Abstract
This paper proposes new analytical and finite element solutions for studying the effects of elastic foundations on the uncontrolled and controlled static and vibration responses of smart multi-layered laminated composite plates with integrated piezoelectric layers, acting as actuators and sensors. A non-polynomial higher-order plate theory with zigzag kinematics involving a trigonometric function and a local segmented zigzag function is adopted for the first time for modeling the deformation of a smart piezoelectric laminated composite plate supported on an elastic foundation. This model has only five independent primary variables like that of the first-order shear deformation theory, yet it considers the realistic parabolic behavior of the transverse shear stresses across the thickness of the laminated composites plates, and also maintains the continuity conditions of transverse shear stresses at the interfaces of the laminated plates. A two-parameter foundation model, namely Pasternak’s foundation, is used to model the deformation and shear interactions of the elastic foundation. The governing set of equations is derived by implementing Hamilton’s principle and variational calculus. Two different solution methods, namely, a generalized closed-form analytical solution of Navier-type, and a C0 isoparametric finite element (FE) formulation, are developed for solving the governing set of equations. The solutions in the time domain are obtained with Newmark’s average acceleration method. Comprehensive parametric studies are presented to investigate the influence of elastic foundation parameters, piezoelectric layers, loading, and boundary conditions on the static and dynamic responses of the smart composite plates with piezoelectric layers. The effects of the elastic foundations on the vibration control of the smart composite plates are also presented by coupling the piezoelectric actuator and sensor with a feedback controller. Several benchmark results are presented to show the influence of the various material and geometrical parameters on the controlled and uncontrolled responses of the smart plates, and also the significant effect of the elastic foundations on the static and dynamic responses of the smart structures. The results obtained are in very good agreement with the available literature, and it can be concluded that the proposed analytical solution and FE formulation can be efficiently used to model the static and dynamic electro-elastic behavior of smart laminated plates supported on elastic foundations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Smart materials like piezoelectric materials are widespread due to their capability of transforming energy forms from mechanical to electrical and vice versa. To utilize the coupled electromechanical properties of piezoelectric materials, they are integrated with traditional composites for the alteration of system characteristics. The idea of integrating piezoelectric materials with structural systems like advanced composite beams, plates, and shells has been implemented in many disciplines, namely mechanical, civil, and aerospace engineering. Such structural configurations are primarily known as smart structures, and their development offers a substantial interest in numerous engineering applications: vibration control, noise control, shape control, structural health monitoring, and damage detection, to name a few.
In the earlier studies, the piezoelectric materials were used as distributed actuators/sensors with the isotropic structural components for modification of the structural characteristics such as stiffness and damping, as well as system responses of stress/strains in a controlled manner [1,2,3,4]. With the advent of composite materials, there has been an increasing interest in developing smart composite structures that are lightweight and superior to their conventional counterparts [5]. Raja et al. [6] carried out experiments to suppress the vibration of a laminated composite plate with piezoelectric actuators and sensors subjected to time-dependent forces. Dong et al. [7] presented both numerical and experimental studies for the vibration control of a cantilevered aluminum plate with piezoelectric patches based on system identification. Han et al. [8] presented an analytical model based on the Ritz method, and also conducted experiments for the active vibration control of composite structures with piezoceramic actuators and piezo-film sensors. Ali et al. [9] studied the dynamic behavior of woven carbon fabric laminates integrated with in-house piezoelectric polyvinylidene fluoride nanofibers. Recently, Rahman et al. [10] carried out experimental investigations for the dynamic analysis of smart laminated composite plates and validated their results through finite element simulations in ANSYS. The load-bearing components in structures during service are subjected to extreme loading conditions and harsh environments due to temperature and moisture, leading to damage. Structural health monitoring (SHM) makes use of piezoelectric sensors for quantifying the damages and determines the locations of damage in composite structures to inspect the health. Ataei et al. [11] developed a damage detection approach for detecting the damage due to delamination in composite structures with piezoceramic transducers. Elahi [12] presented a study on the structural health monitoring of aerospace structural systems with piezoelectric harvesters. Aabid et al. [13] discussed on challenges and future opportunities of the piezoelectric material-based structural health monitoring techniques. The authors concluded that the converse piezoelectric effect, by which the local forces and moments induced in the piezoelectric materials via the application of an electric field, makes it easier for the structure to avert the occurrence of high stress/strain levels, thus lessening the criticality of the damage.
Accurate mathematical modeling of the smart composite plates with piezoelectric materials is crucial for predicting their deformation behavior, which will further enable the research community to utilize them in more industrial applications. In the initial stage of the mathematical developments, the classical laminated plate theory (CLPT) [14, 15] and first-order shear deformation theory (FSDT) [16,17,18] have been employed to derive the deformation responses of advanced composite plates with piezoelectric layers. Mallik and Ray [19] and Shingare and Naskar [20] developed new piezoelectric materials based on piezoelectric fiber-reinforced composites (PFRCs) and graphene-reinforced piezoelectric composites (GRPCs) in an attempt to improve some of the piezoelectric properties useful for developing distributed piezoelectric actuators and sensors. However, for the accurate prediction of the structural behavior of an adaptive smart laminated composite plate, the CLPT and FSDT are not adequate [21]. The higher-order shear deformation theories (HSDTs) that take into account the warping of the cross section of the plates to get the realistic non-linear variations of the transverse shear stresses/strains across the cross-sectional thickness have been developed. Interested readers can refer to the work of Reddy [22], Kant and Manjunatha [23], and Lo et al. [24], to name a few, who have utilized Taylor’s series expansion and developed new HSDTs that take into account the transverse deformation [22], and both transverse shear and normal deformation [23, 24]. Shimpi [25] proposed a two-variable plate model for the bending analysis of composite plates. The plate model in [25] is further upgraded to a four-variable model by Sobhy [26] by taking into account the membrane deformations for the thermal buckling of functionally graded (FG) piezoelectric sandwich plates with a lightweight core. Various shear strain functions have been considered in [26] to get the realistic through-thickness variations of the transverse shear strains, which are of polynomial [22] and non-polynomial [27, 28] types for comparing the results. Shiyekar and Kant [29] adopted the HSDT in [23] for studying the actuation in the electro-elastic responses of smart composite plates with PFRC actuators. Rouzegar and Abad [30] and Rouzegar and Abbasi [31] presented analytical and finite element (FE) solutions for the static analysis of smart composite plates with piezoelectric layers. Ray et al. [32] and Samanta et al. [33] derived a FE model based on the plate model in [24] for the static and dynamic analysis of laminated composite plates with PVDF actuators and sensors. Chanda and Sahoo [34] adopted a five-variable non-polynomial HSDT for deriving analytical solutions for the coupled electromechanical problem of smart laminated composite plates with PFRC layers. Joshan et al. [35] proposed a new non-polynomial HSDT consisting of five variables for the bending responses of smart composite plates with piezoelectric layers. The actuation in the structural responses of the smart composite plates due to the converse piezoelectric effect is observed in the results presented in the references [29,30,31,32,33,34,35]. Also, the non-polynomial HSDTs in [26, 34, 35] accommodate the warping of the transverse cross section with five primary variables, therefore reducing the computational costs. The smeared models adopted in the above references cannot accurately describe the deformation behavior of the smart composite plates across the plate thickness as the continuity requirements of the slopes of in-plane displacement components, and the continuity of the inter-laminar tractions between two layers of different material properties is not satisfied at the interfaces. The HSDTs applied in the framework of Layer-wise (LW) and Zigzag (ZZ) approaches for modeling the deformation behavior of multi-layered composite plates are observed to satisfy the aforementioned requirements. Robbins and Reddy [36], Saravanos et al. [37], Zabihollah et al. [38], and Moita et al. [39], to name a few, have shown the applicability of LW models in capturing the inter-laminar effects in electromechanical problems of smart composite plates. Wu et al. [40] presented the static analysis of stiffened laminated composited plates with piezoelectric layers by considering defects like deboning, cracks, and delamination using an extended layer-wise model. Xiao et al. [41] presented an application of the extended layer-wise model in [40] for studying the thermo-electro-mechanical dynamic fracture behavior of multi-layered laminated composite plates integrated with piezoelectric patches. Xu et al. [42] utilized the extended layer-wise model for the static responses of laminated piezoelectric composite plates with multiple delamination and transverse cracks. Recently, Li [43] presented a review on the applications of the LW models for the structural analysis of laminated composite structures. While the LW models yield satisfactory structural responses for the smart composite plate structures, the computational involvement in modeling the entire problem of a multi-layered structure is huge. On the other hand, HSDTs utilized in the framework of the ZZ approach can efficiently model the problem of smart composites with much lesser computational efforts compared to the LW approach. At the same time, this approach satisfies the continuity conditions of inter-laminar stresses and the slope discontinuity of displacement components at the interfaces between two adjacent layers of different material properties. Significant contributions are made by Di Scuiva [44], Cho and Parmerter [45], Chakrabarti and Sheikh [46], and Kapuria and Kulkarni [47] in developing various ZZ-based HSDT models for the static and dynamic analysis of laminated composites and sandwich plates. Topdar et al. [48] and Khandelwal et al. [49] extended the model developed in [46] for the static and dynamic analysis of smart composite plate structures. Kapuria and Achary [50] studied the dynamics of piezoelectric cross-ply composite plates with a coupled zigzag model. Nath and Kapuria [51] studied the thermoelectric effects on the electromechanical responses of smart cross-ply laminated composite shells with improved zigzag models. The ZZ models employed in the above-mentioned references are based on polynomial shear strain functions based on Taylor’s series expansions. Apart from the polynomial ZZ models, ZZ models are also recently developed, which utilize non-polynomial shear strain functions for accommodating the non-linearity of the transverse shear strains/stresses across the thickness of the plates [52]. Chanda and Sahoo [53] derived an analytical model for the static electromechanical responses of smart laminated composite plates with piezoelectric layers using a non-polynomial ZZ theory. The non-polynomial shear strain functions enhance the efficiency of the mathematical models as they implicitly accommodate the higher-order polynomial terms of Taylor’s series, which contributes to the refinement of the bending behavior. Limited applications of the non-polynomial ZZ models are observed in the literature for studying the electro-elastic responses of smart composite plates. A unified approach is presented by Carrera [54,55,56], coined as ‘Carrera Unified Formulation (CUF)’ for the two-dimensional modeling of layered composite structures. A series of hierarchical plate models can be implemented in a single formulation, thus creating a systematic assessment of various plate models ranging from Equivalent-Single-Layer (ESL) to higher-order LW and ZZ models.
Applications of advanced composite structures supported on elastic foundations also have enormous applications in various engineering structures like buttress foundations, pile foundations, swimming pools, and railway applications, to name a few. The elastic foundations supporting the loaded structure are responsible for reducing the structural vibrations of the system [57]. Akavci et al. [58] used the CLPT and FSDT to derive the structural responses of advanced composite plates supported by elastic foundations. The authors have adopted a two-parameter foundation model referred to as Pasternak’s model for simulating the deformation of the elastic foundations. Shen [59] adopted the FSDT for determining the non-linear bending responses of advanced composite plates subjected to in-plane and transverse mechanical loads. Lal et al. [60] derived the stochastic free-vibration responses of laminated composite plates resting on elastic foundations using Reddy’s HSDT [22]. Further, Akavci [61] adopted various non-polynomial-based HSDTs for deriving the free-vibration and buckling responses of advanced composite plates resting on elastic foundations. The responses reported in [61] reveal that the buckling loads and the natural frequencies of the plates increase due to the presence of the foundations. The effects of the elastic foundation on the buckling responses of smart piezoelectric plates with porosities are investigated by Barati et al. [62] with a higher-order four-variable plate model. Ebrahimi et al. [63] studied the vibration responses of magneto-electro-elastic plates with porosities resting on elastic foundations. Zenkour and Alghanmi [64] derived the static responses of smart functionally graded (FG) plates supported on elastic foundations. Zenkour and Shahrany [65] derived the controlled vibration responses of smart laminated composite plates integrated with magnetostrictive layers in the thickness direction. The combined effects of elastic foundations and hygro-thermal loading conditions on the controlled vibration responses of smart laminated composite plates supported on elastic foundations are reported by Zenkour and Shahrany [66]. Bisheh and Civalek [67] presented the vibration responses of smart carbon nanotube-reinforced cylindrical panels supported on an elastic foundation under hygro-thermal loading conditions. Several studies are presented in [68,69,70,71,72] in which the structural responses of advanced composite plates resting on elastic foundations are investigated.
Based on the literature survey, it is observed that there is no study in the open literature utilizing the kinematics of zigzag-based non-polynomial HSDTs for studying the effects of elastic foundations on the static and dynamic electro-elastic responses of smart composite plate structures. The non-polynomial HSDTs are computationally less expensive as a single non-polynomial function can be utilized to accommodate the higher-order bending behavior of the plate structures. Furthermore, the conjunction of the zigzag functions to the HSDTs can satisfy the piecewise continuity requirements of the displacement components, and inter-laminar transverse shear stresses that are not possible when the HSDTs alone are used to model the multi-layered smart composite plates. Thus, the present work is an addition to the existing literature, which examines the electro-elastic actuation and sensing behavior of piezoelectric materials integrated with multi-layered laminated composite plates supported on elastic foundations. The elastic foundations are represented by vertical springs and a shear layer which takes into account the transverse shear deformation. This model is popularly referred to as Pasternak’s foundation model in the literature. The governing equations of the problem are derived using Hamilton’s principle and variational calculus. Analytical and Finite Element (FE) solution techniques are proposed. A closed-form analytical solution for the spatial approximation of the primary variables is assumed following Navier’s solution technique for diaphragm-supported plates. For the FE solutions, an isoparametric formulation is presented using the eight-noded serendipity elements. In both the analytical and FE solution techniques, the solution forms in the spatial domain generate a system of coupled ordinary differential equations (ODEs) in time. The solutions from the coupled ODEs are further determined using Newmark’s time integration scheme. Computer programs are developed in MATLAB software for both the analytical and FE formulation. Several numerical examples pertaining to static and forced-vibration analysis, including vibration suppression, are solved, and the results obtained are compared with standard solutions reported in the literature to verify the efficiency and the range of applicability of the present models. The effects of the elastic foundations on the structural responses of smart composite plate structures are thoroughly investigated.
2 Theoretical developments
2.1 Introduction
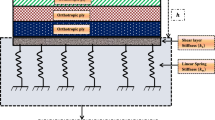
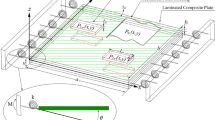
Consider a rectangular laminated composite plate of length, ‘l’ and width ‘b’ with piezoelectric actuator and sensor bonded at the top and bottom surface of the plate resting on Pasternak’s foundation. The rectangular Cartesian coordinate system (x, y, z) is used for the derivation of the equations, with z = 0 coincident with the mid-plane of the smart laminated plate. The laminated composite plate consists of orthotropic layers stacked in the thickness direction (z), with a total thickness of h. The thickness of the piezoelectric layers is denoted as \({t}_{p}\). The schematic diagram of the structure is shown in Fig. 1.
2.2 Kinematic model
Recently developed non-polynomial HSDT with inter-laminar continuity of transverse shear stress [52] is considered to reduce the 3D displacements, ‘U, V, and W’ to 2-D deformation modes defined at the mid-plane (z = 0). The model is a refinement of the CLPT by implicitly accommodating the odd-powered higher-order terms of Taylor’s series with a single non-polynomial mathematical function. Auxiliary variables ‘\({\alpha }_{xu}^{i}\), \({\alpha }_{xl}^{j}\), \({\alpha }_{yu}^{i}\), and \({\alpha }_{yl}^{j}\)’ (i = 1,2… nu-1, j = 1, 2,.. nl-1) are assumed at the interfaces of the plate along with segmented functions of thickness coordinate (z). nu and nl are denoted as the number of layers in the positive and negative z-direction. Figure 2 illustrates the kinematics of the present model. The model is explicitly described as follows:
where, \({u}_{0}\), \({v}_{0}\), \({w}_{0}\), \({\beta }_{x}\), and \({\beta }_{y}\) are denoted as the primary variables defined at the mid-plane. The mathematical function, \(f\left(z\right)\) is adopted as ‘z sec \(\left(\frac{rz}{h}\right)\),’ where ‘r’ is denoted as the transverse shear stress parameter [73] and is ascertained in the post-processing step using an inverse method by comparison of the present results with 3D solutions [73]. Based on the published article [74], the value of r is considered to be 0.1. The inter-laminar continuity equations of the transverse shear stresses generate additional equations by which the auxiliary variables can be written in terms of the primary variables of the mid-plane. The modified displacement field, after imposing the continuity conditions of the transverse shear stresses, is given by
where \({p}_{1}\) = \(z\) sec \(\left(rz/h\right)\) + \(\sum_{i=1}^{{n}_{u}-1}\left(z-{z}^{iu}\right)H\left(z-{z}^{iu}\right){\alpha }_{xu}^{i}+\sum_{j=1}^{{n}_{l}-1}\left(z-{z}^{jl}\right)\) \(H\left(-z+{z}^{jl}\right){\alpha }_{xl}^{j}\)
2.3 Foundation model
The interaction between the supporting elastic medium and the plate is modeled using Pasternak’s foundation model [58]. It is a two-parameter model in which the foundation reaction ‘\({R}_{F}\)’ is expressed in terms of the transverse displacement (W) of the plate and its second-order derivatives \(\left(\frac{{\partial }^{2}{w}_{0}}{\partial {x}^{2}},\frac{{\partial }^{2}{w}_{0}}{\partial {y}^{2}}\right)\) with the Winkler’s stiffness (\({K}_{w}\)) and Pasternak’s stiffness (\({K}_{s}\)) given by the following equations:
where \({{R}_{F}}^{(1)}\) and \({{R}_{F}}^{(2)}\) are given by
Pasternak’s model can be reduced to Winkler’s model by simply neglecting the shear foundation, \({K}_{s}\), i.e., \({K}_{s}\) = 0.
2.4 Strain–displacement equations
Linear strain–displacement relations are written for describing the kinematics of the smart laminated composite plates shown in Fig. 1. The equations for the non-zero strains are given by
where \({q}_{1}\) = \(\frac{\partial {p}_{2}}{\partial z}\) and \({q}_{2}\) = \(\frac{\partial {p}_{1}}{\partial z}\)
2.5 Stress–Strain Constitutive Relations
The linear stress–strain constitutive relations for the laminated composite plate with orthotropic layers are given below:
where the stress vector consists of stresses, ‘\({\sigma }_{11}\), \({\sigma }_{22}\), ...\({\tau }_{13}\)’ defined at a local coordinate system, i.e., along the direction of the fiber (1) and perpendicular to the direction of the fiber (2 and 3). \({\varepsilon }_{11}\), \({\varepsilon }_{22}\)…\({\gamma }_{13}\) are the strains defined along the fiber direction and perpendicular to the fiber direction. The matrix relating the stress and strain vector is the reduced stiffness matrix derived from the plane stress condition. (k) denotes the kth layer along the thickness coordinate (z).
Linear constitutive relations that couple the elastic and electric fields of any point in the piezoelectric layer are given by the following converse and direct piezoelectric relations:
Equation (6a) and (6b) are also known as the actuator and the sensor law, respectively. ‘\({e}_{31}\), \({e}_{32}\), \({e}_{15}\)’ are denoted as the piezoelectric coefficients, and ‘\({\in }_{11}\), \({\in }_{22}\), and \({\in }_{33}\)’ are known as the dielectric coefficients. ‘\({D}_{11}\), \({D}_{22}\), and \({D}_{33}\)’ are known as the electric displacement vectors, and ‘\(\Phi \)’ is the electric potential function of the pth piezoelectric layer. It is assumed that the interface between the piezoelectric layer and the laminated composite plate is suitably grounded. Practically, the thickness of the piezoelectric layer is very low, and a linear variation of the electric potential is assumed across the thickness [18, 30].
where V is the applied voltage at the top surface of the piezoelectric actuator. The applied voltage is further expressed in terms of mathematical functions of space ‘\(\overline{V }\) (x, y)’ and time ‘\({V}_{mn}(t)\).’ Equation (7) is further written as
The details of \(\overline{V }\) (x, y) and \({V}_{mn}(t)\) are further presented in the subsequent sections.
2.6 Derivation of the governing equations of motion
Hamilton’s principle is used to derive the set of governing equations of motion along with the essential and natural boundary conditions of the problem. The variation in the total kinetic energy ‘K’ and the potential energy ‘\({\varvec{\Pi}}\)’ between a time interval t0 to t1 is written as
\({\varvec{\Pi}}\) can be further expressed as the sum of the strain energy of the orthotropic layers of the laminated composite plate, piezoelectric layers, elastic foundation, and the work potential of the applied loads.
The variation of the potential energy and the kinetic energy is expressed as follows:
where \({q}_{z}\) is the applied mechanical load at the top surface of the plate in the z-direction. The 3D stresses in Eq. (10) are further integrated over the thickness, and the integrated quantities are denoted as the stress resultants defined over unit length. The stress resultants of the problem are defined as
Superscripts ‘ES’ and ‘Pz’ are used to indicate the stress resultants of the laminated composite plate and the piezoelectric layers, respectively. The total stress resultant is the sum of the stress resultants of the laminated plate and the piezoelectric layer.
The variation in the kinetic energy (K) is defined as
The density, \({\rho }^{(k)}\), and \({\rho }^{(P)}\) are integrated just like the stresses along the thickness and the integrated quantities are further denoted as the Inertia components. The inertia components are defined as follows:
The inertia terms for the entire system are the sum of the inertia components of the laminated plate in Eq. (14a) and the piezoelectric layers in Eq. (14b).
Substituting Eqs. (10) and (13) in Eq. (9), and integrating the resulting equation by parts in both space (x, y) and time (t) and noting that the variations of the primary variables obtained in space (x, y) at the initial (\({t}_{0}\)) and final time (\({t}_{1}\)) yield the governing equations of the problem. Governing equations for the static and dynamic analysis, along with the essential and natural boundary conditions of the smart composite plate supported on elastic foundation, are written as
2.6.1 Equilibrium Equations
The details of the matrices ‘\(\left[\mathfrak{R}\right]\), \(\left\{\mho \right\}\) and \(\left[\mathcal{R}\right]\)’ are provided in Appendix A.
2.6.2 Boundary Conditions
2.6.3 Boundaries parallel to y-axis, i.e., x = 0 or l
Either
2.6.4 Boundaries parallel to x-axis, i.e., y = 0 or b
Either
2.6.5 At the corners
Either
It is important to note that the inertia components and the external transverse load ‘\({q}_{z}\)’ will be dropped from Eq. (16a) for the static and free-vibration analysis. For the forced-vibration analysis, such terms shall remain in the formulation. The stress results are further expressed in terms of the mid-plane variables and their derivatives with the following plate-constitutive relations.
Different terms in the above equation are defined as
\({\left\{{\varvec{N}}\right\}}^{\left(ES\right)}={\left\{\begin{array}{ccc}{{N}_{xx}}^{(ES)}& {{N}_{yy}}^{(ES)}& {{N}_{xy}}^{(ES)}\end{array}\right\}}^{T}, {\left\{{\varvec{N}}\right\}}^{\left(Pz\right)}={\left\{\begin{array}{ccc}{{N}_{xx}}^{(Pz)}& {{N}_{yy}}^{(Pz)}& {{N}_{xy}}^{(Pz)}\end{array}\right\}}^{T}\)
\({\left\{{\varvec{M}}\right\}}^{\left(ES\right)}={\left\{\begin{array}{ccc}{{M}_{xx}}^{(ES)}& {{M}_{yy}}^{(ES)}& {{M}_{xy}}^{(ES)}\end{array}\right\}}^{T} {\left\{{\varvec{M}}\right\}}^{Pz}={\left\{\begin{array}{ccc}{{M}_{xx}}^{(Pz)}& {{M}_{yy}}^{(Pz)}& {{M}_{xy}}^{(pz)}\end{array}\right\}}^{T}\)
\({\left\{{{\varvec{N}}}^{\boldsymbol{*}}\right\}}^{\left(ES\right)}={\left\{\begin{array}{ccc}{{N}_{xx}^{*}}^{(ES)}& 0& {{N}_{xy}^{*}}^{(ES)}\end{array}\right\}}^{T}, {\left\{{{\varvec{N}}}^{\boldsymbol{*}}\right\}}^{\left(Pz\right)}={\left\{\begin{array}{ccc}{{N}_{xx}^{*}}^{(Pz)}& 0& {{N}_{xy}^{*}}^{(Pz)}\end{array}\right\}}^{T}\)
\({\left\{{{\varvec{M}}}^{\boldsymbol{*}}\right\}}^{\left(ES\right)}={\left\{\begin{array}{ccc}0& {{M}_{yy}^{*}}^{(ES)}& {{M}_{xy}^{*}}^{(ES)}\end{array}\right\}}^{T}, {\left\{{{\varvec{M}}}^{\boldsymbol{*}}\right\}}^{\left(Pz\right)}={\left\{\begin{array}{ccc}0& {{M}_{yy}^{*}}^{(Pz)}& {{M}_{xy}^{*}}^{(Pz)}\end{array}\right\}}^{T}\)
\(\left\{{\varvec{Q}}\right\}={\left\{\begin{array}{cc}{{Q}_{xx}}^{(ES)}& {{Q}_{yy}}^{(ES)}\end{array}\right\}}^{T}, \left\{{\varvec{Q}}\right\}={\left\{\begin{array}{cc}{{Q}_{xx}}^{(Pz)}& {{Q}_{yy}}^{(Pz)}\end{array}\right\}}^{T}\)
\(\left\{{\varvec{T}}\right\}={\left\{\begin{array}{cc}{{T}_{yy}}^{(ES)}& 0\end{array}\right\}}^{T}, \left\{{\varvec{T}}\right\}={\left\{\begin{array}{cc}{{T}_{yy}}^{(Pz)}& 0\end{array}\right\}}^{T}\)
2.6.6 Navier’s solution
For deriving the analytical solution using Navier’s method, we assume that the smart laminated composite plate is supported on all four edges by diaphragm-type supports [75, 85]. The general boundary conditions for the present model are presented in Eqs. 16(b-d), and the boundary conditions for the diaphragm supports are defined with these conditions. The 2-D nature of the deformation modes defined at the mid-plane is exploited by applying the separation of variables approach to define the displacement parameters in the form of double trigonometric series.
Similarly, the mechanical and electrical loading terms are also represented in a similar fashion, just like the displacements.
From Eq. (8), we can write the equation below:
where, \({Q}_{mn}\left(t\right)\) =\(\frac{4}{lb}\) \({\int }_{0}^{l}{\int }_{0}^{b}{q}_{z}(x, y, t)\text{ sin}\left(\frac{m\pi x}{l}\right)\text{ sin}\left(\frac{n\pi y}{b}\right)\) dxdy and
The stress resultants are expressed in terms of the field variables and substituted in the equations of motion. The resulting equations are the partial differential equations (PDEs) in terms of the assumed filed variables. Further substitution of the assumed solutions of the field variables and the loading terms gives a system of five second-order ordinary differential equations (ODEs) in time.
The ODEs in Eq. (21) are finally solved using an analytical or a numerical technique. In this research, Newmark’s constant average acceleration method is utilized for solving the equations in time.\(\left[\overline{M }\right]\), \(\left[\overline{K }\right]\), \({\left\{\overline{F}\right\} }_{M}\), and \({\left\{\overline{F}\right\} }_{E}\) are the mass matrix, stiffness matrix, mechanical force vector, and electrical force vector of the system, respectively. \(\left\{\ddot{U}\right\}\) is the acceleration vector and \(\left\{U\right\}\) is the displacement vector.
2.7 Finite element (FE) formulation
2.7.1 Element selection
The physical domain (x, y) is discretized with an eight-noded serendipity element. The interpolation functions for any node ‘i’ of the element are given below:
2.7.2 Continuity requirements and discretization of kinematic field
The first-order derivatives of the transverse displacement ‘W’ with respect to x and y in Eq. (1) generate second-order derivatives of W in the strain components (ref: Eq. (4a)). Therefore, it requires deriving a C1-continuous FE model. C1-continuous models are computationally difficult in most cases; therefore, the terms ‘\(\frac{\partial {w}_{0}}{\partial x}\) and \(\frac{\partial {w}_{0}}{\partial y}\)’ are assumed to be ‘\({\theta }_{x}\) and \({\theta }_{y}\),’ respectively, to reduce the continuity requirements. As the derivatives are denoted as two new degrees of freedom, therefore, the number of field variables has increased from five to seven. Also, additional constraint equations have now appeared in the formulation, which is written as
The constraint equations are satisfied with the penalty method [76], being in line with [77]. The penalty function of an element is given by
Superscript ‘e’ denotes the eth element from the physical domain (x, y). The variation of the penalty function is written as
The finite element approximations allow the field variables to be expressed in terms of the nodal coordinates of an element ‘e’ with the interpolation functions defined in Eq. (22).
Using Eq. (26), the constraint equations can be discretized to the following set of equations in terms of the nodal coordinates. A generalized displacement vector ‘\(\left\{{d}^{e}\right\}\)’ is considered which contains all the nodal coordinates of an element ‘e’.
From Eq. (27), we can rewrite Eq. (25) in the following manner.
where \(\gamma \) is denoted as the penalty number, and its value is considered to be 106 [73]. The constraint equations are not satisfied when \(\gamma \) is equal to 0, and when the value of \(\gamma \) is sufficiently large, the displacement vector changes in such a way such that the constraint equations are more nearly satisfied. The modified displacement field (Eq. (2a)) with seven degrees of freedom is written as
2.7.3 Discretized Strain–displacement relations
The strains are first expressed in terms of a generalized strain vector, ‘\(\left\{\overline{\varepsilon }\right\}\),’ and the generalized strain vector is further written in terms of the displacement vector. The discrete relations are presented below:
Combining Eqs. 30a and b, we get the final discretized equations for the strains.
where \(\left\{\varepsilon \right\}\) = \({\left\{\begin{array}{ccc}{\varepsilon }_{xx}& {\varepsilon }_{yy}& \begin{array}{ccc}{\gamma }_{xy}& {\gamma }_{yz}& {\gamma }_{xz}\end{array}\end{array}\right\}}^{T}\);
The components of the various submatrices in \(\left[B\right]\) are given in Appendix B.
2.7.4 Discretized Stress–Strain relations
The discretized relationship of the stresses and strains for a laminated composite plate is written as follows:
The electric potential voltage ‘V’ is also approximated over an element ‘e’ in a similar manner like the mechanical displacements as shown in Eq. (26).
where \({{V}_{i}}^{(e)}\) is the voltage applied at the ith node of the eth element. Substituting Eq. (32) in the relationship of the electric potential function ‘\(\Phi \)’ in Eq. (7), we get the following discretized relation.
The electric fields ‘\({E}_{x}\), \({E}_{y}\), and \({E}_{z}\)’ can now be expressed in terms of the voltage coordinates in the following manner:
where \(\left\{E\right\}\) = \({\left\{\begin{array}{ccc}{E}_{x}& {E}_{y}& {E}_{z}\end{array}\right\}}^{T}\), \(\left[\overline{Z }\right]\) = \(\left[\begin{array}{ccc}-\frac{1}{{t}_{p}}\left(z- \frac{h}{2}\right)& 0& 0\\ 0& -\frac{1}{{t}_{p}}\left(z- \frac{h}{2}\right)& 0\\ 0& 0& -\frac{1}{{t}_{p}}\end{array}\right]\) and
Finally, the discretized stress–strain relationships for the piezoelectric materials are written as follows:
2.7.5 Calculation of various energies and governing equation
The total potential energy ‘\({{\varvec{\Pi}}}^{(e)}\)’of an element is the sum of the strain energy of the laminated composite plate ‘\({{\mathbf{U}}_{{\varvec{E}}{\varvec{S}}}}^{(e)}\),’ strain energy of the piezoelectric layers ‘\({{\mathbf{U}}_{{\varvec{P}}{\varvec{z}}}}^{(e)}\),’ strain energy due to the artificial constraints ‘\({{\mathbf{U}}_{{\varvec{C}}}}^{(e)}\),’ strain energy due to the elastic foundation ‘\({{\mathbf{U}}_{{\varvec{E}}{\varvec{F}}}}^{(e)}\),’ and the work potential ‘\({\mathbf{W}}^{e}\)’ of the applied loads. The variation of \({{\varvec{\Pi}}}^{(e)}\) is given by
The discretized expressions for the variations of the energies are derived as follows:
The integrations over the thickness in the above integrals are defined as follows:
The variation of the strain energy due the Pasternak’s foundation is given by
The vector containing the transverse displacement and its derivatives can be further expressed in terms of the displacement vector in the following manner:
where \(\left\{dd\right\}\) = \({\left\{\begin{array}{ccc}{w}_{0}& \frac{\partial {w}_{0}}{\partial x}& \frac{\partial {w}_{0}}{\partial y}\end{array}\right\}}^{T}\), \(\left[{B}_{EF}\right]\) = \(\left[\begin{array}{cc}\left\{{{B}_{EF}}_{1}\right\}& \left\{{{B}_{EF}}_{2}\right\}\end{array} \dots \dots \dots \begin{array}{c}\left\{{{B}_{EF}}_{8}\right\}\end{array}\right]\)
The matrix containing the foundation stiffness in Eq. (41) is denoted as \(\left[{\overline{\overline{K}}}_{EF}\right]\). Finally, the discretized expression of the variation of the strain energy due to Pasternak’s foundation is written as
The variation in the work potential ‘\({\varvec{\delta}}{\mathbf{W}}^{({\varvec{e}})}\)’ is given by
where \(\left\{{f}_{m}\right\}\) =\({\left\{\begin{array}{ccc}0& 0& \begin{array}{ccc}{q}_{z}& 0& \begin{array}{ccc}0& 0& 0\end{array}\end{array}\end{array}\right\}}^{T}\).
The variation in the kinetic energy ‘\({\varvec{\delta}}{\mathbf{K}}^{({\varvec{e}})}\)’ is expressed as
where \(\left[I\right]\) = \({\int }_{-\frac{h}{2}}^{\frac{h}{2}}\left({\left[Z\right]}^{t}{\rho }^{(k)}\left[Z\right]\right){\text{d}}z\) +\({\int }_{-\frac{h}{2}-{t}_{p}}^{\frac{h}{2}}\left({\left[Z\right]}^{t}{\rho }^{(P)}\left[Z\right]\right){\text{d}}z\) + \({\int }_{\frac{h}{2}}^{\frac{h}{2}+{t}_{p}}\left({\left[Z\right]}^{t}{\rho }^{(P)}\left[Z\right]\right){\text{d}}z\).
The variations of the various energies are substituted in Hamilton’s principle to get the discretized governing equations of motion. The integrations in space (x, y) are carried out numerically using the Gauss-quadrature method. A selective integration rule is adopted for thin plate systems so as to avoid any possible numerical disturbances like the shear locking, which might appear with the full integration rule [76]. The discretized governing equations of motion for an element are given by
where \(\left[K\right]\) = \({\int }_{0}^{{l}_{e}}{\int }_{0}^{{b}_{e}}\left({\left[B\right]}^{T}\left[D\right]\left[B\right]\right){{\text{d}}x}^{{\text{e}}}{{\text{d}}y}^{{\text{e}}}\),
\(\left[M\right]\) is the mass matrix of the smart composite plate, \(\left[K\right]\), \(\left[{K}_{P}\right]\), \(\left[{K}_{F}\right]\), and \(\left[{K}_{c}\right]\) are the stiffness matrices of the laminated composite plate, piezoelectric layers, Pasternak’s foundation, and the artificial constraints, respectively. \(\left[{K}_{da}\right]\) is the stiffness matrix generated due to the coupling of the mechanical and electric field. \(\left\{{F}_{mech}\right\}\) is the mechanical force vector due to the external loads. Equation (46) is the governing dynamic equation for an element ‘e’ and the matrices need to be assembled to get the governing equation for the entire system. The final governing equation after assembling the elemental equations presented in Eqs. (46, 47) by following the standard finite element assembling procedure is given by
2.7.6 Active Vibration Control of smart structures on Pasternak’s foundation
The electric potential distribution of the piezoelectric sensor in space (x, y) is obtained in terms of the mechanical displacement vector as a result of the coupling between the elastic and electric fields in the constitutive relations. The electrodes in the piezoelectric layers are at the extreme surfaces, i.e., z = -h/2 and—h/2-tp), and the charges get accumulated at the electrodes. Since the poling is in the z-direction, the charges are calculated by the spatial integration of the electric displacement ‘\({D}_{z}\)’ over the surface area of the electrodes, assuming that the converse piezoelectric effect is negligible. Also, no electric field is applied in the piezoelectric sensor, therefore, \({E}_{xx}\) = \({E}_{yy}\) = \({E}_{zz}\) = 0. The output charge of an element ‘e’ in the piezoelectric sensor is calculated as
From the direct piezoelectric law, the equation of the electric displacement ‘\({D}_{zz}\)’ is written as
and
Substituting for \({D}_{zz}\left(x, y,-\frac{h}{2}\right)\) and \({D}_{zz}\left(x, y,-\frac{h}{2}-{t}_{p}\right)\) from the above equations in the equation of the output charge, we get the following discretized relationship
where \(\left\{{k}_{s}\right\}\) = \(\bigg(\frac{1}{2}{\int }_{0}^{{l}_{e}}{\int }_{0}^{{b}_{e}} \big(\{e\}^{(P)}\big[H\big(-\frac{h}{2}\big)\big][B]\big){{\text{d}}x}^{{\text{e}}}{{\text{d}}y}^{{\text{e}}} + \frac{1}{2}{\int }_{0}^{{l}_{e}}{\int }_{0}^{{b}_{e}}\big(\{e\}^{(P)}\big[H\big(-\frac{h}{2}-{t}_{p}\big)\big][B]\big){{\text{d}}x}^{{\text{e}}}{{\text{d}}y}^{{\text{e}}}\bigg).\)
The total output charge ‘\(Q\)’ of the piezoelectric sensor can be calculated by the summation of the output charges ‘\({Q}^{(e)}\)’ for all the elements. In the present problem, the electrodes are present on the entire surface of the piezoelectric layers. Thus,
The total charge is obtained by the FE assembling of the matrix ‘\(\left\{{k}_{s}\right\}\)’ in Eq. (51). The discretized expression of the output charge after assembling is written as
In this research, we use a negative feedback control system which is based on the velocity measurements of the system. The output voltage of the sensor ‘Vs’ is proportional to the rate of change of the output charge obtained in Eq. (53). Thus,
\({G}_{c}\) is denoted as the constant gain of the amplifier. The sensor voltage is now fed back through an amplifier to the top surface of the actuator with a change in the polarity. Thus, the voltage on the actuator ‘Va’ is given by
\(G\) is the gain of the amplifier. The actuator layer is electroplated; thus, all the nodes on the top surface of the actuator will be equipotential. Therefore, all the entries in the global voltage vector ‘\(\left\{\mathbf{V}\right\}\)’ obtained in Eq. (55) will be equal to Va. Thus,
where \(\mathbf{V}(i)\) is the ith element of \(\left\{\mathbf{V}\right\}\). Using Eqs. (48), (55), and (56), the final governing equation for the active vibration control analysis is given by
where \(\left[{{\varvec{C}}}_{{\varvec{c}}{\varvec{o}}{\varvec{n}}{\varvec{t}}{\varvec{r}}{\varvec{o}}{\varvec{l}}}\right]\) is the active damping matrix identified from Eqs. (55) and (56). It is now perceived from Eq. (57) that the controller has generated a damping matrix which is responsible for the vibration suppression. Apart from the damping generated by the controller, we also introduce the structural damping ‘\(\left[{{\varvec{C}}}_{{\varvec{s}}{\varvec{t}}{\varvec{r}}}\right]\)’ as every structural member is characterized by light damping. For the structural damping, we use the Rayleigh damping, given by
where \({\alpha }_{1}\) and \({\alpha }_{2}\) are Rayleigh’s coefficient of proportionality, and \(\left[{\mathbf{K}}^{\mathbf{*}}\right]\) = \(\left(\left[\mathbf{K}\right] + \left[{\mathbf{K}}_{\mathbf{P}}\right] + \left[{\mathbf{K}}_{\mathbf{F}}\right] + \left[{\mathbf{K}}_{\mathbf{c}}\right]\right)\). Therefore, the governing equation for the active control analysis after including the structural damping is written as
Equation (59) is solved using Newmark’s constant average acceleration method. The equation is subjected to the initial conditions of the problem, i.e., the values of the displacement vector ‘\(\left\{\mathbf{d}\right\}\)’ and velocity vector ‘\(\left\{\dot{\mathbf{d}}\right\}\)’ at time t = 0. In Navier’s analytical solution method presented in Sect. 2.5.1, the mathematical functions assumed for the field variables satisfy the diaphragm-supported boundary conditions as a preliminary. In the FE method, it is essential to enforce the boundary conditions after the formation of the global stiffness matrix, mass matrix, and force vectors. The boundary conditions associated with the field variables for the various types of boundary conditions are as follows:
Diaphragm support (SSSS)
\({u}_{o}\) = \({w}_{o}\)=\({\beta }_{x}\)=\({\theta }_{x}\) = 0 at y = 0, b and \({v}_{o}\) = \({w}_{o}\)=\({\beta }_{y}\)=\({\theta }_{y}\) = 0 at x = 0, l
Clamped support (CCCC)
\({u}_{o}\) = \({w}_{o}\)=\({\beta }_{x}\)=\({\theta }_{x}\)=\({v}_{o}\) = \({\beta }_{y}\)=\({\theta }_{y}\) = 0 at x = 0, l and y = 0, b
Clamped Diaphragm support (CCSS)
\({u}_{o}\) = \({w}_{o}\)=\({\beta }_{x}\)=\({\theta }_{x}\)=\({v}_{o}\) = \({\beta }_{y}\)=\({\theta }_{y}\) = 0 at x = 0 and y = 0.
\({u}_{o}\)= \({w}_{o}\)=\({\beta }_{x}\)=\({\theta }_{x}\) = 0 at y = b and \({v}_{o}\) = \({w}_{o}\)=\({\beta }_{y}\)=\({\theta }_{y}\) = 0 at x = l.
3 Results and discussions
In this section, the numerical results obtained using the analytical and FE formulation derived in the previous section are presented and discussed. The present solutions are validated by the available solutions in the literature. Further, new results for the smart laminated composite plates on elastic foundation are also presented. The material models (MM) and the non-dimensional parameters (ND) used to obtain the results are listed below:
Material Properties
\({E}_{1}\)/\({E}_{2}\) = 25, \({G}_{12}\) = \({G}_{13}\) = 0.5 \({E}_{2}\), \({G}_{23}\) = 0.2 \({E}_{2}\), \({\vartheta }_{12}\) = 0.25.
MM2 [73]
\({E}_{1}\) = 181 GPa, \({E}_{2}\) = 10.3 GPa, \({G}_{12}\) = \({G}_{13}\) = 7.17 GPa, \({G}_{23}\) = 2.87 GPa, \({\vartheta }_{12}\) = 0.28, \(\rho \) = 1578 kg/m3
MM3 [61]
\({E}_{1}\)/\({E}_{2}\) = 40, \({G}_{12}\) = \({G}_{13}\) = 0.6 \({E}_{2}\), \({G}_{23}\) = 0.5 \({E}_{2}\), \({\vartheta }_{12}\) = 0.25.
MM4 [31]
Material properties of the substrate
\({E}_{1}\) = 172.37 GPa, \({E}_{2}\) = 6.89 GPa, \({G}_{12}\) = \({G}_{13}\) = 3.45 GPa, \({G}_{23}\) = 1.38 GPa, \({\vartheta }_{12}\) = 0.25.
Material properties of the piezoelectric layer
E = 2 GPa, \(\vartheta \) = 0.29, \({e}_{31}\) = \({e}_{32}\) = 0.046 C/m2
MM5 [29]
Material properties of the substrate
\({E}_{1}\) = 172.9 GPa, \({E}_{2}\) =\({E}_{1}\)/25, \({G}_{12}\) = \({G}_{13}\) = 0.5 \({E}_{2}\), \({G}_{23}\) = 0.2 \({E}_{2}\), \({\vartheta }_{12}\) = 0.25, \(\rho \)= 1600 kg/m3
Material properties of the piezoelectric layer [84]
\({C}_{11}\)=32.6 GPa; \({C}_{12}\)=4.3 GPa; \({C}_{22}\)=7.2 GPa; \({C}_{66}\)=1.29 GPa;\({C}_{44}\)=1.05 GPa;\({C}_{55}\) = 1.29 GPa.
\({e}_{31}\) = -6.76 C/m2; \({\epsilon }_{11}\) = 0.037 × 10–9 F/m;\({\epsilon }_{22}\) = \({\epsilon }_{33}\)= 10.46 × 10–9 F/m; \(\rho \)= 3640 kg/m3
Material properties of the substrate layers
\({E}_{22}\)= 210 GPa;\({E}_{11}\)=25 \({E}_{22}\); \({G}_{12}\)= \({G}_{13}\)= 0.5 \({E}_{22}\); \({G}_{23}\) = 0.2 \({E}_{22}\); \({\vartheta }_{12}\) = 0.25; \(\rho \)= 800 N s2/m4
Material properties of the piezoelectric layer
E = 2 GPa; \({e}_{31}\)=\({e}_{32}\)= 0.046 C/m2; \({\epsilon }_{11}={\epsilon }_{22}={\epsilon }_{33}\) = 0.1062 × 10–9 F/m; \(\vartheta \) = 0.29;\(\rho \) = 100 N s2/m.4
MM7 [87]
Material properties of the substrate layers
\({E}_{1}\) = 172.5 GPa, \({E}_{2}\) = 6.9 GPa, \({G}_{12}\) = 3.45 GPa, \({\vartheta }_{12}\) = 0.25, \(\rho \)= 1600 kg/m3
Material properties of the piezoelectric layer
\({E}_{1}\) = \({E}_{2}\) =\(2\) GPa, \({G}_{12}\) = 0.775 GPa, \({\vartheta }_{12}\) = 0.29, \(\rho \)= 1600 kg/m3, \({e}_{31}\)=\({e}_{32}\)= 0.046 C/m2
\({\epsilon }_{33}\)= 1.062 × 10–10 F/m.
Non-dimensional Parameters
ND1
\({k}_{w}\) = \(\frac{{\text{K}}_{1}{L}^{4}}{{E}_{2}{h}^{3}}\), \({k}_{s}\) =\(\frac{{\text{K}}_{2}{L}^{2}}{{E}_{2}{h}^{3}}\)
ND2
ND3
3.1 Validation of the static responses of four-layered (00/900) laminated composite plates under sinusoidal mechanical load
A simply supported four-layered laminated composite plate with span-thickness ratios, S = 10 and 100, is considered in this example. The transverse mechanical load acting on the top surface of the plate is assumed to be sinusoidal in both the x- and y-direction. Material properties and the non-dimensional equations in MM1 and ND1, respectively, are used to represent the results of this problem. The static responses of the plate in the form of deflection and stresses are presented in Table 1 and compared with the 3D solutions [78], solutions of Rodrigues et al. [79], Natarajan et al. [80], and Ferreira et al. [81] combined with CUF, and analytical solutions of Reddy [22] using HSDT. It is observed in the table that very precise results of both deflection and stresses are obtained using the present analytical and FE formulation, and a very good agreement can be observed with the elasticity solutions [78], and with the results obtained using radial basis functions [79], cell-based smoothed FE [80], generalized differential quadrature [81], and HSDT [22]. The present results are observed to be more accurate than the other References in the table.
3.2 Validation of the free-vibration responses of four-layered (00/900) laminated composite plates
In this example, we consider another four-layered laminated composite plate with a span–thickness ratio, S = 10, having two types of boundary conditions, namely, simply supported (SSSS) and clamped (CCCC) at all the edges. The material properties and the non-dimensional equations used in this example correspond to MM2 and ND2, respectively. The fundamental natural frequencies of the plate are presented in Table 2. The present solutions are compared with the ZZ, third-order theory (TOT), and 3D solutions obtained in Kulkarni and Kapuria [82] and the HSDT results of Grover et al. [73]. The FE solutions in the table have an excellent convergence, and we also observe a very close agreement of the present solutions with the solutions of the references [73, 82]. The natural frequencies of the plate are observed to be higher in magnitude in the case of the clamped boundary condition due to the greater stiffness as a result of the restraint of all the degrees of freedom at the boundaries. Next, we present the validation of the free-vibration responses of a three-layered (0/90/0) laminated composite resting on a Winkler foundation. The material properties and the non-dimensional parameters in this problem correspond to MM3 and ND2, respectively. The normalized natural frequencies of the plate are presented in Table 3 for various span–thickness ratios, modulus ratios, and boundary conditions. The solutions reported by Akavci [61] and Hui-Shen [83] are also collected in the table for comparison. The present responses are observed to be in a close agreement with the solutions in [61, 83]. The magnitudes of the natural frequencies are observed to increase with the increase in the magnitude of the modulus ratio as there is an increment in the stiffness of the plate.
3.3 Static analysis of smart laminated composite plates integrated with piezoelectric layers supported on elastic foundation
After validation of the present analytical and FE formulations for the cases of static and free-vibration analysis, we now present the static responses of smart composite plates with piezoelectric actuators and sensors. These results can be used as benchmark results for the comparison and assessment of new shear deformation models in the literature. At first, we consider a five-layered simply supported smart composite plate (PVDF/00/900/00/PVDF) with a PVDF actuator and PVDF sensor placed at the top and bottom surface of a 00/900/00 laminated composite plate. The material properties and the non-dimensional equations correspond to MM4 and ND1, respectively. The thickness of each orthotropic layer is considered to be 3 mm, and the thickness of the PVDF layer is 40 \(\mu \)m. A bi-sinusoidal electromechanical load (q = 10 N/m2, V = 0, 100, − 100 V) is assumed to act on the top surface of the smart plate structure. Analytical and FE results of normalized transverse displacement \(\left(\overline{W }\right)\) are presented in Table 4 for various span–thickness ratios. The magnitude of the transverse displacement in the table is observed to decrease due to elastic foundations. The decrease in the magnitude of \(\overline{W }\) is calculated to be 43.46% under the action of electromechanical loads (q = 10 N/m2, V = 100 V) and consideration of Winkler stiffness (K1) for a thick smart composite plate (S = 10). The magnitude further decreases by 69.57% when both Winkler and shear stiffness (K1 and K2) of the foundations are considered. The deflections in the table are the resultant/net deflection due to the combined action of the mechanical and electrical loads. Therefore, the reversal of the deflection in thick plate systems (S = 10, 50) concludes that the piezoelectric actuators are more effective as the value of S decreases.
Next, we consider a piezoelectric fiber-reinforced composite (PFRC) actuator placed on a 00/900/00 composite plate. In the PFRC layer, piezoelectric fibers (PZT5H) are bonded with an epoxy matrix. The PFRC layers have higher electromechanical coupling coefficients, which makes them efficient actuators and sensors for smart structures. The results of the normalized transverse deflection are tabulated in Table 5 for various magnitudes of static electromechanical loads. The thickness of each orthotropic layer is 1 mm, while the thickness of the PFRC layer is 250 \(\mu \)m. The material properties correspond to MM5 for this example. We observe that the magnitude of \(\overline{W }\) has decreased by 41.25% when the Winkler stiffness (K1) of the foundation is considered and 67.62% when both Winker and shear stiffness (K1, K2) of the foundations are considered. The variation of the non-dimensional responses of in-plane displacement \(\overline{U }\)(x, y, \(\frac{h}{2}\)) over the spatial domain of the plate is plotted in Figs. 3a–c for a sinusoidal electrical load of magnitude, V = -− 100 V, and different foundation stiffness values. It is visible in the figures that the magnitude of \(\overline{U }\) is highly influenced by the stiffness of the foundation as the magnitude tends to decrease due to the Winkler and shear stiffness of the foundations. The Winkler foundation stiffness produces in-plane displacement nearly 1.22 times less when K1 = 100 and K2 = 0, and 1.43 times less when K1 = 100 and K2 = 10. Next, the effect of the foundation stiffness on the normalized response of the transverse displacement (\(\overline{W }\)) is shown in Fig. 4 for various combinations of Winkler (K1) and shear foundation stiffness (K2), and electrical loads of magnitude V = 100 V and –100 V. As expected, the plate experiences maximum deflection when K1 = K2 = 0, and the deflection decreases with the increase in the values of the foundation stiffness, with a minimum value attained at K1 = 100 and K2 = 10. It is also observed that the effectiveness of the foundation is much more when the shear stiffness of the foundation is considered. In Winkler’s model, the transverse deflection at any point on the elastic medium is directly proportional to the mechanical pressure applied at that point and is independent of the pressure applied on any other points on the elastic medium. Thus, there is a discontinuity of the adjacent transverse displacements in the mutually independent springs. When the shear layer is also taken into consideration, then the continuity of the adjacent displacements can be established, resulting in more accurate and realistic responses. The same smart plate is now subjected to the electromechanical load of uniform variation of intensity 40 N/m2 and various electrical loads of magnitude V = 0,100 and − 100 V. The variations of the transverse displacement over the spatial domain of the plate are plotted in Fig. 5 by neglecting the effects of the foundation (Fig. 5a, b, c) and by considering both Winkler and shear foundation stiffness (Fig. 5d, e, f). The magnitude of the transverse displacement under the action of uniform variation of the electromechanical load is larger in comparison to the sinusoidal variation. The inclusion of the foundation stiffness results in an increase in the overall stiffness of the plate, resulting in a significant drop in the magnitudes of the displacement, as noticed in Fig. 5d, e, and f. The effect of the boundary conditions on the coupled response of the transverse displacement is examined by considering a fully clamped–clamped (CCCC) condition and a clamped-simply supported (CCSS) condition, and the responses are shown in Figs. 6a, b, c and 7a, b, c for various combinations of foundation stiffness and sinusoidal electromechanical loads. As expected, the plate with CCSS boundary is experiencing more deflection than the plate with CCCC boundary condition. In CCCC boundary conditions, all the degrees of freedom at the boundaries are restrained, resulting in larger stiffness of the plate and producing more resistance against the deformations. The variations of the in-plane shear stress, \({\overline{\tau }}_{xy}\left(x,y,-\frac{h}{2}\right)\) over the spatial domain of the plate are shown in Figs. 8 (a, b, and c). The maximum values of the stress are attained at the corners of the plate boundaries. A significant reduction of the stress is observed when the combined Winkler and shear stiffness of the foundations are considered.
a Variation of in-plane displacement \(\left(\overline{{\varvec{U}} }\left({\varvec{x}},{\varvec{y}},{\varvec{h}}/2\right)\right)\) of a smart composite plate (PFRC/00/900/00) subjected to sinusoidal electromechanical load (V = − 100 V) without foundation stiffness (S = 10); b Variation of the same by considering only Winkler stiffness and electromechanical load (V = − 100 V); c Variation of the same by including both Winkler and shear stiffness of the foundation and electromechanical load (V = − 100 V)
a Variation of transverse displacement of a smart composite plate (PFRC/00/900/00) with the Winkler and shear foundation stiffness subjected to sinusoidal electromechanical load (V = 100 V); b Variation of transverse displacement with the Winkler and shear foundation stiffness subjected to a sinusoidal electromechanical load of opposite polarity (V = − 100 V)
a Static deflection of a smart composite plate (PFRC/00/900/00) subjected to a mechanical load of uniform variation (S = 10); b Static deflection under electromechanical load with positive voltage (V = 100); c Static deflection under electromechanical load with negative voltage (V = − 100); d Static deflection under mechanical load by considering the stiffness of the foundation; e Static deflection under electromechanical load with positive voltage (V = 100) and the stiffness of the foundation (K1 = 100, K2 = 10); f Static deflection under electromechanical load with negative voltage (V = − 100) and the stiffness of foundation (K1 = 100, K2 = 10)
a Static deflection of a clamped (CCCC) smart composite plate (PFRC/00/900/00) subjected to a mechanical load of sinusoidal variation (S = 10); b Static deflection under electromechanical load with positive voltage (V = 100); c Static deflection under electromechanical load with negative voltage (V = − 100); d Static deflection under mechanical load by considering the stiffness of the foundation (K1 = 100, K2 = 10); e Static deflection under electromechanical load with positive voltage (V = 100) and the stiffness of the foundation (K1 = 100, K2 = 10); f Static deflection under electromechanical load with negative voltage (V = − 100) and the stiffness of foundation (K1 = 100, K2 = 10)
a Static deflection of a clamped-simply supported (CCSS) smart composite plate (PFRC/0/90/0) subjected to a mechanical load of sinusoidal variation (S = 10); b Static deflection under electromechanical load with positive voltage (V = 100); c Static deflection under electromechanical load with negative voltage (V = − 100); d Static deflection under mechanical load by considering the stiffness of the foundation (K1 = 100, K2 = 10); e Static deflection under electromechanical load with positive voltage (V = 100) and with the stiffness of the foundation (K1 = 100, K2 = 10); f Static deflection under electromechanical load with negative voltage (V = − 100) and with the stiffness of foundation (K1 = 100, K2 = 10)
a Variation of in-plane shear stress \(\left({\overline{{\varvec{\tau}}} }_{{\varvec{x}}{\varvec{y}}}\left({\varvec{x}},{\varvec{y}},-{\varvec{h}}/2\right)\right)\) of a smart composite plate (PFRC/00/900/00) subjected to sinusoidal electromechanical load (V = 100 V) without foundation stiffness (S = 10); b Variation of the same by considering only Winkler stiffness and electromechanical load (V = 100 V); c Variation of the same by including both Winkler and shear stiffness of the foundation and electromechanical load (V = 100 V)
3.4 Forced vibration analysis of smart laminated composite plates on elastic foundation
In this section, we present the forced-vibration responses of smart composite plates resting on an elastic foundation and integrated with PVDF and PFRC piezoelectric materials. A three-layered laminated composite plate (00/900/00) integrated with a PVDF actuator and a sensor at the top and bottom surface of the plate is subjected to sinusoidal electrical excitations only. The thickness of each orthotropic ply is considered to be 2 mm, and the thickness of the PVDF layer is 0.1 mm. The magnitude and frequency of the electrical excitation are 100 V and 50 Hz, respectively. The material properties and the non-dimensional parameters correspond to MM6 and ND3, respectively. Analytical and FE results of maximum transient deflection of the smart composite plate resting on an elastic foundation are presented in Table 6 for various span–thickness ratios. An excellent correlation of the analytical and FE results can be observed in the table for all the span–thickness ratios. The amplitude of the transient displacement–time response decreases by 56.88% and 79.69% for a thick smart composite plate (S = 6) due to the Winkler stiffness (K1) only and combined Winkler and shear stiffness of the foundation (K1, K2), respectively. Figure 9 shows the forced-vibration response of a four-layered (PFRC/00/900/00) smart composite plate with simply supported boundary conditions at all the edges. The thickness of each orthotropic ply is 1 mm, and the thickness of the PFRC layer is 0.25 mm. The time-dependent electromechanical excitation is constant in the time domain and sinusoidal in the spatial domain. The magnitude of the electrical and mechanical pressure is 100 V and 40 N/m2, respectively. It is observed in the figure that there is a significant decrease and increase in the amplitude and frequency of vibration of the smart composite plate, respectively, under the applied electromechanical excitation. The analytical and the FE responses are also observed to be in excellent correlation with each other in the figure. Figure 10a–c show the 3D variation of the displacement–time response of the smart composite plate for various magnitudes of electrical excitation (− 100 V to 100 V) by neglecting the foundation stiffness (\(\text{K}1=0; \text{K}2=0\)), considering only Winkler stiffness (\(\text{K}1=100; \text{K}2=0\)) and considering the combined Winkler and shear stiffness (\(\text{K}1=100; \text{K}2=10\)) of the foundation. It is observed that the direction of the transverse displacement gets altered when the polarity of the electrical excitations changes from negative to positive and vice versa.
a 3D graphical representation of forced vibration of a smart composite plate (PFRC/00/900/00) without considering foundation stiffness for various magnitudes of pulse electrical excitation (S = 100); b 3D graphical representation of forced vibration of a smart composite plate (PFRC/00/900/00) by considering Winkler foundation stiffness for various magnitudes of pulse electrical excitation; c 3D graphical representation of forced vibration of a smart composite plate (PFRC/00/900/00) by considering both Winkler and shear foundation stiffness for various magnitudes of pulse electrical excitation
3.5 Vibration suppression of smart composite plate supported on an elastic foundation
A simply supported five-layered smart composite plate (PVDF/00/900/00/PVDF) with a PVDF piezoelectric layer bonded on the upper and lower surface of the laminated plate is considered in this example. The material properties of the substrate layers and the PVDF layers correspond to MM7. The in-plane dimensions of the plate are 0.18 m, and the thickness of each orthotropic layer in the substrate and the PVDF layers are 0.002 m and 0.0001 m, respectively. The external mechanical load is assumed to be uniform in the spatial domain and in the time domain, it is assumed to be q sin \(\left(2\pi ft\right)\), where the magnitude, q = 1000 N/m2, and frequency, f = 10 Hz. Figure 11a illustrates the uncontrolled and controlled responses of the plate without considering the effects of the foundation, and Fig. 11b shows the uncontrolled and controlled response of the plate supported on an elastic foundation (K1 = 100, K2 = 10). The uncontrolled responses in the plot are without the negative feedback controller, while the controlled responses are obtained by activating the negative feedback controller via amplifying the voltage generated from the sensors with suitable gain and then fed back to the actuator. The amplitude of the vibration response is observed to decrease, i.e., the vibration of the plate is controlled when the negative feedback controller is activated. In Fig. 11b, it is observed that the reduction in the amplitude of the vibration response is higher compared to the response in Fig. 11a due to the stiffness of the foundation. Next, the smart laminated plate is subjected to a static mechanical load of uniform variation and magnitude, q = 1000 N/m2. The plate is first subjected to a static load and then removed by setting the plate into free vibration. The negative feedback controller is then activated once the plate enters into vibration. The material properties used in this problem are obtained from Wang et al. [88]. The effectiveness of the control strategy can be properly visualized when the structural damping is also included in the formulation. The structural damping matrix is introduced with the Rayleigh damping matrix, in which the proportionality constants, \(\alpha \) and \(\beta \) are adopted to be 0.965 × 103 rad s−1 and 10–6 s [88]. The value of the charge amplifier gain is considered to be 1.6 × 105 \(\Omega \) [88]. The uncontrolled and controlled responses of the plate are plotted in Fig. 12a and b without considering the foundations, and by including the Winkler and shear stiffness of the foundation, respectively. The output voltage from the sensor is amplified with suitable gains, Gi = 50, 100, 150, and 200, and then fed back to the actuator to obtain the equivalent negative velocity feedback. In the previous example, we witnessed that there was no decay in the amplitude of the uncontrolled vibration response with time; however, in this example, we observe the amplitude of the uncontrolled vibration response to be decaying with time due to the structural damping. Also, the overall damping of the system gets more effective when the negative feedback controller is activated as the amplitude of the controlled vibration responses are observed to decay faster with the increase in the magnitude of the feedback gains. In Fig. 12b, we observe that the amplitude of the vibration responses is significantly reduced due to the stiffness of the foundation (K1 = 100, K2 = 10). The frequency of the vibration response is observed to increase due to the foundation stiffness. In this example, the plate vibrates at its natural frequency as the load is removed after setting the plate into vibration. The natural frequency of the plate gets altered due to the presence of the foundations, and as a result, a change in the frequency of the vibration can also be observed in Fig. 12b. The same smart plate is now subjected to constant-pulse load acting up to 0.0015 s, and then removed from the plate. The displacement–time responses of the plate are plotted in Fig. 13a and b. It is observed that the amplitude of the vibration responses is observed to decay faster with the increase in the control gains. The foundation stiffness reduces the amplitude of the displacement–time response while the frequency of the vibration gets increased.
a Uncontrolled and controlled vibration response of smart composite plate subjected to harmonic excitation without considering the foundation stiffness; b Uncontrolled and controlled vibration response of smart composite plate subjected to harmonic excitation by considering the foundation stiffness (K1 = 100, K2 = 10)
a Uncontrolled and controlled free-vibration responses of a smart composite plate with various gains and neglecting the foundation stiffness; b Uncontrolled and controlled free-vibration responses of a smart composite plate with various gains and considering the Winkler (K1) and shear foundation stiffness (K2)
a Uncontrolled and controlled vibration responses of the smart composite plate subjected to constant-pulse mechanical load acting for 0.0015 s with various gains and neglecting the foundation stiffness; b Uncontrolled and controlled vibration responses of the smart composite plate subjected to constant-pulse mechanical load acting for 0.0015 s with various gains and considering the Winkler and shear foundation stiffness
4 Conclusions
This work studies the static and vibration responses of smart composite plates with piezoelectric actuators and sensors resting on elastic foundation. An inter-laminar transverse shear stress continuous plate model, which consists of an equivalent-single-layer (ESL) field in conjunction with a linear zigzag field, is adopted to model the deformation behavior of the plates. A non-polynomial higher-order plate theory with zigzag kinematics involving a trigonometric function and a local segmented zigzag function is adopted for the first time to model the deformation of a smart piezoelectric laminated composite plate supported on elastic foundation. This model has only five independent primary variables like that of the first-order shear deformation theory, yet it considers the realistic parabolic behavior of the transverse shear stresses across the thickness of the laminated composites plates, and also maintains the continuity conditions of transverse shear stresses at the interfaces of the laminated plates. For modeling the soil deformation, the two-parameter foundation model of Pasternak is considered to establish the continuity among the springs, which is neglected in Winkler’s model. New analytical and FE models are derived to solve the governing equations of the problem. A closed-form analytical solution is assumed in the framework of Navier’s method for the diaphragm-supported boundary conditions, and a generalized C0-continuous FE formulation is presented for the general boundary and loading conditions of the problem. Several examples are solved by considering various parameters like the span–thickness ratios, material properties, boundary conditions, foundation stiffness, feedback gains, and various forms of time-dependent electromechanical loads.
The present results are observed to be in very good agreement with the standard solutions available in the literature. The magnitude of the in-plane and transverse displacements and stresses decreases with the increase in the foundation stiffness (K1, K2). The fundamental frequencies of the plate increase with the increase in the stiffness of the foundations (K1, K2). The amplitude and frequency of the vibration responses in the transient analysis are observed to decrease and increase, respectively. Pasternak’s foundation model has more influence on the system responses than Winkler’s foundation model. The negative feedback controller creates an energy dissipation mechanism that is responsible for the control of the mechanical vibrations. Also, the vibration suppression of the displacement–time responses of the system becomes quicker with the increase in the control gain. The effectiveness of the controller increases with the inclusion of the structural damping matrix. The foundation stiffness, together with the feedback control system, results in a more controlled vibrational response of the smart plate. The piezoelectric layer has a higher controlling capacity for the case of plates with a lower span–thickness ratio. Also, significant actuation of the displacement and stresses are observed at various points along the thickness (z) and planform (l, b) of the plate due to the application of the electrical loadings.
Based on the presented results, it can be concluded that the proposed analytical solution and FE formulation can be efficiently used to model the static and dynamic electro-elastic behavior of smart laminated plates supported on elastic foundations.
References
Bailey T, Hubbard JE Jr (1985) Distributed piezoelectric-polymer active vibration control of a cantilever beam. J Guid Control Dyn 8(5):605–611
Im S, Atluri SN (1989) Effects of a piezo-actuator on a finitely deformed beam subjected to general loading. AIAA J 27(12):1801–1807
Gerhold CH, Rocha R (1989) Active control of flexural vibrations in beams. J Aerosp Eng 2(3):141–154
Tzou HS, Tseng CI (1990) Distributed piezoelectric sensor/actuator design for dynamic measurement/control of distributed parameter systems: a piezoelectric finite element approach. J Sound Vib 138(1):17–34
Crawley EF, De Luis J (1987) Use of piezoelectric actuators as elements of intelligent structures. AIAA J 25(10):1373–1385
Raja, S., Sinha, P.K. and Prathap, G., 2003, October. Active vibration control of a laminated composite plate with PZT actuators and sensors: an experimental study. In Smart Materials, Structures, and Systems (Vol. 5062, pp. 637–644). International Society for Optics and Photonics.
Dong XJ, Meng G, Peng JC (2006) Vibration control of piezoelectric smart structures based on system identification technique: Numerical simulation and experimental study. J Sound Vib 297(3–5):680–693
Han JH, Rew KH, Lee I (1997) An experimental study of active vibration control of composite structures with a piezo-ceramic actuator and a piezo-film sensor. Smart Mater Struct 6(5):549
Ali HQ, Tabrizi IE, Khan RMA, Zanjani JSM, Yilmaz C, Poudeh LH, Yildiz M (2019) Experimental study on dynamic behavior of woven carbon fabric laminates using in-house piezoelectric sensors. Smart Mater Struct 28(10):105004
Ur Rahman N, Alam MN, Ansari JA (2021) An experimental study on dynamic analysis and active vibration control of smart laminated plates. Materials Today: Proceedings 46:9550–9554
Ataei MH, Hassanzadeh-Tabrizi SA, Rafiei M, Monshi A (2021) Delamination Detection in a Laminated Carbon Composite Plate Using Lamb Wave by Lead-Free Piezoceramic Transducers. Journal of Advanced Materials and Processing 9(3):3–14
Elahi H (2021) The investigation on structural health monitoring of aerospace structures via piezoelectric aeroelastic energy harvesting. Microsyst Technol 27:2605–2613
Aabid, A., Parveez, B., Raheman, M.A., Ibrahim, Y.E., Anjum, A., Hrairi, M., Parveen, N. and Mohammed Zayan, J., 2021, May. A Review of Piezoelectric Material-Based Structural Control and Health Monitoring Techniques for Engineering Structures: Challenges and Opportunities. In Actuators (Vol. 10, No. 5, 101). Multidisciplinary Digital Publishing Institute.
Moita JMS, Correia IF, Soares CMM, Soares CAM (2004) Active control of adaptive laminated structures with bonded piezoelectric sensors and actuators. Comput Struct 82(17–19):1349–1358
Wang BT, Rogers CA (1991) Laminate plate theory for spatially distributed induced strain actuators. J Compos Mater 25(4):433–452
Chandrashekhara K, Agarwal AN (1993) Active vibration control of laminated composite plates using piezoelectric devices: a finite element approach. J Intell Mater Syst Struct 4(4):496–508
Mahato PK, Maiti DK (2010) Aeroelastic analysis of smart composite structures in hygro-thermal environment. Compos Struct 92(4):1027–1038
Ray MC, Mallik N (2004) Finite element analysis of smart structures containing piezoelectric fiber-reinforced composite actuator. AIAA J 42(7):1398–1405
Mallik N, Ray MC (2003) Effective coefficients of piezoelectric fiber-reinforced composites. AIAA J 41(4):704–710
Shingare KB, Naskar S (2021) Probing the prediction of effective properties for composite materials. European Journal of Mechanics-A/Solids 87:104228
Cho M, Oh J (2004) Higher order zig-zag theory for fully coupled thermo-electric–mechanical smart composite plates. Int J Solids Struct 41(5–6):1331–1356
Reddy, J.N., 1984. A simple higher-order theory for laminated composite plates.
Kant T, Manjunatha BS (1988) An unsymmetric FRC laminate C° finite element model with 12 degrees of freedom per node. Eng Comput 5(4):300–308
Lo KH, Christensen RM, Wu EM (1977) A higher order theory of plate deformation, Part II: Laminated plates. Trans ASME J Appl Mech 44(4):669–676
Shimpi RP (2002) Refined plate theory and its variants. AIAA J 40(1):137–146
Sobhy M (2021) Analytical buckling temperature prediction of FG piezoelectric sandwich plates with lightweight core. Materials Research Express 8(9):095704
Touratier M (1991) An efficient standard plate theory. Int J Eng Sci 29(8):901–916
Karama M, Afaq KS, Mistou S (2003) Mechanical behaviour of laminated composite beam by the new multi-layered laminated composite structures model with transverse shear stress continuity. Int J Solids Struct 40(6):1525–1546
Shiyekar SM, Kant T (2011) Higher order shear deformation effects on analysis of laminates with piezoelectric fibre reinforced composite actuators. Compos Struct 93(12):3252–3261
Rouzegar J, Abad F (2015) Analysis of cross-ply laminates with piezoelectric fiber-reinforced composite actuators using four-variable refined plate theory. J Theor Appl Mech 53(2):439–452
Rouzegar J, Abbasi A (2018) A refined finite element method for bending analysis of laminated plates integrated with piezoelectric fiber-reinforced composite actuators. Acta Mech Sin 34(4):689–705
Ray MC, Bhattacharyya R, Samanta B (1994) Static analysis of an intelligent structure by the finite element method. Comput Struct 52(4):617–631
Samanta B, Ray MC, Bhattacharyya R (1996) Finite element model for active control of intelligent structures. AIAA J 34(9):1885–1893
Chanda, A., Chandel, U., Sahoo, R. and Grover, N., 2020. Stress analysis of smart composite plate structures. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 0954406220975449.
Joshan YS, Santapuri S, Grover N (2020) Analysis of laminated piezoelectric composite plates using an inverse hyperbolic coupled plate theory. Appl Math Model 82:359–378
Robbins DH, Reddy JN (1991) Analysis of piezoelectrically actuated beams using a layer-wise displacement theory. Comput Struct 41(2):265–279
Saravanos DA, Heyliger PR, Hopkins DA (1997) Layerwise mechanics and finite element for the dynamic analysis of piezoelectric composite plates. Int J Solids Struct 34(3):359–378
Zabihollah A, Sedagahti R, Ganesan R (2007) Active vibration suppression of smart laminated beams using layerwise theory and an optimal control strategy. Smart Mater Struct 16(6):2190
Moita JS, Araújo AL, Martins P, Soares CM, Soares CM (2011) A finite element model for the analysis of viscoelastic sandwich structures. Comput Struct 89(21–22):1874–1881
Wu Y, Xiao Z, Li D, Xu J (2022) On numerical static analysis of stiffened laminated composite plates with delaminations, cracks, or debonding of a piezoelectric patch. Mech Adv Mater Struct 29(1):89–103
Xiao Z, Wu Y, Li D (2022) Thermo-electro-mechanical dynamic fracture analysis on laminated piezoelectric plates. Compos Struct 285:115158
Xu JX, Xiao ZG, Wu YG, Li DH (2020) Extended layerwise method for laminated piezoelectric and composite plates with delaminations, cracks or debonding of a piezoelectric patch. Compos Struct 234:111692
Li D (2021) Layerwise theories of laminated composite structures and their applications: A review. Archives of Computational Methods in Engineering 28(2):577–600
Di Sciuva M (1992) Multilayered anisotropic plate models with continuous interlaminar stresses. Compos Struct 22(3):149–167
Cho M, Parmerter RR (1993) Efficient higher order composite plate theory for general lamination configurations. AIAA J 31(7):1299–1306
Chakrabarti A, Sheikh AH (2004) Vibration of laminate-faced sandwich plate by a new refined element. J Aerosp Eng 17(3):123–134
Kapuria S, Kulkarni SD (2007) An improved discrete Kirchhoff quadrilateral element based on third-order zigzag theory for static analysis of composite and sandwich plates. Int J Numer Meth Eng 69(9):1948–1981
Topdar P, Chakraborti A, Sheikh AH (2004) An efficient hybrid plate model for analysis and control of smart sandwich laminates. Comput Methods Appl Mech Eng 193(42–44):4591–4610
Khandelwal RP, Chakrabarti A, Bhargava P (2013) An efficient hybrid plate model for accurate analysis of smart composite laminates. J Intell Mater Syst Struct 24(16):1927–1950
Kapuria S, Achary GGS (2005) A coupled zigzag theory for the dynamics of piezoelectric hybrid cross-ply plates. Arch Appl Mech 75(1):42–57
Nath JK, Kapuria S (2012) Assessment of improved zigzag and smeared theories for smart cross-ply composite cylindrical shells including transverse normal extensibility under thermoelectric loading. Arch Appl Mech 82(7):859–877
Chanda A, Sahoo R (2021) Accurate stress analysis of laminated composite and sandwich plates. The Journal of Strain Analysis for Engineering Design 56(2):96–111
Chanda A, Sahoo R (2020) Analytical modeling of laminated composite plates integrated with piezoelectric layer using Trigonometric Zigzag theory. J Compos Mater 54(29):4691–4708
Carrera E (2003) Theories and finite elements for multilayered plates and shells: a unified compact formulation with numerical assessment and benchmarking. Archives of Computational Methods in Engineering 10(3):215–296
Bharati RB, Filippi M, Mahato PK, Carrera E (2020) Flutter analysis of laminated composite structures using Carrera Unified Formulation. Compos Struct 253:112759
Cinefra M, Carrera E, Valvano S (2015) Variable kinematic shell elements for the analysis of electro-mechanical problems. Mech Adv Mater Struct 22(1–2):77–106
Patil MA, Kadoli R (2020) Influence of Winkler and viscoelastic foundation on free vibration of functionally graded beam integrated with Terfenol-D layer. J Braz Soc Mech Sci Eng 42(11):1–12
Akavci SS, Yerli HR, Dogan A (2007) The first order shear deformation theory for symmetrically laminated composite plates on elastic foundation. Arab J Sci Eng 32(2):341
Shen HS (2000) Nonlinear bending of simply supported rectangular Reissner-Mindlin plates under transverse and in-plane loads and resting on elastic foundations. Eng Struct 22(7):847–856
Lal A, Singh BN, Kumar R (2008) Nonlinear free vibration of laminated composite plates on elastic foundation with random system properties. Int J Mech Sci 50(7):1203–1212
Akavci SS (2007) Buckling and free vibration analysis of symmetric and antisymmetric laminated composite plates on an elastic foundation. J Reinf Plast Compos 26(18):1907–1919
Barati MR, Sadr MH, Zenkour AM (2016) Buckling analysis of higher order graded smart piezoelectric plates with porosities resting on elastic foundation. Int J Mech Sci 117:309–320
Ebrahimi F, Jafari A, Barati MR (2017) Vibration analysis of magneto-electro-elastic heterogeneous porous material plates resting on elastic foundations. Thin-Walled Structures 119:33–46
Zenkour AM, Alghanmi RA (2019) Bending of exponentially graded plates integrated with piezoelectric fiber-reinforced composite actuators resting on elastic foundations. European Journal of Mechanics-A/Solids 75:461–471
Zenkour AM, El-Shahrany HD (2020) Control of a laminated composite plate resting on Pasternak’s foundations using magnetostrictive layers. Arch Appl Mech 90:1943–1959
Zenkour, A.M. and El-Shahrany, H.D., 2021. Hygrothermal Vibration and Damping Behavior of Magnetostrictive Sandwich Plate Resting On Pasternak’s Foundations. Applied Composite Materials, pp.1–26.
Bisheh H, Civalek Ö (2020) Vibration of smart laminated carbon nanotube-reinforced composite cylindrical panels on elastic foundations in hygrothermal environments. Thin-Walled Structures 155:106945
Mashat DS, Zenkour AM, Radwan AF (2020) A quasi-3D higher-order plate theory for bending of FG plates resting on elastic foundations under hygro-thermo-mechanical loads with porosity. European Journal of Mechanics-A/Solids 82:103985
Ghorbanpour Arani A, Khoddami Maraghi Z, Khani Arani H (2017) Vibration control of magnetostrictive plate under multi-physical loads via trigonometric higher order shear deformation theory. J Vib Control 23(19):3057–3070
Bodaghi M, Saidi AR (2011) Stability analysis of functionally graded rectangular plates under nonlinearly varying in-plane loading resting on elastic foundation. Arch Appl Mech 81(6):765–780
Akgoz B, Civalek O (2011) Nonlinear vibration analysis of laminated plates resting on nonlinear two-parameters elastic foundations. Steel Compos Struct 11(5):403–421
Kaddari M, Kaci A, Bousahla AA, Tounsi A, Bourada F, Tounsi A, Bedia EA, Al-Osta MA (2020) A study on the structural behaviour of functionally graded porous plates on elastic foundation using a new quasi-3D model: bending and free vibration analysis. Comput Concr 25(1):37–57
Grover N, Singh BN, Maiti DK (2013) Analytical and finite element modeling of laminated composite and sandwich plates: An assessment of a new shear deformation theory for free vibration response. Int J Mech Sci 67:89–99
Sahoo R, Singh BN (2014) A new trigonometric zigzag theory for static analysis of laminated composite and sandwich plates. Aerosp Sci Technol 35:15–28
Punera D, Kant T (2017) Elastostatics of laminated and functionally graded sandwich cylindrical shells with two refined higher order models. Compos Struct 182:505–523
Cook RD (1995) Finite Element Modeling for Stress Analysis. Wiley, New York
Pandit MK, Sheikh AH, Singh BN (2010) Analysis of laminated sandwich plates based on an improved higher order zigzag theory. J Sandwich Struct Mater 12(3):307–326
Pagano NJ (1970) Exact solutions for rectangular bidirectional composites and sandwich plates. J Compos Mater 4(1):20–34
Rodrigues JD, Roque CMC, Ferreira AJM, Carrera E, Cinefra M (2011) Radial basis functions–finite differences collocation and a Unified Formulation for bending, vibration and buckling analysis of laminated plates, according to Murakami’s zig-zag theory. Compos Struct 93(7):1613–1620
Natarajan S, Ferreira AJM, Bordas SPA, Carrera E, Cinefra M (2013) Analysis of composite plates by a unified formulation-cell based smoothed finite element method and field consistent elements. Compos Struct 105:75–81
Ferreira AJM, Carrera E, Cinefra M, Viola E, Tornabene F, Fantuzzi N, Zenkour AM (2014) Analysis of thick isotropic and cross-ply laminated plates by generalized differential quadrature method and a unified formulation. Compos B Eng 58:544–552
Kulkarni SD, Kapuria S (2008) Free vibration analysis of composite and sandwich plates using an improved discrete Kirchhoff quadrilateral element based on third-order zigzag theory. Comput Mech 42:803–824
Shen HS, Zheng JJ, Huang XL (2003) Dynamic response of shear deformable laminated plates under thermomechanical loading and resting on elastic foundations. Compos Struct 60(1):57–66
Mallik N, Ray MC (2004) Exact solutions for the analysis of piezoelectric fiber reinforced composites as distributed actuators for smart composite plates. Int J Mech Mater Des 1(4):347–364
Mallikarjuna, Kant T (1989) Free vibration of symmetrically laminated plates using a higher-order theory with finite element technique. Int J Numer Meth Eng 28(8):1875–1889
Ray MC, Bhattacharya R, Samanta B (1998) Exact solutions for dynamic analysis of composite plates with distributed piezoelectric layers. Comput Struct 66(6):737–743
Moita JMS, Soares CMM, Soares CAM (2005) Active control of forced vibrations in adaptive structures using a higher order model. Compos Struct 71(3–4):349–355
Wang SY, Quek ST, Ang KK (2001) Vibration control of smart piezoelectric composite plates. Smart Mater Struct 10(4):637
Funding
Open access funding provided by HEAL-Link Greece. No funding was received for conducting this study.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
Appendix B
The components of matrix ‘\(\left[B\right]\)’ are written as
The individual entries in the above matrix are written as
\({\overline{B} }_{{{1,1}}_{i}}={\overline{B} }_{{{3,2}}_{i}}={\overline{B} }_{{{7,4}}_{i}}={\overline{B} }_{{{10,5}}_{i}}={\overline{B} }_{{{12,3}}_{i}}=\frac{\partial {N}_{i}}{\partial x};{\overline{B} }_{{{2,2}}_{i}}={\overline{B} }_{{{3,1}}_{i}}={\overline{B} }_{{{8,5}}_{i}}={\overline{B} }_{{{9,4}}_{i}}={\overline{B} }_{{{11,3}}_{i}}=\frac{\partial {N}_{i}}{\partial y};\)
\({\overline{B} }_{{{4,6}}_{i}}={\overline{B} }_{{{6,7}}_{i}}=-\frac{\partial {N}_{i}}{\partial x}\); \({\overline{B} }_{{{5,7}}_{i}}={\overline{B} }_{{{6,6}}_{i}}=-\frac{\partial {N}_{i}}{\partial y}\); \({\overline{B} }_{{{4,4}}_{i}}={\Omega }_{x}\frac{\partial {N}_{i}}{\partial x}\); \({\overline{B} }_{{{5,5}}_{i}}={\Omega }_{y}\frac{\partial {N}_{i}}{\partial y}\); \({\overline{B} }_{{{6,4}}_{i}}={\Omega }_{x}\frac{\partial {N}_{i}}{\partial y}\);
\({\overline{B} }_{{{6,5}}_{i}}={\Omega }_{y}\frac{\partial {N}_{i}}{\partial x}\); \({\overline{B} }_{{{12,4}}_{i}}={\Omega }_{x}{N}_{i}\); \({\overline{B} }_{{{11,5}}_{i}}={\Omega }_{y}{N}_{i}\); \({\overline{B} }_{{{11,7}}_{i}}={\overline{B} }_{{{12,6}}_{i}}={-N}_{i}\); \({\overline{B} }_{{{13,5}}_{i}}={\overline{B} }_{{{14,4}}_{i}}={N}_{i}.\)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chanda, A.G., Kontoni, DP.N. & Sahoo, R. Development of analytical and FEM solutions for static and dynamic analysis of smart piezoelectric laminated composite plates on elastic foundation. J Eng Math 138, 12 (2023). https://doi.org/10.1007/s10665-022-10251-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10665-022-10251-6
Keywords
- Analytical solution
- Navier’s method
- Finite element method (FEM)
- Zigzag theory
- Smart composites
- Laminated plates
- Elastic foundation
- Pasternak’s foundation model
- Newmark’s time integration
- Vibration control