Fast two-beam collisions in a linear optical medium with weak cubic loss in spatial dimension higher than 1

Abstract

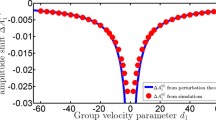
We study the dynamics of fast two-beam collisions in linear bulk optical media with weak cubic loss in spatial dimension higher than 1. The cubic loss arises due to two-photon absorption. We first generalize the perturbation theory that was developed for analyzing two-pulse collisions in spatial dimension 1 to spatial dimension 2. We then use the generalized two-dimensional perturbation theory to show that the collision leads to a change in the beam shapes in the direction transverse to the relative velocity vector. Furthermore, we show that in the important case of a separable initial condition for both beams, the longitudinal part in the expression for the amplitude shift is universal, while the transverse part is not universal. The same behavior holds for collisions between pulsed optical beams in spatial dimension 3. We check these analytic predictions along with other predictions concerning the effects of anisotropy in the initial condition by extensive numerical simulations with the weakly perturbed linear propagation model. The agreement between the perturbation theory and the simulations is very good. Thus, our study extends and generalizes the results of previous works, which were limited to spatial dimension 1. The results are very useful for multiwavelength optical communication systems.

Appendices

Appendix A: Invariance of $\varDelta A_{1}^{(c)}$ under rotations

In this appendix, we show that the change in the coordinate system, in which we rotate the $x'$ and $y'$ axes by an angle $\varDelta \theta$, such that in the new coordinate system the relative velocity vector between the beam centers lies on the x axis, does not change the value of $\varDelta A_{1}^{(c)}$. That is, the value of the collision-induced amplitude shift is invariant under this rotation transformation. This calculation is important for two main reasons. First, only the formulas obtained in the new coordinate system (after the rotation transformation) explicitly preserve the true small parameters in the problem. Second, the latter formulas are simple enough to enable the derivation of explicit expressions for the collision-induced amplitude shift. In this manner, the application of the rotation transformation enables a deeper insight into the collision-induced dynamics in the high-dimensional problem.

We consider the fast two-beam collision problem in the $(x',y',z)$ coordinate system, in which the relative velocity vector $\mathbf {d_{1}'}=(d_{11}', d_{12}')$ does not lie on the $x'$ or $y'$ axes. We assume that $d_{1}'=|\mathbf {d_{1}'}| \gg 1$. The perturbed linear propagation model in the $(x',y',z)$ coordinate system is

$$\begin{aligned}&\mathrm{{i}}\partial _z\psi '_{1} + \partial _{x'}^{2}\psi '_{1} + \partial _{y'}^{2}\psi '_{1}= -\mathrm{{i}}\epsilon _{3}|\psi '_{1}|^2\psi '_{1} -2\mathrm{{i}}\epsilon _{3}|\psi '_{2}|^2\psi '_{1}, \nonumber \\&\mathrm{{i}}\partial _z\psi '_{2} + \mathrm{{i}}d_{11}'\partial _{x'}\psi ' _{2} +\mathrm{{i}}d_{12}'\partial _{y'}\psi ' _{2} +\partial _{x'}^2\psi '_{2} + \partial _{y'}^{2}\psi '_{2} = -\mathrm{{i}}\epsilon _{3}|\psi '_{2}|^2\psi '_{2} -2\mathrm{{i}}\epsilon _{3}|\psi '_{1}|^2\psi '_{2}, \end{aligned}$$

(74)

where $\psi '_{j}(x',y',z)$ is the electric field of the jth beam in this coordinate system. The initial condition is:

$$\begin{aligned}&\psi '_{j}(x',y',0)=A_{j}(0)h'_{j}(x',y')\exp (\mathrm{{i}}\alpha _{j0}), \end{aligned}$$

(75)

where $h'_{j}(x',y')$ is real-valued.

We assume that the solution to the unperturbed propagation equation

$$\begin{aligned}&\mathrm{{i}}\partial _z\psi '_{1} + \partial _{x'}^{2}\psi '_{1} + \partial _{y'}^{2}\psi '_{1}=0 \end{aligned}$$

(76)

does not contain any fast dependence on z. In addition, we assume that the only fast dependence on z in the solution to the unperturbed propagation equation

$$\begin{aligned}&\mathrm{{i}}\partial _z\psi '_{2} + \mathrm{{i}}d_{11}'\partial _{x'}\psi ' _{2} +\mathrm{{i}}d_{12}'\partial _{y'}\psi ' _{2} +\partial _{x'}^2\psi '_{2} + \partial _{y'}^{2}\psi '_{2} = 0 \end{aligned}$$

(77)

is contained in factors of the form $x'-x'_{20}-d_{11}'z$ and $y'-y'_{20}-d_{12}'z$, where $(x'_{20},y'_{20})$ is the initial location of beam 2 in the $x'y'$ plane. Under these assumptions, we can use the perturbation method of Sect. 2.1 to show that within the leading order of the method, the equation for $\varPhi _{1}'$ in the collision interval is

$$\begin{aligned}&\partial _{z}\varPhi '_{1}= -2\epsilon _{3}\varPsi _{20}^{\prime 2}\varPsi '_{10}. \end{aligned}$$

(78)

In addition, in a similar manner to the calculation in Sect. 2.1, we can show that $\varDelta \varPhi '_{1}(x',y',z_\mathrm{{c}})$ can be approximated by

$$\begin{aligned}&\varDelta \varPhi '_{1}(x',y',z_\mathrm{{c}})=- 2\epsilon _{3} A_{1}(z_\mathrm{{c}}^{-}) A_{2}^{2}(z_\mathrm{{c}}^{-}) {\tilde{\varPsi }}'_{10}(x',y',z_\mathrm{{c}}) \int _{-\infty }^{\infty } {\bar{\varPsi }}_{20}^{\prime 2}(x'-x'_{20}-d_{11}'z',y'-y'_{20}-d_{12}'z',z_\mathrm{{c}}) \, \mathrm{{d}}z'. \end{aligned}$$

(79)

It follows that the collision-induced amplitude shift in the $(x',y',z)$ coordinate system is

$$\begin{aligned} \varDelta A_{1}^{\prime (c)}= & {} -\frac{2\epsilon _{3} A_{1}(z_\mathrm{{c}}^{-}) A_{2}^{2}(z_\mathrm{{c}}^{-})}{C'_{p1}}\nonumber \\&\times \int _{-\infty }^{\infty } \, \int _{-\infty }^{\infty } \, \int _{-\infty }^{\infty } {\tilde{\varPsi }}_{10}^{\prime 2}(x',y',z_\mathrm{{c}}) {\bar{\varPsi }}_{20}^{\prime 2}(x'-x'_{20}-d_{11}'z',y'-y'_{20}-d_{12}'z',z_\mathrm{{c}}) \, \mathrm{{d}}z'\,\mathrm{{d}}x'\,\mathrm{{d}}y' , \end{aligned}$$

(80)

where

$$\begin{aligned}&C'_{p1}= \int _{-\infty }^{\infty } \, \int _{-\infty }^{\infty } {\tilde{\varPsi }}_{10}^{\prime 2}(x',y',0) \, \mathrm{{d}}x'\,\mathrm{{d}}y'. \end{aligned}$$

(81)

We see that Eq. (80) contains two parameters $d_{11}'$ and $d_{12}'$ that are associated with the single true large parameter $d_{1}'$. Therefore, this equation does not explicitly preserve the true small parameters in the problem $\epsilon _{3}$ and $1/d_{1}'$. Furthermore, the coordinate $z'$ appears in the expression for ${\bar{\varPsi }}_{20}^{\prime 2}$ in the inner integral twice. As a result, derivation of explicit formulas for the amplitude shift from Eq. (80) is difficult.

We now make a change of variables by going to the (x, y, z) coordinate system, in which the relative velocity vector $\mathbf {d_{1}'}$ lies on the x axis. The (x, y, z) system is found by rotating the $x'$ and $y'$ axes by an angle $\varDelta \theta = \arctan (d_{12}'/d_{11}')$ about the z axis. The equations that define this change of variables are:

$$\begin{aligned} x' = x \cos \varDelta \theta - y\sin \varDelta \theta , \quad y' = x \sin \varDelta \theta + y\cos \varDelta \theta , \end{aligned}$$

(82)

and

$$\begin{aligned} \psi '_{j}(x',y',z) = \psi _{j}(x,y,z). \end{aligned}$$

(83)

It is straightforward to show that the perturbed linear propagation model in the (x, y, z) coordinate system is Eq. (1) and that $|d_{11}|=d_{1}'$. The initial condition for the collision problem is given by Eq. (2), where $h_{j}(x,y) = h'_{j}(x',y')$. We observe that the only large parameter in Eq. (1) is $d_{11}$. Thus, the change of variables in Eqs. (82) and (83) does not change the properties of the fast dependence on z of the solutions to the unperturbed propagation equations (76) and (77). This means that the solution to the unperturbed equation

$$\begin{aligned}&\mathrm{{i}}\partial _z\psi _{1} + \partial _{x}^{2}\psi _{1} + \partial _{y}^{2}\psi _{1}=0 \end{aligned}$$

(84)

does not contain any fast dependence on z. In addition, the only fast dependence on z in the solution to the equation

$$\begin{aligned}&\mathrm{{i}}\partial _z\psi _{2}+\mathrm{{i}}d_{11}\partial _{x}\psi _{2} +\partial _{x}^2\psi _{2} + \partial _{y}^{2}\psi _{2} = 0 \end{aligned}$$

(85)

is contained in factors of the form $x-x_{20}-d_{11}z$. If follows that we can employ the perturbation method of Sect. 2.1 to calculate the collision-induced amplitude shift $\varDelta A_{1}^{(c)}$ in the (x, y, z) system, and that $\varDelta A_{1}^{(c)}$ is given by Eq. (19), where $C_{p1}$ is given by Eq. (18).

Let us show that the value of the amplitude shift $\varDelta A_{1}^{\prime (c)}$ in Eq. (80) is equal to the value $\varDelta A_{1}^{(c)}$ in Eq. (19). For this purpose we note that the determinant of the Jacobian matrix for the transformation (82) is $|J|=1$. Using this together with Eqs. (18), (81), and (83), we obtain $C'_{p1}=C_{p1}$. In addition, from Eq. (83) it follows that ${\tilde{\varPsi }}'_{j0}(x',y',z_\mathrm{{c}}) = {\tilde{\varPsi }}_{j0}(x,y,z_\mathrm{{c}})$. Furthermore, since the transformation in Eqs. (82) and (83) does not change the properties of the fast dependence on z of the solutions to the unperturbed propagation equations, and since $d_{12}=0$, we obtain⁹:

$$\begin{aligned} {\bar{\varPsi }}'_{20}(x'-x'_{20}-d_{11}'z,y'-y'_{20}-d_{12}'z,z_\mathrm{{c}}) = {\bar{\varPsi }}_{20}(x-x_{20}-d_{11}z,y,z_\mathrm{{c}}). \end{aligned}$$

(86)

Using all the relations mentioned in the current paragraph in Eq. (80), we arrive at

$$\begin{aligned}&\varDelta A_{1}^{\prime (c)}=-\frac{2\epsilon _{3} A_{1}(z_\mathrm{{c}}^{-}) A_{2}^{2}(z_\mathrm{{c}}^{-})}{C_{p1}|d_{11}|} \int _{-\infty }^{\infty } \, \int _{-\infty }^{\infty } \, \int _{-\infty }^{\infty } {\tilde{\varPsi }}_{10}^{2}(x,y,z_\mathrm{{c}}) {\bar{\varPsi }}_{20}^{2}({\tilde{x}},y,z_\mathrm{{c}}) \, \mathrm{{d}}{\tilde{x}}\,\mathrm{{d}}x\,\mathrm{{d}}y =\varDelta A_{1}^{(c)}. \end{aligned}$$

(87)

Therefore, the value of $\varDelta A_{1}^{(c)}$ is indeed invariant under rotation transformations in the xy plane.

Appendix B: Amplitude dynamics in the perturbed single-beam propagation problem

In this Appendix, we derive the equation for the dynamics of the beam amplitudes in the perturbed single-beam propagation problem, i.e., for a single beam propagating in the presence of weak cubic loss. This equation is used for calculating the amplitude values in the approximate expressions for the $\psi _{j0}$. It is also used for calculating the values of $A_{j}(z_\mathrm{{c}}^{-})$ in Eqs. (16), (19), (34), and (36) for $\varDelta \varPhi _{1}(x,y,z_\mathrm{{c}})$ and $\varDelta A_{1}^{(c)}$, and in other equations in Sect. 2.

Consider the propagation of a single beam in the presence of diffraction, beam steering, and weak cubic loss. The propagation is described by Eq. (5) for beam 1 and by Eq. (6) for beam 2. Employing energy balance calculations for these two equations, we obtain

$$\begin{aligned}&\partial _{z}\int _{-\infty }^{\infty } \, \int _{-\infty }^{\infty } |\psi _{j0}|^{2} \, \mathrm{{d}}x\,\mathrm{{d}}y = -2\epsilon _{3}\int _{-\infty }^{\infty } \, \int _{-\infty }^{\infty } |\psi _{j0}|^{4} \, \mathrm{{d}}x\,\mathrm{{d}}y. \end{aligned}$$

(88)

We now substitute the approximations to the $\psi _{j0}$, which are given by Eqs. (10)–(12), into Eq. (88). This substitution yields the following equation for the $A_{j}$:

$$\begin{aligned}&C_{pj}\frac{\mathrm{d}A_{j}^{2}}{\mathrm{d}z}= -2\epsilon _{3}H_{4j}(z)A_{j}^{4} \,, \end{aligned}$$

(89)

where $H_{4j}(z)=\int _{-\infty }^{\infty } \, \int _{-\infty }^{\infty } {\tilde{\varPsi }}_{j0}^{4}(x,y,z) \, \mathrm{{d}}x\,\mathrm{{d}}y$, $C_{p1}$ is given by Eq. (18), and $C_{p2}$ is given by a similar equation, in which ${\tilde{\varPsi }}_{10}^{2}(x,y,0)$ is replaced by ${\tilde{\varPsi }}_{20}^{2}(x,y,0)$ on the right hand side. The solution of Eq. (89) on the interval [0, z] is

$$\begin{aligned}&A_{j}(z)=\frac{A_{j}(0)}{\left[ 1+2\epsilon _{3}\tilde{H}_{4j}(0,z)A_{j}^{2}(0)/C_{pj}\right] ^{1/2}} \,, \end{aligned}$$

(90)

where ${\tilde{H}}_{4j}(0,z)=\int _{0}^{z} H_{4j}(z') \, \mathrm{{d}}z'$. The simple effects of linear loss on amplitude dynamics can be incorporated into the analysis in exactly the same manner as was done in Refs. [8, 10] for spatial dimension 1. Furthermore, similar to the one-dimensional case, it can be shown that these effects do not change the form of the expressions for the collision-induced changes in beam amplitudes and shapes.

Appendix C: Derivation of Eq. (65)

In this appendix, we derive Eq. (65) for the inverse Fourier transform of ${\hat{p}}_{12}(k_{2},z_\mathrm{{c}})\exp [-\mathrm{{i}} k_{2}^{2}(z-z_\mathrm{{c}})]$ in the case where the initial condition for the collision problem is given by Eq. (45). Equation (65) is used in the calculation of $\phi _{1}(x,y,z)$ in the post-collision interval in Sect. 3.3.

We first employ Eq. (41) along with Eqs. (45), (103), (105), and (109) to obtain an expression for the function $p_{12}(y,z_\mathrm{{c}})$. We find

$$\begin{aligned}&p_{12}(y,z_\mathrm{{c}})= \frac{W_{10}^{(y)}W_{20}^{(y)2}}{(W_{10}^{(y)4} + 4z_\mathrm{{c}}^{2})^{1/4} (W_{20}^{(y)4} + 4z_\mathrm{{c}}^{2})^{1/2}} \exp \left[ -{\tilde{a}}_{2}^{2}(z_\mathrm{{c}})y^{2} -\frac{\mathrm{{i}}}{2}\arctan \left( \frac{2z_\mathrm{{c}}}{W_{10}^{(y)2}}\right) \right] , \end{aligned}$$

(91)

where

$$\begin{aligned} {\tilde{a}}_{2}^{2}(z_\mathrm{{c}})= q_{1}(z_\mathrm{{c}})+ \mathrm{iq}_{2}(z_\mathrm{{c}}), \end{aligned}$$

(92)

and

$$\begin{aligned}&q_{1}(z_\mathrm{{c}})=\frac{W_{10}^{(y)2}W_{20}^{(y)2} (2W_{10}^{(y)2} + W_{20}^{(y)2}) + 4z_\mathrm{{c}}^{2}(W_{10}^{(y)2} + 2W_{20}^{(y)2})}{2(W_{10}^{(y)4} + 4z_\mathrm{{c}}^{2}) (W_{20}^{(y)4} + 4z_\mathrm{{c}}^{2})}, \;\;\;\;\;\;\; q_{2}(z_\mathrm{{c}}) = -\frac{z_\mathrm{{c}}}{W_{10}^{(y)4} + 4z_\mathrm{{c}}^{2}}. \end{aligned}$$

(93)

The Fourier transform of $p_{12}(y,z_\mathrm{{c}})$ is

$$\begin{aligned}&{\hat{p}}_{12}(k_{2},z_\mathrm{{c}})= \frac{W_{10}^{(y)}W_{20}^{(y)2}(W_{10}^{(y)4} + 4z_\mathrm{{c}}^{2})^{1/4}}{{\tilde{a}}_{3}(z_\mathrm{{c}})} \exp \left[ -\frac{k_{2}^{2}}{4\tilde{a}_{2}^{2}(z_\mathrm{{c}})} -\frac{\mathrm{i}}{2}\arctan \left( \frac{2z_\mathrm{{c}}}{W_{10}^{(y)2}}\right) \right] , \end{aligned}$$

(94)

where

$$\begin{aligned} {\tilde{a}}_{3}(z_\mathrm{{c}})= \left[ 2(W_{10}^{(y)4} + 4z_\mathrm{{c}}^{2}) (W_{20}^{(y)4} + 4z_\mathrm{{c}}^{2})\right] ^{1/2} {\tilde{a}}_{2}(z_\mathrm{{c}}). \end{aligned}$$

(95)

Therefore, the inverse Fourier transform of ${\hat{p}}_{12}(k_{2},z_\mathrm{{c}})\exp [-\mathrm{{i}} k_{2}^{2}(z-z_\mathrm{{c}})]$ is given by

$$\begin{aligned}&{{\mathcal {F}}}^{-1}\left( {\hat{p}}_{12}(k_{2},z_\mathrm{{c}}) \exp [-\mathrm{{i}} k_{2}^{2}(z-z_\mathrm{{c}})]\right) = \frac{W_{10}^{(y)}W_{20}^{(y)2}\exp \left[ -q_{1}(z_\mathrm{{c}})y^{2}/R_{1}^{4}(z,z_\mathrm{{c}}) +\mathrm{{i}}\kappa _{1}(y,z)\right] }{(W_{10}^{(y)4} + 4z_\mathrm{{c}}^{2})^{1/4} (W_{20}^{(y)4} + 4z_\mathrm{{c}}^{2})^{1/2}R_{1}(z,z_\mathrm{{c}})}, \end{aligned}$$

(96)

where

$$\begin{aligned} R_{1}(z,z_\mathrm{{c}})= \left\{ 1 - 8q_{2}(z_\mathrm{{c}})(z-z_\mathrm{{c}}) + 16[q_{1}^{2}(z_\mathrm{{c}}) + q_{2}^{2}(z_\mathrm{{c}})](z-z_\mathrm{{c}})^{2}\right\} ^{1/4}, \end{aligned}$$

(97)

and

$$\begin{aligned} \kappa _{1}(y,z)= & {} -\frac{1}{2}\arctan \left[ \frac{2z_\mathrm{{c}}}{W_{10}^{(y)2}}\right] -\frac{1}{2}\arctan \left[ \frac{4q_{1}(z_\mathrm{{c}})(z-z_\mathrm{{c}})}{1 - 4q_{2}(z_\mathrm{{c}})(z-z_\mathrm{{c}})}\right] \nonumber \\&-\, \frac{y^{2} \left\{ q_{2}(z_\mathrm{{c}}) - 4[q_{1}^{2}(z_\mathrm{{c}}) + q_{2}^{2}(z_\mathrm{{c}})](z-z_\mathrm{{c}})\right\} }{R_{1}^{4}(z,z_\mathrm{{c}})}. \end{aligned}$$

(98)

Equation (96) is Eq. (65) of Sect. 3.3.

Appendix D: The solution of the unperturbed linear propagation equation with a Gaussian initial condition

In Sect. 3, we extensively use the solution of the unperturbed linear propagation equation with a Gaussian initial condition as an example. We therefore present here a brief summary of the different forms of this solution.

We consider the unperturbed linear propagation equation

$$\begin{aligned}&\mathrm{{i}}\partial _z\psi + \partial _{x}^{2}\psi + \partial _{y}^{2}\psi =0 \end{aligned}$$

(99)

with the separable Gaussian initial condition

$$\begin{aligned}&\psi (x,y,0)=A\exp \left[ -\frac{(x-x_{0})^{2}}{2W^{(x)2}_{0}} -\frac{(y-y_{0})^{2}}{2W^{(y)2}_{0}} + \mathrm{{i}}\alpha _{0}\right] . \end{aligned}$$

(100)

The solution of Eq. (99) with the initial condition (100) can be written as:

$$\begin{aligned}&\psi (x,y,z)=Ag({\tilde{x}},z) p({\tilde{y}},z)\exp (\mathrm{{i}}\alpha _{0}), \end{aligned}$$

(101)

where ${\tilde{x}} = x - x_{0}$, ${\tilde{y}} = y - y_{0}$,

$$\begin{aligned}&g({\tilde{x}},z)= \frac{W_{0}^{(x)}}{(W_{0}^{(x)4} + 4z^{2})^{1/4}} \exp \left[ -\frac{W_{0}^{(x)2} {\tilde{x}}^{2}}{2(W_{0}^{(x)4} + 4z^{2})} +\mathrm{{i}}\xi _{0}({\tilde{x}},z)\right] , \end{aligned}$$

(102)

and

$$\begin{aligned}&p({\tilde{y}},z)= \frac{W_{0}^{(y)}}{(W_{0}^{(y)4} + 4z^{2})^{1/4}} \exp \left[ -\frac{W_{0}^{(y)2} {\tilde{y}}^{2}}{2(W_{0}^{(y)4} + 4z^{2})} +\mathrm{{i}}\kappa _{0}({\tilde{y}},z)\right] . \end{aligned}$$

(103)

The phase factors $\xi _{0}({\tilde{x}},z)$ and $\kappa _{0}({\tilde{y}},z)$ in Eqs. (102) and (103) are given by

$$\begin{aligned}&\xi _{0}({\tilde{x}},z)= -\frac{1}{2}\arctan \left( \frac{2z}{W_{0}^{(x)2}}\right) +\frac{{\tilde{x}}^{2}z}{W_{0}^{(x)4} + 4z^{2}}, \end{aligned}$$

(104)

and

$$\begin{aligned}&\kappa _{0}({\tilde{y}},z)= -\frac{1}{2}\arctan \left( \frac{2z}{W_{0}^{(y)2}}\right) +\frac{{\tilde{y}}^{2}z}{W_{0}^{(y)4} + 4z^{2}}. \end{aligned}$$

(105)

One can also write the solution (101) in the form

$$\begin{aligned}&\psi (x,y,z)=A\varPsi (x,y,z)\exp [\mathrm{{i}}\chi _{0}({\tilde{x}},{\tilde{y}},z)], \end{aligned}$$

(106)

where

$$\begin{aligned} \varPsi (x,y,z)=G({\tilde{x}},z)P({\tilde{y}},z), \end{aligned}$$

(107)

$$\begin{aligned} G({\tilde{x}},z)= \frac{W_{0}^{(x)}}{(W_{0}^{(x)4} + 4z^{2})^{1/4}} \exp \left[ -\frac{W_{0}^{(x)2} {\tilde{x}}^{2}}{2(W_{0}^{(x)4} + 4z^{2})}\right] , \end{aligned}$$

(108)

$$\begin{aligned} P({\tilde{y}},z)= \frac{W_{0}^{(y)}}{(W_{0}^{(y)4} + 4z^{2})^{1/4}} \exp \left[ -\frac{W_{0}^{(y)2} {\tilde{y}}^{2}}{2(W_{0}^{(y)4} + 4z^{2})}\right] , \end{aligned}$$

(109)

and

$$\begin{aligned} \chi _{0}({\tilde{x}},{\tilde{y}},z)= \xi _{0}({\tilde{x}},z) + \kappa _{0}({\tilde{y}},z) + \alpha _{0}. \end{aligned}$$

(110)

We also note that the solution of Eq. (99) with the term $\mathrm{{i}}d_{11}\partial _{x}\psi$ on its left hand side and with the initial condition (100) is given by Eqs. (101)–(105) [or by Eqs. (106)–(110)] with ${\tilde{x}} = x - x_{0} - d_{11}z$, and ${\tilde{y}} = y - y_{0}$.