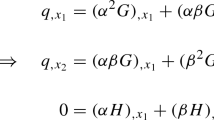Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This brief note discusses the mid-surface scaling invariance of three nonlinear measures of pure bending strain, as introduced in [1] and physically motivated therein more than 20 years ago, in light of the recent work of [3] where the said invariance is introduced.
It is shown that one of the strain measures introduced in [1] possesses scaling invariance, and the other two are easily modified to have the invariance as well. There has been a recent surge of interest in such matters, as can be seen from the works of [3, 5, 6].
We use the notation of [1]: a shell mid-surface is thought of as a 2D surface in ambient 3D space (the qualification ‘mid-surface’ will not be used in all instances; it is hoped that the meaning will be clear from the context). Both the reference and deformed shells are parametrized by the same coordinate system \(((\xi ^{\alpha}), \alpha = 1,2)\) (convected coordinates). Points on the reference geometry are denoted generically by \({\boldsymbol {X}}\) and on the deformed geometry by \({\boldsymbol {x}}\). The reference unit normal is denoted by \({\boldsymbol {N}}\) and the unit normal on the deformed geometry by \({\boldsymbol {n}}\). A subscript comma refers to partial differentiation, e.g. \(\frac{\partial ()}{\partial \xi ^{\alpha}} = ()_{,\alpha}\). Summation over repeated indices will be assumed. The convected coordinate basis vectors in the reference geometry will be referred to by the symbols \(({\boldsymbol {E}}_{\alpha})\) and those in the deformed geometry by \(({\boldsymbol {e}}_{\alpha})\), \(\alpha =1,2\), with corresponding dual bases \(({\boldsymbol {E}}^{\alpha})\), \(({\boldsymbol {e}}^{\alpha})\), respectively. A suitable number of dots placed between two tensors represent the operation of contraction, while the symbol ⊗ will represent a tensor product. The deformation gradient will be denoted by \({\boldsymbol {f}}= {\boldsymbol {e}}_{\alpha }\otimes {\boldsymbol {E}}^{ \alpha}\) and admits the right polar decomposition \({\boldsymbol {f}}= {\boldsymbol {r}}\cdot {\boldsymbol {U}}\), where \({\boldsymbol {U}}({\boldsymbol {X}}): T_{{\boldsymbol {X}}}\to T_{{ \boldsymbol {X}}}\) and \({\boldsymbol {r}}({\boldsymbol {X}}): T_{{\boldsymbol {X}}}\to T_{{ \boldsymbol {x}}}\), where \(T_{{\boldsymbol {c}}}\) represents the tangent space of the shell at the point \({\boldsymbol {c}}\). The curvature tensor on the deformed shell is denoted as \({\boldsymbol {b}} = {\boldsymbol {n}}_{,\beta} \otimes {\boldsymbol {e}}^{\beta}\) and that on the undeformed shell as \({\boldsymbol {B}} = {\boldsymbol {N}}_{,\beta} \otimes {\boldsymbol {E}}^{\beta}\).
2 Some Measures of Pure Bending and Their Invariance Under Mid-Surface Scaling
In [1] three measures of bending strain were proposed, given by
Equation (1c) was unnumbered in that work, as the main emphasis was to obtain a nonlinear generalization of the Koiter-Sanders-Budiansky bending strain measure [2, 4]; \(\widetilde{{\boldsymbol {K}}}\) is introduced as Equation (8) and \(\check{{\boldsymbol {K}}}\) as Equation (10) in [1].
In [3] a physically natural requirement of invariance of bending strain measure under simple scalings of the form
is introduced (for plates, but the requirement is natural for shells as well) and it is shown that the measures \(\widetilde{{\boldsymbol {K}}}\), \(\check{{\boldsymbol {K}}}\) are not invariant under such a scaling. The measure \(\overline{{\boldsymbol {K}}}\) is not discussed in [3].
It is straightforward to see that under the said scaling, the deformation gradient scales as
resulting in the bending measures scaling as
Thus, the bending strain measure \(\overline{{\boldsymbol {K}}}\) from [1], not discussed by [3], is actually invariant under scaling deformations of the deformed shell mid-surface. Furthermore, the simple modifications of the measures \(\widetilde{{\boldsymbol {K}}}\), \(\check{{\boldsymbol {K}}}\) to
where
make them mid-surface scaling invariant.
Data Availability
No datasets were generated or analysed during the current study.
References
Acharya, A.: A nonlinear generalization of the Koiter–Sanders–Budiansky bending strain measure. Int. J. Solids Struct. 37(39), 5517–5528 (2000)
Budiansky, B., Sanders, J.L.: On the ‘Best’ first-order linear shell theory. In: Progress in Applied Mechanics (the Prager Anniversary Volume), pp. 129–140 (1963)
Ghiba, I.D., Bîrsan, M., Lewintan, P., Neff, P.: A constrained Cosserat shell model up to order \(O(h^{5})\): modelling, existence of minimizers, relations to classical shell models and scaling invariance of the bending tensor. J. Elast. 146(1), 83–141 (2021)
Koiter, W.T.: A consistent first approximation in the general theory of thin elastic shells. In: Proceedings of the IUTAM Symposium on the Theory of Thin Shells, pp. 12–33. North-Holland, Amsterdam (1960)
Virga, E.G.: Pure measures of bending for soft plates. Soft Matter 20(1), 144–151 (2024)
Vitral, E., Hanna, J.A.: Dilation-invariant bending of elastic plates, and broken symmetry in shells. J. Elast. 153(4–5), 571–579 (2023)
Funding
Open Access funding provided by Carnegie Mellon University.
Author information
Authors and Affiliations
Contributions
All contributions are those of the sole author.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Acharya, A. Mid-Surface Scaling Invariance of Some Bending Strain Measures. J Elast (2024). https://doi.org/10.1007/s10659-024-10066-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10659-024-10066-9