On the Averaging and Closure of Fiber Orientation Tensors in Virtual Process Chains

Abstract

Fiber orientation tensors (FOT) are widely used to approximate statistical orientation distributions of fibers within fiber-reinforced polymers. The design process of components made of such fiber-reinforced composites is usually accompanied by a virtual process chain. In this virtual process chain, process-induced FOT are computed in a flow simulation and transferred to the structural simulation. Within the structural simulation, effective macroscopic properties are identified based on the averaged information contained in the FOT. Solving the field equations in flow simulations as well as homogenization of effective stiffnesses necessitates the application of a closure scheme, computing higher-order statistical moments based on assumptions. Additionally, non-congruent spatial discretizations require an intermediate mapping operation. This mapping operation is required, if the discretization, i.e., mesh, of the flow simulation differs from the discretization of the structural simulation. The main objective of this work is to give an answer to the question: Does the sequence of closure and mapping influence the achieved results? It will turn out, that the order influences the result, raising the consecutive question: Which order is beneficial? Both questions are addressed by deriving a quantification of the closure-related uncertainty. The two possible sequences, mapping followed by closure and closure followed by mapping, yield strongly different results, with the magnitude of the deviation even exceeding the magnitude of a reference result. Graphical consideration reveals that for both transversely isotropic and planar FOT-input, invalid results occur if the mapping takes place prior to closure. This issue is retrieved by orientation averaging stiffness tensors. As a by-product, we explicitly define for the first time the admissible parameter space of orthotropic fourth-order fiber orientation tensors and define a distance measure in this parameter space.

1 Introduction

Discontinuous fiber-reinforced polymers (DiCoFRP) combine a high degree of design freedom with appealing mechanical properties. Consequently, this class of material is usually deployed within highly functionalized semi-structural components, such as housings or support structures. These parts are typically manufactured by compression molding (CM) or injection molding (IM). The flow process in these manufacturing processes, induces spatial variation of the local fiber orientation, i.e., the microstructure. The effective, macroscopic mechanical properties of the composite are primarily controlled by the underlying microstructure. As this microstructure is the result of the manufacturing process, local and effective stiffness, strength, etc. are mainly determined by the manufacturing process. To take account of this interaction of the process and the resulting microstructure during the design phase, process simulation and structural simulation are interlinked sequentially in a so-called computer aided engineering (CAE) chain. Several methodological and application-oriented contributions on CAE chains indicate the relevance of this approach for both continuous reinforced [1, 2] and discontinuous reinforced [3–5] composites.

In addition, CAE chains have been utilized to quantify the impact of process-induced uncertainties on structural behavior [6]. Feasible computation on the component level requires efficient numerical algorithms. For this reason, macroscopic material models are used within the structural simulation in free as well as commercial state-of-the-art solutions. The flow-induced orientation of the fibers is obtained during the flow simulation [7–9] and described by a spatial field of statistical fiber orientation tensors (FOT) [10, 11]. This field is mapped onto the structural simulation’s spatial discretization. If the identified fiber orientation tensors are of second-order only, closure approximations [7] are commonly used to derive fourth-order fiber orientation tensors, as effective mechanical properties are affected by fourth-order information on the fiber’s orientation [12]. The structural simulation is often limited to linear elasticity with spatially varying local stiffnesses [13–15]. These stiffnesses may be obtained by full field [16–18] or mean field [13–15, 19, 20] homogenization. The latter may follow a two-step approach [21–23], where in a first step, a transversely isotropic stiffness can be obtained by a homogenization method for aligned inclusions, such as Halpin-Tsai [24], Mori-Tanka [25] or Tandon-Weng [26]. In a second step, this stiffness is orientation-averaged based on the local pre-computed FOT from the process simulation.

Within this work, we focus on the mapping and closure of fiber orientation tensors within a virtual process chain. We raise the question: Which order of mapping and closure, i.e., mapping before closure or closure before mapping, is beneficial? Therefore, we study and quantify the difference of both options in terms of resulting fourth-order fiber orientation tensors. The quantification is based on the known variety of fourth-order fiber orientation tensors [12, 27], which for the orthotropic case is specified analytically for the first time. Consequences of the order of mapping and closure for effective linear elastic stiffnesses are demonstrated. We conclude that, if only the second-order fiber orientation tensor is obtained from a flow simulation within a virtual process chain, then the closure should be applied first based on the source discretization.

This paper is organized as follows. In Sect. 2, basic properties of fiber-orientation tensors and parametrizations are recapitulated. Subsequently, a measure for the uncertainty of closure approximations is introduced. In Sect. 3, we study the consequences of the order of mapping and closure and introduce an uncertainty quantification. Consistency of selected closure approximations is evaluated in Sect. 4, before implications for mechanical properties are shown demonstrated in Sect. 5.

1.1 Notation

Symbolic tensor notation is preferred throughout this work. Scalars are denoted by standard Latin and Greek letters, e.g., $a,\lambda , F$. First-order tensors are represented by bold lower case letters, e.g., ${\boldsymbol {p}}, {\boldsymbol {\gamma}}$, whereas upper case Greek or Latin letters are used for second-order tensors such as ${\boldsymbol {A}}, {\boldsymbol {E}}$. Fourth-order tensors are denoted by $\mathbb{C}, \mathbb{S}$. The composition of second and higher-order tensors, e.g., ${\boldsymbol {A}} {\boldsymbol {B}}$ is denoted without taking use of a particular operator symbol. In contrast, a linear mapping of an arbitrary lower order tensor by a corresponding higher order tensor is denoted using brackets, e.g., $\mathbb{C} \left [{\boldsymbol {E}}\right ]$. Scalar products between two tensors of the same order are marked by a dot, e.g., ${\boldsymbol {A}} \cdot {\boldsymbol {C}}$. The dyadic outer product yields a tensor of order $m+n$ from the multiplication of a $m$ by a $n$-order tensor, e.g., ${\boldsymbol {a}} \otimes {\boldsymbol {A}}$. The Frobenius norm $\sqrt{ {\boldsymbol {A}} \cdot {\boldsymbol {A}}}$ is used and abbreviated through $\Vert{\boldsymbol{A}} \Vert$. The rotation of an arbitrary order tensor is denoted by the Rayleigh product ${\boldsymbol {Q}} \star \mathbb{S}$, where the second-order tensor ${\boldsymbol {Q}}$ is member of the special orthogonal group $SO(3)$. The operator $\mathrm{sym}$ returns the weighted sum of all possible permutations (refer to [27, 28] for details). Tensor components in a Cartesian coordinate system, are denoted by indices, e.g., $a_{i} , A_{ij}$ where the number of indices corresponds to the tensor order and the range of the values indicates the dimension. Two types of indices must be distinguished. Iterators in a set of discrete values are denoted by upper case letters $I,J,\ldots \in \mathbb{N}$, whereas the indices of tensor components in the three-dimensional space are denoted by lower case letters $i,j,\ldots$ range from one to three. Unless otherwise indicated, Einstein’s convention for summation holds, thus indices appearing twice in a single expression imply summation.

2 Description of Fiber Orientation States

The scalar-valued fiber orientation distribution function (FODF)

$$ \psi : \mathcal{S}^{2} \mapsto \left [ 0; \infty \right ) $$

(1)

is defined as a mapping from the unit-sphere $\mathcal{S}^{2}$ to non-negative real numbers. The FODF quantifies the probability $P$ of finding fibers in a specific interval $\mathcal{I} \subseteq \mathcal{S}^{2}$ via integration

$$ P\left ( \mathcal{I} \right ) = \int _{\mathcal{I}} \psi \,\mathrm {d}S . $$

(2)

Following the work of Kanatani [10], FOTs of the first-kind are defined as statistical moments of the FODF. Hence, the $n$-th-order FOT ${\boldsymbol {A}}_{\langle n \rangle}$ is given by

$$ {\boldsymbol {A}}_{\langle n \rangle} = \int _{\mathcal{S}^{2}} \psi \left ( {\boldsymbol {n}} \right ) {\boldsymbol {n}}^{ \otimes n} \,\mathrm {d}S, $$

(3)

where ${\boldsymbol {n}}$ is a unit-vector and the operator $\left (\cdot \right )^{ \otimes n}$ represents the $n$-th time dyadic product. For the case of a finite number $N$ of equally weighted discrete fibers, Equation (3) reduces to

$$ {\boldsymbol {A}}_{\langle n \rangle} = \frac{1}{N} \sum _{I}^{N} {\boldsymbol {n}}^{ \otimes n}. $$

(4)

Demanding the FODF to be an even function $\psi \left ( {\boldsymbol {n}} \right ) = \psi \left ( - {\boldsymbol {n}} \right )$, it is obvious that all odd-order FOT vanish, while all even-order FOT are completely symmetric. Further, the $\left (n-2\right )^{\text{th}}$-order FOT is fully contained within the $n^{\text{th}}$-order FOT and can be obtained by a linear mapping of the second-order identity tensor ${\boldsymbol {I}}$ by

$$ {\boldsymbol {A}}_{\langle n - 2 \rangle} = {\boldsymbol {A}}_{\langle n \rangle} \left [ {\boldsymbol {I}} \right ]. $$

(5)

Advani and Tucker III [11] showed that the exact orientation-average of a $n^{\text{th}}$-order transversely isotropic tensor can be computed explicitly if the $n^{\text{th}}$-order FOT is known. They obtained an exact solution for Jeffery’s Equation [29] for an ellipsoidal inclusion in a fluid flow, yielding a transport Equation for the $n^{\text{th}}$-order FOT in space and time

$$ \frac {\partial {\boldsymbol {A}}_{\langle n \rangle} }{\partial t} + \frac {\partial {\boldsymbol {A}}_{\langle n \rangle} }{\partial {\boldsymbol {x}}}\left [ {\boldsymbol {u}} \right ] = {\boldsymbol {f}}_{\langle n \rangle}\left ( {\boldsymbol {A}}_{\langle n \rangle} , {\boldsymbol {A}}_{ \langle n + 2 \rangle}, \frac {\partial {\boldsymbol {u}}}{\partial {\boldsymbol {x}}}, \dots \right ), $$

(6)

with ${\boldsymbol {u}}$ representing the velocity field. Due to the rapidly increasing number of unknowns, Equation (6) is implemented almost exclusively for $n=2$ in available solvers. Hence, only second and fourth-order FOTs are regarded in Equation (6) and are denoted hereafter via ${\boldsymbol {A}}$ and $\mathbb{A}$ respectively. The normalization condition of the FODF implies that the trace of the second-order FOT is equal to one, i.e.,

$$ {\mathrm{tr }}\left ( {\boldsymbol{A}} \right ) = 1 $$

(7)

holds. The set of all admissible fourth-order FOT in dimensions two and three may be obtained by completely symmetric tensors of fourth order which eigenvalues are non-negative and sum to one [12, 27].

2.1 Parameterization of Fiber Orientation Tensors

The normalization constraint in Equation (7) implies $\sum _{i}^{3} \lambda _{i} = 1$ for each FOT of second-order with eigenvalues $\lambda _{i}$. In consequence, a two-parameter representation of the rotation-invariant shape is given by the non-orthogonal decomposition

$$ {\boldsymbol {A}}\left ( \alpha _{1}, \alpha _{3} \right ) = {\boldsymbol {A}}^{\text{iso}} + \alpha _{1} \begin{pmatrix} 1 & & \\ & -\frac{1}{2} & \\ & & -\frac{1}{2} \end{pmatrix} {\boldsymbol {v}}_{i} \otimes {\boldsymbol {v}}_{j} + \alpha _{3} \begin{pmatrix} -\frac{1}{2} & & \\ & -\frac{1}{2} & \\ & & 1 \end{pmatrix} {\boldsymbol {v}}_{i} \otimes {\boldsymbol {v}}_{j} $$

(8)

following Bauer and Böhlke [27]. An orthogonal basis transformation ${\boldsymbol {Q}} \in SO(3)$ of a fixed global basis $\lbrace {\boldsymbol {e}}_{i} \rbrace$ yields the right-handed orientation coordinate system (OCS) $\lbrace {\boldsymbol {v}}_{i} \rbrace$, such that ${\boldsymbol {Q}} = {\boldsymbol {v}}_{i} \otimes {\boldsymbol {e}}_{i}$ holds [27]. Even in the absence of any material symmetry [30], the OCS is not unique, as the indispensable orthotropy of a second-order tensor induces an ambiguity of the sign of pairs of the eigenvectors ${\boldsymbol {v}}_{i}$. However, any choice of the eigensystem is suitable and only effects ${\boldsymbol {Q}}$. Admissible second-order FOT are strictly positive semidefinite, restricting the ranges of $\alpha _{1} , \alpha _{3}$. The set $\mathcal{N}^{\text{com}}$ comprises all pairwise commuting FOT of second-order and is defined by

$$\begin{aligned} \mathcal{N}^{\text{com}} = \bigl\{ & -2/3 \leq \alpha _{1} \leq 2/3, \\ & -1/3 + 1/2\alpha _{1} \leq \alpha _{3} \leq 2/3 + 2\alpha _{1} \wedge 2/3 - \alpha _{1} \bigr\} . \end{aligned}$$

(9)

Two tensors ${\boldsymbol {A}}_{1}$ and ${\boldsymbol {A}}_{2}$ commute, if

$$ {\boldsymbol {A}}_{1} \, {\boldsymbol {A}}_{2} = {\boldsymbol {A}}_{2} \, {\boldsymbol {A}}_{1}\ $$

(10)

holds. Hence, ${\boldsymbol {A}}_{1}$ and ${\boldsymbol {A}}_{2}$ share an equivalent set of eigenvectors. The set $\mathcal{N}^{\text{com}}$ is visualized in Fig. 1. The classical orientation triangle [31], imposing descending order of the eigenvalues, may be represented based on the parameterization (8) by $0\leq \alpha _{1} \leq 2/3, \,\alpha _{1} - 1/3 \leq \alpha _{3} \leq 0$ defining a subspace of $\mathcal{N}^{\text{com}}$ [27].

Fig. 1

Visualization of $\mathcal{N}^{\text{com}}$ adapted from [27]

Based upon harmonic decomposition [30, 32], Bauer and Böhlke [27] derive a parameterization of a generic fourth-order FOT $\mathbb{A}$ containing a constant isotropic part $\mathbb{A}^{\text{iso}}$, a deviatoric distribution being linear in the second-order FOT ${\boldsymbol {A}}$ and the remaining deviatoric harmonic tensor $\mathbb{F}$ with

$$ \mathbb{A} = \mathbb{A}^{\text{iso}} + \frac{6}{7}\mathrm{sym}\left ( {\boldsymbol {A}}^{\prime }\otimes {\boldsymbol {I}} \right ) + \mathbb{F}. $$

(11)

The constant isotropic tensor is $\mathbb{A}^{\text{iso}} = 7/35 \, \mathrm{sym}\left ( {\boldsymbol {I}} \otimes {\boldsymbol {I}} \right )$. The fourth-order deviator $\mathbb{F}$ has nine degrees of freedom and following Bauer and Böhlke [27] might be defined by the tensor coefficient representation

within an ortho-normal Kelvin-Mandel-basis ${\boldsymbol {B}}_{\xi}^{{\boldsymbol {v}}}$ with $\xi =1..6$ spanned by the OCS of the corresponding second-order FOT. Material symmetry constraints have simple representations within the OCS-based parameterization (11). An orthotropic fourth-order FOT is characterized by vanishing coefficients $d_{4}$ to $d_{9}$, i.e.,

$$ \mathbb{F}^{\text{ortho}}\left (d_{1}, d_{2}, d_{3}\right ) = \mathbb{F}\left (d_{1}, d_{2}, d_{3}, 0,0,0,0,0 \right ). $$

(13)

2.2 Closure Approximations for Fiber Orientation Tensors

Closure algorithms based on second-order fiber orientation tensors are frequently used to solve at least two problems. The first problem is solving the transport problem of flowing fibers in Equation (6) defining the spatial and temporal evolution of a given initial field of fiber orientation tensors. The second problem is averaging a transversely isotropic mechanical stiffness with the Advani-Tucker [11] orientation average, if only second-order FOT information is available. A closure approximation $\mathcal{C}$ is a mapping $\mathbb{A} = \mathcal{C}\left ( {\boldsymbol {A}} \right )$ which associates any second-order FOT with exactly one fourth-order FOT. Research has brought forth a large variety of closure approximations. These include early work by Advani and Tucker III [7], Cintra Jr and Tucker III [31], Hand [33], De Frahan et al. [34] as well as significant extensions by Han and Im [35], Chung and Kwon [36,37] and more recent findings [38–41]. Fourth-order FOT obtained by closure approximations should fulfill several requirements. The obtained tensor $\mathbb{A}$ should contract to the second-order FOT ${\boldsymbol {A}}$ it has been obtained for, have full index symmetry, reflect the material symmetry of ${\boldsymbol {A}}$, and be positive semidefinite, meaning all eigenvalues of $\mathbb{A}$ have to be strictly non-negative. The linear closure (LC) [33] and quadratic closure (QC) [11] as well as the hybrid closure (HC) [35] are widely applied due to their simplicity. The formulae are given through

$$\begin{aligned} \mathcal{C}_{\text{LC}}\left ( {\boldsymbol {A}} \right ) = \mathbb{A}^{ \text{iso}} + \frac{6}{7}\mathrm{sym}\left ( {\boldsymbol {A}}^{\prime }\otimes {\boldsymbol {I}} \right ), \end{aligned}$$

(14)

$$\begin{aligned} \mathcal{C}_{\text{QC}}\left ( {\boldsymbol {A}} \right ) = {\boldsymbol {A}} \otimes {\boldsymbol {A}}, \end{aligned}$$

(15)

$$\begin{aligned} \mathcal{C}_{\text{HC}}\left ( {\boldsymbol {A}} \right ) = 27 \, {\mathrm{det }} \left ( {\boldsymbol{A}} \right ) \mathcal{C}_{\text{LC}}\left ( {\boldsymbol {A}} \right ) + (1 - 27\, {\mathrm{det }}\left ( {\boldsymbol{A}} \right )) \mathcal{C}_{\text{QC}}\left ( {\boldsymbol {A}} \right ). \end{aligned}$$

(16)

More physically-consistent, but computationally more expensive, closure approximations are, e.g., the invariant-based optimal fitting closure (IBOF) [37] or orthotropic fitted closure (OFC) [31, 36]. Additionally, closure approaches taking the flow field information into account such as the so-called exact closure [38] or natural closure [34] have been proposed and extended in recent years. For comprehensive overviews and investigations of available closure approximations, the reader is referred to [42]. Most closure methods are constructed to yield orthotropic fourth-order FOT, thus describing the coefficients $d_{1}, d_{2}, d_{3}$ in Equation (12) as functions of $\alpha _{1}$ and $\alpha _{3}$. In addition to the aforementioned direct closure methods, FODF $\psi$ reconstruction methods can be used to post-compute the $\text{fourth}$-order FOT according to Equation (3). A noteworthy candidate can be found in Shannon’s [43] maximum entropy method (MEP) estimating the FODF based on the second-order FOT ${\boldsymbol {A}}$, which can therefore be regarded as indirect closure approximation [14, 44].

2.3 Margin of Closure Uncertainty

While $\mathbb{A}^{\text{iso}}$ is constant and ${\boldsymbol {A}}^{\prime }$ is unambiguously given by the associated second-order FOT ${\boldsymbol {A}}$, the residual deviatoric tensor $\mathbb{F}$ in Equation (11) maps the identity tensor ${\boldsymbol {I}}$ onto the null-space $\mathbb{F} \left [ {\boldsymbol {I}} \right ] = {\boldsymbol {0}}$. In consequence, $\mathbb{F}$ must be constructed on the basis of assumptions when a closure operation is applied. Since only orthotropic closure schemes will be considered in the following investigations, $\mathbb{F}$ is assumed to possess this material symmetry. Note that the variety of valid $\mathbb{F}$ depends on ${\boldsymbol {A}}$ itself. The set of admissible orthotropic fourth-order FOT $\mathcal{N}^{\text{ortho}}$ is obtained by demanding positive semidefiniteness [12, 27]. Bauer and Böhlke [27] graphically presented the variety of orthotropic fourth-order FOT and gave an explicit expression for those orthotropic fourth-order FOT which contract to an isotropic second-order FOT. However, to the authors’ best knowledge an explicit algebraic expression for the complete space of $\mathcal{N}^{\text{ortho}}$ is not given in literature, yet. This gap is closed by the contributions of this work, as an explicit expression and a brief derivation of all admissible orthotropic fourth-order FOT is given in Appendix A.

Having identified the limits of admissible fourth-order information potentially identified by orthotropic closure approximations, scalar measurements for the uncertainty can be formulated. For this work, we propose a strictly-positive margin quantity $\left \Vert \Delta \mathbb{F}^{\text{ortho}}_{\text{max}} \right \Vert$ defined as

$$ \left \Vert \Delta \mathbb{F}^{\text{ortho}}_{\text{max}} \right \Vert \left ({\boldsymbol {A}}\right ) =\max _{\mathbb{A}_{1} , \mathbb{A}_{2}\, \in \left . \mathcal{N}^{\text{ortho}}\right |_{{\boldsymbol {A}}}} \left \Vert \mathbb{A}_{1} - \mathbb{A}_{2} \right \Vert . $$

(17)

A derivation of the explicit expression for $\left \Vert \Delta \mathbb{F}^{\text{ortho}}_{\text{max}}\right \Vert$ is given in Appendix A. The definition allows the comparison of fourth-order deviators of dimensions two and three in the orthogonal space spanned by $\{ d_{1}, d_{2}, d_{3} \}$. Additionally, this measure is invariant under any permutations of the basis vectors of the OSC. The graph of $\left \Vert \Delta \mathbb{F}^{\text{ortho}}_{\text{max}} \right \Vert$ over the orientation triangle is given in Fig. 2. In loose terms the value of the measure $\left \Vert \Delta \mathbb{F}^{\text{ortho}}_{\text{max}} \right \Vert$ at given ${\boldsymbol {A}}$ indicates how many candidates $\mathbb{A}$ exist that contract to this very FOT of second-order. The course of $\left \Vert \Delta \mathbb{F}^{\text{ortho}}_{\text{max}} \right \Vert$ is monotonic along the edges with a global maximum at the planar isotropic state (⊕-marker) and a global minimum of zero for the unidirectional state (⊙-marker). The latter is plausible since a unidirectional FODF and therefore all its higher-order moments are completely described by ${\boldsymbol {A}}^{\text{UD}}$. Along the transversely isotropic line (depicted in blue) the isotropic state at $\lambda _{1}=\lambda _{2}=1/3$ (sphere-shaped marker) represents an inflection point.

Fig. 2

Margin of orthotropic uncertainty $\left \Vert \Delta \mathbb{F}^{\text{ortho}}_{\text{max}} \right \Vert$ as a function of the second-order FOT’s eigenvalues $\lambda _{1}, \lambda _{2}$

2.4 Mapping of Fiber Orientation Tensors

Within a virtual process chain, the transfer of data from one discretization to another is a common task. An example is given by the transfer of FOT data from a flow simulation to a consecutive structural simulation. Consider two non-congruent discretizations of solution domains, e.g., unstructured meshes. A mapping operation is carried out to compute data on a target discretization $\left ( \cdot \right )^{\left (\text{Tgt}\right )}_{I}$ based on data given at specific points of a source discretization $\left ( \cdot \right )^{\left (\text{Src}\right )}$. The data both on the target and the source discretization might be associated with specific locations (nodes, integration points, …) or specific subdomains (elements). FOT data is assumed to be an intensive state function. Thus, the subdomain-rule for integration can be applied to compute the mean value

$$ \left ( \cdot \right )^{\left (\text{Tgt}\right )}_{I} = \frac{1}{\left | \Omega ^{\left (\text{Tgt}\right )}_{I} \right |} \int _{\Omega ^{\left (\text{Tgt}\right )}_{I}} \left ( \cdot \right ) \,\mathrm {d}\Omega $$

(18)

of the $I$-th subvolume of the target discretization, based on a sum of the intersections of all $N$ sub-volumes $\Omega _{J}^{\left (\text{Src}\right )}$ of the source discretization which intersect with the target sub-volume $\Omega _{I}^{\left (\text{Tgt}\right )}$ of interest by

$$ \left ( \cdot \right )^{\left (\text{Tgt}\right )}_{I} \approx \frac{1}{\left | \Omega ^{\left (\text{Tgt}\right )}_{I} \right |} \sum _{J} \int _{\Omega ^{\left (\text{Src}\right )}_{J} \cap \Omega ^{ \left (\text{Tgt}\right )}_{I}} \left ( \cdot \right )^{\left ( \text{Src}\right )}\,\mathrm {d}\Omega . $$

(19)

The size of a subvolume in Equation (19) is depicted by $\left | \Omega \right | = \int _{\Omega }1 \,\mathrm {d}\Omega$ and the procedure is visualized in Fig. 3. Assuming the FOT to be piece-wise constant within each subdomain $\Omega _{J}$, Equation (19) simplifies to

$$ \left ( \cdot \right )^{\left (\text{Tgt}\right )}_{I} = \sum _{J} \underbrace{\frac{\left | \Omega ^{\left (\text{Tgt}\right )}_{I} \cap \Omega ^{\left (\text{Src}\right )}_{J} \right |}{\left | \Omega ^{\left (\text{Tgt}\right )}_{I} \right |}}_{:=w_{J}} \left ( \cdot \right )^{\left (\text{Src}\right )}_{J}. $$

(20)

Based on the introduced assumptions, a specific Euclidean mapping is used hereinafter. The generally unknown FODFs on the target subdomains $\Omega ^{\left (\text{Tgt}\right )}_{I}$ compute to

$$ \psi _{I}^{\left (\text{Tgt}\right )}= \sum _{J} w_{J} \psi _{J}^{\left (\text{Src}\right )}. $$

(21)

The linearity of Eqn. (21) justifies to apply the average scheme directly to all FOTs of order $n$ since

$$ {\boldsymbol {A}}_{\langle n \rangle , I}^{\left (\text{Tgt}\right )}= \int _{\mathcal{S}^{2}} \psi _{I}^{\left (\text{Tgt}\right )}{\boldsymbol {n}}^{\otimes n} \, \,\mathrm {d}S = \sum _{J} w_{J} \int _{\mathcal{S}^{2}} \psi _{J}^{\left (\text{Src}\right )}{\boldsymbol {n}}^{\otimes n} \, \,\mathrm {d}S = \sum _{J} w_{J} {\boldsymbol {A}}_{\langle n \rangle , J}^{\left (\text{Src}\right )}. $$

(22)

Fig. 3

Graphical illustration of the subdomain approach. The target domain $\Omega ^{\left (\text{Tgt}\right )}_{1}$ is subdivided into the subdomains $\Omega ^{\left (\text{Src}\right )}_{J} \cap \Omega ^{\left ( \text{Tgt}\right )}_{1}$ $J=1,2,3$

Thus, the tensor coefficients of the second and fourth-order FOT in a global ortho-normal basis $\left \{{\boldsymbol {e}}_{i}\right \}$ read

$$ \begin{aligned} &A^{\left (\text{Tgt}\right )}_{I, ij} {\boldsymbol {e}}_{i} \otimes {\boldsymbol {e}}_{j} = \sum _{J} w_{J} A^{\left (\text{Src}\right )}_{J, ij} {\boldsymbol {e}}_{i} \otimes {\boldsymbol {e}}_{j}, \\ &A^{\left (\text{Tgt}\right )}_{I, ijkl} {\boldsymbol {e}}_{i} \otimes {\boldsymbol {e}}_{j} \otimes {\boldsymbol {e}}_{k} \otimes {\boldsymbol {e}}_{l} = \sum _{J} w_{J} A^{\left ( \text{Src}\right )}_{J, ijkl} {\boldsymbol {e}}_{i} \otimes {\boldsymbol {e}}_{j} \otimes {\boldsymbol {e}}_{k} \otimes {\boldsymbol {e}}_{l}. \end{aligned} $$

(23)

Throughout this work, we assume the FOT field to be defined over the entire spatial target domain. Therefore, effective values can be determined by averaging following Equation (23). In contrast to this averaging operation, interpolation techniques [45] are intended to increase the resolution of discrete spatial fields. Consequently, interpolation plays an important role if the source field is obtained experimentally or numerically in terms of discrete point data with limited resolution [46].

3 Differences Between Fourth-Order Average and Second-Order Average

Most virtual process chains for discontinuous fiber-reinforced plastics (DiCoFRP) contain both a FOT-closure operation and a FOT-mapping operation. With respect to the ordering of these operations, two routes are possible, either the closure is followed by the mapping or vice versa. Based on those routes the fourth-order average and second-order average of a fourth-order FOT are introduced. An evaluation of the range of deviations between those averages is conducted and accompanied by the comparison of the corresponding tensor glyphs.

3.1 Problem Definition

Usually, at the interface between process simulation and structural simulation, three operations or steps have to be distinguished:

• Closure of available second-order FOTs in order to obtain corresponding fourth-order tensors using a generic closure scheme $\mathcal{C}$.

• Mapping of available data from source (Src) to target (Tgt) discretization utilizing a generic averaging scheme ℱ.

• Homogenization and orientation averaging to receive effective macroscopic properties.

While the homogenization is naturally performed as part of the structural simulation module, either as pre-processing operation or during solver runtime, the order of FOT closure and mapping is arbitrary at first glance. Hence, two conceivable routes remain, which are depicted in Fig. 4. Starting from second-order FOT ${\boldsymbol {A}}^{\left (\text{Src}\right )}_{I}$ on the source discretization (light blue rectangles), the upper row corresponds to the “closing first” method. Herein, the individual fourth-order tensors $\mathbb{N}^{\left (\text{Src}\right )}_{I}$ are computed using a generic closure technique $\mathcal{C}$. Each closure yields an individual margin of uncertainty $\mathbb{F}^{\left (\text{Src}\right )}_{I}$, which depends on the underlying lower-order tensor ${\boldsymbol {A}}^{\left (\text{Src}\right )}_{I}$ and is symbolized through the semi-opaque gray annuli. Subsequently, the results are mapped onto the target discretization (light green rectangles) utilizing a generic mapping technique ℱ. The resulting fourth-order $\bar{\mathbb{A}}^{\left (\text{Tgt}\right )}_{\text{av4, }I}$ tensor is referred to as fourth-order average. Contrary to this, the lower row of Fig. 4 illustrates the alternative approach, called “mapping first”. Firstly, the second-order FOT are mapped yielding an averaged measure $\bar{{\boldsymbol {A}}}^{\left (\text{Tgt}\right )}_{I}$. Afterwards, on the target mesh, the closure operation is applied yielding the second-order average $\bar{\mathbb{A}}^{\left (\text{Tgt}\right )}_{\text{av2 }, I}$ with its individual level of uncertainty.

Fig. 4

Possible routes in virtual process chains. The “closing first” approach is depicted in the upper row. The bottom row corresponds to the “mapping first” approach

A brief overview of available commercial and academic methodologies reveals, that all approaches follow the “mapping first” route and perform FOT-closure on the target discretization after mapping takes place (cf. Table 1). This order appears to be the logical choice in terms of simplicity, since the number of necessary information drastically increases with the tensor order. The tensor characteristics can be expressed by 5 for second- and 14 independent scalars for fourth-order FOT, respectively [27]. However, more commonly used storage of coefficients concerning a global basis using the Voigt or Mandel notation requires 6, respectively 21 scalars per tensor [54], if algorithms are not optimized for symmetry. Another evident argument might be the mapping to be less computationally expensive when applied to second-order tensors.

Table 1 Literature review of CAE-chains, corresponding manufacturing process and order of closure and mapping. In each case the authors decide to follow the “mapping first”-approach, i.e., map second-order FOT and conduct the closure on the target mesh

In the following sections, we consider the problem depicted in Fig. 4. Results on two source domains $\Omega _{I}^{\left (\text{Src}\right )}, \, I=1, 2$ of identical size are mapped onto the target domain $\Omega ^{\left (\text{Tgt}\right )}= \Omega _{1}^{\left (\text{Src} \right )}\cap \Omega _{2}^{\left (\text{Src}\right )}$, yielding a single value. This minimal example covers the main features of applications within real simulation chains, where the number of elements can quickly reach six digits. With the averaging method defined in Equation (19), the fourth-order average $\bar{\mathbb{A}}^{\text{av4}}$ and the second-order average $\bar{\mathbb{A}}^{\text{av2}}$ are obtained by

$$ \begin{aligned} \bar{{\boldsymbol {A}}} &:= {\boldsymbol {A}}^{\left (\text{Tgt}\right )}= \frac{1}{2}\left ( {\boldsymbol {A}}_{1}^{\left (\text{Src}\right )}+ {\boldsymbol {A}}_{2}^{ \left (\text{Src}\right )}\right ), \\ \bar{\mathbb{A}}^{\text{av2}} &:= \bar{\mathbb{A}}^{\left (\text{Tgt} \right )}_{\text{av2}} = \mathcal{C}\left ( \bar{{\boldsymbol {A}}} \right ), \\ \bar{\mathbb{A}}^{\text{av4}} &:= \bar{\mathbb{A}}^{\left (\text{Tgt} \right )}_{\text{av4}} = \frac{1}{2}\left ( \mathcal{C}\left ({\boldsymbol {A}}_{1}^{ \left (\text{Src}\right )}\right ) + \mathcal{C}\left ({\boldsymbol {A}}_{2}^{ \left (\text{Src}\right )}\right ) \right ). \end{aligned} $$

(24)

A relative measure of deviation is introduced via

$$ \|\Delta \mathbb{A}\|_{\text{rel}} := \dfrac{\|\bar{\mathbb{A}}^{\mathrm{av4}} - \bar{\mathbb{A}}^{\mathrm{av2}} \|}{\| \mathbb{A}^{\text{iso}} \|} \quad \text{with } \| \mathbb{A}^{\text{iso}} \| = \frac{\sqrt{5}}{5}. $$

(25)

We visualize FOT in terms of a tensor glyph. A parametric representation of this glyph is obtained by the FOT’s projection on the unit-triad

$$ {\boldsymbol {a}}\left ({\boldsymbol {n}}\right ) = \mathbb{A} \left [{\boldsymbol {n}}^{\otimes 3} \right ] \quad {\boldsymbol {n}} \in \mathcal{S}^{2}. $$

(26)

3.2 Averaging Commuting Fiber Orientation Tensors

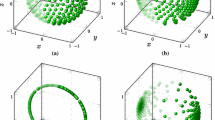
We investigate the problem depicted in Fig. 4 with the first source FOT ${\boldsymbol {A}}^{\left (\text{Src}\right )}_{1}$ being fixed to either full isotropy, planar isotropy or unidirectionality, and the second source FOT ${\boldsymbol {A}}^{\left (\text{Src}\right )}_{2}(\alpha _{1}, \alpha _{3})$ taking arbitrary values within the set of commuting second-order FOT $\mathcal{N}^{\text{com}}$, i.e., being a function of $\alpha _{1}$ and $\alpha _{3}$. We consider the quadratic, hybrid and IBOF closure approximations. For each of those closures combined with every FOT defined by the tuple $(\alpha _{1}, \alpha _{3})$, we calculate the deviation of second-order and fourth-order average following Equations (25) and (24). The results of the numerical experiments are depicted in Fig. 5 as contour courses of $\Delta \| \mathbb{A}\|_{\text{rel}}$ over the admissible range of $( \alpha _{1}, \alpha _{3} )$, which is indicated by the black dashed lines in each subplot.

Fig. 5

Contours of the relative deviation between second-order average $\bar{\mathbb{A}}^{\text{av2}}$ and fourth-order average $\bar{\mathbb{A}}^{\text{av4}}$ over the admissible range of commuting second-order FOT $\mathcal{N}^{\text{com}}$

We draw two conclusions from Fig. 5: Firstly, the co-domain of deviations is remarkably large, ranging from zero to one between two unidirectional states in Fig. 5 (right column). Secondly, for all references the IBOF closure (upper row) yields the lowest deviations $\Delta \| \mathbb{A}\|_{\text{rel}}$. The left column in Fig. 5 shows the case of isotropic reference tensor. For each of the three closures considered, the maxima are located at the three edges of the triangles representing unidirectional states with differing principal axis. Both, quadratic closure (middle row) and IBOF closure (upper row) appear to increase monotonically with increasing separation from the reference FOT ${\boldsymbol {A}}^{\text{iso}}$. The local minima are located on the transversely isotropic lines connecting isotropic and planar isotropic states. In contrast, the hybrid closure (lower row) exhibits significant non-monotonic behavior, which can be visualized best on the planar edges with local maxima at the planar isotropic states. The same observation is discovered, if the reference tensor is fixed at a planar isotropic state (cf. Fig. 5 (middle column)). Here the global maxima are found at the opposing unidirectional state, e.g., if ${\boldsymbol {A}}_{\text{ref}} = \frac{1}{2}\left ( {\boldsymbol {v}}_{1} \otimes {\boldsymbol {v}}_{1} + {\boldsymbol {v}}_{2} \otimes {\boldsymbol {v}}_{2} \right )$, the relative deviation $\Delta \| \mathbb{A}\|_{\text{rel}}$ becomes maximal at ${\boldsymbol {v}}_{3} \otimes {\boldsymbol {v}}_{3}$. Fig. 5 (right column) depicts the results for a unidirectional reference FOT. Analogous to both previously discussed cases, $\Delta \| \mathbb{A}\|_{\text{rel}}$ positively correlates with increasing distance to the reference state with maxima recurring at the opposing unidirectional state. The relative variance between hybrid and quadratic closure is low. To give an example of the influence of the tensor shape, respectively anisotropy, tensor glyphs for the edge-case of two unidirectional second-order FOT with different principal axis ${\boldsymbol {p}}$ are studied in Fig. 6. The second-order volume average ${\boldsymbol {\bar{A}}} = \frac{1}{2} \left ( {\boldsymbol {v}}_{1}^{\otimes 2} + {\boldsymbol {v}}_{ 2}^{\otimes 2} \right )$ yields planar isotropic FOT, which outputs a planar isotropic fourth-order average when processed by a closure method. This behavior is visualized by means of the top row in Fig. 6 leading to disc-shaped tensor glyphs. The different diameters are due to the quadratic and hybrid closure violating the normalization condition $\mathbb{I}^{\text{S}} \cdot \mathbb{A} = 1$, which is a known drawback [40]. In contrast, all closure schemes considered yield unidirectional FOT of fourth order $\mathcal{C}\left ( {\boldsymbol {p}}^{\otimes 2} \right ) = {\boldsymbol {p}}^{\otimes 4}$. Thus, the fourth-order average $\bar{\mathbb{A}}^{\text{av4}}$ computes to $\frac{1}{2}\left ( {\boldsymbol {v}}_{1}^{\otimes 4} + {\boldsymbol {v}}_{2}^{\otimes 4} \right )$ preserving structural information. The corresponding tensor glyphs in the bottom row of Fig. 6 exhibit two distinct maxima in the original unidirectional directions ${\boldsymbol {v}}_{1}$ and ${\boldsymbol {v}}_{2}$.

Fig. 6

Tensor glyphs for resulting $\bar{\mathbb{A}}$ candidates with ${\boldsymbol {A}}_{1} = {\boldsymbol {v}}_{1} \otimes {\boldsymbol {v}}_{1}$, ${\boldsymbol {A}}_{2} = {\boldsymbol {v}}_{2} \otimes {\boldsymbol {v}}_{2}$. The dashed lines indicate the planes of symmetry

4 Consistency of Closure Schemes

The previous studies have revealed notable differences between second-order and fourth-order averages. Section 4.1 proves that the second-order average may yield mathematically and physically inconsistent results within the subspace of commuting transversely isotropic FOT. In Sect. 4.2, we study the subspace of commuting planar FOT.

For the following examples, we define a valid average fourth-order tensor as a special case of Eqn. (21) through the following theorem:

Theorem 4.1

Given two second-order FOT ${\boldsymbol {A}}_{1}$ and ${\boldsymbol {A}}_{2}$ and corresponding weights $w_{1} \in \left [ 0, 1 \right ],\, w_{2} = 1-w_{1}$, an averaged fourth-order FOT $\bar{\mathbb{A}}$ is only valid, if it could be constructed from some FODF $\bar{\psi} = w_{1} \psi _{1} + w_{2} \psi _{2}$ via $\bar{\mathbb{A}} = \int _{\mathcal{S}^{2}} \bar{\psi} \,{\boldsymbol {n}}^{\otimes 4}\, \,\mathrm {d}S$, with ${\boldsymbol {A}}_{1} = \int _{\mathcal{S}^{2}} \psi _{1} \, {\boldsymbol {n}}^{\otimes 2}\, \,\mathrm {d}S$ and ${\boldsymbol {A}}_{2} = \int _{\mathcal{S}^{2}} \psi _{2} \, {\boldsymbol {n}}^{\otimes 2}\, \,\mathrm {d}S$.

4.1 Transversely Isotropic Fiber Orientation Distributions

In this section, we focus on transversely isotropic FODF which represent a subspace of all possible FODF. A transversely isotropic FODF $\psi \left ( {\boldsymbol {n}} \right )$ is isotropic within each plane perpendicular to a distinct axis ${\boldsymbol {v}}_{1}$, i.e., $\psi \left ( {\boldsymbol {v_{\perp}}} \right ) = \psi _{\perp}$ holds with constant value $\psi _{\perp}$ for all directions ${\boldsymbol {v}}_{\perp}$ with ${\boldsymbol {v}}_{\perp }\cdot {\boldsymbol {v}}_{1} = 0$. The second and fourth-order moments can be parameterized following [14, 27] by

$$ {\boldsymbol {A}}^{\text{tv}} \left ( \alpha \right ) = \int _{\mathcal{S}^{2}} \psi \left ( {\boldsymbol {n}}\right ) {\boldsymbol {n}}^{\otimes 2} \, \,\mathrm {d}S = {\boldsymbol {A}}^{ \text{iso}} + \alpha \, {\boldsymbol {F}}^{\text{tv}}, $$

(27)

$$ \mathbb{A}^{\text{tv}}\left (\alpha , \rho \right ) = \int _{ \mathcal{S}^{2}} \psi \left ( {\boldsymbol {n}}\right ) {\boldsymbol {n}}^{\otimes 4} \, \,\mathrm {d}S = \mathbb{A}^{\text{iso}} + \alpha \, \mathrm{sym} \left ( {\boldsymbol {F}}^{ \text{tv}} \otimes {\boldsymbol {I}} \right ) + \rho \, \mathbb{F}^{\text{tv}} $$

(28)

with the second-order structure tensor ${\boldsymbol {F}}^{\text{tv}} = {\boldsymbol {v}}_{1} \otimes {\boldsymbol {v}}_{1} - 1/2 \left ( {\boldsymbol {v}}_{2} \otimes {\boldsymbol {v}}_{2} + {\boldsymbol {v}}_{3} \otimes {\boldsymbol {v}}_{3} \right )$ and the irreducible fourth-order structure tensor $\mathbb{F}^{\text{tv}} = \mathbb{F}^{\text{ortho}}\left ( d_{1}=d_{2}=-4, d_{3}=1 \right )$. The convex set $\mathcal{N}^{\text{tv}}$ is defined as the unity of all positive semidefinite transversely isotropic FOT and gives bounds to the linear coefficients $\alpha$ and $\rho$ [55] by

$$ \mathcal{N}^{\text{tv}} = \Bigl\{ \mathbb{A}^{\text{tv}}\left (\alpha , \rho \right ) \Big| -\frac{1}{3} \leq \alpha \leq \frac{2}{3}, \quad \rho _{\text{min}}\left (\alpha \right ) \leq \rho \leq \rho _{ \text{max}}\left (\alpha \right ) \Bigr\} $$

(29)

with

$$ \rho _{\text{min}}\left (\alpha \right ) = \frac{1}{8}\alpha ^{2} - \frac{1}{42} \alpha - \frac{1}{90}, \quad \rho _{\text{max}}\left ( \alpha \right ) = \frac{1}{56} \alpha + \frac{1}{60}. $$

(30)

If, and only if, two transversely isotropic ${\boldsymbol {A}}$ commute, the deviatoric distributors ${\boldsymbol {F}}^{\text{tv}}$ and $\mathbb{F}^{\text{tv}}$ are constant. Taking the volume average $\bar{\mathbb{A}}$ of two commuting transversely isotropic fourth-order FOT reduces to averaging the parameters $\alpha$ and $\rho$, i.e.,

$$ \bar{\mathbb{A}} = \frac{1}{V} \int _{v} \mathbb{A} \, \,\mathrm {d}v = \mathbb{A}^{\text{iso}} + \frac{1}{V} \int _{v} \alpha \, \,\mathrm {d}v \, \frac{6}{7}\mathrm{sym}\left ( {\boldsymbol {F}}^{\text{tv}} \otimes {\boldsymbol {I}} \right ) + \frac{1}{V} \int _{v} \rho \, \,\mathrm {d}v \, \mathbb{F}^{ \text{tv}} $$

(31)

for the continuous, and

$$ \bar{\mathbb{A}} = \sum _{I} c_{I} \mathbb{A}_{I} = \mathbb{A}^{ \text{iso}} + \underbrace{\sum _{I} c_{I} \alpha _{I}}_{:= \bar{\alpha}} \, \frac{6}{7}\mathrm{sym}\left ( {\boldsymbol {F}}^{\text{tv}} \otimes {\boldsymbol {I}} \right ) + \underbrace{\sum _{I} c_{I} \rho _{I} }_{:= \bar{\rho}} \mathbb{F}^{\text{tv}} $$

(32)

for the subdomain-wise constant case, respectively. The volume fractions $c_{I}$ sum up to one. As a direct consequence, the compact representation of the two closure-related $\text{fourth}$-order candidates, fourth-order average and second-order average, follows as

$$\begin{aligned} \bar{\mathbb{A}}^{\text{av4}} & = \mathbb{A}^{\text{iso}} + \bar{\alpha} \frac{6}{7}\mathrm{sym}\left ( {\boldsymbol {F}}^{\text{tv}} \otimes {\boldsymbol {I}} \right ) + \underbrace{\sum _{I} c_{I} \rho _{\mathcal{C}}\left ( \alpha _{i} \right ) }_{:= \bar{\rho}^{\text{av4}}}\mathbb{F}^{\text{tv}}, \end{aligned}$$

(33)

$$\begin{aligned} \bar{\mathbb{A}}^{\text{av2}} & = \mathbb{A}^{\text{iso}} + \bar{\alpha} \frac{6}{7}\mathrm{sym}\left ( {\boldsymbol {F}}^{\text{tv}} \otimes {\boldsymbol {I}} \right ) + \underbrace{\rho _{\mathcal{C}}\left ( \bar{\alpha} \right )}_{:= \bar{\rho}^{\text{av2}}} \mathbb{F}^{\text{tv}}, \end{aligned}$$

(34)

where $\rho _{\mathcal{C}}$ represents the result of the closure. To be a valid candidate, $\bar{\mathbb{A}}$ has to be a member of $\mathcal{N}^{\text{tv}}$ defined in Equation (29), i.e., $\rho _{\text{min}}\left (\bar{\alpha}\right ) \leq \bar{\rho} \leq \rho _{\text{max}}\left (\bar{\alpha}\right )$. If the chosen closure yields valid FOT for all $\alpha$, the second-order average $\bar{\mathbb{A}}^{\text{av2}}$ automatically fulfills this constraint. The same applies for the fourth-order average $\bar{\mathbb{A}}^{\text{av4}}$ since $\mathcal{N}^{\text{tv}}$ is convex and the arithmetic average is represented by a straight line in this set. However, a stricter constraint is given by the convex set $\mathcal{N}^{\text{tv}}_{\text{average}} (\alpha _{1},\, \alpha _{2}) \subseteq \mathcal{N}^{\text{tv}}$ defined by

$$\begin{aligned} \mathcal{N}^{\text{tv}}_{\text{average}} (\alpha _{1},\, \alpha _{2}) = \Bigl\{ \mathbb{A}^{\text{tv}} (\alpha ,\, \rho ) \Big|\,\, (\alpha , \, \rho ) \in \mathrm{conv} \Bigl( \Bigl\{ & (\alpha _{1}, \rho ^{ \text{min}}(\alpha _{1})), \\ & (\alpha _{1}, \rho ^{\text{max}}(\alpha _{1})), \\ & (\alpha _{2}, \rho ^{\text{min}}(\alpha _{2})), \\ & (\alpha _{2}, \rho ^{\text{max}}(\alpha _{2})), \Bigr\} \Bigr) \Bigr\} \end{aligned}$$

(35)

with the operator $\mathrm{conv}(\cdot )$ constructing the convex hull of a given set of points. Retrieving Theorem 4.1, the constraints forming the set in Equation (35) follow directly from the linearity of the orientation average. The construction of the set $\mathcal{N}^{\text{tv}}_{\text{average}} (\alpha _{1},\, \alpha _{2})$ can easily be extended to more than just two information on FOT of second-order. This stronger constraint does not impose a restriction to the relative volume fraction $c_{I}\, \in \left [0,\, 1\right ]$ and is visualized in Fig. 7 for the example depicted in Fig. 4 with ${\boldsymbol {A}}_{1} = {\boldsymbol {A}}^{\text{iso}} + \alpha _{1} {\boldsymbol {F}}^{\text{tv}}$ and ${\boldsymbol {A}}_{2} = {\boldsymbol {A}}^{\text{iso}} + \alpha _{2} {\boldsymbol {F}}^{\text{tv}}$. The tensors $\mathbb{A}_{1}$ and $\mathbb{A}_{2}$ in Fig. 7 are obtained from $\alpha _{1}$ and $\alpha _{2}$ by the IBOF closure and represented through an up-pointing triangle and down-pointing triangle, respectively. The extrema of $\rho (\alpha _{I})$ yield the extremal fourth-order FOT $\mathbb{A}_{I}^{m}$ with $I=1, 2$ and $m=\text{min}, \text{max}$ which represent edge-points of the set $\mathcal{N}^{\text{tv}}_{\text{average}} (\alpha _{1},\, \alpha _{2})$ (dark gray area) in Fig. 7. For the depicted problem the second-order average $\bar{\mathbb{A}}^{\text{av2}}$ is located outside of $\mathcal{N}^{\text{tv}}_{\text{average}} (\alpha _{1},\, \alpha _{2})$ and therefore is not admissible. In contrast, the fourth-order average $\bar{\mathbb{A}}^{\text{av4}}$ (diamond marker) is valid and located halfway on the straight line connecting $\mathbb{A}_{1}$ and $\mathbb{A}_{2}$. The findings implicate that the IBOF closure is indeed not self-consistent with regard to volumetric subdomain composition. In loose terms, this translates to the following statement: If the second-order FOT ${\boldsymbol {A}}_{1}$ and ${\boldsymbol {A}}_{2}$ of two subdomains are determined exactly, hence the admissible FOT $\bar{{\boldsymbol {A}}}$ of the union of those subsets is also exactly determinable. The IBOF closure of $\bar{{\boldsymbol {A}}}$ however, can yield a physically impossible result. For the special case of transversely isotropic second-order FOT, Müller and Böhlke [14] concluded that the deviations between the closures IBOF, MEP, and ORF schemes are negligible. Thus, it has to be expected that those also suffer from lacking self-consistency.

Fig. 7

Location of the fourth-order average and second-order average of transversely FOT in relation to the sets $\mathcal{N}^{\text{tv}}$ and $\mathcal{N}^{\text{tv}}_{\text{average}}(\alpha _{1},\, \alpha _{2})$. In the depicted case of $\alpha _{1}=-1/5$, $\alpha _{2}=11/20$ the second-order average $\bar{\mathbb{A}}^{\text{av2}}$ is invalid

The difference between fourth-order average and second-order average by means of the linear coefficient $\rho$ as a function of the parameter $\alpha$ of two equally weighted second-order FOT is presented in Fig. 8(a). The graph is symmetric to the line $\alpha _{1} = \alpha _{2}$ since the labeling order is arbitrary. A higher distance between the two basic values with respect to the parameter $\alpha$ yields higher deviations between the values $\bar{\rho}^{\text{av4}}$ and $\bar{\rho}^{\text{av2}}$, reaching a maximum for the average of a unidirectional ($\alpha =2/3$) and planar-isotropic state ($\alpha =-1/3$). Fig. 8(b) visualizes the validity of the second-order average $\bar{\rho}^{\text{av2}}$ for all possible combinations of $\alpha _{1}, \alpha _{2}$. All pairs inside the blue domain yield valid, i.e., physically possible, results. Fig. 8(b) highlights in red all combinations, which violate the subdomain self-consistency. The black dot marks the example shown in Fig. 7.

Fig. 8

Deviations of fourth-order averaged and second-order averaged coefficient $\rho$ (left) and regions of validity for pairwise combinations of $\alpha _{1}, \alpha _{2}$ for transversely isotropic FODFs

4.2 Planar Fiber Orientation Distributions

In this section, we focus on planar FODF which represent a subspace of all possible FODF. We require fibers of a planar FODF to be located solely within a plane spanned by the vectors ${\boldsymbol {v}}_{1}$ and ${\boldsymbol {v_{2}}}$. Following Bauer and Böhlke [27], the second- and fourth-order FOT of a planar FODF can be expressed by

$$\begin{aligned} {\boldsymbol {A}}^{\text{pl}} \left ( \alpha \right ) & = \left ( \frac{1}{2} + \frac{3}{4} \alpha \right ) {\boldsymbol {v}}_{1}^{\otimes 2} + \left ( \frac{1}{2} - \frac{3}{4} \alpha \right ) {\boldsymbol {v}}_{2}^{\otimes 2}, \end{aligned}$$

(36)

$$\begin{aligned} \mathbb{A}^{\text{pl}} \left ( \alpha , d_{1}, d_{8} \right ) & = \mathbb{A}^{\text{iso}} + \frac{6}{7} \mathrm{sym}\left ( \left ( {\boldsymbol {A}}^{\text{pl}} \left (\alpha \right ) \right )^{\prime }\otimes {\boldsymbol {I}} \right ) + \mathbb{F}^{\text{pl}} \left ( \alpha , d_{1}, d_{8} \right ). \end{aligned}$$

(37)

The planar harmonic structure tensor

$$ \mathbb{F}^{\text{pl}} \left ( \alpha , d_{1}, d_{8} \right ) = \mathbb{F}\left ( d_{1}, d_{2}=\frac{-15 \alpha -6}{140}, d_{3}= \frac{15 \alpha -6}{140}, d_{4}...d_{7}=0, d_{8}, d_{9}=-d_{8}, \right ). $$

(38)

is defined as a special case of the triclinic one defined in Equation (12). The linear coefficients $d_{1}, \, d_{8}$ define the degree of orthotropy and triclinity respectively [27]. Bauer and Böhlke [27] derived an explicit representation of the set $\mathcal{N}^{\text{pl}}$ containing all admissible planar fourth-order FOT, which is re-formulated in [44]. The lengthy expressions are not repeated in this context but rather a visualization of the body of admissible parameter combinations for $-2/3 \le \alpha \le 2/3$ is given in Fig. 9. Analogous to the transversely isotropic edge case (cf. Sect. 4.1) closure-related fourth-order and second-order averages are directly applied to the linear coefficients $d_{1}, d_{8}$. The resulting closure-related valid set $\left .\mathcal{N}^{\text{pl}}_{\text{average}}\right |_{{\boldsymbol {A}}}$ follows as convex union by

$$\begin{aligned} &\mathcal{N}^{\text{pl}}_{\text{average}} (\alpha _{1},\, \alpha _{2})\\ &\quad = \Bigl\{ \mathbb{A}^{\text{pl}} (\alpha ,\, d_{1}, d_{8}) \Big|\,\, ( \alpha ,\, d_{1}, d_{8}) \in \mathrm{conv} \Bigl( \Bigl\{ \\ &\qquad \lbrace \alpha _{1}, -4/35 \leq d_{1} \leq d_{1}^{\text{max}} \left ( \alpha _{1} \right ), \, d_{8}^{\text{min}}\left ( \alpha _{1} , d_{1} \right ) \leq d_{8} \leq d_{8}^{\text{max}}\left ( \alpha _{1} , d_{1} \right ) \rbrace , \\ &\qquad \lbrace \alpha _{2}, -4/35 \leq d_{1} \leq d_{1}^{\text{max}} \left ( \alpha _{2} \right ), \, d_{8}^{\text{min}}\left ( \alpha _{2} , d_{1} \right ) \leq d_{8} \leq d_{8}^{\text{max}}\left ( \alpha _{2} , d_{1} \right ) \rbrace , \Bigr\} \Bigr) \Bigr\} . \end{aligned}$$

(39)

Using the same style and nomenclature as in the previous section, the consistency of the closure is inspected graphically. Fig. 9 shows the set $\mathcal{N}^{\text{pl}}$ (light gray body) in the parameter space spanned by $\alpha$, $d_{1}$ and $d_{8}$. For constant second-order information $\alpha$, the admissible values of $d_{1}$ and $d_{8}$ form a disc in the parameter-space. According to Equation (39), the closure-related valid space $\mathcal{N}^{\text{pl}}_{\text{average}}\left ( \alpha _{1}, \alpha _{2} \right )$ forms a convex hull bounded by the admissible ranges at $\alpha _{1, 2 }$, which is depicted in dark-gray color. Admissible orthotropic FOT $\mathbb{A}^{\text{pl}}$ are located on the plane $d_{8} =0$. Since the regarded IBOF-closure exclusively yields orthotropic results, the investigations can be reduced to the subset $\mathcal{N}^{\text{pl,ortho}}$, which circumference is indicated by the black dash-dotted line in Fig. 9. The course of the IBOF-closure $d_{1}^{\text{IBOF}} \left ( \alpha \right )$ (blue bold line) is axis-symmetric to the isotropic state at $\alpha =0$. The derivation of the closure-related average candidates $\bar{\mathbb{A}}^{\text{av2}}$ and $\bar{\mathbb{A}}^{\text{av4}}$ follows Sect. 4.1. The limitations of the transversely isotropic case occur here as well. It is possible to find combinations $\lbrace \alpha _{1}, \alpha _{2}\rbrace$ that yield invalid second-order averages, such as the example depicted in Fig. 9. Fig. 10(a) gives the quantified difference between fourth-order average and second-order average by means of the linear coefficient $d_{1}$ as a function of the parameter $\alpha$ of two equally weighted second-order FOT. Parameter combinations $\lbrace \alpha _{1}, \alpha _{2} \rbrace$ resulting in invalid second-order average $\bar{\mathbb{A}}^{\text{av2}}$ are located in the red domain in Fig. 10(b). To emphasize the argumentation, the extreme case ${\boldsymbol {A}}_{1} = {\boldsymbol {A}}^{\text{pl}}\left ( \alpha = 2/3 \right ) = {\boldsymbol {v}}_{1}^{\otimes 2}$, ${\boldsymbol {A}}_{2} = {\boldsymbol {A}}^{\text{pl}} \left ( \alpha = -2/3 \right ) = {\boldsymbol {v}}_{2}^{\otimes 2}$ is considered in Table 2. For the unidirectional cases, the FODF, and thus all corresponding higher-order FOT, can be reconstructed from the second-order FOT. The fourth-order average results as moment of the exact averaged FODF. On the contrary, the second-order average is planar isotropic, which would indicate an FODF possessing deviators of order six and above at most. Obviously, this distribution deviates from the exact one. That is, $\int _{\mathcal{S}} \frac{1}{2} \left (\psi _{1} + \psi _{2}\right ) \, \,{\boldsymbol {n}}^{\otimes 4} \,\mathrm {d}S \neq \bar{\mathbb{A}}^{\text{av2}}$. The previously discussed graphical access reveals the same interrelation. The convex set $\mathcal{N}^{\text{pl}}_{\text{average}}\left ( 2/3, -2/3 \right )$ degenerates to a single fourth-order tensor $\mathbb{A} = \mathbb{A}^{\text{pl.iso}} = \mathbb{A}^{\text{pl}} \left (\alpha =0, d_{1} = -4/35 \right )$, which coincides with the fourth-order average $\bar{\mathbb{A}}^{\text{av4}}$.

Fig. 9

Location of fourth-order average and second-order average of planar FOT

Fig. 10

Deviations of fourth-order averaged and second-order averaged coefficient $d_{1}$ (left) and regions of validity for pairwise combinations of $\alpha _{1}, \alpha _{2}$ for planar FODFs

Table 2 Statistical entities for the planar averaging case: ${\boldsymbol {A}}_{1} = {\boldsymbol {v}}_{1}^{\otimes 2}$, ${\boldsymbol {A}}_{2} = {\boldsymbol {v}}_{2}^{\otimes 2}$. The vector-valued Dirac distribution is defined as: $\delta \left ({\boldsymbol {n}}, {\boldsymbol {v}}\right ) := \frac{1}{2}\left (\delta \left ( {\boldsymbol {n}} - {\boldsymbol {v}} \right ) + \delta \left ( {\boldsymbol {n}} + {\boldsymbol {v}} \right )\right )$

5 Implications for Mechanical Homogenization

We identify implications of the outlined closure inconsistency in terms of second-order averages on linear elastic material homogenization.

5.1 Two-Step Homogenization Following Tandon & Weng and Tucker

Effective mechanical properties of inhomogeneous materials may be approximated by mean field homogenization. Orientation-averaged mean field homogenization methods combine the analytical solution by Eshelby [56] with an orientation averaging methods, e.g., following Advani and Tucker III [11]. For the following investigations, we use the two-step mean field homogenization approach originally proposed by Tandon and Weng [26] (TW). In the mechanical context, this method is restricted to spheroidal isotropic inclusions in an isotropic matrix. For common glass-fiber-reinforced polymers these assumptions apply [20]. The effective stiffness of interest $\bar{\mathbb{C}}$ is regarded as linear mapping of volume-averaged elastic strains $\langle {\boldsymbol {\varepsilon}} \rangle$ onto volume-averaged stresses $\langle {\boldsymbol {\sigma}} \rangle$, such that the Equation $\langle {\boldsymbol {\sigma}} \rangle = \bar{\mathbb{C}}\left [ {\boldsymbol {\langle \varepsilon}} \rangle \right ]$ holds. The fiber volume content $c_{\text{f}}$ is a one-point characteristic of the microstructure and enters the homogenization method of Tandon and Weng [26] within a first homogenization step leading to the transversely isotropic stiffness tensor $\bar{\mathbb{C}}^{\text{tv}}_{\text{TW}}$ with the transversely isotropic axis ${\boldsymbol {p}}$ by

$$ \bar{\mathbb{C}}^{\text{tv}}_{\text{TW}} \left ( {\boldsymbol {p}} \right ) = \mathbbm{f}\left ( c_{\text{f}}, {\boldsymbol {p}} , \mathbb{C}_{\text{fiber}}, \mathbb{C}_{\text{matrix}} \right ) $$

(40)

with the isotropic stiffness of the fibers $\mathbb{C}_{\text{fiber}}$ and the matrix $\mathbb{C}_{\text{matrix}}$, respectively. Within a second homogenization step, this transversely isotropic stiffness is orientation averaged following Advani and Tucker III [11] based on the fiber orientation tensor $\mathbb{A}$, reflecting the orientation of the fibers within the microstructure, representing another one-point characteristic. In consequence, the anisotropic effective stiffness of the composite $\bar{\mathbb{C}}_{\text{TW}} \left ( \mathbb{A} \right )$

follows in its irreducible form as

$$\begin{aligned} \bar{\mathbb{C}}_{\text{TW}}\left ( \mathbb{A} \right ) & = \langle \bar{\mathbb{C}}_{\text{TW}}^{\text{tv}} \rangle _{\mathcal{S}^{2}}\left ( \mathbb{A} \right ) = \int _{\mathcal{S}^{2}} \psi \left ( {\boldsymbol {n}} \right ) \bar{\mathbb{C}}^{\text{tv}}_{\text{TW}} \left ( {\boldsymbol {n}}\right )\, \,\mathrm {d}S \\ & = b_{1} \,\mathbb{P}_{1} + b_{2} \, \mathbb{P}_{2} + b_{3} \, \mathfrak{J}_{3} \left [ {\boldsymbol {A}}^{\prime }\right ] + b_{4} \, \mathfrak{J}_{4} \left [ {\boldsymbol {A}}^{\prime }\right ] + b_{5} \, \mathbb{F}. \end{aligned}$$

(41)

Here, $\mathbb{P}_{1}$ denotes the identity on second-order spherical tensors, $\mathbb{P}_{2}$ the identity on symmetric traceless second-order tensor, while $\mathfrak{J}_{3}$ and $\mathfrak{J}_{4}$ are isotropic tensors of order six. ${\boldsymbol {A}}^{\prime}$ and $\mathbb{F}$ represent the deviators of $\mathbb{A}$ in accordance with Eqn. (11). The scalar coefficients $b_{i}$ can be obtained from the tensor coefficients of $\bar{\mathbb{C}}^{\text{tv}}_{\text{TW}}$. The authors chose the representation (41) to point out the linearity of the orientation average in $\mathbb{F}$. It should be noted, that the orientation average of the unidirectional stiffness tensor mathematically corresponds to a Voigt-like averaging [57, 58]. Different approaches such as performing orientation average on strain-localization tensor approximations or effective unidirectional compliance tensors (Reuss-like) exist [44, 59].

5.2 Structural Bounds for the Strain Energy

The strain energy density $W\left (\mathbb{C}, {\boldsymbol {n}}\right )$ of a hyperelastic material with stiffness tensor ℂ induced by a virtual unidirectional unit strain ${\boldsymbol {\varepsilon}}_{0} = {\boldsymbol {n}} \otimes {\boldsymbol {n}}$ with ${\boldsymbol {n}} \in \mathcal{S}^{2}$ is

$$ W\left (\mathbb{C}, {\boldsymbol {n}}\right ) = \frac{1}{2} \left ({\boldsymbol {n}} \otimes {\boldsymbol {n}}\right ) \cdot \mathbb{C} \left [ {\boldsymbol {n}} \otimes {\boldsymbol {n}} \right ]. $$

(42)

If for a given microstructure with transversely isotropic material symmetry, only the second-order FOT ${\boldsymbol {A}}^{\text{tv}} = {\boldsymbol {A}}^{\text{iso}} + \alpha {\boldsymbol {F}}^{\text{tv}}$ is known, the corresponding strain energy, which is based on the effective stiffness of the microstructure, e.g., approximated by Equation (41), is subjected to uncertainty, due to the missing fourth-order FOT information. As the fourth-order FOT information is restricted to those FOT which contract to the given second-order FOT, i.e., $\mathbb{A} \in \left .\mathcal{N}^{\text{tv}}\right |_{\bar{\alpha}}$, valid values of the strain energy are bound by

$$ W\left ( \bar{\mathbb{C}}_{\text{TW}} \left (\mathbb{A}\right ) , {\boldsymbol {n}} \right ) \in \underbrace{ \Bigl\{ W\left ( \bar{\mathbb{C}}_{\text{TW}}\left (\mathbb{A} \right ) , {\boldsymbol {n}} \right ) | \mathbb{A} \in \left .\mathcal{N}^{\text{tv}}\right |_{\bar{\alpha}} \Bigr\} }_{:= \left .\mathcal{W}^{\text{tv}}\right |_{\bar{\alpha}}} \quad \quad \forall \,{\boldsymbol {n}} \in \mathcal{S}^{2}. $$

(43)

We consider a microstructure, which is the union of two sub microstructures. Both sub microstructures are assumed to be transversely isotropic and have commuting second-order FOT defined by $\alpha _{1}$ and $\alpha _{2}$, respectively. The admissible range of the strain energy density of the union microstructure is restricted (cf. Sect. 4.1) to

$$\begin{aligned} &W\left ( \bar{\mathbb{C}}_{\text{TW}} \left (\mathbb{A}\right ) , {\boldsymbol {n}} \right ) \in \underbrace{ \Bigl\{ W\left ( \bar{\mathbb{C}}_{\text{TW}}\left (\mathbb{A} \right ) , {\boldsymbol {n}} \right ) | \mathbb{A} \in \left .\mathcal{N}^{\text{tv}}_{\text{average}}\left (\alpha _{1}, \alpha _{2}\right )\right |_{\bar{\alpha}} \Bigr\} }_{:= \left .\mathcal{W}^{\text{tv}}_{\text{average}}\right |_{ \bar{\alpha}}} \subseteq \left .\mathcal{W}^{\text{tv}}\right |_{ \bar{\alpha}}\\ & \quad \forall \,{\boldsymbol {n}} \in \mathcal{S}^{2}. \end{aligned}$$

(44)

The strain energy densities corresponding to $\bar{\mathbb{A}}^{\text{av2}}$ and $\bar{\mathbb{A}}^{\text{av4}}$ are denoted $\bar{W}^{\text{av2}}$ and $\bar{W}^{\text{av4}}$, respectively.

5.3 Validity of Effective Material Properties

The bounds introduced in the previous section are demonstrated for numerical values of isotropic mechanical properties of the fibers and matrix taken from literature and listed in Table 3. For the example depicted in Fig. 7 and marked in Fig. 8 with $\alpha _{1} = -2/10$, $\alpha _{2}=11/20$, $\bar{\alpha} = 7/40$ the strain energy is computed for the effective stiffness $\bar{\mathbb{C}}$ based on either the fourth-order average $\bar{\mathbb{A}}^{\text{av4}}$ or the second-order average $\bar{\mathbb{A}}^{\text{av2}}$. The unit vector ${\boldsymbol {n}}$ is parameterized with a single polar angle $\vartheta$ such that ${\boldsymbol {n}}\left ( \vartheta \right ) = \cos \left (\vartheta \right ) {\boldsymbol {p}}_{\parallel }+ \sin \left ( \vartheta \right ){\boldsymbol {p}}_{\perp}$. The unit vector ${\boldsymbol {p}}_{\parallel }$ corresponds to the symmetry axis of both the stiffness of the first homogenization step $\bar{\mathbb{C}}^{\text{tv}}_{\text{TW}}$ and the fourth-order FOT $\mathbb{A}$. The direction ${\boldsymbol {p}}_{\perp }$ denotes an arbitrary perpendicular unit vector. The resulting strain energy densities are visualized in Fig. 11. The domain of possible values for all positive semidefinite $\mathbb{A}$ is depicted by the region filled in light gray color. This area encapsulates valid energy densities due to averaging (dark gray). The ranges degenerate to points under specific angles, i.e., the strain energy density has to take the exact value for any valid $\bar{\mathbb{A}}$.

Fig. 11

Valid ranges of $W$, $\bar{W}^{\text{av2}}$ and $\bar{W}^{\text{av4}}$ as a function of the polar angle $\vartheta$. Due to the orthotropic symmetry the non-redundant range of $\vartheta$ is restricted to the interval $[0, \pi /2]$

Table 3 Elastic material properties of fiber and matrix. The glass fiber and polypropylene (PP) polymer matrix are assumed to be isotropic

Those angles directly follow from Eqn. (41) representing the roots of the quartic form $\mathbb{F}^{\text{tv}} \cdot {\boldsymbol {n}}^{\otimes 4}\left (\vartheta \right )$. Under loading angles $\hat{\vartheta}$ with $\tan \left (\hat{\vartheta}\right ) = \pm \frac{1}{3} \sqrt{36 \pm 6 \sqrt{30}}$, the part of $\hat{\mathbb{C}}^{\text{TW}}$ being linear in the fourth-order deviator $\mathbb{F}$ does not contribute to the strain energy density $W$, irrespective of the specific value of the material invariant $b_{5}$. This hard constraint is fulfilled by both $\bar{W}^{\text{av2}}$ and $\bar{W}^{\text{av4}}$. However, for all remaining unit strain directions the quantity $\bar{W}^{\text{av2}} \left (\vartheta \right )$ is located in the exterior of the average-related strain energy density bounds. Therefore, the orientation averaged stiffness $\bar{\mathbb{C}}_{\text{TW}} \left (\bar{\mathbb{A}}^{\mathrm{av2}} \right )$ is invalid as it represents a material behavior, that cannot be associated with the given second-order FOT information of the sub-volumes. The qualitative observation of $\bar{W}^{\text{av2}}$ violating the bounds can be reproduced for any combination of elastic properties. The findings implicate that the invalid results of $\bar{\mathbb{A}}^{\text{av2}}$ propagate through the orientation average and yield non-physical stiffness tensors. This is a direct consequence of the orientation average $\langle \cdot \rangle _{\mathcal{S}^{2}}$ being linear in both its argument and $\mathbb{A}$ (cf. Equation (41)).

6 Summary and Conclusions

Mapping and closure of fiber orientation tensors are identified as the two main steps interlinking the process simulation and structural simulation of discontinuous fiber-reinforced polymers components. An analytical expression for the set of admissible orthotropic fourth-order FOT is derived. This set is utilized to quantify the orthotropic uncertainty of closure approximations based on second-order FOT. The scalar uncertainty measure is maximum for isotropic second-order moments and vanishes for the unidirectional state. The terms second-order average and fourth-order average are introduced to distinguish two possible routes linking process and structural simulations. Second-order average indicates mapping before closure whereas fourth-order average indicates closure before mapping. For three distinct reference FOT, the deviation between the second-order and fourth-order average is computed by means of the tensor norm for varying second-order FOT. The norm of the difference is remarkably large, especially if the two basic values exhibit large structural variances. In the edge case of two unidirectional states with different principal axis, the norm of deviations has been found to exceed the norm of the isotropic fourth-order FOT. Tensor glyphs reveal that the second-order average does favor more isotropic states, while the fourth-order average tends to preserve more structural information. For transversely isotropic orientation states with homogeneous principal direction, an inconsistency has been detected. The second-order average yields impossible and thus invalid results for specific combinations of second-order FOT. Such an inconsistency is also present among commuting planar FOT. Using the average FOT of fourth order in the context of orientation averaging of stiffness tensors illustrates how invalid statistical information in form of the FOT average produces invalid material behavior, which is indicated by means of the elastic energy density.

The main findings and contributions of this work are

• The set of admissible orthotropic fourth-order FOT is given analytically. This extends the work of Bauer and Böhlke [27] and enables further investigations.

• Changing the order of closure and averaging within virtual process chains, significantly affects the obtained fourth-order FOT. The deviations vanish if the considered FOT of second-order are structurally similar.

• The magnitude in deviation is lower for the IBOF closure compared to quadratic and hybrid closure schemes.

• Second-order averages of transversely isotropic FOTs may yield invalid results, while the fourth-order average is valid in all cases.

• For a planar FOT, both fourth-order average and second-order average are valid in all cases, if the projectors of basic values are identical. Apart from this subset, invalid states are also feasible in the case of second-order averages.

• Orientation averages of a linear elastic stiffness based on invalid fourth-order FOT yield non-physical strain energy.

The findings justify the following statement: If only the FOT of second-order is available within a virtual process chain, the closure should be applied on the source discretization. Subsequently, the obtained fourth-order FOT can be mapped onto the target discretization guaranteeing valid results. However, the closure-related uncertainty remains still large and is usually restricted to orthotropic states. Additionally, the work considers exclusively the special-case of commuting tensors. An extension towards the general, non-commuting, case is favorable for a holistic approach to this problem. This would comprise cases, in which the averaging yields different symmetries for the second-order and fourth-order averages. With increasing computational performance, micro- and meso-models in process simulations, e.g., [61], are favorable, since those allow the direct computation of fourth-order FOT.

Appendices

Appendix A: The Set of Admissible Orthotropic Fiber Orientation Tensors

We sketch a brief derivation to obtain an explicit formulation of the set of admissible orthotropic fourth-order FOT in terms of the linear deviator coefficients $\alpha _{1}, \alpha _{3}, d_{1}, d_{2}, d_{3}$. Our procedure is based on the theorem comprehensively proved in reference [12] for two and three spatial dimensions:

Theorem 7.1

Let $\mathbb{A}$ be a real-valued fourth-order tensor. If $\mathbb{A}$ is completely symmetric, normalized in the sense of $A_{iijj} = 1$, and generates a non-negative quadratic form ${\boldsymbol {V}} \cdot \mathbb{A}\left [{\boldsymbol {V}}\right ] \geq 0,\, \forall \, {\boldsymbol {V}} \in Sym$, $\mathbb{A}$ is an admissible fiber orientation tensor. The inverse implication holds.

By construction via Equation (11) complete index symmetry and normalization of a fourth-order FOT are trivially fulfilled. A tensor $\mathbb{A}$ suffices ${\boldsymbol {V}} \cdot \mathbb{A}\left [{\boldsymbol {V}}\right ] \geq 0,\, \forall \, {\boldsymbol {V}} \in Sym$, if its coefficient matrix $A_{\xi \zeta}$ in an orthonormal Mandel basis is positive semi-definite. Definiteness is characterized by Sylvester’s law of inertia: For a positive semi-definite matrix, all principal minor determinants have to be non-negative. In this case, all roots of the characteristic polynomial ${\mathrm {det} }\left ( A_{\xi \zeta} - \lambda \delta _{\xi \zeta} \right )$ are non-negative.

The coefficient matrix of an arbitrary orthotropic FOT is explicitly given in [27, Equation (78+82)]. We will use the more general form:

$$ A^{\text{ortho}}_{\xi \zeta} = \begin{bmatrix} a & d & e & 0 & 0 & 0\\ & b & f & 0 & 0 & 0\\ & & c & 0 & 0 & 0\\ & & & 2f & 0 & 0\\ & & & & 2e & 0\\ & & & & & 2d \end{bmatrix}\quad \text{with} \quad M_{\xi \zeta} := \begin{bmatrix} a & d & e \\ & b & f \\ & & c \end{bmatrix}, $$

(45)

where $a,\ldots,f$ are functions of $\alpha _{1}, \alpha _{3}, d_{1}, d_{2}$ and $d_{3}$. As first order minors, the coefficients $d,e,f$ must be non-negative. Those inequalities directly yield the lower limits of $d_{1}, d_{2}$ and $d_{3}$, which are already stated in [27, Equation (79-81)]. Since $2d,2e$ and $2f$ are also roots of the characteristic polynomial, the upper coefficient bounds can be derived from the submatrix $M_{\xi \zeta}$ alone. Again, we demand positive semi-definiteness for $M_{\xi \zeta}$. Hence, all the following inequalities must hold mutually:

$$\begin{aligned} & a \geq 0, \quad b \geq 0, \quad c \geq 0, \end{aligned}$$

(46)

$$\begin{aligned} & ab - d^{2} \geq 0, \quad ac - e^{2} \geq 0, \quad bc - f^{2} \geq 0, \end{aligned}$$

(47)

$$\begin{aligned} & {\mathrm {det} }\left ( M \right ) = abc - af^{2} - be^{2} - cd^{2} + 2def \geq 0 . \end{aligned}$$

(48)

The third-order (3o) bounds follow by applying simple algebraic manipulation: We use ${\mathrm {det} }\left ( M_{\xi \zeta} \right ) \geq 0$ to find $d_{3}^{\text{max, 3o}}$, $\left .{\mathrm {det} }\left ( M_{\xi \zeta} \right )\right |_{d_{3} = d_{3}^{\text{min}}} \geq 0$ for $d_{2}^{\text{max, 3o}}$, and $\left .{\mathrm {det} }\left ( M_{\xi \zeta} \right )\right |_{d_{2} = d_{2}^{\text{min}}, d_{3} = d_{3}^{\text{min}}} \geq 0$ for $d_{1}^{\text{max, 3o}}$. Similarly, first-order bound $d_{i}^{\text{max, 1o}}$ and second-order bounds $d_{i}^{\text{max, 2o}}$ for $i \in [1, 2, 3]$ result from the inequalities comprised in Equation (46) and (47), respectively. A long but basic algebraic comparison shows that

$$ d_{i}^{\text{max, 3o}} \leq d_{i}^{\text{max, 2o}} \quad \text{and} \quad d_{i}^{\text{max, 3o}} \leq d_{i}^{\text{max, 1o}}, \quad i \in [1, 2, 3], \quad \alpha _{1, 3} \in \mathcal{N}^{\text{com}} $$

(49)

in the admissible range of $\alpha _{1, 3}$ (cf. Equation (9)) Thus, Equation (48) is a sufficient condition. For graphical interpretation, Fig. 12 depicts the admissible parameter combinations of $d_{1,2,3}$ for the special case of fixed values $\alpha _{1} = \alpha _{3} = 0$.

Fig. 12

Graphical representation of the admissible ranges of parameter combinations $d_{1,2,3}$ according to the first-order bounds (Eqn. (46)), to the second-order bounds (Eqn. (47)) and to the third-order bounds (Eqn. (48)) for a given isotropic second-order FOT, i.e. $\alpha _{1} = \alpha _{3} = 0$

Finally, each admissible orthotropic FOT of order four is a member of the set $\mathcal{N}^{\text{ortho}}$ given by

$$ \begin{aligned}\mathcal{N}^{\text{ortho}} = \Big\{ \mathbb{A}^{ \text{ortho}} & \left ( {\boldsymbol {A}}, d_{1}, d_{2}, d_{3}\right ) \left | \right .\, {\boldsymbol {A}} = {\boldsymbol {A}}^{\text{iso}} + \alpha _{1} {\boldsymbol {F}}_{1} + \alpha _{3} {\boldsymbol {F}}_{3} \in \mathcal{N}^{\text{comm}}, \\ &d_{1}^{\text{min}} \left ( \alpha _{1}, \alpha _{3} \right ) \leq d_{1} \leq d_{1}^{\text{max}}\left ( \alpha _{1}, \alpha _{3} \right ), \\ & d_{2}^{\text{min}} \left ( \alpha _{1}, \alpha _{3} \right ) \leq d_{2} \leq d_{2}^{\text{max}}\left (\alpha _{1}, \alpha _{3}, d_{1}\right ), \\ & d_{3}^{\text{min}} \left ( \alpha _{1}, \alpha _{3} \right ) \leq d_{3} \leq d_{3}^{\text{max}}\left (\alpha _{1}, \alpha _{3}, d_{1}, d_{2} \right ) \Big\} \end{aligned} $$

(50)

with

$$\begin{aligned} d_{1}^{\text{min}} \left ( \alpha _{1}, \alpha _{3} \right ) &= \frac{1}{14}\left ( 2 \alpha _{3} - \alpha _{1} \right )-\frac{1}{15}, \end{aligned}$$

(51)

$$\begin{aligned} d_{2}^{\text{min}} \left ( \alpha _{1}, \alpha _{3} \right ) &= - \frac{1}{14}\left ( \alpha _{1} + \alpha _{3} \right ) - \frac{1}{15}, \end{aligned}$$

(52)

$$\begin{aligned} d_{3}^{\text{min}} \left ( \alpha _{1}, \alpha _{3} \right ) &= \frac{1}{14}\left ( 2\alpha _{1} - \alpha _{3} \right ) - \frac{1}{15}, \end{aligned}$$

(53)

$$\begin{aligned} d_{1}^{\text{max}}\left ( \alpha _{1}, \alpha _{3} \right ) &= (-225 \alpha _{1}^{2} + (-45\alpha _{3} + 36)\alpha _{1} + 45\alpha _{3}^{2} - 72\alpha _{3} + 28) \end{aligned}$$

(54)

$$\begin{aligned} &\quad / (210\alpha _{1} - 420\alpha _{3} + 280), \\ d_{2}^{\text{max}}\left ( \alpha _{1}, \alpha _{3}, d_{1}\right ) &= \left [\right . -75600\alpha _{1}^{3} \end{aligned}$$

(55)

$$\begin{aligned} &\quad + (-66150d_{1} + 113400\alpha _{3} + 49680)\alpha _{1}^{2} + (28350\alpha _{3}^{2} \\ &\quad + (264600d_{1} - 49680)\alpha _{3} - 63000d_{1})\alpha _{1} - 33075 \alpha _{3}^{3} \\ &\quad + (-264600d_{1} + 31050)\alpha _{3}^{2} + 69300d_{1}\alpha _{3} + 41160d_{1} - 3136 \left .\right ] \\ &\quad / \left [\right . 66150\alpha _{1}^{2} + (132300\alpha _{3} + 63000) \alpha _{1} \\ &\quad + 66150\alpha _{3}^{2} + 264600d_{1} + 6300\alpha _{3} - 41160 \left .\right ], \\ d_{3}^{\text{max}}\left ( \alpha _{1}, \alpha _{3}, d_{1}, d_{2} \right ) &= \left [\right . -33075d_{1}\alpha _{1}^{2} + 132300d_{1} \alpha _{1}\alpha _{3} - 132300d_{1}\alpha _{3}^{2} \\ &\quad - 33075d_{2}\alpha _{1}^{2} - 66150d_{2}\alpha _{1}\alpha _{3} - 33075d_{2}\alpha _{3}^{2} \\ &\quad - 18900\alpha _{1}^{3} + 28350\alpha _{1}^{2}\alpha _{3} + 28350 \alpha _{1}\alpha _{3}^{2} \\ &\quad - 18900\alpha _{3}^{3} - 132300d_{1}d_{2} - 12600d_{1}\alpha _{1} + 25200d_{1}\alpha _{3} \\ &\quad - 12600d_{2}\alpha _{1} - 12600d_{2}\alpha _{3} + 12420\alpha _{1}^{2} - 12420\alpha _{1}\alpha _{3} \\ &\quad + 12420\alpha _{3}^{2} + 11760d_{1} + 11760d_{2} - 784 \left . \right ] \\ &\quad / \left [\right . 132300\alpha _{1}^{2} - 132300\alpha _{1} \alpha _{3} + 33075\alpha _{3}^{2} + 132300d_{1} \\ &\quad + 132300d_{2} - 25200\alpha _{1} + 12600\alpha _{3} - 11760 \left .\right ]. \end{aligned}$$

(56)

Appendix B: Topography of the Space of Orthotropic Fourth-Order Fiber Orientation Tensors

We study the topography of the space of orthotropic fourth-order fiber orientation tensors $\mathcal{N}^{\text{ortho}}$. For an arbitrary but constant second-order fiber orientation tensor ${\boldsymbol {A}}$, the Hessian Determinant of $d_{3}^{\text{max}}$ and thus the intrinsic curvature vanishes except at one singular point. Thus, the set $\left . \mathcal{N}^{\text{ortho}} \right |_{{\boldsymbol {A}}}$ can be topographically interpreted as an intrinsically flat cone in the $\lbrace d_{1}, d_{2}, d_{3} \rbrace$-space, which is sliced by the orthogonal planes $d_{i} = d_{i}^{\text{min}}$ for $i \in [1, 2, 3]$. This is confirmed by the graphical discussion in the work of Bauer and Böhlke [27]. The apex of the cone $\vec{d}^{\text{apex}}$ can be found at the singularity location of the gradient of $d_{3}^{\text{max}}$

$$ \vec{d}^{\text{apex}} \left ( \alpha _{1}, \alpha _{3} \right ) = \begin{bmatrix} d_{1}^{\text{apex}} \\ d_{2}^{\text{apex}} \\ d_{3}^{\text{apex}} \end{bmatrix} = \begin{bmatrix} \frac{1}{4} \alpha _{3}^{2} - \frac{1}{4} \alpha _{3} \alpha _{1} - \frac{4}{21} \alpha _{3} - \frac{1}{2} \alpha _{1}^{2} + \frac{2}{21} \alpha _{1} + \frac{2}{45} \\ -\frac{1}{2} \alpha _{3}^{2} + \frac{5}{4} \alpha _{3} \alpha _{1} + \frac{2}{21} \alpha _{3} - \frac{1}{2} \alpha _{1}^{2} + \frac{2}{21} \alpha _{1} + \frac{2}{45} \\ -\frac{1}{2} \alpha _{3}^{2} - \frac{1}{4} \alpha _{3} \alpha _{1} + \frac{2}{21} \alpha _{3} + \frac{1}{4} \alpha _{1}^{2} - \frac{4}{21} \alpha _{1} + \frac{2}{45} \end{bmatrix} . $$

(57)

The symmetry axis of the cone passes through $\vec{d}^{\text{apex}}$ and the central point $\vec{d}^{\text{center}}$ with

$$ \vec{d}^{\text{center}} \left ( \alpha _{1}, \alpha _{3} \right ) = \begin{bmatrix} d_{1}^{\text{center}} \\ d_{2}^{\text{center}} \\ d_{3}^{\text{center}} \end{bmatrix} = \begin{bmatrix} d_{1}^{\text{min}} \left ( \alpha _{1}, \alpha _{3} \right ) \\ d_{2}^{\text{min}} \left ( \alpha _{1}, \alpha _{3} \right ) \\ d_{3}^{\text{min}} \left ( \alpha _{1}, \alpha _{3} \right ) \end{bmatrix} . $$

(58)

Appendix C: Scalar Distance Between Harmonic Orthotropic Fourth-Order Tensors

We study the distance between two orthotropic fourth-order fiber orientation tensors $\mathbb{A}_{1}$ and $\mathbb{A}_{2}$ which contract to a given second-order fiber orientation tensor $\mathbf{A}$, i.e., $\mathbb{A}_{1}\left [{\boldsymbol {I}}\right ] = \mathbf{A} = \mathbb{A}_{2} \left [{\boldsymbol {I}}\right ]$ or equivalently $\mathbb{A}_{i} \in \left .\mathcal{N}^{\mathrm{ortho}}\right |_{ {\boldsymbol {A}}}$ for $i \in [1,2]$. Such tensors differ solely by their harmonic fourth-order parts $\mathbb{F}_{i}$ with $i \in [1,2]$, see Equation (11). The difference $\Delta \mathbb{F} = \mathbb{F}_{2} - \mathbb{F}_{1}$ of two orthotropic harmonic structure tensors $\mathbb{F}_{1}$ and $\mathbb{F}_{2}$ can be expressed by $\Delta \mathbb{F} = \mathbb{F}^{\text{ortho}} \left ( \Delta d_{1}, \Delta d_{2}, \Delta d_{3} \right )$ based on the differences $\Delta d_{i}$ of the tensors scalar coefficients $d_{i}$ for $i \in [1,2,3]$, defined in Equation (13). The Frobenius norm of $\Delta \mathbb{F} = \mathbb{F}_{2} - \mathbb{F}_{1}$ is given by

$$ \left \Vert \Delta \mathbb{F} \right \Vert = \sqrt{8\left ( \Delta d_{1}^{2} + \Delta d_{2}^{2} + \Delta d_{3}^{2} \right ) + 2 \left ( \Delta d_{1} \Delta d_{2} + \Delta d_{1} \Delta d_{3} + \Delta d_{2} \Delta d_{3} \right )} $$

(59)

and is maximized for the pair $\mathbb{F}_{1} = \mathbb{F}^{\text{ortho}} \left ( \vec{d}^{ \text{apex}} \right )$ and $\mathbb{F}_{2} = \mathbb{F}^{\text{ortho}} \left ( \vec{d}^{ \text{center}} \right )$ with $\vec{d}^{\text{apex}}$ and $\vec{d}^{\text{center}}$ defined in Equation (57) and (58), respectively. Thus, the scalar measurement $\left \Vert \Delta \mathbb{F}^{\text{ortho}}_{\text{max}}\right \Vert \left ( {\boldsymbol {A}} \right )$ follows as

$$\begin{aligned} \left \Vert \Delta \mathbb{F}^{\text{ortho}}_{\text{max}}\right \Vert \left ( {\boldsymbol {A}} \right ) &= \left [\right . 1458 \alpha _{1}^{4} - 2916 \alpha _{1}^{3} \alpha _{3} + 4374 \alpha _{1}^{2} \alpha _{3}^{2} - 2916 \alpha _{1} \alpha _{3}^{3} \\ &\quad + 1458 \alpha _{3}^{4} - 1134 \alpha _{1}^{3} + 1701 \alpha _{1}^{2} \alpha _{3} + 1701 \alpha _{1} \alpha _{3}^{2} \\ &\quad - 1134 \alpha _{3}^{3} - 162 \alpha _{1}^{2} + 162 \alpha _{1} \alpha _{3} - 162 \alpha _{3}^{2} + 120 \left .\right ] / 18. \end{aligned}$$

(60)