Abstract
Fiber-orientation tensors describe the relevant features of the fiber-orientation distribution compactly and are thus ubiquitous in injection-molding simulations and subsequent mechanical analyses. In engineering applications to date, the second-order fiber-orientation tensor is the basic quantity of interest, and the fourth-order fiber-orientation tensor is obtained via a closure approximation. Unfortunately, such a description limits the predictive capabilities of the modeling process significantly, because the wealth of possible fourth-order fiber-orientation tensors is not exploited by such closures, and the restriction to second-order fiber-orientation tensors implies artifacts. Closures based on the second-order fiber-orientation tensor face a fundamental problem – which fourth-order fiber-orientation tensors can be realized? In the literature, only necessary conditions for a fiber-orientation tensor to be connected to a fiber-orientation distribution are found. In this article, we show that the typically considered necessary conditions, positive semidefiniteness and a trace condition, are also sufficient for being a fourth-order fiber-orientation tensor in the physically relevant case of two and three spatial dimensions. Moreover, we show that these conditions are not sufficient in higher dimensions. The argument is based on convex duality and a celebrated theorem of D. Hilbert (1888) on the decomposability of positive and homogeneous polynomials of degree four. The result has numerous implications for modeling the flow and the resulting microstructures of fiber-reinforced composites, in particular for the effective elastic constants of such materials. Based on our findings, we show how to connect optimization problems on fourth-order fiber-orientation tensors to semi-definite programming. The proposed formulation permits to encode symmetries of the fiber-orientation tensor naturally. As an application, we look at the differences between orthotropic and general, i.e., triclinic, fiber-orientation tensors of fourth order in two and three spatial dimensions, revealing the severe limitations inherent to orthotropic closure approximations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 State of the Art
Fiber-orientation tensors [1] date back to the far-reaching works [2, 3] and describe the relevant features of the fiber-orientation distribution of discontinuous fiber-reinforced composites. Within the virtual development and design process of such composites [1, 4–6], fiber-orientation tensors appear in material modeling [7–12], microstructure generation [13–19], mold filling or flow simulations [20–25] and the experimental computer tomography analysis [26–28]. This wide field of application motivates a detailed understanding of the mathematical properties of fiber-orientation tensors. Actually, the motivation and field of application is much more general, as fabric tensors and diffusion tensors share structural properties with fiber-orientation tensors. Fabric tensors [7, 29] share all characteristics with fiber-orientation tensors, except for a normalization constraint and are used in the field of porous materials. Diffusion tensors [30–32] also differ from fiber-orientation tensors only by a missing trace constraint and are used in medicine to describe the orientation of body tissues based on the diffusion motion of water molecules. This procedure is called diffusion-weighted magnetic resonance imaging (DW-MRI) [33, 34] and is, e.g., used on brain tissue to prevent strokes [35]. In particular, insights on the mathematical properties of fiber-orientation tensors might be transferred to diffusion tensors or fabric tensors.
The phase space of second-order fiber-orientation tensors is known [36–40], see the recent review [41]. A spectral decomposition is typically used to separate the structural features of a second-order fiber-orientation tensor, described by two independent eigenvalues with limited admissible parameter ranges, from the spatial alignment of this structural information in terms of a rotation or eigensystem. The limited structural variability of second-order fiber-orientation tensors is a critical ingredient for applications in process simulations [5, 9–11].
In contrast to the second-order case, the phase space of fourth-order fiber-orientation tensors is less well understood, a circumstance which motivated the work at hand. Algebraic properties of symmetry and normalization are agreed upon and discussed in the literature [42–46]. Bauer and Böhlke [41] developed an eigensystem-based parametrization of fourth-order fiber-orientation tensors combining the framework of irreducible tensors [47–53] with the work of Kanatani [2]. This parametrization ensures normalization as well as symmetry conditions automatically and separates second- and fourth-order data. Moreover, additional material-symmetry constraints may be taken into account in a natural way. Bauer and Böhlke [41] assume that positive semidefiniteness of the tensor is a sufficient condition to derive admissible parameter ranges, specifying the variety of fourth-order fiber-orientation tensors. This variety is presented for special cases motivated by material symmetry. The case of planar fourth-order fiber-orientation tensors and derived quantities is studied in successive papers [54, 55]. However, the necessary condition of positive semidefiniteness of the completely symmetric tensor is assumed to be sufficient. In Sect. 2.3 of this work, sufficiency of this condition for the cases inspected by Bauer and Böhlke [41] is proven.
A scientific topic which is intimately connected to the question on the phase space of fourth-order fiber-orientation tensors, is fiber-orientation closure approximations. Such closure approximations [22, 37, 56–61] are tensor-valued functions which postulate a functional relationship between a given second-order fiber-orientation tensor and an unknown fourth-order fiber-orientation tensor [19]. Identifying the phase space of fourth-order fiber-orientation tensors is essential to solve a fundamental problem of closure approximations – which fourth- order fiber-orientation tensors can be realized?
1.2 Contributions
This work is divided into a basic and an applied part. In the first part, we provide a proof for a simple characterization for the phase space of realizable fourth-order fiber-orientation tensors in the physically relevant dimensions two and three. In case of second-order fiber-orientation tensors, such a characterization is straightforward to obtain. Any symmetric second-order tensor whose eigenvalues are non-negative and sum to unity represents such a fiber-orientation tensor. In case of fourth-order tensors, an educated guess gives that completely symmetric fourth-order tensors whose eigenvalues are non-negative and sum to unity should correspond to realizable fourth-order fiber-orientation tensors.
Our arguments are based on two key ingredients. First, we use convex duality theory, in the following form. Two closed convex cones coincide precisely if their dual cones coincide. For the case at hand, the dual cones are a bit simpler to work with. The second insight is based on the natural identification of completely symmetric tensors of order \(k\) with homogeneous polynomials of degree \(k\). Then, a celebrated theorem due to Hilbert [62] on the decomposability of a positive homogeneous polynomial of fourth degree into a sum of squares of homogeneous quadratic polynomials implies the claim. Interestingly, this theorem holds only in spatial dimensions two and three. For higher dimensions, this decomposability does not hold. In particular, the educated guess for characterizing the phase-space of fourth-order fiber-orientation tensors is actually false for spatial dimensions four and above. This fact shows that there are no “elementary”, in particular dimension-independent, arguments for showing this characterization of the phase space to be valid.
As a by-product of our analysis, we show the equivalence of representations of fiber-orientation tensors in terms of integration, sums of monomials (rank-one tensors) and finite sums of monomials with non-negative weights summing to one, a consequence of Carathéodory’s theorem [63].
In the applied part, we investigate the geometry of the phase space of fourth-order fiber-orientation tensors via studying optimization problems on the latter. For this purpose, we consider suitable semidefinite programs, i.e., optimization problems posed on positive semidefinite matrices. Indeed, due to the characterization shown in the first part, we may identify a realizable fourth-oder fiber-orientation tensor with a positive semidefinite matrix in a suitable matrix representation (we use the Kelvin-Mandel notation).
Extreme states of the phase space of fourth-order fiber-orientation tensors are studied based on the parametrizations introduced in previous work [41], which separate second- and fourth-order data and enable to incorporate constraints on material symmetry easily. For fixed second-order information, we identify fourth-order data maximizing the projection onto a specified direction in two and three dimensions. Restricting the parameter space to orthotropic fourth-order information prohibits extreme projections into certain directions. These findings demonstrate the inherent limitations of closure approximations, as closed fourth-order information is automatically orthotropic. Due to the close connection to effective elastic properties, corresponding limitations of the effective stiffnesses become clear, as well.
This paper is organized as follows. After recapitulating basic properties of fiber-orientation tensors and their representation by finite sums, see Sect. 2.1, we specify a set of fiber-orientation tensor candidates in Sect. 2.2. In Sect. 2.3, we establish sufficiency of the conditions these candidates fulfill for tensor order four and dimensions two and three, leading to applications in Sect. 3. In Sect. 3.1, optimization on fiber-orientation tensors is identified as semidefinite programming. Consequences of material symmetry constraints, introduced in Sect. 3.2, on the problem of extreme fourth-order information, defined in Sect. 3.3, are presented in Sects. 3.4 and 3.5 for dimensions three and two.
After submitting this work we became aware of the article by Francfort et al. [64]. The authors were interested in the effective elastic properties of sequential laminates. For a specific scenario, they are led to studying fourth-order moments of Borel measures on the unit sphere, and show a representation theorem similar to the one established in the article at hand. Moreover, they employ the same strategy based on a convex dualization procedure, reducing the question to Hilbert’s theorem on the sum-of-squares decomposition of polynomials.
It is interesting to see how applied questions in different areas of engineering lead to rather similar questions in pure mathematics. In particular, advances in one area may be transferred to another. For instance, Francfort et al. [64] show – in our terminology – that every fourth-order fiber-orientation tensor in three spatial dimensions may be written as the convex combination of at most six quartics.
2 Realizability of Fourth-Order Fiber-Orientation Tensors
2.1 Fiber-Orientation Tensors
A non-polar fiber-orientation distribution is given by a probability measureFootnote 1\(\mu \) on the unit sphere

in \(d\) spatial dimensions which is invariant w.r.t. the involution \(\mathbf{p}\mapsto -\mathbf{p}\) on the unit sphere. This definition includes continuous fiber-orientation distributions, described by non-negative and suitably normalized functions \(\varphi \) via the measure
in terms of the usual surface measure \(dA\) on the unit sphere. Moreover, discrete fiber-orientation states, described in terms of \(N\) vectors \(\mathbf{p}_{i} \in S^{d-1}\) are included via the formulation
where \(\delta _{\mathbf{p}}\) denotes the Dirac measure concentrated on the point \(\mathbf{p}\).
As working with such measures may be cumbersome, Advani-Tucker [3] (compare also Kanatani [2]) introduced the so-called fiber-orientation tensors \(\mathbf{A}^{(k)}\) of order \(k\), where \(k\) denotes a non-negative integer, via the definition
in terms of the \(k\)-fold outer tensor product \(\mathbf{p}^{\otimes k}\) of the unit vector \(\mathbf{p}\), integrated over the unit sphere. The fiber-orientation tensors have the following properties.
-
1.
The fiber-orientation tensors are completely symmetric, i.e., the identity
$$ A^{(k)}_{i_{1} \, i_{2} \, \ldots \, i_{k}} = A^{(k)}_{i_{\sigma (1)} \, i_{\sigma (2)} \, \ldots \, i_{\sigma (k)}}, \quad i_{j} \in \{1, \ldots ,d\}, \quad j\in \{1,\ldots ,k\} $$(2.5)holds for the components of the tensor \(\mathbf{A}^{(k)}\) and any permutation \(\sigma \) of the index set \(\{1,\ldots ,k\}\). Denoting by \(\textrm {Sym}_{d}(k)\) the vector space of completely symmetric \(k\)-th order tensors in \(d\) dimensions, the condition (2.5) is equivalent to the inclusion \(\mathbf{A}^{(k)} \in {\textrm {Sym}_{k}(d)}\).
-
2.
For odd order \(k\), the fiber-orientation tensors vanish.
-
3.
The fiber-orientation tensor \(\mathbf{A}^{(k)}\) is positive semidefinite in the sense that
$$ \mathbf{A}^{(k)} \cdot ^{k} \mathbf{q}^{\otimes k} \geq 0 $$(2.6)holds for all vectors
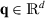 and the \(k\)-fold index contraction \(\cdot ^{k}\) of tensors.
and the \(k\)-fold index contraction \(\cdot ^{k}\) of tensors. -
4.
Double contraction with the \(d \times d\)-identity \(\operatorname{\textrm{Id}}\) recovers the fiber-orientation tensor of two orders lower
$$ \mathbf{A}^{(k+2)}:\operatorname{\textrm{Id}}= \mathbf{A}^{(k)}, \quad k = 0,1,2, \ldots $$(2.7) -
5.
The zeroth-order fiber-orientation tensor is unity, i.e., the equation
$$ A^{(0)} = 1 $$(2.8)holds.
-
6.
Any fixed fiber-orientation tensor \(\mathbf{A}^{(k)}\) of even order may be written as a finite sum
$$ \mathbf{A}^{(k)} = \sum _{i=1}^{r} w_{i} \, \mathbf{q}_{i}^{\otimes k} $$(2.9)with appropriate non-negative weights \(w_{i}\) which sum to unity, directions \(\mathbf{q}_{i} \in S^{d-1}\) and a non-negative integer \(r\) not exceeding \({{k+d-1}\choose {d-1}}\).
These properties 1.-5. are elementary to verify and well-known [3]. We provide a derivation of property 6. in the Appendix A. Property 6. permits us to restrict to finite sums (2.9) when considering fiber-orientation tensors of fixed order. In particular, it is not necessary to resort to the general integration-based definition (2.4).
2.2 Fiber-Orientation Tensor Candidates
The work at hand is specifically concerned with fourth-order fiber-orientation tensors  . More precisely, we are interested in the set of realizable fourth-order fiber-orientation tensors
. More precisely, we are interested in the set of realizable fourth-order fiber-orientation tensors

By Property 6. of the previous section, the set \(\texttt {A}(d)\) may be rewritten in the form

which is more convenient from the mathematical point of view.
The fundamental question we wish to answer in this work is the following. Suppose a fourth-order tensor  is given – under which (easy to verify) conditions can it be represented in the form (2.11)? Here, the non-negativity of the weights is crucial. Indeed, every completely symmetric \(k\)-th order tensor can be written as a linear combination of monomials [65, Lemma 4.2], i.e., with both positive and negative weights.
is given – under which (easy to verify) conditions can it be represented in the form (2.11)? Here, the non-negativity of the weights is crucial. Indeed, every completely symmetric \(k\)-th order tensor can be written as a linear combination of monomials [65, Lemma 4.2], i.e., with both positive and negative weights.
Elements  are completely symmetric (2.5), positive semidefinite on quartics (2.6)
are completely symmetric (2.5), positive semidefinite on quartics (2.6)

and satisfy the trace-conditions (2.7) as well as (2.8). Here, the operator :: stands for a fourth-fold contraction, and gives rise to an inner product on the space \(\textrm {Sym}_{4}(d)\) of completely symmetric fourth-order tensors.
However, it is readily seen that fiber-orientation tensors  satisfy a non-negativity condition which is stronger than the condition (2.12). More precisely, for any tensor
satisfy a non-negativity condition which is stronger than the condition (2.12). More precisely, for any tensor  , the inequality
, the inequality

i.e., symmetric second-order tensors \(\mathbf{S}\) in dimension \(d\). Indeed, in view of the representation (2.11), we observe

for any \(\mathbf{S} \in \textrm {Sym}_{2}(d)\) due to the non-negativity of the weights \(\mu _{i}\). Please notice that the condition (2.13) is stronger than the condition (2.12) as the special symmetric tensor \(\mathbf{S} = \mathbf{q} \otimes \mathbf{q}\) may be chosen in the condition (2.13). Moreover, the condition (2.13) is equivalent to the positive semidefiniteness of the tensor  , considered as a linear operator
, considered as a linear operator

on the vector space \(\textrm {Sym}_{2}(d)\), endowed with the inner product \((\mathbf{S},\mathbf{T})\mapsto \mathbf{S}:\mathbf{T}\).
In the literature, the following set is typically considered [41]

to consist of reasonable candidates for fiber-orientation tensors.
The set (2.16) is much easier to work with in practice than the original set \(\texttt {A}(d)\). Indeed, suppose a candidate tensor  is given. Then, it is elementary to examine its complete symmetry. Moreover, the non-negativity condition (2.13) and the normalization requirement
is given. Then, it is elementary to examine its complete symmetry. Moreover, the non-negativity condition (2.13) and the normalization requirement  are assessed via an eigendecomposition of the fourth-order tensor
are assessed via an eigendecomposition of the fourth-order tensor  , e.g., conveniently computed in an orthogonal basis like the Kelvin-Mandel representation [66, 67]. Indeed, both conditions are satisfied precisely if the eigenvalues are non-negative and sum to unity.
, e.g., conveniently computed in an orthogonal basis like the Kelvin-Mandel representation [66, 67]. Indeed, both conditions are satisfied precisely if the eigenvalues are non-negative and sum to unity.
In contrast, the defining condition of realizable fiber-orientation tensors (2.11) is much harder to check, as it involves a canonical decomposition problem with non-negativity constraints, which is known to be non-trivial [65].
Properties 1., 4. and 5. of fiber-orientation tensors, listed in the previous Sect. 2.1, imply all defining conditions of the set \(\texttt {Cand}(d)\). Moreover, we just established the positive semidefiniteness condition (2.13). Thus, the inclusion of sets
holds. The impending question remains whether the set inclusion (2.17) is strict or not, i.e., whether every element  is also realizable, i.e.,
is also realizable, i.e.,  holds.
holds.
2.3 On Sufficiency of Conditions
The purpose of this section is to check when the inverse direction of the inclusion (2.17)
holds. It will turn out that this is true for spatial dimensions \(d \leq 3\) and false for dimension \(d \geq 4\).
Central to our arguments is the auxiliary set

of sums of fourth-order tensor-powers of vectors with non-negative weights and the set of tensors

which are completely symmetric and positive semidefinite (2.13). Notice that, in contrast to the definition (2.11) of the set \(\texttt {A}(d)\), we use non-negative weights in the definition (2.19) instead of positive weights to include the zero tensor in the set \(\texttt {Q}(d)\). This inclusion is necessary for the set \(\texttt {Q}(d)\) to be closed.
The intersection conditions

and

hold. Thus, we have the implication
In particular, the fiber-orientation realization problem (2.18) may be studied in terms of the sets (2.19) and (2.20). Both sets are closed convex cones, i.e., they are closed, convex and invariant under the action  for \(\lambda \geq 0\). For the set \(\texttt {N}(d)\), the definition (2.20) immediately implies that it is a closed convex cone. Indeed, inequality constraints involving continuous functions lead to closed sets in finite dimensions, and the representation
for \(\lambda \geq 0\). For the set \(\texttt {N}(d)\), the definition (2.20) immediately implies that it is a closed convex cone. Indeed, inequality constraints involving continuous functions lead to closed sets in finite dimensions, and the representation  recasts the set (2.20) as an intersection of half spaces through zero. As the intersection of (a family of) convex cones is a convex cone, we see that the set (2.20) is a convex cone.
recasts the set (2.20) as an intersection of half spaces through zero. As the intersection of (a family of) convex cones is a convex cone, we see that the set (2.20) is a convex cone.
For the set \(\texttt {Q}(d)\), the definition (2.19) implies that the set is a convex cone. The closedness is a consequence of Carathéodory’s theorem [63], as detailed in the Appendix A. Indeed, as a consequence of this theorem, we may assume that no more than \(r_{\max} = {{k+d-1}\choose {d-1}}\) terms enter in the definition (2.19). Suppose a sequence  of elements in \(\texttt {Q}(d)\) converges to some
of elements in \(\texttt {Q}(d)\) converges to some  . Let us write
. Let us write

We observe

Thus, there is a uniform bound \(C\) on the coefficients \(\mu _{i,k}\). As the sets \([0,C]\) and \(S^{d-1}\) are compact, we may extract a subsequence (not relabeled), s.t.
for suitable \(\mu _{i} \in [0,C]\) and \(\mathbf{p}_{i} \in S^{d-1}\). Due to the uniqueness of limits, we obtain the representation

Hence, the set \(\texttt {Q}(d)\) is closed.
For any set  with inner product \(\langle \cdot ,\cdot \rangle \), the dual cone
with inner product \(\langle \cdot ,\cdot \rangle \), the dual cone  is defined by the relation
is defined by the relation

It is immediate to see that the set \(C^{*}\) does indeed define a closed convex cone. If, moreover, the original set \(C\) was a closed convex cone to start with, the dual cone of the dual cone coincides with the original set
This assertion is a consequence of convex duality theory [68].
As we identified the sets \(\texttt {Q}(d)\) and \(\texttt {N}(d)\) as closed convex cones, the equivalence
follows directly, where we fix the inner product

For this assertion to be useful, it is necessary to identify the dual cones explicitly. We have

Indeed, the inclusion ⊆ follows from the definition of the dual cone (2.28)

by selecting  as an element of \(\texttt {Q}(d)\). The inclusion ⊇ follows by considering
as an element of \(\texttt {Q}(d)\). The inclusion ⊇ follows by considering

With a completely analogous argument, we obtain

where \(\texttt{sym}\) refers to the complete symmetrization of all indices. To study when the sets \(\texttt {Q}(d)^{*}\) and \(\texttt {N}(d)^{*}\) coincide, we use the identification of completely symmetric tensors with homogeneous polynomials. More precisely, for any tensor  , the function
, the function

defines a homogeneous polynomial of order four. Conversely, any fourth-order homogeneous polynomial may be represented in the form (2.36). With this interpretation, a tensor  is an element of \(\texttt {Q}(d)^{*}\) (see equation (2.32)) precisely if the polynomial
is an element of \(\texttt {Q}(d)^{*}\) (see equation (2.32)) precisely if the polynomial  is non-negative
is non-negative

Similarly, a tensor  is an element of the set \(\texttt {N}(d)^{*}\) (2.35) precisely if the associated polynomial is a sum of squares
is an element of the set \(\texttt {N}(d)^{*}\) (2.35) precisely if the associated polynomial is a sum of squares

with homogeneous quadratic polynomials \(Q_{i}\). The decomposability of a positive homogeneous polynomial of even order (2.37) into a sum of squares (2.38) is a classical problem of real algebraic geometry, first addressed by Hilbert [62]. In our terminology, Hilbert’s results imply that the identity
holds for dimensions \(d\leq 3\) and is false otherwise. Explicit counterexamples [69, 70] and a quantitative version [71] are available.
The fact that positive polynomials of even order do not split as a sum of squares of polynomials of lower order, in general, led Hilbert to formulate his 17th problem. More precisely, he asked whether positive polynomials of even order may be written as a sum of squares of rational functions, which eventually led to the development of real algebraic geometry.
Unfortunately, Hilbert’s paper [62] is not formulated in contemporary mathematical jargon (in particular, it is in German). Fully detailed accounts of Hilbert’s proof are available in the book [72, Chap. 7] and the articles [73, 74]. We refer to Pfister-Scheiderer [75] for an elementary proof.
Based on the equality (2.39), we obtain the assertion
in the physically relevant cases \(d=2\) and \(d=3\). For higher dimensions, these assertions are false as a result of Hilbert’s results [62] and the fact that the sets \(\texttt {Cand}(d)\) and \(\texttt {A}(d)\) arise via a codimension-one condition, see equations (2.21) and (2.22).
3 Consequences and Variations
3.1 Optimal Microstructure: Programming on Fiber-Orientation Tensors
Identifying microstructures which lead to extreme effective physical properties of microstructured composite materials is a central goal in the field of material design. Following Sect. 2.3, and focusing on the practically relevant case of fourth-order fiber-orientation tensors in two or three dimensions, i.e., \(d=2\) or \(d=3\) and \(k=4\), the condition  with (2.16)
with (2.16)

is sufficient for the tensor  to be realizable, i.e., there exists at least one microstructure composed of fibers which is described by the tensor
to be realizable, i.e., there exists at least one microstructure composed of fibers which is described by the tensor  on average. In consequence, one strategy to identify extreme microstructures is to optimize w.r.t. fiber-orientation tensors. Optimization on the phase space of fourth-order fiber-orientation tensors may be accomplished via semidefinite programming, as the set
on average. In consequence, one strategy to identify extreme microstructures is to optimize w.r.t. fiber-orientation tensors. Optimization on the phase space of fourth-order fiber-orientation tensors may be accomplished via semidefinite programming, as the set

defined in equation (2.20), is a closed convex cone and requires the tensor  to be positive semidefinite. The normalization or trace condition
to be positive semidefinite. The normalization or trace condition  as well as the complete symmetry condition
as well as the complete symmetry condition  represent linear constraints of the semidefinite program. Linear semidefinite programming on the phase space of fourth-order fiber-orientation tensors solves the problem
represent linear constraints of the semidefinite program. Linear semidefinite programming on the phase space of fourth-order fiber-orientation tensors solves the problem

with the fourth-order tensor  entering the objective function and tuples
entering the objective function and tuples  of fourth-order tensors and scalars specifying \(m\) additional linear constraints. In order to solve the problem (3.3), a transition from tensorial notation to the Kelvin-Mandel notation is advised. In Kelvin-Mandel notation, fourth-order tensors with the left and right minor symmetry are represented in an orthonormal basis of symmetric second-order tensors. In contrast to the commonly used Voigt notation [76], the Kelvin-Mandel basis tensors are not only orthogonal but also normalized. As a result, in dimensions two and three, the eigenvalues of the matrix with respect to the Kelvin-Mandel basis tensors are identical to the eigenvalues of a fourth-order tensor with the aforementioned symmetries. The change from tensorial notation to Kelvin-Mandel notation is made possible by the symmetries of the problem and allows to reduce the dimension of the problem by introducing tensor bases. In the case \(d=3\), \(k=4\) and the symmetries at hand, it is possible to represent the tensor
of fourth-order tensors and scalars specifying \(m\) additional linear constraints. In order to solve the problem (3.3), a transition from tensorial notation to the Kelvin-Mandel notation is advised. In Kelvin-Mandel notation, fourth-order tensors with the left and right minor symmetry are represented in an orthonormal basis of symmetric second-order tensors. In contrast to the commonly used Voigt notation [76], the Kelvin-Mandel basis tensors are not only orthogonal but also normalized. As a result, in dimensions two and three, the eigenvalues of the matrix with respect to the Kelvin-Mandel basis tensors are identical to the eigenvalues of a fourth-order tensor with the aforementioned symmetries. The change from tensorial notation to Kelvin-Mandel notation is made possible by the symmetries of the problem and allows to reduce the dimension of the problem by introducing tensor bases. In the case \(d=3\), \(k=4\) and the symmetries at hand, it is possible to represent the tensor

in terms of a six times six coefficient matrix  and the dyads \(\mathbf{B}_{\xi} \otimes \mathbf{B}_{\zeta}\) with the indices \(\xi , \zeta \in \{1,\,\ldots,\, 6\}\). Details of the Kelvin-Mandel notation are given in Bauer and Böhlke [41]. The complete index symmetry of the tensor
and the dyads \(\mathbf{B}_{\xi} \otimes \mathbf{B}_{\zeta}\) with the indices \(\xi , \zeta \in \{1,\,\ldots,\, 6\}\). Details of the Kelvin-Mandel notation are given in Bauer and Böhlke [41]. The complete index symmetry of the tensor  stated in equation (2.5) is easily imposed by linear constraints, since the representation of a completely symmetric tensor
stated in equation (2.5) is easily imposed by linear constraints, since the representation of a completely symmetric tensor  in Kelvin-Mandel notation reads
in Kelvin-Mandel notation reads

with redundant coefficients color-coded following the reference [41] and “symmetric” indicating matrix symmetry of the tensor coefficients in equation (3.5).
An active rotation of a fiber-orientation tensor changes the alignment in space of the averaged directional information on the fibers’ orientation. However, the averaged information itself, apart from its alignment in space, is unaffected. If we are interested in studying the averaged information itself, independent of its alignment in space, we can use an eigensystem-based parametrization of fourth-order fiber-orientation tensors [41]. The 15-dimensional space \(\textrm {Sym}_{4}(3)\), reduced by the normalization constraint (2.8), leaves 14 dimensions, i.e., three defining the spatial alignment of the averaged information and eleven remaining dimensions which represent structural information. In addition to distinguishing alignment and structural information, the parametrization of Bauer and Böhlke [41] separates second- and fourth-order information following the seminal work of Kanatani [2]. Therefore, searching for fourth-order data which maximizes the objective function for given second-order information is possible. Further, material symmetry properties can be easily incorporated by using the additional constraints in equation (3.3). Following Bauer and Böhlke [41, Equation (59)], a general, i.e., triclinic, fourth-order fiber-orientation tensor may be parameterized by

based on an eigensystem-dependent parametrization of the corresponding second-order fiber-orientation tensor
where we apply the common ordering convention
In addition, equation (3.6) contains the isotropic fourth-order fiber-orientation tensor

a triclinic fourth-order deviatoric structure tensor represented in Kelvin-Mandel notation by
the operator \(\text{sym}(\cdot )\) projecting onto the completely symmetric part of a tensor and the operator \(\text{dev}(\cdot )\) extracting the deviatoric part of a tensor [47]. For clarity, the constant and second-order part of equation (3.6) , which corresponds to the linear closure [77], is given explicitly

already including the normalization constraint \(\lambda _{3} = 1- \lambda _{1} - \lambda _{2}\) enforced by the condition (2.8). If we follow the ordering convention on the eigenvalues of \(\mathbf{A}\) in expression (3.8) and decide for either right- or left-handed coordinates, a symmetric second-order tensor, which is automatically orthotropic, will have at least four eigensystems. These four systems differ by the action of elements of the orthotropic symmetry group, each changing signs of two eigenvectors at a time. Without loss of generality, we choose one of the possible four eigensystems to be defined by
mapping the arbitrary but fixed basis \(\left \{\mathbf{e}_{i}\right \}\) onto the eigensystem \(\left \{\mathbf{v}_{i}\right \}\). Selecting one of the other three possible eigensystems results in two sign changes of groups of tensor coefficients but leaves the identified physical quantity unaffected. The Kelvin-Mandel [66, 67] basis \(\mathbf{B}^{\mathbf{v}}_{\xi} \otimes \mathbf{B}^{\mathbf{v}}_{\zeta}\) in (3.10) and (3.11) is spanned in the eigensystem and therefore, e.g., \(\boldsymbol{B}_{1} = \mathbf{v}_{1} \otimes \mathbf{v}_{1}\) holds. This simplifies incorporating specific material symmetry.
3.2 Material Symmetry Constraints
Constraints of material symmetry reduce the dimensionality of the optimization problem stated in equation (3.3). Furthermore, material symmetry constraints arise naturally in the context of closure approximations, as any second-order fiber-orientation tensor is (at least) orthotropic, whereas fourth-order fiber-orientation tensors may not be orthotropic, in general. A rotation \(\mathbf{Q} \in \text{SO}(d)\) is said to belong to the symmetry class  of a given tensor
of a given tensor  , provided its action by rotation leaves the tensor invariant, i.e., the characterization
, provided its action by rotation leaves the tensor invariant, i.e., the characterization

holds with the Rayleigh product ⋆ rotating each tensor basis of the tensor  by the rotation \(\mathbf{Q}\). Forte and Vianello [48] identified the possible symmetry classes of fourth-order tensors, which read – ordered by increasing cardinality of the symmetry group
by the rotation \(\mathbf{Q}\). Forte and Vianello [48] identified the possible symmetry classes of fourth-order tensors, which read – ordered by increasing cardinality of the symmetry group  – triclinic, monoclinic, orthotropic, trigonal, tetragonal, transversely isotropic, cubic and isotropic. Isotropic quantities are symmetric with respect to all rotations, whereas the triclinic symmetry group is trivial,
– triclinic, monoclinic, orthotropic, trigonal, tetragonal, transversely isotropic, cubic and isotropic. Isotropic quantities are symmetric with respect to all rotations, whereas the triclinic symmetry group is trivial,  .
.
Material symmetry constraints impose linear constraints in the optimization problem (3.3). For example, orthotropic symmetry w.r.t. the symmetry axes in three-dimensions is equivalent to vanishing parameters \(d_{i}=0\) for \(i \in \{4,\,5,\,6,\,7,\,8,\,9\}\) in the parametrization (3.6), as the orthotropic symmetry class
consists of the rotations
expressed in a coordinate system \(\bigl\{ \mathbf{v}_{i} \bigr\}\) whose axes are normal to symmetry planes of the orthotropic quantity.
3.3 Extreme Fourth-Order Information
We are interested in the phase space of fourth-order fiber-orientation tensors, extending previous work of Bauer and Böhlke [41]. For this purpose, we fix a second-order fiber-orientation tensor and study the set of all fourth-order fiber-orientation tensors which cover the prescribed second-order tensor in the sense that the condition  holds. This set is closed and convex, and we wish to study the “extreme states” of this set. For this purpose and with the notation introduced in the previous sections, suppose that a fiber-orientation tensor \(\mathbf{A}(\lambda _{1},\, \lambda _{2})\) is given in its principal axes and where \(\lambda _{1}\), \(\lambda _{2}\) refer to the two largest eigenvalues. Then, we consider an arbitrary direction
holds. This set is closed and convex, and we wish to study the “extreme states” of this set. For this purpose and with the notation introduced in the previous sections, suppose that a fiber-orientation tensor \(\mathbf{A}(\lambda _{1},\, \lambda _{2})\) is given in its principal axes and where \(\lambda _{1}\), \(\lambda _{2}\) refer to the two largest eigenvalues. Then, we consider an arbitrary direction
on the unit sphere, parameterized by the angles \(\varphi \) and \(\theta \). We consider the tensor  in problem (3.3) combined with the constraint
in problem (3.3) combined with the constraint  , specifying the second-order information. In addition, material symmetry is ensured by enforcing
, specifying the second-order information. In addition, material symmetry is ensured by enforcing  for all rotations \(\mathbf{Q} \in \mathcal {S}^{\text{problem}}\) of the selected symmetry class \(\mathcal {S}^{\text{problem}}\), leading to the problem
for all rotations \(\mathbf{Q} \in \mathcal {S}^{\text{problem}}\) of the selected symmetry class \(\mathcal {S}^{\text{problem}}\), leading to the problem

For the convenience of the reader, we translated typical constraints of problem (3.18) in terms of expressions  with \(k = 1, \ldots, m\) with tensors
with \(k = 1, \ldots, m\) with tensors  , see Table 1 in appendix B. Before discussing the results, we briefly comment on the motivation for investigation the optimization problem (3.18). The effective stiffness
, see Table 1 in appendix B. Before discussing the results, we briefly comment on the motivation for investigation the optimization problem (3.18). The effective stiffness  of a short-fiber reinforced composite is rather accurately described by a Voigt-type orientation average [3] of the stiffness
of a short-fiber reinforced composite is rather accurately described by a Voigt-type orientation average [3] of the stiffness  of a short-fiber composite with fibers aligned in direction \(\mathbf{p}\). More precisely, it holds
of a short-fiber composite with fibers aligned in direction \(\mathbf{p}\). More precisely, it holds

with the fiber-orientation distribution \(\mu \), see equations (2.2) and (2.3). Based on the observation that the effective stiffness  of a composite with aligned fibers whose centers and lengths are random is transversely isotropic, and thus may be represented in the form
of a composite with aligned fibers whose centers and lengths are random is transversely isotropic, and thus may be represented in the form

for suitable coefficients \(b_{1}, b_{2}, \ldots , b_{5}\), the effective stiffness (3.19) may be expressed explicitly in the form

where the fiber-orientation tensors \(\mathbf{A}\) and  appear explicitly, see Advani-Tucker [3] for details. In equations (3.20) and (3.21),
appear explicitly, see Advani-Tucker [3] for details. In equations (3.20) and (3.21),  stands for the identity tensor on symmetric second-order tensors and the symbol \(\Box _{*}\) is an abbreviation of the product
stands for the identity tensor on symmetric second-order tensors and the symbol \(\Box _{*}\) is an abbreviation of the product
between two symmetric second-order tensors \(\mathbf{B}\) and \(\mathbf{C}\), expressed in index notation.
 with
with 
Typically, the coefficient \(b_{1}\) is large compared to the remaining coefficients. Therefore, monitoring the product  provides a good indication of the stiffness
provides a good indication of the stiffness  in direction \(\mathbf{n}\). Actually, our proposed techniques permit to handle the product
in direction \(\mathbf{n}\). Actually, our proposed techniques permit to handle the product  directly, in view of the representation formula (3.21). However, the results would depend on the arising parameters \(b_{1},b_{2},\ldots ,b_{5}\), and thus obfuscate potential insights. For this reason, we chose to retain the material-independent choice (3.18).
directly, in view of the representation formula (3.21). However, the results would depend on the arising parameters \(b_{1},b_{2},\ldots ,b_{5}\), and thus obfuscate potential insights. For this reason, we chose to retain the material-independent choice (3.18).
3.4 Results in Three Spatial Dimensions
On a regular grid of points on one-eighth of the unit sphere, the maximum values of the objective function of problem (3.18) are visualized in Figs. 1, 2, 3 as spherical plots. Due to the symmetry of the objective function specified by the quartic product \(\mathbf{n}^{\otimes 4}\), inspecting the results on a grid of direction within one-eighth of the unit sphere is sufficient. Figures 1 to 3 differ by the given second-order fiber-orientation information, i.e., tuples \(\mathbf{A}(\lambda _{1}, \lambda _{2})\). Each of the figures contains two surfaces. The first surface plotted in light gray represents the maximum objective function obtained without material constraints on  , whereas the second surface plotted in blue represents the same quantity with
, whereas the second surface plotted in blue represents the same quantity with  restricted to orthotropic fourth-order fiber-orientation tensors, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{orthotropic}}\) in problem (3.18). Figures 1 to 3 demonstrate that restricting to the orthotropic subspace limits the possibility to obtain large values of the objective function in specific directions. Only in directions aligned with the axes of the eigensystem \(\bigl\{ \mathbf{v}_{i} \bigr\}\) as well as in directions with \((\varphi ,\, \theta ) \in \left \{(0,\, 45^{\circ}),\, (90^{\circ}, \, 45^{\circ}),\, (45^{\circ},\, 0)\right \}\), the constraint of orthotropy does not induce a restriction on the extreme value of the objective function. With increasing anisotropy of the specified second-order information, the consequences of the constraint onto the orthotropic subspace decrease.
restricted to orthotropic fourth-order fiber-orientation tensors, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{orthotropic}}\) in problem (3.18). Figures 1 to 3 demonstrate that restricting to the orthotropic subspace limits the possibility to obtain large values of the objective function in specific directions. Only in directions aligned with the axes of the eigensystem \(\bigl\{ \mathbf{v}_{i} \bigr\}\) as well as in directions with \((\varphi ,\, \theta ) \in \left \{(0,\, 45^{\circ}),\, (90^{\circ}, \, 45^{\circ}),\, (45^{\circ},\, 0)\right \}\), the constraint of orthotropy does not induce a restriction on the extreme value of the objective function. With increasing anisotropy of the specified second-order information, the consequences of the constraint onto the orthotropic subspace decrease.
Two views on identical surfaces of polar plots of the maximum objective function value, i.e.,  , of problem (3.18) for values \(\lambda _{1} = 1/3\) and \(\lambda _{2} = 1/3\). Results for the unconstrained triclinic case, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{triclinic}}\) are given in light gray, whereas results with restriction to the orthotropic subspace, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{orthotropic}}\) are shown in blue
, of problem (3.18) for values \(\lambda _{1} = 1/3\) and \(\lambda _{2} = 1/3\). Results for the unconstrained triclinic case, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{triclinic}}\) are given in light gray, whereas results with restriction to the orthotropic subspace, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{orthotropic}}\) are shown in blue
Polar plots of the maximum objective function value, i.e.,  , of problem (3.18) for values \(\lambda _{1} = 1/2\) and \(\lambda _{2} = 3/8\). Results for the unconstrained triclinic case, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{triclinic}}\) are given in light gray, whereas results with restriction to the orthotropic subspace, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{orthotropic}}\) are shown in blue
, of problem (3.18) for values \(\lambda _{1} = 1/2\) and \(\lambda _{2} = 3/8\). Results for the unconstrained triclinic case, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{triclinic}}\) are given in light gray, whereas results with restriction to the orthotropic subspace, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{orthotropic}}\) are shown in blue
Polar plots of the maximum objective function value, i.e.,  , of problem (3.18) for values \(\lambda _{1} = 8/10\) and \(\lambda _{2} = 1/10\). Results for the unconstrained triclinic case, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{triclinic}}\) are given in light gray, whereas results with restriction to the orthotropic subspace, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{orthotropic}}\) are shown in blue
, of problem (3.18) for values \(\lambda _{1} = 8/10\) and \(\lambda _{2} = 1/10\). Results for the unconstrained triclinic case, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{triclinic}}\) are given in light gray, whereas results with restriction to the orthotropic subspace, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{orthotropic}}\) are shown in blue
Some care is advised when interpreting the results shown in Fig. 1. Indeed, as the prescribed second-order fiber-orientation tensor \(\mathbf{A}\) is isotropic, the three mutually orthogonal eigenvectors \(\mathbf{v}_{1}\), \(\mathbf{v}_{2}\) and \(\mathbf{v}_{3}\) are not unique. Thus, the surface in Fig. 1 should be interpreted relative to this orthogonal basis. Changing this orthogonal basis also changes the coordinates of the direction vector \(\textbf{n}\).
Please note also that the fourth-order fiber-orientation tensor  maximizing the product
maximizing the product  will, in general, have a smaller symmetry group than the corresponding second-order fiber-orientation tensor
will, in general, have a smaller symmetry group than the corresponding second-order fiber-orientation tensor  , as the direction \(\mathbf{n}\) “breaks the symmetry” (in physics terminology). For instance, the tensors realizing the maxima shown in Fig. 1 will not be isotropic, but their associated \(\mathbf{A}\)-tensors will be.
, as the direction \(\mathbf{n}\) “breaks the symmetry” (in physics terminology). For instance, the tensors realizing the maxima shown in Fig. 1 will not be isotropic, but their associated \(\mathbf{A}\)-tensors will be.
Similar considerations apply to cases where two eigenvalues of the second-order fiber-orientation tensor \(\mathbf{A}\) coincide, as considered below.
3.5 Results in Two Spatial Dimensions
If the given second-order fiber-orientation \(\mathbf{A}\) is planar, i.e., fulfills the conditions \(\lambda _{2} = 1-\lambda _{1}\) and \(1/2 \le \lambda _{1} \le 1\), the constraint  in problem (3.18) will enforce planarity of the resulting fourth-order fiber-orientation tensor
in problem (3.18) will enforce planarity of the resulting fourth-order fiber-orientation tensor  . Within the plane spanned by the directions \(\mathbf{v}_{1}\) and \(\mathbf{v}_{2}\), the maximum values of the objective function
. Within the plane spanned by the directions \(\mathbf{v}_{1}\) and \(\mathbf{v}_{2}\), the maximum values of the objective function  are plotted in Fig. 4 (a) to (f) with and without constraints in terms of material symmetry. The directions \(\mathbf{n}(\varphi , \theta )\) within the plane \(\mathbf{v}_{1}\) and \(\mathbf{v}_{2}\) are characterized by the condition \(\theta = \pi /2\) and varying angle \(\varphi \). The values of the objective function obtainable for directions aligned with \(\mathbf{v}_{1}\) and \(\mathbf{v}_{2}\) are \(\lambda _{1}\) and \(\lambda _{2}\), respectively. For directions specified by angles \(\varphi \in \{0,\, 45^{\circ},\, 90^{\circ}\}\), the objective values obtained with or without material symmetry constraints are identical. For all other directions, restricting to the class of orthotropic fiber-orientation tensors
are plotted in Fig. 4 (a) to (f) with and without constraints in terms of material symmetry. The directions \(\mathbf{n}(\varphi , \theta )\) within the plane \(\mathbf{v}_{1}\) and \(\mathbf{v}_{2}\) are characterized by the condition \(\theta = \pi /2\) and varying angle \(\varphi \). The values of the objective function obtainable for directions aligned with \(\mathbf{v}_{1}\) and \(\mathbf{v}_{2}\) are \(\lambda _{1}\) and \(\lambda _{2}\), respectively. For directions specified by angles \(\varphi \in \{0,\, 45^{\circ},\, 90^{\circ}\}\), the objective values obtained with or without material symmetry constraints are identical. For all other directions, restricting to the class of orthotropic fiber-orientation tensors  limits the values of the objective function that can be attained. This limitation decreases as second-order fiber-orientation tensor information advances towards the uni-directional state, i.e., \(\lambda _{1} \rightarrow 1\).
limits the values of the objective function that can be attained. This limitation decreases as second-order fiber-orientation tensor information advances towards the uni-directional state, i.e., \(\lambda _{1} \rightarrow 1\).
Polar plots of the maximum objective function value, i.e.,  , of problem (3.18) and \(\lambda _{2} = 1- \lambda _{1}\) for selected values of \(\lambda _{1}\). Results are given for restriction to the triclinic or orthotropic subspace, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{triclinic}}\) or \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{orthotropic}}\) respectively
, of problem (3.18) and \(\lambda _{2} = 1- \lambda _{1}\) for selected values of \(\lambda _{1}\). Results are given for restriction to the triclinic or orthotropic subspace, i.e., \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{triclinic}}\) or \(\mathcal {S}^{\text{problem}} = \mathcal {S}^{\text{orthotropic}}\) respectively
4 Conclusion
The work at hand showed that the set of candidates for fourth-order fiber-orientation tensors

represents all realizable fourth-order fiber-orientation tensors for the practically relevant spatial dimensions \(d=2\) or \(d=3\). This result provides an a-posteriori justification for the approach of Bauer and Böhlke [41] to characterize the variety of fourth-order fiber-orientation tensors based on tensor decompositions.
Our result has a number of interesting implications and applications. For a start, it permits assessing the realizability of a given fourth-order tensor as a fiber-orientation tensor in a simple and straightforward way. Consider, for instance, fiber-microstructure generators [18, 19, 78], which serve as the basis for full-field simulations and where the fourth-order fiber-orientation tensor serves as the input. Then, if the prescribed tensor does not belong to the set \(\texttt {Cand}(d)\), it cannot be realized by a fiber microstructure at all, independent of the size of the microstructure and the number of considered fibers. This simple fact provides constraints on fiber-orientation closure approximations used in fiber-orientation dynamics [37, 38], and may be used to re-evaluate their physical plausibility.
A second consequence concerns the effective elastic properties of short-fiber reinforced composites. It is well-known that, together with the volume fraction and the aspect ratio, the fourth-order fiber-orientation tensor is responsible for the effective elastic properties of such a composite [3, 8, 9, 40]. Classical closure approximations, expressing the fourth-order fiber-orientation tensor as an isotropic tensor function of the second-order fiber-orientation tensor, are restricted, by definition, to orthotropic symmetry. In particular, the set of realizable effective stiffnesses is restricted to being orthotropic. Our computational investigations revealed that this restriction to orthotropy actually underestimates the achievable effective stiffnesses in particular directions for a prescribed second-order fiber-orientation tensor significantly. Thus, we expect that using the full phase space of fourth-order fiber-orientation tensors will be critical for exploiting the full lightweight potential of such short-fiber composites, e.g., by reducing safety factors. First steps in this direction were already proposed [3, 79, 80], and these works may be revisited with fresh impetus.
Last but not least let us stress the simplicity and utility of the connection between optimization of fiber microstructures described by fourth-order fiber-orientation tensors and semi-definite programming introduced in the work at hand. In particular due to the power of the available optimization solvers, new directions were opened to engineers working on fiber-reinforced components and their optimal design.
Notes
On the \(\sigma \)-algebra of Borel sets.
References
Tucker, C.L. III: Fundamentals of Fiber Orientation: Description, Measurement and Prediction. Carl Hanser Verlag, Munich (2022)
Kanatani, K.: Distribution of directional data and fabric tensors. Int. J. Eng. Sci. 22, 149–164 (1984)
Advani, S.G., Tucker, C.L. III: The use of tensors to describe and predict fiber orientation in short fiber composites. J. Rheol. 31, 751–784 (1987)
Böhlke, T., Henning, F., Hrymak, A., Kärger, L., Weidenmann, K., Wood, J.T.: Continuous–Discontinuous Fiber-Reinforced Polymers: An Integrated Engineering Approach. Carl Hanser Verlag, Munich (2019)
Görthofer, J., Meyer, N., Pallicity, T.D., Schöttl, L., Trauth, A., Schemmann, M., Hohberg, M., Pinter, P., Elsner, P., Henning, F., Hrymak, A., Seelig, T., Weidenmann, K., Kärger, L., Böhlke, T.: Virtual process chain of sheet molding compound: development, validation and perspectives. Composites, Part B, Eng. 169, 133–147 (2019)
Meyer, N., Gajek, S., Görthofer, J., Hrymak, A., Kärger, L., Henning, F., Schneider, M., Böhlke, T.: A probabilistic virtual process chain to quantify process-induced uncertainties in Sheet Molding Compounds. Composites, Part B, Eng. 249, 110380 (2022)
Zysset, P.K., Curnier, A.: An alternative model for anisotropic elasticity based on fabric tensors. Mech. Mater. 21(4), 243–250 (1995)
Jack, D.A., Smith, D.E.: The effect of fibre orientation closure approximations on mechanical property predictions. Composites, Part A, Appl. Sci. Manuf. 38(3), 975–982 (2007)
Jack, D.A., Smith, D.E.: Elastic properties of short-fiber polymer composites, derivation and demonstration of analytical forms for expectation and variance from orientation tensors. J. Compos. Mater. 42(3), 277–308 (2008)
Goldberg, N., Ospald, F., Schneider, M.: A fiber orientation-adapted integration scheme for computing the hyperelastic Tucker average for short fiber reinforced composites. Comput. Mech. 60(4), 595–611 (2017)
Köbler, J., Schneider, M., Ospald, F., Andrä, H., Müller, R.: Fiber orientation interpolation for the multiscale analysis of short fiber reinforced composite parts. Comput. Mech. 61(6), 729–750 (2018)
Hessman, P.A., Welschinger, F., Hornberger, K., Böhlke, T.: On mean field homogenization schemes for short fiber reinforced composites: unified formulation, application and benchmark. Int. J. Solids Struct. 230–231, 111141 (2021)
Feder, J.: Random sequential adsorption. J. Theor. Biol. 87(2), 237–254 (1980)
Pan, Y., Iorga, L., Pelegri, A.A.: Numerical generation of a random chopped fiber composite RVE and its elastic properties. Compos. Sci. Technol. 68(13), 2792–2798 (2008)
Altendorf, H., Jeulin, D.: Random-walk-based stochastic modeling of three-dimensional fiber systems. Phys. Rev. E 83(4), 041804 (2011)
Salnikov, V., Choï, D., Karamian-Surville, P.: On efficient and reliable stochastic generation of RVEs for analysis of composites within the framework of homogenization. Comput. Mech. 55(1), 127–144 (2015)
Tian, W., Qi, L., Zhou, J., Liang, J., Ma, Y.: Representative volume element for composites reinforced by spatially randomly distributed discontinuous fibers and its applications. Compos. Struct. 131, 366–373 (2015)
Schneider, M.: The sequential addition and migration method to generate representative volume elements for the homogenization of short fiber reinforced plastics. Comput. Mech. 59(2), 247–263 (2017)
Mehta, A., Schneider, M.: A sequential addition and migration method for generating microstructures of short fibers with prescribed length distribution. Comput. Mech. 70(4), 829–851 (2022)
Jeffery, G.B.: The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. Ser. A, Contain. Pap. Math. Phys. Character, 102(715), 161–179 (1922)
Folgar, F., Tucker, C.L. III: Orientation behaviour of fibers in concentrated suspensions. J. Reinf. Plast. Compos. 3, 98–119 (1984)
Advani, S.G., Tucker, C.L. III: A numerical simulation of short fiber orientation in compression molding. Polym. Compos. 11(3), 164–173 (1990)
Yamamoto, S., Matsuoka, T.: A method for dynamic simulation of rigid and flexible fibers in a flow field. J. Chem. Phys. 98(1), 644–650 (1993)
Wang, J., O’Gara, J.F., Tucker, C.L. III: An objective model for slow orientation kinetics in concentrated fiber suspensions: theory and rheological evidence. J. Rheol. 52(5), 1179–1200 (2008)
Phelps, J.H., Tucker, C.L. III: An anisotropic rotary diffusion model for fiber orientation in short-and long-fiber thermoplastics. J. Non-Newton. Fluid Mech. 156(3), 165–176 (2009)
Bay, R.S., Tucker, C.L. III: Stereological measurement and error estimates for three-dimensional fiber orientation. Polym. Eng. Sci. 32(4), 240–253 (1992)
Clarke, A.R., Archenhold, G., Davidson, N.C.: A novel technique for determining the 3D spatial distribution of glass fibres in polymer composites. Compos. Sci. Technol. 55(1), 75–91 (1995)
Geusebroek, J.-M., Smeulders, A.W.M., van de Weijer, J.: Fast anisotropic Gauss filtering. IEEE Trans. Image Process. 12(8), 938–943 (2003)
Cowin, S.C.: The relationship between the elasticity tensor and the fabric tensor. Mech. Mater. 4(2), 137–147 (1985)
Le Bihan, D., Mangin, J.-F., Poupon, C., Clark, C.A., Pappata, S., Molko, N., Chabriat, H.: Diffusion tensor imaging: concepts and applications. J. Magn. Reson. Imaging 13(4), 534–546 (2001)
Mori, S., van Zijl, P.C.M.: Fiber tracking: principles and strategies–a technical review. NMR Biomed. 15(7–8), 468–480 (2002)
Basser, P.J., Jones, D.K.: Diffusion-tensor MRI: theory, experimental design and data analysis–a technical review. NMR Biomed. 15(7–8), 456–467 (2002)
Taylor, D.G., Bushell, M.C.: The spatial mapping of translational diffusion coefficients by the NMR imaging technique. Phys. Med. Biol. 30(4), 345 (1985)
Le Bihan, D., Breton, E., Lallemand, D., Grenier, P., Cabanis, E., Laval-Jeantet, M.: MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology 161(2), 401–407 (1986)
Schaefer, P.W., Grant, P.E., Gonzalez, R.G.: Diffusion-weighted MR imaging of the brain. Radiology 217(2), 331–345 (2000)
Nomura, S., Kawai, H., Kimura, I., Kagiyama, M.: General description of orientation factors in terms of expansion of orientation distribution function in a series of spherical harmonics. J. Polym. Sci. A-2, Polym. Phys. 8(3), 383–400 (1970)
Cintra, J.S. Jr., Tucker, C.L. III: Orthotropic closure approximations for flow-induced fiber orientation. J. Rheol. 39(6), 1095–1122 (1995)
Chung, D.H., Kwon, T.H.: Improved model of orthotropic closure approximation for flow induced fiber orientation. Polym. Compos. 22(5), 636–649 (2001)
Linn, J.: The Folgar-Tucker model as a differential algebraic system for fiber orientation calculation. Berichte des Fraunhofer-Instituts für Techno- und Wirtschaftsmathematik (ITWM Report) vol. 75 (2005). https://doi.org/10.24406/publica-fhg-292733
Müller, V., Böhlke, T.: Prediction of effective elastic properties of fiber reinforced composites using fiber orientation tensors. Compos. Sci. Technol. 130, 36–45 (2016)
Bauer, J.K., Böhlke, T.: Variety of fiber orientation tensors. Math. Mech. Solids 27(7), 1185–1211 (2022)
Moakher, M.: The algebra of fourth-order tensors with application to diffusion MRI. In: Visualization and Processing of Tensor Fields, pp. 57–80. Springer, Berlin (2009)
Rahmoun, J., Kondo, D., Millet, O.: A 3D fourth order fabric tensor approach of anisotropy in granular media. Comput. Mater. Sci. 46(4), 869–880 (2009)
Weldeselassie, Y.T., Barmpoutis, A., Atkins, M.S.: Symmetric positive semi-definite Cartesian tensor fiber orientation distributions (CT-FOD). Med. Image Anal. 16(6), 1121–1129 (2012)
Ghosh, A., Papadopoulo, T., Deriche, R.: Biomarkers for HARDI: 2nd & 4th order tensor invariants. In: 2012 9th IEEE International Symposium on Biomedical Imaging (ISBI), pp. 26–29. IEEE, Barcelona (2012)
Moreno, R., Smedby, Ö., Pahr, D.H.: Prediction of apparent trabecular bone stiffness through fourth-order fabric tensors. Biomech. Model. Mechanobiol. 15(4), 831–844 (2016)
Spencer, A.J.M.: A note on the decomposition of tensors into traceless symmetric tensors. Int. J. Eng. Sci. 8(6), 475–481 (1970)
Forte, S., Vianello, M.: Symmetry classes for elasticity tensors. J. Elast. 43(2), 81–108 (1996)
Jerphagnon, J., Chemla, D., Bonneville, R.: The description of the physical properties of condensed matter using irreducible tensors. Adv. Phys. 27(4), 609–650 (1978)
Adams, B.L., Boehler, J.P., Guidi, M., Onat, E.T.: Group theory and representation of microstructure and mechanical behavior of polycrystals. J. Mech. Phys. Solids 40(4), 723–737 (1992)
Cowin, S.C.: Properties of the anisotropic elasticity tensor. Q. J. Mech. Appl. Math. 42(2), 249–266 (1989)
Rychlewski, J.: A qualitative approach to Hooke’s tensors. Part I. Arch. Mech. 52(4–5), 737–759 (2000)
Bauer, J.K.: Fiber orientation tensors and mean field homogenization: Application to sheet molding compound. Doctoral thesis. In press
Bauer, J.K., Böhlke, T.: Fiber orientation distributions based on planar fiber orientation tensors of fourth order. Math. Mech. Solids (2022). https://doi.org/10.1177/10812865221093958
Bauer, J.K., Böhlke, T.: On the dependence of orientation averaging mean field homogenization on planar fourth-order fiber orientation tensors. Mech. Mater. 170, 104307 (2022)
Han, K.-H., Im, Y.-T.: Modified hybrid closure approximation for prediction of flow-induced fiber orientation. J. Rheol. 43(3), 569–589 (1999)
Chung, D.H., Kwon, T.H.: Invariant-based optimal fitting closure approximation for the numerical prediction of flow-induced fiber orientation. J. Rheol. 46(1), 169–194 (2002)
Montgomery-Smith, S., He, W., Jack, D.A., Smith, D.E.: Exact tensor closures for the three-dimensional Jeffery’s equation. J. Fluid Mech. 680, 321–335 (2011)
Montgomery-Smith, S., Jack, D.A., Smith, D.E.: The fast exact closure for Jeffery’s equation with diffusion. J. Non-Newton. Fluid Mech. 166(7–8), 343–353 (2011)
Karl, T., Gatti, D., Frohnapfel, B., Böhlke, T.: Asymptotic fiber orientation states of the quadratically closed Folgar–Tucker equation and a subsequent closure improvement. J. Rheol. 65(5), 999–1022 (2021)
Tucker, C.L. III: Planar fiber orientation: Jeffery, non-orthotropic closures, and reconstructing distribution functions. J. Non-Newton. Fluid Mech. 310, 104939 (2022)
Hilbert, D.: Über die Darstellung definiter Formen als Summe von Formenquadraten. Math. Ann. 32(3), 342–350 (1888)
Carathéodory, C.: Über den Variabilitätsbereich der Fourier’schen Konstanten von positiven harmonischen Funktionen. Rend. Circ. Mat. Palermo 32(1), 193–217 (1911)
Francfort, G., Murat, F., Tartar, L.: Fourth-order moments of nonnegative measures on \(S^{2}\) and applications. Arch. Ration. Mech. Anal. 131, 305–333 (1995)
Comon, P., Golub, G., Lim, L.-H., Mourrain, B.: Symmetric tensors and symmetric tensor rank. SIAM J. Matrix Anal. Appl. 30(3), 1254–1279 (2008)
Thomson, W.: Elements of a mathematical theory of elasticity. Philos. Trans. R. Soc. Lond. 146, 481–498 (1856)
Mandel, J.: Généralisation de la théorie de plasticité de WT Koiter. Int. J. Solids Struct. 1, 273–295 (1965)
Rockafellar, R.T.: Convex Analysis. Princeton Landmarks in Mathematics and Physics. Princeton University Press, Princeton (1996)
Choi, M.D., Lam, T.Y., Reznick, B.: Even symmetric sextics. Math. Z. 195, 559–580 (1987)
Reznick, B.: Some concrete aspects of Hilbert’s 17th problem. Contemp. Math. 253, 251–272 (2000)
Blekherman, G.: There are significantly more nonegative polynomials than sums of squares. Isr. J. Math. 153, 355–380 (2006)
Rajwade, A.R.: Squares. In: Lecture Notes of the London Mathematical Society, vol. 171, Cambridge University Press, Cambridge (1993)
Rudin, W.: Sums of squares of polynomials. Am. Math. Mon. 107, 813–821 (2000)
Swan, R.G.: Sums of squares of polynomials. Contemp. Math. 272, 287–293 (2000)
Pfister, A., Scheiderer, C.: A theory of anisotropic fluids. J. Algebra 371, 1–25 (2012)
Voigt, W.: Lehrbuch der Kristallphysik, vol. 34. BG Teubner, Leipzig (1910)
Hand, G.L.: A theory of anisotropic fluids. J. Fluid Mech. 13, 33–46 (1962)
Schneider, M.: An algorithm for generating microstructures of fiber-reinforced composites with long fibers. Int. J. Numer. Methods Eng. 123(24), 6197–6219 (2022)
Altan, M.C., Subbiah, S., Güçeri, S.I., Pipes, R.B.: Numerical prediction of three-dimensional fiber orientation in Hele-Shaw flows. Polym. Eng. Sci. 30, 848–859 (1990)
Jack, D.A.: Sixth-order fitted closures for short-fiber reinforced polymer composites. J. Thermoplast. Compos. Mater. 19(2), 217–246 (2006)
Reznick, B.: Sums of Even Powers of Real Linear Forms. Memoirs of the American Mathematical Society, vol. 96. Am. Math. Soc., Boston (1992)
Simon, B.: Extreme points and the Krein–Milman theorem. In: Cambridge Tracts in Mathematics, pp. 120–135. Cambridge University Press, Cambridge (2011)
Acknowledgements
The authors would like to thank J. Köbler (ITWM) and M. Krause (ITM, KIT) for fruitful discussions. We are grateful to the anonymous reviewers for their suggestions which helped improve the presentation of the arguments. Support by the German Research Foundation (DFG, Deutsche Forschungsgemeinschaft) within the International Research Training Group “Integrated engineering of continuous-discontinuous long fiber reinforced polymer structures” (GRK 2078/2) – project 255730231 – is gratefully acknowledged. Partial support of M.S. by the European Research Council within the Horizon Europe program – project 101040238 – is gratefully acknowledged.
Funding
Open Access funding enabled and organized by Projekt DEAL. T.B. and J.K.B. received funding by German Research Foundation (DFG, Deutsche Forschungsgemeinschaft) within the International Research Training Group “Integrated engineering of continuous-discontinuous long fiber reinforced polymer structures” (GRK 2078/2) – project 255730231. M.S. received partial support by the European Research Council within the Horizon Europe program – project 101040238.
Author information
Authors and Affiliations
Contributions
T.B. and M.S. acquired the funding and were responsible for the conceptualization. M.S. developed the theoretical part. J.K.B. ran the simulations and analyzed the ensuing data. J.K.B. and M.S. wrote the main manuscript text. J.K.B. prepared all figures. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Representing a Fiber-Orientation Tensor as a Non-negative Sum of Monomials
The purpose of this appendix is to show the monomial decomposition (2.9), i.e., that every fixed fiber-orientation tensor \(\mathbf{A}^{(k)}\) of even order may be written as a finite sum
with appropriate non-negative weights \(w_{i}\), directions \(\mathbf{q}_{i} \in S^{d-1}\) and a non-negative integer \(r\) not exceeding \({{k+d-1}\choose {d-1}}\), the dimension of the space of completely symmetric \(k\)-tensors in \(d\) dimensions.
As a prerequisite, we require Carathéodory’s theorem [63], which states that any vector \(\mathbf{z}\) in an \(m\)-dimensional vector space \(V\) which is represented in the form
may also be written in the form
for an index set \(\mathcal{I} \subseteq \{1,\ldots ,r\}\) with at most \(m\) elements and non-negative coefficients \(\rho _{i}\). For the convenience of the reader, we include a short derivation, following Reznick [81]. Let us consider the case
The vectors \(\{\mathbf{x}_{i}\}\) are linearly dependent, i.e., there are coefficients \(c_{i}\), not all zero, s.t. the representation
holds. We may assume that some of the \(c_{i}\) are positive. Indeed, if they were non-positive, we may multiply the coefficients by −1. Furthermore, suppose that the coefficients \(c_{i}\) are ordered, upon possibly reindexing the sequence. In particular, the inequality
holds for all \(i=1,\ldots ,m\) as \(c_{m+1}>0\). We may rearrange equation (A.5) into the form
Inserting this representation into the expression (A.4) yields
Thus, we arrived at the conclusion of Carathéodory’s theorem for the special case (A.4) in view of the non-negativity assertion (A.6) of the coefficients.
The general case (A.2) with more terms \(r>m+1\) follows from applying the special case (A.4) inductively.
Suppose a fiber-orientation tensor \(\mathbf{A}^{(k)}\) is given, i.e., there is some probability measure \(\mu \) and a representation (2.4)
The space of Radon measures may be considered as the continuous dual space of the space of continuous functions on the unit sphere \(S^{d-1}\). It is a classical result of functional analysis (e.g., as a direct consequence of the Krein-Milman theorem [82, Example 8.16]) that the sum of Dirac measures is dense in the space of Radon measures w.r.t. the weak-∗ topology, i.e., there are \(r_{j}\) positive weights \(w_{i,j}\) and directions \(\mathbf{p}_{i,j} \in S^{d-1}\), s.t., for any continuous function  , we have
, we have
Choosing the monomials of homogeneity \(k\) as special continuous functions, we thus obtain the result
By Carathéodory’s theorem (A.3) we can assume a uniform bound on the ranks \(r_{j}\), i.e., it holds
Appendix B: Constraints
Typical constraints of problem (3.18) are translated in terms of the condition  with \(k = 1, \ldots, m\) with
with \(k = 1, \ldots, m\) with  in Table 1.
in Table 1.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bauer, J.K., Schneider, M. & Böhlke, T. On the Phase Space of Fourth-Order Fiber-Orientation Tensors. J Elast 153, 161–184 (2023). https://doi.org/10.1007/s10659-022-09977-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-022-09977-2
Keywords
- Fiber-orientation tensor
- Injection molding
- Closure approximation
- Effective elastic stiffness
- Fiber-reinforced composite


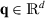 and the
and the 


