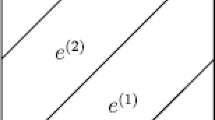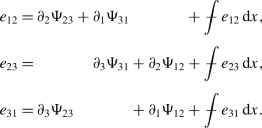1 Introduction

Shape-memory alloys are materials with a thermodynamically very interesting behaviour: They undergo a diffusionless, solid-solid phase transformation in which symmetry is reduced. More precisely, a highly symmetric high temperature phase, the austenite, transforms into a much less symmetric low temperature phase, the martensite, upon cooling below a certain critical temperature [1]. Mathematically, these materials have very successfully been described by an energy minimization [2] of the form

$$\begin{aligned} \int \limits _{\Omega} W(\nabla u, \theta ) \, \mathrm{d}x \rightarrow \min . \end{aligned}$$
(1)

Here \(\Omega \subset \mathbb{R}^{3}\) denotes the reference configuration, which often is chosen to be the austenite state at the critical temperature \(\theta _{c}>0\), the deformation of the material is \(u: \Omega \rightarrow \mathbb{R}^{3}\), the temperature is denoted by \(\theta : \Omega \rightarrow [0,\infty )\) and \(W: \mathbb{R}^{3\times 3}_{+} \times [0,\infty ) \rightarrow [0, \infty )\) corresponds to the stored energy function. Here and in what follows we use the notation \(\mathbb{R}^{3\times 3}_{+}:=\{M \in \mathbb{R}^{3\times 3}: \ \det (M)>0 \}\). The function \(W\) encodes the physical properties of the material and is assumed to be

  1. (i)

    frame indifferent, i.e., \(W(F,\theta ) = W(QF,\theta )\) for all \(F \in \mathbb{R}^{3\times 3}_{+}\) and \(Q\in SO(3)\),

  2. (ii)

    invariant with respect to the material symmetry, i.e., \(W(F,\theta ) = W(F H, \theta )\) for \(H\in \mathcal{P}_{a}\) where \(\mathcal{P}_{a}\) denotes the symmetry group of the austenite phase, which we assume to strictly include the symmetry group of the martensite phase.

Here (i) can be viewed as a geometric nonlinearity, while (ii) encodes the main material nonlinearity which, for instance, reflects the transition from the highly symmetric austenite to the less symmetric martensite phase. Both structure conditions imply that the energies in (1) are highly non-quasiconvex and thus give rise to a rich energy landscape. As a result, minimizing sequences can be rather intricate, which physically leads to various different microstructures.

In this note, it is our objective to study a specific phase transformation for which experimentally interesting microstructures are observed. Seeking to capture “crossing-twin structures” in a fully three-dimensional model (see Fig. 1, left), we focus on the cubic-to-trigonal phase transformation in three dimensions. This deformation, for instance, arises in materials such as Zirconia or in Cu-Cd-alloys but also in the cubic-to-monoclinic transformation in CuZnAl. We refer to [3, 4] for experimental studies, to [5] for an investigation of special microstructures in a geometrically nonlinear context and to [6, 7] for mathematical relaxation results for the associated geometrically nonlinear problems. Since the study of the minimization problem (1) can be rather complex, in this note we make the following three simplifying assumptions which are common in the mathematical analysis of martensitic phase transformations:

  • We fix temperature below the transition temperature,

  • we consider only the material nonlinearity while linearizing the geometric nonlinearity,

  • and we study only exactly stress-free structures.

Instead of investigating the full minimization problem (1), we thus study the differential inclusion

$$\begin{aligned} e(u) \in \{e^{(1)}, e^{(2)}, e^{(3)}, e^{(4)}\} \mbox{ in } \mathbb{T}^{3}, \end{aligned}$$
(2)

where

$$\begin{aligned} \begin{aligned} e^{(1)}= \begin{pmatrix} d_{1} & 1 & 1 \\ 1 & d_{2} & 1 \\ 1 & 1 & d_{3} \end{pmatrix}, \ e^{(2)} = \begin{pmatrix} d_{1} & -1 & -1 \\ -1 & d_{2} & 1 \\ -1 & 1 & d_{3} \end{pmatrix}, \\ e^{(3)} = \begin{pmatrix} d_{1} & 1 & -1 \\ 1 & d_{2} & -1 \\ -1 & -1 & d_{3} \end{pmatrix}, \ \ e^{(4)} = \begin{pmatrix} d_{1} & -1 & 1 \\ -1 & d_{2} & -1 \\ 1 & -1 & d_{3} \end{pmatrix}, \end{aligned} \end{aligned}$$
(3)

and \(d_{1},d_{2},d_{3}\) are material-specific constants. In order to avoid additional mathematical difficulties arising from potential boundaries or non-compactness of the reference configuration, we assume that it is given by the torus \(\mathbb{T}^{3} := \mathbb{T}_{1}\times \mathbb{T}_{2}\times \mathbb{T}_{3}\), where \(\mathbb{T}_{i} := [0,\lambda _{i})\) for some \(\lambda _{i} >0\) and \(i \in \{1,2,3\}\). We observe that all the matrices in (3) are symmetrized rank-one connected, i.e., for each \(i,j\in \{1,2,3,4\}\) there exist (up to their sign unique) \(a_{ij}\in \mathbb{R}^{3} \setminus \{0\}, n_{ij}\in S^{2}\) such that

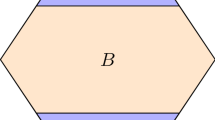
$$\begin{aligned} e^{(i)}-e^{(j)} = \frac{1}{2}(a_{ij}\otimes n_{ij} + n_{ij}\otimes a_{ij}). \end{aligned}$$

It is well-known that, as a consequence, the differential inclusion (2) thus allows for so-called twin or simple laminate solutions, i.e., solutions \(u(x) = u(n_{ij}\cdot x)\) with \(n_{ij}\in S^{2}\) denoting the vectors from above. These are rather rigid, one-dimensional structures, which are frequently observed in experiments [1], see also Fig. 1, right. The possible pairs \((a_{ij}, n_{ij}) \in \mathbb{R}^{3} \times S^{2}\) for the cubic-to-trigonal phase transformation are collected in Table 1.

Fig. 1
figure 1

Schematic illustration of a crossing twin structure (left) and a simple laminate (right). Only very specific twins can be used to form crossing twin structures. These are obtained as a consequence of the compatibility conditions satisfied by the strain equations

Full size image
Table 1 The possible normals arising in simple laminate constructions. For these the strain alternates between the two strain values given in the left column of the table
Full size table

Contrary to other materials such as alloys undergoing a cubic-to-tetragonal phase transformation, simple laminates are not the only possible solutions to (2). As in the (more complex) cubic-to-orthorhombic phase transformation, also in the cubic-to-trigonal phase transformation “crossing-twin structures” can emerge. These are two-dimensional structures involving “laminates within laminates” (see Fig. 1, left). In particular, these patterns locally consist of zero-homogeneous deformations which involve specific “corners” which are formed by four different variants of martensite.

1.1 The Main Result

As our main result, we classify all solutions to the differential inclusion (2) and prove that in addition to the simple laminate solutions only crossing twin structures arise.

Theorem 1

Let \(e(u):= \frac{1}{2}(\nabla u + (\nabla u)^{t})\) with \(e(u): \mathbb{T}^{3} \rightarrow \mathbb{R}^{3\times 3}_{sym}\) be a periodic symmetrized gradient. Assume that

$$\begin{aligned} e(u) \in \{e^{(1)}, e^{(2)}, e^{(3)}, e^{(4)}\}. \end{aligned}$$

Then the following structure result holds:

  1. (i)

    There exists \(j\in \{1,2,3\}\) such that \(\partial _{j} e(u)=0\).

  2. (ii)

    Assuming that \(j = 2\), there exist functions \(f_{1}: \mathbb{T}_{1} \rightarrow \mathbb{R}\) and \(f_{3}:\mathbb{T}_{3} \rightarrow \mathbb{R} \) such that \(f_{1}, f_{3} \in \{-1,1\}\) and either \(e_{13}(u)(x) = f_{1}(x_{1})\) for a.e. \(x\in \Omega \) or \(e_{13}(u)(x) = f_{3}(x_{3})\) for a.e. \(x\in \Omega \).

  3. (iii)

    Assuming that \(e_{13}(u)(x) = f_{3}(x_{3})\), consider \(\Phi (s,t):= (t -F_{3}(s),s)\), where \(F_{3}(s)\) is such that \(F_{3}'(s) = f_{3}(s)\) a.e. and \(F_{3}(0)=0\). Then, there exists \(g: \Phi ^{-1}(\mathbb{T}^{3}) \rightarrow \mathbb{R}\), \((s,t) \mapsto g(t)\) such that

    $$\begin{aligned} (e_{12}\circ \Phi )(s,t) = g(t), \ (e_{23}\circ \Phi )(s,t) = f_{3}(s) g(t). \end{aligned}$$

Remark 1

All cases not listed result from the symmetries of the model under permutation of the space directions, as these only permute the side lengths of the torus \(\mathbb{T}^{3}\) and the constants \(d_{1}\), \(d_{2}\), and \(d_{3}\), the precise values of these constants do not enter the argument. The permutations play the following roles: If an index \(i\in \{1,2,3\}\) has been fixed, the other two can be exchanged via transposition. A fixed index can be transformed into a different fixed index by a full cyclic permutation.

Remark 2

We highlight that, in general, the index \(j \in \{1,2,3\}\) in Theorem 1(i) may not be unique (e.g., in the case of \(e\) being constant or for specific simple laminates). However, for genuine crossing-twin microstructures, since these are genuinely two-dimensional, the choice of \(j\) is indeed unique. We view the statement of Theorem 1(i) as one of our main results: It is at this point that – in spite of the full three-dimensionality of the problem – the symmetry of the problem is broken for the first time. A similar remark on the (non-)unique- ness of \(j\) is valid for the auxiliary results leading up to Theorem 1(i), in particular, for Proposition 2 below.

Let us comment on this result: From a materials science point of view, it gives a complete classification of exactly stress-free solutions for the cubic-to-trigonal phase transformation in the geometrically linear framework. Mathematically, Theorem 1 provides a rigidity result for a phase transformation which leads to more complex structures than simple laminates. While a similar classification and rigidity result had been obtained in [8] for the cubic-to-orthorhombic phase transformation in three dimensions, this required strong geometric assumptions on the smallest possible scales. These assumptions were also necessary as a result of the presence of convex integration solutions for the corresponding differential inclusion in the case of the cubic-to-orthorhombic phase transformation. In contrast, in our model, such conditions are not needed. Due to the smaller degrees of freedom that are present (four instead of six possible strains), in fact any exactly stress-free solution must satisfy the structural conditions and “wild” convex integration solutions are ruled out.

1.2 Relation to the Cubic-to-Orthorhombic Phase Transformation

Due to the outlined rather different behaviour (in terms of rigidity and flexibility) of stress-free solutions of the cubic-to-orthorhombic and the cubic-to-trigonal phase transformation, we explain the algebraic relation between these two transformations: To this end, we recall that for the cubic-to-orthorhombic phase transformation, the exactly stress-free setting in the geometrically linearized situation corresponds to the differential inclusion

$$\begin{aligned} e( u) \in \{e^{(1)},\dots , e^{(6)}\}, \end{aligned}$$

with

$$\begin{aligned} e^{(1)}&:= \begin{pmatrix} 1 & \delta & 0 \\ \delta & 1 & 0 \\ 0 & 0 & -2 \end{pmatrix}, \ e^{(2)}:= \begin{pmatrix} 1 & -\delta & 0 \\ -\delta & 1 & 0 \\ 0 & 0 & -2 \end{pmatrix}, \ e^{(3)}:= \begin{pmatrix} 1 & 0 & \delta \\ 0 & -2 & 0 \\ \delta & 0 & 1 \end{pmatrix}, \\ e^{(4)}&:= \begin{pmatrix} 1 & 0 & -\delta \\ 0 & -2 & 0 \\ -\delta & 0 & 1 \end{pmatrix},\ e^{(5)}:= \begin{pmatrix} -2 & 0 & 0 \\ 0 & 1 & \delta \\ 0 & \delta & 1 \end{pmatrix}, \ e^{(6)}:= \begin{pmatrix} -2 & 0 & 0 \\ 0 & 1 & -\delta \\ 0 & -\delta & 1 \end{pmatrix}. \end{aligned}$$

Here \(\delta >0\) is a material dependent parameter. If now one assumes that a microstructure only involves the infinitesimal strains \(\{e^{(1)},\dots ,e^{(4)}\}\) and if one carries out the change of coordinates \(x\mapsto \hat{x}:=C^{-t}x\), \(u\mapsto \hat{u}:= C u\) with

$$\begin{aligned} C:= \begin{pmatrix} \frac{1}{\sqrt{3}} & 0 & 0 \\ 0 & \frac{\sqrt{3}}{\sqrt{2} \delta} & 0 \\ 0 & 0 &\frac{1}{\sqrt{3}} \end{pmatrix} \cdot \begin{pmatrix} 0 & 1 & 1 \\ \sqrt{2} & 0 & 0 \\ 0 & 1 & -1 \end{pmatrix}, \end{aligned}$$

using that the (infinitesimal) strain transforms according to \(e(\hat{u}) = C e(u) C^{t}\), one exactly arrives at the differential inclusion (2) for the cubic-to-trigonal phase transformation with the parameters \(d_{1} = - \frac{1}{3}\), \(d_{2} = \frac{3}{\delta ^{2}}\), \(d_{3} = - \frac{1}{3}\). This shows that the differential inclusion for the cubic-to-trigonal phase transformation indeed corresponds to a subset of the differential inclusion for the cubic-to-orthorhombic phase transformation. Due to the fewer degrees of freedom, in contrast to the full cubic-to-orthorhombic phase transformation, it however displays strong rigidity properties.

1.3 Main Ideas

The arguments for the proof of Theorem 1 rely on a combination of the linear compatibility conditions for strains in the form of the Saint-Venant equations and the nonlinear constraints in our model. More precisely, the Saint-Venant conditions imply structural conditions on the possible space dependences of the strains. Furthermore, the full classification result requires a breaking of symmetries that can only be deduced in combination with the non-convexity of the problem, i.e., the fact that for all \(i,j \in \{1,2,3\}\) we have that \(e_{ij}( u)\) attains at most three possible values and the nonlinear relation \(e_{23}-e_{12}e_{13}=0\). For a simplified model with only two-dimensional dependences similar arguments had earlier been considered in [8]. However, in contrast to [8], in the present setting we do not need to make use of the additional structural condition of two-dimensionality. Using restrictions to carefully chosen planes, as the key part of our argument, we in fact infer the two-dimensionality of the strains and then combine this with the ideas from [8].

1.4 Relation to the Literature

In the study of minimization problems of the type (1) a common first step consists of the analysis of exactly stress-free structures. This is investigated for particular low energy nucleation problems in [9, 10], for the two-well problem in [11, 12], for the cubic-to-tetragonal phase transformation in [13, 14] and for the cubic-to-orthorhombic transformation in [8, 15]. Moreover, rigidity properties of related differential inclusions without gauge symmetries are studied in [13, 16–21]. For sufficiently complex structures of the energy minima, a striking dichotomy between rigidity of the underlying exactly stress-free structures under relatively high regularity conditions (e.g., \(BV\) conditions for \(\nabla u\)) and flexibility of low regularity solutions arises [13, 22–30]. We expect that if one passes from our geometrically linearized setting of the cubic-to-trigonal phase transformation to the setting of geometrically nonlinear elasticity in which full frame indifference is present, by using ideas as in [14], our model would also display such a dichotomy. In this context, one would expect that above a certain regularity threshold still only rigid structures in the form of crossing twins exist, while at low regularities such a full classification is no longer valid and a plethora of highly irregular, “wild” solutions exist. The latter are expected to no longer satisfy the kinematic compatibility conditions given for crossing twin structures.

Moreover, building on the first (more qualitative) step of investigating exactly stress-free structures, further quantitative properties of the resulting material patterns and the associated energies are studied in the literature. For instance, this includes the scaling and relaxation behaviour of the associated energies [8, 31–42] as well as the stability and fine-scale properties of these patterns [43–46]. We refer to [47] and [1] for a survey of these results. Also for our model a quantification of our crossing twin structures would be of substantial interest. While we believe that the first part of our argument (based on the Saint-Venant conditions) is robust and can be made quantitative with ideas from the literature, the second ingredient (the nonlinear relation between the strains), in which the symmetry of the problem is “broken”, is substantially more fragile and needs new ideas. This, in particular, requires quantifications of the restrictions of the strain components to carefully chosen planes mimicking our stress-free argument which poses substantial technical difficulties. We thus postpone this to possible future studies.

1.5 Outline of the Article

The remainder of the article is structured as follows: In Sect. 2 we first exploit the linear structure conditions which are given by the Saint-Venant compatibility conditions and by the assumption of periodicity. Next, in Sect. 3 we combine these with the nonlinear and non-convex constraints which arise from our differential inclusion and prove the crucial symmetry breaking in the form that the strains must have only two- instead of fully three-dimensional dependences. Last but not least, in Sect. 4 we provide the proof of Theorem 1.

2 First Structure Results: Exploiting the Saint-Venant Conditions

In this section we employ the Saint-Venant compatibility conditions to deduce first structure results for \(e(u)\). Relying on these structural results, in the next section we will carry out a refined analysis of the restrictions of the strains to certain planes in order to prove that \(e(u)\) only depends on two of the three variables.

We begin by recalling the Saint-Venant compatibility conditions (see for instance [8, Lemma 1]):

Lemma 1

Saint-Venant compatibility conditions

Let \(\Omega \subset \mathbb{R}^{3}\) be a simply connected, bounded domain and let \(e:\Omega \rightarrow \mathbb{R}^{3\times 3}_{sym}\) be bounded. Then the following conditions are equivalent:

  1. (i)

    there exists a deformation \(u \in W^{1,p}(\Omega )\) with \(p\in (1,\infty )\) such that \(e = \frac{1}{2}(\nabla u + (\nabla u)^{t})\), i.e., \(e\) is a strain corresponding to a deformation \(u\),

  2. (ii)

    distributionally it holds that \(\nabla \times (\nabla \times e) =0\), i.e., the following system of PDEs hold distributionally in \(\Omega\)

    $$\begin{aligned} \begin{aligned} 2 \partial _{12} e_{12} & = \partial _{22} e_{11} + \partial _{11} e_{22}, \\ 2 \partial _{13} e_{13} & = \partial _{33} e_{11} + \partial _{11} e_{33}, \\ 2 \partial _{23} e_{23} &= \partial _{22} e_{33} + \partial _{33} e_{22}, \end{aligned} \end{aligned}$$
    (4)
    $$\begin{aligned} \begin{aligned} \partial _{23} e_{11} & = \partial _{1} (-\partial _{1} e_{23} + \partial _{2} e_{13} + \partial _{3} e_{12}), \\ \partial _{13} e_{22} & = \partial _{2}(\partial _{1} e_{23} - \partial _{2} e_{13} + \partial _{3} e_{12}), \\ \partial _{12} e_{33} & = \partial _{3}(\partial _{1} e_{23} + \partial _{2} e_{13} - \partial _{3} e_{12}). \end{aligned} \end{aligned}$$
    (5)

In the following sections we will apply these compatibility equations to solutions to our differential inclusion (2). To this end, we note that by virtue of the constant diagonal entries of the wells from (3) the first three strain equations (4) can be simplified to read

$$\begin{aligned} \partial _{12} e_{12} &= 0, \\ \partial _{13} e_{13} &= 0, \\ \partial _{23} e_{23} & = 0. \end{aligned}$$

Integrating this, we directly obtain the following decomposition into two-dimensional waves:

$$\begin{aligned} e_{12}(x_{1},x_{2},x_{3}) & = f_{31}(x_{1},x_{3}) + f_{32}(x_{2},x_{3}), \end{aligned}$$
(6)
$$\begin{aligned} e_{23}(x_{1},x_{2},x_{3}) &= f_{12}(x_{1},x_{2}) + f_{13}(x_{1},x_{3}), \end{aligned}$$
(7)
$$\begin{aligned} e_{31}(x_{1},x_{2},x_{3}) & = f_{21}(x_{1},x_{2}) + f_{23}(x_{2},x_{3}), \end{aligned}$$
(8)

for functions \(f_{ij} : \mathbb{T}_{i}\times \mathbb{T}_{j} \to \mathbb{R}\) (cf. the argument for Lemma 2(4) below).

The two-valuedness of the components of the strain allows to extract further information about these functions.

Lemma 2

Let \(e(u): \mathbb{T}^{3} \rightarrow \mathbb{R}^{3\times 3}_{sym}\) be a \(\mathbb{T}^{3}\)-periodic symmetrized gradient solving the differential inclusion (2). Then one can decompose the strain components as stated in (6)–(8) and choose the functions \(f_{ij}\) for \(i,j\in \{1,2,3\}\) with \(i\neq j\) to satisfy the following three statements for \(\{i,j,k\} = \{1,2,3\}\):

  1. 1.

    The functions \(f_{ij}\) satisfy the inclusion \(f_{ij} \in \{-1,0,1\}\) a.e. for \(i\neq j\).

  2. 2.

    For almost all \(x_{i} \in \mathbb{T}_{i}\) we have either \(f_{ij}(x_{i},\bullet ) = 0\) for almost all \(x_{j} \in \mathbb{T}_{j}\) or \(f_{ik}(x_{i},\bullet ) = 0\) for almost all \(x_{k} \in \mathbb{T}_{k}\).

  3. 3.

    If there exists \(C \in \mathbb{R}\) such that \(e_{ij} = C\), then \(f_{ki}\) and \(f_{kj}\) can be chosen to be constant.

  4. 4.

    The functions \(f_{ij}\) are periodic in both variables, i.e., for almost every \((x_{i}, x_{j}) \in \mathbb{T}_{i} \times \mathbb{T}_{j} \) it holds that \(f_{ij}(x_{i}+\lambda _{i},x_{j})-f_{ij}(x_{i},x_{j})=0\) and \(f_{ij}(x_{i}, x_{j}+ \lambda _{j})- f_{ij}(x_{i}, x_{j}) = 0\).

Proof

The claims follow immediately as by the two-valuedness of the strain components, it is possible to rewrite (6)–(8) as

$$\begin{aligned} \begin{aligned} e_{12}(x_{1},x_{2},x_{3})&= \chi _{3}(x_{3})(1-2\chi _{31}(x_{1},x_{3})) + (1-\chi _{3}(x_{3}))(1-2\chi _{32}(x_{2},x_{3})), \\ e_{23}(x_{1},x_{2},x_{3})&= \chi _{1}(x_{1})(1-2\chi _{12}(x_{1}, x_{2})) + (1-\chi _{1}(x_{1}))(1-2\chi _{13}(x_{1}, x_{3})), \\ e_{31}(x_{1},x_{2},x_{3})&= \chi _{2}(x_{2})(1-2\chi _{21}(x_{1},x_{2})) + (1-\chi _{2}(x_{2}))(1-2\chi _{23}(x_{2},x_{3})), \end{aligned} \end{aligned}$$
(9)

where \(\chi _{j}, \chi _{ik}\) are characteristic functions, which can be chosen to be constant (with both values 0 and 1 being possible) if the corresponding entry of the strain \(e_{ij}\) is constant.

Finally, we turn to the periodicity claim. By symmetry it suffices to consider \(f_{12}\). We note that by the decomposition of the strain into two planar waves, we immediately obtain that for almost every \((x_{1},x_{2}) \in \mathbb{T}_{1} \times \mathbb{T}_{2}\)

$$\begin{aligned} 0 = e_{23}(x_{1},x_{2}+\lambda _{2},x_{3})- e_{23}(x_{1},x_{2},x_{3}) = f_{12}(x_{1},x_{2}+\lambda _{2})- f_{12}(x_{1},x_{2}). \end{aligned}$$

In order to also infer the periodicity in the \(x_{1}\) variable, we use that for almost every \((x_{1},x_{2}) \in \mathbb{T}_{1} \times \mathbb{T}_{2}\)

$$\begin{aligned} \begin{aligned} 0 &= e_{23}(x_{1}+\lambda _{1},x_{2},x_{3})- e_{23}(x_{1},x_{2},x_{3}) \\ &= f_{12}(x_{1}+\lambda _{1},x_{2})- f_{12}(x_{1}, x_{2}) + f_{13}(x_{1}+ \lambda _{1},x_{3})- f_{13}(x_{1}, x_{3}). \end{aligned} \end{aligned}$$
(10)

Varying the \(x_{2},x_{3}\) variables separately, we deduce that for almost every \((x_{1},x_{2}) \in \mathbb{T}_{1} \times \mathbb{T}_{2}\) it holds that \(f_{12}(x_{1}+\lambda _{1},x_{2})- f_{12}(x_{1}, x_{2}) = const\). Due to the structural result from (9) this is only possible if \(\chi _{1}(x_{1}+\lambda _{1}) = \chi _{1}(x_{1})\) for almost every \(x_{1} \in \mathbb{T}_{1}\). For all \(x_{1} \in \mathbb{T}_{1}\) with \(\chi _{1}(x_{1}+\lambda _{1}) = 0\), the claim of the lemma follows immediately. For \(x_{1} \in \mathbb{T}_{1}\) with \(\chi _{1}(x_{1}+\lambda _{1}) =1\), the periodicity condition (10) of the strain and the fact that for these choices of \(x_{1} \in \mathbb{T}_{1}\) it necessarily holds that \(f_{13}(x_{1}+\lambda _{1},x_{3}) = f_{13}(x_{1},x_{3}) = 0\), then also yields the desired periodicity condition for \(f_{12}\). □

Next we consider the second set of strain equations (5) which simplify to become

$$\begin{aligned} 0&= \partial _{1}(-\partial _{1} e_{23} + \partial _{2} e_{13} + \partial _{3} e_{12}), \end{aligned}$$
(11)
$$\begin{aligned} 0&= \partial _{2}(\partial _{1} e_{23} - \partial _{2} e_{13} + \partial _{3} e_{12}), \end{aligned}$$
(12)
$$\begin{aligned} 0&= \partial _{3}(\partial _{1} e_{23} + \partial _{2} e_{13} - \partial _{3} e_{12}). \end{aligned}$$
(13)

By integrating these, we infer a further structure result:

Lemma 3

Let \(e(u): \mathbb{T}^{3} \rightarrow \mathbb{R}^{3\times 3}_{sym}\) be a \(\mathbb{T}^{3}\)-periodic symmetrized gradient solving the differential inclusion (2). Then, for all \({i,j,k} =\{1,2,3\}\) we have that

(14)

Proof

By symmetry, we only have to consider the case \(i=1\), \(j=2\), and \(k=3\). From equation (13), we obtain

$$\begin{aligned} \partial _{1} e_{23} + \partial _{2} e_{13} - \partial _{3} e_{12} = h(x_{1},x_{2}). \end{aligned}$$

Integrating in \(x_{1},x_{2}\) and using the periodicity assumption then yields that for almost every \(x_{3} \in \mathbb{T}_{3}\)

Now, integrating this in \(x_{3}\) and using the periodicity of the strain component \(e_{12}\), implies that

Hence, by the above computation, , which concludes the argument. □

By combining the information from both sets of strain equations, we can prove the existence of a periodic primitive which in turn is closely related to the planar waves from Lemma 2.

Lemma 4

Let \(e(u): \mathbb{T}^{3} \rightarrow \mathbb{R}^{3\times 3}_{sym}\) be a \(\mathbb{T}^{3}\)-periodic symmetrized gradient solving the differential inclusion (2) and let \(f_{ij}\) with \(i,j\in \{1,2,3\}\), \(i\neq j\), denote the functions from Lemma 2. Then there exist periodic Lipschitz vector fields \(\Psi _{i,i+1} : \mathbb{T}_{i} \times \mathbb{T}_{i+1} \to \mathbb{R}\) for the cyclical indices \(i \in \{1,2,3\}\) such that with \(\Psi _{i+1,i}:= \Psi _{i,i+1} \) the following properties hold:

  1. 1.

    We have the decomposition

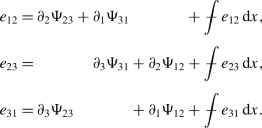
  2. 2.

    The primitives satisfy the discrete differential inclusion

    for \(\{i,j,k\}=\{1,2,3\}\).

  3. 3.

    They allow to efficiently detect whether \(f_{ij} \equiv const\) in some direction for \(i,j\in \{1,2,3\}\) with \(i\neq j\): Let \(x_{i} \in \mathbb{T}_{i}\) be fixed such that \(f_{ij}(x_{i}, \bullet )\) and \(\partial _{j} \Psi _{ij}(x_{i} , \bullet )\) are measurable functions. Then the following properties are equivalent:

    1. (i)

      \(f_{ij}(x_{i},\bullet ) \equiv const\).

    2. (ii)

      \(\partial _{j} \Psi _{ij}(x_{i}, \bullet ) \equiv 0\).

    3. (iii)

      \(\vert \{x_{j} \in \mathbb{T}_{j} : \partial _{j} \Psi _{ij}(x_{i}, x_{j}) = 0 \} \vert > 0\).

Proof

We argue in three steps, first constructing the primitive which yields the identity stated in (1), then derive the properties in (2) and finally deduce the equivalences in (3).

Step 1: Construction of the primitive.

In order to deduce the desired structure result, we combine the strain equations (11)–(13) with the representation formulae from Lemma 2.

We take the \(\partial _{2}\) derivative of the first strain equation (11) and subtract the \(\partial _{1}\) derivative of the second equation (12) to infer the first equation in

$$\begin{aligned} \begin{aligned} 0&= -\partial _{1}^{2} \partial _{2} e_{23} + \partial _{1}\partial _{2}^{2} e_{13} , \\ 0&= - \partial _{2}^{2}\partial _{3} e_{13} + \partial _{2}\partial _{3}^{2} e_{12}, \\ 0&= +\partial _{1}^{2} \partial _{3} e_{23} -\partial _{1}\partial _{3}^{2} e_{12}, \end{aligned} \end{aligned}$$
(15)

while the others follow by symmetry.

Using the representation from Lemma 2 and evaluating the first equation from (15) yields

$$\begin{aligned} \partial _{1}^{2} \partial _{2} f_{12}(x_{1},x_{2}) = h_{12}(x_{1},x_{2})= \partial _{1}\partial _{2}^{2} f_{21}(x_{1},x_{2}). \end{aligned}$$

Here \(h_{12}(x_{1},x_{2})\) denotes a generic function in the \(x_{1},x_{2}\) variables which may change from each block of equations to the next, as do the functions \(g_{12}\), \(g_{21}\), \(k_{12}\), and \(k_{21}\) from what follows for the respective arguments. Integrating in the \(x_{1}\) direction hence results in

$$\begin{aligned} \partial _{1}\partial _{2} f_{12}(x_{1},x_{2}) &= h_{12}(x_{1},x_{2}) + g_{12}(x_{2}), \\ \partial _{2}^{2} f_{21}(x_{1},x_{2}) &= h_{12}(x_{1}, x_{2}) + g_{21}(x_{2}). \end{aligned}$$

Integrating in the \(x_{2}\) direction then gives

$$\begin{aligned} \partial _{1} f_{12}(x_{1},x_{2}) &= h_{12}(x_{1},x_{2}) + g_{12}(x_{2}) + k_{12}(x_{1}), \\ \partial _{2} f_{21}(x_{1},x_{2}) &= h_{12}(x_{1}, x_{2}) + g_{21}(x_{2}) + k_{21}(x_{1}). \end{aligned}$$

In particular, for functions \(\overline{g}_{12}: \mathbb{T}_{2} \to \mathbb{R}\) and \(\overline{k}_{12}: \mathbb{T}_{1} \to \mathbb{R}\) this yields

$$\begin{aligned} \partial _{1} f_{12}(x_{1},x_{2}) = \partial _{2} f_{21}(x_{1},x_{2}) - \overline{g}_{12}(x_{2})+ \overline{k}_{12}(x_{1}). \end{aligned}$$

Defining \(\overline{h}_{12}(x_{1},x_{2}):= \partial _{2} f_{21}(x_{1},x_{2}) - \overline{g}_{12}(x_{2})\), we then infer

$$\begin{aligned} \partial _{1} f_{12}(x_{1},x_{2})&= \overline{h}_{12}(x_{1},x_{2}) + \overline{k}_{12}(x_{1}), \\ \partial _{2} f_{21}(x_{1},x_{2})&= \overline{h}_{12}(x_{1},x_{2}) + \overline{g}_{12}(x_{2}). \end{aligned}$$

For convenience of notation, we drop the bars in the sequel and simply write

$$\begin{aligned} \partial _{1} f_{12}(x_{1},x_{2}) &= h_{12}(x_{1},x_{2}) + k_{12}(x_{1}), \end{aligned}$$
(16)
$$\begin{aligned} \partial _{2} f_{21}(x_{1},x_{2}) &= h_{12}(x_{1}, x_{2}) + g_{12}(x_{2}). \end{aligned}$$
(17)

We next seek to prove that the vector field \(\begin{pmatrix} f_{21} \\ f_{12} \end{pmatrix} \) from equations (16) and (17) essentially comes from a gradient field in the two variables \(x_{1},x_{2}\).

Averaging over \(\mathbb{T}_{1}\times \mathbb{T}_{2}\) in the equations (16), (17) and recalling the periodicity of the functions \(f_{ij}\) implies that

Thus, possibly after modifying \(h_{12}\) by a constant, we can choose

Returning to (16), (17) and invoking the periodicity of \(f_{12}\), \(f_{21}\), we have for each \(\overline{x}_{1} \in \mathbb{T}_{1}\), \(\overline{x}_{2} \in \mathbb{T}_{2}\) that

This in turn implies

For \(i,j\in \{1,2,3\}\) with \(i\neq j\) setting

we see that equations (16) and (17) turn into

$$\begin{aligned} \partial _{1} (f_{12}(x_{1},x_{2}) - G_{12}(x_{1})) &= h_{12}(x_{1},x_{2}) , \\ \partial _{2} (f_{21}(x_{1},x_{2})-G_{21}(x_{2})) &= h_{12}(x_{1}, x_{2}). \end{aligned}$$

Thus, we deduce the existence of a periodic primitive \(\Psi _{12} : \mathbb{T}_{1} \times \mathbb{T}_{2} \to \mathbb{R}\) with

$$\begin{aligned} \partial _{1} \Psi _{12} & = f_{21} - G_{21}, \end{aligned}$$
(18)
$$\begin{aligned} \partial _{2} \Psi _{12} & = f_{12} - G_{12}. \end{aligned}$$
(19)

We note that the periodicity of \(\Psi _{12}\) follows from the fundamental theorem of calculus and the mean zero conditions for \(\partial _{1} \Psi _{12}\) and for \(\partial _{2} \Psi _{12}\). By cyclical symmetry, we also deduce the existence of \(\Psi _{23}\) and \(\Psi _{31}\) such that

$$\begin{aligned} \begin{aligned} \partial _{2} \Psi _{23} & = f_{32} - G_{32}, \\ \partial _{3} \Psi _{23} & = f_{23} - G_{23}, \\ \partial _{3} \Psi _{31} & = f_{13} - G_{13}, \\ \partial _{1} \Psi _{31} & = f_{31} - G_{31}. \end{aligned} \end{aligned}$$
(20)

With this in hand, using the representation (6)–(8), we first obtain

$$\begin{aligned} \begin{aligned} e_{12}(x_{1}, x_{2}, x_{3}) &= f_{31}(x_{1},x_{2}) + f_{32}(x_{2},x_{3}) \\ &= \partial _{1} \Psi _{31}(x_{1},x_{3}) + G_{31}(x_{3}) + \partial _{2} \Psi _{23}(x_{2},x_{3}) + G_{32}(x_{3}). \end{aligned} \end{aligned}$$
(21)

Then, recalling the periodicity of \(\Psi _{ij}\) and applying Lemma 3 implies that

Combining this with (21) then concludes the proof of the first statement of the Proposition up to cyclical symmetry.

Step 2: Proof of (2). In order to observe (2), for simplicity, we consider the case \(i=1\), \(j=2\) and \(k=3\), i.e., we seek to prove that

(22)

We deduce the differential inclusion (22) as a consequence of the definition of \(\Psi _{12}\) in terms of the functions \(f_{12}\) and \(f_{21}\). Indeed,

(23)

Now, using Lemma 2, we have that \(f_{12}\in \{0,1,-1\}\) and that \(e_{23} = f_{12} + f_{13}\). In the following we choose \(\bar{x}_{1}\in \mathbb{T}_{1}\) such that all functions are still measurable as restrictions to \(\{\bar{x}_{1}\} \times \mathbb{T}_{2}\), \(\{\bar{x}_{1}\} \times \mathbb{T}_{3}\) or \(\{\bar{x}_{1}\} \times \mathbb{T}_{2} \times \mathbb{T}_{3}\), which is the case for almost all \(\bar{x}_{1} \in \mathbb{T}_{1}\).

If we have \(f_{12}(\bar{x}_{1},x_{2}) =0\) for a set of positive measure in \(x_{2}\), then by Lemma 2 we obtain that \(f_{12}(\bar{x}_{1},x_{2}) =0\) for almost all \(x_{2}\in \mathbb{T}_{2}\). Thus, by construction (23), also \(\partial _{2} \Psi _{12}(\bar{x}_{1},x_{2}) =0\) for almost all \(x_{2} \in \mathbb{T}_{2}\).

If however we have \(\vert f_{12}(\overline{x}_{1},x_{2}) \vert = 1\) for some set of positive measure in \(x_{2}\), then by Lemma 2 we have \(\vert f_{12}(\overline{x}_{1},x_{2})\vert =1\) for almost all \(x_{2} \in \mathbb{T}_{2}\) and \(f_{13}(\overline{x}_{1},x_{3})=0\) for almost all \(x_{3} \in \mathbb{T}_{3}\). As a consequence,

In the last equality we used Lemma 3. Due to \(\vert f_{12}(\bar{x}_{1},x_{2})\vert =1\) for almost all \(x_{2}\) and due to the representation (23), we finally obtain the differential inclusion (22).

This concludes the argument for (2).

Step 3: Proof of (3). The implications \((i)\Rightarrow (ii)\) and \((ii)\Rightarrow (iii)\) follow directly from the definitions of the functions \(\partial _{j} \Psi _{ij}\). In order to infer the equivalences, it thus suffices to prove that (iii) implies (i). For simplicity of notation, we assume that \(i=1\), \(j=2\), \(k=3\).

Recall that for the fixed \(x_{1}\) all restrictions are measurable. Assuming that (iii) holds, we obtain that there exists a set \(E\subset \mathbb{T}_{2}\) with positive one-dimensional Lebesgue measure such that for \(x_{2} \in E\) we have \(\partial _{2} \Psi _{12}(x_{1},x_{2})=0\). As a consequence, by construction of \(\partial _{2} \Psi _{12}\) for \(x_{2} \in E\) we obtain

(24)

Since by Lemma 2 we also have \(f_{12}\in \{0,\pm 1\}\), the identity (24) yields that also

If , this immediately implies that by discreteness and extremality of the values \(\pm 1\) it holds \(f_{12}(x_{1}, \bullet ) \equiv \pm 1\) which proves the claim.

It hence suffices to consider the case that . Again by (24) this however implies that \(f_{12}(x_{1},\bullet ) = 0\) on a set of positive measure. By Lemma 2(2) this in turn results in \(f_{12}(x_{1},\bullet ) = 0\) for almost all \(x_{2} \in \mathbb{T}_{2}\) which also proves the claim (3) in the last remaining case. □

3 A Refined Analysis of the Functions \(\Psi _{jk}\)

In this section, we use the structure results which were deduced from the Saint-Venant conditions and in particular the conditions from Lemma 5(3) in order to obtain finer information on the potentials \(\Psi _{jk}\). Here we exploit a final, nonlinear property of the strains from (3), namely

$$\begin{aligned} e_{12} e_{23} - e_{13} = 0. \end{aligned}$$

We will use this property (and permutations thereof) on carefully chosen planes in order to obtain further conditions on the potentials \(\Psi _{ij}\). Note that the following result is not symmetric in the indices anymore. Indeed, it is in the following lemma that the symmetry is broken for the first time which then subsequently entails the desired one-dimensional dependence of the strain components.

Lemma 5

Let \(e(u): \mathbb{T}^{3} \rightarrow \mathbb{R}^{3\times 3}_{sym}\) be a \(\mathbb{T}^{3}\)-periodic symmetrized gradient solving the differential inclusion (2) and let \(f_{ij}\) with \(i,j\in \{1,2,3\}\), \(i\neq j\), denote the functions from Lemma 2. Let \(\vert \left \{x_{i} \in \mathbb{T}_{i}: f_{ij}(x_{i},\bullet ) \equiv const \textit{ a.e.}\right \} \vert > 0\) for some \(\{i,j,k\} \in \{1,2,3\}\). Then at least one of the following results holds: Almost everywhere we have

$$\begin{aligned} \Psi _{ij} \equiv const \textit{ or } \Psi _{jk} \equiv \Psi _{jk}(x_{j}) \textit{ or } \Psi _{ik} \equiv \Psi _{ik}(x_{k}). \end{aligned}$$

Proof

For simplicity, we choose \(i=3\) and \(j=2\). Thus, we seek to prove that at least one of the following structure results holds \(\Psi _{32}\equiv const\) or \(\Psi _{21} \equiv \Psi _{21}(x_{2})\) or \(\Psi _{31} \equiv \Psi _{31}(x_{1})\). The other cases follow by symmetry.

Let \(A \subset \mathbb{T}_{3}\) be the set such that for \(x_{3} \in A\) we have \(f_{32}(x_{3},\bullet ) \equiv const\) and such that all involved functions are defined \(\mathcal{L}^{2}\)-a.e. on \(\mathbb{T}_{1}\times \mathbb{T}_{2} \times \{x_{3}\}\). Note that by assumption we have

$$\begin{aligned} \vert A\vert > 0. \end{aligned}$$
(25)

In the following, we will fix \(x_{3} \in A\) and consider all functions to be restricted to this hyperplane by abuse of notation. In particular, on any such plane we have \(e_{12} = e_{12}(x_{1})\).

Step 1: Reduction by means of a transport equation. The identity \(e_{31} - e_{12}e_{23} = 0\) together with the decomposition in Lemma 4 implies

Defining \(E_{12}(x_{1})\) to satisfy

$$\begin{aligned} E_{12}'(x_{1}) = e_{12}(x_{1}) \text{ and } E_{12}(0) = 0, \end{aligned}$$

we infer that almost everywhere

$$\begin{aligned} \partial _{1} \left ( \Psi _{12} \left ( x_{1}, x_{2} - E_{12}(x_{1}) \right ) \right ) = - (\partial _{3} \Psi _{23})(x_{2} - E_{12}(x_{1}) ) + h(x_{1}), \end{aligned}$$

where \(h\) is a generic measurable and bounded function of \(x_{1}\) that may change from line to line. Here the use of the chain rule for the Lipschitz-function \(\Psi _{12}\) is justified as the transformation \((x_{1},x_{2}) \mapsto (x_{1},x_{2} - E_{12}(x_{1}))\) is volume-preserving.

Upon integrating in \(x_{1}\) we get

$$\begin{aligned} \Psi _{12}\left (x_{1},x_{2}-E_{12}(x_{1})\right ) = -\int _{0}^{x_{1}} \partial _{3} \Psi _{23}(x_{2} - E_{12}(s) )\, \mathrm{d}s + h(x_{1}) + k(x_{2}) \end{aligned}$$

almost everywhere, where \(k\) is a measurable function of \(x_{2}\). By taking the difference of the above equation for \(x_{1}, \tilde{x}_{1}\in \mathbb{T}_{1}\) we obtain

$$\begin{aligned} \begin{aligned} & \quad \Psi _{12} \left (x_{1},x_{2} - E_{12}(x_{1}) \right ) - \Psi _{12} \left (\tilde{x}_{1},x_{2} - E_{12}( \tilde{x}_{1}) \right ) - h(x_{1}) + h(\tilde{x}_{1}) \\ & = - \int _{\tilde{x}_{1}}^{x_{1}}\partial _{3} \Psi _{23}(x_{2} - E_{12}(s) )\, \mathrm{d}s. \end{aligned} \end{aligned}$$
(26)

Step 2: Consequences of the transport equation. Let \(B:=\{x_{1} \in \mathbb{T}_{1} : f_{12}(x_{1},\bullet ) \equiv const \} =\{x_{1} \in \mathbb{T}_{1} : \partial _{2} \Psi _{12}(x_{1}, \bullet ) \equiv 0\} \), where the equality of the two sets follows from Lemma 4(3). We now distinguish two cases:

Step 2.1: Firstly, we assume that \(\vert B\vert = 0\). Then, \(f_{12}(x_{1}, \bullet ) \not \equiv const\) for almost all \(x_{1} \in \mathbb{T}_{1}\), which by Lemma 2 implies \(f_{13} \equiv 0\). In turn, we get \(\Psi _{31} \equiv \Psi _{31}(x_{1})\) by Lemma 4.

Step 2.2: Let us consider the case \(\vert B \vert >0\). As for \(x_{1}, \tilde{x}_{1} \in B\), the left hand side of identity (26) is independent of \(x_{2}\), there exists a Lipschitz continuous function \(K : B \to \mathbb{R}\) such that for almost all \((x_{1}, \tilde{x}_{1}) \in B^{2}\) we have

$$\begin{aligned} K(x_{1})-K(\tilde{x}_{1}) = \int _{\tilde{x}_{1}}^{x_{1}}\partial _{3} \Psi _{23}(x_{2} - E_{12}(s) )\, \mathrm{d}s. \end{aligned}$$
(27)

By Kirszbraun’s theorem, we may consider \(K\) to be defined on \(\mathbb{T}_{1}\) and thus it is differentiable almost everywhere by Rademacher’s theorem.

Let \(x_{2} \in \mathbb{T}_{2}\). Then the map \(s \mapsto \partial _{3} \Psi _{23}(x_{2} - E_{12}(s))\) is measurable. Therefore, by the Lebesgue point theorem, we have for almost all \(x_{1} \in \mathbb{T}_{1}\) that

(28)

By a reflection argument, for all \(x_{1} \in B\) of density one there exists \(\varepsilon _{n} >0\) for \(n\in \mathbb{N}\), depending on \(x_{1}\), such that \(\varepsilon _{n} \to 0\) and \(x_{1} \pm \varepsilon _{n} \in B\). The identity (27) implies that for \(x_{1}\) satisfying the above requirements, we have

Therefore, the convergence (28) gives

$$\begin{aligned} \partial _{3} \Psi _{23}(x_{2} - E_{12}(x_{1}) ) = K'(x_{1}) \end{aligned}$$
(29)

for all \(x_{2} \in \mathbb{T}_{2}\) and almost all \(x_{1} \in B\).

Consequently, varying \(x_{2}\) in (29), we observe that \(\partial _{3} \Psi _{23}(\bullet , x_{3}) \equiv const\) for \(x_{3} \in A\), which implies \(\partial _{3} \Psi _{23} (x_{2},x_{3}) = q(x_{3})\) for almost all \((x_{2},x_{3})\in \mathbb{T}_{2} \times A\). We next claim that the fact that \(\partial _{3} \Psi _{23} (x_{2},x_{3}) = q(x_{3})\) for almost all \(x_{2} \in \mathbb{T}_{2}\) and \(x_{3} \in A\) together with Lemma 4(3) implies the dichotomy

$$\begin{aligned} \begin{aligned} f_{23}(x_{2},\bullet ) \equiv const \text{ for a.e. } x_{2} \in \mathbb{T}_{2} \text{ or } f_{23} (x_{2}, \bullet ) \not \equiv const \text{ for a.e. } x_{2} \in \mathbb{T}_{2}. \end{aligned} \end{aligned}$$
(30)

Indeed, we distinguish two cases:

  1. (i)

    If for some set of positive measure in \(x_{2}\in \mathbb{T}_{2}\) and for

    $$\begin{aligned} C(x_{2}):=\{x_{3} \in \mathbb{T}_{3}: \ \partial _{3} \Psi _{23}(x_{2},x_{3})=0 \} \end{aligned}$$

    we have \(\vert C(x_{2})\vert >0\), then by Lemma 4(3) we obtain that for such a value of \(x_{2}\in \mathbb{T}_{2}\) and almost all \(x_{3} \in \mathbb{T}_{3}\) it holds \(\partial _{3} \Psi _{23}(x_{2},x_{3})\equiv 0\). By virtue of the fact that \(\partial _{3} \Psi _{23}(x_{2}, x_{3}) = q(x_{3})\) for \((x_{2},x_{3})\in \mathbb{T}_{2} \times A\), we then obtain that for all \((x_{2},x_{3})\in \mathbb{T}_{2} \times A\) it holds that \(q(x_{3})= 0\) and that \(\partial _{3} \Psi _{23}(x_{2}, x_{3}) =0\). Hence, the condition \(\vert C(x_{2})\vert >0\) holds for almost all \(x_{2} \in \mathbb{T}_{2}\). But then Lemma 4(3) implies that \(f_{23}(x_{2},\bullet ) \equiv const\) holds for almost all \(x_{2} \in \mathbb{T}_{2}\).

  2. (ii)

    If for almost all \(x_{2} \in \mathbb{T}_{2}\) it holds that

    $$\begin{aligned} \vert C(x_{2})\vert = \vert \{x_{3} \in \mathbb{T}_{3}: \ \partial _{3} \Psi _{23}(x_{2},x_{3})=0\}\vert =0, \end{aligned}$$
    (31)

    by Lemma 4(3) we have for all \(x_{2}\in \mathbb{T}_{2}\) that \(f_{23}(x_{2},\bullet ) \not \equiv const\).

Therefore, from (i), (ii) we conclude (30). If combined with Lemma 2, this in turn yields

$$\begin{aligned} f_{23}(x_{2},\bullet ) \equiv const \text{ for a.e. } x_{2} \in \mathbb{T}_{2} \text{ or } f_{21} \equiv 0 \text{ a.e. } \text{ on } \mathbb{T}_{1}\times \mathbb{T}_{2}. \end{aligned}$$
(32)

In the first case of (32) by Lemma 4(3) we have \(\Psi _{23} \equiv \Psi _{23}(x_{2})\). Moreover, by Lemma 4(3), the assumption (25) that there exists \(x_{3} \in \mathbb{T}_{3}\) such that \(f_{32}(x_{3},\bullet ) \equiv const\), gives that there exist \(x_{3} \in \mathbb{T}_{3}\) such that \(\partial _{2} \Psi _{32}(x_{3},\bullet ) \equiv 0\). Hence, since \(\Psi _{23} = \Psi _{32}\), we obtain that \(\Psi _{32} \equiv const\) in this case.

In the second case of (32), Lemma 4(3) implies that \(\Psi _{12} \equiv \Psi _{12}(x_{2})\). □

As a consequence of the previous structure result, we show that we can dispose of one of the functions \(\Psi _{ij}\) in the decomposition of the strain:

Corollary 1

Let \(e(u): \mathbb{T}^{3} \rightarrow \mathbb{R}^{3\times 3}_{sym}\) be a \(\mathbb{T}^{3}\)-periodic symmetrized gradient solving the differential inclusion (2) and let \(\Psi _{i,i+1}\) with \(i\in \{1,2,3\}\) denote the functions from Lemma 4. Then there exists an index \(i\in \{1,2,3\}\) such that \(\Psi _{i,i+1} \equiv const\).

Proof

By Lemma 2(2) we have \(\vert \{x_{1}: f_{12}(x_{1},\bullet ) \equiv const\} \vert >0\) or \(\vert \{x_{1}: f_{13}(x_{1},\bullet ) \equiv const\} \vert >0\). We split the argument into two cases.

Case 1: We assume that either

$$ \vert \{x_{1} \in \mathbb{T}_{1}: f_{12}(x_{1},\bullet ) \equiv const \} \vert = \vert \mathbb{T}_{1} \vert $$

or

$$ \vert \{x_{1}\in \mathbb{T}_{1}: f_{13}(x_{1},\bullet ) \equiv const \} \vert = \vert \mathbb{T}_{1} \vert . $$

Exchanging the indices 2 and 3 if necessary, it is sufficient to consider

$$ \vert \{x_{1}\in \mathbb{T}_{1}: f_{12}(x_{1},\bullet ) \equiv const \} \vert = \vert \mathbb{T}_{1}\vert , $$

which implies \(\partial _{2} \Psi _{12}\equiv 0\). Lemma 5 implies that at least one of the following statements holds: \(\Psi _{12} \equiv const\) or \(\Psi _{23} \equiv \Psi _{23}(x_{2})\) or \(\Psi _{31} \equiv \Psi _{31}(x_{3})\).

In the first case there is nothing left to prove. In the second case, using our assumption, the decomposition of Lemma 4 reads

(33)

Since the only function in the decomposition (33) which depends on \(x_{2}\) is given by \(\partial _{2} \Psi _{23}(x_{2})\) (which in turn only appears in the expression for \(e_{12}\)), the identity \(e_{12} - e_{23}e_{31} \equiv 0\) trivially implies \(\partial _{2}\Psi _{23} (\bullet ) \equiv const\). By periodicity and the fundamental theorem of calculus, we get that the constant has to be zero and thus we obtain \(\Psi _{23} \equiv const\).

In the third case, we have

Similarly as in the previous case we have \(\partial _{1} \Psi _{12} \equiv const\) and thus \(\Psi _{12}= const\).

Case 2: We assume that

$$ \vert \{x_{1} \in \mathbb{T}_{1}: f_{12}(x_{1},\bullet ) \equiv const \} \vert >0 $$

and

$$ \vert \{x_{1} \in \mathbb{T}_{1}: f_{13}(x_{1},\bullet ) \equiv const \} \vert >0. $$

Again, we only have to deal with the cases in which Lemma 5 does not immediately give the desired statement. In that case we have

$$\begin{aligned} \Psi _{23} \equiv \Psi _{23}(x_{2}) \mbox{ or } \Psi _{31} \equiv \Psi _{31}(x_{3}) \end{aligned}$$

and

$$\begin{aligned} \Psi _{23} \equiv \Psi _{23}(x_{3}) \mbox{ or } \Psi _{12} \equiv \Psi _{12}(x_{2}). \end{aligned}$$

However, the statement \(\Psi _{31} \equiv \Psi _{31}(x_{3})\) implies

$$ \vert \{x_{3} \in \mathbb{T}_{3}: f_{31}(x_{3},\bullet ) \equiv const \} \vert = \vert \mathbb{T}_{3} \vert $$

and thus (up to symmetry) this case has already been dealt with in case 1 from above. The case \(\Psi _{12} \equiv \Psi _{12}(x_{2})\) can be handled similarly. Therefore we have \(\Psi _{23} \equiv \Psi _{23}(x_{2})\) and \(\Psi _{23} \equiv \Psi _{23}(x_{3})\), which implies that \(\Psi _{23} \equiv const\). □

Finally, using the nonlinear relation satisfied by the strain components in combination with the previously derived reductions of the potentials, we obtain that the strain only depends on two out of three possible variables:

Proposition 2

Let \(e(u): \mathbb{T}^{3} \rightarrow \mathbb{R}^{3\times 3}_{sym}\) be a \(\mathbb{T}^{3}\)-periodic symmetrized gradient solving the differential inclusion (2) and let \(\Psi _{i,i+1}\) with \(i\in \{1,2,3\}\) denote the functions from Lemma 4. Then there exists an index \(i\in \{1,2,3\}\) such that \(\partial _{i} e \equiv 0\). Moreover, assuming without loss of generality that \(i=2\), we obtain one of the decompositions

(34)

or

(35)

Proof

By symmetry and Corollary 1, we may assume \(\Psi _{12} \equiv const\). Then the decomposition reads

Due to \(e_{12} \in \{-1,1\}\) being a sum of two one-dimensional functions and by periodicity, for \(x_{3} \in \mathbb{T}_{3}\) fixed we can by Lemma 4 additionally assume

$$\begin{aligned} \vert \{x_{3} \in \mathbb{T}_{3}: \partial _{2} \Psi _{23}(\bullet , x_{3}) \equiv 0 \} \vert >0 \end{aligned}$$
(36)

after exchanging the indices 1 and 2 if necessary.

The algebraic relation \(e_{31} - e_{23}e_{12} = 0\) implies

Using that the right hand side of the above expression is independent of \(x_{2}\), defining the discrete differential \(\partial _{2}^{h} f(x_{2}):= f(x_{2}+h) - f(x_{2})\) for \(h>0\) and applying it to the above equation, we get

$$\begin{aligned} \partial _{3} \partial _{2}^{h} \Psi _{23} - e_{23} \partial _{2} \partial _{2}^{h} \Psi _{23} = 0. \end{aligned}$$

Defining

$$\begin{aligned} \partial _{3} E_{23} (x_{1},x_{3}) & = e_{23}(x_{1},x_{3}), \\ E_{23} (x_{1},0) & = 0, \end{aligned}$$

we may invoke the chain rule for the Lipschitz function \(\partial _{2}^{h}\Psi _{23}\) to obtain

$$\begin{aligned} \partial _{3}\left ( \partial _{2}^{h} \Psi _{23}\left (x_{2}- E_{23}(x_{1},x_{3}),x_{3} \right ) \right ) = 0 \end{aligned}$$

for almost all \((x_{1},x_{2},x_{3}) \in \mathbb{T}^{3}\).

Recalling (36), choosing \(\bar{x}_{3} \in \mathbb{T}_{3}\) such that

$$\begin{aligned} \partial _{2} \Psi _{23}(\bullet , \bar{x}_{3}) \equiv 0\text{ and } x_{2} \mapsto \Psi _{23}(x_{2},\bar{x}_{3})\text{ is differentiable a.e.,} \end{aligned}$$
(37)

and integrating in \(x_{3}\) gives

$$\begin{aligned} \partial _{2}^{h} \Psi _{23}\left (x_{2}- E_{23}(x_{1},x_{3}),x_{3} \right ) = \partial _{2}^{h} \Psi _{23}\left (x_{2}- E_{23}(x_{1}, \bar{x}_{3}), \bar{x}_{3} \right ) \end{aligned}$$

almost everywhere. Dividing by \(h \neq 0\), taking the limit \(h\to 0\) and invoking the choice (37) we see that

$$\begin{aligned} \partial _{2} \Psi _{23}\left (x_{2}- E_{23}(x_{1},x_{3}),x_{3} \right ) = \partial _{2} \Psi _{23}\left (x_{2}- E_{23}(x_{1},\bar{x}_{3}), \bar{x}_{3} \right ) = 0 \end{aligned}$$

for almost all \((x_{1},x_{2},x_{3}) \in \mathbb{T}^{3}\).

Consequently, we have \(\partial _{2} \Psi _{23} \equiv 0\) and the decomposition reduces to

which is the first case (34) of the desired statement.

If we had taken the other choice at the inequality (36), by symmetry, we would have deduced

so that \(\partial _{1}e \equiv 0\). A cyclical permutation shifting the index 1 to 2 allows us to deduce the second representation (35). □

4 Proof of Theorem 1

With the result of Proposition 2 the argument for Theorem 1 follows as in [8, Sect. 4.2.1]. We repeat the argument for self-containedness.

Proof of Theorem 1

Since the claims of Theorem 1(i), (ii) already follow from Proposition 2, it suffices to prove the claim of Theorem 1(iii). Without loss of generality we may assume that as in Proposition 2 we have \(\partial _{i} e = 0\) for \(i=2\) as well as the decomposition (34). Moreover, invoking Theorem 1(ii), without loss of generality, we may further assume that \(e_{31}=e_{31}(x_{3})\). Using the notation from [8], we define

Further we set \(\Phi (s,t):= (t-E_{31}(s),s) \), where \(E_{31}'(s) = e_{31}(s)\) and \(E_{31}(0)=0\). We note that the map \(\Phi (s,t)\) is a bilipschitz mapping on \(\mathbb{R}^{2}\). Together with the definition of \(v\) we thus infer

$$\begin{aligned} \frac{d}{ds} v(\Phi (s,t)) = \partial _{3} v\vert _{\Phi (s,t)} - e_{31}(s) \partial _{1} v\vert _{\Phi (s,t)} = e_{23}\vert _{\Phi (s,t)}-e_{31} \vert _{\Phi (s,t)} e_{12}\vert _{\Phi (s,t)}= 0. \end{aligned}$$

As a consequence, \(v(\Phi (s,t)) = \tilde{g}(t)\) for some function \(\tilde{g}\) of only one variable. Hence,

$$\begin{aligned} \begin{pmatrix} e_{12}\circ \Phi (s,t) \\ e_{23}\circ \Phi (s,t) \end{pmatrix} &= \begin{pmatrix} \partial _{1} v \circ \Phi (s,t) \\ \partial _{3} v \circ \Phi (s,t) \end{pmatrix} = \begin{pmatrix} 1 &0 \\ e_{31}(s) & 1 \end{pmatrix} \begin{pmatrix} \partial _{t} (v\circ \Phi )(s,t) \\ \partial _{s} (v\circ \Phi )(s,t) \end{pmatrix} \\ &= \begin{pmatrix} 1 & 0 \\ e_{31}(s) & 1 \end{pmatrix} \begin{pmatrix} \partial _{t} (v\circ \Phi )(s,t) \\ 0 \end{pmatrix} = \begin{pmatrix} \tilde{g}'(t) \\ e_{31}(s) \tilde{g}'(t) \end{pmatrix}. \end{aligned}$$

Defining \(f_{3}(x_{3}) = e_{31}(x_{3}) \) and \(g(t) = \tilde{g}'(t)\), then concludes the proof of the final structure result. □