Abstract
For a given class of materials, universal deformations are those that can be maintained in the absence of body forces by applying only boundary tractions. Universal deformations play a crucial role in nonlinear elasticity. To date, their classification has been accomplished for homogeneous isotropic solids following Ericksen’s seminal work, and homogeneous anisotropic solids and inhomogeneous isotropic solids in our recent works. In this paper we study universal deformations for inhomogeneous anisotropic solids defined as materials whose energy function depends on position. We consider both compressible and incompressible transversely isotropic, orthotropic, and monoclinic solids. We show that the universality constraints—the constraints that are dictated by the equilibrium equations and the arbitrariness of the energy function—for inhomogeneous anisotropic solids include those of inhomogeneous isotropic and homogeneous anisotropic solids. For compressible solids, universal deformations are homogeneous and the material preferred directions are uniform. For each of the three classes of anisotropic solids we find the corresponding universal inhomogeneities—those inhomogeneities that are consistent with the universality constraints. For incompressible anisotropic solids we find the universal inhomogeneities for each of the six known families of universal deformations. This work provides a systematic approach to study analytically functionally-graded fiber-reinforced elastic solids.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In elasticity, for a given class of materials, universal deformations are those deformations that can be maintained in the absence of body forces by applying only boundary tractions for an arbitrary energy function in that class.Footnote 1 They are particularly important in nonlinear elasticity since they exist independently of a particular choice of energy function. Therefore, they can be used experimentally to study material properties and analytically as a basis for more complicated deformations or to gain insight into basic properties of materials. The history of a theory of universal deformations goes back to the seminal work of Ericksen who showed that for homogeneous compressible isotropic solids, universal deformations are homogeneous [9]. From that original seed, grew a large body of work addressing the same problems for materials that have constraints such as incompressibility, may be anisotropic, may be inhomogenous, may be anelastic, or linear as shown in Fig. 1. The problem of finding universal deformations in the presence of internal constraints is more difficult [32]. For homogeneous incompressible isotropic solids, in a second seminal paper that was motivated by the earlier works of Rivlin [29–31], Ericksen [8] found four families of universal deformations. He conjectured that a deformation with constant principal invariants has to be homogeneous. This conjecture turned out to be incorrect [11], and motivated the discovery of a fifth family of universal deformations [20, 34]. The six known families of universal deformations are:
-
Family 0: Homogeneous deformations
-
Family 1: Bending, stretching, and shearing of a rectangular block
-
Family 2: Straightening, stretching, and shearing of a sector of a cylindrical shell
-
Family 3: Inflation, bending, torsion, extension, and shearing of a sector of an annular wedge
-
Family 4: Inflation/inversion of a sector of a spherical shell
-
Family 5: Inflation, bending, extension, and azimuthal shearing of an annular wedge
The universal program: Finding all the universal deformations and displacements, together with the associated universal material preferred directions, and universal inhomogeneities, for both compressible and incompressible solids. These are the different cases considered so far with partial or complete solutions. Here, nonlinear elasticity refers to hyperleasticity and the existence of a strain-energy density \(W\) is assumed that can either be homogeneous or non-homogenous, isotropic or anisotropic
We should emphasize that for incompressible isotropic solids Ericksen’s problem has not been solved completely to this day; the case of deformations with constant principal invariants is still an open problem. However, the conjecture is that there are no other possible families of universal deformations. In related works, there have been several studies of universal deformations and universal steady-state temperature fields in nonlinear thermoelasticity (see [6, 7, 26, 33], and references therein).
Based on Ericksen’s seminal work, we embarked a few years ago into what we now refer to as the universal program: to generalize Ericken’s results to anisotropic and inhomogeneous materials for all hyperelastic materials, anelastic materials, and linear materials (see Fig. 1). Indeed, the analogue of universal deformations in linear elasticity are universal displacements [18, 38, 45]. In [45], it was shown that universal displacements explicitly depend on the symmetry class of the material; the larger the symmetry group is the larger the corresponding space of universal displacements is. More recently, we studied universal inhomogeneities in anisotropic linear elasticity [43]. There have been recent extensions of Ericksen’s analysis to anelasticity. Yavari and Goriely [41] proved that in compressible anelasticity universal deformations must be covariantly homogeneous. In the case of incompressible anelasticity, Goodbrake et al. [15] observed that a key feature of the analysis is that the extra fields entering the analysis should follow the same symmetry as the universal deformations. They also showed that the six known families of universal deformations are invariant under certain Lie subgroups of the special Euclidean group.
Until recently, there was no systematic study of universal deformations in anisotropic solids. There were early studies restricted to a subset of Family 1 deformations for two cases of homogeneous anisotropy, and Family 3 deformations for an example of homogeneous anisotropy [10] (see also [1, 2]). However, many examples of universal deformations for anisotropic fiber-reinforced systems were known and widely used [3, 4, 16, 17, 19, 23, 28, 36]. Recently, we studied universal deformations and universal material preferred directions in homogeneous compressible and incompressible anisotropic solids [42]. More specifically, we considered compressible and incompressible transversely isotropic, orthotropic, and monoclinic solids. We assumed that the material preferred directions can vary from point to point. In the case of compressible solids we showed that universal deformations are homogeneous and universal material preferred directions for the three classes of anisotropic solids must be uniform. In the case of homogeneous incompressible transversely isotropic, orthotropic, and monoclinic solids, we showed that in addition to the nine universality constraints for isotropic solids [8], there are extra 25, 74, and 152, respectively, extra universality constraints that must be satisfied. For each known family of universal deformations we obtained the universal material preferred directions assuming that they have the symmetry of the corresponding universal deformations (that are encoded in the symmetries of the right Cauchy-Green strain).Footnote 2
Motivated by a result in [14], Yavari [40] extended the analysis of universal deformations to inhomogeneous isotropic solids (with position-dependent strain-energy density), and showed that in addition to those of homogeneous isotropic solids there are some extra universality constraints. It was shown that inhomogeneous compressible isotropic solids do not admit universal deformations. In the case of inhomogeneous incompressible solids the following results were obtained for each of the six known families of universal deformations.
-
For inhomogeneous incompressible isotropic solids it was incorrectly concluded that Family 0 deformations are not universal. This is discussed in §4.1, and the corrected statement is given in Footnote 4.
-
Family 1 deformations are universal for any energy function of the form \(W= W(X,I_{1},I_{2})\), where \((X,Y,Z)\) is a Cartesian coordinate system with coordinate lines normal to the faces of an undeformed rectangular block. Note that with respect to cylindrical coordinates \((r,\theta,z)\) in the deformed configuration, Family 1 deformations have the form: \((r,\theta,z)=\left(\sqrt{C_{1}(2X+C_{4})},C_{2}(Y+C_{5}),\frac{Z}{C_{1}\,C_{2}}-C_{2}\,C_{3} Y+C_{6}\right)\), where \(C_{1}, \ldots, C_{6}\) are constants.
-
Families 2, 3, and 4 deformations are universal for any energy function of the form \(W=W(R,I_{1},I_{2})\), where \(R\) is the radial coordinate in the undeformed configuration of a cylindrical shell, an annular wedge, and a spherical shell, for Families 2, 3, and 4, respectively.
-
For inhomogeneous incompressible isotropic solids, Family 5 deformations are not universal.
The remaining problem to be solved to complete Ericksen’s program is to study elastic materials that are inhomogenous, and anisotropic. Therefore, we study universal deformations for inhomogeneous anisotropic solids and generalize the results of [40, 42]. We consider both compressible and incompressible transversely isotropic, orthotropic, and monoclinic solids. It is shown that the universality constraints—the constraints that are dictated by the equilibrium equations and the arbitrariness of the energy function—for inhomogeneous anisotropic solids include those of inhomogeneous isotropic and homogeneous anisotropic solids as special cases. For compressible solids, universal deformations are homogeneous and the material preferred directions are uniform. For each of the three classes of anisotropic solids we find the corresponding universal inhomogeneities—those inhomogeneities (position dependence of the energy function) that are compatible with the universality constraints. For incompressible anisotropic solids we find the universal inhomogeneities for each of the six known families of universal deformations.
This paper is organized as follows. In §2 we tersely review nonlinear anisotropic elasticity. In §3, we consider inhomogeneous compressible transversely isotropic, orthotropic, and monoclinic solids. The universal deformations, universal material preferred directions, and universal inhomogeneities of inhomogeneous incompressible transversely isotropic solids are analyzed for each of the six known families in §4. Similar analyses for inhomogeneous incompressible orthotropic and inhomogeneous incompressible monoclinic solids are given in §5 and §6, respectively. Conclusions are given in §7.
2 Nonlinear Anisotropic Elasticity
Kinematics
Consider an elastic body  . In nonlinear anelasticity the body is identified with a Riemannian manifold
. In nonlinear anelasticity the body is identified with a Riemannian manifold  whose metric \(\mathbf{G}\) is used in calculating the natural distances between material points in the body. In nonlinear elasticity
whose metric \(\mathbf{G}\) is used in calculating the natural distances between material points in the body. In nonlinear elasticity  is flat, and is a submanifold of the Euclidean 3-space. A deformation of the body is a map
is flat, and is a submanifold of the Euclidean 3-space. A deformation of the body is a map  , where
, where  is the Euclidean ambient space, and \(\mathbf{g}\) is the Euclidean metric. The material velocity is defined as
is the Euclidean ambient space, and \(\mathbf{g}\) is the Euclidean metric. The material velocity is defined as

The spatial velocity is defined as \(\mathbf{v}=\mathbf{V}\circ\varphi_{t}^{-1}\). The deformation gradient—the tangent map (or derivative) of \(\varphi\)—is denoted by \(\mathbf{F}=T\varphi\). With respect to local coordinate charts \(\{x^{a}\}\) and \(\{X^{A}\}\) on  and
and  , respectively, deformation gradient is defined as
, respectively, deformation gradient is defined as

The deformation gradient is a linear map that maps vectors in the tangent space at a material point in the reference configuration to vectors in the tangent space of the same material point in the current configuration. The transpose of deformation gradient is defined as

where and are the inner products induced by the material and ambient space metrics, respectively. \(\mathbf{F}^{T }\) has the following components
The right Cauchy-Green deformation tensor is defined as

The pulled-back metric is denoted by \(\mathbf{C}^{\flat}=\varphi^{*}\mathbf{g}\), and is defined as

where \(\flat\) is the flat operator induced by the metric \(\mathbf{g}\). \(\mathbf{C}^{\flat}\) has components \(C_{AB}=(g_{ab}\circ \varphi)F^{a}{}_{A}F^{b}{}_{B}\). The left Cauchy-Green deformation tensor is defined as
The spatial analogues of \(\mathbf{C}^{\flat}\) and \(\mathbf{B}^{\sharp}\) are denoted by \(\mathbf{c}^{\flat}\) and \(\mathbf{b}^{\sharp}\) (the Finger deformation tensor), respectively, and are defined as
The second-order tensors \(\mathbf{C}\) and \(\mathbf{b}\) have the same principal invariants \(I_{1}\), \(I_{2}\), and \(I_{3}\) that are defined as [25]
Balance laws
The referential forms of the mass conservation and the balance of linear and angular momenta read
where \(\rho_{0}\) is the material mass density, \(\mathbf{B}\) is body force per unit referential volume, \(\mathbf{A}\) is the material acceleration, and \(\mathbf{P}\) is the first Piola-Kirchhoff stress. The spatial forms of conservation of mass and balance of linear and angular momenta read
where \(\rho\) is the spatial mass density, \(\boldsymbol{\sigma}\) is the Cauchy stress, \(\mathbf{b}=\mathbf{B}\circ\varphi_{t}^{-1}\), \(\mathbf{a}\) is the spatial acceleration, and \(\mathbf{L}_{\mathbf{v}}\rho\) is the Lie derivative of the spatial mass density with respect to the spatial velocity. \(\mathbf{P}\) and \(\boldsymbol{\sigma}\) are related as \(J\sigma^{ab}=P^{aA}F^{b}{}_{A}\). The Jacobian of deformation \(J=\sqrt{I_{3}}\) relates the material (\(dV\)) and spatial (\(dv\)) Riemannian volume forms as \(dv=J dV\), and is given by
Constitutive equations
For an inhomogeneous anisotropic hyperelastic solid the energy function (per unit undeformed volume) has the following functional form
where \(W\) explicitly depends on \(\mathbf{X}\) (inhomogeneity), and the structural tensors \(\boldsymbol{\zeta}_{i}, i=1,\dots,n\) characterize the material symmetry group of the solid. Using structural tensors the energy function becomes an isotropic function of its arguments. Instead of (2.13) one can write the energy as a function of an integrity basis for the set of tensors \(\{\mathbf{C}^{\flat},\mathbf{G},\boldsymbol{\zeta}_{1},\dots,\boldsymbol{\zeta}_{n}\}\). Denoting the integrity basis by \(I_{j},j=1,\dots,m\), one can write \(W=W(\mathbf{X},I_{1},\ldots,I_{m})\). The second Piola-Kirchhoff stress tensor has the following representation [5, 22, 44]
The relations between the second Piola-Kirchhoff stress, and the first Piola-Kirchhoff and Cauchy stresses are: \(S^{AB}=(F^{-1})^{A}{}_{a} P^{aB}=J (F^{-1})^{A}{}_{a} (F^{-1})^{B}{}_{b}\, \sigma^{ab}\).
Isotropic solids
For an inhomogeneous isotropic solid, \(W=W(\mathbf{X},I_{1},I_{2},I_{3})\), where \(I_{1}, I_{2}\), and \(I_{3}\) were defined in (2.9). From (2.14) one writes
The Cauchy stress has the following representation
where \(c^{ab}=(F^{-1})^{M}{}_{m}(F^{-1})^{N}{}_{n}G_{MN}\,g^{am}\,g^{bn}\). For an incompressible isotropic solid \(I_{3}=1\), and hence
where \(p\) is the Lagrange multiplier associated with the incompressibility constraint \(J=\sqrt{I_{3}}=1\). Equation (2.17)2 in components reads \(\sigma^{ab}=-p\,g^{ab}+2W_{1}\,b^{ab}-2W_{2}\,c^{ab}\).
Transversely isotropic solids
In a transversely isotropic solid at every point there is a single material preferred direction, which is normal to the plane of isotropy at that point. We assume that a unit vector \(\mathbf{N}(\mathbf {X})\) identifies the material preferred direction at  . The energy function for an inhomogeneous transversely isotropic solid has the form \(W=W(\mathbf{X},\mathbf{G},\mathbf{C}^{\flat}, \mathbf{A})\), where \(\mathbf{A}=\mathbf{N}\otimes\mathbf{N}\) is a structural tensor [5, 21, 36]. The energy function \(W\) depends on five independent invariants that are defined as
. The energy function for an inhomogeneous transversely isotropic solid has the form \(W=W(\mathbf{X},\mathbf{G},\mathbf{C}^{\flat}, \mathbf{A})\), where \(\mathbf{A}=\mathbf{N}\otimes\mathbf{N}\) is a structural tensor [5, 21, 36]. The energy function \(W\) depends on five independent invariants that are defined as
The second Piola-Kirchhoff stress tensor has the following representation
where
Thus
The Cauchy stress has the representation [10, 12, 13]
where \(n^{a}=F^{a}{}_{A} N^{A}\), and
In the case of an incompressible transversely isotropic solid (\(I_{3}=1\)), \(W=W(\mathbf{X},I_{1},I_{2}, I_{4},I_{5})\), and hence
Similarly, the Cauchy stress has the following representation [10, 12, 13, 37]
Orthotropic solids
An orthotropic solid has reflection symmetry with respect to three mutually perpendicular planes at every point. Let three \(\mathbf {G}\)-orthonormal vectors \(\mathbf{N}_{1}(\mathbf{X})\), \(\mathbf{N}_{2}(\mathbf{X})\), and \(\mathbf{N}_{3}(\mathbf{X})\) specify the orthotropic axes at a point \(\mathbf{X}\) in the reference configuration. The three tensors \(\mathbf{A}_{1}=\mathbf{N}_{1}\otimes\mathbf{N}_{1}\), \(\mathbf{A}_{2}=\mathbf{N}_{2}\otimes\mathbf{N}_{2}\), and \(\mathbf{A}_{3}=\mathbf{N}_{3}\otimes\mathbf{N}_{3}\) are structural tensors. However, because \(\mathbf{A}_{1}+\mathbf{A}_{2}+\mathbf{A}_{3}=\mathbf{I}\), only two of them are independent. The energy function of an inhomogeneous orthotropic solid has the functional form \(W=W(\mathbf{X},\mathbf{G},\mathbf{C}^{\flat}, \mathbf{A}_{1},\mathbf{A}_{2})\) [5, 21, 36]. It can be rewritten as a function of the following seven independent invariants:
Thus
The second Piola-Kirchhoff stress tensor has the following representation
Similarly, the Cauchy stress is written as [12, 13, 35, 37]
where \(n_{1}^{a}=F^{a}{}_{A}N_{1}^{A}\), and \(n_{2}^{a}=F^{a}{}_{A}N_{2}^{A}\). In the case of an incompressible orthotropic solid (\(I_{3}=1\)), \(W=W\left(\mathbf{X},I_{1},I_{2},I_{4},I_{5},I_{6},I_{7}\right)\). Thus, using (2.28), one has
Similarly, the Cauchy stress tensor is written as
where \(\ell_{1}^{ab}=n_{1}^{a}\, b^{bc}\, n_{1}^{d}\, g_{cd}+n_{1}^{b}\, b^{ac}\, n_{1}^{d} \,g_{cd}\), and \(\ell_{2}^{ab}=n_{2}^{a}\, b^{bc}\, n_{2}^{d} \,g_{cd}+n_{2}^{b}\, b^{ac}\, n_{2}^{d}\, g_{cd}\).
Monoclinic solids
A monoclinic solid has three material preferred directions that are specified by three unit vectors \(\{\mathbf{N}_{1},\mathbf{N}_{2},\mathbf{N}_{3}\}\) such that \(\mathbf{N}_{1}\cdot\mathbf{N}_{2}\neq 0\) and \(\mathbf{N}_{3}\) is normal to the plane of \(\mathbf{N}_{1}\) and \(\mathbf{N}_{2}\) [24]. The energy function of a monoclinic solid depends on nine invariants [37], seven of which are identical to those of orthotropic solids (2.26). The two extra invariants are

where  . Note that
. Note that

For orthotropic solids the second Piola-Kirchhoff stress has the following representation

where \(W_{i}=W_{i}\left(\mathbf{X},I_{1},\ldots,I_{9}\right)\), \(i=1,\ldots,8\). Similarly, the Cauchy stress can be written as

In the case of incompressible monoclinic solids (\(I_{3}=1\)), \(W=W(\mathbf{X},I_{1},I_{2},I_{4},I_{5},I_{6},I_{7}, I_{8},I_{9})\). Thus

Similarly, the Cauchy stress tensor is written as
where  .
.
3 Compressible Inhomogeneous Anisotropic Solids
3.1 Transversely Isotropic Solids
We first consider an inhomogeneous body made of compressible transversely isotropic solids. We do not specify the material preferred direction \(\mathbf{N}(\mathbf{X})\) a priori. In the absence of body forces, the equilibrium equations in Cartesian coordinates read \(\sigma^{ab}{}_{,b}=0\). Substituting (2.22) into the equilibrium equations one obtains [42]
For universal deformations the equilibrium equations hold for an arbitrary energy function \(W\). Knowing that \(W\) is an arbitrary function of its arguments, the coefficient of \(W_{1}\), \(W_{2}\), \(W_{3}\), \(W_{3}\), and \(W_{5}\) must vanish separately. Thus [42]
The above constraints simplify (3.1) to read
Note that \(I_{3,b}=0\) from (3.2)3 and
where
Notice that the first term on the right-hand side of each equation in (3.4) vanishes for homogeneous solids [42]. Substituting the above relations into (3.3) the coefficients of \(W_{13}\) and \(W_{23}\) read
Thus, \(I_{1,b}=I_{2,b}=0\). Substituting these into (3.4) and using (3.3) the coefficients of \(W_{34}\) and \(W_{35}\) read
Hence, \(I_{4,b}=I_{5,b}=0\). Therefore, we have the following universality constraints
Note that (3.8) and (3.9) are the universality constraints for isotropic solids [9, 41] and imply that \(F^{a}{}_{A|B}=0\), i.e., universal deformations are homogeneous. In addition, since \(I_{4,b}=I_{4,A}(F^{-1})^{A}{}_{b}=0\), we have \(I_{4,A}=0\). Similarly, \(I_{5,A}=0\). The constraints (3.10) and (3.11) imply that \(\mathbf{N}\) is a constant unit vector [42].
For inhomogeneous solids one has the following extra five sets of universality constraints:
The first three constraints in (3.12) are identical to those of isotropic solids [40], and imply that
The constraint (3.12)4 implies that \(n^{b} (F^{-1})^{A}{}_{b}\,W_{4,A}=W_{4,A}\,N^{A}=0\). As \(\mathbf{N}\) is a constant unit vector we can choose the Cartesian coordinates \((X^{1},X^{2},X^{3})\) in the reference configuration such that
i.e., \(N^{A}=\delta^{A}_{1}\). Here we have used the notation \({\partial_{X^{i}}}\) to denote the unit (tangent) vector along the \(i\)th Cartesian direction as is customary in differential geometry. With this choice of coordinates the constraint \(W_{4,A}\,N^{A}=0\) reads
Note that \(n^{a}=F^{a}{}_{A} \,N^{A}=F^{a}{}_{A} \,\delta^{A}_{1}=F^{a}{}_{1}\).
Equation (3.12)5 is equivalent to
Using (2.23) the above constraints can be rewritten as
Knowing that \(N^{A}=\delta^{A}_{1}\), this last expression can be rewritten as
For \(B=2\), it implies that \(C^{2}{}_{1}W_{5,1}=0\), which must hold for arbitrary homogeneous deformations, i.e., for arbitrary constant \(C^{2}{}_{1}\). Thus, \(W_{5,1}=0\). Now the constraint for \(B=3\) is trivially satisfied. For \(B=1\), \(C^{2}{}_{1}\,W_{5,2}+C^{3}{}_{1}\,W_{5,3}=0\), which must be satisfied for arbitrary constants \(C^{2}{}_{1}\), and \(C^{3}{}_{1}\). Therefore, \(W_{5,2}=W_{5,3}=0\). Thus, the constraint (3.12)5 implies that \(W_{5,A}=0\). In summary, we have the following constraints
This implies that
for some scalar functions \(f_{A}\). Note that \(\frac{\partial f_{1}}{\partial X^{2}}=\frac{\partial f_{2}}{\partial X^{1}}\). Since \(f_{1}\) does not depend on \(I_{4}\), one has
Similarly, \(\frac{\partial f_{1}}{\partial X^{3}}=\frac{\partial f_{3}}{\partial X^{1}}\) implies that
From (3.20)1, one writes
where \(X_{0}^{1}\) is some fixed value of \(X^{1}\), \(h\) is some scalar function, and \(W(\mathbf{X},I_{i})\) and \(h(X^{2},X^{3},I_{i})\) are short for \(W(\mathbf{X},I_{1},I_{2},I_{3},I_{4},I_{5})\) and \(h(X^{2},X^{3},I_{1},I_{2},I_{3},I_{4},I_{5})\), respectively. Taking partial derivative with respect to \(X^{2}\) of both sides one obtains
From (3.24) and (3.20)2 one concludes that
Thus
where \(X_{0}^{2}\) is some fixed value of \(X^{2}\). Hence
Using the above relation in (3.23), one writes
Taking partial derivative with respect to \(X^{3}\) of the above relation one obtains
Thus using (3.20)3 one concludes that
Hence
where \(X_{0}^{3}\) is some fixed value of \(X^{3}\). Thus
Substituting the above relation into (3.28) one obtains
Substituting (3.21) and (3.22) into the above relation one finds that \(W(\mathbf{X},I_{i})=\hat{W}(\mathbf{X})+\overline{W}(I_{i})+\widetilde{W}(X^{2},X^{3},I_{4})\). Note that the term \(\hat{W}(\mathbf{X})\) is mechanically inconsequential, and hence we have proved that the only universal deformations are homogeneous and the only possible dependence on the position is through \(I_{4}\) and in directions normal to a constant vector \(\mathbf{N}\):
Proposition 3.1
For compressible nonlinear transversely isotropic solids, universal deformations are homogeneous, the universal material preferred direction is at all points a constant unit vector \(\mathbf{N}\), and the universal inhomogeneity has the following form
where the Cartesian \(X^{1}\)-coordinate line is parallel to \(\mathbf{N}\).
3.2 Orthotropic Solids
For inhomogeneous compressible orthotropic solids there are two sets of universality constraints. The first set of constraints are identical to those of homogeneous compressible orthotropic solids and read [42]:
These constraints imply again that universal deformations are homogeneous and the material preferred directions are uniform. In the reference configuration we choose the Cartesian coordinates \((X^{1},X^{2},X^{3})\) such that
The second set of universality constraints are:
The first three constraints are identical to those of isotropic solids [40], and imply that \(W_{1,A}=W_{2,A}=W_{3,A}=0\). Similarly to the universality constraints of transversely isotropic solids, (3.42)4 and (3.42)6 imply that
The universality constraints (3.42)5 and (3.42)7 imply that
This means that
Note that
Thus
Using (3.45)1, one writes
where \(h\) is some scalar function, and \(X_{0}^{1}\) is some fixed value of \(X^{1}\). Taking partial derivative with respect to \(X^{2}\) of both sides one obtains
From (3.49) and (3.45)2 one concludes that
Thus
where \(X_{0}^{2}\) is some fixed value of \(X^{2}\). Hence
Using the above relation in (3.48), one has
Taking partial derivative with respect to \(X^{3}\) of the above relation one obtains
Thus using (3.45)3 one concludes that
Hence
where \(X_{0}^{3}\) is some fixed value of \(X^{3}\). Thus
Using the above relation in (3.53), one obtains
Substituting (3.47) into (3.58) one finds
Noting that the term \(\hat{W}(\mathbf{X})\) is mechanically inconsequential, we have proved the following result.
Proposition 3.2
For compressible nonlinear orthotropic solids universal deformations are homogeneous, the universal material preferred directions are everywhere the same three mutually orthogonal constant unit vectors \(\mathbf{N}_{1}, \mathbf{N}_{2}\), and \(\mathbf{N}_{3}\), and the universal inhomogeneity has the following form
where the Cartesian coordinate lines are the orthotropy directions.
While the form of this strain-energy density seems involved, it can be written explicitly in terms of the Cartesian components of \(\mathbf{C}\) as
3.3 Monoclinic Solids
Note that orthogonality of the material preferred directions was not assumed when deriving the constraints (3.35)-(3.40), i.e., these universality constraints hold for monoclinic solids as well. However, there are the following extra universality constraints [42]:
For compressible monoclinic solids the universality constraints (3.35)-(3.40) imply that universal deformations are homogeneous, and the three unit vectors \(\mathbf{N}_{1}, \mathbf{N}_{2}\), and \(\mathbf{N}_{3}\) are constant. This means that (3.62), (3.63) are trivially satisfied. Let us assume that the angle between \(\mathbf{N}_{1}\) and \(\mathbf{N}_{2}\) is \(\theta\) \((0<\theta<\frac{\pi}{2})\). In the reference configuration we choose a Cartesian coordinate system \((X^{1},X^{2},X^{3})\) such that
In general, \(\mathbf{N}_{1}\) makes and angle \(\alpha\) with the \(X_{1}\)-axis, and thus
The second set of universality constraints for inhomogeneous monoclinic solids include those of orthotropic solids, i.e., Eqs. (3.42). There is one extra universality constrain that reads:
This is equivalent to \(\left(N_{1}^{B} N_{2}^{A}+N_{1}^{A} N_{2}^{B}\right)W_{8,A} =0\), and is trivially satisfied for \(B=3\). For \(B=1,2\) it gives us
These need to be satisfied for arbitrary \(\alpha\), and \(\theta\), and hence
The first three universality constraints in (3.42), and (3.42)5 and (3.42)7 imply that
The constraint (3.42)4 implies that
which must hold for any \(\alpha\), and hence
The constraint (3.42)6 implies that
This needs to hold for any \(0<\theta<\frac{\pi}{2}\), and hence
From Eqs. (3.68), (3.69), (3.71), and (3.73) one has
Using (3.74)1, one can write
Taking partial derivative with respect to \(X^{2}\) of both sides one obtains
From (3.76) and (3.74)2 one concludes that
Thus
Using the above relation in (3.75), one writes
Taking partial derivative with respect to \(X^{3}\) of the above relation one obtains
Thus using (3.74)3 one concludes that
Hence
Using the above relation in (3.79), one obtains
Note that the second and third terms on the right-hand side are mechanically inconsequential, and hence, we have proved the following result.
Proposition 3.3
For compressible nonlinear monoclinic solids universal deformations are homogeneous, the universal material preferred directions are everywhere the same three constant unit vectors \(\mathbf{N}_{1}, \mathbf{N}_{2}\), and \(\mathbf{N}_{3}\), such that \(\mathbf{N}_{3}\) is perpendicular to the plane of \(\mathbf{N}_{1}\) and \(\mathbf{N}_{2}\), and the universal inhomogeneity has the following form
where the Cartesian \(X^{3}\)-coordinate line is along \(\mathbf{N}_{3}\).
Table 1 summarizes our results for inhomogeneous compressible anisotropic solids.
4 Incompressible Inhomogeneous Transversely Isotropic Elastic Solids
For a body made of an incompressible transversely isotropic solid, the equilibrium equations in the absence of body forces read:
This is equivalent to exactness of the 1-form
where
The exactness of \(\boldsymbol{\xi}\) implies that \(\boldsymbol{d}\boldsymbol{\xi}=\mathbf{0}\) [39], or equivalently, \(\xi_{a|b}=\xi_{b|a}\), where
Note that \(W_{i}=W_{i}(\mathbf{X},I_{1},I_{2},I_{4},I_{5})\), \(i=1,2,4,5\), and thus
Note also that
The last term on the right hand-side is simplified as
Notice that
Thus
Let us denote the independent third-order derivatives of the energy function by \(W_{ijk}=\frac{\partial^{3} W}{\partial I_{i}\partial I_{j}\partial I_{k}}\), ( \(i\leq j\leq k\)). Thus
HenceFootnote 3
Similarly,
and
The symmetry \(\xi_{a|b}=\xi_{b|a}\) forces the coefficient of each partial derivative of the energy function to be symmetric. Following the notation introduced in [42], we define  to be the matrix of the coefficient of \(W_{\kappa}\), where \(\kappa\) is a multi-index. The first nine terms are identical to those of homogeneous isotropic solids:
to be the matrix of the coefficient of \(W_{\kappa}\), where \(\kappa\) is a multi-index. The first nine terms are identical to those of homogeneous isotropic solids:  . They read
. They read

where \(b_{a}^{n}=b^{mn}g_{ma}\), and \(c_{a}^{n}=c^{mn}g_{ma}\). It is well known that the symmetry of the above nine terms admits six families of deformations [8, 20, 34]. For both homogeneous and inhomogeneous transversely isotropic solids, we have 25 extra terms:

These terms read [42]:

and

It turns out that the known universal deformations are invariant with respect to certain Lie subgroups of the special Euclidean group [15]. In [42] we conjectured that for each family of universal deformations the corresponding universal material preferred direction vector \(\mathbf{N}\) is invariant under the same Lie subgroup. For each of the six families of universal deformations we found the corresponding universal material preferred directions.
For inhomogeneous incompressible transversely isotropic solids, in addition to the universality constraints (4.15), (4.17), and (4.18), there are the following eighteen extra sets of universality constraints (each term must be symmetric in \((ab)\) for \(A=1,2,3\), and \(B\geq A\)):

and

The set of universality constraints (4.19) are identical to those of inhomogeneous isotropic solids [40]. For a given family of deformations and material preferred directions that are consistent with (4.15), (4.17), and (4.18), the corresponding inhomogeneities that respect (4.19) and (4.20) are called the universal inhomogeneities. In the following subsections, for each of the six families of universal deformations the corresponding universal inhomogeneities will be determined. This will be done by looking at each term in (4.19) and (4.20) and examining its symmetries. If a particular term cannot be symmetric, the corresponding derivative of \(W\) has to vanish, giving us a constraint on the form of \(W\).
4.1 Family 0: Homogeneous Deformations
With respect to the Cartesian coordinates \(\{X^{A}\}\) and \(\{x^{a}\}\) in the reference and current configurations, respectively, a homogeneous deformation has the representation \(x^{a}(\mathbf{X})=F^{a}{}_{A} X^{A}+c^{a}\), where \([F^{a}{}_{A}]\) is a constant matrix and \([c^{a}]\) is a constant vector. The incompressibility constraint is then \(\det [F^{a}{}_{A}]=1\). For a homogeneous deformation the right Cauchy-Green tensor has the constant components \(C_{AB}=F^{a}{}_{A}F^{a}{}_{A}\,\delta_{ab}\), which implies that \(\mathbf{C}^{\flat}\) is invariant under the action of \(T(3)\subset SE(3)\)—the group of translations. In [42] it was assumed that \(\mathbf{N}(\mathbf{X})\) is invariant under \(T(3)\) as well, i.e., \(\mathbf{N}\) is a constant unit vector. We choose the Cartesian coordinates \((X^{1},X^{2},X^{2})\) such that
i.e., \(N^{A}=\delta^{A}_{1}\). With this assumption the universality constraints (4.17) and (4.18) are satisfied. For homogeneous deformations, the first five sets of universality constraints (4.19) are trivially satisfied. The last two sets force the deformation to be the identity [40]. This implies that
For isotropic solids, the relations \(W_{1,AB}=\left(W_{1,A}\right)_{,B}=0\), and \(W_{2,AB}=\left(W_{2,A}\right)_{,B}=0\) imply that
Note that
From (4.23)1, one concludes that
Thus
for some function \(R(\mathbf{X},I_{2})\). Hence
Substituting the above identity into (4.23)2 one concludes that
This implies that
and hence \(R(\mathbf{X},I_{2})=R_{1}(\mathbf{X})+R_{2}(I_{2})\). Using this in (4.26), up to a mechanically inconsequential \(\mathbf{X}\)-dependent term one concludes that for an incompressible isotropic solid the energy function is a linear function of the Cartesian coordinates, i.e.,
for some vector \(\mathbf{H}(I_{1},I_{2})\).Footnote 4
In the case of inhomogeneous transversely isotropic solids, one still has the constraints (4.22). The first nine sets of universality constraints (4.20) are trivially satisfied for homogeneous deformations and constant \(\mathbf{N}\). The last two sets of constraints in (4.20) are nontrivial. The universality constraints corresponding to Eq. (4.20)10 read
Knowing that \(N^{A}=\delta^{A}_{1}\), the above constraints are rewritten as
This is equivalent to
which is simplified to read
These are three constraints corresponding to \((M,N)=(1,2),~(1,3)\), and \((2,3)\), and read
Notice that these need to be satisfied for an arbitrary matrix \([C_{AB}]\) with unit determinant. This means that \(W_{4,11}=W_{4,12}=W_{4,13}=0\).
The universality constraints corresponding to Eq. (4.20)11 read
This can be simplified to read
These are three constraints corresponding to \((M,N)=(1,2),~(1,3)\), and \((2,3)\), and read
These must be satisfied for an arbitrary matrix \([C_{AB}]\) with unit determinant. If \([C_{AB}]\) is diagonal, one concludes that \(W_{5,12}=W_{5,13}=0\). Considering simple shear in the \(X^{1}X^{2}\)-plane (\(C_{13}=C_{23}=0\)), one concludes that \(W_{5,11}=W_{5,22}=W_{5,23}=0\). Substituting these in the above equations, one concludes that \(W_{5,33}=0\). Therefore, \(W_{4,AB}=0\).
In summary, for the universality constraints to hold one must have
Using arguments similar to those used in deriving (4.30), one can show that the above constraints imply the following proposition.
Proposition 4.1
For inhomogeneous incompressible nonlinear transversely isotropic solids with material preferred direction parallel to the \(X^{1}\)-axis in a Cartesian coordinate system \((X^{1},X^{2},X^{3})\), Family 0 deformations are universal for any energy function of the following form
Remark 4.2
Note that the last term of the energy function in (4.40) has a form identical to that of compressible orthotropic solids (3.34).
4.2 Family 1: Bending, Stretching, and Shearing of a Rectangular Block
Consider a rectangular block and a Cartesian coordinate system \((X,Y,Z)\) with coordinate planes parallel to the faces of the block. In the current configuration cylindrical coordinates \((r,\theta,z)\) are used. With respect to these coordinates, the Family 1 deformations have the following representation
where \(C_{1}, \ldots, C_{6}\) are constants. The right Cauchy-Green strain reads
and is independent of \(Y\) and \(Z\), i.e., \(\mathbf{C}^{\flat}\) is invariant under the action of \(T(2)\subset SE(3)\). In [42] it was assumed that \(\mathbf{N}\) has the same symmetry, i.e.,
where \((N^{1}(X))^{2}+(N^{2}(X))^{2}+(N^{3}(X))^{2}=1\). It was shown that the universal material preferred direction has the following possible forms
where \(\psi(X)\) is an arbitrary function. Notice that (4.44)1 corresponds to a uniform distribution of fibers parallel to the \(X\)-axis. In the other universal material preferred direction distribution (4.44)2, for fixed \(X\) fibers make an angle \(\psi(X)\) with the \(Y\)-axis, and are distributed uniformly in the \(YZ\)-plane.
In [40] it was shown that the constraints (4.19) imply that
The above relations hold for inhomogeneous transversely isotropic solids as well. For the universal material preferred direction (4.44)1, one can show thatFootnote 5

These constraints cannot be satisfied, and hence
Similarly, for the universal material preferred direction (4.44)2 one has the following constraints:
-
 , for \((A,a,b)=(2,1,2)\) requires that $$ C_{2} \sqrt{C_{1} (C_{4}+2 X)} \cos\psi \left[2 (C_{4}+2 X) \psi' \sin\psi-3 \cos\psi \right]=0\,. $$(4.48)
, for \((A,a,b)=(2,1,2)\) requires that $$ C_{2} \sqrt{C_{1} (C_{4}+2 X)} \cos\psi \left[2 (C_{4}+2 X) \psi' \sin\psi-3 \cos\psi \right]=0\,. $$(4.48) -
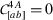 , for \((A,a,b)=(3,1,2)\) implies that $$ C_{2} \sqrt{C_{1} (C_{4}+2 X)} \left[C_{1} C_{2}^{2} C_{3} \cos^{2}\psi+(C_{4}+2 X) \psi' \cos 2\psi+\sin 2\psi \right]=0\,. $$(4.49)
, for \((A,a,b)=(3,1,2)\) implies that $$ C_{2} \sqrt{C_{1} (C_{4}+2 X)} \left[C_{1} C_{2}^{2} C_{3} \cos^{2}\psi+(C_{4}+2 X) \psi' \cos 2\psi+\sin 2\psi \right]=0\,. $$(4.49) -
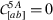 , for \((A,a,b)=(2,1,2)\) requires that $$ \begin{aligned}[b] & C_{2} \sqrt{C_{1} (C_{4}+2 X)} \Big\{ 2 (C_{4}+2 X) \psi'\left[C_{1} C_{2}^{2} \sin 2\psi \left(C_{1} C_{4}+2 C_{1} X+C_{3}^{2}\right)+C_{3} \cos 2\psi \right]\\ & \quad\quad -2 C_{1} \,C_{2}^{2} \cos^{2}\psi \left[5 C_{1} (C_{4}+2 X)+3 C_{3}^{2}\right]+3 C_{3} \sin2\psi \Big\} =0 \,. \end{aligned} $$(4.50)
, for \((A,a,b)=(2,1,2)\) requires that $$ \begin{aligned}[b] & C_{2} \sqrt{C_{1} (C_{4}+2 X)} \Big\{ 2 (C_{4}+2 X) \psi'\left[C_{1} C_{2}^{2} \sin 2\psi \left(C_{1} C_{4}+2 C_{1} X+C_{3}^{2}\right)+C_{3} \cos 2\psi \right]\\ & \quad\quad -2 C_{1} \,C_{2}^{2} \cos^{2}\psi \left[5 C_{1} (C_{4}+2 X)+3 C_{3}^{2}\right]+3 C_{3} \sin2\psi \Big\} =0 \,. \end{aligned} $$(4.50) -
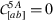 , for \((A,a,b)=(3,1,2)\) requires that $$ \begin{aligned}[b] & (C_{4}+2 X)^{2} \psi' \cos 2\psi \left[C_{1}^{2} \,C_{2}^{4} \left(C_{1} (C_{4}+2 X)+C_{3}^{2}\right)+1\right]\\ & \quad +(C_{4}+2 X) \Big\{ C_{1}^{3} C_{2}^{6} C_{3} \cos 2\psi \left(C_{1} \,C_{4}+2C_{1} X+C_{3}^{2}\right) \\& \quad +\sin 2\psi \left[2 C_{1}^{3} \,C_{2}^{4} (C_{4}+2 X)+1\right] \\ & \quad +C_{1} \,C_{2}^{2} \,C_{3} \left[ C_{1}^{2} \,C_{2}^{4} \left(C_{1} \,C_{4}+2 C_{1}X+C_{3}^{2}\right)-2\right]\Big\} =0 \,. \end{aligned} $$(4.51)
, for \((A,a,b)=(3,1,2)\) requires that $$ \begin{aligned}[b] & (C_{4}+2 X)^{2} \psi' \cos 2\psi \left[C_{1}^{2} \,C_{2}^{4} \left(C_{1} (C_{4}+2 X)+C_{3}^{2}\right)+1\right]\\ & \quad +(C_{4}+2 X) \Big\{ C_{1}^{3} C_{2}^{6} C_{3} \cos 2\psi \left(C_{1} \,C_{4}+2C_{1} X+C_{3}^{2}\right) \\& \quad +\sin 2\psi \left[2 C_{1}^{3} \,C_{2}^{4} (C_{4}+2 X)+1\right] \\ & \quad +C_{1} \,C_{2}^{2} \,C_{3} \left[ C_{1}^{2} \,C_{2}^{4} \left(C_{1} \,C_{4}+2 C_{1}X+C_{3}^{2}\right)-2\right]\Big\} =0 \,. \end{aligned} $$(4.51)
None of the above constraints can be satisfied, and hence, (4.47) holds for this case as well. From (4.45) and (4.47) one concludes that up to a mechanically inconsequential function of \((X,Y,Z)\), the energy function must have the form \(W=W(X,I_{1},I_{2},I_{4},I_{5})\). For energy functions of this form, in (4.19) and (4.20) one only needs to check the symmetry of the terms with \(A=1\), and \(A=B=1\). All those terms are symmetric.
Proposition 4.3
For inhomogeneous incompressible nonlinear transversely isotropic solids with any of the universal material preferred directions given in (4.44), Family 1 deformations are universal for any energy function of the form \(W=W(X,I_{1},I_{2},I_{4},I_{5})\).
4.3 Family 2: Straightening, Stretching, and Shearing of a Sector of a Cylindrical Shell
Consider a sector of a cylindrical shell that is parametrized by cylindrical coordinates \((R,\Theta,Z)\). In the deformed configuration Cartesian coordinates \((x,y,z)\) are used. Family 2 deformations have the following representation
and hence
It is seen that the right Cauchy-Green strain is independent of \(\Theta\) and \(Z\). In [42] it was assumed that \(\mathbf{N}\) has the same symmetry, i.e.,
such that \((N^{1}(R))^{2}+R^{2}(N^{2}(R))^{2}+(N^{3}(R))^{2}=1\). It was shown that there are two solutions for the universal material preferred direction:
where \(\chi(R)\) is an arbitrary function. In the case of (4.55)1 fibers are distributed radially. In the solution (4.55)2, if \(\cos\psi(R)\neq 0,\pm 1\) fibers are distributed helically, if \(\cos\psi(R)=0\) they are distributed parallel to the axis of the shell, and if \(\cos\psi(R)=\pm 1\) they are concentric circles in the \((R,\Theta)\)-plane.
In [40] it was shown that the constraints (4.19) imply that
The above relations hold for inhomogeneous transversely isotropic solids as well. For the universal material preferred direction (4.55)1, one can show that

These constraints cannot be satisfied, and thus
Similarly, for the universal material preferred direction (4.55)2 one has the following constraints:
-
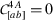 , for \((A,a,b)=(2,1,2)\) requires that $$ \cos\chi(R) \left[R\,\chi'(R) \sin\chi(R)+\cos\chi(R)\right]=0\,. $$(4.59)
, for \((A,a,b)=(2,1,2)\) requires that $$ \cos\chi(R) \left[R\,\chi'(R) \sin\chi(R)+\cos\chi(R)\right]=0\,. $$(4.59) -
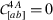 , for \((A,a,b)=(3,1,2)\) implies that $$ \sin2\chi(R)-2R\,\chi'(R)\cos2\chi(R) =0\,. $$(4.60)
, for \((A,a,b)=(3,1,2)\) implies that $$ \sin2\chi(R)-2R\,\chi'(R)\cos2\chi(R) =0\,. $$(4.60) -
 , for \((A,a,b)=(2,1,2)\) requires that $$ \begin{aligned}[b] & R\,\chi'(R) \left[\left(1+C_{3}^{2}\right) \sin 2\chi(R)-C_{1} C_{3} R\cos2\chi(R)\right] \\ & \quad +\cos\chi(R) \left[3 C_{1} C_{3} R \sin\chi(R)+4 \left(1+C_{3}^{2}\right) \cos\chi(R)\right]=0 \,. \end{aligned} $$(4.61)
, for \((A,a,b)=(2,1,2)\) requires that $$ \begin{aligned}[b] & R\,\chi'(R) \left[\left(1+C_{3}^{2}\right) \sin 2\chi(R)-C_{1} C_{3} R\cos2\chi(R)\right] \\ & \quad +\cos\chi(R) \left[3 C_{1} C_{3} R \sin\chi(R)+4 \left(1+C_{3}^{2}\right) \cos\chi(R)\right]=0 \,. \end{aligned} $$(4.61) -
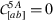 , for \((A,a,b)=(3,1,2)\) requires that $$ \begin{aligned}[b] -R \left(1+C_{1}^{2} R^{2}+C_{3}^{2}\right) \chi'(R) \cos2\chi(R)+\left(3+C_{1}^{2} R^{2}+3 C_{3}^{2}\right) \sin 2\chi(R) +2 C_{1}\, C_{3} R=0 \,. \end{aligned} $$(4.62)
, for \((A,a,b)=(3,1,2)\) requires that $$ \begin{aligned}[b] -R \left(1+C_{1}^{2} R^{2}+C_{3}^{2}\right) \chi'(R) \cos2\chi(R)+\left(3+C_{1}^{2} R^{2}+3 C_{3}^{2}\right) \sin 2\chi(R) +2 C_{1}\, C_{3} R=0 \,. \end{aligned} $$(4.62)
None of the above constraints can be satisfied,Footnote 6 and thus, (4.58) holds for this case as well. From (4.56) and (4.58) one concludes that up to a mechanically inconsequential function of \((R,\Theta,Z)\), the energy function must have the form \(W=W(R,I_{1},I_{2},I_{4},I_{5})\). For energy functions of this form, in (4.19) and (4.20) one only needs to check the symmetry of the terms with \(A=1\), and \(A=B=1\). All those terms are symmetric.
Proposition 4.4
For inhomogeneous incompressible nonlinear transversely isotropic solids with any of the universal material preferred directions given in (4.55), Family 2 deformations are universal for any energy function of the form \(W=W(R,I_{1},I_{2},I_{4},I_{5})\).
4.4 Family 3: Inflation, Bending, Torsion, Extension, and Shearing of a Sector of an Annular Wedge
Family 3 deformations, with respect to the cylindrical coordinates \((R,\Theta,Z)\) and \((r,\theta,z)\) in the reference and current configurations, respectively, have the following representation
and hence
where \(K=C_{1}C_{4}-C_{2} C_{3}\). Notice that \(\mathbf{C}^{\flat}\) is independent of \(\Theta\) and \(Z\). In [42] it was assumed that \(\mathbf{N}\) has the same symmetry, i.e.,
where \((N^{1}(R))^{2}+R^{2}(N^{2}(R))^{2}+(N^{3}(R))^{2}=1\). It was shown that there are two solutions for the universal material preferred direction:
where \(\psi(R)\) is an arbitrary function.
In [40] it was shown that for this family of deformations constraints (4.19) imply that
The above relations hold for inhomogeneous transversely isotropic solids as well. For the universal material preferred direction (4.66)1, one can show that

These constraints cannot be satisfied, and hence
Similarly, for the universal material preferred direction (4.66)2  , for \((A,a,b)=(2,1,2)\) requires that:
, for \((A,a,b)=(2,1,2)\) requires that:
The constraints  , for \((A,a,b)=(3,1,2)\),
, for \((A,a,b)=(3,1,2)\),  , for \((A,a,b)=(2,1,2)\), and
, for \((A,a,b)=(2,1,2)\), and  , for \((A,a,b)=(3,1,2)\) require vanishing of some lengthy expressions that we do not report here. None of these four constraints can be satisfied, and thus, (4.69) holds for this case as well. Similar to Family 2 deformations, from (4.67) and (4.69) one concludes that up to a mechanically inconsequential function of \((R,\Theta,Z)\), the energy function must have the form \(W=W(R,I_{1},I_{2},I_{4},I_{5})\). For energy functions of this form, in (4.19) and (4.20) one only needs to check the symmetry of the terms with \(A=1\), and \(A=B=1\). All those terms are symmetric.
, for \((A,a,b)=(3,1,2)\) require vanishing of some lengthy expressions that we do not report here. None of these four constraints can be satisfied, and thus, (4.69) holds for this case as well. Similar to Family 2 deformations, from (4.67) and (4.69) one concludes that up to a mechanically inconsequential function of \((R,\Theta,Z)\), the energy function must have the form \(W=W(R,I_{1},I_{2},I_{4},I_{5})\). For energy functions of this form, in (4.19) and (4.20) one only needs to check the symmetry of the terms with \(A=1\), and \(A=B=1\). All those terms are symmetric.
Proposition 4.5
For inhomogeneous incompressible nonlinear transversely isotropic solids with any of the universal material preferred directions given in (4.66), Family 3 deformations are universal for any energy function of the form \(W=W(R,I_{1},I_{2},I_{4},I_{5})\).
Physically, this universal inhomogeneity and directions can be understood as follows: A particular case consists of a single homogeneous cylindrical tube with helical preferred directions. Now, consider a series of encased homogeneous cylindrical tubes in the reference configuration, each with its own helical material preferred directions as describe in [16]. The solution from Proposition 4.5 is a continuous version of this problem where the variation in helical fibers and material properties only depends on \(R\).
4.5 Family 4: Inflation/Inversion of a Sector of a Spherical Shell
Family 4 deformations with respect to the spherical coordinates \((R,\Theta,\Phi)\) and \((r,\theta,\phi)\) in the reference and current configurations, respectively, have the following representation
Thus
which can be written as [15]
where \(\mathbf{1}\) is the identity tensor, and \(\hat{\mathbf{R}}=\frac{\mathbf{X}}{|\mathbf{X}|}\). This implies that at a given point \(\mathbf{X}\), \(\mathbf{C}^{\flat}\) is invariant under all those rotations that fix \(\mathbf{X}\). Yavari and Goriely [42] assumed that \(\mathbf{N}(\mathbf{X})\) has the same symmetry, i.e., it is invariant under all those rotations that fix \(\mathbf{X}\). Thus, \(\mathbf{N}(\mathbf{X})\) is parallel to \(\mathbf{X}\), and knowing that it is a unit vector one concludes that
This means that the universal material preferred direction is radial, i.e., with respect to the spherical coordinates
In [40] it was shown that for this family of deformations constraints (4.19) imply that
The above relations hold for inhomogeneous transversely isotropic solids as well. For the universal material preferred direction (4.75), one can show that

These constraints cannot be satisfied, and hence
From (4.76) and (4.78) one concludes that up to a mechanically inconsequential function of \((R,\Theta,\Phi)\), the energy function must have the form \(W=W(R,I_{1},I_{2},I_{4},I_{5})\). For any energy function of this form, in (4.19) and (4.20) one only needs to check the symmetry of the terms with \(A=1\), and \(A=B=1\). All those terms are symmetric.
Proposition 4.6
For inhomogeneous incompressible nonlinear transversely isotropic solids with the universal material preferred directions given in (4.75), Family 4 deformations are universal for any energy function of the form \(W=W(R,I_{1},I_{2},I_{4},I_{5})\).
Again, this result can be understood physically as the continuous limit of a finite number of encased homogeneous spherical shells with different material properties.
4.6 Family 5: Inflation, Bending, Extension, and Azimuthal Shearing of an Annular Wedge
Family 5 deformations with respect to the cylindrical coordinates \((R,\Theta,Z)\) and \((r,\theta,z)\) in the reference and current configurations, respectively, have the following representation
Thus
which only depends on \(R\). Yavari and Goriely [42] assumed that \(\mathbf{N}\) has the same symmetry, i.e.,
where \((N^{1}(R))^{2}+(N^{2}(R))^{2}+(N^{3}(R))^{2}=1\). They obtained the following two solutions for universal material preferred directions
for arbitrary constants \(\eta\), and \(\xi\). Unfortunately, there was a mistake in checking the universality constraints for solution (4.82)1: This solution satisfies all the universality constraints other than the symmetry of the coefficient of \(W_{4}\) for \((a,b)=(1,3)\), which gives \(C_{2}\cos\eta\sin\eta=0\). Note that \(\sin\eta=0\) in (4.82)1 corresponds to \(\cos\xi=0\) in (4.82)2. This means that the correct set of universal material preferred directions for Family 5 are:
for an arbitrary constant \(\xi\).
In [40] it was shown that the for Family 5 deformations constraints (4.19) imply that
The above relations hold for inhomogeneous transversely isotropic solids as well.
For the universal material preferred direction (4.83)1, all the terms in (4.20)\(_{(1-9)}\) are symmetric. In the last two sets of equations the following four terms are not symmetric:

This implies that
From (4.84) and (4.86) one concludes that . For an energy function of this form, in (4.19) and (4.20) one only needs to check the symmetry of the terms with \(A=1\), and \(A=B=1\). It turns out that all those terms are symmetric.
For the universal material preferred direction (4.83)2, one can show that

None of the above constraints can be satisfied,Footnote 7 and hence
From (4.84) and (4.88) one concludes that the energy function must be homogeneous. This means that Family 5 deformations are not universal for inhomogeneous incompressible transversely isotropic solids with the universal material preferred directions (4.83)2.
Proposition 4.7
For inhomogeneous incompressible nonlinear transversely isotropic solids with the universal material preferred directions given in (4.83)1, Family 5 deformations are universal for any energy function of the form . Family 5 deformations are not universal for inhomogeneous incompressible transversely isotropic solids with the universal material preferred directions (4.83)2.
Table 2 summarizes our results for inhomogeneous incompressible transversely isotropic solids.
5 Incompressible Orthotropic Elastic Solids
For inhomogeneous orthotropic solids
In order to satisfy the symmetry \(\xi_{a|b}=\xi_{b|a}\) for an arbitrary energy function the coefficient of each partial derivative of \(W\) must be symmetric. There are five groups of terms. The first four were derived in [42]. In order for this work to be self contained, all the five groups are reported below. The first four groups of terms that must be symmetric for both incompressible and compressible orthotropic solids are:
-
i)
Nine terms that need to be symmetric for isotropic solids as well:
 (5.2)
(5.2) -
ii)
25 terms associated to \(\mathbf{N}_{1}\):
 (5.3)
(5.3) -
iii)
25 terms associated to \(\mathbf{N}_{2}\):
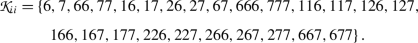 (5.4)
(5.4) -
iv)
24 terms corresponding to coupling of \(\mathbf{N}_{1}\) and \(\mathbf{N}_{2}\):
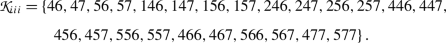 (5.5)
(5.5) -
v)
33 terms that correspond to the inhomogeneity of the energy function. 18 of these are identical to those of isotropic (4.19) and transversely isotropic solids (4.20).
In [42] it was noticed that  and
and  universality constraints have forms identical to those of
universality constraints have forms identical to those of  universality constraints (4.16). This implies that \((\mathbf{N}_{1},\mathbf{N}_{2},\mathbf{N}_{3})\) is universal for orthotropic solids if i) \(\mathbf{N}_{1}\), \(\mathbf{N}_{2}\), and \(\mathbf{N}_{3}\) are universal for transversely isotropic solids, and ii) the three pairs \((\mathbf{N}_{1},\mathbf{N}_{2})\), \((\mathbf{N}_{2},\mathbf{N}_{3})\), and \((\mathbf{N}_{3},\mathbf{N}_{1})\) satisfy the
universality constraints (4.16). This implies that \((\mathbf{N}_{1},\mathbf{N}_{2},\mathbf{N}_{3})\) is universal for orthotropic solids if i) \(\mathbf{N}_{1}\), \(\mathbf{N}_{2}\), and \(\mathbf{N}_{3}\) are universal for transversely isotropic solids, and ii) the three pairs \((\mathbf{N}_{1},\mathbf{N}_{2})\), \((\mathbf{N}_{2},\mathbf{N}_{3})\), and \((\mathbf{N}_{3},\mathbf{N}_{1})\) satisfy the  universality constraints. We follow the notation introduced in [42], and let
universality constraints. We follow the notation introduced in [42], and let  , and
, and  . The coefficients of the derivatives of the energy function associated to the set
. The coefficients of the derivatives of the energy function associated to the set  are:
are:

and

For inhomogeneous incompressible orthotropic solids, in addition to the universality constraints (4.19), and (4.20) there are the following 15 extra sets of universality constraints (each term must be symmetric in \((ab)\) for \(A=1,2,3\), and \(B\geq A\)):

5.1 Family 0
In [42] it was shown that for homogeneous orthotropic solids homogeneous deformations are universal for any three constant unit vectors \((\mathbf{N}_{1},\mathbf{N}_{2},\mathbf{N}_{3})\) that are mutually orthogonal. In the reference configuration we choose the Cartesian coordinates \((X^{1},X^{2},X^{3})\) such that
The universality constraints still imply (4.39). For homogeneous deformations and constant \((\mathbf{N}_{1},\mathbf{N}_{2},\mathbf{N}_{3})\), only the last two sets of universality constraints in (5.8) are nontrivial, and imply that
Using a fairly lengthy but standard argument (similar to those of §3.2) one can show that the constraints (4.39) and (5.10) imply the following result.
Proposition 5.1
For inhomogeneous incompressible nonlinear orthotropic solids, Family 0 deformations are universal for any energy function of the following form
where \((\mathbf{N}_{1},\mathbf{N}_{2},\mathbf{N}_{3})\) are constant unit vectors given in (5.9).
Remark 5.2
Note that the last three terms of the energy function in (5.11) have identical forms to that of compressible orthotropic solids (3.60).
5.2 Family 1
In [42] it was shown that for Family 1 universal deformations the universal material preferred directions are
where \(\psi(X)\) is an arbitrary function. The constraints (4.45) and (4.47) hold for orthotropic solids as well. Similarly, from (5.8)1−2 one concludes that
All the other universality constraints are satisfied. Therefore, we have the following result.
Proposition 5.3
For inhomogeneous incompressible nonlinear orthotropic solids with any of the universal material preferred directions given in (5.12), Family 1 deformations are universal for any energy function of the form \(W=W(X,I_{1},I_{2},I_{4},I_{5},I_{6},I_{7})\).
5.3 Families 2 and 3
In [42] it was shown that for Families 2 and 3 the following family of material preferred directions are universal.
where \(\chi(R)\) is an arbitrary function. The constraints (4.56) and (4.58) still hold. Similarly, from (5.8)1−2 one concludes that
All the other universality constraints are satisfied. Thus, we have the following result.
Proposition 5.4
For inhomogeneous incompressible nonlinear orthotropic solids with any of the universal material preferred directions given in (5.14), Family 2 and 3 deformations are universal for any energy function of the form \(W=W(R,I_{1},I_{2},I_{4},I_{5},I_{6},I_{7})\).
Yavari and Goriely [42] showed that for homogeneous incompressible orthotropic solids Family 4 deformations are not universal. This is the case for inhomogeneous incompressible orthotropic solids as well.
5.4 Family 5
In [42] the following universal material preferred directions were reported.
As was mentioned in §4.6, there was a mistake in one of the families of universal material preferred directions. In (5.16)2 either \(\cos\eta=0\), or \(\sin\eta=0\), which are already included in (5.16)1. Therefore, the correct families of universal material preferred directions are (we have relabelled them so that \(\mathbf{N}_{3}\) is parallel to the \(Z\)-axis):
where \(\xi\) is an arbitrary constant.
In [40] it was shown that the for Family 5 deformations constraints (4.19) imply that
The above relations hold for inhomogeneous orthotropic isotropic solids as well. If we check the universality constraints for the pair \((\mathbf{N}_{1},\mathbf{N}_{2})\) given in (5.17), from §4.6 we know that \(W_{4,A}=W_{5,A}=W_{6,A}=W_{7,A}=0\), and hence the energy function must be uniform:
Proposition 5.5
For inhomogeneous incompressible nonlinear orthotropic solids Family 5 deformations are not universal.
Table 3 summarizes our results for inhomogeneous incompressible orthotropic solids.
6 Incompressible Monoclinic Elastic Solids
In the case of monoclinic solids
The universality constraint \(\xi_{a|b}=\xi_{b|a}\) forces the coefficient of each partial derivative of \(W\) to be symmetric. Yavari and Goriely [42] showed that for monoclinic solids there are an extra 78 terms corresponding to the following set:

We follow the notation in [42] and write  , and
, and  . The terms corresponding to the set
. The terms corresponding to the set  are:
are:




and

For inhomogeneous incompressible monoclinic solids, in addition to the universality constraints (4.19), and (4.20) there are the following 16 extra sets of universality constraints (each term must be symmetric in \((ab)\) for \(A=1,2,3\), and \(B\geq A\)):

6.1 Family 0
In [42] it was shown that for homogeneous incompressible monoclinic solids homogeneous deformations are universal for any three constant unit vectors \((\mathbf{N}_{1},\mathbf{N}_{2},\mathbf{N}_{3})\) such that \(\mathbf{N}_{1}\) and \(\mathbf{N}_{2}\) are non-parallel, and \(\mathbf{N}_{3}\) is normal to the plane of \(\mathbf{N}_{1}\) and \(\mathbf{N}_{2}\). We assume that the angle between \(\mathbf{N}_{1}\) and \(\mathbf{N}_{2}\) is \(\theta\) \((0<\theta<\frac{\pi}{2})\), and hence,  . In the reference configuration let us choose the Cartesian coordinates \((X^{1},X^{2},X^{3})\) such thatFootnote 8
. In the reference configuration let us choose the Cartesian coordinates \((X^{1},X^{2},X^{3})\) such thatFootnote 8
i.e.,
For monoclinic solids the constraints (4.39) still hold. Notice that only the last two sets of constraints in (5.8) are nontrivial. The universality constraint (5.8)14 implies that
Explicitly, we have
These are three constraints corresponding to \((M,N)=(1,2), (1,3), (2,3)\), and read
Suppose \([C_{AB}]\) is diagonal. From (6.13)2, one concludes that \(\cos\theta\,W_{6,13}+\sin\theta\,W_{6,23}=0\), which must hold for any \(\theta\in (0,\frac{\pi}{2})\). This implies that \(W_{6,13}=W_{6,23}=0\). Substituting this back into (6.13)2 one concludes that \(\left(C_{13}\cos\theta+C_{23}\sin\theta\right)\left(\cos\theta\,W_{6,11}+\sin\theta\,W_{6,12}\right)=0\), which implies that \(W_{6,11}=W_{6,12}=0\). Substituting these into (6.13)3 one obtains \(\left(C_{13}\cos\theta\sin\theta+C_{23}\sin^{2}\theta\right)W_{6,22} =0\), which implies that \(W_{6,22}=0\). Therefore, we have shown that
The universality constraint (5.8)15 implies that
is symmetric in \((MN)\). For \(M=1, N=3\), and diagonal \([C_{AB}]\), the universality constraint is simplified to read
This must hold for arbitrary \(C_{11}\) and \(C_{22}\), and hence, \(W_{7,13}=W_{7,23}=0\). Substituting this back into the universality constraint and considering simple shear deformations for which \(C_{12}=C_{13}=0\), one concludes that \(\cos\theta\,W_{7,11}+2\sin\theta\,W_{7,12}=0\), which must hold for an arbitrary \(\theta\). Thus, \(W_{7,11}=W_{7,12}=0\). Substituting these back into the constraint for simple shear, one concludes that \(W_{7,33}=0\). For \(M=2, N=3\), and simple shear deformations for which \(C_{12}=C_{13}=0\), the universality constraint is simplified to read: \(C_{23} \left(2C_{22}+C_{33} \right)\sin^{2}\theta\,W_{7,22}=0\), which implies that \(W_{7,22}=0\). Therefore, we have concluded that \(W_{7,AB}=\left(W_{7,A}\right)_{,B}=0\), \(A,B=1,2,3\).
For homogeneous deformations and uniform material preferred directions only the last set of constraints in (6.8) are non-trivial and are rewritten in terms of the referential quantities as (for \(K,N=1,2,3\))
Thus, we have
Equation (6.18) are three constraints corresponding to \((K,N)=(1,2),~(1,3)\), and \((2,3)\), and read
The above constraints need to be satisfied for an arbitrary matrix \([C_{AB}]\) with unit determinant. For simple shear in the \(X^{2}X^{3}\)-plane (\(C_{12}=C_{13}=0\)), (6.19)3 gives \(C_{23}\sin\theta\,W_{8,12}-C_{22}\sin\theta\,W_{8,13}=0\), which must hold for arbitrary \(C_{23}\), and hence \(W_{8,12}=W_{8,13}=0\). Thus, (6.19) is simplified to read
For simple shear in the \(X^{1}X^{2}\)-plane (\(C_{13}=C_{23}=0\)), (6.20)2 gives \(C_{11}\sin\theta\, W_{8,23}=0\), which implies that \(W_{8,23}=0\). Thus
The last two equations imply that \(W_{8,11}=W_{8,22}=0\). Thus, (6.19) implies that \((W_{8,1})_{,A}=(W_{8,2})_{,A}=0,~A=1,2,3\).
In summary, the universality constraints give us the following
Using a lengthy but standard argument (similar to those of §3.2) one can show that the constraints (6.22) imply the following result.
Proposition 6.1
For inhomogeneous incompressible nonlinear monoclinic solids, Family 0 deformations are universal for any energy function of the following form
where \((\mathbf{N}_{1},\mathbf{N}_{2},\mathbf{N}_{3})\) are constant unit vectors such that \(\mathbf{N}_{3}\) is parallel to the Cartesian \(X^{3}\)-axis.
Remark 6.2
Note that the last term of the energy function in (6.23) has a form identical to that of compressible monoclinic solids (3.84).
6.2 Family 1
In [42] it was shown that for Family 1 deformations of homogeneous incompressible monoclinic solids the universal material preferred directions are
where \(\psi_{1}(X)\) and \(\psi_{2}(X)\) are arbitrary functions such that \(\psi_{1}(X)\neq\psi_{2}(X)\). The constraints (4.45), (4.47), and (5.13) hold for monoclinic solids as well. The constraints  , for \((A,a,b)=(2,1,2)\) and \((A,a,b)=(3,1,2)\), require vanishing of some lengthy expressions that we do not report here. Neither of these two constraints can be satisfied, and hence
, for \((A,a,b)=(2,1,2)\) and \((A,a,b)=(3,1,2)\), require vanishing of some lengthy expressions that we do not report here. Neither of these two constraints can be satisfied, and hence
All the other universality constraints are satisfied. Therefore, we conclude that \(W=\overline{W}(X,I_{1},I_{2},I_{4},I_{5},I_{6},I_{7},I_{8},I_{9})+\widetilde{W}(X,Y,Z,I_{9})\). Noting that the term \(\widetilde{W}(X,Y,Z,I_{9})\) is mechanically inconsequential, we have proved the following result.
Proposition 6.3
For inhomogeneous incompressible nonlinear monoclinic solids with any of the universal material preferred directions given in (6.24), Family 1 deformations are universal for any energy function of the form \(W=W(X,I_{1},I_{2},I_{4},I_{5},I_{6},I_{7},I_{8},I_{9})\).
6.3 Families 2 and 3
In [42] it was shown that for Family 2 and 3 deformations of homogeneous incompressible monoclinic solids the universal material preferred directions are
where \(\chi_{1}(R)\neq\chi_{2}(R)\) are arbitrary functions.
For monoclinic solids, the constraints (4.56), (4.58), and (5.15) still hold. The constraints  , for \((A,a,b)=(2,1,2)\) and \((A,a,b)=(3,1,2)\), require vanishing of some lengthy expressions that we do not report here. Neither of these two constraints can be satisfied, and hence
, for \((A,a,b)=(2,1,2)\) and \((A,a,b)=(3,1,2)\), require vanishing of some lengthy expressions that we do not report here. Neither of these two constraints can be satisfied, and hence
All the other universality constraints are satisfied. Therefore we conclude that \(W=\overline{W}(R,I_{1},I_{2},I_{4},I_{5},I_{6},I_{7},I_{8},I_{9})+\widetilde{W}(R,\Theta,Z,I_{9})\). Noting that the term \(\widetilde{W}(R,\Theta,Z,I_{9})\) is mechanically inconsequential, we have proved the following result.
Proposition 6.4
For inhomogeneous incompressible nonlinear monoclinic solids with any of the universal material preferred directions given in (6.26), Family 2 and 3 deformations are universal for any energy function of the form \(W=W(R,I_{1},I_{2},I_{4},I_{5},I_{6},I_{7},I_{8},I_{9})\).
Yavari and Goriely [42] showed that for homogeneous incompressible monoclinic solids Family 4 deformations are not universal. This is the case for inhomogeneous incompressible monoclinic solids as well.
6.4 Family 5
In [42] the following universal material preferred directions were reported:
Noting that \(\sin\eta\cos\eta=0\), Classes (ii) and (iii) become unacceptable (\(\hat{\mathbf{N}}_{1}\cdot\hat{\mathbf{N}}_{2}=0\)), and hence the correct universal material preferred directions are:
This means that the material preferred directions are two families of fibers that are parallel to the \((R,\Theta)\) plane and are distributed uniformly in two distinct fixed directions.
In [40] it was shown that the for Family 5 deformations constraints (4.19) imply that
The above relations hold for inhomogeneous monoclinic solids as well. As was shown in §4.6 the universality constraints (4.20) imply that \(W_{4,A}=W_{5,A}=W_{6,A}=W_{7,A}=0\). For the universal material preferred direction (6.31), one can show that

None of the above constraints can be satisfied, and hence
In summary, we have proved the following result.
Proposition 6.5
For inhomogeneous incompressible nonlinear monoclinic solids Family 5 deformations are not universal.
Table 4 summarizes our results for inhomogeneous incompressible monoclinic solids.
7 Concluding Remarks
In this paper we studied universal deformations in inhomogeneous anisotropic bodies. Equilibrium equations in the absence of body forces, and arbitrariness of energy functions in a given class of materials impose certain constraints that we call universality constraints. We observed that the universality constraints of inhomogeneous solids include those of the corresponding homogeneous solids. In other words, for a given class of materials universal deformations and universal material preferred directions are determined by the universality constraints of the corresponding homogeneous solids. Universal inhomogeneities (position dependence of the energy function) are those inhomogeneities that are consistent with the universality constraints. We characterized the universal inhomogeneities for inhomogeneous compressible transversely isotropic, orthotropic, and monoclinic solids. In the case of inhomogeneous incompressible solids, for each of the six known families of universal deformations, and material preferred directions we characterized the corresponding universal inhomogeneities for inhomogeneous incompressible transversely isotropic, orthotropic, and monoclinic solids. Table 1 summarizes our results for inhomogeneous compressible transversely isotropic, orthotropic, and monoclinic solids. Tables 2, 3, and 4 summarize our results for inhomogeneous incompressible transversely isotropic, orthotropic, and monoclinic solids, respectively.
This classification of universal solutions concludes our universal program for hyperelastic materials. It provides a complete collection of solutions that can be used for applications and can be systematically analyzed by stability methods to look for the existence of nearby solutions. In our construction for incompressible solids we have assumed that the choice of material preferred directions is consistent with the underlying symmetries of the deformation (e.g., radial fibers for radial deformations). Therefore, our results do not preclude the existence of other universal solutions that would not preserve the underlying symmetry of the deformations. However, we believe that these solutions are unlikely to exist and we conjecture that this classification, like the cases of isotropic incompressible solids, and isotropic anelastic solids is complete.
Notes
See Pucci et al. [27] for definitions of controllable, general, universal, and partial solutions in nonlinear elasticity.
The factor “\(\frac{1}{2}\)” on the sixth line is missing in Eqs. (4.7)-(4.9) in [40]. However, this typo did not affect any of the results of that work.
In [40] from (4.22) it was incorrectly concluded that \(W(\mathbf{X},I_{1},I_{2})=\overline{W}(I_{1},I_{2})\). Proposition 4.1 in [40] should be corrected to read: “For inhomogeneous incompressible nonlinear isotropic solids, Family 0 deformations are universal for any energy function of the form \(W(\mathbf{X},I_{1},I_{2})=\overline{W}(I_{1},I_{2})+\mathbf{H}(I_{1},I_{2})\cdot\mathbf{X}\).”
All the symbolic computations in this paper were performed using Mathematica Version 12.3.0.0, Wolfram Research, Champaign, IL.
Note that we are finding the universal inhomogeneities of the energy function for an arbitrary member of this class. That means that \(\cos\xi\neq0\), in general, i.e., (4.87)1 cannot be satisfied.
In order to make the calculations simpler we have chosen \(\alpha=0\) in (3.65).
References
Adkins, J.E.: Finite deformation of materials exhibiting curvilinear aeolotropy. Proc. R. Soc. Lond. Ser. A 229(1176), 119–134 (1955)
Adkins, J.E.: Some general results in the theory of large elastic deformations. Proc. R. Soc. Lond. Ser. A 231(1184), 75–90 (1955)
Demirkoparan, H., Pence, T.J.: Swelling of an internally pressurized nonlinearly elastic tube with fiber reinforcing. Int. J. Solids Struct. 44(11–12), 4009–4029 (2007)
Demirkoparan, H., Pence, T.J.: Magic angles for fiber reinforcement in rubber-elastic tubes subject to pressure and swelling. Int. J. Non-Linear Mech. 68, 87–95 (2015)
Doyle, T.C., Ericksen, J.L.: Nonlinear elasticity. Adv. Appl. Mech. 4, 53–115 (1956)
Dunwoody, J.: On a class of controllable deformations of isotropic incompressible elastic solids with simple material inhomogeneity. IMA J. Appl. Math. 70(1), 64–79 (2005)
Dunwoody, J.: On a class of controllable deformations of isotropic incompressible elastic solids with simple material inhomogeneity: II. IMA J. Appl. Math. 70(6), 937–953 (2005)
Ericksen, J.L.: Deformations possible in every isotropic, incompressible, perfectly elastic body. Z. Angew. Math. Phys. 5(6), 466–489 (1954)
Ericksen, J.L.: Deformations possible in every compressible, isotropic, perfectly elastic material. Stud. Appl. Math. 34(1–4), 126–128 (1955)
Ericksen, J.L., Rivlin, R.S.: Large elastic deformations of homogeneous anisotropic materials. J. Ration. Mech. Anal. 3, 281–301 (1954)
Fosdick, R.L.: Remarks on Compatibility. Modern Developments in the Mechanics of Continua, pp. 109–127. Academic Press, New York (1966)
Golgoon, A., Yavari, A.: Nonlinear elastic inclusions in anisotropic solids. J. Elast. 130(2), 239–269 (2018)
Golgoon, A., Yavari, A.: Line and point defects in nonlinear anisotropic solids. Z. Angew. Math. Phys. 69(3), 1–28 (2018)
Golgoon, A., Yavari, A.: On Hashin’s hollow cylinder and sphere assemblages in anisotropic nonlinear elasticity. J. Elast. 146(1), 65–82 (2021)
Goodbrake, C., Yavari, A., Goriely, A.: The anelastic Ericksen problem: Universal deformations and universal eigenstrains in incompressible nonlinear anelasticity. J. Elast. 142(2), 291–381 (2020)
Goriely, A.: The Mathematics and Mechanics of Biological Growth. Springer, New York (2017)
Goriely, A., Tabor, M.: Rotation, inversion and perversion in anisotropic elastic cylindrical tubes and membranes. Proc. R. Soc. Lond. Ser. A 469(2153), 20130011 (2013)
Gurtin, M.E.: The linear theory of elasticity. In: Handbuch der Physik, Band VIa/2. Springer, Berlin (1972)
Holzapfel, G.A., Gasser, T.C., Ogden, R.W.: A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. 61, 1–48 (2000)
Klingbeil, W.W., Shield, R.T.: On a class of solutions in plane finite elasticity. Z. Angew. Math. Phys. 17(4), 489–511 (1966)
Lu, J., Papadopoulos, P.: A covariant constitutive description of anisotropic non-linear elasticity. Z. Angew. Math. Phys. 51(2), 204–217 (2000)
Marsden, J.E., Hughes, T.J.R.: Mathematical Foundations of Elasticity. Dover, New York (1994)
Melnik, A.V., Goriely, A.: Dynamic fiber reorientation in a fiber-reinforced hyperelastic material. Math. Mech. Solids 18(6), 634–648 (2013)
Merodio, J., Ogden, R.W.: Finite deformation elasticity theory. In: Constitutive Modelling of Solid Continua, pp. 17–52. Springer, Berlin (2020)
Ogden, R.W.: Non-linear Elastic Deformations. Dover, New York (1984)
Petroski, H.J., Carlson, D.E.: Controllable states of elastic heat conductors. Arch. Ration. Mech. Anal. 31, 127–150 (1968)
Pucci, E., Rajagopal, K.R., Saccomandi, G.: On the determination of semi-inverse solutions of nonlinear Cauchy elasticity: The not so simple case of anti-plane shear. Int. J. Eng. Sci. 88, 3–14 (2015)
Qiu, G.Y., Pence, T.J.: Remarks on the behavior of simple directionally reinforced incompressible nonlinearly elastic solids. J. Elast. 49(1), 1–30 (1997)
Rivlin, R.S.: Large elastic deformations of isotropic materials IV. Further developments of the general theory. Philos. Trans. R. Soc. Lond. A 241(835), 379–397 (1948)
Rivlin, R.S.: Large elastic deformations of isotropic materials. V. The problem of flexure. Proc. R. Soc. Lond. Ser. A 195(1043), 463–473 (1949)
Rivlin, R.S.: A note on the torsion of an incompressible highly elastic cylinder. In: Mathematical Proceedings of the Cambridge Philosophical Society, vol. 45, pp. 485–487. Cambridge University Press, Cambridge (1949)
Saccomandi, G.: Universal solutions and relations in finite elasticity. In: Topics in Finite Elasticity, pp. 95–130. Springer, Berlin (2001)
Saccomandi, G.: On inhomogeneous deformations in finite thermoelasticity. IMA J. Appl. Math. 63(2), 131–148 (1999)
Singh, M., Pipkin, A.C.: Note on Ericksen’s problem. Z. Angew. Math. Phys. 16(5), 706–709 (1965)
Smith, G.F., Rivlin, R.S.: The strain-energy function for anisotropic elastic materials. Trans. Am. Math. Soc. 88(835), 175–193 (1958)
Spencer, A.J.M.: The formulation of constitutive equation for anisotropic solids. In: Mechanical Behavior of Anisotropic Solids/Comportment Méchanique des Solides Anisotropes, pp. 3–26. Springer, Berlin (1982)
Spencer, A.J.M.: Modelling of finite deformations of anisotropic materials. In: Large Deformations of Solids: Physical Basis and Mathematical Modelling, pp. 41–52. Springer, Berlin (1986)
Truesdell, C.: The Elements of Continuum Mechanics. Springer, Berlin (1966)
Yavari, A.: Compatibility equations of nonlinear elasticity for non-simply-connected bodies. Arch. Ration. Mech. Anal. 209(1), 237–253 (2013)
Yavari, A.: Universal deformations in inhomogeneous isotropic nonlinear elastic solids. Proc. R. Soc. A 477(2253), 20210547 (2021)
Yavari, A., Goriely, A.: The anelastic Ericksen problem: Universal eigenstrains and deformations in compressible isotropic elastic solids. Proc. R. Soc. A 472(2196), 20160690 (2016)
Yavari, A., Goriely, A.: Universal deformations in anisotropic nonlinear elastic solids. J. Mech. Phys. Solids 156, 104598 (2021)
Yavari, A., Goriely, A.: The universal program of linear elasticity. Math. Mech. Solids. https://doi.org/10.1177/108128652210913052022
Yavari, A., Marsden, J.E., Ortiz, M.: On the spatial and material covariant balance laws in elasticity. J. Math. Phys. 47, 85–112 (2006)
Yavari, A., Goodbrake, C., Goriely, A.: Universal displacements in linear elasticity. J. Mech. Phys. Solids 135, 103782 (2020)
Acknowledgements
Arash Yavari was supported by ARO W911NF-18-1-0003 and NSF – Grant No. CMMI 1939901. This work was also supported by the Engineering and Physical Sciences Research Council grant EP/R020205/1 to Alain Goriely.
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to Professor Roger L. Fosdick on the occasion of his 85th birthday
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yavari, A., Goriely, A. The Universal Program of Nonlinear Hyperelasticity. J Elast 154, 91–146 (2023). https://doi.org/10.1007/s10659-022-09906-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-022-09906-3
Keywords
- Universal deformations
- Nonlinear elasticity
- Anisotropic elasticity
- Inhomogeneity
- Functionally-graded materials





 , for
, for 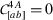 , for
, for 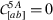 , for
, for 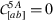 , for
, for 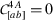 , for
, for 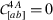 , for
, for  , for
, for 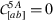 , for
, for