1 Introduction

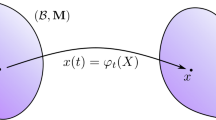
In nonlinear anelasticity, in the notion first defined in [7], strain has an elastic and an anelastic part. In terms of deformation gradient it is written as \(\mathbf{F}=\mathbf{F}^{e}\mathbf{F}^{a}\), where \(\mathbf{F}^{e}\) and \(\mathbf{F}^{a}\) are the elastic and anelastic deformation tensors, respectively [17, 37, 39]. The hybrid German-English portmanteau term eigenstrain has its origin in the pioneering paper of Hans Reissner [31] (Eigenspannung means proper or self stress) and was further popularized by Mura [25, 30]. In the literature several equivalent terms have been used for the same concept; initial strain [27], nuclei of strain [29], transformation strain [11], inherent strain [42], and residual strains [1] (see also [21, 53]). In the setting of linear elasticity, and for infinite bodies, inclusions and their induced stress fields were systematically studied by Eshelby in a celebrated paper [11]. He showed that an ellipsoidal inclusion that has uniform eigenstrain and is embedded in an infinite linear elastic medium, has a uniform stress field. It is known that in the case of finite bodies the stress field of an inclusion with uniform eigenstrain is not necessarily uniform, e.g., a spherical inclusion centered at a finite ball [28]. The extension of Eshelby’s analysis of eigenstrains to nonlinear anelasticity has received attention in the last twenty years. In the case of some special constitutive equations one can mention [6, 22–24, 35, 36]. There are several more recent works that use geometric techniques [13, 14, 16, 43, 45–47].

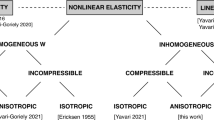
If one is asked to deform an elastic body to a desired arbitrary shape, most likely body forces will be required to achieve the desired deformation, especially when one does not specify a particular material. However, there are special deformations that can be maintained by applying only boundary tractions for any member of a material class. These are called universal deformations. The systematic study of universal deformations began in two seminal papers of Ericksen [8, 9] motivated by earlier works of Rivlin [32–34]. Ericksen proved that for compressible isotropic solids only homogeneous deformations are universal. For incompressible isotropic solids he found four families of universal deformations, in addition to the isochoric homogeneous deformations. He conjectured that only homogeneous deformations have constant principal invariants. This turned out to be incorrect [12], and led to the discovery of a fifth family of universal deformations [26, 38]. Existence of other constant principal invariant inhomogeneous universal deformations is still an open problem, but the current conjecture is that none exists.

We extended Ericksen’s analysis to compressible anelasticity and showed that universal deformations must be covariantly homogeneous [48]. We proved that this implies that for simply-connected bodies universal eigenstrains are impotent. Universal deformations and eigenstrains in incompressible anelasticity were investigated in [18]. It was shown that the six known families of universal deformations in incompressible isotropic elasticity are invariant under certain Lie subgroups of the special Euclidean group. In the analysis of universal eigenstrains it was assumed that for each class of universal deformations the corresponding universal eigenstrains have the same symmetries. Under this assumption, the universal eigenstrains were characterized for each class.

Ericksen’s analysis was extended to inhomogeneous compressible and incompressible isotropic solids in [44] (this was motivated by an earlier result in [15]). It was shown that if the energy function is assumed to be position dependent (in the reference configuration) there are some extra universality constraints, in addition to those of the corresponding homogeneous solids. The universal inhomogeneities—the form of the position dependence of energy function consistent with the universality constraints—were fully characterized for compressible isotropic solids and for the six known families of universal deformations of incompressible isotropic solids.

Ericksen and Rivlin [10] presented a limited analysis of universal deformations in anisotropic solids assuming fixed material preferred directions. We extended Ericksen’s analysis to transversely isotropic, orthotropic, and monoclinic solids in both compressible and incompressible cases [49]. We showed that for compressible transversely isotropic, orthotropic, and monoclinic solids universal deformations are homogeneous and the universal material preferred directions are uniform. For each of the six known families of universal deformations in the incompressible case (that turn out to be universal for anisotropic solids as well) we assumed that the corresponding universal material preferred directions have the same symmetries as those of the universal deformations (these symmetries are encoded in the symmetries of the right Cauchy-Green strain). Under this assumption we fully characterized the universal material preferred directions for each family and material class. Recently, we completed the universal program of nonlinear hyperelastic elasticity by characterizing the universal inhomogeneities for each of the three material classes for both compressible and incompressible cases [50].

Since the central object of linear elasticity is displacement fields rather than deformations, universal displacements are the natural analogue of universal deformations in linear elasticity [20, 41, 52]. These are displacements that can be maintained in the absence of body forces and by applying only boundary tractions for arbitrary elastic constants in a given symmetry class. In [52], universal displacements of linear anisotropic elasticity were fully characterized for each of the eight symmetry classes assuming that the directions of the material anisotropy are known. Recently, we extended the analysis of universal displacements to inhomogeneous anisotropic linear elasticity [51]. It was shown that the universality constraints of inhomogeneous linear elasticity include those of homogeneous linear elasticity. For each of the eight symmetry classes we fully characterized the universal inhomogeneities, i.e., the form of position dependence of the elastic moduli that are consistent with the universality constraints. In the present paper, we study universality in anisotropic linear anelasticity.

This paper is organized as follows. In §2 we define universal elastic strains and eigenstrains in linear anelasticity. Universal elastic strains and eigenstrains of isotropic linear anelasticity are discussed in §3. The same problems are investigated for the other seven symmetry classes (triclinic, monoclinic, tetragonal, trigonal, orthotropic, transversely isotropic, and cubic) in §4. Conclusions are given in §5.

2 Universal elastic strains and eigenstrains in linear anelasticity

In linear anelasticity, linearized strain is additively decomposed into elastic and anelastic parts: \(\boldsymbol{\epsilon}=\boldsymbol{\epsilon}^{e}+\boldsymbol{\epsilon}^{*}\), with

$$ \boldsymbol{\epsilon}=\frac{1}{2}\left (\nabla \mathbf{u}+\nabla \mathbf{u}^{\mathsf{T}}\right ) \,, $$
(2.1)

where \(\mathbf{u}\) is the displacement field and \(\boldsymbol{\epsilon}^{*}\) is the linearized eigenstrain, which in this paper we simply refer to as eigenstrain. Note that, in general, \(\boldsymbol{\epsilon}^{e}\) and \(\boldsymbol{\epsilon}^{*}\) are incompatible, i.e., \(\operatorname{curl}\circ \operatorname{curl}\boldsymbol{\epsilon}^{e}\neq \mathbf{0}\), and \(\operatorname{curl}\circ \operatorname{curl}\boldsymbol{\epsilon}^{*}\neq \mathbf{0}\), where \(\operatorname{curl}\circ \operatorname{curl}\) is the incompatibility operator. The constitutive equations read \(\boldsymbol{\sigma}=\boldsymbol{\mathsf{C}}\cdot \boldsymbol{\epsilon}^{e}\), or in components

$$ \sigma _{\mathit{ab}}=\mathsf{C}_{\mathit{abcd}}\left (u_{c|d}-\epsilon ^{*}_{\mathit{cd}}\right ) \,, $$
(2.2)

where \(\boldsymbol{\mathsf{C}}\) is the elasticity tensor and summation over repeated indices is assumed. Let us consider a homogeneous linear elastic body ℬ. In the Cartesian coordinates \(\{x_{a}\}\) the body has uniform elastic constants \(\mathsf{C}_{\mathit{abcd}}\). At \(\mathbf{x}\in \mathcal{B}\), the displacement and eigenstrain fields have components \(u_{a}(\mathbf{x})\) and \(\epsilon ^{*}_{\mathit{ab}}(\mathbf{x})\), respectively. In the absence of body forces, the equilibrium equations read

$$ \sigma _{\mathit{ab},b}=\mathsf{C}_{\mathit{abcd}}\,u_{c,\mathit{db}}-\mathsf{C}_{\mathit{abcd}}\,\epsilon ^{*}_{\mathit{cd},b}=0 \,. $$
(2.3)

It is more convenient to rewrite this in terms of elastic strains as

$$ \mathsf{C}_{\mathit{abcd}}\,\epsilon ^{e}_{\mathit{cd},b}=0 \,, $$
(2.4)

which must hold for arbitrary \(\mathsf{C}_{\mathit{abcd}}\) in a given symmetry class. We refer to (2.4) as the universality constraints.

Definition 2.1

For a given symmetry class, a strain field that satisfies \(\boldsymbol{\mathsf{C}}\cdot \nabla \boldsymbol{\epsilon}^{e}=\mathbf{0}\), or in components, \(\mathsf{C}_{\mathit{abcd}}\,\epsilon ^{e}_{\mathit{cd},b}=0\), \(a=1,2,3\), for all the elasticity tensors in the symmetry class, is called a universal elastic strain.

The incompatibility tensor is defined as \(\boldsymbol{\mathsf{R}}=\operatorname{curl}\circ \operatorname{curl}\boldsymbol{\epsilon}\), or in components

$$ \mathsf{R}_{\mathit{ij}}=\mathsf{R}_{\mathit{ji}}=\varepsilon _{\mathit{aki}}\,\varepsilon _{\mathit{blj}}\,\epsilon _{\mathit{ab},\mathit{kl}}\,, $$
(2.5)

where \(\varepsilon _{\mathit{abc}}\) is the permutation symbol. The six bulk compatibility equations of linear elasticity are therefore given by \(\mathsf{R}_{\mathit{ij}}=0\) [43]. Knowing that the total strain is compatible, one concludes that \(\boldsymbol{\mathsf{R}}^{*}=-\boldsymbol{\mathsf{R}}^{e}\). For a given symmetry class the universality constraints (2.4) determine the set of universal elastic strains as we will see in the following sections. This leads to the definition of universal eigenstrains.

Definition 2.2

For a given symmetry class, the corresponding universal eigenstrains are the set of solutions to the following linear partial differential equations (PDEs)

$$ \varepsilon _{\mathit{aki}}\,\varepsilon _{\mathit{blj}}\,\epsilon ^{*}_{\mathit{ab},\mathit{kl}}=-\varepsilon _{\mathit{aki}}\,\varepsilon _{\mathit{blj}}\,\epsilon ^{e}_{\mathit{ab},\mathit{kl}}\,, $$
(2.6)

where \(\boldsymbol{\epsilon}^{e}\) is a universal elastic strain fields of the symmetry class. In other words, a universal eigenstrain satisfies (2.6) for at least one universal elastic strain. Note that the above PDEs determine universal eigenstrains up to compatible (impotent) eigenstrains.

3 Isotropic linear anelasticity

For isotropic solids, in a Cartesian coordinate system \(\{x_{a}\}\), the elasticity tensor has the representation \(\mathsf{C}_{\mathit{abcd}}=\lambda \,\delta _{\mathit{ab}}\delta _{\mathit{cd}}+\mu \,(\delta _{\mathit{ac}}\delta _{\mathit{bd}}+\delta _{\mathit{ad}}\delta _{\mathit{bc}})\), where \(\lambda \) and \(\mu \) are the Lamé constants. The universality constraints (2.4) for isotropic solids are simplified to read

$$ \lambda \,\epsilon ^{e}_{\mathit{cc},a}+2\mu \, \epsilon ^{e}_{\mathit{ab},b}=0\,, \quad a=1,2,3\,. $$
(3.1)

Note that the above identity must hold for arbitrary elastic constants \(\lambda \) and \(\mu \), and hence

$$ \epsilon ^{e}_{\mathit{cc},a}=\epsilon ^{e}_{\mathit{ab},b}\,, \quad a=1,2,3\,. $$
(3.2)

Therefore, universal elastic strains have constant trace and are divergence free. A divergence-free second-order tensor can be represented as: \(\epsilon ^{e}_{\mathit{ab}}=\varepsilon _{\mathit{acm}}\,\varepsilon _{\mathit{bdn}}\,\phi _{\mathit{cd},\mathit{mn}}\), where \(\phi _{\mathit{cd}}=\phi _{\mathit{dc}}\) is the Beltrami potential [2, 19]. In other words, any constant-trace divergence-free elastic strain is universal. Note that these universal elastic strains are incompatible as one can show that

$$ \mathsf{R}_{\mathit{ij}}=\phi _{\mathit{kl},\mathit{ijkl}}+\phi _{\mathit{ij},\mathit{kkll}}-\phi _{\mathit{kj},\mathit{ikkll}}-\phi _{\mathit{ik},\mathit{jkll}}\,. $$
(3.3)

Proposition 3.1

For isotropic linear elastic solids universal elastic strains are divergence free and have constant trace. The universal eigenstrains (up to impotent eigenstrains) are the set of solutions of the following linear PDEs:

$$ \varepsilon _{\mathit{aki}}\,\varepsilon _{\mathit{blj}}\,\epsilon ^{*}_{\mathit{ab},\mathit{kl}}= -\phi _{\mathit{kl},\mathit{ijkl}}-\phi _{\mathit{ij},\mathit{kkll}}+\phi _{\mathit{kj},\mathit{ikkll}}+\phi _{\mathit{ik},\mathit{jkll}}\,, $$
(3.4)

where \(\phi _{\mathit{ij}}=\phi _{\mathit{ji}}\) are Beltrami potentials such that \(\epsilon ^{e}_{\mathit{cc}}=\phi _{\mathit{nn},\mathit{mm}}-\phi _{\mathit{mn},\mathit{mn}}\) is constant.

4 Anisotropic linear anelasticity

In the absence of eigenstrains, Yavari et al. [52] characterized the universal displacements of linear elasticity for all the eight anisotropy classes. In this section, we extend their work to anisotropic linear anelasticity for all the eight symmetry classes: triclinic, monoclinic, tetragonal, trigonal, orthotropic, transversely isotropic, and cubic [3–5, 40]. Consider a homogeneous body made of a linear elastic solid with elasticity tensor \(\mathsf{C}_{\mathit{abcd}}\) that has major \(\mathsf{C}_{\mathit{abcd}}=\mathsf{C}_{\mathit{cdab}}\) and minor symmetries \(\mathsf{C}_{\mathit{abcd}}=\mathsf{C}_{\mathit{bacd}}\). We use the Voigt notation with the bijection \((11,22,33,23,31,12)\leftrightarrow (1,2,3,4,5,6)\) to write the constitutive equations as \(\sigma _{\alpha}=c_{\alpha \beta}\epsilon _{\beta}\), where Greek indices run from 1 to 6. The elasticity tensor is then represented by a symmetric \(6\times 6\) stiffness matrix as

$$ \boldsymbol{\mathsf{C}}(\mathbf{x})=\begin{bmatrix} c_{11} & c_{12} & c_{13} & c_{14} & c_{15} & c_{16} \\ c_{12} & c_{22} & c_{23} & c_{24} & c_{25} & c_{26} \\ c_{13} & c_{23} & c_{33} & c_{34} & c_{35} & c_{36} \\ c_{14} & c_{24} & c_{34} & c_{44} & c_{45} & c_{46} \\ c_{15} & c_{25} & c_{35} & c_{45} & c_{55} & c_{56} \\ c_{16} & c_{26} & c_{36} & c_{46} & c_{56} & c_{66} \end{bmatrix}\,. $$
(4.1)

In this notation the equilibrium equations are written as

$$ \begin{bmatrix} \frac{\partial}{\partial x_{1}} & 0 & 0 & 0 & \frac{\partial}{\partial x_{3}} & \frac{\partial}{\partial x_{2}} \\ 0 & \frac{\partial}{\partial x_{2}} & 0 & \frac{\partial}{\partial x_{3}} & 0 & \frac{\partial}{\partial x_{1}} \\ 0 & 0 & \frac{\partial}{\partial x_{3}} & \frac{\partial}{\partial x_{2}} & \frac{\partial}{\partial x_{1}} & 0 \end{bmatrix} \begin{bmatrix} c_{11} & c_{12} & c_{13} & c_{14} & c_{15} & c_{16} \\ c_{12} & c_{22} & c_{23} & c_{24} & c_{25} & c_{26} \\ c_{13} & c_{23} & c_{33} & c_{34} & c_{35} & c_{36} \\ c_{14} & c_{24} & c_{34} & c_{44} & c_{45} & c_{46} \\ c_{15} & c_{25} & c_{35} & c_{45} & c_{55} & c_{56} \\ c_{16} & c_{26} & c_{36} & c_{46} & c_{56} & c_{66} \end{bmatrix} \begin{bmatrix} \epsilon ^{e}_{1} \\ \epsilon ^{e}_{2} \\ \epsilon ^{e}_{3} \\ \epsilon ^{e}_{4} \\ \epsilon ^{e}_{5} \\ \epsilon ^{e}_{6} \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \\ 0 \end{bmatrix}\,, $$
(4.2)

where

$$ \epsilon ^{e}_{1}=\epsilon ^{e}_{11}\,,\quad \epsilon ^{e}_{2}=\epsilon ^{e}_{22}\,,\quad \epsilon ^{e}_{3}=\epsilon ^{e}_{33}\,,\quad \epsilon ^{e}_{4}=2\epsilon ^{e}_{23}\,,\quad \epsilon ^{e}_{5}=2\epsilon ^{e}_{13}\,,\quad \epsilon ^{e}_{6}=2\epsilon ^{e}_{12} \,. $$
(4.3)

Equation (4.2) and the arbitrariness of the elastic constants for a given symmetry class force the elastic strains to satisfy a set of PDEs that we call universality constraints.

4.1 Triclinic solids

Triclinic solids are the least symmetric among the eight symmetry classes; the identity and minus identity are the only symmetry transformations for such materials. This means that triclinic linear elastic solids have twenty one independent elastic constants. In [52] it was shown that for triclinic linear elastic solids homogeneous displacements are the only universal displacements. It is straightforward to show that for triclinic solids, the universality constraints (2.4) read \(\epsilon^{e}_{\beta ,a}=0\), for \(\beta =1,...,6\), and \(a=1,2,3\).Footnote 1 This means that universal elastic strains are constant. This implies that universal elastic strains are compatible, and consequently the universal eigenstrains are impotent.

Proposition 4.1

For triclinic linear elastic solids, universal elastic strains are uniform, and consequently, universal eigenstrains are impotent.

Remark 4.2

The universal eigenstrains are of the form \(\boldsymbol{\epsilon}^{*}(\mathbf{x})=\frac{1}{2}\left [\nabla \mathbf{u}^{*}(\mathbf{x})+\nabla \mathbf{u}^{*}(\mathbf{x})^{\mathsf{T}}\right ]\), where \(\mathbf{u}^{*}(\mathbf{x})\) is any displacement field. For a given impotent eigenstrain \(\boldsymbol{\epsilon}^{*}(\mathbf{x})\), universal displacements are superposition of \(\mathbf{u}^{*}(\mathbf{x})\) and all homogeneous displacements. This implies that all displacement fields are universal. However, if one defines universal eigenstrains modulo impotent eigenstrains, in the case of triclinic solids, only homogeneous displacements are universal.

4.2 Monoclinic solids

In a monoclinic solid there is one plane of material symmetry that we assume to be parallel to the \(x_{1}x_{2}\)-plane. A monoclinic linear elastic solid has thirteen independent elastic constants. The elasticity matrix has the following form:

$$ \mathbf{c}=\begin{bmatrix} c_{11} & c_{12} & c_{13} & 0 & 0 & c_{16} \\ c_{12} & c_{22} & c_{23} & 0 & 0 & c_{26} \\ c_{13} & c_{23} & c_{33} & 0 & 0 & c_{36} \\ 0 & 0 & 0 & c_{44} & c_{45} & 0 \\ 0 & 0 & 0 & c_{45} & c_{55} & 0 \\ c_{16} & c_{26} & c_{36} & 0 & 0 & c_{66} \end{bmatrix}\,. $$
(4.4)

In [52] it was shown that for a monoclinic linear elastic solid with planes of symmetry parallel to the \(x_{1}x_{2}\)-plane, universal displacements are the superposition of homogeneous displacements \(\mathbf{F}\cdot \mathbf{x}\) (\(\mathbf{F}\) is a constant matrix) and the one-parameter inhomogeneous displacement field \((\mathit{cx}_{2}x_{3},-\mathit{cx}_{1}x_{3},0)\).

For monoclinic solids, the universality constraints (4.2) read \(\epsilon^{e}_{\beta ,a}=0\), for \(\beta =1,2,3,6\), and \(a=1,2,3\), and

$$ \begin{aligned} & \frac{\partial \epsilon ^{e}_{23}}{\partial x_{2}} = \frac{\partial \epsilon ^{e}_{23}}{\partial x_{3}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{13}}{\partial x_{2}} = \frac{\partial \epsilon ^{e}_{13}}{\partial x_{3}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{13}}{\partial x_{2}} + \frac{\partial \epsilon ^{e}_{23}}{\partial x_{1}}=0\,. \end{aligned} $$
(4.5)

The first two PDEs imply that \(\epsilon ^{e}_{23}=\epsilon ^{e}_{23}(x_{1})\), and \(\epsilon ^{e}_{13}=\epsilon ^{e}_{13}(x_{2})\), and the third PDE implies that \({\epsilon ^{e}_{23}}'(x_{1})=-{\epsilon ^{e}_{13}}'(x_{2})=c_{0}\), a constant. It is straightforward to check that the universal elastic strains are compatible.

Proposition 4.3

For monoclinic linear elastic solids the universal elastic strains have the following form

$$ \boldsymbol{\epsilon}^{e}(\mathbf{x})=\begin{bmatrix} c_{1} & c_{6} & -c_{0}x_{2}+c_{5} \\ c_{6} & c_{2} & c_{0}x_{1}+c_{4} \\ -c_{0}x_{2}+c_{5} & c_{0}x_{1}+c_{4} & c_{3} \\ \end{bmatrix}\,, $$
(4.6)

where \(c_{i}, i=0,1,...,6\) are constants. These strains are compatible, and consequently, universal eigenstrains are impotent.

Remark 4.4

The universal eigenstrains are of the form \(\boldsymbol{\epsilon}^{*}(\mathbf{x})=\frac{1}{2}\left [\nabla \mathbf{u}^{*}(\mathbf{x})+\nabla \mathbf{u}^{*}(\mathbf{x})^{\mathsf{T}}\right ]\), where \(\mathbf{u}^{*}(\mathbf{x})\) is any displacement field. For a given impotent eigenstrain \(\boldsymbol{\epsilon}^{*}(\mathbf{x})\), universal displacements are superposition of \(\mathbf{u}^{*}(\mathbf{x})\) and all universal displacements in the absence of eigenstrains, i.e., those of linear elasticity [52, Proposition 3.2]. This implies that all displacement fields are universal. However, if one defines universal eigenstrains modulo impotent eigenstrains, in the case of monoclinic solids, universal displacements are identical to those given in [52, Proposition 3.2].

4.3 Tetragonal solids

A tetragonal solid has five symmetry planes. The normals of four of them are coplanar and the fifth plane is normal to the other four. In a Cartesian coordinate system \((x_{1},x_{2},x_{3})\) we assume, without loss of generality, that the fifth normal is parallel to the \(x_{3}\) axis. Two of the symmetry planes are parallel to the \(x_{1}x_{3}\) and \(x_{2}x_{3}\)-planes. The other two symmetry planes are related to the ones parallel to the \(x_{1}x_{3}\)-plane by \(\pi /4\) and \(3\pi /4\) rotations about the \(x_{3}\) axis. A tetragonal solid has six independent elastic constants and the elasticity matrix has the following form:

$$ \mathbf{c}=\begin{bmatrix} c_{11} & c_{12} & c_{13} & 0 & 0 & 0 \\ c_{12} & c_{11} & c_{13} & 0 & 0 & 0 \\ c_{13} & c_{13} & c_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & c_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & c_{44} & 0 \\ 0 & 0 & 0 & 0 & 0 & c_{66} \end{bmatrix}. $$
(4.7)

In [52] it was shown that in a tetragonal linear elastic solid with the tetragonal axes parallel to the \(x_{3}\)-axis, the universal displacements are a superposition of homogeneous displacements and the following inhomogeneous displacements:Footnote 2

$$ \begin{aligned} & u_{1}(x_{1},x_{2},x_{3})=F_{11}x_{1}+F_{12}x_{2}+F_{13}x_{3}+c_{1}x_{2}x_{3}+c_{2}x_{1}x_{3}, \\ & u_{2}(x_{1},x_{2},x_{3})=F_{21}x_{1}+F_{22}x_{2}+F_{23}x_{3}-c_{2}x_{2}x_{3}+c_{3}x_{1}x_{3}, \\ & u_{3}(x_{1},x_{2},x_{3})=F_{31}x_{1}+F_{32}x_{2}+F_{33}x_{3}+g(x_{1},x_{2})\,, \end{aligned} $$
(4.8)

where \(c_{1}\) and \(c_{2}\) are constants, and \(g=g(x_{1},x_{2})\) is any harmonic function.

The universality constraints (4.2) give us the following thirteen PDEs:

$$\begin{aligned} &\frac{\partial \epsilon ^{e}_{11}}{\partial x_{1}} = \frac{\partial \epsilon ^{e}_{11}}{\partial x_{2}}=0\,, \\ &\frac{\partial \epsilon ^{e}_{22}}{\partial x_{1}} = \frac{\partial \epsilon ^{e}_{22}}{\partial x_{2}}=0\,, \\ &\frac{\partial \epsilon ^{e}_{11}}{\partial x_{3}} + \frac{\partial \epsilon ^{e}_{22}}{\partial x_{3}}=0\,, \\ &\frac{\partial \epsilon ^{e}_{33}}{\partial x_{1}} = \frac{\partial \epsilon ^{e}_{33}}{\partial x_{2}}= \frac{\partial \epsilon ^{e}_{33}}{\partial x_{3}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{12}}{\partial x_{1}} = \frac{\partial \epsilon ^{e}_{12}}{\partial x_{2}}=0\,, \\ & \frac{\partial \epsilon ^{e}_{13}}{\partial x_{3}} = \frac{\partial \epsilon ^{e}_{23}}{\partial x_{3}}=0\,, \\ & \frac{\partial \epsilon ^{e}_{13}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{23}}{\partial x_{2}}=0\,. \end{aligned}$$
(4.9)

The first five PDEs imply that \(\epsilon ^{e}_{11}=\epsilon ^{e}_{11}(x_{3})\), \(\epsilon ^{e}_{22}=-\epsilon ^{e}_{11}(x_{3})+c_{0}\), where \(c_{0}\) is a constant. Eq. (4.9)4 implies that \(\epsilon ^{e}_{33}\) is constant. Eq. (4.9)5 implies that \(\epsilon ^{e}_{12}=\epsilon ^{e}_{12}(x_{3})\). The last three PDEs imply that

$$ \epsilon ^{e}_{13}=\epsilon ^{e}_{13}(x_{1},x_{2}),\quad \epsilon ^{e}_{23}=\epsilon ^{e}_{23}(x_{1},x_{2}), \quad \text{with the constraint}\quad \frac{\partial \epsilon ^{e}_{13}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{23}}{\partial x_{2}}=0\,. $$
(4.10)

Therefore, we have the following result.

Proposition 4.5

For a tetragonal linear elastic solid with the tetragonal axis parallel to the \(x_{3}\)-axis in a Cartesian coordinate system \((x_{1},x_{2},x_{3})\), the universal elastic strains have the following form

$$ \boldsymbol{\epsilon}^{e}(\mathbf{x})=\begin{bmatrix} \epsilon ^{e}_{11}(x_{3}) & \epsilon ^{e}_{12}(x_{3}) & \epsilon ^{e}_{13}(x_{1},x_{2}) \\ \epsilon ^{e}_{12}(x_{3}) & -\epsilon ^{e}_{11}(x_{3})+c_{0} & \epsilon ^{e}_{23}(x_{1},x_{2}) \\ \epsilon ^{e}_{13}(x_{1},x_{2}) & \epsilon ^{e}_{23}(x_{1},x_{2}) & \epsilon ^{e}_{33} \\ \end{bmatrix}\,, $$
(4.11)

where \(c_{0}\) and \(\epsilon ^{e}_{33}\) are constants, \(\epsilon ^{e}_{11}(x_{3})\), \(\epsilon ^{e}_{12}(x_{3})\), and \(\epsilon ^{e}_{13}(x_{1},x_{2})\) are arbitrary functions, and \(\epsilon ^{e}_{23}(x_{1},x_{2})\) has the following representation

$$ \epsilon ^{e}_{23}(x_{1},x_{2})=-\int \epsilon ^{e}_{13,1}(x_{1},x_{2})\,\mathit{dx}_{2} + f(x_{1})\,, $$
(4.12)

for an arbitrary function \(f(x_{1})\). Universal egenstrains (up to impotent eigenstrains) are solutions of the six second-order linear PDEs \(\operatorname{curl}\circ \operatorname{curl}\boldsymbol{\epsilon}^{*}=-\boldsymbol{\mathsf{R}}^{e}\).

Remark 4.6

The incompatibility tensor of the universal elastic strains reads

$$ \boldsymbol{\mathsf{R}}^{e}=\begin{bmatrix} -{\epsilon ^{e}_{11}}''(x_{3}) & {\epsilon ^{e}_{12}}''(x_{3}) & -\nabla ^{2}\epsilon ^{e}_{13}(x_{1},x_{2}) \\ {\epsilon ^{e}_{12}}''(x_{3}) & {\epsilon ^{e}_{11}}''(x_{3}) & -\nabla ^{2}\epsilon ^{e}_{23}(x_{1},x_{2}) \\ -\nabla ^{2}\epsilon ^{e}_{13}(x_{1},x_{2}) & -\nabla ^{2}\epsilon ^{e}_{23}(x_{1},x_{2}) & 0 \\ \end{bmatrix}\,. $$
(4.13)

It is seen that the universal elastic strains (and consequently the universal eigenstrains) are impotent if \(\epsilon ^{e}_{11}\) and \(\epsilon ^{e}_{12}\) are linear functions, and \(\epsilon ^{e}_{13}\) and \(\epsilon ^{e}_{23}\) are harmonic.

4.4 Trigonal solids

A trigonal solid has three planes of symmetry whose normals lie in the same plane and are related by \(\pi /3\) rotations. We choose Cartesian coordinates \((x_{1},x_{2},x_{3})\) such that the trigonal axis is parallel to the \(x_{3}\)-axis. A trigonal solid has six independent elastic constants and the elasticity matrix has the following form:

$$ \mathbf{c}=\begin{bmatrix} c_{11} & c_{12} & c_{13} & 0 & c_{15} & 0 \\ c_{12} & c_{11} & c_{13} & 0 & -c_{15} & 0 \\ c_{13} & c_{13} & c_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & c_{44} & 0 & -c_{15} \\ c_{15} & -c_{15} & 0 & 0 & c_{44} & 0 \\ 0 & 0 & 0 & -c_{15} & 0 & \frac{1}{2}(c_{11}-c_{12}) \end{bmatrix}. $$
(4.14)

Yavari et al. [52] showed that in the absence of eigenstrains universal displacements are a superposition of homogeneous displacements and the following inhomogeneous displacements

$$ \begin{aligned} & u_{1}^{\text{inh}}(x_{1},x_{2},x_{3})=a_{123}x_{1}x_{2}x_{3}+a_{12}x_{1}x_{2}+a_{13}x_{1}x_{3}+a_{23}x_{2}x_{3},\\ & u_{2}^{\text{inh}}(x_{1},x_{2},x_{3})=\frac{1}{2}(a_{12}+a_{123}x_{3})(x_{1}^{2}-x_{2}^{2})+b_{13}x_{1}x_{3}-a_{13}x_{2}x_{3},\\ & u_{3}^{\text{inh}}(x_{1},x_{2},x_{3})=-a_{123}x_{1}^{2}x_{2}-(a_{23}+b_{13})x_{1}x_{2}+\frac{1}{3}a_{123}x_{2}^{3} -a_{13}(x_{1}^{2}-x_{2}^{2}). \end{aligned} $$
(4.15)

The universality constraints (4.2) give us the following fourteen PDEs:

$$ \begin{aligned} & \frac{\partial \epsilon ^{e}_{33}}{\partial x_{1}} = \frac{\partial \epsilon ^{e}_{33}}{\partial x_{2}}= \frac{\partial \epsilon ^{e}_{33}}{\partial x_{3}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{13}}{\partial x_{3}} = \frac{\partial \epsilon ^{e}_{23}}{\partial x_{3}}=0\,, \end{aligned} $$
(4.16)

and

$$ \begin{aligned} & \frac{\partial \epsilon ^{e}_{11}}{\partial x_{3}} + \frac{\partial \epsilon ^{e}_{22}}{\partial x_{3}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{11}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{12}}{\partial x_{2}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{22}}{\partial x_{1}} - \frac{\partial \epsilon ^{e}_{12}}{\partial x_{2}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{12}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{22}}{\partial x_{2}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{12}}{\partial x_{1}} - \frac{\partial \epsilon ^{e}_{11}}{\partial x_{2}}=0\,, \end{aligned} $$
(4.17)

and

$$ \begin{aligned} & \frac{\partial \epsilon ^{e}_{13}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{23}}{\partial x_{2}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{11}}{\partial x_{3}} - \frac{\partial \epsilon ^{e}_{22}}{\partial x_{3}} -2\frac{\partial \epsilon ^{e}_{23}}{\partial x_{2}}+2\frac{\partial \epsilon ^{e}_{13}}{\partial x_{2}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{11}}{\partial x_{1}} - \frac{\partial \epsilon ^{e}_{22}}{\partial x_{1}} -2\frac{\partial \epsilon ^{e}_{12}}{\partial x_{2}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{23}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{13}}{\partial x_{2}} +\frac{\partial \epsilon ^{e}_{12}}{\partial x_{3}}=0\,. \end{aligned} $$
(4.18)

From (4.16) one concludes that \(\epsilon ^{e}_{33}\) is constant and \(\epsilon ^{e}_{13}=\epsilon ^{e}_{13}(x_{1},x_{2})\), \(\epsilon ^{e}_{23}=\epsilon ^{e}_{23}(x_{1},x_{2})\). From the last four PDEs in (4.17) one gets

$$ \begin{aligned} & \frac{\partial \epsilon ^{e}_{11}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{22}}{\partial x_{1}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{11}}{\partial x_{2}} + \frac{\partial \epsilon ^{e}_{22}}{\partial x_{2}}=0\,. \end{aligned} $$
(4.19)

These together with (4.17)1 imply that \(\epsilon ^{e}_{22}(x_{1},x_{2},x_{3})=-\epsilon ^{e}_{11}(x_{1},x_{2},x_{3})+c_{0}\), where \(c_{0}\) is a constant. Substituting this into (4.18)3 one obtains

$$ \frac{\partial \epsilon ^{e}_{11}}{\partial x_{1}} - \frac{\partial \epsilon ^{e}_{12}}{\partial x_{2}}=0\,. $$
(4.20)

This together with (4.17)2 implies that

$$ \frac{\partial \epsilon ^{e}_{11}}{\partial x_{1}} = \frac{\partial \epsilon ^{e}_{12}}{\partial x_{2}}=0\,, $$
(4.21)

and hence \(\epsilon ^{e}_{11}=\epsilon ^{e}_{11}(x_{2},x_{3})\) and \(\epsilon ^{e}_{12}=\epsilon ^{e}_{12}(x_{1},x_{3})\). Now the remaining PDEs are simplified to read:

$$ \begin{aligned} & \frac{\partial \epsilon ^{e}_{13}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{23}}{\partial x_{2}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{11}}{\partial x_{3}} -\frac{\partial \epsilon ^{e}_{23}}{\partial x_{2}} +\frac{\partial \epsilon ^{e}_{13}}{\partial x_{1}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{12}}{\partial x_{1}} -\frac{\partial \epsilon ^{e}_{11}}{\partial x_{2}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{23}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{13}}{\partial x_{2}} +\frac{\partial \epsilon ^{e}_{12}}{\partial x_{3}}=0\,. \end{aligned} $$
(4.22)

From (4.22)3, one obtains

$$ \frac{\partial }{\partial x_{1}}\epsilon ^{e}_{12}(x_{1},x_{3}) = \frac{\partial }{\partial x_{2}} \epsilon ^{e}_{11}(x_{2},x_{3}) \quad \Rightarrow \quad \frac{\partial ^{2}}{\partial x_{1}^{2}}\epsilon ^{e}_{12}(x_{1},x_{3}) = \frac{\partial ^{2}}{\partial x_{2}^{2}} \epsilon ^{e}_{11}(x_{2},x_{3})=0 \,. $$
(4.23)

Thus, one has

$$ \begin{aligned} & \epsilon ^{e}_{11}(x_{2},x_{3})=x_{2} f_{11}(x_{3})+g_{11}(x_{3}) \,,\\ & \epsilon ^{e}_{12}(x_{1},x_{3})=x_{1} f_{12}(x_{3})+g_{12}(x_{3}) \,. \end{aligned} $$
(4.24)

From (4.22)3, one concludes that \(f_{12}(x_{3})=f_{11}(x_{3})\). Equation (4.22)2 can be rewritten as

$$ \frac{\partial \epsilon ^{e}_{13}(x_{1},x_{2})}{\partial x_{1}}-\frac{\partial \epsilon ^{e}_{23}(x_{1},x_{2})}{\partial x_{2}} =-x_{2} f'_{11}(x_{3})-g'_{11}(x_{3})\,. $$
(4.25)

Therefore, \(x_{2} f''_{11}(x_{3})+g''_{11}(x_{3})=0\), which implies that \(f''_{11}(x_{3})=g''_{11}(x_{3})=0\). Thus, \(f_{11}(x_{3})=a_{11}x_{3}+a_{0}\), and \(g_{11}(x_{3})=b_{11}x_{3}+c_{1}\). Similarly, from (4.22)4 one concludes that \(g_{12}(x_{3})=b_{12}x_{3}+c_{2}\).

Finally, the three PDEs in (4.22) are simplified to read

$$ \begin{aligned} & \frac{\partial \epsilon ^{e}_{13}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{23}}{\partial x_{2}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{13}}{\partial x_{1}}-\frac{\partial \epsilon ^{e}_{23}}{\partial x_{2}}=-a_{11}x_{2}-b_{11}\,,\\ & \frac{\partial \epsilon ^{e}_{23}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{13}}{\partial x_{2}}=-a_{11}x_{1}-b_{12}\,. \end{aligned} $$
(4.26)

From the first two one obtains

$$ \begin{aligned} & \epsilon ^{e}_{13}(x_{1},x_{2})=-\frac{1}{2}a_{11}x_{1}x_{2}-\frac{1}{2}b_{11}x_{1}+f_{13}(x_{2})\,,\\ & \epsilon ^{e}_{23}(x_{1},x_{2})=\frac{1}{4}a_{11}x_{2}^{2}+\frac{1}{2}b_{11}x_{2}+f_{23}(x_{1})\,. \end{aligned} $$
(4.27)

Substituting these back into (4.26)3, one obtains \(f'_{23}(x_{1})+\frac{1}{2}a_{11}x_{1}+b_{12}=-f'_{13}(x_{2})\). This implies that \(f'_{23}(x_{1})+\frac{1}{2}a_{11}x_{1}+b_{12}=-f'_{13}(x_{2})=c_{3}\), and hence \(f_{23}(x_{1})=-\frac{1}{4}a_{11}x_{1}^{2}+(-b_{12}+c_{3})x_{1}+c_{4}\), and \(f_{13}(x_{2})=-c_{3}x_{2}+c_{5}\).

In summary, we have proved the following result.

Proposition 4.7

For trigonal linear elastic solids whose trigonal axes are parallel to the \(x_{3}\) axis in a Cartesian coordinate system \((x_{1},x_{2},x_{3})\), the universal elastic strains have the following components

$$ \begin{aligned} & \epsilon ^{e}_{11}(x_{1},x_{2},x_{3})=a_{11}x_{2}x_{3}+a_{0}x_{2}+b_{11}x_{3}+c_{1}\,, \quad \epsilon ^{e}_{22}(x_{1},x_{2},x_{3})=-\epsilon ^{e}_{11}(x_{1},x_{2},x_{3})+c_{0} \,, \\ & \epsilon ^{e}_{33}(x_{1},x_{2},x_{3})=\epsilon ^{e}_{23} \,,\quad \epsilon ^{e}_{23}(x_{1},x_{2},x_{3})=\frac{1}{4}a_{11}x_{2}^{2}+\frac{1}{2}b_{11}x_{2}-\frac{1}{4}a_{11}x_{1}^{2} +(-b_{12}+c_{3})x_{1}+c_{4}\,,\\ & \epsilon ^{e}_{13}(x_{1},x_{2},x_{3})=-\frac{1}{2}a_{11}x_{1}x_{2}-\frac{1}{2}b_{11}x_{1}-c_{3}x_{2}+c_{5}\,, \quad \\& \epsilon ^{e}_{12}(x_{1},x_{2},x_{3})= a_{11}x_{1}x_{3}+b_{12}x_{3}+c_{2} \,. \end{aligned} $$
(4.28)

These strains are compatible, and consequently, universal eigenstrains are impotent.

Remark 4.8

The universal eigenstrains are of the form \(\boldsymbol{\epsilon}^{*}(\mathbf{x})=\frac{1}{2}\left [\nabla \mathbf{u}^{*}(\mathbf{x})+\nabla \mathbf{u}^{*}(\mathbf{x})^{\mathsf{T}}\right ]\), where \(\mathbf{u}^{*}(\mathbf{x})\) is any displacement field. For a given impotent eigenstrain \(\boldsymbol{\epsilon}^{*}(\mathbf{x})\), universal displacements are superposition of \(\mathbf{u}^{*}(\mathbf{x})\) and all universal displacements in the absence of eigenstrains, i.e., those of linear elasticity [52, Proposition 3.4]. This implies that all displacement fields are universal. However, if one defines universal eigenstrains modulo impotent eigenstrains, in the case of trigonal solids, universal displacements are identical to those given in [52, Proposition 3.4].

4.5 Orthotropic solids

An orthotropic solid has three mutually orthogonal symmetry planes. Let us choose Cartesian coordinates \((x_{1},x_{2},x_{3})\) whose coordinate planes are parallel to the symmetry planes. An orthotropic solid has nine independent elastic constants, and the elasticity matrix has the following form:

$$ \mathbf{c}=\begin{bmatrix} c_{11} & c_{12} & c_{13} & 0 & 0 & 0 \\ c_{12} & c_{22} & c_{23} & 0 & 0 & 0 \\ c_{13} & c_{23} & c_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & c_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & c_{55} & 0 \\ 0 & 0 & 0 & 0 & 0 & c_{66} \end{bmatrix}. $$
(4.29)

In [52] it was shown that in an orthotropic linear elastic solid whose planes of symmetry are normal to the coordinate axes in a Cartesian coordinate system \((x_{1},x_{2},x_{3})\), and in the absence of eigenstrains the universal displacements are the superposition of homogeneous displacement fields and the three-parameter inhomogeneous displacement field \((a_{1}x_{2}x_{3},a_{2}x_{1}x_{3},a_{3}x_{1}x_{2})\).

The universality constraints (4.2) give us the following fifteen PDEs:

$$ \begin{aligned} & \frac{\partial \epsilon ^{e}_{11}}{\partial x_{1}} = \frac{\partial \epsilon ^{e}_{11}}{\partial x_{2}} = \frac{\partial \epsilon ^{e}_{11}}{\partial x_{3}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{22}}{\partial x_{1}} = \frac{\partial \epsilon ^{e}_{22}}{\partial x_{2}} = \frac{\partial \epsilon ^{e}_{22}}{\partial x_{3}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{33}}{\partial x_{1}} = \frac{\partial \epsilon ^{e}_{33}}{\partial x_{2}}= \frac{\partial \epsilon ^{e}_{33}}{\partial x_{3}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{12}}{\partial x_{1}} = \frac{\partial \epsilon ^{e}_{12}}{\partial x_{2}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{13}}{\partial x_{1}} = \frac{\partial \epsilon ^{e}_{13}}{\partial x_{3}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{23}}{\partial x_{2}} + \frac{\partial \epsilon ^{e}_{23}}{\partial x_{3}}=0\,. \end{aligned} $$
(4.30)

Thus, the normal elastic strains are constant and \(\epsilon ^{e}_{23}=\epsilon ^{e}_{23}(x_{1})\), \(\epsilon ^{e}_{13}=\epsilon ^{e}_{13}(x_{2})\), and \(\epsilon ^{e}_{12}=\epsilon ^{e}_{12}(x_{3})\). Therefore, we have proved the following result.

Proposition 4.9

For orthotropic linear elastic solids with planes of symmetry normal to the coordinate axes in a Cartesian coordinate system \((x_{1},x_{2},x_{3})\), the universal elastic strains have the following form

$$ \boldsymbol{\epsilon}^{e}(\mathbf{x})=\begin{bmatrix} \epsilon ^{e}_{11} & \epsilon ^{e}_{12}(x_{3}) & \epsilon ^{e}_{13}(x_{2}) \\ \epsilon ^{e}_{12}(x_{3}) & \epsilon ^{e}_{22} & \epsilon ^{e}_{23}(x_{1}) \\ \epsilon ^{e}_{13}(x_{2}) & \epsilon ^{e}_{23}(x_{1}) & \epsilon ^{e}_{33} \\ \end{bmatrix}\,, $$
(4.31)

where \(\epsilon ^{e}_{11}\), \(\epsilon ^{e}_{22}\), \(\epsilon ^{e}_{33}\) are constant, and \(\epsilon ^{e}_{23}(x_{1})\), \(\epsilon ^{e}_{13}(x_{2})\), \(\epsilon ^{e}_{12}(x_{3})\) are arbitrary functions. Universal eigenstrains (up to impotent eigenstrains) are the set of solutions to the following six PDEs

$$ \begin{aligned} \frac{\partial ^{2} \epsilon ^{*}_{11}}{\partial x_{2}^{2}} + \frac{\partial ^{2} \epsilon ^{*}_{22}}{\partial x_{1}^{2}} -2\frac{\partial ^{2} \epsilon ^{*}_{12}}{\partial x_{1}\partial x_{2}} &=0\,,\\ \frac{\partial ^{2} \epsilon ^{*}_{11}}{\partial x_{3}^{2}} + \frac{\partial ^{2} \epsilon ^{*}_{33}}{\partial x_{1}^{2}} -2\frac{\partial ^{2} \epsilon ^{*}_{13}}{\partial x_{1}\partial x_{3}} &=0\,,\\ \frac{\partial ^{2} \epsilon ^{*}_{22}}{\partial x_{3}^{2}} + \frac{\partial ^{2} \epsilon ^{*}_{33}}{\partial x_{2}^{2}} -2\frac{\partial ^{2} \epsilon ^{*}_{23}}{\partial x_{2}\partial x_{3}} &=0\,,\\ -\frac{\partial ^{2} \epsilon ^{*}_{11}}{\partial x_{2}\partial x_{3}} -\frac{\partial ^{2} \epsilon ^{*}_{23}}{\partial x_{1}^{2}} +\frac{\partial ^{2} \epsilon ^{*}_{13}}{\partial x_{1}\partial x_{2}}+ \frac{\partial ^{2} \epsilon ^{*}_{12}}{\partial x_{1}\partial x_{3}} & ={\epsilon ^{e}_{23}}''(x_{1})\,,\\ -\frac{\partial ^{2} \epsilon ^{*}_{22}}{\partial x_{1}\partial x_{3}}+\frac{\partial ^{2} \epsilon ^{*}_{23}}{\partial x_{1}\partial x_{2}} - \frac{\partial ^{2} \epsilon ^{*}_{13}}{\partial x_{2}^{2}}+\frac{\partial ^{2} \epsilon ^{*}_{12}}{\partial x_{2}\partial x_{3}} & ={\epsilon ^{e}_{13}}''(x_{2})\,,\\ -\frac{\partial ^{2} \epsilon ^{*}_{33}}{\partial x_{1}\partial x_{2}}+\frac{\partial ^{2} \epsilon ^{*}_{23}}{\partial x_{1}\partial x_{3}} + \frac{\partial ^{2} \epsilon ^{*}_{13}}{\partial x_{2}\partial x_{3}}-\frac{\partial ^{2} \epsilon ^{*}_{12}}{\partial x_{3}^{2}} & ={\epsilon ^{e}_{12}}''(x_{3})\,. \end{aligned} $$
(4.32)

Remark 4.10

The incompatibility tensor of the universal elastic strains reads

$$ \boldsymbol{\mathsf{R}}^{e}=\begin{bmatrix} 0 & -{\epsilon ^{e}_{12}}''(x_{3}) & -{\epsilon ^{e}_{13}}''(x_{2}) \\ -{\epsilon ^{e}_{12}}''(x_{3}) & 0 & -{\epsilon ^{e}_{23}}''(x_{1}) \\ -{\epsilon ^{e}_{13}}''(x_{2}) & -{\epsilon ^{e}_{23}}''(x_{1}) & 0 \\ \end{bmatrix}\,. $$
(4.33)

We observe that the universal elastic strains (and consequently the universal eigenstrains) are impotent if \(\epsilon ^{e}_{23}(x_{1})\), \(\epsilon ^{e}_{13}(x_{2})\), \(\epsilon ^{e}_{12}(x_{3})\) are linear functions.

4.6 Transversely isotropic solids

A transversely isotropic solid has an axis of symmetry that is normal to the isotropy planes. Let us assume that the axis of transverse isotropy is along the \(x_{3}\)-axis in a Cartesian coordinate system \((x_{1},x_{2},x_{3})\). A transversely isotropic solid has five independent elastic constants, and the elasticity matrix has the following representation:

$$ \mathbf{c}=\begin{bmatrix} c_{11} & c_{12} & c_{13} & 0 & 0 & 0 \\ c_{12} & c_{11} & c_{13} & 0 & 0 & 0 \\ c_{13} & c_{13} & c_{33} & 0 & 0 & 0 \\ 0 & 0 & 0 & c_{44} & 0 & 0 \\ 0 & 0 & 0 & 0 & c_{44} & 0 \\ 0 & 0 & 0 & 0 & 0 & \frac{1}{2}(c_{11}-c_{12}) \end{bmatrix}. $$
(4.34)

In [52] it was shown that, in the absence of egenstrains, universal displacements have the following form:

$$ \begin{aligned} & u_{1}(x_{1},x_{2},x_{3})=c_{1}x_{1}+c_{2}x_{2}+\mathit{cx}_{2}x_{3}+x_{3}h_{1}(x_{1},x_{2})+k_{1}(x_{1},x_{2}),\\ & u_{2}(x_{1},x_{2},x_{3})=-c_{2}x_{1}+c_{1}x_{2}-\mathit{cx}_{1}x_{3}+x_{3}h_{2}(x_{1},x_{2})+k_{2}(x_{1},x_{2}),\\ & u_{3}(x_{1},x_{2},x_{3})=c_{3}x_{3}+\hat{u}_{3}(x_{1},x_{2}), \end{aligned} $$
(4.35)

where \(\xi (x_{2}+\mathit{ix}_{1})=h_{2}(x_{1},x_{2})+\mathit{ih}_{1}(x_{1},x_{2})\) and \(\eta \left (x_{2}+\mathit{ix}_{1}\right )=k_{2}(x_{1},x_{2})+\mathit{ik}_{1}(x_{1},x_{2})\)Footnote 3 are holomorphic, and \(\hat{u}_{3}(x_{1},x_{2})\) is harmonic.

The universality constraints (4.2) give us the following fifteen PDEs:

$$ \begin{aligned} & \frac{\partial \epsilon ^{e}_{33}}{\partial x_{1}} = \frac{\partial \epsilon ^{e}_{33}}{\partial x_{2}}= \frac{\partial \epsilon ^{e}_{33}}{\partial x_{3}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{13}}{\partial x_{3}} = \frac{\partial \epsilon ^{e}_{23}}{\partial x_{3}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{13}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{23}}{\partial x_{2}}=0\,, \end{aligned} $$
(4.36)

and

$$ \begin{aligned} & \frac{\partial \epsilon ^{e}_{11}}{\partial x_{3}} + \frac{\partial \epsilon ^{e}_{22}}{\partial x_{3}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{11}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{12}}{\partial x_{2}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{22}}{\partial x_{1}} - \frac{\partial \epsilon ^{e}_{12}}{\partial x_{2}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{12}}{\partial x_{1}} - \frac{\partial \epsilon ^{e}_{11}}{\partial x_{2}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{12}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{22}}{\partial x_{2}}=0\,. \end{aligned} $$
(4.37)

From (4.36)1 one concludes that \(\epsilon ^{e}_{33}\) is constant. The remaining PDEs in (4.36) imply that \(\epsilon ^{e}_{13}=\epsilon ^{e}_{13}(x_{1},x_{2})\), \(\epsilon ^{e}_{23}=\epsilon ^{e}_{23}(x_{1},x_{2})\), and \(\frac{\partial \epsilon ^{e}_{13}(x_{1},x_{2})}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{23}(x_{1},x_{2})}{\partial x_{2}}=0\). Therefore, \(\epsilon ^{e}_{13}(x_{1},x_{2})\) is an arbitrary function and

$$ \epsilon ^{e}_{23}(x_{1},x_{2})=-\int \epsilon ^{e}_{13,1}(x_{1},x_{2})\,\mathit{dx}_{2}+\hat{\epsilon}_{23}(x_{1})\,, $$
(4.38)

where \(\hat{\epsilon}_{23}(x_{1})\) is an arbitrary function. From the last four PDEs in (4.37), one obtains

$$ \frac{\partial \epsilon ^{e}_{11}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{22}}{\partial x_{1}}=0\,,\quad \frac{\partial \epsilon ^{e}_{11}}{\partial x_{2}} + \frac{\partial \epsilon ^{e}_{22}}{\partial x_{2}}=0\,, $$
(4.39)

which together with (4.37)1 imply that \(\epsilon ^{e}_{22}(x_{1},x_{2},x_{3})=-\epsilon ^{e}_{11}(x_{1},x_{2},x_{3})+c_{0}\), where \(c_{0}\) is a constant. The remaining PDEs are (4.37)2 and (4.37)4. They imply that

$$ \begin{aligned} & \frac{\partial ^{2} \epsilon ^{e}_{11}}{\partial x_{1}^{2}} + \frac{\partial ^{2} \epsilon ^{e}_{11}}{\partial x_{2}^{2}}=0\,,\\ & \epsilon ^{e}_{12}(x_{1},x_{2},x_{3})=\int \epsilon ^{e}_{11,2}(x_{1},x_{2},x_{3})\,\mathit{dx}_{1}+\hat{\epsilon}(x_{2},x_{3}) \,, \end{aligned} $$
(4.40)

where \(\hat{\epsilon}(x_{2},x_{3})\) is an arbitrary function. Therefore, we have proved the following result.

Proposition 4.11

For transversely isotropic linear elastic solids with the isotropy plane parallel to the \(x_{1}x_{2}\)-plane in a Cartesian coordinate system \((x_{1},x_{2},x_{3})\), the universal elastic strains have the following form

$$ \boldsymbol{\epsilon}^{e}(\mathbf{x})=\begin{bmatrix} \epsilon ^{e}_{11}(x_{1},x_{2},x_{3}) & \epsilon ^{e}_{12}(x_{1},x_{2},x_{3}) & \epsilon ^{e}_{13}(x_{1},x_{2}) \\ \epsilon ^{e}_{12}(x_{1},x_{2},x_{3}) & -\epsilon ^{e}_{11}(x_{1},x_{2},x_{3})+c_{0} & \epsilon ^{e}_{23}(x_{1},x_{2}) \\ \epsilon ^{e}_{13}(x_{1},x_{2}) & \epsilon ^{e}_{23}(x_{1},x_{2}) & \epsilon ^{e}_{33} \\ \end{bmatrix}\,, $$
(4.41)

where \(\epsilon ^{e}_{33}\) is constant. \(\epsilon ^{e}_{11}(x_{1},x_{2},x_{3})\) satisfies the PDE (4.40)1, and \(\epsilon ^{e}_{12}(x_{1},x_{2},x_{3})\) has the representation (4.40)2. \(\epsilon ^{e}_{13}(x_{1},x_{2})\) is an arbitrary function, while \(\epsilon ^{e}_{23}(x_{1},x_{2})\) has the representation (4.38). Universal egenstrains (up to impotent eigenstrains) are the set of solutions of the six second-order linear PDEs \(\operatorname{curl}\circ \operatorname{curl}\boldsymbol{\epsilon}^{*}=-\boldsymbol{\mathsf{R}}^{e}\), where the incompatibility tensor of the universal elastic strains reads

$$ \boldsymbol{\mathsf{R}}^{e}=\begin{bmatrix} -\frac{\partial ^{2}\epsilon ^{e}_{11}}{\partial x_{3}^{2}} & \frac{\partial ^{2}\epsilon ^{e}_{12}}{\partial x_{3}^{2}} & \frac{\partial}{\partial x_{2}}\! \left (\frac{\partial \epsilon ^{e}_{23}}{\partial x_{1}}- \frac{\partial \epsilon ^{e}_{13}}{\partial x_{2}} \right ) \\ \frac{\partial ^{2}\epsilon ^{e}_{12}}{\partial x_{3}^{2}} & \frac{\partial ^{2}\epsilon ^{e}_{11}}{\partial x_{3}^{2}} & \frac{\partial}{\partial x_{1}}\! \left (\frac{\partial \epsilon ^{e}_{13}}{\partial x_{2}}- \frac{\partial \epsilon ^{e}_{23}}{\partial x_{1}} \right ) \\ \frac{\partial}{\partial x_{2}}\! \left (\frac{\partial \epsilon ^{e}_{23}}{\partial x_{1}} - \frac{\partial \epsilon ^{e}_{13}}{\partial x_{2}} \right ) & \frac{\partial}{\partial x_{1}} \!\left (\frac{\partial \epsilon ^{e}_{13}}{\partial x_{2}}- \frac{\partial \epsilon ^{e}_{23}}{\partial x_{1}} \right ) & 0 \\ \end{bmatrix}\,. $$
(4.42)

4.7 Cubic solids

A cubic solid has nine planes of symmetry at every point such that their normals are parallel to the edges and face diagonals of a cube. Suppose the edges of the cube are parallel to the coordinate axes of a Cartesian coordinate system \((x_{1},x_{2},x_{3})\). A cubic solid has three independent elastic constants and with respect to this coordinate system has an elasticity matrix with the following representation

$$ \mathbf{c}=\begin{bmatrix} c_{11} & c_{12} & c_{12} & 0 & 0 & 0 \\ c_{12} & c_{11} & c_{12} & 0 & 0 & 0 \\ c_{12} & c_{12} & c_{11} & 0 & 0 & 0 \\ 0 & 0 & 0 & c_{44} & 0 & 0 \\ 0 & 0 & 0& 0 & c_{44} & 0 \\ 0 & 0 & 0 & 0 & 0 & c_{44} \end{bmatrix}. $$
(4.43)

In [52] it was shown that for cubic solids and in the absence of eigenstrains universal displacements have the following form

$$ \begin{aligned} & u_{1}(x_{1},x_{2},x_{3})=\frac{a}{2}x_{1}(x_{3}^{2}-x_{2}^{2})+c_{1}x_{1}x_{3}+b_{1}x_{1}x_{2}+d_{1}x_{1}+g_{1}(x_{2},x_{3}),\\ & u_{2}(x_{1},x_{2},x_{3})=\frac{a}{2}x_{2}(x_{1}^{2}-x_{3}^{2})+a_{1}x_{1}x_{2}-c_{1}x_{2}x_{3}+d_{2}x_{2}+g_{2}(x_{1},x_{3}),\\ & u_{3}(x_{1},x_{2},x_{3})=\frac{a}{2}x_{3}(x_{2}^{2}-x_{1}^{2})-a_{1}x_{1}x_{3}-b_{1}x_{2}x_{3}+d_{3}x_{3}+g_{3}(x_{1},x_{2}), \end{aligned} $$
(4.44)

where \(g_{1}\), \(g_{2}\), and \(g_{3}\) are arbitrary harmonic functions.

The universality constraints (4.2) give us the following nine PDEs:

$$ \begin{aligned} & \frac{\partial \epsilon ^{e}_{11}}{\partial x_{1}} = \frac{\partial \epsilon ^{e}_{22}}{\partial x_{2}}= \frac{\partial \epsilon ^{e}_{33}}{\partial x_{3}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{22}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{33}}{\partial x_{1}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{11}}{\partial x_{2}} + \frac{\partial \epsilon ^{e}_{33}}{\partial x_{2}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{11}}{\partial x_{3}} + \frac{\partial \epsilon ^{e}_{22}}{\partial x_{3}}=0\,, \end{aligned} $$
(4.45)

and

$$ \begin{aligned} & \frac{\partial \epsilon ^{e}_{12}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{23}}{\partial x_{3}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{12}}{\partial x_{2}} + \frac{\partial \epsilon ^{e}_{13}}{\partial x_{3}}=0\,,\\ & \frac{\partial \epsilon ^{e}_{13}}{\partial x_{1}} + \frac{\partial \epsilon ^{e}_{23}}{\partial x_{2}}=0\,. \end{aligned} $$
(4.46)

From (4.45)1, \(\epsilon ^{e}_{11}=\epsilon ^{e}_{11}(x_{2},x_{3})\), \(\epsilon ^{e}_{22}=\epsilon ^{e}_{22}(x_{1},x_{3})\), and \(\epsilon ^{e}_{33}=\epsilon ^{e}_{33}(x_{1},x_{2})\). From the remaining PDEs in (4.45) one concludes that

$$ \begin{aligned} & \epsilon ^{e}_{11}(x_{2},x_{3})=g(x_{2})+h(x_{3}) \,,\\ & \epsilon ^{e}_{22}(x_{1},x_{3})=f(x_{1})-h(x_{3})\,,\\ & \epsilon ^{e}_{33}(x_{1},x_{2})=-f(x_{1})-g(x_{2})\,, \end{aligned} $$
(4.47)

where \(f(x_{1})\), \(g(x_{2})\), and \(h(x_{3})\) are arbitrary functions.

From (4.46) one concludes that

$$ \begin{aligned} & \epsilon ^{e}_{12}(x_{1},x_{2},x_{3}) = f_{3}(x_{1},x_{3})+g_{3}(x_{2},x_{3}) \,,\\ & \epsilon ^{e}_{23}(x_{1},x_{2},x_{3}) = f_{1}(x_{1},x_{2})+g_{1}(x_{1},x_{3})\,,\\ & \epsilon ^{e}_{13}(x_{1},x_{2},x_{3}) = f_{2}(x_{1},x_{2})+g_{2}(x_{2},x_{3})\,, \end{aligned} $$
(4.48)

such that

$$ \begin{aligned} & \frac{\partial}{\partial x_{1}}f_{3}(x_{1},x_{3}) + \frac{\partial}{\partial x_{3}}g_{1}(x_{1},x_{3})=0\,,\\ & \frac{\partial}{\partial x_{2}}g_{3}(x_{2},x_{3}) + \frac{\partial}{\partial x_{3}}g_{2}(x_{2},x_{3})=0\,,\\ & \frac{\partial}{\partial x_{1}}f_{2}(x_{1},x_{2}) + \frac{\partial}{\partial x_{2}}f_{1}(x_{1},x_{2})=0\,. \end{aligned} $$
(4.49)

Thus

$$ \begin{aligned} & g_{1}(x_{1},x_{3})=-\int f_{3,1}(x_{1},x_{3}) \,\mathit{dx}_{3}+\alpha (x_{1}) \,,\\ & g_{3}(x_{2},x_{3})=-\int g_{2,3}(x_{2},x_{3}) \,\mathit{dx}_{2} +\gamma (x_{3}) \,,\\ & f_{2}(x_{1},x_{2})=-\int f_{1,2}(x_{1},x_{2}) \,\mathit{dx}_{1}+\beta (x_{2}) \,, \end{aligned} $$
(4.50)

where \(\alpha (x_{1})\), \(\beta (x_{2})\), and \(\gamma (x_{3})\) are arbitrary functions. Therefore, we have proved the following result.

Proposition 4.12

For cubic linear elastic solids the universal elastic strains have the following form

$$ \boldsymbol{\epsilon}^{e}(\mathbf{x})=\begin{bmatrix} g(x_{2})+h(x_{3}) & f_{3}(x_{1},x_{3})+g_{3}(x_{2},x_{3}) & f_{2}(x_{1},x_{2})+g_{2}(x_{2},x_{3}) \\ f_{3}(x_{1},x_{3})+g_{3}(x_{2},x_{3}) & f(x_{1})-h(x_{3}) & f_{1}(x_{1},x_{2})+g_{1}(x_{1},x_{3}) \\ f_{2}(x_{1},x_{2})+g_{2}(x_{2},x_{3}) & f_{1}(x_{1},x_{2})+g_{1}(x_{1},x_{3}) & g(x_{2})+h(x_{3}) \\ \end{bmatrix}\,, $$
(4.51)

where \(g_{1}(x_{1},x_{3})\), \(g_{3}(x_{2},x_{3})\), and \(f_{2}(x_{1},x_{2})\) are given in (4.50), and the remaining functions are arbitrary. Universal egenstrains (up to impotent eigenstrains) are the set of solutions of the six second-order linear PDEs \(\operatorname{curl}\circ \operatorname{curl}\boldsymbol{\epsilon}^{*}=-\boldsymbol{\mathsf{R}}^{e}\), where the incompatibility tensor of the universal elastic strains reads

$$ \boldsymbol{\mathsf{R}}^{e}= {\fontsize{7.6}{7.6}\selectfont \begin{aligned}[b] \begin{bmatrix} -g''(x_{2})-h''(x_{3}) & -\nabla ^{2}f_{3}(x_{1},x_{3})-\nabla ^{2}g_{3}(x_{2},x_{3}) & -\nabla ^{2}f_{1}(x_{1},x_{2})-\nabla ^{2}g_{1}(x_{1},x_{3}) \\ -\nabla ^{2}f_{3}(x_{1},x_{3})-\nabla ^{2}g_{3}(x_{2},x_{3}) & -f''(x_{1})+h''(x_{3}) & -\nabla ^{2}f_{2}(x_{1},x_{2})-\nabla ^{2}g_{2}(x_{2},x_{3}) \\ -\nabla ^{2}f_{1}(x_{1},x_{2})-\nabla ^{2}g_{1}(x_{1},x_{3}) & -\nabla ^{2}f_{2}(x_{1},x_{2})-\nabla ^{2}g_{2}(x_{2},x_{3}) & g''(x_{2})+h''(x_{3}) \\ \end{bmatrix}\,. \end{aligned}} $$
(4.52)

5 Conclusion

We have studied the universality of elastic and anelastic strains in anisotropic linear anelasticity. Universal displacements are those displacement fields that satisfy the equilibrium equations in the absence of body forces for arbitrary elastic constants in a given symmetry class. The universality constraints of linear anelasticity restrict the possible forms of elastic strains. We completely characterized the universal elastic strains for all the eight symmetry classes. We observed that for triclinic, monoclinic, and trigonal solids universal elastic strains are compatible. The total strain \(\boldsymbol{\epsilon}=\boldsymbol{\epsilon}^{e}+\boldsymbol{\epsilon}^{*}\) is compatible, and hence, \(\operatorname{curl}\circ \operatorname{curl}\boldsymbol{\epsilon}^{e}+\operatorname{curl}\circ \operatorname{curl}\boldsymbol{\epsilon}^{*}=\mathbf{0}\). Having determined the set of universal elastic strains for every symmetry class, the corresponding universal eigenstrains are found to be those that satisfy the linear second-order PDEs \(\operatorname{curl}\circ \operatorname{curl}\boldsymbol{\epsilon}^{*}=-\operatorname{curl}\circ \operatorname{curl}\boldsymbol{\epsilon}^{e}\) for at least one universal elastic strain field \(\boldsymbol{\epsilon}^{e}(\mathbf{x})\). For triclinic, monoclinic, and trigonal classes we showed that only compatible eigenstrains are universal. If universal eigenstrains are defined modulo the compatible eigenstrains, for these three classes the universal displacements are identical to the corresponding linear elasticity universal displacements that were characterized in [52]. For the other five classes universal eigenstrains are solutions to a system of inhomogeneous PDEs with forcing terms that are certain arbitrary functions depending on the symmetry class. We observed that the smaller the symmetry group, the smaller the space of universal elastic strains, and consequently, the smaller the space of universal eigenstrains. Hence, we have achieved a complete classification of universal elastic strains in linear anelasticity.