Abstract
An elastic map \(\mathbf {T}\) describes the strain-stress relation at a particular point \(\mathbf {p}\) in some material. A symmetry of \(\mathbf {T}\) is a rotation of the material, about \(\mathbf {p}\), that does not change \(\mathbf {T}\). We describe two ways of inferring the group \(\mathcal {S} _{ \mathbf {T} }\) of symmetries of any elastic map \(\mathbf {T}\); one way is qualitative and visual, the other is quantitative. In the first method, we associate to each \(\mathbf {T}\) its “monoclinic distance function”  on the unit sphere. The function
on the unit sphere. The function  is invariant under all of the symmetries of \(\mathbf {T}\), so the group \(\mathcal {S} _{ \mathbf {T} }\) is seen, approximately, in a contour plot of
is invariant under all of the symmetries of \(\mathbf {T}\), so the group \(\mathcal {S} _{ \mathbf {T} }\) is seen, approximately, in a contour plot of  . The second method is harder to summarize, but it complements the first by providing an algorithm to compute the symmetry group \(\mathcal {S} _{ \mathbf {T} }\). In addition to \(\mathcal {S} _{ \mathbf {T} }\), the algorithm gives a quantitative description of the overall approximate symmetry of \(\mathbf {T}\). Mathematica codes are provided for implementing both the visual and the quantitative approaches.
. The second method is harder to summarize, but it complements the first by providing an algorithm to compute the symmetry group \(\mathcal {S} _{ \mathbf {T} }\). In addition to \(\mathcal {S} _{ \mathbf {T} }\), the algorithm gives a quantitative description of the overall approximate symmetry of \(\mathbf {T}\). Mathematica codes are provided for implementing both the visual and the quantitative approaches.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Elasticity is about the relation between strain and stress. We refer to the function \(\mathbf {T}\) from strain to stress as the elastic map. It expresses the constitutive relations of the material under consideration, or the generalized Hooke’s Law [1].
The map \(\mathbf {T}\) describes the strain-stress relation at a particular point \(\mathbf {p}\) in the material. A symmetry of \(\mathbf {T}\) is a rotation of the material, about \(\mathbf {p}\), that does not change \(\mathbf {T}\).
We assume throughout that \(\mathbf {T}\) is a linear self-adjoint transformation of \(3\times 3\) symmetric matrices. For any such \(\mathbf {T}\) we describe two methods of finding its group of symmetries. One method is qualitative and visual, and the other is quantitative; the two methods complement each other.
The first method is a reformulation and elaboration of that of Diner et al. [8], who in turn drew on François et al. [10]. The method is so accessible and appealing that we can give a preliminary description of it here:
To any elastic map \(\mathbf {T}\) we associate its “monoclinic distance function”  on the unit sphere. The zero-contour \(\mathbb{Z} ^{ \mathbf {T} }\) of
on the unit sphere. The zero-contour \(\mathbb{Z} ^{ \mathbf {T} }\) of  turns out to consist of the points where the axes of the 2-fold symmetries of \(\mathbf {T}\) intersect the unit sphere. Since the 2-fold rotations in any elastic symmetry group generate the group, then \(\mathbb{Z} ^{ \mathbf {T} }\) determines the elastic symmetry group of \(\mathbf {T}\). Figure 1 shows eight instances of \(\mathbb{Z} ^{ \mathbf {T} }\). These are the only possibilities; regardless of \(\mathbf {T}\), the set \(\mathbb{Z} ^{ \mathbf {T} }\) will look like one of these eight, though probably reoriented. Thus the set \(\mathbb{Z} ^{ \mathbf {T} }\) reveals the group of symmetries of \(\mathbf {T}\) by displaying the axes of the 2-fold rotations in the group. Since the identification of elastic symmetries has been traditionally regarded as a challenging problem, this pictorial solution came as a welcome surprise.
turns out to consist of the points where the axes of the 2-fold symmetries of \(\mathbf {T}\) intersect the unit sphere. Since the 2-fold rotations in any elastic symmetry group generate the group, then \(\mathbb{Z} ^{ \mathbf {T} }\) determines the elastic symmetry group of \(\mathbf {T}\). Figure 1 shows eight instances of \(\mathbb{Z} ^{ \mathbf {T} }\). These are the only possibilities; regardless of \(\mathbf {T}\), the set \(\mathbb{Z} ^{ \mathbf {T} }\) will look like one of these eight, though probably reoriented. Thus the set \(\mathbb{Z} ^{ \mathbf {T} }\) reveals the group of symmetries of \(\mathbf {T}\) by displaying the axes of the 2-fold rotations in the group. Since the identification of elastic symmetries has been traditionally regarded as a challenging problem, this pictorial solution came as a welcome surprise.
The zero contour (blue) of  on the unit sphere for various elastic maps \(\mathbf {T}\). Each \(\mathbf {T}\) here has as symmetry group one of eight “reference” groups \(\mathbb{U} _{\textsc{triv}},\ldots , \mathbb{U} _{\textsc{iso}}\) as indicated. The points of the zero contour of
on the unit sphere for various elastic maps \(\mathbf {T}\). Each \(\mathbf {T}\) here has as symmetry group one of eight “reference” groups \(\mathbb{U} _{\textsc{triv}},\ldots , \mathbb{U} _{\textsc{iso}}\) as indicated. The points of the zero contour of  are where the axes of the 2-fold symmetries of \(\mathbf {T}\) intersect the unit sphere. Since the 2-fold rotations in any elastic symmetry group generate the group, the zero contour of
are where the axes of the 2-fold symmetries of \(\mathbf {T}\) intersect the unit sphere. Since the 2-fold rotations in any elastic symmetry group generate the group, the zero contour of  determines the symmetry group of \(\mathbf {T}\). For any elastic map \(\mathbf {T}\), the zero contour of
determines the symmetry group of \(\mathbf {T}\). For any elastic map \(\mathbf {T}\), the zero contour of  is one of the eight shown here, though probably reoriented
is one of the eight shown here, though probably reoriented
The first method of inferring elastic symmetries—the visual method—is derived in Sect. 4. The second method—the quantitative method—is derived in Sect. 5; see especially Theorem 3. Other approaches to finding the symmetry groups of elastic maps are found in [2–4, 6, 8, 10, 11, 13, 15]. Of these, only [6, 8, 10, 15] are directly relevant to the current paper. Papers [4] and [15] use the eigensystems of elastic maps to find symmetries. Papers [2, 3, 13] are algebraic and are more sophisticated than the present paper. The papers [5, 10, 12, 14] have applications to acoustics and seismology. We ourselves, however, do not treat applications in this paper.
Mathematica code for drawing contour plots of  and for finding the symmetry group of any elastic map is available as described in the Code Availability section. Inferring elastic symmetry—by either method—can be done routinely.
and for finding the symmetry group of any elastic map is available as described in the Code Availability section. Inferring elastic symmetry—by either method—can be done routinely.
2 Some Prerequisites
Most of this section is abridged from [15]. Details, including proofs, can be found there.
2.1 The Basis \(\mathbb{B}\)
We let \(\mathbb{M}\) be the vector space of \(3\times 3\) symmetric matrices. The basis \(\mathbb{B}\) for \(\mathbb{M}\) consists of the six elements
Our matrix representations of linear transformations \(\mathbf {S} : \mathbb{M} \rightarrow \mathbb{M} \) are all with respect to the basis \(\mathbb{B}\). The matrix representation of \(\mathbf {S}\) is denoted by \([ \mathbf {S} ]\).
2.2 Inner Products and Norms
The inner product of \(n\times n\) matrices \(M=(m_{ij})\) and \(N=(n_{ij})\) is defined by
(Juxtaposition of matrices, with no dot, signifies matrix multiplication.) Matrix norms are then defined in terms of the inner product as usual:
The inner product of elastic maps \(\mathbf {T} _{1}\) and \(\mathbf {T} _{2}\) is defined via their matrix representations:
Norms of elastic maps are then defined from the inner product.
2.3 Adjoint
For a linear transformation \(\mathbf {S} : \mathbb{M} \rightarrow \mathbb{M} \), the adjoint of \(\mathbf {S}\) is the linear transformation \(\mathbf {S} ^{ \boldsymbol {\ast } }: \mathbb{M} \rightarrow \mathbb{M} \) such that
The matrix of \(\mathbf {S} ^{ \boldsymbol {\ast } }\) with respect to \(\mathbb{B}\) is
where the symbol \(\top \) denotes matrix transpose.
2.4 Rotation Matrices
A square matrix \(U\) is said to be orthogonal if \(U U^{\top}=I\). If also \(\det U = 1\) then \(U\) is a rotation matrix. We let \(\mathbb{U}\) be the group of all \(3\times 3\) rotation matrices. Examples of matrices in \(\mathbb{U}\) would be the \(3\times 3\) rotations \(X_{\xi}\), \(Y_{\xi}\), \(Z_{\xi}\) through angle \(\xi \) about the \(x\), \(y\), \(z\) axes, respectively:
For \(3\times 3\) matrices \(M\) and \(N\) and for \(U\in \mathbb{U} \),
2.5 Conjugation by a Rotation Matrix
For \(U\in \mathbb{U} \), the linear transformation \(\overline {U}: \mathbb{M} \rightarrow \mathbb{M} \) is defined to be conjugation by \(U\). That is,
Since \(\overline {U}(E_{1})\cdot E_{2}=E_{1}\cdot \overline {U^{\top}}(E_{2})\), then by comparison with Eq. (5),
Thus, whereas \(\overline {U}\) is conjugation by \(U\), the transformation \(\overline {U}^{ \boldsymbol {\ast } }\) is conjugation by \(U^{\top}\).
2.5.1 The Matrix of \(\overline {U}\)
The matrix of \(\overline {U}\) with respect to the basis \(\mathbb{B}\) (Eq. (1)) is found to be
The matrix of \(\overline {U}^{ \boldsymbol {\ast } }\) is
For any \(6\times 6\) matrices \(S\) and \(T\), and for \(U\in \mathbb{U} \),
It is enough to verify Eq. (13) for \(U= Y_{t} \) and \(U= Z_{t} \), since any \(3\times 3\) rotation matrix can be written \(Z_{\theta} Y_{\phi} Z_{\sigma} \) and since \([\overline {U_{1} U_{2}}]=[\overline {U_{1}}][\overline {U_{2}}]\). From Eq. (13),
2.6 The Eight Reference Groups
If \(\mathbf {T}\) is the elastic map at a point \(\mathbf {p}\) in some material, then \(\overline {U}\circ \mathbf {T} \circ \overline {U}^{ \boldsymbol {\ast } }\) is the elastic map for the material after it has been rotated about \(\mathbf {p}\) using \(U\). Thus,
In terms of matrices, from Eq. (12),
The symmetry group \(\mathcal {S} _{ \mathbf {T} }\) of \(\mathbf {T} \) is the group of all symmetries of \(\mathbf {T} \).
A group of \(3\times 3\) rotation matrices is said to be an elastic symmetry group if it is the symmetry group of some elastic map. Except for conjugacy, there are exactly eight elastic symmetry groups (Forte and Vianello [9]). More precisely, each symmetry group \(\mathcal {S} _{ \mathbf {T} }\) is a conjugate of one of the eight ‘reference’ groups \(\mathbb{U} _{\Sigma}\) in Table 1, and each of the reference groups is the symmetry group of some elastic map.
From Eq. (15a),
Hence the symmetry group \(\mathcal {S} _{\,\overline {U}\,\circ \, \mathbf {T} \,\circ \,\overline {U}^{ \boldsymbol {\ast } }}\) is conjugate to \(\mathcal {S} _{ \mathbf {T} }\) by \(U\):
2.7 The Eight Reference Matrices
The reference matrices are listed in Table 2. As shown in [15, Sect. 12.1], their fundamental relation with the reference groups is that the symmetry group of an elastic map \(\mathbf {T}\) is at least \(\mathbb{U} _{\Sigma}\) if and only if the matrix of \(\mathbf {T}\) has the form of the reference matrix \(T_{\Sigma}\):
2.8 The Eight Elastic Symmetry Classes
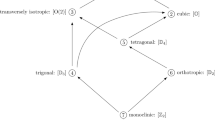
For \(\Sigma =\textsc{triv},\ldots ,\textsc{iso}\), we define the (elastic) symmetry class \(\mathcal {C} _{\Sigma}\) to consist of the groups that are conjugate to \(\mathbb{U} _{\Sigma}\):
Temporarily abbreviating \(\mathcal {C} _{\Sigma _{1}}\) and \(\mathcal {C} _{\Sigma _{2}}\) to \(\mathcal {C} _{1}\) and \(\mathcal {C} _{2}\), we define a partial ordering ≺ of the eight symmetry classes by
Because all members of a symmetry class are conjugate to one another, we get equivalent formulations of Eq. (19a):
With an arrow from \(\mathcal {C} _{\Sigma _{1}}\) to \(\mathcal {C} _{\Sigma _{2}}\) signifying \(\mathcal {C} _{\Sigma _{1}}\! \prec \mathcal {C} _{\Sigma _{2}}\), we have

For an elastic map \(\mathbf {T}\), we define the symmetry class \(\overline { \mathcal {S} _{ \mathbf {T} }}\) of \(\mathbf {T}\) to be the symmetry class that contains the group \(\mathcal {S} _{ \mathbf {T} }\) (as a member). The symmetry class \(\overline { \mathcal {S} _{ \mathbf {T} }}\) is less informative than the symmetry group \(\mathcal {S} _{ \mathbf {T} }\), since the orientation information in \(\mathcal {S} _{ \mathbf {T} }\) is lost in \(\overline { \mathcal {S} _{ \mathbf {T} }}\). Figure 2 shows three members of the symmetry class \(\mathcal {C} _{\textsc{tet}}\).
A suggestion of the elastic symmetry class \(\mathcal {C} _{\textsc{tet}}\), showing only three of its infinitely many members. The class consists of all groups of the form \(U \mathbb{U} _{\textsc{tet}}U^{\top}\). Here each group is shown by its 2-fold symmetry axes; compare with the diagram for \(\mathbb{U} _{\textsc{tet}}\) in Fig. 1
2.9 Regular Angles, Regular Axes
An angle \(\xi \) is said to be regular if a rotation through angle \(\xi \) is neither 1-fold, 2-fold, 3-fold, nor 4-fold. That is, \(\xi \neq \pm 2\pi /n \ (\mathrm{mod}\ 2\pi)\), \(n=1,2,3,4\).
If \(\xi \) is regular and if rotation through angle \(\xi \) about some axis is a symmetry of an elastic map \(\mathbf {T}\), then rotations through all angles about that same axis are symmetries of \(\mathbf {T}\) [15, Theorem 5]. The axis is then said to be a regular axis for \(\mathbf {T}\).
3 Orthogonal Projection
In an inner product space \(\mathbb{V}\), vectors \(\mathbf {v} _{1}\) and \(\mathbf {v} _{2}\) in \(\mathbb{V}\) are said to be orthogonal if \(\mathbf {v} _{1}\cdot \mathbf {v} _{2}=0\). The orthogonal complement of a subspace \(\mathbb{W}\) is
The orthogonal projection \(P( \mathbf {v} , \mathbb{W} )\) of a vector \(\mathbf {v}\) onto a subspace \(\mathbb{W}\) of \(\mathbb{V}\) is characterized by vectors \(\mathbf {w} _{1}\) and \(\mathbf {w} _{2}\) such that
Then
If a vector \(\mathbf {w} \) is in \(\mathbb{W}\), then its distance squared from \(\mathbf {v}\) is
since \(\mathbf {w} _{1}- \mathbf {w} \in \mathbb{W} \) and since \(\mathbf {v} - \mathbf {w} _{1}= \mathbf {w} _{2}\in \mathbb{W} ^{\perp}\). The projected vector \(P( \mathbf {v} , \mathbb{W} )= \mathbf {w} _{1}\) is therefore the closest member of \(\mathbb{W}\) to \(\mathbf {v}\). The distance from \(\mathbf {v}\) to the subspace \(\mathbb{W}\) is
Suppose a linear transformation \(\mathbf {U} : \mathbb{V} \rightarrow \mathbb{V} \) is unitary, that is, \(\mathbf {U} \circ \mathbf {U} ^{ \boldsymbol {\ast } }= \mathbf {U} ^{ \boldsymbol {\ast } }\circ \mathbf {U} = \mathbf {I} \), where \(\mathbf {I}\) is the identity transformation. Applying Eqs. (22a), (22b) to \(\mathbf {U} ^{ \boldsymbol {\ast } }( \mathbf {v} )\) rather than to \(\mathbf {v}\), we have
If \(\mathbf {w} \in \mathbb{W} \) then \(\mathbf {U} ( \mathbf {w} _{2})\cdot \mathbf {U} ( \mathbf {w} )= \mathbf {w} _{2}\cdot \mathbf {w} =0\), so that \(\mathbf {U} ( \mathbf {w} _{2})\in \mathbf {U} ( \mathbb{W} )^{\perp}\). Applying \(\mathbf {U}\) to both sides of Eq. (25a) gives
and so the projection onto \(\mathbf {U} ( \mathbb{W} )\) is related to the projection onto \(\mathbb{W}\) by
4 The Zero Contour of  Expresses the Symmetry Group of \(\mathbf {T}\)
Expresses the Symmetry Group of \(\mathbf {T}\)
In this section we show that the symmetry group of any elastic map \(\mathbf {T}\) is determined by the zero contour of a certain function  (Eq. (40)). The exposition draws on ideas from Diner et al. [8].
(Eq. (40)). The exposition draws on ideas from Diner et al. [8].
We let \(\boldsymbol {\mathcal {T}}\) be the vector space of all elastic maps, and we let \(\mathcal {T}\) (unbold font)—also a vector space—consist of their matrices. Those matrices are the \(6\times 6\) symmetric matrices. We define
Thus \(\boldsymbol {\mathcal {T}} \!_{\textsc{mono}}\) consists of the elastic maps whose symmetry class is at least monoclinic.
For \(U\in \mathbb{U} \) and \(\mathbf {k} =(0,0,1)\), we also let
The set \(\boldsymbol {\mathcal {V}} _{\textsc{mono}}(U)\) is a subspace of \(\boldsymbol {\mathcal {T}}\), whereas \(\boldsymbol {\mathcal {T}} \!_{\textsc{mono}}\) is not. The set \(\mathcal {V} _{\textsc{mono}}(U)\) is likewise a subspace of \(\mathcal {T}\).
From Eq. (24), the distance from an elastic map \(\mathbf {T}\) to the subspace \(\boldsymbol {\mathcal {V}} _{\textsc{mono}}(U)\) is
The projected matrix \(P([ \mathbf {T} ], \mathcal {V} _{\textsc{mono}}(U))\) is indeed the matrix of \(P( \mathbf {T} ,\, \boldsymbol {\mathcal {V}} _{\textsc{mono}}(U))\), hence
We next find the matrix \(P\left (T, \mathcal {V} _{\textsc{mono}}(U)\right )\):
(i) The special case where \(U\) is the \(3\times 3\) identity matrix \(I\). For
we let
From Eqs. (29a), (29b), the subspace \(\mathcal {V} _{\textsc{mono}}(I)\) consists of the matrices of elastic maps that have \(\mathbf {k}\) as a 2-fold axis. They are therefore the matrices having the form of \(T_{\textsc{mono}}\) in Table 2; see Eq. (17). Hence \(W_{1}\in \mathcal {V} _{\textsc{mono}}(I)\). And, from Eq. (2),
so that \(W_{2}\in \mathcal {V} _{\textsc{mono}}(I)^{\perp}\). Thus
By comparison with Eqs. (22a), (22b), the matrix \(W_{1}\) is the orthogonal projection of \(T\) onto \(\mathcal {V} _{\textsc{mono}}(I)\):
(ii) The general case, where \(U\in \mathbb{U} \) is arbitrary. The elastic map \(\mathbf {T}\) has a 2-fold symmetry with axis \(\mathbf {k}\) if and only if \(\overline {U}\circ \mathbf {T} \circ \overline {U}^{ \boldsymbol {\ast } }\) has a 2-fold symmetry with axis \(U \mathbf {k} \). Therefore, from Eq. (29a),
In terms of matrices,
From Eq. (27), with the (unitary) function \(T\rightarrow \overline {U}\,T \,\overline {U}^{\top}\) playing the role of \(\mathbf {U}\), with \(T\) playing the role of \(\mathbf {v}\), and with \(\mathcal {V} _{\textsc{mono}}(I)\) playing the role of \(\mathbb{W}\),
Returning to Eq. (31) and then using Eqs. (38) and (14), we have
where
From Eq. (29a) we find that \(\boldsymbol {\mathcal {V}} _{\textsc{mono}}(U Z_{\xi} )= \boldsymbol {\mathcal {V}} _{\textsc{mono}}(U)\). Hence we can regard \(d( \mathbf {T} , \boldsymbol {\mathcal {V}} _{\textsc{mono}}(U))\) not as a function of orientations \(U\) but as a function  of points \(\mathbf {v}\) on the unit sphere \(\mathbb{S}\):
of points \(\mathbf {v}\) on the unit sphere \(\mathbb{S}\):

From Eqs. (29a), (39a), (39b), (40),
Theorem 1
The number  (Eq. (40)) is the distance from \(\mathbf {T}\) to the subspace of elastic maps having \(\mathbf {v}\) as a 2-fold symmetry axis. Analytically, it is
(Eq. (40)) is the distance from \(\mathbf {T}\) to the subspace of elastic maps having \(\mathbf {v}\) as a 2-fold symmetry axis. Analytically, it is

where
and where \(U\) is any \(3\times 3\) rotation matrix with \(U \mathbf {k} = \mathbf {v} \). The matrix \(P(S,\, \mathcal {V} _{\textsc{mono}}(I))\) is computed using Eq. (36).
In words: To find  , we choose \(U\in \mathbb{U} \) so that \(U \mathbf {k} = \mathbf {v} \), and we calculate the \(6\times 6\) matrix \(S=[\overline {U}]^{\top}\![ \mathbf {T} ]\,[\overline {U}]\). We then set the entries of \(S\) equal to zero, except for those in its upper right \(2\times 4\) submatrix and in its lower left \(4\times 2\) submatrix. The norm of the resulting \(6\times 6\) matrix is
, we choose \(U\in \mathbb{U} \) so that \(U \mathbf {k} = \mathbf {v} \), and we calculate the \(6\times 6\) matrix \(S=[\overline {U}]^{\top}\![ \mathbf {T} ]\,[\overline {U}]\). We then set the entries of \(S\) equal to zero, except for those in its upper right \(2\times 4\) submatrix and in its lower left \(4\times 2\) submatrix. The norm of the resulting \(6\times 6\) matrix is  .
.
From Theorem 1,

4.1 The Zero Contour \(\mathbb{Z} ^{ \mathbf {T} }\) Determines \(\mathcal {S} _{ \mathbf {T} }\)
From Eq. (41), the zero-contour \(\mathbb{Z} ^{ \mathbf {T} }\) of  consists of the points \(\mathbf {v}\) where the axes of the 2-fold symmetries of \(\mathbf {T}\) intersect the unit sphere. Since the 2-fold rotations in any elastic symmetry group generate the group, then \(\mathbb{Z} ^{ \mathbf {T} }\) determines the symmetry group \(\mathcal {S} _{ \mathbf {T} }\) of \(\mathbf {T}\). Except for orientations, there are just eight possibilities for \(\mathbb{Z} ^{ \mathbf {T} }\), as shown in Fig. 1.
consists of the points \(\mathbf {v}\) where the axes of the 2-fold symmetries of \(\mathbf {T}\) intersect the unit sphere. Since the 2-fold rotations in any elastic symmetry group generate the group, then \(\mathbb{Z} ^{ \mathbf {T} }\) determines the symmetry group \(\mathcal {S} _{ \mathbf {T} }\) of \(\mathbf {T}\). Except for orientations, there are just eight possibilities for \(\mathbb{Z} ^{ \mathbf {T} }\), as shown in Fig. 1.
Since the zero contour of  can be calculated (from \(\mathbf {T}\)), then the symmetry group of \(\mathbf {T}\) can be calculated as well. At the moment, however, we are more interested in using the contour plot of
can be calculated (from \(\mathbf {T}\)), then the symmetry group of \(\mathbf {T}\) can be calculated as well. At the moment, however, we are more interested in using the contour plot of  to convey the symmetry of \(\mathbf {T}\) visually.
to convey the symmetry of \(\mathbf {T}\) visually.
4.2 Symmetries of 
A \(3\times 3\) rotation matrix \(V\) is said to be a symmetry of  if
if

In that case the contour map for  appears unchanged when rotated using \(V\).
appears unchanged when rotated using \(V\).
Theorem 2
For any elastic map \(\mathbf {T}\), the symmetries of \(\mathbf {T}\) are symmetries of  .
.
Proof
Let \(V\) be a symmetry of \(\mathbf {T}\) and let \(\mathbf {v} \in \mathbb{S} \). The number  in Theorem 1 is determined by \(S(U)\), where \(U \mathbf {k} = \mathbf {v} \). Since \(VU \mathbf {k} =V \mathbf {v} \), then
in Theorem 1 is determined by \(S(U)\), where \(U \mathbf {k} = \mathbf {v} \). Since \(VU \mathbf {k} =V \mathbf {v} \), then  is determined by \(S(VU)\). Since
is determined by \(S(VU)\). Since
then  . □
. □
The converse of Theorem 2 appears to be true as well, but we have not proved it.
4.3 Some Examples
Although the zero-contour of  entirely determines the symmetry group of \(\mathbf {T}\), a symmetry of \(\mathbf {T}\) is often more conspicuous in the contour plot of
entirely determines the symmetry group of \(\mathbf {T}\), a symmetry of \(\mathbf {T}\) is often more conspicuous in the contour plot of  as a whole, especially when the plot is viewed along the axis of the symmetry; see Figs. 3 and 4.
as a whole, especially when the plot is viewed along the axis of the symmetry; see Figs. 3 and 4.
Contour plots of  for eight elastic maps \(\mathbf {T}\) having symmetry groups \(\mathbb{U} _{\textsc{triv}},\ldots , \mathbb{U} _{\textsc{iso}}\), the same as in Fig. 1. At corresponding locations in this figure and Fig. 1 the zero contours of
for eight elastic maps \(\mathbf {T}\) having symmetry groups \(\mathbb{U} _{\textsc{triv}},\ldots , \mathbb{U} _{\textsc{iso}}\), the same as in Fig. 1. At corresponding locations in this figure and Fig. 1 the zero contours of  are therefore the same. Thus in the lower left sphere in the two figures the zero contours are the same; they consist of the points where the 2-fold axes of \(\mathbb{U} _{\textsc{tet}}\) penetrate the sphere. The symmetries of \(\mathbf {T}\) are symmetries of
are therefore the same. Thus in the lower left sphere in the two figures the zero contours are the same; they consist of the points where the 2-fold axes of \(\mathbb{U} _{\textsc{tet}}\) penetrate the sphere. The symmetries of \(\mathbf {T}\) are symmetries of  and hence are seen in the contour plots. The \(xyz\) axes are the same here as in Fig. 1
and hence are seen in the contour plots. The \(xyz\) axes are the same here as in Fig. 1
Four of the contour plots from Fig. 3 but seen looking down the \(z\)-axis. (The \(x\)-axis is to the right.) From left to right, the \(z\)-axis is a 2-fold, 3-fold, 4-fold, and regular axis, respectively, for the relevant elastic map. Except in the \(\mathbb{U} _{\textsc{mono}}\) diagram, the zero contour is not conspicuous in this view, since most of its points are in the \(xy\)-plane. Compare with Fig. 3
Suppose anisotropic elastic maps \(\mathbf {T} _{1}\) and \(\mathbf {T} _{2}\) have the same symmetry group \(\mathcal {S} _{ \mathbf {T} _{1}}= \mathcal {S} _{ \mathbf {T} _{2}}\). The contour plots of \(f_{\textsc{mono}}^{ \mathbf {T} _{1}}\) and \(f_{\textsc{mono}}^{ \mathbf {T} _{2}}\) can be very different, but the zero contours will be the same for each. In spite of their differences, both plots are invariant under the symmetries in \(\mathcal {S} _{ \mathbf {T} _{i}}\), by Theorem 2. Compare Figs. 4 and 5.
Contour plots of  for four elastic maps \(\mathbf {T}\) whose symmetry groups, like the elastic maps in Fig. 4, are \(\mathbb{U} _{\textsc{mono}}\), \(\mathbb{U} _{\textsc{trig}}\), \(\mathbb{U} _{\textsc{tet}}\), and \(\mathbb{U} _{\textsc{xiso}}\) as indicated. The viewpoint is looking down the \(z\)-axis, the same as in Fig. 4. Corresponding diagrams in the two figures have the same zero contours, since their symmetry groups are the same
for four elastic maps \(\mathbf {T}\) whose symmetry groups, like the elastic maps in Fig. 4, are \(\mathbb{U} _{\textsc{mono}}\), \(\mathbb{U} _{\textsc{trig}}\), \(\mathbb{U} _{\textsc{tet}}\), and \(\mathbb{U} _{\textsc{xiso}}\) as indicated. The viewpoint is looking down the \(z\)-axis, the same as in Fig. 4. Corresponding diagrams in the two figures have the same zero contours, since their symmetry groups are the same
With the exception of 3-fold axes, any non-trivial symmetry axis \(\mathbf {v} \in \mathbb{S} \) of an elastic map \(\mathbf {T}\) is also a 2-fold axis of \(\mathbf {T}\). In that case the point \(\mathbf {v}\) appears in the zero contour \(\mathbb{Z} ^{ \mathbf {T} }\) of  . A 3-fold axis may or may not be a 2-fold axis, but it will nevertheless be recognizable in the contour plot for
. A 3-fold axis may or may not be a 2-fold axis, but it will nevertheless be recognizable in the contour plot for  , due to Theorem 2. Thus in the \(\mathbb{U} _{\textsc{cube}}\) diagram in Fig. 3 the center of each light-colored three-pronged region of the sphere is a 3-fold symmetry axis.
, due to Theorem 2. Thus in the \(\mathbb{U} _{\textsc{cube}}\) diagram in Fig. 3 the center of each light-colored three-pronged region of the sphere is a 3-fold symmetry axis.
Figs. 6, 7, 8 show contour plots of  for three different elastic maps \(\mathbf {T} = \mathbf {T} _{1}, \mathbf {T} _{2}, \mathbf {T} _{3}\). The lattices that appear in the figures are explained in Sect. 5; they can largely be ignored at the moment.
for three different elastic maps \(\mathbf {T} = \mathbf {T} _{1}, \mathbf {T} _{2}, \mathbf {T} _{3}\). The lattices that appear in the figures are explained in Sect. 5; they can largely be ignored at the moment.
Contour plot of  for the elastic map \(\mathbf {T} = \mathbf {T} _{1}\) whose matrix is given in Eq. (75). Except for orientation, the plot is consistent with the diagram labeled \(\mathbb{U} _{\textsc{xiso}}\) in Fig. 1. Thus it appears that the symmetry of \(\mathbf {T} \) is transverse isotropic and that the symmetry group of \(\mathbf {T}\) is the conjugate of \(\mathbb{U} _{\textsc{xiso}}\) (Table 1) that has its regular axis at \(\mathbf {v} _{1}\). Of course such symmetry inferences, based only on a picture, are necessarily approximate. The role of the lattice in confirming the symmetry of \(\mathbf {T}\) quantitatively will be explained in Sect. 5. For \(\Sigma =\textsc{triv},\ldots ,\textsc{iso}\), the angle \(\beta _{\Sigma}^{ \mathbf {T} }\) is a measure of how far \(\mathbf {T}\) is from having symmetry class at least \(\mathcal {C} _{\Sigma}\). Red arrows accentuate the lattice nodes where \(\beta _{\Sigma}^{ \mathbf {T} }=0\), hence where the symmetry class of \(\mathbf {T}\) is at least \(\mathcal {C} _{\Sigma}\)
for the elastic map \(\mathbf {T} = \mathbf {T} _{1}\) whose matrix is given in Eq. (75). Except for orientation, the plot is consistent with the diagram labeled \(\mathbb{U} _{\textsc{xiso}}\) in Fig. 1. Thus it appears that the symmetry of \(\mathbf {T} \) is transverse isotropic and that the symmetry group of \(\mathbf {T}\) is the conjugate of \(\mathbb{U} _{\textsc{xiso}}\) (Table 1) that has its regular axis at \(\mathbf {v} _{1}\). Of course such symmetry inferences, based only on a picture, are necessarily approximate. The role of the lattice in confirming the symmetry of \(\mathbf {T}\) quantitatively will be explained in Sect. 5. For \(\Sigma =\textsc{triv},\ldots ,\textsc{iso}\), the angle \(\beta _{\Sigma}^{ \mathbf {T} }\) is a measure of how far \(\mathbf {T}\) is from having symmetry class at least \(\mathcal {C} _{\Sigma}\). Red arrows accentuate the lattice nodes where \(\beta _{\Sigma}^{ \mathbf {T} }=0\), hence where the symmetry class of \(\mathbf {T}\) is at least \(\mathcal {C} _{\Sigma}\)
Like Fig. 6 but for the elastic map \(\mathbf {T} = \mathbf {T} _{2}\) whose matrix is given in Eq. (76). Except for orientation, the contour plot on the sphere is consistent with the diagram labeled \(\mathbb{U} _{\textsc{tet}}\) in Fig. 1. Thus it appears that the symmetry of \(\mathbf {T} \) is tetragonal and that the symmetry group of \(\mathbf {T}\) is the conjugate of \(\mathbb{U} _{\textsc{tet}}\) that has \(\mathbf {v} _{1}\) as its 4-fold axis and has \(\mathbf {v} _{2}\) as one of its 2-fold axes. (Quantitative confirmation of the symmetry group is given by Theorem 3 of Sect. 5, with \(U\) from Eq. 60. Also see Eq. 62)
Like Fig. 7 but for the elastic map \(\mathbf {T} = \mathbf {T} _{3}\) whose matrix is given in Eq. (77). The zero contour of  on the sphere appears to be a great circle together with its poles, as if the symmetry of \(\mathbf {T} \) were transverse isotropic. The contour plot as a whole, however, shows that the symmetry cannot be transverse isotropic, since the contours would then have to be concentric circles. Instead, it appears that the symmetry is tetragonal and that the symmetry group is one of the conjugates of \(\mathbb{U} _{\textsc{tet}}\) that have \(\mathbf {v} _{1}\) as a 4-fold axis. The 2-fold axes, however, are not easy to discern from the contour plot alone. (The point \(\mathbf {v} _{2}\) is indeed one of them, but it was found quantitatively, from
on the sphere appears to be a great circle together with its poles, as if the symmetry of \(\mathbf {T} \) were transverse isotropic. The contour plot as a whole, however, shows that the symmetry cannot be transverse isotropic, since the contours would then have to be concentric circles. Instead, it appears that the symmetry is tetragonal and that the symmetry group is one of the conjugates of \(\mathbb{U} _{\textsc{tet}}\) that have \(\mathbf {v} _{1}\) as a 4-fold axis. The 2-fold axes, however, are not easy to discern from the contour plot alone. (The point \(\mathbf {v} _{2}\) is indeed one of them, but it was found quantitatively, from  .) The elastic maps \(\mathbf {T} _{2}\) and \(\mathbf {T} _{3}\) are closely related, as explained in the text, and in fact their symmetry groups are the same. Note the much smaller value of \(\beta _{\textsc{xiso}}^{ \mathbf {T} }\) here as compared with Fig. 7
.) The elastic maps \(\mathbf {T} _{2}\) and \(\mathbf {T} _{3}\) are closely related, as explained in the text, and in fact their symmetry groups are the same. Note the much smaller value of \(\beta _{\textsc{xiso}}^{ \mathbf {T} }\) here as compared with Fig. 7
For \(\mathbf {T} = \mathbf {T} _{3}\) (Fig. 8) the zero contour of  appears to be a great circle together with its poles, as if the symmetry of \(\mathbf {T}\) were transverse isotropic. In that case, however, the contours of
appears to be a great circle together with its poles, as if the symmetry of \(\mathbf {T}\) were transverse isotropic. In that case, however, the contours of  would all be concentric circles, which they are not. The contours, especially the cigar-shaped contours, are consistent with tetragonal symmetry. In fact, the symmetry group of \(\mathbf {T}\) here is the same as that of the more conspicuously tetragonal \(\mathbf {T} _{2}\) in Fig. 7.
would all be concentric circles, which they are not. The contours, especially the cigar-shaped contours, are consistent with tetragonal symmetry. In fact, the symmetry group of \(\mathbf {T}\) here is the same as that of the more conspicuously tetragonal \(\mathbf {T} _{2}\) in Fig. 7.
A too casual glance at the contour plot in Fig. 8 can thus mischaracterize the exact symmetry group of \(\mathbf {T} _{2}\). We nevertheless think that the contour plot gives a better sense of the overall symmetry of \(\mathbf {T}\) than does the symmetry group of \(\mathbf {T}\) by itself.
The elastic maps \(\mathbf {T} _{2}\) and \(\mathbf {T} _{3}\) are closely related. Their eigenvectors are exactly the same, and their eigenvalues are nearly the same: the eigenvalues of \(\mathbf {T} _{2}\) are \(2,2,3,4,5,6\), and those of \(\mathbf {T} _{3}\) are \(2,2,3,32/10,5,6\). We could have made the contours of  for \(\mathbf {T} = \mathbf {T} _{3}\) look even more nearly transverse isotropic—without changing the symmetry group of \(\mathbf {T} _{3}\)—just by making the fourth eigenvalue of \(\mathbf {T} _{3}\) closer to 3.
for \(\mathbf {T} = \mathbf {T} _{3}\) look even more nearly transverse isotropic—without changing the symmetry group of \(\mathbf {T} _{3}\)—just by making the fourth eigenvalue of \(\mathbf {T} _{3}\) closer to 3.
5 A Computational Complement to the Contour Plots
In this section we show how to find the symmetry groups of elastic maps by calculation, independently of the contour plots of  . Some of the material here appears also in Diner et al. [7].
. Some of the material here appears also in Diner et al. [7].
5.1 The Set \(\boldsymbol {\mathcal {T}} \!_{\Sigma}\) of Elastic Maps with Symmetry at Least \(\mathcal {C} _{\Sigma}\)
For each \(\Sigma =\textsc{triv},\ldots ,\textsc{iso}\), we generalize Eq. (28) by defining the set \(\boldsymbol {\mathcal {T}} \!_{\Sigma}\) to consist of the elastic maps \(\mathbf {T}\) whose symmetry class \(\overline { \mathcal {S} _{ \mathbf {T} }}\) is at least \(\mathcal {C} _{\Sigma}\) (Sect. 2.8):
From Eqs. (43), (19a), (19c), we get another characterization of \(\boldsymbol {\mathcal {T}} \!_{\Sigma}\):
In Appendix A.2 we show that
The inclusions among the sets \(\boldsymbol {\mathcal {T}} _{\!\Sigma}\) are therefore clear from the lattice of symmetry classes (Eq. (20)).
5.2 The \(\Sigma \)-Subspaces \(\boldsymbol {\mathcal {V}} _{\!\Sigma}(U)\)
For \(U\in \mathbb{U} \) we generalize Eqs. (29a), (29b) by defining
Thus \(\boldsymbol {\mathcal {V}} _{\!\Sigma}(U)\) consists of the elastic maps \(\mathbf {T}\) whose symmetry group \(\mathcal {S} _{ \mathbf {T} }\) is at least \(U \mathbb{U} _{\Sigma}U^{\top}\), and \(\mathcal {V} _{\Sigma}(U)\) consists of their matrices.
We refer to the sets \(\boldsymbol {\mathcal {V}} _{\!\Sigma}(U)\) as the \(\Sigma \)-subspaces of the vector space \(\boldsymbol {\mathcal {T}}\). Although they are indeed subspaces, and although \(\boldsymbol {\mathcal {T}} \!_{\Sigma}\) is the union of them, the set \(\boldsymbol {\mathcal {T}} \!_{\Sigma}\) is not itself a subspace, except for \(\Sigma =\textsc{triv}\) and \(\Sigma =\textsc{iso}\). (\(\boldsymbol {\mathcal {T}} \!_{\textsc{triv}}= \boldsymbol {\mathcal {T}} \) and \(\boldsymbol {\mathcal {T}} \!_{\textsc{iso}}= \boldsymbol {\mathcal {V}} _{\textsc{iso}}(I)\).)
The \(\Sigma \)-subspaces \(\boldsymbol {\mathcal {V}} _{\!\Sigma}(U)\) and \(\boldsymbol {\mathcal {V}} _{\!\Sigma}(I)\) are related as follows.
Hence
From Eqs. (46a), (46b) and (17), the \(\Sigma \)-subspace \(\mathcal {V} _{\Sigma}(I)\) consists of the \(6\times 6\) matrices having the form of the reference matrix \(T_{\Sigma}\) in Table 2:
Then from Eq. (48b),
5.3 Distance from \(\mathbf {T}\) to \(\boldsymbol {\mathcal {V}} _{\!\Sigma}(U)\)
If we mimic the derivation of Eqs. (39a), (39b), but now starting from Eq. (48b) rather than from Eq. (37a), we find the distance from an elastic map \(\mathbf {T}\) to the subspace \(\boldsymbol {\mathcal {V}} _{\!\Sigma}(U)\) to be
where the projected matrix \(P(S,\, \mathcal {V} _{\Sigma}(I))\) is now computed using Appendix A.1.
5.4 Distance from \(\mathbf {T}\) to \(\boldsymbol {\mathcal {T}} \!_{\Sigma}\)
From Eq. (47), the distance from \(\mathbf {T}\) to the set \(\boldsymbol {\mathcal {T}} \!_{\Sigma}\) is
with \(d( \mathbf {T} , \boldsymbol {\mathcal {V}} _{\!\Sigma}(U))\) given by Eq. (50). The minimum in Eq. (51) occurs at many different points (i.e., rotation matrices) of \(\mathbb{U}\). We refer to them as \(\Sigma \)-minimizers for \(\mathbf {T}\). Thus,
Equivalently,
To calculate the minimum in Eq. (51) we parameterize \(\mathbb{U}\). Many parameterizations are possible. We usually use the function \((\theta ,\sigma ,\phi )\rightarrow Z_{\theta} Y_{\phi} Z_{\sigma} \).
5.5 The Angle \(\beta _{\Sigma}^{ \mathbf {T} }\) Between \(\mathbf {T}\) and the Set \(\boldsymbol {\mathcal {T}} \!_{\Sigma}\)
We defineFootnote 1 the angle \(\beta _{\Sigma}^{ \mathbf {T} }\) by
where \(d( \mathbf {T} , \boldsymbol {\mathcal {T}} \!_{\Sigma})\) is from Eq. (51). The angle \(\beta _{\Sigma}^{ \mathbf {T} }\) is therefore a measure of how far \(\mathbf {T}\) is from having symmetry class at least \(\mathcal {C} _{\Sigma}\). It is a feasible measure due in part to the fact that \(\boldsymbol {\mathcal {T}} \!_{\Sigma}\) is closed under multiplication by scalars: \(\mathbf {T} \in \boldsymbol {\mathcal {T}} \!_{\Sigma}\Longrightarrow \lambda \mathbf {T} \in \boldsymbol {\mathcal {T}} \!_{\Sigma}\). As a measure, \(\beta _{\Sigma}^{ \mathbf {T} }\) is preferable to the distance \(d( \mathbf {T} , \boldsymbol {\mathcal {T}} \!_{\Sigma})\) in that \(\beta _{\Sigma}^{\lambda \mathbf {T} }=\beta _{\Sigma}^{ \mathbf {T} }\) for \(\lambda \neq 0\). And a small angle, e.g., \({1}^{\circ }\), is more easily perceived as small, than is a small distance.
Since \(d( \mathbf {T} , \boldsymbol {\mathcal {V}} _{\!\Sigma}(U))\le \|{ \mathbf {T} }\| \) (due to Eq. (23)), then \(d( \mathbf {T} , \boldsymbol {\mathcal {T}} \!_{\Sigma})\le \|{ \mathbf {T} }\| \) as well. Hence \(\beta _{\Sigma}^{ \mathbf {T} }\) in Eq. (54) is real, and \(0\le \beta _{\Sigma}^{ \mathbf {T} }\le \pi /2\).
From Eq. (54),
Then from Eq. (43),
As a consequence,
Hence
5.6 Finding the Symmetry Group \(\mathcal {S} _{ \mathbf {T} }\) from the Angles \(\beta _{\Sigma}^{ \mathbf {T} }\) and a Minimizer
The left-hand lattice below is the same as that in Eq. (20) but with each \(\mathcal {C} _{\Sigma}\) replaced with \(\boldsymbol {\mathcal {T}} \!_{\Sigma}\). For a given elastic map \(\mathbf {T}\), the right-hand lattice is again the same, but with \(\beta _{\Sigma}^{ \mathbf {T} }\) instead of \(\mathcal {C} _{\Sigma}\). From Eqs. (45) and (54),
Arrow direction in the lattice therefore indicates (1) increasing symmetry, (2) decreasing size of the sets \(\boldsymbol {\mathcal {T}} \!_{\Sigma}\) of elastic maps, and (3) increasing (rather, non-decreasing) angles \(\beta _{\Sigma}^{ \mathbf {T} }\).

Once the eight numbers \(\beta _{\Sigma}^{ \mathbf {T} }\) have been calculated, including an appropriate minimizer, the symmetry group of \(\mathbf {T}\) will be known. For an example, we consider the elastic map \(\mathbf {T} = \mathbf {T} _{2}\). Its \(\beta _{\Sigma}^{ \mathbf {T} }\)-values were calculated and found to be as in the lattice in Fig. 7.
Since \(\beta _{\textsc{tet}}^{ \mathbf {T} }=0\) then, from Eq. (56a) and from the lattice, the symmetry class \(\overline{ \mathcal {S} _{ \mathbf {T} }}\) of \(\mathbf {T}\) is \(\mathcal {C} _{\textsc{tet}}\), \(\mathcal {C} _{\textsc{xiso,}}\), \(\mathcal {C} _{\textsc{iso}}\), or \(\mathcal {C} _{\textsc{cube}}\). But since \(\beta _{\textsc{xiso}}^{ \mathbf {T} }\), \(\beta _{\textsc{iso}}^{ \mathbf {T} }\), and \(\beta _{\textsc{cube}}^{ \mathbf {T} }\) are positive, then \(\overline{ \mathcal {S} _{ \mathbf {T} }}\) cannot be \(\mathcal {C} _{\textsc{xiso,}}\), \(\mathcal {C} _{\textsc{iso}}\), or \(\mathcal {C} _{\textsc{cube}}\), by Eq. (56b). Hence \(\overline{ \mathcal {S} _{ \mathbf {T} }}= \mathcal {C} _{\textsc{tet}}\).
In finding \(\beta _{\textsc{tet}} ^{ \mathbf {T} }\) (Eqs. 54 and 51 with \(\Sigma =\textsc{tet}\)), we also get a tet-minimizer for \(\mathbf {T}\), namely,
Then \(\mathbf {T} \in \boldsymbol {\mathcal {V}} _{\textsc{tet}}(U)\), from Eq. (58). Hence from Eq. (46a), the symmetry group \(\mathcal {S} _{ \mathbf {T} }\) satisfies
Since \(\overline{ \mathcal {S} _{ \mathbf {T} }}= \mathcal {C} _{\textsc{tet}}\) then \(\mathcal {S} _{ \mathbf {T} }\) is a conjugate of \(\mathbb{U} _{\textsc{tet}}\). But no conjugate of \(\mathbb{U} _{\textsc{tet}}\) can properly contain another, so \(\mathcal {S} _{ \mathbf {T} }= U \mathbb{U} _{\textsc{tet}} U^{\top}\!\).
Thus the lattice of \(\beta _{\Sigma}^{ \mathbf {T} }\)-values determined the symmetry class \(\overline { \mathcal {S} _{ \mathbf {T} }}\), and then a tet-minimizer for \(\mathbf {T}\) determined the symmetry group \(\mathcal {S} _{ \mathbf {T} }\).
To relate the result \(\mathcal {S} _{ \mathbf {T} }= U \mathbb{U} _{\textsc{tet}} U^{\top}\!\) to the contour plot in Fig. 7, let \(\mathbf {i} \), \(\mathbf {j} \), \(\mathbf {k} \) be the standard basis for \(\mathbb{R} ^{3}\). Then \(\mathbf {k} \) is the 4-fold symmetry axis for the group \(\mathbb{U} _{\textsc{tet}}\) (Table 1), and soFootnote 2\(U \mathbf {k} \) is the 4-fold axis for \(U \mathbb{U} _{\textsc{tet}} U^{\top}\!\). Likewise, \(Z_{i\pi /4} \, \mathbf {i} \), \(i=0,1,2,3\), are 2-fold axes for \(\mathbb{U} _{\textsc{tet}}\), and so \(U Z_{i\pi /4} \, \mathbf {i} \) are 2-fold axes for \(U \mathbb{U} _{\textsc{tet}} U^{\top}\!\). In particular, the points \(\mathbf {v} _{1}\) and \(\mathbf {v} _{2}\) in Fig. 7 are
The vectors \(U \mathbf {i} \) and \(U \mathbf {k} \) are of course the first and third columns of \(U\).
Theorem 3
Calculating the symmetry of \(\mathbf {T}\)
Let \(\mathbf {T}\) be an elastic map, and let \(\mathcal {C} _{\Sigma}\) be a greatest symmetry class for which \(\beta _{\Sigma}^{ \mathbf {T} }=0\). Then the symmetry class \(\overline { \mathcal {S} _{ \mathbf {T} }}\) for \(\mathbf {T}\) is \(\mathcal {C} _{\Sigma}\), and the symmetry group \(\mathcal {S} _{ \mathbf {T} }\) is \(U \mathbb{U} _{\Sigma}U^{\top}\!\), where the reference group \(\mathbb{U} _{\Sigma}\) is from Table 1and where \(U\) is any \(\Sigma \)-minimizer for \(\mathbf {T}\) (Eq. (53)). Here “greatest” means greatest with respect to the partial order ≺ (Eq. (19a)): precisely, \(\Sigma \) is chosen so that \(\beta _{\Sigma}^{ \mathbf {T} }=0\), and so that, if \(\mathcal {C} _{\Psi}\succ \mathcal {C} _{\Sigma}\) and \(\mathcal {C} _{\Psi}\neq \mathcal {C} _{\Sigma}\) then \(\beta _{\Psi}^{ \mathbf {T} }>0\).
Proof
The proof is as in the \(\mathbf {T} = \mathbf {T} _{2}\) example that precedes it, but with \(\Sigma \) substituting for tet. One needs the fact that no conjugate of the group \(\mathbb{U} _{\Sigma}\) properly contains another. This fact is trivial when \(\mathbb{U} _{\Sigma}\) is finite, since all conjugates of \(\mathbb{U} _{\Sigma}\) have the same number of members. It is also trivial for \(\Sigma =\textsc{iso}\). The remaining case \(\Sigma =\textsc{xiso}\) is a consequence of Lemma 2 of [15]. □
The code mentioned in the Code Availability section will compute the angles \(\beta _{\Psi}^{ \mathbf {T} }\) and the \(\Sigma \)-minimizer \(U\) that are needed in the theorem.
Note that for a given \(\mathbf {T}\) there can be only one greatest symmetry class for which \(\beta _{\Sigma}^{ \mathbf {T} }=0\), since according to the theorem, that greatest symmetry class must be \(\overline { \mathcal {S} _{ \mathbf {T} }}\).
5.7 Theorem 3 in Practice
From a purely mathematical standpoint, almost all elastic maps have only the trivial symmetry; the set \(\boldsymbol {\mathcal {T}} \!_{\textsc{mono}}\), which includes all elastic maps having non-trivial symmetry, has dimension 15, whereas the set \(\boldsymbol {\mathcal {T}}\) of all elastic maps has dimension 21. It is nevertheless easy to make up elastic maps that have prescribed non-trivial symmetry. For such maps, Theorem 3 will retrieve their symmetry.
The theorem is not so helpful, however, when the elastic map arises empirically, from observation. Whereas the material under consideration might in principle have some non-trivial symmetry, its measured elastic map \(\mathbf {T}\), being subject to uncertainties, is apt to have only trivial symmetry. Trivial symmetry is then what the theorem will report, if the theorem is interpreted to the letter.
One may nevertheless want to examine the lattice of angles \(\beta _{\Psi}^{ \mathbf {T} }\) to see if one of them, say \(\beta _{\Sigma}^{ \mathbf {T} }\), is fairly small, with higher ones being not so small. One might then consider \(\Sigma \) to be an approximate symmetry class for \(\mathbf {T}\).
Formulating a sensible notion of approximate symmetry group for \(\mathbf {T}\), however, is more challenging, and we are not sure how best to do it. An obvious candidate for “the” approximate symmetry group is \(U \mathbb{U} _{\Sigma}U^{\top}\!\), where \(\Sigma \) is the approximate symmetry class and where \(U\) is a \(\Sigma \)-minimizer for \(\mathbf {T}\). This may be good enough for many applications, but one needs to entertain the possibility that \(U \mathbb{U} _{\Sigma}U^{\top}\!\) might not be unique.
Danek et al. [6] discuss determining the approximate symmetry of elastic maps whose matrix entries are given with uncertainties.
6 Afterthoughts
We have now realized our original goal of describing two methods of inferring elastic symmetries; the visual method is summarized in Sect. 4.1, and the quantitative method is summarized in Theorem 3. Some questions may nevertheless remain. We discuss several in this section.
6.1 When \(\boldsymbol {\mathcal {V}} _{\!\Sigma}(U_{1})= \boldsymbol {\mathcal {V}} _{\!\Sigma}(U_{2})\)
A \(\Sigma \)-subspace \(\boldsymbol {\mathcal {V}} _{\!\Sigma}(U)\) can be specified by \(U\), but the label \(U\) is not unique. In this section we see why.
For \(\Sigma =\textsc{triv},\ldots ,\textsc{iso}\),
where \(\mathbb{U} _{\Sigma}\) is the reference group as in Table 1 and where the subgroup \(\mathbb{G} _{\Sigma}\) of \(\mathbb{U}\) is
The group \(\mathbb{D} _{6}\) is the 12-element group generated by \(Z_{\pi /3}\) and \(X_{\pi}\), and \(\mathbb{D} _{8}\) is the 16-element group generated by \(Z_{\pi /4}\) and \(X_{\pi}\).
To verify Eq. (63a) for \(\Sigma =\textsc{orth}\), for example: The 2-fold axes of rotations in the group \(\mathbb{U} _{\textsc{orth}}\) are \(\pm \mathbf {i} \), \(\pm \mathbf {j} \), \(\pm \mathbf {k} \)—the face centers of the unit cube. For any \(V\in \mathbb{U} \) the 2-fold axes of rotations in \(V \mathbb{U} _{\textsc{orth}}V^{\top}\) are therefore \(\pm V \mathbf {i} \), \(\pm V \mathbf {j} \), \(\pm V \mathbf {k} \). The groups \(V \mathbb{U} _{\textsc{orth}}V^{\top}\) and \(\mathbb{U} _{\textsc{orth}}\) coincide when \(V\) maps the set of face centers of the unit cube to itself. That is, they coincide when \(V\in \mathbb{U} _{\textsc{cube}}\).
Theorem 4
\(\boldsymbol {\mathcal {V}} _{\!\Sigma}(U_{1})= \boldsymbol {\mathcal {V}} _{\!\Sigma}(U_{2})\iff U_{2}= U_{1} V\) for some \(V\in \mathbb{G} _{\Sigma}\)
Proof
Suppose \(\boldsymbol {\mathcal {V}} _{\!\Sigma}(U_{1})= \boldsymbol {\mathcal {V}} _{\!\Sigma}(U_{2})\). Since \(U_{1} \mathbb{U} _{\Sigma}U_{1}^{\top}\) is an elastic symmetry group, there is an elastic map \(\mathbf {T}\) such that \(\mathcal {S} _{ \mathbf {T} }=U_{1} \mathbb{U} _{\Sigma}U_{1}^{\top}\). Then \(\mathbf {T} \in \boldsymbol {\mathcal {V}} _{\!\Sigma}(U_{1})= \boldsymbol {\mathcal {V}} _{\!\Sigma}(U_{2})\) and \(\overline { \mathcal {S} _{ \mathbf {T} }}= \mathcal {C} _{\Sigma}\). Then \(U_{2}= U_{1} V\) for some \(V\in \mathbb{G} _{\Sigma}\), by Lemma 1 of Appendix B.
Conversely, suppose \(U_{2}= U_{1} V\) for some \(V\in \mathbb{G} _{\Sigma}\). Then \(\boldsymbol {\mathcal {V}} _{\!\Sigma}(U_{2})= \boldsymbol {\mathcal {V}} _{\!\Sigma}(U_{1} V)= \boldsymbol {\mathcal {V}} _{ \!\Sigma}(U_{1})\), the latter equality from Eqs. (46a) and (63a). □
A minor consequence of Theorem 4 is that the union in Eq. (47), as well as the minimization in Eq. (51), can be taken not over all of \(\mathbb{U}\) but over a smaller subset \(\widehat{ \mathbb{U} }_{\Sigma}\) of \(\mathbb{U}\). The set \(\widehat{ \mathbb{U} }_{\textsc{xiso}}=\widehat{ \mathbb{U} }_{\textsc{mono}}\) turns out to have dimension two rather than three (as for \(\mathbb{U}\)), and \(\widehat{ \mathbb{U} }_{\textsc{iso}}=\widehat{ \mathbb{U} }_{\textsc{triv}}=\{I\}\).
6.2 Closest Members of \(\boldsymbol {\mathcal {T}} _{\!\Sigma}\) to \(\mathbf {T}\)
By comparison with Sect. 4, the closest elastic map in the \(\Sigma \)-subspace \(\boldsymbol {\mathcal {V}} _{\!\Sigma}(U)\) to an elastic map \(\mathbf {T}\) has matrix
(Compare Eq. (64) with Eq. (38), and compare Eq. (48b) with Eq. (37a).)
Theorem 5
For an elastic map \(\mathbf {T}\), the closest members of \(\boldsymbol {\mathcal {T}} _{\!\Sigma}\) to \(\mathbf {T}\) are the projected maps \(P( \mathbf {T} , \boldsymbol {\mathcal {V}} _{\!\Sigma}(U))\) such that \(U\) is a \(\Sigma \)-minimizer for \(\mathbf {T}\). (The matrix of \(P( \mathbf {T} , \boldsymbol {\mathcal {V}} _{\!\Sigma}(U))\) is then as in Eq. (64).)
Proof
Suppose that \(\mathbf {T} _{0}\) is a closest member of \(\boldsymbol {\mathcal {T}} _{\!\Sigma}\) to \(\mathbf {T}\). That is, \(\mathbf {T} _{0}\in \boldsymbol {\mathcal {T}} _{\!\Sigma}\) and
Since \(\mathbf {T} _{0}\in \boldsymbol {\mathcal {T}} _{\!\Sigma}\) then \(\mathbf {T} _{0}\in \boldsymbol {\mathcal {V}} _{\!\Sigma}(U)\) for some \(U\in \mathbb{U} \), by Eq. (47). Since \(\mathbf {T} _{0}\) is then the closest member of the subspace \(\boldsymbol {\mathcal {V}} _{\!\Sigma}(U)\) to \(\mathbf {T}\), then from Sect. 3,
Then \(d( \mathbf {T} , \boldsymbol {\mathcal {V}} _{\!\Sigma}(U))=d( \mathbf {T} , \boldsymbol {\mathcal {T}} \!_{\Sigma})\) from Eqs. (65) and (66), so that \(U\) is a \(\Sigma \)-minimizer for \(\mathbf {T}\) (Eq. (53)).
Conversely, if \(U\) is a \(\Sigma \)-minimizer for \(\mathbf {T}\), then \(d( \mathbf {T} , \boldsymbol {\mathcal {T}} \!_{\Sigma})=d( \mathbf {T} , \boldsymbol {\mathcal {V}} _{\!\Sigma}(U))= d( \mathbf {T} , P( \mathbf {T} , \boldsymbol {\mathcal {V}} _{\!\Sigma}(U)))\), so that \(P( \mathbf {T} , \boldsymbol {\mathcal {V}} _{\!\Sigma}(U))\) is a closest member of \(\boldsymbol {\mathcal {T}} _{\!\Sigma}\) to \(\mathbf {T}\). □
Note that when the symmetry of \(\mathbf {T}\) is at least \(\Sigma \) then the closest member of \(\boldsymbol {\mathcal {T}} _{\!\Sigma}\) to \(\mathbf {T}\) is \(\mathbf {T}\) itself.
For a given elastic map \(\mathbf {T}\) and symmetry \(\Sigma \), Diner et al. [7] define the effective elastic map to be the closest in \(\boldsymbol {\mathcal {T}} _{\!\Sigma}\) (our notation) to \(\mathbf {T}\). (They give some guidance for specifying \(\Sigma \), based on the qualitative behavior of \(\mathbf {T}\).) In Appendix B.4 we show that “the” closest elastic map in \(\boldsymbol {\mathcal {T}} _{\!\Sigma}\) to \(\mathbf {T}\) is not always unique. This takes some of the luster off the otherwise appealing notion of effective elastic map.
6.3 \(\Sigma \)-Reference Matrices for Elastic Maps
Theorem 6
Let \(\mathbf {T}\) be an elastic map, let \(U\in \mathbb{U} \), let \(\Sigma =\textsc{triv},\ldots ,\textsc{iso}\), and let \(T_{\Sigma}\) be as in Table 2. The following four conditions are equivalent:
(The angle \(\beta _{\Sigma}^{ \mathbf {T} }\) is defined in Eq. (54), and the notion of \(\Sigma \)-minimizer is defined in Eq. (52).)
Proof
To show that Eq. (67a) implies Eq. (67b), suppose \(\beta _{\Sigma}^{ \mathbf {T} }=0\) and \(U\) is a \(\Sigma \)-minimizer for \(\mathbf {T}\). Then
as desired. To see the converse, note that \(\boldsymbol {\mathcal {V}} _{\!\Sigma}(U)\subset \boldsymbol {\mathcal {T}} \!_{\Sigma}\), hence the reasoning reverses.
Eqs. (67b) and (67c) are equivalent by Eq. (49b), and Eqs. (67c) and (67d) are obviously equivalent. □
The matrix \(T_{\Sigma}(a,b,\ldots )\) in Eqs. (67c) and (67d) is said to be a \(\Sigma \)-reference matrix for \(\mathbf {T}\).
To illustrate Theorem 6, we find tet-reference matrices for the elastic map \(\mathbf {T} = \mathbf {T} _{2}\) (Fig. 7). Recall from the discussion preceding Theorem 3 that \(\beta _{\textsc{tet}}^{ \mathbf {T} }=0\) and that the matrix \(U\) in Eq. (60) is a tet-minimizer for \(\mathbf {T}\). From Eq. (53) and Theorem 4:
Although there are 16 such minimizers \(U V\), they give rise to only two distinct tet-reference matrices \(T_{\Sigma}^{1}\) and \(T_{\Sigma}^{2}\) for \(\mathbf {T}\). Letting \(U_{1}=U\) and \(U_{2}=U Z_{\pi /4} \), we have, from Eq. (67d),
Eq. (71) of Appendix B.3 guarantees that Eq. (68) gives all the tet-minimizers for \(\mathbf {T}\) and hence that \(T_{\Sigma}^{1}\) and \(T_{\Sigma}^{2}\) are the only tet-reference matrices for \(\mathbf {T}\). There will, however, be \(\Sigma \)-reference matrices for \(\mathbf {T}\) for \(\Sigma\) = orth and \(\Sigma\) = mono (and trivially for \(\Sigma\) = triv), since \(\beta _{\textsc{orth}}^{ \mathbf {T} }=\beta _{\textsc{mono}}^{ \mathbf {T} }=\beta _{\textsc{triv}}^{ \mathbf {T} }=0\).
6.4 Some History
Equation (69a) (for example) says that if the material in question is reoriented using \(U_{1}^{\top}\) then the matrix of its elastic map takes the form \(T_{\Sigma}^{1}\). Until fairly recently, finding \(U_{1}\) from \(\mathbf {T} = \mathbf {T} _{2}\) (and hence finding \(T_{\Sigma}^{1}\)) would have been tantamount (in a small circle of enthusiasts) to finding the Holy Grail, since Eq. (67c) would then imply that the symmetry group of \(\mathbf {T}\) was at least \(U_{1} \mathbb{U} _{\textsc{tet}} U_{1}^{\top}\!\). Thus Chapman [5, p. 131] wrote in 2004:
Interpreting general anisotropic elastic parameters is difficult. If all 21 parameters are non-zero, is the medium in fact one with a high-order of symmetry, e.g. TI, but with tilted axes …? In other words, would a simple rotation reduce the number of non-zero parametersFootnote 3 significantly?
More precisely, for a given \(\mathbf {T}\) and \(\Sigma \), is there a rotation \(U\) satisfying Eq. (67d), and if so, how does one find it?
By 2007 Bóna et al. [4] had made impressive headway in responding. We ourselves [15] treated the question in 2021. Neither our method nor theirs, however, can handle every elastic map, and both methods are slow, since they require some thought and are not easily automated. Now, however, the angle \(\beta _{\Sigma}^{ \mathbf {T} }\) and a \(\Sigma \)-minimizer \(U\) for \(\mathbf {T}\) are readily found from \(\mathbf {T}\), using Eqs. (54) and (52). Theorem 6 thus gives a completeFootnote 4 answer to Chapman’s questions: If \(\beta _{\Sigma}^{ \mathbf {T} }=0\), then \(U\) can serve as the desired rotation. If \(\beta _{\Sigma}^{ \mathbf {T} }>0\), then no such rotation exists (for the specified \(\Sigma \) and \(\mathbf {T}\)).
We included Theorem 6 in part for historical reasons. For finding symmetry groups of elastic maps, we still recommend Theorem 3.
7 Summary
An elastic map \(\mathbf {T}\) describes the strain-stress relation at a particular point \(\mathbf {p}\) in a material. A symmetry of \(\mathbf {T}\) is a rotation of the material, about \(\mathbf {p}\), that does not change \(\mathbf {T}\).
For a point \(\mathbf {v}\) on the unit sphere, the number  is the distance from \(\mathbf {T}\) to the space of elastic maps having \(\mathbf {v}\) as a 2-fold symmetry axis. The function
is the distance from \(\mathbf {T}\) to the space of elastic maps having \(\mathbf {v}\) as a 2-fold symmetry axis. The function  is invariant under all of the symmetries of \(\mathbf {T}\), so the symmetries are visible in a contour plot of
is invariant under all of the symmetries of \(\mathbf {T}\), so the symmetries are visible in a contour plot of  . In fact, the zero contour alone reveals the symmetry group \(\mathcal {S} _{ \mathbf {T} }\) of \(\mathbf {T}\), and information about the approximate symmetry of \(\mathbf {T}\) is seen in the contour plot as a whole. The function
. In fact, the zero contour alone reveals the symmetry group \(\mathcal {S} _{ \mathbf {T} }\) of \(\mathbf {T}\), and information about the approximate symmetry of \(\mathbf {T}\) is seen in the contour plot as a whole. The function  is calculated using Theorem 1.
is calculated using Theorem 1.
To complement the visual approach of the contour plots, we treat elastic symmetry quantitatively, in Sect. 5. For an elastic map \(\mathbf {T}\) and for \(\Sigma =\textsc{triv},\ldots , \textsc{iso}\), the angle \(\beta _{\Sigma}^{ \mathbf {T} }\) (Eq. (54)) is a measure of how far \(\mathbf {T}\) is from having symmetry class at least \(\mathcal {C} _{\Sigma}\). The lattice of the eight angles \(\beta _{\Sigma}^{ \mathbf {T} }\) determines the symmetry class \(\overline { \mathcal {S} _{ \mathbf {T} }}\) of \(\mathbf {T}\), and the lattice and an appropriate \(\Sigma \)-minimizer for \(\mathbf {T}\) (Eq. (52)) determine the symmetry group \(\mathcal {S} _{ \mathbf {T} }\). The angles \(\beta _{\Sigma}^{ \mathbf {T} }\) as well as \(\Sigma \)-minimizers for \(\mathbf {T}\) can be computed using the code mentioned in the Code Availability section. Theorem 3 then gives \(\mathcal {S} _{ \mathbf {T} }\) immediately.
In practice, where an elastic map \(\mathbf {T}\) arises from observations rather than being constructed mathematically, its symmetry group \(\mathcal {S} _{ \mathbf {T} }\) by itself is not helpful; random errors in the observations mean that the exact symmetry group can never be anything but trivial. Section 5.7 has some thoughts on the notion of an approximate symmetry group. Whether or not that notion turns out to be viable, the approximate symmetry of \(\mathbf {T}\) is well expressed by the contour plot of  , the lattice of angles \(\beta _{\Sigma}^{ \mathbf {T} }\), and \(\Sigma \)-minimizers for \(\mathbf {T}\).
, the lattice of angles \(\beta _{\Sigma}^{ \mathbf {T} }\), and \(\Sigma \)-minimizers for \(\mathbf {T}\).
Code Availability
Code for drawing contour plots of  and for finding the symmetry group of any elastic map is available at https://github.com/carltape/mtbeach.
and for finding the symmetry group of any elastic map is available at https://github.com/carltape/mtbeach.
The file names are ES_ContourPlots.nb and ES_FindSymGroups.nb
Notes
Temporarily letting \(\mathbf {T} _{0}\) denote the zero elastic map, we note that it is not possible to define \(\beta _{\Sigma}^{ \mathbf {T} _{0}}\) so that the function \(\mathbf {T} \rightarrow \beta _{\Sigma}^{ \mathbf {T} }\) is continuous at \(\mathbf {T} _{0}\). Our later results involving \(\beta _{\Sigma}^{ \mathbf {T} }\) are assumed, without further mention, to exclude the case \(\mathbf {T} = \mathbf {T} _{0}\).
We treat members of \(\mathbb{R} ^{3}\) as column vectors when matrix multiplication is involved, but we continue to write them as row vectors.
The emphasis on the number of non-zero entries is misguided. More zero entries does not guarantee more symmetry.
Conceivably there are elastic maps so perverse that the needed minimization in Eq. (51) would defeat the mathematical software, but we have yet to encounter one.
Our analog of \(C^{\text{trigo}}\) of Diner et al. is \(P(T, \mathcal {V} _{\textsc{trig}}(U))\) with \(U= Z_{\pi /2} \), not \(U=I\).
References
Aki, K., Richards, P.G.: Quantitative Seismology, 2nd edn. University Science Books, San Francisco, Calif., USA (2002). 2009 corrected printing
Backus, G.: A geometrical picture of anisotropic elastic tensors. Rev. Geophys. Space Phys. 8(3), 633–671 (1970)
Baerheim, R.: Classification of symmetry by means of Maxwell multipoles. Q. J. Mech. Appl. Math. 51, 73–103 (1998)
Bóna, A., Bucataru, I., Slawinski, M.A.: Coordinate-free characterization of the symmetry classes of elastic tensors. J. Elast. 87, 109–132 (2007)
Chapman, C.H.: Fundamentals of Seismic Wave Propagation. Cambridge University Press, Cambridge, United Kingdom (2004)
Danek, T., Kochetov, M., Slawinski, M.A.: Effective elasticity tensors in context of random errors. J. Elast. 121, 55–67 (2015)
Diner, Ç., Kochetov, M., Slawinski, M.A.: On choosing effective symmetry classes for elasticity tensors. Q. J. Mech. Appl. Math. 64(1), 57–74 (2010)
Diner, Ç., Kochetov, M., Slawinski, M.A.: Identifying symmetry classes of elasticity tensors using monoclinic distance function. J. Elast. 102, 175–190 (2011)
Forte, S., Vianello, M.: Symmetry classes for elasticity tensors. J. Elast. 43, 81–108 (1996)
François, M., Geymonat, G., Berthaud, Y.: Determination of the symmetries of an experimentally determined stiffness tensor: application to acoustic measurements. Int. J. Solids Struct. 35(31–32), 4091–4106 (1998)
Helbig, K.: Foundations of Anisotropy for Exploration Scientists. Pergamon, Elmsford (1994)
Nye, J.: Physical Properties of Crystals. Oxford University Press, Oxford (1957, 1985)
Olive, M., Kolev, B., Desmorat, R., Desmorat, B.: Characterization of the symmetry class of an elasticity tensor using polynomial covariants. Math. Mech. Solids 27(1), 144–190 (2022). https://doi.org/10.1177/10812865211010885
Slawinski, M.A.: Waves and Rays in Elastic Continua, 3rd edn. World Scientific, Singapore (2015)
Tape, W., Tape, C.: Elastic symmetry with beachball pictures. Geophys. J. Int. 227, 970–1003 (2021). https://doi.org/10.1093/gji/ggab183
Acknowledgements
We thank two anonymous reviewers for helpful reviews.
Funding
C. Tape was supported by National Science Foundation grant EAR 1829447.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Supplement for Sect. 5
1.1 A.1 The Projected Matrices \(P(T, \mathcal {V} _{\Sigma}(I))\)
The subspace \(\mathcal {V} _{\Sigma}(I)\) consists of the \(6\times 6\) matrices having the form of the reference matrix \(T_{\Sigma}\) in Table 2; see Eq. (49a). One verifies Eqs. (70a)–(70h), below, as was done for \(P(T, \mathcal {V} _{\textsc{mono}}(I))\) in Eqs. (33)–(36).
For \(T\) as in Eq. (32) the projection of \(T\) onto \(\mathcal {V} _{\Sigma}(I)\) is








The matrices \(P(T, \mathcal {V} _{\Sigma}(I))\) in Eqs. (70b)–(70g) are the analogs of the matrices \(C^{\Sigma}\) in Sect. 4.2 of Diner et al. [7]. Our matrices are simpler due to the fact that our matrix representations of elastic maps are with respect to the basis \(\mathbb{B}\) in Eq. (1). (The Diner et al. matrices are with respect to the basis \(\Phi \) in Eq. (S23) of [15] .) The Diner et al. matrices in their Sect. 4.2 are consistent with ours,Footnote 5 with the exception of their \(C^{\text{TI}}\) (their Eq. (4.10)). Our disagreement also applies to their matrix \(({\tilde{X}_{0}}^{\top}C \tilde{X}_{0})^{\text{TI}}\) in their Sect. 5.3.
1.2 A.2 Proof That \(\boldsymbol {\mathcal {T}} _{\!\Sigma _{1}}\subset \boldsymbol {\mathcal {T}} _{\!\Sigma _{2}}\iff \mathcal {C} _{\Sigma _{1}}\succ \mathcal {C} _{\Sigma _{2}}\) (Eq. 45)
Suppose \(\boldsymbol {\mathcal {T}} _{\!\Sigma _{1}}\subset \boldsymbol {\mathcal {T}} _{\!\Sigma _{2}}\). Since \(\mathbb{U} _{\Sigma _{1}}\) is an elastic symmetry group, there is an elastic map \(\mathbf {T}\) such that \(\mathcal {S} _{ \mathbf {T} }= \mathbb{U} _{\Sigma _{1}}\). Then
Hence \(\boldsymbol {\mathcal {T}} _{\!\Sigma _{1}}\subset \boldsymbol {\mathcal {T}} _{\!\Sigma _{2}}\Longrightarrow \mathcal {C} _{\Sigma _{1}}\succ \mathcal {C} _{\Sigma _{2}}\). The converse is immediate from the definition of \(\boldsymbol {\mathcal {T}} _{\!\Sigma}\) (Eq. (43)).
Appendix B: Supplement for Sect. 6
Lemma 1
Let \(\overline { \mathcal {S} _{ \mathbf {T} }}= \mathcal {C} _{\Sigma}\) and \(\mathbf {T} \in \boldsymbol {\mathcal {V}} _{\!\Sigma}(U_{1})\cap \boldsymbol {\mathcal {V}} _{\!\Sigma}(U_{2})\). Then \(U_{2}= U_{1} V\) for some \(V\in \mathbb{G} _{\Sigma}\).
Proof
For \(i=1,2\),
The fourth step is due to the fact that no conjugate of \(\mathbb{U} _{\Sigma}\) can properly contain another. □
2.1 B.3 Number of \(\Sigma \)-Minimizers for \(\mathbf {T}\)
We let \(N_{\Sigma}^{ \mathbf {T} }\) be the number of \(\Sigma \)-minimizers for the elastic map \(\mathbf {T}\). Equations (52), (53), and Theorem 4 give \(N_{\Sigma}^{ \mathbf {T} }\ge | \mathbb{G} _{\Sigma}|\), where \(| \mathbb{G} _{\Sigma}|\) is the number of elements of \(\mathbb{G} _{\Sigma}\).
If the symmetry of \(\mathbf {T}\) is exactly \(\Sigma \) and if \(U_{1}\) and \(U_{2}\) are \(\Sigma \)-minimizers for \(\mathbf {T}\), then \(\mathbf {T} \in \boldsymbol {\mathcal {V}} _{\!\Sigma}(U_{1})\cap \boldsymbol {\mathcal {V}} _{\!\Sigma}(U_{2})\), by Theorem 6, and then \(U_{2}= U_{1} V\) for some \(V\in \mathbb{G} _{\Sigma}\), by Lemma 1. Thus \(N_{\Sigma}^{ \mathbf {T} }\le | \mathbb{G} _{\Sigma}|\), so that in fact
The assumption \(\overline { \mathcal {S} _{ \mathbf {T} }}= \mathcal {C} _{\Sigma}\) in Eq. (71) matters. The monoclinic map \(\mathbf {T}\) in Eq. (72), for example, has \(N_{\textsc{orth}}^{ \mathbf {T} }=48\), whereas \(| \mathbb{G} _{\textsc{orth}}|=24\). The orth-minimizers are \(Z_{t} V\), where \(t=\pm \pi /12\) and \(V\in \mathbb{U} _{\textsc{cube}}\).
2.2 B.4 An Elastic Map and Two Distinct Elastic Maps That Are Closest Orthorhombic Maps to It
Let \(\mathbf {T}\) be the monoclinic elastic map whose matrix is
For \(U_{1}= Z_{\pi /12} \) and \(U_{2}=U_{1}^{\top}\) we have, from Eq. (64),
Then
The first two equalities are from Eqs. (72) and (73), and the last equality is from Eq. (51). Thus both \(P( \mathbf {T} , \boldsymbol {\mathcal {V}} _{\!\textsc{orth}}(U_{1}))\) and \(P( \mathbf {T} , \boldsymbol {\mathcal {V}} _{\!\textsc{orth}}(U_{2}))\) are closest elastic maps in \(\boldsymbol {\mathcal {T}} \!_{\textsc{orth}}\) to \(\mathbf {T}\), but they are not the same.
Appendix C: Definition of the Elastic Maps \(\mathbf {T} _{1}\), \(\mathbf {T} _{2}\), \(\mathbf {T} _{3}\)
The elastic maps \(\mathbf {T} _{1}\), \(\mathbf {T} _{2}\), \(\mathbf {T} _{3}\) in Figs. 6, 7, 8 are defined via their matrices:
The map \(\mathbf {T} _{1}\) is the same as the elastic map \(\mathbf {T} '\) whose symmetries were found in Sect. 15.4 of [15], and \(\mathbf {T} _{2}\) is the same as \(\mathbf {T} '\) whose symmetries were found in Sect. 15.3. The method of finding symmetries in [15] can therefore be compared with the two methods of the present paper.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Tape, W., Tape, C. Two Complementary Methods of Inferring Elastic Symmetry. J Elast 150, 91–118 (2022). https://doi.org/10.1007/s10659-022-09898-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10659-022-09898-0


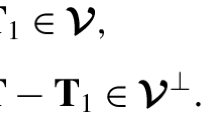



 Expresses the Symmetry Group of
Expresses the Symmetry Group of 





