1 Introduction

Nematic elastic rods are slender, flexible structures made of liquid crystal elastomers (LCEs) [35, 48, 65, 71, 72]. Due to their stimuli-responsive material properties, they can convert light or heat into mechanical work, without the need for batteries, electric wires or gears [58, 67].

Rods are filamentary structures capable of two main reversible deformations causing large displacements, namely, bending and twist. Classically, they are modeled as long, thin elastic bodies defined by a central curve and acted upon by external loads [3, 24, 36, 50]. An extension to anelastic rods where non-elastic deformations and changes in microstructure occur was considered in [19]. A generic one-dimensional strain energy for rod models derived from large-strain finite elasticity was recently proposed in [4] where many related models were also reviewed.

For a nematic rod, significant displacements can be achieved by natural deformations caused by external stimuli. A fundamental problem is then to establish how such spontaneous deformation may lead to the generation of curvatures. Experimental observations for nematic elastomer rods that bend upon exposure to UV light were reported in [35, 72]. Rods with an in-printed helical director field under a remotely controlled rotation were presented in [48]. Light-controlled bending and twisting of nematic rods were investigated in [65, 71]. Theoretically, three-dimensional nematic cylinders under combined stretch and torsion were analyzed in [17], and a nonlinear beam model for photoresponsive structures was proposed in [30].

Light-induced shape changes in nematic solids containing photoisomerizing dye molecules (namely, azobenzene mesogens) were first reported in [16], then [73]. In these materials, when photons are absorbed, the dye molecules change from straight trans- to bent cis-isomers. This so-called Weigert’s effect mechanism [15, 29] then causes a reduction in the nematic order. The strong dependence of photoresponses on the light polarization in aligned monodomain and randomly disordered polydomain nematic elastomers was demonstrated in [26]. Experimental studies showing a range of mechanical behaviors caused by the light intensity, polarization and wavelength have been reviewed, for example, in [1, 10, 28, 31, 38, 52, 55, 57, 59, 66, 68–70].

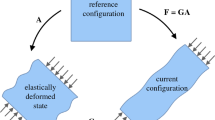
For ideal monodomain nematic elastomers, with the liquid crystal mesogens uniaxially aligned throughout the material, a simple continuum model is provided by the neoclassical strain-energy function proposed in [5, 62, 63]. This is a phenomenological model based on the molecular network theory of rubber [54]. The constitutive parameters appearing in the neo-Hookean-type strain energy can be obtained through statistical averaging at microscopic scale or derived from macroscopic shape changes at small strain [60, 61]. Here, we adopt the neoclassical strain-energy function, and assume the isotropic phase at high temperature as the reference configuration [8, 11–14], instead of the cross-linking nematic phase [2, 5, 56, 62–64, 74]. We exploit theoretically the multiplicative decomposition of the deformation gradient from the reference configuration to the current configuration into an elastic distortion followed by a natural shape change [20, 41–44]. This multiplicative decomposition is similar to those found in the constitutive theories of thermoelasticity, elastoplasticity, and morphoelasticity [19, 37] (see [18, 53] as well), but it is also different in the sense that the stress-free geometric change is superposed on the elastic deformation, which is directly applied to the reference state.

We consider the macroscopic deformation of a nematic rod as the product of a spontaneous deformation inducing curvatures and a finite elastic deformation preserving cylindrical symmetry. We are interested in answering the following main questions:

  1. (i)

    If the shape of a filamentary nematic elastomer structure is known, what is the internal nematic stretch field created by an external stimulus?

  2. (ii)

    Given the local nematic stretch field of a filamentary structure under a stimulus, what are the intrinsic curvatures and what is the shape of a rod subject to external loads and boundary constraint?

As we show, these questions are particularly difficult to resolve since a change of shape also changes the position of the rod with respect to its stimulus. In particular cases, we can decouple the two problems but in general, the two questions cannot be answered in isolation. Our approach consists in reducing the three-dimensional (3D) strain-energy density function of a nematic cylindrical structure to the one-dimensional (1D) energy of a nematic rod. To achieve this, we adapt the strategy developed for morphoelastic rods in [46] (see also [34, 45, 47, 49]), and apply the resulting model to specific scenarios leading to the formation of rods with non-trivial intrinsic curvatures. In particular, we consider rods with square or circular cross-section, and a nematic director uniformly aligned at a given angle relative to the longitudinal axis [65, 71], or a helical director field [48]. In Sect. 2, the 3D neoclassical strain-energy function for ideal nematic elastomers is briefly reviewed. The 1D nematic rod model is derived in Sect. 3. Examples of light-induced deformations are presented in Sect. 4.

2 A Continuum Model for Ideal Nematic Elastomers

To describe an ideal nematic LCE, we assume the following strain-energy density function [20, 40–44],

$$ W^{(nc)}(\textbf{F},\textbf{n})=W(\textbf{A}), $$
(1)

where \(\textbf{F}\) represents the deformation gradient from the isotropic state, \(\textbf{n}\) is a unit vector, known as the director, for the orientation of the nematic field, and \(W(\textbf{A})\) denotes the strain-energy density of the isotropic polymer network, depending only on the (local) elastic deformation tensor \(\textbf{A}\). The tensors \(\textbf{F}\) and \(\textbf{A}\) are related through the identity

$$ \textbf{F}=\textbf{G}\textbf{A}, $$
(2)

where

$$ \textbf{G}=a^{-1/6}\textbf{I}+\left (a^{1/3}-a^{-1/6}\right )\textbf{n} \otimes \textbf{n}, $$
(3)

is the ‘spontaneous’ deformation tensor defining a change of frame of reference from the isotropic phase to a nematic phase. Here, we assume the existence of an isotropic phase that can be reached from a suitably imprinted defect field in the original fabrication process. The exact conditions under which such an intermediary configuration can be mapped to a stress-free reference configuration that is isotropic has been discussed in the general framework of anelasticity in [18]. In (3), \(a>0\) represents a temperature-dependent stretch parameter, ⊗ denotes the tensor product of two vectors, and \(\textbf{I}=\text{diag}(1,1,1)\) is the second-order identity tensor.

3 The Nematic Rod Model

Our goal is to devise a 1D model for a slender nematic solid which is sufficiently long and thin so that it can be approximated by a rod equation. For the derivation of the constitutive equations applicable to nematic rods, we rely on the following conditions assumed a priori:

  1. (R1)

    For the undeformed 3D structure, the dimension in one direction (the axial length) is much larger than in the orthogonal directions (the cross-sectional length scales);

  2. (R2)

    Any curvature-inducing deformation is of the same order of magnitude as the aspect ratio between the cross-sectional dimensions and the axial length.

These kinematic assumptions from the classic rod theory [32] are appropriate for filamentary nematic solids, and allow to reduce the dimensionality of the problem, which can be useful in analytical treatments and numerical simulations. Henceforth, we proceed in a similar manner as in [46] where morphoelastic rods were modeled. Apart from the different order of the multiplicative decomposition between elastic growth and LCE theories, we also bear in mind that, unlike in morphoelasticity, the natural deformation tensor for LCEs is always symmetric, i.e., \(\textbf{G}=\textbf{G}^{T}\), where \(T\) denotes the transpose operator, and this tensor changes if the nematic director rotates. In addition, as LCEs are generally incompressible, their deformations are isochoric, and in particular, \(\det \textbf{G}=1\).

3.1 Model Reduction

We consider a circular cylinder occupying a domain \(\Omega =\mathcal{S}\times [0,L]\in \mathbb{R}^{3}\) in the reference configuration, with Cartesian coordinates \(\left (X,Y,Z\right )\in \Omega \), where

$$ \mathcal{S}(Z)=\left \{ (X,Y)\ \left |\ \int _{\mathcal{S}(Z)}X \text{d}X=\int _{\mathcal{S}(Z)}Y\text{d}Y=\int _{\mathcal{S}(Z)}XY \text{d}X\text{d}Y=0\right .\right \} ,\qquad Z\in [0,L], $$
(4)

are cross-sections with centroids at \(Z\in [0,L]\). In a Cartesian coordinate system, each material point \(\left (X,Y,Z\right )\in \Omega \) is identified with its position given by the vector \(X\textbf{e}_{1}+Y\textbf{e}_{2}+Z\textbf{e}_{3}\), where \((\textbf{e}_{1},\textbf{e}_{2},\textbf{e}_{3})\) is the usual right-handed orthonormal basis.

We assume that the typical length scale \(\ell (Z)\) of every individual cross-section divided by the rod’s length \(L\) is of order \(\mathcal{O}(\varepsilon )\), where \(0<\varepsilon \ll 1\), and that its shape is a slowly varying function of \(Z\), so that, locally, the structure is cylindrical. We define the scaled section

$$ \mathsf{S}(Z)=\left \{ (x,y)\ \left | \ X=\varepsilon x,\ Y= \varepsilon y,\ (X,Y)\in \mathcal{S}(Z) \right .\right \} . $$
(5)

The potential energy takes the form

$$ E=\varepsilon ^{2}\int _{0}^{L}\left \{ \int _{\mathsf{S}(Z)}\left [W \left (\textbf{A}\right )-p\left (\det \textbf{A}-1\right )\right ] \text{d}x\text{d}y\right \} \text{d}Z, $$
(6)

where \(W(\textbf{A})\) is the elastic strain-energy function on which the nematic strain energy \(W^{(nc)}(\textbf{F},\textbf{n})\) is based, and \(p\left (\det \textbf{A}-1\right )\) enforces the incompressibility condition \(\det \textbf{A}=1\).

We analyze deformations that map a right circular cylinder, with the longitudinal axis (centerline) in the \(Z\)-direction, to a filamentary body with the centerline \(\textbf{r}(Z)\), and set a local director basis \((\textbf{d}_{1}(Z),\textbf{d}_{2}(Z),\textbf{d}_{3}(Z))\), such that \(\textbf{r}'(Z)=\left (1+\varepsilon \xi \right )\textbf{d}_{3}(Z)\), where ′ denotes differentiation with respect to \(Z\), and \(\xi \) is the small axial (longitudinal) strain. We define the Darboux curvature vector

$$ \textbf{u}={\mathsf{u}}_{1}\textbf{d}_{1}+{\mathsf{u}}_{2}\textbf{d}_{2}+{ \mathsf{u}}_{3}\textbf{d}_{3}, $$
(7)

to describe the evolution of the director basis along the filament, satisfying

$$ \textbf{d}_{i}'(Z)=\left (1+\varepsilon \xi \right )\textbf{u}\times \textbf{d}_{i},\qquad i=1,2,3, $$
(8)

where × is the usual vector product.

A finite elastic deformation of the cylindrical body from the reference configuration \(\mathcal{B}_{0}\) to the current configuration ℬ is then described in terms of its centerline and director basis by the following one-to-one, orientation-preserving mapping \(\boldsymbol{\chi }\colon \Omega \to \mathbb{R}^{3}\),

$$ \boldsymbol{\chi }(X,Y,Z)=\textbf{r}(Z)+\sum _{i=1}^{3}\rho _{i}(X,Y,Z) \textbf{d}_{i}(Z), $$
(9)

where \(\rho _{i}=\rho _{i}(X,Y,Z)\), \(i=1,2,3\), are functions to be determined that describe the local deformation of each cross-section. Each of these functions satisfies the condition \(\rho _{i}(0,0,Z)=0\), so that the \(Z\)-axis is mapped to the centerline \(\textbf{r}(Z)\). Taking into account the small cross-sectional length scales, we denote \(\rho _{i}=\varepsilon \alpha _{i}\), \(i=1,2,3\).

The corresponding deformation gradient tensor takes the form

$$ \textbf{F}=F_{ij}\ \textbf{d}_{i}\otimes \textbf{e}_{j}= \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \alpha _{1x} & \alpha _{1y} & \varepsilon \left (1+\varepsilon \xi \right )\left ({\mathsf{u}}_{2}\alpha _{3}-{\mathsf{u}}_{3}\alpha _{2} \right ) \\ \alpha _{2x} & \alpha _{2y} & \varepsilon \left (1+\varepsilon \xi \right )\left ({\mathsf{u}}_{3}\alpha _{1}-{\mathsf{u}}_{1}\alpha _{3} \right ) \\ \alpha _{3x} & \alpha _{3y} &\left (1+\varepsilon \xi \right )\left [1+ \varepsilon \left ({\mathsf{u}}_{1}\alpha _{2}-{\mathsf{u}}_{2} \alpha _{1}\right )\right ] \end{array}\displaystyle \right ], $$
(10)

where the indices \(x\) and \(y\) denote the derivatives with respect to \(x\) and \(y\), respectively.

As the rod is slender, we assume a spontaneous deformation tensor of the form

$$ \textbf{G}=\textbf{I}+\varepsilon \textbf{g}, $$
(11)

where \(\textbf{g}\) is an incremental remodeling tensor that may induce curvature, twist, or torsion. We recall that, for a straight rod in torsional deformation, each transverse cross-section is rotated by some angle while the longitudinal axis remains straight, so that the generators on the sides of the rod, which are initially parallel to the axis, become helical.

By writing the Taylor expansions:

$$\begin{aligned} &\alpha _{i}\approx \alpha _{i}^{(0)}+\varepsilon \alpha _{i}^{(1)}+ \cdots ,\qquad i=1,2,3, \end{aligned}$$
(12)
$$\begin{aligned} &p\approx p^{(0)}+\varepsilon p^{(1)}+\cdots , \end{aligned}$$
(13)

and denoting

$$ V(\alpha _{1},\alpha _{2},\alpha _{3},p)=W\left (\textbf{A}\right )-p \left (\det \textbf{A}-1\right ), $$
(14)

we have the approximation

$$\begin{aligned} V(\alpha _{1},\alpha _{2},\alpha _{3},p)&\approx V_{0}\left (\alpha ^{(0)}_{1}, \alpha ^{(0)}_{2},\alpha ^{(0)}_{3},p^{(0)}\right ) \\ &\quad {}+V_{1}\left ( \alpha ^{(0)}_{1},\alpha ^{(0)}_{2},\alpha ^{(0)}_{3},p^{(0)},\alpha ^{(1)}_{1}, \alpha ^{(1)}_{2},\alpha ^{(1)}_{3},p^{(1)}\right )+\cdots . \end{aligned}$$
(15)

The potential energy is then written as follows,

$$ \mathcal{E}\approx \varepsilon ^{2} \mathcal{E}_{0}+\varepsilon ^{3} \mathcal{E}_{1}+\cdots , $$
(16)

where

$$ \mathcal{E}_{k}=\int _{0}^{L}\left (\int _{\mathsf{S}(Z)}\!\!V_{k}\, \text{d}x\text{d}y\right )\text{d}Z,\qquad k=0,1,\ldots , $$
(17)

with \(V_{k}=V_{k}\left (\alpha ^{(0)}_{1},\alpha ^{(0)}_{2},\alpha ^{(0)}_{3},p^{(0)}, \ldots ,\alpha ^{(k)}_{1},\alpha ^{(k)}_{2},\alpha ^{(k)}_{3},p^{(k)} \right )\).

3.2 Equilibrium Equations

On each cross-section \(\mathsf{S}(Z)\), we define a sequence of minimization problems for the functionals

$$ \mathcal{F}_{k}=\int _{\mathsf{S}(Z)}V_{k}\text{d}x\text{d}y, \qquad k=0,1, \ldots . $$
(18)

The associated Euler-Lagrange equations take the form:

$$\begin{aligned} &\frac{\partial ^{2} V_{l}}{\partial x\partial \alpha ^{(k)}_{jx}}+ \frac{\partial ^{2} V_{l}}{\partial y\partial \alpha ^{(k)}_{jy}}- \frac{\partial V_{l}}{\partial \alpha ^{(k)}_{j}}=0,\qquad j=1,2,3, \end{aligned}$$
(19)
$$\begin{aligned} &\frac{\partial ^{2} V_{l}}{\partial x\partial p^{(k)}_{x}}+ \frac{\partial ^{2} V_{l}}{\partial y\partial p^{(k)}_{y}}- \frac{\partial V_{l}}{\partial p^{(k)}}=0, \end{aligned}$$
(20)

with the natural boundary conditions:

$$\begin{aligned} &\widetilde{n}_{1}\frac{\partial V_{l}}{\partial \alpha ^{(k)}_{jx}}+ \widetilde{n}_{2}\frac{\partial V_{l}}{\partial \alpha ^{(k)}_{jy}}=0, \qquad j=1,2,3, \end{aligned}$$
(21)
$$\begin{aligned} &\widetilde{n}_{1}\frac{\partial V_{l}}{\partial p^{(k)}_{x}}+ \widetilde{n}_{2}\frac{\partial V_{l}}{\partial p^{(k)}_{y}}=0, \end{aligned}$$
(22)

where \(\widetilde{\textbf{n}}=[\widetilde{n}_{1},\widetilde{n}_{2}]^{T}\) is the outward unit normal vector to the boundary of \(\mathsf{S}(Z)\). In these equations, at each order \(\varepsilon ^{l}\), the choice of \(k\leq l\) will depend on the solution at previous order.

We note that the above system of equations is linear in \(\alpha _{1}^{(k)}\), \(\alpha _{2}^{(k)}\), \(\alpha _{3}^{(k)}\), and \(p^{(k)}\), for any given strain-energy density \(W(\textbf{A})\) and spontaneous deformation tensor \(\textbf{G}\). For \(l = 1\), the equations are automatically satisfied, hence, \(\alpha _{1}^{(1)}\), \(\alpha _{2}^{(1)}\), \(\alpha _{3}^{(1)}\), and \(p^{(1)}\) are only solved at order \(\varepsilon ^{2}\). These variables take a form similar to the ones given in [46] and lead to the potential energy

$$ \mathcal{E}\approx \varepsilon ^{4}\int _{0}^{L}\left (\int _{ \mathsf{S}(Z)}V_{2}\text{d}x\text{d}y\right )\text{d}Z+\mathcal{O}( \varepsilon ^{5}), $$
(23)

where \(V_{2}=V_{2}\left (\alpha ^{(0)}_{1},\alpha ^{(0)}_{2},\alpha ^{(0)}_{3},p^{(0)}, \alpha ^{(1)}_{1},\alpha ^{(1)}_{2},\alpha ^{(1)}_{3},p^{(1)},{ \mathsf{u}}_{1},{\mathsf{u}}_{2},{\mathsf{u}}_{3},\xi \right )\).

4 Examples of Rod Deformations

Since the strain-energy density of a nematic rod to the approximation considered here only depends on the linear behavior of the 3D strain-energy density [46], without loss of generality, we can use the form

$$ W(\textbf{A})=\frac{\mu }{2}\left [\mathrm{tr}\left (\textbf{H}^{T} \textbf{H}\right )+\mathrm{tr}\left (\textbf{H}^{2}\right )\right ], $$
(24)

where \(\textbf{H}=\textbf{A}-\textbf{I}\) and \(\mu \) is the shear modulus at small strain.

We assume a nematic rod with the director taking the following general form in a reference system with cylindrical polar coordinates \((R,\Theta ,Z)\),

$$ \textbf{n}=\sin \Phi \cos \Psi \ \textbf{e}_{R}+\sin \Phi \sin \Psi \ \textbf{e}_{\Theta }+\cos \Phi \ \textbf{e}_{Z}, $$
(25)

where \(\Phi \in [-\pi /2,\pi /2]\) and \(\Psi \in [0,\pi ]\) are given angles. The handedness of the fiber is given by the sign of \(\Phi \) with right-handedness obtained with angles strictly between 0 and \(\pi /2\). Helical fibers are defined for \(\Psi =\pi /2\) and purely radial fibers are obtained when \(\Phi =\pm \pi /2\). Equivalently, in the rectangular coordinate system, the nematic director is equal to

$$ \textbf{n}=\sin \Phi \cos (\Psi +\Theta )\textbf{e}_{1}+\sin \Phi \sin ( \Psi +\Theta )\textbf{e}_{2}+\cos \Phi \ \textbf{e}_{3}. $$
(26)

4.1 Nematic Rod with Axial Director Field

First, we assume that the nematic field is aligned parallel to the longitudinal axis, i.e., \(\Phi =0\), so that \(\textbf{n}=\textbf{e}_{3}\). The corresponding spontaneous deformation tensor is equal to

$$ \textbf{G}=\mathrm{diag}\left (a^{-1/6},a^{-1/6},a^{1/3}\right ), $$
(27)

with \(\mathrm{diag}(\cdot ,\cdot ,\cdot )\) denoting the diagonal second order tensor. We set \(a^{1/3}=1+\varepsilon g(x,y)\). Hence,

$$ \textbf{G}=\textbf{I}+\varepsilon g(x,y)\ \mathrm{diag}\left (-1/2,-1/2,1 \right )+\mathcal{O}(\varepsilon ^{2}). $$
(28)

When \(\textbf{A}=\textbf{G}^{-1}\textbf{F}\), we can follow the same steps as in [46] to reduce, after solving the Euler-Lagrange equations, the three-dimensional energy functional to a one-dimensional energy of the form

$$ \mathcal{E}=\frac{1}{2}\int _{0}^{L} \left [K_{0} (\zeta - \widehat{\zeta })^{2}+ K_{1} \left (\mathsf{u}_{1}- \widehat{\mathsf{u}}_{1}\right )^{2}+K_{2} \left (\mathsf{u}_{2}- \widehat{\mathsf{u}}_{2}\right )^{2}+K_{3} \mathsf{u}_{3}^{2}\right ] \,\text{d} Z, $$
(29)

where \(\zeta =1+\varepsilon \xi \) and the stiffnesses are

$$\begin{aligned} &K_{0}=\int _{\mathcal{S}}E\, \text{d}X\,\text{d}Y,\qquad K_{1}=\int _{ \mathcal{S}} E Y^{2}\, \text{d}X\,\text{d}Y,\qquad K_{2}=\int _{ \mathcal{S}} E X^{2}\, \text{d}X\,\text{d}Y, \end{aligned}$$
(30)
$$\begin{aligned} &K_{3}=\int _{\mathcal{S}} \mu (Y^{2}+X^{2})\, \text{d}X\,\text{d}Y+ \int _{\mathcal{S}}\mu \left (X\Phi _{Y}-Y\Phi _{X}\right )\, \text{d}X\,\text{d}Y, \end{aligned}$$
(31)

with \(E=3\mu \) representing the Young’s modulus. Here, \(\Phi \) is the so-called warping function, and is a solution of

$$\begin{aligned} & \Delta \Phi =0,\quad (X,Y)\in \mathcal{S}, \end{aligned}$$
(32)
$$\begin{aligned} &\widetilde{\mathbf{n}}\cdot (\Phi _{X},\Phi _{Y})= \widetilde{\mathbf{n}}\cdot (Y,-X), \quad (X,Y)\in \partial \mathcal{S}, \end{aligned}$$
(33)

where \(\widetilde{\mathbf{n}}\) is the unit vector normal to the boundary. The unstressed extension is

$$ \widehat{\zeta }=\frac{H_{0}}{K_{0}},\qquad H_{0}= \int _{\mathcal{S}} E \, G(X,Y)\,\text{d}X\,\text{d}Y, $$
(34)

with \(G(X,Y)=\varepsilon g(X/\varepsilon ,Y/\varepsilon )\). Similarly, the unstressed curvatures are given by

$$ \widehat{\mathsf{u}}_{1}=\frac{H_{1}}{K_{1}},\qquad \widehat{\mathsf{u}}_{2}=-\frac{H_{2}}{K_{2}},\qquad \widehat{\mathsf{u}}_{3}=0, $$
(35)

where

$$ H_{1}=\int _{\mathcal{S}} E Y\, G(X,Y)\, \text{d}X\,\text{d}Y,\qquad H_{2}= \int _{\mathcal{S}} E X\, G(X,Y)\,\text{d}X\,\text{d}Y. $$
(36)

The bending curvature and the torque of the deformed rod are, respectively (see [19, p. 103] for details),

$$ \kappa =\sqrt{\widehat{u}_{1}^{2}+\widehat{u}_{2}^{2}},\qquad \tau = \widehat{u}_{3}- \frac{\widehat{u}_{1}'\widehat{u}_{2}-\widehat{u}_{2}'\widehat{u}_{1}}{\widehat{u}_{1}^{2}+\widehat{u}_{2}^{2}}, $$
(37)

where ′ denotes the first derivative with respect to \(Z\). Taking the arc length \(S\) in a stress-free reference configuration and the twist

$$ \varphi (S)=\arctan \frac{\widehat{u}_{1}}{\widehat{u}_{2}}, $$
(38)

as the angle between the normal vector to the centerline and \(\textbf{d}_{1}\), the quantity

$$ \frac{\partial \varphi }{\partial S}= \frac{\widehat{u}_{1}'\widehat{u}_{2}-\widehat{u}_{2}'\widehat{u}_{1}}{\widehat{u}_{1}^{2}+\widehat{u}_{2}^{2}}, $$
(39)

represents the rotation of local basis with respect to the Frenet frame as the arc length increases.

4.1.1 Photoresponses

Following [9], we assume that the anelastic photostrain \(\epsilon _{p}\) is due to the conversion of straight (trans) to bent (cis) forms of the dye molecules present in the LCE. In the simplest case, we can take the photostrain to be proportional to the cis fraction of chromophores \(n_{c}\), so that

$$ \epsilon _{p}=-A n_{c},\qquad \lambda _{p}=1-A n_{c}, $$
(40)

where \(\lambda _{p}\) is the anelastic photostretch and \(A\) is the proportionality constant (taken to be 1 in all the particular examples and figures). When \(\lambda _{p}=\lambda _{p}(X,Y)\) is given in the cross-section, the rod deformation can be found explicitly.

We can now couple the mechanical theory to the light intensity distribution by using a generalized Beer-Lambert law [27] for light absorbance. We define \(\eta \) to be the arc length along an optic path measured from the point \(\eta =0\) where the ray enters the material. We are interested in the light intensity \(I=I(\eta )\) in the material. Defining \(J=J(\eta )=I(\eta )/I(0)\), the generalized Beer-Lambert law reads

$$ \frac{\text{d} J}{\text{d}\eta }=-\beta n_{t}(J) J, $$
(41)

where \(\beta \) is a material constant, \(n_{t}\) is the proportion of trans molecules with the property \(n_{t}+n_{c}=1\), and

$$ n_{c}=\frac{\alpha J}{1+\alpha J},\qquad n_{t}=\frac{1}{1+\alpha J}, $$
(42)

where \(\alpha =I(0)/I_{c}\) is a measure of incident intensity, with \(I_{c}\) the characteristic intensity [9]. Therefore, (41) reads

$$ \frac{\text{d} J}{\text{d}\eta }=-\frac{\beta J}{1+\alpha J} , \qquad J(0)=1, $$
(43)

which integrates to

$$ J(\eta )= \frac{W_{0}\left (\alpha e^{\alpha -\eta \beta }\right )}{\alpha }, $$
(44)

where \(W_{0}\) denotes the Lambert function. We conclude that, along a single path, we have

$$ \lambda _{p}(\eta )= \frac{1+(1-A)W_{0}\left (\alpha e^{\alpha -\eta \beta }\right )}{1+W_{0}\left (\alpha e^{\alpha -\eta \beta }\right )}. $$
(45)

In general, at a given point \((X,Y)\) in the cross-section, multiple light rays contribute to the light intensity. Then, the total light intensity at that point is given by the sum of these different contributions from which the photostretch can be found.

4.1.2 Uniform Illumination: Axial Director, Square Cross-Section

As a simple first example, we consider a square cross-section and assume that the illumination enters a single side, as shown in Fig. 1(a). Moreover, on the illuminated surface, we assume that \(I_{0}=I(0)\) is constant and that light enters the material along its normal direction, as illustrated in Fig. 1(c). In this case, we have \(\eta =X+1\) and each light ray only contributes to a single point in the cross-section. Using (35) with \(G(X,Y)=A n_{c}\), the only non-vanishing unstressed curvature reads

$$ \widehat{\mathsf{u}}_{2}=-\frac{3}{2}A\int _{0}^{2} (\eta -1)n_{c} \text{d}\eta . $$
(46)

Then, using (42) and (44), we find after simplification, the bending curvature (see Appendix A for details)

$$ \kappa =\widehat{\mathsf{u}}_{2}=\frac{3}{4} \frac{\alpha A}{\beta ^{2}}\left [\alpha J_{2}^{2}+2 J_{2} (1+\beta )+2 \beta -2 -\alpha \right ], $$
(47)

where \(J_{2}=J(2)\). Note that, after a suitable identification of variables, we recover the main result of [9] (viz., Equation 6, with \(d=1/\beta \) and \(w=2\)). Thus, the resulting deformation is pure bending, without torsion or twist. In particular, the principal bending stiffnesses \(K_{1}\) and \(K_{2}\), and the torsional stiffness \(K_{3}\) are the same as for the undeformed rod.

Fig. 1
figure 1

Uniform illumination on (a) a square or (b) a partially coated circular cross-section causing (c) a uniform unstressed curvature. Physically, in the absence of load and body force, this solution can be realized by a central light source placed at the center of a circle with radius \(1/\kappa \)

Full size image

Experimental observations of bending in LCE rods due to illumination are presented, for example, in [35, 65, 72]. Figure 2(a) shows the bending curvature \(\kappa \) scaled by \(\beta \) (note the penetration depth is \(1/\beta \), so \(\kappa /\beta \) is dimensionless) as a function of the thickness to penetration depth ratio \(2\beta \) for various incident reduced light intensities \(\alpha \) (see also Fig. 4 of [9]).

Fig. 2
figure 2

Changes in the bending curvature \(\kappa \), scaled by the light penetration depth \(1/\beta \), for a nematic beam with (a) square or (b) circular cross-section with opening \(\Delta \Theta =\pi \) and thickness 2, when the thickness to penetration depth ratio \(2\beta \) increases under various incident reduced light intensities \(\alpha \)

Full size image

4.1.3 Uniform Illumination: Axial Director, Partially Coated Circular Cross-Section

We also take a circular cylindrical rod and assume again that on the illuminated surface (see Fig. 1(b)), \(I_{0}=I(0)\) is constant, and that light enters the material along its normal direction, i.e., along the radial direction of the cross-section (see Fig. 1(c)). Then, if the cross-section is a unit circle coated in the opening with angle \(\Delta \Theta \), we can write \(X=(\eta -1)\cos \Omega \) and \(Y=(\eta -1)\sin \Omega \), with \(\eta \in [0,2]\) and \(\Omega \in \left [\pi -\Delta \Theta /2,2\pi -\Delta \Theta /2 \right ]\). In this case, using (35) with \(G(X,Y)=A n_{c}\), the non-zero unstressed curvature is equal to (details in Appendix A)

$$ \widehat{\mathsf{u}}_{2}=\frac{8 \sin (\Delta \Theta /2) }{\pi }A \left [\int _{0}^{1} (\eta -1)^{2} n_{c}\text{d}\eta -\int _{1}^{2} ( \eta -1)^{2} n_{c}\text{d}\eta \right ]. $$
(48)

We now obtain the bending curvature

$$ \begin{aligned} \kappa =\widehat{\mathsf{u}}_{2}&=- \frac{4 \alpha A \sin (\Delta \Theta /2) }{3 \pi \beta ^{3}} \left [-2 \alpha ^{2}+6 \alpha \beta -9 \alpha -6 \beta ^{2}+12 \beta +4 \alpha ^{2} J_{1}^{3}-2 \alpha ^{2} J_{2}^{3}\right . \\ & {}-6 \alpha (2 \beta -3) J_{1}^{2}-3 \alpha (2 \beta +3) J_{2}^{2}+12 \left (\beta ^{2}-2 \beta +2\right ) J_{1} \\ &\left. {} -6 \left (\beta ^{2}+2 \beta +2\right ) J_{2}-12\right ], \end{aligned} $$
(49)

where \(J_{1}=J(1)\) and \(J_{2}=J(2)\). Figure 2(b) shows the curvature \(\kappa \) scaled by \(1/\beta \) as a function of \(2\beta \) for various incident reduced light intensities \(\alpha \). Comparison with the mechanical behavior of a rod with a square cross-section suggests that there is very little difference between the two cases (see Figs. 2(a) and (b)).

4.1.4 Non-uniform Illumination: Optical Effects

The light paths in the above scenarios are simple, due to the assumption that the light penetrates the material only in the normal direction. To demonstrate that our modeling approach is also amenable to computing the curvature when the optical paths must be resolved, we consider horizontal light rays entering a material with circular cross-section. In this case, the light rays are refracted into the material at an angle \(\phi _{2}\) from the normal to the material according to Snell’s law [6]

$$ n_{2}\sin \phi _{2}=n_{1}\sin \phi _{1}, $$
(50)

where \(n_{1}\) and \(n_{2}\) are the refractive indices of the external environment and the LCE material, respectively. For light rays traveling in the \(X\)-direction and intersecting the unit circle \((X(s),Y(s))=(\cos s,\sin s)\), we have \(\phi _{1}=s\), and the light rays enter the material in the direction (see Appendix B)

$$ \left [ \textstyle\begin{array}{c} p \\ q\end{array}\displaystyle \right ]= \left [ \textstyle\begin{array}{c} -\sqrt{1-n^{2}\sin ^{2}s}\cos s-n\sin ^{2}s \\ -\sqrt{1-n^{2}\sin ^{2}s}\sin s+n\sin s\cos s \end{array}\displaystyle \right ], $$
(51)

where \(n=n_{1}/n_{2}\) is the ratio of the refractive indices. For \(n\) close to 1, the light is refracted by a very small amount and will continue to travel nearly horizontally, with increasing deflection for decreasing \(n\). Generally, we will restrict our attention to the range \(n<1\); in particular, if the external environment is air, then \(n_{1}\approx 1.00029\), while a typical value for LCE is \(n_{2}\approx 1.64128\) [7, 33, 51].

For given \(n\), the light paths satisfy

$$ \left [ \textstyle\begin{array}{c} X(s,t) \\ Y(s,t)\end{array}\displaystyle \right ]= \left [ \textstyle\begin{array}{c} \cos s+pt \\ \sin s+qt \end{array}\displaystyle \right ]. $$
(52)

Noting that \(p^{2}+q^{2}=1\), \(t\) is the arc length along the path and may be identified with \(\eta \) in (41). We can now compute the curvature by numerically integrating (41) along the light paths, while simultaneously integrating for \(\widehat{\mathsf{u}}_{2}\) by converting equation (36) into an integral over \(s\) and \(t\) (details in Appendix B).

In Fig. 3(a), we plot the scaled curvature \(\kappa /\beta \) against the thickness to penetration depth ratio \(2\beta \) for different values of \(n_{2}>1\) (with \(n_{1}=1\)), for fixed incident intensity \(\alpha =0.5\). Also included in this plot for comparison are the cases of radial rays with \(\Delta \Theta =\pi \), and horizontal rays on a square cross-section; these appear respectively as the black dashed and dotted curves, almost indistinguishable. The first clear difference when comparing the cases of refracted and unrefracted light is that in the refracted cases the quantity \(\kappa /\beta \) diverges as \(\beta \) tends to zero. This is due to the existence of regions that are not reached by the refracted light (unlike the case of Fig. 1(a) or Fig. 1(b) with \(\Delta \Theta =\pi \)). Therefore, even if \(J\equiv 1\) across the entire path of the light rays, \(n_{c}\) will remain 0 in the hidden regions so that a curvature still develops with \(\beta =0\), and thus \(\kappa /\beta \to \infty \) as \(\beta \to 0\).

Fig. 3
figure 3

Curvature generation for horizontal rays refracted into a circular cross-section. In (a), the scaled curvature is plotted against the thickness to penetration depth ratio \(2\beta \) for varying refractive index of the nematic beam (with \(n_{1}=1\)): \(n_{2}=\) 1.01 (red), 1.1 (orange), 1.6 (green), 2 (blue), and 4 (purple). Also included are the cases of radial rays (black dashed) and horizontal rays for a square cross-section (dotted black). The optical paths are illustrated for each case. In (b), the integrated curvature \(\kappa _{\text{int}}\) is plotted against refractive index ratio \(n_{2}/n_{1}\) for the indicated values of incident intensity \(\alpha \). Light paths are shown (at evenly spaced points around the circle) for indicated values of \(n_{2}/n_{1}\), with caustic curves highlighted in red

Full size image

It also appears from Fig. 3 that low refraction generates less curvature: the lowest curvatures occur for \(n_{2}=1.01\) (red) and \(n_{2}=1.1\) (orange), for which the light paths remain nearly horizontal. With increasing \(n_{2}\), there are two competing effects for curvature generation: (i) the light becomes more focused, with the light rays tending to the radial direction as \(n_{2}\to \infty \), and (ii) the size of the hidden domain for which no light paths enter first increases and then decreases with increasing \(n_{2}\). The hidden domain is largest for \(n_{2}\) around 2 (this is more clearly evident in the light paths shown in Fig. 3(b)). When \(\beta \) is small, this second effect is dominant, and the highest curvature is generated when the hidden region is largest. For larger \(\beta \), the light intensity decays too quickly for the second effect to have much consequence; instead the curvature is higher when the light is more focused: thus the case of \(n_{2}=1.6\) (blue) provides highest curvature for small \(\beta \), while \(n_{2}=4\) (purple) gives a higher curvature for larger \(\beta \).

These observations demonstrate a strong dependence of curvature generation on both the optics and the depth of the material, and suggest the potential to balance the competing effects noted above in order to optimize the optical properties for curvature generation. To investigate further, we define an integrated scaled curvature

$$ \kappa _{\text{int}}=\int _{0}^{10} \frac{\kappa (\beta )}{\beta }\;d \beta , $$
(53)

which provides a measure of the ability of the material to generate curvature over a range of thickness to penetration depth ratios. In Fig. 3(b), we plot \(\kappa _{\text{int}}\) as a function of \(1/n=n_{2}/n_{1}\) for a range of values of incident intensity \(\alpha \). We verified numerically that the divergence as \(\beta \to 0\) is slower than \(1/x\) for all values of \(n_{2}/n_{1}\), so that \(\kappa _{\text{int}}\) remains finite. These plots show an optimal value of \(n_{2}\approx 2.2\). We see that the optimal value has almost no dependence on the intensity \(\alpha \), and moreover, the maximum value seems to saturate for \(\alpha \gtrsim 0.5\), suggesting that, once the light intensity is high enough, generating curvature is purely a function of the material geometry and optical properties. The dashed vertical line corresponds to \(n_{2}=1.64\), showing that the value of refractive index typically cited for LCE is not far from the optimal value.

4.1.5 Non-uniform Illumination: Bending Towards the Light

Now, we consider a uniform inextensible transversely isotropic rod with a square cross-section that is clamped at one end. We choose the axes so that the sides of the cross-section at the clamped end are oriented along the rectangular \(X\)- and \(Z\)-directions, respectively, and, in the absence of illumination, the rod’s longitudinal axis is parallel to the \(Y\)-direction. We are interested in finding its configuration when light rays are produced so that they are parallel to the \(X\)-direction, and the rod is illuminated from the negative \(X\)-direction. For simplicity, and to avoid any end effects, we also assume that the top end of the rod is opaque, which prevents the light from entering the material. This basic setup is inspired by the experiments in [35] showing how a clamped rod bends into the light.

In this scenario, the light rays are not oriented with respect to the normal at each point on the rod surface, rather the light distribution will depend on the rod’s inclination that itself depends on the rod’s curvature, dictated by light. The problem can be solved by computing the contribution of different light rays to a given cross-section \(\mathcal{S}\), as depicted in Fig. 4, following Snell’s law.

Fig. 4
figure 4

In a cross-section \(\mathcal{S}\), the light intensity at a point \(p\) depends on the path-length \(\widetilde{\eta }\)

Full size image

The light intensity at a point \(p\in \mathcal{S}\) depends on the light decay along a path of length \(\widetilde{\eta }\). Hence, we can use equation (44) to obtain the light intensity \(J\) at \(p\) as follows,

$$ J(\widetilde{\eta })= \frac{W_{0}\left (\alpha e^{\alpha -\widetilde{\eta } \beta }\right )}{\alpha }, $$
(54)

where \(\widetilde{\eta }\) is now the length along the section \(\mathcal{S}\) from the light entry point. Following Kirchhoff’s assumptions on the geometry of a rod, the curvature and the incidence angle do not vary rapidly with arc length. Therefore the light paths impacting on a given cross-section will be approximately parallel. With this simplification, basic geometry gives \(\widetilde{\eta }=\eta /\cos \theta _{2}\), and therefore, (54) is equivalent to

$$ J(\eta ,\theta _{1})= \frac{W_{0}\left (\alpha e^{\alpha -\eta \beta /\cos {\theta _{2}(\theta _{1})}}\right )}{\alpha }. $$
(55)

We observe that this relationship for the light distribution inside the material is the same as that given by (44), except that the parameter \(\beta \) is now replaced by \(\widetilde{\beta }=\beta /\cos \theta _{2}(\theta _{1})\). The result on the curvature provided by (47) can then be readily adapted by replacing \(\beta \) with \(\widetilde{\beta }\) in (47). Since a cross-section with \(\theta _{1}=\pi /2\) does not receive any light, the curvature vanishes identically on any cross-section that reaches that particular value of the angle. We obtain the following unstressed curvature depending on the incidence angle,

$$ \kappa (\theta _{1})= \textstyle\begin{cases} \frac{3}{4}\frac{\alpha A}{\widetilde{\beta }^{2}}\left [\alpha \widetilde{J}_{2}^{2}+2 \widetilde{J}_{2} (1+\widetilde{\beta })+2 \widetilde{\beta }-2 -\alpha \right ]\quad &\text{if} \quad 0\leq \theta _{1}< \pi /2, \\ 0&\text{if}\quad \theta _{1}=\pi /2,\end{cases} $$
(56)

where

$$ \widetilde{J}_{2}= \frac{W_{0}\left (\alpha e^{\alpha -2 \widetilde{\beta }}\right )}{\alpha } \qquad \text{and}\qquad \widetilde{\beta }= \frac{\beta }{\cos \left (\arcsin \left (\frac{n_{1}}{n_{2}} \sin \theta _{1}\right )\right )}. $$
(57)

From the curvature, we find the unstressed shape by first recalling that the tangent vector is equal to \(\mathbf{r}'(s)=-\sin \theta _{1}\mathbf{e}_{x}+\cos \theta _{1} \mathbf{e}_{y}\) and, second, by connecting the incidence angle to the curvature: \(\theta _{1}'(s)=\kappa \). We then derive the shape by integrating numerically the following system of ordinary differential equations,

$$\begin{aligned} &\frac{\text{d}x}{\text{d}s}=-\sin \theta _{1},\qquad \frac{\text{d}y}{\text{d}s}=\cos \theta _{1},\qquad \frac{\text{d}\theta _{1}}{\text{d}s}=\kappa (\theta _{1}), \end{aligned}$$
(58)

with initial conditions \(x(0)=y(0)=\theta _{1}(0)=0\). An illustration of this integration is shown in Fig. 5, where we see that there is a critical length \(L_{\text{crit}}\) for the rod when \(\theta _{1}(L_{\text{crit}})=\pi /2\). For \(L< L_{\text{crit}}\), a rod of length \(L\) only bends partially towards the light, and for \(L>L_{\text{crit}}\), the rod has an horizontal segment with zero curvature of length \(L-L_{\text{crit}}\).

Fig. 5
figure 5

(a) A rod is illuminated from the left and bends into the light as observed in [35]. (b) The unstressed curvature \(\kappa \) depends on the incidence angle \(\theta _{1}\). (c) According to its length, the rod will bend completely or partially towards the light. Past a critical length, \(L_{\text{crit}}\), the top part of the rod remains horizontal. The parameter values are \(\alpha =\beta =1\), \(A=0.1\), and \(L_{\text{crit}}\approx 98.921\)

Full size image

4.2 Nematic Rod with Helical Director Field

We further consider LCE rods with a helical nematic field (see [48, 71] for relevant experimental tests, and also [17] for a theoretical discussion). In cylindrical polar coordinates, the nematic director takes the form

$$ \textbf{n}=\sin \Phi \ \textbf{e}_{\Theta }+\cos \Phi \ \textbf{e}_{Z}. $$
(59)

Equivalently, in Cartesian coordinates, the director is equal to

$$ \textbf{n}=-\sin \Phi \sin \Theta \ \textbf{e}_{1}+\sin \Phi \cos \Theta \ \textbf{e}_{2}+\cos \Phi \ \textbf{e}_{3}. $$
(60)

Then \(\mathbf{G}\) takes the form

$$ \mathbf{G}=\mathbf{1}-\frac{ \epsilon n_{c}}{4} \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} -2 & 0 & 0 \\ 0 & 1-3 \cos 2 \Phi & 3 \sin 2\Phi \\ 0 &3 \sin 2\Phi & 1+3 \cos 2 \Phi \\ \end{array}\displaystyle \right ]. $$
(61)

Performing similar calculations to those for a cylindrical rod with axial nematic field, we obtain the unstressed extension and curvatures

$$\begin{aligned} &\widehat{\zeta }=-\frac{A}{\pi R_{0}^{4}}\int _{0}^{2\pi }\text{d} \Theta \int _{0}^{R_{0}}R (1+3 \cos 2 \Phi (R,\Theta )) n_{c}(R, \Theta )\, \text{d}R, \end{aligned}$$
(62)
$$\begin{aligned} &\widehat{\mathsf{u}}_{1}=-\frac{A}{\pi R_{0}^{4}}\int _{0}^{2\pi } \text{d}\Theta \sin \Theta \int _{0}^{R_{0}}R^{2} (1+3 \cos 2 \Phi (R, \Theta )) n_{c}(R,\Theta )\, \text{d}R, \end{aligned}$$
(63)
$$\begin{aligned} &\widehat{\mathsf{u}}_{2}=\frac{A}{\pi R_{0}^{4}}\int _{0}^{2\pi } \text{d}\Theta \cos \Theta \int _{0}^{R_{0}}R^{2} (1+3 \cos 2 \Phi (R, \Theta )) n_{c}(R,\Theta )\, \text{d}R, \end{aligned}$$
(64)
$$\begin{aligned} &\widehat{\mathsf{u}}_{3}= - \frac{2 A}{\pi R_{0}^{4}}\int _{0}^{2 \pi }\text{d}\Theta \int _{0}^{R_{0}}R^{2} \sin 2 \Phi (R,\Theta ) n_{c}(R, \Theta )\, \text{d}R, \end{aligned}$$
(65)

where, as before, \(A\) relates the concentration of cis molecules to their stretch (introduced in (40)).

4.2.1 Uniform Illumination: Helical Director, Partially Coated Circular Cross-Section

As an application of the curvatures generated by helical nematic directors, we consider a uniform rod with circular cross-section and a constant helical director field, with \(\Phi >0\), that only exists in a sector \(R\in [R_{1},R_{0}],\Theta \in [0,2 \pi ]\). The rod is partially coated so that light only enters in a section of the boundary circle as shown in Fig. 1(b) following the setup of Sect. 4.1.3. We also assume that the illumination is uniform. In this case, we can adapt the computation of Sect. 4.1.3 for the case of helical fibers to obtain the curvatures

$$\begin{aligned} &\widehat{\mathsf{u}}_{1}=0, \end{aligned}$$
(66)
$$\begin{aligned} & \widehat{\mathsf{u}}_{2}=- \frac{\alpha A (1+3 \cos 2 \Phi )\sin \Delta \Theta }{3 \pi \beta ^{3}} \bigg[-2 \alpha ^{2}+6 \alpha \beta -9 \alpha -6 \beta ^{2}+12 \beta -2 \alpha ^{2} J_{2}^{3}+2 \alpha ^{2} J_{11}^{3} \\ & \left . \phantom{-\frac{\alpha A \sin (\Delta \Theta ) (3 \cos (2 \phi )+1)}{3 \pi \beta ^{3}}} +2 \alpha ^{2} J_{12}^{3}-3 \alpha (2 \beta +3) J_{2}^{2}+9 \alpha J_{12}^{2}-6 \left (\beta ^{2}+2 \beta +2\right ) J_{2}\right . \\ & \left . \phantom{-\frac{\alpha A \sin (\Delta \Theta ) (3 \cos (2 \phi )+1)}{3 \pi \beta ^{3}}} +6 \alpha \beta J_{12}^{2} R_{1}+\alpha J_{11}^{2} \left (9-6 \beta R_{1} \right )+6 \beta ^{2} J_{12} R_{1}^{2}\right . \\ &\left . \phantom{-\frac{\alpha A \sin (\Delta \Theta ) (3 \cos (2 \phi )+1)}{3 \pi \beta ^{3}}} +6 J_{11} \left (\beta ^{2} R_{1}^{2}-2 \beta R_{1}+2\right )+12 \beta J_{12} R_{1}+12 J_{12}-12\right ], \\ \end{aligned}$$
(67)
$$\begin{aligned} & \widehat{\mathsf{u}}_{3}= \frac{2 \alpha A (\pi -\Delta \Theta ) \sin 2 \Phi }{3 \pi \beta ^{3}} \bigg[-2 \alpha ^{2}+6 \alpha \beta -9 \alpha -6 \beta ^{2}+12 \beta +2 \alpha ^{2} J_{2}^{3}+2 \alpha ^{2} J_{11}^{3} \\ & \phantom{\widehat{\mathsf{u}}_{3}=\frac{2 \alpha A (\pi -\Delta \Theta ) \sin (2 \phi )}{3 \pi \beta ^{3}}} -2 \alpha ^{2} J_{12}^{3} +6 \alpha \beta J_{2}^{2}+9 \alpha J_{2}^{2}+6 \beta ^{2} J_{2} \\ & \phantom{\widehat{\mathsf{u}}_{3}=\frac{2 \alpha A (\pi -\Delta \Theta ) \sin (2 \phi )}{3 \pi \beta ^{3}}} +12 \beta J_{2}+6 J_{11} \left(\beta ^{2} R_{1}^{2}-2 \beta R_{1}+2 -6 J_{12} \left (\beta ^{2} R_{1}^{2} \right )\right. \\ & \left. \phantom{\widehat{\mathsf{u}}_{3}=\frac{2 \alpha A (\pi -\Delta \Theta ) \sin (2 \phi )}{3 \pi \beta ^{3}}} +2 \beta R_{1}+2\right )+\alpha J_{11}^{2} (9-6 \beta R_{1})-3 \alpha J_{12}^{2} (2 \beta R_{1}+3) \\ &\left . \phantom{\widehat{\mathsf{u}}_{3}=\frac{2 \alpha A (\pi -\Delta \Theta ) \sin (2 \phi )}{3 \pi \beta ^{3}}} +12 J_{2}-12\right ], \end{aligned}$$
(68)

where we have taken \(R_{0}=1\) and \(J_{2}=J(2)\), \(J_{12}=J(1+R_{1})\), \(J_{11}=J(1-R_{1})\).

An example of the behavior of this twist under different light penetration depths and reduced light intensities is shown in Fig. 6. We note that the intrinsic torsion is negative, creating a left-handed intrinsic helix even though the directors are right-handed. This is due to the fact that the molecules contract, hence applying an anticlockwise rotation of the cylinder that is compensated by a torsional response.

Fig. 6
figure 6

Changes in intrinsic curvature \(\widehat{\mathsf{u}}_{3}\) and intrinsic twist \(\widehat{\mathsf{u}}_{3}\), as a function of the inverse of light penetration depth \(\beta \), for a nematic beam with circular cross-section and \(R_{0}=1\), \(R_{1}=1/2\) (\(\omega =A=1\), \(\Delta \Theta =\pi /2\), \(\Phi =\pi /4\)), under various incident reduced light intensities \(\alpha \). We observe the non-monotonic behavior of the twist as a function of \(\alpha \)

Full size image

We can now use this exact form to compute the critical values at which a straight LCE rod would become unstable when illuminated. For example, we assume that such a straight rod is pulled with an end tension \(T\) and there is no twist before illumination. If the ends are prevented from turning, then, upon illumination, its intrinsic curvatures are given by (66)-(68), and will build elastic energy. Depending on the parameters of the system, this elastic energy can be sufficient to create an instability [23, 39].

To compute the critical value of the parameters where such an instability occurs, we follow the general perturbation method given in [19, pp 136-137]. The Kirchhoff equations for an inextensible and unshearable rod, written in local director basis, are [46]

$$\begin{aligned} &\mathsf{n}_{3} {\mathsf{u}}_{2}-{\mathsf{n}}_{2} {\mathsf{u}}_{3}+{ \mathsf{n}}_{1}'=0, \end{aligned}$$
(69a)
$$\begin{aligned} &{\mathsf{n}}_{1} {\mathsf{u}}_{3}-{\mathsf{n}}_{3} {\mathsf{u}}_{1}+{ \mathsf{n}}_{2}'=0, \end{aligned}$$
(69b)
$$\begin{aligned} &{\mathsf{n}}_{2} {\mathsf{u}}_{1}-{\mathsf{n}}_{1} {\mathsf{u}}_{2}+{ \mathsf{n}}_{3}'=0, \end{aligned}$$
(69c)
$$\begin{aligned} &K_{1} \left ({\mathsf{u}}_{1}'-\widehat{\mathsf{u}}_{1}'\right )+K_{3} {\mathsf{u}}_{2} \left ({\mathsf{u}}_{3}-\widehat{\mathsf{u}}_{3} \right )-K_{1} {\mathsf{u}}_{3} \left ({\mathsf{u}}_{2}- \widehat{\mathsf{u}}_{2}\right )-{\mathsf{n}}_{2}=0, \end{aligned}$$
(69d)
$$\begin{aligned} &K_{1} \left ({\mathsf{u}}_{2}'-\widehat{\mathsf{u}}_{2}'\right )+K_{1} {\mathsf{u}}_{3} \left ({\mathsf{u}}_{1}-\widehat{\mathsf{u}}_{1} \right )-K_{3} {\mathsf{u}}_{1} \left ({\mathsf{u}}_{3}- \widehat{\mathsf{u}}_{3}\right )+{\mathsf{u}}_{1}=0, \end{aligned}$$
(69e)
$$\begin{aligned} &K_{3} \left ({\mathsf{u}}_{3}'-\widehat{\mathsf{u}}_{3}'\right )+K_{1} {\mathsf{u}}_{1} \left ({\mathsf{u}}_{2}-\widehat{\mathsf{u}}_{2} \right )-K_{1} {\mathsf{u}}_{2} \left ({\mathsf{u}}_{1}- \widehat{\mathsf{u}}_{1}\right )=0, \end{aligned}$$
(69f)

where \(\{\mathsf{n}_{1},{\mathsf{n}}_{2},{\mathsf{n}}_{3}\}\) and \(\{\mathsf{u}_{1},{\mathsf{u}}_{2},{\mathsf{u}}_{3}\}\) are the local components of the force and the curvature, respectively (see equation (7)).

One can readily verify that the straight configuration, with \({\mathsf{u}}_{1}={\mathsf{u}}_{2}={\mathsf{u}}_{3}={\mathsf{n}}_{1}={ \mathsf{n}}_{2}=0\), \({\mathsf{n}}_{3}=T\), satisfies equations (69a)-(69f) for all tension values \(T\). We start in a regime of large tension, then decrease the tensile force until one reaches the critical value \(T_{\text{crit}}\). To find this limit, we linearize equations (69a)-(69f) around the straight solution and determine the largest tension that leads to the existence of a non-trivial solution. After simplification, we obtain

$$ T_{\text{crit}}= \frac{E \pi \left (\Gamma ^{3} \widehat{\mathsf{u}}_{3}^{2}+\widehat{\mathsf{u}}_{2}^{2}\right ){}^{2}}{16 \Gamma ^{4}\widehat{\mathsf{u}}_{3}^{2}}, $$
(70)

where \(\Gamma =K_{1}/K_{3}\in [2/3,1]\). We recognize a correction of the well-known twisting instability due to curvature and recover the twisting instability [21, 22] as \(\widehat{\mathsf{u}}_{2}\to 0\). Since we know the values of the intrinsic curvatures from equation (66)-(68), we can compute the critical tension necessary to destabilize the system, as a function of the illumination for different penetration depths (see Fig. 7). We note that the main difference between an infinite and a finite length rod is a delay of the bifurcation, so that the critical tension for a finite length rod is slightly lower than the one given here for an infinite length. This difference vanishes as the rod increases in length.

Fig. 7
figure 7

Critical tension at which a straight pulled (infinite) rod becomes unstable as a function of the illumination intensity \(\alpha \), for \(\beta =1,\ldots ,10\). We assume a nematic rod with circular cross-section and \(R_{0}=1\), \(R_{1}=1/2\) (\(\omega =A=1\), \(\Delta \Theta =\pi /2\), \(\Phi =\pi /4\), \(E=1\)). For a given set of parameter and illumination, the straight rod is stable when the tension is above the critical value, given by equation (70)

Full size image

5 Conclusions

We have presented in this paper a general method to construct an LCE rod model from a 3D material model. As long as the internal changes due to the excitation of the nematic directors remain moderate, so that the intrinsic curvatures are of the same order as the rod’s slenderness ratio, the approximate strain-energy density of the LCE rods can be obtained through dimensional reduction.

We have demonstrated the utility of this approach through a series of examples. In the case of uniform illumination, we have obtained explicit formulas for the light-induced curvature as a function of the incident light intensity and penetration depth of the material. We have shown that our approach is also compatible with cases of non-uniform illumination, in which the light paths are non-trivial to resolve. The approach proposed here thus represents a major step in our ability to model these materials and use them in actual structures that respond to external stimuli such as heliotracking devices [25]. Indeed, the change of shape of a structure can be systematically recomputed by updating continuously the effect of the stimuli on the nematic directors. Rather than using a computationally expensive 3D finite-element approach, the large deformations of the rod can be easily computed as an updated boundary-value problem at each time step as done, for instance, in the case of plant tropism [47].

At the same time, this work hints at a wealth of complexity that exists in the fully general case. Indeed, the curvature depends on the light paths, which depend on both the geometry of the material and the orientation in the light stimulus, which depends on the curvature. Even when solved in an iterative fashion, resolving the paths of refracted light across different cross-sections in a 3D geometry can pose a formidable challenge, particularly when shadowing effects are important. Nevertheless, in principle, our approach is amenable to any scenario, and in most cases analytic progress may be made under reasonable approximations such as uniform rays impacting on a given cross-section.

More generally, LCE materials open a new area of research where mechanics can be coupled with other physical effects affecting in real time the internal microstructure of the material. While great progress has been made in understanding the intrinsic geometry of such materials, much work remains to be done to fully couple geometry to mechanics and other external fields. We are now in a position to use the full power of nonlinear anelasticity to explore the behavior and shape these materials can acquire.