Contact Transform for the Biharmonic Equation Applicable to Plane Stress Elastoplastic Elliptical Hole Problems

Abstract

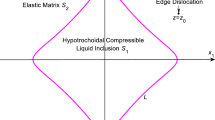
An analytical technique is developed that reduces the unknown elastic-plastic boundary of a linear elastic-perfectly plastic material containing an elliptical hole under tensile plane stress loading conditions into an equivalent mathematical problem with known boundaries. This mathematical transformation may facilitate this problem’s solution by either analytical or numerical means. Yield is assumed to occur in this analysis under the Tresca yield criterion. An example elastic-plastic problem illustrating this method is drawn from existing literature in the form of a perturbation solution for an elliptical hole derived by a series expansion about a circular boundary.

Appendix:  Various Coordinate Transformations

From (4.4) and (3.29), one derives using a chain rule that

$$ \frac{\partial\Delta}{\partial x} = \frac {\partial \Delta}{\partial\xi} \frac{\partial^{2}\psi}{\partial x^{2}} + \frac{\partial\Delta}{\partial\eta} \frac{\partial^{2}\psi}{\partial x\partial y} = \zeta \biggl( \frac{\partial\Delta}{\partial\xi} \frac{\partial^{2}\omega}{\partial\eta^{2}} - \frac{\partial \Delta}{\partial\eta} \frac{\partial^{2}\omega}{\partial\xi\partial \eta} \biggr). $$

(9.1)

Similarly, from (4.6) and (3.29) one finds

$$ \frac{\partial\Delta}{\partial y} = \frac {\partial \Delta}{\partial\xi} \frac{\partial^{2}\psi}{\partial x\partial y} + \frac{\partial\Delta}{\partial\eta} \frac{\partial^{2}\psi}{\partial y^{2}} = \zeta \biggl( - \frac{\partial\Delta}{\partial\xi} \frac{\partial^{2}\omega}{\partial\xi\partial\eta} + \frac {\partial \Delta}{\partial\eta} \frac{\partial^{2}\omega}{\partial\xi^{2}} \biggr). $$

(9.2)

Second order transformations of Δ, for substitution into (4.10), follow analogously as

$$\begin{aligned} \frac{\partial}{\partial x} \biggl( \frac{\partial \Delta}{\partial\xi} \biggr)& = \frac{\partial}{\partial\xi} \biggl( \frac{\partial\Delta}{\partial\xi} \biggr)\frac{\partial\xi}{\partial x} + \frac{\partial}{\partial\eta} \biggl( \frac{\partial\Delta}{\partial\xi} \biggr)\frac{\partial\eta}{\partial x} \\ &= \frac{\partial^{2}\Delta}{\partial \xi^{2}}\frac{\partial^{2}\psi}{\partial x^{2}} + \frac{\partial^{2}\Delta}{\partial\xi\partial\eta} \frac{\partial^{2}\psi}{\partial x\partial y} = \zeta \biggl( \frac{\partial^{2}\Delta}{\partial\xi^{2}}\frac{\partial ^{2}\omega}{\partial\eta^{2}} - \frac{\partial^{2}\Delta}{\partial\xi \partial \eta} \frac{\partial^{2}\omega}{\partial\xi\partial\eta} \biggr), \end{aligned}$$

(9.3)

$$\begin{aligned} \frac{\partial}{\partial x} \biggl( \frac{\partial \Delta}{\partial\eta} \biggr) &= \frac{\partial}{\partial\xi} \biggl( \frac{\partial\Delta}{\partial\eta} \biggr)\frac{\partial\xi}{\partial x} + \frac{\partial}{\partial\eta} \biggl( \frac{\partial\Delta}{\partial\eta} \biggr)\frac{\partial\eta}{\partial x} \\ &= \frac{\partial^{2}\Delta}{\partial\xi\partial \eta} \frac{\partial^{2}\psi}{\partial x^{2}} + \frac{\partial ^{2}\Delta}{\partial\xi\partial\eta} \frac{\partial^{2}\psi}{\partial x\partial y} = \zeta \biggl( \frac{\partial^{2}\Delta}{\partial\xi\partial\eta} \frac{\partial^{2}\omega}{\partial\eta^{2}} - \frac{\partial ^{2}\Delta}{\partial\eta^{2}}\frac{\partial^{2}\omega}{\partial\xi\partial \eta} \biggr), \end{aligned}$$

(9.4)

$$\begin{aligned} \frac{\partial}{\partial y} \biggl( \frac{\partial \Delta}{\partial\xi} \biggr) &= \frac{\partial}{\partial\xi} \biggl( \frac{\partial\Delta}{\partial\xi} \biggr)\frac{\partial\xi}{\partial y} + \frac{\partial}{\partial\eta} \biggl( \frac{\partial\Delta}{\partial\xi} \biggr)\frac{\partial\eta}{\partial y} \\ &= \frac{\partial^{2}\Delta}{\partial \xi^{2}}\frac{\partial^{2}\psi}{\partial x\partial y} + \frac{\partial^{2}\Delta}{\partial\xi\partial\eta} \frac{\partial^{2}\psi}{\partial y^{2}} = \zeta \biggl( - \frac{\partial^{2}\Delta}{\partial\xi^{2}}\frac{\partial ^{2}\omega}{\partial\xi\partial\eta} + \frac{\partial^{2}\Delta}{\partial \xi \partial\eta} \frac{\partial^{2}\omega}{\partial\xi^{2}} \biggr), \end{aligned}$$

(9.5)

$$\begin{aligned} \frac{\partial}{\partial y} \biggl( \frac{\partial \Delta}{\partial\eta} \biggr) &= \frac{\partial}{\partial\xi} \biggl( \frac{\partial\Delta}{\partial\eta} \biggr)\frac{\partial\xi}{\partial y} + \frac{\partial}{\partial\eta} \biggl( \frac{\partial\Delta}{\partial\eta} \biggr)\frac{\partial\eta}{\partial y} \\ &= \frac{\partial^{2}\Delta}{\partial\xi\partial \eta} \frac{\partial^{2}\psi}{\partial x\partial y} + \frac{\partial ^{2}\Delta}{\partial\eta^{2}}\frac{\partial^{2}\psi}{\partial y^{2}} = \zeta \biggl( - \frac{\partial^{2}\Delta}{\partial\xi\partial\eta} \frac{\partial^{2}\omega}{\partial\xi\partial\eta} + \frac{\partial^{2}\Delta}{\partial\eta^{2}}\frac{\partial ^{2}\omega}{\partial\xi^{2}} \biggr). \end{aligned}$$

(9.6)