Characteristics of planar buoyant jets and plumes in a turbulent channel crossflow from direct numerical simulations

Abstract

This paper is motivated by an interest in understanding the characteristics of buoyant fluids discharged from the bottom wall of channels, such as encountered during tunnel fires or in river effluent discharge. Direct numerical simulation is used to model the upward release of a planar buoyant jet or plume from the bottom wall of a channel into an incoming turbulent crossflow. The well-studied jet-in-crossflow with only a momentum source is simulated first, and subsequently, fixing the incoming Reynolds number, buoyancy source as heat flux is added alongside varying momentum source, with two cases where only a buoyancy source is present. Appropriate five non-dimensional parameters relevant for this flow are defined, of which three are fixed and two—source to channel momentum ratio and Richardson number—are varied. The changes in turbulence characteristics as the buoyant jet or plume evolves downstream are presented. In all cases with buoyancy, except for the pure jet case, the plume is initially confined to the lower half of the channel before it suddenly lifts to the top half, an effect that occurs at an increasingly smaller downstream distance with increasing buoyancy, and dividing the flow into a near and far field. The distributions of mean and Reynolds stresses in the near and far field of the source are reported, and it is found that the channel flow becomes more turbulent downstream of the source, and further, the turbulent vertical temperature flux switches sign from near to far field owing the a change in the mean temperature gradient sign. From the input parameters and using the integrated temperature equation a reasonable estimate of the far field mean channel temperature can be obtained by a reference temperature based on the heat conservation that includes the convective and diffusive source heat flux. A monotonic behaviour of the back-layering distance is also observed a function of this reference temperature, which was difficult to obtain with the two specified non-dimensional parameters.

1 Introduction

Plumes in crossflow are of major interest in environmental and industrial flows because of their wide application; for example, road tunnel fire, film cooling and wastewater from sewage treatment plants (e.g. [1,2,3,4]). The discharge of buoyant harmful gases or liquid within enclosed spaces, such as tunnels or in rivers can have serious consequences, such as adverse effects on human health, environmental risk and destruction of the water balance. In the case of road tunnels, usually, the ventilation along the confined spaces is used to impose a crossflow that can dilute and control the hazardous gas from flowing upstream. Similarly, for pollution discharged into rivers, a large main river flow can dilute and minimize the effects of pollution. Generally, the plume in a turbulent crossflow refers to a buoyant jet of fluid that is generated by buoyancy and momentum sources, and exits into the surrounding crossflow. In practical scenarios like tunnel fires and pollution discharged into rivers, the crossflow Reynolds number and plume Richardson number, Ri (the ratio of plume buoyancy and momentum) are such that the crossflow and plumes are turbulent.

Focus of the present study is to understand the interaction between the crossflow and the buoyant jet (and plume) as reflected in their turbulent statistics using direct numerical simulation (DNS) for varying non-dimensional parameters. Here, a line plume (extended in the spanwise and compact in the streamwise direction) is generated from a linear heat source situated at the bottom wall of a three-dimensional channel with turbulent flow through it. The impact of the plume on the top wall and its downstream or upstream propagation are contingent upon the plume intensity and magnitude of the turbulent channel crossflow.

Owing to its practical importance, there have been quite a few studies that have focused on the plume in crossflow (for example, [2,3,4,5,6,7,8,9,10,11,12]). Pratte and Baines [6] were one of the first to carry out experiments on jet trajectories under various jet to crossflow velocity ratios and found that the greater the crossflow velocity greater is bending of the jet trajectory. Patton et al. [7] injected a heated jet into a crossflow, where they focused on the injection angle but did not discuss the contribution of buoyancy. Later, Chen and Hwang [8] considered a row of round jets mimicking a plane jet that was slightly heated. However, since their ratio of the buoyancy to viscous force was small, buoyancy had almost no effect on the buoyant jet.

More recently, computational fluid dynamics (CFD) tools have increasingly been used to investigate (buoyant) jets in crossflow. Jones and Wille [10] performed a large Eddy simulation (LES) for the plane jet in crossflow. Their configuration was similar to [8] but without buoyancy force. Jones and Wille [10] validated the jet trajectory, velocity profile and turbulent intensity with the experiment of [8] and showed efficacy of LES for studying the jet in crossflow problems. Galeazzo et al. [13] compared LES with standard Smagorinsky model and Reynolds-averaged Navier–Stokes (RANS) simulations for a jet in crossflow, showing the advantage of LES over the RANS, especially in the prediction of Reynolds stresses.

From the perspective of tunnel fire, the heat and smoke created by the fire source can act as a momentum and/or buoyancy source, primarily because of the heat release from the fuel. The key here is to use sufficient crossflow (or ventilation) velocity to prevent smoke from propagating upstream of the source location. The top wall location where the upstream front of the smoke (or the buoyant jet) reaches is called ‘back-layering’ distance—it’s negative if smoke propagates upstream. Using data from small-scale experiments, Oka and Atkinson [9] found the one-third power relationships between crossflow velocity and heat release rate for zero back-layering distance—originally proposed by Thomas [14]—and used them to relate laboratory experiment data with full-scale tests. Wu and Bakar [2] used numerical simulations with a RANS $k-\varepsilon$ model and studied the propagation of the warm plume along the top wall. However, both Oka and Atkinson[9] and Wu and Bakar [2] did not consider the effect of the momentum released from the source of the fire.

While most of the above studies concentrate whether the plume propagates downstream and/or upstream (back-layering), the study of flow field resulting from the interaction of the buoyant jets (and plumes) and crossflow has received less attention. Jiang et al. [5] suggested the importance of plume source Richardson number Ri in estimating the ‘critical-ventilation velocity’ – the crossflow velocity that ensures no back-layering. Most of the previous studies have aimed at understanding the formation and evolution of counter-rotating vortex pairs owing to a round jet geometry; however, for a plane jet, the vortex structure would be different and the subsequent evolution of the plane jet has been less studied. Even little attention has been paid to the buoyant jets or plumes mixing behaviours at far-field regions. In addition, knowledge of accurate Reynolds stress and turbulent heat flux distributions are valuable for industrial CFD applications reliant on RANS based solvers for buoyant jets in crossflow problems.

The work presented in this paper uses direct numerical simulations (DNS) data to further our understanding of the dynamics of buoyant jets and plumes in a turbulent channel crossflow, and quantify variations in flow statistics as relevant parameters vary. We use the Boussinesq approximation for the buoyancy term, and plumes emanating with different buoyancy and momentum fluxes will be investigated. The next section (Sect. 2) discusses the computational details for DNS, validation of numerical methodology, relevant non-dimensional parameters that govern this flow, and visualisation of coherent structures generated by these flows. Subsequently we divide the paper into two main sections: Sect. 3 for near-field (closer to the source) and Sect. 4 where flow transition to far-field. Within each section we present mean and Reynolds stress statistics as the flow changes from a purely momentum source, i.e., jet-in-crossflow to a pure buoyancy source, i.e., plume-in-crossflow, and in-between where both momentum and buoyancy sources are present. Finally, we will discuss the dependence of back-layering distance on the parameters in Sect. 5 before presenting summary and conclusions in Sect. 6.

2 Computational setup and non-dimensional parameters

2.1 Governing equations and numerical setup

The present simulations use equations of mass, momentum and energy (or temperature) conservation for an incompressible constant property fluid neglecting any heating of fluid due to viscosity along with the Boussinesq approximation for buoyancy effects:

$$\begin{aligned} \frac{\partial u_{i}}{\partial x_{i}}= & {} 0, \end{aligned}$$

(1a)

$$\begin{aligned} \frac{\partial u_{i}}{\partial t}+u_{j} \frac{\partial u_i}{\partial x_j}= & {} -\frac{1}{\rho } \frac{\partial p}{\partial x_{i}}+\nu \frac{\partial ^2 u_i}{\partial x_j^2} + g_{\delta _{i2}} \beta \left( T -T_0 \right) , \end{aligned}$$

(1b)

$$\begin{aligned} \frac{\partial T}{\partial t}+u_{j} \frac{\partial T}{\partial x_j}= & {} \kappa \frac{\partial ^2 T}{\partial x_j^2}, \end{aligned}$$

(1c)

Fig. 1

Sketch of computational domain for three dimensional simulation

where the subscripts i and j are the usual tensor notation, u is the flow velocity, T is the temperature, $\rho$ and $\nu$ are constant fluid density and kinematic viscosity and $\beta$ is the coefficient of thermal expansion; T and $T_0$ are local fluid temperature and inlet reference temperature and $\kappa$ is thermal diffusivity. All fluid properties are assumed to be constant, and considering the working fluid as air, we take a constant value of Prandtl number $Pr=0.71$, where $Pr=\nu / \kappa$. The acceleration due to gravity g is in the negative y direction (c.f. Fig. 1).

Equations in (1) are solved with a publicly available spectral element code, Nek5000 [15,16,17]. The spectral element method is an accurate numerical method for solving partial differential equations, especially if the geometry is complex. Nek5000 uses high-order Gauss–Lobatto–Legendre (GLL) polynomials with quadrature rules to achieve a high order of accuracy with minimal diffusion and dispersion errors. A third order temporal discretization scheme is applied for these simulations. The semi-implicit backward-difference formulae of order 3 (BDF3) are applied for the adaptive time stepping scheme. For the simulation to be stable, the maximum Courant number is set at 0.5. To enforce continuity, the pressure correction method is used. No subgrid-scale model is used in the computation. Nek5000 has been successfully used in the aerospace and aeronautics, biology, gas industry, nuclear power engineering, etc. to model and simulate practical engineering problems [18,19,20,21].

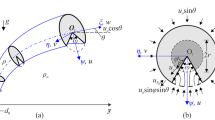
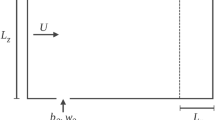
The numerical configuration is depicted in Fig. 1, and involves two stages of domains. The first stage involves a simulation of pure wall turbulence in a stream- and span-wise periodic channel flow without temperature, with the aim of generating a turbulent inlet condition for use in the second stage. The second stage consists of the turbulent channel flow passing over a spanwise homogeneous strip of buoyancy and/or momentum flux source located at the bottom wall, before finally exiting through the outlet. The second-stage domain is not periodic in the streamwise direction but only periodic in the spanwise direction. Note that the use of periodic stage one channel allows us to obtain fully developed instantaneous turbulent velocities with substantially lower computational resources compared to using one extremely long channel for the whole simulation. The dimensions of the main channel are denoted by the length L, width W, and half channel height $\delta$.

Figure 1 shows the boundaries defining the downstream computational region (inlet, side, top-wall, bottom-wall and outlet). The boundary condition for the top and bottom walls is no slip. The top as well as the bottom wall (except where the heat source is present) are also assumed to be adiabatic. The inlet temperature is fixed at ambient temperature $T_0$. The velocity and temperature boundary condition at the outlet is set as zero gradients. As mentioned above, the velocity for the inlet is set as Dirichlet boundary condition and comes from the upstream simulation. The flow is driven at a constant bulk velocity, $u_b$.

Table 1 Simulation parameters for the upstream simulation

Some details of the upstream simulation are given in Table 1. The friction Reynolds number $Re_\tau =\delta u_\tau / \nu =180$, where $u_\tau$ is the friction velocity ($u_\tau = \sqrt{ \nu \frac{\partial {\overline{u}}}{\partial y} |_{wall} }$). The instantaneous turbulent profile from the upstream simulation is the instantaneous inlet boundary condition of the downstream simulation. The streamwise, vertical and spanwise directions are denoted by x, y and z, with u, v and w the corresponding velocities.

Table 2 illustrates the size of the computational domain as well as the resolution for downstream stage two simulations. The distance from the center of the source to the inlet and the outlet is $10\delta$ and $20\delta$ respectively. Here the spacing at the center-line is $\Delta y_c^+$, whereas the averaged spacing in the streamwise and spanwise directions are $\Delta {\overline{x}}^+$ and $\Delta {\overline{z}}^+$ respectively, where the superscript $+$ is the symbol for non-dimensionalization with viscous scales, which $y^+=yu_\tau /\nu$. Note that there are 18 grid points below $y^+=10$. In Tables 1 and 2, $n_x$, $n_y$ and $n_z$ are the number of grid points along x, y and z axis. $L_x$ and $L_z$ are streamwise and spanwise domain lengths and $\Delta y^+_{min}$ is for grid spacing closest to the wall. Consistent with [22, 23], at $Re_{\tau }=180$, $(L_x, L_z)=(4\pi \delta , 4\delta )$ is long and wide enough for a fully developed of channel flow. The macro grid points are equally spaced in the streamwise and spanwise directions. Non-uniform grid points are used in the wall-normal direction with a cosine function used to ensure smaller macro elements near the channel walls. The minimum $\Delta y^+$ is 0.0993 ensuring sufficient wall normal resolution. As shown in "Appendix A.1", we find favourable comparison between the mean velocity as well as fluctuating velocity statistics for our upstream $Re_{\tau }=180$ channel flow simulations with other DNS databases. Furthermore, in "Appendix B" we show the sufficiency of the computational domain width by analysing the two-point correlations in the spanwise direction, as well as discuss the grid resolution compared to the Kolmogorov length-scale $\eta$. The grid spacing is about $2\eta$ to $3\eta$.

Table 2 Geometry of the computational domain of the downstream simulation with the mesh resolution

In the main downstream channel simulation, heat source is introduced as a homogeneous strip of heat flux located at the bottom wall as shown in Fig. 1. The distribution of heat source is set as a Gaussian function,

$$\begin{aligned} f_w=\kappa A \exp \left( -(x-x_0)^2/b_T^2 \right) , \end{aligned}$$

(2)

where A is the magnitude of the temperature gradient, $x_0$ is the source location, $b_T$ is the source half-width. The Gaussian distribution is along the x axis and is uniform along the z axis. The heat release rate per unit length Q $[W\cdot m^{-1}]$ is defined as $Q= \rho c_p \int _{-\infty }^{+\infty }f_w \ dx$, and the buoyancy flux is defined as $F_0= g \beta \int _{-\infty }^{+\infty } {f_w \ dx}$, where $c_p$ is specific heat. The unit of $F_0$ is $[m^3 \cdot s^{-3}]$. Thus, the heat source velocity based on the buoyancy flux is defined as,

$$\begin{aligned} v_s=F_0^{1/3}. \end{aligned}$$

(3)

The Gaussian heat distribution function and buoyancy flux definitions are similar to our more recent works on wall-attached plume [24] and plume in a laminar crossflow [25]. The reference temperature and non-dimensional temperature are respectively defined as

$$\begin{aligned} T_{R}=\frac{v_s^2}{g \beta b_T}; \quad T^*=\frac{T-T_0}{T_{R}-T_0} = \frac{T}{T_{R}}, \end{aligned}$$

(4)

where, without loss of generality, we take $T_0=0$ in our simulations since only the temperature difference matters. Note that the above reference temperature uses $b_T$ as the length scale, rather than $\delta$ as in [25] [25], to obtain a simpler expression for Richardson number (defined below) consistent [5] [5].

For cases where source momentum is present, the homogeneous strip used for the heat source is also used for the momentum source. The jet inflow velocity profile $v_j$ is prescribed on the bottom wall as a Dirichlet boundary condition with a parabolic velocity profile multiplied by a smoothing super-Gaussian function [26,27,28,29]:

$$\begin{aligned} \frac{v_j(x)}{u_b}=R\left( 1-\left( \frac{x-x_0}{b_T}\right) ^2\right) \exp \left( -\left( \frac{x-x_0}{0.7b_T} \right) ^4\right) , \end{aligned}$$

(5)

where R is the velocity ratio of the jet centreline velocity ($v_{jc}$) and free-stream bulk flow velocity ($R=v_{jc}/u_b$). The above equation has been used by others in the past for its convenience in computations, and it has a small negative velocity region close to $\pm b_T$ that corresponds to about $0.01\%$ of volume flux, which is not inconsistent with experimental data [30]. Note that the ratio between $v_{jc}$ and bulk jet inflow velocity $v_{jb}$ ($=\frac{1}{2b_T}\int _{-\infty }^\infty v_j(x) \ dx$) is $v_{jc}/v_{jb}$=1.89. Validation of the numerical simulation for a jet-in-crossflow (without any heat source) is presented in Appendix A.2 by comparing three DNSs that match the parameters of data available in the literature [6, 8, 10, 31,32,33]. Comparisons of jet trajectory are made for three different values of R (equal to 3, 6 and 7.34) with others, as well as the mean velocity profile at $x/b_T=2$ downstream of the jet for $R=7.34$ with results in the existing literature. In all cases we find the comparisons favourable.

We now proceed to categorise the flow into relevant non-dimensional groups, and inform how our different numerical simulations vary one or few of these non-dimensional groups.

2.2 Relevant non-dimensional groups

The present flow configuration has three main inputs that are characterised by appropriate dimensional quantities: (i) the inlet turbulent channel flow governed by the half channel height $\delta$ and bulk velocity $u_b$; (ii) the jet source momentum characterised by the jet centreline velocity $v_{jc}$ (or the bulk jet velocity $v_{jb}$) and source width $b_T$, and (iii) the source buoyancy given by the heat source velocity $v_s$ (or the buoyancy flux $F_0$, or the parameter A in Eq. 2) and $b_T$. Adding viscosity ($\nu$), thermal diffusivity ($\kappa$) and the product of gravitational acceleration and thermal expansion coefficient ($g \beta$) also as relevant parameters appearing in the governing equations will result in a total of 8 dimensional parameters leading to 5 non-dimensional groups, say, Prandtl number (Pr), heat source Reynolds number, $Re_s$, the jet Reynolds number, $Re_j$, the turbulent crossflow Reynolds number within the channel $Re_c$, and they are defined as,

$$\begin{aligned} Re_s=\frac{v_s b_T}{\nu }, \quad Re_j=\frac{v_{jc} b_T}{\nu }, \quad Re_c=\frac{u_b \delta }{\nu }, \end{aligned}$$

(6)

as well as $b_T/\delta$, which we fix at 0.05 suggesting a ‘point’ source. We also fix $Re_c = 2833$ that (as mentioned above) corresponds to the friction Reynolds $Re_\tau =\delta u_\tau / \nu =180$, and $Pr=0.71$.

As such, the focus of this work is to understand the buoyant jet within a channel with constant crossflow that originates from a fixed but small $b_T/\delta$ as we vary $Re_s$ and $Re_j$. In fact, within a large body of work where only momentum source is present (i.e., no source buoyancy), the usual non-dimensional group is defined as the ratio of the jet to the bulk channel flow momentum:

$$\begin{aligned} M \equiv \left( \frac{v_{jc}}{u_b}\right) ^2 \frac{b_T}{\delta } = \left( \frac{Re_j}{Re_c}\right) ^2 \frac{\delta }{b_T}. \end{aligned}$$

(7)

For fixed inlet $u_b$, larger M corresponds to a jet-in-crossflow situation, O(1) for buoyant jets and zero for plumes (c.f. Table 3). On the other hand, when both momentum and buoyancy sources are present Richardson number is used to characterise their respective strengths (as the ratio of source buoyancy to momentum flux):

$$\begin{aligned} Ri \equiv \left( \frac{5}{8 \alpha _p} \right) \frac{g\beta \left( T_{R}-T_0 \right) b_T}{v_{jc}^2} = \left( \frac{5}{8 \alpha _p} \right) \left( \frac{v_s}{v_{jc}} \right) ^2 = \left( \frac{5}{8 \alpha _p} \right) \left( \frac{Re_s}{Re_j} \right) ^2, \end{aligned}$$

(8)

where we have used $T_0=0$ and the definition of $T_R$ from (4); also $\alpha _p=0.12$ is the entrainment coefficient (see for example [5, 34,35,36]). We note that the precise value of $\alpha$ has been found to be slightly smaller (0.055 to 0.11) for 2D buoyant jets issuing into a quiescent fluid (e.g., [37, 38]), and hence, the values of Ri will increase slightly if these smaller $\alpha$ are used in the above equation. For the lazy plume or buoyancy dominant plume $Ri \gg 1$, the momentum effect could be neglected, whereas for the momentum dominated plume, $Ri \ll 1$, and the buoyancy and momentum effects are of similar magnitude for $Ri \sim 1$. Physically, Ri can also be related (within an constant) to the ratio of two length scales, $\delta$ and L. Here the length scale $L\equiv v_{jc}^2 b_T/v_s^2$ is typically used when a buoyant jet issues into an infinite ambient (e.g., [37, 38]) and represents the distance beyond which the plume scaling will overtake the jet scaling, and consequently, L is infinite for momentum jets, finite for buoyant jets and zero for plumes. As such, the appropriate non-dimensional group is:

$$\begin{aligned} \frac{\delta }{L} = \frac{\delta v_s^2}{v_{jc}^2 b_T} = \left( \frac{8 \alpha _p}{5} \right) \left( \frac{\delta }{b_T} \right) Ri = 3.84 \,Ri, \end{aligned}$$

(9)

where, to obtain the last equality we have used $b_T/\delta =0.05$ that is constant for all our cases.

Therefore, rather than the non-dimensional groups $Re_s$ and $Re_j$ one can also specify M and Ri or $\delta /L$ (except when the momentum source is zero and $Ri=\infty$, in which case, if needed, a new Ri can be defined using $u_b$ instead of $v_{jc}$).

2.3 Present data set

Table 3 shows the different DNS cases simulated and the corresponding non-dimensional numbers $Re_s$ and $Re_j$, as well as Ri and M along with the symbols used within the paper. The cases are of three different categories depending on the source conditions: jet (Case J1, Case J2, etc), buoyant jet (Case BJ1, Case BJ2, etc), and two buoyant plumes without any source momentum (Case B1 and Case B2).

Table 3 Details of the configuration for planar non-buoyant jets (J), buoyant jets (BJ) and buoyant plumes (B). Note that quantities $l_S$ and $l_T$ are defined in Sects.3.1 and 5, whereas ${\overline{T}}_{in}^*$ and ${T}_{R_{far}}$ are defined in Sects. 3.1 and 4.2

The jet cases (J1 to J4) are primarily for the investigation of recirculation region immediately downstream of the source and comparison with other researchers (in Sect. 3.2). More importantly, however, a single jet case J5 is isolated, and will used to understand how adding a buoyancy source will change the flow characteristics. There are three cases with the same source momentum (i.e., $Re_j=425$ or $M=0.45$) but with increasing source heat flux (i.e, $Re_s$ or Ri). In the next two case (BJ3 and BJ4) Ri (or $Re_s$) in continuously increased. In the last two cases (B1 and B2) source momentum is zero and the source buoyancy flux is increased. Most the analysis in this paper focuses on cases J5 and below in Table 3 where $Re_s$ is increased monotonically. Other quantities presented in the table (e.g., $l_S/\delta$, $l_T/\delta$, ${\overline{T}}_{in}^*$ and others) would be discussed in subsequent sections.

Before presenting detailed flow analysis, in the following some flow structures are presented for two cases.

2.4 Vortical structures in cases BJ1 and B2

Two cases, Case BJ1 – that is governed by a stronger momentum and weak buoyancy source, and Case B2 – that has no momentum and only buoyancy source, are selected to show flow structures in a 3D view.

Figure 2a, b display the turbulent structures in the flow for Case BJ1 and Case B2, respectively, visualised by the iso-surface of the Q-criterion [39] and coloured by the value of the spanwise vorticity $\omega _z$. The quantity Q is defined as:

$$\begin{aligned} Q \equiv \frac{1}{2}\left( \Omega _{ij}\Omega _{ij} - S_{ij}S_{ij} \right) = \frac{1}{4} \omega ^2 - \frac{1}{2} S_{ij}S_{ij}, \end{aligned}$$

(10)

where $\Omega _{ij} = (1/2)(\partial u_i/\partial x_j - \partial u_j/\partial x_i)$, $S_{ij} = (1/2)(\partial u_i/\partial x_j + \partial u_j/\partial x_i)$ are the anti-symmetric and symmetic part of the velocity gradient tensor, and enstrophy $\omega ^2 = \varvec{\omega } \cdot \varvec{\omega }$ with $\varvec{\omega } = \varvec{\nabla } \times \varvec{u}$. The positive values of Q therefore suggest a dominance of enstrophy over strain, and helps to visualise ‘turbulent’ regions. Top panels of Fig. 2a, b use $Q=3$ whereas the bottom panels use a higher $Q=40$ to visualise more intense vortical structures only downstream of the source that masks the weaker vortices upstream within the turbulent wall-flow.

In Fig. 2a the jet flow appears as a blockage that interacts with the crossflow and creates a vortex tube in the spanwise direction near the bottom wall upstream of the source. Along the streamwise direction, several long structures are visible as they attach to the deflected jet flow, starting from the near bottom wall and ending with the mixing of the jet plume with the crossflow. The high mixing region can be observed downstream of the plume, as well as near the top wall where the plume interacts with the top wall. All of these structures merge with turbulence of the channel flow as they move downstream, and create an overall more intense turbulent state (to be discussed later) than the incoming flow.

Fig. 2

Iso-surface of Q-criterion. a Case BJ1. b Case B2. Top-panel $Q=3$, whereas the bottom panel has $Q=40$. The iso-surfaces are coloured by the spanwise vorticity $\omega _z$ normalized by $u_b$ and $\delta$

Figure 2b with only buoyancy source shows that the majority of the turbulent structures are formed closer to the source owing to the breakup of streak-like structures along the streamwise direction. This breakup process, however, occurs far downstream for low Reynolds number laminar cases, as described in [25]. The source generates a significant amount of turbulent structures rising with the warm plume, characterized by strong spanwise vorticity values. At the impinging region along the top wall ($x/\delta \approx 5$), large vorticity values are visible as a result of the back-flow shear.

3 Near field turbulence statistics

This section presents the results of the spanwise and time-averaged fields in the near field of the source. In the next section we would define more precisely the transition from a near to a far field. First, we show the mean velocities normalised by the channel bulk velocity (${\overline{u}}/u_b$ and ${\overline{v}}/u_b$) and the temperatures profile for Case J5 and all the buoyancy assisted cases (BJ1 to BJ4, B1 and B2—see Table 3), in total seven cases. Next, we will focus on immediate vicinity of source where a re-circulation region can form, especially when a momentum source is involved. We will characterise this re-circulation region and compare with other studies carried out for only pure momentum source. Subsequently, we will present data for the wall shear stress and top-wall temperatures that are also relevant quantities for practical tunnel-fires studies. We would close this section with a discussion of the turbulent stress.

3.1 Mean flow and temperature

Figure 3 shows mean ${\overline{u}}/u_b$ and ${\overline{v}}/u_b$ in the first and second column, and temperature normalised with $T_R$ (${\overline{T}}^* \equiv {\overline{T}}/T_R$) in the last column, with rows top to bottom corresponding to cases J5, BJ1, BJ2, BJ3, BJ4, B1 and B2 that arranged in increasing Ri or $Re_s$, i.e., source heat flux increases from top to bottom panels. Note that the contour scales of ${\overline{v}}/u_b$ and ${\overline{T}}^*$ are multiplied by a constant ($C_v$ and $C_T$ respectively) for different cases to accommodate the variation in values between cases.

Fig. 3

Contours of: a ${\overline{u}}/u_b$ (left column) and contour level at 0 (black dashed lines); b ${\overline{v}}/u_b$ (middle column); c ${\overline{T}}^*$. The seven panels top to bottom are numbered 0 to 6 corresponding respectively to cases J5, BJ1, BJ2, BJ3, BJ4, B1 and B2

Figure 3a0 in the first column shows ${\overline{u}}/u_b$ for the jet Case J5. The crossflow coming from the upstream is accelerates around the source region due to the ‘blockage effect’ resulting in a negative flow region. The black dash contour level at ${\overline{u}}/u_b=0$ shows the boundary of this region, which will be characterised in Sect. 3.2. This near-source negative velocity region diminishes with decreasing jet momentum (in panel a1 - Case BJ1), and even further in (a3) and vanishing for increasing $Re_s$ and decreasing $Re_j$ as we move down to panel (a6). Panel (a2) corresponding to Case BJ2 shows a re-circulation region on the top wall as the buoyant jet impinges on the upper channel wall. Interestingly this effect reduced with decreasing $Re_j$ but resurfaces in panel (a6) for the highest $Re_s$, again owing to the rising plume that reaches the top wall (within the region of flow shown).

This rising flow is better observed in the middle column depicting ${\overline{v}}/u_b$. Notice that in panel (b2) a large ‘blob’ of upward moving fluid is observed at the downstream end of the top wall re-circulation region. The upward moving fluid is associated will all cases where buoyancy flux is present in the source, as can be seen in other middle panels (b2 to b6). The highest $Re_s$ Case B2 (in panel b6) has an increased upward velocity among all cases except Case BJ2 (in panel b2).

The cause of back-flow owing to the rising plume is even better visualised in the temperature contours shown in the rightmost column of Fig. 3. Not surprisingly, panel (c2) shows the hot plume traversing along the top wall. In fact, as will be clarified later, in all cases where a source buoyancy is present (i.e., panels c1 to c6) the plume will eventually reach the top wall, although it might take a longer streamwise distance in some cases. This location where plume hits the top wall in a crucial position in road tunnel fires etc, and called the back-layering distance. It is positive if the plume on the top wall is observed downstream of the source, and negative otherwise. In panel (c2) the back-layering position—defined as the smallest x-location on the top wall where shear-stress becomes negative (e.g., [25]) – normalised by the half-channel height $l_S/\delta$ takes a negative value $\approx -1.7$. Table 3 shows $l_S/\delta$ for all cases with buoyancy.

Notice also that table 3 presents data for the mean temperature obtained at the source inlet (${\overline{T}}_{in}$) under two normalisations:

$$\begin{aligned} {\overline{T}}_{in}^*\equiv \frac{{\overline{T}}_{in}}{T_R}=\frac{{\overline{T}}_{in}}{(u_s^2/g\beta b_T)} {~\mathrm and,~} \frac{{\overline{T}}_{in}}{(u_b^2/g\beta \delta )}. \end{aligned}$$

(11)

For our study, at fixed $u_b$ and $\delta$, the latter normalisation more transparently shows a monotonically increasing value of temperature with increasing $Re_s$. On the other hand, ${\overline{T}}^*$ – normalised with $T_R$ that depends primarily on the source buoyancy flux – first increases and then reaches an approximate constant with increasing $Re_s$. In fact, ${\overline{T}}^*$ reaches towards a constant value as momentum reduces (or is zero) suggesting the efficacy of this normalisation for pure plumes. Furthermore, the highest value of ${\overline{T}}_{in}^*$ corresponds with Case BJ2, which as discussed Fig. 3(c2) also is the first case to show a back-layering and smallest $l_S/\delta$ value.

3.2 Near-field re-circulation region

The re-circulation region discussed above is observed clearly in Fig. 4a, b that shows mean streamlines for cases J5 (only momentum source) and BJ2 (a buoyant jet case) respectively. In Fig. 4a the jet discharges from $x/\delta =0$ into the crossflow, and is deflected to form a confined re-circulation region. (There are two smaller re-circulation regions upstream of the source on which we do not focus here.) The size of the dominant re-circulation vortex zone is primarily affected by the ratio of the jet width to the channel height, as well as the velocity ratio, $R\equiv v_{jc}/u_b$. These two factors are, however, combined into a single non-dimensional parameter, the momentum flux ratio, M that is expected to govern the jet trajectory. The value of M are listed in table 3 for all cases.

Fig. 4

Streamline pattern from the time- and spanwise-averaged flow field. a Case J5. b Case BJ2

The re-circulation vortex zone is usually characterized by its inner length, $L_i$, and inner height, $H_i$, as depicted in Fig. 4. Here $L_i$ is defined as the horizontal distance between the jet and the stagnation point (where the wall shear stress changes sign and indicated by the red point on the bottom wall in Fig. 4), and $H_i$, is the maximum height of the stagnation line. Figure 5 displays how $L_i$ and $H_i$ change with respect to the momentum flux ratio M. The results of this study are compared to those from prior literature and show good agreement. It is challenging to measure the limits of small M values in experiments due to the physically small size of the re-circulation vortex zone. On the other hand, the RANS method may have limitations in accurately predicting smaller vortices. We also show the values for the buoyant jet cases (in blue symbols). We observe re-circulation regions only for the larger M cases (BJ1 and BJ2), but the size of the reverse flow region reduces with increasing buoyancy for the same M value. Decreasing M and increasing $Re_s$ make the re-circulation region disappear ($H_i$ and $L_i$ are zero).

Fig. 5

The relationship between the momentum flux ratio and a normalised re-circulation vortex zone length comparing with [40,41,42,43,44]; b normalised re-circulation vortex zone inner height comparing with [40, 42,43,44]. The coloured symbols,

,

,

 etc, see Table 3, and are from the present DNS

3.3 Top wall shear stress and temperature

As mentioned before, from an application point of view, top-wall temperature as well as occasionally mean shear stress play an important role in characterising buoyant jets in channel crossflows. Figure 6a, b respectively display shear stress ($\tau _w^+$) and temperature profiles of the top wall. For the pure jet case J5 (in red) the increased shear stress is due to flow acceleration above the re-circulation region, and there is reduction in $\tau _w^+$ downstream of the re-circulation region as the flow decelerates. A similar trend is observed for Case BJ1 also, but Case BJ2 with its large top-wall re-circulation region shows a different trend—the large negative $\tau _w^+$ is caused by the reverse flow and a subsequent increase owing to the accelerate flow downstream of this reverse-flow. Interestingly, the other buoyant jet cases, and in particular the plume case (BJ5), show a trend similar to BJ2—which is owing to the hot rising air impinging on the top wall.

On the other hand, top-wall temperature shown in Fig. 6b continues to increase before plateauing to a constant value. Note that the abscissa is on a log scale, which as mentioned before is to accommodate the broad range of ${\overline{T}}^*$ values observed across the cases. As perhaps antipated, for pure buoyant plume cases (B1 and B2) as well as the next larger Ri case BJ4, ${\overline{T}}^*$ approaches a similar value suggestive of a top-wall temperature becoming independent of Ri at high Ri values. The buoyant jet cases (BJ2 is particular) show high top-wall temperature, consistent with the description of back-layering discussed in relation to Fig. 3. More importantly, we observe that the $x-$locations where the top-wall ${\overline{T}}^*$ approaches a constant value is almost at the location of the back-layering $l_S/\delta$ (see table 3). This intimate connection between back-layering location, the top-wall temperature and wall-stress is owing to the flow structures governed by the rising plume overcoming the momentum of the crossflow.

Fig. 6

Top wall profile of a wall shear stress; b wall temperature. Symbols

(J5),

(BJ1),

(BJ2),

(BJ3),

(BJ4),

(B1),

(B2); also see table 3

3.4 Turbulent stresses

Turbulence is created by the interaction between the crossflow and upwards moving jet, which is more intense than the wall-turbulence present in the oncoming channel flow. Turbulent stresses resulting from this interaction is presented in Fig. 7. The left column in (a) shows $\overline{u'u'}^+$ (where $u' = u - {\overline{u}}$ is velocity fluctuation denoted by prime superscript), the middle (b) and right (c) columns respectively show the fluxes $\overline{u'v'}^+$ and $\overline{v'T'}^+$ both of which are present in Reynolds averaged Navier–Stokes (RANS) equation and used in modelling turbulence. The rows of Fig. 7 are arranged in a manner similar to Fig. 3 where the top (0) to bottom (6) row correspond respectively to Case J5 to Case B2. Note that the superscript $+$ indicates quantities scaled by the wall shear velocity of the inlet $u_{\tau }$ for velocity and reference temperature, $T_{R}$. For example, $\overline{v'T'}^+= \overline{v'T'} / (u_{\tau } T_{R})$.

Fig. 7

Contours of: a $\overline{u'u'}^+$ (left column); b $\overline{u'v'}^+$ (middle column); c $\overline{v'T'}^+$. The seven panels top to bottom are numbered 0 to 6 corresponding respectively to cases J5, BJ1, BJ2, BJ3, BJ4, B1 and B2

The location of intense turbulence is best observed in $\overline{u'u'}^+$ on the left column (a) of Fig. 7. For momentum dominated cases (e.g., say J5, BJ1 and BJ2) the high mean shear regions (c.f., Fig. 3) is the main cause of turbulent production, and hence high turbulence. The cases dominated by buoyancy, however, have low mean shear and high regions of turbulence is concentrated where the plume hits the top-wall (see for example Fig. 7(a6)).

Reynolds stresses $\overline{u'v'}^+$ (in the middle column) follow a similar pattern, but now rather than taking only negative values as in wall-turbulence (see upstream values before the source) they also takes positive values. The positive and negative $\overline{u'v'}^+$ are consistent with the sign of the mean shear being negative and positive, respectively, owing to the jet (especially in Fig. 7(b0), (b1) and (b2)). For cases dominated by buoyancy, most positive $\overline{u'v'}^+$ comes from the upward moving (positive $v'$) hotter fluid towards the top wall (where ${\overline{u}}$ is less and hence a positive $u'$).

Fig. 8

Contours of turbulent production $\overline{u'v'}^+ d {\overline{u}}^+/dy^+$: a0 case J5; a2 case BJ2; a6 case B2. These three panels correspond to panels (a0, b0 and c0), (a2, b2 and c2), and (a6, b6 and c6), in Figs.  3 and 7

The vertical temperature flux $\overline{v'T'}^+$ (in the right column) has mostly positive value owing to a rising (positive $v'$) hotter (positive $T'$) fluid, except within the re-circulation regions immediately downstream of the buoyant jet (c.f., Fig. 7 c0 and c1). Again, as mentioned for the mean temperature results, note the large variation in the magnitudes of $\overline{v'T'}^+$ among the cases. Further, temperature in Case J5 represents passive scalar and hence its absolute magnitude is not relevant.

To further illustrate the effect of mean shear on turbulence production, in Fig. 8 contours of turbulent production $\overline{u'v'}^+ d {\overline{u}}^+/dy^+$ are displayed for three cases: J5, BJ2 and B2. Note that a negative $\overline{u'v'}^+ d {\overline{u}}^+/dy^+$ aid in turbulence production, which can be approximately deciphered from $\overline{u'u'}$ contours in Fig. 7’s first column. Figure 8 shows a dominant negative value at most locations roughly coinciding with large $\overline{u'u'}$. As a passing we note that buoyant production: $g \beta \overline{v'T'}$ can be inferred from Fig. 7’s last column.

Thus far, we have considered statistics in the near field of the source. In the following we will focus on the far field statistics. Before that, however, we briefly show that for all cases with buoyancy (almost irrespective of Ri) the flow ‘transitions’ from a near field region where the plume might appear similar to the one developing in a shear flow to far field where plume attaches to the top wall before continuing to mix downstream.

4 Transition to far field and turbulent far field statistics

4.1 Transition from near to far field

The change in flow behaviour progressing downstream is visualised in Figs. 9a, b that respectively show normalised mean temperature field (${\overline{T}}^*$) for cases BJ1 and B2 representing the extreme buoyancy scenarios that we have. Here (unlike Fig. 3 right column) we have extended the abscissa $x/\delta$ to 15 that shows a longer domain. Interestingly, for both cases BJ1 (with large source momentum) and B2 (zero source momentum and largest buoyancy), the plume initially remains in the lower half of the channel, and then within a short axial distance moves up and attaches to the top wall.

The peak temperature across y at each x-location is identified and plotted as a black solid line. The abrupt change in the y-location of the peak temperature as we move downstream is evident. We would refer to the upstream of this temperature jump location as the near field and further downstream as the far field region. Perhaps not surprisingly, this jump location is proportional to the ‘back-layering’ location because both relate to the same physical process of plume lifting to the top wall. The back-layering location ($l_S/\delta$), where the top-wall shear stress first becomes zero, are presented in Table 3, which are 4.6 and 2.2 for cases BJ1 and B2, showing that even though $l_S/\delta$ is mostly proportional but it is smaller than the temperature jump location. Note that particularly for Case B2 Figs. 3a6 and b6 show the small reverse flow and a strong upward velocity both of which aid on the lifting of the plume. We will return to the location of temperature jump in Sect. 5.

The eddies of wall-turbulent flow (that increase in size with distance from the wall, e.g., [45, 46]) has approximately opposite directions of rotation (owing to opposite mean shear sign) in the bottom and top half of the channel. It appears that the bottom plume is therefore confined by these eddies (at least for our set of cases), until buoyancy forces the plume above the centreline, at which point the top-half eddies work in tandem with the buoyancy to attach the plume to the top wall. We observe (although not shown here) that the plume centerlines for all cases roughly follow a similar trajectory, but are lifted to the top wall from a sightly lower y and x location for an increasing value of total buoyancy flux (which is defined later in (13b) as a combined effect of momentum and imposed heat flux). We note that the pure jet case J5 remains within the lower half for the present parameters, with no buoyancy to assist the scalar in moving to the top channel half.

Figure 9a, b also show the top and bottom boundary of the plume (identified as 10% of the peak temperature at a given x) in black dashed-dotted lines. These boundaries become difficult to define where the plume lifts up towards the top wall, and these boundaries do stop closer to the $l/\delta$.

Fig. 9

Mean temperature contours for a Case BJ1 b Case B2. Black solid lines—maximum temperature location a particular x; back dashed lines—y-locations where temperature drops to $10\%$ of the maximum for a given x; and white solid lines—weighted plume centreline $y_c$

For completeness, we also present the weighted ‘plume centreline’ ($y_c$) at each x-location calculated using: $y_c(x)={\int _{0}^{2\delta } y {\overline{T}}dy}/{\int _{0}^{2\delta } {\overline{T}}dy}$ in white solid lines in Fig. 9a, b. In studies of round source (as opposed to our planar plume) defining a centreline, say using peak temperature location, causes difficulties due to the 3D nature of the plume [47]. In our case, it is clear that $y_c$ in Fig. 9a, b is almost insensitive to the lift-up of the plume towards the top wall, which is an important feature that is not captured by $y_c$. As such, we will use the traditional peak temperature location to define the plume centreline.

A plume can only be defined in the near-field region, whereas in the far-field region, the temperature is more mixed with the peak temperature consistently adjacent to the top wall. In the following we present some relevant turbulent statistics in this far-field region.

Fig. 10

Far field velocity and temperature profile at $x/\delta =15$. Top panel: mean quantities, and bottom panel: turbulent stresses. a ${\overline{u}}/u_b$; b ${\overline{v}}/u_b$; c ${\overline{T}}/T_{R_{far}}$; d $\overline{u'u'}^+$; e $\overline{u'v'}^+$; and (f) $\overline{v'T'}/(u_b T_{R_{far}})$. Colours and symbols representing different cases are in table 3. Black dashed lines in (a) and (d) show the corresponding distributions for the turbulent channel flow upstream of the source location

4.2 Far-field turbulence statistics

The mean and turbulence statistics at a downstream location, $x/\delta =15$, are presented in Fig. 10a–f, where the top panel shows mean quantities and the bottom panel selected turbulent stresses. For all cases except Case BJ2 (where we observe back-layering and complicated top and bottom wall recirculation zones) by $x/\delta =15$ the flow has reached a situation that is not changing significantly further downstream.

Figure 10a for ${\overline{u}}/u_b$ shows similarity between all cases, except of course Case BJ2 (that indicates a slight back-flow, owing to another recirulation region). The flow is continuously moving towards the top-wall because of buoyancy, as observed in Fig. 10b, and consequently the mean shear stress ($|d{\overline{u}}/dy|$) at the top wall is greater compared to the bottom wall. Interestingly, in comparison to the turbulent channel flow upstream (shown in black dashed line in Fig. 10a) the developed flows have a larger wall shear stress, which is reflection of a highly turbulent state in the downstream part of the channel.

Temperature (in Fig. 10c) has been reasonably mixed throughout the channel, although the peak mean temperature is still on the top wall. Normalisation of ${\overline{T}}$ with $T_R$, as in Fig. 3(right column), produces an expansive range of values since $T_R$ is exclusively based on the diffusive heat flux, whereas the flow within the buoyant jet will have a convective source component too. Therefore we will try to estimate a far field reference temperature by integrating the temperature Eq. (1c) within the flow volume:

$$\begin{aligned} \int _{0}^{2\delta } \left( {\overline{T}}{\overline{u}} + \overline{T'u'} \right) _{far} \textrm{d}y = \int \left( {\overline{T}}{\overline{v}} - \kappa \frac{\partial T}{\partial y} \right) _{source}\textrm{d}x, \end{aligned}$$

(12)

where we have taken into account that the incoming flow has $T=0$; also, the left-hand-side integral is taken ‘far’ downstream from the source (that we take to be $x/\delta =15$) and the integral on the right-hand-side is along the bottom wall over the source location. From the data we know that the integral of turbulent correlation term ($\overline{T'u'}$) is small (about $0.1\%$) compared to the mean (${\overline{T}}{\overline{u}}$). Therefore, we can define a reference far field temperature (noting that far field bulk flow rate is the sum of incoming channel and the source flow rates):

$$\begin{aligned} T_{R_{far}}\equiv & {} \frac{\int \left( {\overline{T}}{\overline{v}} - \kappa \frac{\partial T}{\partial y} \right) _{source}\textrm{d}x}{(2\delta \,u_b + 2b_T v_{jb})} \end{aligned}$$

(13a)

$$\begin{aligned}\equiv & {} \frac{\int \left( {\overline{T}}{\overline{v}}\right) _{source}\textrm{d}x + F_0/(g\beta )}{(2\delta \,u_b + 2b_T v_{jb})}, \end{aligned}$$

(13b)

where, the numerator of the above equations is the total buoyancy flux. As such, when ${\overline{T}}$ in Fig. 10c is normalised with $T_{R_{far}}$, the range of values are around O(1). This suggests that the far field temperature can be reasonably represented by the known input parameters, especially for lower source momentum cases. The numerical values of $T_{R_{far}}$ (normalised with $(u_b^2/g\beta \delta )$) are presented Table 3. They show that $T_{R_{far}}/(u_b^2/g\beta \delta )$ increases from Case BJ1 to BJ2 owing to convective (first term in LHS of (13b)), and then decreases as the source momentum decreases, and finally peaks for Case B2 because of the highest diffusive flux (second term in LHS of (13b)) but no source momentum.

The non-buoyant case J5 (in red colour), i.e., passive scalar transport from a jet-in-crossflow, is characteristically different to the buoyant cases; ${\overline{v}}$ is negative and peak in passive scalar (${\overline{T}}$) is below the centreline. In fact, this feature of ${\overline{T}}$ is similar to the near-field character of the buoyant cases—see Fig. 9. The fact that the location of scalar peak remains close to the bottom wall (or ‘ground’) is a generic feature of passive scalar dispersion within a turbulent boundary layer when the source is located closer to the ground (see for example, [48,49,50]).

Turbulent stresses $\overline{u'u'}$ and $\overline{u'v'}$ in Fig. 10d, e show trends similar to the upstream channel and the non-buoyant case, but with reduced stresses on the top wall compared to the bottom wall owing to slight turbulence suppression by the buoyancy effects. However, both the top and bottom wall $\overline{u'u'}$ in Fig. 10d is higher than the upstream channel distribution shown by the black dashed line, again indicating the increased turbulence activity when a momentum or buoyancy source is present.

Turbulent buoyancy flux $\overline{v'T'}$ (in Fig. 10f) on the other hand is predominantly positive for the non-buoyant case and negative for buoyant cases because of opposing mean temperature variation with height (for example, in the non-buoyant case an upward fluid parcel with positive $v'$ encounters a positive $T'$ because of reduction in ${\overline{T}}$ with y). We contrast these far field negative $\overline{v'T'}$ values for buoyant cases with the positive $\overline{v'T'}$ in the near field. In the near field, mean temperature predominantly decreases with height, and therefore, a positive $v'$ leads to positive $T'$; hence to a positive $\overline{v'T'}$. Once the plume hits the top wall, the temperature gradient flips, i.e., mean temperature is increasing with height leading to a negative $\overline{v'T'}$. Therefore, a general conclusion (at least within the present simulations) is a positive/negative $\overline{v'T'}$ upstream/downstream of the transition region (i.e., where the plume suddenly rises to the top wall).

5 Discussion—on the back-layering length

Before we present our summary and conclusion, we briefly discuss an important practical application issue the back-layering length. In applications, negative back-layering length ($l_S/\delta$) is not desirable, which is maintained positive by increasing bulk velocity $u_b$. In fact there is standard (1/3rd) scaling of Froude number (based on $u_b$) and heat flux (e.g., [14, 25]) that says that to keep the back-layering length zero $u_b\sim v_s$. In the present study we keep $u_b$ constant and vary $v_s$ as well as momentum flux. Therefore, we now have an extra parameter on which $l_S/\delta$ depends. In Fig. 11a, b we present $l_S/\delta$ as a function of $Re_j$ versus $Re_s$ and M versus Ri, respectively. Since we have only limited cases we have extrapolated the data to fill the contour diagram—which makes it speculative. Nevertheless, this assists in displaying the over trend visually. For small $Re_j$ it is clear that increasing $Re_s$ will reduce the back-layering length, although this trend is not obvious for fixed M and increasing Ri. However, for fixed Ri, increasing M will reduce $l_S/\delta$, whereas for fixed $Re_s$ increasing $Re_j$ produce a non-monotonic change in $l_S/\delta$. Overall, it appears that there is no simple functional form for $l_S/\delta$ either with ($Re_j,~Re_s$) or (M,  Ri).

Fig. 11

a and b Back-layering length ($l_S/\delta$) as a function of parameters—an extrapolated, and hence, speculative view; a $Re_j$ versus $Re_s$, and b M versus Ri, where Ri is on a log-scale. c $l_S/\delta$ (with a white circle inside the symbols) and $l_T/\delta$ (in filled symbols with shades of blue) as a function of normalised $T_{R_{far}}$. For symbols see Table 3, where for $l_T/\delta$ the outer shades of the symbols have been changed to a blue colour

Some progress can be made if we recall that $T_{R_{far}}$ based on the total buoyancy flux (c.f. Eq. 13b) showed a more-or-less monotonic behaviour with $l_S/\delta$ in Table 3. In Fig. 11c normalised $T_{R_{far}}$ is plotted against $l_S/\delta$, and the approximate monotonic behaviour is evident where increasing $T_{R_{far}}$ shows a decreasing $l_S$. Note, however, that for one set increasing $T_{R_{far}}$ increases $l_S$, leading to a slight non-monotonic behaviour. At this point we introduce another ‘back-layering distance’ $l_T$ as the x-location where the maximum temperature lifts off from the bottom half channel to the top (c.f. Fig. 9). This is a sharp jump, and its location for different cases is presented in Table 3 as $l_T/\delta$. In Fig. 11c we plot normalised $T_{R_{far}}$ versus $l_T/\delta$, and a clear monotonic trend is evident. This strongly suggests that the net buoyancy flux presented as $T_{R_{far}}$ is a parameter that might be able to scale the back-layering distance. Further testing will be required to ascertain the efficacy of $T_{R_{far}}$.

6 Summary and conclusions

Motivated by practical applications such as tunnel fires and owing to the dearth of fully resolved simulations, we set up a series of 3D DNS wherein the momentum and heat flux at the bottom wall of a turbulent channel flow are systematically varied. After ensuring the quality of the DNS by comparing with other DNS with only momentum source, and testing for grid resolution, we present the flow structures and turbulence statistics. There are five non-dimensional parameters, and we fix three (Prandtl, $Pr=0.71$, incoming Reynolds number, $Re_\tau =180$ and source width to channel height ratio, $b_T/\delta = 1/20$), and vary the other two (source momentum and heat flux Reynolds $Re_j,~Re_s$ or equivalently jet to crossflow momentum ratio and Richardson numbers M,  Ri). We find that inclusion of buoyancy to the existing momentum source creates smaller turbulent structures.

We separate the results into the near-field and far field. In the near field, observations of mean velocity points to the re-circulation regions downstream of momentum sources at the bottom wall, but these reverse flow regions disappear with the inclusion of heat flux assisted by smaller and more intense turbulence. Interestingly, with increasing buoyancy flux, we start observing re-circulation regions on the top wall instead. These re-circulation zones disappear with increasing heat flux, but when pure plumes (without momentum source) of large magnitudes are introduced, the top-wall re-circulation region reappears. The re-circulation regions are accompanied by the mean vertical velocity created by the buoyancy effects are also visualised in the mean temperature distributions. The Reynolds normal and shear stresses show more complicated behaviours, with a significant increase in turbulence at the appropriate combinations of momentum and heat flux sources. The turbulent vertical temperature flux and shear stress are again governed by the buoyancy fluxes, rather than the mean shear. It is observed that temperature normalised by the source heat flux reference temperature ($T_{ref}$) results in appropriate collapse of temperature when heat flux is stronger, but results in a large variation in the final temperatures when a strong momentum source is present. We also characterise the ‘traditional’ back-layering locations $l_S/\delta$ (where the top-wall shear stress first vanishes) for each case, that shows a non-monotonic change with the heat flux.

We notice that all cases with buoyancy, even with slight buoyancy and strong momentum source results in the plume being lifted up from the bottom half of the channel to the top half. This lift up is quite abrupt, that happens at a sharp x-location. Interestingly, although the lift up location roughly follows proportionately the back-layering distance, lift up happen much downstream of $l_S/\delta$. We, therefore, define a another back-layering distance $l_T$ where the plume lifts to the top half. Subsequently, we observe the ‘far-field’ mean quantities and Reynolds stresses. The flow is found to be more turbulent both from the increased mean wall shear stress and increased turbulence compared to the incoming turbulent channel flow. Again the temperature profiles did not scale with the heat flux reference temperature $T_{ref}$. To resolve this, we use the mean temperature equation and define a new reference temperature ($T_{R_{far}}$) based on the ‘total heat flux’ that is the sum of the input heat flux and the heat carried by source momentum flux owing to source wall temperature. The temperature $T_{R_{far}}$ scales the far-field temperature well.

Finally, in trying to understand the functional relationship between the back-layering length $l_S$ and the input parameters, we plot (an extrapolated) $l_s$ as the function of our two non-dimensional parameters ($Re_j,~Re_s$) or (M,  Ri). Although there was some understandable trends (when source momentum was negligible), unfortunately, we were not able to find a clear relationship on this two dimension parameter plane. Interestingly, however, when $l_S/\delta$ is plotted against $T_{R_{far}}$ an approximate monotonic behaviour is observed. Furthermore, a strict monotonic relationship was found when the new back-layering length $l_T/\delta$ was plotted against $T_{R_{far}}$, providing some hope of a scaling in future.

Appendices

Appendix A: Validation of the numerical simulation

1.1 A.1 Validation of upstream turbulent channel flow

Here comparisons are made with our upstream turbulent channel flow simulations with some of the DNS databases from the existing literature. Figure 12a, b show respectively the mean streamwise velocity profile (${\overline{u}}^+$) and fluctuating velocity statistics ($u^{\prime +}_{rms}, ~v^{\prime +}_{rms},~w^{\prime +}_{rms},~\overline{u^{\prime } v^{\prime }}^+$) obtained from the upstream simulation. The profiles are compared with others [22, 23, 52], showing good agreement.

1.2 A.2 Validation of jet in crossflow results with other literature

Fig. 12

a The mean velocity profile in wall units compared with [52] [52] at $Re_{\tau }=180$. b Root mean square fluctuating velocity and Reynolds shear stress profiles in wall units compared with [22] [22] and [23] [23] at $Re_{\tau }=180$

A few extra simulations (i.e., different to those mentioned in the main text) are carried for comparison with open literature data on jet-in-crossflow, and to validate our numerical method. Three DNSs are performed with an source momentum, and heat source set to zero, i.e., $v_s=0$, at velocity ratios $R=v_{jc}/u_b$ of 3, 6 and 7.34. The details of the flow configuration for validation are shown in Table. 4 where $\delta /b_T$ also has been changed to match with the data in the literature.

Fig. 13

a Jet trajectories for three different velocity ratios (R): ${\textcircled {{A}}}$ for $R=3$, and comparisons made with PB(1967) [6] and V(2002) [31]; ${\textcircled {{B}}}$ for $R=6$, and compared with data from C(1974) [32], V(2002) [31] and C(2002) [33]; ${\textcircled {{C}}}$ at $R=7.34$ compared with CH(1991) [8] and JW(1996) [10]. b Normalised velocity at $x/(2b_T)=2$ downstream of the jet exit at $R=7.34$ comparing with [8, 10]

Table 4 Details of parameter for validation setup

Figure 13a shows mean jet trajectory into the crossflow, where the data are presented as three groups ${\textcircled {{A}}}$, ${\textcircled {{B}}}$ and ${\textcircled {{C}}}$ corresponding to $R=3$, 6 and 7.34. The present DNS is shown with a solid line and data from literature as symbols. The present results are in good agreement with those in the existing literature. Figure 13b shows the normalized velocity profile for $R=7.34$ at $x/(2b_T)=2$ downstream of the jet exit. Here $u_{max}$ is the maximum velocity at the given cross-section. The present work shows the expected back-flow region (indicated by negative streamwise velocity) in the vicinity of the jet exit. The maximum velocity of the profile is located where the jet bends and flows downstream. The present data are, again, consistent with those available in the literature.

Appendix B: Domain width sufficiency from two-point correlation analysis and grid resolutions

In order to properly capture the 3D nature of the flow, it is important to allow sufficient spanwise computational domain width for the turbulent structure to freely develop. However, conducting 3D DNS can be computationally expensive. To balance the trade-off between computational cost and accuracy, it is crucial to choose the appropriate spanwise domain length (W). Ideally, W should be wide enough to allow the free development of turbulent structures without excessive computational costs. To assess the impact of the spanwise direction on the turbulent structures, the two-point spanwise correlation method can be used. When W is sufficiently large, the correlation values in the spanwise direction should approach relatively small values, indicating that the spanwise structures have fully developed.

The two-point spanwise correlation at a particular z-location $z_i$ is defined as,

$$\begin{aligned} R_{uu}(s_z;x,y)=\frac{ \overline{u'(x,y,z,t) u'(x,y,z+s_z,t)} }{\sigma _u(z)\sigma _u(z)} \end{aligned}$$

(B1)

where $\overline{(\cdot )}$ is averaging over different z locations and time, $u'(x,y,z,t)=u(x,y,z,t)-{\overline{u}}(x,y)$ with ${\overline{u}}$ is the mean velocity, $s_z$ is the distance in spanwise direction and $\sigma _u$ is the standard deviation of the fluctuation velocity. The double u subscript in $R_{uu}$ indicates the correlation of a velocity fluctuation component with itself. Similar to $R_{uu}$, we can define $R_{vv}$ and $R_{ww}$. Since the domain is periodic in the spanwise direction, the two-point spanwise correlation is shown only for the half-width of the channel ($W/2\delta$).

Figure 14 shows $R_{uu}$, $R_{vv}$ and $R_{ww}$ for the Case B2 (in Table 3). Nine specific locations are picked to illustrate the spanwise correlation. Figure 14a–c, i.e. each column, shows the locations immediately behind the source ($x/\delta =0.2$), where the plume rises ($x/\delta =2$) and far downstream ($x/\delta =8$), as for each x location, we pick three wall normal location (rows). All the correlations drop rapidly, especially for the first and second columns because the source disturbs the flow and interacts with the crossflow. All the correlations reach close to zero, which means that the computational domain is sufficiently wide. It is interesting that the correlations for the third column do not fall off as fast as the first and second columns. Especially for the near wall region, $R_{uu}$ and $R_{ww}$ drop more gently, see Fig. 14c.1 and c.3. It is because, due to the buoyancy flux, the warm fluid concentrate near the top wall and the cold fluid concentrate near the bottom wall, thus forming the natural temperature gradient. The natural temperature gradient leads to the turbulent structure with a larger coherent length. Still, the two-point spanwise correlation illustrates the adequacy of the computational domain width.

Fig. 14

Spanwise two-point correlation for Case B2. Three columns from a to c represents the streamwise location of $x/\delta =0.2, 2.0, 8.0$. Three rows from 1 to 3 represent to the wall-normal location of $y/\delta =0.2, 1.0, 1.8$ respectively

In order to show that the mesh resolution is fine enough, the spanwise averaged ratio of local mesh size and Kolmogorov microscale is evaluated. The local mesh size is calculated by the geometric mean of local mesh size for each direction: $\Delta \equiv \left( \Delta x \Delta y \Delta z \right) ^{1/3}$. The Kolmogorov scale is calculated as, $\eta =\left( \nu ^3/ \varepsilon \right) ^{1/4}$, where $\varepsilon$ is the dissipation rate, which is calculated as:

$$\begin{aligned} \varepsilon =2\nu \overline{s'_{ij}s'_{ij}}, \quad s'_{ij}=\frac{1}{2}\left( \frac{\partial u'_i}{\partial x_j}+\frac{\partial u'_j}{\partial x_i} \right) \end{aligned}$$

(B2)

Based on Fig. 2, the turbulent structures are abundant near the source where the plume rises. We find that the maximum $\Delta /\eta$ is about 2, which is located far upstream close to the wall region. Furthermore, all the value of $\Delta /\eta$ is smaller than 3, which suggests that the mesh resolution can be considered fine enough for the DNS of the buoyant jet in crossflow.

Figure 15 shows the trajectories comparing three different mesh resolutions, where the details of mesh resolution are shown in Table. 5. We find that for medium mesh resolution, the trajectory overlaps with the one with the fine mesh. Thus, we conclude that the medium mesh is good enough to capture the flow.

Fig. 15

Trajectory with different mesh resolution (see Table. 5)

Table 5 Mesh information for mesh independent test