1 Introduction

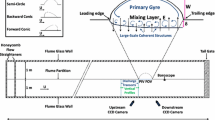
Lateral cavities are commonly found in natural rivers, ocean shores, and hydraulic structures. These cavities significantly impact the mass-exchange process in river systems, including solute transport and dispersion [1,2,3,4,5,6], and exhibit different characteristics from the groin fields [7,8,9,10]. For instance, Juez et al. [7] treated the lateral cavities as one of the macro-roughness elements and revealed a strong relation between the flow hydrodynamics and the sediment dynamics in the lateral cavities. In comparison with the explorations of groin fields by Uijttewaal et al. [8] and McCoy et al. [9], groin fields demonstrated a feature that weakens the mass exchange between the main channel and the lateral embayment due to the interactions among turbulent vortices formed in the corners of the groins. As for the solute transport, Jackson et al. [1] examined the mean residence time in lateral cavities and identified the nondimensional parameters used to calculate it; these parameters include Froude number, Reynolds number, cavity aspect ratio (ratio of cavity width to length), relative depth ratio (ratio of cavity depth to shear layer depth), a shape factor representing the degree of cavity equidimensionality, which is defined by the ratio of the square root of cavity width multiplied by cavity depth to the cavity length, and a roughness factor defined by the ratio of shear velocity to the main channel velocity. Their proposed relationship provides a basic understanding of how the cavity affects solute transport and can be used to predict the time variation characteristics of the dispersion of pollutants or other contaminants. In addition to affecting the mass-exchange process, cavities also affect flow patterns [11,12,13,14] and sediment transportation [7, 15, 16]. For example, Weitbrecht et al. [3] used particle image velocimetry (PIV) in a groin field experiment to measure the instantaneous velocity field and found that the velocity distribution changed sharply around the mixing layer at the connection between the lateral cavity and the mainstream. The recirculating flow inside the lateral cavity increased the streamwise velocity in the mixing layer. Similar findings were observed by Mignot et al. [12], who conducted a two-dimensional (2D) analysis of the vortex motion and examined the coherent structures in the mixing layer. Compared with the transverse velocity, which exhibits a zero-mean periodic signal, the streamwise velocity is strongly affected by the vortices. This highlights the importance of investigating the vortex motion around the cavity to predict the velocity distribution and classify the flow regime. Kadotani et al. [13] conducted experiments and numerical simulations using a large-eddy simulation (LES) model to examine water surface oscillation. They categorized four types of water surface oscillations based on the location of the maximum contribution area to the oscillation using the proper orthogonal decomposition (POD) method and identified the most active type as a high Froude number case with a relatively wide cavity, where intense oscillation occurred between the cavity and the opposite main channel, causing a relatively large increase in the mean water level. In addition to the changes in the flow pattern, sediment transportation and deposition characteristics in cavities have also been widely studied. For instance, de Oliveira et al. [15] investigated the relationship between sediment transport and vegetation density in lateral cavities. According to their results, as the vegetation density increased, the flow velocity inside the cavity decreased, and secondary circulation appeared; this was unexpected with the chosen aspect ratio (cavity length to width = 0.60). The final results showed that an increase in vegetation density promoted deposition inside the cavity. Although this study focused on sediment deposition, the appearance of secondary circulation is an interesting topic for further investigation. Besides, the influence of bank lateral cavities on the fine sediment deposits was studied by Juez et al. [17], with a focus on whether sediment deposits can be flushed away by an increase of flow discharge in the main channel which is practical in the sediment exchange processes in natural rivers conveying fine sediments.

Regarding the problem of secondary circulation, Mignot et al. [11] summarized a basic scheme for identifying the relationship between the geometrical aspect ratio of a cavity and the number of recirculating cells. The results indicate that when the cavity gradually changes from relatively narrow to relatively wide in the length direction, a strong vortex develops and occupies most of the cavity space. It subsequently generates two contra-rotating recirculation vortices aligned along the flow direction, with the upstream vortex located farther from the interface. For wider cavities, the contra-rotating vortices disappear, forming a single strong vortex. However, when the cavity is sufficiently wide, two contra-rotating vortices form again; in this case, the two vortices are aligned perpendicularly to the interface. According to this criterion, there should only be a single cell in the aforementioned case [15], with an aspect ratio of 0.60. However, owing to the impact of other parameters, such as vegetation density, such inconsistencies exist.

Kimura et al. conducted a fundamental investigation of suspended sediment transport in a lateral cavity [16]. The related secondary flow, which exists in the cavity, was considered to evaluate its effect on both flow structures and sediment transport. They proposed a typical tea leaf paradox, also known as the tea-pot effect, which describes the phenomenon of tea leaves in a cup migrating to the center and bottom of the cup after being stirred, rather than being forced to the edges of the cup, as would be expected in a spiral centrifuge. A solution to this paradox was first proposed by Einstein in a paper where he explained the erosion of riverbanks. Similar to tea leaves, sediment is deposited in the bottom center area of the cavity. The secondary flow is also widespread in real three-dimensional (3D) flow and significantly impacts the momentum exchange, velocity redistribution, and sediment movement. Juez et al. studied the sediment transport tendency in multiple lateral cavities in addition to a single lateral cavity [7, 17]. A strong correlation was observed between the vortical structure within the cavity and the sediment settling area. The sediment entrainment and eventual settling in the cavities were attributed to the main recirculating eddy. The analysis of different geometries shows that complex and intricate flow patterns generally favor deposition. The mechanism behind this conclusion is explained by relating the residence times of captured sediments inside the cavity to the possibility of settling. The more intricate the flow with 3D vortex motions and turbulences, the longer the path that the trapped sediments must travel inside the cavity. This corresponds to a longer residence time, indicating a higher probability of sediment settling.

In summary, open-channel cavities have a non-negligible effect on the flow velocity distribution, mass exchange, sediment, and other solute transport. Therefore, simulation and understanding of the flow characteristics around a cavity area are essential for a wide range of further investigations. Although the effects of open-channel cavities on various aspects have been extensively studied, the exploration of 3D flow characteristics is still in its early stages. Most existing studies have focused on the physical scale or arrangement of the cavity; however, research on the shallowness parameter (L/H, where L is the typical horizontal or transverse length scale and H is the representative water depth) [18] and how the 3D flow, including secondary flow, differs from the horizontal 2D flow structures, is limited. This difference can be described as the 3D flow effect, which has been frequently discussed in fluid research [19, 20]. In other words, only one component of vorticity can be considered in 2D models. However, in three dimensions, all three components of vorticity have an important role in the horizontal flow structure. One of the most relevant parameters in the investigation of the strength of the 3D flow effect is the shallowness parameter ɛ (which is discussed in detail in this paper in Sect. 4). Although this shallowness parameter provides a method for quantitatively assessing the strength of the 3D flow effect, the specific manifestation of the 3D flow effect is still unclear. Therefore, a reliable and efficient computational model that can reproduce the flow pattern around a cavity and capture the 3D flow effect is required. Recently, direct numerical simulation (DNS) and large-eddy simulation (LES) methods have been recognized and used as 3D models to simulate simple geometries such as a lateral cavity. For example, Ouro et al. [21] used LES to investigate the main drivers in the mass and momentum exchange between the main channel and lateral cavity. Large streamwise and transversal velocities were mostly found in regions near the bottom and top lids at the mouth of the cavities, which indicated the 3D nature of the exchange processes. However, high computational costs limit their application to complex bed profiles. Therefore, the third-order model to solve the shallow water equations was proposed by Navas-Montilla et al. [22, 23] with high-resolution data of water surface and velocity oscillations as well as the seiche amplitude distributions for different oscillation modes. Moreover, using 3D models alone, although capable of considering 3D flow effect, does not allow the isolation of its specific manifestations compared to a 2D model. In contrast, this study focuses on the effect of incorporating the three-dimensional flow effects, extract and evaluate the role of the 3D flow effect with varying shallowness conditions on the lateral cavity flow dynamics. Similar objectives of revealing the 3D flow hydrodynamics can be found in Ouro et al. [21], where investigations into the mass and momentum transfer mechanisms between the main channel and the lateral embayment were conducted under sufficiently deep-water conditions to induce a pronounced 3D flow characteristic. However, this study concentrated on much shallower water conditions and smaller intervals for case settings, notably distinguished it from the previous one. In other words, this study adopts an advanced 2D calculation model called the bottom velocity computation (BVC) model [24, 25], along with 3D models, to discern differences in simulation results among the 2D, advanced 2D, and 3D models and reveal the role of 3D flow structures on water flow dynamics in an open-channel cavity and its variation with the shallowness parameter. The gap in flow characteristics among the experimental and calculation results with a full-three-dimensional calculation (3DC) model, the BVC model in which 3D flow effects can be partially evaluated in the momentum equations, and the conventional two-dimensional calculation (2DC) model to solve the shallow water equation without considering velocity and pressure distribution in the vertical direction is also explored.

2 Calculation methods and experimental conditions

This study uses a quasi-3D depth-integrated model called the bottom velocity computation method [24, 25] to directly capture and investigate the 3D flow effect. In addition to depth integrated continuity equation and momentum equations which have been used in the 2DC model, this model combines a set of equations, including equations for the depth-integrated vorticity and water surface velocity, and the equation for depth-averaged velocity in the vertical direction to evaluate the bottom velocity and pressure using the vertical velocity distribution of a cubic polynomial Eq. (1) and a non-hydrostatic pressure distribution Eq. (2), respectively.

$$\begin{array}{c}{u}_{i}=\Delta {u}_{i}\left(12{\eta }^{3}-12{\eta }^{2}+1\right)+\delta {u}_{i}\left(-4{\eta }^{3}+3{\eta }^{2}\right)+{U}_{i},\#\end{array}$$
(1)
$$\begin{array}{c}\frac{p}{\rho }=gh\eta +\frac{d{p}_{b}}{\rho }\eta ,\#\end{array}$$
(2)

where \(i,j=1\left(x\right), 2\left(y\right)\); \({u}_{i}=\) horizontal velocity; \(\Delta {u}_{i}={u}_{si}-{U}_{i}\), \({U}_{i}=\) depth-averaged horizontal velocity; \(\eta =\left({z}_{s}-z\right)/h\), where \({z}_{s}=\) water surface elevation, \(z=\) vertical direction, \(h\) is water depth, and \(h={z}_{s}-{z}_{b}\), where \({z}_{b}=\) bottom elevation; \(\delta {u}_{i}={u}_{si}-{u}_{bi}\), where \({u}_{si}=\) horizontal water surface velocity, and \({u}_{bi}=\) horizontal bottom velocity; p is pressure; \(d{p}_{b}=\) bottom pressure deviation. To simplify and maintain computational stability, this study assumed that the pressure deviation from the hydrostatic pressure distribution followed a linear vertical distribution, as shown in Eq. (2), while neglecting the temporal variation term and the horizontal momentum exchange induced by shear stress. Further details regarding the governing equations and numerical schemes can be found in previous reports [24, 25].

By applying the vorticity equations in the horizontal direction, the BVC method can solve the 3D vortex motions (Fig. 1). The governing equations are listed in Table 1. The SBVC model is a reduction of the GBVC model’s solution of vertical velocity and non-hydrostatic pressure and adopts the assumption of shallow water conditions, where the representative horizontal scale is significantly larger than the representative water depth (i.e., ɛ <  < 1). The differences in the calculation results between the GBVC and SBVC indicate the effects of shallow water conditions. The SBVC model reduces to the 2DC model for the equilibrium conditions of the depth-integrated vorticity and surface velocity, in which the vertical velocity distribution becomes the uniform velocity profile such as the log-low velocity distribution [26]. The differences in the calculation results of depth and depth-averaged velocity between SBVC and 2DC indicate the effect of the vertical distribution of the velocity and momentum transfer with the dispersion terms. A one-equation model that solves the transport equation for turbulence energy [27, 28] is applied to the depth integrated models, in which the kinetic turbulence energy production due to the vertical distribution of flow velocity is evaluated [24, 25].

Table 1 Governing equations for the BVC method
Full size table
Fig. 1
figure 1

Unknown variables of the BVC method

Full size image

In this study, 3D calculations using OpenFOAM are also performed for comparison. For the turbulence model, a standard k-ɛ turbulence model was applied.

3 Model validation

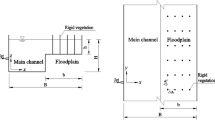
To validate the reliability of the BVC model, the case of a single cavity is first selected for validation in this section. In this case, two sets of experimental results with the same cavity geometric scale but different hydraulic conditions in Kimura and Hosoda [14] and Kimura et al. [16] were used. The basic experimental conditions are illustrated in Fig. 2.

Fig. 2
figure 2

Schematic of the open channel cavity in experiments

Full size image

As shown in Fig. 2, an open-channel lateral cavity with a length L = 22.5 cm is attached to the sidewall of the open channel. The cavity extends W = 15 cm from the main channel, and the width of the main channel is B = 10 cm. For Case 1, which corresponded to Run 1 in Kimura et al. [16], the streamwise velocity distribution at cross-section A-A’ was measured at the middle layer of the water depth. In Case 2, which corresponded to Run 2 in Kimura and Hosoda [14], temporal velocity variations and surface elevation oscillations were measured at Points V and S, respectively. The temporal velocity variations were also measured at half the water depth. Other hydraulic parameters are listed in Table 2.

Table 2 Experimental and numerical parameters
Full size table

For Case 1, OpenFOAM was used as a full three-dimensional calculation model to enable a better comparison of the 2DC, SBVC, and GBVC models with the experimental results. The grid sizes were maintained consistently in the x- and y-directions at 0.0025 m for both the BVC and 3DC models. The differences between the GBVC and 3DC models are attributed to the resolution when calculating the velocity, vertical distribution of pressure, and turbulence models. The grid size in the z-direction of the 3DC model was set to 0.001 m. The mesh used in the BVC model was extended upstream by a distance of five times the cavity length to obtain a stable approaching flow in the main channel. By contrast, in the 3DC model, this distance was exactly equal to the cavity length. For the downstream extension distance, both meshes were the cavity lengths. In this case, the BVC and 3DC models contained 30,600 and 162,000 grids, respectively. Figure 3 shows the overall distribution of the grids around the cavity. For the roughness condition, all the methods were set to smooth-bed calculations, corresponding to the actual experimental conditions. In addition, the time step of the BVC model was set to 0.1 s, whereas it was set automatically in OpenFOAM.

Fig. 3
figure 3

Grid system around the cavity (Left: BVC; Right: OpenFOAM)

Full size image

To validate the BVC model, both the streamwise velocity distribution and temporal variation of the water surface and streamwise velocity are examined. Figure 4 presents the streamwise velocity distribution at cross-section A-A’. The horizontal axis represents the distance from the main channel, where the area of the main channel ranges from 0 to 0.10 m, and beyond 0.10 m is the range within the cavity. The vertical axis shows the streamwise velocity in half the water depth of the 2DC, SBVC, and GBVC models, which were obtained based on the cubic polynomial distribution Eq. (1) to ensure a better comparison with the streamwise velocity in half the water depth layer for the 3DC and experimental results. All results presented in Fig. 4 are time-averaged results calculated for 10 s after reaching the steady state. There were significant differences in the velocity distribution around the junction of the main channel and cavity, as well as near the upper boundary wall of the cavity, especially between the 2DC and other models. The overestimation of velocity magnitude also can be observed in the results of other 2D models, such as the high-resolution 2D model developed by Navas-Montilla et al. [22]. This characteristic should be a general limitation of 2D models considering only one component of vorticity. However, the simulation results of the BVC models demonstrated good agreement with the experimental and 3DC model results under relatively shallow water conditions. This suggests that the shallow water assumption (ɛ <  < 1) is reasonable for this condition; this may also explain the minimal differences between the SBVC and GBVC models.

Fig. 4
figure 4

Streamwise velocity distribution at cross-section A-A’ with various methods

Full size image

The 3D flow effect can be isolated by comparing the results of the BVC and 2DC models. Specifically, the secondary flow contained in the 3D flow, to a certain extent, resists drastic changes in the flow field by transferring momentum outward from the cavity center, thereby increasing the velocity gradient in the junction between the main channel and the cavity and decreasing the velocity gradient near the upper boundary of the cavity.

Further analysis of the temporal variation in streamwise velocity and water surface is shown in Fig. 5. The horizontal axes represent the time elapsed for the experiment or the time after the simulation reaches the steady state. To facilitate a more direct comparison of the differences in the oscillation amplitude and period, the starting points of both the experimental and numerical simulation results are adjusted to coincide with the wave crest. Therefore, the time at which the first wave crest appears in the selected time period for both the experimental and numerical simulation results is identified and denoted as T0. The specific values of the period, varied range, and variances are listed in Table 3. The simulation results obtained using the SBVC and GBVC models accurately reproduce the oscillation amplitude, whereas the 2DC model overestimates the amplifications. This is because the SBVC and GBVC models include a mechanism that converts the horizontal vorticity motion into turbulent energy by generating velocity strain and vertical vorticity with depth-integrated vorticity equations, whereas the 2DC includes no energy attenuation mechanism other than the bottom shear stress unless vertical vorticity exists. All the numerical simulation models provide a time series of velocities at half the water depth calculated from Eq. (1), which closely matches the experimental measurement conditions shown in Fig. 5. However, the models struggle to reproduce small fluctuations in the instantaneous velocities induced by turbulent energy dissipation and shear-layer instability. Consequently, this slightly increases the period and accounts for the observed gaps. Despite this limitation, the overall findings validate the BVC model and its potential in revealing the flow patterns in open-channel lateral cavity areas.

Fig. 5
figure 5

Temporal variation of water surface and streamwise velocity

Full size image
Table 3 Temporal variation characteristics
Full size table

To clarify the importance in considering 3D flow effects in horizontal flow field calculation and calculation scheme for solving the shallow water equations, comparisons with accurate numerical simulation for shallow water flow model become an interest in validation purposes. The following validation part compares the 2DC and GBVC models to previous investigation for a single cavity flow by Navas-Montilla et al. [22], in which a high-resolution depth-averaged unsteady RANS shallow water equation model (HSWE) and experimental measurements are presented. The cavity was configurated with a length (L) of 0.24 m and, width (W) of 0.24 m, connected to the main channel with a width (B) of 0.24 m and a slope of 1/400, as shown in Fig. 6. Five experimental cases with different discharges and water depths were conducted. The corresponding hydraulic conditions are listed in Table 4. The grid sizes were consistently maintained at 0.0048 m in the x- and y-directions for the 2DC and GBVC models, whereas for HSWE, the computational mesh was constructed using square cells with dimensions of 0.0024 m [22].

Fig. 6
figure 6

Sketch of the cavity configuration in Navas-Montilla et al. [22]

Full size image
Table 4 Experimental conditions conducted by Navas-Montilla et al. [22]
Full size table

In Fig. 7a, the 2DC model exhibited similar characteristics to the HSWE results, and both numerical models tended to overestimate velocity magnitudes and gradient within the cavity area—a common weakness or limitation of 2D models or shallow water model. The shallow water models failed to reproduce changes in flow patterns investigated by the experiment with increasing water depth from Case S1 to S5, such as the reduction of the low-velocity magnitude region within the cavity and the expansion of the high streamwise velocity region near the mouth of the cavity. This problem of the shallow water models is considered to be caused by the governing equation, implying the presence of the 3D flow effect. In Fig. 7b, the GBVC model exhibited a better agreement with the experimental measurements illustrated in Fig. B.16, Fig. B.17, and Fig. 6 in Navas-Montilla et al. [22]. The GBVC model showed better performance than shallow water models, especially near the boundary walls of the cavity, with notable improvements observed in the transverse velocity distribution. Furthermore, the GBVC model successfully reproduced the change in velocity distribution patterns: as water depth increased, the velocity increases were suppressed compared to the shallow water models. This underscored the importance of evaluating the effect of 3D flows on the horizontal flow field within the cavity and simultaneously highlighted the potential of employing the GBVC model to investigate the 3D flow effect.

Fig. 7
figure 7figure 7

a Time-averaged streamwise velocity (left), transverse velocity (middle), and horizontal velocity magnitude (right) distribution obtained from the 2DC model. From top to bottom corresponds to cases S5, S4, S3, S2, and S1 in Navas-Montilla et al. [22]. b Time-averaged streamwise velocity (left), transverse velocity (middle), and horizontal velocity magnitude (right) distribution obtained from the GBVC model. From top to bottom corresponds to cases S5, S4, S3, S2, and S1 in Navas-Montilla et al. [22]

Full size image

4 Aspect ratio effect

4.1 Geometrical and shallowness parameters

Aspect ratios, such as the ratio of channel length or width to water depth and the ratio of cavity length to width, are often used to further study their effects [7, 11, 29]. Conventionally, the characteristic length-to-water depth ratio, also known as the shallowness parameter, indicates the relatively deep or shallow water condition. However, in this study, the “shallowness parameter” is defined as the opposite ratio (ε = ratio of water depth to the cavity length) to more accurately reflect changes in water depth. As the cavity length remains constant, the magnitude of ε directly reflects the water depth; the larger the value of ε, the greater the water depth. Generally, a value of approximately 0.05 indicates shallow water, and increasing values indicate greater water depths and stronger 3D flow effects [18]. Mignot et al. [11] selected the geometrical aspect ratio W/L, where W is the cavity width and L is its length (see Fig. 2), as a dimensionless parameter for investigating the evolution of the main flow patterns. They divided lateral cavities into three categories based on W/L: narrow (W/L < 0.6), close-to-square (0.6 ≤ W/L ≤ 2.0), and wide (W/L > 2.0). This study focuses on an intermediate case with W/L = 0.67, which is used to examine 3D flow effects. The cavity configuration in detail is read as follows: a main channel with a width (B) of 10 cm and a cavity with a streamwise length (L) of 22.5 cm and a transverse length (W) of 15 cm. In the previous study [11], the velocity fields were measured; the results indicate that in slightly wider cavities (0.6 ≤ W/L ≤ 2.0), a single cell occupies most of the available area with two small additional secondary cells confined in opposite corners. Similar vortex motions and flow characteristics are also observed in the present study, as shown in Fig. 8.

Fig. 8
figure 8

Secondary vortices observed in the upper corners of the cavity

Full size image

However, this characteristic is only observed under shallow water conditions. As the water depth increases, the two secondary cells become less noticeable and eventually disappear. Further analysis of this phenomenon is presented in Sect. 4.3.

To investigate the relationship between the water depth and 3D vortex motions, numerical simulations were conducted for six different sets of water depths (Table 5) based on the shallowness parameter and the representative velocity in the main channel of Case 1 (Italic in Table 5). Together with a single cavity Case 1, which has a shallowness parameter of approximately 0.04, numerical simulations were conducted using 2DC, BVC, and 3DC models for shallowness parameters ranging from 0.01 to 0.16. To ensure a fair comparison of the results, the same grid division criterion and simulation parameters as in Case 1 were adopted and used for the model validation. This included parameters such as the time step and roughness condition.

Table 5 Numerical simulation conditions
Full size table

Regarding the existence of resonant wave such as a seiche in each configuration, in the validation Case 2, which was also investigated experimentally by Kimura and Hosoda [14], a seiche was reported to be observed with a period of 0.875 s. The simulation results proposed in the validation section also confirmed that. The oscillation mode was identified as a longitudinal mode with a single node along the streamwise direction and none along the transverse direction. This oscillation mode strongly depended on another geometrical aspect ratio, (W + B)/B, where W represents the cavity width and B denotes the main channel width. Experimental studies have consistently demonstrated that the oscillation mode is influenced by this aspect ratio. It is generally accepted that narrow cavities exhibit longitudinal modes, while wider cavities exhibit transverse modes. In this study, the cavity was configured the same as in Run 2 of Kimura and Hosoda [14], with a geometrical aspect ratio (W + B)/B = 2.50. A similar configuration of (W + B)/B = 2.00 was investigated by Wolfinger et al. [30] and Tuna et al. [31], while Perrot-Minot et al. [32] explored (W + B)/B = 2.66. All of these studies reported a longitudinal mode, consistent with the observations in this study. While for the rest of the configurations, the free surface oscillation periods in each configuration were examined based on the GBVC results and compared to the theoretical characteristics periods according to the Eq. (3) proposed by Lamb [33] and Rabinovich [34].

$$\begin{array}{c}\left\{\begin{array}{c}{f}_{{n}_{x}{n}_{y}}=\frac{c}{2}{\left[{\left(\frac{{n}_{x}}{L}\right)}^{2}+{\left(\frac{{n}_{y}}{W+B}\right)}^{2}\right]}^\frac{1}{2}\\ c=\frac{g}{2\pi {f}_{{n}_{x}{n}_{y}}}tanh\frac{2\pi h{f}_{{n}_{x}{n}_{y}}}{c}\end{array}\right.\#\end{array}$$
(3)

where \({n}_{x}\) and \({n}_{y}\) are the numbers of nodes along the streamwise direction and transverse direction, respectively; \(c\) is the celerity of the water waves; \(g\) is the acceleration of gravity.

Moreover, a previous study focused on seiches in lateral cavities conducted by Perrot-Minot et al. [35] revealed that the Froude number in the range of 0.55 to 0.85 does not affect the oscillation mode selection. Instead, it suggested that the geometrical aspect ratio of the cavity governs the mode selection. This finding ensured that the longitudinal mode, with \({n}_{x}\) = 1 and \({n}_{y}\) = 0 in Eq. (3), is suitable for \(\varepsilon\) = 0.01, 0.02, 0.04, and 0.09. Correspondingly, the results in Table 6 showed that the simulation periods obtained from the GBVC model agree with the theoretical periods in the above cases, which indicated the existence of seiche waves. However, in Case \(\varepsilon\) = 0.08, a subsa]ntial disparity was observed between the simulation and theoretical results. Besides, in Cases \(\varepsilon\) = 0.12 and 0.16, the seiche can not be observed through free surface oscillations provided by the simulation results. This should be related to the increase in the energy dissipation with the increasing shallowness parameter, which results in the decrease of seiche energy and its demise. Additionally, in Cases \(\varepsilon\) = 0.08, 0.12, and 0.16, the Froude numbers were lower than 0.55, this suggests that the low Froude numbers should have an impact on the occurrence of seiches. In another investigation conducted under low Froude number conditions by Perrot-Minot et al. [32], the oscillation modes did change with varying Froude numbers, especially those under 0.60. This suggested that not only the geometrical aspect ratio but also the Froude numbers controlled the oscillation modes for Cases \(\varepsilon\) = 0.08, 0.12, and 0.16. More complex oscillation modes may be included by the superposition of more than one specific oscillation mode and the simple theoretical equations do not apply in these cases.

Table 6 Oscillation periods in simulation and analytical estimation
Full size table

4.2 Streamwise velocity distribution

In addition to the results shown in Fig. 4, the longitudinal cross-sectional streamwise velocity distributions at the cavity centerline (i.e., section A-A’) for other shallowness parameter conditions were also extracted for comparison. Figure 9 shows the streamwise velocity at section A-A’, and it is evident that as the shallowness parameter ε increases, the difference in the streamwise velocity within the cavity among the calculation models increases progressively. For instance, when the shallowness parameter is 0.04, as discussed using Fig. 4 in Sect. 3, the gaps are mainly concentrated in the 2DC and other models, occurring in the range of Y > 0.10 m. For a shallowness parameter of 0.08, the SBVC model begins to exhibit a large gap with the 3DC model, whereas the GBVC model still matches the results of the 3DC model. Similar characteristics are observed for the larger shallowness parameters. Table 7 shows the root mean square error (RMSE) calculated for all shallowness parameter cases, where the RMSE is calculated using the 3DC model results as the true values. Overall, the results indicate that the RMSE between 2 and 3DC is significantly larger than that between SBVC/GBVC and 3DC. Moreover, the gap between 2DC/SBVC/GBVC and 3DC gradually increases as the shallowness parameter increases, indicating that the 3D flow effect becomes more prominent as the relative water depth increases. This implies that the 2DC and SBVC models, based on the assumption of shallow water conditions, are no longer suitable for simulating flow characteristics in deeper water.

Fig. 9
figure 9

Streamwise velocity distribution at cross-section A-A’ for different ε

Full size image
Table 7 RMSE of streamwise velocity distribution (m/s)
Full size table

To quantify the strength of the horizontal vortex in the cavity, two points at the A-A' cross-section, namely, the connection area between the main channel and the cavity (Y = 0.10 m) and the inner wall of the cavity (minimum velocity close to the wall), were selected to reflect this strength by calculating the degree of streamwise velocity variation using Eq. (4):

$$\begin{array}{c}\frac{\left|{U}_{min}-{U}_{0.1}\right|}{{U}_{0.1}}\times 100\%.\#\end{array}$$
(4)

Figure 10 (right) illustrates the degree of variation in the streamwise velocity for each shallowness parameter. All the models exhibit the same trend, wherein the degree of variation increases as the shallowness parameter increases. Notably, the 2DC model yields the largest degree of variation, ranging from 140% for a shallowness parameter of 0.01 to 195% for the 0.16 case. This is because, in shallow water conditions, the 3D flow effect is not significant, resulting in similar results across all models. However, for large shallowness parameters, the 2DC model overestimates the degree of velocity change because it fails to consider the momentum exchange and velocity redistribution arising from the 3D flow effect. In other words, the 2DC model cannot evaluate the pressure gradient variation adequately, due to the lack of the momentum transfer induced by secondary flow, resulting in overestimating the horizontal eddy strength in the cavity, which related to the degree of velocity change, and this also explains the differences in predicting the water surface and velocity oscillations.

Fig. 10
figure 10

RMSE of streamwise velocity distribution (left) and streamwise velocity difference for various shallowness parameters (right)

Full size image

Figures 11 and 12 present the flow field characteristics within the cavity by showing the water surface and bottom streamwise velocity distributions, respectively. The horizontal and vertical coordinates in the figures are dimensionless, where the vertical coordinate y/W represents (y-yb)/W, with yb equal to 0.10 m for the boundary between the cavity and the main channel. The three models, 2DC, GBVC, and 3DC, are presented from left to right, and the shallowness parameters 0.04, 0.12, and 0.16 are displayed from top to bottom. Compared to a previous Lagrangian study of a lateral cavity by Engelen et al. [36], who provided horizontal velocity field including streamlines at different elevations above the channel bed, a similar observation can be found in terms of the velocity distribution and extension of streamlines. Figure 13 showed the velocity distribution at the water surface and the bottom elevation obtained from the GBVC model in the case of \(\varepsilon\) = 0.16, which is close to the shallowness condition in Engelen et al. [36]. In Fig. 13, the solid black lines represent the streamlines. The velocity distributions were dimensionless by using the ratio of horizontal velocity magnitude and the bulk velocity in the main channel. To ensure a better comparison, the horizontal and vertical coordinates were adjusted to be consistent with the above-mentioned previous study. For the horizontal velocity distribution, all the results showed that at the center area of the cavity, velocity magnitude was obviously lower than that in the periphery. And near the right boundary wall of the cavity, there existed a significant increase in the velocity magnitude, the GBVC results agreed with the 3D-PTV measurements. For the extension of streamlines, the simulation results are consistent with experimental data both at the bottom elevation and surface elevation. With varying elevations from the bottom to surface, the typical shape of the recirculating flow changed from quasi-circular to a distinct ellipsoidal shape which the main axes were in line with the cavity diagonals. While in terms of the nondimensionalized streamwise velocity distribution among different models, the 2DC model predicts a relatively constant flow pattern in the cavity with symmetrically distributed positive and negative velocity zones across the central section of the cavity (i.e., y/W = 0.5). The same pattern is maintained with the change in the relative water depth; however, the area of the negative velocity zone expands rapidly as the shallowness parameter increases, confirming its overestimation of the streamwise velocity variation. The GBVC and 3DC models exhibit a noticeable asymmetry in the flow pattern, with the distribution of the negative velocity zone significantly different from that predicted by the 2DC model. The maximum negative velocity zone is considerably smaller, and the distribution of the negative velocity zone extends from the lower right corner to the upper left corner of the cavity. Although there are still some differences between the GBVC and 3DC results, they exhibit good consistency in terms of the location of the maximum negative velocity zone in the cavity and its gradual shift toward the lower left as the shallowness parameters increase.

Fig. 11
figure 11

Water surface streamwise velocity distribution with horizontal velocity vectors

Full size image
Fig. 12
figure 12

Bottom streamwise velocity distribution with horizontal velocity vectors

Full size image
Fig. 13
figure 13

Horizontal surface velocity and bottom velocity distribution and streamlines obtained from the GBVC model

Full size image

To gain a more comprehensive understanding of the flow behavior within the cavity, the dimensionless streamwise velocity distribution is presented in Fig. 14. The streamwise velocity profile illustrates the ratio of the streamwise velocity to the approaching flow streamwise velocity in the main channel (U0). The dashed line represents the location where the velocity is zero, whereas nine longitudinal sections along the flow direction, x/L ranging from 0.3 to 0.7, are chosen to exhibit the relative velocity distribution. The figures denoted by a, b, and c correspond to shallowness parameters of ε = 0.04, 0.12, and 0.16, respectively. It is evident that for small shallowness parameters, the flow velocity profiles of the SBVC and GBVC models are consistent with those of the 3DC model. However, the 2DC model overestimates the flow velocity in the area close to the upper boundary wall of the cavity and the main channel. Conversely, for larger shallowness parameters, a considerable deviation exists between the SBVC and 3DC models. Only the GBVC model maintains a good agreement with the 3DC model.

Fig. 14
figure 14figure 14

a Dimensionless streamwise velocity profiles inside the cavity (ɛ = 0.04). b Dimensionless streamwise velocity profiles inside the cavity (ɛ = 0.12). c Dimensionless streamwise velocity profiles inside the cavity (ɛ = 0.16)

Full size image

4.3 Evolution of vortex motions

As shown in Fig. 8 in Sect. 4.1, the open-channel lateral cavity (W/L = 0.67) used in this study should contain a primary vortex that typically occupies most of the cavity area, accompanied by two smaller secondary vortices distributed at the inner corners of the cavity, as presented in previous reports [11]. Nevertheless, the number and distribution patterns of the horizontal eddies undergo significant changes as the relative water depth gradually increases. To quantify the evolution of these horizontal eddies, a vortex identification method, known as the \(\Omega\) vortex identification criterion, was adopted in this study. The details of \(\Omega\) criterion are provided as follows [37, 38]:

A 3D vector field can be decomposed into an irrotational vector and a solenoidal vector field, known as Helmholtz velocity decomposition [39]. Equation (5) shows the velocity gradient tensor, which can be divided into two parts: the first symmetric part, denoted as A, represents the deformation, and the second antisymmetric part, denoted as B, represents the rotation, as shown in Eq. (6). Based on Eq. (6), a parameter \(\Omega\) is introduced and defined as the ratio of the squared norm of the vorticity tensor to the sum of the squared norm of the vorticity tensor and the squared norm of the deformation tensor. This parameter is used to investigate the vortex formation, as shown in Eq. (9). It is noteworthy that \(\Omega\) is dimensionless and normalized within the range of \(\left[\mathrm{0,1}\right]\).

$$\begin{array}{c}\nabla u=\left[\begin{array}{ccc}\frac{\partial U}{\partial x}& \frac{\partial U}{\partial y}& \frac{\partial U}{\partial z}\\ \frac{\partial V}{\partial x}& \frac{\partial V}{\partial y}& \frac{\partial V}{\partial z}\\ \frac{\partial W}{\partial x}& \frac{\partial W}{\partial y}& \frac{\partial W}{\partial z}\end{array}\right],\#\end{array}$$
(5)
$$\begin{array}{c}\nabla u=\frac{1}{2}\left(\nabla u+\nabla {u}^{T}\right)+\frac{1}{2}\left(\nabla u-\nabla {u}^{T}\right)=A+B,\#\end{array}$$
(6)
$$\begin{array}{c}A=\left[\begin{array}{ccc}\frac{\partial U}{\partial x}& \frac{1}{2}\left(\frac{\partial U}{\partial y}+\frac{\partial V}{\partial x}\right)& \frac{1}{2}\left(\frac{\partial U}{\partial z}+\frac{\partial W}{\partial x}\right)\\ \frac{1}{2}\left(\frac{\partial V}{\partial x}+\frac{\partial U}{\partial y}\right)& \frac{\partial V}{\partial y}& \frac{1}{2}\left(\frac{\partial V}{\partial z}+\frac{\partial W}{\partial y}\right)\\ \frac{1}{2}\left(\frac{\partial W}{\partial x}+\frac{\partial U}{\partial z}\right)& \frac{1}{2}\left(\frac{\partial {u}_{k}}{\partial {x}_{j}}+\frac{\partial V}{\partial z}\right)& \frac{\partial W}{\partial z}\end{array}\right],\#\end{array}$$
(7)
$$\begin{array}{c}B=\left[\begin{array}{ccc}0& \frac{1}{2}\left(\frac{\partial U}{\partial y}-\frac{\partial V}{\partial x}\right)& \frac{1}{2}\left(\frac{\partial U}{\partial z}-\frac{\partial W}{\partial x}\right)\\ \frac{1}{2}\left(\frac{\partial V}{\partial x}-\frac{\partial U}{\partial y}\right)& 0& \frac{1}{2}\left(\frac{\partial V}{\partial z}-\frac{\partial W}{\partial y}\right)\\ \frac{1}{2}\left(\frac{\partial W}{\partial x}-\frac{\partial U}{\partial z}\right)& \frac{1}{2}\left(\frac{\partial W}{\partial y}-\frac{\partial V}{\partial z}\right)& 0\end{array}\right],\#\end{array}$$
(8)
$$\begin{array}{c}\Omega =\frac{b}{a+b+\mu },\#\end{array}$$
(9)

where \(U,V,and W\) represent the velocity in \(x,y,and z\) directions, respectively; \(a=trace\left({A}^{T}A\right)=\sum_{i=1}^{3}\sum_{j=1}^{3}{\left({A}_{ij}\right)}^{2}\), the square of Frobenius norm of A; \(b=trace\left({B}^{T}B\right)=\sum_{i=1}^{3}\sum_{j=1}^{3}{\left({B}_{ij}\right)}^{2}\), the square of Frobenius norm of B; \(\mu\) is a small positive number used to prevent the denominator from being zero and can be written as \(\mu =0.001{\times \left(b-a\right)}_{max}\) empirically.

The \(\Omega\) method relies on a threshold to determine the presence of a vortex at a particular point in the flow field, and in practice, a threshold value of 0.52 is recommended [38]. The process used to determine the recommended threshold value is described by Liu et al. in a previous report [40]. Figure 15 illustrates the evolution of the horizontal eddies within the cavity as the shallowness parameter increases from 0.01 to 0.16. The Omega value contour at 0.52 is marked, and the red area highlights the presence of the vortex. The left and right sides show the results of the 2DC, GBVC and 3DC models, respectively. Regarding the primary vortex in the cavity, for low shallowness parameters, the vortex first develops on the right side of the cavity. As the relative water depth increases, the vortex on the right side gradually expands and forms a main vortex that occupies most of the cavity space along with the left-side vortex. This trend is observed through the comparison between the 3DC results and other models. However, the 2DC model predicts a faster main eddy formation rate than the GBVC and 3DC models. These results indicate that the 3D flow effect weakens the development of horizontal eddies to a certain extent and is not conducive to the formation of the main eddy. However, when the relative water depth reaches a certain value (0.16), all the models show almost identical results. Regarding the development of secondary vortices, it can be observed that two small vortices situated in the inner corners of the cavity are present under relatively shallow water conditions. In the 2DC model, two secondary vortices can be identified until the shallowness parameter reaches 0.08. However, the presence of these two secondary vortices is not significantly captured in the GBVC model until the shallowness parameter reached 0.08, but one large secondary vortex occurred in the cases of shallowness parameters 0.08 and 0.12. In the 3DC results, the secondary eddies can be observed at moderate shallowness parameters, which means the secondary eddies were raised by the development of the main vortex but faded away when the main vortex was formed and occupied the cavity area. This phenomenon is similar to the influence of the 3D flow effect on the formation of the primary vortex, wherein the 3D flow effect hinders the formation of the primary vortex, thus suppressing the development of the secondary vortex caused by it under shallow water conditions. This explains why the presence of the secondary vortex is not significant in the GBVC and 3DC models at first. However, as the relative water depth increases, the eddy motion in the horizontal plane becomes significantly stronger than that in the vertical plane. Although the 3D flow effect becomes stronger and hinders the development of the main eddy, the main eddy eventually forms, and the secondary vortex disappears with the gradual formation of the primary vortex.

Fig. 15
figure 15

Omega criterion of vortex identification inside the cavity (0.52 contour lines labeled)

Full size image

With a focus on the horizontal eddy developed inside the cavity, this study did not consider too much on the vortex structures developed in the shear layers, such as the Kelvin–Helmholtz vortices. However, the evolution of the main vortex inside the cavity is not only related to the aspect ratios and shallowness parameters but also indicates the interaction between the main vortex and the Kelvin–Helmholtz vortices. This kind of interaction would affect the mass transfer through the mixing interface between the main channel and the lateral cavity and remains to be further investigated.

The identification of eddies in the flow field also reveals an interesting phenomenon related to the variation in the eddy center location with shallowness parameters. In this study, the vortex center is defined as the point at which the velocity is zero. Figure 16 presents the trends of the vortex center movements in both the streamwise and transverse directions. As the relative water depth increases, the vortex center tends to move from the right half of the cavity to the central part in the streamwise direction, as indicated by the movement of x/L from 0.9 to 0.55.

Fig. 16
figure 16

Movement of vortex center with varying shallowness parameter

Full size image

In the transverse direction, the vortex center moves from the lower half of the cavity to the central part, as indicated by the movement of y/W from 0.30 to 0.50. Overall, the vortex center gradually moves from the lower right part of the cavity to the central area as the relative water depth increases. This feature can be attributed to the influence of the incoming flow direction on vortex formation, as the vortex center tends to be located in the part of the cavity where the flow first enters. In this study, the water flow direction is positive on the x-axis, leading to the concentration of the vortex center in the lower right part of the cavity. If the direction of the water flow is reversed, the vortex center is likely to appear first in the lower-left part of the cavity. The movement trend of the vortex center position can be explained by examining the evolution of the horizontal eddies with respect to the shallowness parameters. Under relatively shallow water conditions, the 3D flow effect hinders the development of horizontal eddies to some extent, resulting in uneven scales and distributions of eddies and preventing the formation of a primary vortex. This leads to significant deviations in the prediction of the vortex center position via numerical simulation models for small shallowness parameter conditions. However, as the relative water depth increases, the resistance of the 3D flow effect gradually becomes less effective, leading to the development of the primary vortex. The horizontal vortex system then has sufficient space in the water depth direction for full development. Consequently, a relatively balanced primary vortex is eventually formed, with the vortex center located at the center of the cavity. In the previous study conducted by Ouro et al. [21], the location of the recirculating main vortex core was also investigated using LES. However, the simulation only covered three different shallowness parameter cases, that is \(\varepsilon\) = 0.14, 0.20, and 0.28, based on the experiments conducted by Juez et al. [7]. As the case of \(\varepsilon\) = 0.14 fell within the interval simulated in this section, the vortex core position was used to compare. The experimental results showed that the core position was (0.58, 0.56) and the LES results showed that the core position was (0.57, 0.52). These two positions were also consistent with the trend of vortex core movements presented in Fig. 16. While for the other two cases with higher shallowness parameters, both the experimental and LES results exhibited similar trends with this paper, that is the vortex core was gradually moving toward the center of the cavity as the shallowness parameter increased.

5 Conclusions

This study investigated the flow patterns and vortex motion characteristics of lateral cavity flow in open channels. To demonstrate the specific performance of the 3D flow effect, a quasi-3D calculation method called the bottom velocity computation model was compared with the traditional 2D and 3D models. The relationship between the 3D flow effect and relative water depth was examined by controlling the shallowness parameter, and the Omega vortex identification criterion was used to analyze the vortex evolution in the cavity. The main findings of this study can be summarized as follows.

  1. (1)

    The 3D flow effect enables resistance to sudden changes in the flow field, such as an increase in the velocity gradient between the main channel and the cavity and a reduction in the velocity gradient at the upper wall of the cavity, thereby reducing the degree of velocity variation.

  2. (2)

    As the relative water depth increases, the strength of the 3D flow effect increases. As the traditional 2DC model does not consider this effect, it tends to overestimate the flow velocity variation.

  3. (3)

    As the relative water depth increases, a primary vortex, which occupies most of the cavity, is gradually formed. However, the 3D flow effect prevents the formation of a horizontal primary vortex and inhibits the formation of secondary vortices.

  4. (4)

    The location of the vortex center in the cavity depends on the direction of the incoming flow. The vortex center tends to appear in the part of the cavity where the flow first enters and gradually moves to the central part of the cavity with the complete development of the primary vortex.

  5. (5)

    The applicability of 2D and advanced 2D models, with an emphasis on the shallowness parameter \(\varepsilon\) (ratio of water depth to the cavity scale), is evaluated by comparing their results to those of the 3D model. The evaluated acceptable ranges of the 2DC, SBVC, and GBVC models are presented to simulate the horizontal flow structure in the lateral cavity as \(\varepsilon\) < 0.04, \(\varepsilon\) < 0.08, and \(\varepsilon\) < 0.16, respectively. Nevertheless, additional investigation into deeper water conditions is required for further clarification.