Skip to main content
SpringerLink
Log in

Flow structure and mean residence times of lateral cavities in open channel flows: influence of bed roughness and shape

  • Original Article
  • Published:
Environmental Fluid Mechanics Aims and scope Submit manuscript

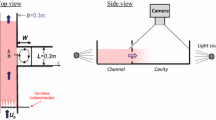
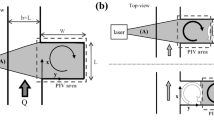
Abstract

Natural lateral cavities in open channels are important because their lower water velocities promote water quality and provide refugia for organisms. Little is known about the influence of natural cavity shapes and roughness on flow structure and exchange dynamics. We investigated the effects of cavity shape (semi-circular, backward conic, and forward conic) and bed roughness on the flow structure and mean residence time (MRT) of a lateral cavity in a flume. All cavity shapes have a flow field dominated by a one-gyre recirculation pattern, contrasting results of rectangular cavities at similar Reynolds number and aspect ratios. Transverse velocity energy spectra indicate the flow is dominated by large-scale quasi-2D coherent structures. Fundamental frequencies of mixing layer vortex shedding are fastest for forward conic cavities and slowest for backward conic cavities. Fluid enters cavities at shallower mixing layer depths, and fluid exits cavities at deeper mixing layer depths. MRTs are smaller for hydraulically smooth cases and forward conic cavities due to higher recirculation velocities. MRTs are larger for rough bed cases and backward conic cavities. Rough flow cases have a strong correlation to a predictive MRT relationship derived by Jackson et al. (Water Resour Res: 10.1002/wrcr.20272, 2013) (R 2 = 0.77); however, this predictive model does not work well for smooth cavities. Two MRT relationships were derived for smooth lateral cavities and both have strong power-law correlations to normalized MRT. Understanding cavity shape and bed roughness effects will provide a guideline for designing lateral embayments in stream restoration projects.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Ahuja K, Mendosa J (1995) Effects of cavity dimensions, boundary layer and temperature on cavity noise with emphasis on benchmark data to validate computational aeroacoustics codes. Final Report Contract NASA-19061, Task 13. NASA Contractor Report

  2. Allan JD (2004) Landscapes and riverscapes: the influence of land use on stream ecosystems. Annu Rev Ecol Evol Syst 35:257–284. doi:10.1146/annurev.ecolsys.35.120202.110122

    Article  Google Scholar 

  3. Anderson EJ, Phanikumar MS (2011) Surface storage dynamics in large rivers: comparing three-dimensional particle transport, one-dimensional fractional derivative, and multi-rate transient storage models. Water Resour Res 47:W09511. doi:10.1029/2010WR010228

    Google Scholar 

  4. Baker DW, Bledsoe BP, Price JM (2012) Stream nitrate uptake and transient storage over a gradient of geomorphic complexity, north-central Colorado, USA. Hydrol Process 26:3241–3252

    Article  Google Scholar 

  5. Becker JF (2012) Natural channel design impacts on reach scale transient storage. M.S. Thesis, State University of New York, New York, New York

  6. Benjamin AS, Denny VE (1979) On the convergence of numerical solutions for two dimensional flows a cavity at large Re. J Comput Phys 33:340–358

    Article  Google Scholar 

  7. Bradshaw N (2012) Design and testing a multi-channel ultrasonic bathymetry probe: comparing turbulence measurements by ADV and PIV methods; and application of potential flow theory to model probe disturbances. MS thesis, University of Idaho, Moscow, ID

  8. Brevis W, García-Villalba M, Niño Y (2014) Experimental and large eddy simulation study of the flow developed by a sequence of lateral obstacles. Environ Fluid Mech. doi:10.1007/s10652-013-9328-x

    Google Scholar 

  9. Budwig R, Goodwin P (2012) The Center for Ecohydraulics Research Mountain StreamLab—a facility for collaborative research and education. In: Aung W, Ilic V, Mertanen O, Moscinski J, Uhomoibhi J (eds), Innovations 2012: world innovations in engineering education and research (pp. 17–28). Potomac, Maryland, USA: iNEER

  10. Buffoni G, Falco P, Griffa A, Zambianchi E (1997) Dispersion processes and residence times in a semi-enclosed basin with recirculating gyres: an application to the Tyrrhenian Sea. J Geophys Res 102(C8):18699–18713

    Article  Google Scholar 

  11. Burggraf OR (1966) Analytical and numerical studies of the structure of steady separated flows. J Fluid Mech 24:113–115

    Article  Google Scholar 

  12. Chang MH, Cheng CH (1999) Predictions of lid-driven flow and heat convection in an arc-shape cavity. Int Commun Heat Mass 26:829–838

    Article  Google Scholar 

  13. Chang K, Constantinescu G, Park SO (2007) Purging of a neutrally buoyant or a dense miscible contaminant from a rectangular cavity. II: case of an incoming fully turbulent overflow. J Hydraul Eng 133(4):373–385. doi:10.1061/(ASCE)0733-9429(2007)133:4(373)

    Article  Google Scholar 

  14. Chang KS, Constantinescu SG, Park S (2006) Analysis of the flow and mass transfer process for the incompressible flow past an open cavity with a laminar and a fully turbulent incoming boundary layer. J Fluid Mech 561:113–145

    Article  Google Scholar 

  15. Chen YH, Cotton GK (1988) Design of roadside channels with flexible linings. Hydraul Eng Circular No. 15, Publication No. FHWA-IP-87-7, U.S. Department of Transportation, Federal Highway Administration, McLean, VA

  16. Cheng M, Hung KC (2006) Vortex structure of steady flow in a rectangular cavity. Comput Fluids 35:1046–1062

    Article  Google Scholar 

  17. Chiang TP, Sheu WH, Hwang RR (1998) Effect of Reynolds number on the eddy structure in a lid-driven cavity. Int J Numer Methods Fluids 26:557–579

    Article  Google Scholar 

  18. Constantinescu G, Sukhodolov A, McCoy A (2009) Mass exchange in a shallow channel flow with a series of groynes: LES study and comparison with laboratory and field experiments. Environ Fluid Mech 9:587–615. doi:10.1007/s10652-009-9155-2

    Article  Google Scholar 

  19. Constantinescu G, Miyawaki S, Rhoads B (2011) The structure of turbulent flow at a river confluence with momentum and velocity ratios close to one: insight provided by an eddy-resolving numerical simulation. Water Resour Res 47(W05507):1–16

    Google Scholar 

  20. Dodds WK (2006) Nutrients and the “dead zone”: the link between nutrient ratios and dissolved oxygen in the northern Gulf of Mexico. Front Ecol Environ 4:211–217

    Article  Google Scholar 

  21. Drost K, Apte SV, Haggerty R, Jackson TR (2014) Parameterization of mean residence times in idealized rectangular dead zones representative of natural streams. J Hydraul Eng. doi:10.1061/(ASCE)HY.1943-7900.0000879,04014035

    Google Scholar 

  22. Drost K, Jackson T, Haggerty R, Apte SV (2012) RANS predictions of turbulent scalar transport in dead zones of natural streams. In: Proceedings of ASME Fluid Eng. Summer Meeting, FEDSM2012-72380, American Society of Mechanical Engineers, Puerto Rico, July 2012

  23. Engelhardt C, Krüger A, Sukhodolov A, Nicklisch A (2004) A study of phytoplankton spatial distributions, flow structure and characteristics of mixing in a river reach with groynes. J Plankton Res 26(11):1351–1366

    Article  Google Scholar 

  24. Ensign SH, Doyle MW (2005) In-channel transient storage and associated nutrient retention: evidence from experimental manipulations. Limnol Oceanogr 50(6):1740–1751

    Article  Google Scholar 

  25. Erturk E, Gokcol C (2006) Fourth-order compact formulation of Navier–Stokes equations and driven cavity flow at high Reynolds numbers. Int J Numer Methods Fluids 50:421–436

    Article  Google Scholar 

  26. Faure TM, Adrianos P, Lusseyran F, Pastur L (2007) Visualizations of the flow inside an open cavity at medium range Reynolds numbers. Exp Fluids 42:169–184

    Article  Google Scholar 

  27. Ghia U, Ghia KN, Shin CT (1982) High-Re solutions for incompressible flow using the Navier–Stokes equations and a multigrid method. J Comput Phys 48:387–411

    Article  Google Scholar 

  28. Glowinski R, Guidoboni G, Pan W (2006) Wall-driven incompressible viscous flow in a two-dimensional semi-circular cavity. J Comput Phys 126:76–91

    Article  Google Scholar 

  29. Gooseff MN, Benson DA, Briggs MA, Weaver M, Wollheim W, Peterson B, Hopkinson CS (2011) Residence time distributions in surface transient storage zones in streams: estimation via signal deconvolution. Water Resour Res 47:W05509. doi:10.1029/2010WR009959

    Google Scholar 

  30. Grace SM, Dewar WG, Wroblewski DE (2004) Experimental investigation of the flow characteristics within a shallow wall cavity for both laminar and turbulent upstream boundary layers. Exp Fluids 36:791–804

    Article  Google Scholar 

  31. Hall RO, Bernhardt ES, Likens GE (2002) Relating nutrient uptake with transient storage in forested mountain streams. Limnol Oceanogr 47:255–265

    Article  Google Scholar 

  32. Hays JR (1966) Mass transport mechanisms in open channel flow. Ph.D Dissertation, Vanderbilt University, Nashville, Tennessee

  33. Henderson FM (1966) Open channel flow. MacMillan Publishing Co., New York

    Google Scholar 

  34. Hinterberger C, Fröhlich J, Rodi W (2007) Three-dimensional and depth-averaged large-eddy simulations of some shallow water flows. J Hydraul Eng 133(8):857–872

    Article  Google Scholar 

  35. Hocut C, Budwig R, Tonina D (2010) Flow disturbances and scour caused by a cylinder that penetrates the free surface of an open channel flow. M.S. Thesis, Center for Ecohydraulics Research, University of Idaho, Boise, ID

  36. Howe MS (1997) Edge, cavity and aperture tones at very low mach numbers. J Fluid Mech 330:61–84

    Article  Google Scholar 

  37. Jackson TR, Haggerty R, Apte SV (2013) A predictive relationship for the mean residence time of lateral cavities in gravel-bed rivers and streams: incorporating streambed roughness and cavity shape. Water Resour Res. doi:10.1002/wrcr.20272

    Google Scholar 

  38. Jackson TR, Haggerty R, Apte SV, Coleman A, Drost KJ (2012) Defining and measuring the mean residence time of lateral surface transient storage zones in small streams. Water Resour Res. doi:10.1029/2012WR012096

    Google Scholar 

  39. Jacobson RB, Femmer SR, McKenney RA (2001) Land-use changes and the physical habitat of streams. U.S. Geological Survey Circular 1175

  40. Kimura I, Hosoda T (1997) Fundamental properties of flows in open channels with dead zone. J Hydraul Eng 123(2):98–107

    Article  Google Scholar 

  41. Kozerski HP, Schwartz R, Hintze T (2006) Tracer measurements in groyne fields for the quantification of mean hydraulic residence times and of the exchange with the stream. Acta Hydrochim Hydrobiol 34:188–200

    Article  Google Scholar 

  42. Kurzke M, Weitbrecht V, Jirka GH (2002) Laboratory concentration measurements for determination of mass exchange between groin fields and main stream. Paper presented at IAHR Conference, ‘River Flow’, Louvain de la Neuve, Belgium

  43. Lancaster J, Hildrew AG (1993) Characterizing in-stream flow refugia. Can J Fish Aquat Sci 50(8):1663–1675

    Article  Google Scholar 

  44. Larson MG, Booth DB, Morley SA (2001) Effectiveness of large woody debris in stream rehabilitation projects in urban basins. Ecol Eng 18(2):211–226

    Article  Google Scholar 

  45. Lin JC, Rockwell D (2001) Organized oscillations of initially turbulent flow past a cavity. AIAA J 39:1139–1151

    Article  Google Scholar 

  46. McCoy A, Constantinescu G, Weber L (2006) Exchange processes in a channel with two vertical emerged obstructions. Flow Turbul Combust 77:97–126. doi:10.1007/s10494-006-9039-1

    Article  Google Scholar 

  47. McCoy A, Constantinescu G, Weber L (2007) A numerical investigation of coherent structures and mass exchange processes in channel flow with two lateral submerged groynes. Water Resour Res 43:W05445. doi:10.01029/02006WR005267

    Google Scholar 

  48. McCoy A, Constantinescu G, Weber L (2008) Numerical investigation of flow hydrodynamics in a channel with a series of groynes. J Hydraul Eng 134(2):157–172

    Article  Google Scholar 

  49. Mercan H, Atalik K (2009) Vortex formation in lid-driven arc-shape cavity flows at high Reynolds numbers. Eur J Mech B. doi:10.1016/j.euromechflu.2008.02.001

    Google Scholar 

  50. Migeon C, Texier A, Pineau G (2000) Effect of lid-driven cavity shape on the flow establishment phase. J Fluid Struct 14:469–488

    Article  Google Scholar 

  51. Moffat RJ (1998) Describing the uncertainties in experimental results. Exp Therm Fluid Sci 1:3–17

    Article  Google Scholar 

  52. Muto Y, Baba Y, Fujita I (2002) Velocity measurements in rectangular embayments attached to a straight open channel. In: Proceedings of river flow 2002, Louvain-la-Neuve, Belgium, 1213–1219

  53. Nauman EB (1981) Residence time distributions in systems governed by the dispersion equation. Chem Eng Sci 36:957–966

    Article  Google Scholar 

  54. O’Connor B, Hondzo M, Harvey JW (2010) Predictive modeling of transient storage and nutrient uptake: implications for stream restoration. J Hydraul Eng 136(12):1018–1032

    Article  Google Scholar 

  55. Ozalp C, Pinarbasi A, Sahin B (2010) Experimental measurement of flow past cavities of different shapes. Exp Therm Fluid Sci 34:505–515

    Article  Google Scholar 

  56. Parker G, Toro-Escobar CM, Ramey M, Beck S (2003) Effect of floodwater extraction on mountain stream morphology. J Hydraul Eng 129(11):885–895

    Article  Google Scholar 

  57. Pereira JCF, Sousa JMM (1995) Experimental and numerical investigation of flow oscillations in a rectangular cavity. J Fluids Eng 117:68–73

    Article  Google Scholar 

  58. Rockwell D (1998) Vortex-body interactions. Ann Rev Fluid Mech 30:199–229

    Article  Google Scholar 

  59. Rockwell D (1983) Invited lecture: oscillations of impinging shear layers. AIAA J 21(5):645–664

    Article  Google Scholar 

  60. Rockwell D, Knisely C (1979) Unsteady features of flow past a cavity. J Hydraul Div 105(8):969–979

    Google Scholar 

  61. Rockwell D, Knisely C (1980) Observation of the three-dimensional nature of unstable flow past a cavity. Phys Fluids 23:425–431

    Article  Google Scholar 

  62. Rockwell D, Naudascher E (1979) Self-sustained oscillations of impinging free shear layers. Ann Rev Fluid Mech 11:67–94

    Article  Google Scholar 

  63. Rockwell D, Naudascher E (1978) Review-self-sustaining oscillations of flow past cavities. J Fluids Eng 100:152–165

    Article  Google Scholar 

  64. Rockwell D (1977) Prediction of oscillation frequencies for unstable flow past cavities. J Fluids Eng 99:294–300

    Article  Google Scholar 

  65. Runkel RL (1998) One-dimensional transport with inflow and storage (OTIS): a solute transport model for streams and rivers. U.S.G.S. Water Resour. Inv. Rep. 98–4018, Denver, Colorado, 73 p

  66. Sarohia V (1977) Experimental investigation of oscillations in flows over shallow cavities. AIAA J 15:984–991

    Article  Google Scholar 

  67. Scavia D, Rabalais NN, Turner RE, Dubravko J, Wiseman WJ Jr (2003) Predicting the response of Gulf of Mexico hypoxia to variations in Mississippi River nitrogen load. Limnol Oceanogr 48:951–956

    Article  Google Scholar 

  68. Schall JD, Richardson EV, Morris JL (2008) Introduction to highway hydraulics hydraulic design series no. 4. U.S. Dept. of Transportation Federal Highway Administration Technical Report, No. FHWA NHI-08-090 (HDS-4), 4th edition

  69. Schreiber R, Keller HB (1983) Spurious solutions in driven cavity calculations. J Comput Phys 49:165–172

    Article  Google Scholar 

  70. Shankar PN (1993) The eddy structure in Stokes flow in a cavity. J Fluid Mech 250:371–383

    Article  Google Scholar 

  71. Shankar PN (1997) Three-dimensional eddy structure in a cylindrical container. J Fluid Mech 342:97–118

    Article  Google Scholar 

  72. Shen C, Floryan JM (1985) Low Reynolds number flow over cavities. Phys Fluids 28:3191–3202

    Article  Google Scholar 

  73. Sinha SN, Gupta AK, Oberai MM (1982) Laminar separating flow over backsteps and cavities part II: cavities. AIAA J 20(3):370–375

    Article  Google Scholar 

  74. Thomas SA, Valett HM, Mulholland PJ, Fellows CS, Webster JR, Dahm CN, Peterson CG (2001) Nitrogen retention in headwater streams: the influence of groundwater-surface water exchange: optimizing nitrogen management in food and energy production and environmental protection. In: Proceedings of 2nd international nitrogen conference on science and policy, 1(S2), 623–631

  75. Uijttewaal W, Lehmann D, van Mazijk A (2001) Exchange processes between a river and its groyne fields: model experiments. J Hydraul Eng 127:928–936

    Article  Google Scholar 

  76. Uijttewaal WSJ (2005) Effects of groyne layout on the flow in groyne fields: laboratory experiments. J Hydraul Eng 131(9):782–791

    Article  Google Scholar 

  77. Uzol O, Camci C (2001) The effect of sample size, turbulence intensity and velocity field on the experimental accuracy of ensemble averaged PIV measurements. In: Proceedings of the 4th international symposium on particle image velocimetry, September 17–19, 2001, Göttingen, Germany

  78. Wallast I, Uijttewaal W, van Mazijk A (1999) Exchange processes between groyne field and main stream. In: Proceedings of 28th IAHR Congress, IAHR, Madrid, Spain

  79. Weitbrecht V, Socolofsky SA, Jirka GH (2008) Experiments on mass exchange between groin fields and main stream in rivers. J Hydraul Eng 134(2):173–183

    Article  Google Scholar 

  80. Weitbrecht V, Jirka GH (2001) Flow patterns in dead zones of rivers and their effect on exchange processes. Paper presented at Proceedings of IAHR 3rd international symposium on environmental hydraulics, Tempe, Arizona

  81. Yao H, Cooper RK, Raghunathan S (2004) Numerical simulation of incompressible laminar flow over three-dimensional rectangular cavities. J Fluids Eng 126:919–927

    Article  Google Scholar 

  82. Yossef MFM, de Vriend HJ (2011) Flow details near river groynes: experimental investigation. J Hydraul Eng 137(5):504–516

    Article  Google Scholar 

  83. Yu G, Huang HQ, Wang Z, Brierley G, Zhang K (2012) Rehabilitation of a debris-flow prone mountain stream in southwestern China—strategies, effects and implications. J Hydrol 414–415:231–243

    Article  Google Scholar 

Download references

Acknowledgments

This work was supported by the National Science Foundation, EAR 09-43570 and by the CUAHSI Pathfinder Fellowship to T. R. Jackson. We would especially like to thank Bob Basham for his exceptional assistance and instrumentation training during the laboratory experiments. We would like to thank Daniele Tonina for his sponsorship and support during the laboratory experiments. We also would like to thank the reviewers for their insightful comments, which have helped to improve the quality of this manuscript.

Author information

Authors and Affiliations

  1. Water Resources Engineering Program, College of Earth, Ocean, and Atmospheric Sciences, Oregon State University, 104 CEOAS Admin. Bldg., Corvallis, OR, 97331-5503, USA

    Tracie R. Jackson

  2. Department of Mechanical, Industrial, and Manufacturing Engineering, Oregon State University, 204 Rogers Hall, Corvallis, OR, 97331, USA

    Sourabh V. Apte

  3. College of Earth, Ocean, and Atmospheric Sciences, Institute for Water and Watersheds, Oregon State University, 104 CEOAS Admin. Bldg., Corvallis, OR, 97331-5503, USA

    Roy Haggerty

  4. Department of Civil Engineering, Center for Ecohydraulics Research, University of Idaho, 322 E. Front St, Boise, ID, 83702, USA

    Ralph Budwig

Authors
  1. Tracie R. Jackson
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Sourabh V. Apte
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Roy Haggerty
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ralph Budwig
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tracie R. Jackson.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jackson, T.R., Apte, S.V., Haggerty, R. et al. Flow structure and mean residence times of lateral cavities in open channel flows: influence of bed roughness and shape. Environ Fluid Mech 15, 1069–1100 (2015). https://doi.org/10.1007/s10652-015-9407-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10652-015-9407-2

Keywords

Search

Navigation