1 Introduction

The global demand for freshwater continues to increase with population growth, economic expansion and urbanization. According to the United Nations [1] in the past 100 years, the global water use has increase by a factor of six and is currently increasing at a rate of approximately 1% per year. The water scarcity caused by both population growth and climate change has led to the development of a number of innovative freshwater production processes including increasingly sophisticated desalination technologies. Jones et al. [2] estimated there were 15,906 desalination plants operating in the world at that time, producing approximately 95 million m3/day of desalinated water. The high concentration brine effluent produced by large scale desalination plants has higher salinity and density than the surrounding ocean, and is normally discharged back into the sea from which the saltwater was sourced. Jones et al. [2] estimated the brine production associated with the above plants to be approximately 142 million m3/day. Changes in the salinity of marine habitats can be harmful to aquatic ecology e.g. [3, 4]. Other than salt, effluent from desalination plants is normally characterized by elevated levels of chemicals, such as trace elements, residuals of pretreatment and cleaning agents e.g. [3, 5, 6]. Therefore, an effective wastewater dispersion process is essential in reducing contaminant concentrations to acceptable levels, so that potential environmental impacts are mitigated for large-scale desalination discharges.

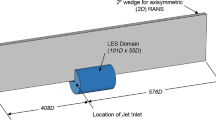
Brine effluent from large-scale desalination plants is typically discharged at offshore sites via submerged outfall diffuser ports mounted on the ocean floor. These ports are inclined towards the ocean surface to enhance the initial mixing of the discharged fluid. Figure 1 shows a schematic diagram of an idealized discharge configuration. This discharge flow configuration is commonly referred to as an inclined negatively buoyant jet (INBJ). Near the source, the flow is dominated by its initial momentum flux, and it rises towards the water surface. As the flow rises, the vertical momentum flux decreases because of the negative buoyancy forces (due to the elevated salt concentration), and hence the flow trajectory is deflected downwards. In addition, the discharge becomes increasingly asymmetric about the centerline as the flow progresses because of additional mixing on the inner/lower side of the discharge associated with the presence of buoyancy-induced instabilities. This feature of the flow is clearly evident in the experimental studies of Kikkert et al. [7]; Oliver et al. (planar concentration fields) [8]; Crowe et al. (planar velocity fields) [9]; Abessi and Roberts, 2015 (planar concentration fields extracted from 3D experiments) [10]; Abessi and Roberts, 2016 (3D concentration fields of INBJs in shallow water) [11].

Fig. 1
figure 1

Schematic diagram of an inclined negatively buoyant jet. xm: horizontal distance to the maximum centerline height. zm: vertical distance to the maximum centerline height. zme: maximum edge height. xr: horizontal distance to the return point where the centerline falls back to the source height

Full size image

Modelling the effects of the buoyancy-induced instabilities is challenging, and it has been widely discussed that being able to capture this phenomenon is important in accurately predicting the behaviour of INBJs [12,13,14,15,16,17,18,19,20]. However, as discussed in these papers, all numerical models to date have been unable to accurately capture the effects of the buoyancy-induced instabilities, and hence unable to accurately predict the behaviour of INBJs.

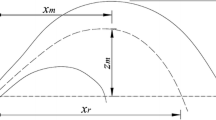
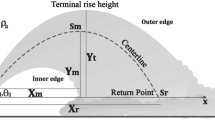
The reduction in vertical momentum flux noted above eventually results in the flow reaching the centerline maximum height at coordinate \({({x}_{m},z}_{m})\). The flow then descends, passes its source height and eventually impacts the seafloor. The point at which the descending centerline returns to the source height is referred to as the return point \(({x}_{r},0)\). The discharge configuration show in Fig. 1 is idealized in the sense that the potential influences of ambient motion and ambient stratification are not considered here. Improvements in our understanding of the mixing processes associated with the above idealized discharge configuration provides a foundation for the future introduction of additional complexities associated with variations in the surrounding ambient fluid.

Existing experimental and theoretical studies demonstrate that the geometric, velocity and dilution parameters of INBJs are dependent on the densimetric Froude number \({F}_{0}\):

$$\begin{array}{*{20}c} {F_{0} = \frac{{U_{0} }}{{\sqrt {\hat{g}_{0} d} }},} \\ \end{array}$$
(1)

where \(U_{0}\) is the initial velocity, \(d\) is the source diameter, and \(\hat{g}_{0}\) is the initial reduced gravity:

$$\begin{array}{*{20}c} {\hat{g}_{0} = \frac{{\left( {\rho_{0} - \rho_{a} } \right)}}{{\rho_{a} }}g,} \\ \end{array}$$
(2)

\({\rho }_{0}\) and \({\rho }_{a}\) are the initial density and the density of the ambient fluid, respectively. The preferred discharge configuration maximises the dilution at the disposal site. Thus, it is essential to be able to accurately predict the behavior of INBJs to guide the design of marine outfalls from desalination facilities.

Zeitoun et al. [21] were the first to perform detailed experiments on INBJs, measuring the flow trajectories and dilution of discharges at inclinations of 30°, 45°, 60° to the horizontal. Following this relatively crude study by present day standards, numerous researchers have investigated the geometric and dilution characteristics on INBJs to various levels of detail and under a broader range of discharge conditions [7, 22,23,24,25,26,27,28,29,30]. Despite the number of studies listed, there remains significant scatter in key parameters reported and thus uncertainty remains in terms of characterizing the behaviour of INBJs for the purposes of evaluating environmental effects.

One of the potential sources of this uncertainty is variations in the bottom boundary condition for these studies. Shao and Law [31] and more recently Ramakanth et al. [32] systematically examined the effects of the bottom boundary (seabed) on the trajectories and dilution of INBJs, and their studies have resolved some of the discrepancies evident in the previously published results. However, Oliver et al. [8] took the approach of removing the influence of the bottom boundary from return point data to provide a basis for comparing experimental studies and the predictive capabilities of numerical models prior to introducing the additional complexities associated with boundary interaction. Oliver et al. [8] employed a high-quality Laser-induced Fluorescence (LIF) system to provide comprehensive concentration field data for INBJs under this simplified condition. Crowe et al. [9] adopted the same approach and measured detailed velocity field information using a Particle Tracking Velocimetry (PTV) system. Ramakanth [33] also verified the measurements made by Oliver et al. [8] by conducting LIF experiments under similar conditions. The numerical investigation detailed in this paper does not attempt to model boundary interaction and hence the studies of Oliver et al. [8], Crowe et al. [9] and Ramakanth [33] are most relevant when comparing predictions with measured behaviour.

Relatively simple numerical models, often referred as integral models because they are based on integral forms of the equations of motion, are commonly employed to guide the design and assessment of environmental effects for these types of marine discharges. In general, these models do not attempt to model boundary interaction, but instead assume that values immediately prior to reaching the boundary (seabed) are representative of conditions at the impact point located on the boundary. These models are only capable of predicting bulk flow parameters, and they are semi-empirical in that they utilize coefficients determined from experimental studies to determine critical mixing parameters (entrainment or spread coefficients and mean turbulent fluxes). Examples relevant to INBJs include models developed by Papanicolaou et al. [34], Yannopoulos and Bloutsos [35]; Oliver et al. [36] and Crowe et al. [37]. The more recent modified reduced buoyancy flux (RBF) model of Crowe et al. adopts a physically based approach to directly model the bulk influences of the buoyancy-induced instabilities by treating the detrainment on the lower side of the INBJs as a reduction in buoyancy flux in the main flow. However, while integral model predictions are improved through the RBF formulation, significant predictive errors remain when comparisons are made with experimental measurements.

More sophisticated numerical simulations have the potential to provide increased insights into the details of the flow. The next level of predictive models in terms of complexity (sophistication) and resources required are based on the Reynolds Averaged Navier Stokes (RANS) equations. Relevant studies in this context include those by Vafeiadou et al. [38], Oliver et al. [12], Kheirkhah Gildeh et al. [13,14,15], Robinson et al. [16] and Tahmooresi and Ahmadyar [39]. RANS models have also been employed to simulate specific discharge configurations in the laboratory and in the field. For example, Yan and Mohammadian [40] performed simulations of 60° INBJs from multiport diffusers with a bottom boundary; Baum and Gibbes [20] simulated the discharge configurations defined by the site conditions of the Gold Coast Desalination Plant. In the above studies, the RANS models have been shown to provide some level of agreement with experimental studies based on specific closure schemes and methods of incorporating buoyancy effects, but in general they have a tendency to under-predict both dilutions and geometric parameters. Thus, the suitability of RANS models for particular applications is dependent on the accuracy required to meet expectations and achieve the necessary outcomes.

Large Eddy Simulations (LES) resolve the large-scale turbulent motions that drive the mixing processes, and hence have the potential to improve the quality of predictions of INBJ behaviour. In particular, they provide access to an increased level of detail in terms of the evolution of the flow structure, and associated velocity and concentration fields. A number of more recent studies have explored the application of LES to INBJs. In order to provide these benefits, a significant increase in the level of computational resources is needed. Robinson et al. [16] confirmed this when they compared predictions from a low-resolution LES model with those from a standard k-ε model and noted that the LES model provided no significant advantages in this context with both models under-predicting the measured behaviour.

Higher resolution LES models of INBJ’s have been implemented by Zhang et al. [17], Zhang et al. [18] and Jiang et al. [19]. Zhang et al. [17] modelled 45° INBJs using both Smargorinksy (\({F}_{0}=11.3, 15.0, 20.0\) and \(30\)), and Dynamic sub-grid scale (SGS) models (\({F}_{0}=11.3\) and \({F}_{0}=15.0\)). The simulations were performed on a static structured grid, which was stretched such that the grid spacing increased from the center of the discharge port to the domain boundaries. The resolution of a region expected to be covered by the flow was doubled. Experiments were also performed to provide additional data for the verification of the LES results. These simulations employed an open boundary condition at the bottom boundary, so interaction with the “sea floor” was not modelled. This makes comparisons with data measured on a solid bottom boundary potentially problematic and the least contaminated data in this respect is that of Oliver et al. [8], where elevated source heights (ranging from \(2.33{DF}_{0}\) to \(8.07{DF}_{0}\)) enabled potential boundary influences to be removed from the measured region.

Importantly, Zhang et al. [17] demonstrated that their higher resolutions LES predictions were more accurate than the previously published numerical models of INBJs. However, some significant discrepancies remained (based on comparisons with Oliver et al. [8] and Ramakanth [33]). This LES model over-predicted the horizontal and vertical locations of the maximum height, and the horizontal location of the return point. The dilutions at the maximum height and return point given by the Smagorinsky model were under-predicted by up to 37% and 29%, respectively. The Dynamic SGS model also under-predicted the dilution at these two locations by up to 34% and 32%. A summary of the geometrical and dilution coefficients is presented in Tables 3, 4, 5 and 6. Concentration and velocity spreads, especially on the inner/lower side, were substantially under-predicted and the LES model also predicted variations in flow spread that are not observed in experimental data. The quality of predictions of concentration fluctuation intensities also varied significantly—under-predicting some areas and over-predicting in others. The authors concluded that both the Smagorinsky and Dynamic SGS models were unable to fully capture the behavior of the turbulent flow under the influence of buoyancy, and an improved SGS model was needed.

Zhang et al. [18] performed LES and RANS simulations for 45° and 60° INBJs with bottom boundary interaction. The Dynamic SGS model and the k-ε model were chosen for the LES and RANS simulations, respectively. The near-wall modelling approach was used for the wall modelling in the LES simulations; and both the near-wall modelling and the wall function approaches were used for the k-ε simulations. The initial densimetric Froude number ranged from \({F}_{0}=10-40\). Overall, their LES predictions were more accurate than the previously published numerical studies of INBJs with bottom impact. While the k-ε model greatly under-predicted all the key geometric coefficients, the LES outputs of the 45° cases were found to agree well with the experimental data of Shao and Law [31] and Lai and Lee [30]. For 60° discharges, the experimental data available for comparison were more limited and variable, and therefore more difficult to interpret. This in part reflects a lack of consistency in terms of the non-dimensional source heights for these studies. In the context of dilution, the LES model underpredicted measured values at the maximum height and return point by \(\sim 18\%\) (based on comparisons with Oliver et al. [8] and Ramakanth [33]) and \(\sim 20\%\) (as noted by Zhang et al. [18]), respectively.

More recently, Jiang et al. [19] performed experiments and LES of 45° INBJs, with an emphasis on the turbulent characteristics. The initial densimetric Froude number of the experiments and LES ranged from \({F}_{0}=11-35\) and \({F}_{0}=11-30\), respectively. A grid scheme similar to that adopted by Zhang et al. [17] and Zhang et al. [18] was used. The turbulent intensity of streamwise velocity along the trajectory was slightly underestimated near the nozzle, and the error continued to increase downstream. The turbulent intensity of radial velocity, however, showed good agreement with their experiment data. The cross-section streamwise turbulent intensity profiles were consistently under-predicted at several locations along the flow centerline when compared to experimental data. The turbulent kinetic energy spectrum at different locations along the flow centerline demonstrated that the predicted turbulence energy densities at low frequencies were close to experimental data, but those at higher frequencies were significantly under-predicted. With regards to the flow spread along the flow trajectory, while the predicted spread on the outer/upper edge showed good agreement with their experimental data, the predicted spread on the inner/under side was significantly lower than the measured data. The authors noted that their LES model was unable to capture the higher frequency turbulence created by the buoyancy-induced instabilities because the resolution of the model was limited. They also concluded that the turbulent models need to be improved in the future to incorporate sub-grid scale stratification effects.

While recent higher resolution LES studies have demonstrated the superiority and potential of the LES approach in capturing the behavior of INBJs, significant errors in the predicted geometric, mixing, and turbulent characteristics persists. The errors are potentially associated with of the inability of the existing SGS model to sufficiently capture the effects of the buoyancy-induced instabilities on the sub-grid scale turbulence, given the imposed static limits on the mesh resolution. Here we address this issue by moving away from a static mesh, the structure of which is informed by limited information based on existing experimental studies, to an adaptive mesh that reacts dynamically to the instantaneous flow structure. This approach enables the LES simulations to refine the grid in areas where higher resolution is needed and reduce in the grid resolution in areas where a lower resolution grid is able to capture sufficient detail. The adaptive mesh approach combined with a Lagrangian Dynamic SGS model provides the basis for generating a very detailed three-dimensional data set. This level of detail is well beyond that which can be captured by current experimental systems, and the new data can be used to inform the development of less sophisticated models which can be more readily applied in practice. This paper describes the Adaptive LES model (Sect. 2), and then demonstrates this model’s predictive capabilities in the context of existing experimental data sets and model predictions of INBJ behaviour (Sect. 3). Subsequent publications will focus on extracting additional insights into the flow behaviour from the comprehensive data set that the simulations have created.

2 Numerical methods

2.1 Governing equations

In LES, large-scale and small-scale flow structures are separated by filtering the transport equations. The large-scale motions are resolved, while the effects of the small-scale motions are modeled by SGS models. The filtered continuity, momentum and scalar transport equations for the present problems are:

$$\begin{array}{*{20}c} {\frac{{\partial \overline{u}_{i} }}{{\partial x_{i} }} = 0,} \\ \end{array}$$
(3)
$$\begin{array}{*{20}c} {\frac{{\partial \overline{u}_{j} }}{\partial t} + \frac{{\partial \left( {\overline{u}_{i} \overline{u}_{j} } \right)}}{{\partial x_{i} }} = - \frac{1}{{\rho_{0} }}\frac{{\partial \overline{P}}}{{\partial x_{j} }} + \nu \frac{{\partial^{2} \overline{u}_{j} }}{{\partial x_{i} x_{i} }} - \frac{{\partial \tau_{ij}^{r} }}{{\partial x_{i} }} + g_{j} - g_{j} \beta \left( {\overline{C} - \overline{C}_{0} } \right),} \\ \end{array}$$
(4)
$$\begin{array}{*{20}c} {\frac{{\partial \overline{C}}}{\partial t} + \frac{{\partial \left( {\overline{C}\overline{u}_{i} } \right)}}{{\partial x_{i} }} = \Gamma \frac{{\partial^{2} \overline{C}}}{{\partial x_{i} x_{i} }} - \frac{{\partial Q_{i} }}{{\partial x_{i} }},} \\ \end{array}$$
(5)

where the overbar denotes spatially filtered variables; \({u}_{i}\) and \({u}_{j}\) are the \(i\)th and \(j\)th velocity components in the \({x}_{i}\) and \({x}_{j}\) directions, \(t\) is time, \(P\) is pressure, \(\nu\) is the kinematic viscosity, \({\rho }_{0}\) is the ambient density, \({g}_{i}\) is the gravitational acceleration, \({C}_{0}\) is the ambient scalar concentration, \(C\) is the local scalar concentration, \(\Gamma\) is the molecular diffusivity of the scalar; \({\tau }_{ij}^{r}\) is the SGS residual-stress tensor, \({Q}_{i}\) is the SGS scalar flux, and \(\beta =\frac{1}{{\rho }_{0}}\frac{\overline{\rho }-{\rho }_{0}}{\overline{C}-{C}_{0}}\) is the coefficient of saline contraction under the Boussinesq approximation for buoyancy, where \(\rho\) is the local density.

2.2 Turbulence modelling

The most commonly used approach to model the SGS residual-stress tensor \({\tau }_{ij}^{r}\) is the linear eddy-viscosity model:

$$\begin{array}{*{20}c} {\tau_{ij}^{r} = - 2\nu_{t} \overline{S}_{ij} ,} \\ \end{array}$$
(6)

where \(\overline{S}_{ij} = \frac{1}{2}\left( {\frac{{\partial \overline{u}_{i} }}{{\partial x_{j} }} + \frac{{\partial \overline{u}_{j} }}{{\partial x_{i} }}} \right)\) is the resolved rate of strain tensor, and the eddy viscosity \(\nu_{t}\) is modeled as:

$$\begin{array}{*{20}c} {\nu_{t} = C_{s}^{2} {\Delta }^{2} \left| {\overline{S}} \right|,} \\ \end{array}$$
(7)

where \(\Delta\) is the LES filter width defined by the grid spacing, and \(\left|\overline{S}\right|=\sqrt{2{\overline{S}}_{ij}{\overline{S}}_{ij}}\) is the characteristic filtered rate of strain. The treatment of the coefficient \({C}_{s}\) defines the difference between the Smagorinsky model and the Lagrangian Dynamic SGS model. In the Smagorinsky model, the coefficient \({C}_{s}\) is set to a constant value, typically \(\sim 0.17\) [41, 42], while in the Lagrangian Dynamic SGS model, \({C}_{s}\) is determined by a dynamic procedure proposed by Meneveau et al. [43]:

$$\begin{array}{*{20}c} { C_{s}^{2} = \frac{{{\mathcal{I}}_{LM} }}{{{\mathcal{I}}_{MM} }},} \\ \end{array}$$
(8)

where \({\mathcal{I}}_{LM}\) and \({\mathcal{I}}_{MM}\) are the solutions to the equations:

$$\begin{array}{*{20}c} { \frac{{\partial {\mathcal{I}}_{LM} }}{\partial t} + \frac{{\partial (u_{i} {\mathcal{I}}_{LM} )}}{{\partial x_{i} }} = \frac{1}{T}\left( {L_{ij} M_{ij} - {\mathcal{I}}_{LM} } \right)} \\ \end{array}$$
(9)
$$\begin{array}{*{20}c} { \frac{{\partial {\mathcal{I}}_{MM} }}{\partial t} + \frac{{\partial \left( {u_{i} {\mathcal{I}}_{MM} } \right)}}{{\partial x_{i} }} = \frac{1}{T}\left( {M_{ij} M_{ij} - {\mathcal{I}}_{MM} } \right),} \\ \end{array}$$
(10)

in which

$$\begin{array}{*{20}c} { L_{ij} = \widehat{{\overline{u}_{j} \overline{u}_{j} }} - \widehat{{\overline{u}_{j} }}\widehat{{\overline{u}_{j} }}} \\ \end{array}$$
(11)
$$\begin{array}{*{20}c} { M_{ij} = 2\Delta^{2} \left[ {\widehat{{\left| {\overline{S}} \right|\overline{S}_{ij} }} - \hat{\Delta }^{2} \widehat{{\left| {\overline{S}} \right|}}\widehat{{\overline{S}}}_{ij} } \right]} \\ \end{array}$$
(12)
$$\begin{array}{*{20}c} { T = \theta \Delta \left( {{\mathcal{I}}_{LM} {\mathcal{I}}_{MM} } \right)^{ - 1/8} ,} \\ \end{array}$$
(13)

where the hat denotes variables spatially filtered at scale \(2\Delta\), and \(\theta =1.5\) is a dimensionless coefficient. It was shown that the \({\mathcal{I}}_{LM}\) and \({\mathcal{I}}_{MM}\) obtained from solving Eqs. (9) to (10) are equivalent to the Lagrangian averaged \({L}_{ij}{M}_{ij}\) and \({M}_{ij}{M}_{ij}\), respectively, over the historical particle trajectories with an exponentially decreasing weighting. The time scale \(T\) effectively determines the memory length of the Lagrangian averaging [43].

It is worth noting that the Dynamic SGS model used by Zhang et al. [17], Zhang et al. [18] and Jiang et al. [19], was originally proposed by Germano et al. [44] and subsequently modified by Lily [45]. This Dynamic SGS model involves an intermediate step that performs a spatial averaging procedure over directions of statistical homogeneity. Ghosal et al. [46] and Meneveau et al. [43] noted that the simulated flows need to be statistically homogeneous in at least one direction in order to make the spatial averaging procedure possible in this Dynamic SGS model. However, for flows that spatially vary in all the three dimensions, such as the INBJs, the prescription of the averaging directions is problematic, and the sensitivity of the previously published simulations to the choice of the averaging directions in the context of INBJs is not clear.

With the Lagrangian Dynamic SGS model implemented here, temporal averaging along fluid-particle paths avoids the need of performing spatial averages along directions of statistical homogeneity. The dynamic determination of \({C}_{s}\) also allows the eddy viscosity to vanish in laminar regions, including regions where local shear is present in the filtered velocity field. Hence this dynamic determination better differentiates the behavior of eddy viscosity in different flow regimes [47], which is important when modelling free shear flows. In contrast for the Smagorinsky model, where \({C}_{s}\) is a constant, Eq. (7) suggests that as long as there is local shear in the filtered velocity field, the eddy viscosity would be present even in laminar flow regions.

Nevertheless, the eddy viscosity given by the Smagorinsky model has some beneficial properties that are useful in the adaptive meshing procedure developed for the present study. First, it increases with the magnitude of velocity gradient, which is an indicator of the need for higher resolution. Second, unlike the velocity gradient magnitude, it decreases as \(\Delta\) in Eq. (7) decreases (i.e. as the cell is refined). In the limit that the small eddies are well resolved, the resolved molecular shear stresses would dominate the SGS residual-stresses, and the eddy viscosity would no longer be significant [47]. Therefore, the eddy viscosity given by the Smagorinsky model reflects the level of refinement relative to the resolution required by the velocity gradient magnitude.

On the contrary, if the velocity gradient magnitude alone was used as the adaptive refinement criterion, when a region with a relatively coarse grid is refined, the local velocity gradient could further increase because smaller scale eddies are resolved. Consequently, the region would be refined repeatedly and result in a local resolution that is unnecessary and unaffordable for LES. Therefore, in the present simulations both eddy viscosities given by the Lagrangian Dynamic SGS model and the Smagorinsky model were calculated. While the former is used to determine the SGS stresses, the latter is used as the cell refinement criterion in the adaptive meshing procedure, but is not involved in the turbulence modelling.

The SGS scalar flux \({Q}_{i}\) in Eq. (5) is modeled with the gradient diffusion hypothesis to avoid additional computational cost [48]:

$$\begin{array}{*{20}c} {Q_{i} = \frac{{\upsilon_{t} }}{{Sc_{t} }}\frac{{\partial \overline{\phi }}}{{\partial x_{i} }},} \\ \end{array}$$
(14)

where \({Sc}_{t}=0.7\) [17, 49, 50] is the SGS turbulent Schmidt number.

2.3 Numerical configuration

In the present study, the equations were discretised with the finite volume method. The solver buoyantBoussinesqPimpleFoam in the open-source CFD library, OpenFOAM-v1712 was modified to include the adaptive meshing function that is already available in another part of the library, dynamicFvMesh. This study focuses on 45° discharges, future studies may adapt the modelling approach to extend the simulations to a wider range of discharge configurations. The flow configurations of the simulations are summarised in Table 1. The kinematic viscosity and molecular scalar diffusivity were \({10}^{-6}{\text{m}}^{2}\text{/s}\) and \({10}^{-9}{\text{m}}^{2}\text{/s}\), respectively, giving a Schmidt number \(Sc=1000\). However, given the inherently limited resolution in LES, the Batchelor scale (i.e. the smallest length scale of the scalar field fluctuation) is far from resolved, so the resolved \(Sc\) of the simulations is relatively small. Nevertheless, for the turbulent discharges simulated in the present study, scalar dispersion is expected to be dominated by turbulent diffusion as opposed to molecular diffusion. Therefore, it is expected that the LES results would be relatively insensitive to the value of the scalar diffusivity, given that \(Sc\) is large. The ambient and discharged brine concentration was normalised to be 0 and 1, respectively. The coefficient of saline contraction \(\beta\) was set to be 0.03 such that there is a 3% density difference between the discharged and ambient fluid. For both cases, the simulation time from the beginning of the discharge was 75 s to provide sufficient time-averaged results.

Table 1 Flow configurations of the simulations
Full size table

A second order implicit backward scheme was used to discretise the temporal terms. A second order linear scheme and a limited linear scheme was used to discretise the divergence terms for the velocity and concentration, respectively. An upwind scheme was used for the divergence terms for \({\mathcal{I}}_{LM}\) and \({\mathcal{I}}_{MM}\). The Laplacian terms were discretised with a linear scheme. The convergence criteria for the residuals of the flow field parameters were set to be \({10}^{-6}\).

2.4 Computational domain and boundary conditions

A schematic diagram of the computational domain for the simulations is shown in Fig. 2. The center of the circular discharge pipe is located at the origin. The distance from the pipe center to the bottom (\(H1\)), top (\(H2\)), back (\(L1\)), front (\(L2\)) and side (\(W\)) boundaries in both simulations are summarized in Table 2.

Fig. 2
figure 2

Schematic diagram of the computational domain

Full size image
Table 2 Dimensions of the computational domains
Full size table

The boundary conditions for all the six domain boundaries were set to “zero-gradient open boundary”, which allows both inflow and outflow. The circular discharge surface of the pipe was set to be a velocity inlet with a uniform mean velocity and 10% turbulent fluctuating component. The other surfaces of the discharge port were set to be no-slip walls.

2.5 Adaptive mesh

Unlike previous LES studies of INBJs, the simulations in the present study were performed on adaptive meshes. Initially, a uniform structured mesh was created across the whole computational domain. The cells surrounding the discharge pipe were then repeatedly divided into smaller cells to fit the geometry of the pipe using a tool in OpenFOAM called snappyHexMesh. This process created the initial mesh for the simulation shown in Fig. 3a. Once the simulation began, the mesh was automatically refined and unrefined at every time step based on the local turbulent viscosity given by the Smagorinsky SGS model. As noted above, this turbulent viscosity was only used as the cell refinement criterion, but it was not involved in the turbulence modelling. The reason for choosing the Smagorinsky eddy viscosity as the adaptive refinement criterion is discussed in Sect. 2.2. Figure 3b shows a typical instantaneous snapshot of the adaptive mesh on the center-plane of the INBJ for case C1. It can be seen that refined regions resemble the instantaneous shape of an INBJ. As the simulations reached a statistically steady state, the total numbers of computational cells in the domains were approximately 17 million and 3.4 million for cases C1 and C2, respectively.

Fig. 3
figure 3

a The initial mesh at the start of the simulation; b An instantaneous snapshot of the adaptive mesh on the centre plane

Full size image

2.6 Grid convergence

Normally, assessment of grid convergence involves repeating the simulations with a different resolution, and then comparing the outputs. However, since the LES presented here were performed with an adaptive meshing approach, repeating the simulations with doubled/halved resolution while preserving the exact same cell distribution is not possible.

As far as the present authors are aware, there is no well-established way of assessing grid convergence for adaptive meshes in the literature. Therefore, for the Adaptive LES presented here, grid-convergence is supported by the following evidence. First, simulation case C1 was repeated, but with a different threshold of refinement criterion that triggers the refinement. The threshold was chosen such that the resulting total number of cells after temporal convergence is approximately 1/8 of the original case C1. This reduction in number of cells is equivalent to halving the resolution in a static mesh. Results of dilution at maximum height and return point showed only 0.1% and 0.8% differences from the original case C1, respectively.

Second, as discussed in Sect. 3, the mean flow field and turbulent statistics predicted by the Adaptive LES agree well with benchmark experimental data in the literature.

Third, in the limit that small eddies are well resolved, the resolved molecular shear stresses would dominate the SGS residual-stresses, and the eddy viscosity would no longer be significant. In the present Adaptive LES, the eddy viscosity calculated by the Smagorinsky model was used as the refinement criteria. The threshold ensured that the highest eddy viscosity (Smagorinsky) in the domain was of the same order of magnitude as the molecular viscosity (10−6). This provides increased confidence that the Adaptive LES has resolved sufficient flow detail.

Finally, as discussed in Sect.  3.5.2, the turbulent spectrum predicted by the Adaptive LES captured at least part of the  − 5/3 decay profiles at the locations considered, which confirms that the Adaptive LES captures part of the inertial sub-range, where the residual is nearly isotropic and scale-invariant. This filtering scale is considered to be appropriate in the LES approach [47, 51, 52]. Simulating this level of detail also provides additional confidence that the Adaptive LES has captured a sufficient range of scales to adequately resolve the simulated flows.

The evidence above supports the independence of the simulated flows from the grids generated through the adaptive process.

3 Results and discussion

As discussed in Sect. 1, the experiments of Oliver et al. [8], Crowe et al. [9] and Ramakanth [33] were conducted with the bottom boundary influence removed. The LIF concentration field measurements of Oliver et al. and Ramakanth also agree with (and hence verified) each other. Therefore, in the following discussion, the Adaptive LES predictions are primarily compared with these three sets of experimental data and other published LES results where appropriate. Other than the instantaneous concentration field shown in Fig. 4, all the results presented are time-averaged data.

Fig. 4
figure 4

Instantaneous concentration field on the centre-plane: a the present Adaptive LES. b Figure 17 from Zhang et al. [17]—LES. c Figure 5 from Zhang et al. [18]—LES with solid bottom boundary. d Figure 17 from Zhang et al. [17]—experiment. e Figure 5.2 from Ramakanth [33]—experiment

Full size image

3.1 General flow features and bulk flow parameters

Figure 4a shows a typical instantaneous concentration field predicted by the Adaptive LES taken from the centre-plane of case C1. As expected, near the source, the INBJ behaviour is dominated by the discharge momentum flux and the behavior of the flow is jet-like. In this region, the width of the INBJ on both the inner and outer sides are almost symmetrical. As the jet rises, detrainment is observed on the inner side of the flow due to buoyancy-induced instabilities [7,8,9, 53], and the INBJ becomes increasingly asymmetrical. Under the influence of the negative buoyancy forces, the vertical momentum flux of the rising INBJ decreases. Subsequently, the INBJ reaches its maximum height and begins to descend. The observed behaviour is consistent with those reported in published laboratory experiments.

The LES and experimental instantaneous concentration field on the centre-plane from Zhang et al. [17], Zhang et al. [18] and Ramakanth [33] are reproduced here in Fig. 4b to e for comparison. Compared to the LES predictions from the literature (Zhang et al. [17, 18]), the LES study presented here is able to resolve much finer eddy structures. This is also reflected in the simulation’s ability to capture the detraining flow on the inner side of the jet in much greater detail. Qualitatively this figure demonstrates that the instantaneous concentration fields from the current simulations are much more consistent with experimental observations (Ramakanth [33] and Zhang et al. [17]) when compared with those from previously published LES studies.

Table 3 summarizes the key geometric and dilution coefficients predicted by the present and previously published LES without bottom impact, together with appropriate benchmark experimental data from the literature. Dilution \(S={C}_{0}/C\) is defined as the ratio between the source concentration \({C}_{0}\) and the local concentration \(C.\) Note that the experiment of Zhang et al. [17] was performed with the discharge port located at \(0.76D{F}_{0}\) above the bottom boundary—with this source height, the effect of the bottom boundary on the bulk flow coefficients before the return point is expected to be small [32]. Therefore, the experimental data of Zhang et al. [17] is also included for comparison. Note that Jiang et al. [19] also performed LES of 45° INBJs, but their analysis was focused on the turbulent characteristics and the coefficients listed in Table 3 were not presented. Therefore, direct comparison with their results in this context is not possible.

Table 3 Comparison of key geometric and dilution coefficients
Full size table

Table 4 summarizes the percentage errors of the LES-predicted coefficients presented in Table 3 based on comparisons with the relevant experimental data. It is evident that the errors of all the geometric parameters from the Adaptive LES predictions are relatively low. The predicted locations of the terminal rise height \({z}_{me}\) in both cases are very close to the experimental measurements. The locations of the return points \({x}_{r}\) in both simulations also agree with the experimental data of Ramakanth [33] reasonably well. It is interesting to note that while the LES of Zhang et al. under-predicted the dilution at both the centerline maximum height and return points because their model was unable to fully capture the buoyancy-induced instability, the Adaptive LES over-predicted the dilution at these locations. The errors of the dilution at the centerline maximum height and return point are somewhat higher than that of the geometric parameters. In case C1, the errors of the dilution at these two locations ranged from approximately 7.32% to 13.1%. In case C2, while the dilution at the return point was predicted to be close to the experimental measurement, the error at maximum height is high, being 28.2%. Nevertheless, it should be noted that these comparisons are based on the mean values in the experimental data; but as will be seen in in the next section (Fig. 6), it is evident that the Adaptive LES predicted dilutions along the whole centerline in case C1 that are within the scatter of the experimental data of Oliver et al. [8]. While case C2 slightly over-predicted the rate of dilution along the rising part of the flow, in other parts of the trajectory the dilution is also within the scatter of the experimental data (Fig. 6). The more noticeable errors associated with the C2 simulation are potentially explained by the lower effective resolution of this simulation.

Table 4 Percentage error of key geometric and dilution coefficients against benchmarking experimental data
Full size table

Tables 5 and 6 summarize the percentage improvement of the present LES from the Smagorinsky and Dynamic SGS LES of Zhang et al. [17], respectively. The percentage improvement is defined as:

$$\begin{array}{*{20}c} {\frac{{\left| {k_{z} - k_{e} } \right| - \left| {k_{p} - k_{e} } \right|}}{{\left| {k_{z} - k_{e} } \right|}} \times 100\% ,} \\ \end{array}$$
(15)

where the subscript \(p\) denotes predicted values in the present LES, subscript \(z\) denotes predicted values in the LES of Zhang et al., subscript \(e\) denotes experimental values from either Oliver et al. [8], Ramakanth [33] or Zhang et al. [17], and \(k\) can be any of the six non-dimensional coefficients. It can be seen that the predictions given by the present simulations are consistently closer to the benchmark experimental data than the previous LES predictions of these flows. The few exceptions are that the \({z}_{m}/D{F}_{0}\) and \({x}_{r}/D{F}_{0}\) predicted by the LES (Dynamic SGS) of Zhang et al. [17] were closer to the experimental data from the same study. However, for all other comparisons, the predictions from the present Adaptive LES were closer to the experimental data. Most of the coefficients are improved by more than 50%, and some of the geometric predictions are improved by approximately 90%. When compared with the experimental data of Zhang et al. [17], the present LES with the higher resolution (Case C1) provided 74–80% improvements in dilution relative to their LES. Case C2 with the lower resolution, however, provided relatively less improvements in dilution: 36–60% improve relative to the Zhang et al. [17] LES when compared with their experiments. The same is true when comparing with the experimental data of Oliver et al. [8] and Ramakanth [33]—while both of the Adaptive LES simulations provided improvements relative to the literature LES, Case C1 provided more improvement than Case C2.

Table 5 Percentage improvement in quantities against Zhang et al. [17] LES (Smagorinsky). Positive numbers refer to improvement
Full size table
Table 6 Percentage improvement in quantities against Zhang et al. [17] LES (Dynamic SGS). Positive numbers refer to improvement
Full size table

3.2 Trajectory and mixing characteristics

Figure 5 compares the non-dimensionalized jet trajectories predicted by the Adaptive LES with the experimental concentration data of Oliver et al. [8] and the LES prediction of Zhang et al. [17]. The trajectories, also known as the flow centerlines, are defined along the locations of maximum concentration in cross-sectional profiles perpendicular to the mean flow direction and are determined from an iterative process; details of this process are given in Law [54].

Fig. 5
figure 5

Non-dimensionalised concentration trajectories

Full size image

While the LES-predicted trajectory for case C1 sits on the lower side of the experimental data, it follows the experimental trajectory data very closely. Referring to Table 4, the predicted \({z}_{m}/DFr\) and \({x}_{r}/DFr\) are 5.5% and 2.88% below the experimental data of Oliver et al. [8]. The trajectory for case C2, however, sits below the experimental data, with the \({z}_{m}/DFr\) and \({x}_{r}/DFr\) being 6.42% and 8.31% below the experimental data of Oliver et al. This is potentially related to the lower effective resolution (number of cells) of case C2 as noted above. Nevertheless, the predicted trajectories show noticeable improvements when compared with existing LES predictions of Zhang et al. [17], and these improvements are also reflected in Tables 5 and 6 discussed in Sect. 3.1.

Similar to the trajectory, Fig. 6 shows agreement between the normalized centerline dilution predicted by the Adaptive LES and the experimental data of Oliver et al. [8]. The simulations captured the consistent rate of dilution on the falling side of the INBJ against vertical height. The consistent slope of dilution beyond the return point also indicates that both the present simulations and the experimental data of Oliver et al. were not affected by the bottom boundary. As already seen in Fig. 5, the predicted vertical location of the maximum height in case C2 sits on the lower side of the experimental data. Nevertheless, as discussed in Tables 3, 4, 5 and 6, the predicted locations of critical points along the trajectory still show noticeable improvement (up to 80% improvement in \({S}_{m}\) and 77% improvements in \({S}_{r}\)) when compared with other published LES studies.

Fig. 6
figure 6

Non-dimensionalised dilution along the centerline trajectory against vertical height. The LES predictions of Zhang et al. [17] at the maximum height and return point are also presented for comparison

Full size image

Figure 7 compares the horizontal (\(u\)) and vertical (\(w\)) velocity components along the jet centerline predicted by the LES with the PTV experimental data of Crowe et al. [9]. In both cases, the horizontal and vertical velocity components were predicted to decay slightly faster than the rate measured in experiments.

Fig. 7
figure 7

Non-dimensionalised velocity components along the centerline trajectory

Full size image

Case C2, the case with fewer computational cells, showed slightly faster decay rate in both velocity components than case C1. However, overall both LES predictions are reasonably consistent with the experimental data.

3.3 Profile shapes of mean quantities

Figure 8 compares the non-dimensional cross-sectional concentration profiles at the maximum height and return point with the experimental data of Oliver et al. [8]. The radial distance from the centerline, \(r\), is non-dimensionalized by the concentration spread width on the outer side of the flow, \({b}_{c}\). The concentration spread \({b}_{c}\) is defined as the radial distance from the concentration centerline to the location where the concentration is equal to \({e}^{-1}{C}_{m}\), where \({C}_{m}\) is the centerline concentration. Note that the coordinate \(r\) is perpendicular to the flow centerline, and negative refers to the inner side of the jet (Fig. 1). At both locations, the simulation results of both cases are consistent with the experimental data. The Adaptive LES predicts the near-Gaussian profile on the outer/upper side of the jet. The predicted concentration profile near the outer edge is lower than the Gaussian curve. This discrepancy is associated with the stable density gradients present in this region of the flow [8] and is consistent with experimental results. The simulations also capture the wider spread on the inner side of the jet, which is caused by detrainment due to buoyancy-induced instabilities. The rate of concentration decay on the inner side of the flow is also very consistent with the experimental measurements at both locations.

Fig. 8
figure 8

Non-dimensionalized cross-sectional concentration profiles at the a maximum height b return point. Unfilled symbols are experimental data of Oliver et al. [8]. Figure adapted from Oliver [56]

Full size image

Figure 9 compares the non-dimensional velocity profiles along the cross-sections at the maximum height and return point with the experimental data of Crowe et al. [9]. Again, negative \(r\) refers to the inner side of the jet, and the velocity spread \(b\) is defined as the radial distance from the velocity centerline to the location where the velocity is equal to \({e}^{-1}{U}_{m}\), where \({U}_{m}\) is the centerline velocity. Similar to the concentration profiles, the predicted velocity profiles follow the experimental measurements very well. The Adaptive LES captures the near-Gaussian axial velocity profile on the outer side of the flow where the density gradients are stable. The magnitude and profile shape of the axial velocity on the inner side of the flow where the density gradients are unstable also agrees with the experimental data. For the transverse velocity component, at both locations the simulations follow the positive values on the outer side of the flow, indicating that ambient fluid is being entrained into the jet. On the inner side, the Adaptive LES predicts positive transverse velocities, which is consistent with the detraining flow. As observed by Crowe et al., while the transverse velocity on the inner side is significantly larger than the outer side at the maximum height, at the return point they are more similar in magnitude.

Fig. 9
figure 9

Non-dimensionalized cross-sectional profiles of velocity components at the a maximum height b return point

Full size image

3.4 Spread

Figure 10a shows the spread of the concentration field along the centre-plane of these flows. In both cases, the Adaptive LES predictions on the outer side of the flow agree with the experimental data of Ramakanth [33] very well, this is particularly evident prior to the return point (\(s/d{F}_{0}\approx 3.8\)). Further downstream, increased scatter is evident in both the Adaptive LES predictions and experimental results, which reflects the limited duration of the temporal averaging of the data relative to the longer time scales of the turbulent motions in this region.

Fig. 10
figure 10

Spread of the a concentration and b velocity field. Note that the spread data of Zhang et al. [17] is defined as the distance from the centerline to the location where concentration (or velocity) decays to 0.05cm (or 0.05um), instead of e − 1cm (or e − 1um) used in the present study and the compared experiments. Therefore, the error of the Zhang et al. LES is under-represented in this figure. The inner concentration spread and the velocity spread predicted by the dynamic SGS LES of Zhang et al. [17] was not presented in their paper and therefore not available for comparison

Full size image

On the inner side of the flow, the LES predictions follow the experimental data relatively closely. However, at around \(s/{F}_{0}d=1\), the LES-predicted spreading rate in both cases started to increase closer to the source than that observed in the experiments. This results in the downstream simulation data sitting slightly higher than the experimental data. This discrepancy is consistent with the slightly lower \({x}_{m}/D{F}_{0}\) predicted by the Adaptive LES in comparison to the experimental data of Ramakanth (see Table 4). Nevertheless, overall the new simulation results provide significant improvements in the concentration spread predictions relative to the LES study by Zhang et al. [17], with their simulations predicting a significantly lower concentration spread on the inner side of the flow in comparison with experimental data. Note that the spread data of Zhang et al. [17] is defined as the distance from the centerline to the location where concentration decays to 0.05 \({\mathrm{c}}_{\mathrm{m}}\), in contrast to the \({\mathrm{e}}^{-1}{\mathrm{c}}_{\mathrm{m}}\) (\(\sim 0.37{c}_{m}\)) used in the present study and for the experimental data. If a consistent definition is used, the difference between the Zhang et al. [17] LES and the experimental data would be larger than that visualised in Fig. 10. In addition, On the outer side, the LES of Zhang et al. [17] predicted a decrease in concentration jet spread on at around \(s/{F}_{0}d=2\) to \(2.7\) before it increased again. This reduction in spreading rate has not been observed in the experimental data. Zhang et al. suggested that these discrepancies indicated that the Smagorinsky and Dynamic SGS models were not able to fully capture the buoyancy-induced instabilities on the inner side of the jet because of the limited grid resolution. In the present study, these issues are resolved by using the adaptive meshing approach and the Lagrangian Dynamic SGS model.

Figure 10b shows the velocity spread of the flow. The Adaptive LES results on the outer side in both cases agree with the experimental data of Crowe [55] very well. Similar to the concentration spread, the velocity spreading rate on the inner side of the flow is predicted to begin increasing slightly earlier than that observed in experiments. However, overall the LES predictions are reasonably close to the experimental measurements. Compared with the LES study of Zhang et al. [17] where their predicted spreading rate increases significantly further downstream, the present Adaptive LES has provided significant improvements. Note again that Zhang et al. has adopted a 0.05 \({\mathrm{c}}_{\mathrm{m}}\) threshold for defining the spread, so the actual difference between their simulation results and experimental data is larger than that visualised in Fig. 11.

Fig. 11
figure 11

Cross-sectional concentration turbulent intensity profiles at the a maximum height b return point. Unfilled symbols are experimental data of Oliver et al. [8]. Figure adapted from Oliver et al. [56]

Full size image

3.5 Turbulent characteristics

As seen in Fig. 4, the Adaptive LES captures significantly finer eddy structures than the previously published LES predictions for these flows. Qualitatively, the fuller range of eddy sizes in the present LES look very similar to experimental images. In this section, the Adaptive LES predictions of the INBJ’s turbulent characteristics are compared quantitatively against results from previously published LES and experimental studies.

3.5.1 Profile shapes of turbulent statistics

Figure 11 compares the cross-sectional concentration turbulent intensity with the experimental data of Oliver et al. [8] and LES predictions of Zhang et al. [17]. Here, positive \(r\) on the horizontal coordinate refers to the outer side of the jet. Overall, the turbulent intensity at both the maximum height and return point in the two LES cases follow the experimental measurements closely. Case C1 predicts a slightly higher peak value than the experimental data. However, for both cross-sections of the two simulated cases, the locations of the peak agree with the experimental data very well. The predictions of the magnitudes and profile forms are also very consistent with the experimental data. In contrast to the previously published study by Zhang et al. [17], the Adaptive LESs capture the influences of the buoyancy-induced instabilities and do not under-predict the turbulent intensity in the inner region. Similarly, when compared with Zhang et al., the Adaptive LESs do not over-predict the turbulent intensity at the return point.

Figure 12 shows the cross-sectional turbulent kinetic energy (TKE) profiles at the maximum height and return point. Positive \(r\) on the horizontal coordinate refers to the outer side of the jet. In both LES cases, the TKE for the two cross-sections follow the experimental data of Crowe et al. [9] relatively well, and the locations of the peaks match the experimental data. The magnitude and profile shape in most regions also agree with the experimental measurements on both the inner and outer sides of the flow. At the maximum height, the Adaptive LES predicts the TKE beyond \(r/b=2\) to gradually decay to zero as the velocity field transitions into the ambient fluid (laminar flow); which is consistent with the LES and experimental concentration turbulent intensity profiles presented in Fig. 12a. However, the experiments show small non-zero values within the reported range of \(2<r/b<5\). A similar pattern is also observed at the return point on the outer side of the flow: while the TKE predicted by the Adaptive LES gradually reduces to zero, the experiments show non-zero values. Some of the experimental data in this region also increased beyond \(r/b=2\), which is inconsistent with laminar ambient fluid motion. The concentration turbulent intensity profiles in Fig. 11b also supports that in this region, the flow gradually transitions to a laminar regime. These discrepancies are possibly related to fluctuations in the background noise and the limited resolution inherent to the PTV system utilized in the Crowe et al. [9] study. Therefore, it is possible that the experimental profiles have over-estimated the TKE, and this potentially explains the slightly higher TKE levels across the experimental profiles compared to the Adaptive LES profiles in Figs. 12a and b.

Fig. 12
figure 12

Cross-sectional turbulent kinetic energy profiles at the a maximum height b return point. The TKE is calculated with two velocity components only (u and w)

Full size image

Figure 13 shows the cross-sectional turbulent shear intensity profiles at the maximum height and return point. Again, for both LES, the shear intensities at these two locations show relatively good agreement with the experimental data of Crowe et al. [9] in terms of magnitude and profile shape. While the predicted peak locations in the maximum height profiles do not necessarily coincide with the peaks in the experimental data, the differences are small and the simulation results are within the scatter of the experimental data. The locations of the predicted profile peaks at the return point are in agreement with the experiments.

Fig. 13
figure 13

Cross-sectional turbulent shear intensity profiles at the a maximum height b return point

Full size image

Figure 14 shows the cross-sectional vorticity profiles from cases C1 and C2 at the maximum height and return point. In most portions of both cross-sections, the magnitude of the predicted vorticity agrees with the experimental data of Crowe et al. [9] reasonably well. The locations of the peaks on both the inner and outer sides of the INBJ at the maximum height are also captured. However, near the peak of both profiles, the Adaptive LES appears to over-predict the magnitude of the vorticity. These discrepancies are potentially related to the spatial interpolation processes employed in the PTV algorithm of Crowe et al. [9] during the production of the Eulerian velocity fields from instantaneous velocities of individual tracked particles. Since vorticity is computed from the gradients of velocity components, it is naturally more sensitive to spatial resolution and averaging duration than concentration and velocity fields. For a direct comparison, the present simulation results are also spatially filtered with a resolution equivalent to the post-processing system of Crowe et al. These filtered results are also presented in Fig. 15. After applying the filter, the vorticity in both cross-sections follows the experimental data very well. The magnitude and level of fluctuation are also consistent with the experimental measurements.

Fig. 14
figure 14

Cross-sectional vorticity profiles at the a maximum point b return point

Full size image
Fig. 15
figure 15

The eight points for the analysis of turbulent kinetic energy spectrum. Locations are the same as Jiang et al. [19] (x/DF0 = 0.3, 0.5, 0.9, 1.2, 1.5, 1.8, 2.1, 2.4)

Full size image

3.5.2 Turbulent kinetic energy spectrum

Analysis of the streamwise turbulent kinetic energy (TKE) spectra were performed at eight locations along the velocity centerline shown in Fig. 15. These locations are the same as those presented in Jiang et al. [19] (\(x/D{F}_{0}=\) 0.3, 0.5, 0.9, 1.2, 1.5, 1.8, 2.1, 2.4). For direct comparison, only the streamwise velocity component is used in the analysis.

Figure 16 compares the streamwise TKE spectrum of the present LES prediction with the experimental and LES data of Jiang et al. [19]. Compared with the LES of Jiang et al., the Adaptive LES is in better agreement with the experimental data in terms of both magnitude and profile form of the spectra at all eight locations.

Fig. 16
figure 16

Turbulent kinetic energy spectrum at different locations along the trajectory. Figure adapted from Jiang et al. [19]. Blue line: the Adaptive LES. Dashed black line: experimental data of Jiang et al. Solid black line: LES of Jiang et al. Red line: slope  − 5/3

Full size image

At Points 1 and 2 (\(\frac{x}{D{F}_{0}}=\)0.3 and 0.5), the Adaptive LES results almost completely follow the experimental spectrum. The spectral profiles at these two locations are relatively flat because they are within the zone of flow establishment. At Point 2, near the highest frequencies of around 25 Hz, the Adaptive LES predicted spectrum is lower than the experimental data. This is likely attributed to the (by definition) limited resolution of LES, as the motions of the higher frequencies correspond to the motions of smaller length-scale. Here again the differences between the measured and predicted behaviour are small.

At Points 3 and 4 (\(\frac{x}{D{F}_{0}}=\)0.9 and 1.2), the Adaptive LES simulated turbulence is developing and the spectra progresses towards the  − 5/3 slope gradually, which agrees with the experimental data. The reduced magnitude of the predicted spectrum relative to the experimental data at high frequencies becomes more evident further downstream. This is expected as the principle of LES is to only resolve the lower frequencies (larger length-scale) motions, while the effects of the higher frequency motions are included in the SGS models. At Point 4 (\(\frac{x}{D{F}_{0}}=\)1.2), the slope of the simulated spectrum is closer to the fully developed  − 5/3 inertial subrange profile than the experimental data. This suggests that the fully developed turbulence occurs earlier in the Adaptive LES.

At Point 5 and 6 (\(\frac{x}{D{F}_{0}}=\)1.5 and 1.8), the spectral profiles clearly follow the  − 5/3 slope, which implies that the inertial subrange is fully developed and captured by the Adaptive LES. At Points 7 and 8 (\(\frac{x}{D{F}_{0}}=\) 2.1 and 2.4), the spectral profiles at lower frequencies also follow the experimental data and the  − 5/3 profile very well. The smaller magnitude at high frequencies compared with experiment is expected, as noted above. Nevertheless, the resolved frequencies are sufficient to provide relatively accurate mean and turbulent quantities in INBJs as is evident in other data presented in this paper.

4 Conclusions

Large eddy simulations of 45° inclined negatively buoyant jets (INBJs) have been performed. The new simulation predictions are more accurate than other existing LES studies in the literature based on comparisons with experimental data of bulk parameters and turbulent statistics.

Previous studies have highlighted the difficulties in capturing the detrainment fluxes driven by buoyancy-induced instabilities because of the limited grid resolution. The Adaptive LES presented here addresses this issue by using an adaptive meshing approach with a novel refinement criterion. In addition, these previous studies have suggested that with the limited resolution, existing sub-grid scale (SGS) models are insufficient to fully capture the behaviour of the buoyancy induced instabilities, and improved SGS models should be developed. The present study has shown that with the novel adaptive meshing approach, the Lagrangian Dynamic SGS model is adequate in capturing this phenomenon. Using the Lagrangian Dynamic SGS model also addressed potential issues associated with the averaging direction in the Dynamic SGS model used in previous studies. This is the first study that has applied the Lagrangian Dynamic SGS model to INBJs.

Importantly, this study has provided a set of methods for generating high-quality LES data, well beyond the level of detail that can be captured by current experimental systems. The simulation output will be further analyzed to provide information on the behaviour of INBJs that has not been previously reported from experimental studies because of the limitations of experimental methods. This new information can potentially guide the more practical aspects of research on INBJs, such as developing new integral models—as well as the more fundamental aspects, such as studying the mechanisms of detrainment. In addition, future studies can apply the methods described here to simulate INBJs for different discharge configurations, and extend the approach to include different environmental conditions, such as ambient motion and stratification, and the presence of a seabed.