Skip to main content
SpringerLink
Log in

Effects of turbulent Schmidt number on CFD simulation of \(45^\circ \) inclined negatively buoyant jets

  • Original Article
  • Published:
Environmental Fluid Mechanics Aims and scope Submit manuscript

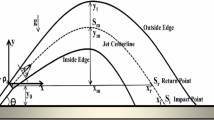
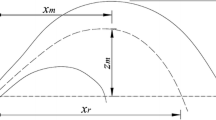
Abstract

Employing inclined negatively buoyant jets is one of the most advantageous means to discharge brine or waste in coastal environments. However, numerical prediction of mixing parameters for this kind of flow is still a challenge. In this investigation, CFD simulations of \(45^\circ \) inclined dense jets were conducted using realizable k–\(\epsilon \) model with buoyancy corrections and different values of turbulent Schmidt number (\(Sc_t\)) within two approaches in a finite volume model (Open FOAM). In the first approach, seven scenarios with different values of \(Sc_t\) were simulated. In the second one, a Regional Turbulent Schmidt Number (RTSN) configuration was introduced based on different behaviors of the flow in jet-like, plume-like, and inner/outer regions. Regarding the first approach, results showed that changing the turbulent Schmidt number has significant consequences for mixing and geometrical parameters. Reducing \(Sc_t\) from 1.0 to 0.4 led to more than \(\sim 60\%\) and \(\sim 40\%\) improvements in dilution ratio at return point and centerline peak, respectively. Using RTSN approach successfully improved the mixing parameters along with keeping nearly unchanged the accuracy of geometrical parameters. That was the case, specifically at return point in comparison with using any other constant \(Sc_t\) for the whole domain (first approach). This local (regional) change in turbulent Schmidt number compensates for flaws of Boussinesq approximation in the linear two-equation turbulence modeling of inclined negatively buoyant jets. Comparing to the previous LES results, the RTSN approach combined with the realizable k–\(\epsilon \) model stands as an economically superior solution employing much lower grid numbers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

Notes

  1. The open source CFD toolbox https://www.openfoam.com.

  2. Launder, Reece, and Rodi.

Abbreviations

\(b_c\) :

Charachteristic radial distance

C :

Concentration/salinity

\(C_0\) :

Initial concentration at nozzle

\(C_m\) :

Maximum local concentration

\(C_{1\epsilon }\),\(C_{2\epsilon }\),\(C_{3\epsilon }\) :

Constant

D :

Diameter

\(D_t\) :

Turbulent diffusion rate

\(Fr_d, Fr\) :

Densimetric Froude number

G :

Production due to buoyancy

g :

Acceleration due to gravity

\(H_0\) :

Nozzle tap height

k :

Turbulent kinetic energy

\(l_m\) :

Momentum length scale

M :

Initial momentum flux

P :

Pressure/production due to shear

\(Pr_t\) :

Turbulent Prandtl number

Q :

Initial volume flux

\(R_e\) :

Reynolds number

\(R_f\) :

Flux Richardson number

S :

Salinity/concentration/dilution ratio

\(Sc_t\) :

Turbulent Schmidt number

\(S_m\) :

Dilution ratio at centerline peak

\(S_r\) :

Dilution ratio at return point

\(S_\varPhi \) :

Source term

s :

Streamwise distance

T :

Temperature

\(U_0\) :

Initial velocity at nozzle

\(\overline{u'_i u'_j}\) :

Reynolds stress tensor

\(\overline{u'_i\phi '}\) :

Turbulent scalar flux

\(X_m\) :

Horizontal distance of centerline peak from nozzle level

\(X_r\) :

Horizontal distance of return point from nozzle level

\(Y_m\) :

Vertical distance of centerline peak from nozzle level

\(Y_t\) :

Vertical distance of terminal rise height location from nozzle level

\(\beta \) :

Thermal/saline expansion/contraction coefficient

\(\varGamma _{total}\) :

Total diffusion rate

\(\varDelta \rho \) :

Density difference

\(\delta _{ij}\) :

Kronecker delta

\(\zeta _{ij}\) :

Stress tensor

\(\epsilon \) :

Dissipation rate of turbulent kinetic energy

\(\theta _0\) :

Nozzle angle to horizontal

\(\nu \) :

Kinematic viscosity

\(\nu _t\) :

Eddy viscosity

\(\rho _a\) :

Ambient density

\(\rho _r\) :

Reference fluid density

\(\rho _0\) :

Initial density/jet density at nozzle

\(\sigma _t\) :

Schmidt/Prandtle number

\(\varPhi \) :

Scalar

References

  1. Papakonstantis IG, Christodoulou GC, Papanicolaou PN (2011) Inclined negatively buoyant jets 1: geometrical characteristics. J Hydraul Res 49(1):3–12

    Google Scholar 

  2. Roberts PJ, Ferrier A, Daviero G (1997) Mixing in inclined dense jets. J Hydraul Eng 123(8):693–699

    Google Scholar 

  3. Ardalan H, Vafaei F (2019) CFD and experimental study of 45\(^\circ \) inclined thermal-saline reversible buoyant jets in stationary ambient. Environ Process 6:1–21

    Google Scholar 

  4. Zeitoun M, Reid R, McHilhenny W, Mitchell T (1972) Model studies of outfall systems for desalination plants. Office of Saline Water, US Department of the Interior, Washington, DC

    Google Scholar 

  5. Kikkert GA, Davidson M, Nokes R (2007) Inclined negatively buoyant discharges. J Hydraul Eng 133(5):545–554

    Google Scholar 

  6. Shao D, Law AWK (2010) Mixing and boundary interactions of 30 and 45 inclined dense jets. Environ Fluid Mech 10(5):521–553

    Google Scholar 

  7. Lai CC, Lee JH (2012) Mixing of inclined dense jets in stationary ambient. J Hydro-Environ Res 6(1):9–28

    Google Scholar 

  8. Oliver C, Davidson M, Nokes R (2013) Removing the boundary influence on negatively buoyant jets. Environ Fluid Mech 13(6):625–648

    Google Scholar 

  9. Cipollina A, Brucato A, Grisafi F, Nicosia S (2005) Bench-scale investigation of inclined dense jets. J Hydraul Eng 131(11):1017–1022

    Google Scholar 

  10. Papakonstantis IG, Christodoulou GC, Papanicolaou PN (2011) Inclined negatively buoyant jets 2: concentration measurements. J Hydraul Res 49(1):13–22

    Google Scholar 

  11. Bashitialshaaer R, Larson M, Persson KM (2012) An experimental investigation on inclined negatively buoyant jets. Water 4(3):720–738

    Google Scholar 

  12. Abessi O, Roberts PJ (2015) Effect of nozzle orientation on dense jets in stagnant environments. J Hydraul Eng 141(8):06015009

    Google Scholar 

  13. Crowe A, Davidson M, Nokes R (2016) Velocity measurements in inclined negatively buoyant jets. Environ Fluid Mech 16(3):503–520

    Google Scholar 

  14. Papakonstantis IG, Tsatsara EI (2018) Trajectory characteristics of inclined turbulent dense jets. Environ Process 5(3):539–554

    Google Scholar 

  15. Papakonstantis IG, Tsatsara EI (2019) Mixing characteristics of inclined turbulent dense jets. Environ Process 6:1–17

    Google Scholar 

  16. Shao D (2010) Desalination discharge in shallow coastal waters. Ph.D. thesis, Nanyang Technological University

  17. Zhang W, Zhu DZ (2010) Near-field mixing downstream of a multiport diffuser in a shallow river. J Environ Eng 137(4):230–240

    Google Scholar 

  18. Jiang B, Law AWK, Lee JHW (2013) Mixing of 30 and 45 inclined dense jets in shallow coastal waters. J Hydraul Eng 140(3):241–253

    Google Scholar 

  19. Abessi O, Roberts PJ (2015) Dense jet discharges in shallow water. J Hydraul Eng 142(1):04015033

    Google Scholar 

  20. Vafeiadou P, Papakonstantis I, Christodoulou G (2005) Numerical simulation of inclined negatively buoyant jets. In: The 9th international conference on environmental science and technology, September, pp 1–3

  21. Oliver C, Davidson M, Nokes R (2008) k-\(\varepsilon \) predictions of the initial mixing of desalination discharges. Environ Fluid Mech 8(5–6):617

    Google Scholar 

  22. Kheirkhah Gildeh H, Mohammadian A, Nistor I, Qiblawey H, Yan X (2015a) CFD modeling and analysis of the behavior of 30 and 45 inclined dense jets-new numerical insights. J Appl Water Eng Res 4(2):112–127

    Google Scholar 

  23. Kheirkhah Gildeh H, Mohammadian A, Nistor I, Qiblawey H (2015b) Numerical modeling of 30 and 45 degree inclined dense turbulent jets in stationary ambient. Environ Fluid Mech 15(3):537–562

    Google Scholar 

  24. Zhang S, Jiang B, Law AWK, Zhao B (2015) Large eddy simulations of 45 inclined dense jets. Environ Fluid Mech 16(1):101–121

    Google Scholar 

  25. Zhang S, Law AWK, Jiang M (2017) Large eddy simulations of 45 and 60 inclined dense jets with bottom impact. J Hydro-Environ Res 15:54–66

    Google Scholar 

  26. Jiang M, Law AWK, Lai AC (2019) Turbulence characteristics of 45 inclined dense jets. Environ Fluid Mech 19(1):27–54

    Google Scholar 

  27. Nemlioglu S, Roberts P (2006) Experiments on dense jets using three-dimensional laser-induced fluorescence (3dlif). In: 4th International conference on marine waste water disposal and marine environment

  28. Palomar P, Lara J, Losada I (2012) Near field brine discharge modeling part 2: validation of commercial tools. Desalination 290:28–42

    Google Scholar 

  29. Crowe A, Davidson M, Nokes R (2016) Modified reduced buoyancy flux model for desalination discharges. Desalination 378:53–59

    Google Scholar 

  30. Gualtieri C, Angeloudis A, Bombardelli F, Jha S, Stoesser T (2017) On the values for the turbulent schmidt number in environmental flows. Fluids 2(2):17

    Google Scholar 

  31. Millero FJ, Poisson A (1981) International one-atmosphere equation of state of seawater. Deep Sea Res A Oceanogr Res Pap 28(6):625–629

    Google Scholar 

  32. Shih TH, Liou WW, Shabbir A, Yang Z, Zhu J (1995) A new k-\(\epsilon \) eddy viscosity model for high Reynolds number turbulent flows. Comput Fluids 24(3):227–238

    Google Scholar 

  33. Van Maele K, Merci B (2006) Application of two buoyancy-modified k-\(\varepsilon \) turbulence models to different types of buoyant plumes. Fire Saf J 41(2):122–138

    Google Scholar 

  34. Heindel T, Ramadhyani S, Incropera F (1994) Assessment of turbulence models for natural convection in an enclosure. Numer Heat Transf 26(2):147–172

    Google Scholar 

  35. Daly BJ, Harlow FH (1970) Transport equations in turbulence. Phys Fluids 13(11):2634–2649

    Google Scholar 

  36. Commission IO, et al. (2010) The international thermodynamic equation of seawater—2010: calculation and use of thermodynamic properties. (includes corrections up to 31st October 2015)

  37. Baurle R (2004) Modeling of high speed reacting flows: established practices and future challenges. In: 42nd AIAA aerospace sciences meeting and exhibit, p 267

  38. Liu Y, Feng H, Olsen MG, Fox RO, Hill JC (2006) Turbulent mixing in a confined rectangular wake. Chem Eng Sci 61(21):6946–6962

    Google Scholar 

  39. Tominaga Y, Stathopoulos T (2007) Turbulent Schmidt numbers for CFD analysis with various types of flowfield. Atmos Environ 41(37):8091–8099

    Google Scholar 

  40. He G, Guo Y, Hsu AT, Brankovic A, Syed S, Liu NS (1999) The effect of Schmidt number on turbulent scalar mixing in a jet-in-crossflow. In: ASME 1999 international gas turbine and aeroengine congress and exhibition, American Society of Mechanical Engineers, pp V002T02A029–V002T02A029

  41. Reynolds A (1975) The prediction of turbulent Prandtl and Schmidt numbers. Int J Heat Mass Transf 18(9):1055–1069

    Google Scholar 

  42. Shao D, Law AWK (2009) Turbulent mass and momentum transport of a circular offset dense jet. J Turbul 10(10):N40

    Google Scholar 

  43. Xu D, Chen J (2012) Experimental study of stratified jet by simultaneous measurements of velocity and density fields. Exp Fluids 53(1):145–162

    Google Scholar 

  44. Shi Z, Chen J, Chen Q (2016) On the turbulence models and turbulent Schmidt number in simulating stratified flows. J Build Perform Simul 9(2):134–148

    Google Scholar 

  45. Roberts PJ, Toms G (1987) Inclined dense jets in flowing current. J Hydraul Eng 113(3):323–340

    Google Scholar 

  46. Papanicolaou PN, List EJ (1988) Investigations of round vertical turbulent buoyant jets. J Fluid Mech 195:341–391

    Google Scholar 

  47. Riddle A, Carruthers D, Sharpe A, McHugh C, Stocker J (2004) Comparisons between fluent and adms for atmospheric dispersion modelling. Atmos Environ 38(7):1029–1038

    Google Scholar 

  48. Kikkert GA (2006) Buoyant jets with two and three-dimensional trajectories. Ph.D. thesis, University of Canterbury

  49. Rodi W (1980) Turbulence models and their application in hydraulics. University of Karlsruhe, Germany

    Google Scholar 

  50. Galeazzo FCC, Donnert G, Cárdenas C, Sedlmaier J, Habisreuther P, Zarzalis N, Beck C, Krebs W (2013) Computational modeling of turbulent mixing in a jet in crossflow. Int J Heat Fluid Flow 41:55–65

    Google Scholar 

  51. Huq P, Stewart EJ (2008) Measurements and analysis of the turbulent Schmidt number in density stratified turbulence. Geophys Res Lett 35(23):L23604

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Civil Engineering, K.N. Toosi University of Technology, P. O. Box 15876-4416, Tehran, Iran

    Sina Tahmooresi & Davoud Ahmadyar

Authors
  1. Sina Tahmooresi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Davoud Ahmadyar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sina Tahmooresi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tahmooresi, S., Ahmadyar, D. Effects of turbulent Schmidt number on CFD simulation of \(45^\circ \) inclined negatively buoyant jets. Environ Fluid Mech 21, 39–62 (2021). https://doi.org/10.1007/s10652-020-09762-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10652-020-09762-6

Keywords

Search

Navigation