Predicting flow resistance in open-channel flows with submerged vegetation

Abstract

In vegetated flows, hydrodynamic parameters, such as drag coefficient, frontal area and deflected canopy height, influence velocity distributions, mean velocity and flow resistance. Previous studies have focused on flow–structure interaction in sparse vegetation, dense vegetation or transitional canopies, respectively. To date, a unifying approach to estimate hydrodynamic properties of submerged vegetated flows across the full vegetation density spectrum is missing. Herein, published data sets across a wide range of vegetation conditions were re-analysed using a previously proposed four-layer velocity superposition model. For the investigated vegetation conditions, the velocity model was able to match measured velocity distributions and depth-averaged mean velocity. The contribution of each velocity layer to the mean velocity was analyzed, showing that the mixing layer is dominant in transitional canopies with shallow submergence, and that the log-law layer is dominant in denser canopies with deeper submergence. Based upon velocity distributions, an explicit equation for the Darcy–Weisbach friction factors was deduced that is able to predict flow resistance as function of relative submergence. While each velocity distribution could be well described with the four-layer model across the range of vegetation conditions, some data scatter in model parameters was observed. To improve predictive capabilities of the model, future research should focus on detailed velocity measurements with high spatial resolution.

1 Introduction

Vegetated open-channel flow systems such as grassed waterways or levees are important nature-based solutions. The vegetation helps to create a balanced ecosystem [1], improves nutrients and oxygen content [2], mitigates soil loss, promotes sedimentation [3, 4], and increases groundwater replenishment [5], while maintaining the function of water conveyance [6]. From an engineering perspective, the use of grass and vegetation in open-channels can contribute to low-impact developments.

Flows over vegetation have attracted significant research attention, spanning from flows with submerged vegetation in rivers and estuaries [7, 8], over overland flows in flood plains [9,10,11], to supercritical flows over grass-lined dikes [12, 13] and embankments [14, 15]. A general distinction between (1) emergent vegetation and (2) submerged vegetation can be made. In flows with emergent vegetation, the vegetation exceeds the flow depth while the interactions between flow and vegetation are reduced [8]. For instance, the large-scale canopy vortices generated by the turbulent mixing between inside-canopy and above-canopy flows are absent in emergent vegetation [16]. For flows with submerged vegetation, research has focused on improving the understanding of interactions between vegetation and flows [5, 17,18,19], flow resistance estimations [18, 20], as well as stability considerations [21,22,23]. Both, emergent and submerged vegetation, generate flow resistance through similar mechanism of canopy drag [24, 25]. The current study focuses on channels with a uniformly distributed submerged vegetation layer, while natural riverine and floodplain can also have a heterogeneous mixture of different vegetation species (e.g., shrubs and grass) [26,27,28].

Table 1 Selected laboratory studies of open-channel flows with submerged vegetation, resembling transitional canopies (top, $C_Dah_c < 0.5$) and dense canopies (bottom, $0.5 \le C_Dah_c$); note that all studies besides [29] were performed in subcritical flows

Table 1 summarizes laboratory studies in open channels with submerged vegetation as typically found in grassed waterways and vegetated channels or floodplains. The vegetation type is differentiated into three categories: (i) natural or artificial, (ii) rigid or flexible, and (iii) grass-like or stem-like or leafy. The vegetated channels and floodplains listed in Table 1 were modeled using rigid (stem-like) cylinders [30, 31, 33, 35, 37], flexible plastic stripes [33, 34, 36], or flexible leafy vegetation [32], while engineered and well-maintained grassed waterways were represented by a dense layer of artificial turf [16, 29]. All studies in Table 1 had uniformly distributed vegetation elements, assuming spatially homogeneous flow properties, and most studies were conducted in subcritical flows with dense vegetation (Table 1, bottom). Fewer researchers studied subcritical flows with transitional vegetation (Table 1, top) and limited research investigated dense supercritical flows [29]. Note that the selection of studies in Table 1 was based upon availability of required hydrodynamic information (including velocity profiles), and other relevant studies were therefore not considered (e.g., [20, 38, 39]).

The vegetation can be classified using a hydrodynamic density definition $C_Dah_c$, in which $C_D$ is the drag coefficient, $h_c$ is the deflected vegetation height, and a is the frontal area per unit volume, defined as $a=mw$ for grass-like and stem-like vegetation, with m being the number of canopies/stems per unit area, and w the canopy width or stem diameter. Note that the drag coefficient and frontal area were treated as temporally and spatially averaged parameters. Previous studies reduced the hydrodynamic density ($C_Dah_c$) to vegetation density ($ah_c$), assuming $C_D = 1$ [40, 41]. On the basis of different velocity distributions, Nepf et al. (2007) [42] classified the vegetation density as sparse ($ah_c<< 0.1$), transitional ($ah_c \approx 0.1$) and dense ($ah_c \ge 0.1$), see [19, 43, 44]. It is noted that multiple threshold definitions between transitional and dense canopies have been used by other researchers, e.g., $ah_c \ge 0.15$ [45], $ah_c \ge 0.23$ [19], and $ah_c \ge 0.56$ [46].

Because the collated vegetation data sets include cases with $C_D \ne 1$ (see also Table 2 in Appendix 1), the hydrodynamic density definition $C_Dah_c$ was used herein to separate transitional from dense canopies. With increasing $C_Dah_c$, gradual changes in velocity distributions from transitional canopy to dense canopy were found in the re-analysed data, and a noticeable change in velocity distributions was observed at $C_Dah_c \approx 0.5$. Consequently, sparse canopies were defined as $C_Dah_c < 0.03$ [47], transitional canopies as $0.03 \le C_Dah_c < 0.5$, and dense canopies as $0.5 \le C_Dah_c$ (Table 1).

1.1 Velocity profiles for different canopy densities

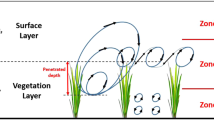
Figure 1 conceptualises streamwise time-averaged velocity distributions in flows with submerged vegetation, differentiating between sparse, transitional and dense canopies. The individual velocity contributions of the four-layer velocity model of [16] are included, comprising (i) quasi-constant velocity distribution ($\overline{u}_{\text {UD}}$), (ii) mixing layer ($\overline{u}_{\text {ML}}$), (iii) log-law layer ($\overline{u}_{\text {LL}}$), and (iv) wake region ($\overline{u}_{\text {WF}}$). Single- and double-layer velocity models have also been proposed to characterise velocity distributions in vegetated channels [30, 33, 37, 39, 48], but the four-layer velocity superposition provides a complete description of individual physical effects on velocity profiles for different canopy densities.

Fig. 1

Conceptualization of the four-layer velocity profile from [16] for vegetated channels with a sparse canopy ($C_Dah_c < 0.03$) b transitional canopy ($0.03 \le C_Dah_c < 0.5$) c dense canopy ($0.5 \le C_Dah_C$) (with d = flow depth, y = bed normal coordinate)

From an engineering point of view, sparse canopies ($C_Dah_c < 0.03$) contribute little to erosion prevention and soil retention [49], which implies that they are rarely found in human-made vegetated waterways. Experiments in sparse canopies ($C_Dah_c < 0.03$) have shown that the canopy drag provided by the vegetation has only localized effects, implying that the drag is generally negligible when compared to the bed roughness [50], and that the Reynolds stress distribution is similar to bare soil condition [51] or smooth beds [52]. Therefore, velocity distributions in sparse canopies can be modeled using classic boundary layer theory with log-law layer and wake function [41] (Fig. 1a). Sparse canopies are therefore not considered in the remainder of this manuscript.

In flows with transitional canopies ($0.03 \le C_Dah_c < 0.5$), the effect of the vegetation is more pronounced, and a sudden increase of Reynolds stress has been observed near the canopy top [53], which is due to Kelvin–Helmholtz instabilities induced by the canopy drag discontinuity [41]. However, the canopy drag is not strong enough to dissipate these Kelvin–Helmholtz instabilities, implying that canopy-scale vortices can penetrate towards the channel bed, thereby influencing the in-canopy velocity (Fig. 1b). In flows with transitional canopies, a mixing layer has been observed, starting in the vicinity of the channel bed and occupying the majority of the in-canopy flow depth [19, 38, 54]. This mixing layer is typically characterised by an inflection point, located approximately midway between slow moving in-canopy flows and fast moving above-canopy flows [10, 54, 55], and usually ends below the canopy top, followed by the start of log-law layer and wake function layer [30, 32]. As demonstrated in Fig. 1b, the complete velocity profiles of transitional canopies are S-shaped, and can be described through a superposition of mixing layer, log-law layer and wake function.

In flows across dense canopies ($0.5 \le C_Dah_c$), the mixing layer thickness is reduced by the strong canopy drag, and, with increasing density, a quasi-uniform velocity layer gradually appears inside the canopy [16, 44, 56] (see Fig. 1c). Within this uniform velocity layer, Reynolds stresses and turbulent kinetic energy are near-zero due to the strong canopy drag [18, 35, 57]. The mixing layer starts on top of the uniform velocity layer and occupies a smaller fraction of the in-canopy flow depth when compared to transitional densities. The inflection point is typically located near the canopy top. Above the canopy top, the log-law layer typically starts to form near the deflected canopy height $h_c$ [58], while its starting location has been found to be as high as $2h_c$ [17].

1.2 Research objectives

Despite extensive research of vegetated flows, the majority of velocity profile models have been established for one type of vegetation density, and have rarely been tested in other vegetation conditions. Re-analysing 40 velocity distributions measured in previous studies across a wide range of vegetation densities ($0.03 \le C_Dah_c \le 9.66$, see Table 2 in Appendix 1) provided an opportunity to test the applicability of the velocity model of [16] across the full range of vegetation density conditions. Up to date, this superposition model has only been applied to vegetated channels with high canopy density [16, 29, 59], while its applicability to sparse or transitional densities remains unknown. The current re-analysis shows that the superposition model is able to consistently predict velocity distributions and depth-averaged mean velocity of the diverse data sets of Table 1.

Previous experimental and analytical studies have also shown a dependency of depth-averaged mean velocity ($\langle \overline{u} \rangle$) and Darcy–Weisbach friction factor (f) on canopy densities [18, 19, 29, 32, 37, 60], in which larger canopy densities decrease mean velocity and increase flow resistance. Yet, limited number of studies provided expressions of $\langle \overline{u} \rangle$ and f for the full range of densities [61, 62], despite the complex phenomenological closure model for velocity distribution and flow resistance by [18, 63]. The current study expanded [16]’s velocity superposition model, defining an explicit equation for the prediction of Darcy–Weisbach friction factors.

2 Methodology

2.1 Superposition velocity model

The four-layer velocity superposition model of Nikora et al. [16] was originally developed to describe the streamwise time-averaged velocity distribution ($\overline{u}$) of subcritical open-channel flows over dense artificial grass:

$$\begin{aligned} \overline{u} = \underbrace{\sqrt{\frac{2gS_0}{aC_D}}}_{\overline{u}_\text {UD}} +\underbrace{(\overline{u}_i-\overline{u}_{\text {UD}}) \left( 1+\tanh {\frac{y-y_i}{L_e}}\right) }_{\overline{u}_\text {ML}} +\underbrace{\frac{u_{*_\text {c}}}{\kappa } \left( \ln {\frac{y-y_i-d_i}{y_0}}+2\Pi \sin ^2 \left( {\frac{\pi y}{2d}}\right) \right) }_{\overline{u}_\text {LL} + \overline{u}_\text {WF}} \end{aligned}$$

(1)

where g is the gravitational acceleration, $\overline{u}_{i}$ is the time-averaged velocity at the inflection point, $y_i$ is the bed-normal elevation of the inflection point, $L_e$ is a characteristic length scale describing the penetration depth of vortices [54, 64], $u_{*_\text {c}}$ is the shear velocity at the canopy top, $\kappa$ is the von Karman constant (taken as $\kappa = 0.41$), $d_i$ is a deviation length scale, $y_0$ is the roughness height, $\Pi$ is the wake parameter [65], d is the flow depth, and $S_0$ is the bed slope, which is equal to the friction slope $S_f$ for uniform flows.

Equation (1) was applied to a wide range of collected data sets. Herein, $\overline{u}_\text {UD}$ was evaluated from vegetation characteristics and channel slope, $u_{*_\text {c}} = \rho gS_0(d-h_c)$ was computed using the deflected vegetation height ($h_c$) and channel slope ($S_0$), whereas $\overline{u}_i$ and $y_i$ were directly extracted from measured velocity profiles. Other parameters in Eq. (1) were obtained through velocity profile fitting based on minimizing the root-mean-squared error (RMSE) between model and measurements. The mixing layer velocity $\overline{u}_\text {ML}$ was fitted to in-canopy velocities through adjustment of $L_e$, the log-layer velocity $\overline{u}_\text {LL}$ was fitted to measurements for elevations $h_c< y < h_c + 0.2 \, \cdot \, (d-h_c)$ by adapting $d_i$ and $y_0$, and $\overline{u}_\text {WF}$ was fitted to elevations $y > 0.2 \, \cdot \, (d-h_c)$ through variation of $\Pi$. Note that the log-law layer and wake function layer only start above $y \ge y_i+d_i+y_0$.

An integration of Eq. (1) between the channel bed ($y = 0$) and the free-surface ($y = d$) provided the depth-averaged mean velocity [16]:

$$\begin{aligned} \begin{aligned} \langle \overline{u} \rangle&= \frac{1}{d} \left( \int _{0}^{d}\overline{u}_{\text {UD}} \, \text {d}y + \int _{0}^{d}\overline{u}_{\text {ML}} \, \text {d}y +\int _{y_i}^{d} \overline{u}_{\text {LL}} \, \text {d}y +\int _{0}^{d}\overline{u}_{\text {WF}} \, \text {d}y \right) \\&=\underbrace{\sqrt{\frac{2gS_0}{C_Da}}}_{\langle \overline{u}_{\text {UD}} \rangle } + \underbrace{\sqrt{\frac{2gS_0}{C_Da}} (\zeta -1) \, \left( 1+\frac{ \alpha h_c}{d} \, \ln \left[ \frac{\cosh \left( \frac{\beta }{\alpha }-\frac{d}{ \alpha h_c} \right) }{\cosh \left( \frac{\beta }{\alpha } \right) }\right] \right) }_{\langle \overline{u}_{\text {ML}} \rangle } \\&\quad \quad + \underbrace{\frac{1}{d} \frac{u_{*_\text {c}}}{\kappa }\left( d -\beta h_c\right) \left( \ln \left[ \frac{d-\beta h_c}{h_c}\right] + \kappa C -1\right) }_{\langle \overline{u}_{\text {LL}} \rangle } + \underbrace{u_{*_\text {c}} \frac{\Pi }{\kappa }\, }_{\langle \overline{u}_{\text {WF}} \rangle } \end{aligned} \end{aligned}$$

(2)

where the operator $\langle \rangle$ stands for depth-averaging, and the following substitution parameters were used: $\alpha = \frac{L_e}{h_c}$, $\beta = \frac{y_i}{h_c}$, $\zeta = \frac{\overline{u}_i}{\overline{u}_{\text {UD}}}$, $C = -1/\kappa \ln (y_0/h_c)$ (further details in Sect. 3.2). Equation (2) was simplified by omitting $y_i$ in the lower integration limit of $\overline{u}_{\text {WF}}$, $y_0$ in the lower integration limits of $\overline{u}_{\text {LL}}$ and $\overline{u}_{\text {WF}}$, and assuming $d_i = 0$ [16]. These simplifications resulted in a deviation $\le 4.5 \%$ and are consistent with integration limits suggested by [16].

2.2 Explicit friction factor equation

The Darcy–Weisbach friction factor f is commonly used to characterise flow resistance in open channel flows. In the present study, the Darcy–Weisbach friction factor f was considered as point flow resistance coefficient related to the velocity distribution [66], and was computed as ratio of shear velocity ($u_*$) and mean velocity ($\langle \overline{u}\rangle$) [67]:

$$\begin{aligned} f = 8\left( \frac{u_*}{\langle \overline{u} \rangle }\right) ^2 \end{aligned}$$

(3)

For uniform flows in vegetated channels, the shear velocity ($u_*$) can be computed as [68]:

$$\begin{aligned} u_{*} = \sqrt{g S_0 (d + h_c(\phi -1))} \end{aligned}$$

(4)

where $\phi$ is the porosity of the vegetation, defined as ratio of fluid volume and total canopy volume, which is $\phi \approx 1.0$ in vegetated channels [16, 19, 69, 70]. Combining Eqs. (2), (3), and (4), the friction factor is herein expressed as:

$$\begin{aligned} \begin{aligned} f&= 8\left( \frac{u_*}{\langle \overline{u} \rangle }\right) ^2 \\&= \frac{8d}{\left( \begin{array}{r}{\sqrt{\frac{1}{\frac{1}{2} C_D a }} \Biggl \lbrace 1 + (\zeta -1) \left( 1 + \frac{\alpha h_c}{d} \ln \left[ \frac{\cosh \left( \frac{\beta }{\alpha } - \frac{d}{\alpha h_c} \right) }{\cosh \left( \frac{\beta }{\alpha }\right) } \right] \right) \Biggl \rbrace +}\\ {\sqrt{h_c \left( \frac{d}{h_c} - 1 \right) }\left[ \frac{1}{\kappa }\frac{(d-\beta h_c)}{d} \left( \ln \left[ \frac{d-\beta h_c}{h_c}\right] + \kappa C -1\right) +\frac{\Pi }{\kappa } \right] }\end{array}\right) ^2} \end{aligned} \end{aligned}$$

(5)

where it was assumed that $\phi =1$ and that the flow is uniform. It is noteworthy that the channel slope was eliminated in Eq. (5), demonstrating that the friction factor is independent of $S_0$.

2.3 Data sets

In this work, 40 previously published data sets were collated, comprising flow rates (q), flow depths (d), channel slope ($S_0$), deflected vegetation/grass height ($h_c$), unit frontal area (a), drag coefficients ($C_D$), and velocity profiles. A summary is presented in Table 2 (Appendix 1), where only studies with available velocity distributions were considered, ranging from transitional [30,31,32,33] to dense canopies [16, 17, 29, 34,35,36,37]. A detailed re-analysis of these velocity distributions resulted in values of model parameters ($\alpha$, $\beta$, C, $\zeta$, $\Pi$) for both, transitional and dense canopies (Fig. 3 and Table 3).

3 Results

3.1 Streamwise time-averaged velocity profiles

Examples of measured velocity distributions as well as the fitted superposition model (Eq. 1) are presented in Fig. 2a–c for transitional canopies, and in Fig. 2d–f for dense canopies. A detailed velocity decomposition is shown in Fig. 2c,f for both vegetation densities, as well as in the Supplementary Material for all data sets.

Fig. 2

Superposition velocity model predicts velocity distributions in vegetated channels with varying hydrodynamic densities a nr. 9 (Table 2, [33]) b nr. 3 (Table 2, [31]) c nr. 1 (Table 2, [30]) d nr. 15 (Table 2, [35]) e nr. 18 (Table 2, [17]) f nr. 14 (Table 2, [34])

The deflected vegetation/grass height ($h_c$) and shear velocity at the channel bed ($u_*$) (Eq. 4) were used for normalization. For transitional canopies (Fig. 2a–c), the mixing layer started immediately above the channel bed ($\overline{u}=\overline{u}_\text {UD}+\overline{u}_\text {ML}$ at $y \approx 0$), indicating that the Kelvin–Helmholtz instabilities penetrated deep into the canopy. Inflection points were observed near the canopy top and the log-law layer with wake function matched the above-canopy velocities (Fig. 2a–c). It is noted that the the log-law layer started below the canopy top, which is in agreement with previous observations [30, 32]. Overall, velocity distributions in transitional canopies were well characterised by Eq. (1).

For flows across dense canopies, the velocity distributions were also well predicted with Eq. (1), as demonstrated in Fig. 2d–f. Uniform velocities occupied a considerable proportion of the in-canopy depth, which is explained by the strong canopy drag, limiting the penetration of Kevin-Helmholtz instabilities [71]. The uniform layer occupied more than half of the in-canopy depth, while high densities in the experiments of [36] and [16] resulted in $\overline{u}_{\text {UD}}$ $\approx$ 0 m s$^{-1}$ (not shown). Due to the enhanced drag, the mixing layer thickness was significantly reduced in dense canopies when compared to transitional canopies. In some cases, such as shown in Fig. 2f, the mixing layer started and finished within the upper half of the in-canopy flow depth. The inflection point was typically located below the canopy top for dense canopies, and the above- canopy velocities were modeled well with a log-law layer and wake function (Fig. 2d–f).

3.2 Model parameters

Modeling the velocity distribution and depth-averaged velocity with Eqs. (1) and (2) involves hydrodynamic density parameters ($C_D, a, h_c$) and model parameters ($L_e$, $y_i$, $\overline{u}_i$, $d_i$, $y_0$, $\Pi$), including their dimensionless versions ($\alpha = L_e/h_c$, $\beta = y_i/h_c$, $\zeta = \overline{u}_i/\overline{u}_\text {UD}$, $C = -1/\kappa \ln (y_0/h_c)$). Hydrodynamic density parameters were used to calculate the uniform velocity $\overline{u}_\text {UD}$, while model parameters relating to the mixing layer, log-layer, and wake function were evaluated as described in Sect. 2.1. All derived model parameters are listed and illustrated in Table 3 (Appendix 1) and Fig. 3, respectively.

Fig. 3

Model parameters for the superposition velocity model in vegetated flows a $\alpha =$ dimensionless characteristic length scale of the mixing layer b $\beta =$ dimensionless elevation of the inflection point c $y_0/h_c =$ dimensionless roughness height d $\zeta =$ dimensionless inflection point velocity e $\Pi =$ Coles’ wake function parameter

3.2.1 Mixing layer

Figure 3a shows the dimensionless mixing layer length scale ($\alpha$) as a function of vegetation hydrodynamic density ($C_D a h_c$). An increase in hydrodynamic density was associated with a decrease in $\alpha$, which implies that a denser vegetation limits the penetration of vortices into the canopy [16,17,18, 71]. The majority of inflection points were located below the canopy top ($\beta < 1$; Fig. 3b), and an inverse trend with respect to $C_D a h_c$ was observed, i.e., the inflection point elevation increased with increasing vegetation density. Note that the suggested value of $\beta = 0.75$ [16] for dense canopies confirms these observations. For higher vegetation densities, the momentum transfer between above-canopy and in-canopy flows decreases, which is associated with a smaller extent and a higher elevation of the mixing layer. It is further noted that bottom slope $S_0$ and relative submergence $d/h_c$ may also influence the mixing layer thickness [16]. For example, an increase in slope can lead to an increase in stem-wake-scale turbulence and thus enhanced turbulent viscosity, which would slow down the growth of the mixing layer.

The dimensionless ratio ($\zeta$) of the inflection point velocity ($\overline{u}_i$) to the uniform velocity ($\overline{u}_{\text {UD}}$) is shown in Fig. 3c as function of a dimensionless friction velocity at the canopy top ($u_{*_c}/\overline{u}_\text {UD}$). For all data sets, there was a strong correlation between $\zeta$ and $u_{*_c}/\overline{u}_\text {UD}$. An increase in $u_{*_c}/\overline{u}_\text {UD}$ implies stronger canopy drag which quickly dissipates the canopy-scale vortices [18], resulting in an updwars shift of the mixing layer, and consequently a larger inflection point velocity $\overline{u}_i$.

3.2.2 Log-layer and wake function

The calculation of the log-law layer as per Eq. (1) requires further knowledge of the deviation length scale $d_i$ and the roughness height $y_0$. It is noted that $d_i$ was relatively small and could be neglected in first instance, i.e. $d_i \approx 0$. The dimensionless roughness height $y_0/h_c$ increased with increasing mixing layer length scale, and was approximately $y_0/h_c = 2 \alpha$ for smaller densities, as shown in Fig. 3d.

Coles’ wake parameter ($\Pi$) is the main parameter of the wake region and describes the departure of the velocity profile from a pure log-law behaviour in the upper flow. The wake function parameter is approximately $\Pi = 0.2$ for uniform flows with zero pressure gradient (see dashed blue line in Fig. 3e), while a dependence on relative submergence $d/h_c$ and channel aspect ratio has been discussed [16]. As the aspect ratio and relative submergence are inversely connected, a separation of such different effects is difficult. For consistency, $\Pi$ is plotted against $C_D a h_c$ in Fig. 3e. Some smaller $\Pi$-values were observed for transitional canopies. One may argue that a larger roughness may lead to a increase in $\Pi$, as shown in [72], but a conclusive statement on $\Pi$-values is not feasible and would require more systematic investigations.

3.3 Mean velocities

Depth-averaged velocities were evaluated using Eq. (2), together with hydrodynamic density parameters and model parameters as provided in Tables 2 and 3. Figure 4a compares estimated depth-averaged velocities with measured depth-averaged velocities for the 40 data sets, demonstrating a close agreement between measurements and model calculations (RMSE = 0.058 ms$^{-1}$), which highlights the applicability of Eq. (2).

Fig. 4

Comparison of estimated depth-averaged velocities $\langle \overline{u} \rangle$ with measured depth-averaged velocities $\langle \overline{u} \rangle _\text {meas}$ for flows in channels with transitional and dense canopies; mean velocities calculated using Eq. (2) and vegetation/model parameters listed in Tables 2 and 3

Fig. 5

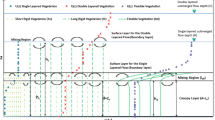
Contribution of individual velocity layers to the mean velocity (Eq. (2)) for varying relative submergence levels; profiles ordered with increasing $C_d a h_c$ a nr. 7 (Table 2, [33]) b nr. 3 (Table 2, [31]) c nr. 1 (Table 2, [30]) d nr. 14 (Table 2, [35]) e nr. 17 (Table 2, [17]) f nr. 13 (Table 2, [34]); note that the submergence level of each study is marked by a dashed line

The relative contribution of each velocity layer to the mean velocity was computed to understand how individual physical processes affected the composition of the velocity profiles. For different submergence levels, Eq. (2) was evaluated using hydrodynamic density and model parameters (as per Tables 2 and 3) for exemplary transitional data sets of [30, 31, 33] (Fig. 5a–c) and exemplary dense data sets of [17, 34, 35] (Fig. 5d–f).

For transitional data sets (Fig. 5a–c), the in-canopy mixing layer contributed significantly to the mean velocity for small submergence levels, while the contribution of the above-canopy log-law layer increased with increasing submergence. The proportion of the wake region was $< 0.1$, which implies that parameters associated with the mixing layer ($C_D$, $\beta$) and the log-law layer ($\beta$, $y_0$, $h_c$) have strong influence on the estimation of mean velocity and friction factor. For dense canopies (Fig. 5d–f), the in-canopy contribution of the uniform layer exceeded the contribution of the mixing layer in low submergence ($d/h_c \le 4$), while the contribution of the in-canopy velocities $\langle \overline{u}_\text {UD} \rangle + \langle \overline{u}_\text {ML} \rangle$ decreased naturally with increasing relative submergence. Overall, the model parameters associated with mixing and log-law layers ($\beta$, C, $h_c$) contributed the most to the estimation of mean velocities (and consequently friction factors), and should be carefully selected when applying the explicit Eqs. (2) and (5).

3.4 Friction factors

Darcy–Weisbach friction factors were evaluated for all 40 data sets. Figure 6 shows exemplary values of “measured” (markers) and “predicted” (lines) friction factors for different canopy densities, where submergence levels represented shallow submergence ($1< d/h_c < 5$) and intermediate submergence ($5 \le d/h_c \le 10$) [41]. “Measured” friction factors were computed using Eqs. (3) and (4), while “predicted” friction factors were estimated with Eq. (5), using data-set averaged model parameters and hydrodynamic density parameters as indicated in the legend of Fig. 6.

Fig. 6

Comparison of “measured” and “predicted” Darcy–Weisbach friction factors a transitional canopies b dense canopies c measured versus predicted friction factors

For transitional canopies (Fig. 6a), two data sets with varying values of $C_Dah_c$ are presented ([31, 33], showing a close match with friction factors calculated with Eq. (5). Friction factors declined with increasing submergence and lower $C_Dah_c$ values (Fig. 6a). The values of f were in the range of $0.18 \le f \le 0.68$, suggesting a reduced flow resistance for less dense transitional canopies compared to denser transitional canopies. With increasing $d/h_c$, the mean velocity increased due to the increased proportion of the log-law layer (Fig. 5), which decreased the friction factor. Lastly, there was a lack of data points for $d/h_c > 4$ (Fig. 6a), and the validity of the model for transitional canopies needs to be confirmed for higher relative submergence.

Exemplary friction factors for dense canopies [29, 36] are presented in Fig. 6b, showing higher f values for denser canopies, which is linked to the increasing roughness. In all data sets, the friction factor declined with increasing submergence and lower $C_Dah_c$ values. Friction factors for $C_Dah_c\ge 2.5$ ($0.13 \le f \le 2.55$) showed close agreement with each other across two studies with different $C_Dah_c$ values, implying the reduced sensitivity of friction factors on vegetation properties. Friction factors from [73] were comparable to denser canopies, which may be a results of their higher canopy stiffness (artificial rigid stem-like versus artificial flexible grass-like). All friction factors were well modeled with Eq. (5), which is also shown in Fig. 6c, comparing “measured” friction factors with “predicted” friction factors for both canopy densities. The uncertainty in $\langle \overline{u} \rangle$ (± 10%, Fig. 4b) affected the computation of the friction factor per Eq. (5), which is herein estimated to be up to ± 22% using a Monte-Carlo simulation (not shown).

4 Discussion: Model limitations

This study demonstrates that velocity profiles, depth-averaged mean velocities and friction factors of flows over transitional and dense canopies can be characterised using a four-layer superposition model. This finding is of high relevance for practical design of vegetated channels. Given a design flow rate, the uniform flow depth can be found numerically by equating Eq. (2) with $\langle \overline{u} \rangle = q/d$, subsequently yielding mean velocity and friction factor. However, the application of Eqs. (1), (2), and (5) requires a priori knowledge of model parameters ($\alpha$, $\beta$, $\zeta$, C, $\Pi$), hydrodynamic density parameters ($C_D$, a, $h_c$), and channel slope $S_0$. Some limitations are discussed in the following.

4.1 Model parameters

The current re-analysis suggests some trends of model parameters in relation to the hydrodynamic vegetation density (Fig. 3). For example, the elevation and thickness of the mixing layer was shown to be linked to $C_D a h_c$ (Figs. 3a, b). However, these result should be treated as qualitative, as effects of bottom slope and relative submergence on model parameters have been found elsewhere [16]. There was some larger scatter for the wake function parameter $\Pi$ (Fig. 3e), which is believed to be linked to measurement uncertainties and limited spatial resolution of previous measurements. As such, the data scatter limits predictive capabilities of the superposition velocity model, while it was shown that its application can yield a fine characterisation of the contribution of different physical effects to the mean velocity (Fig. 5). Therefore, future research is required to improve the characterisation of model parameter dependence on bulk flow parameters, aiming to improve predictive capabilities of the superposition model.

4.2 Hydrodynamic density parameters

In this study, time- and depth-averaged values of $C_D$, a and $h_c$ were adopted in Eqs. (1), 2), and (5). As such, the model is able to describe the time-averaged velocity distribution and associated time-averaged parameters, while it does not provide further insights into time-varying processes such as change of vegetation parameters due to reconfiguration of canopy postures caused by the coherent canopy waves [71, 74], and change of vegetation conditions due to scouring damage [75], which could subsequently influence instantaneous canopy drag, frontal area and canopy height [76,77,78].

A sensitivity analysis (Appendix 1) shows that a careful evaluation of key vegetation properties, including drag coefficient ($C_D$), frontal area (a), and deflected canopy height ($h_c$), is important for model accuracy. Some additional considerations on the estimation of $C_D$ and $h_c$ are presented below:

Fig. 7

Estimation of drag coefficients $C_D$ for different vegetation types a reported range of $C_D$ values for R = rigid vegetation [83], L = leafy plants [85], F = fluvial and coastal vegetation [86], B = bushes [87], G = grass [18], and A = artificial turf [16] b drag coefficient as function of the canopy-width Reynolds number

• Drag coefficient $C_D$

  The drag coefficient is an important parameter in the modeling of vegetated flows. Using previously published data, a range of $C_D$ values for selected vegetation types is shown in Fig. 7a. The drag coefficient is often assumed to be vertically uniform for rigid stem-like or flexible grass-like vegetation [30, 40], and its value is affected by Froude number [79], stem density [80], vegetation distribution [81], stem diameter [82], and deflected vegetation height [83]. Figure 7b shows drag coefficients of the re-analysed data sets as function of the canopy-width Reynolds number ($Re_\text {w} = \overline{u}_{\text {UD}}w / \nu$), together with additional data from [16]. In agreement with results of [84], the present re-analysis found $C_D$ to decline with increasing $Re_{\text {w}}$, approaching unity for larger Reynolds numbers.

• Deflected canopy height $h_c$

  In vegetated flows with flexible canopy, the vegetation height is reduced due to bending. [88] explored the connection between deflected vegetation height and mechanical properties of the vegetation such as canopy density, elasticity, and moment of inertia. [89] predicted the deflected vegetation height for a given flow rate and vegetation properties, and his model served the development of numerical solutions by [90] and [91]. Recently, [92] and [93] modeled the vegetation deflection considering the influence of leaf sheltering. A relatively crude and simplistic approach to evaluate the deflected vegetation height was provided by [94] after analyzing the bending of grass-like vegetation (16 mm $\le h_v \le$ 280 mm) with data sets of [10, 36, 94]. An empirical correlation between deflected canopy height ($h_c$), non-deflected canopy height ($h_v$), and depth-averaged mean velocity ($\langle \overline{u} \rangle$) reads:

  $$\begin{aligned} \frac{h_c}{h_v} = (-1.44\langle \overline{u} \rangle +1) \end{aligned}$$

  (6)

  Note that Eq. (6) is only valid for low velocity flows with $\langle \overline{u} \rangle \lessapprox 0.7$ ms$^{-1}$, while it yields non-physical results for higher flow velocities.

5 Conclusion

Vegetated channels and waterways are nature-based solutions for modern water resources management. For flows with submerged vegetation, most previous studies considered a small range of vegetation densities while changes in vegetation density results in different velocity distributions. This manuscript systematically investigated a wide range of vegetation densities ($0.03 \le C_Dah_c \le 9.66$) using published data, and demonstrated the transition of velocity distributions from transitional to dense canopies. The superposition model of [16] was found to be a valid velocity model for all tested data sets in submerged spatially homogeneous vegetation conditions. Critical design parameters such as depth-averaged mean velocity and Darcy-Weisbach friction factors were successfully predicted by explicit equations for different vegetation conditions, including artificial, natural, flexible, rigid, grass-like, stem-like, and leafy vegetation.

The practical application of the superposition model relies on the appropriate evaluation of all model parameters. Indicative values for vegetation properties were recommended based on previous literature and rigorous data analysis, while a sensitivity analysis identified the log-law fitting parameters and the vegetation properties (drag coefficient, frontal area and deflected vegetation height) as the key parameters for the estimation of mean velocity and friction factors.

Future research should look into expanding the model into further aspects related to vegetation properties, including (i) time-variation of all model and vegetation parameters, which were treated as time- and depth-averaged in this study, (ii) non-uniform distributions of vegetation elements, which would require the application of double-averaging techniques, and (iii) a systematic investigation on the generalization of model parameters. A meaningful extension of the present work would comprise a systematic study of these aspects (i to iii) on flow resistance and velocity distributions for a wide range of flows in vegetated channels.

Appendices

Appendix A: Data sets and model parameters

This Appendix summarises re-analysed data sets in terms of key flow parameters and vegetation/grass properties, including specific flow rate (q), flow depth (d), deflected vegetation height ($h_c$), bed slope ($S_0$), unit frontal area (a), and drag coefficient ($C_D$). Table 2 expands the collection of [18] through a novel classification of vegetation types (natural/artificial, rigid/flexible, grass-like/stem-like/leafy) and through additional data sets of [30, 33] (transitional canopies) and [16, 29, 37] (dense canopies).

Nikora’s superposition model [16] was fitted to 40 velocity profiles of flows across transitional and dense canopies. Hydrodynamic density parameters ($C_D$, a, $h_c$) and resulting model parameters are listed in Table 3, including the dimensionless length scale of the mixing layer ($\alpha =L_e/h_c$), the dimensionless elevation of the inflection point ($\beta = y_i/h_c$), the dimensionless inflection point velocity ($\zeta = \overline{u}_i/\overline{u}_{\text {UD}}$), the dimensionless roughness height ($y_0/h_c$), and Coles’ wake parameter ($\Pi$). Model parameters were evaluated based on a minimization of the root-mean-squared error between Eq. (1) and velocity measurements.

Table 2 Data collection for transitional (top, $C_Dah_c < 0.5$) and dense (bottom, $C_Dah_c \ge 0.5$) canopies

Table 3 Model parameters for transitional (top, $C_Dah_c < 0.5$) and dense canopies (bottom, $C_Dah_c \ge 0.5$)

Appendix B: Sensitivity analysis

A sensitivity analysis was performed to quantify the influence of hydrodynamic vegetation properties ($C_D$, a, $h_c$) on estimated mean velocities (Eq. (2)), using respective model parameters for transitional and dense canopies (Fig. 3). Running Monte-Carlo simulations with 10,000 runs each, vegetation parameters were assumed to follow normal distributions with mean/expected values ($\mu$) and standard deviations ($\sigma$) specified in Table 4, where the first three rows and the last three rows represent transitional and dense canopies, respectively. The Monte-Carlo simulations were conducted for relative submergence of $d/h_c =2$ and 5. For each simulation, one vegetation parameter was varied while the other two were constant (Table 4).

Figure 8 shows the results of the sensitivity analysis in form of probability distributions of depth-averaged (mean) velocities. For transitional canopies, Eq. (2) was most sensitive to $C_D$ and a (Fig. 8a–c). An increase in $d/h_c$ was found to reduce this sensitivity, while the variation of $h_c$ resulted in deviations in the order of 20% (Fig. 8c). This is because the log-law layer becomes more dominant at higher submergence, with $h_c$ being closely linked to this layer through $u_{*_\text {c}}$. In contrast, the increase in submergence ($d/h_c$) induced negligible change to the sensitivity of $C_D$, a and $h_c$ for dense canopies. The highest sensitivity of depth-averaged velocity in dense canopies was found in $h_c$, which is due to the dominant log-layer in such flows. As a result, estimations of mean velocity and friction factors via Eqs. (2) and (5) require careful estimation of hydrodynamic vegetation properties for both, transitional and dense canopies.

Table 4 Sensitivity analysis of vegetation properties on mean velocity estimations for representative transitional (top, $C_Dah_c < 0.5$) and dense canopies (bottom, $0.5 \le C_Dah_c$)

Fig. 8

Effects of hydrodynamic vegetation properties on the estimation of mean velocities (Eq. (2)); varied properties are indicated in each sub-figure as per Table 4a–c results for transitional canopies d–f results for dense canopies