Abstract
The oceanic bottom mixed layer (BML) is a well mixed, weakly stratified, turbulent boundary layer. Adjacent to the seabed, the BML is of intrinsic importance for studying ocean mixing, energy dissipation, particle cycling and sediment-water interactions. While deep-seabed mining of polymetallic nodules is anticipated to commence in the Clarion-Clipperton Zone (CCZ) of the northeastern tropical Pacific Ocean, knowledge gaps regarding the form of the BML and its potentially key influence on the dispersal of sediment plumes generated by deep-seabed mining activities are yet to be addressed. Here, we report recent field observations from the German mining licence area in the CCZ that characterise the structure and variability of the BML locally. Quasi-uniform profiles of potential temperature extending from the seafloor reveal the presence of a spatially and temporally variable BML with an average local thickness of approximately 250 m. Deep horizontal currents in the region have a mean speed of 3.5 cm s\(^{-1}\) and a maximum speed of 12 cm s\(^{-1}\) at 18.63 ms above bottom over an 11 month record. The near-bottom currents initially have a net southeastward flow, followed by westward and southward flows with the development of complex, anticyclonic flow patterns. Theoretical predictions and historical data show broad consistency with mean BML thickness but cannot explain the observed heterogeneity of local BML thickness. We postulate that deep pressure anomalies induced by passing surface mesoscale eddies and abyssal thermal fronts could affect BML thickness, in addition to local topographic effects. A simplified transport model is then used to study the influence of the BML on the interplay between turbulent diffusion and sediment settling in the transport of deep-seabed mining induced sediment plumes. Over a range of realistic parameter values, the effects of BML on plume evolution can vary significantly, highlighting that resolving the BML will be a crucial step for accurate numerical modelling of plume dispersal.
Article Highlights
-
Field observations detail the presence of bottom mixed layer in the abyss of the Clarion-Clipperton Zone in the northeastern tropical Pacific
-
Mean local thickness of the layer is approximately 250 m, with large spatial and temporal heterogeneity that needs further understanding
-
The transport of benthic sediment plumes generated by deep-seabed mining can be greatly influenced by bottom mixed layer variability
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The oceanic bottom mixed layer (BML), also known as the benthic boundary layer when it was initially described [1], is a widespread feature of the global ocean abyss and refers to the lowermost part of the water column directly adjacent to the seafloor. Active mixing promoted by processes such as bottom shear and internal wave breaking leads to weak stratification and a quasi-homogeneous layer characterised by quasi-uniform vertical profiles of potential temperature, salinity, density, and other properties [2, 3]. First documented and characterised extensively in the western North Atlantic to be of \(\mathcal {O}\)(10 – 100 m) in thickness [4], the BML is considered to play a critical role in ocean mixing, circulation, and energy dissipation [5,6,7], as well as in the cycling of particles and particle-reactive biogeochemical constituents [8,9,10].
The turbulent nature of the BML has largely been measured indirectly. In the Hatteras abyssal plain of the western North Atlantic, apparent vertical eddy diffusivities were estimated from radon-222 (\(^{222}\)Rn), a naturally-occurring short-lived radioisotope, to be of \(\mathcal {O}\)(50 cm\(^2\) s\(^{-1}\)) in the BML and of \(\mathcal {O}\)(1 cm\(^2\) s\(^{-1}\)) above it in the interior ocean [11]. In efforts to characterise the spatial distribution of deep ocean mixing intensity, field studies found that in the deep equatorial and South Atlantic, the diapycnal diffusivities at mid-depths were of \(\mathcal {O}\)(0.1 cm\(^2\) s\(^{-1}\)) but reached values above 5 cm\(^2\) s\(^{-1}\) in the bottom-most 150 m of the water column above the Mid-Atlantic Ridge; the greatest estimated diapycnal diffusivity of 150 cm\(^2\) s\(^{-1}\) was found at the Romanche Fracture Zone along the equatorial section of the Mid-Atlantic Ridge [12, 13].
The physical conditions prevailing at abyssal depths in the Eastern Pacific have been poorly investigated. With recent rising interests in polymetallic nodule mining in the Clarion-Clipperton Zone (CCZ), a deep region (depths > 4000 m) with a gently westward sloping seafloor and scattered abyssal hills with occasional 1000–2000 m tall seamounts extending from the East Pacific Rise to Hawaii, there is a pressing need to understand the flow and dynamics of the bottom water column in the region [14]. In an extensive field hydrographic survey in the late 1970s, Hayes [15] noted weak benthic stratification, yet the author was unable to conclude on whether a BML was present in the region due to inadequate resolution of the temperature measurements. Two recent global compilations of BML thickness estimates, based on hydrographic data from the World Ocean Database and the archived World Ocean Circulation Experiment (WOCE) data, found that a BML up to 500 m in thickness may exist in the region [3, 16]; however, no recent observational study of the BML had been conducted specific to the region. Sporadic current meter observations in deep water column were made in this region during the Deep Ocean Mining Environmental Study (DOMES) program, the Manganese Nodule Project (MANOP), and a series of field experiments of the Russian Academy of Science between the 1970s and 1980s. Bottom currents were found to be predominantly weak (averaged 2–6 cm s\(^{-1}\)), with maximum speeds of approximately 12–15 cm s\(^{-1}\) between 4 and 8 metres above bottom (m.a.b.), and they were characterised by alternations of strong, quasi-unidirectional currents with low frequency motions [15, 17, 18].
Commercial mining activities of polymetallic nodules (baseball sized concretions on the seabed comprising critical minerals such as nickel and cobalt), regulated by the International Seabed Authority, are expected to commence in the CCZ in the coming decade, yet many asepcts of the potential environmental impact are still poorly understood [14]. In the deep water column, a key environmental consideration is the release of sediment plumes generated by nodule collector vehicles traversing on the seabed [19]. The released plume particles would form (i) gravity currents [20] and (ii) associated ambient plumes with suspended small particles (typically with diameter < 63 \(\mu\)m) that behave largely as passive tracers [21]. The creation and dispersal of ambient plumes can be considered essentially as the artificial processes of resuspension and transport of sediment particles. In the eastern tropical Pacific Ocean, long-term nephelometer observations found that the deep water column had low suspended particulate matter concentrations of typically 4–8 \(\mu\)g l\(^{-1}\) [17]. Although occurrences of benthic storms (also known as deep-sea storms) induced by deep-reaching surface anticyclonic eddies were reported in the region, there was little evidence of natural sediment resuspension events due to abyssal current flows [17, 18, 22, 23]. Nevertheless, eddy-related abyssal current variability has been characterised by changes in both directions and speeds of the flow, and therefore benthic storm occurrences may be important in predicting the horizontal extent of mining-generated benthic plume dispersal [18, 22,23,24].
Little attention has been paid to the vertical extent of benthic plume dispersal, especially in the context of deep-seabed mining. Elevated levels of particle concentration originating from recurring natural resuspension of seabed sediments have been observed in the abyssal water column of global oceans where strong bottom flows (typically with speeds \(>\,\) 20 cm s\(^{-1}\)) have been reported [25]. Intense turbulent mixing in the BML has been found to partially explain the high particle concentration levels in the lower portion of the benthic nepheloid layer formed of naturally resuspended fine sediments, particularly in the western North Atlantic [10, 26]. In the CCZ, whilst the relatively tranquil abyssal flows may not be sufficiently strong to resuspend bottom sediments locally [17], the mining-generated ambient plume may provide a persisting anthropogenic particle source analogous to recurring natural resuspension.
Recently, a long array with high-resolution temperature sensors deployed by the Royal Netherlands Institute for Sea Research in the CCZ showed a well-mixed, near-homogeneous turbulent bottom layer, with strong temporal variation in its thickness between 7 and 100 m with a mean around 65 m [27]. The vertical eddy diffusivity was estimated to vary between \(\mathcal {O}(10^{-5}-10^{-2}\) m\(^2\) s\(^{-1})\) from the top to the bottom, with two peaks at 10 m.a.b. and 65 m.a.b. attributable to bottom friction and internal-wave induced turbulence, respectively (Figure 11 of van Haren [27]), which can affect sediment resuspension and transport. The release and farfield transport of fine sediments from deep-seabed mining operations can introduce anthropogenic disturbances to abyssal ecosystems [28]. While deep-sea ecology, and to what extent the sediment plumes could influence the benthic biota and ecosystem functioning, is beyond the scope of this study, the scales and extent to which the fine sediments can be transported away from mining sites are central to their environmental impact assessment [19]. Important questions concerning the potential environmental impact of mining-generated bottom plumes therefore arise: (i) What are the characteristics of water properties and flows in the deep water column in the CCZ? (ii) How homogeneous or heterogeneous is the BML in the CCZ? (iii) In what way does the presence of BML affect the transport of fine sediment plumes?
In this study, we address these aforementioned questions by examining the bottom water and current conditions in the deep-seabed mining trial area licensed to the German Federal Institute for Geosciences and Natural Resources (BGR) in the CCZ from recent field experiments (Fig. 1). The paper is organised as follows. First, the data from BGR licensed area used in this study is described, followed by a characterisation of the water properties, benthic stratification, and flow conditions. We then compare the estimates of BML thicknesses from field data to theoretical scaling prediction in an attempt to rationalise the estimates. Thereafter, we discuss the observed variability of BML in comparison with hydrographic data from an eastern tropical Pacific transect of WOCE Hydrographic Programme (P04E), as well as the potential influence of mesoscale eddies on its variability. Finally, we use a simplified model of sediment transport to investigate the influence of the BML on the dispersal of sediment plumes induced by deep-seabed mining. Brief concluding remarks and prospects for future research follow at the end.
2 Field sampling
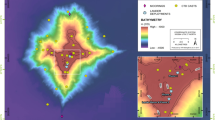
The BGR holds an exploration license for manganese nodules with the International Seabed Authority since 2006. To study the impacts and risks of deep sea mining during the early-stage prototype trials, the European Joint Programming Initiative for Healthy and Productive Seas and Oceans (JPI Oceans) launched the environmental monitoring programme Mining Impact. As part of this programme, R/V Kilo Moana cruises KM-13 (April 2013), KM-14 (April 2014) and R/V Sonne cruise SO-262 (May–June 2018) collected a total of 12 Sea-Bird Scientific SBE 19 plus conductivity-temperature-depth (CTD) measurements with a sampling frequency of 4 Hz and a temperature sensor precision of \(0.0001^{\circ }\hbox {C}\), throughout the entire water column in the BGR licensed area of CCZ (Fig. 1). In 2013, three full-depth CTD cast profiles were sampled closely at sites near \(117.0^{\circ }\hbox {W}\), \(11.9^{\circ }\hbox {N}\); in 2014, the three full-depth CTD cast profiles were sampled at sites near \(117.2^{\circ }\hbox {W}\), \(11.3^{\circ }\hbox {N}\); and in 2018, the first three cast profiles were sampled at sites almost identical to 2013 sites, with another three cast profiles sampled further to the west or east, with one site particularly located next to a seamount at \(116.5^{\circ }\hbox {W}\), \(11.8^{\circ }\hbox {N}\) (Fig. 1). Bottom depths at the CTD sampling sites varied between 4083 and 4343 m (Table 1).
In addition to hydrographic data, bottom current velocity was measured by an upward-oriented Teledyne RD Instrument Workhorse Sentinel 600 kHz acoustic-Doppler current profiler (ADCP) on an ocean bottom mooring (OBM) deployed during the SO-262 cruise near the mining trial site at \(117.0^{\circ }\hbox {W}\), \(11.9^{\circ }\hbox {N}\) with a bottom depth of 4089 m (Fig. 1). The ADCP had a sampling precision of 0.1 cm s\(^{-1}\), a bin size of 1.5 m and a blanking distance of 2.66 m, with a a sampling frequency of 0.56 Hz and an ensemble time of 45 min. Time series of current velocities at four heights between 8 and 20 m.a.b. were recorded for 320 days from 14 April 2018 to 1 March 2019.
Oceanographic context of the Clarion-Clipperton Zone: a Regional bathymetric map with major topographic features, b Inset bathymetric map of the BGR licensed area, c Potential temperature (\(\theta\))–salinity (S) diagram based on full-depth CTD casts from the BGR area. Dot points in a and b are locations of full-depth CTD casts considered in this study. The white cross in b marks the location of the ADCP ocean bottom mooring (OBM) deployed during the BGR 2018 experiment. Bathymetric data from the 2-minute resolution ocean depth database Global Multi-Resolution Topography [29]. Overlaid in c are water masses characteristic of the Tropical Surface Water (TSW), Subtropical Surface Water (STSW), Antarctic Intermediate Water (AAIW), and the Lower Circumpolar Water (LCPW) [30]. Potential density anomaly contours (in kg m\(^{-3}\)) in c are calculated from the Gibbs-SeaWater Oceanographic Toolbox [31])
3 Observations
3.1 Hydrography
To eliminate the effect of compression at great depths, in situ temperature was converted into potential temperature, with a reference pressure at 4000 dbar, using the nonlinear equation of state in the Gibbs-SeaWater Oceanographic Toolbox [31, 32]. Compilation of potential temperature (\(\theta\)) and salinity (S) data from CTD casts in the BGR region from years 2013, 2014, and 2018 reveals that several water masses are present in this region from the surface to the abyss. The \(\theta -S\) diagram shows the presence of the Tropical Surface Water (TSW), the Subtropical Surface Water (STSW), the Antarctic Intermediate Water (AAIW), and the Lower Circumpolar Water (LCPW), typical of the hydrography of the eastern tropical North Pacific [30] (Fig. 1). In the upper water column where TSW and STSW are present, salinity increases monotonically as potential temperature decreases down to approximately \(10\,^{\circ }\hbox {C}\), where a gradient reversal in salinity is present. Freshening of the mid-water column, characterised by a salinity minimum on the \(\theta -S\) diagram, is attributed to the presence of southern-sourced AAIW, consistent with previous observations along P04E section [33]. Below the salinity minimum, salinity increases again monotonically as potential temperature decreases; the deepest waters (from the seabed to 1000 m.a.b. at each sampling station) have an average \(\theta\) of \(1.6\,^{\circ }\hbox {C}\) and an average S of 34.68. These values are characteristic of LCPW (see inset Fig. 1c) and consistent with historical observations in the region [15, 34].
3.2 Bottom mixed layer
The vertical profiles of \(\theta\) show that the lowermost 1000 m of the water columns can be characterised by two regions (Fig. 2): a lower region adjacent to the seabed with a quasi-uniform \(\theta\) and small vertical gradients, overlaid by an upper region with non-uniform values of \(\theta\) with larger vertical gradients. Close visual examination of the vertical profiles of \(\theta\) reveals that the vertical extent of the lower region varied between approximately 50 m and 500 m, indicating the presence of a heterogeneous, well-mixed boundary layer that resembles the characteristics of a BML [4, 35,36,37]. While there is no consensus on the exact definition of a BML, a number of operational definitions have been proposed to quantify the thickness of this bottom layer. For its well-mixed nature, we first use a mixed-layer quality index (QI) as an attempt to quantify the degree of uniformity of the vertical profile of \(\theta\) [38]:
Here, \(\sigma _{ML}\) is the standard deviation of \(\theta\) within the proposed mixed layer, and \(\sigma _{1.5 ML}\) is the standard deviation of \(\theta\) over the depth interval extending from the seabed to 1.5 times the proposed mixed layer thickness. A value of QI exceeding 0.8 would indicate that the proposed layer is a well-developed mixed layer, whereas a value of QI smaller than 0.5 would indicate that a mixed layer is not present [38]. This method has been used as part of a study to map the global distribution of the BML thickness [3] and an attempt to characterise the BML thickness at a number of sites in the western North Atlantic region where a turbid benthic nepheloid layer was observed [10]. Using this definition, we find that a BML with a thickness between 68 m and 475 m is present at all 12 BGR sampling sites, with an average BML thickness of 277 m and a standard deviation of 150 m (Table 1).
Vertical profiles of the difference in potential temperature from the lowermost measurement in the water column for CTD casts taken in 2013, 2014, and 2018 in the BGR region (from left to right panels, respectively). Coloured vertical profiles in 2018 are CTD casts taken in areas away from the \(117^{\circ }\hbox {W}\) meridien: SO262-121 (green) is located near \(116^{\circ }\hbox {W}\) away from topographic features, SO262-164 (blue) is west to \(117^{\circ }\hbox {W}\) to the north of a seamount, SO262-169 (red) is east to \(117^{\circ }\hbox {W}\) at the base of a 2000-m tall seamount
The definition of QI (Eq. 1) could appear arbitrary, however, as it is unclear why a height scale difference by a factor of 1.5 is considered, instead of other values. Field observations, on the other hand, further motivate us to consider the two following properties for identifying the BML: (i) the vertical \(\theta\) gradient criterion and (ii) the vertical buoyancy gradient criterion. Both methods allow us to identify regions with well-mixed properties, with (i) identifying the super-adiabatic region of the water column and (ii) identifying the region with small buoyancy flux and weak stratification. In a region close to our study area within the CCZ, Hayes [15] noted that within the bottom 200 m at two sampling sites (with water depths \(\sim\)4500 m), the vertial \(\theta\) gradients were found to be of \(\mathcal {O}(1 \times 10^{-5}\,^{\circ }\hbox {C}\,\hbox {m}^{-1})\), with a mean buoyancy frequency within the bottom 200 m of \(1.9 \times 10^{-4}\) s\(^{-1}\) and \(3.0 \times 10^{-4}\) s\(^{-1}\) found at the two sites, respectively. Motivated by the visible difference between the vertical \(\theta\) gradients within the BML and the water column above it (Fig. 2), we quantify the thickness of the BML by introducing a vertical \(\theta\) gradient threshold of \(1 \times 10^{-4}\, ^{\circ }\hbox {C}\,\hbox {m}^{-1}\), as indicated by Thorpe [39] for identifying the super-adiabatic region of the water column (a similar value of \(1.2 \times 10^{-4}\,^{\circ }\hbox {C}\,\hbox {m}^{-1}\) was first proposed by Wimbush and Munk [1]). With the criterion of \(\partial \theta / \partial z \le 1 \times 10^{-4}\,^{\circ }\hbox {C}\,\hbox {m}^{-1}\), the BML is found among all 12 sampling sites, with varying thicknesses between 170 and 465 m. The average thickness is 298 m, with a standard deviation of 97 m (Table 1).
The vertical buoyancy gradient, related to buoyancy frequency and as a function of the vertical density gradient, describes stratification and is an alternative property that can be used to identify the BML:
where N is known as the buoyancy frequency, b is buoyancy, g is gravitational acceleration, \(\rho _0\) is the reference density at 4000 dbar, \(\rho\) is potential density referenced to 4000 dbar, calculated from measured in situ temperature and salinity using the nonlinear equation of state in the Gibbs-SeaWater Oceanographic Toolbox [31, 32], and z is height above seabed. Note that z is positive upward. Field observations have found that vertical density gradient in the BML is generally smaller than in the interior ocean. In a recent attempt to map the global distribution of the weakly stratified BML, Banyte et al [16] used a vertical density gradient threshold of \(-1 \times 10^{-5}\) kg m\(^{-4}\) to define the top of the layer. For consistency, we use the criterion \(N^2 \le 1.0 \times 10^{-7}\,\text {s}^{-2}\) to identify the BML and find that the BML is present among all sampling sites, with thicknesses between 124 m and 378 m. The average thickness is 236 m, with a standard deviation of 96 m (Table 1). Note that van Haren [27] used a similar criterion of \(N^2 \le 9.0 \times 10^{-8}\,\text {s}^{-1}\) to define the BML in the same region of our study.
3.3 Abyssal flows
The bottom currents are weak with low-frequency motions over the duration of current meter record (Fig. 3). The mean horizontal flow speeds over the entire time series are 0.0357 \(\mathrm {m\,s} ^{-1}\), 0.0349 \(\mathrm {m\,s}^{-1}\), 0.0347 \(\mathrm {m\,s}^{-1}\), and 0.0334 \(\mathrm {m\,s}^{-1}\) at 18.63 m.a.b, 15.63 m.a.b, 12.63 m.a.b, and 9.63 m.a.b, respectively. Maximum bottom speeds are 0.12 \(\mathrm {m\,s}^{-1}\), 0.11 \(\mathrm {m\,s}^{-1}\), 0.11 \(\mathrm {m\,s}^{-1}\), and 0.10 \(\mathrm {m\,s}^{-1}\) at those heights, respectively. These bottom flow speeds are consistent with previous observations of \(\mathcal {O}(0.01\) \(\mathrm {m\,s}^{-1}\)) near the bottom in the region [15, 17, 18]. The mean vertical velocities are \(-0.0018 \; \mathrm {m\,s}^{-1}\), \(-0.0022\; \mathrm {m\,s}^{-1}\), \(-0.0025 \; \mathrm {m\,s}^{-1}\), and \(-0.0028\; \mathrm {m\,s}^{-1}\) at 18.63 m.a.b, 15.63 m.a.b, 12.63 m.a.b, and 9.63 m.a.b, respectively. Throughout the recrod period, vertical motion tends to be downward, with occasional upward vertical velocity above 0.0020 \(\mathrm {m\,s}^{-1}\) only at 18.63 m.a.b. Visually, the currents appear coherent over the bottom 20 m. Both low-frequency and small high-frequency features can be traced throughout the records (Fig. 3). Applying a symmetric Gaussian low-pass filter [40] with a cut-off frequency at the local inertial frequency (\(f = 3.0 \times 10^{-5}\) s\(^{-1}\)) to the current time series reveals low-frequency features with periods of motion between one and two months that likely reflect the passage of mesoscale eddies in the region, particularly between May and Sep 2018.
Time series of horizontal current speed and vertical velocity measured at SO262-005 ocean bottom mooring site. Black lines are original current speeds measured by the acoustic doppler current profiler, red lines are low-pass Gaussian-filtered current speeds with a cut-off frequency at inertial frequency
Directional plots of current observations at SO262-005 ocean bottom mooring site between April 2018 and March 2019: a Rose diagram of current heading directions based on horizontal velocity components measured at 18 m.a.b; contour labels show the frequency of a particular direction out of all measurements. b Progressive vector diagram of currents at different measurement heights above seabed over the entire record duration
The near-bottom current at the site had a predominant heading direction either towards southeast or towards northwest (Fig. 4). At 18.63 m.a.b., approximately 35% of the horizontal current measured had a heading in the southeast quadrant, and 27% had a heading in the northwest quadrant (Fig. 4a). Southeast and south-heading currents (with a bearing between \(135^{\circ }\) and \(180^{\circ }\)) are faster flowing than currents in other directions. The progressive vector diagram shows that the current direction was initially towards southeast, followed by a westward flow with complex, anticyclonic patterns, and eventually southward and westward (Fig. 4b). The patterns of the current progressive vector at different height levels are nearly coherent, but the cumulative flows at lower levels (12.63 m.a.b. and 9.63 m.a.b.) appear weaker than those at upper levels (18.63 m.a.b. and 15.83 m.a.b.) and have a greater net eastward component. The discrepancies in the cumulative flow direction and pattern could be attributed to veering due to the presence of bottom Ekman layer [41]. Although historical analyses attempted to establish the bottom veering from near-bottom velocity measurements [15], the vertical spatial resolution of their records (4 m.a.b. and 50 m.a.b. as two lowest depth levels) was too sparse to illustrate veering within the bottom Ekman layer.
At this mooring site, the height of the turbulent Ekman layer \(h_E\) in unstratified water can be calculated by [42, 43]
where f is the inertial frequency, \(U_*\) is the frictional velocity, which has the following expression [4, 44]:
where U is the mean velocity of the flow away from the boundary, or the geostrophic flow in the ocean interior. In this study, while the lack of velocity measurements above 18.63 m.a.b. restricts our ability to establish whether the mean flow velocity measured at this level could be considered a suitable value of U, historical studies of the region suggests a speed of 0.05 m s\(^{-1}\) can be considered a representative value of interior flow U [15, 17], which leads to an estimated Ekman layer thickness \(h_E = 22\) m. This suggests that all current velocity measurements were from within the bottom Ekman layer. In the northern hemisphere, the veering in the bottom Ekman layer is anti-clockwise looking down, and thus the net northeast-ward displacement of the flow observed near the bottom (at 12.63 m.a.b. and 9.63 m.a.b.) with respect to the flow away from the bottom (at 18.63 m.a.b. and 15.63 m.a.b.) is consistent with the theory for a bottom Ekman layer [44].
Power spectral density of the horizontal current speeds measured at SO262-005 ocean bottom mooring site. The inertial subrange of the energy spectrum lies between the inertial and buoyancy periods. Spectral density calculated using Welch method [45]
The horizontal kinetic energy spectra at all levels for the site are shown in Fig. 5. All spectra are red and have no significant low-frequency structure, and spectra of all depth levels appear near-identical. At higher frequencies, energy peaks at near-inertial, diurnal, semi-diurnal periods, as well as the first harmonic of semi-diurnal period. The near-inertial and semi-diurnal signals are most pronounced, and the displacement of the inertial peak towards higher frequencies could be attributed to the response to free vertical modes at depths, as shorter waves forced at the surface would dissipate before reaching the ocean bottom in the near equatorial region [46,47,48]. These findings are consistent with the historical studies in the CCZ [15, 17].
4 Discussion
The varying estimates of BML thickness at different sites in the study area affirms that the BML is not a steady, spatially homogeneous structure, and its dynamics may well affect the dispersal of fine sediment plumes that are generated from seabed mining vehicles during their operations. Below, we discuss the following aspects of the BML observation presented in this study. First, the estimated BML thicknesses are compared with similar studies from other regions and theoretical model predictions. Then, we explore additional archived field data from a 1989 trans-Pacific hydrographic cruise in an attempt to establish the heterogeneity of BML in the eastern tropical North Pacific region. Next, we discuss how westward propagating mesoscale eddies passing through the region could contribute to the spatial and temporal heterogeneity.
4.1 Theoretical estimates
The height of the boundary layer, for a horizontally homogeneous flow over a flat topography, depends on the effect of planetary rotation, stratification, and the unsteadiness of the flow [37]. Although horizontal advection appears to be an important factor in determining the height of BML particularly when the site is close to bathymetric features [36], one-dimensional models can be instructive in predicting the vertical scale of the boundary layer. Weatherly and Martin [49] used a one-dimensional second-order turbulence closure model to study the development of the oceanic BML and proposed a relationship between the frictional velocity (\(U_*\)), local inertial frequency (f), and the buoyancy frequency (N) such that
where A is a constant with an approximate value of 1.3 over the range \(0 \le N/f \le 200\). Using Eq. 4 for \(U_*\), with \(U = 0.05\) m s\(^{-1}\), \(f = 3.0 \times 10^{-5}\) s\(^{-1}\) and \(N = 3.0 \times 10^{-4}\) s\(^{-1}\), the thickness of BML is estimated 227 m from Eq. 5, consistent with the estimates from hydrographic observations (Table 1).
The theoretical relationship appears to explain, to some extent, the discrepancy between the thicknesses of BML found in the CCZ in this study and those found in the deep western North Atlantic region based on potential temperature profiles. Detailed profiles of potential temperature and radon-222 measurements and in the Hatteras abyssal plain (depths > 5500 m) revealed a turbulent BML with varying thicknesses between approximately 15 and 60 m [4, 11]. Along Line W segment of the GEOTRACES North Atlantic transect (GA03) between the New England continental rise and Bermuda, Chen et al. [10] reported the presence of a well mixed boundary layer adjacent to the seabed with a thickness between 95 and 105 m at various stations (depths between 3772 and 4926 m) with no obvious bathymetric features on the New England continental rise and the abyssal plain. These values are all smaller than the observations of BML in the BGR region of CCZ found in this study, the predicted value of BML thickness based on Eq. 5, and the historical estimates [15]. The difference can be explained by the apparent dependence of \(h_{BML}\) on f based on Eq. 5, which yields a BML thickness of 44 m in the mid-latitude northern hemisphere (\(35^{\circ }\)N). This predicted value is similar to those documented in the Hatteras abyssal plain [4, 11] but half of those reported in the New England abyssal plain region [10]. Note that while this theoretical relationship appears to suggest some predictability of BML thickness based on its local inertial frequency and buoyancy frequency, it assumes flat topography and neglects horizontal advection that is an important process especially near topographic features [36, 37], and predictions from this theoretical relationship cannot explain the global distribution of BML thickness [3].
4.2 Heterogeneity of BML
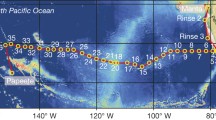
While the theoretical estimate appears to be consistent with the majority of our estimates of BML thickness in the BGR area, the large range of BML thickness found in the area highlights its transient and heterogeneous nature. This finding motivates further understanding of the spatial variability of BML not only within the local area, but also the wider region of the CCZ. A recent global synthesis study used CTD profiles archived by WOCE to estimate the distribution of BML averaged in \(10^{\circ }\) \(\times\) \(10^{\circ }\) bin [3]. However, it did not establish an estimated BML thickness for parts of the CCZ, including the BGR region and its vicinity. Here, we use additional full-depth CTD data archived from a WOCE Hydrographic Programme (WHP) trans-Pacific hydrographic cruise R/V Moana Wave (from January to May 1989) along \(10^{\circ }\)N transect (P04E) (Fig. 1) [50] in an attempt to map out the zonal distribution of BML across the eastern tropical North Pacific Ocean.
Zonal sections along the P04E transect: a potential temperature (\(\theta\)), b potential density, c vertical gradient of potential temperature, and d buoyancy frequency (as \(N^2\)); in c and d, the colourbar limits are set to illustrate the presence of BML based on respective definitions (see main text)
The vertical extent of the BML is illustrated by mapping the vertical \(\theta\) gradient and \(N^2\), as in the Sect. 3.2 two operating definitions of BML based on these two properties were introduced: regions of the bottom water column where (i) \(\partial \theta / \partial z \le 1 \times 10^{-4}\,^{\circ }\hbox {C}\,\hbox {m}^{-1}\) or (ii) \(N^2 \le 1.0 \times 10^{-7}\) s\(^{-2}\), respectively. Zonal sections of \(\partial \theta / \partial z\) and \(N^2\) reveal a heterogeneous BML along the \(10^{\circ }\)N transect, with a thickness up to \(\mathcal {O}(1000\) m) between \(155^{\circ }\)W and \(125^{\circ }\)W, a region with bathymetry depths greater than 4500 m in the CCZ, and between \(100\) and \(90^{\circ }\hbox {W}\), a region of bathymetric low between the East Pacific Rise and the Pacific coast of America Fig. 6. In these two regions, the surfaces of constant potential temperature and approximate isopycnal surfaces within 1000 m above the bottom show great changes in thickness along the section (Fig. 6 upper panels), similar to those profiles observed within a hilly region in the Madeira abyssal plain [37]. On the other hand, between \(115\) and \(105^{\circ }\hbox {W}\), an area between the Clarion Fracture Zone and the East Pacific Rise, the BML appears to be thin, with a thickness of \(\mathcal {O}(10\) m), and cannot be quantified visually on the zonal sections (Fig. 6 lower panels). Curiously, this finding appears inconsistent with our observations of BML from the CTD profiles recently collected in the BGR region, within the same longitudinal band and approximately \(2^{\circ }-3^{\circ }\) latitude north to the transect.
The apparently inconsistent findings in BML observation between P04E transect and CTD profiles from the BGR region can be attributed to the localised and transient nature of BML. This, in fact, is not surprising, as previous studies on the Hatteras abyssal plain in the western North Atlantic showed that the boundary layer thickness varied both spatially and temporally with length scales up to \(\sim\)20 km [36], yet to date few studies have attempted to characterise such variability over basin scale based on hydrographic measurements in detail. Richards [37] outlined that typically four processes can contribute to the horizontal variation of a benthic boundary layer: passing of a thermal front, isopycnal surfaces intersecting with a sloping bottom, synoptic scale eddies, and flow-topography interactions. The transient nature of the BML was established in a numerical modelling study, where a second-order turbulence closure model was applied to study the development of the BML [51]. The study found that under the effects of a time-dependent oscillatory forcing flow and an initially stably stratified density gradient, the timescale for BML development was approximately 10 days, and the growth rate of the boundary layer was found to decrease with time [51].
It is worth noting that van Haren [27] reported a BML with a thickness that varied strongly with time between 7 and 100 m, with a mean around 65 m, from shipboard CTD data collected in 2015 in the same BGR region. The turbulent nature of this layer is highlighted by the time-averaged turbulent diffusivities of up to \(\mathcal {O}(10^{-2}\) m\(^{2}\) s\(^{-1})\) close to the bottom, two to three magnitudes greater than those in the interior above the layer [27]. While the range of estimated thickness is smaller than those found in this study, the values are similar to those inferred from P04E data. The transient nature, and the effect of lateral advection due to presence of local topography, of this layer can also be found in the potential temperature profile of SO262-169 site in this study (Fig. 2 right panel), where van Haren [27] attributed such step-like, sheet-and-layer structured stratification to the propagation, breaking, and overturning of short length-scale internal waves near the buoyancy frequency. The association between a thicker boundary layer with complex bathymetry has been well documented. Based on observations in the Hatteras abyssal plain of the western North Atlantic [4, 35], Armi [52] inferred that stratified fluid could be advected towards topography from the interior by either mesoscale motion or the mean flow, subsequently forming mixed layers at the topography; these boundary mixed layers would then detach from the topography, advected along isopycnal surfaces, forming the sheet-and-layer structures. A laboratory experiment later showed that the distortion of isopycnals due to mixing near a sloping bottom would give rise to buoyancy forces that would tend to drive denser water upslope and lighter water downslope, enhancing boundary mixing [53]. As a result, topographic effect on BML variability is likely local yet profound, and the opportunistic nature of field sampling means that only snapshots of the BML are captured.
The short timescales for local BML heterogeneity suggest that local processes, such as the passing of abyssal thermal fronts and mixing at the interface between the mixed layer and interior, could play an important role and may deserve attention for further research. Mooring observations on the Madeira Abyssal Plain in the Mediterranean Sea found benthic fronts \(\sim\)300 m wide with frontal surfaces tilted \(\sim 10^{\circ }\) and temperature difference of 0.002 to \(0.004\,^{\circ }\hbox {C}\) across the fronts [54, 55]. These benthic fronts are analogous to atmospheric fronts and could form as a consequence of straining of mesoscale motions and the distortion weak horizontal thermal gradients, for example by flow interacting with topographic bumps, resulting in modifying the mixed layer properties over periods as short as one day [37, 55, 56]. Although there is no direct observation of benthic thermal fronts in the CCZ, their influence on BML variability cannot be ruled out, particularly for sampling sites close to each other with different BML profiles (Figs. 1 and 2). In addition, entrainment and mixing of fluid at the interface between BML and the interior is another process that can contribute to variability over short time and length scales [37, 57].
4.3 Influence of mesoscale eddies
Mesoscale eddies that propagate westward over the region likely also contribute to the variability of the vertical structure of the water column and, possibly, the variability of the BML. The eastern tropical North Pacific is one of the most eddying regions, typically at the mesoscale, in the world ocean [58]. Strong easterly wind bursts, channelled through gaps in the Sierra Madre mountains in Central America, are the main sources of forcing for eddy genesis [59]. Eddies that form as a result of these intense high-frequency winds, known as Tehuantepec and Papagayo eddies [60, 61], then propagate westward due to the latitudinal variation in the Coriolis parameter, i.e. the \(\beta\)-effect [62, 63], at an average translation speed of 12.5 cm s\(^{-1}\) [23]. Typically 4 to 18 cyclonic or anticyclonic eddies form off the coastal region between southern Mexico and Panama from boreal late autumn to early spring, with anticyclonic eddies being stronger, lasting longer, and potentially penetrating deeper than the cyclonic eddies [64, 65].
The attribution of deep current variability to the passing of surface eddies in the region was first discussed by Kontar and Sokov [18], where the authors found that the cyclonic eddy signals could be traced down to the levels of 4500–4750 m, as reflected by strong abyssal currents with average speeds of 10–15 cm s\(^{-1}\). More recently, Aleynik et al [22] found that the passing anticyclonic eddies at the surface partly contributed to the abyssal current variability in addition to tides and surface wind forcings. Comparing deep current property measurements and satellite altimetry data, Purkiani et al. [23] showed an enhancement of deep-ocean currents with a lag of about three weeks in response to passing anticyclonic mesoscale eddies in the surface near the BGR region. While recent field observations found that eddy-induced transport could penetrate down to 1500 m depth by strong anticyclonic eddies in the northeastearn tropical Pacific [66], to what extent and through what dynamical mechanism can these eddies affect the deeper water column remain to be elucidated. Field observations and modelling studies in the western North Atlantic and the Agulhas regions have shown that instability-driven cyclonic eddies could form a quasi-barotropic vertical structure [67,68,69,70,71]. Instability-driven mesoscale eddies also occur in the northeastern tropical Pacific region [61, 65]. The barotropic and baroclinic instabilities of the North Equatorial Current induced by the low frequency components of the easterly winds, as well as the instability of coastal currents induced by poleward propagating coastal Kelvin waves, are additional generation mechanisms for eddies not directly associated with the Central American gap winds [65, 72, 73]. The passing eddies could affect the variability of BML thickness, if they could perturb the vertical structure of the abyssal ocean, by disturbing the isopycnals [37]. Using a theoretical model of a quasi-geostrophic two-layer fluid above a mixed layer, Richards [57] demonstrated that horizontal advection plays a dominant role in the dynamics and energetics of the BML. Savidge and Bane, in their study of surface-intensified deep cyclones in the western North Atlantic [74], noted that within a cyclonic eddy, horizontal convergence of the ageostrophic velocity field is associated with the increasingly cyclonic circular flow in the deep ocean, leading to upward vertical motion; conversely, horizontal divergence is associated with the anticyclonic circular flow at depth, leading to downward vertical motion. These phenomena are analogous to cyclonic and anticyclonic flows in the atmospheric boundary layer [75].
Although multiple records of bottom-current observations suggest that anticyclonic flow conditions near the seabed typically coincide with passing surface anticyclonic eddies [18, 22, 23, 76, 77], in an idealised model study on larval dispersal at the East Pacific Rise by a westward propagating anticyclonic eddy, Adams and Flierl [78], using a two-layer quasi-geostrophic model, demonstrated that a cyclonic eddy developed in the deep layer and accompanied the surface anticyclone propagating westward, in their words a “vertical dipole”, regardless of the initial conditions in the lower layer or topography in the numerical simulations. Paired vortices initially developed with an anticyclone to the west and a cyclone to the east, but the initial anticyclonic vorticity in the lower layer quickly decayed due to rapid radiation of Rossby waves [78]. However, observational evidence supporting this structure has yet to be established. While further research is needed, both through detailed field monitoring and theoretical modelling studies, it can be inferred that if anticyclonic vorticity is present near the seabed, horizontal divergence is expected due to friction, accompanied by downwelling vertical motion; this could lead to depression of isopycnals and, therefore, a decrease in local BML thickness. Vice versa, cyclonic vorticity near the seabed would lead to an increase in local BML thickness (Fig. 7).
Cartoons of the isopycnal displacements associated with abyssal anticyclonic and cyclonic flows in the northern hemisphere. The red/blue area indicates a region of anticyclonic/cyclonic vorticity in the deep water column. The thin, wavy dashed lines represent different isopycnalsurfaces, denoted by \(\sigma\); note that the three-layer structure is only a schematic to illustrate continuous stratification in reality. The region between \(\sigma _{L1}\) surface and the seabed represents a weakly stratified BML. The large arrows indicate the horizontal divergence/convergence and downward/upward vertical motions within the eddying region. Black dots in this near-bottom layer represent fine suspended particles. Small black circular arrows indicate entrainment and detrainment processes at the BML–interior interface [37]
5 Effects of BML on plume dispersal
Of great interest is the potential effect of BML on the dispersal of resuspended sediment plume from the discharge of deep-seabed mining nodule-collecting vehicles operating at the seabed [14, 19, 20]. The discharged plume initially behaves as a high Reynolds number turbulent wake (with an outflow Reynolds number \(\mathrm{{Re}}_o \sim \mathcal {O}(10^{6})\)) upon its release from a collector vehicle. It is expected that following the initial discharge phase from the collector vehicle, the plume dynamics becomes a buoyancy-driven turbidity current, characterised by the presence of a high-concentration head followed by a thinner body [79, 80], with the magnitude of concentration estimated to be \(\mathcal {O}(1-10\) kg m\(^{-3})\), asserting a disturbance of 0.1% to 1% from the ambient water density [81]. The initial discharge and buoyancy-driven phases then set the initial conditions for a passive transport phase of the plume. During this phase, three key processes are present: (i) advection of fine particles by background flows, (ii) gravitational settling of fine particles, and (iii) turbulent diffusion in the horizontal and vertical directions.
To gain a fundamental understanding of how the extent of benthic deep-seabed mining sediment plumes varies with key environmental and operational parameters, Ouillon et al. [21] derived a simple reduced-order model of particle transport. Their analysis showed in particular that the interplay of vertical turbulent diffusion and settling plays a key role in setting the extent of plumes. However, their analysis was limited to a constant vertical turbulent diffusion. Here, we extend their analysis to include spatially variable turbulent diffusivities in the vertical direction, in order to study the potential role of BML on plume evolution. Following Ouillon et al [21], the vertical transport equation writes as
where C is the concentration of particles, t is time, z is height above seabed, \(w_s\) is the settling speed of particles, \(\kappa _z\) is the vertical turbulent diffusivity. To solve Eq. 6, we use the initial condition \(C(z,t=0) = \mathcal {H}(H-z)\), where \(\mathcal {H}\) is a heaviside function. Note that C is non-dimensional. At the bottom, particles are assumed to settle through without accumulation, such that the lower boundary condition can simply be given by a zero gradient condition [21],
The upper boundary condition, on the other hand, is a free surface boundary condition such that there is no particle flux at the upper boundary, assuming that the top boundary is placed far enough so that it has negligible effect on the evolution of the vertical concentration profile [82],
As noted in Ouillon et al. [21], the interplay of settling and vertical diffusion results in a strongly non-linear evolution of the seabed particle concentration. Therefore it is more insightful to discuss the solution to Eq. 6 in non-dimensional terms. The solution of C can be expressed as a function of the non-dimensional vertical position \(z' = z/H\) and non-dimensional time \(t' = \frac{t}{H/w_s}\), such that the equation (6), written in non-dimensional form, becomes
where \(Pe_z\) is the vertical Péclet number \(\left( Pe_z = \frac{H w_s}{\kappa _z^0} \right)\) for a particle settling at a speed of \(w_s\) in a flow with a reference turbulent diffusivity of \(\kappa _z^0\), and \(\xi (z)=\kappa _z(z)/\kappa _z^0\) is the ratio of the local turbulent diffusivity to the reference turbulent diffusivity. Following Ouillon et al. [21], Eq. 9 is solved numerically using a simple finite difference method. The diffusion term is discretised with a second-order central difference scheme, while the settling term is discretised with a first-order upwind scheme and integrated in time using the Crank-Nicholson method.
Ouillon et al. [21] show that the temporal evolution of the seabed concentration of suspended particles is controlled by the vertical Péclet number, which reflects the relative strength of settling to vertical diffusion, with a series of regime changes, in a one-dimensional set-up with no differentiation of vertical layers. In order to represent the effect of BML on the interplay between vertical diffusion and settling, we expand the model to a two-layer model, with the lower layer representing the BML and the upper layer representing the interior ocean away from the boundary. The interface between the two layers at \(H_{bml}\) marks the upper limit of the BML. Since the upper layer has a diffusivity \(\kappa _z^1\) that is at least one or two orders of magnitude smaller than the diffusivity \(\kappa _z^0\) of the lower layer (e.g., [11, 27]), \(z = H_{bml}\) effectively acts as a lid that prevents the upward diffusion of suspended particles, and \(\kappa _z^1=0\) can be assumed without loss of generality. We then introduce an additional non-dimensional parameter, the BML Péclet number \(Pe_{bml} = \frac{H_{bml} w_s}{\kappa _z^0}\) and investigate the sensitivity of the temporal evolution of seabed particle concentration to \(Pe_{bml}\), under the same condition of \(Pe_z\). Note that since \(H_{bml} \ge H\), \(Pe_{bml}\) is always greater or equal to \(Pe_z\), if a constant value of \(w_s\) is assumed.
Temporal evolution of the non-dimensional vertical solution C to equation (9) at the lowest vertical position (i.e. the seabed concentration), with an initial plume of \(Pe_z = 0.1\) and \(Pe_z = 0.01\) under different \(Pe_{bml}\) conditions. Note that \(Pe_{bml}\) becomes \(+\infty\) when the model considers only a one-layer domain and thus assumes no upper boundary for the BML
To choose a vertical Péclet number characteristic of the fine particles settling in the deep ocean, we assume a particle settling speed of \(2 \times 10^{-5}\) m s\(^{-1}\), a vertical turbulent diffusivity of \(1 \times 10^{-3}\) m s\(^{-2}\), and a plume vertical length scale of 5 m [21]. These parameters give a vertical Péclet number \(Pe_z = 0.1\). Recall that the initial condition of the solution to Eq. 9 is a heaviside function, and the initial concentration of the plume is C = 1. The non-dimensionalised governing Eq. (9) for the two-layer set up is solved with a range of \(Pe_{bml}\) values. Note that the ratio between \(Pe_{bml}\) and \(Pe_z\) is effectively the ratio between the thickness of the BML imposed in the two-layer model and the thickness of the plume at the initial condition, when \(w_s\) and \(\kappa _z\) are assumed constant within the BML.
Our results with \(Pe_z = 0.1\) demonstrate that the temporal evolution of seabed concentration (\(C(0,t')\)) is affected by the value of \(Pe_{bml}\) (Fig. 8). Qualitatively, \(C(0,t')\) is initially controlled by diffusion for all \(Pe_{bml}\) values. For \(Pe_{bml}\) smaller than 0.5, turbulent diffusion of materials upward appears to be limited by the presence of the upper bound of the BML acting as a lid, and settling quickly becomes the dominant process instead, leading to a sharp decline of \(C(0,t')\), resulting in smaller values of C at the seabed. When \(Pe_{bml}\) is greater than 0.5 but smaller than 10, similarly, diffusion initially dominates the transport, but the transition from a diffusion-dominated regime to a settling-dominated regime occurs later as \(Pe_{bml}\) becomes larger, leading to an increase of C at the seabed with the increase of \(Pe_{bml}\). These effects of \(Pe_{bml}\) on \(C(0,t')\) indicate that the presence of BML could inhibit the upward diffusive transport and shorten the timescale over which a diffusion-dominated regime transitions into a settling-dominated regime. Finally, as \(Pe_{bml}\) approaches 10 and larger values, \(C(0,t')\) evolution converges with the model set up without the presence of a BML upper bound, suggesting that a BML with \(Pe_{bml} \ge 10\) does not affect \(C(0,t')\) evolution of a plume that has a characteristic \(Pe_z = 0.1\). This suggests that when \(Pe_{bml}\) is sufficiently large, either due to a large value of \(H_{bml}\) or \(w_s\) (or both), the presence of strong stratification at the top of the BML may no longer affect the the evolution of the plume. Whether the BML affects the evolution of the plume is also a question of the sediment concentrations of interest. Indeed, while the case of \(Pe_{bml}=5\) is seen to deviate from the 1-layer solution, it does so at relatively low concentrations (or high dilution levels).
The results with \(Pe_z=0.01\) show that for the same ratio \(\frac{Pe_{bml}}{Pe_z}\), i.e. the same ratio of BML height to initial plume height \(\frac{H_{bml}}{H}\), a lower value of \(Pe_z\) leads to a more pronounced effect of the BML. Indeed, as the Péclet number is reduced, so is the time scale of diffusion relative to the time scale of settling. Consequently, the plume is better able to stretch vertically, thereby encountering the top of the BML more quickly and at higher concentrations. In order to better quantify the dynamical regime in which the BML affects the concentration at the seabed, we define the time \(t_{div}\) at which the 1-layer and the 2-layer case diverge from each other. For illustration purposes, \(t_{div}\) is defined as the time when the concentration at the seabed in the 1-layer case is \(50\%\) larger than in the 2-layer case, such that at \(t_{div}\), a significantly lower concentration is measured at the seabed as a result of the influence of the BML. To \(t_{div}\) corresponds a dilution factor \(D_{div} = C(z=0,t=0)/C(t=0,t=t_{div})\), which gives insight into how diluted the plume is by the time the BML starts playing a role at the seabed. The values of \(t_{div}\) and \(D_{div}\) are shown in Fig. 9 as nonlinear functions of \(Pe_z\) and the ratio \(Pe_{bml}/Pe_z\) (ensuring that \(Pe_{bml}/Pe_z>1\), see discussion above). A striking observation is that over a short range of values of \(Pe_z\), the divergence time and dilution factor vary over a large range of values (note in particular the logarithmic scale in figure Fig. 9). This observation further highlights that the balance between vertical diffusion and settling plays a highly nonlinear role in the context of deep-seabed mining sediment plumes, as noted in Ouillon et al [21]. It also shows that for small values of the Péclet number, for instance those associated with slow-settling particles, the BML is likely to play a key role, leading to significantly more rapid sediment deposition than in the 1-layer scenario. Table 2 illustrates this role of the BML by calculating the dimensional values of \(t_{div}\) and \(D_{div}\) for realistic values of the operational parameters. We find the time to divergence varies between as little as a few hours, to over a year.Footnote 1 Similarly, the dilution level varies from approximately 40 to nearly \(10^{14}\), further demonstrating that over a range of realistic parameters, the BML can either play a significant role on the evolution of the plume, or indeed play no role at all.
6 Conclusions
A weakly stratified, temporally and spatially variable BML can be identified in the German licensed area of the CCZ from locally collected CTD hydrographic data during a number of expeditions between 2013 and 2018 as part of the JPI Oceans Mining Impact environmental monitoring programme. The local thickness of the layer varies between 68 m and 475 m among different stations, with an approximate mean thickness of 250 m. The flow in this layer can be characterised by alternating southeast-ward and northwest-ward flowing currents with a mean flow speed of 3.5 cm s\(^{-1}\) within the bottom 20 m of the water column, likely within the bottom Ekman layer, and with energy peaks at near-inertial, diurnal, and semidiurnal frequencies. The finding is consistent with historical analyses [15] and confirms their speculation that a well-mixed bottom layer is present in the region. The mean thickness of this layer is found to be broadly consistent with the prediction based on a theoretical scaling relationship [49].
The observations of the BML in the study area highlight both temporal and spatial heterogeneity of the boundary layer. An attempt was made to characterise such heterogeneity over a broader spatial scale across the eastern segment of the tropical North Pacific transect (P04E) of a WHP trans-Pacific cruise from archived hydrographic data. Discrepancies were found in the thickness of BML estimated from site-specific CTD analyses and those mapped out using P04E cruise data near the study area (between 110 and \(120^{\circ }\hbox {W}\) longitude range). The differences in the estimates emphasise the local and transient nature of BML and highlight the difficulties to capture the exact picture of this boundary layer based solely on opportunistic point sampling. The passing of benthic thermal fronts and fluid entrainment at the mixed layer–interior interface likely contribute to the changes in local BML thickness, in addition to topographic effects, but the data available in this study is insufficient to determine this. Westward propagating mesoscale eddies passing the area could also affect the BML thickness by vertical motion and displacement of isopycnals in the water column, but further research is needed to elucidate the vertical structure of these eddies. For a more comprehensive picture of the BML, future dedicated deep-ocean field monitoring programmes in the CCZ will be essential to establish the physical processes responsible for, and the influence of, BML variability over the temporal and spatial scales relevant to mining plume dispersal.
Although estimating turbulent mixing within and above this layer is beyond the scope of this study, one can infer that the presence of this layer may affect vertical mixing and ultimately the transport of fine-particle plumes released during deep-seabed mining operations that enter a passive transport phase. Indeed, by modifying a simple, reduced-order model of particle transport [21], we devise a two-layer model with two different values of vertical turbulent diffusivity in an attempt to study the potential role of BML on plume evolution. The findings suggest that both the timescale for a BML to affect the vertical dispersal of the plume and the level of dilution of the plume particle concentration are non-linear functions of the Péclet number of the initial plume and the Péclet number of the BML. With a range of realistic values of the parameters, the presence of a BML can vary significantly, and when the BML thickness is large, the effects of BML may be considered negligible. While caution is needed in the interpretation of our results given the simplicity and the theoretical nature of the model, these findings point to the importance of resolving the BML for accurate numerical modelling of the dispersal of sediment plumes associated with deep-seabed mining.
Notes
Note that it is not implied that the model of Ouillon et al [21] can accurately consider the evolution of the sediment concentration over such time scales, but rather that \(t_{div}\) varies nonlinearly with the choice of parameters.
References
Wimbush M, Munk W (1970) The benthic boundary layer. The Sea 4(1):731–758
Armi L (1977) The dynamics of the bottom boundary layer of the deep ocean. In: Elsevier oceanography series, Elsevier, pp 153–164
Huang PQ, Cen XR, Lu YZ et al (2019) Global distribution of the oceanic bottom mixed layer thickness. Geophys Res Lett 46(3):1547–1554
Armi L, Millard RC Jr (1976) The bottom boundary layer of the deep ocean. J Geophys Res 81(27):4983–4990
Wunsch C (1970) On oceanic boundary mixing. In: Deep Sea Research and Oceanographic Abstracts, Elsevier, pp 293–301
Trowbridge JH, Lentz SJ (2018) The bottom boundary layer. Ann Rev Mar sci 10:397–420
Drake HF, Ferrari R, Callies J (2020) Abyssal circulation driven by near-boundary mixing: Water mass transformations and interior stratification. J Phys Oceanogr 50(8):2203–2226
Boudreau BP, Jørgensen BB (2001) The benthic boundary layer: Transport processes and biogeochemistry. Oxford University Press, Oxford
Turnewitsch R, Springer BM (2001) Do bottom mixed layers influence \(^{234}\)Th dynamics in the abyssal near-bottom water column. Deep Sea Res Part I Oceanogr Res Papers 48:1279–1307
Chen SYS, Marchal O, Lerner PE et al (2021) On the cycling of \(^{231}\)Pa and \(^{230}\)Th in benthic nepheloid layers. Deep Sea Res Part I Oceanogr Res Papers. https://doi.org/10.1016/j.dsr.2021.103627
Sarmiento JL, Biscaye PE (1986) Radon 222 in the benthic boundary layer. J Geophys Res Oceans 91(C1):833–844
Polzin KL, Speer KG, Toole JM et al (1996) Intense mixing of antarctic bottom water in the equatorial Atlantic ocean. Nature 380:54–57
Polzin KL, Toole JM, Ledwell JR et al (1997) Spatial variability of turbulent mixing in the abyssal ocean. Science 276:93–96
Miller KA, Thompson KF, Johnston P et al (2018) An overview of seabed mining including the current state of development, environmental impacts, and knowledge gaps. Front Mar Sci 4:418
Hayes S (1980) The bottom boundary layer in the eastern tropical pacific. J Phys Oceanogr 10(3):315–329
Banyte D, Smeed D, Morales Maqueda M (2018) The weakly stratified bottom boundary layer of the global ocean. J Geophys Res Oceans 123(8):5587–5598
Gardner W, Sullivan LG, Thorndike EM (1984) Long-term photographic, current, and nephelometer observations of manganese nodule environments in the pacific. Earth Planet Sci Lett 70(1):95–109
Kontar EA, Sokov AV (1994) A benthic storm in the northeastern tropical pacific over the fields of manganese nodules. Deep Sea Res Part I Oceanogr Res Papers 41(7):1069–1089
Peacock T, Ouillon R (2023) The fluid mechanics of deep-sea mining. Ann Rev Fluid Mech. https://doi.org/10.1146/annurev-fluid-031822-010257
Muñoz-Royo C, Ouillon R, El Mousadik S et al (2022) An in situ study of abyssal turbidity-current sediment plumes generated by a deep seabed polymetallic nodule mining preprototype collector vehicle. Sci Adv. https://doi.org/10.1126/sciadv.abn1219
Ouillon R, Muñoz-Royo C, Alford MH et al (2022) Advection-diffusion settling of deep-sea mining sediment plumes. part 2. collector plumes. Flow 2:E23. https://doi.org/10.1017/flo.2022.19
Aleynik D, Inall ME, Dale A et al (2017) Impact of remotely generated eddies on plume dispersion at abyssal mining sites in the Pacific. Sci Rep 7(1):1–14
Purkiani K, Paul A, Vink A et al (2020) Evidence of eddy-related deep-ocean current variability in the northeast tropical pacific ocean induced by remote gap winds. Biogeosciences 17(24):6527–6544
Purkiani K, Gillard B, Paul A et al (2021) Numerical simulation of deep-sea sediment transport induced by a dredge experiment in the northeastern pacific ocean. Front Mar Sci. https://doi.org/10.3389/fmars.2021.71946
Gardner W, Richardson MJ, Mishonov A (2018) Global assessment of benthic nepheloid layers and linkage with upper ocean dynamics. Earth Planet Sci Lett 482:126–134
McCave IN (1986) Local and global aspects of the bottom nepheloid layers in the world ocean. Neth J Sea Res 20:167–181
van Haren H (2018) Abyssal plain hills and internal wave turbulence. Biogeosciences 15(14):4387–4403
Smith CR, Levin LA, Koslow A, et al (2008) The near future of the deep seafloor ecosystems. Aquatic ecosystems: trends and global prospects pp 334–352
Ryan W, Carbotte S, Coplan J et al (2009) Global multi-resolution topography synthesis. Geochem Geophys Geosys. https://doi.org/10.1029/2008GC002332
Fiedler PC, Talley LD (2006) Hydrography of the eastern tropical Pacific: a review. Prog Oceanogr 69(2–4):143–180
McDougall TJ, Barker PM (2011) Getting started with teos-10 and the gibbs seawater (gsw) oceanographic toolbox. SCOR/IAPSO WG 127:1–28
Jackett DR, McDougall TJ, Feistel R et al (2006) Algorithms for density, potential temperature, conservative temperature, and the freezing temperature of seawater. J Atmos Ocean Technol 23(12):1709–1728
Johnson GC, Toole JM (1993) Flow of deep and bottom waters in the pacific at 10n. Deep Sea Res Part I Oceanogr Res Papers 40(2):371–394
Wong C (1972) Deep zonal water masses in the equatorial pacific ocean inferred from anomalous oceanographic properties. J Geophys Res 77(36):7196–7202
Armi L (1978) Some evidence for boundary mixing in the deep ocean. J Geophys Res Oceans 83(C4):1971–1979
Armi L, D’Asaro E (1980) Flow structures of the benthic ocean. J Geophys Res Oceans 85(C1):469–484
Richards K (1990) Physical processes in the benthic boundary layer. Philos Trans R Soc London Ser A Math Phys Sci 331(1616):3–13
Lorbacher K, Dommenget D, Niiler P et al (2006) Ocean mixed layer depth: a subsurface proxy of ocean-atmosphere variability. J Geophys Res Oceans 111(C7):22
Thorpe SA (2005) The turbulent ocean. Cambridge University Press
Schmitz WJ (1974) Observations of low frequency current fluctuations on the continental slope and rise near site d. J Mar Res 32(2):233–251
Pedlosky J (1987) Geophysical Fluid Dynamics, 2nd edn. Springer-Verlag, New York, p 710
Caldwell D, Van Atta C, Helland K (1972) A laboratory study of the turbulent ekman layer. Geophys Fluid Dyn 3(2):125–160
Howroyd G, Slawson P (1975) The characteristics of a laboratory produced turbulent Ekman layer. Bound Layer Meteorol 8(2):201–219
Csanady G (1967) On the “resistance law’’ of a turbulent Ekman layer. J Atmos Sci 24(5):467–471
Stoica P, Moses RL et al (2005) Spectral analysis of signals, vol 452. Pearson Prentice Hall Upper Saddle River, NJ
Wunsch C (1977) Response of an equatorial ocean to a periodic monsoon. J Phys Oceanogr 7(4):497–511
Munk W, Phillips N (1968) Coherence and band structure of inertial motion in the sea. Rev Geophys 6(4):447–472
Eriksen CC (1980) Evidence for a continuous spectrum of equatorial waves in the Indian Ocean. J Geophys Res Oceans 85(C6):3285–3303
Weatherly GL, Martin PG (1978) On the structure and dynamics of the oceanic bottom boundary layer. J Phys Oceanogr 8:557–570
Toole J, Joyce T, Bryden HL (1989) WHP Cruise Summary Information of section P04. WOCE
Richards K (1982) Modeling the benthic boundary layer. J Phys Oceanogr 12(5):428–439
Armi L (1979) Effects of variations in eddy diffusivity on property distributions in the oceans. J Mar Res 37(3):515–530
Phillips O, Shyu JH, Salmun H (1986) An experiment on boundary mixing: mean circulation and transport rates. J Fluid Mech 173:473–499
Elliott A, Thorpe S (1983) Benthic observations on the madeira abyssal-plain. Oceanologica Acta 6(4):463–466
Thorpe S (1983) Benthic observations on the madeira abyssal plain: fronts. J Phys Oceanogr 13(8):1430–1440
Hoskins BJ, Bretherton FP (1972) Atmospheric frontogenesis models: mathematical formulation and solution. J Atmos Sci 29:11–37
Richards K (1984) The interaction between the bottom mixed layer and mesoscale motions of the ocean: a numerical study. J Phys Oceanogr 14(4):754–768
Chelton DB, Schlax MG, Samelson RM et al (2007) Global observations of large oceanic eddies. Geophys Res Lett. https://doi.org/10.1029/2007GL030812
Chelton DB, Freilich MH, Esbensen SK (2000) Satellite observations of the wind jets off the pacific coast of central america. Part I: case studies and statistical characteristics. Mon Weather Rev 128(7):1993–2018
Palacios DM, Bograd SJ (2005) A census of tehuantepec and papagayo eddies in the northeastern tropical pacific. Geophys Res Lett 32(23):4
Liang JH, McWilliams JC, Gruber N (2009) High-frequency response of the ocean to mountain gap winds in the northeastern tropical pacific. J Geophys Res Oceans 114(C12):12
Nof D (1981) On the \(\beta\)-induced movement of isolated baroclinic eddies. J Phys Oceanogr 11(12):1662–1672
Cushman-Roisin B, Tang B, Chassignet EP (1990) Westward motion of mesoscale eddies. J Phys Oceanogr 20(5):758–768
Willett CS, Leben RR, Lavín MF (2006) Eddies and tropical instability waves in the eastern tropical pacific: a review. Prog Oceanogr 69(2–4):218–238
Liang JH, McWilliams JC, Kurian J et al (2012) Mesoscale variability in the northeastern tropical pacific: forcing mechanisms and eddy properties. J Geophys Res Oceans 117(C7):13
Purkiani K, Haeckel M, Haalboom S et al (2022) Impact of a long-lived anticyclonic mesoscale eddy on seawater anomalies in the northeastern tropical pacific ocean: a composite analysis from hydrographic measurements, sea level altimetry data, and reanalysis model products. Ocean Sci 18(4):1163–1181. https://doi.org/10.5194/os-18-1163-2022
Savidge DK, Bane JM (1999) Cyclogenesis in the deep ocean beneath the Gulf Stream: 1. Description. J Geophys Res Oceans 104(C8):18111–18126
Kämpf J (2005) Cyclogenesis in the deep ocean beneath western boundary currents: a process-oriented numerical study. J Geophys Res Oceans 110(C3):13
Cronin MF, Tozuka T, Biastoch A et al (2013) Prevalence of strong bottom currents in the greater Agulhas system. Geophys Res Lett 40(9):1772–1776
Andres M, Toole J, Torres D et al (2016) Stirring by deep cyclones and the evolution of Denmark Strait Overflow Water observed at line W. Deep Sea Res Part I Oceanogr Res Papers 109:10–26
Schubert R, Biastoch A, Cronin MF et al (2018) Instability-driven benthic storms below the separated Gulf Stream and the North Atlantic Current in a high-resolution ocean model. J Phys Oceanogr 48(10):2283–2303
Hansen DV, Maul GA (1991) Anticyclonic current rings in the eastern tropical pacific ocean. J Geophys Res 96(C4):6965–6979
Zamudio L, Hurlburt HE, Metzger EJ et al (2006) Interannual variability of tehuantepec eddies. J Geophys Res Oceans 111(C5):21
Savidge DK, Bane JM (1999) Cyclogenesis in the deep ocean beneath the Gulf Stream: 2. Dynamics. J Geophys Res Oceans 104(C8):18,127-18,140
Holton JR (1979) An Introduction to Dynamic Meteorology, vol 23. Internationa Geophysics Series. Academic Press, New York, p 389
Adams DK, McGillicuddy DJ, Zamudio L et al (2011) Surface-generated mesoscale eddies transport deep-sea products from hydrothermal vents. Science 332(6029):580–583
Zhang Z, Tian J, Qiu B et al (2016) Observed 3d structure, generation, and dissipation of oceanic mesoscale eddies in the south china sea. Sci Rep 6(1):1–11
Adams DK, Flierl GR (2010) Modeled interactions of mesoscale eddies with the east pacific rise: implications for larval dispersal. Deep Sea Res Part I Oceanogr Res Papers 57(10):1163–1176
Meiburg E, Kneller B (2010) Turbidity currents and their deposits. Ann Rev Fluid Mechn 42:135–156
Ouillon R, Kakoutas C, Meiburg E et al (2021) Gravity currents from moving sources. J Fluid Mech. https://doi.org/10.1017/jfm.2021.654
Lavelle J, Ozturgut E, Swift S et al (1981) Dispersal and resedimentation of the benthic plume from deep-sea mining operations: a model with calibration. Mar Min 3(1/2):59–93
Davies C (1949) The sedimentation and diffusion of small particles. Proc R Soc London Ser A Math Phys Sci 200(1060):100–113
Acknowledgements
We would like to thank Annemiek Vink (BGR) for providing the field data for this study. We are grateful to Matthew Alford (UCSD), Wilford Gardner (Texas A&M), Geoffrey Gebbie (WHOI), Olivier Marchal (WHOI), Amala Mahadevan (WHOI), and Kurt Polzin (WHOI) for discussions and constructive feedback. Two anonymous reviewers provided helpful comments for improving the manuscript.
Funding
Open Access funding provided by the MIT Libraries. Sources of funding support for this study include the MIT–WHOI Joint Program, the Office of Naval Research grant N000141812762, the NSF grant CBET-2139277, and the Benioff Ocean Initiative. The funders had no role in any aspects of the research.
Author information
Authors and Affiliations
Contributions
Authors contribution
SYC led the study and wrote the main manuscript text. RO contributed to the model section of the manuscript. CMR processed the ADCP data used in this study. TP conceived of and supervised the study. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that no known competing financial interests or personal relationships could have appeared to influence the work reported in this study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, SY.S., Ouillon, R., Muñoz-Royo, C. et al. Oceanic bottom mixed layer in the Clarion-Clipperton Zone: potential influence on deep-seabed mining plume dispersal. Environ Fluid Mech 23, 579–602 (2023). https://doi.org/10.1007/s10652-023-09920-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10652-023-09920-6