1 Introduction

Tides in the Gulf of California play a significant role in the circulation and vertical mixing thereby influencing the coastal lagoon dynamics [1]. The Urias coastal lagoon (URCOL), which includes the Mazatlan harbour, is relevant for the economic development of the northwestern Mexico. The harbour is the outlet overseas and for cargo from several states of Mexico. The ecosystems of the lagoon constitute substantial fishery grounds and excellent conditions for aquaculture; in fact, the lagoon provides a nursery ground for post-larval shrimp [2]. Since most of these grounds are exposed to accretion or erosion threats caused by tidal hydrodynamics or meteorological events, understanding the hydrodynamic regime and sediment transport processes in the URCOL is critical for environment protection and preservation. To achieve this, it is important to know the sediment transport characteristics and erosion and accretion patterns within the lagoon, as well as the mechanisms that force morphological changes. Eventually, the generated information inherent to the URCOL morphodynamics may help solve accretion or erosion problems, and to conserve this invaluable coastal ecosystem.

Regardless of the relevance of URCOL, little is known about the sediment transport processes of this subtropical coastal lagoon. To our knowledge, there are just a few studies on the transport of sediments in the Urias Coastal Lagoon. One was conducted only in the URCOL entrance [3], and the other was about bottom sediment distribution within the lagoon [4]. Montaño-Ley et al. [5] investigated the hydrodynamics and pollutant dispersion in the URCOL. Cardoso-Mohedano et al. [6] implemented a hydrodynamic-biogeochemical model to evaluate the dispersion, under specific tidal conditions, of nutrient discharges from a semi-intensive shrimp farm during spring and neap tide.

In a broad geographical context, in recent years, relevant studies have been addressed to investigate the sediment transport and the morphodynamics of coastal lagoons: Carbajal et al. [7] investigated the tide-driven bed load transport of sediments in the shallow coastal lagoon of Yavaros, located in the southeastern part of the Gulf of California, Mexico. Petti et al. [8] studied the morphodynamics of the Marano and Grado lagoon in Italy using a two-dimensional horizontal (2DH) morphological-hydrodynamic model.

Ahmed-Syed et al. [9] evaluated the morphodynamics of Miani Hor, a coastal lagoon of Lasbela, Balochistan, Pakistan. Mengual et al. [10] investigated bed load transport in the Seine Estuary (France). In the literature, few investigations exist concerning bed load sediment transport and the morphodynamics in coastal lagoons. Hence, it is imperative to investigate this issue.

The main objective of this research was to investigate the sediment transport and the seabed morphodynamics of the URCOL. It has been emphasized the investigation of the influence of the bathymetry, tidal asymmetries, geometry of the lagoon in the tidal hydrodynamics, and the mechanism that forces the bed load sediment transport and sea bottom morphodynamics of the lagoon. This investigation may contribute to the better understanding of similar coastal lagoons in a broader geographical context.

The principal characteristics of field velocities were computed to analyze the mechanisms involved in the lagoon’s sediment transport and bottom morphodynamics processes. A two-dimensional non-linear hydro-dynamical-finite difference, semi-implicit model like that described by Backaus [11] and implemented by Carbajal [1], was applied. Van-Rijn [12] parameterized the bed load sediment transport. Also, we incorporated the sediment conservation equation into the two-dimensional hydrodynamic model to determine the seafloor morphodynamics. The seabed erosion/accretion areas have been delineated, providing a conceptual understanding of the sub-aquatic geomorphology development of URCOL.

2 Study area

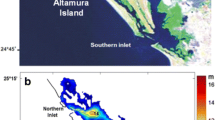
The Urias coastal lagoon (23° 11′ N–106° 22′ W) is adjacent to Mazatlán City, Sinaloa State, is located on the western coast of Mexico in the Gulf of California (Fig. 1). URCOL has been classified by Lankford [28] as a coastal lagoon with an internal platform barrier with an L shape. It has a surface area of 18 km2 and a length of 17 km. A mixed tide dominates this coastal lagoon with an average range of about 1.0 m [13]. Montaño-Ley et al. [5] reports a maximum tidal velocity of 0.6 m s−1 in the navigation channel and predicted tidal ranges of 1.2 m under the spring tide. Soto-Jiménez and Páez-Osuna [14] described estuarine behaviour during the rainy season in this water body but anti-estuarine in the dry season. Its complex morphology causes abrupt changes in the tidal current speed along the lagoon, of 0.91 m s−1 in the harbour area, 0.83 m s−1 in the intermediate area, and 0.31 m s−1 in the upper area [6]. According to Alvarez-Leon [15], the average annual rainfall in the area is 800 mm, the average annual surface temperature is 25 °C, and the monthly average temperature ranges from 19.7 °C in February to 28 °C in August.

Fig. 1
figure 1

a Location and b bathymetry of the Urias Coastal Lagoon. The position and names of relevant zones are shown

Full size image

Because of limited freshwater discharges, mainly through Jabalies creek (site b in Fig. 1) during the rainy seasons, the salinity is usually high throughout the year. The average annual salinity has been reported to have a value of 34 PSU (practical salinity unit), a maximum during the drought season (39.4 PSU) and a minimum during the rainy season (31.7 PSU) [6]. Water depth varies between 1 and 3 m except in the navigation channel, which is up to 13 m. Prevailing winds are associated with weather systems from the NW [5]. Occasionally, tropical storms migrate along the Pacific Coast of Mexico from the SW, striking Mazatlán city. Confined by two breakwaters, the Mazatlán Harbor is within the Urias Coastal Lagoon. Between the breakwaters (inlet), a water depth of up to 13 m allows the exchange of lagoon and ocean waters and the ship to enter safely the harbour through a navigation channel extends for about 3 km inside the coastal lagoon.

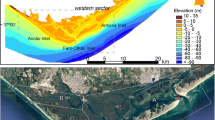
It is essential to emphasize the spatial scales of some specific locations in URCOL, including the mouth of the Infiernillo creek (located approximately 4 km from the inlet and 12 km from the head of the lagoon, with 4 m in water depth), the inlet (13 m in water depth and 300 m wide), and head of the lagoon (2 m in water depth and 400 m wide). The middle part of the URCOL is about 2 km wide and consists of a narrow channel and a wide shallow area (less than 2 m in water depth).

3 Model description and model set-up

The model area of the URCOL comprises a matrix of 81 × 144 elements representing the coastal lagoon’s bathymetry. The mesh spacing used was ΔL = 75 m. All data sets are referred to as the mean low water level datum, MLW.

We applied a two-dimensional semi-implicit non-linear model like that described by Backaus [11] and Carbajal [1]. It considers only the effect of tidal hydrodynamics in a homogeneous sea. It has been successfully used to calculate the propagation of tidal waves in regions like the North Sea, Indonesian Archipelago, and coastal lagoons of the Gulf of California [5, 16, 17]. The model, based on the vertically integrated Navier–Stokes equations of motion for shallow water and the continuity equation, is described as:

$$\frac{\partial U}{{\partial t}} + \frac{U}{H + \zeta }\frac{\partial U}{{\partial x}} + \frac{V}{H + \zeta }\frac{\partial U}{{\partial y}} - fV = - g(H + \zeta )\frac{\partial \zeta }{{\partial x}} + A_{H} \left( {\frac{{\partial^{2} U}}{{\partial x^{2} }} + \frac{{\partial^{2} U}}{{\partial y^{2} }}} \right) - r\frac{{\left( {U^{2} + V^{2} } \right)^{\frac{1}{2}} U}}{{\left( {H + \zeta } \right)^{2} }}$$
(1)
$$\frac{\partial V}{{\partial t}} + \frac{U}{H + \zeta }\frac{\partial V}{{\partial x}} + \frac{V}{H + \zeta }\frac{\partial V}{{\partial y}} + fU = - g(H + \zeta )\frac{\partial \zeta }{{\partial y}} + A_{H} \left( {\frac{{\partial^{2} V}}{{\partial x^{2} }} + \frac{{\partial^{2} V}}{{\partial y^{2} }}} \right) - r\frac{{\left( {U^{2} + V^{2} } \right)^{\frac{1}{2}} V}}{{\left( {H + \zeta } \right)^{2} }}$$
(2)
$$\frac{\partial \zeta }{{\partial t}} + \frac{\partial U}{{\partial x}} + \frac{\partial V}{{\partial y}} = 0$$
(3)

where x and y are the horizontal space variables, \(t\) is the time, \(U\) is the water transport (m2 s−1) in the \(x\) direction, \(V\) is the water transport (m2 s−1) in the \(y\) direction, \(\zeta\) is the sea surface elevation (m); \(A_{H}\) is the horizontal turbulent exchange coefficient (m2 s−1), \(f = 2\Omega \sin \varphi\) is the Coriolis parameter, \(\Omega = 7.29 \times 10^{ - 5} \,s^{ - 1}\) is the angular velocity of the earth, \(\varphi\) is the latitude (~ 23°12ʹ N in these calculations), \(H\) is the depth (m); \(g\) is the gravitational acceleration (ms−2); and \(r\) is the friction coefficient.

The system was forced at the open boundary by seven tidal constituents, each one of the form:

$$\zeta = \zeta_{0} \cos (\omega t - \phi )$$
(4)

where \(\zeta_{0}\) is the amplitude, \(\phi\) the phase and \(\omega\) the frequency of the forcing wave. The tidal amplitudes and phase data were available from Carbajal (1993). The values of the tidal harmonics K2, S2, M2, N2, K1, P1, and O1. (amplitudes) at the inlet were 0.349, 0.242, 0.201, 0.139, 0.081, 0.064, 0.067 m while the phases were 255.93, 252.19, 72.24, 67.36, 254.58, 251.08, 69.61, respectively. The dominant tidal harmonic is the M2 type. At the open boundary, the gradient of the velocity perpendicular to the boundary was equal to zero.

The hydrodynamic model applied in the present investigation was calibrated by Montaño-Ley et al. [5] with water level data recorded with a tidal gauge placed at site T (the location has been shown in Fig. 1b). The tidal elevation observations were used to calibrate the model (Fig. 2a). In addition, the observed and predicted current velocities have been shown in Fig. 2b, c, respectively. The current velocities observations have been carried out with a Sensor Data Current meter deployed at site b of the URCOL (Fig. 1). More details of the hydrodynamic model can be seen in Carbajal (1993). A friction coefficient r = 0.003, previously used by Montaño-Ley et al. [5] in the Urias coastal lagoon was also applied in this research.

Fig. 2
figure 2

a Time series of predicted and observed tidal elevation in m at site T (see in Fig. 1a) of the Urias Coastal Lagoon (modified from [5]). b Stick diagram of currents observed at point B (see in Fig. 1a). c Stick diagram of tidal currents predicted at point B

Full size image

The erosion-accretion patterns of sediments, i.e., the changes of the sea bottom, were determined by the sediment transport divergence:

$$\frac{\partial H}{{\partial t}} = \,\vec{\nabla } \cdot \,\vec{S}_{b} \,$$
(5)

where H is the water depth, and \(\vec{S}_{b} \,\) is the sediment transport.

A review of approaches to long-term modeling of coastal morphology is given by De Vriend et al. [18]. The seabed shape in our URCOL model is updated at every time interval, and the current and sediment transport patterns are recomputed using the new bathymetry. The water elevation over the reference level was imposed at the open ocean boundary using tidal predictions.

The depth-integrated tidal velocities calculated through the 2D hydrodynamic model were used as input data to calculate the sediment transport through Eq. 7. The transport parameterized in flow models as a function of the depth-averaged velocities is given by Huthnance [19], Hulsher [20], Schuttelaars and De Swart [21], and Carbajal and Montaño [22]. The volumetric sediment flux (bed load transport) in the active layer, given by Van Rijn [12], is:

$$\vec{S}_{b} \, = s\frac{{\left| {\vec{u}} \right|^{b} }}{{u\mathop {cr}\nolimits_{{}}^{b} }}\left( {\frac{{\vec{u}}}{{\left| {\vec{u}} \right|}} + k_{ * } \vec{\nabla }H} \right)$$
(6)

Here |\(\vec{u}\)| is the magnitude of the velocity vector, ucr is the critical velocity for erosion, which for fine sand is 0.3 m s−1. The term s is the ratio of densities of sediment and water [23]. The diffusive term measured by k* is a bed slope correction term, which models the preferred downhill transport of sediment. The typical value of b = 3 and k* = 2 was chosen in this work.

The parameter s is a function of the sediment properties (Eqs. 7–8), ρs is the sediment density (2,650 kg/m3) and d50 the mean sediment diameter. The value of s was calculated for d50 = 170 microns, according to Eqs. (8) and (9) [12, 24, 25] that define s as:

$$s = \sqrt {\,\,g^{1} \,\,\,\,d_{50}^{3} } \,\,\,\,\,$$
(7)
$$g^{1} = (\rho_{s} - \rho )g/\rho$$
(8)

Sediment properties are fundamentals for obtaining the value of s. Very often, the assumption of homogeneous grain size is considered to study sediment transport in coastal lagoons or coastal areas [26, 27]. According to this, and with existing data of URCOL indicating that the dominant sediment in the study area is fine and medium sands, homogeneous grain size values of 170 μ were used to run the sediment transport model [14]. The water density is given by ρ.

4 Results

This study investigated the tidal hydrodynamic and seabed interaction processes that generate the bed load sediment transport producing areas, either of erosion or accretion, focusing on the seabed morphodynamics. We have gained an insight into the bed load sediment transport in the study area for fine sand (170 μ) and the seabed sedimentation and morphodynamics controlled by tidal hydrodynamics.

Numerous experiments were performed to investigate the hydrodynamic and bedload sediment transport in the Urias Coastal Lagoon. The experiments consisted of running a modified 2D hydrodynamic finite differences model for the actual topography of the seabed (Fig. 1b). The output data consist of the depth-integrated velocity components, which are used as input for the parameterization of the bed load sediment transport module. After their discretization, the bed load sediment transport and the mass conservation equation for sediment were solved numerically to obtain the seafloor changes. The sediment transport computation did not include the effect of orbital velocities generated by the gravity waves or the wind effect.

Because the critical threshold velocity should be exceeded by the tidal flow to start the transport of sediments, the knowledge of patterns of instantaneous velocities is relevant. The spatial distribution of the instantaneous tidal currents at two different tidal stages in the URCOL is shown in Fig. 3.

Fig. 3
figure 3

Instantaneous tidal currents show the flood and the ebb flow patterns at two different times

Full size image

In general, the magnitude of the velocities in the navigation channel is large and undergoes attenuation as it travels away from the main channels. In the upper part of the lagoon, at the head, tidal currents are small, hardly reaching 0.10–0.30 m s−1 in magnitude. The tidal prism is discharged into the ocean during the ebb (Fig. 3a) and the water from the Ocean enters through the gap between the breakwaters into the lagoon during the flood (Fig. 3b). After leaving the main channel, the intensity of velocities becomes weaker due to bottom friction in the shallower area of the lagoon. In this location, the channel turns east, presenting the most significant tidal velocities.

The predicted tidal signals at four different locations inside the URCOL have been included in Fig. 4. The tidal elevation and the horizontal components of the x-direction, u, and in the y-direction, v, reflect the diurnal–semidiurnal mixed character of the tidal signal. Near the lagoon entrance at point A (see Fig. 1a for the position of the points), v component of the velocity is overriding, tidal currents are aligned along the principal channel, and u component close to zero. At point B, the two components of the velocity are out of phase by \(\frac{\pi }{2}\) and v is slightly larger than u. The calculated duration of rising and fall of the tide revealed in the sea surface elevation a signal distortion of ebb-dominant type, i.e., a longer rise and a short tidal fall. These few time series provide an idea of the complex behavior of the tidal flow in the shallow and relatively small URCOL. Bathymetry control these flows. The time series of the components (u, v) of the horizontal velocity vector show a considerable distortion of the tidal signal, indicating a complicated behavior of acceleration processes. The duration of falling and rising tidal velocities varied for the different flats and channels. At sites C and D (see Fig. 1a for the position of the points), the y component of the tidal velocities v is almost zero, and the u velocity component is also tiny.

Fig. 4
figure 4

Time series of the predicted tidal elevation in m (serie1 blue), tidal velocities components u in the x-direction in m s−1 (serie2 red) and tidal velocity component v in the y-direction m s−1 (serie3 black) at sites A, B, C and D (see Fig. 1a for sites location)

Full size image

The instantaneous bed load sediment transport fields for different tidal stages: t = T/4, t = T/2, t = 3 T/4, and t = T have been displayed in Fig. 5. For the tidal stages, t = T/4 and t = T/2 prevail in the ebb conditions, and the bed load sediment transport is toward the lower part of the lagoon. The bed load transport reverses direction for the flood conditions when t = 3 T/4 and t = T and sediment moves toward the upper part of the lagoon. The order of magnitude of the sediment transport rate is 10–5 m3 m−1 s−1.

Fig. 5
figure 5

Instantaneous bed load sediment transport fields for different tidal stages a t = T/4 b t = T/2 c t = 3 T/4 d t = T

Full size image

The net sediment transport distribution field after one tidal period (M2) has been plotted in Fig. 6. The highest sediment transport rates were predicted in the channel's middle part, right where the channel starts curving, changing its alignment.

Fig. 6
figure 6

Net bed load sediment transport field in one tidal period of the M2 tide and bathymetry (m)

Full size image

The time series of cumulative sediment transport at point P in the y-direction has been shown for 60 M2 tidal periods in Fig. 7a. The units are m3 per m of transversal bottom length or m2. It may be observed that the y component keeps growing negatively, indicating the outflux of sediment from the lagoon into the Ocean. It is worth mentioning that between the tidal periods 9 and 18 and between periods 34 and 48, the cumulative sediment transport is not growing. These intervals correspond to the interval of neap tides (Fig. 7b) when the tidal range is relatively small (approximately 0.65 m) and the critical velocities to move sediment are below the threshold values. After 60 M2 tidal periods, the cumulative sediment transport has reached 1.0 × 10−1 m2. This implies that has occurred a net sediment transport to seaward of 1 × 10–1 m3 per depth meter.

Fig. 7
figure 7

a Cumulative bed load sediment transport in the y direction predicted (m2) at point P (see in Fig. 1a). b Tidal elevation (m) at point P. c Cumulative bed load sediment transport through the inlet in m3 (see in Fig. 1b)

Full size image

Figure 7c shows the computed net bed load sediment transport at the inlet of URCOL. The outcome of the computed time series indicates a seaward net transport of sediment toward the Gulf of California. The seaward net transport reflects the difference between the imported and exported bed load transport in about a year. For extended period, expected changes in sediment transport rates or reverse in the net transport direction might be expected.

Bed erosion and accretion patterns of sediment were determined from the divergence of the bed load sediment transport. The patterns in URCOL related to the vertical changes of the seafloor have been displayed in Fig. 8. The magnitude of the vertical changes of the bottom of the coastal lagoon is shown in 2 (Fig. 8a), 4 (Fig. 8b), 6 (Fig. 8c), and 8 (Fig. 8d) months of calculation. Changes of about 2 × 10−2 m in the sea bottom have been predicted in this process. After 1.5 years of numerical simulation of sediment transport and applying a constant threshold velocity (0.3 ms−1) and friction coefficient (0.003), the areas of noticeable vertical changes on the seafloor have been revealed in the middle section (MS) of the lagoon (see Fig. 1b for location). The affected areas are larger, and the bottom changes are about 5 × 10–2 m. The influence of the lagoon’s L-shape alignment on the bed's vertical changes is displayed in Fig. 9 (see square A).

Fig. 8
figure 8

Predicted Sea bottom vertical changes in m (positive values correspond to accretion and negative values to erosion) after a t = 2 months, b t = 4 months, c t = 6 months and d t = 8 months of numerical simulation

Full size image
Fig. 9
figure 9

Predicted erosion and accretion areas caused by the bed load sediment transport after 1.5 years in the middle section (MS) of the lagoon. Square A corresponds to the zoomed middle area

Full size image

5 Discussion

The hydrodynamics and the induced sediment transport in coastal lagoons are essentially modulated by the astronomical ocean tides, the geometry of the lagoons, and sediment availability [28]. The energy available to transport the sediment is provided by tidal forcing, which in Urias coastal lagoon, according to the results of the present study, can generate tidal current speeds close to 1.0 m s−1 at the central section (MS) of the lagoon. Most of the URCOL is very shallow (less than 2 m water depth) with extensive flat areas (Fig. 1b), and the amplitude of the M2 tidal component to the mean water depth of the lagoon exceeds 0.1. Under these circumstances, a depth-integrated two-dimensional numerical model is justified in studying the tidal hydrodynamics at the URCOL. The model implemented was barotropic because it considers only the effect of the tidal hydrodynamics without density effect due to salinity and temperature changes. URCOL receives only negligible freshwater inputs. Because of this, gravitational effects are minimal. According to Aubrey [29], when river inflow is absent, “sedimentation in coastal lagoons primarily depends on the reworking of material within the lagoon, the influx of sediment through the tidal inlet from the ocean, runoff from marginal areas, and biological sources (i.e., marsh grass and shell material)”. Therefore, without river influx, as in URCOL, the tidal velocities (Fig. 3) will govern most of the sediment transport regardless sediment transport occurs as bedload or suspended. Hence the flow velocity pattern in URCOL controls much of the sediment transport. We predicted the highest sediment transport rates (Fig. 5) in the middle part of the channel (MS) where the fastest tidal currents, the maxima velocity gradients, and morphological changes of the seafloor occurred.

Two principal factors indicate whether a coastal lagoon or estuary undergoes an asymmetry of the tidal signal [30]. A lagoon dominantly characterized by channels develops an asymmetry typified by a longer falling tide. As the tide propagates, the asymmetry increases with greater friction and a time-variable channel cross-sectional area. If channels and flats characterizes the coastal lagoon, it can produce a longer rising tide if the area with tidal flats is large enough to overcome the effect of channels. According to the above discussion, the effect of channels is overruled in the URCOL lagoon by the tidal flats. Consequently, it produces an asymmetry with a longer rising tide (Fig. 4), i.e., it is an ebb-dominant coastal lagoon. The present investigation reveals that the URCOL contains both characteristics—a channel mesh and extensive flat areas.

Montaño-Ley et al. [3] investigated the sediment exchange between the ocean and URCOL. Based on observations of water–sediment concentration and currents velocities measured at the lagoon entrance, they suggest the advection of sediment in suspension from the lagoon to the adjacent Ocean. The authors also found high suspended sediment concentrations in the upper part of the lagoon. The outcome of present investigation indicates moderated exchange of sediment between the lagoon and the Gulf of California through the inlet. The net bed load sediment transport calculated through the gap between the two breakwaters, shown by the computed time series, resulted in low and seaward transport toward the Gulf of California (Fig. 7). The time series also indicated that in URCOL, lower low water, follows higher high water. This condition usually produces maximum velocities during ebb tide. The low seaward net transport computed does not mean, in any way, low exchange between the coastal lagoon and the Gulf of California but just reflects the difference between the imported and exported bed load transport in about a year. On a longer time, expected changes in sediment transport rates or even an inflection or reversing in the net transport direction might be expected since the rate of export and import of sediments exhibit semi-annual, monthly, and fortnightly oscillations.

Other investigations carried out in coastal lagoons of the region of the Gulf of California like Topolobampo [16] and Yavaros [7], indicate exchange of sediment between the lagoon and the Ocean through the inlets. Both lagoons are exposed to similar tidal conditions than the Urias Coastal Lagoon. The net bed load sediment transport, as in the present investigation, was seaward toward the Gulf of California. In the case of Topolobampo it was also found that the largest bedload sediment transport rates and seabed morphodynamics took place in a narrow passage that connect the northern and southern part of the lagoon. Similarly, in Urias coastal lagoon the more intense sediment transport took place in a narrow area (400 m wide) located in the middle section of the lagoon. In this section also developed the most intense bottom morphodynamics (Figs. 8 and 9), The geometry of the Topolobampo and Urias Lagoon seemed to affect the sediment dynamics of both lagoons. In the case of Yavaros, as the lagoon has a more regular shape, it does not seem to exist any relation between geometry and sediment dynamics.

In other regions of the world like Miani Hor (a coastal lagoon of Lasbela, Balochistan, Pakistan) as in the present investigation, the tidal hydrodynamics is the main forcing function of the sediment transport. According to Ahmed-Syed et al. [9], the rise and fall of the tide in the adjacent sea generates horizontal flow of water into and out of the channel that in turn causes fluctuation of water level of the lagoon. As in the present investigation, wave condition within the lagoon and adjacent sea indicates that offshore deep-water waves do not penetrate the lagoon due to the single narrow inlet. Strong tidal currents generate most of the erosion and accretion within and out of the lagoon.

The bed load sediment transport according to Eq. (6) [12] depends on sediment properties. Seabed sediment in URCOL was assumed to be non-cohesive of uniform grain size. A review of the scientific literature on this subject revealed that strong assumptions had to be made in most sediment transport modeling. A frequent assumption is to consider a uniform grain size in coastal lagoons or coastal areas to study sediment transport [26, 27]. On these bases, and with existing data of URCOL indicating that the dominant sediment in the study area is fine and medium sand, uniform grain size values of 170 μ were selected to run the sediment transport model. Using a uniform grain size in the model probably leads to an overestimate of the transport in some areas of the lagoon where the presence of coarser sediment limits the actual transport [26].

A seabed area’s net accretion or erosion rates depends on the balance in the entering or leaving sediments. The erosion and accretion patterns were obtained from the bed load sediment transport divergence. Seabed will be eroded if the value of the divergence is positive, whereas sediment will be accreted if the value is negative. The distribution patterns of the erosion and accretion rates are consistent with the convergent and divergent character of the vectors of sediment transport rates. The accretion of sediments has been predicted, mainly shoals on the middle part of the lagoon right where the channel starts curving. The predicted erosion areas were usually very close to where sediment was accumulated, shaping some pattern, as was already expected from the sediment conservation equations.

A seabed area’s net accretion or erosion rates depends on the balance in the entering or leaving sediments. The erosion and accretion patterns were obtained from the bed load sediment transport divergence. Seabed will be eroded if the value of the divergence is positive, whereas sediment will be accreted if the value is negative. The distribution patterns of the erosion and accretion rates are consistent with the convergent and divergent character of the vectors of sediment transport rates. The accretion of sediments has been predicted, mainly shoals on the middle part of the lagoon right where the channel starts curving (Figs. 8 and 9). The predicted erosion areas were usually very close to where sediment was accumulated, shaping some pattern, as was already expected from the sediment conservation equations.

The bedload transport in the Seine Estuary (France), according to Mengual et al. [10] appears as a non-dominant but relevant contributor to the sediment dynamics of the Seine Estuary causing, as in the present investigation of the URCOL lagoon, erosion-accretion patterns, especially over shoals. The sediment flux and the resulting patterns of erosion and accretion look usually similar between suspended load and bedload dynamics. Petti et al. [8] studied the morphodynamics of the Marano and Grado lagoon in Italy, by means of a two-dimensional horizontal (2DH) morphological-hydrodynamic model. They found that most of the erosion areas were concentrated in tidal flats and marshes. In the present investigation, the narrow middle section (MS) of the lagoon (see Fig. 1b for location) showed the largest vertical changes of the seabed of about 5 × 10–2 m. The influence of the lagoon's inverted L-shape as well as the shallow water (2–6 m) in the narrow (400 m wide) middle section (MS) of the lagoon, seemed to be relevant for the increase of the bottom morphodynamics, either erosion or accretion (Fig. 8) in this part of the lagoon.

This investigation provides an insight into the local seabed geomorphic changes in the Urias Coastal Lagoon. In a broad geographical context, comparison of the present investigation with other coastal lagoons of the Gulf California and around the world, shows that tidal asymmetries were determinant of the net bedload sediment transport direction though the inlets, and that the tidal hydrodynamics and geometry of the lagoons (like narrow channels) play an important role on the location of the intense bed load sediment transport and accretion-erosion areas within the lagoons.

6 Conclusions

The bedload sediment transport induced by the tidal hydrodynamics and the consequent erosion and accretion process in Urias Coastal Lagoon in the Gulf of California coast was investigated, providing insight into the local seabed geomorphic evolution.

The instantaneous tidal currents predicted in the URCOL showed high spatial and temporal variability. This investigation provides a first approach of the complex behavior of the tidal flow and induced bedload sediment transport in the URCOL. These flows appeared controlled by bathymetric features. The instantaneous velocities patterns indicate that the magnitude of the velocities in the navigation channel is large and undergoes attenuation as it travels away from the main channels. At the head of the lagoon, the tidal currents are relatively minor in magnitude. The location where the channel turns to the east, resembling an inverted L, presented the largest tidal velocities.

The highest sediment transport rates were predicted in the middle part of the lagoon, right on the place where sharp topographic gradients occur and the channel starts curving, changing the lagoon alignment. The sediment pattern suggests sediment exchange between the lagoon and the Gulf of California. The net movement of bedload sediment transport caused by the tidal hydrodynamics resulted in being seaward. The time series indicated that in URCOL, lower low water follows higher high water. This condition usually produces maximum velocities during ebb tide. Ebb velocities affect the flushing sediments from the coastal lagoon into the Gulf of California. The calculations indicate that a relatively stable bed prevails nearby the head of the lagoon.

The distribution patterns of the erosion and accretion rates are consistent with the convergent and divergent character of the vectors of sediment transport rates. The sediment accretion was predicted mainly in the middle part of the channel, right at the place where the channel starts curving to the SW.

Noticeable vertical changes (0.01–0.04 m) in the seabed level of the lagoon were found in the middle part of the channel, where the sediment transport gradients were also more significant.