1 Introduction

Penetrative convection is a phenomenon whereby thermal convection may commence in a sub-layer of a horizontal layer of fluid, or in a horizontal layer of fluid saturated porous medium, and the ensuing convective motion will induce motion in other part(s) of the layer. It typically induces counter rotating convection cells. Mathematical models for penetrative convection typically involve either a quadratic density in the buoyancy force or an internal heat source, see e.g. Straughan [1, pages 97–102]. We here concentrate on the model where density is a quadratic function of temperature, as introduced by Veronis [2], for the case of a layer of incompressible viscous fluid.

The fact that penetrative convection is of such interest is primarily due to the realization that it is an area with a multitude of real physical applications. As pointed out in Straughan [1], there are applications in planetary physics, DietrichWicht [3], van den berg et al. [4], in internally cooled convection,Berlengiero et al. [5], in environmental fluid mechanics, Fernando [6],Pol and Fernando [7], in the cloud cover of Venus, Imamura et al. [8], in aiding the rise of volcanic plumes in the Earth’s atmosphere, Kaminski et al. [9], in mixing in the Laptev Sea, Kirillov et al. [10], in cloud to ground discharges,Machado et al. [11], Mharzi et al. [12], in biochemical decay,Prudhomme and Jasmin [13], in flow in the Sun, Tikhomolov [14], and in particular in penetrative convection in a porous medium where application is to formation of stones into regular patterns, George et al. [15], and in building insulation, Straughan and Walker [16]. Theoretical analyses of penetrative convection have ensued such as Veronis [2], Musman [17], Carr [18, 19], Carr and Putter [20], Carr and Straughan [21], Harfash [22, 23], Krishnamurti [24], Larson [25], Straughan [26,27,28]. Further references may be found in the books of Straughan [29, 30].

DietrichWicht [3] write,...“Many celestial objects are thought to host interfaces between convective and stable stratified interior regions. The interaction between both, e.g. the transfer of heat, mass, or angular momentum depends on whether and how flows penetrate into the stable layer. Powered from the unstable, convective regions, radial flows can pierce into the stable region depending on their inertia (overshooting). Veronis [2] developed and analysed a model for penetrative convection in an infinite horizontal layer of water where the temperature at the bottom of the layer is kept fixed at \(0~^{\circ }\)C while the temperature of the upper plane is kept fixed at temperature \(T_U(\ge 4~^{\circ }\mathrm{C})\). Water possesses a density maximum at approximately \(4~^{\circ }\)C and thus the Veronis [2] situation has water in the \(0~^{\circ }\)C to \(4~^{\circ }\)C range in a potentially gravitationally unstable configuration. When convective motion commences it can penetrate into the part of the layer where the temperature is above \(4~^{\circ }\)C, and if the upper temperature is sufficiently high then a second counter rotating fluid cell may arise in the upper part of the layer, see e.g. the streamlines shown in Musman [17]. In this article we are interested in finding critical Rayleigh numbers and wave numbers for when penetrative convection may occur in a porous medium saturated with water where the geometric configuration is the Veronis [2] one, i.e. the lower boundary temperature held at \(0~^{\circ }\)C with the upper temperature fixed at \(T_U\). Of particular interest to us is to determine the conditions under which one convection cell occurs, and when two or more will occur. Since we are employing a porous medium we have several influences to consider, such as whether the porous medium is isotropic or anisotropic, what conditions are imposed on the fluid at the upper boundary, and what theory is employed to describe the porous medium, e.g. Darcy theory or Brinkman theory. Flow patterns in the porous medium are important in transporting micro particles or contaminants which may subsequently be distributed into the surrounding environment where they may degrade quantities such as air quality. Therefore, an understanding of the flow patterns in saturated porous media due to penetrative motions is essential for a complete knowledge of the physics of the environment.

The goal of this work is to analyse models for penetrative convection in a porous material of Darcy or Brinkman type allowing for the porous structure to be of horizontally isotropic type. We consider a fixed boundary condition for the fluid at the upper boundary of the layer but alternatively we allow a condition of constant pressure. We derive critical Rayleigh numbers and wave numbers for the onset of penetrative convection and investigate in detail the conditions on the upper boundary temperature which give rise to a single convection cell or multiple cells. This is achieved by finding the associated eigenfunctions of the instability problem and our results vary strongly depending on the degree of anisotropy, the upper boundary condition on the velocity, or which porous medium theeory is utilized.

2 Equations for penetrative convection

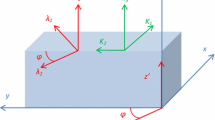
Suppose the porous medium occupies the horizontal layer \({\mathbb {R}}^2\times \{z\in (0,d)\}\) with gravity g acting in the downward direction, i.e. \(g_i=-gk_i\), where \(\mathbf{k}=(0,0,1)\). The lower plane \(z=0\) is held at fixed temperature \(0~^{\circ }\)C while the upper plane at \(z=d\) is held at fixed temperature \(T_U\ge 4~^{\circ }\)C.

For a linear density–temperature relationship the governing equations for an isotropic Darcy porous medium are given by Straughan [30] in equations (4.1), p. 148, and we repeat these here but we allow for a density which is quadratic in temperature T. Thus, the governing equations are

$$\begin{aligned} \begin{aligned}&0=-\frac{\mu }{K}\,v_i-p_{,i}-\rho (T)gk_i,\\&v_{i,i}=0,\\&T_{,t}+v_iT_{,i}=\kappa \varDelta T, \end{aligned} \end{aligned}$$
(1)

where the density \(\rho\) is given by

$$\begin{aligned} \rho (T)=\rho _0(1-\alpha [T-4]^2), \end{aligned}$$
(2)

with \(\rho _0\) the density of water at \(4~^{\circ }\)C and where \(\alpha\) is the coefficient of thermal expansion. In (1) \(v_i,\mu ,K,p,g\) and \(\kappa\) are the velocity field, the dynamic viscosity of water, the permeability of the porous material, the pressure of the water in the saturated porous medium, gravity, and the thermal diffusivity of the porous medium. Standard indicial notation is used throughout in conjunction with the Einstein summation convention, so that for example, if \(\mathbf{v}=(v_1,v_2,v_3)\equiv (u,v,w)\) and \(\mathbf{x}=(x_1,x_2,x_3)\equiv (x,y,z)\), then we write the divergence of the velocity field in the forms

$$\begin{aligned} v_{i,i}\equiv \sum _{i=1}^3v_{i,i}=&\frac{\partial v_1}{\partial x_1}+\frac{\partial v_2}{\partial x_2}+\frac{\partial v_3}{\partial x_3}\,,\\ =&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}\,. \end{aligned}$$

For an example involving a nonlinearity, we write

$$\begin{aligned} v_iT_{,i}\equiv \sum ^3_{i=1}v_iT_{,i}= u\frac{\partial T}{\partial x} +v\frac{\partial T}{\partial y} +w\frac{\partial T}{\partial z}. \end{aligned}$$

Many porous materials display distinct anisotropy in their structure and this may be manifest by replacing the scalar permeability K with a tensor \(K_{ij}\). In this case the relevant equations are

$$\begin{aligned} \begin{aligned}&0=-\mu v_i-K_{ij}p_{,j}-\rho (T)gK_{ij}k_j,\\&v_{i,i}=0,\\&T_{,t}+v_iT_{,i}=\kappa \varDelta T, \end{aligned} \end{aligned}$$
(3)

cf. Straughan [30, page 149].

If we consider an isotropic Brinkman theory then the equations are

$$\begin{aligned} \begin{aligned}&0=-\frac{\mu }{K}\,v_i-p_{,i}+{\tilde{\mu }}\varDelta v_i-\rho (T)gk_i,\\&v_{i,i}=0,\\&T_{,t}+v_iT_{,i}=\kappa \varDelta T, \end{aligned} \end{aligned}$$
(4)

where \({\tilde{\mu }}\) is a Brinkman effective viscosity, cf. Straughan [30, page 150].

The boundary conditions we consider in this article are

$$\begin{aligned} T=0~^{\circ }\mathrm{C}\,\,\mathrm{at}\,\,z=0;\quad T=T_U\,\,\mathrm{at}\,\,z=d;\quad W=0\,\,\mathrm{at}\,\,z=0, \end{aligned}$$
(5)

and either

$$\begin{aligned} W=0\,\,\mathrm{at}\,\,z=d, \end{aligned}$$
(6)

or

$$\begin{aligned} p=p_a\,\,\mathrm{at}\,\,z=d, \end{aligned}$$
(7)

where \(p_a\) is a constant ambient surface pressure.

The steady temperature field for all cases is

$$\begin{aligned} {{\bar{T}}}=\beta z, \end{aligned}$$
(8)

where \(\beta =T_U/d\). The steady velocity field in whose stability we are interested is

$$\begin{aligned} {{\bar{W}}}\equiv 0. \end{aligned}$$
(9)

3 Effects on penetrative convection

Our main concern here is to investigate the effect of anisotropy via \(K_{ij}\), the changes due to the Brinkman term with coefficient \({\tilde{\mu }}\), and the effect of the boundary conditions (6) or (7), upon the critical parameters of penetrative convection.

Anisotropic effects upon thermal convection in saturated porous media have been the subject of many recent investigations, see e.g. Capone et al. [31,32,33,34,35], Hemanthkumar et al. [36,37,38]. In particular the ramifications of anisotropy in porous media have proved of interest in the application to healthcare materials and in human tissues, see Fang et al. [39], Mirbod et al. [40].

The Brinkman effect upon thermal convection in porous media has also inspired recent research such as Rees [41], Gentile and Straughan [28, 42] and Wu and Mirbod [43]. Of particular note is the observation by Wu and Mirbod [43] that \(\mu\) and \({\tilde{\mu }}\) in (4)\(_1\) will not in general be the same. In [28] it is also shown that the Darcy theory in equations (1) and the Brinkman theory in (4) can lead to very different physical effects and thus the two theories should always be considered separately.

The influence of non-Dirichlet boundary conditions on either the velocity field or the temperature field is also an area which has attracted much recent attention in thermal convection in porous media, see e.g. Barletta et al. [44], Barletta [45], Barletta [46], Barletta and Celli [47], Barletta and Rees [48], Celli and Kuznetsov [49], Mohammad and Rees [50], Nield and Kuznetsov [51], Rees and Barletta [52], Rees and Mojtabi [53, 54], Brandao et al. [55].

In order to place the mathematical theories of flow in porous media on a firm mathematical footing there have been many recent articles studying structural stability aspects of the equations themselves, see e.g. Li et al. [56],Liu and Xiao [57], Liu et al. [58], Liu et al. [59], Liu et al. [60],Gentile and Straughan [61].

We next investigate instability of the basic solution (8), (9), under variation of the effects of anisotropy, the Brinkman coefficient, boundary conditions, and the upper temperature \(T_U\).

4 Instability

To investigate instability of the conduction solution (8), (9), we introduce perturbations \(u_i,\pi ,\theta\) to \(v_i,p,T\) as

$$\begin{aligned} v_i={{\bar{v}}}_i+u_i,\quad p={{\bar{p}}}+\pi ,\quad T={{\bar{T}}}+\theta , \end{aligned}$$

and we then non-dimensionalize with the scales given in George et al. [15] and Straughan [37]. The scalings needed are

$$\begin{aligned}&u_i=u_i^*U,\qquad \theta =\theta ^*T^{\sharp },\qquad x_i=x_i^*d,\qquad t=t^*{{\mathcal {T}}},\\&{{\mathcal {T}}}=\frac{d^2\rho _0}{\mu }\,,\qquad U=\frac{\mu }{\rho _0d}\,,\qquad P=\frac{\mu Ud}{K}\,\qquad T^{\sharp }=U\Bigl [\frac{\beta d^2\mu }{\kappa \rho _0g\alpha (T_U-T_L)K}\Bigr ]^{1/2}\,, \end{aligned}$$

with K replaced by \(K_H\) in the anisotropic permeability case. This yields the non-dimensional perturbation equations for (1) as

$$\begin{aligned} \begin{aligned}&0=-\pi _{,i}-u_i-2R\theta (\xi -z)k_i+Pr\theta ^2k_i,\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=-Rw+\varDelta \theta , \end{aligned} \end{aligned}$$
(10)

where the domain is \({\mathbb {R}}^2\times \{z\in (0,1)\}\times \{t>0\}\), \(Pr=\mu /\kappa \rho _0\) is the Prandtl number, \(\xi =(T_0-T_L)/(T_U-T_L)\), \(T_0=4~^{\circ }\mathrm{C}\), \(T_L=0~^{\circ }\mathrm{C}\), and R is defined by

$$\begin{aligned} R^2=\frac{g\alpha \rho _0\beta ^2d^3K}{\kappa \mu }\,. \end{aligned}$$
(11)

When dealing with the Darcy models we present results in terms of a Rayleigh number

$$\begin{aligned} Ra=\xi ^3R^2, \end{aligned}$$
(12)

which reflects the depth of the destabilizing layer in the steady state, cf. George et al. [15].

For the Darcy anisotropic case we suppose the permeability tensor is that appropriate to horizontal isotropy so that \(K_{ij}\equiv diag\{K_H,K_H,K_V\}\) cf. Straughan [37]. Then with \(\ell ^2=K_H/K_V\) the non-dimensional perturbation equations are

$$\begin{aligned} \begin{aligned}&0=-\pi _{,i}-D_{ij}u_j-2R\theta (\xi -z)k_i+Pr\theta ^2k_i,\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=-Rw+\varDelta \theta , \end{aligned} \end{aligned}$$
(13)

which are again defined on the domain \({\mathbb {R}}^2\times \{z\in (0,1)\}\times \{t>0\}\), and where \(D_{ij}\equiv diag\{1,1,\ell ^2\}\), and now \(R^2=g\alpha \rho _0\beta ^2d^3K_H/\kappa \mu\). It is worth observing that Straughan [37] provides many instances of real geophysical situations where the horizontally isotropic form \(D_{ij}\) is valid.

For the Brinkman system (4), a form of the non-dimensional perturbation equations which incorporates a horizontally isotropic permeability is

$$\begin{aligned} \begin{aligned}&0=-\pi _{,i}-D_{ij}u_j+B\varDelta u_i-2R\theta (\xi -z)k_i+Pr\theta ^2k_i,\\&u_{i,i}=0,\\&Pr(\theta _{,t}+u_i\theta _{,i})=-Rw+\varDelta \theta , \end{aligned} \end{aligned}$$
(14)

where \(B={\tilde{\mu }}K_H/\mu d^2\) is a non-dimensional form of \({\tilde{\mu }}\) and the domain of definition is \({\mathbb {R}}^2\times \{z\in (0,1)\}\times \{t>0\}\).

For equations (10) the boundary conditions are that \((u_i,\pi ,\theta )\) satisfies a plane tiling periodicity in x and y commensurate with the form of periodic cells (typically hexagonal shaped) and on the planes \(z=0,1\),

$$\begin{aligned} w=0,\quad z=0,1;\qquad \theta =0,\quad z=0,1. \end{aligned}$$
(15)

We shall also consider the case where the upper boundary is such that the pressure is constant there at the ambient atmospheric pressure \(p_a\), and then the boundary conditions (15) are replaced by

$$\begin{aligned} w=0,\quad z=0;\qquad \frac{\partial w}{\partial z}=0,\quad z=1; \qquad \theta =0,\quad z=0,1. \end{aligned}$$
(16)

We only consider equations (16) for the Darcy isotropic case. From equation (10)\(_1\) applied on the boundary \(z=1\), \(\pi =0\) when \(z=1\), and this yields u, v zero there, and so from the equation of continuity \(w_z=0\) when \(z=1\). This case is referred by Barletta et al. [44] as corresponding to a perfectly permeable upper boundary. For the non - penetrative convection situation boundary conditions (16) are analysed in detail by Barletta et al. [44], by taking \(a_1=a_2=b_1=0\), \(b_2=\infty\), in their notation. They analyse this class of solutions in section 4.2.4 of their paper and the Rayleigh number against wavenumber curve is given in their Fig. 5 (lower frame) with \(a_1=0\).

For the Brinkman perturbation equations (14) the boundary conditions are again periodicity in the (x, y) plane and on the boundaries \(z=0,1\),

$$\begin{aligned} u_i=0,\quad z=0,1;\qquad \theta =0,\quad z=0,1. \end{aligned}$$
(17)

To find the critical Rayleigh number, wavenumber, and associated eigenfunction, we discard the \(Pr\theta ^2\) terms and take curlcurl of each of equations (10)\(_1\), (13)\(_1\), (14)\(_1\). We then look for a normal mode solution of form

$$\begin{aligned} w=e^{\sigma t}W(z)h(x,y),\qquad \theta =e^{\sigma t}\varTheta (z)h(x,y), \end{aligned}$$

where h(x, y) is a plane tiling function, which satisfies \(\varDelta ^*h=-a^2h\), for a wavenumber a where \(\varDelta ^*\) is the horizontal Laplacian, cf. [29, page 51]. This results in having to solve the system of equations

$$\begin{aligned} \begin{aligned}&(D^2-a^2)W-2R(\xi -z)a^2\varTheta =0,\\&(D^2-a^2)\varTheta -RW=\sigma \varTheta , \end{aligned} \end{aligned}$$
(18)

in the isotropic Darcy case,

$$\begin{aligned} \begin{aligned}&(D^2-a^2\ell ^2)W-2R(\xi -z)a^2\varTheta =0,\\&(D^2-a^2)\varTheta -RW=\sigma \varTheta , \end{aligned} \end{aligned}$$
(19)

in the horizontally isotropic Darcy case, and

$$\begin{aligned} \begin{aligned}&(D^2-a^2\ell ^2)W-B(D^2-a^2)^2W-2R(\xi -z)a^2\varTheta =0,\\&(D^2-a^2)\varTheta -RW=\sigma \varTheta , \end{aligned} \end{aligned}$$
(20)

in the horizontally isotropic Brinkman case, where \(D=d/dz\) and \(z\in (0,1)\).

The boundary conditions for (18) and (19) are

$$\begin{aligned} W=0,\quad z=0,1;\qquad \varTheta =0,\quad z=0,1; \end{aligned}$$
(21)

or for the constant pressure case

$$\begin{aligned} W=0,\quad z=0;\qquad DW=0,\quad z=1;\qquad \varTheta =0,\quad z=0,1; \end{aligned}$$
(22)

and for (20) for two fixed surfaces

$$\begin{aligned} W=DW=0,\quad z=0,1;\qquad \varTheta =0,\quad z=0,1. \end{aligned}$$
(23)

5 Global nonlinear stability

For any of the systems of equations (10), (13), or (14), a standard energy stability analysis will not lead to global nonlinear stability due to the presence of the quadratic term \(Pr\theta ^2k_i\). Instead, we may employ an energy function which has a weight, of form

$$\begin{aligned} E(t)=\frac{Pr}{2}\int _V(\zeta -2z)\theta ^2dx, \end{aligned}$$
(24)

where \(\zeta >2\) is a constant at our disposal and V is a period cell for the solution, cf. [29, pages 342–343]. When dE/dt is calculated the weight \(\zeta -2z\) gives rise to a term of form \(-w\theta ^2\) and this cancels out with the analogous term which arises from the momentum equation. Thus, the energy equation which arises contains only quadratic terms which then lead to unconditional (global) nonlinear stability. This leads to an energy equation of form, in the Darcy situation,

$$\begin{aligned} \frac{dE}{dt}=RI-D, \end{aligned}$$
(25)

where the dissipation D and the production term I are given by

$$\begin{aligned} I=-\int _V(2\xi +\zeta -4z)w\theta \,dx\,, \end{aligned}$$

and

$$\begin{aligned} D=\int _VD_{ij}u_iu_jdx+\int _V(\zeta -2z)\vert \nabla \theta \vert ^2dx. \end{aligned}$$

A global nonlinear stability analysis may be developed from (25) as follows

$$\begin{aligned} \frac{dE}{dt}\le -D\Bigl (\frac{R}{R_E}-1\Bigr )\,, \end{aligned}$$
(26)

where

$$\begin{aligned} \frac{1}{R_E}=\max _H\,\frac{I}{D}\,, \end{aligned}$$
(27)

with \(H=\{u_i\in L^2(V),\theta \in H^1(V)\}\) with (x, y) periodicity, being the space of admissible solutions. One has then to calculate the Euler-Lagrange equations from (27) and solve these for the critical value of \(R_E\). This calculation is similar to that done for the linear instability problem in Sect. 7 of this paper. We do not present numerical results for this calculation here since we are primarily interested in the effects of anisotropy and boundary conditions upon penetrative convection. However, the numerical results follow those of Straughan and Walker [16] on a different problem and show that the nonlinear stability threshold is close to the linear instability one for \(T_U\) values not exceeding \(8~^{\circ }\)C.Veronis [2] shows that sub-critical instabilities are possible in the pure fluid penetrative convection problem and so we do not expect coincidence of the energy stability and linear instability Rayleigh number values, especially for \(T_U\) larger, where in Sect. 7 we find multi-cellular structures form.

6 Numerical method

To solve equations (18), (19), (20) with boundary conditions (21), (22), (23) numerically we employ a \(D^2\) Chebyshev tau method, as described in Dongarra et al. [62]. We treat \(\sigma\) as the eigenvalue and recast each system into a generalized matrix eigenvalue problem of form

$$\begin{aligned} A\mathbf{x}=\sigma B\mathbf{x}, \end{aligned}$$
(28)

where

$$\begin{aligned} \mathbf{x}=(W_0,\cdots ,W_N,\varTheta _0,\cdots ,\varTheta _N), \end{aligned}$$

for the Darcy cases with

$$\begin{aligned} W=\sum _{i=0}^NW_iT_i(z),\qquad \varTheta =\sum _{i=0}^N\varTheta _iT_i(z), \end{aligned}$$
(29)

where \(T_i(z)\) are Chebyshev polynomials. For the Brinkman case we introduce a variable \(\chi\) by \(\chi =(D^2-a^2)W\) and then we still have a system like (28) to solve but now

$$\begin{aligned} \mathbf{x}=(W_0,\cdots ,W_N,\chi _0,\cdots ,\chi _N,\varTheta _0,\cdots ,\varTheta _N). \end{aligned}$$
(30)

The boundary conditions (21) and (23) are inserted as rows \(N-1,N,2N-1,2N\) for the Darcy problem and rows \(N-1,N,2N-1,2N,3N-1,3N\) for the Brinkman problem. For these cases the resulting generalized matrix eigenvalue problem was solved by the QZ algorithm of Moler and Stewart [63]. The eigenfunctions W(z) are calculated from the eigenvalues \(W_i\) as in (29) or (30).

For the constant pressure boundary condition (22) we found significant problems with the production of spurious eigenvalues if we used the method of writing in the boundary conditions as rows of the matrices. To overcome this it was necessary to use the discrete form of the boundary conditions to remove variables \(W_{N+1}\) and \(W_{N+2}\) and in this manner to incorporate the boundary conditions into all rows of the matrices. The relevant expressions are given by (2.15) and (2.16) of Payne and Straughan [64] taking their variable \({{\mathcal {A}}}=0\). In our case the appropriate conditions are

$$\begin{aligned}&W_{N+1}=-\sum _{i=0}^N\Biggl (\frac{i^2+(-1)^i(N+2)^2}{2N^2+6N+5}\biggr )W_i,\\&\quad W_{N+2}=\sum _{i=0}^N\Biggl (\frac{-i^2+(-1)^i(N+1)^2}{2N^2+6N+5}\biggr )W_i. \end{aligned}$$

The conditions on \(W_{N+1}\) and \(W_{N+2}\) may be found by using the relations \(T_n(\pm 1)=(\pm 1)^n,\) \(T^{\prime }_n(\pm 1)=n^2(\pm 1)^{n-1}.\) The domain (0,1) is transformed to the Chebyshev domain (-1,1) by \(z=2{{\hat{z}}}-1\) and then the boundary conditions \(W=0,\,\,z=0\) and \(DW=0,\,\,z=1\) are

$$\begin{aligned}&W_0-W_1+W_2-\cdots +W_{N+1}-W_{N+2}=0,\\&\quad W_1+4W_2+\cdots +(N+1)^2W_{N+1}+(N+2)^2W_{N+2}=0. \end{aligned}$$

The expressions for \(W_{N+1}\) and \(W_{N+2}\) are obtained by elimination from these two equations.

We put \(\sigma =\sigma _r+\sigma _1\), \(\sigma _r,\sigma _1\in {\mathbb {R}}\), and the secant method is employed to locate where \(\sigma _r=0\). We then minimize the value of Ra so found in \(a^2\) to yield the critical values of Ra and a. It is of interest to note that for all the cases we have performed we found \(\sigma _1=0\) at criticality. While we do not have a rigorous proof that \(\sigma \in {\mathbb {R}}\), i.e. that the principle of exchange of stabilties holds, it is certainly found numerically in all the results shown here.

7 Numerical results

Numerical results for critical wavenumbers, a, and Rayleigh numbers, Ra, are presented in tables 1 - 6. The W eigenfunctions associated to the critical values of a and Ra are displayed in Figs. 1, 2, 3, 4.

Tables 1, 2, 3 concentrate on isotropic theory and concern, respectively, the Darcy model with \(W=0\) on the upper surface, the Darcy model with constant pressure on the upper surface, and the Brinkman model for two fixed surfaces. The corresponding eigenfunctions are presented in Figs. 1, 2, 3. For the Brinkman model the results are presented in terms of a Rayleigh number

$$\begin{aligned} Ra=\xi ^5R^2, \end{aligned}$$

so that the depth of the destabilizing layer is reflected in that case.

Table 1 shows that the critical wavenumber increases as \(T_U\) increases, which is equivalent to the aspect ratio of the convection cell (width/depth) for constant depth decreasing. We do not witness counter cells for \(T_U=4,6,\) but there is one counter cell when \(T_U=8,\) but the aspect ratio is less. When \(T_U=12\) we find 3 cells and when \(T_U=16\) there are 4 cells, with the cell width being approximately one third of that when \(T_U=4\). The pattern of cell formation is repeated in Tables 2, 3, for Darcy theory with a constant pressure boundary condition, and Brinkman theory, respectively. As \(T_U\) increases the critical Ra values tend to a constant which is different in the Brinkman case to the two Darcy theories. The value of Ra as \(T_U\) increases is the same for both of the Darcy theories and the eigenfunctions are very similar which suggests that for \(T_U\ge 12\) the upper boundary condition on W is less relevant. The narrowness of the convection cells and greater temperature variation appears to be more influential to cell formation.

The transition value from one cell to two cells varies for each model. For the Darcy theory with \(W=0\) on the upper boundary we find two cells are present when \(T_U=6.5\), whereas with a constant pressure boundary condition \(T_U=6.6\). For the Brinkman theory with \(B=1\) or 10 we find two cells when \(T_U=7.2\). When \(B=0.1\) the relevant value is \(T_U=7.1\) and when \(B=0.01\), \(T_U=6.8\).

The eigenfunctions for Darcy theory with \(W=0\) on the upper surface or for a constant pressure boundary condition are very close for \(T_U=8,12,16\), apart from near to the upper surface \(z=1\). When \(T_U=8\) the strength of the counter cell is 0.0877 for the constant pressure boundary condition whereas it is 0.0718 for \(W=0\) at \(z=1\). When \(T_U=12\) the second cells have the same strength with the strength of the third cell being 1.6 times greater for the constant pressure case. When \(T_U=16\) the strengths of the second and third cells are the same for \(W=0\) or constant pressure boundary conditions, but the fourth cell is approximately 1/3 times stronger for the constant pressure boundary condition.

There is a greater variation of strength in the Brinkman case where the Laplacian term plays a strong role. The second counter cells for \(T_U=12,16\) are much stronger for the Brinkman theory as is witnessed in Fig. 3.

In Table 4 we show critical wavenumber and Rayleigh number values for the Darcy problem with \(T_U=6\) and \(W=0\) on the upper boundary, the corresponding W(z) eigenfunction behaviour is seen in Fig. 4. The effect of anisotropy is observed. This was also investigated by Carr and Putter [20], but for different values. The horizontal isotropy has a strong effect upon critical values and, indeed, upon convection cell structure. As \(\ell ^2\) increases a decreases which means the aspect ratio increases and the cells become wider. Also, for \(\ell ^2=10\) we see a second cell has formed. This is in complete agreement with the observations by Musman [17] for penetrative convection in a layer of pure water, who writes,... “The most important penetration of convective motions takes place in the form of nearly horizontal motions in the lowest part of the stable region, corresponding to the upper part of the principal cell." For \(\ell ^2\) large the horizontal permeability is significantly larger than the vertical one and this will assist horizontal motion and so extra cells will be expected physically for larger values of \(\ell ^2\).

In Table 5 critical Ra and a values are given for the Darcy theories and they are compared with the Brinkman values over a similar \(T_U\) range. The variation of critical wavenumbers and Rayleigh numbers as \(\ell ^2\) changes for the Brinkman theory is noticeable. When \(T_U=6.8\) we see that \(\ell ^2\) has to be very large for a counter cell to form.

The effect of the variation of the Brinkman parameter B is displayed in Table 6. It is noted that the counter cell occurence does not appear to be influenced much by B variation, e.g. for \(T_U=7.1\), \(B=1,10\) indicates only one principal cell, and when \(T_U=7.2\) a counter cell appears for \(B=0.1,1\) and 10. The effect of variation of \(T_U\) for \(B=0.01\) is given and a counter cell is observed when \(T_U=6.8\).

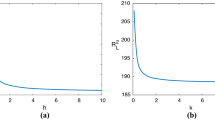
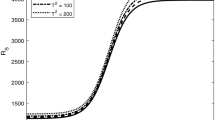
Table 7 shows how the critical Rayleigh number varies with the upper surface temperature \(T_U\) (which is equivalent to varying \(\xi\)) for fixed values of the Brinkman number, 0.1 and 1. Figures 5 and 6 display this variation. The behaviour is similar in each figure although the scale is different. Tables 8, 9, 10 show how the critical Rayleigh number varies with the Brinkman number B for fixed values of \(T_U\) and anisotropy \(\ell ^2\). These results are displayed graphically in Fig. 7. For \(\ell ^2=1\) or 10 we find that the graphs of \(log_{10}\,Ra\) against \(log_{10}\,B\) are almost straight lines, thus displaying nearly linear variation. For \(\ell ^2=100\) where the horizontal permeability is much greater than the vertical one this is not true for small B although as B increases the curves approach a linear relationship. This is understandable since for B small the Darcy term is dominating via the strong horizontal permeability.

8 Conclusions

Penetrative convection in a horizontal layer of water saturated porous material has been studied. The problem is much richer in a porous material than in the pure fluid case since one must consider the appropriate porous medium model, the porous medium may be strongly anisotropic, and if a Brinkman theory is employed the strength of this effect has to be investigated.

We have analysed two porous medium theories, that of Darcy and also that of Brinkman. We have also allowed for different boundary conditions on the velocity on the upper surface of the layer. We have shown that anisotropy and the Brinkman effect may alter the critical wave and Rayleigh numbers substantially, and may also affect the structure of convection cell formation. For the Darcy theory the upper boundary condition of zero vertical velocity or constant pressure is important when the upper temperature is less than 8 \(^{\circ }\)C, but the difference in the effect of the boundary conditions becomes much less when the upper temperature takes the values of \(12~^{\circ }\)C or \(16~^{\circ }\)C.

Table 1 Critical wavenumber, a, critical Rayleigh number, \(Ra=\xi ^3R^2\), number of convection cells (if any, denoted by change of sign in W), for varying upper temperature, \(T_U\). Isotropic Darcy theory with \(W=0\) at \(z=1\)
Full size table
Table 2 Critical wavenumber, a, critical Rayleigh number, \(Ra=\xi ^3R^2\), number of convection cells (if any, denoted by change of sign in W), for varying upper temperature, \(T_U\). Isotropic Darcy theory with \(DW=0\) at \(z=1\)
Full size table
Table 3 Critical wavenumber, a, critical Rayleigh number, \(Ra=\xi ^5R^2\), number of convection cells (if any, denoted by change of sign in W), for varying upper temperature, \(T_U\). Isotropic Brinkman theory with \(W=0\) at \(z=1\)
Full size table
Table 4 Critical wavenumber, a, critical Rayleigh number, \(Ra=\xi ^3R^2\), whether W changes sign in (0, 1), for fixed upper temperature, \(T_U=6\), with varying anisotropy parameter \(\ell ^2\). Darcy theory with \(W=0\) at \(z=1\)
Full size table
Table 5 Critical wavenumber, a, critical Rayleigh number, \(Ra=\xi ^3R^2\), whether W changes sign in (0, 1), for various upper temperatures, with varying anisotropy parameter \(\ell ^2\), for Darcy theory, Darcy theory with constant pressure boundary condition, or Brinkman theory as indicated. For the Darcy theories \(Ra=\xi ^3R^2\), whereas for the Brinkman theory \(Ra=\xi ^5R^2\)
Full size table
Table 6 Critical wavenumber, a, critical Rayleigh number, \(Ra=\xi ^5R^2\), whether W changes sign in (0, 1), for various upper temperatures, with varying Brinkman parameter B
Full size table
Table 7 Critical wavenumber, a, critical Rayleigh number, \(Ra=\xi ^5R^2\), with varying \(T_U\) (alternatively varying \(\xi \equiv 4/T_U\)) for \(B=0.1, 1\). Brinkman theory with \(\ell ^2=1\)
Full size table
Table 8 Critical wavenumber, a, critical Rayleigh number, \(Ra=\xi ^5R^2\), with varying B, \(T_U=8\), (\(\xi =0.5\)). Brinkman theory, with horizontally isotropic Darcy coefficient
Full size table
Table 9 Critical wavenumber, a, critical Rayleigh number, \(Ra=\xi ^5R^2\), with varying B, \(T_U=6\), (\(\xi =0.6667\)). Brinkman theory, with horizontally isotropic Darcy coefficient
Full size table
Table 10 Critical wavenumber, a, critical Rayleigh number, \(Ra=\xi ^5R^2\), with varying B, \(T_U=4\), (\(\xi =1\)). Brinkman theory, with horizontally isotropic Darcy coefficient
Full size table
Fig. 1
figure 1

Graph of W against \(T_U\) for Darcy isotropic theory with \(W=0\) at \(z=1\). The values of \(T_U\) are marked on the graph

Full size image
Fig. 2
figure 2

Graph of W against \(T_U\) for Darcy isotropic theory with \(DW=0\) at \(z=1\). The values of \(T_U\) are marked on the graph

Full size image
Fig. 3
figure 3

Graph of W against \(T_U\) for Brinkman isotropic theory with two fixed surfaces. The values of \(T_U\) are marked on the graph

Full size image
Fig. 4
figure 4

Graph of W against \(\ell ^2\) for Darcy isotropic theory with \(W=0\) at \(z=1\). The upper temperature is fixed at \(T_U=6~^{\circ }\)C. The values of \(\ell ^2\) are 10, 2, 0.5 and 0.1, with \(\ell ^2=1\) being in figure 1

Full size image
Fig. 5
figure 5

Graph of Ra against \(T_U\) for Brinkman isotropic theory with two fixed surfaces. The Brinkman parameter has value \(B=0.1\)

Full size image
Fig. 6
figure 6

Graph of Ra against \(T_U\) for Brinkman isotropic theory with two fixed surfaces. The Brinkman parameter has value \(B=1\)

Full size image
Fig. 7
figure 7

Graph of \(log_{10}\,Ra\) against \(log_{10}\,B\) for Brinkman theory with two fixed surfaces. The solid circle is for \(T_U=8\), (\(\xi =0.5\)), \(\ell ^2=1\), the cross is for \(T_U=6\), (\(\xi =0.6667\)), \(\ell ^2=1\), the open circle is for \(T_U=8\), (\(\xi =0.5\)), \(\ell ^2=10\), the triangle is for \(T_U=4\), (\(\xi =1\)), \(\ell ^2=1\), the open square is for \(T_U=6\), (\(\xi =0.6667\)), \(\ell ^2=100\). the plus sign is for \(T_U=4\), (\(\xi =1\)), \(\ell ^2=100\)

Full size image