1 Introduction

In a pioneering paper Reid and Kajiura [18] investigate the linear interaction between surface wave motion in a fluid layer of finite depth and the motion in an underlying saturated porous medium of infinite depth. The fluid is inviscid, and the flow in the porous medium is governed by Darcy’s law. It is found that the exchange of fluid between the porous layer and the overlying fluid causes the waves to become spatially attenuated.

The present paper takes a new look at this problem, assuming that the porous layer has a finite depth; see also [20]. The main emphasis of the present investigation will be on the mean particle drift in the porous medium. For this purpose, we apply a Lagrangian description of fluid motion in the fluid layer and the porous bed. The novelty here is that the pressure gradient in Darcy’s law becomes nonlinear in the Lagrangian description, yielding a direct wave-induced drift in the porous medium. In particular, for spatially damped waves, we consider the effect of radiation stress [12] at the surface on the mean motion. The Lagrangian mean surface gradient must be balanced by the gradient of the radiation stress in this case; see e.g. Phillips [16] for a discussion of this problem in Eulerian terms. Then, the Lagrangian mean drift in the fluid layer is given by the Stokes drift [19]. In the long-wave approximation, the horizontal mean pressure gradient is continuous into the porous bed. Accordingly, the gradient of the radiation stress component in long waves induces a mean horizontal drift in the porous layer, in addition to the small Stokes drift.

We also point out that the exchange of mass between the upper fluid and the porous medium may cause temporal attenuation of the waves. This follows directly from the dispersion relation (52) in the “Appendix”. Again, through nonlinearity, this leads to a small horizontal Stokes drift in the porous layer, but now damped in time.

The present problem has some interesting parallels to processes in the natural environment. For example, Luthar et al. [13] have found mean currents induced by surface waves in a seagrass meadow. This is of course a more complicated problem, since the fibrous porous matrix is not fixed but is moving in the oscillatory current. A closer similarity to the present problem is the investigation by Webber and Huppert [20, 21], who calculate the wave-induced Stokes drift in corals reefs.

Another important environmental aspect of the present analysis is the application to the transport of microplastics in the porous oceanic bottom layer. Microplastics are defined as plastic fragments less than 5 mm in length. It originates from surface plastic debris and finally ends up at the ocean bottom. In natural pore systems, like coral reefs, the permeability typically is \(K = 5 \times 10^{ - 7} \;{\text{m}}^{2}\) [20, 21]. This corresponds to pore dimensions of order centimeters, and we realize that microplastics at the bottom may penetrate the bottom layer due to the oscillatory surface wave field. When inside the porous bottom layer, these plastic fragments may spread horizontally by the wave-induced Lagrangian mean current.

Apart from reefs and beaches, shallow banks in the open ocean are locations where surface waves may induce oscillatory flow at the ocean bottom. For example, on Spitsbergenbanken in the Barents Sea, the minimum water depths are 26–53 m [2], so the sea bottom is well in reach of long ocean swells. Spitsbergenbanken has a porous bottom layer of depth 5–20 m of loose carbonate material consisting of a mixture of shells, stones and gravel [24]. The permeability is typically \(K = 2.62 \times 10^{ - 7} \;{\text{m}}^{2}\) [14], corresponding to an average grain diameter of about 2 cm. A considerable accumulation of floating debris (mostly plastic) is observed at the nearby Tromsøflaket [3]; see Fig. 1.

Fig. 1
figure 1

Map of the western Barents Sea. NwAC is the Norwegian Atlantic Current

Full size image

This makes Tromsøflaket a potential source of microplastics in the western Barents Sea. The proximity to the shallow Spitsbergenbanken, and the direction of the ocean currents, could lead to the accumulation of microplastics in the porous bottom layer of Spitsbergenbanken. The wave-induced Lagrangian transport would then, depending on the direction of the swell, extend laterally the contaminated region. We discuss this problem in some detail at the end of Sect. 7.

2 Mathematical formulation

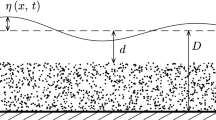
We study surface gravity waves in a horizontal fluid layer of undisturbed depth \(H_{1}\) overlying a fluid-saturated porous layer of thickness \(H_{2}\). The fluid is incompressible and homogeneous in both layers and has density \(\rho\). In the fluid, we neglect the effect of friction, while in the porous layer the motion is governed by Darcy’s law [1]. We take that the \(X\)-axis is horizontal and situated at the interface between the porous layer and the fluid layer, while the \(Z\)-axis is vertical, and positive upwards. The pressure is \(P\), and upper and lower layer variables are denoted by subscripts 1 and 2, respectively. The free surface of the upper layer is given by \(Z_{1} = H_{1} + \eta \left( {X,t} \right)\). Here we assume that the pressure vanishes, i.e. \(P_{1} = 0\). The impermeable bottom of the porous layer is given by \(Z_{2} = - H_{2}\). This configuration is sketched in Fig. 2.

Fig. 2
figure 2

A diagram showing the configuration, with a free surface wave in the upper fluid layer above a porous bed. The floor at \(Z_{2} = - H_{2}\) is impermeable

Full size image

We assume that the surface wave in the upper layer has a wavelength \(\lambda\) that is much larger than the thickness of both layers, i.e. \(\lambda \gg H_{1} ,H_{2}\). Then we can assume that the pressure is hydrostatic in the vertical. Hence, in both layers

$$ P_{Z} /\rho = - g, $$
(1)

where \(g\) is the acceleration due to gravity. Utilizing that the pressure is continuous at the interface between the upper and lower layer, where \(Z_{1} = Z_{2} = \xi \left( {X,t} \right)\), we find by integration in the vertical that

$$ P_{1} /\rho = - gZ_{1} + g\left( {H_{1} + \eta } \right), $$
(2)
$$ P_{2} /\rho = - gZ_{2} + g\left( {H_{1} + \eta } \right). $$
(3)

In the horizontal direction we have for the fluid layer

$$ X_{1tt} = - g\eta_{{X_{1} }} , $$
(4)

where subscripts denote partial differentiation. In the porous medium, using Darcy’s law [1], the momentum equation has the form

$$ (\nu /K_{H} )X_{2t} = - g\eta_{{X_{2} }} , $$
(5)

where \(\nu\) is the kinematic viscosity of the fluid in the pores, and \(K_{H}\) is the horizontal component of the permeability of the porous medium. We note right away that the vertical component of the permeability \(K_{V}\) does not enter the problem because of the shallow-water assumption.

For the mathematical analysis, we apply Lagrangian coordinates. Let a fluid particle \(\left( {a,c} \right)\) initially have coordinates \(\left( {X_{0} ,Z_{0} } \right)\). Its position \(\left( {X,Z} \right)\) at later times will then be a function of \(a,c\) and time \(t\). Velocity components and accelerations are given by \(\left( {X_{t} ,Z_{t} } \right)\) and \(\left( {X_{tt} ,Z_{tt} } \right)\), respectively. It is trivial to express Eqs. (4) and (5) in terms of the independent Lagrangian spatial coordinates \(\left( {a,c} \right)\); see [9]. These equations now become

$$ X_{1tt} X_{1a} = - g\eta_{a} , $$
(6)
$$ (\nu /K_{H} )X_{2t} X_{2a} = - g\eta_{a} . $$
(7)

We note that because of the shallow-water assumption, the horizontal displacements \(X_{1} ,X_{2}\) are not functions of the Lagrangian independent vertical variable \(c\). Furthermore, it is interesting to notice that the governing Eq. (7) in the porous medium becomes nonlinear in the Lagrangian formulation. Even though \(\left( {a,c} \right)\) is not the initial particle position, it is convenient to write the displacements of the form (e.g., Pierson [17])

$$ X_{1,2} = a + x_{1,2} \left( {a,t} \right),\;\;Z_{1,2} = c + z_{1,2} \left( {a,c,t} \right), $$
(8)

where the deviations (\(x_{1,2} ,z_{1,2} )\) can be expanded in series after a small parameter \(\varepsilon\) proportional to the wave amplitude [23]. Equations (6) and (7) can thus be written

$$ x_{1tt} (1 + x_{1a} ) = - g\eta_{a} , $$
(9)
$$ \left( {\nu /K_{H} )x_{2t} (1 + x_{2a} } \right) = - g\eta_{a} . $$
(10)

The conservation of mass (here volume) leads to [9],

$$ J\left( {X,Z} \right) \equiv X_{a} Z_{c} - X_{c} Z_{a} = J\left( {X_{0} ,Z_{0} } \right). $$
(11)

From Eqs. (8), (11) becomes in each layer

$$ x_{ta} + z_{tc} + \left( {x_{a} z_{c} } \right)_{t} - \left( {x_{c} z_{a} } \right)_{t} = 0. $$
(12)

In the Lagrangian formulation, the boundary of the upper layer is given by \(c = H_{1}\). This is a freely moving material surface, along which the pressure must be constant. At the horizontal bottom boundary of the porous bed, given by \(c = - H_{2}\), the vertical velocity must vanish. Particles originally situated at the horizontal separation line between the fluid layer and the porous bed are given by \(c = 0\). After the perturbation by the surface wave, these particles will still be found at \(c = 0\), irrespective of whether they are located in the fluid or in the porous layer. The complicating factor is that the Darcy velocity in the porous medium is defined as an average, which makes the problem of mass and momentum transfer far from trivial; see the comprehensive discussion by Lācis et al. [8]. We here follow the approach in [7, 10], and take that normal component of the velocity and the normal stress (here the pressure) are continuous at the interface, which characterizes a material surface.

Although Eqs. (9) and (10), together with the continuity Eq. (12), are nonlinear, it is seen that the hydrostatic approximation simplifies the problem considerably. In addition, as noted before, only the permeability in the horizontal direction enters the problem. This is an advantage since it appears that the permeability in nature is often anisotropic.

3 The Lagrangian mean drift

The linear problem is trivial, and the details have been deferred to the “Appendix”. Here we consider the nonlinear problem to second order for the Lagrangian mean quantities. The mean is defined by averaging over the wave cycle, and this process is denoted by an over-bar. From Eq. (9), we obtain to second order in the fluid layer

$$ u_{1t}^{\left( L \right)} = - \overline{{\tilde{x}_{1tt} \tilde{x}_{1a } }} - g\overline{\eta }_{a} , $$
(13)

where real parts are used for the linear variables and the Lagrangian mean drift in the fluid is defined as \(u_{1}^{\left( L \right)} = \overline{x}_{1t}\). Longuet-Higgins [11] derived the Stokes drift \(u_{1}^{\left( S \right)}\) to second order in Eulerian variables. In Lagrangian terms it can be written

$$ u_{1}^{\left( S \right)} = \overline{{\tilde{x}_{1} \tilde{x}_{1ta} }} + \overline{{\tilde{z}_{1} \tilde{x}_{1tc} }} = - \overline{{\tilde{x}_{1t} \tilde{x}_{1a} }} - \overline{{\tilde{z}_{1t} \tilde{z}_{1a} }} , $$
(14)

where we in the last expression have utilized that the flow is irrotational, i.e. \(\tilde{x}_{1c} = \tilde{z}_{1a}\). It should be pointed out that for irrotational flow, Eames and McIntyre [5] have given an exact expression for the Stokes drift (not limited to second order in wave steepness).

In the Lagrangian formulation the Stokes drift is generally obtained from the governing equations by allowing for a small viscosity (whatever small, as long as it is non-zero). This singular behavior is discussed in the review [23]. In the present inviscid case, the vorticity vanishes in the fluid layer. By expressing this fact in Lagrangian terms, the Stokes drift can be calculated for irrotational waves [4, 22].

We define the mean quantity \(\overline{Q}\) by

$$ \overline{Q} \equiv - \overline{{\tilde{x}_{1tt} \tilde{x}_{1a } }} - \overline{{\tilde{z}_{1tt} \tilde{z}_{1a} }} . $$
(15)

In the shallow-water approximation, the last term on the right-hand side is negligible, and we notice that \(\overline{Q}\) appears in Eq. (13). Generally, by simple manipulations

$$ \overline{Q} = - \left( {\overline{{\tilde{x}_{1t} \tilde{x}_{1a} }} + \overline{{\tilde{z}_{1t} \tilde{z}_{1a} }} } \right)_{t} + \frac{1}{2}\left( {\overline{{\tilde{x}_{1t}^{2} }} + \overline{{\tilde{z}_{1t}^{2} }} } \right)_{a} . $$
(16)

We note from Eq. (14) that the first term in Eq. (16) is the time derivative of the Stokes drift. The second term is the spatial gradient of the kinetic energy per unit depth and density for long gravity waves. Since we have equal partition of kinetic and potential energy in non-rotating waves, we can write for the total mechanical energy \(E\),

$$ E = \rho H_{1} \left( {\overline{{\tilde{x}_{1t}^{2} }} + \overline{{\tilde{z}_{1t}^{2} }} } \right). $$
(17)

Hence, in Eq. (16),

$$ \overline{Q} = u_{1t}^{\left( S \right)} + \frac{1}{{2\rho H_{1} }}E_{a} . $$
(18)

We finally utilize that wave energy \(E\) and wave mean momentum \(M\) are connected by

$$ E = C_{0} M = C_{0} \rho U_{1}^{\left( S \right)} , $$
(19)

(Phillips [16]). Here \(U_{1}^{\left( S \right)}\) is the vertically integrated Stokes drift (the Stokes flux) in the fluid layer, and \(C_{0} = \omega /k = \left( {gH_{1} } \right)^{1/2}\) is the phase speed (and the group velocity) of long waves. Since Eqs. (18) and (19) also are valid in the long-wave approximation, we obtain by insertion into Eq. (13) that

$$ u_{1t}^{\left( L \right)} = - g\overline{\eta }_{a} + u_{1t}^{\left( S \right)} + \frac{1}{{2H_{1} }}C_{0} U_{1a}^{\left( S \right)} . $$
(20)

This equation for the Lagrangian drift in high-frequency long gravity waves is also found in [23], (Eq. 114), when the effects of viscosity and the Earth’s rotation are disregarded.

In the porous layer, we obtain from Eq. (10) to second order

$$ u_{2}^{\left( L \right)} = - \overline{{\tilde{x}_{2t} \tilde{x}_{2a} }} - gK_{H} \overline{\eta }_{a} /\nu , $$
(21)

where \(u_{2}^{\left( L \right)} = \overline{x}_{2t}\) is the horizontal Lagrangian mean drift in the porous bed. We observe from Eq. (14) that the first term on the right-hand side of Eq. (21) is just the Stokes drift for long waves in the porous bed, and we can write

$$ u_{2}^{\left( L \right)} = u_{2}^{\left( S \right)} - gK_{H} \overline{\eta }_{a} /\nu . $$
(22)

We thus see that the surface mean gradient in the fluid layer yields an additional drift contribution in the porous bed. It will be demonstrated in Sect. 5 that the surface gradient is proportional to the tensor component of radiation stress per unit density in shallow-water waves when the mean flow is steady.

4 Drift in temporally damped waves

When \(\alpha = 0\) in Eq. (42), the drift problem becomes particularly simple. We can then assume that the mean variables do not depend on the horizontal coordinate \(a\). Hence, from Eq. (20) we find

$$ u_{1}^{\left( L \right)} = u_{1}^{\left( S \right)} = \frac{1}{{2H_{1}^{2} }}C_{0} A^{2} e^{ - 2\beta t} , $$
(23)

where we have inserted from the “Appendix” for the real part of the variables to obtain \(u_{1}^{\left( S \right)}\) from Eq. (14). We note that the horizontal Lagrangian mean flow in this case is just the Stokes drift.

In the porous layer Eq. (22) reduces to

$$ u_{2}^{\left( L \right)} = u_{2}^{\left( S \right)} = \frac{1}{{2H_{1}^{2} }}R^{2} C_{0} A^{2} e^{ - 2\beta t} , $$
(24)

where the small parameter \(R\) is defined by Eq. (55). Again, the Lagrangian mean flow in the porous bed equals the Stokes drift. We notice that the Stokes drift here is a factor \(R^{2}\) smaller than the Stokes drift in the fluid layer.

We also remark that since \(\overline{x}_{ta} = 0\) in both layers, we obtain from the continuity Eq. (12) that \(\overline{z}_{tc} = 0\). With a rigid bottom at \(c = - H_{2}\), and continuity of mean velocities at \(c = 0\), this means that \(\overline{z}_{t} = 0\) in both layers. In the next section where we consider spatially damped waves, we shall see that this change and we have vertical mean drift velocities in the porous bed as well as in the fluid layer.

5 Drift in spatially damped waves

For spatially damped waves, i.e., \(\beta = 0\) in Eq. (43), we have that \(\overline{\eta }_{a} \ne 0\). A steady balance in Eq. (20) then requires

$$ g\overline{\eta }_{a} = \frac{1}{{2H_{1} }}C_{0} U_{1a}^{\left( S \right)} . $$
(25)

Following Longuet-Higgins and Stewart [12], we can write the tensor component \(S^{{\left( {22} \right)}}\) of radiation stress per unit density in shallow-water waves along the 1-axis as

$$ S^{{\left( {22} \right)}} = E/\left( {2\rho } \right) = C_{0} U_{1}^{\left( S \right)} /2, $$
(26)

where we have used Eq. (19). Hence, from Eq. (25) we find

$$ g\overline{\eta }_{a} = S_{a}^{{\left( {22} \right)}} /H_{1} . $$
(27)

This means that the mean pressure gradient at the surface due to the presence of spatially damped waves must be balanced by the radiation stress gradient per unit depth in order to achieve steady horizontal mean motion. In fact, this balance must hold also in the case when the wave amplitude varies slowly in time.

Utilizing Eq. (25), we find from Eq. (20) in the upper fluid in the long-wave approximation

$$ u_{1}^{\left( L \right)} = u_{1}^{\left( S \right)} = \frac{1}{{2H_{1}^{2} }}C_{0} A^{2} e^{ - 2\alpha a} $$
(28)

Again, the Lagrangian horizontal mean flow in the fluid layer is just the Stokes drift, exactly as it was for temporally damped waves; see Eq. (23).

Now the Stokes flux becomes

$$ U_{1}^{\left( S \right)} = \int_{0}^{{H_{1} }} {u_{1}^{\left( S \right)} dc} = \frac{1}{{2H_{1} }}C_{0} A^{2} e^{ - 2\alpha a} . $$
(29)

Hence, from Eq. (25) we obtain for the mean surface elevation that

$$ \overline{\eta } = \frac{1}{{4H_{1} }}A^{2} e^{ - 2\alpha a} , $$
(30)

where \(A\) in this case is a slowly varying function of time, as will be demonstrated in Sect. 6.

Using the spatial damping rate given by Eq. (56), we can write Eq. (22) in the porous bed, when we insert from Eq. (25),

$$ u_{2}^{\left( L \right)} = u_{2}^{\left( S \right)} - gK_{H} \overline{\eta }_{a} /\nu = \frac{1}{{4H_{1}^{2} }}C_{0} R^{2} [2 + H_{2} /H_{1} ]A^{2} e^{ - 2\alpha a} . $$
(31)

We remark that the effect of the radiation stress on the horizontal Lagrangian drift in the porous bed (last term in the brackets) will dominate when \(H_{2} > 2H_{1}\).

6 Vertical mean drift for spatially damped waves

Continuity in the porous layer yields \(\overline{x}_{2ta} = - \overline{z}_{2tc}\) from Eq. (12). By integrating in the vertical, and using that \(\overline{z}_{2t} \left( {c = - H_{2} } \right) = 0\), we find

$$ w_{2}^{\left( L \right)} = \frac{1}{{4H_{1}^{3} }}\omega H_{2} R^{3} (2 + H_{2} /H_{1} )\left( {c + H_{2} } \right)A^{2} e^{ - 2\alpha a} . $$
(32)

where \(w_{2}^{\left( L \right)} = \overline{z}_{2t}\) is the vertical Lagrangian mean drift in the porous bed. We note that this is very small.

From Eq. (12) we find in the fluid layer to second order

$$ w_{1c}^{\left( L \right)} = \overline{z}_{1tc} = - u_{1a}^{\left( L \right)} . $$
(33)

Integration in the vertical yields

$$ w_{1}^{\left( L \right)} \left( {c = H_{1} } \right) - w_{1}^{\left( L \right)} \left( {c = 0} \right) = 2\alpha H_{1} u_{1}^{\left( L \right)} . $$
(34)

The kinematic boundary condition is

$$ w_{1}^{\left( L \right)} \left( {c = 0} \right) = w_{2}^{\left( L \right)} \left( {c = 0} \right). $$
(35)

Hence, we have that

$$ w_{1}^{\left( L \right)} \left( {c = H_{1} } \right) = w_{2}^{\left( L \right)} \left( {c = 0} \right) + 2\alpha H_{1} u_{1}^{\left( L \right)} . $$
(36)

From Eq. (32) we note that the first term on the right-hand side of Eq. (36) is of \(O\left( {R^{3} } \right)\) compared to the second term, which is of \(O\left( R \right)\) from Eq. (28). Hence, the first term can be neglected. We may then write

$$ w_{1}^{\left( L \right)} \left( {c = H_{1} } \right) = \overline{\eta }_{t} = 2\alpha H_{1} u_{1}^{\left( L \right)} . $$
(37)

Inserting from Eqs. (28) and (30) into Eq. (37), we find

$$ (A^{2} )_{t} - 4\alpha C_{0} A^{2} = 0. $$
(38)

Accordingly, in the case of spatially damped waves the mean free surface has the form

$$ \overline{\eta } = \frac{1}{{4H_{1} }}A_{0}^{2} e^{{ - 2\alpha \left( {a - 2C_{0} t} \right)}} . $$
(39)

Here \(A_{0}\) is the initial wave amplitude at \(a = 0\), where the surface wave enters our domain. We thus see that the free surface in this case has a small upward motion in addition to the small horizontal attenuation.

7 Discussion and concluding remarks

It is worth noting that if we require a steady position of the free surface, i.e. \(w_{1}^{\left( L \right)} \left( {c = H_{1} } \right) = 0\), this would imply that \(w_{2}^{\left( L \right)} \left( {c = 0} \right) = - 2\alpha H_{1} u_{1}^{\left( L \right)}\) from Eq. (36). However, by integrating the continuity equation in the porous bed, we find \(w_{2}^{\left( L \right)} \left( {c = 0} \right) = 2\alpha H_{2} u_{2}^{\left( L \right)}\) which combines to yield

$$ u_{2}^{\left( L \right)} = - H_{1} u_{1}^{\left( L \right)} /H_{2} . $$
(40)

This means that the volume fluxes for the drift in each layer would be equal in magnitude and oppositely directed. However, this is highly unrealistic. The mean flow in a porous medium must be much smaller than in the fluid above, since the Reynolds number based on the pore diameter must be of order 1 or less for Darcy’s law to be valid [1, 15]. In fact, the vertical drift velocity at the interface between the porous bed and the fluid must depend directly on the pore diameter through the permeability; see Eq. (32). When the pore diameter approaches zero, and hence \(K_{H} \to 0\), the interface becomes impermeable, which requires \(w_{1}^{\left( L \right)} \left( {c = 0} \right) = w_{2}^{\left( L \right)} \left( {c = 0} \right) = 0\). This shows that the free surface position cannot be stationary when we consider drift due to spatially damped waves in this problem.

Assuming that marine microplastic particles are non-inertial and passive, our results in Sect. 5 may be applied to Spitsbergenbanken, which has a lateral dimension of about 100 km; see Fig. 1. We take \(H_{1} = 30\;{\text{m}}\) for the ocean layer, and \(H_{2} = 10\;{\text{m}}\), \(K_{H} = 2.62 \times 10^{ - 7} \;{\text{m}}^{2}\) and \(\nu = 10^{ - 6} \;{\text{m}}^{2} \;{\text{s}}^{ - 1}\) for the porous bed. Furthermore, we consider a long swell of period 16 s (wavelength 400 m) and typical amplitude 1 m, arriving at the bank from the Norwegian Sea. From (28) and (31), this swell will for a period of 24 h cause a net horizontal drift of particles above the bed of about 1200 m. In the porous bed, the corresponding drift distance will be about 15 m. From the spatial damping rate (56) such waves will typically attenuate over a distance of 4 km, so swell due to repeated storm events in the Norwegian Sea will cause accumulation of microplastics at the western part of the bank.

To the authors’ knowledge, the application of a Lagrangian description to flow in porous media is not common. It yields directly the mean particle drift in oscillatory wave motion. Of particular interest is the application of the long-wave approximation, which is relevant for a considerable range of physical and geophysical applications. As pointed out before, a consequence of this approximation is that the vertical component of the permeability of the porous medium does not enter the problem. This simplifies the analysis of the drift in the porous bed considerably. In addition, our results are valid even if the medium is anisotropic.