1 Introduction

The importance of wave-driven flows and their role in mass transport within the world’s oceans has long been recognised on a macroscopic scale, carrying waste and driftwood [25]. One of the key processes which is understood to facilitate this large-scale transport (‘drifting’) is the second-order Stokes drift, a net motion in the direction of wave propagation, first introduced by Stokes [24], arising from the important long-term difference between the Lagrangian and Eulerian velocities of fluid particles undergoing oscillatory motion.

The case of Stokes drift arising from surface gravity waves is well-studied, and a detailed exposition of its derivation can be found, for example, in Phillips [19]. For a fluid particle with initial position \(\varvec{x_0}\) and a Lagrangian velocity field \(\varvec{u_L}\left( \varvec{x_0},\,t\right)\), the particle’s position at time t is

$$\begin{aligned} \varvec{x}\left( t\right) = \varvec{x_0} + \int ^t_0{\varvec{u_L}\left( \varvec{x_0},\,s\right) \,\mathrm {d}s}, \end{aligned}$$
(1)

and the Eulerian velocity \(\varvec{u}\left( \varvec{x},\,t\right)\) is given, upon expansion of a Taylor series, by

$$\begin{aligned} \varvec{u}\left( \varvec{x},\,t\right) = \varvec{u}\left( \varvec{x_0},\,t\right) + \left( \int ^t_0{\varvec{u_L}\left( \varvec{x_0},\,s\right) \,\mathrm {d}s}\right) \cdot \varvec{\nabla u} + \cdots . \end{aligned}$$
(2)

Following the approach of Longuet-Higgins [11], this first-order difference term can be time-averaged over a period of oscillation to give the Stokes drift velocity that we will henceforth denote \(\varvec{u_S}\). Letting \(\left\langle \dots \right\rangle\) denote an average over an oscillation and dropping the subscript from the Lagrangian velocity, we obtain

$$\begin{aligned} \varvec{u_S} = \left\langle \left( \int ^t_0{\varvec{u}\left( \varvec{x_0},\,s\right) \,\mathrm {d}s}\right) \cdot \varvec{\nabla u} \right\rangle . \end{aligned}$$
(3)

In the case of linear water waves on an ocean surface with mean position \(z=0\) and total depth D [described by \(z = A\exp {\left\{ \mathrm {i}\left( kx - \omega t\right) \right\} }\)where the x coordinate is horizontal], [19] shows that the Stokes drift effect is entirely horizontal, with magnitude

$$\begin{aligned} u_S = \frac{\omega k A^2 \cosh {\left[ 2k\left( z+D\right) \right] }}{2\sinh ^2{kD}}, \end{aligned}$$
(4)

which decreases exponentially with depth. However, in many oceanographic contexts, it is not realistic to treat the water as a layer of fixed depth D with an impenetrable boundary at \(z=-D\) – perhaps the simplest example of this is the case of shorelines where the sea overlies a saturated bed of sand, and is known to induce some flow within the sand (as discussed by Phillips [20]). Another such potential extension is to a coral reef underlying the ocean. Unlike the dense sand beds discussed by Phillips, flow between the two layers is of great importance because the reef layer is much more permeable on average. A typical coral reef also has a much deeper vertical extent than the porous sand layer typically modelled, before one reaches an effectively solid rock layer below.

The importance of mass transport into and throughout coral reefs is indisputable. Monismith [17] states the importance of flow throughout the reef in trapping nutrients and plankton, as well as the role of mass transfer in preventing coral bleaching events [18]. Further studies have investigated the effects of such flows on larval accumulation [21] and underlined the importance of vertical flows as well as the purely horizontal effects seen in the absence of a porous layer [8].

Fluid-mechanically, however, existing studies of the hydrodynamics of coral reefs tend to consider the porous layer as a boundary condition, exerting drag on the flow above (see, for example, Rosman and Hench [22]). Monismith [17] uses the model of Longuet-Higgins and Stewart [12] to treat the effect of propagating waves as a body force on the mean flow, and also cites a number of studies on wave-breaking on the faces of reefs. Other studies such as Falter et al. [4] predict the rates of uptake of nutrients across a reef interface, but neglect consideration of slow mean flows through the reef. However, on smaller scales, there has not, to the present authors’ knowledge, been any studies on Stokes drift within the coral reef itself, and how the damping effect of this porous layer affects the drift velocities both above and within, aside from the model discussed here and first mentioned in [27].

Other transport processes involving coral reefs have been discussed in the literature, with Lowe et al. [13] determining that the breaking of waves, inducing currents of the order of 2 cm s\(^{-1}\), is a dominant effect in determining the currents above reefs in Kaneohe Bay, Hawaii. It is noted in that article that the currents induced by such effects are weak in reefs with a gentle slope, where effects of radiation stress through wave-breaking (‘set-up and set-down’) are small.

In this article, we will describe a two-layer model, coupling potential inviscid theory (as first treated in [24]) above a viscously-dominated porous layer, where the flow is governed by Darcy’s law [20], to derive not only expressions for how incident waves are damped by the presence of a porous layer, but also analytical expressions for the Stokes drift velocities that result. These (second order) drift velocities are different from the flow fields evaluated previously, as by Liu [10], Gu and Wang [5], Lowe et al. [15] and Luhar et al. [16]. We find that the difference between Eulerian and Lagrangian velocities gives rise not just to a horizontal drift effect, but also to the vertical drifts observed in the field by Koehl et al. [8], and offer quantitative explanations for this behaviour in terms of the damping of the waves. Finally, we discuss the applicability of the model to complicated real-world coral reefs, and compare the predictions of our model with measurements made in the field.

2 A two-layer model for a waves over porous media

We consider a layer of water of total depth D bounded below by an impenetrable floor at \(z=-D\). This lower boundary directly underlies a saturated porous medium, of permeability \(\varPi \left( z\right)\), which occupies the space between \(z=-D\) and \(z=-d\). Such a configuration, with surface waves \(z=\eta \left( x,\,t\right)\), is shown in Fig. 1. In the case \(d \rightarrow D\) or \(\varPi \rightarrow \infty\), we recover the classical result derived by Stokes, an example of which is shown in Eq. (4), which will later serve to provide a check on our results.

Fig. 1
figure 1

A diagram showing the two-layer configuration under consideration, with a porous medium overlying an impermeable bottom boundary

Full size image

2.1 Flow above the porous layer

Above the porous layer, we follow [24] in letting the fluid velocity be described by a velocity potential \(\phi\), such that \(\varvec{u} = \varvec{\nabla }\phi\). Incompressibility then imposes that \(\nabla ^2 \phi = 0\), which is to be solved in \(z > -d\) subject to boundary conditions which we will determine.

We start by making the usual assumption that

$$\begin{aligned} \eta {\left( x,\,t\right) } = \mathrm {Re}\left[ A e^{\mathrm {i}\left( kx -\omega t\right) }\right] , \end{aligned}$$
(5)

where the wavenumber k may be complex, to allow for damping effects, which we will later see are key to describing the novel internal vertical drifts driven by horizontal wave motion at the surface. At the free surface \(z=\eta \left( x,\,t\right)\), the dynamic boundary condition indicates

$$\begin{aligned} \frac{\partial \phi }{\partial z} =\frac{\partial \eta }{\partial t} + \frac{\partial \phi }{\partial x}\frac{\partial \eta }{\partial x}, \end{aligned}$$
(6)

which, making the assumptions of linear theory, can be linearised to give \(\partial \phi / \partial z = \partial \eta / \partial t\) at \(z=0\). Furthermore, we can impose a kinematic boundary condition arising from the Bernoulli equation for unsteady potential flow (see, for example, Batchelor [1]), such that at \(z=\eta \left( x,\,t\right)\),

$$\begin{aligned} \rho \frac{\partial \phi }{\partial t} + \frac{\rho }{2}\left| \varvec{\nabla }\phi \right| ^2 + \rho g \eta = f\left( t\right) , \end{aligned}$$
(7)

for f an arbitrary function of time. Without loss of generality, this \(f\left( t\right)\) can be set to equal zero, absorbing constants, and so the linearised boundary condition becomes

$$\begin{aligned} \frac{\partial \phi }{\partial t} + g \eta = 0. \end{aligned}$$
(8)

These conditions imply that \(\phi\) must have the same form of x- and t-dependence as \(\eta \left( x,\,t\right)\), such that

$$\begin{aligned} \phi \left( x,\,z,t\right) = \tilde{\phi }\left( z\right) e^{\mathrm {i}\left( kx -\omega t\right) }, \end{aligned}$$
(9)

where the real part is implicit (henceforth we will always make this assumption). We can then solve Laplace’s equation for \(\phi\) with this assumed form, something which allows us to determine \(\tilde{\phi }\) up to constants to be determined. Thence,

$$\begin{aligned} \phi \left( x,\,z,t\right) = C_1 \cosh {\left( kz + C_2\right) }e^{\mathrm {i}\left( kx -\omega t\right) }, \end{aligned}$$
(10)

and the linearised form of Eq. (6) shows that

$$\begin{aligned} k C_1 \sinh {C_2} = -\mathrm {i}\omega A. \end{aligned}$$
(11)

The linearised kinematic boundary condition provides a second relation between the constants \(C_1\) and \(C_2\), namely that

$$\begin{aligned} \mathrm {i} \omega C_1\cosh {C_2} = gA. \end{aligned}$$
(12)

2.2 Flow within the porous layer

The modelling of flow within porous layers is based on the well-documented use of Darcy’s law (Phillips [20]), relating the volumetric flux to pressure gradients within the fluid. For a porous medium with isotropic permeability \(\varPi \left( z\right)\), this flux \(\varvec{q}\) is given by

$$\begin{aligned} \varvec{q} = -\frac{\varPi \left( z\right) }{\mu }\varvec{\nabla }p, \end{aligned}$$
(13)

where p is the pressure field within the porous medium and \(\mu\) is the dynamic viscosity. In order to enable matching with the oscillatory pressure field above the porous medium, we postulate that this pressure field must take the form

$$\begin{aligned} p\left( x,\,z,\,t\right) = \tilde{p}\left( z\right) e^{\mathrm {i}\left( kx -\omega t\right) } + C_3, \end{aligned}$$
(14)

for constant \(C_3\) and a function \(\tilde{p}\left( z\right)\) to be determined. Because we consider incompressible flow, and the matrix of the porous layer is fixed, \(\varvec{\nabla }\cdot \varvec{q} = 0\), so \(\nabla ^2 p = 0\). Further imposing the condition of zero vertical flux across the impermeable boundary at \(z=-D\), the pressure field must take the form

$$\begin{aligned} p\left( x,\,z,\,t\right) = C_3 + C_4 \cosh {\left[ k\left( z+D\right) \right] }e^{\mathrm {i}\left( kx -\omega t\right) }. \end{aligned}$$
(15)

Therefore, if \(\varvec{q} = \left( u,\,v\right)\),

$$\begin{aligned} u\left( x,\,z,\,t\right)&= - \left[ \mathrm {i} k \varPi \left( z\right) C_4/\mu \right] \cosh {\left[ k\left( z+D\right) \right] }e^{\mathrm {i}\left( kx -\omega t\right) }, \end{aligned}$$
(16a)
$$\begin{aligned} v\left( x,\,z,\,t\right)&= -\left[ k \varPi \left( z\right) C_4/\mu \right] \sinh {\left[ k\left( z+D\right) \right] }e^{\mathrm {i}\left( kx -\omega t\right) }. \end{aligned}$$
(16b)

2.3 Matching the two layers

Having defined our model, we are left with four constants \(C_1\), \(C_2\), \(C_3\) and \(C_4\) to be determined. We combine Eqs. (11) and (12) to find that

$$\begin{aligned} \omega ^2 = g k \tanh {C_2}, \end{aligned}$$
(17)

which, as expected, gives the well-known dispersion relation \(\omega ^2 = gk \tanh {kD}\) [9] in the case of no porous layer (fixing \(C_2 = kD\) to ensure zero vertical velocity at the lower boundary).

Matching of the inviscid flow above the porous layer and the viscously-dominated Darcy flow within is a non-trivial task. The velocities above the porous layer have a different intrinsic meaning to the spatially-averaged volume fluxes within the porous layer, and it is not immediately clear whether considering the classical matching conditions of velocities and pressures is a valid approach. It is, however, clear that mass conservation requires vertical velocities to match at the interface between the two flow regimes, allowing us to derive the matching condition

$$\begin{aligned} - \varPi \left( -d\right) C_4 \sinh {\left[ k\left( D-d\right) \right] } = \mu C_1 \sinh {\left( C_2 - kd\right) }. \end{aligned}$$
(18)

It is clear that we should not match tangential velocities at the interface, however. Beavers and Joseph [3] remark that there is a ‘slip’ discontinuity between layers, and the forces exerted by the reef on the flow could complicate matters, for example by imposing shear stresses (as is the case in many existing models such as Rosman and Hench [22]). Indeed, shear layers of varying thicknesses (measured in Hawai’i by Shashar et al. [23]) are found at the interface between reefs and the ocean above, implying that continuity of horizontal velocities is not an appropriate condition to impose. The model in [3] does, however, also require continuity of pressure at the interface, and the linearisied Navier–Stokes equations suggest, in \(z\ge -d\),

$$\begin{aligned} \rho \frac{\partial \varvec{u}}{\partial t} = -\varvec{\nabla }p - \rho g \varvec{\hat{z}} \quad \text {so} \quad \mathrm {i}\rho \omega \varvec{\nabla } \phi = \varvec{\nabla } p + \rho g \varvec{\hat{z}}. \end{aligned}$$
(19)

Then, if we take the (constant) pressure above the surface waves to be zero,

$$\begin{aligned} p = \rho g d + \mathrm {i}\rho \omega C_1 \cosh {\left( C_2 - kd\right) } e^{\mathrm {i}\left( kx -\omega t\right) } \quad \text {at}~ z=-d. \end{aligned}$$
(20)

Hence, matching this with the expression in (15), it is seen that \(C_3 = \rho g d\) and

$$\begin{aligned} C_4 \cosh {\left[ k\left( D-d\right) \right] } = \mathrm {i}\rho \omega C_1 \cosh {\left( C_2 - kd\right) }. \end{aligned}$$
(21)

2.3.1 Deriving the dispersion relation

This condition now means that the solution can be fully determined. Starting from (17), which determines \(C_2\), we can also determine \(C_1\) from (12), namely that

$$\begin{aligned} C_1 = -\frac{\mathrm {i}A}{\omega k}\sqrt{\left( gk\right) ^2 - \omega ^4} \quad \text {and} \quad C_2 = \mathrm {arctanh}\left( \omega ^2/gk\right) . \end{aligned}$$
(22)

It is then straightforward to determine the value of \(C_4\) using either (18) or (21). This gives

$$\begin{aligned} C_4 = -\frac{\mathrm {i} \mu A \sinh {\left[ \mathrm {arctanh}\left( \frac{\omega ^2}{gk}\right) - kd\right] }}{\omega k \varPi \left( -d\right) \sinh {\left[ k\left( D-d\right) \right] }} \sqrt{\left( gk\right) ^2 - \omega ^4}. \end{aligned}$$
(23)

Perhaps of more interest, however, (18) and (21) can be divided to give

$$\begin{aligned} \mathrm {i} \rho \omega \varPi _I\tanh {\left[ k\left( D-d\right) \right] } = -\mu \tanh {\left[ \mathrm {arctanh}\left( \frac{\omega ^2}{gk}\right) - kd\right] }, \end{aligned}$$
(24)

where \(\varPi _I = \varPi \left( -d\right)\) is the interfacial permeability. This is the dispersion relation linking the frequency \(\omega\) of surface waves to their complex wavenumber k for the situation under consideration. It is important to note from the outset that only the value of permeability at the porous layer interface, \(\varPi _I\), is of any importance in this relation; this is a consequence of the fact that there is no stress matching condition and instead all matching conditions depend only on values at the boundary.

2.4 Special cases of the dispersion relation

Define the dimensionless constant \(J = \rho \omega \varPi \left( -d\right) / \mu\) such that the dispersion relation of Eq. (24) can be written

$$\begin{aligned} J \tanh {\left[ k\left( D-d\right) \right] } = \mathrm {i} \tanh {\left[ \mathrm {arctanh}\left( \frac{\omega ^2}{gk}\right) - kd\right] }. \end{aligned}$$
(25)

Owing to the nature of this dispersion relation, it will usually need to be solved numerically for k given \(\omega\) and the parameters of the model. To investigate the properties of the relation, define

$$\begin{aligned} f\left( k,\,\omega ;\,J,\,D,\,d,\,g\right) = J \tanh {\left[ k\left( D-d\right) \right] } - \mathrm {i} \tanh {\left[ \mathrm {arctanh}\left( \frac{\omega ^2}{gk}\right) - kd\right] }, \end{aligned}$$
(26)

such that, for fixed \(\omega\), zeros of f correspond to suitable values of the wavenumber k. Making the assumption that waves propagate in the positive x-direction and are therefore damped in this direction (i.e. their amplitude decreases as x increases), we will only seek (the physically-relevant) solutions with \(\mathrm {Re}\left( k\right) > 0\) and \(\mathrm {Im}\left( k\right) > 0\).

An initial investigation shows that it is possible to find multiple solutions for k that satisfy this assumption, even with all of the other parameters fixed. Figure 2 shows that there exists one (mostly) propagating solution with a small imaginary part and larger real part, which decays slowly, in addition to one highly evanescent solution with a very small real part and larger imaginary part. For our purposes, we will consider the propagating solutions because we would expect the highly-evanescent solutions to decay quickly as they are damped over the reef.

Fig. 2
figure 2

Contour plots of the function \(\left| f\left( k,\,\omega ;\,1,\,1,\,1/2,\,10\right) \right|\), with f defined by Eq. (26), showing two solutions for k in each case. Blue represents small magnitudes

Full size image

2.4.1 Limit of no porous layer

As mentioned above, one would expect that the classical dispersion relation \(\omega ^2 = gk \tanh {kd}\) [9] would be recovered in the limit of no porous layer. Indeed, taking either \(d \rightarrow D\) or \(\varPi \left( -d\right) = 0\) (i.e. setting the porous layer interface to have zero permeability) sets the left-hand side of Eq. (25) to zero, such that

$$\begin{aligned} \tanh {\left[ \mathrm {arctanh}\left( \frac{\omega ^2}{gk}\right) - kd\right] } = 0 \Rightarrow \omega ^2 = gk \tanh {kd}. \end{aligned}$$
(27)

2.4.2 Limit of small frequencies

In the case of low-frequency waves, we would expect k to be small, giving longer wavelengths. Using the addition formula for \(\tanh\),

$$\begin{aligned} J \tanh {\left[ k\left( D-d\right) \right] } = \mathrm {i} \frac{\omega ^2 / gk - \tanh {\left( kd\right) }}{1 - \omega ^2 \tanh {\left( kd\right) }/gk}, \end{aligned}$$
(28)

and thus, in the limit of small kd,

$$\begin{aligned} k \approx \left( \frac{\mathrm {i}\omega ^2}{J\left( D-d\right) (g - d\omega ^2) + \mathrm {i}gd}\right) ^{1/2}. \end{aligned}$$
(29)

This approximation is shown in Fig. 3.

2.4.3 Limit of high frequencies

Conversely, we would expect \(k \rightarrow \infty\) as \(\omega \rightarrow \infty\) and therefore, again starting from Eq. (28),

$$\begin{aligned} J \approx \mathrm {i}\left( \omega ^2 - gk\right) /\left( gk - \omega ^2\right) , \end{aligned}$$
(30)

but because J is real, \(\omega ^2 = gk\), or, alternatively, \(k = \omega ^2 / g\). Note here that k is real in this limit, so the asymptotic expression for \(\mathrm {Im}\left( k\right)\) is simply zero to leading order. Considering the next order, as detailed in the “Appendix”, we obtain the asymptotic expansion

$$\begin{aligned} \mathrm {Im}\left( k\right) \approx \frac{2 J \omega ^2}{g\left( 1+J^2\right) }\left( E_1 + E_2\right) , \end{aligned}$$
(31)

where \(E_1 = e^{-2 \omega ^2 d / g}\) and \(E_2 = e^{-2\omega ^2 \left( D-d\right) / g}\). As above in the low-frequency case, this approximation is compared to the full numerical result in Fig. 3.

Fig. 3
figure 3

Plots of the real and imaginary parts of k as functions of \(\omega\) in the case \(S=1\), \(D=1\,\mathrm {m}\), \(d=0.5\,\mathrm {m}\) and \(g=10\,\mathrm {ms}^{-2}\). The numerical approximations of (29) and (30) are plotted in red, showing close comparison. The inset on the first figure shows the exchange in validity between the large-\(\omega\) and small-\(\omega\) limits

Full size image

3 Stokes drift velocities

Following the approach detailed in [19], given the expressions for velocities both above and within the porous layer, it is possible to calculate the Stokes drift velocities in these layers. Provided that particles do not cross between these two layers, a complication which will be later discussed in more detail, this gives an indication of the wave-driven fluid velocities.

3.1 Above the porous layer

Given the expression of (10) for the velocity potential, it is a straightforward task to calculate Stokes drift velocities following the mechanism outlined in [19] [Eq. (3)]. Using the result that \(\left\langle \mathrm {Re}\left[ a e^{\mathrm {i}\omega t}\right] \mathrm {Re}\left[ b e^{\mathrm {i}\omega t} + c\right] \right\rangle = \frac{1}{2} \mathrm {Re}\left[ a\bar{b}\right]\), where a, b and c are time-independent complex numbers, we can find the Stokes drift velocity above the porous layer to be

$$\begin{aligned} \varvec{u_S} = \frac{\left| C_1\right| ^2 \left| k\right| ^2 e^{-2 k_I x}}{2 \omega } \Big \lbrace k_R \cosh {\left( 2 \mathrm {Re}\left[ kz+C_2\right] \right) }\varvec{\hat{x}} + k_I \sinh {\left( 2 \mathrm {Re}\left[ kz+C_2\right] \right) }\varvec{\hat{z}}\Big \rbrace , \end{aligned}$$
(32)

where \(\mathrm {Re}\left[ k\right] = k_R\) and \(\mathrm {Im}\left[ k\right] = k_I\) for brevity.

3.2 Within the porous layer

Analogously within the porous medium, recall that

$$\begin{aligned} \varvec{q} = -\mathrm {Re}\Bigg [\frac{k \varPi \left( z\right) C_4 e^{\mathrm {i}\left( kx-\omega t\right) }}{\mu }\Big \lbrace \mathrm {i}\cosh {\left[ k\left( z+D\right) \right] }\varvec{\hat{x}} + \sinh {\left[ k\left( z+D\right) \right] }\varvec{\hat{z}} \Big \rbrace \Bigg ] \end{aligned}$$
(33)

is an analogue for velocity \(\varvec{u}\). Thus, in exactly the same way as above, we can write the two components \(\varvec{u_S} = \left( u_S, v_S\right)\) in the form

$$\begin{aligned} u_S = \frac{\left| C_4\right| ^2 \left| k\right| ^2 \varPi e^{-2 k_I x}}{2 \mu ^2 \omega } \Big \lbrace \varPi k_R \cosh {\left( 2 \mathrm {Re}\left[ k\left( z+D\right) \right] \right) } + \frac{\varPi '}{2} \sinh {\left( 2\mathrm {Re}\left[ k\left( z+D\right) \right] \right) } \Big \rbrace \end{aligned}$$
(34a)

and

$$\begin{aligned} v_S = \frac{\left| C_4\right| ^2 \left| k\right| ^2 \varPi ^2 e^{-2 k_I x}}{2 \mu ^2 \omega } k_I \sinh {\left( 2 \mathrm {Re}\left[ k\left( z+D\right) \right] \right) }, \end{aligned}$$
(34b)

where again \(k = k_R + \mathrm {i}k_I\) and \(\varPi = \varPi \left( z\right)\) with \(\varPi ' = \partial \varPi / \partial z\).

3.3 Interpretation of the results

Parallels can be seen between the expressions of Eqs. (32) and (34) and the classical expressions first derived by [24]. In both cases, the magnitudes of the drift velocities are second order and scale like the square of the amplitude of fluid motion, with the damping effect of the porous layer manifested in the \(e^{-2\mathrm {Im}\left[ k\right] x}\) term. This damping can be seen very clearly in Fig. 4, which considers waves with amplitude \(0.05\,\mathrm {m}\) at position \(x=0\).

Fig. 4
figure 4

Horizontal Stokes drift velocity profiles for the model with parameters detailed in Table 1 measured at different horizontal positions. The damping action of the porous layer results in a reduction in wave amplitude, in turn reducing the magnitude of drift velocities

Full size image

It is also of interest to consider the case where \(d\rightarrow D\) and there is no porous layer. As was seen in the case where there is no porous layer, the dispersion relation becomes \(\omega ^2 = gk \tanh {kd}\) and thus \(C_2 = kd\). This means that

$$\begin{aligned} C_1 = -\mathrm {i}gA/\left( \omega \cosh {kd}\right) \; \text {and} \; C_4 = \rho gA/\left( \cosh {kd}\right) . \end{aligned}$$
(35)

Then, above the porous layer, Eq. (32) becomes

$$\begin{aligned} \varvec{u_S} = \frac{g^2 A^2 k^3}{2 \omega ^3 \cosh ^2{kd}} \cosh {\left[ 2k\left( z+d\right) \right] }, \end{aligned}$$
(36)

which simplifies precisely to the form of (4) in this limit, as would be expected.

4 Stokes drift in coral reefs

It becomes useful at this stage to introduce representative dimensional paramters—dependence on properties of the porous layer such as the permeability and its geometry cannot be encapsulated in a simple dimensionless parameter like J above. As discussed in the introduction, an understanding of the hydrodynamics of coral reefs is of great importance, and there is a wealth of data available on their structure and composition. Though this can vary widely, we choose the well-documented reefs in Kaneohe Bay, Hawai’i as a basis for this modelling, which are primarily comprised of Porites compressa coral [6].

On the assumption that the kinematic viscosity of water is \(\nu \approx 10^{-6}\,\mathrm {m}^2\,\mathrm{s}^{-1}\) and the flow within the reef has characteristic velocity scale \(U = 10^{-2}\,\mathrm {ms}^{-1}\) [6], the Reynolds number of the flow in the porous layer is

$$\begin{aligned} Re = \frac{Ul}{\nu } \approx 10^{4} l, \end{aligned}$$
(37)

where l is a characteristic length scale for the problem—the grain diameter of the reef. This lengthscale refers to the mean size of the ‘gaps’ in heads of coral through which the water flows—in denser corals these can be very small pore-sized gaps (Wang et al. [26]). Provided this diameter is of the order \(10^{-3}\,\mathrm {m}\) (i.e. millimetre-scale), we can expect Darcy’s law to be a valid description of the flow therein (Bear [2] states that Darcy’s law is a valid model for \(Re \lesssim 10\)). There will be some reefs where turbulence is an important effect and the pore size is too large for such modelling to be valid (see, for example, Lowe et al. [14]) but we would also expect this model to be valid for denser reef structures, such as sorted sands, gravels or shells. Of course, such a model will not hold if the flow is turbulent, since Darcy’s law rests on the assumption of laminar flow—and then other phenomena such as Taylor dispersion would be of importance. However, the reefs on Kaneohe Bay are especially simple to model, given that Koehl and Hadfield [6] remark that waves break on the outside of the reef and then propagate steadily, and uniformly, over the water surface, satisfying our modelling assumptions. For the sake of simplicity, we start by modelling reefs where the permeability is a constant \(\varPi \left( z\right) = \varPi _0\). The parameter values which are used in this model are summarised in Table 1.

Table 1 Representative values of different parameters for the reef and the water flowing through it, determined through Koehl and Hadfield [6] and private communication with Koehl (2019)
Full size table

4.1 Stokes drift velocities

Plotting the paths of fluid particles undergoing oscillatory motion in this model, as shown in Fig. 5, we can see not only a drift effect in the positive x-direction (i.e. in the direction of wave propagation), as would be expected from Stokes’ theory, but also a new vertical drift. This drift can be seen to arise from the damping of the waves, as the amplitude of vertical motion decreases with horizontal distance.

As an individual fluid ‘parcel’ moves forwards, it also moves downwards, before the direction of its horizontal velocity changes and it moves backwards, behind its original position. At this point, the parcel is moving upwards, but the magnitude of this upwards velocity is greater than that of the downward section of motion, owing to the damped amplitude. Therefore, over an entire period of motion, the fluid parcel not only experiences a net drift in the horizontal direction, but also a net upwards vertical drift.

Such a simplified model, however, breaks down close to the boundary between the reef and the fluid overlying it. An example of this behaviour is shown in the second plot of fFig. 5, indicating that the expressions of Eqs. (32) and (34) are no longer valid, and a direct numerical approach is required. It is for this reason that we also see discontinuities in the drift velocities—we would expect our model to be deficient close to the boundary due to the presence of (comparatively) thin shear layers [23], the properties of which will differ widely between reefs, the existence of which motivates the lack of a velocity continuity condition in the model. In the case where these equations are valid, however, Fig. 6 shows representative horizontal and vertical drift velocities, of the order of a few millimetres per second, largely in agreement with the mean (drifting) velocities measured by Koehl and Hadfield [6].

Fig. 5
figure 5

Paths of individual fluid ‘parcels’ over 4 wave periods (i.e. from \(t=0\) to \(t=8\pi /\omega\)), showing the net drift in their position, calculated by integration of Eulerian fluid velocities. Starting positions are marked in green and final positions in red—note the complicated paths taken by fluid parcels near the interface when they cross between regions; the horizontal drift is backwards in these cases and the behaviour quickly becomes somewhat chaotic. The reef region is shaded in both plots, with the water above given a white background

Full size image

In addition to these field measurements, we can consult the existing literature on nutrient uptake across the ocean-reef interface (for example [4]), also measured at Kaneohe Bay, where it was estimated that phosphate, ammonium and nitrate were all transported vertically into the reef at rates around 10 m per day. With our model predicting vertical velocities of the order of \(10^{-3}\) m per second, this produces daily drifts of the order of \(10^{1}{-}10^{2}\) m per day, not more than one order of magnitude difference with these other models.

Fig. 6
figure 6

Plots of the horizontal and vertical Stokes drift velocities in the model with parameter values shown in Table 1

Full size image

4.2 Varying reef depths

It is apparent that changing the depth of the porous layer underlying the water will affect the amount by which waves are damped. Considering the model of Table 1, but varying the parameter d, it can be seen that the imaginary part of the wavenumber varies too, as shown in Table 2.

Table 2 Wavenumbers k for different depths of coral reef in a shallow sea of total depth \(D=2\,\mathrm {m}\), with all other parameters as in Table 1
Full size table

This results in different drift velocities—two cases where \(d=0.5\,\mathrm {m}\) and \(d=1.9\,\mathrm {m}\) with all other parameters the same are shown in Fig. 7. It may appear counterintuitive that the presence of the reef increases horizontal drift velocities relative to the case with no porous layer, since the porous medium has a damping effect on waves and absorbs their energy. However, increasing the damping effect of the waves also leads to a less circular fluid path as parcels of fluid oscillate with wave motion, exaggerating any Stokes drift effect. These two competing factors imply that there is not a direct relationship between d and drift velocity.

Fig. 7
figure 7

Plots of the horizontal and vertical Stokes drift velocities in the model with parameter values shown in Table 1, for two different values of the parameter d. The contrasting case of no porous layer is shown as a dashed line (there is no vertical drift with no porous layer)

Full size image

4.3 Varying permeabilities

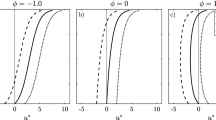
If the permeability \(\varPi _0\) of the coral reef layer is increased, this will increase the magnitude of the velocities within the reef itself, but this will also affect the calculated value of k—changing the permeability affects the amount of damping that the reef has on the surface waves. There are two competing effects here: the increase in flow velocities from a greater permeability and the decrease due to wave damping.

The plots in Fig. 8 show that increasing the reef permeability increases the drift velocities within the reef layer itself, since the velocities there are greater, but decreases the drift velocities above the reef, since the wave damping effect wins out here. This is the case both for the vertical and horizontal velocity components.

Fig. 8
figure 8

Plots of the horizontal and vertical Stokes drift velocities in the model with parameter values shown in Table 1, but allowing for the parameter \(\varPi _0\) to vary. Note the opposite effect an increase in the permeability has above and below the reef

Full size image

4.4 Role of spatial variation in permeability

Webber and Huppert [27] discuss in more detail the effect of taking the permeability to be a function of depth \(\varPi \left( z\right)\) as opposed to a constant \(\varPi _0\). Such a consideration is important physically, with marine reefs decreasing in permeability with depth. The dispersion relation is local, however, only dependent on the value of the permeability at the interface, and therefore any non-uniform permeability structure only manifests itself in the flows within the reef.

The expressions for the Stokes drift velocity within the porous layer, Eq. (34), show that permeability variations add an additional term in the horizontal drift, proportional to \(\varPi '\left( z\right)\), when compared to expressions with constant \(\varPi\). If we assume that the characteristic lengthscale of permeability variations is L,

$$\begin{aligned} \frac{\frac{1}{2}\varPi ' \sinh {\left( 2\mathrm {Re}\left[ k\left( z+D\right) \right] \right) }}{\varPi \, \mathrm {Re}\left[ k\right] \cosh {\left( 2\mathrm {Re}\left[ k\left( z+D\right) \right] \right) }} \sim \frac{ \tanh {\left( 2\mathrm {Re}\left[ k\left( z+D\right) \right] \right) }}{L\mathrm {Re}\left[ k\right] } \end{aligned}$$
(38)

and so we can only reasonably neglect this term in cases where the permeability changes are slight or the waves are propagating at especially large or small wavenumbers.

A second application of a model incorporating spatial variation in permeability is when an algal turf overlies a coral reef (as discussed in more depth in [27]). In this case, the reef is covered with a thin layer of algal material, typically of a lower permeability than the bulk of the reef itself, the presence of which is seen in the field to have dramatic effects on the flow within the reef, with subsequent effects on marine life within (Koehl et al. [7]). By modelling the permeability field of the coral reef as two sandwiched layers of different constant permeability, we can therefore model the effect of varying the permeability or thickness of algal turf without resorting to a more complicated three-phase model.

5 Conclusion

It has been shown that an analysis of surface gravity waves can be extended to a system where the fluid sits atop a saturated porous bed, incorporating the damping effect of this bed on the fluid motion. By matching a viscously-dominated Darcy flow law in this lower porous layer with inviscid potential flow above, a complete description of flow both above and within the bed can be derived, from which one can derive Stokes drift velocities in both layers.

In addition to the well-known horizontal drift in the direction of wave propagation first derived in [24], it is seen that the damping of the waves on the surface leads to a second-order vertical drift in both layers. Though this model does not apply for fluid that crosses the boundary between the porous medium and the overlying water, in both regions the calculated drifts match actual measurements made by Koehl and Hadfield [6] in a Hawaiian coral reef in order of magnitude. Further field measurements in different reef locations around the world are awaited to both confirm the generality of this result and provide more accurate parameter values for modelling.

This different, and possibly simplified, model can be extended to consider permeable layers where the permeability varies with depth, as explored in more detail in Webber and Huppert [27], and could then be further extended to consider other features of ‘real-world’ coral reefs, including variable topographies and sloping sea floors, as well as incorporating existing work on the breaking of waves on reef lagoons and its effects on mass transport [17]. However, we would expect to still see this novel vertical drift effect as a major contributor to mass transport in reefs.