Are the income and price elasticities of economy-wide electricity demand in middle-income countries time-varying? Evidence from panels and individual countries

Abstract

Understanding the income/GDP and price elasticities of electricity demand is important for forecasting demand and evaluating the potential impact of energy/climate policies. Yet, there has been little work on this topic that focuses on countries outside the OECD. We employ a new database of cross-country real economy-wide electricity prices and apply a set of panel-based and time-series-based methods that together account for temporal heterogeneity and cross-sectional heterogeneity on a group of middle-income/rapidly growing countries. Both our panel results and the eight individual country analyses that applied structural time series modeling determined that both the income and price elasticities of economy-wide electricity demand are stable/effectively constant over time. In addition, our results suggested that the income elasticity of economy-wide electricity demand for these middle-income countries was on average 0.8. The price elasticity—which displayed more movement over time (at least in percentage terms)—was on average -0.09. The results of essentially constant income and price elasticities is analogous to recent findings focused on economy-wide energy demand in middle-income countries.

1 Introduction

Increasing the share of energy services that are delivered via electricity is one of two challenges/strategies for mitigating climate change (decarbonizing electricity generation being the other). Thus, the shift towards electricity consumption will be a dominant feature in future world energy systems. Nowhere has this trend been more rapid than in the middle-income economies. Not only is per-capita economic growth faster in middle-income economies than within the (high-income) OECD, but middle-income countries also have shifted more of their energy use towards electricity as they have become richer.

While economy-wide energy demand has been studied frequently (for recent examples, see Liddle and Huntington 2020; Liddle et al. 2020; Gao et al. 2021), economy-wide electricity demand has been considered rarely—particularly outside the OECD. We employ a new database of cross-country real economy-wide electricity prices and apply a set of panel-based and time-series-based methods that, taken in total, account for nonstationarity, cross-sectional dependence, temporal heterogeneity (as well as exogenous and endogenous breaks), and cross-sectional heterogeneity. By doing so we aim to improve the understanding of both the current levels and temporal change in income/GDP and price elasticities of economy-wide electricity demand in middle-income countries, as well as the diversity of those elasticities in eight¹ particular such countries.

One reason we care about income and price elasticities is that they are employed in electricity forecasts and integrated models (e.g., economy and environment models). There are two reasons income and price elasticities may not be constant over time: (1) they may change systematically, perhaps, because of specific events; or (2) they may display temporal variance the same way panel estimations are known to contain cross-unit variation. In the first case, not understanding this time variance could cause misleading conclusions/forecasts. In the second case, a single panel coefficient may lead to reasonable conclusions/forecasts, but its precision would be improved were it to be developed from over-time averaging in addition to cross-unit averaging.

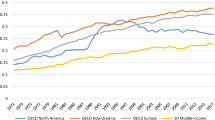
The income elasticity may decline with increases in income because of demand saturation effects. However, two recent time-varying analyses of middle-income/non-OECD country panels found that the income/GDP elasticity of economy-wide energy demand only varied within a relatively small band (Liddle et al. 2020; Gao et al. 2021). Furthermore, the electricity consumption paths of most of the middle-income countries we consider do not suggest saturation of demand (e.g., see Fig. 1). Events like the Asian Financial Crisis (circa 1997) and the Great Recession could impact demand—through their impact on income—but this would not mean that the income elasticity would change.

Fig. 1

Economy-wide per capita electricity consumption (kWh/person), 31 countries and average for OECD as a whole, 1980–2019. Data from US Energy Information Administration (November 2021) (https://www.eia.gov/international/data/world), except for the OECD series, which is based on IEA data from the IEA (2020) World Energy Balances, www.iea.org/statistics. All rights reserved; as modified by authors

Price elasticities could fall because of technical change, spurred, for example, by the energy crises of the 1970s and early-1980s. Indeed, several studies have found evidence of declining price elasticities in OECD countries, e.g., Dargay and Gately (1997) (for transport) and Gately and Huntington (2002) (for economy-wide energy demand), because of reactions to those substantial price peaks. However, analyses that considered only more recent experience (i.e., beginning in 1990 or later) have not necessarily uncovered such price elasticity changes (Liddle and Huntington 2021a).

Ultimately, we find that the income and price elasticities of economy-wide electricity demand are stable/effectively constant over time (with a few exceptions of elasticities that increased slightly over time for the individually analyzed countries). In addition, most of our results suggested that the income elasticity of economy-wide electricity demand for these middle-income countries was on average between 0.7 and 0.9; although, for three of the individually analyzed countries, the income elasticity was substantially above unity. These findings of a stable income elasticity around 0.8 are similar to/slightly higher than previous analyses of economy-wide energy demand for middle-income panels (e.g., Liddle and Huntington 2020), but are different from the results of OECD-focused studies that have uncovered a declining income/GDP elasticity of economy-wide electricity demand that may be as low as 0.2 (e.g., Arcabic et al. 2021; Liddle et al. 2023).

2 Literature review

Likely in no small part because of the lack of availability of non-OECD country price data, it was difficult to locate income and price elasticity of economy-wide electricity demand panel estimations that included middle-income/non-OECD countries. Indeed, one analysis we did find, Sadorsky (2012), used the CPI instead of electricity prices and focused on an unbalanced panel spanning 1993–2008 of 19 so-called emerging market economies that included (i) high-income Czech Republic, Hungary, and Poland; (ii) 11 countries that appear in our middle-income panel, too²; and (iii) another five middle-income countries for which we have insufficient price observations. The paper reported time-invariant, statistically significant long-run elasticities of 0.76 for income and 0.1 for prices. The finding of a positive price elasticity might be interpreted as evidence that the CPI is not a suitable proxy for electricity prices.

2.1 Previous (panel and individual) middle-income/non-OECD country studies of aggregations of electricity demand

Two recent papers estimated time-invariant sectoral electricity demand elasticities (residential and industry) for middle-income country panels by applying the Dynamic Common Correlated Effects (DCCE) estimator of Chudik and Pesaran (2015). Liddle and Huntington (2021b) estimated elasticities of residential electricity demand for a panel of 29 middle-income countries with data spanning 1978–2013. Their significant income and price elasticities for middle-income countries were 0.8 and -0.1, respectively. Liddle and Hasanov (2022) analyzed industry electricity demand for a panel of 30 middle-income countries with data spanning 1978–2016. They estimated output elasticities of unity or larger and price elasticities that were small and insignificant.

Two of the countries that we consider—Korea and Turkey—have been analyzed individually using different aggregations of electricity demand in a time-varying context. Chang et al. (2014) used a smooth time-varying coefficient cointegration method to analyze residential, commercial, and industrial electricity demand in Korea by considering monthly data. They focused their time-varying analysis on the income/output elasticities; price elasticities were time-invariant. All three of the income/output elasticities increased over time (more or less linearly). The output elasticities of commercial and industrial demand increased by about 25% and 50%, respectively, over 1985–2012. The residential income elasticity increased the most in percentage terms—nearly doubling from 1995 to 2012—but was still less than 0.14.

Arisoy and Ozturk (2014) analyzed annual data over 1960–2008 for residential and industrial electricity demand in Turkey by employing the Kalman filter. They found that all four elasticities (price and income/output for residential and industrial demand) were significant and effectively constant since 1970. The income elasticity for both industrial and residential electricity demand was near unity; whereas, the price elasticities were small at − 0.01 and − 0.02 for industry and residential, respectively.

So, there has been very little previous work on economy-wide electricity demand elasticity estimates based on middle-income countries—whether time-varying or not.³ Further, we found only one paper—focused on Turkey—that estimated time-varying income and price elasticities for industrial and residential electricity demand separately. Thus, our panel analysis is unique, and our eight-country individual analyses are unique too.

3 Data and electricity consumption trends

We assemble a panel of middle-income (or high-growth) countries that is reasonably large in both the cross-sectional and time dimensions. For 31 such countries, we collected electricity consumption per capita (in kWh per capita) and GDP per capita data (in constant 2010 US$ at PPP) data from IEA. These series span 1971–2019 and are complete for all countries.

Price data are what typically constrain energy demand datasets. We draw from a particularly large dataset of economy-wide electricity real prices (in 2015 US cents per kilowatt hour and including taxes) from Liddle (2022).⁴ These highly unbalanced data also span 1971–2019, but full-to-nearly-full data are available only for Iran (beginning in 1971); India, Indonesia, Korea, Thailand, and Chinese Taipei (all beginning in 1973); and Mexico, South Africa,⁵ and Turkey (all beginning in 1978).

Single-country, time-varying estimation methods typically require substantial time observations; so, we analyze these eight countries individually (methods discussed explicitly in the following section). However, while not necessarily a requirement, for the time-varying panel analysis, we believe it is best if the panels are balanced since we do not want the revealed dynamics of income and price elasticities to be impacted by changes in panel composition/size. So, we create a balanced panel that spans 1990–2019.

To create this panel we had to fill in several missing price observations. These missing observations usually occurred at the beginning of the time period and sometimes at the end (for four countries). We imputed the missing price observation with the closest observed one (i.e., previous or following year’s price).⁶ This approach was used by Gao et al. (2021) and has been justified in, e.g., Jin et al. (2021). Even though including prices in the model restricts the size of the panel, we believe doing so is important since excluding prices has been demonstrated to impart an upward bias on time-invariant estimates of the income/GDP elasticity (Liddle 2022), and this bias has been shown consistently to exist over different time spans (Liddle et al. 2023).

Appendix 1, Table 5 outlines the limits of the price data. Table 1 shows the summary statistics for both the entire sample and the balanced sample.

Table 1 Summary statistics

Figure 1 displays electricity consumption per capita from 1980 to 2019 for our 31 countries and for the OECD as a whole (dashed line). The highest per capita consumers in our panel are (in order) Chinese Taipei (Taiwan), Korea, Saudia Arabia, and Trinidad and Tobago. While Chinese Taipei, Korea, and Saudia Arabia are considered high-income⁷ as opposed to middle-income, we nevertheless include them in our panel since their consumption pattern is one of high, mostly consistent, growth unlike most of the OECD, for which consumption has leveled for some time. Further, these three countries have surpassed the average OECD level of per capita electricity consumption.

Indeed, unlike consumption in most of the OECD, per capita electricity consumption has been increasing throughout the countries in our panel. Notable exceptions are South Africa, where consumption has not increased much since 1990 (even though the share of the population with access to electricity has more than doubled over that span), and Trinidad and Tobago, where consumption has declined slightly since 2013 (after a substantial increase). (Romania’s per capita electricity consumption peaked in 1989, but after a decline has been increasing steadily since about 2000.)

In 21 countries, populations enjoy full (100% according to the World Bank) access to electricity. In only four countries is the share of population with electricity access less than 96%: Honduras (93%), Nicaragua (88%), South Africa (85%), and Ivory Coast (69% but increasing steadily). While the share of all energy services that are provided via electricity has increased, it is still fairly low, ranging from 25% in Korea to only 6% in Trinidad and Tobago. Not surprisingly, transport has a low penetration for electricity—for only two countries is electricity’s share of energy in agriculture and transport over 7%⁸; but there is much room for electrification growth in many countries for buildings (commercial and residential) and industry. For example, electricity’s share of building energy consumption ranges from 76% (in Costa Rica) to 7% (in Guatemala), and electricity’s share of industry energy consumption ranges from 50% (in Korea) to 13% (in Paraguay). So, the increase in electricity consumption results from rising incomes, increasing access to electricity, and supplying more energy services via electricity.

4 Models and methods

4.1 Time invariant panel estimations

In addition to the possibility of time heterogeneity (i.e., elasticities changing over time), it is likely that elasticities will be different across countries. Hence, we use a mean group estimator (MG) that first estimates cross-sectional specific regressions and then averages those estimated individual-country coefficients to arrive at panel coefficients.⁹ (Indeed, that the country-specific slopes are not homogenous was confirmed by a test based on Pesaran and Yamagata (2008),¹⁰ which compares the difference between coefficients obtained from a pooled, fixed effects regression and the coefficients obtained from an MG-based regression.)

Two other well-known statistical issues for macro-panels are cross-sectional dependence and non-stationarity. The Pesaran (2015a) cross-sectional dependence (CD) test¹¹ rejects the null hypothesis of weak cross-sectional dependence at very high levels of significance for all the variables (results shown in Appendix 2, Table 6). Also, the Pesaran (2007) panel unit root test (results shown in Appendix 2, Table 7), which allows for cross-sectional dependence to be caused by a single (unobserved) common factor,¹² suggests that the variables are nonstationary (i.e., have nonconstant means). Thus, we include in the regression cross-sectional averages of the dependent and independent variables (following the Pesaran 2006 Common Correlated Effects (CCE) approach) to account for cross-sectional dependence (in the time-invariant and breaks regressions). In addition to addressing cross-sectional dependence, these cross-sectional average terms represent unobserved common factors, e.g., technology. Additionally, CCE is robust to nonstationarity, cointegration, breaks, and serial correlation.

As is common in the economics literature, we start with the classic demand model in which (i) all variables have been converted via natural logs and (ii) electricity consumption is a function of income (GDP per capita) and electricity price:

$$ln\,Electricity_{it} \, = \,\alpha_{i} \, + \,\beta_{i}^{1} ln GDP_{it} \, + \,\beta_{i}^{2} ln price_{it} \, + \,\varepsilon_{it}$$

(1)

where t represents the time dimension and i the country dimension; α is a cross-sectional specific constant; the βs are cross-sectional specific coefficients to be estimated; and ε_it is the error term. In such a model, the coefficients are interpreted as elasticities, and are expected to be positive for income and negative for price. While demand models often include a lag of the dependent variable, we consider a static model to conserve degrees of freedom (since we have only 30 time observations in our balanced panel).¹³

In addition to using Eq. 1 for the estimation of time-invariant elasticities, we consider an exogenous break at the balanced sample mid-point (i.e., 2004) that allows for the income and price elasticities to be different over the first- and second-halves of the sample. Specifically, Eq. 1 is adjusted to:

$$ln\,Electricity_{it} \, = \,\alpha_{i} \, + \,\beta_{i}^{1} ln GDP_{it} \, + \,\beta_{i}^{2} bk \cdot ln GDP_{it} \, + \,\beta_{i}^{3} ln price_{it} + \beta_{i}^{4} bk \cdot ln price_{it} + \varepsilon_{it}$$

(2)

where bk is a dummy variable that takes on zero from 1990 to 2004 and one from 2005 to 2019. We consider three break possibilities: (i) breaks in both the income and price elasticities; (ii) a break in the income but not the price elasticity; and (iii) a break in the price but not the income elasticity.

Further, we test for the possibility of multiple endogenous breaks using a new method, Ditzen et al. (2021), that extends to a panel setting the Bia and Perron (2003) approach. While the Ditzen et al. method is fixed effects-based (as opposed to MG), it addresses cross-sectional dependence a la Pesaran (2006). Ditzen et al. (2021) determines the number of breaks (if any) and estimates their timing.

4.2 Panel estimations of time-varying elasticities

To consider explicitly whether the panel elasticities have changed over time, we consider a novel panel approach that allows for both cross-sectional and temporal heterogeneity in both intercepts and slopes: mean observation OLS (MO–OLS), which was introduced by Keane and Neal (2020). The method estimates coefficients (and a constant) for each cross-section and each time period and averages across these NxT values to arrive at the panel coefficients. MO–OLS applies a series of regressions to the data along the time and cross-sectional dimensions that (potentially) initially produce biased estimates. This bias is then reduced to an inconsequential amount via an iterative procedure of further regressions (Neal 2019). MO–OLS adjusts Eq. 1 to:

$$ln\,Electricity_{it} \, = \,\alpha_{it} \, + \,\beta_{it}^{1} ln GDP_{it} \, + \,\beta_{it}^{2} ln price_{it} \, + \,\varepsilon_{it}$$

(3)

where the estimated coefficients now vary according to both i and t.

MO–OLS assumes stationary and cross-sectionally independent data, but, like mean-group based methods, can produce stationary residuals even in the presence of nonstationary regressors. In addition, Neal (2020) argued that if the cross-sectional dependence is caused by time-varying slope parameters, MO–OLS will be more effective in removing this dependence than even CCE-based methods.

Since we are interested in the over-time variation, we calculate and plot the cross-sectional mean for each time period.¹⁴ Also, on those plots we show the 95/05 and 75/25 percentile ranges for those individual cross-sectional means (similar to Keane and Neal 2020). So, the long-run income and price elasticities at each time, t, are:

$$\beta_{t}^{1} \, = \,\frac{{\mathop \sum \nolimits_{i = 1}^{31} \beta_{it}^{1} }}{31}\,and\,\beta_{t}^{2} \, = \,\frac{{\mathop \sum \nolimits_{i = 1}^{31} \beta_{it}^{2} }}{31}$$

(4)

4.3 Individual country time-varying elasticity estimations

We use the structural time series modeling (STSM) approach as developed by Harvey (1989), Koopman (1993), Anderson and Moore (1979), and de Jong (1991) to assess whether eight individual country’s electricity demand elasticities vary over time. The static version of Eq. 1 in the STSM framework—considering only the trend component of electricity demand (not cyclical and seasonal components) since we have annualized data—can be expressed, as in Dilaver and Hunt (2011) and Mikayilov et al. (2020), by:

$$ln\,Electricity_{t} \, = \,\mu_{t} \, + \,\beta_{t}^{1} ln GDP_{t} \, + \,\beta_{t}^{2} ln\,Price_{t} \, + \,e_{t}$$

(5)

where ${\beta }_{t}^{i}$ are the time-varying elasticities of electricity consumption with respect to income and price, and ${\mu }_{t}$ and ${e}_{t}$ are the trend component and irregular (error) component, respectively. The trend component can be specified in level (Eq. 6) and in slope (Eq. 7):

$$\mu_{t} \, = \,\mu_{t - 1} \, + \,\gamma_{t - 1} + v_{t}$$

(6)

$$\gamma_{t} \, = \,\gamma_{t - 1} + w_{t}$$

(7)

where ${v}_{t}$ and ${w}_{t}$ are the level disturbance and slope disturbance, respectively.

It is assumed that ${e}_{t}, {v}_{t}$ and ${w}_{t}$ are mutually uncorrelated, and they are $NID(0,{\delta }_{e}^{2})$, $NID\left(0,{\delta }_{v}^{2}\right), \mathrm{and }NID(0,{\delta }_{w}^{2})$, respectively. The specifications can vary depending on whether variances from Eqs. 6–7 are zero or greater than zero. For example, if ${\delta }_{w}^{2}=0$, then the slope of the trend component is fixed (i.e., not time-varying)—this is the option that we consider (i.e., we assume that only the intercept component can be time-varying). Similarly, if ${\delta }_{v}^{2}=0$, then the level of the trend (intercept) component is fixed. In addition, our method tests for year outliers (in Eqs. 5–7) and adds interventions/dummy variables to account for such (outlying) cases. Lastly, we confirmed the stationarity of ${e}_{t}$ in Eq. 5 for all regressions.

5 Results and discussion

5.1 Time invariant/point elasticity estimations

First, we employ on the full, unbalanced sample, two heterogenous, residual-based first-generation cointegration tests (Pedroni 2004; Westerlund 2005), in which we subtract the cross-sectional averages from each series (a procedure Levin et al. 2002 recommended to mitigate cross-sectional dependence). The main difference between the Pedroni (2004) and the Westerlund (2005) cointegration tests is in their varying alternative hypotheses: Pedroni’s alternative hypothesis is that all cross-sections are cointegrated; whereas the alternative for the Westerlund test is that some of the cross-sections are cointegrated (the null hypothesis for both tests is no cointegration). The results of both tests (shown in Appendix 2, Table 8) strongly reject the null of no cointegration, and thus establish that there is a meaningful long-run relationship among the variables.

Table 2 displays the time invariant, panel average elasticity estimations for the balanced panel and three different MG-based estimators. For all three estimators, both the income and price elasticities were statistically significant and had the expected signs. The MG estimator (no adjustment for cross-sectional dependence and time-invariant) produces a large income elasticity, but the residuals are problematic—weak cross-sectional dependence was rejected (in favor of strong dependence), and nonstationarity could not be rejected when a trend was included. Both CCE and MO–OLS produced stationary residuals, and for both, weak cross-sectional dependence could not be rejected when considering the test of Juodis and Reese (2022), which corrects for over-rejection when used on residuals of the Pesaran (2015a, b) test. The MO–OLS panel elasticities were between the MG and CCE ones.

Table 2 Panel elasticity estimates. Balanced sample: 31 countries, 1990–2019

Comparing these economy-wide electricity results with the long-run residential income electricity estimates of Liddle and Huntington (2021b) and the long-run industry electricity estimates of Liddle and Hasanov (2022) (both considered dynamic models) from those papers’ middle-income country panels, the price elasticity from CCE and MO–OLS is just below the significant residential price elasticity of − 0.1 but larger than the insignificant industry price elasticity. On the other hand, the economy-wide income electricity estimates from CCE and MO–OLS bracket the residential income elasticity of 0.8, but are smaller than the industry output (i.e., value added) elasticity of 1.2 from those same two studies.

A long-run income elasticity of 0.7 (from CCE) could seem low given the typical growth of energy consumption displayed in Fig. 1. However, that estimate is nearly the same as the recent time-invariant economy-wide energy demand income elasticity estimation for a middle-income country panel from Liddle and Huntington (2020). (In contrast to the results here, all of Liddle and Huntington’s price estimates for middle-income panels were insignificant.) Also, that 0.7 income elasticity of economy-wide electricity consumption is considerably higher than two recent OECD/EU economy-wide electricity estimates—i.e., Arcabic et al. (2021) and Liddle et al. (2023)—that were in the 0.4–0.3 range. As Fig. 1 suggested, electricity consumption has stagnated in OECD countries in contrast to most of the middle-income countries in our panel. Lastly, as discussed above, there is substantial room to increase the share of energy services that are provided by electricity; so, electricity demand could increase despite an income elasticity that is (significantly) below unity.

5.1.1 Exogenous and endogenous breaks analysis

Table 3 displays the results of the exogenous (pre-determined) break analysis. Here we allow the income and price elasticities to be different over the period 1990–2004 from the period 2005–2019. Again, we consider three cases: (i) where both the income and price elasticities are different/have breaks; (ii) where only the income elasticity differs between the two periods; and (iii) where only the price elasticity differs between the two periods. As Table 3 indicates, the elasticity over 2005–2019 is always insignificant. This is particularly so for the two cases where only one break is allowed.

Table 3 Exogenous breaks analysis (Eq. 2). Balanced sample: 31 countries, 1990–2019. CCE estimator

This exogenous break test would uncover a monotonic change in elasticities, where the elasticity became either smaller or larger over time, either as a result of a shock or in a smooth transition. However, this approach would not necessarily reveal whether the elasticities had changed in a more complex pattern. So, we consider the multiple, endogenous panel break test of Ditzen et al. (2021). Both the sequential test for multiple breaks and the separate test of the null of no breaks against the alternative of up to five breaks always rejected the null of no breaks, even at the 10% level, thus, supporting the previous exogenous, single break analysis.

5.2 Time-varying panel estimations

Figures 2a and b display the MO-OLS results over the 1990–2019 time span. Again, the overall panel averages for MO-OLS were 0.86 for the income elasticity and -0.086 for the price elasticity. The income elasticity (Fig. 2a) displays a little movement over time, but this movement could be interpreted as variation in the MO–OLS estimate rather than an increasing trend followed by a decreasing trend. The income elasticity estimates range from 0.78 to 0.95, so they are never far from their average of 0.86 (i.e., never off by more than 10%). The typical MG estimation displays variance among the country-specific estimates (again, the panel estimate is an average of those country estimates). MO–OLS allows such variance across both country and time. If we calculate the country income elasticities (by averaging their estimates over time), these estimates display considerably more variance, e.g., the range is from 0.17 to 1.87. In other words, MO–OLS suggests much more variance/heterogeneity across countries than over time for the income elasticity.

Fig. 2

a Time-varying income elasticity estimates from MO-OLS, 1990–2019. The bold line is the yearly mean of the slope coefficient. The dark gray and light gray areas represent the 25th to 75th and the 5th to 95th percentiles, respectively. b Time-varying price elasticity estimates from MO-OLS, 1990–2019. The bold line is the yearly mean of the slope coefficient. The dark gray and light gray areas represent the 25th to 75th and the 5th to 95th percentiles, respectively

The price elasticity (Fig. 2b) displays somewhat more movement over time, with a range of − 0.01 to − 0.17. Again, the overall average (− 0.086) falls roughly in the middle of the range, but, in percentage terms, assuming a time-invariant elasticity would result in larger error. On the other hand, the price elasticity may be small enough that forecasts could assume constant income and price elasticities without incurring substantial loss of precision. As with income, the temporal pattern of the price elasticity is one of an inverted-U shape with the high point near the mid-point of the sample. Also, as with income, the range of country-specific price elasticities was much larger: 0.30 to − 0.56.

5.3 Individual country time-varying estimations

For the eight countries for which we had the most time observations, we performed an individual time-varying demand elasticity analysis via STSM. These estimations have the advantage of using all our available data and being fully temporally and cross-sectionally heterogenous. A drawback of these results is that the cross-sectional sample is considerably smaller than our panel for generalizing about middle-income countries as a group.

Table 4 summarizes the results for each country—the key statistics is the range (minimum and maximum) of the elasticity estimates over the sample period. The few results that display variance over time are shown in Figs. 3 (income) and 4 (price). The results that are effectively constant over time are shown in Appendix 3, Figures 5 (income) and 6 (price).

Table 4 Summary of individual country STSM results

Fig. 3

a-c STSM results for the income elasticity for India, Iran, and Mexico. The middle (red) line is the elasticity; the top and bottom lines represent the 95% confidence intervals

Focusing on the income elasticity results, they are very much consistent with the panel results discussed above. Heterogeneity in the level of the income elasticity is clearly present; yet, the average elasticity (based on the mid-point of the country ranges) is 0.90, i.e., virtually the same as the panel average from MO–OLS. Judging from the reported elasticity ranges, for most (six) countries, their income elasticity is effectively constant over time (the elasticity for Turkey moves slightly more than the other five, but is the same at the end of the period as it was at the beginning). Again, these elasticity trajectories are displayed in Appendix 3, Figure 5.

The income elasticities for India, Iran, and Mexico are shown in Fig. 3. These elasticities do change slightly over time, but the pattern is the same for all three: a more-or-less linear increase; albeit, the income elasticity for India stops increasing around 1995. So, perhaps only for Iran and Mexico would a time-varying income elasticity—or at least one based on more recent observations—lead to more precise long-run projections of electricity demand.

In general, the individual country price elasticities are small as in the previous panel estimates, and the individual country estimates are not always statistically significant. For three countries, Indonesia, Iran and Taiwan, the time-varying price elasticities move enough over time to be visualized with standard resolution y-axes. So, we show them in Fig. 4 below. The other countries’ price elasticities are displayed in Appendix 3, Figure 6. (While Thailand’s price elasticity does vary over time, it is nearly always insignificant and positive; so, we place it in Figure 6 also.)

Fig. 4

a-c STSM results for the price elasticity for Indonesia, Iran, and Taiwan. The middle (red) line is the elasticity; the top and bottom lines represent the 95% confidence intervals

For both Indonesia and Iran, the price elasticity declines in absolute value over time in a nonlinear fashion. For Indonesia, the movement over time is less than that for Iran, but Indonesia’s price elasticity is mostly insignificant at the 5% level. For Taiwan, the price elasticity takes an inverted-U shape over time, but for the periods at the beginning and end of the sample, for which the elasticity is statistically significant, the elasticity is contained within the relatively tight interval of − 0.28 to − 0.15, and it appears to end with roughly the same value that it began with (so, a time-invariant elasticity may not be a bad approximation).

Lastly, we can compare our individual country results with the two previous papers that considered the same countries. Our Turkey results for economy-wide electricity elasticities were similar to the results of Arisoy and Ozturk (2014) for residential and industrial electricity elasticities in that all the elasticities were mostly constant over time. But our income elasticity was less than half of theirs (both their residential and industrial sector results were similar—about unity); whereas, our price elasticity (while small and not statistically significant at the 5% level) was larger (in absolute terms) than theirs. While our methods were similar to theirs, the time spans considered were quite different: 1978–2019 for our analysis compared to 1960–2008 for theirs.

Chang et al. (2014) estimated price elasticities (assumed to be constant) that were significant for residential (− 0.4) and industry (− 0.5). Their positive and insignificant estimate of price elasticity for the commercial sector electricity demand is very similar to our economy-wide estimate, which was positive and insignificant, too. Our income elasticity for economy-wide consumption, while effectively constant, was twice as high as the ultimate output elasticity for industry and commercial from Chang et al. (2014).

6 Conclusions

It is important to have a greater understanding of electricity demand in middle-income countries—countries that are growing fastest in terms of both GDP and electricity and energy consumption. We take advantage of a new dataset of economy-wide electricity prices and employ two panel methods that address both cross-sectional and temporal heterogeneity; we also consider a third time-series approach to model electricity demand over a relatively long time horizon for an additional eight countries. Our work is particularly novel in terms of the number of middle-income countries considered as well as in the time span.

All three of our methods—both panel approaches and the individual country analyses—determined that the income and price elasticities of economy-wide electricity demand are stable/effectively constant over time. In addition, the majority of our results suggested that the income elasticity of economy-wide electricity demand for these middle-income countries was on average between 0.7 and 0.9.

While our work is also unique in terms of analyzing economy-wide electricity demand for a large group of middle-income countries, comparisons can be made to similar work on economy-wide energy demand for high- and middle-income countries and to similar work on economy-wide electricity demand for OECD/high-income countries. For example, our result of effectively constant income and price elasticities is analogous to recent findings focused on economy-wide energy demand in both middle-income countries (e.g., Liddle et al. 2020; Gao et al. 2021) and OECD/high-income countries (e.g., Gao et al. 2021). However, our finding of the constancy of the economy-wide electricity demand income elasticity contrasts with findings on OECD/high-income country economy-wide electricity demand, for which the income elasticity has been determined to be declining over time (e.g., Liddle et al. 2023).

Also, our income elasticity of economy-wide electricity demand estimate for middle-income countries is similar to (albeit, slightly higher than) recent estimations of the income elasticity of economy-wide energy demand for both OECD/high-income and middle-income countries (e.g., Liddle and Huntington 2020; Gao et al. 2021). However, our economy-wide income elasticity of electricity demand estimate for middle-income countries is substantially higher than income elasticity estimates of economy-wide electricity demand for OECD/EU countries, which are closer to 0.3–0.2 (e.g., Arcabic et al. 2021; Liddle et al. 2023). Given that our panel does include some high-income countries (Chinese Taipei, Korea, Saudi Arabia), we would caution against deducing from those different panel results that the income elasticity of electricity demand falls with income.

For modelers the implications of our results are that modelers analyzing panel data can focus on areas like cross-sectional heterogeneity and cross-sectional dependence and spend less effort/degrees of freedom being concerned with possible temporal heterogeneity of coefficients. However, if sufficient data exist to allow for both cross-sectional and temporal heterogeneity, panel averaging will likely be improved. As for limitations/future work, as is typical in these analyses, more data—were it available—would be helpful. For example, quarterly data would allow the study of seasonal impacts. In addition, the price of substitutes, like natural gas, are sometimes included in energy demand equations.

In terms of policy implications, an income elasticity of electricity demand of less than unity (say, around 0.8) may seem encouraging for climate mitigations focused on increasing the electrification of energy services. As we mentioned before, there indeed is much room to increase such electrification in the middle-income countries studied here. However, rising rates of energy service electrification could result in an increase in the income/GDP elasticity (e.g., see Liddle et al. 2023 for such an analysis focused on OECD countries). Lastly, the findings of a nearly/effectively constant income elasticity over time could be interpreted as evidence of a large (i.e., near 100%) economy-wide rebound effect that offsets efficiency improvements in electricity consumption (an interpretation suggested by, e.g., Brockway et al. 2021).

Appendices

Appendix 1

See Table 5

Table 5 Unbalanced price data

Appendix 2

Pre-testing results (See Tables 6, 7 and 8).

Table 6 Pesaran (2015a) CD test. Full 31 country, 1971–2019 unbalanced panel

Table 7 Pesaran (2007) Panel Unit Root Test Results. Full 31 country, 1971–2019 unbalanced panel

Table 8 Panel cointegration tests. Full 31 country, 1971–2019 unbalanced panel

Appendix 3

Graphical STSM results (See Figs. 5 and 6).

Fig. 5

STSM results for the time-varying income elasticity for five countries (for which the elasticity is effectively constant). The middle (red) line is the elasticity; the top and bottom lines represent the 95% confidence intervals

Fig. 6

STSM results for the time-varying price elasticity for five countries (for which the elasticity is effectively constant). The middle (red) line is the elasticity; the top and bottom lines represent the 95% confidence intervals