1 Introduction

Marine habitats are complex and can be difficult to systematically describe due in part to the difficulty of systematic sampling across relevant space and time scales (Everett et al. 2017). With regard to modeling resource distribution (Everett et al. 2017), while data are available from different sources, the use of different collection methods with different temporal and spatial scales confounds the process. Critical to the management of marine habitats are the distribution, abundance, and composition of marine zooplankton, a community that is central to the energy flow through the system from primary producers to higher trophic levels such as invertebrates, fish, and baleen whales (Lenz 2000; Everett et al. 2017). The diverse zooplankton groups have multiple functional roles in the marine food web including controlling the biomass by grazers, nutrient recycling via excrement, and vertical transport of material either by sinking, direct transport, or diel vertical migration (Andersen et al. 1993; Richardson 2008). Therefore, modeling the abundance and dynamics of zooplankton is critical in understanding the flow of energy to higher trophic levels (Mitra et al. 2014; Everett et al. 2017) and provides the motivation for the work presented here.

We use a zooplankton database that informs management of the Cape Cod Bay (CCB), MA, USA habitat, specifically related to those characteristics that impact the critically endangered North Atlantic right whales (Eubalaena glacialis; NARW; Cooke 2020). The study of the NARW prey resource in CCB suffers from intermittent sampling, both spatially and temporally. Despite the difficulty in describing the distribution and abundance of the zooplankton, such methodology is important for the development of conservation strategies related to the habitat use patterns of the NARW’s.

We describe the distribution and abundance of sea surface zooplankton utilizing the following data. At irregularly spaced locations (in CCB) and times (in 2003–2019), we have two sources of space-time data collection for zooplankton, both of which inform about sea surface zooplankton abundance. These data are the product of two methods of collection, as described below. We offer a fusion of these two response sources which requires calibration. Further, an important environmental factor that affects sea surface zooplankton abundance is sea surface temperature (SST; Mauchline 1998; Richardson 2008). Here, we also have two different data sources for SST, also described below. We need to fuse these sources as well in order to develop an SST regressor. These sources also require calibration; hence we adopt the terminology of double fusion and double calibration for our modeling.

The notions of fusion and calibration arise here from the well-discussed issue of measurement error (or errors in variables) in the Statistics literature (see, e.g., Fuller 1987; Carroll et al. 2006). Substantial published literature is available on stochastic spatial or spatiotemporal data fusion modeling for environmental and ecological data. For example, Fuentes and Raftery (2005) consider fusion of air pollution data sources. In this regard, Liu et al. (2011) and Zidek et al. (2012) consider fusion for ozone sources. Foley and Fuentes (2008) present wind data modeling fusion. Finley et al. (2011) offer a fusion for agricultural crop yields. Liu et al. (2016) investigate fusion to predict spatial tracks for marine mammals. Very recent work (Villejo et al. 2023) introduces the INLA-SPDE approach for spatial data fusion.

Our context is spatiotemporal data fusion, and neither the SST sources nor the zooplankton abundance sources observe the true value; they are observed with measurement error. However, there is a conceptual true SST which, in part, influences a conceptual true zooplankton abundance and we seek to learn about the latter surface for CCB over space and time. For each variable, we have two data sources, which inform us about the true values. For each variable, one source is essentially observed up to measurement error while the other requires calibration relative to the truth. An attractive generative modeling strategy (i.e., modeling which could actually have produced the observations) is to use a hierarchical specification, introducing a latent true surface and then connecting the observed data to the truth (Fuentes and Raftery 2005; Banerjee et al. 2014, Chapter 15).

The benefit of the fusion is to provide a more appropriate assessment of uncertainty, yielding prediction that is better centered. Ignoring measurement error underestimates uncertainty and leads to poorer prediction. This can be argued technically but is challenging to demonstrate with real data since the truth is not known. So, in the interest of illuminating the benefit, justifying the additional modeling effort to implement the fusion and calibration, we also provide a simplified simulation illustration where we know the truth.

Observed zooplankton abundance is also connected to the spatial variable, presence or absence of NARW’s at the location of collection, i.e., where whales are present, we would expect higher zooplankton abundance. However, this presence/absence regressor is only recorded at sites where abundance data are collected. Further, data are collected at a combination of regular stations (i.e., spatially-fixed) and non-regular (spatially-varying) sites for varying number of days within the first half of the year over the 17 year period. The regular stations supply repeated measurements over time; the non-regular sites are essentially opportunistic, providing site measurements only at the unique time of collection and predominantly collected in the vicinity of feeding whales.

More precisely, we propose a continuous-space, discrete-time multi-level/hierarchical model, implemented via the foregoing fusion and calibration processes. We use this model to develop a prediction of daily spatial zooplankton abundance surfaces over CCB, enabling an assessment of spatial variability as well as inference regarding average abundance over CCB or subregions. The partial observation of the NARW presence/absence variable adds complication to such prediction. Is our prediction based on the assumption the indicator is 1 (presence) everywhere? Or should our prediction be based on the assumption the indicator is 0 (absence) everywhere? Neither surface would be what we want. Rather, we seek to provide an average surface, averaged over a spatial probability of presence surface. In fact, this averaging requires the estimation of the probability of whale presence at an arbitrary location on an arbitrary day in an arbitrary year. For this purpose, a further modeling component is needed; we develop a predictive spatiotemporal logistic regression for the probability of presence. The above modeling enables inference for spatial abundance at selected temporal scales, e.g., averaged to bi-weekly or annual scale as well as to make inter-annual comparisons. As is evident, the modeling is complex and model fitting is challenging. However, again, the reward is prediction with better precision and more appropriate accuracy.

Returning to the data sources, for both the zooplankton data and the SST data, fusion and calibration are needed. As above, our spatial fusion approach assumes a latent true surface for the variable with each of the sources varying in some fashion around this truth. Calibration is required for the fusion. See, e.g., Fuentes and Raftery (2005) or Rundel et al. (2015) for an illustration of this so-called Bayesian melding or latent truth approach. For instance, below, we assume that the surface zooplankton measurements, since they are surface measurements, are observed as the true surface zooplankton plus error. However, since an oblique measurement is obtained by pulling the tow up from 19 ms, it is anticipated to overestimate surface zooplankton; as a result, it needs to be calibrated. We have a similar challenge with the temperature. Here, we also have two sources, one is highly accurate and available across all of CCB but is not observed exactly at the locations where the zooplankton is collected. The other is measured at the boat when the collection was made. It is expected to be less reliable due to variability in the depth of the measuring device on the boat and is available more sparsely over CCB. Consequently, we assume the former is observed as true SST plus error, while the latter may benefit from calibration.

The format of the paper is as follows. Section 2 offers the details on the datasets that were employed along with associated exploratory summaries. Section 3 demonstrates the benefit of our fusion and calibration through a simpler illustration. Section 4 develops the full spatiotemporal hierarchical specification with associated fitting details and model comparison. Section 5 presents a rich range of results from the model fitting. Finally, Sect. 6 concludes with a brief summary and directions for future work.

2 The dataset

Zooplankton abundances and temperature measurements were obtained from the Center for Coastal Studies (CCS) zooplankton database, which was established in 1981 (Hudak et al. 2023). The primary goal of CCS’ long term monitoring is to assess the critically endangered NARW’s prey resource within CCB, by using a 333-μm mesh filtration to mimic the filtration efficiency of the right whale’s baleen (Mayo et al. 2001). While this database provides an invaluable resource, it presents several spatial and temporal challenges for statistical analysis, as sampling varied spatially over time, depending on the field objectives of a given research cruise.

The dataset contained 2012 observations collected within CCB over a 17-year period (2003–2019) in the first 6 months of each year (January through June). Each observation consisted of the following elements: (1) zooplankton abundance measurements from one or two types of plankton collection (surface and oblique net tows); (2) one or two types of SST measurements (CTD and thermistor, specified below); and (3) a binary variable indicating the presence/absence of a NARW at the time of collection. The zooplankton collection methods included surface samples collected from a 30-cm diameter conical plankton net and flow meter towed at the surface, and oblique samples collected from a 60-cm diameter conical plankton net and flow meter dropped vertically to 19 ms then towed back to the surface obliquely. This deep drop associated with the oblique tows anticipates higher zooplankton per cubic meter than surface tows, motivating the need to calibrate the former. All samples were subsampled and each subsample was enumerated to obtain the abundance measurement (\(\text {organisms}/\text {m}^3\)) (Hudak et al. 2023). While the primary copepod prey species of NARW is Calanus finmarchicus, NARW feed on other species, including those from the Pseudocalanus complex (i.e., Pseudocalanus, Paracalanus, and Clausocalanus species) and Centropages genera (Waktins and Schevill 1976; Mayo and Marx 1990; Hudak et al. 2023). In CCB, the above mentioned taxa dominate the zooplankton resource in a successive pattern of three regimes (i.e., abundance dominance among the three taxa groups), with the turnover between the regimes within years at days \(34 \pm 3\) and \(92 \pm 3\) (Hudak et al. 2023); therefore, we use the total zooplankton abundance to account for the shift in dominance between the taxa through the study period.

The temperature collection methods included the Sea-Bird SBE-19 conductivity-temperature-depth (CTD) profiler, and temperature measurements recorded at the time of zooplankton collections from the negative temperature coefficient (NTC) thermistor sensor. Both temperature measurements are available in degrees Celsius (ºC). The CTD profiler was used intermittently throughout the years to sample ocean temperatures (Mayo et al. 2004). The profiler was mounted on a steel cage and lowered through the water column to the bottom or specific depths, with a scan rate of every 0.5 s. Only temperature measurements taken in less than 1.25 ms in depth for SST’s were used. To increase the temperature data pool we included temperature measurements recorded at the time of zooplankton collections from the NTC thermistor sensor positioned on the keel of the vessel at \(\sim\) 1 m depth (Mayo et al. 2004). The SST’s obtained from the thermistor data may also benefit from calibration since they depend upon the depth of the thermistor in the water, which varies over time of collection.

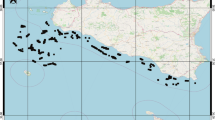
All observations had the binary NARW sighting variable, at least one type of zooplankton measurement, and either one, both, or no temperature measurement associated with it. See Sect. S1 of the Supplementary Information (SI) for additional details on the proportion of non-missing measurements in the observations. The observations were partitioned into regular (1595, \(79.3\%\)) and non-regular stations (417, \(20.7\%\)). Figure 1 shows the position of the observations at non-regular stations (grey points) and regular stations (red crosses) within CCB. Regular stations had fixed coordinates and were repeatedly observed at these coordinates over time. A total of 20 regular stations were used of which 8 had more than 100 observations each over the study period. In contrast, non-regular stations had unique coordinate locations over time. Their collection was generally motivated by the presence of NARW’s, as part of an effort to describe the environment selected by right whales. NARW presence at regular stations was \(5.8\%\) of the observations and \(87.6\%\) in non-regular stations, revealing the strong sampling bias for NARW’s in non-regular stations. However, in order to employ as much zooplankton data as is available, we use the data from both the regular and non-regular stations, using the presence indicator variable as a regressor. That is, we expect more zooplankton (more prey) at the non-regular stations in response to whale presence.

Fig. 1
figure 1

Position of the observations at non-regular stations (grey points) and regular stations (red crosses) in CCB, MA, USA

Full size image

Section S1.1 of the SI includes additional information about observation counts per year and day, as well as within year, by type of station, plankton collection method, and SST measurement.

2.1 Exploratory data analysis

We summarized an extensive exploratory data analysis of the zooplankton abundance per cubic meter, SST, and NARW presence data to establish the hierarchical structures in the model (see Sect. S1 of the SI for additional details). Kernel density estimation and normal quantile–quantile plots were plotted on the two measurement scales, original and logarithmic, for zooplankton measurements. Both zooplankton measurements on the original scale had a high positive skew, but, on the log scale, the variance stabilized (working at the log scale is usual for zooplankton data, see, e.g., Plourde et al. 2019; Record et al. 2019).

Figure 2 shows the seasonal pattern by days within years using moving averages (top) and the average annual long-term trend using annual averages (bottom) of the two types of temperature measurement (left), the two types of zooplankton measurement (center), and the proportion of NARW presence (right). Both temperature measurements have the same strong seasonal component and a slight increase in the long-term trend, with the measurements from the thermistor differing by 1 °C above those from the CTD. Both zooplankton measurements have a similar seasonal pattern with log oblique shifted above log surface. The transition points of the regime effect are clear in the zooplankton plot, with three distinguished levels; two higher in January and later from April, and a lower one in February and March. The seasonal component in the NARW presence is strongly unimodal with a maximum in March and a NARW presence close to zero in January and June.

Fig. 2
figure 2

For temperature (left), zooplankton (center), and proportion of NARW presence (right). Top: Moving average of data in a window of 7 and 30 days on each side (for days within years) and all years. Bottom: Average by year. (For NARW presence, we only average data for regular stations. At the bottom, for temperature and zooplankton we only average data where both collection methods are available)

Full size image

Section S1.2 of the SI includes additional exploration about the influential covariates in the zooplankton modeling; i.e., SST, the binary variable indicating the presence of NARW’s, and regime. Linear regression models were fitted as exploratory tools to examine the components needed to capture the seasonal component of the temperature, zooplankton, and NARW’s processes; these were generally modeled using harmonics (or regime for zooplankton).

Once the processes of interest and their relationships have been described, we delve into the relationship between the two types of measurement of zooplankton and of temperature, since they will be fused in the modeling. Section S1.3 of the SI includes additional exploration about the calibration of the zooplankton and temperature sources. In summary, the relationship between log surface and oblique measurements appears linear, but there is some variability associated with each type of measurement; this relationship is expected to vary in space and across years. Thermistor and CTD measurements show an exceptionally strong linear relationship that could vary spatially, but does not appear to vary in time.

3 A simulation example to demonstrate the benefit of the fusion

As discussed in the Sect. 1, it is challenging to demonstrate the benefit of calibration and fusion with real data. Specifically, in the context of more than one source informing about the true value of a variable, neither source provides observations that are the true values. Each source has measurement error and, in the absence of external validation data, the true value of the variable is not observed. In a regression setting, whether a predictor or the response (or both) is observed with measurement error, learning about the true regression relationship is the objective. Therefore, in the absence of the true values, using the observed values implies increased uncertainty in this inference objective. Ignoring measurement errors leads to potentially inaccurate assessment of precision and accuracy. In order to demonstrate the improvement in inference by incorporating measurement error, in the form of calibration and fusion, into our modeling specification, we present a simple simulation example, in the spirit of our setting, where the truth is known.

We generated 100 points inside the unit square, as realizations from \(Y_{true}({\textbf {s}})\). We captured spatial dependence with a mean \(\mu = 4\) Gaussian process (GP) arising from an exponential covariance function with variance \(\sigma _{true}^{2} = 4\) and decay parameter \(\phi _{true} = 3/0.5\), so the spatial range is 0.5. Then, we sampled 80 locations at random. We randomly assigned half of these locations to source 1 and the other half to source 2. For source 1, we obtain the responses using \(Y_{1}({\textbf {s}}) = Y_{true}({\textbf {s}}) + \epsilon _{1}({\textbf {s}})\) where the \(\epsilon _{1}({\textbf {s}})\) are i.i.d. \(N(0, \sigma _{1}^{2} = 4)\). This is the measurement error sample. For source 2, we obtain the responses using \(Y_{2}({\textbf {s}}) = \lambda _{0} + \lambda _{1}Y_{true}({\textbf {s}}) + \epsilon _{2}({\textbf {s}})\) where the \(\epsilon _{2}({\textbf {s}})\) are i.i.d. \(N(0, \sigma _{2}^{2} = 1)\) for fixed \(\lambda _{0} = 2\) and \(\lambda _{1} = 2\). This is the calibration sample. The remaining 20 locations are employed as “out of sample” for both sources and are viewed for validation. We predict the \(Y_{true}({\textbf {s}})\) for these points using kriging.

We fit Model 1 using just the source 1 data in a standard spatial linear regression model, \(Y_{1}({\textbf {s}}) = \mu + w({\textbf {s}}) + e({\textbf {s}})\) where \(w({\textbf {s}})\) is a mean-zero spatial GP (with known decay parameter) and \(e({\textbf {s}})\) is pure error. So, this model has three parameters, \((\mu , \sigma _{w}^{2}, \sigma _{e}^{2})\). We fit Model 2 using the source 1 and source 2 data. This model specifies \(Y_{1}({\textbf {s}})\) and \(Y_{2}({\textbf {s}})\) as above. It has six parameters, \((\mu , \sigma _{true}^{2}, \sigma _{1}^{2}, \lambda _{0}, \lambda _{1}, \sigma _{2}^{2})\). Under each model, we do posterior prediction for the 20 hold out true values. We repeat the entire simulation 100 times. Table 1 summarizes across simulations, using the predictive performance metrics described in Sect. 4.5 below, RMSE, MAE, and CRPS. Model 2 improves Model 1 by roughly 15–20% based on all metrics, demonstrating the benefits of the fusion in terms of predictive performance.

Table 1 Performance metrics (RMSE, MAE, and CRPS) for the two models summarized by their average across 100 simulations
Full size table

4 Modeling

We propose a hierarchical model for zooplankton abundance per cubic meter that requires double calibration using fusion of the two SST sources as a regressor and the two zooplankton measurement methods as a response. The model operates over continuous space and two discrete temporal scales, years and days within years. The fundamental assumption underlying the calibration modeling is that there are “true” unobserved daily spatial processes for zooplankton and for temperature, and that the two sources of observations are related to these processes via measurement error models. As we elaborate below, the measurement error models assume that one data source is the truth plus error while the other needs spatiotemporal calibration. The models for true zooplankton and true temperature capture spatial dependence through spatial process modeling of yearly or constant-in-time intercepts, respectively. The amount of zooplankton is, presumably, associated with the presence of whales, but here we only attempt to model abundance of the former, introducing presence/absence of the latter at a site as a predictor. Prediction under this modeling of zooplankton abundance at unobserved locations requires averaging/marginalization over this unobserved binary regressor at arbitrary locations. In order to address this, we propose a simple logistic regression response model for the presence of a whale at any zooplankton location of interest which operates only on temporal scales. We detail the calibration modeling below and then discuss model fitting, validation and model comparison. We also present details of prediction under the calibration and the marginalization using a binary response model.

We specify geostatistical, i.e., point level models. While there is a SST at every location in CCB, conceptually there is no zooplankton abundance at a point. The recorded abundance arises from the tow collection procedure and is scaled to a per cubic meter value. That value is assigned to the geo-coded location of the collection site. This does not prevent us from inferring a zooplankton abundance surface; rather, it clarifies how to interpret the value at a selected location. Further, if we seek an average zooplankton abundance over CCB for a given day in a given year, we will interpret it as a block average of these point level abundances.

4.1 The temperature model

We begin with the space-time calibration modeling for true temperature; in fact, since we seek sea surface zooplankton, we confine this predictor to “true” SST. Let t denote year and let j denote day within year, with years running from 2003 to 2019 and days from 1 (January 1) to 181 (June 30, except for leap years). Let \(temp_{t,j}({\textbf {s}})\) denote the true SST for day j in year t at location \({\textbf {s}}\) in CCB. We have two data sources for temperature to fuse: CTD, which we take as truth up to error, and the thermistor data, which we expect to benefit from calibration. We propose the following joint model to implement the fusion of the two sources:

$$\begin{aligned} \begin{aligned} CTD_{t,j}({\textbf {s}})&= temp_{t,j}({\textbf {s}}) + \epsilon _{t,j}^{CTD}({\textbf {s}}), \quad{} & {} \epsilon _{t,j}^{CTD}({\textbf {s}}) \sim \text { i.i.d. } N\big (0, \sigma _{CTD}^2\big ), \\ Therm_{t,j}({\textbf {s}})&= {\tilde{\alpha }}_{0}({\textbf {s}}) + {\tilde{\alpha }}_{1}({\textbf {s}}) temp_{t,j}({\textbf {s}}) + \epsilon _{t,j}^{Therm}({\textbf {s}}), \quad{} & {} \epsilon _{t,j}^{Therm}({\textbf {s}}) \sim \text { i.i.d. } N\big (0, \sigma _{Therm}^2\big ), \end{aligned} \end{aligned}$$
(1)

where

$$\begin{aligned} \begin{aligned} {\tilde{\alpha }}_{0}({\textbf {s}})&= \alpha _0 + \alpha _{0}({\textbf {s}}), \\ {\tilde{\alpha }}_{1}({\textbf {s}})&= \alpha _1 + \alpha _{1}({\textbf {s}}), \end{aligned} \end{aligned}$$
(2)

and the \(\epsilon _{t,j}({\textbf {s}})\)’s are pure errors at sites for days within years for both data sources. They provide learning about the uncertainty associated with the CTD and thermistor measurement processes.

Here, \(\alpha _0\) and \(\alpha _1\) provide the overall slope and intercept bias of the thermistor model, while \(\alpha _0({\textbf {s}})\) and \(\alpha _1({\textbf {s}})\) provide local adjustments, respectively. The spatially-varying coefficients \(\alpha _0({\textbf {s}})\) and \(\alpha _1({\textbf {s}})\) are in turn modeled as bivariate mean-zero spatial GP’s using the method of coregionalization (Banerjee et al. 2014, Chapter 9). Therefore, we suppose that there exist two mean-zero unit variance independent GP’s, \(v_0({\textbf {s}})\) and \(v_1({\textbf {s}})\), with exponential covariance functions having decay parameters \(\phi _{v_0}\) and \(\phi _{v_1}\), respectively. Then, we specify \(\alpha _0({\textbf {s}}) = a_{00} v_0({\textbf {s}})\) and \(\alpha _1({\textbf {s}}) = a_{10} v_0({\textbf {s}}) + a_{11} v_1({\textbf {s}})\), where \(a_{10}\) captures the dependence between the two processes.

Next, the true temperature for day j, year t, and location \({\textbf {s}}\) is modeled additively in space and time by

$$\begin{aligned} temp_{t,j}({\textbf {s}}) = \gamma _{0} + \gamma _{0t} + \gamma _0({\textbf {s}}) + \gamma _{1}\text {sin}(2\pi j/365) + \gamma _2 \text {cos}(2\pi j/365) \end{aligned}$$
(3)

in which \(\gamma _{0}\) is a global intercept, and the \(\sin\) and \(\cos\) terms are introduced to provide a semi-annual seasonal component. Based on the exploratory analysis, additional harmonic terms are not necessary. We consider an autoregression in years with \(\gamma _{0t} \sim N(\rho _{\gamma } \gamma _{0t-1}, \sigma _{\gamma }^2)\) and \(\gamma _{0,2002} \equiv 0\), providing annual intercepts. This specification can help to capture factors yielding correlation across years, such as naturally occurring ocean–atmosphere oscillations or the slight increase in temperatures observed in the exploratory analysis. In addition, \(\gamma _0({\textbf {s}})\) provides local spatial adjustment to the intercept and it is modeled by a mean-zero spatial GP with an exponential covariance function having variance parameter \(\sigma _{\gamma _{0}({\textbf {s}})}^2\) and decay parameter \(\phi _{\gamma _{0}({\textbf {s}})}\). With this specification the data models consider pure errors but the true temperature has no pure error and, in accord with the behavior of the true process, it is continuous over space.

4.2 The zooplankton model

Turning to the zooplankton data, let \(Y_{t,j}^{sur}({\textbf {s}})\) denote the logarithm of the surface collection at day j in year t at location \({\textbf {s}}\) in CCB, similarly, for the logarithm of the oblique collection, \(Y_{t,j}^{obl}({\textbf {s}})\). Let \({{\textbf {1}}}_{t,j}({\textbf {s}})\) be the indicator as to whether there was a whale sited when zooplankton was collected at day j, year t, site \({\textbf {s}}\). Let \(r_{j}\) indicate the regime (one of three regimes) associated with day j. Following Hudak et al. (2023), the first regime corresponds to \(j \in [1,32]\), the second to \(j \in [33,89]\), and the third to \(j \in [90,181]\). Then, with the goal of obtaining zooplankton abundance at the sea surface, we have that for \(\text {ZOOP}_{t,j}^{true}({\textbf {s}})\), the true surface zooplankton log abundance per cubic meter is additive in space and time; i.e., at day j, year t, site \({\textbf {s}}\):

$$\begin{aligned} \log \text {ZOOP}_{t,j}^{true}({\textbf {s}}) = \beta _{0} + \beta _{1} temp_{t,j}({\textbf {s}}) + \delta {{\textbf {1}}}_{t,j}({\textbf {s}}) + r_{j} + \eta _{t}({\textbf {s}}). \end{aligned}$$
(4)

Here, \(\beta _{0}\) is a global intercept, \(\beta _{1}\) is the coefficient that accompanies the true temperature modeled earlier, and \(\delta\) accompanies the binary variable indicating NARW presence (i.e., the presence of a whale increases in \(\delta\) units the logarithm of zooplankton abundance). Again, \(r_{j}\) indicate regime and is modeled with a dummy variable having three categories where the first regime is the reference. Finally, \(\eta _{t}({\textbf {s}})\) is a yearly spatial process providing local adjustment, centered around \(\eta _{t}\) which introduces a global annual effect. We could consider dynamics as an autoregression in the \(\eta _t\)’s. However, with a fairly small number of years we found no evidence of such autoregression. Consequently, we model \(\eta _t \sim \text { i.i.d. } N(0,\sigma _{\eta }^2)\). As for the \(\eta _{t}({\textbf {s}})\), for each t, they follow a GP with mean parameter \(\eta _t\) and a common exponential covariance function having a variance parameter \(\sigma _{\eta _{t}({\textbf {s}})}^2\) and decay parameter \(\phi _{\eta _{t}({\textbf {s}})}\).

There is no error term in (4). Again, the true surface for any day within any year is assumed to be smooth. Error terms appear when we connect the observed collection to the true. That is:

$$\begin{aligned} Y_{t,j}^{sur}({\textbf {s}})&= \log \text {ZOOP}_{t,j}^{true}({\textbf {s}}) + \epsilon _{t,j}^{sur}({\textbf {s}}), \quad{} & {} \epsilon _{t,j}^{sur}({\textbf {s}}) \sim \text { i.i.d. } N\big (0, \sigma _{sur}^2\big ), \\ Y_{t,j}^{obl}({\textbf {s}})&= {\tilde{\lambda }}_{0t}({\textbf {s}}) + {\tilde{\lambda }}_{1t}({\textbf {s}}) \log \text {ZOOP}_{t,j}^{true}({\textbf {s}}) + \epsilon _{t,j}^{obl}({\textbf {s}}), \quad{} & {} \epsilon _{t,j}^{obl}({\textbf {s}}) \sim \text { i.i.d. } N\big (0, \sigma _{obl}^2\big ), \end{aligned}$$
(5)

calibrating the oblique net tows. The \(\epsilon _{t,j}({\textbf {s}})\)’s are pure errors where we attempt to learn about the uncertainty associated with the surface and oblique measurement processes. Finally, the space-time calibration coefficients are given by

$$\begin{aligned} \begin{aligned} {\tilde{\lambda }}_{0t}({\textbf {s}})&= \lambda _0 + \lambda _{0t} + \lambda _{0}({\textbf {s}}), \\ {\tilde{\lambda }}_{1t}({\textbf {s}})&= \lambda _1 + \lambda _{1t} + \lambda _{1}({\textbf {s}}), \end{aligned} \end{aligned}$$
(6)

where \(\lambda\)’s and \(\lambda ({\textbf {s}})\)’s are defined analogously to (2) changing the notation from a’s to b’s and from v’s to w’s. In addition, \({\varvec{\lambda }} _t = (\lambda _{0t}, \lambda _{1t})^\top\) are yearly adjustments to the intercept and slope bias, respectively. These coefficients are modeled dynamically in time (West and Harrison 1997) by \({\varvec{\lambda }} _t \sim N_2({\textbf {P}} {\varvec{\lambda }} _{t-1}, {\textbf {V}}_{\varvec{\lambda }})\) and \({\varvec{\lambda }} _{2002} \equiv {{\textbf {0}}}\) where \({\textbf {P}}\) has \(\rho _{\lambda _0}\) and \(\rho _{\lambda _1}\) in the diagonal and 0’s otherwise.

As an aside, the true surface zooplankton is of direct interest with regard to connection to whale abundance (observed at the surface). However, we could be interested in overall zooplankton biomass, a more 3-dimensional view. In this regard, we could consider the oblique zooplankton observations as an appropriate measure since they collect zooplankton down to 19 ms. If so, then we would reverse the roles of the calibration above; we would view the oblique observations as varying around the truth and calibrate the surface observations.

We refer to the above specifications as a “double calibration” model and fit it to the data using all sites observed for all days within years. We fit the temperature specification and the zooplankton specification jointly as one fully hierarchical model. At any time and location, there are, potentially, four observable measurements, two temperature measurements and two zooplankton measurements. If at least one of the four measurements is observed, the observation is employed in the model fitting, i.e., we use all of the data. For a missing zooplankton or temperature measurement, we simply remove that value from the corresponding likelihood.

4.3 Model fitting details

4.3.1 Priors

The double fusion and calibration model is proposed as a Bayesian hierarchical formulation and is completely specified given priors for all the parameters. In general, these priors are weak or diffuse and, when available, conjugate prior distributions are chosen.

We consider the parameters of the temperature and zooplankton models in (3) and (4), respectively. We assign to each of the regression coefficients independent and diffuse normal priors with mean 0 and variance \(100^2\), i.e., for \(\gamma _0\), \(\gamma _1\), \(\gamma _2\), \(\beta _0\), \(\beta _1\), \(\delta\), and the two non-reference categories in \(r_j\). Additionally, the variance parameters of the spatial and temporal random effects are assigned inverse gamma priors with scale parameter and mean equal to 1, i.e., for \(\sigma _{\gamma }^2\), \(\sigma _{\gamma _0({\textbf {s}})}^2\), \(\sigma _{\eta }^2\), \(\sigma _{\eta _t({\textbf {s}})}^2\). It is not possible to estimate consistently all of the exponential covariance parameters under noninformative priors (Zhang 2004). However, with the decay parameter equal to \(3/\text {range}\), we set \(\phi \equiv \phi _{\gamma _0({\textbf {s}})} = \phi _{\eta _t({\textbf {s}})} = 3 / d_{max}\), where \(d_{max} \approx 46.6\) km is the maximum distance between any pair of spatial locations. With concern regarding prior sensitivity, we have also explored model performance over a 2-dimensional grid of \(\phi\)’s taking values \(3 / d_{max}\), \(6 / d_{max}\), \(12 / d_{max}\), \(21 / d_{max}\), and \(30 / d_{max}\). These values correspond to approximate ranges of 46.6, 23.3, 11.6, 6.7, and 4.7 km, respectively. We have found that the model performance metrics described in Sect. 4.5 are essentially insensitive to the choice of the decay parameters and the selected combination of decay choices yields the same or slightly better results than the others. In addition, the spatial interpolation using Bayesian methods becomes computationally much more manageable if \(\phi\) is kept fixed during model fitting. Finally, for the autoregressive term \(\rho _\gamma\) we assign a uniform prior over the interval \((-1,1)\).

Regarding priors for the parameters in the calibration specifications (1) and (5), we adopt inverse gamma priors as above for all the variance terms, i.e., for \(\sigma _{CTD}^2\), \(\sigma _{Therm}^2\), \(\sigma _{sur}^2\), \(\sigma _{obl}^2\). Global calibration of thermistor and log oblique is captured by \((\alpha _0,\alpha _1)^{\top }\) and \((\lambda _0,\lambda _1)^{\top }\). For these, we employ independent bivariate normal priors with prior mean equal to \((0,1)^{\top }\) and a diagonal prior covariance matrix with large diagonal entries, \(100^2\), corresponding to vague prior variances. For the coregionalization coefficients, we place vague half/folded normal priors with scale parameter 10 on \(a_{00}\), \(a_{11}\), \(b_{00}\) and \(b_{11}\), as they are related to the variances of the local adjustments; we add a vague zero-mean normal prior with variance \(100^2\) on \(a_{10}\) and \(b_{10}\), as they are related to the correlation. Noting the identifiability problem in the decay parameters mentioned above, we employ an informative uniform over the interval \((3 / d_{max}, 30 / d_{max})\) for the decay parameters \(\phi _{v_0}\), \(\phi _{v_1}\), \(\phi _{w_0}\) and \(\phi _{w_1}\) (Banerjee et al. 2014, Chapter 6). For the dynamic coefficients, \({\textbf {V}}_{\varvec{\lambda }}\) is assigned an inverse Wishart prior with 2 degrees of freedom and \({\textbf {I}}_2\) as the positive definite scale matrix. For the autoregressive terms, \(\rho _{\lambda _0}\) and \(\rho _{\lambda _1}\), we assign a uniform over \((-1,1)\).

4.3.2 Computational details

Markov chain Monte Carlo (MCMC) is used to fit the model and obtain realizations from the joint posterior distribution of all the model parameters; we employ a Metropolis-within-Gibbs version. The regression coefficients have normal full conditional distributions, the variance parameters have inverse gamma full conditionals, the autoregressive coefficients have truncated normal full conditionals, the coregionalization coefficients, as well as the covariance matrix from the dynamic specification are also conjugate. The only parameters that are not conditionally conjugate are the decay parameters that have not been fixed. They are sampled using a random-walk Metropolis–Hastings step with truncated normal proposals. We implement hierarchical centering reparameterizations to improve the mixing of the algorithm (Gelfand et al. 1995; Pitt and Shephard 1999).

4.4 Prediction to obtain zooplankton abundance

Here, we show how we implement space-time interpolation to produce zooplankton abundance maps over CCB for a given day within a given year. This is a post model fitting activity. Furthermore, and perhaps more usefully, afterward, we can create bi-weekly or yearly maps by averaging in time. In addition, averaging in space, we can obtain daily, bi-weekly or yearly time series of averages in CCB.

4.4.1 Spatial zooplankton surfaces

In order to obtain the posterior predictive distribution for true zooplankton for day j within year t at an unobserved site \({\textbf {s}}_0\), \(\text {ZOOP}^{true}_{t,j}({\textbf {s}}_{0})\), we need to introduce into (4) posterior samples of the model parameters, posterior realizations of the spatial processes, the true temperature at that time and site, \(temp_{t,j}({\textbf {s}}_{0})\), and a value of the indicator function, \({{\textbf {1}}}_{t,j}({\textbf {s}}_0)\). To obtain predictions on the original scale, we exponentiate the predictive realizations drawn from (4). Posterior samples of the model parameters are obtained from model fitting and posterior realizations of the GP’s are obtained through Bayesian kriging (Banerjee et al. 2014, Chapter 6) using posterior samples of the parameters. In a similar manner, the fusion model for the CTD data and thermistor data enables a posterior predictive distribution for true temperature at any location in CCB. For prediction, we introduce posterior predictive realizations for the true temperature at the location.

As noted above, the \({{\textbf {1}}}_{t,j}({\textbf {s}}_0)\) are supplied only for the actual observations. They are not known for the desired grid of prediction locations across the 181 days within the 17-year period. To address this, we can create a conditional zooplankton abundance map assuming the indicator is 0 everywhere or assuming the indicator is 1 everywhere. Since conditional abundance surfaces given a value of the indicator are of limited interest, we seek to marginalize over the indicator. That is, in principle, we need the probability surface, \(P({{\textbf {1}}}_{t,j}({\textbf {s}}_{0}) = 1)\), hence \(P({{\textbf {1}}}_{t,j}({\textbf {s}}_{0})=0)\), to obtain a marginal abundance for any location on a given day in a given year. Such a task is more than the currently available data can support. Instead, we focus on modeling temporal dependence for these probabilities, but we assume that they are constant over space for any given time. That is, we obtain a day within year weighting, but the weighting is global. The maps will still be spatial because the zooplankton abundance maps are; it is only the weighting for the indicator that is global.

Specifically, then, we model \(p_{t,j}\), the probability of a sighting on day j within year t on the logit scale as:

$$\begin{aligned} \text {logit } p_{t,j} = \omega _{0} + \omega _{0t} + \omega _{1} \sin (2 \pi j/365) + \omega _{2} \cos (2 \pi j/365). \end{aligned}$$
(7)

Again, \(\omega _{0}\) is the intercept, and the \(\sin\) and \(\cos\) terms are introduced to provide an annual seasonal component. Exploratory analysis shows that one harmonic is enough to capture the seasonal component of the data. The \(\omega _{0t}\)’s are i.i.d. annual random effects \(\sim N(0,\sigma _{\omega }^2)\). We note that this specification is additive in day and year. As above, the priors are \(\omega _{0}, \omega _{1}, \omega _{2} \sim N(0, 100^2)\) and \(\sigma _{\omega }^2 \sim IG(2,1)\). We fit this model using only the data from the regular stations due to concerns regarding introducing sampling bias.

After fitting the model, from the true zooplankton model in (4), according to the value of \({{\textbf {1}}}_{t,j}({\textbf {s}})\), we can obtain conditional posterior predictive realizations of \(\text {ZOOP}^{true}_{t,j}({\textbf {s}})\) for any location at any day within any year. In order to develop a marginal posterior predictive distribution at unobserved locations and times, we average these conditioned realizations using the global weights, \(p_{t,j,b}\) for \(b=1,\ldots ,B\), yielding

$$\begin{aligned} \text {ZOOP}^{true}_{t,j,b}({\textbf {s}}) = \text {ZOOP}^{true}_{t,j,b}({\textbf {s}}) \mid {{\textbf {1}}}_{t,j}({\textbf {s}})=1) p_{t,j,b} + \text {ZOOP}^{true}_{t,j,b}({\textbf {s}}) \mid {{\textbf {1}}}_{t,j}({\textbf {s}})=0) (1-p_{t,j,b}). \end{aligned}$$
(8)

With kriging, these samples can be used to provide marginal posterior predictive inference at any \({\textbf {s}}\). In particular, we can obtain the posterior predictive mean zooplankton at \({\textbf {s}}\) on day j in year t.

Continuing with (8), researchers have documented critical zooplankton density thresholds needed to promote feeding in NARW (cf. Table 5 in Gavrilchuk et al. 2021). To investigate the nature of such patches, we can use the above modeling to create the posterior predictive probability of exceedance of a specified zooplankton threshold, i.e., \(P(\text {ZOOP}^{true}_{t,j}({\textbf {s}}) > c \mid data)\). Hence, we can develop a posterior predictive probability of exceedance surface for any threshold of interest. In this regard, the realized exceedance surface is a binary map, i.e., a 0 or 1 at each location in CCB. We can not show this but rather, we can show the posterior expectation of the map, i.e., \(E({{\textbf {1}}}(\text {ZOOP}^{true}_{t,j}({\textbf {s}})> c) \mid \text {data}) = P(\text {ZOOP}^{true}_{t,j}({\textbf {s}}) > c \mid \text {data})\), the posterior predictive probability surface.

4.4.2 Zooplankton time series through block averaging

It is of key interest to infer about average zooplankton abundance over CCB for a given day j within a given year t. This becomes a block average (Banerjee et al. 2014, Chapter 7), which is a stochastic integral defined by

$$\begin{aligned} \text {ZOOP}_{t,j}^{true}(CCB) = \frac{1}{|CCB |} \int _{CCB} \text {ZOOP}_{t,j}^{true}({\textbf {s}}) \,d{\textbf {s}}, \end{aligned}$$
(9)

where \(|CCB |\) denotes the area of CCB. We approximate this integral by Monte Carlo integration of the form

$$\begin{aligned} \widehat{\text {ZOOP}}_{t,j}^{true}(CCB) = \frac{1}{|G |} \sum _{{\textbf {s}}_k \in G} \text {ZOOP}_{t,j}^{true}({\textbf {s}}_k), \end{aligned}$$
(10)

where G is a sufficiently fine spatial grid of CCB and \(|G |\) is the number of grid cells in G. In this way, with arbitrarily many posterior predictive realizations, we can learn arbitrarily well about the posterior predictive distribution for \(\text {ZOOP}_{t,j}^{true}(CCB)\). We can plot the posterior mean of these integrals versus time to see daily trends in zooplankton abundance. In addition, we can average zooplankton at a site over days within a week, a month, or within a year. Lastly, implementing the block average can lead to annual time series. We denote the yearly averages by \(\text {ZOOP}_{t.}^{true}(CCB)\), with analogous notation for their Monte Carlo version.

Instead of integrating over all of CCB in (9), a subregion of CCB could also be considered, so that the time trends in zooplankton abundance of different subregions could be compared. In a different direction, the idea of block averaging could be extended to the concept of extent (Cebrián et al. 2022). Defining the block average of the indicator \({{\textbf {1}}}(\text {ZOOP}^{true}_{t,j}({\textbf {s}}) > c)\), we can formally define the spatiotemporal extent of the exceedance of a specified zooplankton threshold. Precisely, it is the proportion of CCB which is exceeding the specified zooplankton threshold c on day j within year t.

4.5 Metrics for validation and model comparison

Model validation can only be done with regard to observed measurements. In that sense, we can validate the temperature calibration using solely the CTD and thermistor data. The zooplankton validation can be done with both the surface and oblique measurements but must be done using the full model. Since zooplankton prediction is our primary objective, we confine our validation to the full model.

For model assessment, we leave out 402 (\(20\%\)) observations as test data and we fit the models with the remaining 1610 (\(80\%\)) observations. Once MCMC samples of the model parameters are obtained, subsequent posterior predictive realizations of the true temperature are sampled for the test data. These samples are used to obtain the posterior predictive realizations for CTD and thermistor, and also to obtain posterior predictive realizations for true zooplankton. Again, these zooplankton samples are used to obtain posterior predictive realizations from surface and oblique.

We conduct model validation and comparison employing the following metrics (Castillo-Mateo et al. 2022): (1) root mean square error (RMSE), (2) mean absolute error (MAE), (3) continuous ranked probability score (CRPS), and (4) \(90\%\) coverage (CVG). The smaller the RMSE, MAE, and CRPS values, the better the model performance, and the target for CVG is proximity to 0.90. In the next section, we investigate comparison of four models.

5 Analysis

This section summarizes the results of the double calibration model in Sect. 4 fitted to the dataset described in Sect. 2. First, we validate and compare the proposed model with some parsimonious versions of it. Then, after preferring the full model (as we shall see in Sect. 5.1), we show the posterior inference for the model parameters as well as the posterior predictive spatial surfaces and time series of average zooplankton abundance.

For each fitting in the validation and comparison part as well as the fitting for the final model we use the MCMC described in Sect. 4.3. For each model, we ran two chains of the Gibbs sampling algorithm, each with different initial values, running 500,000 iterations for each chain, to obtain samples from the joint posterior distribution. The first 250,000 samples were discarded as burn-in and the remaining 250,000 samples were thinned to retain 1000 samples from each chain for posterior inference. Convergence of the algorithms (not shown) was monitored by usual trace plots and the potential scale reduction factors (Brooks and Gelman 1998).

5.1 Validation and model comparison

We compare the predictive performance of several models, according to the specification of the calibration coefficients in (2) and (6). We denote models with \({\mathcal {M}}\) and one subscript. The choices are: 1 indicates constant parameters over space and time, i.e., \({\tilde{\alpha }}_k({\textbf {s}}) \equiv \alpha _k\) and \({\tilde{\lambda }}_{kt}({\textbf {s}}) \equiv \lambda _k\) (\(k=0,1\)); 2 indicates spatially varying intercepts but constant slope parameters; 3 indicates all four coefficients spatially varying but fixed in time; and 4 indicates the full model for the calibration coefficients described in Sect. 4.

Following Sect. 4.5, Table 2 shows the performance metrics RMSE, MAE, CRPS and CVG for the test data for the four models described above. According to this table, all models perform similarly, with the full model presented in Sect. 4, \({\mathcal {M}}_{4}\), being the best. So, from here on we present the results from \({\mathcal {M}}_{4}\). The \(90\%\) prediction intervals for the test measurements with this model are plotted in Fig. 3. Beyond the summary table of RMSE’s, MAE’s, CRPS’s, and CVG’s; it is useful to show a few posterior predictive distributions for test surface, oblique, CTD and thermistor data with the observed values overlaid, to give a visual illustration of the predictive performance. Out of the 402 observations for each type of measurement to be validated, 26 were missing for oblique, 58 for surface, 303 for CTD, and 74 for thermistor. Among the available measurements, \(88.6\%\), \(90.7\%\), \(87.9\%\), and \(88.1\%\) of the \(90\%\) predictive intervals correctly included the observed values, indicating that the model is performing as it should for out-of-sample predictions.

Table 2 Performance metrics (RMSE, MAE, CRPS and CVG) for the four elements of interest (log surface, log oblique, CTD and thermistor) in the models \({\mathcal {M}}_{1}\), \({\mathcal {M}}_{2}\), \({\mathcal {M}}_{3}\) and \({\mathcal {M}}_{4}\)
Full size table
Fig. 3
figure 3

Posterior predictive mean and \(90\%\) intervals (gray) for test log surface, log oblique, CTD and thermistor measurements (black), respectively

Full size image

5.2 Parameter estimates

Section S2.1 of the SI gives a detailed description with tables and figures of each of the parameters and processes of the model \({\mathcal {M}}_{4}\). Here, we give a summary of the main conclusions regarding zooplankton modeling in (4) and the calibration of measurements with (1) and (5). The most important parameters are summarized in Table 3.

Table 3 Posterior mean and \(90\%\) credible intervals for some model parameters
Full size table

Regarding the zooplankton modeling from (4), since \(\beta _1\) is significantly positive, higher SST explains higher concentrations of zooplankton. The significance of \(\delta\) asserts a larger intercept in the presence of whales than without it. This increases expected zooplankton abundance when a whale is near a site, in agreement with the expectation that whales identify areas of rich prey. However, whales are not continuously feeding and may be displaying other behaviors, e.g., engaging in surface active groups or traveling. In these instances we would not necessarily expect zooplankton abundance to be higher in the vicinity of whales. Distinguishing between these behaviors is beyond the scope of the present work. Further parameter inference is supplied in the SI, where we see that only the second regime is significant with the first as the base. However, the annual random effects show temporal variability across years. The estimates of the variance components show that there is more unexplained variability in the pure errors than variability in the spatiotemporal effects. It is also seen that the surface measurement process has approximately three times more variance than the oblique measurement process on the log scale.

Focusing on the calibration of measurements with (1) and (5), the main result is given by the global coefficients of the calibrations, i.e., \(\alpha _0,\alpha _1,\lambda _0,\lambda _1\). On average, thermistor measurements are shifted by 1 °C from true temperature and for every degree that it increases, the thermistor measurements increase by almost 1 °C. On the other hand, the log oblique measurements have a shift of four and a half units (\(\text {organisms}/\text {m}^3\) on a log scale) with respect to the true log zooplankton; each unit that this increases results in an increase in the log oblique measurements by an average of half a unit.

5.3 Prediction of zooplankton surfaces and time series

For prediction, we need the probabilities of NARW presence, and the parameter estimates associated with its temporal model (7) are given in Sect. S2.2 of the SI. We also need a fine grid of G points within CCB. We choose G with resolution of \(1 \text { km} \times 1 \text { km}\) yielding \(|G |= 1580\) grid cells. This grid is shown in Fig. S14 of the SI. Altogether, the entire posterior predictive time series results in very large data files from which maps and time series are computed. For instance, we have 17 years by 181 days by 1580 grid centroids by 2000 replicates yielding approximately 10 billion points.

With regard to space, we illustrate daily predictions of spatial surfaces for three illustrative days: 29 April 2011, 21 March 2017, and 17 April 2019. The predicted mean surfaces of zooplankton abundance and their standard deviation at these days are given in Fig. 4, at the top and the bottom, respectively. At the top, there are large differences with regard to the locations of highs and lows between the three maps. Also, there is more spatial variation in the predicted means for day 29 April 2011 than for days 21 March 2017 and 17 April 2019. The maps of the standard deviations show similar spatial patterns. They tend to be larger where mean levels are larger. Because the mean levels were larger for day 29 April 2011, the standard deviations are larger for day 29 April 2011. The block averages for these days are 1090.3, 383.0, and 442.3 \(\text {organisms}/\text {m}^3\), respectively.

In addition to the average zooplankton of CCB, the probability of threshold exceedance is of interest because it provides inference on the response of NARW to higher prey availability (Gavrilchuk et al. 2021). We started with a threshold value of 1000 \(\text {organisms}/\text {m}^3\) (Mayo and Marx 1990), with recent analyses suggesting both higher and habitat-specific threshold values (Sorochan et al. 2021). Figure 5 show \(P(\text {ZOOP}^{true}_{t,j}({\textbf {s}}) > 1000 \mid data)\) at the top and \(P(\text {ZOOP}^{true}_{t,j}({\textbf {s}}) > 1500 \mid data)\) at the bottom. Note that the scale is different for each plot and the “white” is set to the mean level of the bay for that particular day. The spatial pattern is the same as in the previous figure, the day 29 April 2011 has a much higher average probability of exceeding the thresholds than the other 2 days, whose probabilities do not exceed 0.1.

Fig. 4
figure 4

Maps of the mean (top) and standard deviation (bottom) of the posterior predictive distribution of zooplankton abundance at 29 April 2011, 21 March 2017, and 17 April 2019, respectively

Full size image
Fig. 5
figure 5

Maps of the posterior probability of exceeding zooplankton thresholds \(c = 1000\) (top) and 1500 (bottom) at 29 April 2011, 21 March 2017, and 17 April 2019, respectively

Full size image

To show inference for a longer period of time we represent the posterior mean of the annual prediction surface in Fig. 6. Illustrative bi-weekly predictions are shown in Sect. S2.2. Here, we observe both, variation across space and time of zooplankton abundance.

Fig. 6
figure 6

Map of the posterior mean of the spatial predictions of annual average zooplankton abundance, \(\text {ZOOP}_{t.}^{true}({\textbf {s}}) = \frac{1}{181} \sum _{j=1}^{181} \text {ZOOP}_{t,j}^{true}({\textbf {s}})\), for \(t=2003,\ldots ,2019\)

Full size image

With regard to time, we illustrate block average daily and annual predictions, i.e., \(\widehat{\text {ZOOP}}^{true}_{t,j}(CCB)\) and \(\widehat{\text {ZOOP}}^{true}_{t.}(CCB)\). We also consider \(\widehat{\text {ZOOP}}^{true}_{t,r_j=3}(CCB)\), i.e., rather than averaging zooplankton abundance across all the period, only predictions from the third regime are considered. In addition, we show extents of the event \({{\textbf {1}}}(\text {ZOOP}_{t,j}^{true}({\textbf {s}}) > 1000)\) across days and years. The predicted time series and extents on a daily scale are given in Fig. 7. Figure 8 shows annual dynamics, showing years with higher abundance of zooplankton than others, and consequently, years with higher average extents than others. The years 2010 and 2017 have the greatest abundance and extent; 2015 is the year with the least. Some of this variability is due to the NARW-focused sampling, e.g., in 2010 there was a considerable amount of sampling in the vicinity of skim-feeding NARW’s. These higher observed abundances likely increased the estimates for 2010. In 2017, while the zooplankton abundance followed the typical increasing-decreasing pattern seen in other years during the winter/spring period, higher concentrations were observed throughout the seasonal period. In addition, high concentrations of Calanus finmarchicus resulted in an extended zooplankton enriched resource.

In general, variability of the mean total zooplankton concentrations can be attributed to the high spatial variability with zooplankton found in very high concentrations in relatively small patches and extensive areas of low concentration. We assume that the spatial variability is due to environmental factors that form these patches along with the seasonal and behavioral responses of the zooplankton resource that varies by taxon (Folt et al. 1999; Hudak et al. 2023). In addition, the annual estimates of zooplankton abundance fit well with observations of NARW abundance (results not shown).

Fig. 7
figure 7

Posterior mean of the time series of zooplankton abundance per cubic meter (top) and of the extent of the event \({{\textbf {1}}}(\text {ZOOP}_{t,j}^{true}({\textbf {s}}) > 1000)\) (bottom) in CCB by day through block average

Full size image
Fig. 8
figure 8

Posterior mean of the time series of zooplankton abundance per cubic meter (left) and of the extent of the event \({{\textbf {1}}}(\text {ZOOP}_{t,j}^{true}({\textbf {s}}) > 1000)\) (right) in CCB averaged by year through block average

Full size image

6 Summary, discussion, and future work

Zooplankton are an important food source for fish and whale species. To better understand their dynamics in a critical habitat for planktivorous NARW’s, we have developed a multi-level model to learn about the spatial and temporal sea surface abundance of this prey. While a better understanding of the foraging ecology of NARW has motivated much of the data collection in CCB, here we have focused primarily on understanding the spatial and temporal distribution of zooplankton. We have used two sources for zooplankton collection along with two sources for SST, as a regressor to build this model. The modeling required fusion and calibration for each of the two data sources. The resulting model was applied to data collected over 17 years from CCB, MA, USA, and enables us to develop space-time abundance surfaces as well as probability exceedance surfaces over CCB. Using block averaging, the abundance surfaces were employed to yield average daily abundance for CCB. Also averaging to weeks, months, or years enables a useful, coarser picture of average abundance.

The issue of scale for foraging NARW is critical, and there are likely several scales over which they make foraging decisions. The spatial and temporal scales at which right whales actually open their mouths to feed are smaller than we are able to capture here; there is likely local increase/decline in abundance that is critical to NARW, which we cannot capture. However, with estimates of exceedance probability (Fig. 5) we can make initial comparisons of the prey resources to CCB-wide aerial observations of feeding NARW. Nevertheless, CCB remains a critical foraging habitat for right whales due to the phenological cycle of their prey and limited inter-annual changes in prey abundance (Hudak et al. 2023).

Acknowledging substantial seasonal variation in abundance behavior for the primary species included in the zooplankton database, future work will explore joint space-time modeling for copepods and NARW. Also, there is an additional SST data source available, HYCOM (Cummings and Smedstad 2013) that has wide coverage over the bay, but is recorded at a coarse spatial resolution relative to the spatial extent of CCB. Future work will assess whether this additional source of temperature data can help the fusion for a SST regressor. Also, there is an additional zooplankton catch data source, vertical pump sampling up through the water column. Fusion with this source will also require careful calibration, particularly because it is never collected jointly with the surface and oblique tow net collection. A further opportunity will move our modeling to a larger spatial area to attempt to extract a zooplankton gradient over the spatial domain, driven by SST, e.g., through joint modeling of the ECOMON dataset (Hare 2021).

An exciting future challenge involves the consideration of bioenergetics. That is, can we demonstrate an association between high zooplankton abundance and high NARW abundance. This will require joint modeling for both abundances. In a generative sense, we will attempt the joint modeling through a conditional times marginal specification, i.e., a marginal model for zooplankton abundance (using some of what we have learned from the present work) and then a conditional whale abundance model given zooplankton abundance. For this modeling, we will have several whale abundance data sources, including distance sampling data (Ganley et al. 2019), passive acoustic monitoring data (Clark et al. 2010), and opportunistic data collection (i.e., the whale sighting data noted herein), resulting in a very demanding space-time data fusion challenge.