1 Introduction

There is general acceptance of the idea that “the primary goal of mathematics instruction should be to have students become competent problem solvers” (Schoenfeld, 1992, p. 334). Indeed, problem solving is widely considered the cornerstone of educational curricula and a keystone of theoretical frameworks to assess international student achievement. However, the degree of success in developing this skill varies substantially across students from different countries. According to the latest Trends in Mathematics and Science Study (TIMSS) report (Mullis et al., 2020), 55% of fourth-grade Singaporean students achieved an advanced level of mathematical proficiency that enabled them to solve the most complex problems presented to them. In contrast, only 4% of Spanish students reached that level. These disparities could be attributed to how Singaporean families approach their children’s education (e.g., family involvement in school education, the general importance of education in society, and the value placed on the meritocracy) and to education policies, such as the available budget for education (Rao et al., 2010). However, there are other elements of mathematics education—for instance, how math problems are implemented in lesson plans—that can help us to understand the reasons behind that performance gap (Chapman, 2006).

The current study is focused on primary school math textbooks, as they are widely used by teachers to support student mastery of math problems (Depaepe et al., 2009; Hiebert et al., 2003). Furthermore, there is evidence that the content of textbooks may influence the level of competence that students develop (e.g., Fagginger Auer et al., 2016; Heinze et al., 2009; Törnroos, 2005; Siegler & Oppenzato, 2021; Sievert et al., 2019, 2021). Specifically, we looked at arithmetic word problems (AWPs) since they are considered prime tools for promoting the development of student problem-solving competence in primary school (Verschaffel et al., 2020). The aim of this study was to compare how math textbooks from Singapore and Spain promote the skills to solve arithmetic word problems. To that end, we analyzed whether there are differences in the quantity and characteristics of AWPs and illustrations that accompany AWPs in primary education textbooks from both countries. In what follows, we define what AWPs are, which problem-solving strategies are available for solving different types of AWPs, which characteristics of AWPs may affect how children approach and solve word problems, how illustrations may support problem solving, and how textbooks in general contribute to students’ mathematical performance.

1.1 What are arithmetic word problems?

There are multiple interpretations of the term “math problem solving”. Schoenfeld (1992) differentiates between working routine exercises aimed at providing practice on a particular mathematical technique—a skill worthy of instruction in its own right—and solving difficult or perplexing problems (Schoenfeld, 1992).

One type of mathematical problem that is considered a prime tool for teaching both the skills to use mathematics to make sense of everyday situations and general heuristic and metacognitive skills that are needed to solve difficult problems (in terms of Polya, 1945) are AWPs (Verschaffel et al., 2020). An operational definition is that AWPs are verbal descriptions of problematic situations that give rise to one or more questions whose answers can be obtained by applying mathematical operations to the numerical data presented in the problem (Verschaffel et al., 2020).

Different models have been formulated to describe how children approach and solve arithmetic word problems. For example, Verschaffel et al. (2000) suggest two approaches to arithmetic word problem solving: genuine and superficial. The first would allow students to solve any type of word problem—independent of complexity and difficulty—and involves an understanding of the problem’s mathematical structure by using mathematical reasoning. The superficial approach involves a direct leap from the data to the operation and then to the result. This approach to word problem solving may be useful for simple problems that can be solved in a straightforward manner by applying little or no reasoning, but it is problematic in regard to more complex problems that do require different types of reasoning to be solved (see below how simple and complex problems are operationalized). Among the strategies that rely on that superficial approach are (i) direct modeling of the actions suggested by the problem text by means of concrete materials, such as blocks or fingers (Riley & Greeno, 1988) and (ii) “key word strategy”, once children face AWPs at the symbolic level with numerals, by taking some words (e.g., “won”) as a cue for choosing an arithmetic operation (e.g., addition), without paying attention to other (con)textual inputs (Hegarty et al., 1995; Verschaffel et al., 1992).

Verschaffel et al.’s model indeed underscores the idea that there are different types of AWPs whose representation and resolution involve different levels of complexity and, therefore, problem-solving strategies. In the same vein, the theoretical framework underlying TIMSS links achievement on different kinds of word problems to a general achievement level in mathematics. Students who have low to intermediate levels of math achievement can only solve the simplest word problems. However, those who have high or advanced math achievement levels can solve problems that require deep conceptual understanding and/or heuristic or metacognitive thinking.

To determine the level of complexity of AWPs, different criteria have been suggested (see Daroczy et al., 2015). Among these criteria, the semantic-mathematical structure of the problem has been found to determine the level of complexity of a problem to a large extent (Carpenter & Moser, 1984; Greer, 1992; Heller & Greeno, 1978; Vergnaud 1991) as well as the strategies required to solve it (Carpenter et al., 1981). One-step additive AWPs can be categorized following the well-established classification proposed by Heller and Greeno (1978) and Carpenter and Moser (1984) as change, compare, combine, and equalize problems. Furthermore, different subcategories can be established depending on the unknown set and the association (additive or subtractive) between the sets involved in the problem (see Fig. 1).

Fig. 1
figure 1

Types of additive structure AWPs (adapted from Heller & Greeno, 1978 and Carpenter & Moser, 1984)

Full size image

Based on a similar analysis, multiplicative AWPs, which are intrinsically more complex (Verschaffel et al., 2007), can be classified according to the semantic-mathematical structure (although the categorization is less established). For instance, depending on the operation required and the unknown set, four types of multiplicative AWPs can be distinguished, each of which consists of different subcategories: (1) rate (or equal groups), (2) multiplicative comparison (or scalars), (3) Cartesian product, and (4) rectangular matrix (Greer, 1992; and Vergnaud 1991, see Fig. 2).

Fig. 2
figure 2

Types of multiplicative structured AWPs (adapted from Greer, 1992 and Vergnaud, 1991)

Full size image

This classification also reflects different processing levels. Following Verschaffel et al. (2000), some of these AWPs can be solved in a direct and straightforward manner, while others require deeper levels of comprehension. Simple AWPs (e.g., Change 1, according to Fig. 1) can be solved by using the word “won” and directly modeling the action described in the word problem (i.e., joining the $5 I had to the $3 I earned). Alternatively, “won” can be used as a cue for adding the two numbers provided in the problem. However, more difficult AWPs can only be solved by reasoning about the relations among numbers and applying specific conceptual knowledge, such as understanding part-whole relations or proportional reasoning. For example, the multiplicative multiple-rate AWPs in Fig. 2 cannot be solved by direct modeling or simply using the keyword strategy; the complex structure of such an AWP must be unraveled before the student is able to solve the problem by applying, for instance, a rule-of-three or another solution strategy.

In line with this theoretical framework, it is assumed that the adequate development of a genuine approach to solving AWPs is contingent on facing a variety of AWPs that include both simple and complex problems (Despina & Harikleia, 2014; Schoen et al., 2021; Xin, 2007). This idea is also in line with the variation theory of learning (Marton, 2015). According to this theory, learners must experience variation in the types of problems they face to discern and focus on the fundamental aspects of problem solving. In other words, to generalize the idea of what solving AWPs entails and to develop adequate problem-solving strategies, students must perceive the similarities associated with solving different types of AWPs. This skill leads students to avoid focusing on superficial cues (e.g., the keyword strategy) as a general approach to solving any type of arithmetic word problem. It is noted that even problems that require only one-step addition or subtraction involve different semantic-mathematical structures, which makes the superficial approach to problem solving prone to error.

1.2 Influence of illustrations on arithmetic problem solving

The mathematical reasoning that is necessary to solve a wide variety of AWPs (and using strategies other than direct modeling or the keyword strategy) can be scaffolded by providing graphical cues such as illustrations that facilitate comprehension of mathematical information (see, for example, Chan & Kwan 2021). Illustrations can be defined as any pictorially or schematically depicted information that is presented next to a word problem (e.g., drawings, photographs, graphs, schemata; see Dewolf et al., 2014).

It is important to note that various taxonomies of illustrations have been distinguished (Berends & van Lieshout, 2009; Dewolf et al., 2015). For example, Elia & Philippou (2004) classified illustrations as decorative (when no information concerning the solution of the problem is provided), representational (when information concerning the content of the problem is provided), informational (the illustration can be considered the basis of the problem), and organizational (those that support the solution procedure, for example, by means of schematic representations of the mathematical structure of the problem).

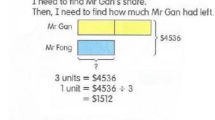
Several studies have found that providing students with schematic organizational representations of the problem contributes effectively to solving word problems (see Xin, 2019). In contrast, representational illustrations have shown inconclusive evidence (Hegarty & Kozhevnikov, 1999; Vicente et al., 2008). The idea that schematic representations of the semantic-mathematical structure of AWPs improve student performance has received wide empirical support from so-called schema-based instruction (SBI), which is a method of teaching problem solving that emphasizes both the semantic structure of the problem and its mathematical structure (Marshall, 2012). SBI integrates schema theory with the effectiveness of relational diagrams. Relying on Bruner’s (1973) stage theory of development, it is assumed that presenting math problems in an enactive or iconic way may overcome the difficulties associated with problems that cannot be understood symbolically. The model method (Kho, 1987), which can be considered one of the basic elements of mathematics education in Singapore, is an example of SBI (Kaur, 2019). This method uses structured processes whereby students are taught to visualize abstract mathematical relations and their varying problem structures through schematic representations (Ferrucci et al., 2008) before solving the word problem (see Kaur 2019). Thus, illustrations used by the model method can be considered organizational illustrations in terms of the classification of Ellia and Philippou (2004) because these illustrations represent the mathematical structure of the problem and support students’ problem solving.

1.3 Textbooks as part of the educational system

Textbooks constitute a fundamental part of the teaching-learning process in the classroom. According to activity theory (Rezat, 2006), textbooks can be considered a type of cultural artifact that teachers and students use in a culturally mediated context (i.e., the classroom) to achieve a given objective (e.g., that students learn to solve problems), hence establishing a triad “subject-mediating artifact-object”. Textbooks are important cultural artifacts for teaching mathematics because they are frequently and intensively used by teachers in most countries around the world (Depaepe et al., 2009; Hiebert et al., 2003). Therefore, textbooks determine what is taught and learned in the classroom to a large extent (Apple, 1992; Oates, 2014). There is empirical evidence that certain aspects of textbook design influence students’ mathematical proficiency, including word problem solving (see Chang & Silalahi 2017, and Sievert et al., 2019, for a review). Indeed, students perform better on topics that are more extensively covered in textbooks (Schmidt et al., 2001; Törnroos, 2005). For instance, students learn basic arithmetic principles better when the frequency of related activities is higher (e.g., Sievert et al., 2021); similarly, students more frequently use the problem-solving strategies that are more emphasized in textbooks (e.g., Fagginger Auer et al., 2016; Heinze et al., 2009, Sievert et al., 2019, 2021). In fact, topics that are not included in textbooks are not usually taught and learned in class (Schmidt et al., 1997). For instance, students are often less proficient in solving certain fraction and decimal mathematical problems, which are rarely found in books (Siegler & Oppenzato, 2021).

In this vein, it is feasible that textbooks from high-performing countries such as Singapore may present more opportunities for students to solve a wider variety of AWPs than those from low- to mid-performing countries. Indeed, lack of experience with some types of problems and/or certain types of schematic representations may hinder children’s learning (Siegler & Oppenzato, 2021). There is evidence that textbooks in high-performing countries contain a more diversified and balanced distribution of both additive and multiplicative AWPs across different problem types than textbooks in countries such as the U.S. (e.g., Schoenfeld, 1991; Stigler et al., 1986; Xin, 2007) and Spain (e.g., Orrantia et al., 2005: Tárraga et al., 2021; Vicente et al., 2018). There is also evidence that textbooks from high-performing countries provide richer illustrations (i.e., diagrams, graphs, models, tables, pictures, manipulatives) that may support student understanding of mathematical structures (Chang & Silalahi, 2017). For example, Mayer et al. (1995) found that Japanese textbooks contained more relevant illustrations than U.S. textbooks and used more meaningful instructional methods that emphasized using different ways of representing problems as words, symbols, and pictures. In the same vein, Vicente et al. (2020) found that while 75% of problem-solving approaches proposed by primary education mathematics textbooks from Singapore included a step to represent the mathematical structure of the problem, only 15% of approaches in Spanish textbooks contained that step.

In sum, although we cannot assume a direct and causal link between the content and design of mathematical textbooks and how well students perform in international assessments, the literature suggests that textbooks play a significant role in the effectiveness of mathematical teaching and learning processes by providing (i) sufficient opportunities to solve AWPs, (ii) a wide variety of AWPs that stimulate different strategies and levels of mathematics reasoning, and (iii) graphical support to enable the understanding and learning of different semantic-mathematical structures.

2 The present study

The aim of the present study was to investigate whether math textbooks from high-performing countries such as Singapore are more effective in supporting student reasoning and learning than those from average-performing countries such as Spain. We argued that such effectiveness relates to students’ access to a variety of AWPs. To this end, we focused on three aspects of math textbooks: (1) proportion of AWP activities in textbooks; (2) variety of AWPs according to their semantic-mathematical structure; and (3) whether AWPs are accompanied by schematic illustrations.

When comparing textbooks from different countries, it is important to examine some aspects of the broader educational systems in which they are used (Li, 2007). In both the Singaporean and Spanish educational systems, the math curriculum is designed in a spiral or cascade form so that the concepts and skills of each piece of content are reviewed and built upon at each new level to achieve greater depth and understanding (Kelly et al., 2020). As such, both curricula reflect a constructivist approach to mathematics education. There are also some differences. First, the Singaporean curriculum includes some types of problems (i.e., algebra and ratios) that are not included in the Spanish curriculum. Second, while no theoretical framework is explicitly used in the Spanish curriculum, in Singapore, the Mathematics Curriculum Framework (Ministry of Education, 2020) has been used as a basis to design the mathematics curriculum. This framework considers the concrete-pictorial abstract (C-P-A) approach as a central aspect of developing mathematical ability.

3 Method

3.1 Procedure

All AWPs included in primary school math textbook series of the main publishers (in terms of percentage of distribution across schools) in Singapore and Spain—Marshall Cavendish 2015 edition (hereafter, MC) and Santillana 2010 edition, respectively—were considered in the current study. In Singapore, mathematics textbooks produced by MC were used in 86% of schools (Clark, 2013), while Santillana’s textbook, from the largest publisher in Spain, was used in 43.16% of schools (see Vicente et al., 2020).

The AWPs that were analyzed corresponded to tasks that (i) included a verbal description of real or imaginary situations by posing a mathematical question that required at least one of the four basic arithmetic operations and (ii) could be classified as any of the research-based additive or multiplicative AWP structures described in Figs. 1 and 2. AWPs that were contextualized as worked-out examples were also considered. Arithmetic problems that did not meet the abovementioned criteria, such as solving arithmetic operations or using calculations to solve situations insufficiently contextualized as problems (for instance, “multiply to calculate the number of flowers”, based on the drawing of five vases with four flowers each), were not considered AWPs. Other types of math problems (e.g., algebra, statistics, and geometric problems such as calculating perimeters) were not considered for the purposes of the current study.

3.2 Categories of analysis: AWPs vs. other Mathematical Activities (OMAs)

We considered “activity” as each task or set of related tasks that constituted a separate instructional activity on a textbook’s page, as indicated by the heading, number or instruction on top of the activity or by any other layout aspect. In these activities, students had to provide or were shown how to provide an answer to one or more questions usually requiring calculations or the application of other types of mathematical knowledge. Each activity presented in the textbooks was assigned to two different categories: (1) AWP solving activity and (2) other mathematical activity (hereafter OMA). AWP-solving activities included one or more AWPs. Therefore, the number of AWP-solving activities was lower than the number of AWPs. OMAs included mostly exercises and, to a much lesser extent, mathematical problems other than AWPs. We identified 14,570 activities (7,989 in MC and 6,581 in Santillana), of which 3,439 were AWP activities (2,131 in MC and 1,308 in Santillana). Only these AWP activities were further analyzed. They included a total number of 5,155 AWPs (2,646 in MC and 2,509 in Santillana).

3.3 Categories of analysis: Semantic/Mathematical structure

Two different classifications were used depending on whether the problem involved an additive or a multiplicative structure. Multistep AWPs were first decomposed into their constituent parts, and then each part was classified in terms of its semantic/mathematical structure. In the current study, 7,755 semantic/mathematical structures were analyzed (3,832 in MC and 3,923 in Santillana).

Types of additive AWPs

These structures corresponded to problems that involved, exclusively, addition or subtraction. Problems were categorized as change, compare, combine, and equalize problems, following Heller and Greeno (1978) and Carpenter and Moser (1984). Different subcategories (20) were established depending on the unknown set and the existing relationships (additive or subtractive) between the sets involved in each AWP (see Fig. 1 above).

Types of multiplicative AWPs

These problems exclusively involved multiplication or division. Following Greer (1992) and Vergnaud (1991), four types of multiplicative AWPs were distinguished: (1) rate (or equal groups), (2) multiplicative comparison (or scalars), (3) Cartesian product, and (4) rectangular matrix. Different subcategories (14) were established depending on the unknown set and the operation (multiplication or division) necessary to solve each AWP (see Fig. 2 above).

3.4 Categories of analysis: illustrations

Only illustrations directly provided by the textbooks were included in the analyses. We considered whether illustrations helped students understand the mathematical structure of problems and whether illustrations provided data as part of the wording of the problem. Thus, for the purposes of the current study, we used an adaptation of the classification suggested by Ellia and Philippou (2004) and distinguished three distinctive types (see Fig. 3):

  1. a)

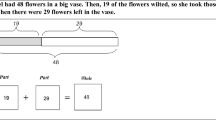
    Figurative: These are pictorial illustrations that depict an element, part, or the whole situation of the problem, but (i) no information concerning the solution is given (this corresponds to decorative illustrations in Elia & Philippou, 2004), (ii) no numerical data are provided, and (iii) no reference to the mathematical structure is shown (this corresponds to representational illustrations in Elia & Philippou, 2004).

  2. b)

    Informational: These are pictorial illustrations, tables, and graphs that contain data that are needed to solve the problem (i.e., these illustrations replace the text of the problem as a source of information).

  3. c)

    Organizational: These are schematic illustrations that represent a part or the whole mathematical structure of the problem in such a way that enables students to understand the mathematical relations between the problem sets. These illustrations can also include the numerical data of the problem. Singaporean “bar modeling” would be included in this category.

Fig. 3
figure 3

Examples of each type of illustration analyzed. Note: The figurative illustration was adapted from Santillana, Book 2, p. 49. Informational and organizational illustrations were adapted from the same AWP found in MC, Book 2B, p. 23

Full size image

3.5 Data coding

First, the percentage of activities devoted to solving AWPs (as defined in the procedure) in each textbook was calculated. Second, to determine the variety of semantic-mathematical structures included in each textbook, each one-step problem was categorized as additive or multiplicative and assigned to one of the subcategories mentioned above (see Figs. 1 and 2). AWPs that must be solved with two, three, four, or more steps were decomposed into individual structures, which were categorized separately, so the number of structures was larger than the total number of AWPs that were identified. Finally, to analyze the role of illustrations, we first calculated the percentage of AWPs accompanied by illustrations. In this regard, it should be noted that a small proportion of problems in the Singaporean-published textbook (1.93% of the total) and the Spanish-published textbook (5.46%) were accompanied by two illustrations (a figurative and an organizational illustration in all cases in the Singaporean textbook and a figurative and an informational illustration in all cases in the Spanish textbook; see Fig. 3 for an example). All illustrations were then classified according to their functions as figurative, informational, or organizational. AWPs with double illustrations received two scores.

The different categorizations (AWP activities vs. OMAs, the AWP semantic-mathematical structure, and type of illustration) were initially carried out jointly by the first and third authors of the paper until the criteria necessary for a reliable analysis had been established. Discrepancies were resolved by discussion among all authors. Once these criteria were established, the first author focused on the semantic-mathematical structure of the AWPs, while the third author analyzed the other categorizations.

3.6 Data analysis

Given the amount and type of data that were generated, a quantitative analysis was performed. Because of the nature of the data, we used nonparametric statistics. Pearson’s chi-square test (or Fisher’s exact test where necessary) was used to determine whether there was an association between the textbook publisher and (1) the frequency of tasks devoted to AWP solving, (2) the variety of types of semantic-mathematical structures, and (3) the types of illustrations. To compare specific types of AWPs between publishers, z-tests with Bonferronni adjustment for multiple comparisons were performed. To check the effect size, we used the Cramer V statisticFootnote 1, which, according to Cohen (1988), indicates whether the effect is small (0.1), moderate (0.3) or large (0.5).

To provide additional evidence regarding the variety of semantic-mathematical structures in each publisher, we followed the approach described in Petersson et al. (2021) and estimated Lorenz curves to assess whether the distribution of types of AWPs was balanced. Note that wider variety does not imply that the distribution of types of AWPs is balanced, since some types may be more frequent than others. The Lorenz curve is often used to describe and compare inequality in income or wealth distribution. The Lorenz curve is defined as the relation between the cumulative proportions of population (%Pi) and the cumulative proportions of income (%Yi), so if each percentage of the population has the same percentage of income (Pi = Yi; ∀ i), a 45° line is observed (the so-called “perfect equity line”). Equity refers to homogeneity in the distribution of categories. Thus, since the Lorenz curve shows a relative cumulative distribution and represents the proportional totality of all sorted or ordered data, it can be used to show the cumulative distribution of each kind of AWP as a proportion of all AWPs in the textbook. In the current study, as the Lorenz curve approaches the diagonal, greater equality across problem structures would be observed, i.e., different problem structures are equally presented in textbooks.

3.7 Hypotheses

According to both the theoretical framework presented above and findings from previous studies regarding the relation between mathematics textbooks and the level of mathematics competence (as well as findings from international assessments), our hypotheses were as follows:

First, given that Singaporean students are more proficient AWP solvers than Spanish students (Mullis et al., 2020) and that previous studies have shown that proficiency with specific math concepts corresponded to what is more frequently practiced (Törnroos, 2005; Schmidt et al., 2001), we expected that Singaporean math textbooks contained a higher proportion of AWP-solving tasks in relation to the total number of math tasks (Hypothesis 1).

Second, given that experience with different types of problems may enhance children’s learning (Siegler & Oppenzato, 2021), we expected that Singaporean textbooks would include a richer or wider variety of AWPs according to the semantic-mathematical structure (Hypothesis 2a). Furthermore, we expected that the distribution of AWPs by type of structure (additive and multiplicative) in Singaporean textbooks would be more balanced. The Lorenz curve regarding the Singaporean textbook would be closer to the perfect equity line (Hypothesis 2b).

Third, the literature review does not suggest that AWPs in Singaporean textbooks are more frequently accompanied by illustrations than those in Spanish textbooks. Nonetheless, given that the model method is the basis of mathematics education in Singapore (Kho, 1987) and that this model shows students how to visualize abstract mathematical relationships through schematic representations (Ferrucci et al., 2008), we expected that Singaporean textbooks presented a higher proportion of organizational illustrations than Spanish textbooks (Hypothesis 3).

4 Results

4.1 Frequency of AWP-solving activities

The Singaporean textbook contained 7,989 math activities; 2,131 (26.67%) were AWP-solving activities. The Spanish textbook contained 6,581 activities, and 1,308 (19.87%) corresponded to AWP-solving activities. A chi-square test revealed that as predicted in Hypothesis 1, math textbooks in Singapore had a larger proportion of AWP-solving activities than those in Spain (AWPs vs. OMAs), χ2 (1, n = 14,570) = 92.49, p < .001. It is noted that the effect size was small (0.08).

4.2 Problem variability

A total of 7,755 structures were analyzed. Out of the 3,923 basic structures that were analyzed in the Singaporean textbook, 59.19% were additive structures. Out of the 3,832 structures that were analyzed in the Spanish textbook, 53.3% were additive.

4.2.1 Additive structures

Table 1 shows that Singaporean textbooks included problems corresponding to 18 different types of structures (90% of all possible additive structures), while problems in Spanish textbooks corresponded to 16 different types of structures (80%). Fisher’s exact test revealed similar variability in regard to additive structures (p > .66).

Table 1 Frequencies in absolute numbers and percentages of each type of additive structure per publisher
Full size table

Regarding the balance of the distribution of AWPs across types of additive structures, the Lorenz curves (see Fig. 4) showed that this distribution was slightly more balanced in the Singaporean textbook than in the Spanish textbook.

Fig. 4
figure 4

Adapted Lorenz curves for the distribution of additive semantic-mathematical structures found in Singaporean and Spanish textbooks

Full size image

Nonetheless, a chi-square goodness-of-fit test showed that neither the Singaporean textbook nor the Spanish textbook provided students with a balanced distribution of experience across different types of structures, MC: χ2 (17) = 4,417.69, p < .001; Santillana: χ2 (15) = 5,198, p < .001). A closer look at Table 1 shows that even if 90% of the 20 different structures were included in the Singaporean textbook, students were not provided with a similar experience across all mathematical structures. In fact, most types of structures in Singaporean textbooks were observed to have frequencies that were either well below or well above 113 (or 5% of the total number of structures that were identified); this was the expected frequency for each type of structure in an equiprobability model, in which textbooks would provide students with a similar experience across different types of structures (i.e., similar observed frequencies). Data pertaining to the Spanish textbook showed a similar pattern.

It is worth mentioning that three types of basic structures—Combine 1 and 2 and Change 2, which can be considered low- (Combine 1 and Change 2) or medium-difficulty (Combine 2) problems according to several studies (Nesher, 1981; Rathmell, 1986; Riley & Greeno, 1988; Riley et al., 1983)—together amounted to 61.8% and 69.9% of additive structures in Singaporean and Spanish textbooks, respectively, while the vast majority of categories showed very small frequencies in both textbook series. This result challenges the interpretation of problem variety in math textbooks. Note that some categories (e.g., Change 5 and 6, Compare 5 and 6, and all categories of Equalize problems) were almost nonexistent in the Spanish textbook, so the distribution of problems in the Spanish textbook could be considered even more unbalanced than in the Singaporean textbook.

Some differences between textbooks were observed in specific types of structures. For instance, the Singaporean textbook included significantly more Change 3, 4, 5 and 6 problems and Compare 4, 5 and 6 problems than the Spanish textbook. It is noted that these problems can be considered medium- and high-difficulty problems according to the studies reported above. Conversely, the Spanish textbook included more Combine 1, Change 2 and Compare 1 and 2 problems, which can be considered easy-to-solve problems.

4.2.2 Multiplicative structures

As seen in Table 2, Singaporean and Spanish textbooks included math problems corresponding to 11 out of 14 types of multiplicative structures (78%). Fisher’s exact test revealed similar variability regarding multiplicative structures (p = 1).

Table 2 Frequencies in absolute numbers and percentages of each type of multiplicative structure per publisher
Full size table

As mentioned for additive structures, the percentages in Table 2 did not reflect with fidelity the degree of variety of multiplicative structures that each textbook provided. The adapted Lorenz curves (see Fig. 5) showed that the distribution of AWPs across different types of multiplicative structures was slightly more balanced in the Singaporean textbook than in the Spanish textbook, although both distributions were highly unbalanced (chi-square goodness-of-fit test: MC: χ2 (10) = 2,531.07, p < .001; Santillana: χ2 (10) = 5,905.31, p < .001).

Fig. 5
figure 5

Adapted Lorenz curves for the distribution of multiplicative semantic-mathematical structures found in Singaporean and Spanish textbooks

Full size image

It is worth noting that three types of structures in both textbooks that correspond to simple rate problems amounted to 72.8% and 87.6% of the multiplicative structures in Singaporean and Spanish textbooks, respectively.

Although some differences between textbooks were observed for specific types of structures, the effect sizes were small (0.28). For instance, the Singaporean textbook presented significantly fewer simple-rate problems and more multiple-rate problems in multiplication structures, and similarly presented more Division compare reference unknown “times more” and more rate partition problems in division structures than the Spanish textbook.

Taken together, the results did not support Hypotheses 2a and 2b, either for the additive or for the multiplicative structures.

4.3 Illustrations

The Singaporean textbook included a lower proportion of AWPs accompanied by illustrations than the Spanish textbook, at 46.1% (n = 1,219) vs. 53.9% (n = 1, 427); χ2 (1, n = 5,155) = 74.80, p < .001); nonetheless, the effect size was small (0.12). Regarding the functions of these illustrations (see Table 3), a chi-square difference test revealed an association between publisher and type of illustration: χ2 (2, n = 2,865) = 594.49, p < .001. The magnitude of this association was moderate (0.46). The Singaporean textbook included a substantially higher proportion of organizational illustrations aimed at supporting and clarifying the mathematical structure of the problem, whereas the Spanish textbook included a higher percentage of figurative representations (see Table 3). Furthermore, when we looked at the percentage of illustrations that were not for figurative purposes, e.g., those that served an informational purpose by presenting data that are not included in the wording of the problem or depicting the mathematical structure of the problem, there was a higher proportion in the Singaporean textbook than in the Spanish textbook (82.4% vs. 52.2%; z = 16.75, p < .001). These results confirmed Hypothesis 3.

Table 3 Frequency in absolute numbers and percentages of type of illustration per publisher
Full size table

5 Discussion

In the current study, we investigated how math textbooks from two countries that differ in terms of achievement in international assessments of mathematics, Singapore and Spain, promoted children’s arithmetic word problem solving skills. To that end, we looked at the presence of AWP activities, the variety of semantic-mathematical structures that the AWP activities included, and the types of illustrations accompanying these AWPs in textbooks from the main publishers in Singapore and Spain. We pursued this research because, firstly, textbooks are thought to influence the teaching and learning of word problem solving, the content and activities of math curricula (Apple, 1992; Oates, 2014), and the development of student learning (Fagginger Auer et al., 2016; Heinze et al., 2009; Schmidt et al., 2001; Törnroos, 2005). Secondly, there is evidence that the design of mathematics textbooks influences student performance (Chang & Silalahi, 2017; Sievert et al., 2019) and, more specifically, that math textbooks from countries where students have a high level of mathematical competence contain a richer and more balanced distribution of AWPs (e.g., Schoenfeld, 1991; Stigler et al., 1986; Vicente et al., 2018; Xin, 2007). Thirdly, there is evidence that textbooks from high-achieving countries contain more relevant illustrations to solve worked-out examples (Mayer et al., 1995) or illustrations that serve as a step of the approach to the solution of the word problem (Vicente et al., 2020).

In the case of Singapore, the outstanding ability of Singaporean students to solve word problems (Mullis et al., 2020) could be related (to some extent) to the opportunities provided by Singaporean textbooks in terms of math problem variety (as suggested by variation theory, Marton, 2015). In particular, AWPs with different semantic-mathematical structures may provide children with the opportunity to learn to solve not only simple problems that can be solved in a straightforward way (i.e., using the keyword strategy; Hegarty et al., 1995; or direct modeling, Riley & Greeno, 1988) but also more difficult problems that require deep mathematical reasoning. Furthermore, providing illustrations that support the understanding of the semantic-mathematical structure of a problem is a cornerstone of the Singaporean educational approach to teaching and learning mathematics (Kaur, 2019).

Our findings showed that the Singaporean textbook placed a higher emphasis on AWPs than the Spanish textbook, as they contained more AWP-solving activities. AWPs in Singaporean textbooks were also more frequently accompanied by illustrations representing the underlying semantic-mathematical structure. These results were found for both additive and multiplicative problems. However, the effect sizes of these differences (except for those related to illustrations) were small, and it is noteworthy that both textbook series contained more OMAs than AWPs. Our study also revealed that (1) Singaporean and Spanish textbooks provided similar problem variety in regard to types of semantic-mathematical structures and (2) the distribution of types of semantic-mathematical structures was unbalanced in both textbook series. This finding about the variety of semantic-mathematical structures is at odds with previous studies that have reported country-related differences and may be attributable to differences in the sample analyzed. For instance, the educational level of the textbooks may alter the results: Mayer et al. (1995) and Xin (2007) analyzed lower secondary school textbooks, while our study analyzed primary school textbooks. Discrepancies with other studies may also respond to the level of analysis and variables that are analyzed. For instance, Schoenfeld (1991) estimated the percentage of problems that could be solved with the “keyword” strategy.

Nonetheless, some differences were found between Singaporean and Spanish textbooks regarding specific types of AWPs. For instance, the Singaporean textbook included structures that were not found (such as Equalize 2 and 6, or Division compare partition “times more”) or were almost nonexistent (such as Compare 5 and 6) in the Spanish textbook. The Singaporean textbook also included a higher proportion of problems that posed higher difficulty (Change 5 and 6 and Compare 5 and 6 with additive structures as well as multiplication-rate problems with multiplicative structures can be considered more challenging AWPs; Carpenter & Moser, 1984; Greer, 1992; Heller & Greeno, 1978; Vergnaud, 1991). The higher proportion of some types of problems in the Singaporean textbook could be explained by the different curricular goals of the two countries. For example, multiple-rate problems (with multiplicative structures) could act as an introduction to the solution of different types of ratio problems (see Musa & Malone, 2012). It should be noted that solving ratio problems is one of the objectives of the Singaporean curriculum, but not of the Spanish one.

Regarding illustrations, we found that AWP-solving tasks in Spanish textbooks were accompanied by illustrations to a larger extent, although the effect size was small. We also observed substantial differences in the functions of illustrations. In Singaporean textbooks, we found a larger percentage of organizational illustrations that helped students learn how to solve AWPs through reasoning. When this type of graphical aid is shown, even in the context of simple problems, students grasp an understanding of the different mathematical structures that can underlie similarly worded problems. This prevents students from relying on superficial strategies such as using “keywords” to solve both simple and difficult problems. Furthermore, such illustrations contribute to student learning of solution strategies that are applicable to any type of problem, regardless of the level of semantic-mathematical complexity. When these organizational illustrations are presented with simple problems in the Singaporean textbook (see example in Fig. 3, above), students learn to solve problems, but above all, students are expected to understand the functioning and relevance of these aids so that they are able to apply these organizational tools themselves to solve more complex problems, both arithmetically in lower grades (as the multiplication compare “times more” problem shown in Fig. 6, left panel) and other types of problems in higher grades (i.e., ratios and algebra, see Fig. 6, right panel).

Fig. 6
figure 6

Example of multiplication comparing “times more” (left) and of algebra problem (right), accompanied by organizational illustration. Note: Adapted from MC, Book 3A, p. 113 and MC, Book 5A, p. 62. The algebra problem was not included in the sample of our study

Full size image

Examples of organizational illustrations in Figs. 3 and 6 show how schematic representations scaffold learning to solve AWPs of different levels of difficulty (in this case, compare problems); from (easy, additive) Compare 2 problems and the more difficult multiplication problem compare “times more” to the algebra problem expressed in comparative terms in Fig. 6. This is in line with the constructivist approach of the Singaporean mathematics curriculum, which is based on their concrete-pictorial-abstract (C-P-A) approach.

Finally, the larger proportion (46%) of purely figurative illustrations in Spanish textbooks compared to Singaporean textbooks (20%) is noteworthy. Such illustrations are known to have little or no positive effect on supporting students’ problem solving (Linder, 2020).

In sum, if math textbooks affect to some extent how students perform on international assessments of mathematical problem solving (Mullis et al., 2020), then our findings suggest that differences between students from high- and low-achieving countries do not primarily relate to the quantity and variety of AWP-solving tasks that are presented in textbooks, but mainly to the nature of illustrations that accompany those tasks. The fact that Singaporean textbooks included a higher proportion of problems with schematic representations of their mathematical structure aligns with results from other studies that have focused on the role of external representations that support the mathematical structure of the problem (Ng & Lee, 2009; Xin, 2019).

6 Educational implications

The findings of our study may have educational implications for two agents involved in teaching how to solve AWPs, namely, teachers and textbook publishers. Firstly, our study suggests an additional quality criterion for the introduction or reinforcement of a theory-based and empirically proven regulation for textbook approval (see Sievert et al., 2019). Secondly, our findings also call attention to strengthening teacher criteria for choosing textbooks and to raising teacher awareness of textbook quality. Thirdly, it is recommended that textbooks introduce additional aids for reasoning and that such aids be applied to different stages involved in learning and solving AWPs. For instance, schematic representations of the mathematical structure in problem-solving tasks and in the proposed solution models could be provided. In the same vein, teachers are encouraged to make aids for reasoning available to students, as proposed by the Schema Based Instruction (Marshall, 2012) and Cognitively Guided Instruction (Carpenter et al., 1999) models. This is relevant when novel mathematical structures are introduced since students can understand similarities and differences between similarly worded problems. Extant evidence shows that in Spanish textbooks, this type of approach is not considered (see Vicente et al., 2020). In this sense, graphic representations such as the bar modeling provided in Singaporean textbooks seem to be a good option for improvement. This would prevent students from solving problems superficially by using, for example, the keyword strategy that can be applied to a large proportion of the AWPs analyzed in the current study.

7 Limitations and future studies

The scope of the results obtained is constrained by several limitations. Firstly, although AWPs are the most frequent tasks in textbooks used in primary schools, they are not the only types of mathematical word problems. The Singaporean textbook included problems other than AWPs, such as algebra (Yang & Sianturi, 2020) and ratios (Musa & Malone, 2012), especially in higher grades of elementary school. These problems, which were hardly to be found in the Spanish textbook, are based on knowledge that has been previously acquired by solving AWPs. Those problems are more difficult than the AWPs in our analyses; if included, the results might show an increase in the variety and difficulty of problems in Singaporean textbooks. Thus, additional studies that consider these types of problems are needed to possibly complete the description undertaken in the current study.

Secondly, it would be advisable to expand the sample of books analyzed in both countries to increase the validity of the results found in our study.

Thirdly, our analyses are based on the frequency and variety of AWPs, but the role that AWPs play within the didactic unit has not been investigated. Future studies should investigate the location, type, and purpose of problems in the didactic unit. These questions may provide a more accurate snapshot of how textbooks contribute to teaching problem-solving skills.

Finally, it is worth mentioning that in addition to factors related to AWPs, educational practices can also influence the way in which students learn and solve problems (i.e., the pragmatic or paradigmatic approach used by teachers in the classroom; see Chapman, 2006). Thus, the results and conclusions of this study should be interpreted in a more general context of how Singaporean and Spanish children learn to solve problems in math classes. This means that other aspects, such as how teachers implement tasks from textbooks and promote learning from textbooks, should be considered (see Rosales et al., 2012).