1 Introduction

Congruence transformations are important mathematical skills that are required in many geometrical constructions far beyond primary school (Boulter & Kirby, 1994). Furthermore, transformations are considered important for supporting children’s development of geometric and spatial thinking (Hollebrands, 2003). Reflection, being the first congruence transformation introduced in primary school, is among the most significant geometry concepts children should learn in mathematics education in primary school (e.g., Kultusministerkonferenz [KMK], 2005; National Council for Teachers of Mathematics [NCTM], 2000).

Teaching symmetry and reflection follows a spiral curriculum (Bruner, 1960) by integrating the concept of symmetry and reflection in the school curriculum in a repetitive manner. First experiences with reflection as a congruence transformation and symmetry already occur in the first grades of primary school.Footnote 1 Children experience that symmetrical figures are invariant under a reflection and learn to interpret symmetry as a property of shapes. Through secondary school, students should be enabled to apply transformations and use symmetry to analyse mathematical situations and solve problems (KMK, 2004; NCTM, 2000).

According to general theories describing the development of an understanding of geometrical concepts at different levels (e.g., van Hiele, 1986; Vollrath, 1984; Weigand, 2014), the elaboration of the first concept of symmetry starts with enactive approaches of mirroring or folding of 2D shapes. Subsequently, an increasingly formal understanding of reflection and symmetry is developed, passing the dynamic aspect of folding towards geometric aspects such as properties of reflections in further years of schooling (Common Core State Standards Initiative [CCSSI], 2010; KMK, 2005; Kirsche, 1992). A sustainable acquisition of the concepts of symmetry and reflection is particularly important as it plays a key role in problem solving and connects various branches of mathematics such as algebra and geometry (e.g., Boulter & Kirby, 1994; Leikin et al., 2000; Panaoura et al., 2009).

Teaching and learning geometry in primary school follow these general theories of concept acquisition: at the beginning, the emphasis lies on an intuitive understanding of the concept. The primary school curriculum requires solving reflection tasks, even though properties of reflection (like perpendicularity) have not been explicitly taught.Footnote 2 However, developing a compatible and meaningfully linked understanding of transformations which supports further acquisition of geometrical competencies is part of primary school mathematics education. For this reason, teaching and learning geometry in primary school must take the students’ abilities into account (coming from an intuitive understanding) and should not hinder further learning of reflections based on a property-related understanding. Primary students’ abilities at the end of primary school are crucial for further concept acquisition in secondary school.

Reviewing available literature in the field, little is known about primary students’ individual abilities and processes when acquiring the concept of reflection in primary school. Also, it is unknown how their understanding of reflection is manifested at the end of primary school and if children’s individual concepts allow coherent mathematical learning in further education. First indications were gathered from research conducted in the field of teaching and learning symmetry and reflection in the form of descriptions of students’ errors when solving reflection tasks. These studies shed light on difficulties encountered by students but were mainly conducted with older students (Denys, 1985; Denys & Grenier, 1986; Grenier, 1985b; Küchemann, 1981; Lima, 2006) and less with primary school students (Götz, 2020; Götz & Gasteiger, 2018; Höglinger & Senftleben, 1997). Errors that occur upon encountering specific tasks can give first insights on the ability of solving reflection tasks and make a certain quality of the students’ understanding of reflection evident but do not elucidate all aspects that encompass the students’ processes of understanding.

Some researchers conducted qualitative interview studies with students solving reflection tasks (Boulter & Kirby, 1994; Ho & Logan, 2013; Hoyles & Healy, 1997; Ramful et al., 2015). Although these studies have different aims, they show that the method of interviewing and observing students can give deeper insights into the students’ solving procedures and they extract aspects of children’s thinking as well as their strategies. However, they did not systematically analyse the sources of typical errors in reflection tasks in relation to the students’ solving approaches.

What (further) hinders or promotes the acquisition of the concept of reflection and symmetry is not yet known. Consciously selected tasks reveal typical errors — and thus lacks in the students’ understanding. Particularly the observation of the students’ errors combined with the approaches students use to solve reflection tasks can provide important information on children’s individual abilities. For the teaching and learning of symmetry and reflection, this knowledge is crucial in order to choose adequate teaching methods in primary school.

The research presented here aims to describe students’ approaches towards solving reflection tasks and to identify which ideas and what kind of understanding lead to errors or correct solutions. Our results should help to elaborate which of the children’s approaches to solve reflection tasks are mathematically coherent and sustainable for further concept acquisition in secondary school geometry.

2 Theoretical framework

To analyse which ideas lead primary school students to correct or incorrect solutions of reflection tasks, we first constituted a framework within which we defined all likely influences on the students’ solution processes. Thus, we will first outline which spatial skills are required to solve reflection tasks. Subsequently, we will relate to empirical research on solutions of reflection tasks and describe already known strategies as well as errors that occur. These different perspectives will aid to describe components of students’ understanding of reflection and show differences in their way of solving reflection tasks.

2.1 The role of spatial reasoning and mental images

It is widely recognized that spatial reasoning plays an important role when dealing with geometry tasks (Clements & Battista, 1992), and consequently, when solving reflection tasks. In the following, central concepts of spatial reasoning and mental images are clarified for the context of reflection tasks.

Spatial visualization is described as the ability to generate and manipulate images (Yakimanskaya, 1991). Integrating different aspects of visualization, Gutierrez (1996) proposes a definition of visualizationFootnote 3 within mathematics education: visualization is “the kind of reasoning activity based on the use of visual or spatial elements, either mental or physical, performed to solve problems or prove properties” (Gutierrez, 1996, p. 9). Visualization encompasses four main elements: mental images, external representations, processes of visualization and abilities of visualization (Gutierrez, 1996). In the students’ process of solving tasks, abilities of visualization are used, and mental images and/or external representations may be produced to solve the task (cf. Gutierrez, 1996). In the following, we illustrate the role of visualization in reflection tasks, especially when approaching them intuitively.

One of the basic elements of visualization is building mental images (Gutierrez, 1996; Yakimanskaya, 1991). Gutierrez (1996, p. 9) defines a mental image as “any kind of cognitive representation of a mathematical concept or property by means of visual or spatial elements.” Therefore, reflecting a shape means operating with the (mental) image of the given shape and having a representation of the shape to mentally reflect. When framing students’ understanding of solving reflection tasks, their mental images are a component to take into consideration. In the Piagetian theory, the construction of mental images as well as geometric knowledge occurs progressively through internalization of actions (with real objects) and the development of mental images of these objects (e.g., Piaget & Inhelder, 1971). Approaching the concept of a mental image, Presmeg (1986, pp. 43–44) identified different kinds of visual images in her students’ solutions: (1) concrete, pictorial imagery (meaning “the pictures-in-mind”), (2) pattern imagery (meaning “pure relationships depicted in a visual-spatial scheme”), (3) memory images of formulae (meaning students “visualize” a formula in their minds as if written down), (4) kinaesthetic imagery (meaning “imagery involving muscular activity”) and (5) dynamic imagery (meaning “images with movement in the mind”). Ho and Logan (2013) used this classification to analyse and categorize students’ answers on a reflection task to conclude on the type of method the students used in their solution. According to the authors, a majority of students used concrete imagery or visualized to solve the symmetry task (Ho & Logan, 2013, p. 748). Their findings also showed that 22.4% of the students used kinaesthetic imagery (within a total of 14.8% who solved the task correctly); the authors identified that most of their students used folding along the line of symmetry. In accordance with these results, Grenier (1985a) described mental paper folding being used by students who successfully solved reflection tasks at inclined mirror lines.

Several other studies addressed the importance of gestures (cf. kinaesthetic imagery (Presmeg, 1986)) in mathematical teaching, learning and thinking processes (Arzarello et al., 2009; Huth, 2010; Krause & Salle, 2018). According to Goldin-Meadow (2003), gestures influence and support problem solving. This result is supported by the description of processes of visualization, in which physically performed reasoning is a part (cf. a. o. Gutierrez, 1996). Following the gesture-for-conceptualization hypothesis (Kita et al., 2017), gestures support the processing of spatio-motoric information. The central theses of this hypothesis are, firstly, that the more difficult a task is, the more gestures are produced (for an overview, Kita et al., 2017). Second, the production of gestures improves “manipulation performance” (such as in mental rotation tasks) (cf. Kita et al., 2017). Thus, gestures contribute to the conceptualization of information and, in this way, support thinking and reasoning.

2.2 Solution strategies

When discussing visualization, not only mental images (a.o.) play a central role (cf. Gutierrez, 1996), but also the interaction between mental images and external representations (e.g., symbols) is viewed as a part of visualization when solving tasks (Arcavi, 2003; Zimmerman & Cunningham, 1991). Considering the students’ solution strategies may show how students deal with external information and therefore help to get a deeper insight when scrutinizing for the students’ understanding and their approaches to solve reflection tasks.

Solution strategies in transformational geometry tasks can be characterized within two broad strategies which both deal with spatial information (Boulter & Kirby, 1994): the analytical strategy (or part approach) and the holistic strategy (or global approach) (cf. Barratt, 1953; Cooper, 1976; Just & Carpenter, 1985; Schultz, 1991). In addition to these two approaches, a third one, the semi-analytic strategy, was identified (Lima, 2006; Tahri, 1993).

Within the holistic approach, the object which has to be operated is treated as a whole, without paying attention to and comparing detailed information of the object (Boulter & Kirby, 1994). The object image then is constructed perceptively by freehand drawing (Lima, 2006; Tahri, 1993). In a case study, Ramful et al. (2015) identified different aspects students refer to when solving reflection tasks. They identified the criterion exactly opposite as the intuitive counterpart of the notion perpendicularity. Furthermore, qualitative analyses identified students taking into account that the reflected “image is (of) the same size and shape (as) the original” (Hoyles & Healy, 1997). Bringing this together with the role of spatial visualization, one could conclude that there seems to be a mental representation to operate with, yet the kind of mathematical operation is not clear. Ramful et al. (2015, p. 466) identified this as a global strategy (“visual check”), which is described as being used to verify whether the drawn solution of reflection as a whole “looks correct.”

In contrast, the meaning of part approach is that specific details of an object are compared and put into relation with other details to solve the spatial problem (cf. Boulter & Kirby, 1994). Within this strategy, students obtain the object image by constructing the images of each vertex of the object before connecting those vertices (Lima, 2006; Tahri, 1993). Interviews conducted show analytical aspects frequently referred to by the students: (1) equidistance between object/image and line of symmetry (Ramful et al., 2015; cf. Hoyles & Healy, 1997), (2) perpendicularity between a point on the object or image and the line of symmetry and (3) congruence of sides, i.e., the notion that the lengths of the sides of object and image object are the same.

The semi-analytic approach combines analytic and global procedures; the image of an object is obtained by first constructing one or several image points before subsequently globally constructing the rest of the image (Küchemann, 1981; Lima, 2006; Ramful et al., 2015; Tahri, 1993; cf. Hoyles & Healy, 1997).

Furthermore, it was observed that students show some inconsistency in the notions they respect during their solution processes (as, e.g., perpendicularity) (Hoyles & Healy, 1997; Ramful et al., 2015).

2.3 Students typical errors in reflection tasks

Strategies describe ways students can generally use to solve reflection tasks. In addition to strategies, errors that occur in specific tasks can give first insights on the students’ ability of solving reflection tasks and thus of their understanding of reflection. By knowing the students’ errors and, moreover, the students’ approaches that may lead to the respective errors, conclusions on the connectivity of their approaches and understanding of reflection can be drawn. In the following, we therefore give a resume on common errors identified in reflection tasks.

Research has shown that the concept of symmetry and reflection is problematic for many students in primary but also in secondary school (Götz, 2020; Götz & Gasteiger, 2019; Grenier, 1985a, 1985b; Küchemann, 1981; Schmidt, 1986). In several studies, a common error in tasks with an inclined mirror line was described as the tendency to reflect horizontally or vertically: students ignored the slope of the mirror line and instead reflected at an imaginary vertical or horizontal mirror line. This error occurred with primary school students (Götz & Gasteiger, 2018) and secondary school students (Götz, 2020; Grenier, 1985a, 1985b; Küchemann, 1981; Lima, 2006). Furthermore, there is a tendency to draw the image shape (or the image segment) parallel to the object (Denys, 1985; Grenier, 1985a, 1985b; Küchemann, 1981; Tahri, 1993) or to translate the object in parallel to the other side of the mirror line (Götz, 2020; Götz & Gasteiger, 2018; Grenier, 1985a, 1985b; Lima, 2006). Another common error with reflection tasks was the rotation of the object about a point (Götz, 2020; Götz & Gasteiger, 2018; Tahri, 1993). In addition, other authors described a prolonging mechanism in the students’ answers, especially in tasks with an inclined mirror line (Lima, 2006; cf. Hoyles & Healy, 1997). This means students focus on one salient side of the object and draw the image object in prolongation to this side.

2.4 Summary and research questions

The acquisition of the concept of reflection throughout the geometry curriculum goes through a change from an action-bound intuitive to an analytical property-based understanding. It is of particular interest to analyse primary students’ approaches on reflection tasks, given their curriculum-caused lack of property-based understanding. The understanding of reflection built up in primary school is to serve as a foundation for sustainable and mathematically connected conceptions of reflection and congruence transformations in further mathematics education.

Especially, how primary school students approach reflection tasks has not been thoroughly investigated yet. The theoretical findings focus particularly on secondary students’ errors. Studies which take into account the students’ strategies remain rather general. Only a few studies in this field focussed on primary students’ understanding.

To grasp primary students’ ideas and their understanding of reflection, a deeper insight in children’s thinking is necessary. We assume that during the solution process, students set various foci and use different approaches that structure their thinking and operating. Focusing on an approach may either lead to a correct solution product or to a wrong solution product. We define approach as all possible perspectives on the students’ thinking and acting: visualization strategies (e.g., mental imagery), gestures and solution strategies such as holistic and analytic strategies that give an indication of the students’ thinking and understanding. Analysing the students’ errors in reflection tasks and their individual approaches can be a tool to find out which of the approaches are sustainable and mathematically connectable and which are not. Therefore, we define the following research questions:

  1. 1.

    Which approaches or strategies do primary students use in their processes of solving reflection tasks?

  2. 2.

    To what extent are students’ solution products related to the approaches primary students use when solving reflection tasks?

3 Methods

3.1 Sample

For our sample, we chose fourth grade students from two German schools (Lower Saxony). A total of n = 42 (f = 26, m = 16) students participated in this study (mean age, 9.84; SD = 0.72). According to the German school curriculum, all primary students study reflective symmetry of 2D shapes during their third and fourth year of school. At the end of grade 4, they designate mirror lines in 2D shapes and reflect given shapes on grid paper at vertical, horizontal and inclined lines of reflection (KMK, 2005). Usually, they do not use right angles and do not work in coordinate systems. Our aim for the study was to select a broad sample regarding the students’ mathematical achievement. Therefore, students with different levels of mathematical abilities were selected on the basis of teacher judgements. For the final interpretation, only 39 transcripts could be used. The quality of three videos was too poor to transcribe the students’ actions properly.

3.2 Instruments

3.2.1 Set of tasks

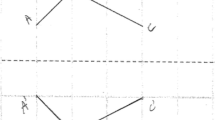
To investigate the students’ approaches while solving reflection tasks, we used a task-based interview. The set of tasks contained four reflection tasks (see Fig. 1Footnote 4) which are typically used in primary school lessons and textbooks. The tasks were explicitly selected to differ in typical task characteristics; the criteria for the selection of tasks were based on difficulty-generating characteristics on reflection items (Götz & Gasteiger, 2019).Footnote 5 We know from previous studies (e.g., Götz & Gasteiger, 2019) that students’ errors vary depending on the task set. Therefore, especially, the slope of the mirror line was varied. Reflections at vertical mirror lines are known to be easier than reflections at horizontal or inclined mirror lines (Götz & Gasteiger, 2019; Grenier, 1985b; Küchemann, 1981) (Fig. 1, task 1). Additionally, sides c and b of the shape in task 1 do not intersect the underlying grid squares diagonally, but somehow this task characteristic allows us to distinguish randomly correct procedures from analytical procedures (Götz & Gasteiger, 2019). Reflections at horizontal mirror lines are known to be more difficult than reflections at vertical mirror lines (Götz & Gasteiger, 2019; Grenier, 1985b; Küchemann, 1981) (Fig. 1, task 2). Task 3 and 4 require the reflection on inclined mirror lines. To differentiate between answers using the (wrong) concept of translation and answers using the (right) concept of reflection (see Section 2.3), a part of the rectangle is coloured in black (Fig. 1, task 3). In task 4, a small rectangle is “added” to the big square. Thus, the shape in task 4 is in itself not vertically symmetrical and the answers using the wrong concept of “reflection at a vertical mirror line” can be distinguished from wrong concepts of translation and rotation (see Section 2.3).

Fig. 1
figure 1

Task overview

Full size image

3.2.2 Thinking aloud

To gain additional insight and understanding, the students were asked to think out loud while working. This method was chosen due to the fact that we needed oral utterances belonging to the students’ actions and actual thinking processes.Footnote 6 Before beginning with the tasks, we gave an example of how to describe what they are thinking and doing (“think-out-loud”) to all students. We did not interrupt the students as long as they worked on the different items. Video recording allowed us to capture the movements of the students’ pencils and their kinaesthetic actions.

3.2.3 Semi-structured interviews

Furthermore, we carried out semi-structured interviews. The interviews are necessary to guarantee the comparability of all task-based observations and to compare the students’ utterances on each task. Solely using the method of thinking out loud would not suffice at this point, as the students might only pronounce for each task what comes to their mind first — according to their language skills. Therefore, the interview guideline contained a variety of predefined questions which could be asked at the end of each paper–pencil task when a student made no comment on this subject during the solution process. One question was, for example, how the students came to their solution product or why the shape of their solution product is oriented this or that way.

3.3 Evaluation method

3.3.1 Procedure

Data were collected in June 2019. The task-based interviews were carried out by two especially trained interviewers. The videos were transcribed in their entirety including the students’ actions and gestures related to their solution process. For the analysis of the answers, a category system was developed in an iterative, multi-step process in which a deductive, theory-based approach alternated with an inductive, data-based approach. Based on the method of qualitative content analysis (Mayring, 2014), we analysed the data task by task with a focus on approaches children refer to during their process of solving. A coding guide was developed, which contained detailed descriptions and an anchor example for each subcategory. In every task (Fig. 1), each subcategory could only be coded once.

3.3.2 Category system

In its latest form, the category system contains four main categories — each containing several approaches students used to solve the tasks (Tables 1, 2, 3, 4).

Table 1 First main category: properties of axial reflections. Subcategories displayed in italic
Full size table
Table 2 Second main category: holistic approaches
Full size table
Table 3 Third main category: gestures and actions illustrating the process of reflection
Full size table
Table 4 Fourth main category: mental images illustrating the process of reflection
Full size table

The first two main categories are based on the main strategies for solving reflection tasks — analytical and holistic strategies (Boulter & Kirby, 1994; Lima, 2006; Tahri, 1993). The first main category contains properties of axial reflections (analytical approaches) (Table 1). Some of the categories were deductively drawn from previous research and were initially included in the coding, namely, congruence of sides and exactly opposite (Hoyles & Healy, 1997; Ramful et al., 2015). Unlike Ramful et al. (2015), who classify exactly opposite more as a holistic procedure, we understand exactly opposite, following Hoyles and Healy (1997), as a property in the sense of “reversed”, meaning turned the other way around. Knowledge of perpendicularity (cf. Ramful et al., 2015) is not part of the primary school curriculum.Footnote 7 Thus, it does not make sense to expect obvious signs of it in the students’ answers. Nevertheless, an intuitive approach to the criterion perpendicularity seems to be possible. Therefore, we split up the equidistance criterion (Ramful et al., 2015) into the two subcategories distance and shortest distance. For tasks with vertical or horizontal mirror lines (task 1 and 2), no visual difference in the students’ solution products between the subcategories distance and shortest distance can be seen, because the distance between a point/mirror point and the axis is always the shortest distance given the fact that with an intuitive understanding, the line segment connecting point and mirror point lies orthogonal to the axis (cf. subcategory (shortest) distance to vertical or horizontal mirror lines). For tasks with inclined mirror lines (task 3 and 4), however, this distinction between shortest distance and distance matters in particular. The shortest distance describes the length of the shortest connection between point and mirror point, which is always a line segment orthogonal to the axis. Contrarily, by distance to inclined mirror lines, we understand a connection between point (mirror point) and axis, which is not the shortest connection of both points. During the coding process, we additionally identified the approach points have mirror points in some of the students’ answers. In the category definitions, we include oral utterances as well as actions specifically supporting property-related reasoning of the students.

Besides analytic properties, we also coded holistic approaches in the students’ processes while solving the reflection tasks (Table 2). This we defined as a main focus, not on properties of reflections but rather on a reproduction of the appearance of the shape itself (cf. Boulter & Kirby, 1994; Lima, 2006; Tahri, 1993). We distinguish the two subcategories holistic procedure in general and congruence of shape (cf. invariance that the image “is the same size and shape of the original” by Hoyles & Healy, 1997). In the category definitions, we include oral utterances as well as students’ actions supporting the thought of a reproduction of the appearance of the shape itself.

The third main category goes back on the relevance of gestures in processes of reasoning already outlined (cf. Kita et al., 2017) and the fact that mental images can be shown as kinaesthetic imagery (Presmeg, 1986). This category was introduced in addition to the actions described in the main categories one (Table 1) and two (Table 2) which are supporting reasoning on properties or in a holistic way. Gestures in this category differ from gestures described above by illustrating the process of reflection itself. We distinguish four different types of actions and gestures illustrating the process of reflection (Table 3) one of which, gestural folding, was already described by Ho and Logan (2013).

The fourth main category focuses on students’ oral utterances describing a mental image or a mental operation illustrating the process of reflection (Table 4). Based on the different kinds of mental images which can be identified in students’ products (Presmeg, 1986; cf. Ho & Logan, 2013), we were looking for visualization in mental images. Therefore, we distinguished two different processes in which the oral utterances illustrate explicitly the process of reflection (Table 4).

A testing of the inter-coder reliability was conducted to guarantee the reliability of the category system. Two research assistants were trained to analyse the video transcripts. The two coders carried out a double coding for 20% (8 videos) of a randomly selected sub-sample of the data material. For the reliability analyses of the double coding, Kappa value was calculated (Brennan & Prediger, 1981) and, with 0.83, achieved a high mean value (Wirtz & Caspar, 2002).

3.3.3 Coding of the documents

To identify patterns describing a link between the approaches used while working on the reflection tasks and the students’ solution products (RQ 2), the paper–pencil data were coded on different levels. In a first step, we coded dichotomous categories (right, wrong) for the students’ products for each task. Additionally, each wrong solution product was coded qualitatively (Table 5), based on the previously reported typical errors on reflection tasks (cf. 2.3). In a final step, the approaches used in the solution process (Section 3.3.2) were related to each task with a dichotomous recoding of the approaches: 1, signifying approach is given in the students’ task solution process; 0, approach is not given. To analyse the relation between the qualitatively coded solution products and approaches observed during processes of solving for each task, we used relative frequencies of each approach per task.

Table 5 Categories of students’ solution products on all four reflection tasks
Full size table

4 Results

After a brief descriptive overview, the following section is composed of two parts. First, we report our results on approaches primary students use in their processes of solving reflection tasks (RQ 1). Second, we analyse to which extent the students’ solution products are related to their approaches during their solution processes (RQ 2).

Descriptive statistics for the solutions of the reflection tasks are given in Table 6. As expected, tasks 3 and 4 with inclined mirror lines have the lowest solution rates. Task 2 has the highest solution rate — even better than task 1, which was the task with a vertical mirror line.

Table 6 Solution ratesA for reflection tasks
Full size table

4.1 Approaches primary students use in their processes of solving reflection tasks

To analyse whether there are task-specific differences, Fig. 2 provides an overview of the different approaches identified in the primary students solving procedures for each task separately.

Fig. 2
figure 2

Overview over absolute frequencies for the different approaches by tasks, grouped according to the four main categories described in 3.3.2 (A to D)

Full size image

In general, the main category properties of reflection were identified most often (see Fig. 2A). The analysis of students’ approaches shows that of the properties of reflection identified, predominantly congruence of sides and the distance to the mirror line were considered in evidence in all of the four tasks. A property of reflection that less attention is paid to was the congruence of sides in task 1 (Fig. 2). The category exactly opposite is mostly referred to in tasks with inclined mirror lines (task 3 and 4). The distance to the mirror lineFootnote 8 was one of the properties of reflection identified very often (Fig. 2). In addition to the information presented in Fig. 2, it was observed that the exact distribution of the three subcategories of distance to the mirror line (c.f., Table 1) revealed more details. For tasks with vertical cf. horizontal mirror lines (tasks 1 and 2), no statement can be made as to whether the students took the shortest distance or the distance into account. Concerning the solution of tasks with inclined mirror lines, both concepts of distance can be differentiated. Out of 28 students who considered the distance in task 3, only five considered the distance in the sense of the shortest distance. In task 4, only two out of 26 students considered the shortest distance.

Notably, for the absolute frequencies in the main category holistic approaches (see Fig. 2B), holistic procedures were observed often in task 1 which is interesting since analytical properties have been observed less in task 1 than in the other tasks.

Regarding the absolute frequencies for the main category gestures and actions illustrating the process of reflection (see Fig. 2C), increased gestural mirroring was noticed compared to gestural folding and increasingly in the solution processes of task 3 and 4 than of task 1 and 2 (Fig. 2).

Concerning the main category mental images illustrating the process of reflection (see Fig. 2D), in general, more students used mental mirroring than mental folding while solving reflection tasks. Also, there is a tendency to do so with increasing difficulty of the task.

4.2 Relation between solution products and approaches used in the solution processes

In a second step, we analysed the relation between the students’ solution products and the students’ approaches for solving the reflection tasks to draw conclusions on which approaches are more sustainable and mathematically connectable (RQ 2).

A closer look on the students’ errors (Fig. 3) shows that incorrect solutions correspond to errors described in previous research (cf. 2.3).

Fig. 3
figure 3

Categories of students incorrect solution products and examples

Full size image

Table 6 shows the frequency of the errors made by the primary students in this study. To draw conclusions on more or less sustainable approaches, we analysed the relation between the approaches used for the solution of each task and each category of errors or correct solution, respectively (see Table 7).

In the following, we will consider each solution product separately by taking into account the approaches students used to solve the tasks. We will use excerpts to further illustrate the students’ approaches. This way, differences in the frequencies of error patterns per task become comprehensible by examining different student approaches.

The error reflection at a given mirror line, but position of mirror shape incorrect (Table 7, columns 1–2) (cf. Fig. 3, task 1), was made by 19 students in tasks 1 and 7 in task 2. It is noticeable for task 1 that the relative frequencies of approaching with a holistic procedure are increased compared to task 2 (relative frequency [RF], 0.68 vs. 0.29), and congruence of sides was less considered (RF: 0.58 vs. 0.86). The distance to the vertical or horizontal mirror line was considered by more than half of the students in both tasks. In general, for task 1, only a few (or no) students made utterances concerning gestures and mental images illustrating the process of reflection (Table 7, relative frequencies between 0.00 and 0.16), whereas in task 2, students often used mental or gestural mirroring (RF, 0.43).

Table 7 Relative frequencies of the approaches used per solution product and task (with a grey background, relative frequencies \(\ge\) 0.50; in light grey, frequencies \(\le\) 0.10; in bold type, values of particular importance which are mentioned separately in the text).
Full size table

For the error translation of the shape to the other side (Table 7, columns 3–6) (cf. Fig. 3, task 2), congruence of sides was, over all tasks, considered the most and was often the dominant approach (see v, relative frequencies between 0.67 and 1.00) (cf. excerpt 1). The example of Student 10 illustrates the dominance of the congruence of sides.

Excerpt 1 Solution process of Student 10 on task 2 with a solution product of a translation of the shape to the other side (cf. Fig. 3, p. 16)
Full size table

Even after further requests by the interviewer, the student did not refer to any other category and even mentioned that it does not matter which position you choose to start drawing the image shape.

The analysis of the excerpts also shows solution processes considering the congruence of sides and the distance (excerpt 2), but still coming to a wrong solution product.

Excerpt 2 Solution process of Student 1 on task 2 with a solution product of a translation of the shape to the other side (cf. Fig. 3, p. 16)
Full size table

When asked how the student obtained this shape, it becomes clear that when considering the distance, the student only looked at the shape as a whole and marked one point for its distance to the axis. Then the student simply counted the squares of the sides of the shape, and from his starting point of the mirror shape, he drew mirror points for each point and then connected them.

The (shortest) distance was rarely observed within these solution products (RF, 0.17 (task 1), 0.46 (task 2) and 0.00 (tasks 3 and 4)); in contrast, some students who slid the shape to the other side referred to the distance to the edge during their solution of tasks 1, 2 and 3 (RF, 0.17 (task 1), 0.31 (task 2) and 0.20 (task 3). Besides considering the congruence of sides, students translating the shape to the other side showed the second highest relative frequency for holistic approaches. For task 1, holistic procedures were coded for 50% of the students; for task 3 and 4 holistic utterances mostly referred to the congruence of the shape (RF, 0.60 (task 3); 0.50 (task 4)). Except for task 3, these students rarely made gestures or utterances alluding to mental images illustrating the process of reflection.

The error reflection at an imaginary vertical or horizontal mirror line (Table 7, columns 7–8) (cf. Fig. 3, task 4) occurred only for reflection tasks with inclined mirror lines. In general, the relative frequencies of these students showing utterances concerning the congruence of sides are high (0.80 (task 3) and 0.82 (task 4)). More than 60% of the students showed utterances concerning exactly opposite (RF, 0.60 (task 3) and 0.64 (task 4)). In addition, more than 75% of the students considered the distance (but not the shortest distance) to the inclined mirror line in their solution processes. Of particular note is that at least in 40% of the students’ solutions, gestural or mental mirroring could be identified. This is more than for nearly all other solution products (except for the error reflection at an imaginary mirror line and translation in task 3; RF, 0.45). The fact that there is a strong idea of mirroring (mental and gestural) can be seen in the approaches of Student 18 working on tasks 3 and 4, when the student explains the orientation of the two shapes he drew (excerpts 3 and 4).

Excerpt 3 Solution process of Student 18 on task 3 with a solution product of a reflection at an imaginary vertical mirror line
Full size table
Excerpt 4 Solution process of Student 18 on task 4 with a solution product of a reflection at an imaginary vertical mirror line (cf. Fig. 3, p. 16)
Full size table

The error reflection at an imaginary mirror line and translation (Table 7, columns 9–10) (cf. Fig. 3, task 3) only occurred in tasks with inclined mirror lines. Similar to the error reflection at an imaginary vertical or horizontal mirror line, the relative frequencies of considering the congruence of sides were high (RF, 0.73 and 0.83). In all the solution processes for this error, students referred to the category exactly opposite. Regarding the occurrence of gestures and actions or mental images illustrating the process of reflection, students referred more to gestural (RF, 0.45) and mental mirroring in task 3 (RF, 0.45) and more to gestural (RF, 0.50) and mental folding (RF, 0.50) in task 4 (Table 7, columns 9 to 10, relative frequencies in bold type). Twenty-seven percent of the students who made this error in task 3 referred to the shortest distance (inclined mirror line) (cf. excerpt 5), whereas in task 4 the students mostly referred to the distance (inclined mirror line) (RF, 0.50). This is the only incorrect solution product in which students considered the shortest distance (inclined mirror line). Excerpt 5 illustrates a typical working process for students with this solution product (cf. Fig. 3).

Excerpt 5 Solution process of Student 15 on task 3 with a solution product of a reflection at an imaginary vertical mirror line and translation (cf. Fig. 3, p. 16)
Full size table

Student 15 takes into account the shortest distance at inclined mirror lines for the first point reflected (excerpt 5, first sentence). From this point on, the student finishes the shape without referring to the shortest distance of other points again.

A large majority of the students reflecting correctly (Table 7, columns 11–14) referred to the congruence of sides and the (shortest) distance to the vertical/horizontal mirror line cf. the shortest distance to the inclined mirror line. For correct solution products for tasks 1, 3 and 4, students considered the category points have mirror points more often than in other solution products (Table 7). Furthermore, there are almost no students referring to holistic approaches (except task 1). For tasks 3 and 4, a rotating of the sheet was coded to a high percentage (RF, 1.00 (task 3), 0.80 (task 4)), more often than in other solution products. One student used the ruler as a Mira mirror and found the correct solutions for tasks 2, 3 and 4. Except for task 3, the relative frequencies for mental and gestural mirroring were almost the same as for other solution products. For task 4, students made spoken or gestural utterances concerning gestural and mental folding and mental mirroring.

5 Summary and discussion

Our detailed multi-faceted analyses of the students’ solving procedures on reflection tasks show their wide variety of approaches used. These approaches differ depending on the characteristics of the tasks. It also emerged that some approaches only become apparent when looking at tasks with inclined mirror lines. Approaches which are not sustainable and not mathematically connectable have been revealed by analysing the students’ errors in relation to the approaches used to solve these tasks. In the following, the results are summarized and discussed along the two research questions.

5.1 Approaches of primary students in their processes of solving reflection tasks and task-specific differences

The students mainly focused on two properties of reflection, namely, congruence of sides and distance. It seems that the approaches students used differ not only (inter-)individually but were also influenced by the characteristics of the task. Exemplary is the observation of the properties of the shape in task 1 (oblique lines intersecting the underlying grid squares somehow but not diagonally, see Fig. 1) in relation to the approaches used: in task 1, the congruence of sides was considered significantly less often than in all other tasks, and at the same time, holistic approaches were chosen significantly more often (Table 7). Students considered the (shortest) distance to vertical cf. horizontal mirror lines to a high percentage in the solutions of tasks 1 and 2, whereas in tasks 3 and 4, mainly the distance to the inclined mirror line was considered. Reference to the shortest distance to the inclined mirror line was only observed by a few students in correct solutions and in the solution product of reflection at an imaginary mirror line and translation. This may be due to the fact that this category would include the notion of perpendicularity, a concept which is not yet exclusively taught in mathematics in primary school (in Germany). It seems that at the end of primary school, an intuitive way of concept acquisition may not seem to be sufficient to correctly refer to the shortest distance to inclined mirror lines. This is supported by a closer look on the task characteristics aligned with the solution products: in task 3, the shape lies closer to the inclined mirror line (cf. Fig. 1, task 3, vertex A) than in task 4 (Fig. 1, task 4, vertex D or B); students’ approaches refer less to the shortest distance (inclined mirror line) in the task with an increased distance to the mirror line (cf. task 3 vs. task 4).

At the same time, the category “exactly opposite” numerically occurred more often in students’ processes in task 3 and 4 than in task 1 and 2. Mental folding, mental mirroring, gestural folding and gestural mirroring were increasingly identified in tasks with inclined mirror lines. A possible reason might be that, in general, tasks with inclined mirror lines demand higher spatial abilities and the development of mental images therefore is more complex than for tasks with vertical and horizontal mirror lines. Concrete acting can facilitate the development of mental images (e.g., Battista, 2007; Kita et al., 2017). This considered, students might use more gestures (actions) for the solution of complex tasks in order to build a mental image they can operate with.

5.2 Relation between solution products and approaches used in the solution process

At this point, we would like to analyse the solution products in conjunction with the approaches students used when solving the reflection tasks. We especially refer to the errors in tasks at inclined mirror lines where a certain hierarchy in the quality of understanding of reflection and, therefore, more or less sustainable approaches can be identified.

Although approaches referring to properties of reflection were identified in the students’ solution processes, these are no guarantors for correct solutions. Most of the students refer to the congruence of sides, but this in itself will not lead to a correct solution product automatically.

Students whose solution product was a translated mirror shape focussed on congruence of sides; however, they did not solve the tasks correctly. One reason could be that next to an approach referring to the congruence of sides, they used holistic approaches or focused predominantly on the (shortest) distance to the mirror line (task 2) (Table 7). This indicates a less comprehensive level of understanding as even the visual image of a reflection (i.e., that the orientation of the mirror shape changes) is not yet understood.

It is noticeable that for the solution products’ reflection at an imaginary vertical or horizontal mirror line, students also referred to the congruence of sides yet without correct solution. Additionally, excerpts 3 and 4 underline that “mirroring” is dominant in their approaches and that students literally seem to imagine putting a vertically oriented mirror in front of themselves (students mainly refer to mental mirroring, gestural mirroring, exactly opposite and distance to the inclined mirror line). Referring back to the Piagetian theory, this could be explained by the development of space, in which a mental concept is an internalized imitation of an action (Piaget & Inhelder, 1971) and aligns with previous research stating that the persistence of a prototypical image (mirroring means reflecting at a vertical line) could be a hindrance for successful problem solving (Ho & Logan, 2013). Equally, this presumption is supported by the analysis of Ramful et al. (2015) that sometimes errors occur when the holistic strategy “takes over as a more intuitive fallback measure” (Ramful et al., 2015, p. 466). For these students, a higher understanding of reflection than for students with the solution product translation of the shape can be assumed because they understood the notion of “exactly opposite” — and thus the direction reversing property of reflections.

Another solution product where students referred to the congruence of sides is the reflection at an imaginary mirror line and translation (Fig. 2). Students’ solution processes for this solution product also show oral and gestural utterances concerning exactly opposite. They made utterances showing gestural and mental mirroring (task 3) and gestural and mental folding (task 4). A few students considered the shortest distance to the inclined mirror line, which is applied to only one point (and its mirror point) of the shape: i.e., the first one reflected (Fig. 1, task 3, vertex A). Considering the solution process of reflecting only one point correctly against the background of analytical and holistic strategies, it can be described as semi-analytical (Lima, 2006; Tahri, 1993) and the defining of the first point being the analytical part (“Here it is now half a square away from the vertex. Then again, I mark this point,” excerpt 5), followed by a reproduction of the image of the shape kept in mind which could be either interpreted as a holistic procedure or a mental visual reproduction of the shape, while no reference is made to other points and their mirror points of the shape (“Then I draw those down. […] then I draw the five squares from here to there. […] And then I connect these two lines.”). This procedure may lead to errors in tasks with inclined mirror lines, whereas it may lead to the right solution product in tasks with vertical and horizontal mirror lines. It appears that this solution product could be seen as a transition on the way to a next step of understanding: from an intuitive understanding to an analytical understanding of reflection. In general, students with the solution product reflection at an imaginary mirror line and translation used many approaches and even referred to the shortest distance. Therefore, a higher understanding of reflection can be assumed for these students.

Correct solutions are different from other solution products, not by considering the congruence of sides, but rather by the fact that the shortest distance to vertical, horizontal and also (mostly) to inclined mirror lines is considered. Taking a closer look at the students’ solution processes revealed that almost all students rotated the sheet in a vertical or horizontal position to solve the tasks. In addition, there were students who first defined mirror points to the points of the shape for solving the tasks or others used a ruler as a Mira mirror to find the correct solutions. It seems that all the students who solved the tasks correctly already had an idea of where the shape has to be positioned in mind and they helped themselves with strategies to draw this mirror shape in their mind — thus compensating their lack of knowledge for orthogonality. These findings agree with research on spatial abilities, indicating that for more complex tasks, solution processes are more efficient when referring to analytical processes (Grüßing, 2002; Linn & Petersen, 1985). Other authors found that students with a high spatial and geometrical level were able to find alternative solution strategies or switch between strategies (e.g., Grüßing, 2002). Applying this to our findings means that either high spatial abilities are necessary or that students’ solution strategies need to be flexible to find the correct solution at inclined mirror lines. At the same time, applying analytical strategies does not indicate success in solving reflectional problems in general (cf. approach congruence of sides or distance).

We conclude that successful solving procedures share the common feature of students using approaches that rely on precise mental images they can adequately operate, rather than sticking to prototypical images (as described by Ho & Logan, 2013). It seems to be a way for students to help themselves to find a solution without needing such images, for example, by turning the sheet or intuitively referring to all the necessary analytical properties (e.g., by finding a mirror point to each point).

It seems that a too distinctive image of vertical reflection can lead to mistakes and thus could be predominant over analytical strategies. Moreover, it might impede understanding of the analytical notion of perpendicularity or the shortest distance. Especially, the large number of students that still reflect at an imaginary vertical (or horizontal) mirror line indicates that the strong image of real mirroring does not seem to be a suitable aid for building a sustainable understanding of reflections. This is supported by an additional qualitative analysis of the errors of this study showing that 17 students reflected at an imaginary mirror line in tasks 3 and 4.

6 Limitations and perspectives

In this study, we conducted task-based interviews with primary school students which were supported by a thinking out loud method. This method was chosen in order to get the largest possible insight in the students’ thinking and turned out to be suitable. Nevertheless, there are large individual differences in how students are aware of their cognitive processes and to what extent they are able to describe these processes orally. Thus, the interpretation of the students’ oral and gestural utterances is not always evident since minor details make differences — hence, the process of coding the documents is an interpretative and subjective process. Nonetheless, by validating the coding system with a second coder, we tried to minimize this subjective interpretation range. Although we tried to get the most thorough understanding of what the students think while they work on the reflection task, we can never really know what the students think. Therefore, our interpretations should be seen as conclusions on the students’ thinking based on the approaches they used. A second limitation is the influence of the instruction methods. It might be possible that the students’ utterances depend on the explanations their teachers gave. We decided not to focus on the instruction part. For our aim to get a first insight into primary school students’ reflection knowledge, we try to guarantee that all teachers followed the curricular requirements concerning symmetry and reflection.

Essentially, the new central aspect we can draw from our study is for teaching and learning reflection: our analyses allow to take students’ errors as a starting point for individualized adaptation of teaching methods according to the students’ current understanding of reflection. A differentiated view on the students’ solution products is required as major differences in the approaches students used emerged in this study — portending to wide disparities in the sustainability of the students’ understanding. Whether the strategies students use remain stable over different tasks or whether they vary according to different task characteristics is yet a research perspective. The results of these analyses indicate that for primary school students, the interaction of holistic and analytical strategies and the transition from one to the other is not “nature given.” Particularly when teaching reflection in primary school, it is the teachers’ responsibility to focus on this. With regard to secondary education, especially, the transition from concrete operational thinking to analytical thinking should be taken into account. Put another way, attention has to be given to instruction methods developing approaches that support analytical properties when reflecting at a given mirror line. Above all, productive methods seem to be those that integrate a flexible mental image or develop the concept of each point has a mirror point and the referring to the shortest distance. As orthogonality is not part of the primary school curriculum, enactive methods initiating a basic sustainable knowledge, on which secondary mathematics can build, have to be developed. Qualitative studies indicate that programming language supports sustainable learning of symmetry and reflection (Edwards & Zazkis, 1993; Hoyles & Healy, 1997), because the students set their focus on actions, visual relationships and symbolic representations at the same time and therefore construct new meanings of reflection. Other authors found that dynamic geometry environments (DGE) help to develop a deeper understanding of reflection (Hollebrands, 2007; Ng & Sinclair, 2015; Xistouri & Pitta-Panzati, 2013). A deeper understanding was particularly observed when primary students focussed on functional relationships of a preimage and its image (Ng & Sinclair, 2015, p. 433) or when students focussed more on properties and relations (Hollebrands, 2007) as before the respective intervention. Other conceivable methods could be graphic kinematical techniques as proposed by Kirsche (1996), such as flipping shapes over a mirror line or practice pin-prick reflection. In this context, this means that pupils fold a sheet of paper and draw a simple straight-line shape. Then, they pin prick through the paper at each vertex. The paper is opened out, and the mirror shape is drawn by joining the pin-pricks. This enactive method puts the emphasis on the reflection of single points while reflecting a shape. Connecting this method with classroom discussions on where and how the mirror image of the given shape is located can be fruitful for an adequate understanding of reflection.