Abstract
Mathematical word problem solving is influenced by various characteristics of the task and the person solving it. Yet, previous research has rarely related these characteristics to holistically answer which word problem requires which set of individual cognitive skills. In the present study, we conducted a secondary data analysis on a dataset of N = 1282 undergraduate students solving six mathematical word problems from the Programme for International Student Assessment (PISA). Previous results had indicated substantial variability in the contribution of individual cognitive skills to the correct solution of the different tasks. Here, we exploratively reanalyzed the data to investigate which task characteristics may account for this variability, considering verbal, arithmetic, spatial, and general reasoning skills simultaneously. Results indicate that verbal skills were the most consistent predictor of successful word problem solving in these tasks, arithmetic skills only predicted the correct solution of word problems containing calculations, spatial skills predicted solution rates in the presence of a visual representation, and general reasoning skills were more relevant in simpler problems that could be easily solved using heuristics. We discuss possible implications, emphasizing how word problems may differ with regard to the cognitive skills required to solve them correctly.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Word problems have been a focus of research in mathematics education for the past 50 years (Verschaffel et al., 2000). Mathematical word problems are considered mathematical tasks in which relevant information is presented as text rather than in mathematical notation (Boonen et al., 2016; Daroczy et al., 2015; Verschaffel et al., 2020). They exist in various forms, ranging from a simple verbal description of a basic mathematical operation (e.g., de Koning et al., 2017) to advanced modeling problems (e.g., Leiss et al., 2019; Vorhölter et al., 2019). We consider complex word problems to be mathematical word problems that typically (1) present information in a syntax that does not merely mirror the mathematical task, (2) contain information that might be redundant or superficial, (3) contain multiple representations, and (4) revolve around a context that is functional for the problem solution (Strohmaier, 2020). Examples for complex word problems can be found in the appendix. In contrast, we refer to prototype word problems as mathematical word problems that follow a simple, linear syntax and are relatively short, typically consisting of about three main clauses (Tom has two apples. Lilly gives Tom one apple. How many apples does Tom have?). They often refer to one of the four basic arithmetic operations. They may be contextualized, but unlike complex word problems, the context is not of functional importance for solving the problem (Strohmaier, 2020).
The relevance of complex word problems for mathematics education has arguably increased over the past decade as the goals of mathematics as a school subject have shifted toward more functional and real-world applications, reasoning, mathematical modeling, and non-routine thinking (e.g., CCSSI, 2017; National Council of Teachers of Mathematics [NCTM], 2000; OECD, 2013a; Sekretatiat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland [KMK], 2004; Stacey, 2015). Complex word problems offer a way to address these goals by embedding the mathematical problem into a realistic context and by enriching it with additional text and visual representations. Accordingly, complex word problems are considered a comprehensive indicator of mathematical skills and are used, for example, to assess mathematical literacy in the Programme for International Student Assessment (PISA; OECD, 2013a). However, only a minor part of research on word problem solving has focused on these more demanding and complex-structured word problems (Pongsakdi et al., 2020).
By introducing a context and by framing mathematics as realistic or authentic problems, complex word problems require a variety of skills beyond calculation (Daroczy et al., 2015; Reinhold et al., 2020; Verschaffel et al., 2020). At the same time, they can take various forms, for example with regard to the amount of text, the type of visual representations used, or the underlying mathematical concepts, ideas, and operations. Because of this variety in task characteristics and required skills, successful complex word problem solving reflects a multifaceted interaction between the student and the task (Pongsakdi et al., 2020). However, previous research has often focused on one of the two perspectives, either addressing student characteristics without also systematically investigating task characteristics, or vice versa (Boonen et al., 2014; Daroczy et al., 2015).
Considering the student perspective, several individual factors influencing the solution of word problems have been investigated apart from arithmetic skills (Daroczy et al., 2020; Verschaffel et al., 2020), including linguistic skills (Boonen et al., 2013; Boonen et al., 2016; Daroczy et al., 2015; Fuchs et al., 2006, 2018; Pongsakdi et al., 2020; Swanson et al., 1993; Vilenius-Tuohimaa et al., 2008), spatial skills (Casey et al., 1997; Geary et al., 2000; Hegarty & Kozhevnikov, 1999; Resnick et al., 2020) and reasoning skills (Fuchs et al., 2015, 2020; Spencer et al., 2020; Vilenius-Tuohimaa et al., 2008). At the same time, Daroczy et al. (2015) point out that few studies compared these factors in a comprehensive design that could reveal unique effects and interactions, and that these studies rarely considered task characteristics at the same time. Pongsakdi et al. (2020) further reported that existing studies typically investigated the role of word problem-solving performance on prototype word problems and did not address the differences in the difficulty levels of more complex word problems.
In a previous study, we investigated the role of predictors of word problem solving by comparing the effects of arithmetic skills, verbal skills, spatial skills, and general reasoning skills on word problem solving performance (Reinhold et al., 2020). In a comprehensive analysis, we found that all four skills independently and positively influenced performance, with verbal skills showing the strongest positive effect. In that study, we found a notable amount of variance in the effect sizes of these predictors, which we assumed might indicate substantial differences in effects between the tasks used. However, we did not address task differences in that study because it focused on the interaction between the four cognitive skills and gender differences. In the following, we first review how cognitive skills influence complex word problem solving. Thereafter, we expand upon these findings by reviewing why and how this influence may vary across different complex word problems, justifying a secondary data analysis that accounts for task characteristics.
2 Cognitive Skills in word problem solving
2.1 Verbal skills
A large body of research has shown that verbal skills are of great importance for mathematical thinking and learning (Aiken, 1972; Fuchs et al., 2006; Jordan et al., 2013; Leung, 2017; Morgan et al., 2014; Peng et al., 2020; Prediger et al., 2018; Seethaler et al., 2011; but see also Deary et al., 2007 for conflicting results), and for word problem solving in particular (Daroczy et al., 2015). In these studies, the term verbal skills is used to describe various different student characteristics. In their review, Peng et al. (2020) analyzed how different types of verbal skills (ranging from phonological processing to oral comprehension) influence different types of mathematical skills. Regarding word problem solving, they found that reading comprehension had a stronger effect than phonological processing skills. Accordingly, verbal skills in studies on word problem solving are primarily assessed as text or reading comprehension (e.g., Leiss et al., 2019; Pongsakdi et al., 2020), or oral comprehension (Fuchs et al., 2020). However, Vilenius-Tuohimaa et al. (2008) analyzed the effect of technical reading skills and reading comprehension on prototype word problem solving and found that both aspects of language skills uniquely and positively contributed to successful word problem solving. Therefore, it seems appropriate to assess verbal skills with a broader measure that accounts for technical reading skills, text comprehension, and verbal reasoning skills. For example, Hegarty and Kozhevnikov (1999) used verbal analogy problems (Liepmann et al., 2007).
Verbal analogical reasoning combines aspects of word production, text comprehension, and reasoning with verbal information (Gick & Holyoak, 1980). Although it does not specifically address decoding and technical reading, it is substantially correlated with both students’ overall achievement in language (Alexander et al., 1987) as well as with more specific measures of technical reading skills and text comprehension (Liepmann et al., 2007). Verbal analogies can be expressed in a variety of forms (Ichien et al., 2020). Typically, two given words A and B are related in a particular way, and this relationship needs to be transferred to a second pair of words C and D (e.g., winter : cold = summer : ?).
Therefore, in the present study, verbal skills were considered a set of skills to successfully decode and comprehend text, including both technical reading skills and text comprehension. Verbal skills are assumed to fundamentally interact with mathematical processes during word problem solving (Cummins et al., 1988; Fuchs et al., 2015; Kintsch & Greeno, 1985; Nathan et al., 1992; Reusser, 1990; Strohmaier, 2020; Strohmaier et al., 2019). For complex word problem solving in particular, verbal skills contribute to task performance in at least two ways (Abedi, 2006; Leiss et al., 2019): First, basic decoding skills are required to translate the word problem into the text base, which is a coherent conceptual cognitive representation of the word problem. Second, text comprehension skills are required to derive the mathematical problem model by inferring missing information, excluding irrelevant information, and structuring the text base to fit the solution process (Kintsch & Greeno, 1985; Strohmaier et al., 2019).
2.2 Arithmetic skills
Arithmetic skills are a fundamental prerequisite for mathematical word problem solving (e.g., Fuchs et al., 2006; Pongsakdi et al., 2020). Similar to verbal skills, previous research has operationalized arithmetic skills in different ways, ranging from the concept of arithmetic fact fluency, which is substantially built on automated retrieval (e.g., Fuchs et al., 2006), to tests that focus on operational fluency (Pongsakdi et al., 2020, see Peng et al., 2020 for an overview). In complex word problem solving, the underlying mathematical task often cannot be solved by fact retrieval but requires calculations. Therefore, we refer to arithmetic skills as the ability to correctly solve arithmetic tasks through fact retrieval or calculation.
Often, the core of a mathematical word problem reflects an arithmetic task, usually one that requires calculation. However, a number of studies suggest that arithmetic skills, although a necessary foundation, are not sufficient to fully explain word problem solving performance (e.g., Daroczy et al., 2015; Fuchs et al., 2006, 2018, 2020; Geary et al., 2000; Pongsakdi et al., 2020). For complex word problems, we found that arithmetic skills positively affect the solution probability of PISA items in adults, although this effect was smallest than the influence found for verbal, spatial, and general reasoning skills (Reinhold et al., 2020).
2.3 Spatial skills
Previous studies have used different definitions of spatial skills; however, they generally agree that spatial skills involve the retrieval and handling of visual information in a spatial context (Boonen et al., 2013; Uttal et al., 2013). The construct of spatial visualization (Hawes & Ansari, 2020) is an important aspect of these skills (see Xie et al., 2020, for an overview) and is sometimes used interchangeably with the term spatial skills (Boonen et al., 2013, 2014). Spatial visualization is often assessed through tasks requiring a mental manipulation of objects in space, for example mental rotation or mental folding (for an overview, see Hawes & Ansari, 2020).
Importantly, spatial skills are not only required to solve geometric tasks but are also known to interact with mathematical thinking with regard to reasoning and arithmetic (e.g., Hawes & Ansari, 2020; Mix & Cheng, 2012). In a meta-analysis, Xie et al. (2020) reviewed the relationship between spatial skills and different domains of mathematical ability in a total of 73 studies. They reported the strongest relations between spatial skills and logical reasoning ability (r = .32) and geometric ability (r = .30) but also highly significant relations with arithmetic ability (r = .25) and numerical ability (r = .22). The authors argue that solving problems in domains other than geometry often requires spatial skills for creating visual representations, mental transformations and visualizations, and for processing spatial representations, for example formulae and equations.
The link between spatial skills and mathematical word problem solving has been addressed by a number of studies (e.g., Casey et al., 1997; Geary et al., 2000; Hegarty & Kozhevnikov, 1999; Resnick et al., 2020). Previous studies show that visual representations can contribute to the construction of a mental model and the interpretation of the situation in word problem solving (Boonen et al., 2014; Múñez et al., 2013; Schnotz & Bannert, 2003), however, there are also conflicting findings (Dewolf et al., 2014; Dewolf et al., 2015; Elia et al., 2007). Spatial skills are thought to support an effective use of such visual representations and the construction of a suitable mental model. For example, when integrating different modes of representation (e.g., text and pictures), it is important to combine these sources of information into a coherent mental model, which poses additional cognitive challenges (Elia, 2020; Schnotz & Bannert, 2003).
2.4 General reasoning skills
General reasoning (or fluid reasoning) refers to abstract, logical thought processes of inference and deduction that are loosely tied to the type of perceptual inputs (Carpenter et al., 1990; Lohman & Lakin, 2011; Thurstone, 1938). General reasoning skills are closely associated to intelligence (e.g., Peng et al., 2020), problem solving (e.g., Spencer et al., 2020), and heuristics and metacognition (Mevarech et al., 2018; Mevarech & Kramarski, 2014). They are typically assessed with matrix reasoning tests (e.g., Arthur & Day, 1994), which require identifying and continuing patterns. Although these tasks bear some resemblance to instruments assessing spatial skills, Schweizer et al. (2007) showed that the scales are only moderately correlated (r = .27) and that general reasoning can be adequately assessed with a matrix reasoning test. The essential difference between matrix reasoning tasks and spatial ability tests is that the former focus on logical rule inferences, whereas the latter focus on the visuospatial mental manipulation itself.
Strategic thinking and reasoning are important for word problem solving (Pongsakdi et al., 2020). Fuchs et al. (2020) showed that differences in reasoning skills explained variance in the development of word problem-solving skills (Fuchs et al., 2015; Spencer et al., 2020). Similarly, Vilenius-Tuohimaa et al. (2008) argue that the process of word problem solving involves general reasoning. Moreover, research has highlighted the important role of heuristic and metacognitive processes in successful word problem solving (Mevarech et al., 2018; Mevarech & Kramarski, 2014).
2.5 Task characteristics of complex word problems
Word problems cover a wide range of mathematical tasks that can differ with respect to numerous characteristics. Although no overview has focused on complex word problems, many task characteristics from prototype word problems can be generalized to this particular task type.
Daroczy et al. (2015) distinguish mathematical, linguistic, and general task characteristics that have been shown to influence word problem solving. Mathematical characteristics included, among others, the properties of numbers (single-digit or multi-digit, fractions or decimal numbers, number magnitude, etc.), the required operation and its complexity, the number of solution steps, the required mathematical processes (fact retrieval, problem solving, calculation, etc.), and the mathematical content area. Linguistic factors include syntactic and semantic complexity, text length, the presence of distractors or redundancies, and the relationship between language and mathematical terms. General factors include the answer format, aspects of the contextualization (stereotypes, real-world knowledge, cultural aspects), and the presence of visual representations as well as their relevance.
Relating the previously reported findings to the aforementioned cognitive skills, it is plausible that a number of task characteristics of complex word problems could influence the role that students’ cognitive skills play in solving them.
2.6 Task characteristics and verbal skills
Previous research on the role of verbal skills has shown that linguistic features of word problems such as text length, word difficulty, or the role of pronouns can influence prototype word problem difficulty (Daroczy et al., 2015; Walkington et al., 2017). Mullis et al. (2013) showed that this linguistic complexity primarily affected performance of students with lower reading abilities. A simple explanation for this is that verbal skills increase in importance as linguistic complexity increases (Mullis et al., 2013; Walkington et al., 2017). Because complex word problems typically differ substantially in terms of the amount of text, the linguistic complexity, and the situational context of a task, there could be considerable differences in the influence of verbal skills between different complex word problems (Pongsakdi et al., 2020). Possibly, the influence of verbal skills diminishes when no particular linguistic difficulties are present.
2.7 Task characteristics and arithmetic skills
Task characteristics could affect students with varying arithmetic skills differently. In complex word problems, the mathematical content usually covers a wide range of mathematical domains and underlying mathematical operations and principles. Tasks that involve larger numbers, more complex number representations (e.g., fractions), or more complex mathematical operations might build more strongly on arithmetic skills (Daroczy et al., 2015). On the other hand, if the core of the complex word problem is focusing on other topics like reasoning and argumentation, arithmetical skills might be less important for a successful solution.
2.8 Task characteristics and spatial skills
The role of spatial skills may differ greatly between various forms of complex word problems. Although spatial skills are assumed to be important for mathematical problems across all domains, their influence might differ between geometry problems, where they are explicitly required, and other problems, where they are helpful but not necessary. Furthermore, spatial skills might be particularly beneficial in solving word problems that involve visual representations. To detect, decode, and process information embedded in visual representations is a key aspect of spatial skills (Xie et al., 2020). Even if visual representations are merely decorative, the ability to correctly distinguish important from irrelevant information will potentially influence the process of word problem solving.
2.9 Task characteristics and general reasoning skills
Reasoning is assumed to increase in importance with more complex word problems (Verschaffel et al., 2000; Wyndhamn & Säljö, 1997), suggesting that it should have a stronger effect with increasing task difficulty. At the same time, implicit or incomplete information and more complex mathematical solutions might require flexible and non-routine thinking, but are not necessarily tied to task difficulty. This could mean that the influence of general reasoning abilities differs from task to task, depending on the combination of these specific characteristics.
3 The present study
It is well established that word problem solving requires a multifaceted set of individual skills. However, there are still critical questions that need to be answered. Daroczy et al. (2015) pointed out that previous studies on word problem solving used different word problems and compared groups of students without capturing the interaction between task characteristics and individual student characteristics. They emphasize that due to the various factors influencing word problem solving, different students may have difficulties with different word problems. Accordingly, Daroczy et al. (2015) call for studies that differentiate at both the task level and the individual level to understand why particular students have difficulties with particular word problems. To our knowledge, the few studies that considered both the individual level and the task level usually focused on one or two specific aspects like verbal skills (Mullis et al., 2013; Pongsakdi et al., 2020; Vilenius-Tuohimaa et al., 2008), student background (Walkington et al., 2017), or environmental factors (Daroczy et al., 2020).
In the present study, we sought to address this research gap by exploratively comparing the task characteristics of six complex word problems in terms of the influence of verbal, arithmetic, spatial, and general reasoning skills. By investigating if and how the influence of these facets differs across tasks, we aim to gain insights into which task characteristics might be responsible for such variability.
The present study reflects a secondary data analysis of data previously reported in Reinhold et al. (2020), where all six tasks were combined into one instrument for complex word problem-solving performance. In the current study, we expanded upon these results by qualitatively taking into account differences between the tasks. This approach combined the advantages of a substantial sample size and strong statistical evidence with open-ended, explorative analyses. We formulated the following research questions:
-
RQ1: Does the influence of verbal, arithmetic, spatial, and general reasoning skills on the probability of a correct solution differ between complex word problems?
-
RQ2: If so, can we identify task characteristics that affect this influence?
With regard to RQ1, we expected that certain differences should be observable in the role that the four facets of skills play in the correct solution of the different complex word problems, as it has been shown by previous research that various task characteristics can affect the requirements for successful word problem solving. To our knowledge, however, this has not yet been investigated by addressing this wide spectrum of skills in complex word problem solving simultaneously.
RQ2 was necessarily explorative and aimed to provide a starting point for more systematic research. Nevertheless, this secondary data analysis was guided by several assumptions derived from previous research. We expected that linguistic features such as text length or semantic and syntactical complexity could increase the role of verbal skills. Further, we expected that arithmetic skills would be more important for successfully solving complex word problems constructed around an arithmetic problem and increase with numerical and operational complexity, whereas the influence might be smaller for the geometry or statistics problems. Spatial skills should be relevant for complex word problems containing visual representations and geometric problems. Finally, we expected that general reasoning skills would be more important for more difficult complex word problems and for tasks that contained redundant or irrelevant information.
4 Method
4.1 Sample
The study was conducted during a regular first-year university lecture for engineering students at the Technical University of Munich. All students attending the course participated, but data were only used if the students gave written informed consent on a voluntary basis on a separate sheet handed out with the questionnaires. A total of 15.4% of students was excluded from the analyses due to not giving consent. The remaining participants were N = 1282 students (25.6% female) with a mean age of 19.98 years (SD = 2.73). The study was conducted according to the 2017 Ethical Principles of Psychologists and Code of Conduct of the American Psychological Association. Ethics approval was not required by institutional guidelines or national regulations. Students participated without reimbursement on a voluntary basis. Their informed consent could be withdrawn within 2 months without giving reasons.
4.2 Material
Complex word problems
Six complex word problems were taken from the pool of published PISA mathematics items (see Figs. 2, 3,4, 5, 6, and 7 in the appendix; OECD, 2006, 2013b; the order of the tasks in the study corresponded to the order in which the tasks are presented in the appendix). Answers were coded in line with the PISA coding manual, which is unequivocal and therefore was not further tested for inter-rater reliability. In accordance with this manual, tasks that were left blank were coded as incorrect. The tasks are intended to assess different aspects of mathematical literacy and covered different PISA content areas (change and relationships, space and shape, and uncertainty and data; OECD, 2013a). Although PISA items are designed for 15-year-olds, empirical research indicates that those items are suitable to assess complex word problem-solving performance in undergraduate students (Ehmke et al., 2005; Strohmaier et al., 2019).
Cognitive skills
All cognitive skills were assessed with items in single-choice format and coded according to the respective manuals. In accordance with the design of these scales, missing values were coded as incorrect.
Verbal skills were measured with a verbal analogies scale that required participants to reproduce a relationship given by a pair of words by completing another pair of words with the second word missing, choosing from five given options (e.g., meter : length = second : ?; a) time, b) minute, c) kilometer, d) clock, e) width; Liepmann et al., 2007). Arithmetic skills were measured with non-verbal tasks that had to be solved without a calculator and ranged from basic arithmetic (e.g., 144 : 4 = A) to equations (e.g., 4(B-3) = 64), with natural numbers as solutions (Liepmann et al., 2007). Spatial skills were measured with the Mental Rotations Test (MRT; Peters et al., 1995, 2006; see also Vandenberg & Kuse, 1978), which required participants to identify two correctly rotated structures from four possibilities corresponding to an initial three-dimensional geometrical structure of cubes. General reasoning skills were measured with a reduced item set of Raven’s advanced progressive matrices (Arthur & Day, 1994), using non-verbal, visual geometric stimuli with a missing piece that must be chosen from eight possibilities to complete a pattern. Possible and observed ranges as well as Cronbach’s alpha values, mean scores, and standard deviations for each scale are given in Table 1. Reliability for the verbal skills scale was relatively low but consistent with observations reported by Liepmann et al. (2007). The relatively low reliability of the general reasoning skills scale appears to be atypical, but could result from the limited number of items, with a similar observation reported by Arthur and Day (1994). Since the general reasoning skills scale was already the most time-consuming scale (see Section 4.3), this issue seems difficult to avoid under the given circumstances.
4.3 Procedure
The test was administered by some of the authors in paper-based format under controlled and standardized conditions within the main lectures during the first weeks of the first semester of the students’ university studies. The students received a 40-page booklet (DIN A4) containing all the questionnaires, scales, and tasks, which were worked on part-by-part. Before working on each part, students were asked to read the specific part’s introduction, which contained information about the nature of the tasks within that part and a solved example task (however, no example word problem was given). If no questions arose after reading the introduction to each scale or the complex word problem tasks, the test administrator instructed students to turn the page and start solving this part of the booklet. We followed the test time recommended for each scale: 8 min for complex word problems, 10 min for the arithmetic skills scale, 12 min for the general reasoning skills scale, 3 + 3 min for the spatial skills scale (with 12 items in each cluster), and 7 min for the verbal skills scale. No calculators were allowed.
4.4 Analyses
To estimate the effects of general cognitive skills on complex word problem solving in each of the six tasks, we ran separate logistic regressions for each complex word problem. The models included z-standardized sum scores of arithmetic skills, verbal skills, spatial skills, and general reasoning skills as independent variables and the solution probability (the likelihood of correctly solving the item) as dependent variable. Gender was included as a control variable, because gender differences have been previously reported on several of our outcome measures (Reinhold et al., 2020). Coefficients are given as odds ratios (OR), which are an indicator of the multiplicative change in the solution probability per standard deviation change of the predictor variable (see also Field, 2009). For example, an odds ratio of 1.40 for arithmetic skills for one task means that participants who scored one standard deviation above average in the arithmetic skills test had a 40% higher chance of solving this task than an average participant. Odds ratios are similar to the coefficient b in logistic regressions but represent the proportional changes of the solution probabilities, which are easier to interpret than absolute values (as in linear regressions), as they do not require a logistic transformation and are comparable across items of varying difficulty (Field, 2009). Because all four cognitive skills were included in the models, each coefficient represents a unique effect, which is controlled for the remaining three cognitive skills. This was important because it was expected that the cognitive skills would be interrelated to some degree. All analyses were conducted in R (R Core Team, 2008).
To test whether the effects differed meaningfully between tasks, we conducted a model-fit comparison using chi-squared and AIC model comparisons. We compared generalized linear mixed models with task as an additional independent variable and a student random intercept that (a) included only the main effects of cognitive skills and task to predict the solution probability or (b) also included the cognitive skills × task interaction.
To answer research question 2, we conducted an exploratory data analysis. To this end, we (a) restructured and visualized the data, (b) interpreted the data with two independent coders, and (c) iterated the process based on this evaluation. First, we collected a list of task characteristics that we assumed might account for differences in the influence of the four cognitive skills. These were the following characteristics: answer format, authenticity, required calculation, content area, difficulty (in PISA), gender-specific context, linguistic complexity (semantics), linguistic complexity (syntax), redundancies, number of solution steps, text length (number of characters), numerical difficulty, operational difficulty, relevance of representations, solution rate, and use of representations. For each cognitive skill, we then ranked the tasks in order of their odds ratios for the respective cognitive skill. The resulting table was inspected independently by the first two authors, who flagged possible patterns or systematic effects. The two raters then compared and discussed their results. This process was repeated after the first round to refine and add task characteristics. We only report those cases in which both authors agreed on possibly meaningful patterns and relationships.
5 Results
5.1 Descriptive results
The correlations between the four different general cognitive skills are given in Table 2. Correlations were all statistically significant (p < 0.001) and varied between r = .22 and r = .30. Table 3 illustrates the correlations between the solution rates (the percentage of correct answers given by all participants) of the six complex word problems. The ICC of the overall scale was .15. Solution rates of the tasks varied between 23 and 78%. The tasks are reported in decreasing order of difficulty in the following tables and figures.
5.2 Differences in the influence of cognitive skills
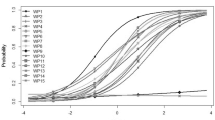
The odds ratios for each task and all cognitive skills are given in Table 4 and illustrated in Fig. 1. Verbal skills were the only predictor that influenced the solution probability of all tasks significantly, with odds ratios ranging from 1.24 to 1.44. The odds ratios of arithmetic skills varied between 0.95 and 1.40, with half of the tasks showing odds ratios that were not significantly different from 1.00 (p > 0.05). For spatial skills, odds ratios varied between 1.12 and 1.39, with only one task showing no significant effect (Mount Fuji, OR = 1.12, p = .110). For general reasoning skills, all tasks except Spring Fair (OR = 1.13, p = .065) showed odds ratios that were statistically significant. Odds ratios of this skill varied between 1.13 and 1.47. Overall, the odds ratios of all cognitive skills on all tasks varied between 0.95 and 1.47.
The model-fit comparison showed that the model including the cognitive skills × task interaction fitted the data significantly better than the model including only main effects (X2(20) = 48.54, p < .001), with a lower AIC (ΔAIC = 8.54).
These results are in line with our hypotheses of RQ1, showing that the influence of the cognitive skills differed both descriptively and statistically between the six complex word problems.
5.3 Task differences
Verbal skills significantly and positively influenced the solution probability of all six tasks. No substantial differences between the tasks or systematic associations with linguistic task features were observed in our data. The only task for which the influence of verbal skills was notably smaller was Mount Fuji (OR = 1.24). It had an average text length compared to the other tasks and was arguably not more difficult with respect to other linguistic features.
The three tasks with a significantly higher solution probability for students with higher arithmetic skills were Revolving Door, Mount Fuji, and Spring Fair. In the first two tasks, students that showed arithmetic skills of 1 SD above average had about a 1.4-times higher probability to solve the task correctly. These tasks required an open numerical answer, derived from appropriate calculations. In contrast to the others, these two tasks were the only ones that were not in single-choice format. Revolving Door was the most difficult task, Mount Fuji was the second easiest. For the task Spring Fair, the influence was still significant, but substantially smaller (OR = 1.24). For Spring Fair, calculations were not necessary, but could provide a result. The solution probability of the three tasks that did not require calculations for their solution (Selling Newspaper, Racing Car, and Water Tank) was not significantly influenced by arithmetic skills when controlling for the other three cognitive skills.
Spatial skills were related to solution probabilities of all tasks except Mount Fuji (OR = 1.12), which was the only task that did not contain any form of visual representation. There was no clear difference between tasks that addressed the content area of space and shape (Water Tank, OR = 1.27; Revolving Door, OR = 1.39) and the tasks that used pictures to illustrate mathematical problems from other content areas (OR = 1.29–1.33).
General reasoning skills significantly predicted the solution probability of all tasks but Spring Fair (OR = 1.13). The two tasks with by far the strongest effect were Mount Fuji and Water Tank (OR = 1.47; OR = 1.41). These two tasks were the easiest to solve and were also the two tasks that contained clearly irrelevant or redundant information. Together with Selling Newspapers, which had the third largest odds ratio for general reasoning skills (OR = 1.23), these tasks were the only ones from the content area change and relationships.
These results concur with the assumption of RQ2 that task characteristics can be identified, which may be responsible for the differences in the influence of the six cognitive skills. These characteristics are discussed in the following section.
6 Discussion
6.1 Different predictors of complex word problems solving
Our findings illustrate a number of aspects that were anticipated based on previous research regarding predictors of successful word problem solving, and others that were less expected. We add to existing studies by taking into account several cognitive skills and task characteristics simultaneously and by investigating complex word problems rather than simple-structured prototype word problems.
Complex word problems vary in terms of their mathematical content and also address a wide range of other cognitive skills (Reinhold et al., 2020). Our results show that the role of these skills differs even within this specific type of word problems (i.e., PISA mathematics items). This underscores the approach to consider task characteristics in research on word problem solving, and to account for their interaction with cognitive skills—for instance, by using statistical models that allow for variance between both students and tasks. At the same time, existing findings should be interpreted carefully when generalized or transferred to different kinds of mathematical word problems. In particular, findings from the large number of studies that used prototype word problems need to be interpreted very cautiously when transferred to complex word problem solving.
6.2 Task differences
A number of task characteristics may have affected the unique influences of one or another cognitive skill on complex word problem solving, whereas other task characteristics did not show a conclusive relation in the present study.
Verbal skills were a consistent predictor of the solution probability of all tasks. This emphasizes the close association between language and mathematics that emerges in complex word problem solving in general (Daroczy et al., 2015; Reinhold et al., 2020; Strohmaier, 2020). The results seemingly conflict with findings by Mullis et al. (2013) who found that the solution of word problems with lower reading demands was less affected by reading abilities. However, Mullis et al. (2013) used reading literacy as a predictor, whereas verbal analogies (as used in the present study) reflect both elements of verbal comprehension and reasoning with verbal information. The general assumption in research on word problem solving is that language serves as a tool to not only decode written information, but also to support the process of successfully building a problem model (Kintsch & Greeno, 1985; Leiss et al., 2019; Reusser, 1990). If word problems differ in terms of linguistic features like text length or the use of pronouns, like analyzed by Mullis et al. (2013), this might be more strongly related to difficulties in reading and decoding of text. On the other hand, more fundamental verbal skills— as also addressed by verbal analogies—might be more strongly related to the process of building a problem model, which in turn might depend less on superficial linguistic features of the complex word problem. This would further support the idea that comprehensive verbal skills reflect one of the core skills that are utilized during complex word problem solving.
The effect of arithmetic skills was strongest in tasks that required calculations in open-ended questions. When no calculation was necessary, arithmetic skills had no influence on the solution probability when controlled for the other cognitive skills. Task difficulty did not seem to systematically influence the effect of arithmetic skills, which is in line with findings by Pongsakdi et al. (2020) who found an association between arithmetic skills and complex word problem solving irrespective of task difficulty. The mere possibility to use a calculation to solve the task does not seem to be a decisive factor, as both Selling Newspapers and Spring Fair could benefit from (but did not require) calculations, but only the latter’s solution probability was influenced significantly by arithmetic skills. Possibly, all solution strategies (including heuristics) need to be taken into account to distinguish which tasks actually offer a way to benefit from arithmetic skills.
This finding seems somewhat obvious, but nevertheless noteworthy, as all six tasks are considered to address aspects of mathematical literacy. This illustrates that mathematical literacy covers areas of mathematics where arithmetic skills are not required and not even particularly helpful. However, it seems that this fact is not reflected in the common perception of mathematics education, educational practice, and research on word problem solving. In schools, arithmetic skills are often considered a necessary foundation for all further mathematical skills. Although this may be true for certain areas of mathematics, this notion seems too narrow for our recent understanding of mathematical literacy. Similarly, research on word problems focuses mostly on contextualized arithmetic problems. However, to fully understand processes of word problem solving in educational practice, non-arithmetic problems should be considered in more detail.
Spatial skills predicted the solution probability of all tasks but one, which was the only one that did not include a visual representation. This indicates that spatial skills are a unique requirement for processing visual representations in complex word problems. However, all of the visual representations in these tasks were necessary or helpful for their solution. Previous research indicates that, in contrast, merely decorative illustrations do not affect performance in complex word problems (Lindner, 2020). Similarly, van Lieshout and Xenidou-Dervou (2018) showed that more demanding visual representations in prototype word problems affect solution rates than less demanding illustrations. Dewolf et al. (2014, 2015) found that representational visual representations in word problems that were not essential for their solution were often not leading to higher solution rates or were not even considered. Because none of the tasks in the present study included decorative illustrations, we cannot say if spatial skills are required in all complex word problems with visual representations, or only when the visual representation explicitly supports the solution process. Our results do however indicate that spatial skills are not limited to the content area of space and shape, which is consistent with findings from Sorby and Panther (2020). It seems plausible that processing visual representations requires additional skills and working memory resources (van Lieshout & Xenidou-Dervou, 2018, 2020) independent of the mathematical requirements of the complex word problem.
Contrary to our expectations, general reasoning skills were more strongly related to easier than to more difficult word problems. Moreover, problems containing irrelevant and redundant information were influenced more strongly. Although the relation to task difficulty is not necessarily causal in our data, it seems plausible that these complex word problems were easier to solve because domain-general reasoning could be used to compensate for missing task-specific knowledge, possibly by exploiting heuristic solution strategies. For example, Water Tank can be effectively solved by eliminating answers in the single-choice answer, but this also applies to tasks like Racing Car. Mount Fuji can be adequately solved by working backwards step-by-step. These two described strategies represent examples of generic problem-solving heuristics—not necessarily related to mathematics—that may build upon general reasoning skills. Such heuristic and metacognitive strategies are an important factor in word problem solving (Verschaffel et al., 2020; Vilenius-Tuohimaa et al., 2008), but to our knowledge, it has not yet been investigated how this effect differs between word problems of varying difficulty. Based on our findings, it would be interesting to address the hypothesis that domain-general heuristic and metacognitive strategies are particularly helpful in easier word problems (where strategies like elimination can replace a mathematical approach) or in word problems where domain-specific requirements are less demanding (and therefore, nonspecific problem-solving strategies can be applied). Moreover, the use of process data such as think-aloud protocols, logfile data, or eye-tracking data could be used to distinguish heuristic solution strategies from the intended mathematical solution strategies during word problem solving.
7 Limitations and implications
The results presented here provide a very focused, but powerful view on determinants of complex word problem solving. Initially, the study was not designed to systematically manipulate specific task features but derived from the observation in Reinhold et al. (2020) that complex word problems varied considerably with regard to their relation to basic cognitive skills. In the analyses presented here, we investigated this variability in more detail, following an explorative approach and applying secondary data analyses to search for possible explanations. However, this can only be a starting point for further research. Our results provide support for the assumption that task characteristics of complex word problems can fundamentally change the skills required for their solution, but our suggestions as to what these characteristics are remain discussable, and their generalizability needs to be addressed with more tasks and a priori hypotheses. This lack of systematic variation has been reported similarly by Pongsakdi et al. (2020) and we agree with their call for a more systematic approach to validate some of the explorative findings from existing research by explicitly comparing larger sets of word problems that differ only in a limited number of task characteristics.
A strength of this study is the large number of participants, which provides strong statistical evidence for the reported findings. On the other hand, the necessity to code all answers solely by their correctness limits the possibilities for qualitative analyses of written answers. Starting with the findings presented here, a next step should identify the specific reasons why students with a particular set of individual skills solve particular complex word problems correctly more often or, in contrast, what particular deficit leads to an incorrect answer. This would help to better understand the processes behind the reported results and the mechanisms behind the influence of basic cognitive skills and complex word problem solving.
Our study reiterates that mathematical word problems have the potential to address cognitive skills beyond mere calculation, but that this potential is very distinct in each word problem. Gaining more knowledge and a stronger awareness of these differences can ensure that the potential of mathematical word problems is utilized optimally in education and in research.
Although our study was conducted with undergraduate students, previous research indicates that the influence of basic cognitive skills on mathematical thinking does not change substantially with age, for example regarding spatial skills (Xie et al., 2020), verbal skills (Peng et al., 2020), and arithmetic skills (Geary et al., 2017). Thus, our findings may also provide practical implications for K-12 education in light of the shift in mathematics education toward more functional, real-world applications, reasoning, mathematical modeling, and non-routine thinking (e.g., CCSSI, 2017; KMK, 2004; NCTM, 2000; OECD, 2013a; Stacey, 2015). Given that complex word problems are considered a suitable tool to assess mathematical literacy and that the present study shows that their solution requires a broad set of cognitive skills, this implies that the focus of educational practice should similarly shift further toward cognitive abilities beyond arithmetic skills in mathematics classrooms. Judging from our results as well as previous studies, it seems appropriate to devote substantial resources to also address verbal, spatial, and general reasoning skills during regular mathematics instruction, thereby broadening our understanding of mathematics not only in assessment, but also in educational practice.
8 Conclusion
The study presented here is based on the notion that mathematical word problem solving is a multifaceted and complex task. Building on findings from studies that have analyzed prerequisites of word problem solving in isolation, our approach was to include multiple student and task characteristics simultaneously. This approach offered a new perspective on the interplay among the various predictors of successful word problem solving. While many of our analyses were explorative in nature and call for more systematic studies, the results suggest that different complex word problems can vary considerably in terms of the required set of cognitive skills beyond arithmetic, and that only verbal skills seem to be a constant prerequisite for this type of mathematical tasks.
References
Abedi, J. (2006). Language issues in item-development. In S. M. Downing & T. M. Haladyna (Eds.), Handbook of test development (pp. 377–398). Erlbaum.
Aiken, L. R. (1972). Language factors in learning mathematics. Review of Educational Research, 42, 359–385. https://doi.org/10.3102/00346543042003359
Alexander, P. A., White, C. S., Haensly, P. A., & Crimmins-Jeanes, M. (1987). Training in analogical reasoning. American Educational Research Journal, 24(3), 387–404. https://doi.org/10.3102/00028312024003387
Arthur, W., & Day, D. V. (1994). Development of a short form for the raven advanced progressive matrices test. Educational and Psychological Measurement, 54(2), 394–403. https://doi.org/10.1177/0013164494054002013
Boonen, A. J. H., van der Schoot, M., van Wesel, F., de Vries, M. H., & Jolles, J. (2013). What underlies successful word problem solving? A path analysis in sixth grade students. Contemporary Educational Psychology, 38, 271–279. https://doi.org/10.1016/j.cedpsych.2013.05.001
Boonen, A. J. H., van Wesel, F., Jolles, J., & van der Schoot, M. (2014). The role of visual representation type, spatial ability, and reading comprehension in word problem solving: An item-level analysis in elementary school children. International Journal of Educational Research, 68, 15–26. https://doi.org/10.1016/j.ijer.2014.08.001
Boonen, A. J. H., de Koning, B. B., Jolles, J., & van der Schoot, M. (2016). Word problem solving in contemporary math education: A plea for reading comprehension skills training. Frontiers in Psychology, 7, Article 191. https://doi.org/10.3389/fpsyg.2016.00191
Carpenter, P. A., Just, M. A., & Shell, P. (1990). What one intelligence test measures: A theoretical account of the processing in the Raven Progressive Matrices Test. Psychological Review, 97(3), 404–431. https://doi.org/10.1037/0033-295X.97.3.404
Casey, M. B., Nuttall, R. L., & Pezaris, E. (1997). Mediators of gender differences in mathematics college entrance test scores: A comparison of spatial skills with internalized beliefs and anxieties. Developmental Psychology, 33(4), 669–680. https://doi.org/10.1037/0012-1649.33.4.669
CCSSI. (2017). Common core standards for mathematics. Retrieved from http://www.corestandards.org/Math/Practice/#CCSS.Math.Practice.MP1
Core Team, R. (2008). R: A language and environment for statistical computing. R Foundation for Statistical Computing.
Cummins, D. D., Kintsch, W., Reusser, K., & Weimer, R. (1988). The role of understanding in solving word problems. Cognitive Psychology, 20(4), 405–438. https://doi.org/10.1016/0010-0285(88)90011-4
Daroczy, G., Wolska, M., Meurers, W. D., & Nuerk, H. C. (2015). Word problems: A review of linguistic and numerical factors contributing to their difficulty. Frontiers in Psychology, 6, Article 348. https://doi.org/10.3389/fpsyg.2015.00348
Daroczy, G., Fauth, B., Cipora, K., Meurers, D., & Nuerk, H. C. (2020). The relation of environmental factors to the task difficulty in word problems. PsyArXiv. https://doi.org/10.31234/osf.io/dz9he
de Koning, B. B., Boonen, A. J. H., & van der Schoot, M. (2017). The consistency effect in word problem solving is effectively reduced through verbal instruction. Contemporary Educational Psychology, 49, 121–129. https://doi.org/10.1016/j.cedpsych.2017.01.006
Deary, I. J., Strand, S., Smith, P., & Fernandes, C. (2007). Intelligence and educational achievement. Intelligence, 35(1), 13–21. https://doi.org/10.1016/j.intell.2006.02.001
Dewolf, T., Van Dooren, W., Ev Cimen, E., & Verschaffel, L. (2014). The impact of illustrations and warnings on solving mathematical word problems realistically. The Journal of Experimental Education, 82(1), 103–120. https://doi.org/10.1080/00220973.2012.745468
Dewolf, T., Van Dooren, W., Hermens, F., & Verschaffel, L. (2015). Do students attend to representational illustrations of non-standard mathematical word problems, and, if so, how helpful are they? Instructional Science, 43(1), 147–171. https://doi.org/10.1007/s11251-014-9332-7
Ehmke, T., Wild, E., & Müller-Kalhoff, T. (2005). Comparing adult mathematical literacy with PISA students: Results of a pilot study. ZDM–Mathematics Education, 37(3), 159–167. https://doi.org/10.1007/s11858-005-0005-5
Elia, I. (2020). Word problem solving and pictorial representations: Insights from an exploratory study in kindergarten. ZDM–Mathematics Education, 52(1), 17–31. https://doi.org/10.1007/s11858-019-01113-0
Elia, I., Gagatsis, A., & Demetriou, A. (2007). The effects of different modes of representation on the solution of one-step additive problems. Learning and Instruction, 17(6), 658–672. https://doi.org/10.1016/j.learninstruc.2007.09.011
Field, A. (2009). Discovering statistics using SPSS (3rd ed.). Sage Publications.
Fuchs, L. S., Fuchs, D., Compton, D. L., Powell, S. R., Seethaler, P. M., Capizzi, A. M., … Fletcher, J. M. (2006). The cognitive correlates of third-grade skill in arithmetic, algorithmic computation, and arithmetic word problems. Journal of Educational Psychology, 98(1), 29–43. https://doi.org/10.1037/0022-0663.98.1.29
Fuchs, L. S., Fuchs, D., Compton, D. L., Hamlett, C. L., & Wang, A. Y. (2015). Is word-problem solving a form of text comprehension? Scientific Studies of Reading, 19(3), 204–223. https://doi.org/10.1080/10888438.2015.1005745
Fuchs, L. S., Gilbert, J. K., Fuchs, D., Seethaler, P. M., & Martin, B. N. (2018). Text comprehension and oral language as predictors of word-problem solving: Insights into word-problem solving as a form of text comprehension. Scientific Studies of Reading, 22(2), 152–166. https://doi.org/10.1080/10888438.2017.1398259
Fuchs, L. S., Fuchs, D., Seethaler, P. M., & Barnes, M. A. (2020). Addressing the role of working memory in mathematical word-problem solving when designing intervention for struggling learners. ZDM–Mathematics Education, 52(1), 87–96. https://doi.org/10.1007/s11858-019-01070-8
Geary, D. C., Saults, S. J., Liu, F., & Hoard, M. K. (2000). Sex differences in spatial cognition, computational fluency, and arithmetical reasoning. Journal of Experimental Child Psychology, 77(4), 337–353. https://doi.org/10.1006/jecp.2000.2594
Geary, D. C., Nicholas, A., Li, Y., & Sun, J. (2017). Developmental change in the influence of domain-general abilities and domain-specific knowledge on mathematics achievement: An eight-year longitudinal study. Journal of Educational Psychology, 109(5), 680–693. https://doi.org/10.1037/edu0000159
Gick, M. L., & Holyoak, K. J. (1980). Analogical problem solving. Cognitive Psychology, 12(3), 306–355. https://doi.org/10.1016/0010-0285(80)90013-4
Hawes, Z., & Ansari, D. (2020). What explains the relationship between spatial and mathematical skills? A review of evidence from brain and behavior. Psychonomic Bulletin & Review, 27, 465–482. https://doi.org/10.3758/s13423-019-01694-7
Hegarty, M., & Kozhevnikov, M. (1999). Types of visual-spatial representations and mathematical problem solving. Journal of Educational Psychology, 91(4), 648–689. https://doi.org/10.1037/0022-0663.91.4.684
Ichien, N., Lu, H., & Holyoak, K. J. (2020). Verbal analogy problem sets: An inventory of testing materials. Behavior Research Methods, 52(5), 1803–1816. https://doi.org/10.3758/s13428-019-01312-3
Jordan, N. C., Hansen, N., Fuchs, L. S., Siegler, R. S., Gersten, R., & Micklos, D. (2013). Developmental predictors of fraction concepts and procedures. Journal of Experimental Child Psychology, 116(1), 45–58. https://doi.org/10.1016/j.jecp.2013.02.001
Kintsch, W., & Greeno, J. G. (1985). Understanding and solving word arithmetic problems. Psychological Review, 92(1), 109–129. https://doi.org/10.1037/0033-295X.92.1.109
Leiss, D., Plath, J., & Schwippert, K. (2019). Language and mathematics - key factors influencing the comprehension process in reality-based tasks. Mathematical Thinking and Learning, 21(2), 131–153. https://doi.org/10.1080/10986065.2019.1570835
Leung, F. K. S. (2017). Making sense of mathematics achievement in East Asia: Does culture really matter? In G. Kaiser (Ed.), Proceedings of the 13th Internatioal Congress on Mathematical Education (pp. 201–218). Springer.
Liepmann, D., Beauducel, A., Brocke, B., & Amthauer, R. (2007). Intelligenz-Struktur-Test 2000 R (2nd ed.). Hogrefe.
Lindner, M. A. (2020). Representational and decorative pictures in science and mathematics tests: Do they make a difference? Learning and Instruction, 68, 101345. https://doi.org/10.1016/j.learninstruc.2020.101345
Lohman, D. F., & Lakin, J. M. (2011). Intelligence and reasoning. In R. J. Sternberg & S. B. Kaufman (Eds.), The Cambridge handbook of intelligence (pp. 419–441). Cambridge University Press. https://doi.org/10.1017/CBO9780511977244.022
Mevarech, Z. R., & Kramarski, B. (2014). Critical maths in innovative societies: The effects of metacognitive pedagogies on mathematical reasoning. OECD.
Mevarech, Z. R., Verschaffel, L., & De Corte, E. (2018). Metacognitive pedagogies in mathematics classrooms: From kindergarten to college and beyond. In D. H. Schunk & J. A. Greene (Eds.), Handbook of self-regulation of learning and performance (pp. 109–123). Routledge.
Mix, K. S., & Cheng, Y.-L. (2012). The relation between space and math: Developmental and educational implications. In J. B. Benson (Ed.), Advances in child development and behavior (vol. 42, pp. 197–243). Elsevier.
Morgan, C., Craig, T. S., Schuette, M., & Wagner, D. (2014). Language and communication in mathematics education: An overview of research in the field. ZDM–Mathematics Education, 46, 843–853. https://doi.org/10.1007/s11858-014-0624-9
Mullis, I. V., Martin, M. O., & Foy, P. (2013). The impact of reading and science achievement at the fourth grade: An analysis by item reading demands. In M. O. Martin & I. V. S. Mullis (Eds.), TIMSS and PIRLS 2011: Relationships among reading, mathematics, and schience anchievement at the fourth grade—implications for ealy learning (pp. 67–108). IEA.
Múñez, D., Orrantia, J., & Rosales, J. (2013). The effect of external representations on compare word problems: Supporting mental model construction. The Journal of Experimental Education, 81(3), 337–355. https://doi.org/10.1080/00220973.2012.715095
Nathan, M. J., Kintsch, W., & Young, E. (1992). A theory of algebra-word-problem comprehension and its implications for the design of learning environments. Cognition and Instruction, 9(4), 329–389. https://doi.org/10.1207/s1532690xci0904_2
National Council of Teachers of Mathematics [NCTM]. (2000). Principles and standards for mathematics. NCTM.
OECD. (2006). PISA released items - mathematics. Retrieved from http://www.oecd.org/pisa/38709418.pdf
OECD. (2013a). PISA 2012 assessment and analytical framework: Mathematics, reading, science, problem solving and financial literacy. OECD Publishing.
OECD. (2013b). PISA 2012 released mathematics items. Retrieved from https://www.oecd.org/pisa/pisaproducts/pisa2012-2006-rel-items-maths-ENG.pdf
Peng, P., Lin, X., Ünal, Z. E., Lee, K., Namkung, J., Chow, J., & Sales, A. (2020). Examining the mutual relations between language and mathematics: A meta-analysis. Psychological Bulletin, 146(7), 595–634. https://doi.org/10.1037/bul0000231
Peters, M., Laeng, B., Latham, K., Jackson, M., Zaiyouna, R., & Richardson, C. (1995). A redrawn Vandenberg and Kuse mental rotations test – different versions and factors that affect performance. Brain and Cognition, 28(1), 39–58. https://doi.org/10.1006/brcg.1995.1032
Peters, M., Lehmann, W., Takahira, S., Takeuchi, Y., & Jordan, K. (2006). Mental rotation test performance in four cross-cultural samples (N = 3367): Overall sex differences and the role of academic program in performance. Cortex, 42(7), 1005–1014. https://doi.org/10.1016/S0010-9452(08)70206-5
Pongsakdi, N., Kajamies, A., Veermans, K., Lertola, K., Vauras, M., & Lehtinen, E. (2020). What makes mathematical word problem solving challenging? Exploring the roles of word problem characteristics, text comprehension, and arithmetic skills. ZDM–Mathematics Education, 52(1), 33–44. https://doi.org/10.1007/s11858-019-01118-9
Prediger, S., Wilhelm, N., Büchter, A., Gürsoy, E., & Benholz, C. (2018). Language proficiency and mathematics achievement. Journal für Mathematik-Didaktik, 39, 1–26. https://doi.org/10.1007/s13138-018-0126-3
Reinhold, F., Hofer, S., Berkowitz, M., Strohmaier, A., Scheuerer, S., Loch, F., … Reiss, K. (2020). The role of spatial, verbal, numerical, and general reasoning abilities in complex word problem solving for young female and male adults. Mathematics Education Research Journal, 32(2), 189–211. https://doi.org/10.1007/s13394-020-00331-0
Resnick, I., Harris, D., Logan, T., & Lowrie, T. (2020). The relation between mathematics achievement and spatial reasoning. Mathematics Education Research Journal, 32, 171–174. https://doi.org/10.1007/s13394-020-00338-7
Reusser, K. (1990). From text to situation to equation: cognitive simulation of understanding and solving mathematical word problems. In H. Mandl, E. De Corte, N. S. Bennett, & H. F. Friedrich (Eds.), Learning and instruction in an international context (pp. 477–498). Pergamon.
Schnotz, W., & Bannert, M. (2003). Construction and interference in learning from multiple representation. Learning and Instruction, 13(2), 141–156. https://doi.org/10.1016/S0959-4752(02)00017-8
Schweizer, K., Goldhammer, F., Rauch, W., & Moosbrugger, H. (2007). On the validity of Raven’s matrices test: Does spatial ability contribute to performance? Personality and Individual Differences, 43(8), 1998–2010. https://doi.org/10.1016/j.paid.2007.06.008
Seethaler, P. M., Fuchs, L. S., Star, J. R., & Bryant, J. (2011). The cognitive predictors of computational skill with whole versus rational numbers: An exploratory study. Learning and Individual Differences, 21(5), 536–542. https://doi.org/10.1016/j.lindif.2011.05.002
Sekretatiat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland [KMK]. (2004). Bildungsstandards im Fach Mathematik für den Mittleren Schulabschluss. Wolters Kluwer.
Sorby, S. A., & Panther, G. C. (2020). Is the key to better PISA math scores improving spatial skills? Mathematics Education Research Journal, 32, 213–233. https://doi.org/10.1007/s13394-020-00328-9
Spencer, M., Fuchs, L. S., & Fuchs, D. (2020). Language-related longitudinal predictors of arithmetic word problem solving: a structural equation modeling approach. Contemporary Educational Psychology, 60, 101825. https://doi.org/10.1016/j.cedpsych.2019.101825
Stacey, K. (2015). The real world and the mathematical world. In K. Stacey & R. Turner (Eds.), Assessing Mathematical Literacy. The PISA Experience (pp. 57–84). Springer.
Strohmaier, A. R. (2020). When reading meets mathematics. Using eye movements to analyze complex word problem solving. [Doctoral dissertation, Technical University of Munich]. Technical University of Munich. https://doi.org/10.14459/2020md1521471
Strohmaier, A. R., Lehner, M. C., Beitlich, J. T., & Reiss, K. M. (2019). Eye movements during mathematical word problem solving - Global measures and individual differences. Journal für Mathematik-Didaktik, 40, 255–287. https://doi.org/10.1007/s13138-019-001
Swanson, H. L., Cooney, J. B., & Brock, S. (1993). The influence of working memory and classification ability on children’s word problem solution. Journal of Experimental Child Psychology, 55(3), 374–395. https://doi.org/10.1006/jecp.1993.1021
Thurstone, L. L. (1938). Primary mental abilities. University of Chicago Press.
Uttal, D. H., Meadow, N. G., Tipton, E., Hand, L. L., Alden, A. R., Warren, C., & Newcombe, N. S. (2013). The malleability of spatial skills: A meta-analysis of training studies. Psychological Bulletin, 139(2), 352–403. https://doi.org/10.1037/a0028446
van Lieshout, E. C. D. M., & Xenidou-Dervou, I. (2018). Pictorial representations of simple arithmetic problems are not always helpful: A cognitive load perspective. Educational Studies in Mathematics, 98(1), 39–55. https://doi.org/10.1007/s10649-017-9802-3
van Lieshout, E. C. D. M., & Xenidou-Dervou, I. (2020). Simple pictorial mathematics problems for children: Locating sources of cognitive load and how to reduce it. ZDM–Mathematics Education, 52(1), 73–85. https://doi.org/10.1007/s11858-019-01091-3
Vandenberg, S. G., & Kuse, A. R. (1978). Mental rotations, a group test of three-dimensional spatial visualization. Perceptual and Motor Skills, 47(2), 599–604. https://doi.org/10.2466/pms.1978.47.2.599
Verschaffel, L., Greer, B., & De Corte, E. (2000). Making sense of word problems. Swets & Zeitlinger.
Verschaffel, L., Schukajlow, S., Star, J., & Van Dooren, W. (2020). Word problems in mathematics education: A survey. ZDM–Mathematics Education, 52(1), 1–16. https://doi.org/10.1007/s11858-020-01130-4
Vilenius-Tuohimaa, P. M., Aunola, K., & Nurmi, J. E. (2008). The association between mathematical word problems and reading comprehension. Educational Psychology, 28(4), 409–426. https://doi.org/10.1080/01443410701708228
Vorhölter, K., Greefrath, G., Borromeo Ferri, R., Leiß, D., & Schukajlow, S. (2019). Mathematical Modelling. In H. Jahnke & L. Hefendehl-Hebeker (Eds.), Traditions in German-Speaking Mathematics Education Research (pp. 91–114). Springer.
Walkington, C., Clinton, V., & Shivraj, P. (2017). How readability factors are differentially associated with performance for students of different backgrounds when solving mathematics word problems. American Educational Research Journal, 55(2), 362–414. https://doi.org/10.3102/0002831217737028
Wyndhamn, J., & Säljö, R. (1997). Word problems and mathematical reasoning—a study of children’s mastery of reference and meaning in textual realities. Learning and Instruction, 7(4), 361–382. https://doi.org/10.1016/S0959-4752(97)00009-1
Xie, F., Zhang, L., Chen, X., & Xin, Z. (2020). Is spatial ability related to mathematical ability: A meta-analysis. Educational Psychology Review, 32(1), 113–155. https://doi.org/10.1007/s10648-019-09496-y
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
English version of the item Racing Car (M159Q04). Adapted from PISA Released Items - Mathematics (p. 33), by OECD (2006). Copyright 2006 by the OECD. Used under CC BY-NC-SA 3.0 IGO
English version of the item Mount Fuji (PM942Q02). Adapted from PISA 2012 Released Mathematics Items (p. 20), by OECD (2013b). Copyright 2013 by the OECD. Used under CC BY-NC-SA 3.0 IGO
English version of the item Water Tank (M465Q01). Adapted from PISA Released Items - Mathematics (p. 60), by OECD (2006). Copyright 2006 by the OECD. Used under CC BY-NC-SA 3.0 IGO
English version of the item Revolving Door (PM995Q02). Adapted from PISA 2012 Released Mathematics Items (p. 34), by OECD (2013b). Copyright 2013 by the OECD. Used under CC BY-NC-SA 3.0 IGO
English version of the item Selling Newspapers (PM994Q03). Adapted from PISA 2012 Released Mathematics Items (p. 78), by OECD (2013b). Copyright 2013 by the OECD. Used under CC BY-NC-SA 3.0 IGO
English version of the item Spring Fair (M471Q01). Adapted from PISA Released Items - Mathematics (p. 63), by OECD (2006). Copyright 2006 by the OECD. Used under CC BY-NC-SA 3.0 IGO
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Strohmaier, A.R., Reinhold, F., Hofer, S. et al. Different complex word problems require different combinations of cognitive skills. Educ Stud Math 109, 89–114 (2022). https://doi.org/10.1007/s10649-021-10079-4
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10649-021-10079-4