Research on how teachers provide feedback in mathematics shows that teachers mainly tend to address procedural skills (Stovner & Klette, in review; Casey et al., 2018; Runnalls & Hong, 2019; Sánchez-Matamoros et al., 2019; Son, 2013). This is of concern, because research in mathematics education (Burkhardt, 2014; Niss et al., 2016) and mathematics curricula (National Governors Association Center for Best Practices, Council of Chief State School Officers, 2010; Norwegian Directorate for Education and Training [UDIR], 2013b) emphasizes that teaching should foster other competencies in addition to procedural skills, such as conceptual understanding and the ability to engage in mathematical practices. Given the importance of providing feedback on mathematical competencies other than procedures, it is crucial that we understand the situations in which teachers provide such advanced feedback in the classroom to help improve their instructional repertoire in this critical area.

The research on feedback is extensive and shows that it is an instructional practice that can have substantial effects on student learning (Hattie & Timperley, 2007). However, most studies on feedback have been content-generic (Wiliam, 2018) and not content-specific; additionally, few studies are on feedback in mathematics (Ruiz-Primo & Li, 2013). Moreover, most were conducted in researcher-created situations (Ruiz-Primo & Li, 2013), such as in interventions (e.g., Inagaki et al., 1998) or using student work or videos of lessons as prompts (e.g., Son, 2016). How teachers provide feedback in day-to-day mathematics classroom teaching is not well documented. In this study, we contribute to the extant literature by describing the feedback practices of teachers who provide substantive feedback, feedback that pushes students toward deeper content engagement and understanding rather than executing procedures only.

A main contribution in the present study is that we investigate feedback in authentic in situ mathematics lessons and not in experimental or other artificial situations. This complements previous laboratory and intervention studies by elucidating the repertoire required to provide substantive feedback while managing the complexity of the instructional situations. We purposefully sampled teachers from a large representative video corpus of mathematics lessons in Norwegian lower secondary school (Klette et al., 2017). Most teachers (N = 47) in these lessons mainly provided procedural feedback, but five teachers provided strong evidence of substantive feedback (Stovner & Klette, in review) for parts of their lessons and are the focal teachers in the present study. We aimed to answer the following research question: What distinguishes the instructional situations in which these teachers provide procedural feedback from the situations when they provide substantive feedback? We focus on oral feedback provided during lessons, because this constitutes the majority of feedback provided by teachers (Ruiz-Primo & Kroog, 2018) and may impact students more than written feedback on assessments and homework (Shavelson, 2003). In the theoretical framework that follows, we situate feedback within assessment for learning (AfL) and define the main analytical terms in the study: procedural and substantive feedback and instructional situations.

1 Theoretical framework

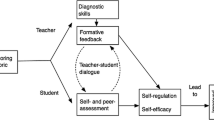
This study is based on a conception of feedback that is inherent in assessment for learning (see Black & Wiliam, 1998). AfL refers to a set of teaching practices in which teachers continually (and mostly informally) assess student learning and use the assessments to adapt their instruction and provide feedback to students. AfL has influenced educational policy around the world (Birenbaum et al., 2015) including the context of the present study, Norway, where a nationwide professional development program in 2010–2018 targeted AfL and teachers’ use of feedback (UDIR, 2018). Within AfL, feedback is communication to students about how they are doing and what they can do to improve, so that they may direct their learning (Wiliam, 2007).

The two defining features of feedback that distinguish it from other kinds of communication are that feedback concerns student performance and is evaluative (Smith & Lipnevich, 2018). Performance denotes a student’s work or understanding, as evident in written work or answers to a teacher’s question or similar. Evaluative in this context means that the comment assesses qualities of student work and understandings or suggests how to improve. Feedback can be very short, such as when acknowledging whether student answers are correct, or more elaborated, for instance, when remediating students’ conceptual difficulties. Feedback may—and often does—form an integral part of teacher–student communication (Small & Lin, 2018): The teacher and the student discuss the student’s work or understanding, often initiated by the student’s question, and the teacher assesses that the student needs some input in order to progress, whereupon the teacher gives the student feedback. Students are active participants who, when receiving feedback from their teacher, may discuss and negotiate with the teacher to create an understanding of the feedback (Hattie & Gan, 2011).

Common feedback frameworks do not distinguish between feedback that addresses procedural skills and feedback that addresses other mathematical competencies, such as conceptual understanding or the ability to engage in mathematical practices. For instance, Hattie and Timperley’s (2007) framework distinguishes between feedback that focuses on the task, the process, self-regulation, and the self. If a teacher gives feedback to a student who has written 3(x + 1) = 3x + 1 by saying “first multiply 3 with x and then 3 with 1,” it would be task feedback as it concerns that specific task, whereas saying “always multiply with all terms in the parentheses” would be process feedback. However, both feedback examples address procedural skills. Therefore, we use a mathematics-specific framework to distinguish between different mathematical competencies addressed in the feedback.

1.1 Mathematical focus of the feedback

In this study, we distinguish between substantive feedback and procedural feedback. See Table 1 for an overview. Procedural feedback focuses on steps in a solution procedure to successfully complete a task. It evaluates whether students have executed the correct steps in a set solution procedure or suggests steps to continue with when stuck. An example is feedback that reminds a student to put fractions on a common denominator before adding. Such feedback may be provided for procedural exercises but also for cognitively demanding tasks—for example if the teacher guides students through a series of steps in a solution procedure. Feedback that focuses on procedures aids students in solving similar problems (Alibali, 1999; Fyfe et al., 2015), at least for learners with little background knowledge (Fyfe et al., 2012).

Table 1 Definitions and examples of procedural and substantive feedback
Full size table

Substantive feedback is feedback that focuses on deeper understanding and content engagement and includes what might be termed conceptual feedback and feedback on mathematical practices. Conceptual feedback focuses on mathematical concepts and the relationships among them. When teachers provide conceptual feedback, they draw on definitions or representations of concepts to explain to students why their work is erroneous or what they need to understand to continue. An example is feedback that draws a graphical representation of the sum of two fractions to explain why the student’s method for adding them was erroneous (see Table 1). There is little evidence of the effect of conceptual feedback on learning, but one study showed that conceptual feedback aids task performance on far-transfer tasks but that procedural feedback is more effective for increased performance on near-transfer tasks (Alibali, 1999). Feedback on mathematical practices focuses on how students engage in mathematical practices (Moschkovich, 2015). Mathematical practices are the practices users of mathematics engage in when doing mathematics, such as problem solving, proving, and conjecturing (Weber et al., 2020). By making students’ engagement in a mathematical practice explicit, a teacher may support students in noticing and attending to the practice (Selling, 2016). An example is when a teacher praises that a student drew a figure to understand a mathematical problem. This feedback contains information regarding a strategy (drawing a figure) that helps the student with a mathematical practice (problem solving). In the example in Table 1, the teacher gives feedback on the practices of conjecturing and justifying.

Because procedural skills, conceptual understanding, and the ability to engage in mathematical practices are important aspects of the Norwegian curriculum in mathematics (UDIR, 2013a), teacher feedback should help students progress in these key areas. In this study, we are especially interested in teachers’ use of substantive feedback—not because procedural feedback cannot be valuable, but because results from laboratory studies (Casey et al., 2018; Son & Sinclair, 2010) and our previous analyses (Stovner & Klette, in review) showed that procedural feedback is far more prevalent than feedback on conceptual understanding or mathematical practices.

1.2 Instructional situations

An instructional situation is defined as a stretch of time during a lesson in which the teachers and students have customary ways of interacting with each other and the mathematics (Herbst, 2006). It captures the notion that teachers and students have expectations for each other regarding who drives the mathematics forward and what counts as valuable mathematical work (Herbst & Chazan, 2012). The instructional situation may change during a lesson, meaning that the teachers and students interact in different ways and take on different responsibilities for the mathematics at hand (Chazan, 2013). We use the notion of instructional situations as a theoretical tool to parse lessons to analyze when teachers provide procedural and substantive feedback and how the situations differ.

Using the instructional situation as a lens to study feedback acknowledges that not only the teachers’ individual resources (e.g., knowledge), but also the students, the mathematics at stake, and the interactions between them, shape and are shaped by the feedback. If introducing new ways of working with the content and providing feedback lead to an instructional situation with which the teachers or students are unaccustomed, it may lead them to default to an instructional situation that they are used to enacting (Herbst & Chazan, 2012). Therefore, changing the instructional situation may require negotiation, clarifying new expectations for the students’ and teacher’s roles as well as what counts as mathematical work (Herbst & Chazan, 2012).

We use the instructional situation as a theoretical tool to answer the question of when and how teachers provide procedural and substantive feedback. This entails viewing feedback as embedded in the larger interaction patterns among the teacher, the students, and the content. To distinguish the instructional situations in which procedural and substantive feedback is provided, we analyzed characteristics of the mathematics at stake in the situation, how teachers and students interact about it, and whether they negotiate the change in the situation.

2 Methods

In this study, we analyzed 16 mathematics lessons taught by five teachers purposefully sampled from a larger video study. The data were drawn from the large-scale video study Linking Instruction and Student Achievement (LISA; Klette et al., 2017). LISA included 172 mathematics lessons taught by 47 teachers in 47 schools (Grade 8). Video recordings of four consecutive lessons were planned for, but in some classrooms, only two or three lessons were possible. The LISA project aimed at investigating the instructional quality of Language Arts and Mathematics lessons in Norway. To measure this, LISA used the observation instrument Protocol for Language Arts Teaching Observation (PLATO; Grossman et al., 2013). In this study, we used the PLATO ratings to sample teachers who provided substantive feedback in their lessons.

2.1 The PLATO instrument

The theoretical outlook of PLATO stresses “rigorous content and intellectually challenging tasks, the centrality of classroom discourse in developing sophisticated understanding of content and disciplinary skills, and the critical role of teachers in providing instructional scaffolding for students to help them succeed” (Grossman et al., 2014, p. 295). The instrument was originally developed to measure Language Arts instruction but has since been used to measure mathematics teaching (Luoto & Klette, in review; Cohen, 2018). The teaching practices measured by PLATO in mathematics have been found to correspond well with quality mathematics teaching as conceptualized in Norway (Klette et al., 2017) and the USA (Cohen, 2018), but other measures of predictive validity or construct validity in mathematics do not exist. In this study, we used the PLATO ratings in the LISA data to sample teachers who provided strong evidence of substantive feedback. Although PLATO measures 12 elements, we used only the feedback element.

We chose PLATO’s feedback element to sample teachers for this study for three reasons. First, it distinguishes between procedural feedback on the low end and substantive feedback on the high end. Second, PLATO’s conception of feedback relates to AfL and formative assessment (Black & Wiliam, 1998; Sadler, 1989) that align well with how feedback is conceptualized in the Norwegian educational context (see Munthe & Melting, 2016; UDIR, 2018). Third, existing mathematics-specific observation instruments do not have feedback dimensions (Praetorius & Charalambous, 2018). While there are also hybrid instruments that mix mathematics-specific and general dimensions, such as TEDS-Instruct (Schlesinger et al., 2018), they have subject-general feedback dimensions. Thus, PLATO’s feedback dimension aligns with our goal of analyzing substantive feedback, the instrument is relevant for the Norwegian educational context, and other instruments would not be a better fit.

When the PLATO instrument is used, lessons are subdivided into 15-min segments, and each segment is assigned a score from 1 to 4. At the low end, segments rated 1 and 2 indicate misleading, vague, and procedural feedback. A score of 3 is provided if a 15-min segment has at least two feedback instances that are specific and substantive. Specific means that the feedback clearly communicates qualities of student work and how to improve. Substantive means that the feedback addresses underlying skills, such as conceptual understanding or problem solving. A score of 4 is provided if the feedback is consistently specific and substantive, and it is easy to infer that students are helped by the feedback.

In the LISA data, there were 512 segments (in the 172 lessons), eight of which were rated 4. They were taught by five teachers (Stovner & Klette, in review). These five teachers constituted the focal teachers in the present analysis, and their 16 recorded lessons are the primary data source. This sampling procedure presupposed that the raters correctly assigned a rating of 4. Fifteen percent of the lessons were double coded, showing a 72% exact overlap between the raters for the feedback element. To ascertain whether the segments rated 4 were correctly coded, we reanalyzed these segments to reach consensus about the true score. We decided all segments rated 4 had a true score of 4.

2.2 Sample

Table 2 displays background data on the teachers, lessons, schools, and student achievement on national numeracy tests. The background data showed a wide variety of characteristics. The five teachers had 2–17 years of teaching experience and 0.5–1.5 years of university courses in mathematics or mathematics education. The teachers taught in urban and rural schools whose intake areas included various socioeconomic backgrounds. The teachers also taught different content in the recorded lessons. The students in three teachers’ classes achieved close to the average on national mathematics tests at intake; the two other teachers’ classes achieved high above and below the national mean.

Table 2 Background data on the teachers and classes
Full size table

2.3 Analysis

The first author created narrative summaries by watching each lesson and taking notes on instructional aspects relevant for identifying instructional situations (e.g., the teacher and student interactions and negotiations, the mathematical tasks and how students worked on them, lesson activities, and the types of feedback provided). Narrative summaries are descriptive accounts of video data that are useful for identifying patterns across large video data sets (Derry et al., 2010). Following Braun and Clarke (2006), the first author conducted a thematic analysis of the narrative summaries. He began the thematic analysis inductively by assigning codes that closely aligned with the data about how teachers and students interacted about the mathematics. He reviewed and refined the codes by combining similar codes into broader ones, eventually naming themes that were descriptive of the instructional situations in which teachers provided procedural and substantive feedback. This process yielded themes of different instructional situations in which teachers provided procedural and substantive feedback and codes that typified the characteristics of these situations. The videos were consulted frequently throughout this process to validate our interpretations. The second author ensured confirmability (Jensen, 2008) of the analysis at the end by rewatching the videos to ensure that the identified themes and characteristics were accurate, and that all instances of each theme cohered together thematically. Last, examples that illustrated the characteristics of the instructional situations were transcribed and translated for presentation in the results section.

2.4 Limitations

The findings in our study are based on a small number of teachers and are not generalizable. We acknowledge that there might be segments in the data that should have been rated 4 but were not rated 4 due to rater error (Bell et al., 2014). Although we might not have found all segments rated 4, the design afforded us the opportunity to study a rare teaching practice, providing substantive feedback, in depth, including when and how teachers provide it.

Because of observer effects, we may not capture feedback as it is provided in regular teaching. Although the teachers were told that we wanted to see their regular lessons, placing cameras and microphones in the classroom is an obvious intervention that may have changed how the teachers taught or the students behaved. However, previous research on camera reactivity suggests that this is of very limited concern when using video observation (Ball et al., 2009; Klette et al., 2016), except for the first few minutes of the first lesson filmed (Praetorius et al., 2017).

3 Results

We identified two types of instructional situations where teachers provided procedural feedback and two types of instructional situations where they provided substantive feedback. We remind the reader that an instructional situation is a stretch of time with a distinct pattern of interactions among the teacher, the students, and the content. The types of instructional situations we identified occurred similarly across the lessons of the different teachers and demarcated when procedural and substantive feedback was provided. Condensed descriptions of the situations are shown in Table 3. We first present the overall pattern of how the situations appeared in the lessons, before we provide two examples of instructional situations when substantive feedback was provided.

Table 3 Types of instructional situations identified in this study
Full size table

Procedural feedback was provided when Developing new content and Practicing exercise tasks. The teachers developed new content in whole-class discussions by engaging students with questions. The teacher–student interactions about the mathematics were characterized by short teacher prompts and student answers, to which the teacher responded with very brief feedback, mostly about whether the students had answered correctly. The situation Practicing exercise tasks mostly followed directly afterward, when the teachers had let students practice tasks that required using the content developed on the board. Students worked individually or in pairs, and the interactions were characterized by teachers providing feedback by correcting steps in a calculation, demonstrating a solution procedure, or telling students how to improve the format of the answer, such as whether it was neatly written or included the correct unit.

Substantive feedback was provided when Working on a cognitively demanding task and Remediating student mathematical issues. Mathematical issues refer to situations where students made errors, contradicted each other, or stated that they were confused or did not know how to solve a task. Cognitively demanding tasks are tasks that require problem solving or sense-making and where students do not have a readily available solution method (Stein et al., 1996). There was a difference in how the two situations appeared in lessons. Working on cognitively demanding tasks appeared as a planned activity, as the teachers had prepared slides or handouts. The situation Remediating student mathematical issues appeared seemingly spontaneously in the middle of instructional situations with procedural feedback when the teacher noticed that several students had a mathematical issue. When remediating the issues, the interactions in the classroom changed, thus marking a different type of instructional situation. The teacher and students temporarily left the preceding situation to discuss the issue at length, during which the teacher provided substantive feedback. Afterward, they returned to the preceding situation. The characteristics of the instructional situations in which substantive feedback was provided are presented in two examples below.

We observed all instructional situations in most of the teachers’ lessons (see Table 4 for an overview). The main pattern was that situations with procedural feedback occurred often, whereas situations with substantive feedback were observed only one to three times for each teacher. In two teachers’ classrooms, the situations with substantive feedback were not as clearly distinguished from those with procedural feedback. For example, the teacher–student interactions in the situation Working on a cognitively demanding task in teacher S01’s classroom shared some features of the situation Practicing exercise tasks, as she gave procedural feedback to some students.

Table 4 The instructional situations appearing in the different teachers’ classrooms
Full size table

In the following sections, we describe characteristics of the instructional situations and how teachers switched from procedural to substantive feedback.

3.1 Characteristics of the situations Remediating student mathematical issues

The most common trigger for substantive feedback was students’ mathematical issues. When individual students had an issue, they often received brief corrective feedback. But when it became evident that several students shared the same issue, the teachers often brought the issue up for discussion with the whole class, changing the instructional situation. The distinguishing characteristics of these situations are summarized in Table 5. The teacher elicited student thinking and used this as the basis for the discussions. The mathematical focus shifted from solution procedures to the meaning behind the procedures, and the feedback provided was mainly conceptual. These situations were often complex: The teachers stated they did not understand student responses, the students expressed resistance to the feedback, and the class was noisy and occasionally off-task. We interpret this noise and complexity as a sign of both deeper content engagement but also unfamiliarity with the situation. This was time-consuming and the situations ended up being long-lasting compared to when teachers provided procedural feedback.

Table 5 Characteristics of the instructional situations when Remediating student mathematical issues
Full size table

These characteristics were intertwined, with one characteristic leading to another. An example is necessary to show how the characteristics featured in a concrete situation. The example begins with an instructional situation with procedural feedback to show how the situation shifted when it became evident that several students had a mathematical issue.

Example 1

Teacher S07 presented a worksheet requiring students to compare various fractions by size, e.g.,

1/2 □ 2/3

The teacher showed the students how to solve the tasks, before they worked individually for 7 minutes. The teacher provided feedback to a few students by giving them a procedure to find the answer or by pointing out errors. Thereafter, the teacher instructed the class to provide a choir response shouting out “greater than,” “lesser than,” or “equal” to each task upon his cue. The students provided strong, confident, and correct answers on all tasks from a) to h). The teacher confirmed that the responses were correct.

Remediating students’ mathematical issue begins

 

For task i) \( \frac{2}{7}\square \frac{1}{3} \) only a few students mumbled answers, some of which were incorrect.

Mathematical issue evident in several students

1

Teacher: “Oh, we were less sure on this one. It is correct that 2/7 is less than 1/3, but this one is a little difficult. I am very interested in hearing how you did it, how you thought. I spoke to one student who said he did it on intuition, he just had the feeling, and while that is correct, in mathematics you have to explain why it is that way. … Magnus?”

Elicit student thinking

2

Magnus: “I found that the common denominator was 21. Then I multiplied the numerator and denominator by 3 and got six twenty-oneths. And seven twenty-oneths on the other.”

 

3

Teacher: “You did it the advanced way, you know a lot about fractions. You did it very professionally, in the way you will learn next lesson. [Teacher continued recounting what Magnus had said while pointing at the board.] Are there other ways? Mari?”

Elicit student thinking

4

Mari: “I see that two sevenths is not quite a third, since two, four, six, two sixths would be a third. So two sevenths is lesser.”

 

5

Teacher: “Erm.” [pauses] “Ah, I see what you mean! You mean that two sevenths is not quite a third of the whole, since to get a third it would be two sixths. Let me try to show the class.”

 

6

[The teacher draws a circle divided into three parts while explaining what represents one-third. The teacher attempts to draw another circle subdivided into seven, but fails to draw this.]

Highlight multiple representations

7

Teacher: “I am not certain how to draw this or to explain this. It’s sort of, if you divide 7 into 3, 2 is not enough to add up to 7. How can we explain this? Ole?”

Teacher states they do not understand

8

Ole: “I think it is easier if you draw rectangles and not circles. A rectangle in thirds, and another one in sevenths.”

 

9

Teacher: “Yes, that was clever. Wonderful! Let’s see if I manage to make them approximately equal.”

 
 

[The teacher draws two rectangles divided into thirds and sevenths while explaining what he does, occasionally asking the class how to proceed.]

 

10

Teacher: “This shows it quite clearly. This third only needs to be repeated three times to cover the whole. If we repeat the two sevenths, two four six, there is still one left. That’s how I understand it. Was this how you thought, Mari?”

 

11

Mari: “Yes.”

 

12

Teacher: “There are many ways of seeing this, and no method is better or worse, the important thing is to be able to explain it mathematically. Great!”

Highlight multiple representations

13

[The teacher continued with choir responses and prompt procedural feedback on the remaining tasks. The students responded confidently and correctly until task q) 3/7 4/9.]

Mathematical issue evident in several students

14

[The teacher again asked several students to explain how they thought.

One student had put the fractions on a common denominator. Another said he compared 28 with 27 “because of 7 · 4 and 3 · 9”.]

Elicit student thinking

15

Teacher: “Interesting. I’ve never seen that method before. I am not quite certain I understand. Could anyone explain it to me?”

Teacher states they do not understand

16

[The class argued loudly over each other (without the teacher intervening).]Teacher: [Repeatedly attempting to get the class’ attention] “OK, so we multiply this … OK, so the idea is ….”

Students are noisy or off-task

17

The students continued discussing before agreeing that it was the same method as with common denominators. The teacher praised the discussion, stated that he enjoyed exploring new methods, and summarized the main points to the class.

 
 

The entire example lasted 21.5 minutes.

Long-lasting

Most students answered confidently until they encountered one task that they were unsure about (line 1). We inferred that the teacher noticed that students had an issue and addressed it. This marked a shift between instructional situations because the interactions among the teacher, the students, and the content changed. The teacher responded to the situation by eliciting student thinking several times (lines 1, 3, and 12) and commenting on the answers. Two of the methods proposed by students were nonstandard (lines 4 and 14), leading to various complications and productive discussions. First, the teacher had difficulty drawing a graphical representation to explain the solution (lines 6–7) and needed help from a student (lines 8–9). Second, the students started arguing loudly, some students became confused, and the teacher’s interventions to calm the class were ineffective at first (lines 15–16). These complications lasted for 11 minutes. Throughout, the feedback was conceptual because it connected several solutions and linked them to a graphical representation (lines 6, 10, and 17).

In summary, instructional situations when remediating student mathematical issues were strikingly different from the more prevalent situations when teachers provided procedural feedback. In the procedural situations, the classroom was orderly, and the lesson proceeded with a consistent method. In contrast, when remediating student mathematical issues, the situations were messy. They involved back-and-forths between the teacher and the class that were confusing and to which students sometimes uttered their resistance.

3.2 Characteristics of the situation Working on a cognitively demanding task

The second instructional situation that demarcated when teachers provided substantive feedback was when they assigned a cognitively demanding task. Note that this differs from Example 1 in which the tasks were short practice tasks. All five teachers provided cognitively demanding tasks in at least one of their lessons, always shifting their feedback from procedural to substantive. Three teachers consistently provided substantive feedback during work on these tasks, whereas two teachers provided a mix of substantive and procedural feedback to different students, see Table 4.

The most salient characteristic of the situation Working on a cognitively demanding task was that when introducing the task, the teachers set expectations for how the students should work and the task’s purposes and success criteria. We called this the negotiation phase: The teachers negotiated the instructional situation by setting expectations for how students should work and the purpose of the task; see Table 6. All teachers told students to discuss with their peers while solving the task. Some teachers told their students to explore the problem and try different strategies, to devise a plan before executing it, to show their thought processes and not only final answers, and to investigate their errors and try to understand them. The teachers also emphasized that the purpose of the task was to be challenging and that the goal was not to complete the task quickly but to understand new mathematics or practice problem solving. During this phase, students asked clarifying questions (e.g., “Can there be more than one answer?” (S07), “Must we write our answers, or only our thoughts?” (S49)).

Table 6 Characteristics of the instructional situation Working on a cognitively demanding task
Full size table

While the students worked on the task, the teachers provided feedback focused on the aspects laid out in the negotiation phase: If the teacher had told the students to explore the problem and try different strategies, the feedback related to how the students could achieve this. Since the expectations concerned engagement in mathematical practices (e.g., problem solving and engaging in mathematical discussions), the feedback addressed mathematical practices. In the following example, we highlight the expectations and purposes set by the teacher in the negotiation phase and how the feedback related to these expectations.

Example 2

Teacher S49’s lessons mostly consisted of developing new content on the board and practicing on exercises in the textbook during seatwork. Her feedback was mostly procedural and consisted of demonstrating how to correctly solve the tasks, although she occasionally included substantive elements like justifications for why the methods were valid.

The task was provided at the beginning of the lesson. It concerned a seating arrangement around a long table made up of a line of small tables with chairs arranged as in Fig. 1. The task was to calculate the required number of chairs when there were a) 4 small tables, b) 25 small tables, and c) n small tables.

 

Negotiation phase

Expectations

1

While presenting the task, the teacher managed students’ expectations about how to work:

Teacher: Do not answer now, we are discussing in groups. And equally important as the answer is how you have thought to arrive at the answer.

[…]

Discuss with peers

Show thought process

2

Teacher: If you have the wrong answer, it will not suffice to only correct the answer, you have to try to find out what the error is, and if you find out, that’s good.

Investigate one’s errors

 

[…]

 

3

Teacher: This is a big challenge so you’ll get to think about how we can use algebra in practical tasks. Start working. Discuss. Work. Show clearly on paper how you have thought.

Discuss with peers

Show thought process

 

Work phase

Feedback

 

The teacher provided feedback to students in pairs. She provided the following feedback to one pair of students who had just completed task b):

 

4

Tim: I believe there are 150 chairs.

 

5

Teacher: You believe there are 150 chairs?

 

6

Tim: I think there are 4 around each table. I multiply by 25 tables, but I remove those [pointing to the chairs at the end of the table]. And I multiply 2 by 25.

 

7

Teacher: Okay, does Helen agree with that interpretation? Erm, have you done task a) first? When there were only four small tables?

 

8

Helen: That’s 18.

 

9

Tim: That’s one, two, three, [counting] eighteen.

 

10

Teacher: Do you see any pattern in this?

 

11

Tim: That you only add one such table with four. Because these on the side stay the same. You only take a new table with four chairs, therefore it’s multiplication.

 

12

Teacher: Is that what you have shown with your calculation in b)? What you said now?

Investigate thought process

13

Tim: No, I haven’t shown it with algebra.

 

14

Teacher: I’m not so concerned with algebra now, but I wonder if the calculation you explained agrees with the calculations you’ve written. Go over it once more. See if you both agree. Count, think, and draw!

Investigate one’s errors

Discuss with Peers

Fig. 1
figure 1

Seating arrangement of task in example 8. The middle tables have four chairs, and the end tables have five

Full size image

In this excerpt, the teacher set expectations for how the students should work on the task (lines 1–3). This revolved around discussing with peers, investigating one’s errors, and showing one’s thought processes. She also made it clear that the purpose of the task was to be challenging, so students had a chance to think carefully about using algebra (line 3). The teacher’s feedback focused on these points. She prompted the students to explain more of their thinking (line 5) but did not correct them or show them how to do the task correctly as she did when solving textbook tasks. Instead, she asked if the other student agreed with the interpretation (line 7) and encouraged the students to identify patterns in their answers to the tasks (line 10). Last, she gave pointers for how the students could identify whether their work was correct and what to discuss (lines 12 and 14). This feedback provided clear suggestions to the students about how to work as set out by the expectations for the task: investigating one’s errors, discussing with peers, and showing one’s thought processes. This is not procedural feedback, but feedback on mathematical practices as it included suggestions for how to engage in the mathematical practices of problem solving and constructing viable arguments.

The other teachers also provided feedback that fit the expectations set in the negotiation phase. Teacher S07’s expectations were that students would explore many ways of solving a challenging problem. He said he did not know how to solve the cognitively demanding task he had just assigned and gave feedback by exploring the task with students. He suggested ways to move forward, the students critiqued his suggestions if they were not feasible, and he, in turn, critiqued the students’ suggestions. When teacher S01 assigned a cognitively demanding task, she mostly provided conceptual feedback, but more procedural feedback to students who had not progressed as far with the task. Teacher S40 launched a group project asking students to devise a plan for estimating the number of spectators in rock concerts based on aerial photos of the event and then execute it. She provided substantive feedback on the groups’ plans by suggesting how to evaluate and improve them. These examples show that the feedback provided during cognitively demanding tasks differed from that provided on routine problems, and that the common feature was that the feedback was substantive rather than procedural and related to the expectations set during the negotiation phase. Unlike the instructional situation when remediating student issues, the situation when working on cognitively demanding tasks appeared to run smoothly, although the students struggled to complete the tasks.

One anomalous example was found with teacher S40. In addition to the cognitively demanding task that she presented to the whole class, some of the textbook tasks were also cognitively demanding. As she helped students during individual work, some worked on procedural tasks and some on the cognitively demanding tasks. Irrespective of the type of task the students were working on, the teacher provided procedural feedback, showing them steps they could take to complete the task. Therefore, the pattern of providing substantive feedback on cognitively demanding tasks was only apparent with tasks that the teacher presented on the board and set expectations for how the students should work.

4 Discussion

To analyze how teachers provide substantive and procedural feedback during regular classroom teaching, we sampled lessons from a large-scale video study (172 lessons) of mathematics teaching in Norwegian lower secondary school. Only five of the 47 teachers showed evidence of consistently providing what we defined as substantive feedback, yielding a sample of 16 lessons for in-depth analysis. The design complements previous studies on how teachers provide feedback by adopting an in situ classroom perspective that details when teachers switch from providing procedural to substantive feedback and how the situations unfold.

4.1 Consistent patterns of procedural and substantive feedback in the instructional situations

We identified two instructional situations where teachers provided substantive feedback: when remediating students’ mathematical issues and when working on cognitively demanding tasks. Researchers have highlighted how students may benefit if teachers reply nonprocedurally in these situations (Borasi, 1994; Stein & Lane, 1996), but also that this is difficult for teachers (Son & Sinclair, 2010; Warshauer, 2015). Conceptual feedback was mainly provided on students’ mathematical issues, and feedback on mathematical practices was mainly provided during work on cognitively demanding tasks. Although we sampled teachers specifically to obtain lessons with substantive feedback, instructional situations with procedural feedback were most common. The teachers returned to procedural feedback as a staple in their teaching although they provided substantive feedback in other situations. This is interesting because the mathematics education community has paid little attention to procedural skills and regarded it as rote knowledge (Star, 2007), but the systematic way these teachers used procedural and substantive feedback suggests that they deliberately fit both types of feedback to the situation. Going forward, it may be fruitful to investigate accomplished teachers’ reasons for providing procedural and substantive feedback and their views on what part these play in helping students acquire mathematical competence.

4.2 Studying feedback as part of instructional situations gave new insights into the challenges of providing feedback in classrooms

The complexity of the instructional situations that arose when students had mathematical issues highlights the importance of studying feedback in classrooms. In laboratory studies, researchers have asked teachers how they would respond to video vignettes (Rougée, 2017) or student written work (Son & Sinclair, 2010), but these studies do not reflect the long chain of decisions teachers in this study had to make. Providing feedback on students’ mathematical issues required not only interpreting student work and creating a feedback message but also handling complex ensuing classroom events. Thus, this study points to at least two other competencies that are required when providing feedback—handling student resistance and not understanding a student’s contribution. Teachers tend to abandon the practices that students show resistance to (Gaspard & Gainsburg, 2019) and to respond emotionally with stress or anxiety to confusing student responses (Rougée, 2017). The situations when remediating students’ mathematical issues involved handling both factors, as evident from the students expressing resistance to the feedback, the students’ answers being occasionally confusing, and the teachers stating that they did not understand. Nevertheless, the teachers persisted and did not default to providing procedural feedback.

The students’ resistance to the feedback may have been caused by not having accepted the new instructional situation. When the student stated, “Why must you always make it so difficult? Can’t you just tell me what to do?” (Table 5), she expressed a wish that the teacher return to providing procedural feedback. When presenting cognitively demanding tasks, the teachers explicitly shared the purpose of the task and set expectations for the students in a negotiation phase beforehand, possibly preempting such questions. However, no negotiation took place before the instructional situations when remediating students’ mathematical issues, effectively requiring the students to understand, accept, and adapt to the new instructional situation without further notice. Future research may investigate whether negotiating the new instructional situation when remediating student mathematical issues may lead to less resistance from students.

4.3 The negotiation phase may serve as a catalyst to changing the instructional situations and providing substantive feedback

There were large differences in the instructional situations when working on cognitively demanding tasks and when practicing exercise tasks. Such differences in the instructional situation may need to be negotiated for students to accept them and understand what is going on. For instance, students worked on only one cognitively demanding task in the same timespan as they would have solved many exercise tasks. Moreover, when working on exercise tasks, students received procedural feedback that quickly gave them the correct answers, but on the cognitively demanding tasks, the feedback addressed concepts or mathematical practices that did not quickly help the students find the right answer. Research on cognitively demanding tasks has shown that students have problems adapting to task demands and instead press to proceduralize the tasks (Tekkumru-Kisa et al., 2020). Therefore, we hypothesize that the teachers’ explicit focus on what was expected of the students during the negotiation phase was crucial in making them understand and accept the new student and teacher roles, including that teachers provide substantive instead of procedural feedback.

In the instructional situations when remediating students’ mathematical issues, the teachers included no negotiation phase. Instead, they abruptly changed how they interacted with the students when it became clear that several students had a shared mathematical issue. The students showed confusion and resistance to the substantive feedback that was provided, the classroom became noisier, and some students were off-task. This contrasts with the situation when teachers provided cognitively demanding tasks in which the students accepted the work and the substantive feedback although they often struggled with the tasks. This suggests that to implement the change from procedural to substantive feedback, the new expectations for the instructional situations need to be made explicit to the students.

5 Concluding remarks

The analysis showed that providing substantive feedback entailed a complex interplay between the tasks, students, and teacher and occurred in two types of situations: when remediating students’ mathematical issues and when working on cognitively demanding tasks. The research from laboratory studies on how teachers provide feedback to students has focused on the utterances of the teacher in response to some aspect of student work (e.g., Sánchez-Matamoros et al., 2019; Son & Sinclair, 2010). Investigating instructional situations when teachers provided procedural and substantive feedback brought additional aspects into focus, namely how teachers negotiate new instructional situations beforehand and how they manage complications that arise. This is a step toward understanding the insights gained from controlled laboratory studies in a more ecologically valid classroom setting.

In this study, we used a small sample of teachers purposefully sampled to have high-rated feedback practices. The design could be expanded to larger video studies that rate the teachers’ feedback quality, such as the new TALIS video study (OECD, 2020). Such studies could determine whether the feedback patterns in the instructional situations described here are valid in larger samples and in other contexts. Future research can examine whether the identified differences in the instructional situations when teachers provided procedural and substantive feedback can be used to help other teachers provide substantive feedback. In time, this could pinpoint areas that can be addressed in teacher training to better train teachers to provide substantive feedback in the classroom.