Abstract
After being taught how to perform a new mathematical operation, students are often given several practice problems in a single set, such as a homework assignment or quiz (i.e., massed practice). An alternative approach is to distribute problems across multiple homeworks or quizzes, increasing the temporal interval between practice (i.e., spaced practice). Spaced practice has been shown to increase the long-term retention of various types of mathematics knowledge. Less clear is whether spacing decreases performance during practice, with some studies indicating that it does and others indicating it does not. To increase clarity, we tested whether spacing produces long-term retention gains, but short-term practice costs, in a calculus course. On practice quizzes, students worked problems on various learning objectives in either massed fashion (3 problems on a single quiz) or spaced fashion (3 problems across 3 quizzes). Spacing increased retention of learning objectives on an end-of-semester test but reduced performance on the practice quizzes. The reduction in practice performance was nuanced: Spacing reduced performance only on the first two quiz questions, leaving performance on the third question unaffected. We interpret these findings as evidence that spacing led to more protracted, but ultimately more robust, learning. We, therefore, conclude that spacing imposes a desirable form of difficulty in calculus learning.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Learning depends not only on what learners do but also on when they do it. Multiple episodes of study or practice are more beneficial for the long-term retention of knowledge when they are distributed over longer, versus shorter, periods of time (Carpenter, 2021). This is known as the distributed practice or spacing effect. Many reviews from different periods and with different emphases are available (e.g., Cepeda et al., 2006; Donovan & Radosevich, 1999; Janiszewski et al., 2003; Latimier et al., 2021; Maddox, 2016; Melton, 1970). The authors of one review call the spacing effect “one of the…most reliable findings in research on human learning” (Carpenter et al., 2012). Given such an endorsement, it is unsurprising that many researchers recommend spacing as a means to enhance knowledge retention in educational contexts (Carpenter et al., 2012; Dunlosky et al., 2013; Kang, 2016; Pashler et al., 2007; Roediger & Pyc, 2012). Taking this recommendation to heart, we have been studying whether spacing can help students retain complex bodies of mathematical knowledge (Hopkins et al., 2016; Lyle et al., 2020).
Existing Research on Spaced Mathematics Practice
The literature on spaced mathematics practice is nascent but promising. Emeny et al. (2021) provided a succinct review. Spaced mathematics practice has been tested in the lab and in the classroom with a variety of populations (from 3rd graders to college students) and with different types of mathematics knowledge (e.g., multiplication, geometry, algebra, and precalculus). Most studies have found superior mathematics performance following a practice that is more spaced versus less. Studies by one group are illustrative (Hopkins et al., 2016; Lyle et al., 2020). They manipulated the spacing of quiz questions in a precalculus course for engineering undergraduates. The manipulation was authentic to the classroom setting because quizzes are a common vehicle for practice in mathematics courses. After students were introduced to a given learning objective (e.g., solve polynomial inequalities), they answered multiple quiz questions about it. These questions were either all presented on the first quiz following the objective’s introduction, which is probably standard practice in many courses (Rohrer et al., 2020), or they were distributed across multiple quizzes over several weeks (i.e., massed and spaced conditions, respectively). In two separate cohorts of students, spaced quizzing led to superior retention of objective-specific knowledge as measured on the final exam in the course. Both studies also provided evidence, particularly clear in Lyle et al. (2020), that superior retention due to spacing persisted into the following semester. Additional research indicates that spacing not only increases the long-term retention of mathematics knowledge but also improves metacognition (Winne & Azevedo, 2014). Specifically, Emeny et al. (2021) found that massed practice led students to be overconfident about how well they would perform on a later mathematics test, whereas spaced practice resulted in realistic confidence levels.
The benefits of spacing for mathematics learning appear substantial, but they may come at a cost, at least in the short term. Some prior research suggests that spacing reduces performance in mathematics practice activities. In Lyle et al. (2020), average performance was worse on precalculus quiz questions that were spaced versus massed. In another study, performance on spaced permutations practice problems was worse than on massed problems (Rohrer & Taylor, 2006). This suggests that spacing imposes “desirable difficulty” during mathematics learning, increasing retention in the long run but impeding performance on practice activities in the short term (Bjork, 1994). Many readers will find this unsurprising since spacing has become almost synonymous with desirable difficulty (e.g., Bjork & Bjork, 2011; Bjork et al., 2013; Clark & Bjork, 2014), but, in fact, several studies have found no negative effect of spacing on practice math tasks (Barzagar Nazari & Ebersbach, 2019; Ebersbach & Barzagar Nazari, 2020a; Rohrer & Taylor, 2007). Clarifying whether or how spacing affects mathematics performance during practice is an important aim for future research.
The Effect of Spacing on Calculus Retention and Practice Performance
As mentioned, the effect of spacing has been investigated in a variety of mathematical domains, but one that has received little attention is calculus. Calculus is important in many fields, such as physics, economics, and meteorology, and, in engineering, it is nothing less than indispensable. Students rarely, if ever, obtain an undergraduate engineering degree without successfully completing at least three college calculus courses (Pearson & Miller, 2012). Unfortunately, mastery of calculus is elusive. Many students who take their first calculus course in college fail and even students who took calculus in high school often test into college precalculus or algebra, rather than calculus itself (Bressoud, 2021). Could the simple act of spacing out practice exercises help students retain calculus knowledge? It is tempting to assume so, given the positive effects of spacing in the closely aligned field of precalculus (Hopkins et al., 2016; Lyle et al., 2020) and given that the spacing effect has been characterized as broadly applicable (Dunlosky et al., 2013). However, the spacing effect does not invariably occur (e.g., Wiseheart et al., 2017), and one review has suggested that spacing might not be beneficial when to-be-learned tasks are of high complexity, have high mental and physical requirements, and when the interval between practice is greater than one day (Donovan & Radosevich, 1999). These conditions, aside from the physical requirement, could easily apply to spaced calculus practice.
An initial attempt to study the effect of spacing on retention of the calculus was made by Beagley and Capaldi (2020), who randomly assigned students in four sections of college calculus to work on homework problems that either exclusively covered recently learned material (massed practice) or covered a mixture of recent and more remote material (spaced practice). Students who engaged in spaced practice, versus massed, performed about 3% better on final exams in their sections. Disappointingly, this effect was not statistically significant, but it may be that the manipulation of spacing was not particularly strong or effective. The research report does not provide the number of homework problems for each topic or the length of the interval between initial and delayed retrieval attempts. Moreover, the authors combined data from first- and second-semester calculus courses, potentially adding noise to the analysis. Additional research is warranted, in our view.
Hand-in-hand with the question of whether spacing increases the retention of calculus knowledge is the question of whether spacing impairs performance in calculus practice activities. Beagley and Capaldi (2020) did not address the issue, and the larger literature on spacing and mathematics learning has often been silent about the effect of spacing on practice performance (Budé et al., 2011; Chen et al., 2018; Gay, 1973; Hopkins et al., 2016; Yazdani & Zebrowski, 2006). It may again be tempting to think that spacing will necessarily impair practice performance in mathematics, generally, and in calculus, specifically, since the spacing is often listed among the factors that induce difficulty during training (Bjork, 1994; Bjork & Bjork, 2011; Bjork et al., 2013; Clark & Bjork, 2014). But that characterization is based largely on studies with verbal materials. When practice performance has been examined in mathematical domains, only two studies have shown negative effects of spacing (Lyle et al., 2020; Rohrer & Taylor, 2006; cf. Barzagar Nazari & Ebersbach, 2019; Ebersbach & Barzagar Nazari, 2020a; Rohrer & Taylor, 2007). From a theoretical perspective, it would be quite remarkable if spacing proved desirable, by increasing calculus retention, but did not impose difficulty during practice. Alternatively, if spacing does harm practice performance, it would be of interest to students and instructors alike since practice activities such as homework and quizzes are often credit-bearing in educational settings.
Overview of Present Research
The present study was the first to examine the effect of spaced practice on calculus retention while simultaneously examining practice performance. We examined these dual effects in a calculus course for engineering undergraduates. As in the precalculus studies (Hopkins et al., 2016; Lyle et al., 2020), the spacing of practice was manipulated by varying the temporal distribution of quiz questions. There were three questions for each of the 24 learning objectives. Utilizing a within-participants research design, the three questions in a triplet were presented on a single quiz for some objectives and were distributed across three separate quizzes spaced weeks apart for other objectives. On the last day of class, we measured the retention of all learning objectives by administering a criterial test containing one question targeting each objective. If spacing produces desirable difficulty during calculus learning, we should see poorer performance on spaced quiz questions than on massed ones, but superior retention of learning objectives following spaced quizzing versus massed quizzing.
Method
The dataset on which analyses were conducted is available at https://osf.io/7u9pa/.
Participants
This study was conducted in a calculus course for engineering undergraduates during the Fall 2020 semester. Enrollment was 235, but analyses were restricted to students who completed all assignments that were part of the experimental procedure (N = 180). Students in our final sample predominantly identified as male (72.8%) and White (76.7%), as is typical at our institution and in many schools of engineering (Anderson et al., 2018).
Course Format and Materials
We first describe the format of the course in which the research study was embedded and then describe materials central to the research itself. The course was conducted in a hybrid fashion. Lectures were recorded and delivered via an online learning platform called MyMathLab®. To support and reinforce learning, the course instructors, one of whom was also part of the research team (BLIND), led in-person activities on Mondays, Wednesdays, and Fridays. Due to distancing constraints during the semester of implementation, students were invited to attend only one day of activities per week. For all students, there were weekly homework assignments and biweekly quizzes, which students completed using MyMathLab®. In addition, there were 13 unit exams, administered on Tuesdays and taken either in-person or online.
For the purposes of the research study, the critical course materials were 24 target learning objectives, five quizzes, and the criterial test. We describe each in turn. The target learning objectives were selected by the course instructor from a larger pool of 97 objectives that were taught in the first seven weeks of the 15-week course. We focused on objectives from the first half of the course so that we could distribute quiz questions covering the objectives across several weeks, including, when necessitated by the quizzing schedule (see below), weeks in the second half of the course. The 24 target learning objectives, shown in Table 1, comprised eight objectives from weeks 1–3, eight from weeks 4–5, and eight from weeks 6–7. All were deemed fundamental to a sound understanding of calculus.
The biweekly quizzes consisted of questions aimed at the target learning objectives. Quiz questions were drawn from the MyMathLab® question library, primarily from the Thomas’ Calculus textbook (Hass et al., 2018). We selected one question for each objective. Questions were almost entirely fill-in-the-blank, requiring students to use mathematical procedures to calculate an answer in numerical or variable form. If not fill-in-the-blank, questions were multiple choice. MyMathLab® generated three random algorithmic variants of the question for each student to produce a total of three quiz questions per objective. Variants differed only in their superficial features (e.g., coefficients, exponents, variable names) and correct answers.
To manipulate the massing or spacing of quiz questions, we varied whether three algorithmic variants of a question appeared on a single quiz or were distributed across three consecutive quizzes. Learning objectives were divided into two sets of 12 by numbering them sequentially and assigning even-numbered objectives to one set and odd-numbered objectives to the other set. Objectives in one set received massed quizzing, and objectives in the other set received spaced quizzing. Assignment of set to condition was counterbalanced across students. In the massed condition, all three versions of the question targeting a given objective appeared on the first quiz following the objective’s introduction in the course. In the spaced condition, one version of the question appeared on the first quiz and the other two versions appeared on the two subsequent quizzes (one question per quiz). The quizzing schedule is shown in Table 2.
The criterial test assessed understanding of all 24 target learning objectives. There was one question per objective, each question being an algorithmic variant of the same question that appeared during quizzing. Hence, the total number of test questions was 24.
Procedure
Prior to the start of the semester, all students enrolled in the course were randomly assigned to one of two groups for the purpose of counterbalancing the assignment of objectives to condition. Objectives that were massed for one group of students were spaced for the other and vice versa. Since initial enrollment was 235, 117 students were assigned to one group and 118 to the other. Among students who completed all assignments that were part of the experimental procedure (N = 180), 92 were assigned to one group and 88 to the other. Although perfect counterbalancing would have been optimal, the slight difference in attrition from the two groups was beyond the researcher’s control.
Students engaged with the course much as they would with any other, watching lectures, participating in course activities, and completing homework, quizzes, and exams at prespecified times. Only the quizzes and criterial test were part of the research study. These assessments contributed to the final letter grades in the course. At the end of the semester, scores on the five quizzes and the criterial test were averaged together and this average counted for 7% of students’ overall grade. To incentivize participation, the average was increased by 10% (up to 100%) if a student completed all five quizzes and the criterial test.
Quizzes were administered at the end of weeks 3, 5, 7, 9, and 11. The syllabus stated that quizzes were cumulative and that any content covered in the class before the quiz could be tested. Quizzes were accessible using MyMathLab® from 1 pm on Friday to 11:59 pm on Sunday. Students had a limited amount of time to complete the quizzes upon opening them. The amount of time was proportional to the number of questions per quiz (approximately 3 min per question). Students were required to complete the quizzes in one sitting without closing their browsers. For objectives in the massed condition, three algorithmic variants of the same question were presented in random serial positions throughout the quiz. Consequently, variants appeared consecutively only when dictated by the randomization process. For objectives in the spaced condition, a single question was presented in a random serial position. Question order was randomized anew for each student. Quizzes were not proctored, but we assumed that the time limit, randomization of question order, and use of algorithmic variants would deter students from working together and sharing answers.
After the submission deadline for each quiz had passed, students could review item-by-item feedback. During the review, students first saw whether each question had been answered correctly or incorrectly. They could then look at their given responses and the correct answers for specific questions. Students also had the option of viewing specific feedback on how to complete any problem they missed.
The criterial test was administered via MyMathLab® on the last day of class (Tuesday of week 15) during a single 75-min window. Question order was randomized for each student. Proctoring was accomplished using Pearson’s ProctorU© technology, which features student webcams and automatic identification of potential test-taking violations (i.e., use of additional resources during the test).
Results
Quiz Performance
To examine the effect of spacing on calculus practice activities, we submitted quiz scores to a 2 (question timing: massed vs. spaced) X 3 (question order: first, second, or third) completely within-participants ANOVA. There was a main effect of timing, F(1, 179) = 9.64, p = 0.002, ηp2 = 0.051, such that, as anticipated, performance was overall worse when questions were spaced (M = 0.78, SD = 0.13) versus massed (M = 0.81, SD = 0.13). There was also a main effect of order, F(2, 358) = 33.67, p < 0.001, ηp2 = 0.158, but this was superseded by a significant interaction between order and timing, F(2, 358) = 26.92, p < 0.001, ηp2 = 0.131. As shown in Fig. 1, performance in the massed condition clearly exceeded the spaced condition on the first question (Ms = 0.80 and 0.74, SDs = 0.14 and 0.16, respectively) and, to a lesser extent, on the second question (Ms = 0.82 and 0.78, SDs = 0.13 and 0.15, respectively). On the third question, however, performance in the spaced condition slightly outstripped the massed condition (Ms = 0.82 and 0.80, SDs = 0.14 and 0.13, respectively). It is apparent from the figure that performance was quite stable across the three questions in the massed condition whereas it steadily increased in the spaced condition. We conducted paired t tests, with Bonferroni correction, to assess the significance of the difference between conditions for each question. Massing was associated with significantly better performance on the first question, t(179) = 5.81, p < 0.001, Hedges’ gav = 0.42, and second question, t(179) = 3.04, p = 0.003, Hedges’ gav = 0.24. The conditions did not differ significantly on the third question, t(179) = 1.33, p = 0.185.
Criterial Test Performance
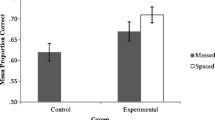
Figure 2 shows the proportion correct in the massed and spaced conditions for all participants. To assess the effect of spacing on long-term retention, we submitted criterial-test scores to a paired t test. Mean performance was higher on spaced objectives (M = 0.77, SD = 0.17) than massed objectives (M = 0.71, SD = 0.18). This difference was statistically significant, t(179) = 4.64, p < 0.001, Hedges’ gav = 0.32. The common-language effect size indicates that, after controlling for individual differences, the likelihood that a person scores higher on spaced objectives than on massed objectives is 63.5% (Lakens, 2013). Hence, distributing calculus practice appears to have helped students retain objective-specific knowledge.
Proportion correct on the criterial test for massed and spaced objectives. Lines connect scores across conditions for individual participants. For increased clarity in the online version of the figure, gray lines denote participants who scored higher in the spaced condition than the massed condition whereas blue lines denote all other participants
Discussion
Spaced retrieval practice increased retention of calculus knowledge. This is consistent with other recent studies showing spacing effects in various types of mathematics learning (e.g., Ebersbach & Barzagar Nazari, 2020a; Emeny et al., 2021; Yazdani & Zebrowski, 2006). Most notably, our finding resembles previous ones in precalculus. Spacing increased the average proportion correct on an end-of-semester test by 0.03 in Hopkins et al. (2016) and by 0.05 in Lyle et al. (2020).Footnote 1 In the present research, the increase was 0.06. Because the criterial test in all these studies was a genuine classroom assessment, with real consequences for students’ overall course grade, we can say that spacing increases actual math test scores by one-third to one-half of a letter grade. These spacing effects have been obtained even though precalculus and calculus are highly complex domains of knowledge, and the spacing interval in the relevant studies was more than one day—conditions previously identified as not necessarily conducive to the spacing effect (Donovan & Radosevich, 1999). This supports the conclusion that the spacing effect has wide-ranging applicability (Dunlosky et al., 2013) and, specifically in mathematics, is not bounded by the nature or complexity of the task (Emeny et al., 2021; cf. Ebersbach & Barzagar Nazari, 2020b). Given that spacing is a low- or no-cost intervention, gains of one-third to one-half of a letter grade are a not-insignificant return on investment. Instructors may be able to bolster students’ mastery of mathematics to a meaningful degree simply by altering the timing of when work is done, with no increase in the amount of work assigned.
Our finding of a significant spacing effect in a calculus course contrasts with Beagley and Capaldi’s (2020) finding of a nonsignificant effect. It is possible that Beagley and Capaldi’s manipulation was not sufficiently strong to fully realize the power of spacing. From their report, we do not know exactly how many delayed retrievals were involved in their procedure, but it seems possible that there was only one, as opposed to two in our procedure. Several other procedural differences existed between our study and the previous one, and any attempt to explain the divergent results must be proffered with caution.
Spacing increased retention of calculus knowledge in the present study, but it also reduced performance on practice questions. This is consistent with the idea that spacing induces desirable difficulty, as argued in a prior study of precalculus (Lyle et al., 2020; see also Rohrer & Taylor, 2006). However, our analysis of question-order effects provides novel insight into the exact nature of the difficulty. Spacing did not globally reduce performance across all practice questions. Rather, there was a large spacing-induced decrement on the first question, a smaller decrement on the second question, and no decrement on the third question. Performance was uniformly high in the massed condition, whereas it was low on the first question in the spaced condition and steadily increased thereafter. How can we explain this striking pattern?
It is important to recognize first that, in our procedure, the lag between classroom presentation of learning objectives and the first quiz question was the same in the massed and spaced condition. Consequently, poor performance on the first question in the spaced condition cannot be attributed to greater opportunity for forgetting, unlike in the verbal learning tradition where spacing-induced difficulty has been attributed to longer lags between study and initial test (Bjork, 1988). We also note that the performance increase across questions in the spaced condition needs not to be attributed to the provision of feedback following quiz submission. Although students had the opportunity to review feedback, they were not required to do so and we do not know to what extent they availed themselves of it. Moreover, although feedback can have powerful effects on learning, its effects are highly variable (Hattie & Gan, 2011) and there are known cases in which people learn more without feedback than with it (Fyfe & Rittle-Johnson, 2017). Finally, and perhaps most tellingly, students were able to perform at a high level on questions in the massed condition even though all those questions were submitted before feedback was made available. It, therefore, seems unnecessary to posit that feedback played a critical role in learning in the spaced condition.
Our preferred explanation for the pattern of practice performance we observed rests on the idea that answering multiple quiz questions gave students the opportunity to construct new knowledge and deepen their understanding of the learning objectives. Recent research indicates that simply working practice math problems, even without feedback, is sufficient to raise scores on a subsequent math test (Avvisati & Borgonovi, 2020; see also Fyfe & Rittle-Johnson, 2017). This suggests that people gain important insights while actively attempting to solve practice problems. In the massed condition of our procedure, students could accumulate insights from seeing three similar problems on the same assignment. Knowledge amassed later during the quiz, after seeing multiple similar questions, could be applied to earlier questions because, as in many real-world test settings, students could move back and forth between questions before submitting the entire quiz. Performance on any one question could, therefore, reflect knowledge gained from all three, explaining equivalent performance across question order in the massed condition. The situation is quite different in the spaced condition, where students had to submit earlier questions before working on later ones. Performance on each question, therefore, reflects only what was learned prior to and while working on that particular question. By our theorizing, this would produce the lowest level of performance on the first question, when students had not worked on any previous problems, intermediate performance on the second question, after working on exactly one previous problem, and highest performance on the third question, after working two problems. We note that performance in the spaced and massed conditions converged on the third question, when the amount of prior practice was equated and, theoretically, so too was new-knowledge construction.
Given our interpretation of the practice-phase data, we conclude that spacing imposed difficulty by protracting the knowledge acquisition process. Equivalent knowledge was ultimately acquired in the massed and spaced conditions, as revealed by performance on the third practice problem, but the process unfolded over several weeks in the spaced condition as opposed to mere minutes in the massed condition. This is distinct from the idea that spacing makes retrieval more effortful (Bjork, 1994; Maddox & Balota, 2015; Maddox et al., 2018; Pyc & Rawson, 2009). While it may well have that effect in some situations, we would argue that, in this particular context, no amount of effort would allow students to retrieve knowledge they have not yet acquired.
Utilizing the learning versus performance distinction (Soderstrom & Bjork, 2015), we can say that protracted knowledge acquisition in the spaced condition, versus the more rapid process in the massed condition, led to lower performance in the short run (on quizzes) but greater learning in the long run (as measured on the final criterial test). We suggest that spreading the acquisition of objective-specific knowledge over several weeks, during which time knowledge about subsequent learning objectives was also being acquired, provided opportunities to integrate knowledge about older and newer objectives, resulting in a more cohesive mental model of calculus and thereby fostering learning (Soderstrom & Bjork, 2015).
Conclusion
Massing is the typical approach to constructing quizzes and other practice activities in many math education settings (see Rohrer et al., 2020). Based on practice performance alone, this may seem like a smart move. Our findings from an undergraduate calculus course suggest that, on massed practice questions, performance will be consistently high, whereas it will take time to “ramp up” in the spaced condition. But our findings also suggest, as previously remarked, that “manipulations facilitating performance during training will often reduce the degree or quality of learning” (Rickard et al., 2008). Despite the promising start during practice, massing yielded poorer performance on the end-of-semester test. We, therefore, encourage instructors and students alike to embrace the short-term pain of spacing in order to reap its long-term gain.
Notes
Hopkins et al. (2016) included both a within- and a between-participants test of the spacing effect. The value given here derives from the within-participants test.
References
Anderson, E. L., Williams, K. L., Ponjuan, L., & Frierson, H. (2018). The 2018 status report on engineering education: A snapshot of diversity in degrees conferred in engineering. Association of Public & Land-grant Universities, Washington, D.C.
Avvisati, F., & Borgonovi, F. (2020). Learning mathematics problem solving through test practice: A randomized field experiment on a global scale. Educational Psychology Review, 32, 791–814.
Barzagar Nazari, K., & Ebersbach, M. (2019). Distributing mathematical practice of third and seventh graders: Applicability of the spacing effect in the classroom. Applied Cognitive Psychology, 33, 288–298.
Beagley, J., & Capaldi, M. (2020). Using cumulative homework in calculus classes. Primus, 30, 335–348.
Bressoud, D. (2021). Decades later, problematic role of calculus as gatekeeper to opportunity persists. https://www.utdanacenter.org/blog/decades-later-problematic-role-calculus-gatekeeper-opportunity-persists.
Bjork, R. A. (1988). Retrieval practice and the maintenance of knowledge. In M. M. Grunberg, P. E. Morris, & R. N. Sykes (Eds.), Practical aspects of memory II (pp. 396–401). Wiley.
Bjork, R. A. (1994). Memory and metamemory considerations in the training of human beings. In J. Metcalfe & A. Shimamura (Eds.), Metacognition: Knowing about knowing (pp. 185–205). MIT Press.
Bjork, E. L., & Bjork, R. A. (2011). Making things hard on yourself, but in a good way: Creating desirable difficulties to enhance learning. In M. A. Gersbacher, R. W. Pew, L. M. Hough, & J. R. Pomerantz (Eds.), & FABBS Foundation, Psychology and the real world: Essays illustrating fundamental contributions to society (pp. 56–64). Worth Publishers.
Bjork, R. A., Dunlosky, J., & Kornell, N. (2013). Self-regulated learning: Beliefs, techniques, and illusions. Annual Review of Psychology, 64, 417–444.
Budé, L., Imbos, T., van de Wiel, M. W., & Berger, M. P. (2011). The effect of distributed practice on students’ conceptual understanding of statistics. Higher Education, 62, 69–79.
Carpenter, S. K., Cepeda, N. J., Rohrer, D., Kang, S. H. K., & Pashler, H. (2012). Using spacing to enhance diverse forms of learning: Review of recent research and implications for instruction. Educational Psychology Review, 24, 369–378
Carpenter, S. K. (2021). Distributed practice or spacing effect. In L.-F. Zhang (Ed.), Oxford research encyclopedia of education. Oxford University Press.
Cepeda, N. J., Pashler, H., Vul, E., Wixted, J. T., & Rohrer, D. (2006). Distributed practice in verbal recall tasks: A review and quantitative synthesis. Psychological Bulletin, 132, 354–380.
Chen, O., Castro-Alonso, J. C., Paas, F., & Sweller, J. (2018). Extending cognitive load theory to incorporate working memory resource depletion: Evidence from the spacing effect. Educational Psychology Review, 30, 483–501.
Clark, C. M., & Bjork, R. A. (2014). When and why introducing difficulties and errors can enhance instruction. In V. A. Benassi, C. E. Overson, & C. M. Hakala (Eds.), Applying science of learning in education: Infusing psychological science into the curriculum (pp. 20–30). Society for the Teaching of Psychology.
Donovan, J. J., & Radosevich, D. J. (1999). A meta-analytic review of the distribution of practice effect: Now you see it, now you don’t. Journal of Applied Psychology, 84, 795–805.
Dunlosky, J., Rawson, K. A., Marsh, E. J., Nathan, M. J., & Willingham, D. T. (2013). Improving students’ learning with effective learning techniques: Promising directions from cognitive and educational psychology. Psychological Science in the Public Interest, 14, 4–58.
Ebersbach, M., & Barzagar Nazari, K. (2020a). Implementing distributed practice in statistics courses: Benefits for retention and transfer. Journal of Applied Research in Memory and Cognition, 9, 532–541.
Ebersbach, M., & Barzagar Nazari, K. (2020b). No robust effect of distributed practice on the short- and long-term retention of mathematical procedures. Frontiers in Psychology, 11, 811.
Emeny, W. G., Hartwig, M. K., & Rohrer, D. (2021). Spaced mathematics practice improves test scores and reduces overconfidence. Applied Cognitive Psychology, 35, 1082–1089.
Fyfe, E. R., & Rittle-Johnson, B. (2017). Mathematics practice without feedback: A desirable difficulty in a classroom setting. Instructional Science, 45, 177–194.
Gay, L. R. (1973). Temporal position of reviews and its effects on retention of mathematical rules. Journal of Educational Psychology, 64, 171–182.
Hass, J. R., Heil, C. E., & Weir, M. D. (2018). Thomas’ calculus (14th ed.). Pearson Education Canada.
Hattie, J., & Gan, M. (2011). Instruction based on feedback. In R. Mayer & P. Alexander (Eds.), Handbook of research on learning and instruction (pp. 249–271). Routledge.
Hopkins, R. F., Lyle, K. B., Hieb, J. L., & Ralston, P. A. S. (2016). Spaced retrieval practice increases college students’ short- and long-term retention of mathematics knowledge. Educational Psychology Review, 28, 853–873.
Janiszewski, C., Noel, H., & Sawyer, A. G. (2003). A meta-analysis of the spacing effect in verbal learning: Implications for research on advertising repetition and consumer memory. Journal of Consumer Research, 30, 138–149.
Kang, S. H. K. (2016). Spaced repetition promotes efficient and effective learning: Policy implications for instruction. Policy Insights from the Behavioral and Brain Sciences, 3, 12–19.
Lakens, D. (2013). Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t-tests and ANOVAs. Frontiers in Psychology, 4, 863.
Latimier, A., Peyre, H., & Ramus, F. (2021). A meta-analytic review of the benefit of spacing out retrieval practice episodes on retention. Educational Psychology Review, 33, 959–987.
Lyle, K. B., Bego, C. R., Hopkins, R. F., Hieb, J. L., & Ralston, P. A. S. (2020). How the amount and spacing of retrieval practice affect the short- and long-term retention of mathematics knowledge. Educational Psychology Review, 32, 277–295.
Maddox, G. B. (2016). Understanding the underlying mechanism of the spacing effect in verbal learning: A case for encoding variability and study-phase retrieval. Journal of Cognitive Psychology, 28, 684–706.
Maddox, G. B., & Balota, D. A. (2015). Retrieval practice and spacing effects in young and older adults: An examination of the benefits of desirable difficulty. Memory & Cognition, 43, 760–774.
Maddox, G. B., Pyc, M. A., Kauffman, Z. S., Gatewood, J. D., & Schonhoff, A. M. (2018). Examining the contributions of desirable difficulty and reminding to the spacing effect. Memory & Cognition, 46, 1376–1388.
Melton, A. W. (1970). The situation with respect to the spacing of repetitions and memory. Journal of Verbal Learning and Verbal Behavior, 9, 596–606.
Pashler, H., Bain, P., Bottge, B., Graesser, A., Koedinger, K., McDaniel, M., & Metcalfe, J. (2007). Organizing instruction and study to improve student learning (NCER 2007–2004). Washington, DC: National Center for Education Research, Institute of Education Sciences, U.S. Department of Education. Retrieved from http://ncer.ed.gov.
Pearson, W., & Miller, J. D. (2012). Pathways to an engineering career. Peabody Journal of Education: Issues of Leadership, Policy, and Organizations, 87, 46–61.
Pyc, M. A., & Rawson, K. A. (2009). Testing the retrieval effort hypothesis: Does greater difficulty correctly recalling information lead to higher levels of memory? Journal of Memory and Language, 60, 437–447.
Rickard, T. C., Lau, J.S.-H., & Pashler, H. (2008). Spacing and the transition from calculation to retrieval. Psychonomic Bulletin & Review, 15, 656–661.
Roediger, H. L., III., & Pyc, M. A. (2012). Inexpensive techniques to improve education: Applying cognitive psychology to enhance educational practice. Journal of Applied Research in Memory and Cognition, 1, 242–248.
Rohrer, D., & Taylor, K. (2006). The effects of overlearning and distributed practice on the retention of mathematics knowledge. Applied Cognitive Psychology, 20, 1209–1224.
Rohrer, D., & Taylor, K. (2007). The shuffling of mathematics problems improves learning. Instructional Science, 35, 481–498.
Rohrer, D., Dedrick, R. F., & Hartwig, M. K. (2020). The scarcity of interleaved practice in mathematics textbooks. Educational Psychology Review, 32, 873–883.
Soderstrom, N. C., & Bjork, R. A. (2015). Learning versus performance: An integrative review. Perspectives on Psychological Science, 10, 176–199.
Winne, P. H., & Azevedo, R. (2014). Metacognition. In R. K. Sawyer (Ed.), The Cambridge handbook of the learning sciences (pp. 63–87). Cambridge University Press.
Wiseheart, M., D’Souza, A. A., & Chae, J. (2017). Lack of spacing effect during piano learning. PLoS One, 12.
Yazdani, M. A., & Zebrowski, E. (2006). Spaced reinforcement: An effective approach to enhance the achievement in plane geometry. Journal of Mathematical Sciences and Mathematics Education, 1, 37–43.
Acknowledgements
Keith B. Lyle is now an independent researcher in Louisville, Kentucky. Results of this study were presented in part at the Frontiers in Engineering Education Conferences (Virtual, October 2020; Lincoln, NE, October 2021) and the annual meetings of the American Society for Engineering Education (Virtual, July 2021) and the Psychonomic Society (November 2021). This research was supported by a National Science Foundation Improving Undergraduate STEM Education Award.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visithttp://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lyle, K.B., Bego, C.R., Ralston, P.A.S. et al. Spaced Retrieval Practice Imposes Desirable Difficulty in Calculus Learning. Educ Psychol Rev 34, 1799–1812 (2022). https://doi.org/10.1007/s10648-022-09677-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10648-022-09677-2