[T]he hand’s essence can never be determined, or explained, by its being an organ which can grasp . . . . Every motion of the hand in every one of its works carries itself through the element of thinking, every bearing of the hand bears itself in that element.

(Heidegger, 1977, p. 357, cf. Pallasmaa, 2017)

An educational researcher and a movement scientist walk into a bar.

Dor: Hi, I’m Dor.

Franz: I’m Franz. I heard you do research on mathematics education?

Dor: Yes, Franz, I run a lab that studies the teaching and learning of math concepts. Wait, you investigate human movements, right? Didn’t you publish in Nature?

Franz: Yes, Dor, in fact we did. I mainly study bimanual coordination. Psychological factors like perception seem to be much more important in this than traditionally thought, even fundamental. So, well, nice to meet you, but seems that our activities don’t have much in common.

Dor: Oh, on the contrary! We should talk! Barman, two scotches, make mine neat. You know, Franz, that’s curious. My lab’s experimental paradigms, just like yours, involve kids moving both hands. We think they learn new concepts that way.

Franz: One ice cube for me. …Uhm… What? Really? Children develop their mathematical understanding by moving their hands? Sounds strange but fascinating. If this is true, you are my man, Dor!

Dor: Honored, Franz! And, you know, a fine single malt is really better neat, perhaps with a few drops of water to loosen the flavor molecules. So, yeah, my lab’s been impressed with the embodiment paradigm in the cognitive sciences. We say, “Learning is moving in new ways.”

Franz: Ha! We say “Moving is learning in new ways”!

Dor: What? Really? You’re kidding.

Franz: L’chayim!

Dor: Prost!

Well, here we are in the bar, more and more astonished yet inspired by an amazing parallelism of our separate ventures. From across our respective disciplines—math-education research and human-movement science—we stumbled independently on rather similar, and even identical fundamental guiding ideas and conclusions. We both understand moving primarily as a psychological (= mental) activity, and we both view thinking as movement-grounded and learning as moving in new ways, where the cognitive work is figuring out new perceptual orientations to situations at hand. Would it, perhaps, be worthwhile to explore for greater synergy and collaboration? Upon reading each other’s work, the answer, to us, is a clear “yes.” To begin with, there are significant commonalities in our basic ideas and research approaches, in spirit and agenda, overall and in detail, even in conclusions from experiments. With this, we well might contribute to an ongoing interdisciplinary discussion regarding the role of movement in human cognition, development, and learning. The aim of this paper is to hopefully make fruitful our personal encounter to narrate the conceptual convergence of two research programs as charting a theoretical foundation for future interdisciplinary efforts.

Educational research constructs draw on fundamental psychology constructs, such as perception, cognition, emotion, and memory. The reputation of movement, in this regard, has been ambivalent and controversial. While the topic has largely been off the agenda in psychology and education, some psychologists and educators have considered movement an important or even fundamental issue to consider. The following quotation from Maria Montessori (1949) well characterizes the spirit of our endeavors:

If mental development is spoken of, people say, “Movement? There is no need for movement; we are talking about mental growth!” When they think of mental improvement, they imagine all are sitting down, moving nothing. But mental development must be connected with movement and is dependent on it. This is the new idea that must enter educational theory and practice. (p. 203)

Stepping back, we affiliate with contemporary attempts to develop a unified embodied-mind approach. The “4E cognition” program suggests that the mind is embodied, embedded, extended, and enactive (Newen et al., 2018). Embodied: The body is vital for cognition. Embedded: The “thinking body” is inextricably situated in an environment. Extended: Processes and tool-enabled manipulations outside the body (such as writing or knitting) are part of cognition. Enactive: The living and thinking person produces itself (i.e., its biological and psychological identity) in an adaptive way, of which cognition is an aspect. Our general aim and hope are to demonstrate how the 4E conceptualization of cognitive activity could potentially serve as a unifying approach across scientific disciplines as well as their applications.

The paper is built as a back-and-forth dialogue between the two research programs that each draws on its respective discipline. It discusses four hypotheses, which we presume to be fundamental for a basic understanding of human movement as mentally organized events, while, in turn, a basic understanding of mental events as movements. The hypotheses are the following:

  • Hypothesis 1: Movements are directly mentally organized and executed, with the underlying neuro-muscular patterns spontaneously and flexibly tuned in.

  • Hypothesis 2: Very difficult movements may become easy as part of a well-perceptible whole.

  • Hypothesis 3: Mental movement structure (= strategy) integrates body and environment in a unified processual “Gestalt.”

  • Hypothesis 4: Physical tasks in movement execution are mentally mastered.

A remark regarding our use of the term “mental”: We use the word for any phenomena and processes in the psychological domain, such as perception, cognition, emotion, or memory. Our guiding idea is that human movements, too, are organized in this domain and are thus psychological, or mental, in nature.

To set the stage, we shall start with an experiment on bimanual coordination by Mechsner that illustrates the connection and unity of mind and movement in a particularly simple way, and illustrates Hypothesis 1. We will then describe in some detail Abrahamson’s work on the Mathematics Imagery Trainer, a learning environment that guides students first to enact a challenging bimanual movement and then analyze their strategy to ground a new mathematical concept. Hypotheses 2, 3, and 4 will then be discussed along further experiments on human movement by Mechsner, while pointing out commonalities with Abrahamson’s work. The final section further brings together the two research programs under a common call for collaborative work that would clarify concepts and terms as well as develop novel approaches and programs. The dialogue will be broadened to include more general perspectives on sciences, applications, and fields of practice, particularly on educational research, teaching, and learning.

Setting the Stage: a Finger-Wiggling Approach to Investigating Mind and Movement

Mechsner’s research program is dedicated to the question: What is the role of perception (including perceptual imagery) and other mental factors in human movement performance? In traditional understanding, the act of moving is primarily the act of switching on and off the correct efferent neuronal pathways and muscles in the correct sequence at the correct times. Richard Schmidt’s theory of “Generalized Motor Programs” (Schmidt, 1975, 1985) offers the most elaborated version of this conjecture. Perceptual or, more generally, psychological factors play a role in initiating the movements, controlling their results, and supporting the formation of suitable spatio-temporal neuro-muscular patterns. However, during the very act of moving, psychological aspects are insignificant, per Schmidt, i.e., physiology reigns here via execution of the learned or to-be-learned neuro-muscular programs.

In contrast to the above common notions, Mechsner adheres to the guiding hypothesis that human movements are basically and intrinsically psychological (= mental) events and can be investigated and understood as such. An illustrative experiment by Mechsner et al. (2001) builds on a now-classical series of studies by Scott Kelso and collaborators (Haken et al., 1985; Kelso, 1984), who investigated spontaneous movement slips in bimanual finger coordination as a possible window into the basic organization of human motor behavior. You can easily observe the crucial phenomenon of a “symmetry tendency” yourself without any equipment:

Place both fists on the table in a palm-down position and stretch out both index fingers away from you in a parasagittal direction. Then move the fingers slowly and periodically at the root (= metacarpophalangeal) joint to the left and to the right, perhaps sliding your finger tips on the table for support. First do so in symmetry with the fingers converging and diverging rhythmically (see Fig. 1A). Like most persons, you will probably be able to maintain the symmetric pattern up to the highest possible oscillation frequencies of the individual fingers.

Fig. 1
figure 1

A Symmetrical finger oscillation; B parallel finger oscillation; C incongruous hand positions

Full size image

Now we come to the crucial effect: Start, again, by moving the fingers slowly, but this time in parallel, i.e., with both fingers synchronously going to the right and to the left (see Fig. 1B). Once again, gradually speed up. Most probably, you will not be able to maintain the parallel pattern with increasing speed. Instead, above a certain speed, your fingers will surprisingly and involuntarily switch into a symmetrical oscillation pattern! With speeding up further, only the symmetrical pattern can be maintained.

Kelso and co-workers investigated the described finger oscillation paradigm systematically. They interpreted the observed symmetry tendency as a physiological tendency toward synchronous activation of homologous muscles. This interpretation was widely adopted by scientists who referred to Kelso’s work and explored the effects further.

But is that physiological interpretation correct as the highest level of explanation? After all, it might also well be that the symmetry tendency of movement is a tendency toward perceptual symmetry, which would imply a psychological interpretation as the highest level of explanation (which, albeit, does not deny underlying physiological processes). To dissociate the alternatives, Mechsner et al. (2001) repeated Kelso’s experiment, in a variation not only with the hands palm-down, but rather in all four combinations of palm-down and palm-up positions (Fig. 1C). Crucial are the two “incongruous” positions with one hand palm-down and the other palm-up. Here, symmetric finger oscillation is not brought about by synchronous activation of homologous muscles. Thus, if a neuro-muscular mechanism is at work, symmetry should not be stable any more with increasing oscillation frequencies.

But this is not what Mechsner et al. (2001) found. Instead, completely independent of congruous or incongruous hand positions, the symmetrical oscillation pattern was always stable up to the highest oscillation frequencies, while the parallel pattern disintegrated with increasing metronome speed and switched into a symmetrical pattern.

Mechsner et al.’s (2001) conclusion:

  • The symmetry tendency in bimanual finger oscillation (adduction–abduction) is not a neurophysiological tendency toward co-activation of homologous muscles (“physiological” interpretation).

  • The symmetry tendency seems to originate on a higher systemic level involving mental (perceptual) planning and control processes (“psychological” interpretation).

To emphasize: By using the term “mental,” we in no way intend to suggest a dualistic world view. Rather, we understand mental (= psychological) phenomena as system properties of the material–physiological brain–body–world system.

To note, the symmetrical finger oscillation pattern is certainly not learned: most persons perform it for the first time in their life, but nevertheless quickly and perfectly. This implies that the involved muscles are organized spontaneously in service of the perceptually defined movement pattern. If the system can work without the need for previously learned neuro-muscular patterns in this case, it seems likely that this result can be extended to the following, more general hypothesis:

  • Hypothesis 1: Movements are directly mentally organized and executed, with the underlying neuro-muscular patterns spontaneously and flexibly tuned in.

Mathematics Learning Is Moving in New Ways: an Embodiment View on Educational Design

If Mechsner’s foregoing hypothesis holds, there are ample possibilities for creatively and spontaneously performing perceptually guided novel movements. This is exactly what Abrahamson and his collaborators observed in an experiment on the role of physical movement and associated perceptual activity, including perceptual imagination and anticipation, in learning mathematical concepts (Duijzer et al., 2017). Again, you can observe the crucial phenomenon yourself without any equipment: The reader is invited to sit at a desk. Envision the origin of a rectangular Cartesian coordinate system ahead of you (or mark it, e.g., with a small object), slightly to the left, together with the positive extensions of the x- and y-axes (you may also draw them).

Now slide your left-hand (LH) index fingertip back and forth along the imaginary y-axis, and your right-hand (RH) index fingertip right and left along the imaginary x-axis (see Fig. 2). But there is more to the task: The distance of RH from the origin should always be double the distance of LH from the origin. So your hands should be moving simultaneously, orthogonally, and proportionately according to a 1:2 ratio. How is this working for you?

Fig. 2
figure 2

Moving the fingertips along the positive extensions of a Cartesian coordinate system

Full size image

Though the action assignments of each individual hand can easily be executed, most people find this motor-control problem difficult, if not overwhelming. However, performing this challenging bimanual task can be dramatically facilitated, if you now introduce an auxiliary imaginary construction into the activity space (see Fig. 3). Begin by placing LH and RH at any pair of 1:2 distances from the origin. Now, visualize an imaginary LH–RH diagonal connector, then move that diagonal line to the right, all the while keeping constant its angular orientation relative to the axes. In consequence, the legs of the right triangle between the Cartesian origin and the fingertips always maintain a 1:2 proportion in length, because all transitory triangles are similar, thus solving the task. How is this working for you now?

In numerous experiments, we found that the key to solving difficult movement problems is often to find a suitable imaginary construction that supports movement execution (for a review of a decade of work, see Alberto et al., 2021). We call this type of strategically useful imaginary Gestalt, such as the diagonal line, an attentional anchor, because it orients, focalizes, and shapes perception toward an environment to facilitate the situated enactment of some goal movement form (Abrahamson and Sánchez-García, 2016; Hutto and Sánchez-García, 2015). We suppose that the phenomenon is quite universal; thus, one could detect attentional anchors in human performance of any mundane practice, from knitting to juggling.

Fig. 3
figure 3

Solving the Orthogonal 1:2 Proportion movement task by moving an imaginary straight line cast diagonally between the fingertips, while keeping its angular orientation constant

Full size image

The hypothetical construct of attentional anchors draws most directly from enactivist theory of cognition, and in particular from the analysis that “cognitive structures emerge from the recurrent sensorimotor patterns that enable action to be perceptually guided” (Varela et al., 1991, p. 173). The construct can also be related to theories in the research field of mathematics education pertaining to images, including imaginary percepts, that ground and mobilize conceptual reasoning, particularly Pirie and Kieren (1994) on dynamical images or Steffe and Kieren (1994) on schemes, but also Tall and Vinner (1981) on concept images and Radford (2008) on iconicity and contraction. Close analyses of shifts in perceptual attention toward mathematical representations and their relation to conceptual insight are found in Mason (1989).

Abrahamson’s empirical work has been centered on evaluating a new type of technologically enabled activity architecture for mathematics education, the aforementioned Mathematics Imagery Trainer (hence, “Trainer”). We now explain the rationale underlying our design-based research program to implement and theorize learning environments in which students learn to move in new ways before making mathematical sense of their movements. Central to our discussion will be the discovery of attentional anchors as a construct bearing on both the theory and practice of mathematics education. As we will explain, it is this new construct arising from our design-based research (i.e., an ontological innovation, diSessa & Cobb, 2004) that motivated us to seek alliance from the movement sciences in a quest for an evidence-based systematic account of perceptual solutions to movement problems.

Continuing with the Orthogonal Proportion task you have tried out, we will illustrate typical student experiences with Trainer activities intended to induce ideas of proportionality. Text and figures, below, will draw from the respective empirical work of Duijzer et al. (2017) and Bongers (2020; Bongers et al., 2018). The illustrative design-research cases discussed below are selected to exemplify findings from the broader research program, which has demonstrated deep learning in transfer tasks and conceptual coordination as well as unique affordances for in-person and remote learning of elementary-, secondary-, and tertiary-school content (for reviews, see Alberto et al., 2021; Abrahamson, 2019).

This section builds on substantive qualitative analyses to offer an account of the ontogenesis of an attentional anchor, here the diagonal line, and its conceptual reach through to normative mathematical practice. As such, we wish to detail the cascade of semiotic actions by which subjectively experienced perceptual structures that come forth to facilitate motor action are step-by-step endorsed into mathematical discourse. This discourse imbues and articulates the perceptual structures with conceptual meanings by implicating the structures’ quantitative invariance.

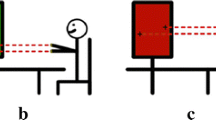
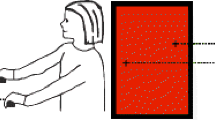
The activity begins by presenting the student with a bimanual motor-control problem. The student is tasked to manipulate the orthogonal dimensions of a rectangle, which initially is red (see Fig. 4a). LH index finger slides the rectangle’s top-left vertex up and down along the y-axis to change its height, and RH index finger slides the rectangle’s bottom-right vertex right and left along the x-axis to change its width. The student is tasked first to make the rectangle green and, once that is accomplished, to keep moving the two vertices while keeping the rectangle green. The rectangle is green when the quotient of its height:width measured values is some yet-unknown constant number, for example 0.5 (see Fig. 4b). As such, once a green rectangle is generated, moving forward its dimensions must be adjusted simultaneously so as to maintain the rectangle continuously in its preset green aspect ratio.

Fig. 4
figure 4

a A Mathematics Imagery Trainer tablet activity. Initially, the manipulated geometrical figure, a rectangle, is colored red, because its selected dimensions do not comply with the yet-unknown specifications. b Reconfigured at a 1:2 height-to-width ratio, the rectangle turns green. Next, both hands must move simultaneously so as to keep the rectangle green while changing its dimensions

Full size image

In the course of solving Orthogonal Proportion problems, study participants typically develop some new perceptual Gestalt to coordinate moving their LH–RH fingers simultaneously at different rates along orthogonal paths. For example, Lars (see Fig. 5a) worked on a variant problem, where he was tasked to move cursors along the orthogonal axes. This is the problem you yourself worked on earlier. When Lars achieved fluent movement in green, he was asked to explain his method. Lars said he was attending to an imaginary diagonal line connecting the cursors (cf. “property noticing,” Pirie & Kieren, 1994). The color blots in the images are post-production data-visualization overlays marking the location of Lars’s foveal eye gaze. Soon after (see Fig. 5b), Lars demonstrated how he moves the diagonal line to the right. The eye-gaze markers indicate that he is no longer foveating on his fingers but, rather, near the center of the diagonal lines. As you scan the sequence of five photographs in Fig. 5b, note the successive locations of the eye-gaze marker: Curiously, Lars’s gaze path, as he imagines the successive LH–RH diagonals, runs along a different diagonal line—a diagonal trajectory from the origin (on the bottom left) and up to the right that describes a y = 0.5 x function. Lars’s diagonal solution was quite typical. Yet, across participants, we found evidence for a variety of attentional anchors, such as gazing at the imaginary top-right corner closing a rectangle subtending between the fingertips and the origin (see Duijzer et al., 2017, for an array of attentional anchors recurring across participants).

Fig. 5
figure 5

a Sequence: Lars, a 14-year-old Dutch student, gestures an imaginary diagonal line that would connect his LH and RH points of contact on the axes. b Sequence: Lars uses his emergent attentional anchor to guide proportional bimanual coordination: He moves sideways the imaginary diagonal between his fingertips

Full size image

Once students have achieved a pre-specified criterion of minimal performance level, the activity proceeds with the teacher—who may be either a human (Abrahamson et al., 2012) or a virtual pedagogical avatar (Abdullah et al., 2017)—introducing supplementary resources designed to steer the students to develop quantitative re-articulations of their movement forms. For example, Fig. 6 shows the presentation of a grid (Fig. 6a) and then numbers (Fig. 6b) onto the tablet interface. Undirected, students count grid lines or units corresponding to their actions and, thus, are able to (1) describe their strategy quantitatively, (2) draw on their arithmetic skills, (3) confirm the veracity of their strategy, (4) determine with greater precision the location and trajectory of the attentional anchor, (5) enact the movement form correctly independent of the color feedback, and (6) predict properties of yet-unenacted geometrical shapes satisfying the interaction regimen (Abrahamson et al., 2011).

Fig. 6
figure 6

a A grid is overlaid onto the movement space. The continuous space thus becomes discrete, affording the enumerative quantification of uniform spatial intervals. b Numerals are supplemented onto the grid. Strategies of iterative manual incrementation are substituted by explicit arithmetic functions enabling multiplicative prediction of green rectangles

Full size image

Students are now equipped with quantitative rules derived from the tablet activity, so that, given a new “green” geometric shape, they are able to calculate a set of additional “green” shapes. The lesson activity now disengages from the tablet and turns to paper. Figure 7 demonstrates a paper-and-pen activity, where the geometrical form presented to the students “materializes” the imaginary diagonal attentional anchor, which they had previously generated on the tablet as their means of solving the interaction problem of expanding the rectangle in green. Students are asked to use the pen to show what would be other “green” triangles. As students engage with the paper-and-pen offline tasks, they no longer have recourse to immediate real-time interactive feedback on the quality of their performance. Nevertheless, the students now have a formalized rule (cf. Pirie & Kieren, 1994) for generating additional instances of the new equivalence class, which has yet to receive a mathematical name.

Fig. 7
figure 7

a Anna places a sheet of paper alongside the triangle’s hypotenuse. b Anna slowly slides the page away, keeping it parallel to the hypotenuse. c Using the sheet of paper as straightedge, Anna draws a parallel line

Full size image

In Fig. 8, Bongers et al. (2018) illustrate study participants’ typical quantitative strategies for drafting diagonals that would generate further “green” triangles. Both the hand-gauge and unit-counting techniques, here used on paper, draw directly on their earlier tablet work with the virtual grid. With that, the tablet-based perceptual strategy of handling an imaginary Gestalt has materialized as a paper-based geometrical strategy of generating a set of “green” triangles. The lines’ mutual affinity—what makes them a coherent set—draws on an assumed empiricism, namely that these lines would satisfy the tablet-based task. Yet the lines’ setness in turn draws also on new perceptual criteria associated with their geometrical construction process—the lines’ salient parallelism and the similitude of the triangles they configure. A set of triangles thus produced through rule-base iterated co-expansion of the legs (e.g., 3-per-2 in Fig. 8) is named as bearing the mathematical quality of “proportionality,” as negotiated with a teacher who revoices students’ multimodal utterance (Flood, 2018; Flood et al., 2016, 2020).

Fig. 8
figure 8

a A participant gauges a vertical span, transports it upwards to form an equivalent concatenated span, and marks the reach. b The participant next performs analogous actions along the horizontal span. c The participant draws units alongside the triangle legs, then extends 3 and 2 units, respectively, along the vertical and horizontal legs

Full size image

The spontaneous emergence of attentional anchors has been documented in a range of empirical studies that implemented the action-based genre of embodied design (Abrahamson, 2014). In each case, articulating the attentional anchor and then elaborating on it with the aid of available mathematical instruments shifted students into mathematical discourse (see Alberto et al., 2021). For example, Fig. 9, from Shvarts et al. (2021), shows a design for understanding the logic of trigonometry graphs by coordinating finger locations along the circumference of the unit circle (LH) and the x-axis (RH). Green feedback appears when the locations subtend equivalent distances from the origin.

Fig. 9
figure 9

a, b Coordinating the distances along the circumference of the unit circle (LH) and along the x-axis (RH). The frame turns green when these two distances from the origin are the same. Red notations of the points are added, here, for clarity and were not shown to the students

Full size image

For another example, Fig. 10, from Shvarts (2022), features a design for parabolas, where the curve emerges as the attentional anchor for moving “in green” along the screen surface, dynamically maintaining an isosceles triangle (see also Shvarts & Abrahamson 2019, for results from dual-eye-tracked tutorial sessions with this embodied design).

Fig. 10
figure 10

A parabola emerges as the attentional anchor for tracing the collection of screen locations where point C causes triangle ABC to be green. It is green when it is isosceles. Point A is fixed, and point B moves along the x-axis “shadowing” directly below point C. The parabola and letters were added here for clarity—the student never sees the graph or labels

Full size image

Embodied-design research employs mixed methods. Attentional anchors were discovered using qualitative micro-genetic analyses of multimodal action and utterance recorded in semi-structured clinical interviews, including data from screen manipulation, verbal–gestural conversation with a human or virtual tutor, and eye-tracking instruments (Abrahamson, 2019). We then employed Cross-Recurrent Quantitative Analysis (Marwan et al., 2007) and found that mathematical insight, transitioning through phases of exploration, discovery, and fluency, bears quantitative markers of complex dynamic systems in flux, both in bimanual coordination (Tancredi et al., 2021a) and between the manual actions and visual attentional anchors (Abdu et al., under review). These findings led to new conjectures about the intermodal grounding of mathematical concepts (Tancredi et al., 2022). Whereas previous work has demonstrated the self-organization of insight in logical problem-solving (Stephen & Dixon, 2009), to date, our work may be the first to demonstrate the self-organization of insight in mathematical problem-solving. For a related action-based approach to “abstract” reasoning and problem solving, see Ross and Vallée-Tourangeau (2021), and see Boncoddo et al. (2010) on the emergence of representations in problem-solving actions.

Whereas embodied designs are tackling increasingly complex concepts (Abrahamson, 2009, 2014; Alberto et al., 2021), these studies have been cross-sectional rather than longitudinal. It would be valuable to monitor the evolution of conceptual Gestalts. Already, though, we have witnessed the emergence of secondary attentional anchors from primary attentional anchors, as demonstrated, above, in the case study of Lars. Lars oriented on a “negative slope” diagonal to coordinate the bimanual “green” movement along the orthogonal axes. In so doing, though, a new “positive slope” diagonal trajectory emerged as a more-encompassing advanced attentional anchor. These clues from our qualitative analyses suggest new directions for design, teaching, and research methods. For example, the idea of a secondary attentional anchor is reminiscent of Peirce’s hypothetical construct of hypostatic abstraction (see Bakker, 2007).

Having presented the Trainer rationale, procedure, findings, and future speculations, we have demonstrated the evolution of mathematical concepts grounded in attentional anchors. The attentional anchor in our account was a Gestalt composed of actual and imaginary percepts behaving in particular invariant dynamics.

A Psychological Approach to Human Movement

To evaluate for connections and discussion themes between our research programs, we will now return to Mechsner’s research in the empirical study of perceptual phenomenology in human movement performance and align it with Abrahamson’s work. As reported above, Mechsner et al. (2001) conducted a variant replication of Kelso and collaborators’ (Haken et al., 1985; Kelso, 1984) bimanual index finger oscillation paradigm. Mechsner’s team found that the highest level of interpretation, and thus the primary locus of control, of the symmetry tendency seems to be found on a psychological (= mental) rather than on a physiological level. Recall that, in light of these results, a more general hypothesis seems worth considering:

  • Hypothesis 1: Movements are directly mentally organized and executed, with the underlying neuro-muscular patterns spontaneously and flexibly tuned in.

Hypothesis 1 resonates with Abrahamson’s empirical findings of study participants’ behaviors: Once the youth conjured an effigy, such as the diagonal line, as their (imaginary or factual) perceptual means of controlling a situation, their attention and discourse shifted away from their hands to that object. Moreover, the students did not appear to experience significant challenge in operating this conjured object, even as its properties changed along a span of variables, both inherent and relational: location within their peripersonal space (position on screen); spatial magnitude (constant increase or decrease); cardinal orientation (in the case of the Parallel task, see Abrahamson et al., 2011); and proportional deformation (e.g., from a 1:2 task to a 2:3 task). In connection with Hypothesis 1, note that effecting all these simultaneous changes piecemeal would likely overwhelm a cognitive system monitoring independent neuromuscular efferent impulses, and yet the students quite casually performed the movement pattern once they had generated a perceptual anchor. Therefore, Occam’s razor favors the perceptual over the neuromuscular explanation for the evident aptitude, fluency, and versatility of study participants’ performance in Abrahamson’s bimanual tasks. Slightly extending Hypothesis 1, we suggest that the patterns of neuromuscular impulses are not explicitly but implicitly organized. This means that neuromuscular patterns are never addressed and organized as such in the process. By way of analogy, when driving a car, we explicitly address and organize only its perceptible path, leaving the steering itself to the implicit control of the car’s machinery.

In another experiment, Mechsner et al. (2001) investigated bimanual circling. If a person circles both hands on a table, a symmetrical pattern, or 0° difference between the circling hands (Fig. 11a), is spontaneously preferred and can be maintained up to the highest possible circling frequencies. Several other patterns, such as antiphase, or 180° difference (Fig. 11b), can also be performed at a slow speed but disintegrate at increasing circling frequencies and finally switch into symmetry, which is the only stable pattern up to the highest possible speed.

Fig. 11
figure 11

a Symmetrical bimanual circling; and b antiphase bimanual circling. In both panels a and b, LH turns clockwise, RH turns anticlockwise

Full size image

Notably, there are bimanual circling patterns that are not only difficult but virtually impossible to perform even at slow circling frequencies. A striking example is bimanual circling in a 4:3 frequency relationship of the hands, (i.e., one hand performs four circles while the other performs three circles in the same amount of time). However, Mechsner et al.’s (2001) experiment showed that such an “impossible” bimanual circling pattern with a 4:3 frequency relationship between the hands can actually rather comfortably be performed in a suitable setting that allows the establishment of a well-perceptible visual movement Gestalt (see also Mechsner, 2003). Figure 12 shows the apparatus used.

Fig. 12
figure 12

a 1:1 circling apparatus; b 4:3 circling apparatus

Full size image

In Fig. 12a, the participant circles a pair of handles that they cannot see (the handles are under a tabletop). Connected to these handles are visible flags as proxies that move directly above the hands: What the invisible hands do is identical with what the visible flags do. Thus, if the hands circle, for instance, in symmetry, the proxies also circle in symmetry. In Fig. 12b, the setup is varied: There is a gear system between RH and the proxy which transforms the movement between hand and proxy to the effect that the right flag circles 4/3 times faster than the hand. In other words, 3 circling rounds of the RH bring about 4 circling rounds of the flag. This setup has the interesting consequence that symmetrical circling of the flags requires a 4:3 frequency relationship in the circling hands (i.e., LH per RH). To remind, such a movement is “impossible” to enact as such. However, if participants are instructed to circle the flags in symmetry (after a few minutes of unimanual training with the RH handle–flag gear system), they are well able to do so (after a further few minutes of bimanual training). The interesting point here is, while circling the flags in symmetry, they (implicitly and without knowing) circle the hands in an otherwise “impossible” 4:3 frequency relationship.

Mechsner et al.’s (2001) conclusion:

  • The hands may circle with ease in an “impossible” 4:3 frequency relation, in service of visual symmetry.

  • Very difficult movements can become easy as part of a well-perceptible whole.

  • This outcome points to a possible general principle: action control is basically psychological (= mental) in nature (rather than physiological).

  • General conjecture: the perceptual/mental structure of a task and action is of crucial importance for performance.

The result provides support for a more general hypothesis:

  • Hypothesis 2: Very difficult movements may become easy as part of a well-perceptible whole.

Human movements may well involve aspects (here: the 4:3 frequency relationship of the circling hands) that are difficult or even impossible to perform as such, but can easily be performed (in this case, implicitly) as part of the respective whole movement (here: circling the flags in symmetry).

Hypothesis 2 also resonates with Abrahamson’s empirical findings of study participants’ behaviors: Abrahamson found that students’ enactment of proto-mathematical movement forms improved dramatically once they perceived/imagined a global structure that encompassed, integrated, and thus facilitated the coordinated enactment of the required movements as functionally related sub-movements. While the tasked bimanual pattern was very difficult or even impossible to perform as such, discovery or construction of a suitable attentional anchor rendered the movement easy. These Gestalts that study participants generated oriented them toward a strategically supportive perceptual pattern or object they could operate as their means of acting on the environment according to the feedback regimen.

If, up until this point, we have mostly been discussing emergent subjective percepts of spatial intervals between two hands, such as the imaginary diagonal line, we now turn to the crucial role of the environment in human movement planning and performance. The paradigm is again bimanual circling, but on a table rather than using the apparatus described above. As said earlier, a symmetrical bimanual circling pattern (Fig. 12a) is stable up to the highest possible circling frequencies. If one presents, say, two well-visible drawn circles of 10-cm diameter on a table, with a 15-cm left-to-right distance between their center points, participants experience no problem in circling their index fingertips inwards symmetrically along these guiding circles, and they can speed up. You can try this yourself.

Then, why not try another pattern: circle the fingertips inwards in a way that the right fingertip is ahead of the left one by about a ¼ circle, i.e., a 90° difference. You may start with the left finger at the top of the left circle synchronously with the right finger at the left edge of the right circle, maintain the relationship while circling, and speed up (Fig. 13a). Anecdotal evidence and unpublished pilot observations by Mechsner suggest that most people are hardly able to maintain the relationship at all and, in any case, lose the pattern when speeding up. Even if one shows them the movement or guides them with a visual demonstration, still, they invariably lose the pattern upon removal of the guidance and finally fall into symmetry at increasing speed.

Fig. 13
figure 13

90° phase-shifted inward circling exercise: a without cues; and b with cues

Full size image

Proponents of the physiological view of motor-control problems might say that performing this bimanual pattern is difficult because doing so is not supported by co-activation of homologous muscles. However, most persons can perform the pattern rather easily with the following setting and instruction: one puts a mark (say, a coin) at “12 o’clock” of the left circle, and a mark at “9 o’clock” of the right circle (Fig. 13b). The instruction is “Circle both hands at the same velocity and pass the marks on the left and the right circle simultaneously. Start slowly and then gradually speed up.” Anecdotal evidence and unpublished pilot data suggest that people can perform the pattern even if they only imagine the marks. Try yourself!

Mechsner’s preliminary conclusions:

  • Difficulties with bimanual circling in a 1/4-circle phase difference are not due to neuro-muscular constraints.

  • Such difficulties reflect an unsuitable strategy (= perceptual/mental movement structure).

  • A more suitable strategy renders the task easy.

  • To note: In a good strategy, the experience of body and environment forms a unified holistic mental structure.

The result—though preliminary—provides support for a more general hypothesis:

  • Hypothesis 3: Mental movement structure (= strategy) integrates body and environment in a unified processual “Gestalt”.

Hypothesis 3 is again also supported by Abrahamson’s results. As reported above, placing horizontal grid lines along his participants’ vertical hand trajectories caused the participants to spontaneously select particular lines as destinations for their hands’ respective motion. For example, to move their two hands at a 1:2 ratio, students move their hands 1 and 2 lines up, respectively (Abrahamson et al., 2011). As such, the participants had to decide which gridlines make for effective targets, and this decision became a form of mathematical reasoning.

Abrahamson and Sánchez-García (2016) argue that students implicitly treat gridlines as interactive features of the environment—as things they can actually grasp (see also Abrahamson, 2021a). Abrahamson and Trninic (2015) describe a case of a student who, still before the grid was introduced, was attracted to an incidental environmental feature extraneous to the virtual working space (the “DELL” logo on the computer screen’s plastic encasement) as her perceptual means of marking a destination for her hand movement. As such, one might speak about the auxiliary inscriptions we place onto mathematical representations to promote our inquiry not just as “frames of reference” but as “frames of action” or as perceptuomotor aides affording interaction.

Hypothesis 4, which we herewith will elaborate, leads away from “simple” bimanual coordination to the overall complexity of skilled whole-body movements, be it in normal everyday undertakings, like flipping an omelet, or in specialized expert abilities in dancing, soccer playing, and the like. Is it even imaginable that such intricate movements are planned and performed completely on a psychological level, i.e., as mental events, as suggested in the forgoing sections? According to Schmidt’s (1975, 1985) abovementioned movement schema theory, humans rely on “generalized motor programs” in such complex activities. The crucial point here is that these motor programs are learned neuro-muscular coordination patterns that can be flexibly adapted to changing situational demands. In essence, the theory is conceived in physiological terms.

Could there be an alternative approach in psychological terms? Thomas Schack proposed an intriguing hypothesis regarding mental control of skilled movements (Schack & Mechsner, 2006). The basic idea: Any purposeful movement has to fulfill distinct functional demands that pose corresponding biomechanical problems to be solved by way of appropriate sub-movements. If movement control is essentially mental, then the mental system has to solve these problems. According to Schack, there are mental concepts stored in human long-term memory for the necessary partial movements, which he calls basic action concepts (BACs).

To give an example, the tennis serve has three distinct phases, namely pre-activation, strike, and final swing, which can be mentally planned, experienced, and perceived and, thus, at least in some aspects, take place in a psychological medium. Working with tennis experts, Schack identified sub-movements that solve the elemental problems of tennis-serve performance. Most interestingly, the identified set of inherent movement problems corresponds 1:1 to a set of basic action concepts (BACs), whose instigation can solve them. First, in the pre-activation phase, body and ball are brought into position, and tension energy is provided to prepare the strike. The following BACs—mental concepts that solve physical problems—were identified: (1) ball throw, (2) forward movement of the pelvis, (3) bending the knees, and (4) bending the elbow. Second, in the strike phase, energy is conveyed to the ball. The following BACs were identified: (5) frontal upper body rotation, (6) racket acceleration, (7) whole-body stretch motion, and (8) hitting point. Third, in the final swing phase, the body is prevented from falling, and the racket movement is decelerated after the strike, where the following BACs were identified: (9) wrist flap, (10) forward bending of the body, and (11) racket follow-through. As mentioned above, each individual BAC is characterized by a set of closely interconnected perceptual and functional features. For example, BAC 7 (whole-body stretch motion) is functionally related to providing energy to the ball, transforming tension into swing, stretching but remaining stable, and the like. Perceptual features of the corresponding sub-movement that allow monitoring of the initial conditions are bent knees, tilted shoulder axis, and body weight on the left foot (for right-handed players). Sensory feedback allows monitoring of whether the functional demands of the sub-movements have been addressed successfully. Using a sophisticated picture-sorting task, Schack was able to show that these BACs are actually present in the long-term memory of tennis players. In skilled players, these are integrated into a coherent memory network (Schack & Mechsner, 2006).

In conclusion, Schack and Mechsner (2006) suggest:

  • The physical sub-tasks of complex movements are solved by making use of mental BACs.

  • Complex movements of experts are flexibly controlled via strategically integrated mental networks of BACs (learned and stabilized by training in long-term memory).

One may generally hypothesize:

  • Hypothesis 4: Physical tasks in movement execution are mentally mastered.

As far as we can see, there is no immediately obvious parallelism and evidence in Abrahamson’s work that might support the hypothesis. This is not surprising, because the research program has so far primarily focused on extremity actions (e.g., the hands), without explicit regard to the rest of the body and supportive sub-movements (e.g., the core muscles). However, every movement is a whole-body movement after all. Thus, it may be worthwhile to not only focus on extremity actions enacting a movement but attempt a more fine-grained kinesiological decomposition of the movement. How might we determine what these sub-movements are? Students’ multimodal utterances, as they engage in mathematical discourse, reveal perceptual facets of their conceptual actions (Abrahamson, 2004; Alibali et al., 1999). Abrahamson can re-analyze earlier video data to implicate multimodal perceptions “under” what he has already found. Furthermore, Abrahamson is motivated to use the research instrument of micro-phenomenological interview (Petitmengin, 2017) to investigate with greater nuance the implicit multimodality of mathematical perception. These musings suggest directions of future research and theorization quite incongruous with prevalent models focusing on the cognitive function of hand movements only (cf. Sweller et al., 2021).

For a target article on Mechsner’s research with commentaries, see Mechsner (2004a, 2004b). See also Muraoka et al. (2016), for a thorough refutation of common criticisms of Mechsner’s ideas. See Abrahamson (2019) for an overview of his research.

The Bigger Picture: Speculating on Broader Implications of Our Theoretical Convergences

The foregoing review of our two research programs showed fundamental commonalities in our basic ideas as well as in our experimental insights. We found strong parallel results in support of our four guiding hypotheses. To repeat them here:

  • Hypothesis 1: Movements are directly mentally organized and executed, with the underlying neuro-muscular patterns spontaneously and flexibly tuned in.

  • Hypothesis 2: Very difficult movements may become easy as part of a well-perceptible whole.

  • Hypothesis 3: Mental movement structure (= strategy) integrates body and environment in a unified processual “Gestalt.”

  • Hypothesis 4: Physical tasks in movement execution are mentally mastered.

We suggest that the set of the foregoing four hypotheses forms a fundamental system for a basic understanding of human movements as mentally organized events.

We hold that not only genuine bodily movements but also mental movements are covered by these hypotheses. In this understanding, cognition is action and action is cognition. Within an embodied-mind framework, bodily movement in an environment has largely been understood as the basis and foundation of all human activity, including “higher” cognition. As such, to understand how people think, we need to understand how they move. However, the exact ontological status, pragmatic function, and processual dynamics of movement in human activity of different kinds are still far from clear. How are the mental and the bodily intertwined in actual physical movement? How does the social factor play into movement? How might physical movement be important also in so-called “abstract” thinking? Is physical movement present in “higher” cognition only via analogous processual schemes, or might every form of cognition without overt movement adequately be understood as a form of internalized, or simulated, physical movement?

Here is what we agree on, which, we believe, could serve as a valid foundation for understanding all human activities, be it solving a number theoretical problem or developing a novel strategy for high jumping. We both (1) appreciate the human capacity to enact perceptually guided movement as an overarching psychological model of thinking, problem-solving, and learning; (2) theorize the mental development of perceptual structures, including actual and imaginary percepts, as the key epistemic vehicle of solving motor-control problems; and (3) promote a view of would-be higher cognition about abstract ideas as grounded perceptuomotor dynamics.

So perception influences movement, or more generally, action, and movement influences perception. To note aside, there is a developmental component here. That is, as infants/toddlers mature, they develop more and more sorts of actions, e.g., from crawling to walking. Novel action possibilities stimulate new perceptual structures which in turn can be used to control action. A compelling example is the work by Campos et al., (1992; cf. Bertenthal et al., 1994; Corbetta, 2021). Without active movement, sensory development may even be basically disturbed as shown in classical experiments by Held and Hein (1963) for the visual sense of kittens. As Fiebelkorn and Kastner (2019) put it succinctly:

The brain’s sensory and motor systems have historically been studied in isolation. The sensory system is considered the point of input, processing environmental stimulation, while the motor system is considered the point of output, generating reactions to environmental stimulation. But this is clearly an oversimplification. The sensory and motor systems evolved together and are functionally integrated. (p. 88)

To this we add, yes, and perception reigns in enacting this functional integration.

A further step to bring the research programs even closer together is to unify the in-part still disparate theoretical insights and terms. A striking example is the concept of an attentional anchor, from Abrahamson and his collaborators, which has not been part of Mechsner’s theoretical notions but can well be integrated. Actually, the attentional anchor seems to be a most fruitful theoretical concept to generally understand essential mental processes in human movement performance involving bimanual coordination. To enrich the interpretation of Mechsner’s experiments with Abrahamson’s concept seems rather straightforward. For example, recall the difficult task of bimanual circling with the right hand leading by a ¼-circle difference. As described above, performance can be dramatically improved if the participant is requested to “synchronously pass NORTH in the left circle and WEST in the right circle,” placing marks at these positions, or even by imagining these marks. These imagined marks in bimanual circling with a ¼-circle difference between the hands can well be conceived as attentional anchors: To emphasize, there is no functional difference between imagined and real marks. Therefore, it seems adequate to conceptualize any guiding item, be it real or imagined, as an attentional anchor. Seen in this way, it seems plausible to suppose that not only well-performed and successful movements, but any purposeful movement, is tacitly guided by strategically chosen attentional anchors, i.e., imagined or real artifacts that are used in a way that is assumed to be supportive. As such, improving a movement may often involve finding and applying a novel, strategically helpful, attentional anchor. A classical hypothesis in this regard is the proposal by McBeath et al. (1995) that baseball outfielders catch flyballs by selecting a running path that maintains a simple linear optical trajectory for the ball (see also Gigerenzer, 2021; Wilson & Golonka, 2013).

Whereas the controlled experimental conditions of Abrahamson’s Mathematics Imagery Trainer lend themselves to observing the emergence of attentional anchors (Abdu et al., under review; Tancredi et al., 2021a), it could be that every single movement we learn to enact requires us to develop an attentional anchor. This embodied-design hypothesis may bear important implications for the most fundamental theoretical and practical considerations of mathematics education.

For further joint work, we see four interlinked perspectives, which we will explain in the following.

Perspective 1: Further Developing Our Respective Research Programs in Close Conversation

A primary task for the future is to further clarify, explore, and develop the concept of attentional anchor in movement tasks. Such theoretical progress could draw on continuous search for experimental empirical paradigms in the literature. By way of an example, object manipulations, such as lifting a mug, involve mental anticipation of the object’s desired end-state, here, pre-optimizing for mug–lip contact ergonomics (Comalli et al., 2016; Rosenbaum et al., 1990). Our reading of empirical research on end-state anticipation suggests that such tasks might well be mastered by relying on a pattern of several interconnected and nested attentional anchors during the process. In the context of a Mathematics Imagery Trainer, appropriately designed end-state motion planning could serve as a perceptual basis for mathematical conceptualization. Of potential relevance is the finding that children’s capacity to intercept a moving object predicts their mathematical attainment (Giles et al., 2018).

What else is “out there”? We plan a systematic survey of the cognitive-psychology and movement literature to identify other possible forms of spontaneous or guided perceptual/imaginary solutions to movement problems. Equipped with this knowledge, Abrahamson’s team could (1) improve the understanding of grounded learning processes; (2) expand and diversify instructional offerings through designing new technological activities that explicitly solicit those types of hitherto-unconsidered perceptual solutions; (3) potentially reach toward more complex mathematical concepts by way of soliciting more complex perceptual achievement; and (4) continue to develop inclusive design frameworks for differently abled students to access mathematical concepts (Abrahamson et al., 2019; Lambert et al., 2022; Tancredi et al., 2021b).

We wish to detect, characterize, label, and classify the various ways and forms that perception (including imagery) comes to organize motor action in the service of performing mundane physical tasks. We are particularly interested in imaginary and strategic percepts that mediate or enable more effective interactions. These attentional anchors may inspire technological innovation in educational design, even as they focalize explorative dialogues between researchers in the hitherto disparate fields of PAC (perception, action, and cognition) and mathematics education (Abrahamson & Abdu, 2020; Tancredi et al. 2021a).

Perspective 2: Toward a Psychological Approach to Movement and a Movement Approach to Psychology

As said, we adhere to the guiding idea that movement is cognition and cognition is movement, as a possible unifying theoretical basis for all human bodily and mental activities. However, it is far from clear whether it would actually be possible to theorize the concrete and would-be abstract via one unified framework. Regarding this question and problem, Abrahamson and Mechsner consider Piaget’s pioneering notion of the sensorimotor grounding of would-be abstract ideas, such as number (Piaget, 1952). We are less aligned with the cognitive semantics theory of conceptual metaphor (Lakoff & Núñez, 2000; see Abrahamson, 2020, 2021b) or with authors promoting “assembled” views of cognition, where mind and objects share in agential status (de Freitas & Sinclair, 2014). Instead, we take a strong stance by following the guiding idea that concrete and would-be abstract mental spaces and activities can be integrated in a unified framework, submitting that all human mental processes basically involve the same categories of spaces, objects, and actions (cf. Glenberg, 2010; Glenberg & Gallese, 2012). Such an approach would imply that human psychology is fundamentally movement-based.

So far, we see the following issues, among others, as important to consider in this context:

  • The basic unit for psychological science is the perceptual–phenomenal field of a human person in its situation, as an inextricably integrated processual gestalt.

  • In connection, a Gestalt-theoretical approach needs to be adopted and developed further to understand human activity in its environment (cf. Isaac & Ward, 2021).

  • This implies, as a hallmark of the Gestalt approach, that any perceptual or cognitive feature of a situation does not stand for itself but is always related to other aspects of the situation.

  • It seems central to understand any human activity in light of the involved strategies—how strategies are applied, changed, developed, discovered, and taught. In a corresponding to-be-developed consistent theoretical framework, the status and role of concepts such as “affordance” and “attentional anchor” need be clarified and perhaps refined and in part re-defined (cf. Abrahamson, 2020, 2021a; Mota, 2021).

  • Movement and movement learning should be understood as problem-solving activities. They should not be judged in terms of an ideal “expert” form, but in terms of the subjective phenomenology of their functional utility (cf. Chow et al, 2007).

  • An “action ontology” characterizes the perceptual–phenomenal field. Anticipatory and, more generally, functional and teleological aspects of perception are of crucial importance (Gallese & Metzinger, 2003). The insights in this regard are to be integrated and developed as important aspects of a movement-based psychology.

Utilizing embodied design as their empirical contexts, PAC researchers could refine their explanatory models for how perception organizes the enactment of movements. PAC researchers would examine how perception is selectively directed to features of the environment to construct dynamically invariant mental structures guiding effective motor action. In particular, polysemous concepts such as proportionality, which lend themselves to several complementary mathematical models, and are thus handled in different ways (Abrahamson & Shulman, 2019; Abrahamson et al., 2014), offer PAC researchers propitious opportunities to investigate how people generate, negotiate, and coordinate a set of operationally distinct yet functionally equivalent perceptual strategies for motor control. In this respect, the interview methodology of micro-phenomenology (Petitmengin, 2007) may offer an additional advantageous instrument of inquiry.

Perspective 3: Joining, Enriching, and Applying the 4E Discussion

Beyond its interdisciplinary mutual benefits, dialogue between educational researchers and movement scientists could illuminate some of the debates in the cognitive sciences over theories that account for human learning and performance of physical skills. An abundance of empirical research has evidenced people acting on the world through attending to imaginary structures or a mix of actual and imaginary percepts, where these perceptions may be bottom-up spontaneous (Duijzer et al., 2017; Kirsh, 2009) or top-down prompted (Abrahamson, 2020; Liao & Masters, 2001; Mechsner, 2004a, b). Yet, we argue, many of these theoretical concepts need clarification and, in case, amendment for the sake of precision, coherence, and integration in a 4E-inspired embodied cognition framework.

By way of example, we hold that the ontology and role of affordances has to be reexamined: Our findings on the emergence of attentional anchors from students’ interactions with material and digital media raise questions for ecological psychologists positing the a priori ontological quality of affordances as agent–environment irreducible dualities (Gibson, 1977; Heft, 1989; Turvey, 2019). Consider the above-discussed 90° bimanual circling paradigm: has a coin on a table an a priori affordance to be used as a mark for movement guidance? Or has a certain location on a uniform table top an a priori affordance to be used as an imagined mark to serve as an attentional anchor never before experienced by anyone anywhere (cf. Tao, 2016)? To say so seems not to make much sense. Maybe, one may adapt the concept by saying that affordances can be created by the acting person. As we consider the formative role of emergent perception as governing action and cognition (Abrahamson, 2019; Mechsner et al., 2001), we may help to undo the Gordian knot of ecological psychology versus enactivism (Cosentino, 2021; Di Paolo et al., 2021; Heft, 2021; Isaac & Ward, 2021).

In Closing

In a traditional understanding, mathematical education research and movement sciences seem disparate in every conceivable characteristic: Is not mathematics essentially abstract, intellectual, and sophisticated, while movement is down-to-earth, physical, and simple? So, are not these areas separate and distinct already in their very conception? Contrary to this view, this article promotes the guiding programmatic idea that a movement-based unified integrated perspective on mental and bodily activity needs to be developed in a consistent theoretical framework and practical applications, for example, in pedagogy. In short, human movement is mental activity, and mental activity is movement. It is the tenet of the present article that only under such an integrative perspective an adequate foundation for understanding human activity of any kind can be developed (cf. Montessori, 1949; Sheets-Johnstone, 1999, 2015).

Our article implies, in a broader perspective, a call for an intensified dialogue of educational researchers with scientists and practitioners from most disparate fields under the leading and unifying idea that cognition is action-oriented perceptual activity. It also implies a call “back to the roots,” under the leading idea that mentally guided physical movement is phylogenetically and ontogenetically the origin and foundation of all mental activities, even of activities that do not present overt movements (cf. Allen & Bickhard, 2013). Per embodied design (Abrahamson, 2014), the teaching and learning of even so-called abstract concepts should begin with physical movement tasks that instantiate—and thus seed—the concepts to be learned.

Students’ physical activity in embodied-design tasks should not be considered a bit of preparatory fuss before the truly relevant to-be-learned material is introduced. Rather, figuring out how to enact movements that satisfy a task criterion, such as making a screen green, is already a full-fledged learning-and-thinking activity. As Pallasmaa (2017) puts it:

Knowledge is normally supposed to reside in verbalized concepts, but any grasp of a life situation and a meaningful reaction to it can, and indeed should, be regarded as knowledge …. It is evident that an educational change concerning the significance of the sensory and mental realm is urgently needed in order to enable us to re-discover ourselves as complete physical and mental beings. (pp. 105–108)

Thus seeing things, we could move forward.

Dor: So it seems we have more in common than a predilection for single malts, Franz. A math education researcher and a movement scientist arrived at the same basic hypotheses and experimental results. And our findings go against the grain of our respective fields… Amazing. This is where I say, “What were the chances the two of us walked into the same elevator at the same time?!”

Franz: I think it was a bar...

Dor: Of course, that explains the drinks.

Franz: But it does not explain that we met. Oh, I am already a bit…

Dor: We should write a paper together.

Franz: Let’s drink to that. Barman!