Exploring Different Assumptions about Outcome-Related Risk Perceptions in Discrete Choice Experiments

Abstract

Environmental outcomes are often affected by the stochastic nature of the environment and ecosystem, as well as the effectiveness of governmental policy in combination with human activities. Incorporating information about risk in discrete choice experiments has been suggested to enhance survey credibility. Although some studies have incorporated risk in the design and treated it as either the weights of the corresponding environmental outcomes or as a stand-alone factor, little research has discussed the implications of those behavioural assumptions under risk and explored individuals’ outcome-related risk perceptions in a context where environmental outcomes can be either described as improvement or deterioration. This paper investigates outcome-related risk perceptions for environmental outcomes in the gain and loss domains together and examines differences in choices about air quality changes in China using a discrete choice experiment. Results suggest that respondents consider the information of risk in both domains, and their elicited behavioural patterns are best described by direct risk aversion, which states that individuals obtain disutility directly from the increasing risk regardless of the associated environmental outcomes. We discuss the implication of our results and provide recommendations on the choice of model specification when incorporating risk.

1 Introduction

In most discrete choice experiment (DCE) studies, policy outcomes associated with environmental goods are generally presented as certain (Roberts et al., 2008). Yet, when policies are implemented, outcome delivery is unlikely to be certain, and this is especially true when environmental outcomes are affected by the stochastic nature of the environment and ecosystems (Torres et al., 2017). Further uncertainty arises from the environmental policies themselves, as social, political and economic factors may influence the effectiveness of the policy, the subsequent effect on human behaviour and hence the environmental outcome (Rolfe and Windle, 2015). Failing to account for outcome uncertainty may not only result in biased willingness-to-pay (WTP) estimates (Cameron, 2005), but also make the scenario seem unrealistic to DCE respondents (Wielgus et al., 2009; Glenk and Colombo, 2011), thus posing a challenge to the external validity of the experiment.

In the DCE literature, an increasing number of studies investigate the effects of embedding information on stated risk of outcome delivery with some including risk in the valuation scenarios, (implicitly) in the attributes or their levels (Wielgus et al. 2009; Torres et al., 2017; Bujosa et al., 2018),and others as an attribute (Roberts et al., 2008; Rigby et al. 2010; Glenk and Colombo, 2011, 2013; Akter et al., 2012; Rolfe and Windle, 2015).¹ Classic economic theory on stated risk perception is based on the expected utility (EU) framework (Von Neumann and Morgenstern, 1947). In this framework, individuals are assumed to combine the information on risk with the associated outcomes and calculate expected outcomes with linearly weighted probabilities (representing risk) in the process of decision-making. However, under prospect theory (Kahneman and Tversky, 1979; Tversky and Shafir, 1992) individuals may over- or under-weigh low and high probabilities, respectively. Moreover, some studies report direct utility risk aversion (DR) behaviour which was first found in a lab experiment where respondent were asked to state their WTP for a gift certificate valuing $50 (for certain) and WTP for entering into a binary-outcome lottery in which they would win either a $50 or $100 gift certificate with a range of probabilities. The results show that the WTP for the lottery was even lower than that for the sure gain of the $50 gift certificate that (Gneezy et al, 2006). Despite some disputes, this behaviour has also been observed in several contexts (Simonsohn, 2009; Newman and Mochon, 2012).² The findings indicate that contrasting to the standard economic assumptions where individuals make decisions according to the probability-weighted outcomes, a separate evaluation process between probability and its associated outcomes may have been applied by respondents (Gneezy et al., 2006; Simonsohn, 2009). In the DCE literature where information on risk is conveyed directly as an attribute of a policy, a number of studies focus on respondents’ behaviour in risky situations with environmental goods specified as either improvements or deteriorations. Results generally suggest that people are willing to pay more to reduce the risk of failing to deliver better environmental outcomes (Glenk and Colombo, 2011; Lundhede et al., 2015) or reduce the chance of worsened environmental conditions (Roberts et al., 2008; Torres et al., 2017). For example, Roberts et al. (2008) tested whether incorporating information on risk affected individuals’ preferences for reducing algal blooms. Under the assumption of expected utility theory, they embedded the information on risk together with environmental attributes in their uncertain treatment and compared it to a certain treatment without the explicit information on risk. Results suggest that individuals are willing to pay more to eliminate algal blooms in the uncertain treatment than in the treatment where occurrence of algal blooms is certain.

Nevertheless, most DCE applications in environmental valuation fail to investigate multiple possible behavioural assumptions when risk is incorporated in the experimental scenario. Past studies have often rejected the premise that respondents behave according to expected utility theory and suggest that risk is considered according to prospect theory (Roberts et al., 2008; Wibbenmeyer et al., 2013; Hand et al., 2015; Dekker et al., 2016). Glenk and Colombo (2013) compared the performance of DCE model specifications following expected utility, prospect theory and direct risk aversion (DR) assumptions. Their results show that the simple additive-in-attribute specification under a direct risk aversion assumption performs best statistically compared to models under other assumptions with linear or non-linear utility functions. Their results also suggest that different utility specifications with different behavioural implications under risk could lead to significant differences in WTP estimates. Rolfe and Windle (2015) also compared a series of different utility specifications and found that respondents place value on an environmental attribute in addition to expected environmental outcomes, implying an underestimation of environmental values under standard expected utility theory.³Overall, there is limited and mixed evidence regarding which behavioural patterns individuals use to reach environmental decisions in risky scenarios, and fail to examine different behavioural specifications under risk could result in biased WTP estimates.

Furthermore, the investigation of the possible multiplicity of behavioural rules can be complicated when the estimated environmental goods are subject to potential improvements as well as deteriorations in the future. Most existing DCE studies that explore individual behaviour under risk assess either future gains or future losses, with the exception of Faccioli et al. (2019). In recent DCE studies that incorporate risk, a linear additive attribute specification is commonly applied, where the probability is specified as independent of the associated environmental impact (Glenk and Colombo, 2011; Akter et al., 2012; Lundhede et al. 2015; Williams and Rolfe, 2017), yet the behavioural implication behind this DR specification has been largely ignored. The consequence of ignoring the underlying behavioural assumptions is especially severe when both environmental gains and losses are possible as a policy outcome and could lead to biased WTP estimates. A DR model postulates that the information of risk is evaluated separately from the corresponding environmental attributes, and therefore a change in the probability of occurrence of the environmental policy does not affect the final state of the environmental outcome. This feature makes the interpretation of the DR results distinctive from that under the expected utility assumptions, which is especially true when the probable change of an environmental outcome indicates a deterioration. For example, under a DR assumption where risk and outcome are separately evaluated, respondents would value an increased probability of the occurrence of wild species population decline partly as “bad news (i.e., reduced number of wild species)” and partly as “good news (i.e., increased certainty itself regardless of population change of the wild species)”. In this study, we provide evidence for both gain and loss domains, by investigating both within-domain and between-domain differences in outcome-related risk perceptions for a number of behavioural assumptions (i.e., expected utility theory, prospect theory and direct risk aversion assumptions) about decision making under risk. Specifically, we carefully examine the property of the DR specification in the loss domain and contrast the WTP estimate with those under other specifications.

This is the first study that extends the investigation of outcome-related risk perceptions in choices for environmental policies to both gain and loss domains, allowing tests of behavioural rule adoption within domain, as well as tests of possible mixed behavioural rules adoption between domains.⁴⁵ Risk is incorporated as an attribute to represent the probability of attribute outcomes, here defined as changes in annual hospital admissions due to air pollution in Beijing, China. Environmental attributes in our design are specified as either possible improvements or deteriorations under risk to reflect uncertainty about the direction of policy implementation (i.e., whether the current air policy regulation will be relaxed or tightened by the government in the future).

We compare statistical performance, consistency between behavioural assumptions and parameters estimation of different specifications of utility functions. For within-domain tests, we assume individuals apply a common behavioural rule across both domains and explore which behavioural assumption best predicts respondents’ decision-making. For between-domain tests, we explore whether risk perception is asymmetric between gain and loss domains. Firstly, we allow for the possibility that individuals apply asymmetric behavioural rules between the gain and loss domains. Secondly, we test whether respondents use the same behavioural rule, but place different importance on the risk between the two domains. In response to past findings around the heterogeneity of risk perception (Dorresteijn, 2017), posterior analysis is applied on the best-fit model specification, to explore the source of heterogeneity of the risk parameter in each domain, as well as the source of heterogeneity of the mean difference of the risk parameters between the gain and the loss domain.

In brief, our results suggest that the elicited behavioural patterns are better described by direct risk aversion in both domains, which states that people obtain disutility directly from risk increase itself regardless of the associated goods (Gneezy et al 2006; Simonsohn, 2009). Moreover, we find that respondents place different weights on the risk attribute in the gain and loss domains. Posterior analysis suggests that ignoring the risk attribute and the self-reported opinion that deteriorating air quality is unacceptable significantly affect the asymmetry in outcome-related risk perceptions. Although our results suggest that a specification under the DR assumption fits our data best, we provide several possible explanations for the adoption of the DR rather than EU behavioural rule in decision making. We therefore provide recommendations on the interpretation of results from an adopted DR behavioural rule and suggest possible directions for future research.

Section 2 presents the experimental design and details of the survey. Section 3 presents the modelling framework of this paper followed by results in Sect. 4. Section 5 discusses the results and implications and provides conclusions.

2 Study Background and Experimental Design

2.1 Study Background

The study area in this paper is Beijing, China, which has been battling with heavy air pollution since 2008. According to data from the Institute for Health Metrics and Evaluation, there are about 1,600,000 deaths annually from air pollution in China (Institute for Health Metrics and Evaluation, 2015). Air pollution has triggered both public and official concern in China, and a number of policies have been implemented in response. Although the Chinese government has implemented a series of stringent policies to combat air pollution, the heavy reliance on non-clean primary energy (e.g., coal) suggests that the implementation of further air pollution reduction policies may harm the country’s economic growth. Therefore, as a developing country, its government needs to consider the trade-off between economic growth and air quality improvement. Given the current strict air pollution policies and much-improved air quality, the government may opt for reduced implementation to maintain economic growth, which implies that the air quality may deteriorate. It thus becomes important for policymakers to decide whether to improve air quality at the expense of economic growth, or to favour economic growth and let air quality deteriorate. Additionally, as environmental outcomes are probabilistic and predictions are estimates, risk and uncertainty play important roles in preference elicitation in the context of air pollution. First, the effects of air pollution on human health are not homogenous. The health complications of air pollution can be condition-specific, while heterogeneous individual health behaviours will further influence the effects of air pollution on individual and public health outcomes. Second, the level of air pollution is affected by unpredictable weather conditions (Sario et al., 2013; Jhun et al., 2015). For example, rain reduces particulate matter (PM) concentrations and sunshine will exaggerate ground ozone pollution (Li et al., 2019). Thus, realistic elicitation preference mechanisms must account for both air quality improvement and deterioration, as well as the presence of risk in health outcomes.

2.2 Design of the Choice Experiment

2.2.1 Attributes and Levels

We selected four attributes, namely health, chance of success (probability of occurrence of the health outcomes), visibility and cost. These attributes and their levels were based on a number of existing DCE studies on outdoor air pollution with a total of 15 potential attributes among them that describe relevant characteristics (Diener et al., 1997; Jara-Díaz et al., 2006; Rizzi et al., 2014; Tang and Zhang, 2015). Furthermore, we consulted experts to assess the realism and possible correlations among these attributes, and conducted one focus group and 15 interviews to assess validity, relevance and comprehensibility with Chinese students from a UK university. Ten supplementary questionnaires were sent to the lay people in Beijing, through an online survey system, to collect more feedback about the realism of payment vehicle and the appropriateness of the attribute levels.

• (1) Health

  
  

  In this study, the health outcome was defined by the number of hospital admissions due to air pollution in the study area, which is a common adverse health effect caused by air pollution and ethically less pressing for respondents to consider in choice tasks compared to mortality. The status quo hospital admissions level due to air pollution was based on the overall hospital admission in Beijing in 2017 published by Beijing Municipal Environmental Protection Bureau and studies on the relationship between hospital admission and air pollution (Xu et al. 2016; Zhang et al., 2015; Tian et al., 2018). The percentage of improvement or deterioration was inferred from the Chinese Ambient Air Quality Standards implemented in 2012. The annual average PM2.5 (one of the main pollutants of air pollution) level in Beijing is 58 ug/m³ in year 2017, while the PM2.5 requirement for class I air quality is < 15 ug/m³ and for the class II air quality < 35ug/m3. Therefore, an assumption of maximum 15% air quality change seemed reasonable and realistic within our study context. The health attribute was presented in both absolute and relative forms (i.e., relative to the current situation of hospital admission due to air pollution per year in Beijing) to facilitate easier decision making.

• (2) Chance of success

  
  

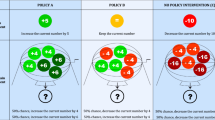
  In order to understand individuals’ decision-making process in risky situations, we incorporated a risk attribute that describes the probability with which the health outcomes stated in the choice experiment will come to fruition. The DCE respondents were informed that health is specified as probabilistic due to the complications of human health behaviour and the unpredictable atmospheric impact on the formation of main air pollutants. A step-by-step description about the concept of probability was then provided, with the underlying health outcomes of both scenarios (i.e., the health outcomes in case of success or failure) being explicitly explained. To ensure that respondents understand the meaning of risk in both the gain and loss domains, we used two policy scenarios with detailed descriptions as examples where risky health outcomes were specified as either increased hospital admissions in Policy A (representing a loss) or decreased hospital admissions in Policy B (representing a gain) in the “warm-up” section of the questionnaire. A bar graph accompanied the attribute on the choice card, which has frequently been used as a visual aid to improve understanding of the probabilities (see Harrison et al., 2014). The probability range was chosen based on previous studies on the relationship between air pollution and hospital admission, and the impact of weather conditions on air pollution (Xu et al. 2016; Zhang et al., 2015; Tian et al., 2018). These studies helped to develop the lower bound of 20% (i.e., lowest chance of success) of the risk attribute.⁶ To make the hypothetical scenario more convincing and enhance respondents’ comprehension that the probability was only applied to the health attribute, a short introduction was embedded in the survey about the scientific rationale behind the unpredictable nature of air pollution and its health effects compared to the other possible outcomes, e.g., visibility. (i.e., the survey text stated explicitly that the uncertainty of outcomes is applied to health, but not to visibility).

• (3) Visibility

  
  

  Poor visibility can cause flight cancellations, traffic jams and accidents, as well as visual dissatisfaction. In this study, visibility was defined as number of ‘bad visibility’ days in Beijing per month, following Rizzi et al. (2014).⁷

• (4) CostThe household electricity, gas and central heating bill was chosen as the payment vehicle, where households pay (get compensation) through the increase (decrease) of their bill to support an improvement (accept a deterioration) in the local air pollution. Such bill changes are frequently used to support environmental services in China (Sun et al., 2016; Sergi et al. 2019). Furthermore, this payment vehicle has appeal and relevance as almost all citizens in Beijing pay electricity, gas and central heating bills and the related energy industries are responsible for a large proportion of air pollution in the area. Thus, money raised by the government through imposed energy bill changes can be earmarked for the installation of new technologies on these targeted industries in an effort to improve their environmental performance. Respondents were told that the health or visibility outcomes can be improved by enhanced implementation on air pollution control, yet they need to pay for the improvement due to the limited governmental budget. Meanwhile, the government could also reduce the level of implementation, and the health or visibility outcomes hence would be worse. If the degree of governmental enforcement is reduced, the cost of R&D and installation of air purification appliances for energy generators would thus decrease, and as a result, the energy bill transferred to customers would be reduced.

A World Bank report (2007) estimates the economic cost of health effects due to air pollution between 1.16% and 3.8% of GDP per year. To define attribute levels, we used the mean value of these cost estimates, adjusted to 2017 GDP estimates (National Statistical Bureaus of China, 2017), and divided by the population of Beijing in 2017 (National Statistical Bureaus of China, 2017) to calculate the estimated cost of air pollution per person per year. Cost levels were repeatedly pre-tested and were increased after respondents in the initial pre-test noted that the amounts were too low to be considered meaningful for trade-offs.

The final attributes and their levels are presented in Table 1. An English translation of the example of a choice card that was presented to respondents is given in Fig. 1. Also see details in Appendix B for the questionnaire used in this study.

Table 1 Attributes and levels selected for the discrete choice experiment

Fig. 1

provides an example of the choice card that was presented to respondents in our experiment

2.2.2 Experimental Design and Procedures

We constructed a D-efficient fractional-factorial design with three blocks of ten choice sets using the Ngene software version 1.2.0. Each choice set consists of two alternatives plus a status-quo option, with the current state of air-pollution and its effects in Beijing as its levels. We randomised the presentation of choice cards to individuals to minimize order effects. Restrictions on experimental design were imposed to avoid unrealistic combinations in choice sets; for any given alternative, the bill cannot decrease (increase) if both health and visibility attributes improve (deteriorate). Otherwise, the health, visibility and the cost attributes are allowed to vary independently. Before starting the choice tasks in the DCE, respondents were told that the health and visibility effects are independent and that the sources that contribute to these effects are different. If the government would prioritise combating visibility and implemented measures to reduce air pollutants that negatively affect visibility, limited budgets could mean that fewer measures would be imposed on the reduction of other pollutants that contribute to the health effect; for this reason, visibility can improve while health worsens.

Participants were first presented with a participation and consent form. After agreeing to participate, respondents were given an introduction on the issues of air pollution and relevant governmental policies. Next, a warm-up DCE question intended to familiarize respondents with the question format (World Health Organisation, 2012), followed by ten DCE scenarios, in which people were asked to choose a preferred option among Policy A, Policy B and Current Policies (the status quo option) (see Fig. 1). At completion, respondents were asked questions about the experiment itself and a set of socio-demographic questions. Ethical approval for the survey was obtained from the Ethics Board of a UK university (Ref. No. 30107 A4). No further ethical approval in China was necessary according to the reputable Chinese marketing company that administered the survey.

Data collection was conducted through an online platform. Respondents from Beijing were randomly sampled and were provided with a personalized link that led them to their assigned questionnaire. Data quality was controlled by setting a minimum time before respondents were able to move to a next page to ensure that respondents would spend sufficient time on reading the scenario description. Respondents who successfully finished the questionnaire obtained eight credit points in the marketing company’s system, exchangeable for 8 RMB or other equivalent consumption goods.

3 Modelling Framework

3.1 Random Utility Model

Within a random utility framework (McFadden, 1974), respondents obtain utility from choosing alternative i:

$${\mathrm{U}}_{nit}={\mathrm{v}}_{nit}+{\upvarepsilon }_{nit}$$

(1)

where ${\mathrm{U}}_{nit}$ is the utility of individual n choosing alternative i in choice set t. ${\mathrm{v}}_{nit}$ is the value function, which represents the deterministic part of the utility function, while ${\upvarepsilon }_{nit}$ represents a stochastic component following some known distribution. Under certainty and symmetry in the gain and loss domains, the value function is specified as Eq. (2), where ${H}_{nit}$, ${V}_{nit}$ and ${C}_{nit}$ are the health, visibility and cost attributes, respectively.

$${\mathrm{v}}_{nit}={\beta }_{H}{H}_{nit}+{\beta }_{V}{V}_{nit}+{\beta }_{C}{C}_{nit}$$

(2)

Equation (2) can also be specified as asymmetric in the gain and loss domains for the health attribute, i.e., according to whether changes in health are stated as an improvement or deterioration. We only consider an asymmetric specification for the health attribute as only this attribute is subject to uncertainty in our scenario; visibility and cost are not uncertain and assumed to have linear and symmetric effects on individual utility.⁸ The asymmetric specification without considering risk is stated in Eq. (3) (model 1)⁹:

$${\mathrm{v}}_{nit}={\beta }_{H}^{imp}{H}_{nit}^{imp}+{{\beta }_{H}^{det}H}_{nit}^{det}+{\beta }_{V}{V}_{nit}+{\beta }_{C}{C}_{nit}$$

(3)

where ${H}^{\mathrm{imp}}$= max(${H}_{SQ}$–$H$, 0) indicates an improvement in health in alternative i relative to the reference point (i.e., the current situation of the health level, ${H}_{SQ}$), and ${H}^{det}$ = max(${H-H}_{SQ}$, 0) indicates a deterioration in health relative to the reference point.

3.2 Research Questions

3.2.1 Research Question 1: What is the Best Utility Specification Within the Gain–Loss Framework under Uncertainty?

The first question is to identify the model specification that fits our data best among all candidate value functions specifications with different assumptions about risk perceptions.¹⁰ Three behavioural assumptions are frequently mentioned in the literature of behavioural economics and DCE that reflect respondents’ behavioural rules in decision-making under risk, namely expected utility, prospect theory and direct risk aversion. Model selection is based on statistical performance and whether the estimated parameters are consistent with their corresponding theoretical assumptions. BIC values are used to evaluate relative statistical performance among different utility specifications.

• (1) Expected utility specification

  
  

  The most common way to incorporate risk in one’s utility function is through the expected utility theory (EU) (Von Neumann and Morgenstern, 1947), in which respondents are assumed to consider the absolute health outcome due to air pollution effect, together with its probability. Empirical evidence from DCE studies suggests that at least some respondents behave according to EU in environmental decision-making (Glenk and Colombo, 2013; Rolfe and Windle, 2015). We specify a value function approximating EU in Eq. 4 (model 2) as:

  $${\mathrm{v}}_{nit}={\beta }_{HR}^{imp}({H}_{nit}^{imp}*{R}_{nit}^{G})+{{\beta }_{HR}^{det}(H}_{nit}^{det}*{R}_{nit}^{L})+{\beta }_{V}{V}_{nit}+{\beta }_{C}{C}_{nit}$$

  (4)

  where${R}_{nit}^{G}$(${R}_{nit}^{L})$ is the risk attribute that represents the probability of success of the associated health outcomes in the gain (loss) domain. It enters estimation as a continuous variable taking three possible values (i.e., 0.2, 0.5 or 0.9) when the associated health outcome implies an improvement (deterioration) compared with the current situation and is set to 0 otherwise. The risk takes the value 1 for the current policy scenario (i.e., no risk of failure). ${H}_{nit}^{imp}*{R}_{nit}^{G}$ (${H}_{nit}^{det}*{R}_{nit}^{L}$) represents the interaction of the risk and health attribute in alternative i in the gain (loss) domain. For the EU specification, we expect ${\beta }_{HR}^{imp}>0$ and ${\beta }_{HR}^{det}<0$ (i.e., utility is expected to increase (decrease) when the expected health outcomes improve (deteriorate)). Parameter signs contradicting this expectation would imply that estimated parameters for this value function specification are not consistent with EU theory. Note that the value function over the health outcome is assumed to be linear here for simplicity, whilst the modelling and the results of a standard EU specification with a non-linear value function is discussed in Appendix A1.3.

  A dummy-coded EU specification (where possible non-linear effects of health are examined) is also applied to understand the change of risk perceptions under different health levels, which is shown in Eq. (5).

  $${\mathrm{v}}_{nit}={D}_{p}^{h}{HR}_{nit}+{\beta }_{V}{V}_{nit}+{\beta }_{C}{C}_{nit}$$

  (5)

  where ${HR}_{nit}$ represents the dummy-coded interaction terms between the health and the risk attributes, and ${D}_{p}^{h}$ is a parameter vector for the interaction terms. Six health levels and three risk levels are considered in the experiment, resulting in 17 dummy-coded interaction variables. In the regression, ${H}^{11}*{R}^{20}$, representing health level 110,000 number of hospital admissions with 20% of achieving this outcome, is treated as the reference level.

• (2) Prospect theory specification

  
  

  Different from the EU specification where linearity is assumed in probability, prospect theory (PT) (Kahneman and Tversky 1979) states that people overweigh small probabilities and underweigh large probabilities (i.e., a specific type of risk non-linearity). In an early DCE attempt, Roberts et al. (2008) incorporated a risk factor using an EU and a PT specification in eliciting individuals’ environmental preference for lake conservation and found that the PT specification outperformed the EU one. A better performance of the PT specification is also found in other DCE studies for environmental problems (Wibbenmeyer et al., 2013; Hand et al., 2015; Dekker et al., 2016). In our specific context where improved and deteriorated health outcomes are specified separately, weighting functions may be different in the gain and loss domain, as people may have different risk perceptions between the two domains (Abdellaoui et al., 2005; Booij et al., 2010). The corresponding value function is given in Eq. (6) (model 3):

  $${\mathrm{v}}_{nit}={\beta }_{HW}^{imp}{{[W}^{+}\left({R}_{nit}^{G}\right)*H}_{nit}^{imp}]+{{\beta }_{HW}^{det}{[W}^{-}\left({R}_{nit}^{L}\right)*H}_{nit}^{det}]+{\beta }_{V}{V}_{nit}+{\beta }_{C}{C}_{nit}$$

  (6)

  where ${W}^{+}(\cdot )$ and ${W}^{-}(\cdot )$ represent the weighting functions in the gain and loss domains, respectively. For the weighting function specification, we choose two possible functional forms proposed by Tversky and Shafir (1992) and Prelec (1998), which are frequently used in applications of prospect theory (Wibbenmeyer et al., 2013; Hand et al., 2015):

  $$W\left(\mathrm{p}\right)=\frac{{p}^{\Upsilon}}{{[{p}^{\Upsilon}+{\left(1-p\right)}^{\Upsilon}]}^{1/\Upsilon}}$$

  (7)
  $$W\left(\mathrm{p}\right)={e}^{{[-(-\mathrm{ln}\left(p\right))}^{\theta }]}$$

  (8)

  where p is the probability representing the risk attribute. In Eq. (7), $\Upsilon$ is the probability weighting parameter, where $\Upsilon\in (\mathrm{0,1}]$ denotes the degree of curvature. For $\Upsilon$= 1, $W\left(\mathrm{p}\right)=\mathrm{p}$ implies a linear weighting function, while $\Upsilon\in (\mathrm{0,1})$ implies an inverse-S shape weighting function, denoting that people generally overweigh small probabilities and underweigh medium and large probabilities. In Eq. (8), $\theta \in (\mathrm{0,1}]$, with the weighting function collapses to a linear probability weighting for $\theta =1$. Different weighting function parameters are estimated in the gain and the loss domain to account for differences in probability distortion in the two domains, and similar to attribute parameters, the estimates for the weighting function parameters can be obtained through maximum likelihood estimation. Overall, empirical values of $\Upsilon<1$ and $\theta <1$ would suggest that respondents treat probabilities non-linearly. Again, the value function over the health outcome is assumed to be linear here for simplicity, while the modelling and the results of a standard PT specification with non-linear value function are provided in Appendix 1.3.

• (3) Direct risk aversion specification

  Risk can also be treated as an attribute separate to its corresponding health outcomes, implying a behavioural assumption that respondents experience direct disutility from risk itself, regardless of the associated outcomes. The underlying assumption of the DR specification stresses two characteristics that are distinct from expected utility or prospect theory. (i) Separability, which means respondents evaluate risk and its outcome in a separate manner, rather than balancing different outcomes according to their probabilities. The feature of separability is summarised as a two-step decision-making process under risk in Gneezy et al. (2006). (ii) Non-monotonicity, which represents the U-shaped relationship between the WTP values and risk found in Gneezy et al. (2006), in which WTP decreases from the certain smaller gain (p = 0) to a lower value when risk is involved (p > 0), and then beyond a mid-level of p increases again as the outcome becomes more certain (p = 1). The non-monotonicity feature reflects their finding that WTP for certainly achieving either outcome of a binary lottery is higher than that for the lottery when a medium level of risk is involved. The DR assumption is less common in behavioural economics literature, but it has been more widely applied in DCE studies incorporating risky scenarios (Glenk and Colombo, 2011, 2013; Akter et al., 2012; Lundhede et al. 2015; Rolfe and Windle, 2015; Williams and Rolfe, 2017), with most of these studies applying a linear additive specification where only separability is assumed. Rolfe and Windle (2015) explicitly tested non-linear risk perceptions by applying a quadratic specification.

To account for the two features of the DR assumption, we propose the following three models:

• (a) Direct risk aversion – quadratic specification (DR-quadratic)

  $$\begin{aligned}{\mathrm{v}}_{nit}&={{\beta }_{HR}^{imp}\left({H}_{nit}^{imp}*{R}_{nit}^{G}\right)+\beta }_{R}^{G}*{R}_{nit}^{G}+{\beta }_{R}^{G2}*{\left({R}_{nit}^{G}\right)}^{2}+{{\beta }_{HR}^{det}(H}_{nit}^{det}*{R}_{nit}^{L})+{\beta }_{R}^{L}*{R}_{nit}^{L}\\& \quad +{\beta }_{R}^{L2}*{({R}_{nit}^{L})}^{2}+{\beta }_{V}{V}_{nit}+{\beta }_{C}{C}_{nit}\end{aligned}$$

  (9)

  In the DR-quadratic specification (model 4), in addition to the probability-weighted health outcomes, linear risk terms, i.e., ${R}_{nit}^{G}$ and ${R}_{nit}^{L}$, is specified to simulate the separable decision-making process of direct risk aversion described in Gneezy et al. (2006). In our case, the specification accounts for the separability feature that risk is evaluated independently from the health outcomes in the gain or loss domain. The quadratic form of the risk terms, i.e., ${\left({R}_{nit}^{G}\right)}^{2}$ and ${\left({R}_{nit}^{L}\right)}^{2}$ capture the non-monotonicity feature of the utility function, if present, in the gain and loss domains. Deriving theoretical expectation regarding the sign of the parameters of the linear risk terms is mathematically complex and beyond the scope of this study. Therefore, we opt for the comparisons of statistical performance across models. Nevertheless, for a basic quadratic functional form, positive parameters would be expected to reflect the convexity of the utility function.

• (b) Direct risk aversion – linear specification (DR-linear)

  $${\mathrm{v}}_{nit}={{\beta }_{HR}^{imp}({H}_{nit}^{imp}*{R}_{nit}^{G})+\beta }_{R}^{G}*{R}_{nit}^{G}+{{\beta }_{HR}^{det}(H}_{nit}^{det}*{R}_{nit}^{L})+{\beta }_{R}^{L}*{R}_{nit}^{L}+{\beta }_{V}{V}_{nit}+{\beta }_{C}{C}_{nit}$$

  (10)

When the quadratic terms are not significantly different from zero, Eq. (9) collapses to Eq. (10) (model 5), i.e., the linear DR specification, implying that risk non-linearity (which includes the characteristic of non-monotonicity) is not observed empirically. Also, compared with the EU specification, the additive linear probability term (i.e., ${R}_{nit}^{G}$ or ${R}_{nit}^{L}$) suggests that individuals place additional penalty on risk of failure. It is expected that the risk parameters are positive in both the gain and the loss domains to reflect the expectation that respondents prefer to reduce risk of failure (i.e., increase success rate) and that this preference is independent of its associated health outcome, whilst insignificant risk parameters would imply that respondents ignore the risk attribute in gain and loss domains.

(c) Pure direct risk aversion specification (Pure DR)

$${\mathrm{v}}_{nit}={\beta }_{R}^{G}*{R}_{nit}^{G}+{\beta }_{R}^{L}*{R}_{nit}^{L}+{\beta }_{H}^{imp}{H}_{nit}^{imp}+{{\beta }_{H}^{det}H}_{nit}^{det}+{\beta }_{V}{V}_{nit}+{\beta }_{C}{C}_{nit}$$

(11)

Compared with Eqs. (9) and (10), Eq. (11) (model 6) goes further and allows a complete separation in the evaluation of health and risk attributes. A risky prospect under this assumption is separately coded as an outcome of certainty plus a risk penalty. Similar to Eq. (10), the linear additive risk terms are expected to be positive in both domains. This formulation is the DR specification commonly used in the DCE literature.

3.2.2 Research Question 2: Is Risk Perceived Asymmetrically in Gain and Loss Domains?

We split this research questions into two sub-questions:

• (1) Research question 2.1: Do respondents impose different behavioural rules in gain and loss domains

  In attribute trade-offs, respondents may impose a different behavioural rule in the loss domain than the gain domain due to unfamiliarity or unimaginability with choice scenarios that involve air quality deterioration. For the between-domain test, we construct a mixed behavioural model where an EU or a PT specification is assumed in the gain domain and a Pure-DR specification is assumed in the loss domain.^{11, 12} This model is then compared with the best-fit model from the within-domain tests (i.e., research question 1).The corresponding value functions for these two domain-asymmetric models according to the EU and PT in the gain domain and Pure-DR in the loss domain are presented in Eq. (12) and (13) (model 7 and 8), respectively:

  $${\mathrm{v}}_{i}={\beta }_{HR}^{imp}\left({H}_{nit}^{imp}*{R}_{nit}^{G}\right)+{{\beta }_{H}^{det}H}_{nit}^{det}+{\beta }_{R}^{L}*{R}_{nit}^{L}+{\beta }_{V}{V}_{nit}+{\beta }_{C}{C}_{nit}$$

  (12)
  $${\mathrm{v}}_{i}={\beta }_{HW}^{imp}{{[W}^{+}\left({R}_{nit}^{G}\right)*H}_{nit}^{imp}]+{{\beta }_{H}^{det}H}_{nit}^{det}+{\beta }_{R}^{L}*{R}_{nit}^{L}+{\beta }_{V}{V}_{nit}+{\beta }_{C}{C}_{nit}$$

  (13)

• (2) Research question 2.2: For the model with the best statistical performance, are risk effects in the gain and loss domain of similar magnitude?

We explore whether respondents place equal importance on the risk attribute in the two domains by testing whether the mean parameter of the risk attribute in the gain domain is significantly different from the one in the loss domain for the statistically superior model obtained in research question 1. For example, if the Pure-DR specification results in the best model fit, then in Eq. (11), ${\beta }_{R}^{G}$≠${\beta }_{R}^{L}$ could be seen as evidence that respondents place different importance on the risk attribute in the two domains.

3.3 Econometric Models

In the various model specifications, when assuming an IID error term ${(\upvarepsilon }_{ni})$ following an extreme value type I distribution, McFadden’s conditional logit is obtained (McFadden, 1974). Yet, the IID assumption of the error term is often violated in empirical analyses implying a lack of preference homogeneity across respondents or correlation across alternatives. We model unobserved preference heterogeneity through a mixed logit model (Hensher and Greene, 2003), where attribute parameters have a fixed and a random component following some known distribution. The general form of a utility function is:

$${\mathrm{U}}_{nit}={\beta }_{n}{X}_{nit}+{\upvarepsilon }_{nit}={\alpha }{X}_{nit}+{\upzeta }_{n}{X}_{nit}++{\upvarepsilon }_{nit}$$

(14)

where ${\beta }_{n}$ is now split to two parts: ${\alpha }$ captures the mean of the unconditional distribution of the preference for a certain attribute, and ${\upzeta }_{n}$ captures the standard deviation around this mean. The IID assumption is relaxed as the utility can be correlated across alternatives. The probability of subject n choosing alternative i in the mixed logit is given by:

$${P}_{ni}=\int (\prod_{t}\frac{\mathrm{exp}\left({\beta }_{n}{X}_{nit}\right)}{{\sum }_{i=1}^{I}{\mathrm{exp}(\beta }_{n}{X}_{nit}) }f(\beta )d\beta$$

(15)

with $f(\beta )$ being the density function of coefficient $\beta .$

To illustrate to what extent different models leads to the differences in welfare estimates, we calculate compensating surplus according to (Hanemann, 1984), which is presented in Eq. (16):

$${CS}_{s}=\frac{lnexp{V}_{s}^{1}-lnexp{V}_{s}^{0}}{-{\beta }^{c}}=\frac{{V}_{s}^{1}-{V}_{s}^{0}}{-{\beta }^{c}}$$

(16)

where ${CS}_{s}$ is the compensating surplus for scenario s, ${V}_{s}^{0}$ and ${V}_{s}^{1}$ represent the value function before and after a change of attributes for this scenario, respectively. ${\beta }^{c}$ refers to the coefficient of the monetary attribute.

We construct six scenarios where both the number of hospital admissions and the chance of success change relative to a base scenario (detailed scenario changes are presented in the results section). Confidence intervals of the WTP estimates from compensating surplus analysis are estimated using the approach proposed by Krinsky and Robb (1986) with 2000 draws to obtain empirical distributions of WTPs of each scenario. The Poe et al. (2005) test is used as a conservative test to examine the statistical significance of differences of WTP estimates between model specifications.¹³

Models are estimated using the Apollo package (Hess & Palma, 2019) based on 500 MLHS (Modified Latin Hypercube Sampling) draws for random parameters. The alternative specific constant term and all environmental attribute parameters are assumed to be random following normal distributions, and the cost parameter is assumed to follow a lognormal distribution.

3.4 Posterior Analysis

As risk is explicitly stated as an attribute in our DCE, ignoring this attribute can be seen as an indication of heuristic information processing, which can be related to cognitive ability (Kaiser et al., 1999; Akter et al., 2009; Taylor, 2016; Dohmen et al., 2018), environmental attitudes (e.g., pro-environmental individuals may prefer policymakers to apply a precautionary principle instead of a cost–benefit analysis to deal with environmental uncertainty) and socio-demographic characteristics (Dorresteijn, 2017). Through posterior analysis we explore how individual characteristics, environmental attitude and cognitive burden affect risk perceptions in the gain and loss domains in three models: two models for the gain and loss domain separately and one model on the gain–loss difference in risk perceptions. The posterior analysis is based on the results of the best-fit mixed logit model, where the dependent variables are the individual-level conditional means of the risk parameters inferred from the mixed logit model, and independent variables being the individual-level demographic factors, variables representing respondents’ cognitive burden (i.e., self-reported attribute non-attendance and self-reported perception about the complexity of the survey) and a variable representing environmental attitude (i.e., self-stated inability to accept air quality to be deteriorated). Individual-level conditional means are obtained using simulation with 500 draws, representing the most likely position of each individual on the pre-assumed distribution of risk attribute parameters. This is an increasingly popular way to interpret preference heterogeneity, in which variation in the conditional means of the random parameters are linked to individual characteristics (Revelt and Train, 2000; Greene, 2002; Hess, 2010).

4 Results

4.1 Descriptive Statistics

Summary statistics for the sample are given in Table 2. Comparing sample characteristics with the Beijing general population, the sample tends to be more educated and younger. This is potentially due to the use of a web-based experiment where selected respondents must have online access and a registered account with the marketing company.

Table 2 Summary statistics of the demographic variables

Of the respondents who completed the survey, we exclude those who had no variation in their DCE answers (i.e., always choose Policy A or Policy B and those who chose the SQ option for the belief that citizens do not need to pay for air quality improvement), which accounts for 1.2% (4 subjects) of the whole sample. Therefore, 341 respondents are included in the data analysis.

4.2 Estimation Results

Estimation results for models 1–6 are given in Table 3. For the No Risk specification (model 1), health, visibility and cost variables are all significant at the 1% level with the expected sign, suggesting that respondents in general behave according to theoretical expectations. More bad visibility days, more hospital admissions due to air pollution and higher cost all lead to higher disutility, while fewer hospital admissions increase utility. A negative coefficient for the status quo alternative indicates a tendency to opt for the proposed new policies rather than staying with the current policies, which is consistent with Yao et al. (2019).

Table 3 Estimation results of mixed logit models with different utility function specifications

For research question 1, we compare model 1 without the risk attribute (No Risk) to model 2 that considers risk according to the expected utility model (EU), model 3 under the prospect theory assumption (PT) and models 4 to 6 under the direct risk aversion assumption. Firstly, we observe significant risk coefficients in both the gain and loss domains for all models, suggesting that individuals incorporate risk in their decision making. Secondly, the results from model 4–6 suggest that: (a) the Pure-DR specification outperforms the DR-linear and DR-quadratic specifications in terms of BIC values; (b) parameters for the Pure-DR specification (model 6) have signs consistent with the DR assumptions—respondents prefer a higher chance of success (lower risk of failure) in both the gain and the loss domain, regardless of the associated health outcomes. These results suggest that the Pure-DR specification (Eq. 11), which contains the characteristic of separability only, fits our data better than the other two DR specifications (Eq. 9 and Eq. 10). We also observe that the Pure-DR specification (model 6) has a smaller BIC value compared with the models under the EU and PT assumptions, suggesting that the Pure-DR model outperforms all other models in terms of model fit, which is consistent with the finding in Glenk and Colombo (2013). Looking at the PT model (model 3), the mean and the standard deviation parameters of the probability-weighted health attribute in the loss domain (i.e., W(${\mathrm{R}}^{L}$)) are much larger compared with the other parameter estimates. The estimated weighting function parameter in the loss domain is 0.13; much lower than the estimates found in many empirical studies.¹⁴ This result implies that respondents under-weighed all probabilities presented in our experiment (i.e., 20%, 50% and 90%).¹⁵ This is a first indication that the PT specification in this study cannot well approximate respondents’ behaviour in the loss domain.¹⁶

To further understand whether respondents apply a weighted average algorithm in decision making that conforms to EU or PT, we conducted the analysis using a dummy-coded specification of the EU model (Eq. 5). The results are provided in Table 4 and visualised in Fig. 2a and (b). The results suggest that for the same health level, utility in the gain domain increases as the probability increases, which is in line with EU assumption. However, inconsistent with the EU assumption, the average trend in Fig. 2b suggests that utility in the loss domain increases as the probability increases (although less salient than that in the gain domain), which implies that holding health levels constant, respondents prefer worse expected health outcomes. The counter-intuitive finding in the loss domain provides evidence that respondents neither make decisions according to EU theory, and by extension nor according to PT theory (where individuals are also assumed to prefer better expected health outcomes). In summary, we find that the parameters in the EU and PT models do not conform to their corresponding theoretical assumptions in the loss domain. Additionally, we conducted a series of robustness checks (e.g., testing non-linear value function for the EU and PT models) and results are consistent with our finding that the Pure-DR specification outperforms other specifications (see Appendix A1 for details).

Table 4 Estimation results of the dummy-coded mixed logit model with expected utility assumption

Fig. 2

(a): Coefficients at each health level in the gain domain from the dummy-coded EU specification. This figure presents the coefficients at each health level in the gain domain from the dummy-coded EU specification. “Level 11”, “Level 11.5”, or “Level 12” is the fitted line for the coefficients of the risk attribute when hospital admissions is at the level of 110,000/115,000/120,000 per year due to air pollution. “Average (linear)” is the fitted line for the average of the coefficients of risk. As can be seen in this figure, the Average (linear) line shows an increasing trend when probability level increases. (b): Coefficients at each health level in the loss domain from the dummy-coded EU specification This figure presents the coefficients at each health level in the loss domain from the dummy-coded EU specification. “Level 14”, “Level 14.5”, or “Level 15” is the fitted line for the coefficients of the risk attribute when hospital admissions is at the level of 140,000/145,000/150,000 per year due to air pollution. “Average (linear)” is the fitted line for the average of the coefficients of risk. As can be seen in this figure, the Average (linear) line shows an increasing trend when probability level increases

For research question 2.1, we test whether the two model specifications with EU or PT in the gain domain and Pure-DR in the loss domain (i.e., model 7 and model 8) conform to the corresponding theoretical assumptions and whether they outperform the best-fit model (i.e. model 6 with a Pure-DR specification in both domains). As shown in Table 3, the attribute coefficients for model 7 and model 8 are consistent with their corresponding theoretical assumptions. For the PT(gain)-PureDR(loss) (model 8), the $\Upsilon$ parameter is 0.49 (and significantly different from 1, with p-value < 0.01), implying an inverse S-shape probability weighting function, in which the small probability (20%) is overestimated, whereas the medium and large probabilities (50% and 90%) are underestimated. Testing Prelec (1998) one-parameter weighting function produces comparable results where small probabilities are overestimated, and medium and large probabilities are underestimated, whilst a slightly worse fit is observed (BIC = 5982; see Fig. 3). This empirical finding is consistent with Wibbenmeyer et al. (2013) and Hand et al. (2015) in the gain domain where respondents distort probabilities when they evaluate environmental goods in risky scenarios. However, the Pure-DR model (model 6) outperforms the both EU (gain)-PureDR (loss) (model 7) and PT(gain)-PureDR(loss) (model 8), as measured by BIC values. In summary, our results suggest that respondents do not apply different behavioural rules between gain and loss domains, and that the Pure-DR specification in both domains fits the data best. Moving onto research question 2.2, we test whether respondents place equal importance on risk in the gain and loss domain. For the Pure-DR specification (model 6 in Table 3), significant differences between the mean parameters of risk attribute in the gain and the loss domain are found using the Wald test (Wald statistic = 3.195; p-value < 0.01), implying different magnitudes for risk between the gain and loss domain.

Fig. 3

Estimated probability weighting function. Note: Tversky & Shafir is the Tversky and Shafir (1992) probability weighting function applied in the gain domain for the PT (gain)-PureDR (loss); Prelec is the Prelec (1998) probability weighting function applied in the gain domain for the PT (gain)-PureDR (loss); Y = X is a line that assumes a linear probability weighting

We also conduct compensating surplus analysis to illustrate the impact of different model specifications on WTP. The description and the results of compensating surplus estimates for the six constructed scenarios are presented in Table 5. In scenarios 1–3 for the gain domain, hospital admissions are assumed to decrease from 120,000 to 110,000 due to improved air quality, while the probability of this achievement varies. In scenarios 4–6 for the loss domain, health is assumed to deteriorate from 140,000 to 150,000 hospital admissions while risk again varies. Visibility is kept constant. For the comparisons in the gain domain (scenarios 1–3), WTP estimates are overall largest for the EU model, while the smallest for the PT(gain)-PureDR(loss) specification; yet in scenario 5–6 in the loss domain, the Pure-DR specification generates the smallest WTP estimates (in absolute value). In scenario 1, the Pure-DR model predicts that respondents would like to pay 720 RMB/month (about £80/month) for an air quality improvement policy that results in a 7.5% reduction in the number of hospital admission, when the success rate of this policy increases by 30% (from 20 to 50%).

Table 5 Scenario changes and the results of compensating surplus estimation (means)

Scenario 1 involves a small decrease in risk (from 20 to 50%) while scenario 2 involves a large decrease (from 20 to 90%). As expected, WTP estimates for all model specifications show that people prefer to pay for a reduction in risk of failure in these two scenarios, and the larger the risk reduction, the more people are willing to pay. For scenario 4–6, WTP estimates are negative due to deteriorated air quality. We observe that for the EU model, WTP in scenario 5 decreases compared with that in scenario 4, and the extent of decrease is even larger for the PT model, due to the highly distorted probability in this domain. However, a distinctive pattern can be found for all other models where DR specifications are applied in the loss domain—WTP in scenario 5 increases compared with that in scenario 4.

The results of the Poe et al. (2005) tests are presented in Table 6. Within the DR family, WTP estimates for the Pure-DR model are significantly different from those for the DR-quadratic specification, but not for the DR-linear specification. WTP estimates also differ significantly between the Pure-DR and the EU models—the equality of WTP values is rejected for all six scenarios, both in the gain and loss domain. The differences are also observed between the Pure-DR and the other specifications in some scenarios, except for the PT(gain)- Pure DR(loss) specification, which produces similar WTP estimates as the Pure-DR model. We also observe that WTP estimates are significantly different for scenarios 4–6 between the PT and EU models. The lower WTP estimates in absolute value (i.e., less negative WTP values) for the PT model compared to the EU model can be explained by the estimated weighting function parameter which implies a sizable underestimation of probabilities in the loss domain. Overall, the welfare analysis suggests that different model specifications could lead to significantly different WTP estimates.

Table 6 Results of WTP (means) comparisons between models using Poe et al. (2005) test

To explore preference heterogeneity in outcome-related risk perceptions, we evaluate the results of the posterior analysis under the best-fit model, the Pure-DR model, in Table 7. Findings suggest that self-reported non-attendance of the risk attribute and rejecting air quality deterioration options significantly affect outcome-related risk perceptions. Respondents who reported that they did not ignore the risk attribute have larger risk coefficients in the gain domain and higher gain–loss asymmetry in outcome-related risk perceptions than others. Additionally, we find that in model (3), Table 7, those who found air quality deterioration scenarios unacceptable show a larger asymmetry in their outcome-related risk perceptions. As a robustness check, we also run a hybrid choice model in which attitudinal variables are incorporated as a function of latent attitude to avoid introducing measurement errors in the regression (Czajkowski et al., 2017). Key results remain qualitatively unchanged, except that the effect of self-reported non-attendance to the risk attribute becomes insignificant, suggesting that the posterior analysis may suffer from measurement error. This is consistent with findings in Carlsson et al. (2010) questioning the reliability of self-reported attribute non-attendance. Details of the hybrid choice model specification and results can be found in Table 9, Appendix 3.

Table 7 Posterior analysis of the conditional mean estimates under direct risk aversion assumption

5 Discussion

Incorporating uncertainty into DCEs has been claimed to increase the credibility of the experiment and mitigate the hypothetical bias of welfare estimates for environmental goods (Wielgus et al., 2009). Yet, despite policy outcomes often being uncertain, most DCEs in the literature fail to consider information about risk in their experimental design. Among studies in which outcome-related risk is incorporated in the design, with a few exceptions, studies use a pre-assumed model specification, usually based on either EU or DR theory.

Our unique experimental design accounts for outcome-related risk and allows us to accommodate both scenarios of environmental improvement and deterioration. In the loss domain where air quality deteriorates due to a more relaxed policy implementation in the future, results of the dummy-coded EU specification show that individuals’ utility increase when the probability of achieving worse outcomes increases (holding health levels constant), which contradicts the EU assumption. Our results suggest that elicited behavioural patterns are better described by the DR behaviour (rather than the EU or PT) in both the gain and the loss domains. From a policy perspective, WTP estimates for the Pure-DR specification, which is the best-fit specification in our context, are notably different from the EU and PT specifications in some or all simulated scenarios. A behavioural implication of the DR specification is that individuals evaluate the risk and the environmental outcome separately, yet most previous studies using the DR model do not discuss the implications of this assumption for the interpretation of results. In the loss domain (where a policy reflects an environmental deterioration), holding the health levels constant, lowering the risk of failure should theoretically imply a worse environmental outcome, and thus results in a decrease in utility under the EU assumption. Yet, under DR assumptions, it implies an increase in utility, because individuals dislike risk regardless of the associated outcome.

A systematic exploration of why the DR assumption (instead of EU or PT assumptions) describes the response behaviour in our study best is beyond our scope, but several explanations can be put forward. First, including risk as an independent attribute in DCE scenarios enables researchers to examine different model specifications, but at the same time such a design may lead respondents to treat risk separately from the associated environmental outcomes. Previous DCE studies with a separate risk attribute have also found that the DR specification fits the data better or equally well as other specifications (e.g. Glenk and Colombo, 2013; Lundhede et al., 2015). For studies where it is plausible and credible to assume outcome uncertainty and risk varying across policy alternatives, future researchers could design an experiment where the attributes of risk and environmental outcome are presented as one, but allowed to vary independently in the experimental design, and compare the results to those of a design where risk and outcome are presented as two separate attributes to assess the extent of this presentation effect. Second, research has found that heterogeneity in numeracy skills and knowledge about expected values explains part of the noise in risk preference elicitation studies (Dave et al., 2010; Taylor, 2016) and difficulties in comprehending risk information in DCEs (Kjær et al., 2018). In our experiment, not all respondents may have had the necessary resources (e.g. a calculator) to compute the expected values of each choice, and hence may not have behaved according to EU theory even if they wanted to. Therefore, a heterogenous decision rules may have been applied where those with good numeracy skills evaluate the outcomes together with their possibilities whilst those with lower numeracy skills may treat risk as a stand-alone attribute irrespective of the associated environmental outcomes. A number of studies propose several flexible modelling approaches based on the latent class framework where different behavioural rules are allowed to be adopted across different groups within the same sample (Hess et al., 2012; Daniel et al., 2018; Sandorf and Campbell, 2019), which can be a potential direction for future research on mixed behavioural rules in risky choices. For future research aiming to better understand what behavioural rules are adopted by respondents when risk is incorporated in a DCE, we also suggest using simple follow-up questions to elicit respondents’ information processing strategies. Another promising approach is to use eye-tracking technology, by which respondents’ eye movements (e.g., saccades directions) can be recorded and analysed (Krucien et al., 2017; Ryan et al., 2018).¹⁷

We cannot rule out the possibility that due to the complexity of our experimental design (i.e., allowing for both improvement and deterioration in air quality outcomes), respondents may have experienced cognitive difficulty and used heuristics to process the information in the attributes and hypothetical scenarios, leading them to assess the associated risk levels in a more parsimonious way (Visschers et al. 2009). We find that the mean score of the self-reported survey difficulty variable suggests that in general the perceived complexity of the survey is close to normal levels (i.e., the mean score of this Likert scale question is 3.002, with Level 3 meaning “neither too easy nor too difficult”), yet we acknowledge that about one third of the respondents are located at the right side of the mean (i.e., consider the survey as either “a bit difficult” or “very difficult”). The relationship between choice complexity (represented by number of attributes/levels/alternatives) and WTP/error variance has been investigated in the DCE literature (Caussade et al. 2005; Hensher, 2006; Boxall, et al., 2009; Rolfe and Bennett, 2009), yet the findings do not show a clear pattern. There is also no agreement on the effect of self-reported experimental complexity on choice behaviour. Intuitively, perceived difficulty could be an indication of misunderstanding of the survey, yet it could also be an indication of a high willingness-to-engage in the survey (Burton and Rigby, 2012), and reported easiness of the survey maybe a manifestation of using heuristics. In addition, about one third of the respondents reported that they have ignored at least one of the attributes, among which the most important reason is that too many attributes needed to be considered during decision making, implying that cognitive burden may play a role in the selection of behavioural rules. Although applying a lognormally distributed cost parameter has reduced the WTP values, we acknowledge that our WTP estimates are still somewhat higher than some earlier SP studies on air pollution in China (Sun et al., 2016; Tang and Zhang 2015; Yin et al., 2018). However, only 12% of the total respondents reported to have ignored the cost-attribute in the choice tasks; much lower than the inferred cost non-attendance in some DCE studies (Scarpa et al., 2009; Campbell et al., 2011), suggesting that some common explanations (e.g., non-attendance to the cost attribute) behind inflated WTP values do not seem to be an issue for the present study. We also acknowledge that sampling bias may affect the generalisability of our findings to the population level. Our sample is younger and more educated relative to the general public in the study area, yet education and age have been found to be correlated with individuals’ environmental preferences (Birol et al., 2006; Ruto and Garrod, 2009). Thus, estimates of environmental preference (and hence WTP) in this sample are potentially larger than those among the general public in Beijing. Therefore, although the objective of the study is investigating risk perceptions with different model specifications, one should be cautious about taking our welfare estimates at face value. WTP estimates may also relate to how the cost attribute is defined and future research could explore different ways of setting cost levels. One option would be to calculate the expenditure needed to achieve given health and visibility outcomes by implementing given policies using different technologies.

We find that the coefficients of the risk attribute differ in magnitude between the two domains for the Pure-DR specification, where respondents put higher weight on the risk attribute in the gain domain. Our posterior analysis to assess the determinants of the asymmetric outcome-related risk perceptions under the direct risk aversion assumption suggests that rejecting air quality deterioration is found to significantly affect the asymmetric risk perceptions. A possible explanation is that trade-offs in the loss domain, where the environment is sacrificed in return for monetary compensation, trigger moral outrage or decision difficulties (Tetlock et al., 2000; Hanselmann and Tanner, 2008; Zaal et al., 2014; Daw et al., 2015), especially among respondents who find environmental losses unacceptable and do not consider options in the loss domain.

Overall, this study incorporates scenario uncertainty associated with air quality outcomes into the DCE and extends the investigation of outcome-related risk perceptions to both the gain and the loss domains. The results show that respondents have a preference to reduce the risk of the outcomes of air pollution policy, and this preference is independent of the associated environmental outcomes (i.e., direct risk aversion). Under the assumption of risk neutrality, where a utility maximiser only cares about the expected outcomes of the policy, ex post welfare estimates can be calculated as the elicited welfare estimates multiplied by the probabilities, and the presentation of probability in the survey is irrelevant. Yet, the results of this study imply that the risk of outcome delivery itself is important to respondents when making choices. Therefore, the information of risk should be included in the stated preference design.

DCE practitioners should strive to generate policy-relevant results based on multiple model specifications when outcome-related risk is incorporated in choice scenarios and plausible to be assumed varying across policy alternatives. Whilst, in the present study, the direct risk behavioural rule performed best, it is important to understand that the best-fit specification can vary depending on the experimental designs and context (e.g., how risk is incorporated and described in the DCE design), and therefore a one-size-fits-all solution might not possible. From a policy perspective, the extent to which a different behavioural assumption leads to a difference in WTP should also be considered in addition to model fit—a best-fit model may have little advantage against an alternative model if the WTP difference is marginal. Therefore, presenting WTPs guided by different behavioural rules forms a range of welfare estimates within which “true” WTP is expected to lie. More importantly (but rarely discussed in environmental studies), more ex-ante efforts should be made to provide respondents with a step-by-step description of the role of risk in choice scenarios at the stage of experimental design (see Harrison et al., 2014; Vass et al. 2019, 2020 for risk communication in DCE studies).

Appendices

Appendices

Appendix A.1: Robustness Checks

2.1 A1.1 Additional Test for Non-Nested Models

We also use J-test (Davidson-MacKinnon, 1981) to compare the model fit of the Pure-DR and EU models. Results from the J-test suggest that the Pure-DR model fits our data better. The fitted values term from the Pure-DR model has significant impact as a covariate in the EU model, whilst it is not the case for the opposite test.

2.2 A1.2 Different Distributional Assumptions for the Random Parameters

We test whether the Pure-DR specification also performs better when imposing other distributional assumptions (i.e., log-normal, symmetric triangular and Johnson SB) on the health and risk attributes instead of a normal distribution. In summary, the results indicate that for models that successfully converged, the Pure-DR specification still outperforms the other models. A detailed summary is as the following: (a) symmetric triangle distribution generally gives a poorer model fit; (b) models under the log-normal distribution or Johnson SB distribution are often impossible to converge, and when converged in a few cases, the model fit of these models are worse than that with a normal distribution.

2.3 A1.3 Non-Linear Value Function specifications

We estimate an additional parameter for the health attribute in the EU specification in the gain domain to account for nonlinearity. A power functional form is used to measure the concavity of the value function, which is calculated as $\frac{({{\mathrm{H}}^{\mathrm{imp}})}^{1-{\alpha }}}{1-{\alpha }}$ (Holt and Laury 2002). ${\alpha }$ >0 indicates a concave value function and ${\alpha }$ =0 indicates linear value function. The results suggest that ${\alpha }$ =0.36, not significantly different from 0 (p.value > 0.1), and the model fit (BIC = 6004) is still worse than the Pure-DR specification.

We also test if allowing for nonlinearity in the value function counterbalances the effect of the independent risk by adding an independent risk attribute in the non-linear EU specification in the gain domain, as suggested by Glenk and Colombo (2013). The results show that the independent risk attribute is still significant (p.value < 0.01). Additionally, we estimate a PT specification with non-linear health attribute specification in the gain domain. The results show a slightly concave value function (α = 0.38; but insignificantly different from zero) and an inverse-S shape weighting function (γ = 0.44) with the BIC value equalling to 5985. The model fit of the non-linear PT (gain)-DR(loss) specification is similar to its linear counterpart, yet outperforming the one for the Pure-DR specification. We also find that if adding an additional independent risk attribute in the non-linear PT (gain)-DR(loss) specification, the risk attribute is still significant (p.value < 0.01). These results suggest that whether specifying the value function as linear or non-linear does not affect our conclusion that Pure-DR specification has the best statistical performance in our study.

2.4 A1.4 Partial Expected Utility Models Specifications and Results

In addition to the traditional expected utility theory specification, respondents may also consider attributes with partial expected utility (Partial-EU) assumption, or a Partial-EU-PureDR model in which a combined EU and Pure-DR specification is assumed (Rolfe and Windle, 2015).

In research question 1, the utility functions of a Partial-EU and a Partial-EU-PureDR models are specified in eq. (A.1) and (A.2) respectively.

$${\mathrm{v}}_{\mathrm{nit}}={\upbeta }_{\mathrm{HR}}^{\mathrm{imp}}({\mathrm{H}}_{\mathrm{nit}}^{\mathrm{imp}} * {\mathrm{R}}_{\mathrm{nit}}^{\mathrm{G}})+{{\upbeta }_{\mathrm{HR}}^{\mathrm{det}}(\mathrm{H}}_{\mathrm{nit}}^{\mathrm{det}} * {\mathrm{R}}_{\mathrm{nit}}^{\mathrm{L}})+{\upbeta }_{\mathrm{H}}^{\mathrm{imp}}{\mathrm{H}}_{\mathrm{nit}}^{\mathrm{imp}}+{{\upbeta }_{\mathrm{H}}^{\mathrm{det}}\mathrm{H}}_{\mathrm{nit}}^{\mathrm{det}}+{\upbeta }_{\mathrm{V}}{\mathrm{V}}_{\mathrm{nit}}+{\upbeta }_{\mathrm{C}}{\mathrm{C}}_{\mathrm{nit}}$$

(A.1)

$${\mathrm{v}}_{\mathrm{nit}}={\upbeta }_{\mathrm{HR}}^{\mathrm{imp}}({\mathrm{H}}_{\mathrm{nit}}^{\mathrm{imp}} *{\mathrm{ R}}_{\mathrm{nit}}^{\mathrm{G}})+{{\upbeta }_{\mathrm{HR}}^{\mathrm{det}}(\mathrm{H}}_{\mathrm{nit}}^{\mathrm{det}} *{\mathrm{ R}}_{\mathrm{nit}}^{\mathrm{L}})+{\upbeta }_{\mathrm{H}}^{\mathrm{imp}}{\mathrm{H}}_{\mathrm{nit}}^{\mathrm{imp}}+{{\upbeta }_{\mathrm{H}}^{\mathrm{det}}\mathrm{H}}_{\mathrm{nit}}^{\mathrm{det}}+{\upbeta }_{\mathrm{R}}^{\mathrm{G}}{\mathrm{R}}_{\mathrm{nit}}^{\mathrm{G}}+{\upbeta }_{\mathrm{R}}^{\mathrm{L}}{\mathrm{R}}_{\mathrm{nit}}^{\mathrm{L}}+{\upbeta }_{\mathrm{V}}{\mathrm{V}}_{\mathrm{nit}}+{\upbeta }_{\mathrm{C}}{\mathrm{C}}_{\mathrm{nit}}$$

(A.2)

where ${\mathrm{H}}_{\mathrm{nit}}^{\mathrm{imp}} * {\mathrm{R}}_{\mathrm{nit}}^{\mathrm{G}}$ and ${\mathrm{H}}_{\mathrm{nit}}^{\mathrm{det}} * {\mathrm{R}}_{\mathrm{nit}}^{\mathrm{L}}$ represent the interactions of the risk and health attributes in alternative i in the gain and loss domain, respectively. ${\mathrm{H}}_{\mathrm{nit}}^{\mathrm{imp}}$ and ${\mathrm{H}}_{\mathrm{nit}}^{\mathrm{det}}$ in Eq. (A.1) represent the additional independent health attribute in alternative i in the gain and loss domain, respectively. In Eq. (A.2), both additional risk and health terms are specified.

We expect that:

${\upbeta }_{\mathrm{HR}}^{\mathrm{imp}}>0, {\upbeta }_{\mathrm{HR}}^{\mathrm{det}}<0$ and ${\upbeta }_{\mathrm{H}}^{\mathrm{imp}}>0 , {\upbeta }_{\mathrm{H}}^{\mathrm{det}}<$ 0 for the Partial-EU1 model (in Eq. A.1).

${\upbeta }_{\mathrm{HR}}^{\mathrm{imp}}>0 , {\upbeta }_{\mathrm{HR}}^{\mathrm{det}}<0, {\upbeta }_{\mathrm{H}}^{\mathrm{imp}}>0 , {\upbeta }_{\mathrm{H}}^{\mathrm{det}}<0 , {\upbeta }_{\mathrm{R}}^{\mathrm{G}}>0\mathrm{ and }{\upbeta }_{\mathrm{R}}^{\mathrm{L}}>$ 0 for the Partial-EU-PureDR model (in Eq. A.2).

Any parameter sign contradicting our expectation implies that the estimated parameters for this utility specification are not consistent with their corresponding theoretical assumptions.

Results from Table 8 shows the interaction term (${\mathrm{H}}^{\mathrm{det}}\times {\mathrm{R}}^{\mathrm{L}}$) in the Partial-EU specification (model 2) and the interaction term (${\mathrm{H}}^{\mathrm{imp}}\times {\mathrm{R}}^{\mathrm{G}}$) in the Partial-EU-PureDR specification (model 3) imply inconsistency with theoretical assumptions as respondents should obtain utility when the expected health outcomes improve and obtain disutility when expected health outcomes deteriorate. As for the statistical performance, the smaller BIC value of the Pure-DR model (Pure-DR, model 1) compared with the Partial-EU and Partial-EU-PureDR model suggest that Pure-DR has the best model fit.

Table 8 Estimation results of the mixed logit models with partial expected utility specifications

In research question 2.1, the corresponding equations for the domain-asymmetric model according to the Partial-EU is presented in Eq. (A.3).

$${\mathrm{v}}_{\mathrm{nit}}={\upbeta }_{\mathrm{HR}}^{\mathrm{imp}}({\mathrm{H}}_{\mathrm{nit}}^{\mathrm{imp}} * {\mathrm{R}}_{\mathrm{nit}}^{\mathrm{G}})+{\upbeta }_{\mathrm{H}}^{\mathrm{imp}}{\mathrm{H}}_{\mathrm{nit}}^{\mathrm{imp}}+{{\upbeta }_{\mathrm{H}}^{\mathrm{det}}\mathrm{H}}_{\mathrm{nit}}^{\mathrm{det}}+{\upbeta }_{\mathrm{R}}^{\mathrm{L}}*{\mathrm{R}}_{\mathrm{nit}}^{\mathrm{L}}+{\upbeta }_{\mathrm{V}}{\mathrm{V}}_{\mathrm{nit}}+{\upbeta }_{\mathrm{C}}{\mathrm{C}}_{\mathrm{nit}}$$

(A.3)

Results in Table 8 show that the coefficient of the ${\mathrm{H}}^{\mathrm{imp}}$ in the PartialEU (gain)-PureDR(loss) model (model 4) is not significant at 5%, and thus do not conform to their corresponding theoretical assumptions. In terms of model fit (measured by BIC values), the Pure-DR model (model 1) still fits the data better.

2.5 A1.5 Asymmetric Visibility or Cost Specification

In the main text, we assume an asymmetric specification for the health attribute. Here, we test whether allowing for an asymmetric specification for visibility or cost attribute affects the conclusion that Pure-DR performs the best. Results suggest that under either asymmetric visibility or asymmetric cost assumption, the Pure-DR specification still outperforms the other models. Therefore, we keep simple linear term for visibility and cost for all models. We observe that for a given model specification, allowing for gain–loss asymmetry for the visibility or cost attribute improves the model fit in some cases. The phenomenon of gain–loss asymmetry (i.e., loss aversion) has been found in some environmental studies and is related to the interpretation of the welfare estimates of the relevant attributes (Glenk, 2011; Ahtiainen et al. 2015). Therefore, although this is not the main concern of this study, future research may accommodate gain–loss asymmetry when future policies imply the possibility of either environmental improvements or deteriorations.

Appendix A2: Estimated Probability Weighting Function

See Fig. 3.

Appendix A3: Results of Hybrid Choice Model

In the measurement equations, three attitudinal questions, namely a variable representing self-reported difficulty of the experiment (Survey difficulty), a variable representing the self-reported ignoring of the risk attribute (Ignore risk) and a variable representing the self-reported acceptance of air quality deterioration scenarios (Not accepting air deterioration) is associated with latent variable 1, latent variable 2 and latent variable 3, respectively. The attitudinal answers are modelled as ordered logit model, in which K-1 thresholds parameters are estimated, with K being the number of levels of each attitudinal question. In the structural equation, latent variable is related associated with a set of socio-demographic variables, which are age, income and education level. An error term following a normal distribution is also included in the equation to reflect random disturbance. In the discrete choice model, the alternative specific constant term is set as normally distributed (using 500 Halton draws) to allow for correlation across alternatives, whilst attributes are non-random (i.e., an error component logit model) (Table 9).

Table 9 The results of hybrid choice model