A Cap-and-Trade Commitment Policy with Allowance Banking

Abstract

We examine the planner’s dynamic regulation problem in an emission trading system (ETS) with allowance banking. The planner sets the emissions cap for the next period after the current period allowance market has cleared, but before knowing the next period’s abatement cost realization. This creates a time consistency problem when banking is possible. We examine two policies to overcome the consistency problem: a commitment solution and the Markov perfect solution. We show that the endogenous price floor generated by the banking demand becomes an integral feature of the two policies. Hence, they can be best described as hybrid policies that combine elements from emissions taxes and tradable allowances. This reveals new welfare implications that have an influence on instrument choice in the traditional prices versus quantities setup. We compare the expected welfare outcomes of four different policy instruments: the commitment policy, the Markov policy, a Pigouvian tax, and a no-banking ETS. We show that allowing banking can yield welfare gains compared to tax and quantity regulation, with or without commitment.

1 Introduction

The relative performance of price and quantity policies in the presence of abatement cost uncertainty has been an active area of research since Weitzman’s (1974) seminal paper. In the canonical form, the regulator has to set the policy before the realization of the cost shock and rank the alternative instruments, e.g. a Pigouvian tax or an emissions quota, based on their expected welfare performance. Whether one instrument dominates over the other depends on the relative slopes of the marginal benefit and marginal damage curves. Such an information structure provides a relatively accurate description for many real world policies, such as those in the European Union Emissions Trading System (EU ETS), where the regulator must set the cap for the next regulation period before knowing the true abatement cost realization.

To complicate matters, banking of allowances is also a typical feature of emission trading systems. Using a two-period model setup, the prices versus quantities approach has been applied to determine the conditions for intertemporal trading of allowances, i.e., banking and borrowing, to improve expected welfare relative to taxes and no-banking cap-and-trade systems (Yates and Cronshaw 2001; Feng and Zhao 2006; Weitzman 2018).¹ The conclusions from these studies seem somewhat surprising: banking and borrowing can improve the expected welfare outcome only if the regulator uses intertemporal trading ratios which are designed to modify the rate of return of banked allowances.² However, such trading ratios are not explicitly used in real world policies. Instead, emission trading systems impose restrictions on borrowing of allowances from future allocations. This creates a policy and theory challenge since it is not fully known how the cap should be set when only banking (saving) of allowances is possible but borrowing is not, and how such restrictions influence the welfare ranking of policies in the prices versus quantities setup.

The purpose of our paper is to solve the dynamic policy rules for setting the periodic cap when the regulation problem has an infinite horizon and when banking of allowances is possible (but not borrowing), and to evaluate the welfare performance of the alternative rules. The policy rules are derived from the regulator’s goal of maximizing the net present value of net benefits from the emissions, given that the regulator can set the cap for each period after observing cost realization in the previous period. We use the regulation of flow pollutants as our policy example, with the steepness of marginal damages allowed to vary to represent different pollutants. We furthermore use a simple IID shock process to capture the perpetual uncertainty in marginal benefits which gives rise to stochastic allowance demand and, hence, creates an incentive and opportunity for banking.

Banking of allowances complicates the regulation problem in two important ways in the infinite horizon prices versus quantities setup. First, it raises the question of time consistency of the policy plan, which stems from the information structure of the regulation game (Lintunen and Kuusela 2018). Namely, the decision to save allowances depends on the expectations of the allowance price in the next period; however, the next period’s allowance price depends on the regulator’s cap decision which is set after the banking decision has been made. Hence, before actually deciding the cap for the next period, the regulator may want to directly influence the price expectations to further control the emissions outcome in the current period. However, such a policy is not time consistent since the regulator may have an incentive to deviate from the plan at some subsequent point in time (Groot et al. 2003). To credibly steer the price expectations, the regulator has to be able to commit to the cap rule.

Second, the presence of banking motives separates the allowance market realizations into two distinct contingencies: one where the emissions cap is binding and one where it is not. By a binding cap, we refer to a market outcome where all available allowances are used in the current period and hence no allowances are saved to be used in the subsequent period. A non-binding cap refers to a situation where some share of the available allowances are banked and not used in the current period. Whether the cap binds or not in any given period will be a stochastic outcome that is influenced by the regulator’s policy and by the strength of the banking demand. While the possibility of a binding cap may first seem unlikely, we show that these two possible outcomes are integral features of the regulator’s dynamic policy rules. In fact, the dynamic adjustments to allowance injections prevent the accumulation of allowance surpluses and hence support the possibility of binding outcomes.³

The main contribution of our paper is to derive a policy rule that relies on the regulator’s ability to commit to a cap in the presence of allowance banking demand, and to compare its welfare performance to three alternative policy instruments. The first alternative is the time consistent policy rule with banking, which we formulate as a purely forward looking Markov perfect solution. Markov policy is consistent by definition since the regulator’s policy is conditional only on the current state of the regulation game (e.g. Groot et al. 2003). We show that the regulator’s commitment solution and the Markov solution differ mainly in the way they account for possible shock contingencies. The commitment regulator takes into account all shock contingencies, whereas the Markov regulator simply disregards the non-binding shock contingencies when choosing the optimal cap. Hence, the commitment policy provides a better expected welfare outcome since the regulator controls both binding and non-binding market outcomes. The two other alternative instruments are an emissions tax and a cap-and-trade without banking.

The regulator’s credibility and the ability to commit to a policy rule, or lack thereof, have been identified as important determinants of environmental policy outcomes (Helm et al. 2003; Brunner et al. 2012; Ulph and Ulph 2013; Jakob and Brunner 2014). In studies of banking and borrowing, on the other hand, the regulator’s commitment has been an explicit, but often overlooked, assumption (Yates and Cronshaw 2001; Newell et al. 2005; Feng and Zhao 2006). Lintunen and Kuusela (2018) have recently characterized the consistent policy in a cap-and-trade system with banking that is subject to persistent business cycle shocks.⁴ However, their results focus on the constant marginal damage case, where the Pigovian tax is always preferable to a quantity-based instrument, and they do not solve the model with commitment. The present paper focuses on the general case where marginal benefits and damages are important determinants of the welfare ranking of the different environmental policies. The above features also set our paper apart from a related body of research on credibility and commitment in environmental policies (Ulph and Ulph 2013; Jakob and Brunner 2014). Most importantly, the role of banking has not been included in previous studies focusing on policy commitment.

Banking of allowances can be understood as a form of forward-looking, speculative storage (e.g. Wright and Williams 1982; Deaton and Laroque 1992). We show that, given the presence of banking motives, the commitment and Markov rules generate a “hybrid policy” with both price and quantity features. The resulting “policy locus” has a form of an inverted L-shape, with the discounted expected price determining the horizontal part and the cap determining the vertical part. The horizontal part forms an endogenous price floor which becomes an essential feature of the dynamic policy rules. The advantage of hybrid policies has been recognized and modeled at least since Roberts and Spence (1976) and Weitzman (1978). This literature typically finds that hybrid policy instruments, by combining elements of price-based and quantity-based regulation, can improve the expected outcomes from regulation (Pizer 2002; Grüll and Taschini 2011; Mandell 2008; Burtraw et al. 2010; Fell and Morgenstern 2010; Wood and Jotzo 2011; Fell et al. 2012a). Previous research has recognized that banking of allowances for future use is another form of a safety valve (Newell and Pizer 2003a; Newell et al. 2005).⁵ However, a formal analysis of the optimal hybrid policy with endogenous price floor is missing in the prices versus quantities literature.

Recently, Weitzman (2018) finds using a two-period model with additively separable damages that it is never optimal to allow banking and borrowing of allowances, since either a tax or a cap without intertemporal trading is always more efficient. Feng and Zhao (2006) show that the option to bank and borrow allowances enhances welfare when the marginal benefits are steeper than the marginal damages. However, for this result to hold requires the design and use of intertemporal trading ratios. In contrast to these studies, we demonstrate that a cap-and-trade system with banking but no borrowing can in fact dominate alternative policy instruments, even without such trading ratios. This occurs in pollutant cases where the marginal benefits and marginal damages have similar slopes in absolute terms. Such dominance holds for both the commitment rule and the time consistent Markov policy. The difference of our results in comparison to previous findings is explained by the non-linear policy locus in our model that can mimic the marginal damage function better than simple price and quantity instruments. The welfare effect of allowing banking but not borrowing has also been analyzed in a related paper by Fell et al. (2012b). They conduct a welfare analysis based on optimal firm decisions under uncertainty while the allowance allocation path, i.e. the emissions cap, is exogenously given. We depart from this by identifying and solving the regulator’s periodic allowance allocation rule both with and without commitment.

Using quadratic benefit and damage functions, we demonstrate how the optimal banking policies operate and highlight the important determinants of the policies, such as the discount rate and the degree of uncertainty in the shock process. For example, we show that the commitment solution tries to keep the expected emissions at the same level as an optimal tax or a cap-and-trade policy without banking. Our welfare comparisons reveal that the banking policy with commitment is never the worst instrument (but in some instances equally bad as the worst alternative), whereas the Markov policy can become the worst instrument when marginal damages have a steep slope and the discount rate is small. Our results demonstrate the value of commitment which is defined as the welfare advantage of the commitment solution over the Markov solution. Finally, we also show that the commitment cap is greater than the Markov cap in certain contingencies but smaller in others.

While we do not focus on analyzing any particular emissions trading system, our modeling work and results provide useful information for interpreting and guiding the developments of real world systems, such as the EU ETS. Recent changes in the EU ETS have emphasized and strengthened rule-based approaches to adjusting the cap in response to business cycle fluctuations (Perino and Willner 2016; Perino 2018).⁶ In principle, such rules function similarly to our dynamic policies. Given the absence of allowance price targets in the EU ETS, such new rules can be characterized to bear more resemblance to the Markov policy in our paper than to the commitment policy. Our results suggest that the value of commitment becomes greater when the market discount rates are low (or when the compliance period is short) and when the degree of uncertainty around the demand shock is high, i.e., when banking demand is expected to be strong.

The rest of the paper is organized as follows. Section 2 first presents a model of speculative banking demand, followed by the regulator’s dynamic policy with and without commitment. Section 3 presents and derives the optimal no-banking cap policy and the emissions tax policy. Section 4 demonstrates and compares the performance of the different instruments using quadratic benefit and damage functions. Section 5 provides a discussion and conclusions.

2 ETS with Banking

2.1 The Setup

Consider a polluting industry that causes aggregate emissions, $q_t$, as a byproduct in each period t. The firms in the industry can reduce their emissions, but only at a cost. Since avoided abatement is associated with higher profits, we define an aggregate profit function, $B(q_t,\theta _t)$, that is strictly concave in the level of emissions.⁷ Profits from avoiding abatement are subject to random shocks, $\theta _t$, that represent fluctuations impacting the demand for the industry’s products, or random variation in the cost of polluting inputs.⁸ We let high shock realizations lead to higher marginal profits, $B_{q\theta }>0$, where subscripts indicate partial derivatives. This means that the cost of abatement is also varying from one period to another. In the absence of regulation the aggregate emissions correspond to the profit maximizing level of production, which we define here via the first-order condition $B_q(\bar{q}_t,\theta _t)=0$. Unregulated emission, $\bar{q}_t$, are higher when the shock realization is high, and lower with low shock realizations. To keep the model as simple as possible, we assume that the periodic shocks are identically and independently distributed (IID).

Emissions cause environmental damages denoted by an increasing and convex damage function $D(q_t)$. These damages represent a classic externality problem. Using a chosen policy instrument, the regulator’s objective is to maximize the expected net present value of welfare that comprises of the industry’s profits net of the emission damages:

$$\begin{aligned} \mathbb {E}_{0} \sum _{t=1}^\infty \beta ^{t} \left[ B(q_t,\theta _t) - D(q_t) \right] , \end{aligned}$$

(1)

where β=(1+r)⁻¹ is the discount factor and r the periodic discount rate. The main policy instruments of interest are the quantity based ETS with and without banking, and an emissions tax. In this section, we develop a model of an ETS with banking. The next section develops the optimality conditions for emission taxes and for an ETS without banking. For each policy instrument, the timing of actions is as follows. At the end of each compliance period, t, the regulator sets the policy level (a tax or a cap) for the next period $t+1$ before observing the next shock realization $\theta _{t+1}$, but after the realization of $\theta _t$. In the beginning of period $t+1$, the firms under regulation observe the period $t+1$ shock and make their abatement decision. With this timing of actions, each time period could be interpreted to mean the time segment between cap setting decisions and not the actual trading periods (i.e. phases in ETS terminology), in case they do not coincide.⁹ In what follows, we first derive the industry’s emission response, and then in the following subsections, we derive the optimal policy rules that are subject to the emissions response.

2.2 Allowance Market Response

Under an ETS policy, scarcity of allowances generates a market price, $p_t$. To comply with the policy, each firm in the industry has to surrender enough allowances to cover its emissions at the end of each compliance period, t.¹⁰ We call this demand as the allowance compliance demand to distinguish it from speculative banking demand. The amount of emissions, and hence the level of compliance demand, is given as a solution to the following problem

$$\begin{aligned} \max _{q_t} B(q_t,\theta _t) - p_t q_t. \end{aligned}$$

(2)

The compliance demand for allowances, $q_t=q(p_t,\theta _t)$, is implicitly given by the first-order condition

$$\begin{aligned} B_q(q_t,\theta _t) - p_t = 0. \end{aligned}$$

(3)

To model banking of allowances for future use, we introduce speculative banking demand, denoted by $b_t$. Whether the speculators and producers are the same entities or distinct does not matter; the only critical requirement is that their expectations are rational (Williams and Wright 2005). The decision to bank allowances depends on the following intertemporal arbitrage condition:

$$\begin{aligned} b_t\ge 0, \qquad -p_t + \beta \mathbb {E}_t p_{t+1} \le 0 \qquad {\text{and}} \qquad (-p_t + \beta \mathbb {E}_t p_{t+1})b_t=0. \end{aligned}$$

(4)

This arbitrage condition means that when the expected present value of the next period’s allowance price, $\beta \mathbb {E}_t p_{t+1}$, is lower than the current allowance price, banking is not profitable and hence $b_t=0$. If the opposite holds, banking becomes profitable, and $b_t>0$. In the competitive equilibrium, all intertemporal arbitrage possibilities are fully exploited, with banking demand increasing the current allowance price until the second inequality in (4) holds as an equation, $p_t = \beta \mathbb {E}_t p_{t+1}$. Since borrowing of allowances is not possible, the amount of banked allowances can be zero or positive.

Banked allowances add to the available supply of allowances in the next compliance period. The regulator injects $I_t$ new allowances for period t, totaling in an allowance supply, $Q_t$:

$$\begin{aligned} Q_t := I_t + b_{t-1}. \end{aligned}$$

(5)

We refer to variable $Q_t$ as the periodic cap or the periodic supply of allowances. The market equilibrium condition can be written as

$$\begin{aligned} Q_t-q_t-b_t = 0, \end{aligned}$$

(6)

where the total demand is the sum of compliance and banking demands, $q_t+b_t$.

There are two possible types of market outcomes depending on the shock realization $\theta _t$. When the shock realization is high enough, the emissions will be equal to the periodic cap, $Q_t$. When the shock realization is low enough, the emissions will be less than the cap. The two outcomes are divided by a cut-off shock level ${\tilde{\theta }}_t$. We provide a formal definition for the cut-off shock in “Appendix 1” and discuss it in more detail when we derive the necessary condition for the commitment solution. More importantly, the way the market price is determined differs under the two outcomes. When the emissions are equal to the cap, $q_t=Q_t$ (the cap is binding), the allowance price is simply determined by the market equilibrium condition (3): $p_t=B_q(Q_t,\theta _t)$. When the cap is not binding, $q_t<Q_t$, there is positive banking $b_t>0$, and according to the speculative market rule (4), the current allowance price is equal to the present value of the expected allowance price in the next period, $\beta E_t p_{t+1}$. In this case, we call the resulting price level the non-binding price. Compliance use of allowances, and hence the emissions, is then given by $q(\beta E_t p_{t+1},\theta _t)$.

The market’s emissions reaction function to the cap $Q_t$ can be defined in a compact form as:

$$\begin{aligned} q_t={\hat{q}}(Q_t,\mathbb {E}_t p_{t+1},\theta _t) := \min \left\{ q(\beta \mathbb {E}_t p_{t+1}, \theta _t) , \, Q_t \right\} . \end{aligned}$$

(7)

The first part of the right-hand side refers to the outcome where the cap is not binding, and the second part to the binding outcome. This form of the reaction function will have an important effect on the optimal policy as will be seen in the next sections. The emissions reaction, ${\hat{q}}$, depends on the shock, $\theta _t$, the cap, $Q_t$, and the expected allowance price in the next period, $\mathbb {E}_t p_{t+1}$ (and also on the parameter $\beta$). We assume that these expectations are rational (Muth 1961). Before defining the rational expectations equilibrium, we first write the allowance price function in a more compact form:

$$\begin{aligned} p_t = \max \left\{ \beta \mathbb {E}_t p_{t+1} , \, B_q(Q_t,\theta _t) \right\} . \end{aligned}$$

(8)

The above expression simply summarizes the possibility of a binding and a non-binding price outcome.

Using the price function in (8), we define an equilibrium price function $p(Q_t,\theta _t)$ that is similar to Deaton and Laroque (1996) and Lintunen and Kuusela (2018), and that will depend on the allowance cap and on the shock realization:

Definition 1

A stationary rational expectations equilibrium is a price function $p(Q_t,\theta _t)$ implicitly defined as a solution to the functional equation

$$\begin{aligned} p(Q_t,\theta _t) = \max \left\{ \beta \mathbb {E}_t p(Q_{t+1},\theta _{t+1}) , \, B_q(Q_t,\theta _t) \right\} . \end{aligned}$$

(9)

The equilibrium conditions (7) and (9) are the optimal responses of the private agents to the emission regulation. They act as constraints in the regulator’s planning problem.

2.3 The Planning Problem

The regulator maximizes (1) by determining the optimal sequence of injections $\{I_t\}_{t=0}^\infty$. Each periodic injection decision is made under uncertainty as the allocation for period t is decided at the end of period $t-1$. The regulator observes the amount of banked allowances, $b_{t-1}$, and therefore can effectively decide the resulting supply of allowances (total cap), $Q_t = I_t + b_{t-1}$. The regulator’s problem hence becomes one of setting the sequence of optimal allowance caps, $\{Q_t\}_{t=0}^\infty .$

Using the reaction functions in (7) and (9), we can write the objective function (1) as:¹¹

$$\begin{aligned} \mathbb {E}_{0} \sum _{t=1}^\infty \beta ^{t} \left[ B\left( {\hat{q}}\left( Q_t,\mathbb {E}_t p\left( Q_{t+1},\theta _{t+1}\right) ,\theta _t\right) ,\theta _t\right) - D\left( {\hat{q}}\left( Q_t,\mathbb {E}_t p(Q_{t+1},\theta _{t+1}),\theta _t\right) \right) \right] . \end{aligned}$$

(10)

Notice that the net benefits in any period t depend on the current period cap $Q_{t}$, and on the next period cap $Q_{t+1}$ via price expectations. Since the caps are set sequentially, it is possible that the regulator that sets $Q_{t}$ and announces $Q_{t+1}$ at the end of period $t-1$ has an incentive to choose different $Q_{t+1}$ once the period t shock is observed. This raises a dynamic consistency problem (Kydland 1975; Groot et al. 2003; Lintunen and Kuusela 2018).

When $\theta _t$ is an IID shock process, the regulator’s cap setting problem remains identical from period to period. As a result, the regulator sets the same cap level for each period. However, the cap, $Q_t$, depends on the regulator’s ability to commit to the announced $Q_{t+1}$. To examine the effects of the ability to commit, we provide two solutions to the maximization of (10). The first one is a commitment solution, in which we assume that the regulator has the ability to commit to $Q_{t+1}$. The commitment solution is compared to a Markov solution, in which case the regulator cannot commit to $Q_{t+1}$. Instead, the regulator decides the cap, $Q_t$, with the understanding that the next period cap, $Q_{t+1}$, will be set with the same strategy in the next period. This Markov perfect equilibrium policy is time-consistent but inefficient compared to the policy with commitment.¹²

2.4 A Commitment Solution

In this section, we specify a periodic cap level that maximizes the objective function (10). We maintain that the regulator is able to commit and solve the commitment outcome.¹³ Such a commitment policy is interesting in at least two respects. First, it is very simple, consisting of a single cap for all periods. Second, it provides a welfare maximizing benchmark for the banking only regulation.¹⁴

From Eq. (10), it is evident that the anticipated choice of $Q_t$ has an effect on the equilibrium emissions in period $t-1$ via the expected allowance price, $\mathbb {E}_{t-1} p_t$. We can write the direct dependency between the cap and the expected price as $\mu (Q_t):=\mathbb {E}_{t-1} p\left( Q_{t},\theta _{t}\right)$ for all t where the price function is defined in Eq. (9). Hence, the regulator uses cap $Q_t$ to control both period t and $t-1$ emissions, where the latter effect works through the expectations channel. By applying the IID assumption, we can therefore write the regulator’s problem in the following two-period format using unconditional expectations:

$$\begin{aligned} \max _{Q_t} \mathbb {E} \left\{ \left[ B(q_{t-1},\theta _{t-1}) - D(q_{t-1}) \right] + \beta \left[ B(q_{t}, \theta _t) - D(q_{t}) \right] \right\} , \end{aligned}$$

(11)

where the equilibrium emissions are $q_{t-1} = {\hat{q}}(Q_{t-1},\mu (Q_t),\theta _{t-1})$ and $q_t = {\hat{q}}(Q_t,\mu (Q_{t+1}),\theta _t)$, with function ${\hat{q}}$ defined by Eq. (7). Due to the IID assumption, the above problem remains the same from period to period, and hence the solution to (11) defines a constant cap, $Q_t=Q$ for all periods.

For each period, the first-order condition to the regulator’s problem (11) is

$$\begin{aligned} \mathbb {E} \left\{ \left[ B_q({\hat{q}}(Q,\mu (Q),\theta ),\theta ) - D_q({\hat{q}}(Q,\mu (Q),\theta )) \right] \left[ \beta \frac{\partial {\hat{q}}}{\partial Q} + \frac{\partial {\hat{q}}}{\partial \mu }\frac{\partial \mu (Q)}{\partial Q} \right] \right\} = 0 . \end{aligned}$$

(12)

Hence, the optimal policy equalizes the expected values of marginal benefits and marginal costs, with additional “weighting” given by the partial derivatives inside the second square brackets. These partial derivatives capture the impact of the cap on the emissions. The first term inside the second square brackets represents the direct effect of the cap on next period’s emissions and it is therefore discounted. The second weighting term captures the regulator’s influence on the current price expectations. Its presence stems from the regulator’s ability to commit to the cap level even after observing the actual $q_{t-1}$ realization. In the next section, we show that the time-consistent Markov policy rule omits this term. Hence, the commitment policy rule (12) is not time consistent.

It can be shown that the term $\partial \hat{q} / \partial Q$ in condition (12) has a non-zero value only when the cap is binding, whereas the term $\partial \hat{q} / \partial \mu$ in the same condition has a non-zero value only when the cap does not bind (“Appendix 1”). The two outcomes (binding vs. non-binding) are separated by the cut-off shock $\tilde{\theta }$. The cut-off shock is endogenous and it is implicitly defined by the following condition which equalizes the binding and non-binding allowance prices:

$$\begin{aligned} B_q(Q,\tilde{\theta }) = \beta \mu (Q). \end{aligned}$$

(13)

Using the explicit forms of the partial derivatives $\partial \hat{q} / \partial Q$, $\partial \hat{q} / \partial \mu$, and $\partial \mu / \partial Q$ (“Appendix 1”), the first-order condition of the commitment solution (12) can be written using two distinct terms, one for each contingency. This is presented in the following proposition:

Proposition 1

The regulator’s optimal commitment policy, $Q^{C}$, satisfies

$$\begin{aligned}&P^C \frac{ \mathbb {E} \left[ B_q(Q^C,\theta ) - D_q(Q^C)| \theta>\tilde{\theta }^C\right] }{\mathbb {E} \left[ B_{qq}(Q^C,\theta ) | \theta >\tilde{\theta }^C\right] } \nonumber \\&\quad + (1-P^C) \frac{P^C}{1 - (1-P^C)\beta } \mathbb {E} \left[ \frac{B_q(\hat{q},\theta ) - D_q(\hat{q})}{B_{qq}(\hat{q},\theta )} |\theta \le \tilde{\theta }^C \right] =0, \end{aligned}$$

(14)

where $\tilde{\theta }^C$ is the cut-off shock level and $P^C$ the probability that the cap is binding.

Proof

“Appendix 1”. $\square$

The first part of the above condition is related to the expected marginal net benefit when the cap is binding, i.e., when the shock realizations are above the cut-off shock level $\tilde{\theta }^C$. This has a probability of $P^C$. The second part is related to the expected marginal net benefit when the cap is not binding, i.e., when the shock realizations are below the cut-off shock level. This has a corresponding probability of $1-P^C$. In the second term, the ratio $P/(1-(1-P)\beta )$ stems from the link between the emissions cap and the price expectations (see more details in “Appendix 1”). Additionally, both parts are weighted by the curvature term $1/B_{qq}$, which denotes the price sensitivity of compliance demand (Eq. (3)). We will see in the next two sections that the inclusion of the curvature term has similarities with the optimal tax policy, but it is redundant in the necessary condition of the Markov solution (19).

The equilibrium is fully specified by the emission cap $Q^C$, cut-off shock level ${\tilde{\theta }}^C$, and the expected price level $\mu ^C$. The expression for the expected price can be written as:

$$\begin{aligned} \mu ^C = ( 1 - P^C ) \beta \mu ^C + P^C \mathbb {E} \left[ B_q(Q^C,\theta _t) | \theta _t > \tilde{\theta }^C \right] . \end{aligned}$$

(15)

The probability of a binding cap, $P^C$, is defined as the probability of $\theta >{\tilde{\theta }}^C$, which is given by the function

$$\begin{aligned} P({\tilde{\theta }}^C):=\int _{{\tilde{\theta }}^C}^{\infty }{dF(\theta )}, \end{aligned}$$

(16)

where $F(\theta )$ is the cumulative distribution function of the random variable $\theta$. Equations (13)–(15) together with the definition in (16) determine the equilibrium solution of the commitment policy.

The expression in (15) states that the expected price is the sum of the expected non-binding and binding allowance prices, adjusted with probability weights. Note that the possibility for the cap to bind, $P^C>0$, is a requirement for positive equilibrium price expectation, $\mu ^C>0$. The equation (15) also highlights the hybrid nature of the policy. With probability $1-P^C$ the price is equal to the non-binding price level $\beta \mu ^C$. This is the endogenous price floor created by the speculative banking demand (Lintunen and Kuusela 2018). We illustrate this feature in Sect. 4 in more detail using quadratic functional forms.

2.5 The Markov Perfect Solution

Since the regulator sets $Q_t$ after the $t-1$ emissions have already been realized, any attempt to influence the expectations $\mathbb {E}_{t-1} p_t$ with $Q_t$ is susceptible to dynamic inconsistency.¹⁵ One solution around the consistency issue is for the regulator to simply disregard the expected price effect when deliberating the choice for $Q_t$. This results in a Markov perfect solution which is time consistent by construction. The market will also anticipate such a consistent policy. In the Markov perfect solution, the price expectations are determined in the equilibrium, and the regulator takes the expected price as given.

Denote the expected price by $\mu _{t}:=\mathbb {E}_{t-1} p\left( Q_{t},\theta _{t}\right)$. When the regulator takes $\mu _t$ as given for every period t, the maximization of (10) leads to the following period-by-period optimization problem:¹⁶

$$\begin{aligned} \max _{Q_t} \mathbb {E}_{t-1} \left[ B({\hat{q}}(Q_t,\mu _{t+1},\theta _t),\theta _t) - D({\hat{q}}(Q_t,\mu _{t+1},\theta _t)) \right] . \end{aligned}$$

(17)

Furthermore, since the shock process is assumed to be IID, there are no explicit linkages between subsequent periods. Hence, the conditioning can be removed from the expectation operator. This directly implies that there is one periodic cap level $Q_t=Q$ and a constant expected price, $\mu _{t+1}=\mu$, for all periods t.¹⁷ While the above problem looks relatively simple, the main complication arises from the equilibrium dependence of the price expectation, $\mu$, on the regulator’s policy, and vice versa.

Under the IID shock assumption, the first-order condition of (17) can be formally written as:

$$\begin{aligned} \mathbb {E}\left\{ \left[ B_q({\hat{q}}(Q,\mu ,\theta _t),\theta _t) - D_q({\hat{q}}(Q,\mu ,\theta _t)) \right] \frac{\partial {\hat{q}}}{\partial Q} \right\} =0, \end{aligned}$$

(18)

where emissions ${\hat{q}}$ are given by (7). As in the commitment case, the partial derivative $\partial \hat{q} / \partial Q$ differs between binding and non-binding contingencies. Hence, the approach to refining the condition in (18) is the same as in the commitment case. We formally state it in the following proposition.

Proposition 2

Suppose the shock process is IID. The regulator’s optimal Markov policy, $Q^{M}$, satisfies

$$\begin{aligned} \mathbb {E}\left\{ B_q(Q^M,\theta )|\theta >\tilde{\theta }^M\right\} = D_q(Q^M), \end{aligned}$$

(19)

where $\tilde{\theta }^M$ is the equilibrium specific cut-off shock level.

Proof

“Appendix 1”. $\square$

The above proposition is the same as in Lintunen and Kuusela (2018), but here we have derived it using the IID assumption. As can be seen from Proposition 2, the regulator chooses the Markov perfect cap to equate the marginal damages from emissions with the expected marginal benefits from emission, conditional on the cap being binding, and simply ignores the contingencies when the cap is not binding. Such a restricted attention to binding contingencies only is the key difference between the Markov and the commitment policies. Recall that in the commitment case the regulator consideres all contingencies (Eq. (12)).

The equilibrium Markov policy is determined by the same system of Eqs. (13) and (15), with the variables replaced by $Q^M$ and $\tilde{\theta }^M$, in combination with the condition (19). Since the optimal policy differs between the commitment solution and the Markov perfect solution, the level of the price floor will also differ in general. We show in Sect. 4 that the difference in the commitment and the Markov solutions has a distinct impact on the optimal cap levels and on the expected price level.

To summarize, the main difference between the commitment and Markov perfect policy is in the way the regulator accounts for possible shock contingencies. With the commitment policy, the regulator attempts to directly influence the expected price, $\mu$, by committing to a cap level $Q^C$ for all periods. Hence, in Proposition 1, the necessary condition assigns weight for both the binding and the non-binding contingencies. With the Markov perfect policy, the regulator disregards the explicit effect of the current cap, $Q^M$, on the expected allowance price. Therefore, the necessary condition (19) is not conditional on those shock contingencies that occur in the non-binding regime.

3 ETS Without Banking and a Pigouvian Tax

Even though there is no banking demand, we can still use the above framework to model the market reaction under the no-banking ETS policy. Replacing the intertemporal banking condition (4), we now have a similar type of a market equilibrium condition:

$$\begin{aligned} p_t\ge 0, \qquad Q_t-q_t\ge 0 \qquad {\text{and}} \qquad (Q_t-q_t)p_t=0. \end{aligned}$$

(20)

There are two possible market outcomes: either the emissions are equal to the periodic cap, $Q_t$ or the emissions are equal to the unregulated level of emissions, $\bar{q}_t$. The former case represents a binding cap and the latter a non-binding cap. In the non-binding case, the allowance price is zero. The current realization of the shock $\theta _t$ ultimately determines whether or not the cap is binding.

The cap is now equal to the number of injected allowances, $Q_t=I_t$. Using the same formulation as in Eqs. (7) and (8), the market’s emissions reaction function is now defined as

$$\begin{aligned} q_t = {\hat{q}}^{NO}(Q_t,\theta _t) := \min \left\{ \bar{q}_t , \, Q_t \right\} , \end{aligned}$$

(21)

and the current allowance price by

$$\begin{aligned} p(Q_t,\theta _t) = \max \left\{ 0 , \, B_q(Q_t,\theta _t) \right\} . \end{aligned}$$

(22)

The absence of speculative banking demand makes the market’s reaction function much simpler. Instead of an endogenously determined price floor $p_t=\beta \mathbb {E}_t p_{t+1}$, there is now a fixed price floor $p_t=0$. Typical of hybrid policies, even a price floor that is simply the non-negativity constraint can be useful in some situations.

The regulator again sets the sequence of optimal caps, $\{Q_t\}_{t=0}^\infty$. The regulator’s problem is essentially the same as in (17) since the only state variable is the exogenous shock. Although there is no banking demand, and hence no rational expectation equilibrium, we can use the same approach as in the banking case and derive the optimality condition (see “Appendix 1”). Hence, Proposition 2 continues to hold even under the no-banking policy. Notice that there is no commitment problem in the no-banking case since the speculative banking demand is absent. This is a standard result in situations where the follower’s current response does not depend on the leader’s decision in the next period (Basar and Olsder 1982). The non-binding regime now refers to outcomes where the allowance price is zero. We can define the cut-off shock value using the condition $B(Q^{N},\tilde{\theta })=0$. With IID shocks, the optimal cap will be constant.

Interestingly, the optimality condition is similar to the one in the banking case, but now the price floor is fixed at zero. The regulator again sets the optimal cap so that the expected marginal benefits conditional on a binding cap equal to the expected marginal damages. The intuition here is that the price floor forms a kink in the policy, and depending on the type of damages, the regulator can sometimes prefer an outcome where the cap is non-binding. For example, with flat marginal damages the non-binding price floor forms essentially a safety valve for the policy maker. In other words, the policy may not strictly fix emissions to be $q_t=Q$, but the emissions can also be lower. The same intuition holds with the banking policy case.

An emissions tax, $\tau _t$, sets an exogenous price per a unit of emissions. We can directly write the market’s emissions response function as $q_t=q(\tau _t,\theta _t)$, where the tax replaces the allowance price as the argument. The regulator decides the sequence of optimal emissions taxes, $\{\tau _t\}_{t=0}^\infty$. Since the only state variable is the exogenous shock, the problem of setting the optimal tax is sequential:

$$\begin{aligned} \max _{\tau _t} \mathbb {E}_{t-1}[ B(q(\tau _t,\theta _t),\theta _t) - D(q(\tau _t,\theta _t)) ]. \end{aligned}$$

(23)

The necessary first-order condition to this problem is:

$$\begin{aligned} \mathbb {E}_{t-1}[ B_q(q(\tau _t,\theta _t),\theta _t) q_\tau (\tau _t,\theta _t)] - \mathbb {E}_{t-1}[D_q(q(\tau _t,\theta _t)) q_\tau (\tau _t,\theta _t)]=0. \end{aligned}$$

(24)

From the market’s reaction, we have $B_q(q_t,\theta _t)=\tau _t$, and substituting in this expression, we get:

$$\begin{aligned} \tau _t \mathbb {E}_{t-1}[ q_\tau (\tau _t,\theta _t) ] - \mathbb {E}_{t-1}[ D_q(q(\tau _t,\theta _t)) q_\tau (\tau _t,\theta _t) ]=0. \end{aligned}$$

(25)

The above equation implicitly determines the optimal tax level, $\tau ^{*}$. Under the assumption of IID shock process, the optimality condition in (25) does not change from one period to another, and the optimal tax is constant. Term $q_{\tau }(\tau _t,\theta _t) = B_{qq}^{-1}(q_t,\theta _t)$ describes the changing curvature of the marginal benefit function.¹⁸ Tax policy enables simple solutions in two special cases: If the marginal damages are constant, $D_q(q) = d$ for all q, then $\tau ^{*} = d$, for each period as the curvature terms cancel out.¹⁹ If the benefit function is quadratic, the curvature term is constant and tax is implicitly determined by $\tau ^{*} = \mathbb {E}_{t-1} D_q(q(\tau ^{*},\theta _t))$.

4 Results

4.1 The Setup

As discussed in the previous sections, the presence of speculative banking demand creates an endogenous price floor $\beta \mu$. There are two critical parameters that influence the likelihood of banking demand. The first one is the intertemporal discount factor $\beta$. Speculators purchase allowances today only if the current price is low enough to justify non-negative expected profits in present value terms ($\beta \mu \ge p_t$). The smaller the discount factor (banking is costly), the less likely it is to witness a low enough shock realization that induces positive banking demand. The value of $\beta$ parameter depends on the type of speculators that are in the market, and it can also vary depending on the length of the compliance period. The second parameter is the degree of uncertainty inherent in the shock process, measured by the variance term $\sigma ^2$. This variability is linked to the likelihood of observing positive banking demand. When the distribution becomes tighter around the mean, the less likely it will be to observe positive banking demand, since sufficiently large negative demand shocks are less frequent. Hence, it again becomes less likely for speculators to buy allowances with the expectation of non-negative profits.

To examine the policies in more detail, we assume that the benefit and damage functions are quadratic polynomials, and that the IID shock process has a symmetric mean zero distribution. Formally, we assume linear marginal benefit

$$\begin{aligned} B_q(q,\theta ) = \theta + \bar{d} - |B_{qq}| (q-\bar{q}), \end{aligned}$$

(26)

and marginal damage functions

$$\begin{aligned} D_q(q) = \bar{d} + D_{qq} (q-\bar{q}), \end{aligned}$$

(27)

where parameters $D_{qq} \ge 0$ and $B_{qq} < 0$ denote the constant slopes of the marginal damage and the marginal benefit lines, respectively. Since $\mathbb {E}\theta =0$, the above specification can be understood as a quadratic approximation of arbitrary benefit and damage functions in the neighborhood of point (${\bar{q}}$, ${\bar{d}}$).

Given the above functional form assumptions, the Markov and the commitment solutions $(Q^M,Q^C)$ can be derived using the systems of equations as explained in previous sub-sections. Since $B_{qq}$ is constant, we are able to simplify the planner’s first-order conditions and write them in a more compact form:

$$\begin{aligned} \mathbb {E} \left[ B_q(Q,\theta ) - D_q(Q)| \theta >\tilde{\theta }\right] + \frac{1-P}{1 - (1-P)\beta } \mathbb {E} \left[ B_q({\hat{q}},\theta ) - D_q({\hat{q}}) |\theta \le \tilde{\theta } \right] I_{C}=0, \end{aligned}$$

(28)

where the indicator parameter $I_{C}=1$ for the commitment case and $I_{C}=0$ for the Markov case. For both solutions, the equilibrium is defined by the first-order condition (28), together with Eqs. (13), (15), and definition (16). Given the above solution structure, it is not possible to derive simple closed form expressions or measures for welfare differences, as is typically the case in prices versus quantities papers. We now turn to numerical policy solutions under differing parameter values to characterize and compare the different policy outcomes and to illustrate the effect of relative marginal slopes on policy outcomes.

4.2 A Comparison of Policies

There are six parameters of interest that determine the optimal policy: ${\bar{q}}$, ${\bar{d}}$, $\beta$, $\sigma$, $B_{qq}$, and $D_{qq}$. Parameters, ${\bar{q}}$ and ${\bar{d}}$, define the point where the marginal benefit and the marginal damage lines are expected to intersect. Under the linearity assumption, these two parameters are sufficient to define the optimal tax and the optimal emission cap when banking is not allowed, that is, $\tau = {\bar{d}}$ and $Q^N={\bar{q}}$, respectively (see Sect. 3).²⁰ However, the optimal cap in the two banking cases will also depend on the four other parameters $\beta$, $\sigma$, $B_{qq}$, and $D_{qq}$. In this subsection, we examine the effects of these four parameters on the banking policy outcomes. The next subsection examines their impacts on welfare.

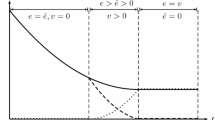
In the numerical solutions that follow, we use a normally distributed shock variable, $\theta _t \sim N(0,\sigma ^2)$. To keep our results comparable to previous studies (cf. Weitzman 1974; Feng and Zhao 2006), we start from a set of policy solutions where we vary the relative slopes of marginal damages and marginal benefits, $|D_{qq}/B_{qq}|$, while keeping the no-banking cap level and the emission tax level constant, at point (${\bar{q}}$, ${\bar{d}}$). In other words, the point of intersection for the marginal damage line and the expected marginal benefit line remains the same, even when we vary the steepness of the marginal damage line. These solutions are illustrated in Figs. 1 and 2 where we compare the non-linear policy loci under the commitment and Markov policies. The downward sloping blue lines represent the expected, $\mathbb {E}\theta =0$, marginal benefit function, i.e., compliance demand, and the red lines represent the different marginal damage functions (flat, intermediate, steep). High (i.e., above average) demand shock realizations lead to the marginal benefit function that is above the depicted blue line (see Eq. (26)). The opposite holds for low shocks.

Fig. 1

The three sub-figures in each row illustrate the commitment and Markov policies for different levels of marginal damages: $|D_{qq}/B_{qq}| \in \{0,1,10\}$ (in columns, respectively). In all sub-figures, the blue line represents the expected marginal benefit function and the red lines represent marginal damage functions. The slope of the marginal benefit line is held fixed at $B_{qq}=-1$. The black lines correspond to optimal policies under three different levels of discount factor. The optimal no banking cap $Q^N=0.5$ and optimal second best tax $\tau =0.5$ in all cases ($\bar{d}=0.5$ and $\bar{q}=0.5$). The shock is normally distributed, $\theta _t \sim N(0,\sigma ^2)$, with $\sigma =0.05$

In all sub-figures, the policy loci are the kinked black curves (inverted L-shape) and they illustrate the hybrid nature of the optimal policy. The horizontal part is the price floor, $\beta \mu$, and the vertical part is the cap, Q. Since the policy loci represent the supply of allowances for the compliant firms, the actual emissions and price realizations, $(q_t,p_t)$, are determined by the intersection of the relevant policy locus and the marginal benefit line realization. The deviations of emission realizations from the first-best emissions, which are determined by the intersection of the actual marginal benefit and damage lines, cause welfare losses. Therefore, the regulator will attempt to set the cap so that the resulting equilibrium policy locus approximates the marginal damage function as closely as possible.

The sub-figures in Fig. 1 illustrate the regulator’s optimal policy under three different scenarios of increasing severity of marginal damages (red lines) relative to the marginal benefits, $|D_{qq}/B_{qq}| \in \{0,1,10\}$. The first row of figures shows the commitment policy, and the second row the Markov policy. In the first scenario from the left, the ratio of marginal damages to marginal benefits is zero, representing a constant marginal damage function.²¹ In the second scenario this ratio is one, representing moderately increasing marginal damages, and in the third scenario, the ratio is 10, representing steeply increasing marginal damages. The inverted L-shaped curves represent optimal policy loci, each corresponding to a different level of the discount factor, $\beta$.

The first observation from Fig. 1 is that the Markov policy is very responsive to the steepness of the marginal damages. Both the cap and the price floor are changing across the sub-figures for a given discount factor. In contrast, the commitment policy is virtually identical across the subfigures for a given discount factor. This is an interesting feature of the commitment solution, and we will explain the reason behind this stability in more detail in our subsequent discussion. Under both policies, higher discount factor translates to a higher cap for a given marginal damage scenario.

The advantage of hybrid policies is commonly framed as their potential to more closely mimic the marginal damages than a simple price or a quantity instrument can. In the above setup, a tax or an emissions cap without banking would create horizontal and vertical policy loci, respectively, that would pass through the point (0.5, 0.5) (not shown). From the sub-figures, it can be seen that, with banking, the vertical part of the inverted L-shaped policy locus can indeed provide a better match for the marginal damage line than a simple tax would when the marginal damages are not flat. In turn, when the slope of marginal damages is moderate or low, banking can provide a better match for the marginal damage line compared to the no-banking case by introducing horizontal price-like part in the policy locus.

The closeness of the approximation seems to depend on the discount factor, especially in the case of the Markov policy. By inspecting the first sub-figure, it can be seen that a high discount factor is beneficial for the Markov regulator since the dotted line mimics the flat marginal damages most closely. By inspecting the third sub-figure, it can be seen that high discount factor provides the worst fit for the Markov regulator, as now the L-shaped policy locus resembles the marginal damages the least (in the next subsection, we measure the welfare outcomes in more detail). In other words, with pollutants associated with flat marginal damages, the presence of high banking demand (high discount factor) can be beneficial. With pollutants associated with steep marginal damages, the Markov regulator may actually prefer a low discount factor. The same observations continue to hold under the commitment policy, but the contrast to the Markov policy is significant. Especially in the case of steep marginal damages, the policy locus in these two policies follows a very different pattern. The commitment policy prescribes a higher cap level and a lower price floor, whereas under the Markov policy, the cap is smaller and the price floor is higher. We return to these observations shortly.

Fig. 2

The optimal policies are solved under the same setup as in Fig. 1. Here the black lines now correspond to the optimal policies under the three different levels of standard deviation. The discount factor is held fixed at value $\beta =0.975$

Figure 2 shows the impact of higher risk in the form of a wider shock distribution while holding the discount factor constant. The interpretation of the lines in all sub-figures is the same as in Fig. 1, except now each of the three kinked policies relate to a different standard deviation, $\sigma$. As can be seen, the Markov policy is again more responsive to the steepness of marginal damages and also to the shock variability, while the commitment policy remains stable across the sub-figures. The Markov regulator increases the cap (vertical line) in response to higher values of $\sigma$. The commitment policy does the same. However, under the commitment policy the price floor remains virtually the same in all sub-figures, indicating the same price expectations, $\mu$, despite the increase in shock dispersion. The change in the price floor is more pronounced under the Markov policy. In the first sub-figure in the second line, the Markov regulator actually increases the cap enough to lead to a decrease in the price floor. In other marginal damage scenarios, the responses are qualitatively the same as in Fig. 1.

Fig. 3

The effect of discount factor, $\beta$, on the policy outcomes under three different marginal damage scenarios. The shock dispersion parameter $\sigma$ is held fixed at value $\sigma =0.05$

Figure 3 presents the optimal caps $(Q^C,Q^M)$, the expected share of banking, $\mathbb {E}b/Q$, the expected emissions, $\mathbb {E}q$, and the expected allowance price, $\mathbb {E}p$, as functions of the discount factor $\beta$. The expression for the expected price under the commitment and the Markov perfect policy was given in Eq. (15).²² We again compare the outcomes under the three different fixed slope ratios ($|D_{qq}/B_{qq}| \in \{0,1,10\}$). In line with our above results, Fig. 3 shows that a greater discount factor leads to larger emissions caps. Under the Markov policy, the increase in the cap is much more pronounced with flat marginal damages than with steep marginal damages. The expected proportion of banking demand is also increasing in $\beta$, since the probability of observing a low enough shock realization is increasing as well ($\sigma$ is held constant).

Fig. 4

The effect of shock dispersion parameter, $\sigma$, on the policy outcomes under three different marginal damage scenarios. The discount factor is held fixed at value $\beta =0.975$

Interestingly, the response in the expected emissions, $\mathbb {E}q$, differs between the Markov and commitment policies. In the commitment case, the expected emissions are the same across the marginal damage scenarios, whereas in the Markov case, both the steepness of marginal damages and the discount factor clearly influence the expected emissions. These results suggest that in the commitment case the regulator chooses the cap so that the expected price and the emissions are (almost) identical to the tax level and the no-banking cap $(\tau =0.5,Q^N=0.5)$. The slope ratio $|D_{qq}/B_{qq}|$ does not affect the tax or the no-banking solutions and, in a correspondent way, we observe a similar outcome in the commitment case. However, we will show below that the correspondence is not straightforward. The critical difference is that the commitment solution actually depends on the steepness of marginal benefits. Hence, examination of the ratio of marginal damages to marginal benefits is not enough.

In the Markov case, the steepness of marginal damages does influence the expected emissions and the optimal cap. The explanation for this is the Markov regulator’s first-order condition that relies only on those shock realizations that are in the binding regime. This causes the steepness of the marginal damage curve to have an impact on the Markov cap. When the Markov cap is compared to the optimal no-banking cap ($Q^N=0.5$), we see that the steeper marginal damages result in lower expected emissions ($\mathbb {E}q<0.5$), whereas with flatter damages the expected emissions are higher ($\mathbb {E}q>0.5$).

Figure 4 presents the same outcomes as in Fig. 3 but now we have fixed the level of the discount factor and allow the variance of the shock term to change. The results are qualitatively similar to Fig. 3. In the next subsection, we will see, however, that the welfare effects of $\beta$ and $\sigma$ are not the same.

As alluded to earlier, the results in Figs. 1, 2, 3 and 4 seem to collectively suggest that the regulator’s commitment policy does not depend on the ratio of the slopes, $|D_{qq}/B_{qq}|$. However, in all these figures, we have fixed the slope of the marginal benefits to equal $B_{qq}=-1$. Hence, the role of the slopes is not yet fully explored. Figure 5 shows the impact of both parameters $B_{qq}$ and $D_{qq}$ on the commitment and Markov caps. Again, we set $({\bar{q}}, {\bar{d}}) = (1/2,1/2)$, which implies the same optimal tax and no-banking solutions as before. The left sub-figure shows that the optimal cap under the commitment policy is decreasing in parameter $B_{qq}$, but for a given $B_{qq}$, it does not respond to parameter $D_{qq}$. The right sub-figure contrasts the cap response under the Markov policy which can be seen to depend on parameter $D_{qq}$ as well.

Fig. 5

The effect of slope parameters $B_{qq}$ and $D_{qq}$ on the emissions cap Q in commitment and Markov policies. Here $\sigma =0.05$ and $\beta =0.975$

The explanation for this difference stems from the necessary condition of the planner’s problem (28). The first-order condition in the commitment case can be formulated as:

$$\begin{aligned}&(1-\beta )(1-P)\mathbb {E}\left[ B_q(Q,\theta )-D_q(Q)|\theta <\tilde{\theta }\right] \\&\quad +\mathbb {E}\left[ B_q(q(Q,\mu (Q),\theta ),\theta )-D_q(q(Q,\mu (Q),\theta ))\right] =0 \end{aligned}$$

The second term in the above equation is essentially the same first-order condition as in the case of the tax policy and the no-banking policy. The first term is typically close to zero when the discount factor is close to 1. On the other hand, when $\beta<<1$, the probability of binding cap should be fairly large since the price floor will be at a low level. Hence the term $(1-P)\approx 0$ when $\beta$ is small. As a result, the condition $\mathbb {E}(B_q-D_q)\approx 0$ is likely to hold for a large set of $\beta$ values (especially for the ones used in Figs. 1, 2, 3 and 4).²³

The above explains why we observed the expected emissions and the expected prices to be the same in the commitment case as in the tax and the no-banking cases. Furthermore, the steepness of marginal damages does not influence the cap level that achieves $\mathbb {E}(B_q-D_q)\approx 0$, since it is the intersection of the marginal benefits and the policy locus that determines the emissions outcome. However, the policy locus depends on marginal benefits, since the price floor depends on demand. Therefore, in response to different $B_{qq}$ parameter values, the commitment regulator has to adjust the cap to maintain an expected emissions outcome that still achieves $\mathbb {E}(B_q-D_q)\approx 0$.

4.3 Welfare Comparisons

To compare the social welfare (SW) outcomes under the alternative policy instruments, we define the ratio of the expected welfare loss relative to the expected welfare under a first-best policy ($SW^{*}$):

$$\begin{aligned} \frac{\mathbb {E}_\theta SW_{SB}-\mathbb {E}_\theta SW^{*}}{\mathbb {E}_\theta SW^{*}} \end{aligned}$$

(29)

This type of a welfare comparison has been common in the literature since Weitzman (1974). First-best policy means that the regulator can set the policy for period t after observing the shock realization, $\theta _t$.

In Fig. 6, we compare the relative expected social welfare under the four policy instruments with differing values of the discount factor, $\beta$. These results are based on the same solution setup as in Figs. 1, 2, 3 and 4. In other words, we are comparing the welfare outcomes under different slope ratios, $|D_{qq}/B_{qq}|\in \{0,1,10\}$, while keeping the point of intersection of the marginal damage and the expected marginal benefit lines fixed at $({\bar{q}}, {\bar{d}})=(1/2,1/2)$. Consequently, the no-banking cap and the emissions tax solutions remain the same. The difference in welfare outcomes between the Markov solution and the commitment solution can be understood as the value of commitment.

In Fig. 6, the welfare outcomes under the commitment and Markov policies are contrasted to a tax instrument (dotted line) and a no-banking ETS policy (broken line). The figure shows that 1) a tax is optimal when marginal damages are constant (left panel), 2) a no-banking policy is best when the marginal damages are much steeper than the marginal benefits, and 3) a tax and a no-banking policy perform equally well when the marginal benefits and marginal damages are equally steep (Weitzman 1974). The discount factor does not have an effect on these two policies, and hence the welfare outcomes remain constant within each sub-figure. In contrast, both of our banking policies respond to changes in the discount factor, and their welfare outcomes also vary when the discount factor changes. The value of commitment can be seen to be increasing in the discount factor.

Fig. 6

The effect of discount factor, $\beta$, on the social welfare outcomes relative to the first-best. Here, $\sigma =0.05$ and $B_{qq}=-\,1$

As explained before, the presence of banking demand creates an endogenous price floor in the regulator’s solution. Therefore, we expect the welfare outcomes with banking to lie between the tax and the no-banking outcomes most of the time. This is true when the marginal damages are flat (Fig. 6, left panel). In the case of steep marginal damages, this is true for the commitment solution (right panel). However, with steep marginal damages the Markov solution actually performs the worst as the discount factor approaches unity. This deterioration could be anticipated from the lower right panel of Fig. 1 since the Markov policy, which only considers the contingencies where the cap is binding, sets a relatively tight emissions cap. Together with the high discount factor, this leads to a relatively high expected allowance price and, consequently, to high price floor. As a result, the inverted L-shaped policy locus can mimic the marginal damages only with high demand realizations, and the realized intersections of the marginal benefit line and the policy locus are typically far above the expected intersection of the marginal benefit and damage lines; hence the poor welfare performance.

However, when the discount factor approaches unity in the case of flat marginal damages, the welfare outcomes with both banking policies approach the optimal tax regulation (cf. Fig. 1, left column). Thus, we can conclude from these observations that the introduction of banking in an ETS: (1) improves the welfare outcome when the marginal damages are flat, with the benefit increasing in the discount factor, and (2) deteriorates the welfare outcome when the marginal damages are steep.

As indicated earlier, the inverted L-shape of the policy locus can best mimic the marginal damages, when they are moderately sloped (cf. Fig. 1, middle column). The middle panel of Fig. 6 shows that this property can yield welfare gains when compared to the tax and no-banking policies. Again, a very high discount factor deteriorates the performance of the Markov policy, but in general, both banking policies yield a better welfare outcome than the tax and the no-banking case.

Fig. 7

The effect of shock dispersion, $\sigma$, on the social welfare outcomes relative to the first-best. Here, $\beta =0.975$ and $B_{qq}=-\,1$

Figure 7 compares the efficiencies of alternative policies when the degree of uncertainty is increasing while keeping the discount factor constant at $\beta =0.975$. The sub-figures show similar welfare rankings as in Fig. 6. The main difference is that an increasing shock dispersion leads to lower welfare in all cases (except when the tax is the first best policy). In contrast to the effect of an increasing discount rate in Fig. 6, the expected welfare of the two banking policies is decreasing in the shock dispersion. When the marginal damages are steep (right panel), the banking solutions experience significant deterioration as the shock dispersion increases. The Markov solution may actually become even worse than the tax policy. This is comparable to the case of a high discount factor (Fig. 6, right panel). In general, an increasing dispersion widens the welfare difference between the Markov and the commitment solutions. Hence the value of commitment becomes greater when the extent of the uncertainty increases.

Fig. 8

The effect of slope parameters $B_{qq}$ and $D_{qq}$ on the expected social welfare. Here $\beta =0.975$ and $\sigma =0.05$

Finally, in Fig. 8, we examine the effects of different slopes $B_{qq}$ and $D_{qq}$, like we did in Fig. 5. Each sub-figure shows the welfare outcomes under different marginal damage values conditional on four different levels of marginal benefit parameter, $B_{qq}$. The regions in the sub-figures where the Markov and the commitment curves are higher than either of the tax instrument or the no-banking curves, represent the values of $D_{qq}$ where banking is preferred to the alternative instruments, conditional on the given parameter $B_{qq}$. These results are also conditional on the chosen $\beta =0.975$ and $\sigma =0.05$.

Figure 8 replicates the well-known result for the condition that determines the choice between the tax and the no-banking quota instrument. The tax and the no-banking curves intersect at the point where $B_{qq}=D_{qq}$, and to the left of that point ($B_{qq}>D_{qq}$), the tax instrument dominates the no-banking instrument, and to the right ($B_{qq}<D_{qq}$), the opposite holds. The graphs show that there is typically a region around the point $B_{qq}=D_{qq}$ where the banking policies dominate both the tax and the no-banking cap policy. This differs from Feng and Zhao (2006, Proposition 2). They observe that with intertemporal trading ratio equal to unity, intertemporal trade (banking and borrowing) will decrease welfare if $D_{qq} > |B_{qq}|$. Figure 8 shows that it is possible that banking increases expected welfare even when $D_{qq} > |B_{qq}|$. Finally, the commitment policy is always better than the Markov policy. Under the chosen parameter values for $\beta$ and $\sigma$, the welfare difference (the value of commitment) between the two banking policies seems small in the region where banking is better than the tax policy and the no-banking cap policy.

4.4 Comparative Statics Results

To characterize the properties of the solutions, the standard approach is to derive comparative statics with respect to the model parameters. In the Markov case, we can directly study these comparative statics effects if we assume a uniform distribution $\theta \sim U[-\sigma ,\sigma ]$. In “Appendix 2”, we show that in this case the optimal cap is defined by a quadratic equation.²⁴ The comparative static results for the Markov solution are collected in the following proposition:

Proposition 3

Assume linear marginal benefit and damage functions,  (26) and (27), and a uniform shock distribution, $\theta \sim U[-\sigma ,\sigma ]$. The optimal cap $Q^M$ is increasing in the dispersion parameter $\sigma$ and in the discount factor $\beta$. Furthermore, the optimal cap is decreasing when either the marginal benefit line or the marginal damage line becomes steeper. The optimal cap is increasing in ${\bar{q}}$ and decreasing in ${\bar{d}}$.

Proof

Direct application of comparative statics. See “Appendix B.2” for details. $\square$

In the Markov case, the regulator responds to a greater demand variation ($\sigma$) and to a higher discount factor ($\beta$) by increasing the cap. The common element and explanation in these two cases is that the likelihood of banking demand is increasing in both parameters. The regulator responds to this higher likelihood by allocating more allowances into the market.

5 Discussion and Conclusions

5.1 Policy Implications and Relevance

Our results show that an ETS with banking but no borrowing of allowances can in certain situations outperform an emissions tax and a quantity instrument with no intertemporal trading. This is in contrast to some earlier findings with less favorable conclusions on the role of intertemporal trading of allowances (Feng and Zhao 2006; Weitzman 2018). Hence, from welfare perspective, there may very well be a justification for allowing banking in an ETS. In addition, banking motives can improve the welfare performance of quantity regulation when the marginal damages are relatively flat. Such a case provides a reasonable approximation for climate change related damages (Hoel and Karp 2002; Newell and Pizer 2003a). Thus, the possibility to bank allowances should be viewed as an useful feature in an ETS that regulates greenhouse gas emissions, at least when the regulator is also actively adjusting the emissions cap. However, with pollutants that have steep marginal damages, banking may undermine the welfare performance of a cap and trade scheme.

The comparisons between the commitment and Markov policies revealed that the welfare gain from commitment seems relatively modest. The largest welfare differences occur when the discount factor is close to unity and the allowance demand uncertainty is high. In such situations, the regulator benefits from commitment and is worse off from using the Markov policy. One policy relevant question is whether commitment, as it is defined in our paper, is easily achieved. Experiences from the EU ETS suggest that it can be challenging, especially if the trading period is long. For example, during the last trading period (phase 3), the EU ETS used “backloading” of auctions to alter the time profile of new allowance injections (EU 2014). While the policy did not change the total emissions cap, it did raise questions about the credibility of the rules governing the trading system.

To address such concerns about credibility, the latest reforms in the EU ETS have focused on creating rule-based adjustments to the allowance supply (Jakob and Brunner 2014). The Market Stability Reserve (MSR) was proposed in 2015 and it began functioning in 2019 (EU 2015) In 2017, the phase 4 MSR rules were appended to incorporate the cancellation of allowances if the reserve exceeds certain threshold (EU 2018; Perino 2018; Beck and Kruse-Andersen 2018). The goal is to create an endogenized cap that is rule-based and hence predictable and transparent.²⁵ In our model, the regulator also actively adjusts the injection of new allowances based on the allowance demand realizations, which prevents the accumulation of unused allowances and thus helps to maintain price stability. One of the benefits of such an endogenous cap is that it helps to preserve, at least partly, the emissions reductions achieved by other policies which have been implemented in addition to an ETS (Perino 2018) Hence, our results and analysis can be understood as providing policy rules for endogenizing the cap given the objective of maximizing social welfare. Such rules can be either implemented using legislation or by an agency with more discretion (Brunner et al. 2012).

One could also ask whether the recent changes to the MSR rules are more aligned with the Markov policy or with the commitment policy, at least in principle. The low EU ETS allowance prices prior to 2018 suggest that the expectations of phase 4 price level have been low prior to the revision of the rules. Recent increases in the allowance prices, on the other hand, highlight the revised expectations of allowance prices in phase 4. Such an increase in prices is in line with both the Markov and commitment policies that prescribe adjustment rules for the cap. However, we could surmise that the reform creates a policy rule that resembles the Markov policy because the rules in the MSR do not refer to a specific price level.²⁶ Given the absence of such price target means that the regulator is not aiming to directly influence the expected price either, which would be reasonable requirement in the commitment policy case. However, our model and the MSR mechanism are not perfectly comparable, and to analyze the differences between our two policies in the context of the EU ETS would require finding numerical solutions to a fully parametrized model that includes time-dependent functional forms and a correlated shock process. We leave such development for future research.

5.2 Intertemporal Trading Ratio

Early research on intertemporal trading of allowances showed that banking and borrowing adjust the time profile of emissions in a manner that guarantees cost-effective intertemporal abatement effort (Cronshaw and Kruse 1996; Rubin 1996). Additionally, a correctly specified intertemporal trading ratio (ITR) can bring further improvements in efficiency by encouraging socially more beneficial banking behavior (Kling and Rubin 1997; Yates and Cronshaw 2001; Feng and Zhao 2006). Returning back to the intermediate case in Fig. 6, we observed that there can be some optimal discount factor that minimizes the welfare loss relative to the first best. Similarly, in the case of constant marginal damages, a higher discount factor improves the relative expected efficiency as well. This suggests that, given the market discount factor $\beta$, the regulator can potentially use an ITR to achieve an improvement in efficiency.

Define an effective discount factor, $\tilde{\beta }$, as

$$\begin{aligned} \tilde{\beta } = \frac{1+\gamma }{1+r} \end{aligned}$$

(30)

Here $\gamma$ denotes the ITR and it can be negative or positive depending on the speculative discount rate. A positive ITR means that the regulator pays interest for saved allowances. This has the effect of increasing the effective discount factor. A negative ITR means that the regulator imposes a penalty on saved allowances. This has the effect of decreasing the effective discount factor. For example, if the original discount factor is low and we are dealing with moderately increasing marginal damages, the regulator can introduce a positive $\gamma$ that would effectively raise the price floor and enable the regulator to improve efficiency. Naturally, the budgetary cost of introducing positive $\gamma$ must be included in the analysis to determine whether such an ITR is justifiable. On the other hand, if we are dealing with steep marginal damages and a high initial discount factor, the regulator could discourage excessive banking by introducing a negative $\gamma$ that will drive the price floor lower and enable the regulator to again improve efficiency.²⁷

5.3 Possible Extensions

Since the random shocks in our model are not correlated, the focus of our analysis can be understood to be on managing uncertainty in an ETS and not on information asymmetries and learning. Future work should examine the effect of relaxing the IID assumption, as the allowance demand shocks can be persistent, at least to some extent. However, while the IID assumption may seem restrictive, it may not actually be that limiting after all given our research question. If the shocks were autocorrelated, the expected effects of autocorrelation would be anticipated by all rational agents but the uncorrelated shock innovation would remain unpredictable and it would hence still be an essential part of the model solution (Lintunen and Kuusela 2018). Therefore, our model can be understood as a residual model where the autocorrelation has been removed from the original model setup. Hence, relaxing the IID assumption would not change the underlying results regarding the implications of a hybrid policy instrument. With the quadratic approximation of benefits and damages, the welfare effects of random shocks would be the same as before. But shock correlation could cause persistent variation in both quantities and prices.

It would be possible to write the model using time dependent benefit and damage functions. Such modeling choice would enable us to study the case for a decreasing emission cap, as seen for example in the EU ETS. However, such generality would complicate the solution of the model by preventing a stationary solution. We can speculate on the possible regulation outcomes if, for example, marginal damages were increasing in time. The regulator would respond to this by decreasing the number of allowances injected in future years, assuming the marginal benefits would remain constant. Formally, the Eq. (11) would have different damage functions in the current period and the next period. A decreasing and anticipated profile for allowance injections would make banking more attractive since future allowance prices would be expected to be higher than in the case with a constant cap. This would increase the endogenous price floor. The regulator would anticipate this and use this knowledge in setting the cap levels for the current and the next period. However, the regulator would still set the cap in such a way that the cap would be binding in random periods. The exact reaction would be an interesting research question. However, we would like to stress here that the presence of these types of additional features would not necessarily yield any more insight on the main question of our study: how the regulator should deal with the randomness in demand shocks (abatement costs) given the possibility to bank allowances.

The regulation of stock based externalities have been examined in the past prices versus quantities literature (Hoel and Karp 2002; Newell and Pizer 2003b). Our model could be extended to a case with a stock pollutant, but as to be expected, this would complicate the solution and the optimal policy. Namely, the optimal policy would depend on the current level of the pollution stock, which would be a state variable in the model. The shadow price of the pollution stock would depend on the current emissions and the past emissions. In the flow pollutant setup, such a case could be approximated by positively autocorrelated marginal damages. If marginal damages are increasing in time due to stock accumulation, the regulator might restrict the injection of future allowances thus potentially making banking more attractive (this is a comparable to time-dependent functional forms). Overall, this would again add structure on how the optimal cap is set in each contingency, but it would not change the qualitative aspects of the Markov and commitment policies to managing allowance demand risk in the presence of allowance banking. We leave the implications of these extensions on the optimal dynamic policy design to be determined in future research.

Appendices

Appendix 1: Proofs of Propositions 1 and 2

1.1 Cut-Off Shock, ${\tilde{\theta }}$

The current shock realization, $\theta _t$, determines whether the cap is binding. A high shock realization leads to high compliance demand and to a greater likelihood of a binding cap. We can hence define a cut-off level, $\tilde{\theta }$, for the shock realization that separates the two shock regimes where the cap is either binding (there is no banking, $b_t=0$) or non-binding (banking is positive, $b_t>0$).

Definition 2

The cut-off value of the shock, $\tilde{\theta }$, is the highest shock realization for which the equilibrium cap level Q is not binding and there is positive banking demand, i.e.

$$\begin{aligned} \tilde{\theta } := \sup \{\theta _t | b_t > 0\}. \end{aligned}$$

(31)

Under IID shocks, the cut-off shock level is implicitly defined by $\beta \mu = B_q(Q, {\tilde{\theta }})$

The response in current emissions to a changing cap level Q differs depending on whether the current shock is above or below the cut-off shock. This will be shown below.

1.2 Commitment Solution (Proposition 1)

The optimality condition for the commitment solution (12) is

$$\begin{aligned} E\left[ \left( B_q (q,\theta )-D_q (q)\right) \left( \beta \frac{\partial \hat{q}}{\partial Q} + \frac{\partial \hat{q}}{\partial \mu } \frac{\partial \mu }{\partial Q}\right) \right] = 0, \end{aligned}$$

where $q=\hat{q}\left( Q,\mu (Q),\theta \right) :=\min \{q\left( \beta \mu (Q),\theta \right) ,Q\}$.

Proposition 1 is proved by analyzing the partial derivatives $\partial \hat{q}/\partial Q$, $\partial \hat{q}/\partial \mu$, and $\partial \mu /\partial Q$. These partial derivatives have different values depending on whether the cap is binding or not, i.e., $\theta > {\tilde{\theta }}$ or $\theta < {\tilde{\theta }}$, respectively. This dichotomy is caused by the form of the market response function (7). The values of the partial derivatives are presented in the following series of lemmas.

Lemma 1

Denote the cut-off shock level, $\tilde{\theta }$. When the cap is binding $(\theta >\tilde{\theta })$:

$$\begin{aligned} \frac{\partial {\hat{q}}}{\partial Q} = 1. \end{aligned}$$

(32)

When the cap is not binding $(\theta \le \tilde{\theta })$:

$$\begin{aligned} \frac{\partial {\hat{q}}}{\partial Q} = 0. \end{aligned}$$

(33)

Proof

The proof of Lemma 1 is shown in Lintunen and Kuusela (2018). It follows from using the Definition 2 and the emissions response function (7). In the binding shock regime, a small change in the cap translates to an identical change in the emissions. In the non-binding shock regime, a small change in the cap has no effect on the emissions because the emission level is determined by the expected price, and not by $Q_t$. $\square$

Lemma 2

Denote the cut-off shock level, $\tilde{\theta }$. When the cap is binding $(\theta >\tilde{\theta })$:

$$\begin{aligned} \frac{\partial {\hat{q}}}{\partial \mu } = 0. \end{aligned}$$

(34)

When the cap is not binding $(\theta \le \tilde{\theta })$:

$$\begin{aligned} \frac{\partial {\hat{q}}}{\partial \mu } = \beta B_{qq}^{-1}(q,\theta )<0. \end{aligned}$$

(35)

Proof

The results in Lemma 2 can be directly derived using the emission response function $\hat{q}\left( Q,\mu ,\theta \right) :=\min \{q\left( \beta \mu (Q),\theta \right) ,Q\}$.

When the cap binds, the partial derivative is zero as the cap Q determines the emissions. When the cap does not bind, $\partial {\hat{q}}/\partial \mu = \partial q/\partial \mu$. Since function $q(p,\theta )$ is defined by the FOC $B_q(q,\theta )=p$, $\partial q/\partial p = B_{qq}^{-1}(q,\theta )$. The result follows from the fact that, when cap does not bind, $p=\beta \mu$. $\square$

Using Lemmas 1 and 2, the first-order condition in the commitment case (12) can be rewritten as:

$$\begin{aligned}&P \mathbb {E}\left[ \left( B_q(q,\theta )-D_q(q)\right) | BIND\right] \nonumber \\&\quad - (1-P)\mathbb {E}\left[ \left( B_q(q,\theta )-D_q(q)\right) \frac{1}{B_{qq}(q,\theta )}\frac{\partial \mu }{\partial Q} | NO BIND\right] \end{aligned}$$

(36)

The final partial derivative, $\partial \mu /\partial Q$, determines the effect of the periodic cap on the price expectations. It depends on the probability for the cap to bind, $P:=Pr(\theta >{\tilde{\theta }})$, the curvature of the benefit function, $B_{qq}$, and the discount factor, $\beta$. The partial derivative is given in the following lemma:

Lemma 3

The effect of the cap on the equilibrium expected price is given by

$$\begin{aligned} \frac{\partial \mu }{\partial Q} = \frac{P \mathbb {E}[B_{qq}(Q,\theta )|\theta > {\tilde{\theta }}]}{1-(1-P)\beta }. \end{aligned}$$

(37)

Proof

Take the accounting identity:

$$\begin{aligned} \mu = (1-P)\beta \mu +P\mathbb {E}\left[ B_q(Q,\theta )|BIND\right] = (1-P)\beta \mu + \int _{\tilde{\theta }}^{\infty }f(\theta )B_q(Q,\theta )d\theta \end{aligned}$$

and definition

$$\begin{aligned} P:=\int _{\tilde{\theta }}^{\infty } f(\theta ) d\theta \end{aligned}$$

Total differentiation

$$\begin{aligned} d\mu = (1-P)\beta d\mu - \beta \mu d \int _{\tilde{\theta }}^{\infty }f(\theta )d\theta + d\int _{\tilde{\theta }}^{\infty }f(\theta ) B_q(Q,\theta ) d\theta \end{aligned}$$

(38)

leads to

$$\begin{aligned} \left( 1-\left( 1-P\right) \beta \right) d\mu = \beta \mu f({\tilde{\theta }})d{\tilde{\theta }} - B_q\left( Q,{\tilde{\theta }}\right) f({\tilde{\theta }})d{\tilde{\theta }} + dQ\int _{\tilde{\theta }}^{\infty }f(\theta ) B_{qq}(Q,\theta ) d\theta \end{aligned}$$

(39)

By definition of cut-off shock realization $\beta \mu =B_q(Q,\tilde{\theta })$, and hence the two first terms in the RHS cancel out and we end up with:

$$\begin{aligned} \frac{\partial \mu }{\partial Q} = \frac{\int _{\tilde{\theta }}^{\infty }f(\theta ) B_{qq}(Q,\theta ) d\theta }{1-(1-P)\beta } = \frac{P\mathbb {E}\left[ B_{qq}(Q,\theta )|BIND\right] }{1-(1-P)\beta } \end{aligned}$$

The second equality follows from the definition of the conditional expectation value. $\square$

Some intuition can be provided using a simple exercise. Assuming a small change in cap $\Delta Q$, the mean price change when cap binds (probability P) is $\Delta p^{BIND} = \mathbb {E} [B_{qq}|BIND]\Delta Q$, and when cap is not binding (probability $1-P$) the price change is $\Delta p^{NO} = \beta \Delta \mu$. Since $\Delta \mu = P\Delta p^{BIND} + (1-P)\Delta p^{NO}$, we get $\Delta \mu /\Delta Q = P \mathbb {E}[B_{qq}|BIND] /(1-(1-P)\beta )$. Hence, the denominator follows from the fact that $\Delta \mu$ is on both sides of the equilibrium equation.

Finally, we can prove Proposition 1:

Proof

Inserting the expression in Lemma 3 into the first-order condition in (36) yields the expression in Proposition 1. $\square$

1.3 Markov Perfect Solution (Proposition 2)

Proposition 2 is proved in Lintunen and Kuusela (2018) but we will present it here for the IID case.

Proof

From Lemma 1, we know that the function $q(Q_t,\theta _t)$ is differentiable almost everywhere and the zero-measure point of non-differentiability does not contribute to the expectation value, as the function $q(Q_t,\theta _t)$ is continuous. Thus, we can directly obtain the first-order condition presented in (18):

$$\begin{aligned} \mathbb {E}[ B_q(\hat{q}_t,\theta _t)\hat{q}_{Qt}] - \mathbb {E}[D_q(\hat{q}_t)\hat{q}_{Qt} ]=0, \end{aligned}$$

(40)

where we have used the following shorthand notation: $\hat{q}_t := q(Q_t,\theta _t)$ and $\hat{q}_{Qt} := q_Q(Q_t,\theta _t)$. From Lemma 1, we also know that $\hat{q}_{Qt} = 1$, if $\theta _t>\tilde{\theta }$ and zero elsewhere. In addition, $\hat{q}_t = Q_t$, if $\theta _t>\tilde{\theta }$. Making use of these properties, we can rewrite the optimality condition as:

$$\begin{aligned} \int B_q(Q_t,\theta _t) \varvec{1}_{\text {BIND}}(\theta _t) d F(\theta _t) = D_q(Q_t) \int \varvec{1}_{\text {BIND}}(\theta _t) d F(\theta _t), \end{aligned}$$

where $F(\theta _t)$ is the distribution function of an IID shock process. Indicator function $\varvec{1}_{\text {BIND}}(\theta )$, has value one when $\theta \in \text {BIND}$ and zero elsewhere. The set $\text {BIND}$ consists of shock realizations in which the emissions are bound by the cap, i.e. $\text {BIND} := \{\theta _t | \theta _t>\tilde{\theta } \}$. Thus, we can write

$$\begin{aligned} \int _{\text {BIND}} B_q(Q_t,\theta _t) d F(\theta _t) = D_q(Q_t) \int _{\text {BIND}} d F(\theta _t). \end{aligned}$$

Since $\int _{\text {BIND}} d F(\theta _t) = Pr(\theta \in \text {BIND})$, this directly leads to the optimality conditions

$$\begin{aligned} \mathbb {E}[ B_q(Q_t,\theta _t)|\theta _t>{\tilde{\theta }}] = D_q(Q_t), \end{aligned}$$

(41)

Recall that ${\tilde{\theta }}$ is implicitly defined by the condition $B(Q,{\tilde{\theta }})=\beta \mu$. $\square$

Appendix 2: Analytical Solution with IID Uniform Shocks

1.1 Setup

The benefit and damage functions are quadratic polynomials, and the shock $\theta$ is IID and follows a continuous, uniform distribution $\theta \sim U[-\sigma , \sigma ]$. Thus, the expected value $\mathbb {E} \theta = 0$. We furthermore calibrate the benefits and damages so that the linear marginal benefits and damages intersect on average at the point (${\bar{q}}$, ${\bar{d}}$) in (q, p) -plane. Thus, we denote the marginal damages as

$$\begin{aligned} D_q(q) = {\bar{d}} + D_{qq} (q - {\bar{q}}) \end{aligned}$$

and marginal benefits

$$\begin{aligned} B_q(q,\theta ) = \theta + {\bar{d}} - |B_{qq}| (q - {\bar{q}}), \end{aligned}$$

where $D_{qq} \ge 0$ and $|B_{qq}| >0$. The above specification can be understood as a quadratic approximation of arbitrary benefit and damage functions in the neighborhood of point (${\bar{q}}$, ${\bar{d}}$).

We assume two additional parametric restrictions that make sense given the scope of our analysis. First, without banking the optimal cap is binding under all the realizations of the shock $\theta$, that is, $\sigma < {\bar{d}}$. Second, with banking there is always a positive probability for positive banking, that is, $\sigma > (1-\beta ) {\bar{d}}$. If $\sigma$ is smaller, there is never banking and the policy reduces to the cap and trade without banking. Together, these restriction imply that $\sigma \in \left( (1-\beta ){\bar{d}}, {\bar{d}} \right)$.

Given the above setup, it is easy to show that the optimal tax is $\tau = {\bar{d}}$, and the optimal cap without banking $Q^{N}={\bar{q}}$.

1.2 Markov Solution

The optimality condition (19) is

$$\begin{aligned} \mathbb {E}[ B_q(Q,\theta )|\theta >{\tilde{\theta }}] = D_q(Q) \end{aligned}$$

with cut-off shock value

$$\begin{aligned} {\tilde{\theta }} = \beta \mathbb {E} p(Q,\theta ) - {\bar{d}} + |B_{qq}| Q, \end{aligned}$$

(42)

and price function

$$\begin{aligned} p(Q,\theta ) = \max \{ \beta \mathbb {E} p(Q, \theta ) ,\, B_q(Q,\theta ) \}. \end{aligned}$$

Directly taking the expectation of the price function, we get:

$$\begin{aligned} \mathbb {E} p(Q,\theta ) = (1-P({\tilde{\theta }})) \beta \mathbb {E} p(Q, \theta ) + P({\tilde{\theta }}) \, \mathbb {E}[B_q(Q,\theta )|\theta > {\tilde{\theta }}], \end{aligned}$$

where $P({\tilde{\theta }})$ stands for probability that the cap is binding, i.e.

$$\begin{aligned} P({\tilde{\theta }}) = \int _{{\tilde{\theta }}}^\infty d F(\theta ) = \frac{1}{2} - \frac{{\tilde{\theta }}}{2\sigma } , \end{aligned}$$

(43)

Using the first-order condition and a short-hand notation $\mu := \mathbb {E} p(Q,\theta )$ we end up with

$$\begin{aligned} \mu = (1-P) \beta \mu + P \, D_q(Q). \end{aligned}$$

(44)

Finally we need to calculate the expectation value explicitly:

$$\begin{aligned} \mathbb {E}[ B_q(Q,\theta )|\theta >{\tilde{\theta }}] = \int _{{\tilde{\theta }}}^{\sigma } \frac{\theta +{\bar{d}} -|B_{qq}| Q}{\sigma - {\tilde{\theta }}}d\theta = (\sigma + {\tilde{\theta }})/2 + {\bar{d}} - |B_{qq}| Q, \end{aligned}$$

(45)

This leads to the first-order condition:

$$\begin{aligned} {\tilde{\theta }} = 2(|B_{qq}| + D_{qq}) (Q-{\bar{q}}) - \sigma . \end{aligned}$$

(46)

Equation (46) is the first equation of the two that define the equilibrium. The second equation is the expected price Eq. (44), which can be rewritten, using Eqs. (42), (43), and (45), as

$$\begin{aligned} 4\sigma (1-\beta ) ({\tilde{\theta }} + {\bar{d}} - |B_{qq}| Q) = \beta (\sigma - {\tilde{\theta }} )^2. \end{aligned}$$

(47)

Inserting Eqs. (46)–(47) we end up with a quadratic equation for the optimal cap

$$\begin{aligned} \varphi (Q) := a_2 (Q-{\bar{q}})^2 + a_1 (Q -{\bar{q}}) + a_0 =0, \end{aligned}$$

where

$$\begin{aligned} a_2= & {} \beta (|B_{qq}| + D_{qq})^2, \\ a_1= & {} -( 2 D_{qq} + (1+\beta ) |B_{qq}| ) \sigma , \end{aligned}$$

and

$$\begin{aligned} a_0= ( \sigma - (1-\beta ) {\bar{d}}) \sigma \end{aligned}$$

Since $a_2>0$ the parabola opens upwards. By the positive banking probability assumption ($\sigma > (1-\beta ) {\bar{d}}$), $a_0>0$, which implies that both roots of the polynomial are positive. This confirms that the optimal cap is greater than ${\bar{q}}$, which is the optimal non-banking cap level. If there is no uncertainty, that is, $\sigma =0$, the solution reduces to the one without banking ($Q={\bar{q}}$) since $a_1$=0 and $a_0=0$. Thus, if there is no stochasticity present, the banking has no role in the optimal policy.

The minimum of the quadratic polynomial, $\varphi (Q)$, is at the emission level

$$\begin{aligned} Q_{min} = {\bar{q}} - \frac{a_1}{2 a_2} = {\bar{q}} + \frac{\sigma }{|B_{qq}| + D_{qq}} + \frac{(1-\beta )(|B_{qq}|+2D_{qq})}{2\beta (|B_{qq}|+D_{qq})^2}, \end{aligned}$$

where the first two terms in the RHS form the emission level at which the maximum realization of marginal benefits crosses the marginal damages, that is, $B_q(q,\sigma ) = D_q(q)$. The last term is positive. Thus, it follows directly that the optimal cap, $Q^*$, is the smaller of the two roots of the polynomial as the larger one is non-optimal solution to the planner’s problem. As the parabola opens upwards and the optimal cap level is the smaller of the two roots, we know that $\varphi _Q(Q^*)<0$.

1.3 Comparative Statics

The optimal solution is uniquely determined by the level parameter of the marginal damages, ${\bar{d}}$, the slope parameters of the marginal damage and benefit lines, $D_{qq}$ and $|B_{qq}|$, the dispersion of the random marginal benefit shocks, $\sigma$, and by the discount factor $\beta$.

The comparative statics results can be directly derived from the results in the preceding sub-section. However, it proves useful to define an auxiliary function that gives the price level associated with the cut-off shock realization ${\tilde{\theta }}$ that also satisfies the planner’s first-order condition (46). This “price floor” function is defined as:

$$\begin{aligned} {\underline{p}} (Q) := B_q(Q;{\tilde{\theta }} (Q)) = - \sigma + {\bar{d}} + (|B_{qq}| + 2 D_{qq}) (Q-{\bar{q}}), \end{aligned}$$

(48)

where ${\tilde{\theta }} (Q)$ is obtained from (46). With the optimal cap, ${\underline{p}} (Q^*) = \beta \mu$ holds.

The effect of the dispersion parameter on the optimal cap is directly obtained as:

$$\begin{aligned} \frac{\partial Q}{\partial \sigma } = \frac{ (2 D_{qq} + (1+\beta )|B_{qq}|) (Q^*-{\bar{q}}) - 2 \sigma + (1-\beta ){\bar{d}}}{\varphi _Q(Q^*)}. \end{aligned}$$

Using Eq. (48), a short manipulation leads to

$$\begin{aligned} \frac{\partial Q}{\partial \sigma } = \frac{ \beta [B_q(Q^*,{\bar{\theta }}) - \mu ] + (1-\beta )\sigma }{|\varphi _Q(Q^*)|}>0. \end{aligned}$$

The positive sign follows directly from the fact that the maximum price realization $B_q(Q,{\bar{\theta }})$ is bound to be higher than the expected value, as long as $\sigma >0$ and $\beta < 1$. Thus, the optimal cap increases with increasing dispersion.

By direct calculation we can similarly derive the effect of the discount factor on the optimal cap:

$$\begin{aligned} \frac{\partial Q}{\partial \beta } =\frac{(|B_{qq}|+D_{qq})^2(Q^*-{\bar{q}})^2 + [{\bar{d}} - |B_{qq}| (Q^* -{\bar{q}})]\sigma }{|\varphi _Q(Q^*)|}>0. \end{aligned}$$

The last term is positive since it is the expected marginal benefit at $q_t=Q^*$, which is greater than or equal to $\beta \mu >0$.

The level variables: The effect of the emission baseline, ${\bar{q}}$, is directly

$$\begin{aligned} \frac{\partial Q}{\partial {\bar{q}}} =\frac{\varphi _Q(Q^*)}{\varphi _Q(Q^*)}=1. \end{aligned}$$

The effect of damage baseline, ${\bar{d}}$, is

$$\begin{aligned} \frac{\partial Q}{\partial {\bar{d}}} =-\frac{(1-\beta )\sigma }{|\varphi _Q(Q^*)|}<0. \end{aligned}$$

The cap is decreasing in both of the slope parameters $|B_{qq}|$ and $D_{qq}$:

$$\begin{aligned} \frac{\partial Q}{\partial |B_{qq}|} =-\frac{1-(1-2P({\tilde{\theta }}))\beta }{|\varphi _Q(Q^*)|} \sigma (Q^* -{\bar{q}})<0. \\ \frac{\partial Q}{\partial D_{qq}} =-2\frac{1-\beta (1-P({\tilde{\theta }}))}{|\varphi _Q(Q^*)|} \sigma (Q^* -{\bar{q}})<0. \end{aligned}$$

In both cases, we have used the function (43) and the facts that $P({\tilde{\theta }})\in (0,1)$ and $Q^*>{\bar{q}}$.