1 Introduction

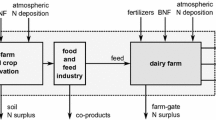
Negative externalities (undesirable outputs) such as nitrogen (N) surplus that accompany agricultural activities and in particular dairy production have been identified as a significant contributor to ground water and surface water pollution, greenhouse gas (GHGs) emissions and the build-up in soil of contaminants, such as heavy metals (McLellan et al. 2018; Buckley et al. 2016). These externalities result mainly from inappropriate manure management and the overuse of external inputs such as fertilizers and concentrates feeds in intensive dairy production systems. They impact directly on the local environment causing damage to the ecosystems and human health (Cecchini et al. 2018; McLellan et al. 2018; Erisman et al. 2011). Although the European Union (EU) through the Common Agricultural Policy (CAP), has enacted a number of environmental policies (for example, the Nitrates Directive and the Water Framework Directive) aimed at ensuring sustainable agricultural production, excess nutrient from dairy production remains an issue of serious concern in the continent (European Communities 2010).

The proper management of negative agricultural externalities require that they are measured and incorporated when evaluating production performance (Skevas et al. 2018; Pérez-Urdiales et al. 2016; Orea and Wall 2017; Mamardashvili et al. 2016; Zhou et al. 2014, 2016; Picazo-Tadeo and Prior 2009; Tyteca 1996). It is difficult to manage what you cannot measure. Unlike the desirable outputs, (milk for example), the undesirable outputs are not accounted for in the market place, either from an individual producer or society’s perspective, and are therefore not costed. In fact, they are not often taken into consideration by the farmers in making their production decisions. The implication of this is that, their economic values are unknown and difficult to assess such that the undesirable outputs are usually in excess of what can be considered as economically and environmentally sustainable. With less quantitative information about the degree of damage undesirable outputs inflict on the environment, the formulation of appropriate and efficient agri-environmental policies acceptable to all stakeholders within the dairy production system becomes difficult. The knowledge of a composite environmental efficiency index and marginal abatement costs of nutrient surplus would provide room for assessing the economic impacts of different farms strategies aimed at reducing polluting emissions and consequently climate change effects. Also, an estimate of the abatement costs of nutrient surplus can provide the relevant parameters in the design of incentive mechanisms relating to the reward for efficient management of negative production externalities by public decision makers. By quantifying the opportunity costs of reducing N surplus, policy makers can better understand the burden that abatement costs would have on the performance of the dairy farms. This will be relevant in making economic and policy decisions affecting the design of regulatory environmental policies and the management of dairy farms.

The dairy sector is an important agricultural sub-sector on the island of Ireland which comprises Northern Ireland, which is part of the United Kingdom and the Republic of Ireland (see Fig. 1). The dairy sector accounts for about 32% of the total agricultural output in both countries (CSO 2018; DAERA 2017; DAFM 2017). However, compared to other agricultural sectors, the dairy sector in both countries has the highest stocking densities and fertilizer inputs, putting pressure on the environment (Buckley et al. 2016). There are indications that the expansion of the dairy sector resulting from the abolition of the milk quotaFootnote 1 regime in 2015 after 31 years of its existence might lead to further environmental concerns. Already, the elevated nutrient concentrations contribute significantly to the problem of environmental pollution and puts pressure on marginal habitats and landscape features. There is widespread water quality issues with some of the water bodies usually exceeding the 50 mg/l limit on the levels of nitrate allowable in drinking water. Agriculture account for more than 30% of the incidence of water pollution on the island of Ireland (Cave and McKibbin 2016; Summary of Findings of Northern Ireland 2012; Environmental Protection Agency (EPA) 2017). More than 50% of all rivers in Northern Ireland are classified as “moderate/poor status”. and about 70% of lakes are classed as eutrophic under the “water framework directive” (Cave and McKibbin 2016; “Summary of Findings of Northern Ireland Nitrates” 2012).The situation is similar in the Republic of Ireland where about 69% of the transitional water bodies, 43% of rivers and 54% of lakes are classified as moderate or worse status (EPA 2017). The quality of surface waters in the region has remained relatively static in the last few years and the objective of the water framework directives to achieve a 13% improvement in surface water standards between 2010 and 2015 has not been achieved (EPA 2017).

Fig. 1
figure 1

Source: Author’s compilation

Map of the study area; inset is the map of the United Kingdom.

Full size image

In this paper we employed the parametric hyperbolic environmental technology distance function approach in a stochastic frontier framework to analyse the environmental performance and consequently estimate the abatement costs (shadow price) of N surplus in dairy farms on the island of Ireland. The farm level N pollution costs ratio and its determinants are also analysed using the within-between (WB) farm random effect modelling approach. The contribution of this paper to the existing literature is three-fold. Firstly, this work provides the first attempt to parametrically estimate the environmental performance and shadow price of N surplus in dairy farms using a hyperbolic distance function approach with farm level panel data. The applied hyperbolic environmental technology distance function is less restrictive compared to the output or input distance function allowing for more robust estimates to be obtained. Secondly, the comparison of environmental performance and shadow price of N surplus in two separate countries with differing, but largely pasture based dairy production systems gives room for greater generalisation of results and provides the basis for spatial comparison of the environmental performance of different dairy production systems. Thirdly, this is the first study to investigate the factors influencing the N pollution cost ratio in dairy farms employing the within-between econometric approach. The methodology is able to analyse the within (time) and between (individual) effects in a single model of the Random effects (RE) modelling framework.

The rest of the paper is organized as follows: In Sect. 2, we review relevant empirical literature. We describe the methodology used in the research by illustrating the theoretical framework in Sect. 3 while in Sect. 4 we provide a detailed description of the data and empirical specification of the model. The estimated results are reported and discussed in Sect. 5. Finally, we conclude in Sect. 6 by presenting an overview of the study outcomes alongside relevant policy recommendations.

2 Literature Review

Various approaches have been suggested in the environmental economics literature as viable techniques to estimate abatement costs and internalise production externalities in agriculture (Novikova 2014). One such approach is the survey based stated preference methods of contingent valuation and choice modelling (Markantonis and Kostas 2010; Dupras et al. 2018). These methods although they fit quite well to the evaluation needs of complex, multidimensional policies due to their flexibility in designing valuation models, they are nevertheless subjective. This is because respondents could over- or underestimate the value of the agricultural externality being measured, which causes the wrong interpretation of the research results (Novikova 2014). To overcome this shortcoming, the concept of shadow price to value production externalities based on the traditional production theory was popularised by Pittman (1981, 1983). This approach is less subjective compared to survey-based approaches and represents the economic valuation of production externalities in the strict scientific sense (Farnsworth et al. 2015). The shadow price approach measures the trade-off between the desirable and undesirable outputs in the production process by estimating the marginal sacrifice needed to comply with environmental restrictions that prevent free disposal of a given pollutant (Pittman 1981, 1983; Färe and Grosskopf 1998; Orea and Wall 2017). Hailu and Veeman (2000) described the shadow price of undesirable outputs as the opportunity cost of reducing additional undesirable output by one unit in terms of less production of desirable outputs.

The first step in the estimation of the shadow price (abatement costs) is the modelling of a multiple outputs (including undesirable outputs) and multiple inputs, environmentally sensitive distance function production technology (Bokusheva and Kumbhakar 2014; Kumbhakar et al. 2015). The distance function is then used to derive the marginal abatement costs of the undesirable output by employing the duality between the distance function and the profitability function (Tang et al. 2016). Different variants of the distance function can be found in the literature. They include the radial input or output distance functions, the directional output distance function and the hyperbolic distance function (Shephard 1953, 1970; Färe et al. 1993; Chambers et al. 1996; Coggins and Swinton 1996). Most of the earlier studies incorporating undesirable outputs into the production possibility set have employed the output or input distance functions (Färe et al. 1993; Hadley 1998). One disadvantage of this methodology is that it treats all outputs and inputs symmetrically. That is, it assumes a proportional expansion of all outputs (both desirable and undesirable outputs) or contraction of all inputs without giving credit to the reduction of undesirable output or increase in desirable outputs (Chung et al. 1997). By contrast, the directional or the hyperbolic distance function which were recently introduced in the literature can treat desirable and undesirable outputs asymmetrically by seeking to simultaneously expand desirable outputs and contract undesirable outputs (Wang et al. 2017; Mamardashvili et al. 2016; Hou et al. 2015; Du et al. 2015; Murty et al. 2007; Chambers et al. 1998; Färe et al. 2005).

Although the directional and hyperbolic distance functions are aimed at achieving similar goals, they are nevertheless differentiated based on their homogeneity property. While the hyperbolic distance function is based on the multiplicative homogeneity property of Shephard’s (1970) distance function, the directional distance function makes use of the translation property which is an additive analogue of the multiplicative homogeneity property of the hyperbolic distance function (Färe et al. 2005; Cuesta et al. 2009; Cuesta and Zofío 2005; Chambers et al. 1998).

Distance functions can be estimated in any of two ways: parametrically or non-parametrically. The non-parametric technique otherwise called the Data Envelopment Analysis (DEA) technique developed by Charnes et al. (1978), employs mathematical programming techniques and does not require the specification of a functional form (Picazo-Tadeo et al. 2011; Macpherson et al. 2010; Chung et al. 1997). However, DEA does not account for any stochastic variance from the frontier. It assumes that all observations in the sample belong to the potential production frontier which make it sensitive to the presence of outliers in the data and may lead to unrealistic frontier construction. Except under constant returns to scale, the program is non-linear and inference is not possible without bootstrapping (Adenuga et al. 2018a; Duman and Kasman 2018; Aragon et al. 2005). Previous studies that have employed the DEA approach for the estimation of environmental efficiency and abatement costs include: Cecchini et al. (2018) who employed the Slacks-Based Measure-Data Envelopment Analysis (SBM-DEA) with undesirable output to estimate the environmental efficiency and marginal abatement costs of CO2 from 10 dairy farms in Umbria region of Italy. March et al. (2016) analysed the environmental efficiency of diverse milk production systems making use data from experimental dairy farms. Toma et al. (2013) compared the environmental efficiency of two divergent strains of Holstein–Friesian cows across two contrasting dairy management systems. Picazo-Tadeo et al. (2011) estimated the eco-efficiency scores at both farm and environmental pressure-specific levels for a sample of Spanish farmers operating in the rain-fed agricultural system of Campos County. Unlike the non-parametric approach, the parametric technique is able to account for statistical noise, it is differentiable and less sensitive to outliers. The approach allows for conducting statistical inference without bootstrapping in contrast to non-parametric technique (Boyd et al. 2002; Hailu and Chambers 2012; Wei et al. 2013; Färe et al. 2005).

On the basis of the above, we adopted the parametric hyperbolic distance function for this study. The methodology in contrast to the directional distance function, can assume a flexible translog functional form (Mamardashvili et al. 2016; Färe et al. 1989; Cuesta et al. 2009). The approach is flexible and has become increasingly popular among productivity studies. Previous studies that have employed this approach include: Cuesta et al. (2009) who employed the hyperbolic and the enhanced hyperbolic distance function to estimate the efficiency scores for a set of U.S. electric industries and consequently estimated the shadow price of SO2 emissions which was considered as undesirable output. Mamardashvili et al. (2016) applied the hyperbolic distance function to analyse the environmental performance and consequently estimated the abatements costs of N surplus for conventional and organic Swiss dairy farms using cross sectional data. Peña et al. (2018) studied agricultural eco-efficiency in the Amazon, using hyperbolic distance functions with a stochastic frontier based on the classical variables of the multi-product production function and considered areas of degraded land as environmentally undesired output. Cuesta and Zofío (2005) using the translog hyperbolic distance function estimated the efficiency of Spanish savings banks. Glass et al. (2014) employed the enhanced hyperbolic distance function to measure the relative performance of Japanese cooperative banks modelling non-performing loans as an undesirable output. Suta et al. (2010) using the hyperbolic distance function approach, calculated the environmental technical efficiency scores of selected EU farms (Bulgaria, Romania and Poland). Duman and Kasman (2018) investigated the environmental technical efficiency for a panel of European Union (EU) member and candidate countries using parametric hyperbolic distance function.

Although, the use of the hyperbolic distance function approach has been popular in recent years, to the best of our knowledge, only one study, Mamardashvili et al. (2016) has employed the parametric hyperbolic distance function in the context of dairy production systems. Even then, this study has only made use of cross sectional data in their analyses and did not analyse the pollution costs ratio and its determinants. Studies have shown that compared to a cross-sectional data, panel data modelling have more variability especially in terms of isolating the effects of unobserved differences between individuals (Kennedy 2008; Baltagi 2001).

3 Model

In this section we present the theoretical model for our study which allows us to estimate the environmental efficiency of dairy farms by incorporating N surplus as undesirable output into the parametric hyperbolic distance function framework. We consequently describe the derivation of the shadow price (abatement costs) of N surplus based on the duality between the hyperbolic environmental technology distance function and the maximisation of the profitability function. In the final subsection, the soil surface budget approach employed in estimating N surplus in dairy farms is presented.

3.1 The Translog Hyperbolic Environmental Technology Distance Function

The hyperbolic environmental technology distance function \(({\text{D}}_{\text{H}} )\) employed in this study represents the maximum expansion of the desirable output vector (y) and the equi-proportionate contraction of the undesirable output vector (s) that places a producer on the boundary of the technology (Cuesta et al. 2009; Färe et al. 1989). Although alternative functional forms such as the quadratic directional distance functions have been proposed in the literature (Färe et al. 2006), we opted for the translog functional form for our hyperbolic distance function. This is because it provides a more flexible approximation to the production technology. It is differentiable, quite amenable to the imposition of the almost homogeneity conditions and has been extensively used the empirical literature (Mamardashvili et al. 2016; Cuesta et al. 2009; Cuesta and Zofío 2005; Peña et al. 2018).

Suppose there are n (n = 1, 2, …, N) dairy farms employing multiple inputs denoted by vector \({\text{x}}_{\text{n}} = \left( {{\text{x}}_{{1{\text{n}}, }} {\text{x}}_{{2{\text{n }}}} , \ldots , {\text{x}}_{\text{Jn }} } \right)\) ∈ \({\text{R}}_{ + }^{\text{J}}\) to produce a vector of desirable outputs (milk and other outputs) \({\text{y}}_{\text{n}} = \left( {{\text{y}}_{{1{\text{n}}}} , {\text{y}}_{{2{\text{n}}}} , \ldots ,{\text{y}}_{\text{Mn}} } \right)\) ∈ \({\text{R}}_{ + }^{\text{M}}\) and a vector of undesirable outputs (N surplus) \({\text{s}}_{\text{n}} = \left( { {\text{s}}_{{1{\text{n}}}} , {\text{s}}_{{2{\text{n}}}} , \ldots , {\text{s}}_{{1{\text{Kn}}}} } \right)\) ∈ \({\text{R}}_{ + }^{\text{K}}\). Then, the environmental production technology can be represented by the output possibility set P(x) given in Eq. (1) (Chung et al. 1997; Zhou et al. 2016; Cuesta et al. 2009).

$${\text{P}}\left( {\text{x}} \right) = \left\{ {{\left( {{\text{x}},{\text{y}},{\text{s}}} \right):} {\text{x }} \in {\text{R}}_{ + }^{\text{J}} \;{\text{can}}\;{\text{produce}}\;\left( {{\text{y}},{\text{s}}} \right);\;{\text{y }} \in {\text{R}}_{ + }^{\text{M}} ,\quad {\text{s }} \in {\text{R}}_{ + }^{\text{K}} } \right\}$$
(1)

where the superscripts j, m, and k represents the number of inputs, desirable outputs, and undesirable outputs respectively. Given the above, the hyperbolic environmental technology distance function \(({\text{D}}_{\text{H}} )\) can be expressed as presented in Eq. (2).

$${\text{D}}_{\text{H}} \left( {{\text{x}},{\text{y}},{\text{s}}} \right) = { \inf }\left\{{ {{{\upeta }} > 0:}\left( {x,\frac{\text{y}}{{{\upeta }}},{\text{s}}\upeta } \right) \in {\text{P}}} \right\}$$
(2)

As indicated by \({{\upeta }}\) in Eq. (2), the desirable and undesirable output changes in the same proportion but in opposite direction. The range of the hyperbolic environmental technology distance function is 0 < \({\text{D}}_{\text{H}}\) (x, y, s) ≤ 1. Farms are said to be fully efficient if \({\text{D}}_{\text{H}} \left( {{\text{x}}, {\text{y}}, {\text{s}}} \right)\) = 1 implying that the estimated observation lies on the boundary of the production possibilities set such that it will not be possible to reduce N surplus without reducing the revenue from dairy production. On the other hand, if the value of the distance functions is less than 1 (\({\text{D}}_{\text{H}} \left( {{\text{x}}, {\text{y}}, {\text{s}}} \right)\) < 1), then the farm is inefficient leaving room for enhancing efficiency by increasing revenue from dairy production and simultaneously reducing N surplus. The hyperbolic environmental technology distance function is almost homogeneous of degrees 0, 1, − 1, 1. This implies that, at a given input level, if the set of desirable outputs is increased by a given proportion, the set of undesirable output is reduced by the same proportion and the distance function will increase by the same proportion. It is non-decreasing in desirable outputs, \({\text{D}}_{\text{H}} \left( {{\text{x}},\upeta{\text{y}},{\text{s}}} \right) \le {\text{D}}_{\text{H}} \left( {{\text{x}},{\text{y}},{\text{s}}} \right), {{\upeta }} \in \left[ {0.1} \right];\) non-increasing in undesirable output \({\text{D}}_{\text{H}} \left( {{\text{x}},{\text{y}},\upeta{\text{s}}} \right) \le {\text{D}}_{\text{H}} \left( {{\text{x}},{\text{y}},{\text{s}}} \right), {{\upeta }} \ge 1\) and non-increasing in inputs \({\text{D}}_{\text{H}} \left( {\upeta{\text{x}}, {\text{y}},{\text{s}}} \right) \le {\text{D}}_{\text{H}} \left( {{\text{x}},{\text{y}},{\text{s}}} \right), {{\upeta }} \ge 1\). Following Mamardashvili et al. (2016), and Cuesta et al. (2009), the almost homogeneity property can be employed to derive the hyperbolic environmental technology distance function. Given a set of inputs data, desirable output and undesirable output, the function can be expressed as given in Eq. (3).

$${\text{D}}_{\text{H}} \left( {{\text{x}},\upphi {\text{y}},\upphi ^{ - 1} {\text{s}}} \right) = \upphi {\text{D}}_{\text{H}} \left( {{\text{x}},{\text{y}},{\text{s}}} \right),\upphi > 0$$
(3)

Given that \(\upphi\) in Eq. (3) is greater than 0, then imposing the almost homogeneity condition by setting \(\upphi = \frac{1}{{{\text{y}}_{\text{m}} }}\) (where \({\text{y}}_{\text{m}}\) is, without loss of generality, the Mth output), the equation is transformed to:

$$ {\text{D}}_{{\text{H}}} \,\left( {{\text{x}}_{{\text{i}}} ,\frac{{{\text{y}}_{{\text{i}}} }}{{{\text{y}}_{{\text{m}}} }},{\text{s}}_{{\text{i}}} \,{\text{y}}_{{\text{m}}} } \right) = \frac{1}{{{\text{y}}_{{\text{m}}} }}\,{\text{D}}_{{\text{H}}} \,\left( {{\text{x}}_{{\text{i}}} ,{\text{y}}_{{\text{i}}} ,{\text{s}}_{{\text{i}}} } \right) $$
(4)

Taking the logarithm of both sides and rearranging the expression, Eq. (4) becomes:

$$ \frac{{{\text{lnD}}_{{\text{H}}} \left( {{\text{x}}_{{\text{i}}} ,{\text{y}}_{{\text{i}}} ,{\text{s}}_{{\text{i}}} } \right)}}{{{\text{lny}}_{{\text{m}}} }} = {\text{lnD}}_{{\text{H}}} \left( {{\text{x}}_{{\text{i}}} ,\frac{{{\text{y}}_{{\text{i}}} }}{{{\text{y}}_{{\text{m}}} }},{\text{s}}_{{\text{i}}} \,{\text{y}}_{{\text{m}}} } \right) $$
(5)

Equation (5) is a specification of the hyperbolic environmental technology distance function. The stochastic frontier analysis framework (SFA) provides room for the estimation of the frontier of best production practices that envelop the data while assuming the existence of an idiosyncratic error term. Taking \({\text{y}}_{{{\text{o}} - {\text{th}}}}\) output as the normalising variable to satisfy the almost homogeneity condition and appending a random error term, \({\text{v}}_{\text{it}}\) ~ N (0, \({{\upsigma}}_{\text{v}}^{2}\)), the stochastic translog hyperbolic environmental technology distance function can be specified as presented in Eq. (6). The model is enhanced by allowing for a multi-period framework making use of panel data, hence, all variables are indexed with a year subscript t.

$$ \begin{aligned} & \frac{{{\text{lnD}}_{\text{H}} \left( {{\text{x}}_{\text{i}} ,{\text{y}}_{\text{i}} ,{\text{s}}_{\text{i}} } \right)}}{{{\text{y}}_{{{\text{mo}},{\text{it}}}} }}\begin{array}{*{20}c} = & {{{\upalpha}}_{0} } \\ \end{array} + \mathop \sum \limits_{{{\text{j}} = 1}}^{\text{J}} {{\upalpha}}_{\text{j}}\,{\text{lnx}}_{{{\text{j}},{\text{it}}}} + \frac{1}{2}\mathop \sum \limits_{{{\text{j}} = 1}}^{\text{J}} \mathop \sum \limits_{{{\text{j}}^{\prime} = 1}}^{\text{J}} {{\upalpha}}_{{{\text{jj}}^{\prime} }}\, {\text{lnx}}_{{{\text{j}},{\text{it}}}} \,{\text{lnx}}_{{{\text{j}}^{\prime} ,{\text{it}}}} + \mathop \sum \limits_{{{\text{m}} = 1}}^{{{\text{M}} - 1}} {{\upbeta}}_{\text{m}} \,{\text{lny}}_{{{\text{m}},{\text{it}}}}^{ *} \\ & \quad + \frac{1}{2}\mathop \sum \limits_{{{\text{m}} = 1}}^{{{\text{M}} - 1}} \mathop \sum \limits_{{{\text{m}}^{\prime} = 1}}^{{{\text{M}} - 1}} {{\upbeta}}_{{{\text{mm}}^{\prime } }} \,{\text{lny}}_{{{\text{m}},{\text{it}}}}^{ *} \,{\text{lny}}_{{{\text{m}}^{\prime } ,{\text{it}}}}^{ *} + \mathop \sum \limits_{{{\text{k}} = 1}}^{\text{K}} {{\upgamma}}_{\text{k}}\, {\text{lns}}_{{{\text{k}},{\text{it}}}}^{ *} + \frac{1}{2}\mathop \sum \limits_{{{\text{k}} = 1}}^{\text{K}} \mathop \sum \limits_{{{\text{k}}^{\prime} = 1}}^{\text{K}} {{\upgamma}}_{{{\text{kk}}^{\prime} }} \,{\text{lns}}_{{{\text{k}},{\text{it}}}}^{ *}\, {\text{lns}}_{{{\text{k}}^{\prime} {\text{it}}}}^{ *} \\ & \quad + \mathop \sum \limits_{{{\text{j}} = 1}}^{\text{J}} \mathop \sum \limits_{{{\text{m}} = 1}}^{{{\text{M}} - 1}} {{\updelta}}_{\text{jm}}\, {\text{lnx}}_{{{\text{j}},{\text{it}}}} \,{\text{lny}}_{{{\text{m}},{\text{it}}}}^{ *} + \mathop \sum \limits_{{{\text{j}} = 1}}^{\text{J}} \mathop \sum \limits_{{{\text{k}} = 1}}^{\text{K}} {{\uppsi}}_{\text{jk}} \,{\text{lnx}}_{{{\text{j}},{\text{it}}}} \,{\text{lns}}_{{{\text{k}},{\text{it}}}}^{ *} + \mathop \sum \limits_{{{\text{m}} = 1}}^{{{\text{M}} - 1}} \mathop \sum \limits_{{{\text{k}} = 1}}^{\text{K}} {{\upmu}}_{\text{mk}}\, {\text{lny}}_{{{\text{m}},{\text{it}}}}^{ *} \,{\text{lns}}_{{{\text{k}},{\text{it}}}}^{ *} + {\text{v}}_{\text{it}} \\ \end{aligned} $$
(6)

where \({\text{y}}_{{{\text{m}},{\text{it}}}}^{ *} = \frac{{{\text{y}}_{{{\text{m}},{\text{it}}}} }}{{{\text{y}}_{{{\text{mo}},{\text{it}}}} }}\); \({\text{s}}_{{{\text{k}},{\text{it}}}}^{ *} = {\text{s}}_{{{\text{k}},{\text{it}}}} \times {\text{y}}_{{{\text{mo}},{\text{it}}}}\).\({{\upalpha}},{{\upbeta}}, {{\upgamma}}, {{\updelta}}, {{\uppsi}}\;{\text{and}}\;{{\upmu}}\) are parameters to be estimated. Equation (6) cannot be directly estimated given that \({\text{lnD}}_{\text{H}} \left( {{\text{x}}_{\text{i}} ,{\text{y}}_{\text{i}} ,{\text{s}}_{\text{i}} } \right)\) is not directly observed. This problem can be solved by making use of the logarithmic properties and denoting \({\text{lnD}}_{\text{H}} \left( {{\text{x}}_{\text{i}} ,{\text{y}}_{\text{i}} ,{\text{s}}_{\text{i}} } \right) = {\text{u}}_{\text{i }}\) (this can be interpreted as a one-sided error term which is assumed to account for farm-specific effects following Aigner et al. (1977)). Moving it to the right-hand side of the equation, an estimable form of the model can be obtained as presented in Eq. (7)

$$ \begin{aligned} & - {\text{lny}}_{{{\text{mo}},{\text{it}}}} = {{\upalpha}}_{0} + \mathop \sum \limits_{{{\text{j}} = 1}}^{\text{J}} {{\upalpha}}_{\text{j}}\, {\text{lnx}}_{{{\text{j}},{\text{it}}}} + \frac{1}{2}\mathop \sum \limits_{{{\text{j}} = 1}}^{\text{J}} \mathop \sum \limits_{{{\text{j}}^{\prime} = 1}}^{\text{J}} {{\upalpha}}_{{{\text{jj}}^{\prime } }} \,{\text{lnx}}_{{{\text{j}},{\text{it}}}} \,{\text{lnx}}_{{{\text{j}}^{\prime } ,{\text{it}}}} + \mathop \sum \limits_{{{\text{m}} = 1}}^{{{\text{M}} - 1}} {{\upbeta}}_{\text{m}} \,{\text{lny}}_{{{\text{m}},{\text{it}}}}^{ *} \\ & \quad + \frac{1}{2}\mathop \sum \limits_{{{\text{m}} = 1}}^{{{\text{M}} - 1}} \mathop \sum \limits_{{{\text{m}}^{\prime } = 1}}^{{{\text{M}} - 1}} {{\upbeta}}_{{{\text{mm}}^{\prime } }} \,{\text{lny}}_{{{\text{m}},{\text{it}}}}^{ *} \,{\text{lny}}_{{{\text{m}}^{\prime } ,{\text{it}}}}^{ *} + \mathop \sum \limits_{{{\text{k}} = 1}}^{\text{K}} {{\upgamma}}_{\text{k}} \,{\text{lns}}_{{{\text{k}},{\text{it}}}}^{ *} + \frac{1}{2}\mathop \sum \limits_{{{\text{k}} = 1}}^{\text{K}} \mathop \sum \limits_{{{\text{k}}^{\prime } = 1}}^{\text{K}} {{\upgamma}}_{{{\text{kk}}^{\prime } }} \,{\text{lns}}_{{{\text{k}},{\text{it}}}}^{ *} \,{\text{lns}}_{{{\text{k}}^{\prime } {\text{it}}}}^{ *} \\ & \quad + \mathop \sum \limits_{{{\text{j}} = 1}}^{\text{J}} \mathop \sum \limits_{{{\text{m}} = 1}}^{{{\text{M}} - 1}} {{\updelta}}_{\text{jm}} \,{\text{lnx}}_{{{\text{j}},{\text{it}}}} \,{\text{lny}}_{{{\text{m}},{\text{it}}}}^{ *} + \mathop \sum \limits_{{{\text{j}} = 1}}^{\text{J}} \mathop \sum \limits_{{{\text{k}} = 1}}^{\text{K}} {{\uppsi}}_{\text{jk}} \,{\text{lnx}}_{{{\text{j}},{\text{it}}}} \,{\text{lns}}_{{{\text{k}},{\text{it}}}}^{ *} + \mathop \sum \limits_{{{\text{m}} = 1}}^{{{\text{M}} - 1}} \mathop \sum \limits_{{{\text{k}} = 1}}^{\text{K}} {{\upmu}}_{\text{mk}} \,{\text{lny}}_{{{\text{m}},{\text{it}}}}^{ *} \,{\text{lns}}_{{{\text{k}},{\text{it}}}}^{ *} + \left( {{\text{v}}_{\text{it}} - {\text{u}}_{\text{i}} } \right) \\ \end{aligned} $$
(7)

Here the composed error term \(\varepsilon_{\text{it}} = \left( {{\text{v}}_{\text{it}} - {\text{u}}_{\text{i}} } \right)\) includes \({\text{u}}_{\text{i}}\), the one-sided error term that captures time invariant inefficiency, that is, the distance that separates a farm from the production frontier and it is assumed to have a half normal distribution \({\text{u}}_{\text{i}}\) ~ |N (0, \({{\upsigma}}_{\text{u}}^{2}\))|, and \({\text{v}}_{\text{it}}\) is the standard random term which captures the statistical noise and is assumed to be symmetrically distributed around zero, \({\text{v}}_{\text{it}}\) ~ N (0, \({{\upsigma}}_{\text{v}}^{2}\)). Terms involving the normalising output \({\text{y}}_{{{\text{mo}},{\text{it}}}}\) are null. This is because the ratio \({\text{y}}_{{{\text{m}},{\text{it}}}}^{ *}\) is equal to one. We are however, able to recover the distance function elasticity with respect to the desirable output by making use of the almost homogeneity condition (Cuesta et al. 2009).

3.2 Estimation of Shadow Price

We derive the shadow price of N surplus by employing Shephard duality lemma between the hyperbolic environmental technology distance function and the maximisation of the profitability function (Färe et al. 2002; Zhou et al. 2014; Shaik et al. 2002; Shephard 1970; Färe and Grosskopf 1998; Hadley 1998). Given \({\text{y}}_{\text{m}}\) as the vector of desirable outputs and \({\text{p}}_{\text{m}}\) as its corresponding prices, the shadow price of N surplus can be derived from the profitability maximising function presented in Eq. (8) (Cuesta et al. 2009; Mamardashvili et al. 2016). See derivation steps in Eqs. (8)–(12).

$${{\uprho}}\left( {{\text{x}},{\text{y}},{\text{s}}} \right) = \mathop {\hbox{max} }\limits_{{{\text{y}},{\text{s}}}} \left\{ {{\text{p}}_{\text{m}} \,{\text{y}}_{\text{m}} /{\text{p}}_{\text{s}}\, {{\text{s}}}{:}{\text{D}}_{\text{H}} \left( {{\text{x}},{\text{y}},{\text{s}}} \right) \le 1} \right\}$$
(8)

where \({\text{p}}_{\text{s}}\) is the (unknown) price of the undesirable output.

$$\frac{{p_{m} }}{{p_{s} s}} = \lambda \frac{{\partial D_{H} \left( {x,y,s} \right)}}{{\partial y_{m} }}, \quad m = 1,2 \ldots , M$$
(9)
$$- \frac{{\mathop \sum \nolimits_{m = 1}^{M} p_{m} y_{m} }}{{p_{s} s^{2} }} = \lambda \frac{{\partial D_{H} \left( {x,y,s} \right)}}{\partial s}$$
(10)

Taking the ratio of the last condition to any first-order condition in the first set we obtain

$$\frac{{\mathop \sum \nolimits_{m = 1}^{M} p_{m} y_{m} }}{s} = - {\text{p}}_{\text{m}} \left[ {\frac{{\partial {\text{D}}_{\text{H}} \left( {{\text{x}},{\text{y}},{\text{s}}} \right)}}{{\partial {\text{y}}_{1} }}} \right]^{ - 1} \frac{{\partial {\text{D}}_{\text{H}} \left( {{\text{x}},{\text{y}},{\text{s}}} \right)}}{{\partial {\text{s}}}}$$
(11)

Given that the frontier of the production possibility set is a representation of the locus of points for which the distance function is equal to unity, the ratio of partial derivatives on the right-hand side of Eq. (11) can be expressed as the slope of the relationship between \({\text{y}}_{\text{m}}\) and s at the frontier. That is, by applying the implicit function theorem on the distance function we get :

$$- {\text{p}}_{\text{m}} \left[ {\frac{{\partial {\text{D}}_{\text{H}} \left( {{\text{x}},{\text{y}},{\text{s}}} \right)}}{{\partial {\text{y}}_{\text{m}} }}} \right]^{ - 1} \frac{{\partial {\text{D}}_{\text{H}} \left( {{\text{x}},{\text{y}},{\text{s}}} \right)}}{{\partial {\rm{s}}}} = {\text{p}}_{\text{m}} \left.{\frac{{\partial {\text{y}}_{{m}} }}{{\partial {{s}}}}}\right| _{{{D}_{H} \left( {x,y,s} \right) = 1}}$$
(12)

This can be interpreted as the shadow price of s in terms of \({\text{y}}_{\text{m}}\). That is, the extent to which the revenue from desirable outputs \({\text{y}}_{\text{m}}\) can be reduced if the undesirable output s is reduced by one unit when the point (x, y, s) is on the production frontier. It describes the trade-off between the desirable output and the undesirable output on the boundary of P(x). The implication of this is that, if dairy farmers are both environmentally efficient (\({\text{D}}_{\text{H}} \left( {{\text{x}},{\text{y}},{\text{s}}} \right)\) = 1) and allocatively efficient (all first-order conditions are satisfied), then the shadow price of a unit of s should be the same irrespective of which first-order conditions have been used to estimate it (Mamardashvili et al. 2016).

3.3 Nutrient Budget Methodology

To estimate the N surplus in the dairy farms, we employed the soil surface budget approach, in which gross N surplus is estimated as the difference between total inputs and outputs (Eurostat 2007, 2013). This is because it provides a more meaningful assessment of risk to the aquatic environment compared to farm gate approach (Eurostat 2007, 2013). An outline of the inputs and output variables according to the OECD/Eurostat methodology and the sources of the information used for our analysis is given in Table 1.

Table 1 Terms used in estimation of the gross nitrogen surplus
Full size table

Unlike other variables in the estimation of N surplus, the calculation of N output from grazed grass at the farm level is relatively complex. Previous studies such as Humphreys et al. (2008), Loro et al. (2013) employed expert judgement assuming a fixed amount of nutrient output per hectare. However, such blank assumptions on the amount of pasture consumed is not able to take into consideration the difference in dairy farm management systems and might lead to a biased result on the level on nutrient balance.

To overcome this shortcoming, we developed a feed requirement model based on the difference between the net energy (NE) provided by feed purchased from off the farm (dry matter of concentrates and forages) and the total NE requirements of livestock on the farm for milk production, pregnancy, maintenance, grazing and walking and body weight change (Gourley et al. 2012). Mathematical representation of the model is given in Eq. (13). It can be described as a back-calculation approach based on an accurate description of the number of grazing animals on the farm, the area under consideration and milk production data (McCarthy et al. 2011). The total NE requirements, converted to units of feed for lactation (UFL) and adapted to local farm conditions, are computed based on relevant equations published in the National Research Council publication on “nutrient requirement for dairy cattle” (NRC 2001). It was assumed that 1 kg dry matter of grass equals 1 unit of feed for lactation (UFL) (McCarthy et al. 2011). Stocking rate was expressed in terms of livestock units (LU) per hectare. The amount of nutrient output from grass was then obtained by multiplying the quantity of grazed grass by the N coefficients in grass (Eurostat 2013). This method provides a logical and quantitative framework for analysing between farm differences in productivity and pasture utilisation.

$${\text{NE}}\;{\text{supplied}}\;{\text{by}}\;{\text{grass}} = {\text{Total }}\;{\text{NE}}\;{\text{requirements }} - {\text{Total}}\;{\text{NE}}\;{\text{from }}\;{\text{supplemetary}}\;{\text{feed}}$$
(13)

4 Data and Empirical Specification

The area of study for this paper is the island of Ireland which accommodates two countries; the Republic of Ireland (IE) and Northern Ireland (NI). The later forms part of the United Kingdom. The dataset employed is obtained from two different sources, the Teagasc National Farm Survey (NFS, Republic of Ireland) and the Northern Ireland Farm Business Survey (FBS, Northern Ireland). Each dataset represents a detailed, stratified, nationally representative random sample of farms surveyed annually. Variables captured in both data sources are directly comparable, given that both are components of the EU Farm Accountancy Data Network (FADN). Figure 1 is a map of the study area showing the two countries of the island of Ireland. Although, the dairy system in both countries is relatively grass-based, there is a good degree of variability with respect to production and inputs management (Gillespie et al. 2016; Hennessy et al. 2015). For example, the dairy production system in Northern Ireland is more intensive with higher use of concentrates feed compared to the Republic of Ireland (Adenuga et al. 2018b). The difference in production systems is influenced to a large extent by the operation of a single market for milk quota within the constituent countries of the United Kingdom during the milk quota era which allowed farms in Northern Ireland to purchase or lease milk quota from Great Britain leading to greater productivity growth as opposed to the Republic of Ireland were quota was regionally constrained (Donnellan and Hennessy 2015).

For this study, balanced panel data sets over a period of 10 years (2005–2014) consisting of 1120 observations for 112 specialist dairy farms for the Republic of Ireland and 498 observations from 83 specialist dairy farms over a period of 6 years (2009–2014) for Northern Ireland was extracted and used for analysis. The difference in the length of time for the panel data is due to data limitation for Northern Ireland. A specialist dairy farm here is defined as a system where a minimum of two-thirds of farm standard output is from grazing livestock and dairy cows are responsible for a minimum of three quarters of the grazing livestock output. The variables considered in the analysis are based upon the production process of specialised dairy farms. The five inputs included in the specification of hyperbolic environmental technology distance function include:

  1. 1.

    labour measured in standardized labour units,

  2. 2.

    total utilized agricultural area measured in hectares,

  3. 3.

    capital measured in terms of depreciation values for building and machinery,

  4. 4.

    the number of livestock on the farm measured in standardized livestock units (LU),

  5. 5.

    variable inputs which consist of costs of livestock feed, fertilizers, seed and others measured in monetary units and

The desirable outputs are:

  1. 1.

    revenue from the sales of milk and

  2. 2.

    revenue from the sales of other outputs (sales of crops and other livestock).

The undesirable output

  1. 1.

    N surplus estimated based on the methodology presented in Sect. 3.2 and measured in kg.

A summary statistic of the variables included in the model is given in Table 2 while Table 3 gives a breakdown of the estimation of the N surplus. The stochastic hyperbolic environmental technology distance function following Aigner et al. (1977) based on Eq. (7) is presented in Eq. (14). With i = 1, 2, …, N representing the observed dairy farms in time t = 1, 2, …, T time periods. The variables measured in monetary units were corrected for inflation using the appropriate annual producer price indices published by DEFRA and DAFM. To impose the almost homogeneity condition, the milk output (\({\text{y}}_{1}\)) was chosen for normalising. We also incorporated a time variable to capture the presence of neutral technical change as well as other temporal effects.

Table 2 Structural and socioeconomic variables (averages across the 6 and 10 years period respectively)
Full size table
Table 3 Estimates of gross N balance (GNB) (averages across the 6 and 10 years period respectively)
Full size table
$$ \begin{aligned} & - {\text{lny}}_{{1,{\text{it}}}} = {{\upalpha}}_{0} + \mathop \sum \limits_{{{\text{j}} = 1}}^{5} {{\upalpha}}_{\text{j}} \,{\text{lnx}}_{{{\text{j}},{\text{it}}}} + \frac{1}{2}\mathop \sum \limits_{{{\text{j}} = 1}}^{5} \mathop \sum \limits_{{{\text{j}}^{\prime} = 1}}^{5} {{\upalpha}}_{{{\text{jj}}^{\prime} }} \,{\text{lnx}}_{{{\text{j}},{\text{it}}}} \,{\text{lnx}}_{{{\text{j}}^{\prime} ,{\text{it}}}} + {{\upbeta}}_{2} { \ln }\frac{{{\text{y}}_{{2,{\text{it}}}} }}{{{\text{y}}_{{1,{\text{it}}}} }} + \frac{1}{2}{{\upbeta}}_{22} \left( {{ \ln }\frac{{{\text{y}}_{{2,{\text{it}}}} }}{{{\text{y}}_{{1,{\text{it}}}} }}} \right)^{2} \\ & \quad + {{\upgamma}}_{\text{o}} \ln \left( {{\text{s}}_{\text{it}} \,{\text{y}}_{{1,{\text{it}}}} } \right) + \frac{1}{2}{{\upgamma}}_{\text{oo}} \left( {\ln \left( {{\text{s}}_{\text{it}}\, {\text{y}}_{{1,{\text{it}}}} } \right)} \right)^{2} + \mathop \sum \limits_{{{\text{j}} = 1}}^{5} {{\updelta}}_{{{\text{j}}2}} \,{\text{lnx}}_{{{\text{j}},{\text{it}}}} { \ln }\frac{{{\text{y}}_{{2,{\text{it}}}} }}{{{\text{y}}_{{1,{\text{it}}}} }} + \mathop \sum \limits_{{{\text{j}} = 1}}^{5} {{\uppsi}}_{\text{jo}} \,{\text{lnx}}_{{{\text{j}},{\text{it}}}} \ln \left( {{\text{s}}_{\text{it}}\, {\text{y}}_{{1,{\text{it}}}} } \right) \\ & \quad + {{\upmu}}_{{2{\text{o}}}} { \ln }\frac{{{\text{y}}_{{2,{\text{it}}}} }}{{{\text{y}}_{{1,{\text{it}}}} }}\ln \left( {{\text{s}}_{\text{it}} \,{\text{y}}_{{1,{\text{it}}}} } \right) + \mathop \sum \limits_{{{{\uptau}} = 1}}^{\text{T}} {{\uprho}}_{{{\uptau}}} {\text{d}}_{{{\uptau}}}^{\text{t}} + \left( {{\text{v}}_{\text{it}} - {\text{u}}_{\text{i}} } \right) \\ \end{aligned} $$
(14)

In Eq. (14), \({\text{y}}_{1}\) and \({\text{y}}_{2}\) represent the revenue from the sales of milk (dairy gross output) and the revenue from sales of crops and other livestock (other output) respectively. \({\text{x}}_{1}\) is the standardised labour units (labour), \({\text{x}}_{2}\) is the total utilised agricultural area (land), \({\text{x}}_{3}\) is the capital in terms of the depreciation values for building and machinery (capital), \({\text{x}}_{4}\) is the number of livestock on the farm (livestock units) and \({\text{x}}_{5}\) is the costs of livestock feed, fertilizers, seed and other variable inputs (variable inputs). s is N surplus. \(\upalpha,\upbeta,\upgamma,\updelta,\uppsi,\upmu\;{\text{and}}\;\uprho\) are parameters to be estimated. All other variables are as earlier defined. Following standard practice in the literature all variables are scaled by their geometric mean to avoid convergence issues in the maximum likelihood algorithm and allow for the interpretation of the estimated first order parameters as elasticities at the sample mean (Färe et al. 2005; Cuesta et al. 2009). We employed the standard maximum likelihood technique (Battese and Coelli 1988) to estimate the panel data specification using STATA (Belotti et al. 2013). The time invariant efficiency estimates EE were calculated for each farm by using the point estimator proposed by Battese and Coelli (1988):

$${\text{EE}} = {\text{E}}\left( {{\text{e}}^{{ - {\text{ui}}}} | {\upvarepsilon\text{i}}} \right)$$
(15)

where E is the mathematical expectation operator. The model expressed in Eq. (14) was analysed separately for Northern Ireland and the Republic of Ireland.

5 Results and Discussion

5.1 Environmental Efficiency

The maximum likelihood estimates (MLE) and associated standard errors of the stochastic hyperbolic environmental technology distance function model for both Republic of Ireland and Northern Ireland are presented in Table 4. The estimated parameters for desirable and undesirable outputs as well as the inputs all have the expected sign at the mean of the data and are significantly different from zero. For example, the negative sign of the inputs and undesirable output parameters implies that any increase in the amount of these variables would increase the value of the distance functions. The reverse is true for the desirable output. These results provide an indication that the monotonicity conditions are fully satisfied at the sample mean for the estimated hyperbolic environmental technology distance functions (Cuesta and Zofío 2005). The average environmental efficiency estimates for the Republic of Ireland and Northern Ireland are 0.89 and 0.92 respectively. The implication of this is that on average, dairy farmers in the Republic of Ireland can improve their productive performance by increasing desirable output from dairy production by 12.35% (1/0.89 = 1.123) and simultaneously contract N surplus by 11% (1 − 0.89 = 0.11). For Northern Ireland, dairy farmers can improve productive performance by increasing desirable output by 8.7% (1/0.92 = 1.087) and simultaneously contract N surplus by 8% (1 − 0.92). In explaining our results, it should be emphasized that higher environmental efficiency level does not necessarily imply higher environmental management system or guarantee sustainability of the dairy production system (Picazo-Tadeo et al. 2011). This is because the coefficient of environmental efficiency only measures the relative level of environmental burden in relation to the volume of economic activity within the sample of farms. The results however, imply that there is greater potential for the average dairy farm in the Republic of Ireland compared to Northern Ireland to improve environmental performance relative to the best performing farms in their respective countries.

Table 4 MLE estimates of the translog hyperbolic distance functions for dairy farms in the island of Ireland
Full size table

The parameter estimates of the year variable \(({{\uprho}}_{{{\uptau}}} )\) which is intended to capture the neutral technical change has the expected negative sign and was statistically different from zero. This gives an indication of the presence of technical progress in both countries over the years with a value of 2.8% for the Republic of Ireland and 4.2% for Northern Ireland. The technical progress values give an indication that the leading dairy farms in both countries are able to increase dairy production while making use of more environmentally friendly technologies. The higher values for Northern Ireland may be connected to the fact that, unlike the Republic of Ireland where milk quota was binding during the milk quota years, in Northern Ireland farmers were able to purchase quota at low cost from other parts of the United Kingdom and were therefore able to maintain or increase cow numbers and increase yield per dairy cow by feeding more concentrate feeds.

5.2 Shadow Price of Nitrogen Surplus

The shadow price of N surplus with respect to the desirable outputs (milk and non-milk outputs) is estimated based on Eq. (11) and the results are presented in Table 5. We inflate the frontier shadow price by multiplying the ratio of the average value of output by the average value of N surplus because all input and output variables have been normalized to estimate the unknown parameters (Färe et al. 2005; Tang et al. 2016). The price of the desirable outputs in the model are also implicitly normalised to 1 given that they are measured in monetary units (Mamardashvili et al. 2016; Tang et al. 2016).

Table 5 Shadow price estimates of N surplus in dairy farms
Full size table

The results presented in Table 5 shows a relative increase in the shadow price of N surplus with respect to milk output and non-milk output in both countries over the years. This result provides an indication of lower substitution possibilities between the desirable output and N surplus. In other words, it has become increasingly costly to reduce N surplus in the dairy production systems of both countries over time. This upward trend in shadow price of N surplus is consistent with those of Bokusheva and Kumbhakar (2014), Shaik et al. (2002) and Hailu and Veeman (2000).

On average, the shadow price is higher for non-milk output compared to the milk output in all the years with higher differences observed in Northern Ireland compared to the Republic of Ireland. This result is similar to that obtained by Mamardashvili et al. (2016) in which they found a higher shadow price for N surplus when measured with respect to non-milk output compared to milk output.

The discrepancies in shadow price with respect to milk and non-milk output can also provide an indication of the allocative efficiency of the dairy farms. This is because, for a farm to be fully allocatively efficient, the shadow price with respect to milk and non-milk output should be equal. This is however, not the case in both countries where the ratio of shadow price with respect to non-milk output to the shadow price with respect to milk output is greater than 1 across all years. It can therefore be concluded that the dairy farms in both countries are not allocatively efficient.

The shadow price evaluated at the mean of the data with respect to milk output and non-milk output for Northern Ireland have a value of £5.26 (€ 6.2) and £10.17 (€11.90) respectively. Whereas for the Republic of Ireland the values are €4.02 and €5.37 respectively. These values can be interpreted as the opportunity cost of reducing an additional unit of N surplus in terms of forgone revenue from milk and non-milk output once all inefficient production has been eliminated.

These results show that the marginal costs of N pollution abatement in terms of farm revenue is higher in Northern Ireland compared to the Republic of Ireland. In other words, it is cheaper to control for N pollution in the Republic of Ireland compared to Northern Ireland. The difference in shadow prices might be traced to the heterogeneity in dairy production systems across the two countries. While in the Republic of Ireland, the pasture-based system with higher grazed grass per hectare prodominates (Table 2), in Northern Ireland feed import-based concentrate system with lower grazed grass per hectare tend to dominate. Another likely reason for the higher shadow price for N surplus in Northern Ireland may be attributed to the higher revenue per farm resulting from higher yield per dairy cow (Table 2).

It should be noted however that within each region, there is a reasonable degree of variation in the spectrum of shadow prices across the dairy farms and across all years. For example, for the Republic of Ireland with respect to milk output, the 25th percentile is 2.53 €/kg, while the 75th percentile is 5.08 €/kg and the maximum value is 29.05€/kg. With respect to non-milk output, the 25% percentile has a value of 3.26 €/kg and the 75th percentile has a value of 6.75 €/kg with a maximum value of 50.63 €/kg. For Northern Ireland, the 25th percentile with respect to milk output is 3.01 €/kg while the 75th percentile is 7.48 €/kg and the maximum value is 38.94 €/kg and with respect to non-milk output, the 25th percentile is 3.15 €/kg and the 75th percentile is 11.29 €/kg with a maximum value of 162 €/kg.

In the interpretation of our results, it should be noted that the estimated shadow price is a measure of opportunity costs based on the assumption of full efficiency of the dairy farms. That is, farms located on the production possibility frontier. The implication of this is that the average shadow price of farms located within the production frontier may not be as high as what we have estimated. (Murty et al. 2007). Also, in trying to compare these results with previous studies in the literature, some care is needed. This is because of differences in the underlying data, units of expression, scope, model, and estimation methodologies both in terms of N surplus and the shadow price estimation.

Taking the above into account, we compare our results to a limited extent to that obtained by Mamardashvili et al. (2016) which employed the hyperbolic distance function in the context of Swiss dairy farms. Our values for both countries are lower, which may be due to the fact that our study is based mainly on conventional dairy farms, whereas the Mamardashvili et al. (2016) study combines conventional and organic farms. Results from previous studies have shown that shadow prices of undesirable outputs are usually higher for organic farms compared to conventional farms (Arandia and Aldanondo-Ochoa 2011; Mamardashvili et al. 2016).

Another reason for the difference might be explained in terms of the mean N surplus per hectare. While the mean N balance for both countries in our study is greater than 100 kg/ha, it is about 53 kg/ha for the Mamardashvili et al. (2016) study. The implication of this is that more N must have been abated by the Swiss dairy farms over the years so that further abatement is more expensive at the margin (assuming that the marginal cost of abatement is increasing). Our result is however higher than that of Malikov et al. (2016) and relatively lower than that of Bokusheva and Kumbhakar (2014) which employed a different methodology using the Farm Data Accountancy Network (FADN) data for Dutch dairy farms. Higher values compared to ours were also obtained by Hadley (1998). This again, may be due to differences in the methodology employed.

5.3 Nitrogen Pollution Costs Ratio of Dairy Farms

The total cost of N pollution per farm was estimated by multiplying the derived average shadow price of N surplus with respect to milk output by the average estimated volume of N surplus per farm for each year. The results of our estimation showed that it will cost about €28,149 and £79,959 (€93,552) per farm to fully abate N surplus for the Republic of Ireland and Northern Ireland respectively. These values constitute about 22% and 33% respectively of revenue from milk output over the stipulated time period. Similar values were obtained by Mamardashvili et al. (2016). These high costs of abatements might contribute to the difficulties in the political implementation of environmental tax on N surpluses. It is important to bear in mind that these estimated costs refer to the full abatement of the N surplus. Achieving full abatement is likely to be difficult to achieve in practice, but there are currently no universally defined limits of allowable N surplus in the EU Common Agricultural Policy (CAP) legislation. Hence, the pollution costs will be lower if some level of N surplus is allowed in soil.

Given the heterogeneity in the level of outputs across farms in both countries and to be able to relate pollution costs to dairy output, we computed the pollution costs ratio for each farm by multiplying the derived average shadow price of N surplus with respect to milk output by the average estimated volume of N surplus per farm for each year. This provides an opportunity for spatial and temporal comparison. An average pollution cost ratio is obtained by dividing the aggregated pollution costs by the aggregated value of output from dairy production across all the farms. Figure 2 shows the annual average pollution costs ratio for Northern Ireland (NI) and the Republic of Ireland (IE) over the years considered.

Fig. 2
figure 2

Annual average N pollution costs ratio

Full size image

It can be observed that the N pollution costs ratio is higher for Northern Ireland compared to the Republic of Ireland. Whereas there has been a relative increase in the N pollution costs ratio in Northern Ireland from about 34% in 2009 to about 48% in 2014, the reverse is the case for the Republic of Ireland which apart from the upward surge in 2009, has experienced a relative decline from about 32% in 2005 to about 21% in 2014. The higher value of pollution costs ratio for Northern Ireland reflects the higher shadow price of N surplus with respect to output from dairy production.

5.4 Factors Influencing Pollution Costs Ratio

To analyse the factors influencing the N pollution costs ratio, we employed the within-between (WB) farm random effect econometric modelling approach. Studies have shown that the approach is more attractive and outperforms the Random (RE) or Fixed (FE) effects models that are normally used to analyse panel and time series data in the economics and social science literature (Dieleman and Templin 2014; Bell and Jones 2015). This is because unlike the RE and FE models, it explicitly models the within (time) and between (individual) effects in a single model of the RE modelling framework, producing smaller absolute errors and within estimates of time variant variables (Bell and Jones 2015; Mela et al. 2016; Schunck 2013; Vincens and Stafström 2015; Teachman 2011; Fairbrother 2013; Adenuga et al. 2018b). The approach is flexible and does not require the assumption of exogeneity of covariates and the normality of residuals which might lead to biased results in the usual RE models (Mundlak 1978; Snijders and Bosker 2011; Bell and Jones 2015). The model specification is given in Eq. (16):

$${\text{y}}_{\text{it}} = {{\upbeta}}_{0} + {{\upbeta}}_{1} \left( {{\text{x}}_{\text{it}} - {\bar{\text{x}}}_{\text{i}} } \right) + \upgamma {\bar{\text{x}}}_{\text{i}} + {{\upbeta}}_{2} {\text{z}}_{\text{i}} + {{\upmu}}_{\text{i}} + {\upvarepsilon}_{\text{it}}$$
(16)

where yjt is the dependent variable for individual farm i at time t, which in this case is the N pollution costs ratio, \({\text{x}}_{\text{it}}\) is a level 1 variable for individual farm i at time t that varies over time within and between the dairy farmers, \({{\upmu}}_{\text{i}}\) is the single, aggregated, unobserved group-level effect otherwise referred to as the level 2 error and the random intercept, and \({{\upvarepsilon }}_{\text{it}}\) is the level 1 error term. \({{\upbeta}}_{1}\) gives the within-effect estimate that is, the fixed-effects estimate, \({{\upgamma}}\) estimates the between effect while \({{\upbeta}}_{2}\) is a measure the effect of level 2 variables. \({\bar{\text{x}}}_{\text{i}}\)  is the group-level mean of the explanatory variables included in the model and estimated as \({\bar{\text{x}}}_{\text{i}} = {\text{n}}_{\text{i}}^{ - 1} \sum\nolimits_{{{\text{t}} = 1}}^{{{\text{n}}_{\text{i}} }} {{\text{x}}_{\text{it}} } ,\) while γ is the ‘contextual’ effect which explicitly models the between effect. The within and between effects are clearly separated and the correlation between \({\bar{\text{x}}}_{\text{i}}\) and \(\left( {{\text{x}}_{\text{it}} - {\bar{\text{x}}}_{\text{i}} } \right)\) will be zero which can facilitate model convergence.

To estimate the within and between effects in one model, we first generate the cluster-specific mean of \(({\text{x}}_{\text{it}} )\). The second step is to create the deviation scores, which is also known as group mean centering used to estimate the within effect. A number of variables \(({\text{x}}_{\text{it}} )\) were hypothesized to influence the dependent variable at the within and between level. They include:

  1. 1.

    the total utilised agricultural area (farm size) measured in hectares,

  2. 2.

    the age of the farm manager (age) in years,

  3. 3.

    stocking densities (stocking density) measured in livestock units per hectare,

  4. 4.

    amount of forage consumed (Grass grazed) measured in kg dry mater per hectare,

  5. 5.

    Farmers with off-farm employment (Off-farm income), measured as a dummy variable

  6. 6.

    investment per cow (Invest. per cow) measured in €/cow,

  7. 7.

    Farmers who engage a milk recording activities relating to the performance of individual cow on the dairy farm (Milk recording) measured as a dummy variable,

  8. 8.

    Farmers that participate in discussion groups on good practices in managing a dairy enterprise (Discussion group) measured as a dummy variable and

  9. 9.

    farmers with access to farm advisory services (Advisory contact) measured as a dummy variable.

The econometric model is estimated separately for Northern Ireland and the Republic of Ireland. Due to data limitation, some of the variables were not included in the Northern Ireland model. The analyses employed the feasible generalized least squares (FGLS) using STATA econometric software. The results of the model analysis are presented in Table 6.

Table 6 Determinants of nitrogen pollution costs ratio: within-between model estimates
Full size table

The two sets of coefficients represent the between and within effects of the time variant variables which are explicitly modelled. The results of our analysis showed that for the Northern Ireland model, stocking density and the amount of grazed grass per hectare were the statistically significant variables influencing pollution costs ratio at the within and between level whereas for the Republic of Ireland model, age and investment per cow is found to be the significant variables at the within and between level. Farm size and age of the farmer are found to be statistically significant only at the between level for the Northern Ireland model and for the Republic of Ireland model advisory contact and milk recording is found to be statistically significant only at the within effect level. Only age at the between effect level is significant in both the Northern Ireland and the Republic of Ireland model. This difference in the significant variables may be linked to the differences in dairy production systems of both countries. The relatively small standard errors justify the adoption of the within-between approach.

Stocking density has a positive relationship with pollution costs ratio in Northern Ireland. This implies that an increase in stocking density results in an increase in the pollution costs ratio. Though a negative relationship is observed for the Republic of Ireland, it is however not significant. The negative relationship of age to pollution costs ratio suggest that older farmers are more likely to have a lower pollution costs ratio. This may imply that the older farmers are more experienced and therefore are more responsive to potentially more environmentally friendly technologies. It may also be the case that the older farmers are correlated with lower stocking density. Older farmers on larger land areas would be more likely to restrict stocking density to limit the amount of labour they need to contribute to the dairy farm. The amount of forage consumed in grazed grass had an inverse relationship with pollution costs ratio in Northern Ireland. It is however not significant in the Republic of Ireland model which may reflect less variation in the amount of forage consumed. This implies that increasing the amount of grass grazed will result in a decline in the pollution costs ratio. The same analogy applies to land which was significant at the between level in the Northern Ireland model. Pollution costs ratio tends to be reduce with higher investment per cow as shown in the Republic of Ireland model at the within and between level. Finally, the results indicate that dairy farmers’ access to advisory contact and the recording of milk outputs also tend to reduce pollution costs ratio.

6 Conclusion

Analysing environmental performance and the cost of negative externalities in the production process is essential to promote sustainable production practices and consequently contribute towards a production process that is more environmentally sustainable. This paper evaluates the performance of dairy farms in the two countries that make up the island of Ireland and estimated the value of agricultural externalities in the form of N surplus by employing the duality between the environmental technology hyperbolic distance function and the profitability function. The pollution costs ratio and its determinants in dairy production systems is also analysed. The results of our analyses show the potentials to simultaneously increase dairy outputs and reduce environmental impacts. A relatively high level of shadow prices of N surplus is obtained in both countries with the cost of abating one unit of N surplus in dairy farms being higher in Northern Ireland compared to the Republic of Ireland. A relatively increasing trend in the shadow price of N surplus is also observed suggesting limited opportunities to reduce N surplus in the efficient farms without substantial cuts in desirable outputs.

Some important implications for policy can be drawn from these findings. First, hyperbolic environmental efficiency scores for both countries show that there are potentials in both countries to simultaneously increase dairy production outputs and reduce N surplus with available resources or technology. The results of this study also provide a possibility for the internalisation of externalities in dairy production in the island of Ireland as it gives an indication of how much has to be given up in order to abate one more unit of N pollution in each farm. Given the high value of the pollution costs especially in Northern Ireland and the fact dairy farms closer to the production frontier have higher shadow prices, reflecting the greater opportunity cost of reducing the undesirable output by one unit, a low cost approach to reduce environmental pressures will be to encourage farmers still operating below the production frontier to adopt the best farming techniques and better input management. This can be achieved through improved nutrient and grazing management plans, increased investment per dairy cow to raise performance, proper management of stocking density and effective recording of dairy cow performances.

Some caution may be needed in the interpretation of results however. This is because the shadow price estimate is only a short-run partial equilibrium calculation to reflect the amount of revenue forgone to achieve reductions in N surplus at the margin. This value is likely to change in the long-run with the development of improved environmental technologies and practices. Also, the gross N balance estimated for the dairy farms gives only an indication of the potential risk to the environment and does not constitute actual risk which apart from economic and management practices is influenced by other factors. Further research will be required in the form of soil test analysis to ascertain the extent to which the high nutrient balances translates into water quality or other environmental degradation problem.