Abstract
Linkages between Emissions Trading Systems are deemed an important element of the future climate policy landscape. They are, however, difficult to agree and remain few and far between. Temporary restrictions on permit trading have potential to facilitate and gradually approach unrestricted, full linkage. We compare the relative merits of several link restrictions in this respect, namely quantitative transfer limits, border taxes on transfers, exchange and discount rates, and unilateral linkage. To this end, we develop a simple model to have a unifying framework which, in conjunction with lessons we draw from real-world experiences, serves as a basis for a broader, policy-oriented discussion. While quantitative restrictions seem to be the natural route to full linkage, they can lead to uncertain distributional effects and weaken price signals. These aspects are mitigated under a border permit tax, but this policy seems harder to implement. Exchange rates have potential to adjust for programmes’ stringencies and raise ambition over time, but can be challenging to select. As experience corroborates, unilateral linkage can be a convenient approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Linkages between Emissions Trading Systems (ETSs) are deemed a key element of the future climate policy landscape (Bodansky et al. 2016; Mehling et al. 2018).Footnote 1 Indeed, for many parties to the Paris Agreement, one of the instruments of choice to deliver on the pledged emissions reductions is carbon markets, 21 of which are in operation along with others in the pipeline (ICAP 2018). Against this backdrop, linkage has become high on the climate policy agenda because it has potential to unleash cost-efficiency gains and help ratchet up ambition. Although most jurisdictions with operating or planned ETSs have engaged in some form of linking negotiations, links are difficult to agree and remain few and far between.
Indeed, the multi-faceted nature of linkage as well as growing heterogeneity in market designs and governance frameworks pose many challenges to prospective partners (Ranson and Stavins 2016). First, discrepancies in autarky prices reflect different ambition levels or views about the desirable price signal (Fankhauser and Hepburn 2010).Footnote 2 Although a wide autarky price gap would increase attendant economic linkage gains, this may also raise concerns about rent transfer, equity, exported abatement co-benefits and so on, thereby impeding on the political feasibility of a link. Second, a certain degree of design harmonization is required to ensure market compatibility and avoid disruptions to the linked system, which also reduces regulatory autonomy (Jaffe et al. 2009).Footnote 3 Third, even when jurisdictions have compatible systems and are seeing eye to eye in terms of ambition, there are still risks that link outcomes do not unfold as anticipated. For instance, linkage creates exposure to ‘imported risks’, i.e., developments originating abroad that propagate throughout the linked system (Flachsland et al. 2009).
Therefore, forging linkage agreements that reconcile and accommodate every party’s interests is proving difficult and the most suitable way for interconnection may well fall short of a full, unrestricted link, at least in the near term. Two types of approaches can be contemplated to palliate the acknowledged difficulties in initiating linkage. First, interties through a common hub might constitute a first step toward further market integration, e.g. networking or indirect linkage via offsetting.Footnote 4 For instance, Jaffe et al. (2009), Tuerk et al. (2009) and Fankhauser and Hepburn (2010) conceived of a progressive mechanism of market integration via unilateral connections to the Clean Development Mechanism, envisaged as a common hub in the Kyoto era.Footnote 5 Second, permit trade restrictions might be established in the perspective of full linkage. According to Mehling and Haites (2009), «a bilateral link can be approached gradually; quantity restrictions could be applied to the other scheme’s units initially and can be loosened over time as the effects [associated with the link] become clear».
In essence, restrictions provide levers to adjust for the reach of the link and their potential is threefold. First, they can contain some link-induced effects (e.g., price variation or abatement relocation) that otherwise stymie link formation (Jaffe et al. 2009; Schneider et al. 2017).Footnote 6 Second, they can provide leverage in linkage negotiations through induced rents or revenues (Gavard et al. 2016). Third but not least, they can help gradually overcome some obstacles to full linkage while giving a taste of it, essentially facilitating negotiations by breaking down a lengthy linking process into progressive steps in the sense of ‘linking by degrees’ (Burtraw et al. 2013).Footnote 7 Our focus primarily lies on the latter aspect. Indeed, such a gradual approach and the various forms it may take have not yet been analyzed carefully.
We consider three main types of link restrictions, namely quantitative transfer limits, border taxes on permit transfers and exchange rates on permits’ compliance values. We also discuss two other forms of restrictions, namely unilateral linkage and discount rates. To evaluate their relative effects we use a partial-equilibrium model of linkage between two markets in a static and deterministic framework. Our stylized model is simple which offers analytical tractability and, crucially, enables us to compare all types of link restrictions in a unifying framework.Footnote 8 This greatly enhances insight and constitutes our first contribution.
No less importantly, our model has enough structure to highlight key differences across restrictions. In particular, we adopt a descriptive approach in comparing their relative implications in terms of cost efficiency, location and volume of abatement, price formation and inter-jurisdictional distributional aspects. By design, therefore, we lack a normative criterion for establishing a clear ranking between them.Footnote 9 However, we take our modelling results, along with lessons we draw from real-world experiences with emissions trading and linkage, as a basis for a policy-oriented discussion of the comparative merits of each restriction—thereby offering a policy menu, as it were—especially in their ability to initiate linkage and gradually scale up the link. This is our second contribution.
Restrictions are distortionary and drive a wedge between jurisdictional prices relative to a full link.Footnote 10 Hence, they create a trade-off between eliminating some impediments to linkage and undermining a fundamental reason for linking in the first place, i.e., cost efficiency. More precisely, by fixing the maximum authorized net permit transfer, a quantitative restriction provides a direct quantity handle on the reach of the link but the ratio of inter-system price convergence is unknown ex ante. Symmetrically, a border tax sets the price ratio but there is uncertainty about the resulting permit transfers. In both cases, the restricted link outcomes are comprised between autarky and full linkage, and aggregate emissions are constant. Just like a border tax, an exchange rate specifies the ratio of jurisdictional marginal abatement costs in equilibrium but further alters the relative compliance value of permits. Aggregate emissions are thus allowed to vary as a result of inter-system permit trading.
On the face of it, quantitative restrictions seem to be the natural route to full linkage between two quantity instruments. However, under a binding quantitative restriction two distinct jurisdictional prices coexist and inter-system transaction prices may not reflect marginal abatement costs, which can generate uncertainty about price formation and undesirable price fluctuations. The binding restriction also generates a scarcity rent whose distribution across jurisdictions is not clear ex ante. Quantitative restrictions can thus lead to uncertain distributional effects and weakened price signals, which may impair the transition to a full link.
Some of these aspects can be mitigated under a border tax on permits. First, since the price ratio is fixed by the tax rate, there should be less undesirable price fluctuations and transaction prices should convey better information on marginal abatement costs. Second, where a quantitative limit creates a rent whose inter-jurisdictional distribution is uncertain, a tax raises revenues collected by a given jurisdiction. Some distributional aspects of the link can thus be better managed and tax revenues can be seen as a form of inter-jurisdictional transfers which might help spur cooperation. Border taxes, however, may be more complicated to implement and pursue legislatively speaking, for instance at the EU level.
By altering the fungibility of jurisdictional abatement efforts, exchange rates can be employed to adjust for differences in programmes’ stringencies—and potentially other economic as well as non-economic criteria. In addition, we show how exchange rates, when skillfully selected, have potential to increase ambition over time. On the flip side, however, difficulties precisely pertain to the selection and subsequent adjustment of the exchange rate, which might possibly lead to environmental and economic outcomes worse than autarky.
Therefore, this analysis allows us to pinpoint comparative advantages and weaknesses for each restriction. Although there is no ‘ideal’ transitional restricted linkage, we finally show how experience suggests that unilateral linkage—whereby permits can flow in one direction but not vice versa—can be a practical way of gradually approaching a full, two-way link.Footnote 11
By comparing all types of restrictions in a unifying framework, we complement and provide an analytical underpinning to Schneider et al. (2017). Closer to our model, but conceptually different, Rehdanz and Tol (2005) and Eyckmans and Kverndokk (2010) consider trade restrictions as an expedient for importing jurisdictions to deter exporting jurisdictions from issuing additional permits relative to autarky—a perverse effect occurring when inter-jurisdictional permit trading in the future is anticipated as first shown by Helm (2003).Footnote 12
The rest of the related literature largely resorts to CGE-based simulations. For instance, Bernstein et al. (1999), Bollen et al. (1999) and Criqui et al. (1999) compared the economic consequences of different emissions trading scenarios to understand the opportunity cost of quantitative restrictions under the Kyoto Protocol.Footnote 13 In particular, Ellerman and Sue Wing (2000) demonstrated the monopsonistic effects and rents induced by restrictions on permit imports. More recently, trade restrictions gained renewed attention in the context of linking and networking. For instance, Burtraw et al. (2017) quantify the impacts of a link between the California ETS and RGGI with a 3-for-1 exchange rate in comparison with full linkage (1-for-1 trading) and Gavard et al. (2016) appraise the benefits of a quantity-restricted link between China and the US (or Europe).Footnote 14
In practice, restrictions have been used to regulate offset credits for ‘supplementarity’ reasons in the form of both quantitative and qualitative limits on compliance usage and discount rates on compliance value (Trotignon 2012; Braun et al. 2015; Gronwald and Hintermann 2016).Footnote 15 To the best of our knowledge, the closest example of border taxes on inter-jurisdictional abatement transfers was on exports of Chinese Certified Emission Reductions, whose purported objective was to split the CDM rent between the government and projects owners (Liu 2010; Zhu 2014). The distortionary effects, tax incidence and revenue potential of the CDM levy were also analyzed by Fankhauser and Martin (2010). So far, exchange rates have not been used to regulate uniformly-mixed pollutants but are contemplated in the context of networking. Usually they are advocated for non-uniformly mixed pollutants to account for the heterogeneity in both pollutants and reception points, and were for instance considered in the ozone-targeting RECLAIM programme (Tietenberg 1995; Johnson and Pekelney 1996).Footnote 16 Finally, linkage has sometimes been initiated via restrictions, as attest transitional one-way links integrating Norway and the European aviation sector to the EU ETS.
The remainder proceeds as follows. Section 2 sets forth the unifying modelling framework. Section 3 describes the implications of each link restriction analytically. Section 4 provides a policy discussion on the relative merits of each restriction with a special focus on the transition to full linkage. Section 5 concludes. An Appendix contains the analytical derivations and proofs (A), numerical simulations (B) and endogenizes domestic cap selection (C).
2 Modelling framework
There are two jurisdictions 1 and 2 with domestic ETSs in place to regulate uniformly-mixed pollution.Footnote 17 Permits markets are competitive and we abstract from market designs to single out restriction-specific effects.Footnote 18 We let \(e_i\) denote jurisdiction i’s emission level for \(i \in \{1,2\}\). For clarity and without loss of generality, jurisdictions have the same unregulated emission level \(e_0\) and binding cap on emissions \(\omega < e_0\).Footnote 19 They thus face the domestic abatement target \(a=e_0-\omega >0\). For comparability, we assume caps are enforced under autarky, full linkage and all other forms of restricted linkages. As we make clear below, it does not matter how permits are handed out for the purpose of our analysis.
We consider a representative firm in each jurisdiction, i.e. the aggregate of all firms located within its geographical boundaries (Montgomery 1972; Krupnick et al. 1983). Abatement costs \(C_i\) in jurisdiction i are increasing and convex in the abatement level \(a_i=e_0-e_i \ge 0\) with \(C_i(0)=0\). For analytical tractability and as is standard practice, these functions are equipped with a quadratic specification (Newell and Stavins 2003). Without loss of generality and up to a translation of the results the linear term is omitted for convenience and we let \(c_i\) denote jurisdiction i’s linear marginal abatement cost slope. That is, the higher \(c_i\) the less sensitive (i.e., elastic) i’s emissions (\( {\rm d} e_i\)) to a shift in the permit price (\({\rm d} \tau \)) since \({\rm d} \tau = c_i {\rm d} e_i\). In other words, jurisdictions are identical but for abatement technology and \(1/c_i\) measures jurisdiction i’s flexibility in abatement.
Autarky Compliance cost minimization under autarky in jurisdiction i requires
Because abatement is costly, jurisdictions emit up to their binding caps and \(\tau _i=c_ia\) denotes i’s autarky permit price. When autarky prices differ across jurisdictions, cost efficiency can be improved upon by relocating some abatement from the high-price to the low-price system. Let jurisdiction 1 (resp. 2) be the high-price (resp. low-price) system, i.e., \(\tau _1 > \tau _2\). Therefore, jurisdiction 1 has less flexibility in abatement than jurisdiction 2, i.e., \(1/c_1<1/c_2\) and the natural direction of the net inter-jurisdictional permit flow is from 2 to 1.
Full linkage Jurisdictional permits are fungible, i.e. mutually recognized as valid compliance instruments in either jurisdiction, and can flow both ways without limitation. Abatement thus occurs where it is least expensive. At the full-linkage equilibrium joint compliance costs with the overall emissions cap \(2\omega \) are minimized, that is
We let \(\Delta ^* > 0\) denote the equilibrium variation in emissions in jurisdiction 1 as a result of full linkage relative to autarky. As the linked market clears, the full-link equilibrium is entirely characterized by
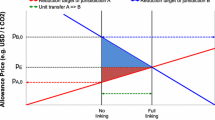
where \(\tau ^*\) is the full-link equilibrium price. With quadratic abatement costs it comes
where \(1/c=1/c_1+1/c_2\) denotes the flexibility in abatement of the linked system. Overall abatement is the same as under autarky but is now apportioned across jurisdictions in proportion to their flexibility in abatement, i.e., jurisdiction i abates \(\tau ^*/c_i\) in equilibrium. That is, cost efficiency obtains and the autarky price differential is arbitraged away. The situation is graphically depicted in Fig. 1 where the thick-edged triangles demarcate the jurisdictional efficiency gains from the full link, \(\Gamma _i^*=c_i\Delta ^{*2}/2=(\tau _i-\tau ^*)^2/(2c_i)\).Footnote 20 Note that they are proportional to the square of the autarky-linking price wedges and that aggregate efficiency gains are distributed in inverse proportion to flexibility, i.e., \(\Gamma _1^*/\Gamma _2^*=c_1/c_2\).
Autarky and full-linkage equilibria. Baselines (\(e_0\)) and domestic caps (\(\omega \)) are common to both jurisdictions. \(c_i\) and \(\tau _i\) denote jurisdiction i’s marginal abatement cost slope and autarky permit price. \(\Delta ^*\) and \(\tau ^*\) denote the full-link equilibrium transfer volume and permit price. c is the marginal abatement cost slope of the linked market. Area \(\Gamma _i^*\) demarcates the efficiency gains accruing to jurisdiction i under unrestricted permit trading
Jurisdictional gains Our focus lies on efficiency and inter- (but not intra-) jurisdictional distributional aspects of linkage. That is, we treat each jurisdiction as a monolithic entity comprising the regulatory authority and the firms, which are themselves further aggregated into a representative firm. In the following when we refer to jurisdictional gains, we thus implicitly refer to the net combination of efficiency gains from linkage accruing to firms and the asset value created by carbon pricing (i.e., the monetary value of freely-allocated permits for firms and auction proceeds for the regulator). This simple structure will prove sufficient for salient divergences between link restrictions to emerge although we acknowledge that intra-jurisdictional distributional aspects can be key in assessing the relative political-economy implications of link restrictions.Footnote 21
In this context, note also that the permit allocation method is irrelevant as it influences intra-jurisdictional gains from linkage but not the net jurisdictional gains. Consider jurisdiction 1 for instance. As a result of the link, if permits are auctioned, firms would save \((\tau _1-\tau ^*)\omega \) in purchasing permits at auctions which would exactly offset the loss in proceeds for the regulator. In turn, the net jurisdictional gains amount to the efficiency gains \(\Gamma _1^*\) just as with free allocation. More specifically, with free allocation linkage is always beneficial on net for the representative firm but we cannot distinguish between ‘winning’ and ‘losing’ firms within jurisdiction 1—here, for instance, selling (resp. buying) firms that are worse (resp. better) off from the link-induced price decrease.Footnote 22
3 Relative Implications of Link Restrictions
3.1 Linkage with Quantitative Limits on Permit Transfers
Consider that jurisdiction 1 limits net imports of permits for compliance or alternatively, that jurisdiction 2 imposes a limit on the net quantity of permits it is willing to export. Either way, we assume the restriction to be binding and let \(\alpha \in \left[ 0;1\right] \) denote the allowed share of the cost-efficient, unrestricted transfer.Footnote 23 Abatement transfer is thus restricted to \(\bar{\Delta }(\alpha )=\alpha \Delta ^*\) and the level of abatement undertaken by jurisdiction 1 (resp. 2) is \(a-\bar{\Delta }(\alpha )\) (resp. \(a+\bar{\Delta }(\alpha )\)). On the face of it, a quantitative restriction should thus limit the reach of the link and associated impacts, i.e. its implications should be comprised between autarky and full linkage. As it turns out, there are more subtle implications.
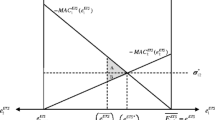
The convergence in jurisdictional shadow prices is incomplete and cost efficiency does not obtain. The restriction \(\alpha \in (0;1)\) drives a wedge between these two prices denoted \(\bar{\tau }_1(\alpha )=c_1(a-\bar{\Delta }(\alpha ))\) and \(\bar{\tau }_2(\alpha )=c_2(a+\bar{\Delta }(\alpha ))\) such that \(\tau _1>\bar{\tau }_1(\alpha )>\tau ^*>\bar{\tau }_2(\alpha )>\tau _2\). This generates a deadweight loss \(L(\alpha ) \propto (1-\alpha )^2\) that is the sum of the deadweight losses on the importer and exporter’s sides of the market (triangles \(L_1\) and \(L_2\) in Fig. 2), the magnitude of which depends on jurisdictional abatement flexibilities. Specifically, because overall abatement is maintained, cost efficiency relative to full linkage can be measured by the index
Even a stringent limit can bring about a high share of the full-link gains: \(I\left( 10\%\right) =19\%\) and \(I\left( 50\% \right) =75\%\). The less stringent the restriction, the bigger the overall efficiency gain from the restricted link, but the lower the increase in gain at the margin. This is so because when \(\alpha \) increases, inter-jurisdictional price disparities narrow down and net gains per permit exchanged decrease accordingly. In turn, the efficiency gains accruing to jurisdiction i reduces to \(\bar{\Gamma }_i (\alpha ) = \alpha ^2 \Gamma _i^*\).
There are two crucial implications of the inter-jurisdictional price wedge. First, jurisdiction 1 is willing to buy up 2-permits for a price of \(\bar{\tau }_1\) at most while jurisdiction 2 is willing to sell off 2-permits for a price of \(\bar{\tau }_2\) at least. This implies that transaction prices are undetermined in the present model (they can settle anywhere in \([\bar{\tau }_2;\,\bar{\tau }_1]\)) and that jurisdictional permits are not entirely fungible commodities.Footnote 24 Second, there exists a scarcity rent \(S(\alpha ) \propto \alpha (1-\alpha )\) of size \(f+g\) in Fig. 2 whose apportionment between the two representative firms ultimately depends on these transaction prices.Footnote 25 Note that the scarcity rent is at its highest when \(\alpha =1 / 2\) and exceeds the joint efficiency gains \(\bar{\Gamma }_1+\bar{\Gamma }_2\) when \(\alpha \le 2 / 3\).
Quantity and tax restricted linkage equilibria. \(\bar{\Delta }\) is the constrained transfer volume and \(\bar{\tau }_i\) the shadow price of emissions in jurisdiction i under the restriction. Area \(\bar{\Gamma }_i\) measures the efficiency gains from restricted permit trading accruing to i. Area \(L_i\) is the deadweight loss associated with the restriction on i’s side of the market. Area \(f+g\) alternatively measures the scarcity rent under a quantity restriction or tax revenues under a border tax
To pin down both the rent extraction and transaction prices we must specify something about bargaining. The market structure we consider is a bilateral monopoly and we assume a Nash bargaining game for the rent extraction (Nash 1950) with zero-value outside options where \(\theta \in [0;1]\) (resp. \(1-\theta \)) denotes the bargaining power of jurisdiction 1 (resp. 2).Footnote 26 In this case jurisdictions capture a share of the rent that is proportional to their respective bargaining power
which also determines the permit transaction price
By contrast, the literature considers that the rent splitting ultimately depends on the way the restriction is set. For instance, Ellerman and Sue Wing (2000) consider the case of a competitive permit supply on the linked market with restricted demand and Forner and Jotzo (2002) that of a competitive demand with restricted supply. Typically, it is assumed that a restriction on imports, i.e., on demand for 2-permits in jurisdiction 1, grants monopsony power (\(\theta =1\)) to jurisdiction 1 which captures the entire rent. Symmetrically, a restriction on exports, i.e., on supply of 2-permits for jurisdiction 1, grants monopoly power (\(\theta =0\)) to jurisdiction 2 which pockets the entire rent. There is, however, no reason to postulate the existence of a link between the definition of the restriction and the market structure itself.Footnote 27
It is noteworthy that one jurisdiction may be better off from the restricted link relative to full linkage. To see this, fix \(\theta =1\), i.e., jurisdiction 1 is monopsonistic and makes the transaction price. We reason around the full-link equilibrium to analyze the effects of a binding restriction on jurisdictions’ total compliance costs, denoted \(TC_i\) in jurisdiction i. A restriction that is binding by a slightly enough margin leads to an infinitesimally small increase in abatement in jurisdiction 1 (\(\mathrm {d}\varepsilon >0\)) and decrease in the price (\(\mathrm {d}\tau < 0\)). Any such active restriction changes the total costs of compliance in both jurisdictions. In particular for jurisdiction 1,
The first term on the right-hand side of Eq. (8) is positive and corresponds to the incremental increase in domestic abatement costs due to more expensive domestic abatement being substituted for imported permits. The second term is negative and measures the incremental cost savings on remaining imports. The sign of \(\mathrm {d}TC_1\) is thus ambiguous and depends on the relative magnitude of these two countervailing effects. When the restriction is lax (i.e., \(\alpha \) close to 1), the import price effect dominates the domestic abatement effect and jurisdiction 1 is better off under the restriction than unrestricted linkage. The converse holds when the restriction is stringent (i.e., \(\alpha \) close to 0). By a continuity argument there exists an optimal restriction from the perspective of the monopsonistic jurisdiction. Note that the price effect is absent in the case of price-taking jurisdiction 2 and the sign of \(\mathrm {d}TC_2\) is hence unambiguous
This corresponds to a direct income transfer to jurisdiction 1. By the same token, we can define jurisdictions’ optimal restrictions in the general case.
Proposition 3.1
Given\(\theta \in [0;\,1]\)jurisdictional optimal quantitative limits are
In the relevant ranges, \(\alpha _1^*\) (resp. \(\alpha _2^*\)) is a decreasing (resp. increasing), convex function of \(\theta \) with \(\alpha _1^*(1) > \alpha _2^*(0)\), \(\mathrm {inf}\{\alpha _1^*\}=\lim _{c_1 \rightarrow c_2^+} \alpha _1^*(1)=2/3\) and \(\mathrm {inf}\{\alpha _2^*\}=\lim _{c_2 \rightarrow 0^+} \alpha _2^*(0)=1/2\).
Proof
Relegated to “Quantity-Restricted Linkage”. \(\square \)
First, because \(\alpha _1^*\) and \(\alpha _2^*\) intersect once at \(\theta =\bar{\theta }\), the two jurisdictions can never prefer a given quantity-restricted linkage simultaneously (relative to full linkage). Second, the range of relative bargaining powers over which the high-cost jurisdiction prefers a quantity-restricted link over full linkage is smaller than for the low-cost jurisdiction. This is so because the former gains relatively more from the full link than the latter. Third, optimal restrictions always authorize at least 50% of the full-link volume of transfers and the one under monopoly power is more stringent than the one under monopsony power (\(\alpha _2^*(0) < \alpha _1^*(1)\)).
3.2 Linkage with Border Taxes on Permit Transfers
A border tax on inter-jurisdictional permit transfers corresponds to the dual link restriction of a quantitative limit. That is, to each tax rate there corresponds a unique authorized share of permit transfers and vice versa.Footnote 28 While both instruments are equivalent in terms of equilibrium characterization in our deterministic framework, they will nonetheless differ in their distributional aspects as well as political and linkage implications. Without loss of generality, consider that jurisdiction 1 imposes a proportional tax \(\mu \) on 2-permit imports.Footnote 29 This tariff only concerns inter-jurisdictional transfers and there is no levy on domestic transactions.Footnote 30 Given \(\mu \), the restricted equilibrium is defined by the triplet \((\bar{\tau }_1,\bar{\tau }_2,\bar{\Delta })\) which, depending on the dispersion in autarky prices, satisfies
Again, the situation is depicted in Fig. 2. Equilibrium (11) is constrained to autarky if the tax rate is set at too high a level for given autarky prices. For instance, if \(\tau _1=2\tau _2\) then the levy on import transactions should not exceed 50% for some transfers to occur. The border tax thus locates the restricted link outcome between autarky (\(\mu \ge 1-\tau _2/\tau _1\)) and full linkage (\(\mu =0\)).
The tax is distortionary and cost efficiency does not obtain. Specifically, the spread in jurisdictional prices is linearly proportional to the tax rate and the deadweight loss rises at the square of it. Overall abatement is constant but some mutually beneficial transfers absent the tax do not take place (\(\bar{\Delta } \le \Delta ^*\), where \(\bar{\Delta }\) is decreasing with the tax rate). Additionally, the increase in the permit price in 1 relative to full linkage is less than the tax because part of it is passed on to 2 where the permit price declines. The magnitude of these price variations, i.e. the tax incidence, depends on relative jurisdictional abatement flexibilities.Footnote 31
However, there are two key differences from quantitative restrictions. First, a border tax allows for trades of permits whose jurisdictional prices differ as jurisdiction 1 pays a markup on each 2-permit it imports. That is, jurisdictional permits are fungible. Second, a border tax raises revenues where a quantitative restriction generates a scarcity rent instead. Distributional aspects of the restriction are thus clearer as the revenues \(f+g\) are collected by (the regulator in) 1 while under an equivalent quantitative restriction the corresponding scarcity rent is unclearly divided between (the representative firms in) 1 and 2.
Specifically, relative to full linkage the imposition of a border tax by jurisdiction 1 is unambiguously detrimental to jurisdiction 2. This is attributable to impeded inter-jurisdictional trade (\(L_2\)) and diminished terms of trade (g). Although its efficiency gains are reduced, jurisdiction 1 also raises tax revenues \(f+g\). It is thus better off with the tax than under full linkage provided that \(g>L_1\). This holds true for small tax rates, which highlights the standard trade-off between the level of the tax rate (\(\mu \)) and the width of the tax base (\(\bar{\Delta }\)).
Corollary 3.2
The optimal tax rate is\(\mu ^*=(c_1-c_2)/(3c_1)\)and jurisdiction 1 is better off from the border tax regime than full linkage if\(\mu \in \left[ 0;\,\bar{\mu }\right] \)where\(\bar{\mu }>\mu ^*\).
Proof
Special case of Proposition 3.1 with \(\theta =1\). See also “Border Tax-Restricted Linkage”. \(\square \)
3.3 Linkage with Exchange Rates on Relative Permit Values
We let \(\rho >0\) denote the rate at which emission reductions occurring in 1 are converted into emission reductions occurring in 2 through inter-jurisdictional exchange of permits. That is, one unit of abatement in 1 is worth \(\rho \) unit of abatement in 2. We define the linked market \(\rho \)-equilibrium by the following joint compliance cost minimization programme
We assume the aggregate constraint on emissions binds and let \(\bar{\Delta }_i(\rho )\) denote the variation in emissions in jurisdiction i at the \(\rho \)-equilibrium relative to autarky. Market closure yields \(\bar{\Delta }_2(\rho )=-\rho \bar{\Delta }_1(\rho )\) and the interior market \(\rho \)-equilibrium is characterized by the necessary first-order condition
With quadratic abatement cost functions, abatement unit transfers from 2 to 1 amount to
There are two effects consecutive to the introduction of an exchange rate, namely fungibility of jurisdictional abatement units does not hold (emission conversion, or EC effect) and jurisdictional marginal abatement costs are adjusted for the exchange rate in equilibrium (MAC effect). First, for a given volume of inter-jurisdictional permit transfer, an exchange rate specifies a rate of conversion between emission reductions in 1 and 2, thereby changing overall abatement. Accounting for the sole EC effect, more or less overall abatement occurs in equilibrium relative to the benchmark. Second, the ratio of jurisdictional marginal abatement costs in equilibrium is determined by the exchange rate. Accounting for the sole MAC effect, an exchange rate induces a deadweight loss and modifies incentives for inter-jurisdictional transfers in a fashion akin to a border tax.
Proposition 3.3
Relative to full linkage, in an interior market \(\rho \) -equilibrium
- (i):
-
jurisdiction 1 raises emissions i.f.f.\(\rho <1\)and jurisdiction 2 curbs emissions i.f.f.\((\rho -1)(\rho -\bar{\rho })<0\)with\(\bar{\rho }\doteq \frac{c_1(\tau _1-\tau _2)}{c_1 \tau _2+c_2 \tau _1} \in (0;\,\tau _1 / \tau _2)\);
- (ii):
-
the additional aggregate level of abatement satisfies\(\gamma (\rho ) \doteq (\rho -1)\bar{\Delta }_1(\rho )\), which is positive i.f.f.\(\rho \in (1;\,\tau _1 / \tau _2)\)and maximal at\(\rho =\hat{\rho }\doteq (\tau _1 / \tau _2)^{1/2}\).
Proof
Relegated to “Linkage with Exchange Rates”. \(\square \)
When parity does not hold, jurisdictional abatements are not equivalent and aggregate emissions vary as a result of inter-jurisdictional permit trading. We see from Eq. (14) that permits flow in the natural direction provided that the exchange rate is smaller than the ratio of autarky prices. We also note from Eq. (13) that cost efficiency obtains only under parity (\(\rho =1\)) and that the \((\tau _1 / \tau _2)\)-equilibrium replicates autarky. Indeed, this rate makes up for the autarky price wedge and there is no incentive to trade. These observations delineate three trading regimes depending on the value of the exchange rate w.r.t. parity (full linkage) and \(\tau _1 / \tau _2\) (autarky) whose properties are listed in Table 1.Footnote 32
Reduction zone (\(1 \le \rho \le \tau _1 / \tau _2\)) The dispersion in jurisdictional marginal abatement costs adjusted for the exchange rate is reduced and the conversion rate is favorable to jurisdiction 1. The market \(\rho \)-equilibrium is depicted in Fig. 3. Controlling for the EC effect, this leads to less abatement transfers than is mutually beneficial in a full link. Controlling for the MAC effect, the 1-permit value is inflated, i.e. the exchange rate reduces the demand for 2-permits in jurisdiction 1 while increasing the demand for 1-permits in both jurisdictions (but jurisdiction 2 remains net exporter). Consequently, holding 2-permit imports constant, less emissions are allowed into jurisdiction 1 than under full linkage. In other words, holding abatement transfers constant, jurisdiction 2 abates \(\rho \)-as-many times more. These two effects combined yield higher overall abatement relative to the benchmark. Relative to full linkage, jurisdiction 1 emits less while jurisdiction 2 may emit more (\(\rho > \bar{\rho }\)) or less (\(\rho < \bar{\rho }\)) but overall, total abatement increases.
Amplification zone (\(\rho \le 1\)) The dispersion in jurisdictional marginal abatement costs adjusted for the exchange rate is amplified and the conversion rate is favorable to jurisdiction 2. Controlling for the EC effect, this is conducive to more exchanges of abatement than under full linkage. Controlling for the MAC effect, the 1-permit value is deflated. Permits keep on flowing in the natural direction but since one 2-permit is worth \(\rho \)-as-many 1-permit more emissions occur overall. These two effects combined yield less aggregate abatement than in the benchmark. Relative to full linkage, jurisdiction 1 emits more while jurisdiction 2 may emit more (\(\rho <\bar{\rho }\)) or less (\(\bar{\rho }<\rho \)) but overall, total abatement decreases.
Restricted linkage equilibrium in the reduction zone (with \(\rho> \bar{\rho } > 1\)). The two curved dotted arrows rotate the line of slope \(\rho c_2\) to the amplification zone (AZ) and the inversion zone (IZ) and point outside of the reduction zone represented by the hull \(\left\langle e_0c_2,e_0c_1 \right\rangle \)
Inversion zone (\(\rho >\tau _1 / \tau _2\)) The dispersion in jurisdictional marginal abatement costs adjusted for the exchange rate is inverted and the conversion rate is favorable to jurisdiction 1 (even more so than in the reduction zone). The exchange rate sufficiently reduces the demand for 2-permits in jurisdiction 1 and increases the demand for 1-permits in both jurisdictions for jurisdiction 1 to become the net permit exporter. This regime is less cost efficient than autarky since abatement occurs where it is most expensive. Relative to autarky, jurisdiction 1 (resp. 2) abates (resp. emits) more. Since the exchange rate inflates the 1-permit value, this results in aggregate emissions higher than in the benchmark.
Note that aggregate efficiency gains no longer are a proper measure of cost efficiency since overall abatement varies with the exchange rate. Loosely speaking, the more distant \(\rho \) from parity, the bigger the dispersion in jurisdictional marginal abatement costs at the \(\rho \)-equilibrium and the lower the degree of cost efficiency.Footnote 33 An exchange rate affects both the size of the aggregate efficiency gains and its repartition across jurisdictions in the following manner
Aggregate efficiency gains decrease with \(\rho \) as long as \(\rho \le \tau _1 / \tau _2\), are nil at \(\rho = \tau _1 / \tau _2\) and increase with \(\rho \) thereafter. In addition, jurisdiction 1 (resp. 2) gets a higher share of these gains when \(\rho \le (\text {resp.} \, \ge ) \hat{\rho }\). Thus, with only efficiency gains in mind, jurisdiction 1 (resp. 2) would like the exchange rate to be as small (resp. large) as possible. This line of reasoning, however, does not account for the induced variation in aggregate emissions. In “Appendix 3” we show that factoring in this shift in emissions mitigates jurisdictional preferences for otherwise unrealistically large or small rates. Here, in the following special case, we illustrate an important implication of the exchange rate induced flexibility in overall emissions in terms of ambition setting as a dynamic process.
Corollary 3.4
Both jurisdictions are better off under full linkage with adjusted caps\((\omega _1,\omega _2)=(\omega ,\omega -\gamma (\hat{\rho }))\)than under\(\hat{\rho }\)-equilibrium with initial caps\((\omega ,\omega )\).
Proof
Relegated to “Linkage with Exchange Rates”. \(\square \)
This highlights that exchange rates have potential to increase environmental ambition over time. Indeed, consider that jurisdictions initiate linkage with an exchange rate that triggers additional abatement relative to autarky. Corollary 3.4 then suggests that, all else equal, both jurisdictions have an incentive to transition to full linkage with domestic caps adjusted so as to generate overall abatement commensurate with that under the exchange rate.Footnote 34
4 Policy Discussion and Comparative Analysis
We take our modelling exercise as a basis for a policy-oriented discussion of the comparative merits and political feasibility of each type of restriction. We further draw on real-world experiences with emissions trading, linking and restrictions. In order to both accommodate these facts and enrich the discussion, we will, at times, slightly deviate from the simple model of Sects. 2 and 3.
To start with, Fig. 4 is helpful in displaying the comparative effects of link restrictions in the overall-abatement-cost-efficiency space relative to autarky. Details on the calibration and additional numerical illustrations can be found in “Appendix 2”. The grey line describes the economic outcomes along the continuum of quantitative restrictions and border taxes. The black curve depicts relative cost efficiency as a function of relative overall abatement along the continuum of exchange rates. It delineates the reduction zone in the upper-right quadrant, the amplification zone in the upper-left quadrant and the inversion zone in the lower-left quadrant. Specifically, Fig. 4 clearly shows that both quantitative restrictions and border taxes affect cost efficiency but preserve overall abatement while exchange rates have an impact along both of these two dimensions.
4.1 Quantitative Transfer Restrictions
Under a quantitative restriction transfers are restricted up to the authorized limit if binding; if not, full linkage should obtain. Thus, because transfers are confined within a predefined range a quantitative restriction is an attractive instrument if jurisdictions seek to have a direct handle on the quantity-side consequences of a link and retain a certain degree of oversight over their domestic systems. On the one hand, a high-price environmentally-inclined jurisdiction may wish to limit imports to avoid those link-induced consequences potentially pitting the economic gains from linkage against broader environmental or equity concerns. This would ensure that a certain volume of abatement occurs domestically (along with the ancillary benefits and reputational aspects thereof) or assuage fears about over-allocation in exporting jurisdictions that could dilute domestic ambition. On the other hand, a low-price jurisdiction may desire to limit exports in a bid to contain the link-induced permit price rise.
That said, some implications of a binding quantitative restriction are not as straightforward as they seem to be on the face of it. This is attributable to the coexistence of different price signals and undetermined transaction prices. Since one permit may have two distinct prices whether it is sold domestically (\(\bar{\tau }_i(\alpha )\)) or abroad (\(\bar{\tau }(\alpha ;\,\theta )\)) quantitative restrictions may lead to speculative transactions by creating perverse incentives for firms to make profits on secondary markets that are disconnected from abatement-related fundamentals.
A related issue is the existence of a scarcity rent whose apportionment among jurisdictions’ constituent firms is not clear ex ante. To mitigate these uncertain distributional effects, some mechanisms may be devised to allocate the rent between them. For instance, restrictions could be formulated at firm levels, e.g., as a percentage of firms’ individual compliance obligations. Alternatively, authorities could issue a certain number of licenses and require that firms attach, say, one license to each foreign permit they remit for compliance. Because the rent distribution may serve as a negotiation lever, linkage can be facilitated if jurisdictions are able to agree on how to allocate these licenses among them. While this parallel license market may offer a better management of the distributional aspects of the restricted link it does not determine how transaction license prices are fixed and, ultimately, the share of the total rent one can extract.Footnote 35 Additionally, administrative and transaction costs associated with setting up and running this parallel market might shrink the gross benefits of linkage. Note, however, that auctioning off licenses may limit these costs and redirect the rent from the firms to the regulatory authority.
Under conditions of uncertainty, we note that a restriction that turns out to be non-binding ex post might still affect permit trading and price formation. Indeed, Gronwald and Hintermann (2016) provide evidence that the probability of non-bindingness of the usage quota on Kyoto credits affected the offset-permit price spread in the EU ETS. Thus, in a context where abatement potentials, costs and baseline emissions have proven to be uncertain, a relatively stringent restriction has joint potential to bring about a relatively important share of the full-link gains, effectively contain the reach of the link as well as reduce uncertainty about its bindingness and related impact on price formation.
As a transitory linkage mechanism, quantity restrictions seem to be the natural route to gradually allow for unlimited trading between two quantity instruments. However, the ratio of jurisdictional shadow prices is undetermined ex ante, hard to infer ex post and transaction prices may fluctuate independently of fundamentals. Permit prices may thus no longer reflect jurisdictional marginal abatement costs, which is essential information in the political process of gradually scaling up the link in order to assess alignment in programs and ambition.
4.2 Border Taxes on Permit Transfers
Although there is a bijection between price and quantity restrictions in terms of equilibrium characterization, their distributional and other link-related effects differ. Because the ratio of jurisdictional prices is fixed by the tax rate, price signals are stronger as they better reflect marginal abatement costs, which is key information for regulators in scaling up the link. Moreover, a border tax raises revenues so that regulators have a better handle on some distributional effects of their policy relative to a quantitative restriction which generates a scarcity rent whose distribution between jurisdictional firms is unclear a priori.Footnote 36 Controlling for the induced deadweight loss, a border tax operates an inter-jurisdictional surplus transfer. In other words, taxes have a redistributive potential that may serve as leverage to foster linkage negotiations and can thus be seen as surrogates for otherwise politically unpalatable lump-sum transfers (Victor 2015).
Under conditions of uncertainty, the dual property between price and quantity restrictions would vanish (Weitzman 1974). In practice, this relates to the comparative advantage of having a fixed maximum level of permit transfers with a variable ratio of jurisdictional prices versus a fixed price ratio and variable permit transfers. Note that because a border tax concerns permit prices the link equilibrium will always be affected and potentially brought to autarky if the rate is set at too high a level. By contrast, quantitative restrictions may turn out to be non-binding, though this might still bear on price formation.
As a transitory linkage mechanism, border taxes may be more seamless than quantitative restrictions in informing a full-link scale-up and managing associated distributional aspects. Note that small tax rates generate a sizeable share of the full-link gains but do not reduce much of its effects. Conversely, too high a tax rate risks turning out to be detrimental (w.r.t. full linkage) even for the jurisdiction that collects revenues. Finally note that a border tax is a fiscal policy and might thus be relatively more complicated to pursue legislatively speaking than a quantity-based approach, for instance in the EU.Footnote 37
4.3 Linkage with Exchange Rates
As with a border tax an exchange rate sets the ratio of jurisdictional marginal abatement costs (MAC effect). Additionally, it also modifies the one-for-one compliance value of jurisdictional permits, i.e., jurisdictional abatement efforts are not equivalent (EC effect). As noted by Burtraw et al. (2017), exchange rates thus have potential to adjust for programmes’ stringencies even though cost efficiency is reduced.Footnote 38 Note that taking this line of reasoning to its logical extreme (i.e., \(\rho \sim \tau _1/\tau _2\)) implies the link would resemble autarky. Additionally, an exchange rate may also serve as a means to accommodate other economic criteria or types of political and environmental preferences.Footnote 39
Cost efficiency may be higher or lower than under autarky but is always lower than under full linkage. Moreover, aggregate emissions vary as a result of inter-jurisdictional trading due to the EC effect. In particular, the volume of unit transfers can increase, decrease or even be reversed relative to full linkage. Thus, as compared to autarky, the aggregate implications of an exchange rate in both economic and environmental terms could happen to be beneficial (reduction zone) as well detrimental (inversion zone). In loose terms, one can imagine that the reduction zone is likely to be targeted by regulators. In particular, if they prioritize environmental outcomes they should aim for a rate close to \(\hat{\rho }=(\tau _1/\tau _2)^{1/2}\). If, instead, they wish to increase market liquidity without bearing much of the other effects of a full link, they should set \(\rho \) close to \(\tau _1/\tau _2\).
Under conditions of uncertainty, however, selecting an exchange rate is likely to prove difficult which can lead to unintended and possibly detrimental consequences. The difficulty is indeed twofold. First, due to ex-ante uncertainty about programmes’ actual stringencies (hence autarky prices) it is complicated to select the rate right in the first place.Footnote 40 Second, it is also challenging to duly adjust the rate ex post since autarky prices that would have prevailed absent the link restriction are not directly observable. Although counterfactual autarky prices could be inferred, it would only be so with a lag of one compliance period at best. The risk of error and possible detrimental outcomes (e.g., of the inversion zone) in selecting the policy handle is higher than for the other two restrictions, whose associated outcomes are always confined within autarky and full linkage.
As a transitory linkage mechanism, an exchange rate has potential to increase environmental ambition over time when emissions cap diminution is not feasible up front. Indeed, penalized schemes—that is, schemes for which conversion rates are not favorable—have an incentive to raise domestic ambition provided that their domestic abatement units become gradually traded with parity. In fact, Corollary 3.4 shows that this ratcheting up of ambition would be in the interest of each party. Note also that since an exchange rate does not induce explicit rents, the transition to a full link may be easier than for a quantitative restriction.
4.4 Two Special Cases of Link Restrictions
We now discuss two additional restrictions, namely unilateral linkage and discount rates, as special cases of quantitative restrictions and exchange rates, respectively.
Unilateral (or conditional) linkage Unilateral linkage is a special case of quantitative restrictions whereby entities in one jurisdiction can remit foreign permits for domestic compliance but not vice versa. Should the unilateral link be established in the natural direction of trade its implications would closely resemble those of a full link save for the non-fungibility of permits. Conversely, the one-way link may also be inactive, i.e., an autarky-like situation persists. In other words, unilateral linkage can be observationally indistinguishable from a full link until until some uncertainty about the cost structure is resolved.
Note that unilateral linkage is thus of a conditional nature, which may entice jurisdictions to increase ambition. Indeed, imagine a one-way link between a ‘high-ambition, high-price’ system 1 and a ‘low-ambition, low-price’ system 2 whereby only 1 can purchase 2-units. In this sense, full linkage is conditional on 2 increasing ambition and note that the unilateral link constitutes a soft price floor for 1. Additionally, unilateral linkage can mitigate price uncertainty and distributional aspects (there is no scarcity rent) associated with quantitative restrictions.
A good example of active one-way linkage is the unilateral integration of the European aviation sector into the EU ETS as of 2012 whereby aircraft operators can surrender permits from the stationary sector (EUAs) in lieu of aviation permits (EUAAs) for compliance but not the other way around. Since 2013, the aviation sector has been short by around 20 \(\hbox {MtCO}_2\hbox {eq}\) each year, which represents about a third of covered emissions (EEA 2017). The aviation sector is thus a net buyer of EUAs and the EUAA price closely follows the EUA price.Footnote 41
Both the Norway-EU and aborted Australia-EU unilateral links were envisaged as initial, transitory steps toward fully-fledged links. In Phase I of the EU ETS and until the extension of the EU ETS to EEA–EFTA countries by late 2007, Norwegian firms could surrender EUAs domestically but not vice versa.Footnote 42 This one-way link originated in a unilateral decision on the part of Norway to help prepare for full integration to the EU ETS, e.g. gradual market design alignment. In mid-2012 Australia and the EU Commission agreed to link up their domestic ETSs following a two-step process whereby Australia would first be unilaterally linked to the EU (EUAs recognized in Australia, but not vice versa) before the link would become two-way three years later. For compatibility with the EU ETS, each step was contingent upon gradual design adjustments in Australia.Footnote 43
These three experiencesFootnote 44 indicate that unilateral links (1) can be established pursuant to unilateral or joint decisions; (2) do not require market designs to be as much aligned as for bilateral links; (3) may help initiate linkage while giving more time to bring schemes into sufficient alignment deemed necessary for bilateral links to be established seamlessly.
The elaboration of the RECLAIM programme also underlines the practical merits of unilateral linkage.Footnote 45 To account for spatial factors the Los Angeles air basin was initially divided into 38 zones without interzonal trading. This would have massively reduced the economic gains from using a market-based policy relative to command and control. One alternative was to create a single market with trading ratios accounting for spatial discrepancies but quantification of these ratios proved complicated and the resulting scheme altogether would have been cumbersome and unworkable. The final programme solely comprised two geographical zones (upwind sources, located near the coast and contributing more to elevated ozone levels and downwind sources, located inland) with interzonal trading allowed only from upwind to downwind sources (Tietenberg 1995; Fromm and Hansjürgens 1996; Johnson and Pekelney 1996).
Discount rates Discount rates are the unilateral version of exchange rates. That is, when jurisdiction 1 applies a given conversion ratio to 2-permits, 2 need not impose a conversion ratio to 1-permits that is equal to the inverse of the former. Therefore, discount rates may be asymmetrical, i.e., of different magnitudes depending on the direction of trade. When the differential in autarky prices surpasses the discount rate its implications are similar to those of an equivalent exchange rate (same EC and MAC effects) but full permit fungibility does not obtain. As noted by Schneider et al. (2017) this asymmetry may have potential to overcome some challenges inherent to exchanges rates. First, discount rates need not be mutually agreed upon so that jurisdictions can maintain relatively more flexibility in selecting and adjusting the discount rates they use. Second, if both jurisdictions were to implement discount rates higher than unity on inflowing foreign permits, then, whatever the realized direction of the permit flow, overall abatement and cost efficiency would increase relative to autarky, which is congruent with the ‘desirable’ characteristics of the reduction zone.
5 Conclusion
We compared various restrictions on permit trading in the context of a bilateral link between ETSs in gradually approaching unrestricted, full linkage. Restricted linkage creates a trade-off between eliminating some impediments to full linkage and undermining a fundamental reason for linking in the first place (i.e., cost efficiency) which justifies a temporary use of restrictions moving toward unrestricted linkage. This trial phase may allow to test the effects of the link and, by limiting its reach, assuage some of the induced effects and perceived risks. This also gives more time and flexibility for partners to reconcile their policy differences and bring their respective schemes further into alignment for a full link to be established seamlessly. A few years down the road, partners may decide to scale up the link. Otherwise, should trial not be conclusive the link may be severed.Footnote 46
We tried to keep the model as simple as possible to have a clear, unifying framework which, in conjunction with lessons from real-world experiences, served as a basis for a less formal, policy-oriented discussion of comparative advantages and weaknesses of link restrictions. On the face of it, quantitative restrictions seem to be the most implementation-friendly route to a full link between quantity instruments. In particular, they provide a direct quantity handle on the reach of the link. However, there is uncertainty about price formation and the distribution of the scarcity rent, which may hinder the transition to a full link. These aspects are mitigated with a border tax, which should ensure a better management of distributional outcomes, less undesirable price fluctuations and better information on jurisdictional marginal abatement costs. Exchange rates can be used to correct for discrepancies in programmes’ stringencies and have potential to increase ambition over time. On the flip side, however, they can be challenging to select and adjust, which might lead detrimental outcomes.
In order to hammer out a linkage agreement as workable and wieldy as possible, regulators can pick the restriction (or combination thereof) that best assuages dominant link-related risks and fits the negotiation and domestic contexts. As experience corroborates, transitory unilateral linkage may well strike a good balance between the ‘ideal’ and the ‘practical’ in translating economic theory into specific policy design elements.Footnote 47 In addition, the insights gained from this simple framework can help evaluate the effects of trade restrictions in the context of networked ETSs. An recent example is the ICAR Platform proposed by Füssler et al. (2016), which provides a structure to which ETSs may dock on a voluntary basis contingent upon their meeting a set of predefined requirements. Docked ETSs retain some discretion in the form of unilateral imposition of both quantitative restrictions on permit outflows/inflows and qualitative restrictions (e.g., discount rates) de facto assigning relative compliance values to foreign permits.
Finally, we identify three alleys for future research. First, although we treat jurisdictions as monolithic entities and abstract from intra-jurisdictional distributional aspects, we stress that this issue deserves more attention.Footnote 48 Indeed, the way restricted linkage affects firms and other jurisdictional constituencies is bound to shape regulators’ room for maneuver in selecting and implementing restrictions.Footnote 49 Second, while our model is static, it is of key interest to understand the interplay between permit banking and alternative link restrictions.Footnote 50 Indeed, each link restriction will distort firms’ inter-temporal decisions and market functioning in its own way. One can conjecture that, like in the static case we consider, unilateral linking may limit the amount of additional induced distortions.Footnote 51 Third, in a strategic environment, we underline that letting jurisdictions bargain over future linking rules (e.g., in the form of restrictions) rather than over domestic caps (that are strategic substitutes and thus prone to free-riding) may be more suitable for the emergence of voluntary cooperation through linkage.Footnote 52
Notes
Broadly speaking, linkage refers to connections between separate jurisdictional climate policies allowing for abatement efforts to be redistributed across jurisdictions in a way that diminishes the aggregate costs of achieving the overall target. Linkage is defined herein in its typical frame, i.e., between two ETSs, but linkage among heterogeneous policies may be feasible (Metcalf and Weisbach 2012; Mehling et al. 2017).
Explicit carbon prices are undoubtedly excessively narrow measures of mitigation efforts and as such cannot constitute an appropriate metric to compare effort across jurisdictions, see Aldy and Pizer (2016) and Aldy et al. (2017) for a detailed discussion. As market signals that drive private-sector behavior and long-term investment decisions, however, regulators can hold their own views about what price level is desirable.
Market designs and caps reflect jurisdictional circumstances and have often been critical to striking an internal political deal (Flachsland et al. 2009). This complicates inter-system design alignment as one may be limited in its inclination to cede sovereign control over entrenched policy objectives and design features.
The concept of networking has recently emerged as a substitute for direct multilateral linkages (Füssler et al. 2016; Keohane et al. 2017). The idea is to allow for trades of ‘carbon assets’ between systems that are inherently different (e.g., in terms of design, ambition, MRV standards) by placing a ‘mitigation value’ on such assets that account for these differences and possibly using trade restrictions as analyzed here.
Such an international offsetting scheme is currently missing. The Sustainable Development Mechanism established under Article 6.4 of the Paris Agreement could allow for indirect links, but has yet to be developed.
As further discussed in Jaffe et al. (2009), restrictions can be employed «to reduce inter-system trading, or if there is a desire, to require that trading with other systems lead to a net reduction in emissions».
Symmetrically, link restrictions may provide levers to maneuver if partners are not satisfied with the link and wish it be severed. That is, they offer alternative ways for the termination of a link, whose organization affects inter-temporal cost effectiveness and price formation (Pizer and Yates 2015).
Throughout the paper, we discuss how some of our results would fare under less restrictive assumptions.
Given the multi-faceted nature of linkage, there is a multitude of factors—often of a political-economy dimension—that may influence the desirable type and level of a restriction. Because this falls well beyond the scope of our model we take restrictions as exogenously given. That said, we provide examples of why restrictions may arise in practice based on general-equilibrium effects or political-economy considerations throughout the paper and especially in the policy discussion in Sect. 4.
Restrictions are always detrimental w.r.t. full linkage in aggregate economic terms but they can improve upon full linkage from the point of view of a jurisdiction, whose optimal restriction level we characterize.
Though a one-way link can be observationally equivalent to a two-way link, it may suddenly revert to autarky as some cost or abatement uncertainty is resolved.
These studies show that greater flexibility reduces overall costs of compliance with the Protocol but that limited flexibility can be preferable for some parties due to the induced rents they are able to capture. See also Westskog (2002) who discusses the relevance of various arguments for trading restrictions in this context.
Gavard et al. (2016) highlight an advantageous general-equilibrium effect from the quantitative limit relative to full linkage. In addition to the captured rent China also benefits from a limited consumption loss (due to a link-induced rise in permit and thus electricity prices) that otherwise swamps the gains from selling permits.
In general, quantitative limits do not exceed 15% of entities’ compliance obligations and, since offset quotas usually span several compliance periods, offset usage need also be timed. To give but one example of discount rate, France applies a 10% discount on the mitigation value of Emission Reduction Units.
In this case, volume efficiency requires that trading ratios be set equal to the ratio of delivery coefficients so that marginal abatement costs vary across emission sources in accordance with associated marginal damages (Montgomery 1972; Mendelsohn 1986) although cost efficiency can generally not be achieved (Førsund and Nævdal 1998).
We limit the analysis to a bilateral link for ease of exposition but we note this is not entirely innocuous. For instance, in a multilateral linkage, permit importers may benefit from binding quantitative restrictions on imports in other jurisdictions/sectors as this contains the permit price increase relative to a full link but not their own demands.
Even when autarky prices are equal and there are no ‘immediate’ efficiency gains, linkage still brings about benefits in terms of increased market liquidity (as a thicker market ought to reduce bid-ask spreads) and risk sharing (Doda et al. 2018).
We leave this approach for future work as further outlined in Conclusion.
Because gains accrue infra-marginally to constituent firms the total gains, on a constituent basis, can be larger than the net gains accruing to the representative firm.
In reality, quantitative restrictions are likely to be expressed in the form of concrete ceilings on the share of domestic caps that can be outsourced or exported. In practice, these restrictions could be implemented in a fashion akin to the ‘gateway mechanism’ proposed by Sterk et al. (2006) or by creating an additional market for licenses which must be attached to permits to allow for imports/exports as e.g., in Bernstein et al. (1999) or Gavard et al. (2016). Here, our notation clarifies exposition because the continuum of quantity-constrained link equilibria between autarky and full linkage is described when \(\alpha \) spans \(\left[ 0;\,1\right] \).
We note that this could reduce the gains in liquidity as compared to unrestricted linkage.
We underline that the scarcity rent results from the binding quantitative restriction and is independent of how permits are distributed in both jurisdictions in the first place.
For instance, when demand is restricted, the standard argument is that the linked market is a pure buyers’ market (buyers’ cartel) in which acquiescent sellers are compelled to compete to sell off their permits (and vice versa for a restricted supply). But one could as well conceive of the situation where sellers collude and/or buyers compete so that the model is underspecified without further assumptions on bargaining.
The effects of a tax on permit imports (resp. exports) levied by jurisdiction 1 (resp. 2) can be assimilated to those of an equivalent quantitative restriction with \(\theta =1\) (resp. \(\theta =0\)).
The opposite situation where jurisdiction 2 imposes the same levy \(\mu \) on permit exports would also satisfy the tax restricted-linkage equilibrium defined in Eq. (11). The only difference is that tax revenues would accrue to (the regulator in) jurisdiction 2 instead.
Heindl et al. (2014) consider a bilateral link where one jurisdiction levies a domestic tax on intra-jurisdictional emissions on top of the linked market price. Some abatement undertaken in this jurisdiction is thus attributable to this tax system, which undermines the price signal in the linked permit system.
Whether a tax is raised on demand or supply, the tax burden falls on both sellers and buyers. The tax incidence then depends on the relative price elasticity of demand and supply, with the more price-inelastic side of the market incurring most of the burden.
Schneider et al. (2017) identify the three same trading zones but name them differently.
Gains in liquidity should be similar to those under full linkage because permits are fungible.
This finding invites a follow-on analysis to formally examine such sequential cap-adjustment processes.
With a binding restriction the license price would also be determined by Eq. (7).
Note that unless tax revenues are redistributed to firms, they will always be worse off as a result of the tax-restricted link relative to full linkage and might thus voice opposition.
Indeed, pursuant to Article 192 §2 of the Lisbon Treaty (2007), policies that are deemed to be ‘primarily of a fiscal nature’ require unanimity between Member States to be enacted. Additionally, we note the indirect but related concern about WTO-compatibility voiced in the broader case of border (tax) adjustments.
Burtraw et al. (2017) implement a 3-for-1 rate in linking California and RGGI (one CCA is worth three RGAs) arguing that this «provides a rough adjustment for the relative stringencies of the two programmes but reduces the opportunities for cost savings from shifting \(\hbox {CO}_2\) emissions from RGGI to California» . Note that this reverses the natural direction of abatement flows, i.e., the 3-for-1 rate belongs to the inversion zone.
Exchange rates could adjust for discrepancies in permits’ mitigation value. In this respect, see the documentation provided under the auspices of the World Bank’s Globally Networked Carbon Markets Initiative.
This issue is somewhat mitigated if markets to be linked are already in operation as historical price levels can help guide the selection of the exchange rate. Moreover, selecting an exchange rate can be challenging if there exist information asymmetries between covered firms and regulators (Holland and Yates 2015).
Though the demand for EUAs from the aviation sector is bound to increase over time, the future of this unilateral link depends on the pending international CORSIA regulation.
Only one EUA transaction was recorded as the price for Norwegian permits was well below the price of CERs (Mehling and Haites 2009). The unilateral link could thus be seen as a de facto soft price ceiling for Norway.
For instance, Australia committed to gradually scrap its price floor and ceiling. See Jotzo and Betz (2009) for more details on the compatibility between the EU ETS and Australia Carbon Pricing Mechanism (CPM). Although linkage negotiations were conducted pursuant to Article 25 of the EU ETS Directive concessions pertaining to design alignment were exclusively envisaged on the Australian side of the link because Europe had more political weight and thus ‘design pull’. The project of an intercontinental link between Australia and Europe stalled when the CPM was officially repealed in mid-2014.
California is also currently examining rules that would specifically allow for Californian permits to be used in other jurisdictions, i.e., de facto unilateral links. We thank a reviewer for bringing this to our attention.
The REgional CLean Air Incentives Market was launched in 1994 to regulate ozone (a non-uniformly mixed pollutant) levels in the Los Angeles basin. Environmental objectives were reached (without hot spots) and compliance costs were reduced w.r.t. command-and-control approaches (Fowlie et al. 2012).
Restriction-induced rents may not entice recipients to roll out a full link. In a different but similar context, Tol (2009) underlines that less stringent restrictions are not Pareto-superior precisely for this reason. It should thus ideally be spelt out in the agreement that the use of restrictions is only temporary.
This echoes the words of Tietenberg (2006) that «in practice, one common approach to resolving spatial concerns involves a system of directional trading».
Different regimes of revenue recycling can have important implications in assessing link restrictions as is the case with first-best instrument selection (Pezzey and Jotzo 2012).
A first step in this direction is Pizer and Yates (2015) who compare how different rules for the treatment of banked permits in the context of future delinking alter present price formation and cost effectiveness.
As is the case in trial phases in nascent ETSs, another option which can be contemplated is to forbid banking in a full-link transition. However this would cancel the gains due to inter-temporal efficiency and additional work is required to provide a more precise analysis of this option.
Relatedly, Açıkgöz and Benchekroun (2017) analyze the anticipatory non-cooperative emission responses of signatories to various exogenously-given types of climate agreements to be implemented in the future.
References
Açıkgöz ÖT, Benchekroun H (2017) Anticipated international environmental agreements. Eur Econ Rev 92:306–36
Aldy JE, Pizer WA (2016) Alternative metrics for comparing domestic climate change mitigation efforts and the emerging international climate policy architecture. Rev Environ Econ Policy 10(1):3–24
Aldy JE, Pizer WA, Akimoto K (2017) Comparing emissions mitigation efforts across countries. Climate Policy 17(4):501–15
Bernstein PM, Montgomery WD, Rutherford TF, Yang GF (1999) Effects of restrictions on international permit trading: the MS-MRT model. Energy J 20:221–56
Bodansky DM, Hoedl SA, Metcalf GE, Stavins RN (2016) Facilitating linkage of climate policies through the Paris outcome. Climate Policy 16(8):956–72
Bollen J, Gielen A, Timmer H (1999) Clubs, ceilings and CDM: macroeconomics of compliance with the kyoto protocol. Energy J 20:177–206
Braun N, Fitzgerald T, Pearcy J (2015) Tradable emissions permits with offsets. In: Hintermann B, Gronwald M (eds) Emissions trading as a policy instrument: evaluation and prospects. MIT Press, Cambridge, pp 239–266
Burtraw D, Palmer KL, Munnings C, Weber P, Woerman M (2013) Linking by degrees: incremental alignment of cap-and-trade markets. Discussion Paper 13-04, Resources for the Future
Burtraw D, Munnings C, Palmer KL, Woerman M (2017) Linking carbon markets with different initial conditions. Working Paper 17-16, Resources for the Future
Carbone JC, Helm C, Rutherford TF (2009) The case for international emission trade in the absence of cooperative climate policy. J Environ Econ Manag 58(3):266–80
Criqui P, Mima S, Viguier L (1999) Marginal abatement costs of \(\text{ CO }_2\) emission reductions, geographical flexibility and concrete ceilings: an assessment using the POLES model. Energy Policy 27(10):585–601
Doda B, Quemin S, Taschini L (2018) Linking permit markets multilaterally. Working Paper 311/275, ESRC Centre for Climate Change Economics and Policy & Grantham Research Institute, London School of Economics
EEA (2017) Trends and Projections in the EU ETS in 2017. European Environment Agency
Ellerman AD, Sue Wing I (2000) Supplementarity: an invitation to monopsony? Energy J 21(4):29–59
Eyckmans J, Kverndokk S (2010) Moral concerns on tradable pollution permits in international environmental agreements. Ecol Econ 69(9):1814–23
Fankhauser S, Hepburn C (2010) Designing carbon markets, Part II: carbon markets in space. Energy Policy 38(8):4381–7
Fankhauser S, Martin N (2010) The economics of the CDM Levy: revenue potential, tax incidence and distortionary effects. Energy Policy 38(1):357–63
Feng H, Zhao J (2006) Alternative intertemporal permit trading regimes with stochastic abatement costs. Resour Energy Econ 28(1):24–40
Flachsland C, Marschinski R, Edenhofer O (2009) To link or not to link: benefits and disadvantages of linking cap-and-trade systems. Climate Policy 9(4):358–72
Forner C, Jotzo F (2002) Future restrictions for sinks in the CDM: how about a cap on supply? Climate Policy 2(4):353–65
Førsund FR, Nævdal E (1998) Efficiency gains under exchange-rate emission trading. Environ Resour Econ 12(4):403–23
Fowlie M, Holland SP, Mansur ET (2012) What do emissions markets deliver and to whom? Evidence from Southern California’s NOx trading program. Am Econ Rev 102(2):965–93
Fromm O, Hansjürgens B (1996) Emission trading in theory and practice: an analysis of RECLAIM in Southern California. Environ Plan C Govern Policy 14(3):367–84
Füssler J, Wunderlich A, Taschini L (2016) International carbon asset reserve: prototyping for instruments reducing risks and linking carbon markets. Final Report, The World Bank Group \(-\) Networked Carbon Markets, INFRAS: Zürich/London
Gavard C, Winchester N, Paltsev S (2016) Limited trading of emissions permits as a climate cooperation mechanism? US-China and EU-China examples. Energy Econ 58:95–104
Gronwald M, Hintermann B (2016) Explaining the EUA-CER Spread. Working Paper 5795, CESifo
Grüll G, Taschini L (2012) Linking emission trading schemes: a short note. Econ Energy Environ Policy 1(3):31–8
Habla W, Winkler R (2017) Strategic delegation and international permit markets: Why linking may fail. Working Paper 6515-2017, CESifo
Hahn RW (1984) Market power and transferable property rights. Q J Econ 99(4):753–65
Heindl P, Wood PJ, Jotzo F (2014) Combining international cap-and-trade with national carbon taxes. In: CCEP Working Paper 1418, Crawford School of Public Policy, The Australian National University
Helm C (2003) International emissions trading with endogenous allowance choices. J Public Econ 87(12):2737–47
Holland SP, Yates AJ (2015) Optimal trading ratios for pollution permit markets. J Public Econ 125:16–27
Holt CA, Shobe WM (2016) Price and quantity collars for stabilizing emission allowance prices: laboratory experiments on the EUETS market stability reserve. J Environ Econ Manag 80:69–86
Holtsmark B, Sommervoll DE (2012) International emissions trading: good or bad? Econ Lett 117(1):362–4
ICAP (2018) Status Report 2018. International Carbon Action Partnership, Berlin
Innes R (2003) Stochastic pollution, costly sanctions, and optimality of emission permit banking. J Environ Econ Manag 45(3):546–68
Jaffe J, Ranson M, Stavins RN (2009) Linking tradable permit systems: a key element of emerging international climate change architecture. Ecol Law Q 36(4):789–809
Johnson SL, Pekelney DM (1996) Economic assessment of the regional clean air incentives market: a new emissions trading program for Los Angeles. Land Econ 72(3):277–97
Jotzo F, Betz R (2009) Australia’s emissions trading scheme: opportunities and obstacles for linking. Climate Policy 9(4):402–14
Keohane N, Petsonk A, Hanafi A (2017) Toward a club of carbon markets. Climatic Change 144(1):81–95
Krupnick AJ, Oates WE, Verg EVD (1983) On marketable air-pollution permits: the case for a system of pollution offsets. J Environ Econ Manag 10(3):233–47
Leiby P, Rubin J (2001) Intertemporal permit trading for the control of greenhouse gas emissions. Environ Resour Econ 19(3):229–56
Liu X (2010) Extracting the resource rent from the CDM projects: can the Chinese government do better? Energy Policy 38(2):1004–9
Marchiori C, Dietz S, Tavoni A (2017) Domestic politics and the formation of international environmental agreements. J Environ Econ Manag 81:115–31
Mehling MA, Haites E (2009) Mechanisms for linking emissions trading schemes. Climate Policy 9(2):169–84
Mehling MA, Metcalf GE, Stavins RN (2017) Linking heterogeneous climate policies (Consistent with the Paris Agreement). Discussion Paper ES 2017-6, Harvard Project on Climate Agreements
Mehling MA, Metcalf GE, Stavins RN (2018) Linking climate policies to advance global mitigation. Science 359(6379):997–8
Mendelsohn R (1986) Regulating heterogeneous emissions. J Environ Econ Manag 13(4):301–12
Metcalf GE, Weisbach D (2012) Linking policies when tastes differ: global climate policy in a heterogeneous world. Rev Environ Econ Policy 6(1):110–29
Montgomery WD (1972) Markets in licenses and efficient pollution control programs. J Econ Theory 5(3):395–418
Nash JFJ (1950) The bargaining problem. Econometrica 18(2):155–62
Newell RG, Stavins RN (2003) Cost heterogeneity and the potential savings from market-based policies. J Regul Econ 23(1):43–59
Pezzey JC, Jotzo F (2012) Tax-versus-trading and efficient revenue recycling as issues for greenhouse gas abatement. J Environ Econ Manag 64(2):230–6
Pizer WA, Yates AJ (2015) Terminating links between emission trading programs. J Environ Econ Manag 71:142–59
Ranson M, Stavins RN (2016) Linkage of greenhouse gas emissions trading systems: learning from experience. Climate Policy 16(3):284–300
Rehdanz K, Tol RS (2005) Unilateral regulation of bilateral trade in greenhouse gas emission permits. Ecol Econ 54(4):397–416
Schneider L, Lazarus M, Lee C, van Asselt H (2017) Restricted linking of emissions trading systems: options, benefits, and challenges. Int Environ Agreem Polit Law Econ 17(6):883–98
Sterk W, Braun M, Haug C, Korytarova K, Scholten A (2006) Ready to link up? Implications of design differences for linking emissions trading schemes. Working Paper 1-06, Wuppertal Institute for Climate, Environment and Energy
Tietenberg T (1995) Tradeable permits for pollution control when emission location matters: what have we learned? Environ Resour Econ 5(2):95–113
Tietenberg T (2006) Emissions Trading: principles & practice, 2nd edn. Resources for the Future Press, Washington
Tol RS (2009) Intra-union flexibility of non-ETS emission reduction obligations in the European Union. Energy Policy 37(5):1745–52
Trotignon R (2012) Combining cap-and-trade with offsets: lessons from the EUETS. Climate Policy 12(3):273–87
Tuerk A, Mehling M, Flachsland C, Sterk W (2009) Linking carbon markets: concepts, case studies and pathways. Climate Policy 9(4):341–57
Victor DG (2015) The case for climate clubs. Policy paper, E15Initiative (International Centre for Trade and Sustainable Development & World Economic Forum)
Weitzman ML (1974) Prices vs quantities. Rev Econ Stud 41(4):477–91
Westskog H (2002) Why should emissions trading be restricted? Climate Policy 2(1):97–103
Yates AJ, Cronshaw MB (2001) Pollution permit markets with intertemporal trading and asymmetric information. J Environ Econ Manag 42(1):104–18
Zhu J (2014) Assessing China’s discriminative tax on clean development mechanism projects: does China’s tax have so many functions? J Environ Plan Manag 57(3):447–66
Acknowledgements
We would like to thank Anna Cretì, Baran Doda, Meredith Fowlie, Sabine Fuss, Larry Goulder, Jean-Pierre Ponssard, Philippe Quirion and an anonymous reviewer from the FAERE for their helpful comments on a previous version of this paper. We also wish to thank two anonymous reviewers and the editor for their comments and suggestions. All remaining errors are ours.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Statement of Exclusive Submission
This paper has not been submitted elsewhere in identical or similar form, nor will it be during the first three months after its submission to the Publisher.
Funding Information
S. Quemin acknowledges funding from LABEX Louis Bachelier Finance and Sustainable Growth (ANR 11-LABX-0019 project) under the ‘Investments for the Future’ programme (in accordance with Article 8 of the Assignment Agreements for Communication Assistance).
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Analytical Derivations and Collected Proofs
1.1 Quantity-Restricted Linkage
Let \(\alpha \in [0;\,1]\) be the authorized share of inter-jurisdictional abatement transfers relative to full linkage. In the constrained link, jurisdiction 1 (resp. 2) abates \(a-\alpha \Delta ^*\) (resp. \(a+\alpha \Delta ^*\)) and the equilibrium marginal abatement cost is \(\bar{\tau }_1(\alpha ) = c_1 (a-\alpha \Delta ^*)\) (resp. \(\bar{\tau }_2(\alpha ) = c_2 (a+\alpha \Delta ^*)\)). Note also that \(\bar{\tau }_1(\alpha )-\bar{\tau }_2(\alpha ) = (1-\alpha ) ( \tau _1 -\tau _2 )\) and that \(|\tau _i-\bar{\tau }_i(\alpha )| = c_i \alpha \Delta ^*\), for \(i=\{1,2\}\). The scarcity rent S, the deadweight loss L and jurisdictional economic gains from trade \(\bar{\Gamma }_i\) then obtain from simple area computations (e.g., from Fig. 2), that is
The scarcity rent S is increasing (resp. decreasing) in \(\alpha \) for \(\alpha \le \)(resp. \(\ge \))1/2. The deadweight loss L is decreasing in \(\alpha \) at a decreasing rate. Jurisdictional economic gains \(\bar{\Gamma }_i\) are increasing in \(\alpha \) less than linearly but at an increasing rate. Addintionally, note that
That is, the size of the scarcity rent relative to that of the economic gains from trade accruing to jurisdictions is significant for a wide range of quantitative restrictions. The way the rent is apportioned among jurisdictions is thus of political importance in terms of linkage design. Finally note that since overall abatement is constant the degree of cost efficiency relative to full linkage can be measured by the ratio of the total surplus under the restriction \(\alpha \) to the total surplus under full linkage, which is given by the index
Although any binding quantitative restriction is detrimental in aggregate terms, this is not necessarily so from a jurisdictional perspective, as shown below.
Proof of Proposition 3.1
Fix \(\theta \in [0;\,1]\). The surplus accruing to jurisdiction 1 under the restriction \(\alpha \) consists of gains from trade and a share of the scarcity rent, that is
The optimal restriction from jurisdiction 1’s perspective thus satisfies
for which the first-order condition simplifies to
provided that \(\alpha _1^*\) belongs to [0; 1]; otherwise, full linkage is preferred, i.e. \(\alpha _1^*=1\). Note that \(\alpha _1^* \ge 0\) and \(\alpha _1^* \le 1\) require \(\theta \ge \bar{\theta }/2\) and \(\theta \ge \bar{\theta }\) where \(\bar{\theta }\doteq c_1/(c_1+c_2) \ge 1/2\), respectively. Equation (A.6) thus holds for \(\theta \ge \bar{\theta }\), which is congruent with Equation (10a). The proof proceeds similarly for jurisdiction 2 where \(\alpha _2^*(\theta ) \doteq \mathrm {arg} \, \max _{\alpha \in [0;1]} \left\langle \Gamma _2(\alpha ;\,\theta ) \doteq \Gamma _2^* \alpha ^2 + (1-\theta ) S(\alpha ) \right\rangle \). \(\square \)
1.2 Border Tax-Restricted Linkage
Consider that jurisdiction 1 unilaterally taxes imports of 2-permits at a proportional rate \(\mu \) and does not share any of the revenues it collects. In the admissible tax range \(\left[ 1;\,1-\tau _2/\tau _1 \right] \), net permit imports are limited to a volume of \(\bar{\Delta }(\mu )\) such that
Jurisdictional economic gains from trade are reduced to \(\bar{\Gamma }_i(\mu )=c_i (\bar{\Delta }(\mu ))^2 / 2\) and decreasing in the tax rate. The total surplus accruing to jurisdiction 1 is \(\Gamma _{1,t}(\mu )=\bar{\Gamma }_1(\mu )+\mu \bar{\tau }_1(\mu )\bar{\Delta }(\mu )=c_1 (\bar{\Delta }(\mu ))^2 / 2 + \mu \bar{\Delta }(\mu )(\tau _1-c_1\bar{\Delta }(\mu ))\) where the second term corresponds to tax revenues. Therefore, jurisdiction 2 is always worse off w.r.t. full linkage but still better off w.r.t. autarky (\(\Gamma ^*_2=\bar{\Gamma }_2(0)\ge \bar{\Gamma }_2(\mu )\ge 0\)) while jurisdiction 1 can be better or worse off w.r.t. full linkage (but always better off w.r.t. autarky) as the diminution in economic gains from trade can be more or less than offset by tax revenues. Indeed, it holds that
where the two bracketed terms are positive for all admissible rate \(\mu \). The sign of \(\Gamma _{1,t}'\) is thus ambiguous. However, by continuity of both \(\Gamma _{1,t}\) and \(\Gamma _{1,t}'\) and by noting that
along with \(\Gamma _{1,t} \left( 1-\frac{\tau _2}{\tau _1} \right) =0 < \Gamma _{1,t}(0)\), there exist \(\mu _1^* \le \bar{\mu }_1\) both admissible such that jurisdiction 1’s surplus is maximized at \(\mu _1^*\) (\(\bar{\Gamma }_1'(\mu _1^*)=0\)) and jurisdiction 1 is indifferent between a tax on imports at a rate \(\bar{\mu }_1>\mu _1^*\) and no tax at all (\(\Gamma _{1,t}(\bar{\mu }_1)=\Gamma _{1,t}(0)=\Gamma _1^*\)). In aggregate, the tax on 2-permit imports results in a deadweight loss of
and taking the derivative gives
which is the sum of three positive terms. The deadweight loss is hence increasing in the tax rate or, equivalently, the aggregate surplus from the link is decreasing in the tax rate.
Notice the bijection between binding quantitative restrictions and admissible tax rates that exists in the deterministic, partial-equilibrium framework we consider. In particular, the tax rate that restricts net permit transfers up to an authorized share \(\alpha \in [0;\,1]\) is such that
with \(\mu = 0 \Leftrightarrow \alpha =1\) and \(\mu =1-c_2/c_1 \Leftrightarrow \alpha =0\). However, a limit and a tax rate linked via Eq. (A.12) are not equivalent in terms of distributional aspects (e.g., for a scarcity rent and tax revenues of identical sizes, the rent apportionment depends on relative bargaining powers) or market functioning (e.g., transaction price formation). Finally, notice that the optimal tax rate on permit imports obtains as a special case of Eq. (10a) with \(\theta =1\), that is
There is no particular interest in determining an analytical value for \(\bar{\mu }_1\). In the symmetric case where jurisdiction 2 unilaterally imposes a tax \(\mu _2\) on 2-permit exports and keeps all the revenues to itself the optimal tax rate would satisfy \(\bar{\Delta }(\mu _2^*) = \alpha _2^*(0) \Delta ^* \, \Leftrightarrow \, \mu _2^* = \frac{c_1-c_2}{c_1+2c_2}>\mu _1^*\).
1.3 Linkage with Exchange Rates
Proof of Proposition 3.3
From Eq. (13) and market closure, any interior linked market \(\rho \)-equilibrium is characterized by
Since \(\Delta _1(\rho ) \sim _{0^+} \frac{\tau _1}{c_1}\) and \(\Delta _1(\rho ) \sim _{+\infty } \frac{- \tau _2}{\rho c_2} \rightarrow _{+\infty } 0^-\), it holds that \(\lim _{0^+}e_1(\rho )=e_0\) and \(\lim _{+\infty }e_1(\rho )=\omega \). The only relevant (positive) root of \(\Delta _1'(\rho )=0\) is \(\rho ^+=\frac{\tau _1}{\tau _2}+ \sqrt{\frac{\tau _1^2}{\tau _2^2}+\frac{c_1}{c_2}}\). Similarly, \(\Delta _2(\rho ) \sim _{+\infty } \frac{\tau _2}{c_2}\) and \(\Delta _2(\rho ) \sim _{0^+} \frac{\rho ^2\tau _2}{c_1} \rightarrow _{0^+}0\) so that \(\lim _{+\infty }e_2(\rho )=e_0\) and \(\lim _{0^+}e_2(\rho )=\omega \). The only relevant (positive) root of \(\Delta _2'(\rho )=0\) is \(\rho ^{++}=\frac{c_1\tau _2}{c_2\tau _1} \left( \sqrt{1+\frac{c_2\tau _1}{c_1\tau _2}}-1 \right) \). Noting that \(\rho =1\) is an obvious root of \(\Delta _i(\rho )=\Delta ^*\) for \(i=\{1,2\}\), it follows that
where \(\bar{\rho }_1 \doteq \frac{c_1 \tau _2 + c_2 \tau _1}{c_2 (\tau _1-\tau _2)} >0\) and \(\bar{\rho }_2 \doteq \frac{c_1(\tau _1-\tau _2)}{c_1\tau _2+c_2\tau _1} \in (0;\,\tau _1 / \tau _2)\). Statements (i) thus follows immediately. Note that the threshold \(\bar{\rho }_2\) satisfies
In our special case where \(\omega _1=\omega _2\), \(\bar{\rho }_2=1 \Leftrightarrow \tau _1 = 3 \tau _2 \Leftrightarrow c_1 = 3 c_2\). Note that when \(\bar{\rho }_2=1\) emissions in jurisdiction 2 never pass below their full-linkage level.
Relative to the benchmark, additional aggregate abatement \(\gamma (\rho )\) obtains as the difference between aggregate emissions in the benchmark and in the \(\rho \)-equilibrium, that is
Recall that \(\bar{\Delta }_1(\rho ) \ge 0\) i.f.f. \(\rho \in [0;\,\tau _1 / \tau _2 ]\). Hence \(\gamma (\rho ) \ge 0\) i.f.f. \(\rho \in [1;\,\tau _1 / \tau _2 ]\). We then solve for
Noting that by assumption \(\tau _i=c_ia\), \(i=\{1,2\}\), then \(c_2\tau _1=c_1\tau _2\) and additional aggregate abatement is maximized at \(\rho =\hat{\rho }\doteq (\tau _1 / \tau _2)^{1/2}\). \(\square \)
Proof of Corollary 3.4
In the linked market \(\hat{\rho }\)-equilibrium variations in jurisdictional emission levels as compared to autarky read
In total, aggregate abatement increases by
Assume that in lieu of implementing the exchange rate regime \(\hat{\rho }\) jurisdictions were to agree upon a full link where jurisdiction 2 would reduce its domestic cap in such a fashion that aggregate abatement would be equal to that in the \(\hat{\rho }\)-equilibrium. That is, jurisdictional caps would be such that \(\hat{\omega }_1=\omega \) and \(\hat{\omega }_2=\omega -\gamma (\hat{\rho })\). Under full linkage with jurisdictional caps \((\hat{\omega }_1,\hat{\omega }_2)\) permits continue to flow in the natural direction and unit transfers amount to
These two linkage regimes can be compared in terms of sole economic gains from trade because they are generative of the same aggregate level of emissions. In particular, jurisdiction i prefers the full link with domestic caps \((\hat{\omega }_1,\hat{\omega }_2)\) over the \(\hat{\rho }\)-equilibrium with domestic caps \((\omega ,\omega )\) i.f.f. \(\hat{\Delta } \ge |\hat{\Delta }_i| \), which holds for \(i=\{1,2\}\) since
Another interpretation than that proposed in the body of the paper is that, if the two jurisdictions were to establish a link with an exchange rate aimed at correcting for too low an ambition level in jurisdiction 2, then they would both be better off from a full link with an equivalent downward-adjusted cap in jurisdiction 2. \(\square \)
Appendix 2: Numerical Simulations
Jurisdictions have the same domestic abatement objective, thus \(c_1/c_2 = \tau _1/\tau _2\). Equating this ratio to 3 ensures that \(\bar{\rho }_2=1\) and provides clear-cut results in terms of emission variations for jurisdiction 2 (see Eq. (A.15b)). The numerical results are presented in relative values (with full linkage or autarky taken as benchmarks) and hold irrespective of the stringency of the common domestic abatement objective. In the following and without loss of generality we set \(e_0=1000\), \(\omega =900\) and \(c_1=3c_2=0.3\), which gives \(\tau _1=3\tau _2=30\).
Border taxes on permit transfers Relative to full linkage, the implications of a border tax on permit imports in the admissible tax range \(\left[ 0;\,2/3 \right] \) are displayed in Fig. 5. This also depicts the effects of a quantitative transfer restriction when jurisdiction 1 has monopsony power (\(\theta =1\)). As the tax rate rises, Fig. 5a shows that trade decreases while the price wedge increases, i.e. cost efficiency decreases. In particular, \(\mu =0\) corresponds to full linkage and for \(\mu \ge 2/3\) the tax regime replicates autarky. Figure 5b shows that jurisdiction 1’s surplus (gains from trade + tax revenues) is increasing with \(\mu \) as long as \(\mu <\mu ^* \simeq .22\) and at that \(\bar{\mu } \simeq .40\) it is indifferent between a tax \(\bar{\mu }\) and full linkage. Both aggregate and jurisdiction 2’s surpluses decrease with the tax rate and remain positive. However, note that jurisdiction 2’s surplus is quasi linearly decreasing while the aggregate surplus is concave and relatively flat for small tax rates. For instance, when the tax rate is \(\mu \simeq .3\) jurisdiction 2 loses about half of its full-link gains while the deadweight loss remains small (\(\sim \) 10%).
Quantitative transfer restrictions Figure 6a depicts the optimal quantitative restrictions for jurisdiction 1 (black line) and 2 (grey line) as a function of relative bargaining power. The black and grey circles denote restrictions that constitute an improvement w.r.t. full linkage for jurisdictions 1 and 2, respectively. Note that the range of such quantity-restricted linkages is wider for the lower-cost jurisdiction. Although both jurisdictions cannot simultaneously be better off under a quantitative restriction w.r.t. full linkage, one jurisdiction may accept to lose out a share of its full-link gains if this is necessary for the other jurisdiction to initiate linking. As an illustration, the black circles in Fig. 6b indicate quantitative restrictions that are potentially acceptable in the sense that jurisdictions are willing to give up on (at most) half of their full-linkage gains in the restricted link. In this case, \(\alpha \simeq .7\) (resp. \(\alpha \simeq .3\)) is the most stringent limit to be potentially acceptable when \(\theta = \{0;1\}\) (resp. \(\theta = \bar{\theta }\)).
Jurisdictional preferences for quantitative linkage restrictions. a Thick black and grey lines are optimal quantitative restrictions for jurisdiction 1 and 2, respectively, and intersect at \(\theta =\bar{\theta }=.75\); black and grey circles indicate volume-restricted linkages better than full linkage for jurisdiction 1 and 2, respectively. b Black (grey) bullets denote restrictions that are (not) potentially acceptable at a 50% level of full-linkage gains from trade by both jurisdictions
Linkage with exchange rates We first define three indexes measuring overall abatement (B.1a), average abatement cost (B.1b) and cost efficiency (B.1c) relative to autarky.
The black curve in Fig. 4 plots \(I^{CE}\) as a function of \(I^{A}\). Note that \(I^{CE}\) merely gives an indication (and not a proper measure) of the degree of cost efficiency. The kink at \(\rho =1\) is due to the max operator: at this point there is a discontinuity since the higher marginal abatement cost jurisdiction switches (\(\bar{\tau }_1 \ge \bar{\tau }_2 \Leftrightarrow \rho \ge 1\)).
Figure 7 describes both the economic and environmental outcomes along the continuum of \(\rho \)-equilibria. The black curve in Fig. 7a shows that the degree of cost efficiency is the lower the farther away the exchange rate from parity, where it is maximal. The grey curve in Fig. 7a shows that overall abatement is higher than in the benchmark provided that the exchange rate lies in \(\left[ 1;\,\tau _1 / \tau _2 \right] \) and is maximal at \(\rho =\hat{\rho }\). Another way to see this is to consider Fig. 7b. In the reduction zone, overall abatement is higher than in the benchmark since the volume of abatement undertaken in jurisdiction 2 is higher than the corresponding increase in emissions occurring in jurisdiction 1 (the dotted grey line is above the continuous grey line and the spread between them is maximal at \(\rho =\hat{\rho }\)). The converse holds outside of this zone. Note also that as the exchange rate runs from autarky to parity both abatement and permit flows from 2 to 1 increase. In the amplification zone the wedge in jurisdictional prices (relative to autarky) widens out as compared to full linkage while it is reversed in the inversion zone. In the latter zone, the negative values associated with the continuous and dotted grey lines indicate that permit trading occurs opposite to the natural direction.
Appendix 3: Cap Selection and Environmental Damages
We assume that damage functions are linear and let \(d_i >0\) denote jurisdiction i’s constant marginal damage from aggregate emissions. This ensures jurisdictional cap reaction functions are orthogonal, i.e., jurisdictions select the same domestic cap whatever the other jurisdiction’s choice. Note that this is a mild assumption as there is evidence that marginal benefits from mitigation are much flatter than marginal abatement costs over the range of annual emissions (Newell and Stavins 2003). We abstract from the strategic anticipatory effects of (different types of restricted) linkage on domestic cap selection à la Helm (2003). For instance, when cap selection is non-cooperative and linkage is not anticipated, the Cournot-Nash caps satisfy
Note that each domestic cap is strictly binding (\(\omega _i < e_0\)) and independent of the cap-setting decision in the other jurisdiction (\(\omega _{-i})\). We abstract from corners by assuming that \(d_i < c_i e_0\), i.e., \(\omega _i>0\) for \(i=\{1,2\}\). Note that our assumption of identical caps in the main text obtains if we assume that \(c_1/c_2 = d_1/d_2\). Note also that jurisdictions do not internalize the negative externality generated by their emissions on the other jurisdiction. By contrast, cooperative caps are socially efficient and satisfy \(\omega _i^*=e_0-(d_i+d_{-i})/c_i < \omega _i\).
The optimal exchange rate \(\rho _i^*\) for jurisdiction i maximizes the difference in compliance costs between autarky and \(\rho _i^*\)-equilibrium, knowing how both jurisdictions react to a rate \(\rho \), that is
This mitigates jurisdictional preferences for unrealistically large/small rates as mentioned in the text. We do not provide an analytical solution to Programme (C.2) and refer the reader to the literature on optimal inter-temporal trading ratios, e.g., Leiby and Rubin (2001), Yates and Cronshaw (2001), Innes (2003) and Feng and Zhao (2006), for similar analytical problems.
Note that the socially efficient level of emissions \(2e_0- (d_1+d_2)/c\) need not coincide with that triggered under \(\hat{\rho }\)-linkage. In particular, we numerically show that when \(d_i/c_i\) is relatively small (resp. big) then the two jurisdictions overabate (resp. underabate) at the \(\hat{\rho }\)-equilibrium as compared to the social optimum. Additionally, we numerically show that jurisdictionally-preferred exchange rates defined in Programme (C.2) that are potentially acceptable at a 50% level of full-link gains are centred around parity within the range [0.61; 1.44].
Rights and permissions
OpenAccess This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Quemin, S., de Perthuis, C. Transitional Restricted Linkage Between Emissions Trading Schemes. Environ Resource Econ 74, 1–32 (2019). https://doi.org/10.1007/s10640-018-00307-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10640-018-00307-6