Abstract
While existing studies acknowledge the importance of using technology in the mathematical modelling process, questions about how to integrate digital tools into mathematical modelling are not still answered. This study aims to examine pre-service mathematics teachers’ designing and solving mathematical modelling problems by using different digital tools through the collaboration of two different courses in their education program. The GeoGebra-supported modelling cycle was adopted as the conceptual framework of the study. The case study was used to design the research. The participants of the study were three volunteer pre-service secondary mathematics teachers, who were able to use and integrate digital tools in mathematics education. The pre-service teachers were asked to design a mathematical modelling problem by integrating different digital tools as the final assignment in both courses. The designed mathematical modelling problem, the video records of pre-service teachers’ explanations including the designing and solving process, and the video records of the focus group interview were the data of the study. The results showed that the pre-service teachers were able to design and solve an effective and comprehensive mathematical modelling problem using technology by combining their skills that they had learnt through different courses. In particular, they were able to use different digital tools in both designing and solving a mathematical modelling problem. Their solution also led to the extension of the adopted framework by adding new technological actions into the modelling stages.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Over the last decades, research has acknowledged the central role of using technology in mathematics education for contributing to students’ development of learning mathematical concepts, and digital toolsFootnote 1 have been accepted as effective tools in learning and teaching mathematics (Bozkurt & Ruthven, 2017; Bozkurt & Yigit Koyunkaya, 2022; Clark-Wilson et al., 2014, 2023; de Villiers, 1998; Laborde, 2001). In line with this idea, the use of digital tools to improve the teaching and learning of mathematical modelling has become an important research area (Greefrath et al., 2018; Kaiser et al., 2006). New technological tools (particularly digital tools) play a pivotal role in mathematical modelling by providing opportunities for exploring mathematical situations.These tools also foster new ways of understanding, evaluating, and interpreting real-world situations (Cevikbas et al., 2023; Molina-Toro et al., 2022). Although the use of technological tools in the mathematical modelling process has many advantages (Siller & Greefrath, 2010; Greefrath & Siller, 2017, 2018), the question of how technology should be integrated into the implementation to effectively support students’ modelling skills has not yet been clearly answered (English, 2016). Although researchers have not yet been able to provide a clear answer to this question, ongoing research shows that more concrete studies on the use of technology in mathematical modelling are emerging.
Molina-Toro et al.’s (2019) research on the articulation of mathematical modelling and digital technologies and Cevikbas et al.’s (2023) research on the educational opportunities offered by digital technologies in mathematical modelling revealed that the importance of technology in modelling is of a current interest in the research area. However, a limited number of studies have been conducted on the effective integration of digital tools into learning environments (Siller et al., 2022). Hence, existing research (Cevikbas et al., 2023) suggested conducting studies on the opportunities and challenges of using different digital tools in mathematical modelling. Following this suggestion, in this study, we aim to extend this limited number of studies by concentrating on the use of different digital tools in both designing and solving mathematical modelling problems. In particular, we focused on how pre-service mathematics teachers (PMTs) used different digital tools to design a mathematical modelling problem and examined their solution throughout the modelling process by highlighting the intended use of different digital tools. Accordingly, the research questions are as follows:
-
How do PMTs use different digital tools in designing a mathematical modelling problem?
-
How do PMTs plan to solve a mathematical modelling problem using different digital tools?
The following section focuses on existing studies related to the aim of this study and discusses the selected conceptual framework that guided the study.
1.1 Importance of digital tools in mathematical modelling
The use of technology in mathematical modelling enables students to improve their modelling skills (Greefrath et al., 2018). The existing studies have illuminated the need for using technology to support the mathematical modelling process. For instance, Fuchs and Blum (2008) indicated that integrating technological tools into the modelling process could support students in achieving different goals. According to these researchers, the use of various digital tools at different stages of the modelling process could encourage students in terms of different pedagogical, psychological, cultural and pragmatical aims. These aims support students to learn application competencies in elementary or complex situations aimed at teaching; to comprehend and remember mathematical contents; to see a balanced picture of mathematics as a science and its impact on culture and society; and to understand, cope with, and evaluate known situations (Siller & Greefrath, 2010). From this perspective, students’ abilities to use digital tools could promote the approaches related to their solutions in the modelling process (Greefrath et al., 2018).
Existing studies have highlighted the advantages of using digital tools during the modelling process (Blum & Leiß, 2007; Greefrath, 2020; Greefrath & Siller, 2017, 2018; Siller & Greefrath, 2010). In particular, using digital tools in this process supports the stages of the modelling process in terms of learning of mathematical concepts (Viseu & Leite, 2019), inquiring, reasoning and exploring some mathematical situations and concepts (Confrey & Maloney, 2007), realizing the importance of mathematical concepts in real life (Frassia & Serpe, 2017; Siller & Greefrath, 2010), constructing different representations (Arzarello et al., 2012), checking and validating mathematical solutions (Cevikbas et al., 2023), working experimentally (Villarreal et al., 2018), and making mathematical modelling a more accessible activity for students (Viseu & Leite, 2019). Furthermore, in the part of the modelling process, it is impossible to work on the problem without using digital tools in some cases. For example, it is inevitable to use digital tools in computationally intensive activities, in studying, structuring, or evaluating large data sets, in visualizing processes and results, and in some experimental studies (Siller & Greefrath, 2010) or in calculating and validating numerical and algebraic results (Greefrath et al., 2018; Lingefjärd, 2000). Therefore, teachers need to have comprehensive knowledge and skills in both using digital tools in mathematics education and integrating them into their teaching (Siller & Greefrath, 2010).
Lingefjärd (2007) states that if pre-service teachers are convinced of the benefit and necessity of using technology in mathematical modelling, they will be able to integrate it into their future teaching. From this viewpoint, it is important to educate pre-service teachers about the use of technology and mathematical modelling in their teacher education programs. Although researching the use of digital tools in mathematical modelling with pre-service teachers is crucially important to improve their teaching of mathematical modelling problems with the use of technology, Villarreal et al. (2018) assert that studies about the use of digital tools that support and enhance pre-service teachers’ knowledge and experiences in the modelling process are less prevalent. In one of these few studies, for example, Lingefjärd (2013) examined modelling tasks including technology and indicated that technology could broaden and enhance pre-service teachers’ experiences with modelling processes. In another study, Daher and Shahbari (2015) investigated middle school pre-service mathematics teachers’ modelling processes and concluded that the use of technology enabled meaningful mathematical learning. Therefore, we aimed to combine two different courses, Mathematical Modelling and Information and Communication Technologies in Mathematics Education, for educating pre-service teachers in terms of using digital tools to design and solve a mathematical modelling problem.
In the literature review on using digital technologies in modelling education, Cevikbas et al. (2023) stated that although there were well-founded findings about modelling with digital tools, many concrete questions remain unanswered. One of these questions is how technology is used for modelling and what the interaction between humans and media is (Schukajlow et al., 2018). In our study, we illuminated how technology was used for modelling by investigating which and how digital tools were used in both designing and solving a modelling problem. This study, in particular, extended the existing literature about the use of digital tools in designing and solving a mathematical modelling problem by suggesting the use of different digital tools such as GeoGebra, Desmos (particularly a graphic calculator), Google Earth, or Youtube, which have not been used together in both designing and solving a mathematical modelling problem with technology before. In the next section, we present Greefrath et al.’s (2018) framework that leads the examination of the modelling problem solution process.
1.2 Conceptual framework
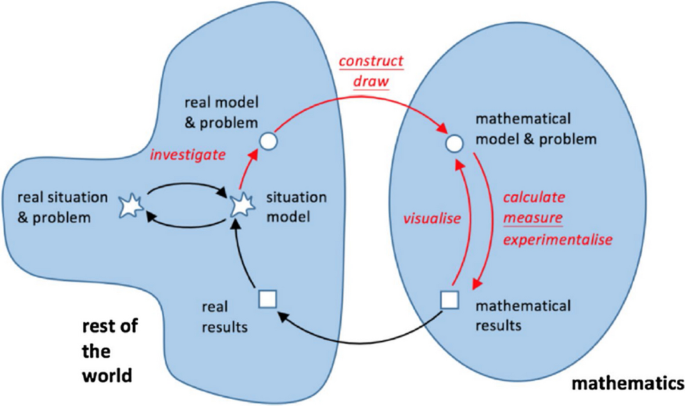
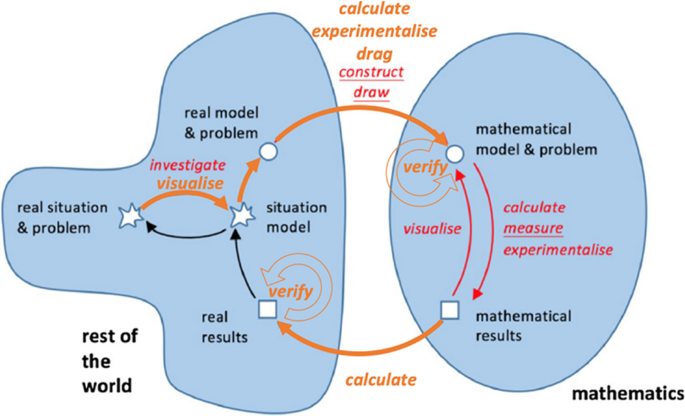
The use of technology plays a pivotal role in the modelling process, which cannot be accepted as an independent domain. Therefore, digital tools can be usefully integrated in every stage of the modelling cycle (Geiger, 2011; Greefrath et al., 2011; Greefrath & Vorhölter, 2016) depending on the purpose (Ludwig & Jablonski, 2021). Although different digital tools used in the modelling cycle have been discussed in the studies, the researchers mainly used dynamic geometry software (specifically, GeoGebra) or computer algebra software. In particular, these studies indicated that GeoGebra supports the modelling process through the use of program-specific features such as using different kinds of representations, self-checking by comparing chart and spreadsheet windows or controlling the geometric constructions by changing a point (Greefrath & Siller, 2018). In this study, Greefrath et al.’s (2018) GeoGebra-supported modelling cycle, which describes technological actions on Blum and Leiß’s (2007) modelling cycle, was chosen as the conceptual framework to examine the pre-service teachers’ possible solution in the modelling process (see Fig. 1).
GeoGebra-supported modelling cycle (Greefrath et al., 2018, p. 236)
According to Blum and Leiß’s (2007) cycle, first students understand a real-life problem and construct a situation model explaining the problem. Then, they simplify the situation model and construct the real model by making the necessary assumptions. During the mathematization process, students construct mathematical models and then obtain mathematical results by solving the models. Students consider mathematical results in the context of real life situation, discuss the effectiveness of the results, and obtain real results by interpreting them. They validate real results by re-examining assumptions, mathematical models, mathematical results, and correctness of calculations (Tekin Dede & Bukova Güzel, 2018). The technological actions that occur when the use of digital tools is integrated into the modelling process are shown in red ink in Fig. 1. Greefrath et al. (2018) developed the cycle based on empirical data and found that GeoGebra was only applied in the modelling cycle among the construction of a real model, a mathematical model, and mathematical results. Particularly, in this figure, the actions of investigate, experimentalise, calculate and visualize are the actions that could be confirmed by empirical data, but the researchers added other actions (construct, draw and measure) by working on GeoGebra (Greefrath et al., 2018). In the aforementioned study, they did not find any evidence for the use of GeoGebra in other steps of the modelling cycle due to reasons such as the small number of students or the problem itself. However, in their previous studies, they stated that visualization and controlling/verifying are possible technological actions that can be used in the transition from mathematical results to real results, in other words, in the interpretation step as several possibilities for applying digital tools in the modelling cycle (Greefrath, 2011). These technological actions are adopted and interpreted as given in Table 1.
For the examination of the actions, there are studies in which GeoGebra is used as a digital tool. In contrast to the existing studies, in this study, we suggest a new perspective on technological actions on the modelling cycle by providing different digital tools that can be used in both designing and solving mathematical modelling problems. In addition, we aimed to expand the use of digital tools in the stages of modelling cycles, such as the validation stage, where student work is rarely seen (Blum & Leiß, 2007), in response to Greefrath and Vorhölter’s (2016) call regarding the necessity of extending the modelling cycle and the necessary translation process (e.g. interpreting and validating) by using digital tools.
2 Method
In this study, a qualitative research paradigm was adopted and the research was designed using a case study. The case study examines and answers the research questions of what, how, and why to analyze the identified case in depth in its context or environment (Yin, 2018). Using the case study design helped us explore the PMTs' ability to design and solve a mathematical modeling problem with the use of different technological tools, which also showed us the effects of integration of two courses in a teacher education program. In particular, we accepted the PMTs’ designing and solving of a mathematical modelling problem as a unit to understand and illustrate the process, in detail (Stake, 2005).
2.1 Participants, context, and procedure
The participants of the study were three pre-service secondary mathematics teachers in their third year of the teacher education program in Türkiye. We conducted this research by combining two different university-based courses during the Spring Semester of 2021. Two authors were instructors of different courses namely Mathematical Modelling (MM) and Information and Communication Technologies in Mathematics Education (ICTME). The MM course (21 PMTs were enrolled in this course) was compulsory, and the ICTME course (14 PMTs were enrolled in this course) was the elective course in their program. Fourteen PMTs were taking both courses, and we selected three of them based on a purposive sampling method (Merriam, 1998). In particular, we considered a couple of criteria in selecting the participants of the study. The PMTs’ use of different technological tools in designing and solving mathematical modelling problem is our first criterion. Most of the students integrated technology into their mathematical modelling problems, but the selected participants used various technological tools for different purposes while designing and solving their problem as the final assignment. Additionally, their ability to use of technological tools was considered another criterion in the selection. These three PMTs provided evidence regarding the development of their ability to select, appropriately use, and integrate technological tools in designing technology-based tasks during the course. Based on the authors’ experiences in the courses, the PMTs’ ability to explain and justify their thoughts, reasoning, and decisions was considered as another criterion, which was a crucial aspect in both collecting and examining the data. In addition, these three participants had different academic achievements, and they were willing to participate in the research and volunteered for participation. The PMTs also indicated that it is almost impossible to solve their modelling problem without using technology, which also supported our decision to work with these pre-service teachers.
Even though two different courses have different aims and outcomes, as instructors, we discussed and collaboratively worked to combine some parts of the courses. The MM course aims to teach PMTs how to learn and realize the nature of mathematical modelling and modelling process; to be able to design and solve mathematical modelling problems; to learn how to use technology in mathematical modelling; and to understand the place of mathematical modelling in the curriculum. The ICTME course aims to provide students with the ability to integrate different technological tools into mathematics education and to use dynamic mathematics software (particularly GeoGebra), various web 2.0 tools (particularly Desmos), and web-based education applications. The goal of this course is not only to improve students’ ability to use technology in mathematics education but also to develop their existing mathematical knowledge by discussing the role of technology in mathematics teaching and learning. The contents of the courses are given in Table 2. As instructors, we discussed and selected a few mathematical modelling problems that were designed or solved in technological environments. In the same week, while implementing the example, the instructor of the MM course introduced and discussed how to solve modelling problems throughout the stages of the modelling cycle by using technology. The instructor of the ICTME course taught and discussed how to design or solve problems using various technologies and how to use the interface or technological tools in these technologies. For instance, in week 11, we provided the Buca Arena Stadium problem (Yiğit Koyunkaya & Tekin Dede, 2021) to the PMTs, and the instructor of the MM course taught how to design the problem considering the stages of the modelling cycle. The instructor of the ICTME course taught how to create and construct a custom activity in Desmos by focusing on how to integrate pictures or videos, how to add the notes, free-response, math-response, multiple choice, checkbox or order list, media and links, how to use the graphic calculator, sketching or geometry tool, and discussing the importance of adding the teachers’ role, students’ support, and sample responses. At the end of the courses, 14 PMTs were required to do a final assignment in which they had to design a mathematical modelling problem in Desmos. In the assignment, the PMTs were also asked to use/integrate various technologies learned in the ICTME course, and they were free to work in groups (including 2 or 3 people). In the assignment, the PMTs were asked to design the problem in Desmos by considering mathematical modelling problem criteria (Borromeo Ferri, 2018) and a possible solution regarding the stages of modeling cycle (Blum & Leiß, 2007). In each Desmos window, they were free to select and integrate any digital tools and were required to include teachers’ role, students’ support, and sample responses. Additionally, they were required to prepare a report explaining the design and solving process. They were free to select the type of their reports; some of the PMTs prepared a written report while other returned audio/video records.
The data in this paper were collected through one group’s final assignment of the courses. The three selected PMTs were members of one group, and they designed a modelling problem in Desmos by integrating various technologies into it and solved it in GeoGebra and Desmos.
2.2 Data collection and analysis
The data of the study consisted of a modelling problem (Festival in the City)Footnote 2 designed by the three PMTs as a group in Desmos, files related to a possible solution in both Desmos and GeoGebra, three video records in which the PMTs explained their design and solving of the problem that captured their screen and voice, and a video record of the focus-group interview. As a final assignment, the PMTs initially designed mathematical modelling problem using the criteria and constructed 14 windows in Desmos by considering the stages of the modelling cycle. In the assignment, they were required to prepare a report, and the selected group preferred to return their report as video recordings. In the report, they self-recorded three different videos to explain their reasoning of their actions regarding the design process, content, and possible solution of the problem using digital tools. In all of the video recordings, the PMTs used a program to record both the computer screen (in which they introduced or solved their mathematical modeling problem) and their voice. In the first video, they explained how they used a particular tool in each window in Desmos, and how and why they used and integrated different digital tools in different windows (The length of the video was 6 min.). For instance, while explaining the second window in Desmos, they explained how and why they provided YouTube and Google Earth links. In the second video, for each Desmos window, they focused on explaining how a teacher could implement the task by indicating the teachers’ role, students’ support, and sample responses regarding the problem (The length of the video was 10 min.). In the last video, they explained how the problem could be solved using both GeoGebra and Desmos, and solved the problem using GeoGebra first and Desmos then (The length of the video was 15 min.). In that video, they also discussed the challenges they faced while solving the problem as well as affordance related to solving the problem with the use of digital tools. After initially examining their problem and video-based reports, we prepared semi-structured questions to reveal their thoughts, decisions and reasoning about the whole process in the focus group interview. In the interview, two researchers and three PMTs met, and the video camera zoomed in on the PMTs’ computer screen and captured their voices. Throughout the focus group interview, they discussed the content of each Desmos windows to reveal the PMTs’ aims in using digital tools throughout the mathematical modelling process. For instance, we asked them “What are your expectations from students in window 7? Why did you prefer to add the graphic calculator in this window? What is the role of this window in the modelling process?”, “What are your goals in adding the teachers’ role and students’ support in each window?”, and “Why did you use both GeoGebra and Desmos for the possible solution of the problem?”, etc. The focus group interview was conducted over 60 min.
In the analysis, we initially examined the modelling problem in each window in Desmos by examining which digital tools the PMTs used and how they used these tools in each stage of the modelling cycle. After identifying the digital tool, we focused on how the tools served the modelling process by considering the codes identified by Greefrath et al.’s (2018) study. We then transcribed all the records of their video-based reports and focus group interview. After transcribing, we initially read whole data and divided it into parts in terms of the stages of the modelling cycle considering Blum and Leiß’s (2007) study. In each part, we identified and colored the digital tools and examined how the digital tools were used to support the related stage. To reveal their purpose of using the digital tools, we coded the technological actions in terms of Greefrath et al.’s (2018) framework. In this process, in addition to the identified codes, we also found new codes regarding PMTs’ use of digital tools in the stages of the modelling cycle, and extended the existing framework by adding new technological actions.
In the analysis, we used a six-row table, and an example of the table can be seen in Table 3. In the first row, we took a screenshot of the examined Desmos window, and labeled which digital tool the PMTs used in the second row. The table also included a third row that explained how the PMTs used the digital tools (particularly in this step, we looked for the function of the tool in the problem). The fourth row represented the PMTs’ planning that focused on what they suggested to the teachers and how they planned to support the students while implementing the problem. In the fifth row, we analysed how digital tools serve the modelling process by considering the stages of the modelling cycle and the technological actions within the framework (Greefrath et al., 2018). The last row included the PMTs’ quotes from the video records or from the focus group interview that explained the design process of the problem, and suggestions for teachers during the implementation. We used these quotes to support our analysis of the use of digital tools in the design process of the problem.
Afterwards, we analyzed the transcriptions regarding the problem’s possible solution in both GeoGebra and Desmos by using the components of the framework (Greefrath et al., 2018). For this purpose, we initially re-read the the entire transcription, re-examined the PMTs’ solution approaches in GeoGebra and Desmos, and identified the PMTs’ modelling approach in each stage of the cycle (Blum & Leiß, 2007). Additionally, we examined how the selected digital tools served their solution in terms of their modelling approach. In this process, we also identified the technological action they performed to reach their intention. For instance, if the PMTs constructed mathematical models in their possible solution, we coded their work as their approaches in the mathematization stage. Related to their solution, in the focus group interview, the PMTs explained how and why they found the area under the curve by using the graphic calculator, and we related that part to the mathematization stage in the analysis.
In this process, we used another table, as shown in Table 4. The first row represents the screenshot that showed which digital tool (GeoGebra or Desmos) the PMTs used and their purpose of using it; the second row includes the modelling stages; the third row explains how they used the digital tools for solving the problem (particularly we focused on the function of the tool in the process); the fourth row represents the technological actions they performed to solve the problem; and the last row includes the PMTs’ quotes from the video records.
To increase the validity of the data, we triangulated different data sources by focusing on the roles and functions of digital tools in designing and solution of the mathematical modelling problem, which also helped us ensure the trustworthiness of the data. To ensure the reliability, we analyzed the whole data together and discussed our different codes and interpretations until we reached a consensus (Miles & Huberman, 1994). After 3-months, we re-analyzed the whole data to ensure the stability of the analysis (Krippendorff, 1980). Additionally, we provided a consent letter to the PMTs by indicating that their names were anonymous, their participation was voluntary, and they could withdraw from the study at any time without providing any reason (Patton, 2014).
3 Results
In this section, we present the design process of the PMTs’ modelling problem and their possible solution approaches using different digital tools. In the text, the bold words represent the technological action identified through the process and the italics represent the digital tools used by the PMTs. We have added these actions to Greefrath et al.’s (2018) framework and expanded it as presented at the end of this section.
3.1 Design process of the problem
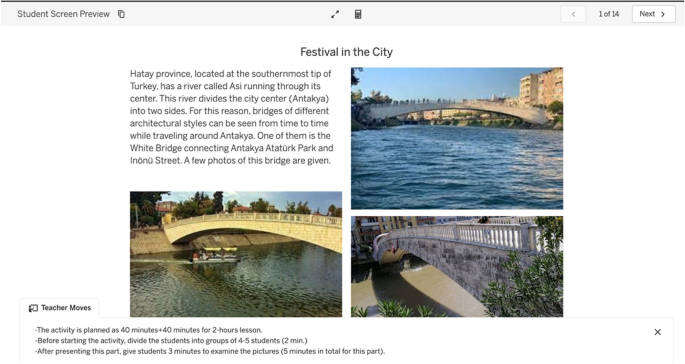
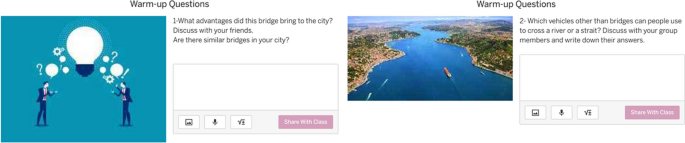
The PMTs planned to implement the warm-up step of the problem by integrating images or videos in four different Desmos windows. In the first window, they used images of the bridge taken from different perspectives/angles and planned to use them as a visual amplifier. They, particularly, aimed to contribute to realism by providing different pictures of the bridge for students without real life experience regarding the context. PMTs explained their actions as follows:
In fact, we intentionally used the pictures. At the beginning, we only included one picture of the bridge; however, we wanted students not to look at the bridge from a single viewpoint. We aimed to support the students in discovering the bridge by looking at it from different perspectives. We thought that students may find different approaches regarding the solution to the problem, or they may start to solve the problem using different solution strategies. Therefore, we have added different pictures of the bridge.
Additionally, in these windows, the PMTs included various supportive actions for teachers that could be used while implementing the problem (see Fig. 2). For instance, they suggested implementing the problem in a 2-hour lesson, dividing the students into groups (4–5 people in each group), and giving 3 min. for students to examine the problem.
In the second window, the PMTs used a video-based application as a technological tool, and they thought of doing warm-up exercises for the real appearance of the bridge with a 30-second video recorded over the bridge (Youtube)Footnote 3and a web-based application (Google earth)Footnote 4. Regarding the reasons for using these digital tools, they stated that some students may take objects of different scales on the bridge as a reference to construct the model, and it would be useful to allow them to explore these objects better to calculate the possible length and area related to the bridge. They expressed their purpose as follows:
We thought that students could think as if they were on or near a bridge using these tools. We also considered that the pictures may not be sufficient to provide an approach to solving the problem. The objects are a little far away in the pictures, but by using Google Earth, they can visualize the people and use them as a reference. In addition, you can walk around the bridge using this tool. We have added it to visualize the real context … We could not have described the bridge in any other way without the use of these digital tools.
The PMTs considered that the technological tools integrated into the problem provided students with the opportunity to experience and explore the real situation related to the existing condition of the context. As a warm-up activity, to support the students’ exploration and experimentation with the context, the PMTs also added two windows that included questions about the advantages of the bridge to the city, and whether they have ever seen a similar bridge. In the interview, they explained the purpose of adding the warm-up activities as supporting the students in visualizing the context of the bridge in their minds and enabling different solution strategies regarding the use of different objects around or on it (See Fig. 3). In this sense, the tools used by the PMTs in the warm-up step of the modelling cycle contributed to the exploration, visualization, and experimentalization of the context.
In the fifth window, the PMTs presented the modelling problem, and they expected students to read and understand the problem (See Fig. 4). The PMTs emphasized that it is crucially important for students to understand the problem, so they planned to use the ‘Students Support’ tab in the Desmos. In this sense, as student support, they provided the following suggestion; ‘If any group has difficulties in understanding the problem, you (as a teacher) lead them and give a clue about where they should start to solve the problem.' They also planned to help with questions such as ‘What do I need to know first to determine how much paint to use?’ or ‘What do you think about finding the length of the cable? How can we find the length?’. The PMTs thought that these questions could trigger students’ thinking about finding knowledge regarding the real-life context. In other words, these questions encouraged students to construct a situation model and transition to a real model by simplifying the problem.
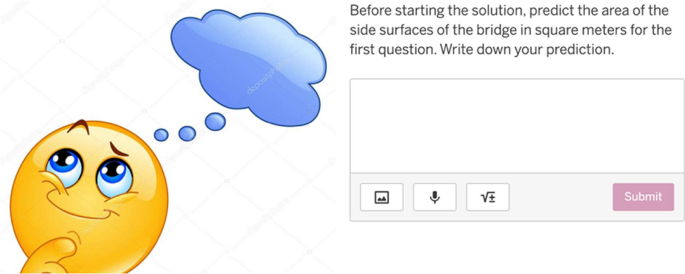
The next windows comprised sections designed to calculate the total area of the surfaces to be painted and the lengths of the LED cables to be installed on the bridge. These steps (the following eight windows in Desmos) included, respectively, windows for making predictions (6 and 10), graphing calculator windows for constructing mathematical models (7 and 11), windows for solving the mathematical models using real life data (8 and 12), and windows for comparing the results obtained by solving the mathematical models with the predictions (9 and 13). In detail, in the sixth window, the PMTs planned to encourage students to make a prediction about the solution of the problem, and they considered measuring and assessing students’ modelling approaches through comparison (See Fig. 5). This prediction activity could support students’ transition from the situation model to the real model. The PMTs expressed the reason for adding prediction windows as follows:
We asked about their predictions because we wanted the students to compare whether they could get closer to the value they predicted when they reached the result. We wanted them to realize how close they had come to the exact result and to see the difference between them.
In the following window, the PMTs planned for students to construct a mathematical model for finding the area of the bridge to be painted. In this window, using the graphical calculator in the Desmos, the PMTs planned for students to construct parabolas representing the bridge and calculate the area between the parabolas with the help of the integral to determine the surface area of the bridge.
In window 8, by providing a free response feature in Desmos, the PMTs planned to ask students to search the properties of the paint they planned to use for coloring the bridge (as well as the LED cable in the following windows), and explain why they chose that particular paint. At this stage, the PMTs aimed for students to identify the assumptions they should use to solve the mathematical models by comprehensively using search engines. They explained their intention as follows:
Searching on the internet is of crucial importance in calculating the cost of paints. We expect them to calculate the cost in the most appropriate way by including these studies in their work.
In the following window, the PMTs aimed for students to compare their predictions with their mathematical results. In particular, this window is effective in validating the solution to the problem. Similar to the previous windows, the PMTs designed the next four windows (10–13) by following similar steps to find the length of the arc using the concept of integral. Similarly, their main expectations from students are to find the length of the LED lights required for the decoration of the bridge and to validate their predictions for the cost calculation by comparing it with their results. In these stages, the PMTs planned to use the graphic calculator in Desmos and search engine tools.
In the last window of the problem, the PMTs planned for students to perform self-validation through the stages of the modelling cycle in the checklist. This checklist is helpful to validate students’ approaches regarding the stages of the modelling cycle, including understanding the problem, simplifying, and evaluating the mathematical model and its’ solution. Additionally, they used a free-response feature to reveal students’ thoughts regarding the advantages and disadvantages of solving the problem using digital tools.
3.2 A possible solution to the problem
The PMTs used both the GeoGebra software and the graphic calculator in Desmos to solve the designed problem. Initially, they considered that the mathematical concept to represent the bridge could be a curve or a function. In line with this idea, they first focused on investigating and visualizing the real-life context given in the problem to construct a situation and real model of the problem. They chose a picture given in the warm-up activities in the first window while constructing the real model. They explained their reasoning for choosing the picture as follows:
They [Students] need to identify the most useful picture so that they can easily calculate the area and the length of the curve… The student should be able to identify and select the necessary picture for the solution. The selected picture should be taken from a wide angle to determine and calculate the length and scale.
According to the PMTs, they selected the most appropriate picture to work on their necessary predictions while constructing the model. Then, they decided to construct the mathematical model in GeoGebra and initially added the picture to the screen using the insert image tool. While inserting it, they intentionally positioned the left corner of the picture at the origin and parallel to the axes.
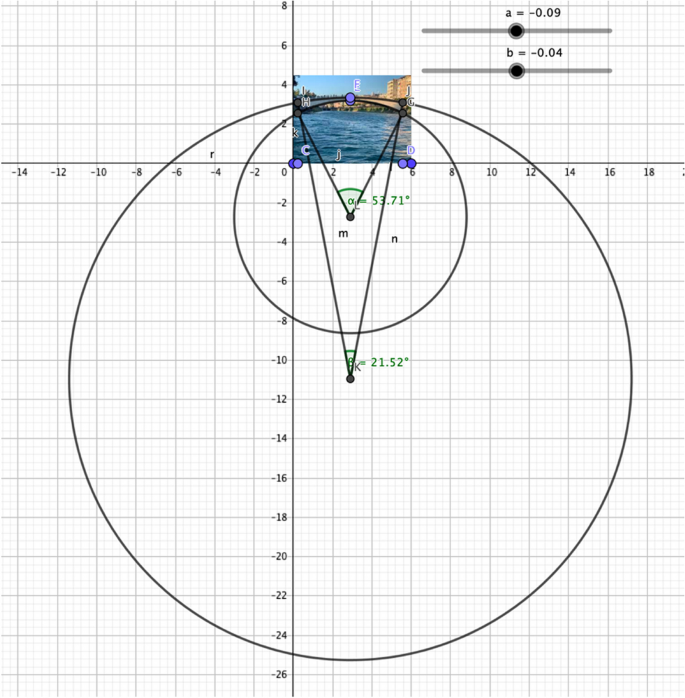
After the PMTs placed the image on the coordinate plane, they began to work on the mathematization stage. They considered the possibility of using the parabola to calculate the surface area and the lengths of the arcs, and continued to work on the mathematical model. In line with this purpose, they initially decided to determine the boundaries of the bridge by drawing the parabola on GeoGebra. During the drawing process, they thought that experimenting with the software could help contruct the mathematical model. While experimenting, they considered that the bridge could be a curve; therefore, they needed to find a quadratic equation to represent it. At this stage, the PMTs attempted to construct the mathematical model and to find the necessary equation by performing different experiments on the software. For instance, they considered using circles (particularly an arc on the circle) to construct mathematical models and used the circle tool in GeoGebra to find the length of the LED lights (See Fig. 6). Additionally, they focused on the sector on the circle to calculate the surface area and the lengths of the arcs. They drew circles as shown in Fig. 6; however, by working on the circle, they were not able to construct the mathematical models.
They explained their actions as follows:
At one point, we even stated that a curve could be found using a sector instead of a parabola. Then, we drew a circle that could be placed on the bridge. At first, we thought that the circle matched better with the bridge; however, the circle was too big [they indicated that the center was far away from the bridge for calculations on the screen as given in Fig. 6].
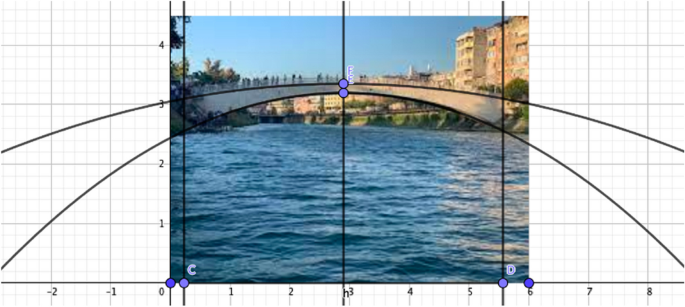
The PMTs then decided to work on the parabola to construct the mathematical model. In this process, they decided to work on the equations \(\text{a}(\text{x}-\text{r})^2\text{and} \ \text{b}(\text{x}-\text{r})^2\), and constructed two sliders to represent the coefficients a and b using the slider tool in GeoGebra. They intentionally drew two different parabolas because one of them represented the upper side of the bridge, and the other represented the lower part of the bridge. In the screen, the PMTs constructed slider a (representing the coefficient a for the parabola in the red color) to draw the parabola for bounding from the bottom and slider b (representing the coefficient b for the parabola in the blue color) to draw the parabola for bounding from the top (See Fig. 7).
The PMTs' explanation regarding the process of constructing the quadratic equations is as follows:
We started by writing a random parabola equation and then changed the coefficient a. However, we could not find the exact parabola representing the bridge. While thinking about how we can do it, we finally thought to find the vertex, and then we can work on it. Next, we drew two different parabolas with coefficients a and b, and the vertex was exactly centered on the bridge. We dragged the sliders to precisely position the arms of the parabola over the bridge.
By experimentalizing the image, the PMTs initially attempted to find the parabola equation representing the curves on the bridge. When they realized that it was impossible to find the value of coefficient a using this, they decided to drag the slider to represent the coefficient. At this point, they wrote a general formula for the quadratic equation on the input tool in GeoGebra and used the slider’s increment feature to determine the exact values of coefficients a and b (which were negligibledecimals). Then, by dragging the slider, they found the coefficients required for the best positioning parabola equation formed the curve of the bridge. In this process, the PMTs attempted to construct the mathematical models by experimenting with the slider tool. In their own words, they explained their actions as follows:
We used the zoom in tool to enlarge the image… We changed the settings of the slider to place the curve exactly on the bridge. We assigned value as 0.001 in the slider and struggled to find the exact value of the coefficient a. As difficult as it was, it was a fun process for us anyway; we think that it was much simpler than the normal solution process… After finding the first parabola equation, everything was easier, and we found the other parabola using the same method.
The PMTs’ actions related to finding the exact value of the coefficients revealed that they validated and verified their initial mathematical models, and revised these models (See Fig. 8).
Afterwards, in the working mathematically stage, the PMTs reached the mathematical results (shared in the following paragraphs) by solving the models they constructed. In this process, to find the results, they used the integral command in GeoGebra.
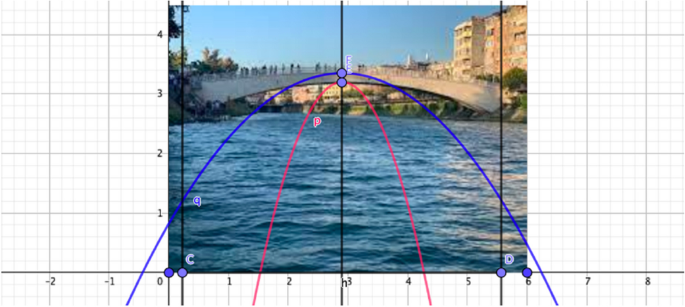
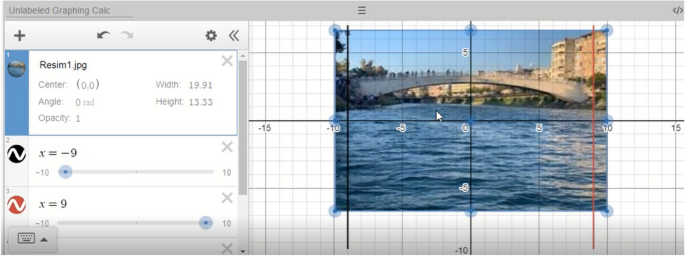
After experimenting in GeoGebra and constructing the necessary mathematical models, the PMTs also solved the problem using the graphing calculator in Desmos (windows 7 and 11 in the problem). After inserting the selected image into Desmos, the PMTs initially determined the boundaries of the quadratic equation representing the parabola. Hence, they set the boundaries as the interval [-9,9], as shown in Fig. 9, and arranged the position of the image such that the starting and ending points of the bridge coincided on the x=-9 and x = 9 lines (see Fig. 9). At this stage, the PMTs constructed the real model needed to solve the problem by simplifying.
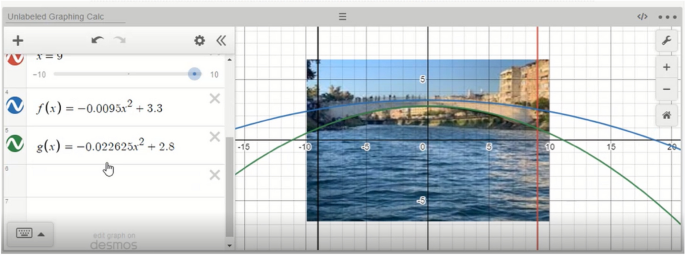
After determining the boundaries, similar to their actions in GeoGebra, they constructed the algebraic expressions of the parabola (in other words, mathematical models) representing the upper and lower boundaries of the bridge (See Fig. 10). The PMTs stated that they determined the coefficients of the equation by experimenting and indicated the differences between GeoGebra and Desmos in this process as follows:
By experimentation, we changed the coefficients and the position of the vertex and tried to fit the parabola on the bridge. In this section, the GeoGebra software has a little more advantage than Desmos. However, Desmos also has other advantages; for example, calculating and writing the integral formula better, easier, and fast.
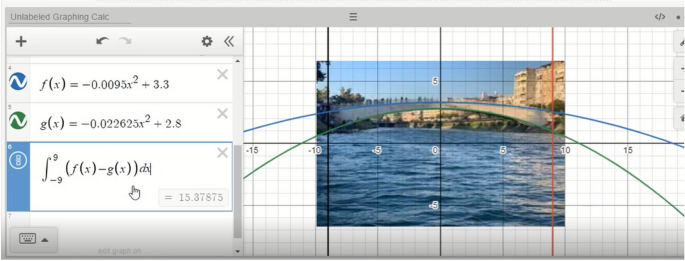
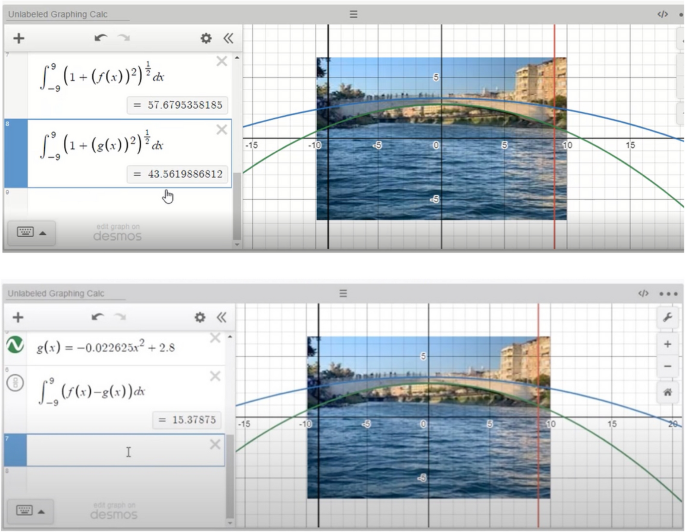
After constructing the mathematical models for the identified intervals and drawing quadratic equations, the PMTs solved the models using definite integrals. In the working mathematically stage, the PMTs calculated the arc length and the area under the curve using integral formulas similar to the actions performed in GeoGebra. They worked on the graphic calculator and calculated the area between the two curves and the lengths of the arcs (see Fig. 11).
However, as seen in Fig. 11, their solution was not correct because the mathematical model they constructed for the arc length was incorrect (they forgot to take the derivative of the function) (see Fig. 12). Then, they realized that they had misremembered the formula for the length of the arc with a definite integral, and afterwards, they revised their solution (as we mentioned in the following paragraphs).
By solving the mathematical models, the PMTs found the arc lengths to be approximately 57.7 and 43.6 units, respectively, and the area between the curves to be approximately 15.4 square units. The PMTs then needed to transform the numerical solutions they found in units into real-life conditions. The PMTs considered the different objects in the image and decided to use the height of a person on the bridge as a reference point. To identify the real value corresponding 1 unit, they first decided to find how many units equal the average person height using the graphic calculator in Desmos. At this point, the teachers drew a line segment corresponding to the height of a person, and measured and calculated the length of this line segment as 0.59 units. They made a prediction regarding the average height of a person as 1.65 m, and focused on solving the problem using their assumption. By proportioning, they assumed that 1 unit corresponds 2.79 m with the help of a calculator. In this process, by calculating, the PMTs transitioned from the mathematical results to the real results. They explained this process as follows:
At this point, I should take these values and apply them to real life. For this, I need to determine the unit. To determine the unit, we used the height of the person over there. When I zoomed [zooming in and showing a person on a bridge], we determined two points from the head to the foot of this person. This made 0.59 units. As a result of research on the internet, we found that the average height of men in the world is 1.70 and that of women is 1.60. We took the average because we did not know the gender of the person. We took the person’s height as 1.65 m. Thus, 0.59 units correspond to 1.65 m. This means that 1 unit is 2.79 m. Then, if we use the unit, we found for the integral value we found here, the students will reach the real value because of the calculation.
They calculated the area between the curves to be approximately 120 m2 as a real result. They found the total area to be approximately 240 m2 considering the two sides of the bridge. They previously found 207 m2 in GeoGebra, and by comparing the two results, they evaluated both results and stated that they found close values even when using different digital tools. During the verification process, they expressed their thoughts regarding the differences between Desmos and GeoGebra as follows:
In our previous solution in GeoGebra, we found approximately 250 m2. Therefore, we can actually say that we found almost the same values. Because after all, the people we take as a reference are different. Here (Desmos), the picture is a little blurred in Desmos. It is a bit clearer in GeoGebra. In Desmos, this clarity is a bit more distorted. It also has an effect on determining the points. This difference may be because of that. However, when students find values almost similar to this, it is acceptable.
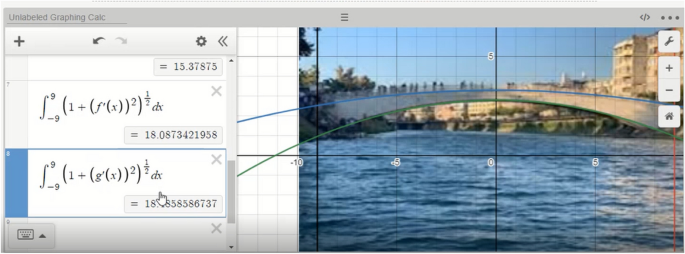
Subsequently, they calculated the lengths of the arcs using the same unit measure and realized that the mathematical model they constructed was not correct. Hence, they needed to revise the integral formula and the mathematical models in the graphic calculator, as shown in Fig. 13.
After their revision, they re-calculated the necessary values using a calculator. They found the length of the upper curve to be approximately 50 m. and the length of the lower curve to be approximately 51.5 m. The PMTs stated that the values they found in GeoGebra were 44.5 and 46 m, respectively, and emphasized that they verified the solution considering the close values they found. Their revisions illuminated that PMTs validated their mathematical models and solutions.
After solving the mathematical models, they searched the engine based on the real-life data necessary to find the costs. As a result of their searching, they assumed that 1 L of paint could be used to paint 7 m2 area, and the total cost would be approximately 3800 TL. In addition, they calculated the cost of 10 m led light as 87,20 TL. The PMTs interpreted the real results in terms of the real context by considering an economic solution as follows:
After this, students will search for the necessary values. Because of this research, they will identify which paint is more suitable and economic, which led light is better, and then calculate the cost. The students’ answers could be different at this point.
The PMTs revealed two different solution approaches by solving the designed modelling problem in both GeoGebra and Desmos. They stated that they initially solved the problem in GeoGebra and transformed their solution to Desmos because they validated their solution in Desmos. Regarding the digital tools they used to solve the problem, they indicated the following:
We really don’t know how we could solve the problem without using GeoGebra or Desmos. We really tried to solve it and thought about the solution, but it is impossible to solve it on paper. I mean, we could draw the curves with a paper and pencil if we had the skills of an architect, but that is not possible for us. In this way, it is crucially important to teach students that such tools are really effective for solving these types of problems. They can solve the problems with 4–5 actions in these digital tools.
The PMTs’ approaches for solving the problems revealed that various digital tools and their features could be used differently and effectively in solving a mathematical modelling problem. The technological actions of the PMTs’ used in the solution process led to the development of the adopted conceptual framework of the study (see Fig. 14). In particular, their possible solution of the problem using different digital tools (dynamic mathematics software, web 2.0 tools, video-based application, web-based application, calculator, search engine) led us to extend the framework by adding a couple of technological actions. In detail, while constructing the situation and the real model, they planned to implement the warm-up activities using visual amplifiers or video/web-based applications. Their actions demonstrated their intention to support students by encouraging them to visualize and imagine (or have an experience if they did not know the context) the real-life context. In particular, the visualization action was effective in selecting and using the most appropriate image/picture when constructing the situation and real model required to solve the problem. In this sense, visualization could be defined as “providing visual amplifiers or video/web-based applications to construct the situation and real model”. Afterwards, while constructing the mathematical models, in addition to constructing and drawing, the PMTs tried to find the quadratic equation by experimenting with GeoGebra software (i.e. using the circle). While experimenting with the parabola equation to construct the most appropriate mathematical model for solving the problem, they benefitted from the dynamic features of the digital tools by adding and dragging the sliders. In particular, dragging provided a crucial effect when experimenting was not sufficient for mathematical model construction that best fits the real model. In this context, we defined the experimenting as “assumptions and conditions tested using the dynamic features (i.e. dragging) in the digital tools”. Dragging action could be defined as “providing immediate feedback to realize the instant changes in the mathematical model based on the assumptions and conditions”. Additionally, the action of calculation could be described as “calculating numerical or algebraic results by conducting operations on any digital tools”. Then, they verified their mathematical model by experimenting with different quadratic equations at the end of the mathematization step. We defined verification as “a judgment based on acceptance, revision, or rejection of the mathematical model”. While transitioning from mathematical results to real results, they used the real data by operating on the calculator to construct the representation of the real data and then calculated the necessary values. They solved the problem using two different digital tools and compared their results to support them verify the real results. In this step, the definition of verification could be similar to the given one, and accepted as “a judgment appeared based on acceptance, revision, or rejection of the real results”. We accepted the definitions of other actions that occurred in the solution process similar to those given by Greefrath et al. (2018). The figure given below (Fig. 14) represents the revised cycle, and the actions given in orange text were added by the authors.
4 Conclusion and discussion
The main goal of this study is to examine the PMTs’ designing and solving mathematical modelling problem using different technologies. In this regard, the PMTs designed their problem in Desmos using various pictures, videos, and links (i.e., Google Earth and graphic calculator) and solved it using both the features of GeoGebra software and Desmos. In particular, the Activity Builder in Desmos, which is a unique strength of the program (DeGilio, 2022; McCulloch et al., 2018), enabled the PMTs to include and construct multiple learning opportunities for students (Chechan et al., 2023; Gulati, 2017). Additionally, constructing the problem in Desmos was easy and fun for the PMTs, as demonstrated by the teachers in McCulloch et al.’s (2018) study.
The PMTs used various digital technologies to design their modelling problem. It is obvious that their integration of pictures, and video-based and web-based (i.e. Google-earth) applications during warm-up activities supported the students in investigating the real-life context, as stated by Greefrath and Vos’ (2021) study. Specifically, the PMTs stated that watching the video and taking a 3D-tour in Google Earth could allow the students to explore, visualize, and incorporate the real-context for constructing both the real and mathematical models, as the students in Aytemiz and Çakmak Gürel’s study (2023). In the modelling problem, experimenting and exploring the problem context by using different sources could enable students to construct multiple solutions to the problem, which is due to the nature of the mathematical modelling.
After presenting the problem statement, the PMTs used different windows in Desmos to lead the students for solving the problem throughout the stages of the modelling cycle. Even though there is no linear direction in solving a mathematical modelling problem (Borromeo Ferri, 2007), designing a problem in Desmos could provide a direction for students in transition between different windows in Desmos, which also supported students in non-linear transition through modelling stages. In detail, by designing the problem in Desmos, the PMTs expected the students to make predictions regarding the context based on the data they collected during the warm-up activities. Additionally, the PMTs wanted students to construct a mathematical model using a graphic calculator, which supported them in creating graphs and operating on functions (McCulloch et al., 2018). While transforming from a mathematical solution to a real solution, the PMTs expected students to use a search-engine to investigate and formulate the required data for solving the problem based on their own interests (Borba et al., 2016; Villarreal et al., 2018), specifically in calculating the cost given in the problem. According to Blum and Leiß (2007), validation is defined as checking whether the predictions are reasonable and accurate. Existing studies acknowledge that the validation stage is the most challenging stage for students in solving a mathematical problem (Galbraith & Stillman, 2006). In this study, the PMTs provided an opportunity for students in the validation stage by constructing a window including a checklist in Desmos to compare their predictions with their mathematical results. In other words, the PMTs designed this problem by offering students the opportunity to predict, test, and explain their assumptions or solutions (Chorney, 2022).
While solving the problem, during transitioning from one stage to another, particular technological actions were revealed based on the PMTS’ aims of using different digital tools. In the transition from the real situation to both the situation and the real model, students must investigate and visualize the context. In particular, visualization allows the investigation of the real context. Additionally, visualization helped them investigate the necessary data in the images during the construction of the real model (Yiğit Koyunkaya & Tekin Dede, 2021). Therefore, the use of images integrated into GeoGebra and Desmos and web/video-based resources attracted students’ attention (Sinclair, 2003, 2004) during the warm-up activities, and influenced them to visualize or imagine the real context. In other words, because the students had no experience with the real situation, the PMTs considered that the students were able to visualize the situation more clearly (Chamberlin & Moon, 2005). Therefore, they can initially construct the situation model and then the real model appropriately. This situation also supported the accuracy of the mathematical models that the students would construct in the following steps. In other words, using the features of GeoGebra (Greefrath et al., 2018) and Desmos (Chorney, 2022) supported both the PMTs (as well as the students) in visualizing the real context to make realistic assumptions for solving the problem.
While the PMTs constructed the possible mathematical models, they tested different quadratic equations that best represented the bridge by experimenting with different drawings. Greefrath and Siller (2017, 2018) included the experimentalise action in working mathematically step, the PMTs provided evidence regarding the use of experiments for testing their assumptions and conditions by using the dynamic features in the simplifying step. After deciding to find the quadratic equation instead of using the circle arc, the PMTs used different technological actions. They constructed a slider to determine which quadratic equation best represented the bridge. In particular, they identified the coefficient in the equation by linking and dragging the point on the parabola (Arzarello et al., 2002). Even though initial models may be inadequate (Zawojewski, 2010), the PMTs’ decision to construct the slider and the dragging actions they used enabled them to verify the mathematical model to be the most appropriate to reality. Hence, their actions performed on GeoGebra triggered them to verify the mathematical model, as Greefrath (2011) stated. We also identified the action of verification in the interpretation step in which the real results were reconsidered. While Ramirez-Montes et al. (2021) stated that the digital tool could not support the interpretation step in their study, in contrast to this study, the PMTs provided evidence of using digital tools effectively at the interpretation step in our study. Another noteworthy result at this point is that comparing their results found in GeoGebra and Desmos triggered the PMTs to verify their real solutions. In terms of the modelling process, using digital tools in verification provided a validation of their real results as Schaap et al. (2011) stated. Borromeo Ferri (2006) described validation as knowledge-based and intuitive validation. In this study, the use of different digital tools allowed the PMTs to consciously use knowledge-based validation by using real data.
In their study, Greefrath (2011) and Greefrath et al. (2018) stated that constructing, drawing, measuring, visualizing, and controlling/verifying are possible technological actions that could be used in different modeling stages. In addition to their interpretations, our study provides evidence of possibilities for using different technological actions in the modelling cycle despite the small number of participants. To conclude, the integration of two different courses in the teacher education program revealed that the PMTs develop knowledge and experiences regarding the collaborative use of different contexts. This study could extend existing studies by providing opportunities as well as challenges to PMTs in designing and solving mathematical modelling problems using different digital tools, as Cevikbas et al. (2023) suggested. In this study, one group’s approaches in designing and solving a mathematical modelling problem helped extend Greefrath et al.’s (2018) framework; however, different actions could occur in different modelling stages while working with a larger number of participants as well as different mathematical modelling problems.
Data availability
The data analysed during this study are included in this article.
Notes
Through this paper, the definition of digital tools is accepted as digital media (e.g. computers, tablets, calculators, softwares, web 2.0 tools) used to support students’ learning specifically in mathematics lessons (Greefrath et al., 2018).
The Desmos link of the modelling problem named Festival in the City is as follows: https://teacher.desmos.com/activitybuilder/custom/65c21aa48e3a5be42f30577e.
References
Arzarello, F., Ferrara, F., & Robutti, O. (2012). Mathematical modelling with technology: The role of dynamic representations. Teaching Mathematics and its Applications, 31(1), 20–30. https://doi.org/10.1093/teamat/hrr027
Arzarello, F., Olivero, F., Paola, D., & Robutti, O. (2002). A cognitive analysis of dragging practises in Cabri environments. Zentralblatt für Didaktik Der Mathematik, 34, 66–72. https://doi.org/10.1007/BF02655708
Aytemiz, H., & Çakmak Gürel, Z. (2023). Examining students’ mathematical modeling competences in video-based modeling tasks. The Journal of Educational Research, 116(6), 336–348.
Blum, W., & Leiß, D. (2007). How do students and teachers deal with mathematical modelling problems? The example sugarloaf and the DISUM project. In C. Haines, P. L. Galbraith, W. Blum & S. Khan (Eds.), Mathematical modelling (ICTMA 12): Education, engineering and economics (pp. 222–231). Horwood. https://doi.org/10.1533/9780857099419.5.221
Borba, M. C., Askar, P., Engelbrecht, J., Gadanidis, G., Llinares, S., & Aguilar, M. S. (2016). Blended learning, e-learning and mobile learning in mathematics education. Zentralblatt für Didaktik der Mathematik-ZDM, 48(5), 589–610.
Borromeo Ferri, R. (2006). Theoretical and empirical differentiations of phases in the modelling process. Zentralblatt für Didaktik der Mathematik-ZDM, 38(2), 86–95.
Borromeo Ferri, R. (2007). Modelling problems from a cognitive perspective. In C. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical modeling: Education, engineering, and economics (pp. 260–270). Woodhead Publishing Limited.
Borromeo Ferri, R. (2018). Learning how to teach mathematical modeling in school and teacher education. Springer. https://doi.org/10.1007/978-3-319-68072-9
Bozkurt, G., & Ruthven, K. (2017). Classroom-based professional expertise: A mathematics teacher’s practice with technology. Educational Studies in Mathematics, 94(3), 309–328.
Bozkurt, G., & Yigit Koyunkaya, M. (2022). Supporting prospective mathematics teachers’ planning and teaching technology-based tasks in the context of a practicum course. Teaching and Teacher Education, 119, 103830. https://doi.org/10.1016/j.tate.2022.103830
Cevikbas, M., Greefrath, G., & Siller, H. S. (2023). Advantages and challenges of using digital technologies in mathematical modelling education – a descriptive systematic literature review. Frontiers in Education, 8, 1–17. https://doi.org/10.3389/feduc.2023.1142556
Chamberlin, S. A., & Moon, S. M. (2005). Model eliciting activities as a tool to develop and identify creatively gifted mathematicians. Journal of Secondary Gifted Education, 17(1), 37–47. https://doi.org/10.4219/jsge-2005-393
Chechan, B., Ampadu, E., & Pears, A. (2023). Effect of using desmos on high school students’ understanding and learning of functions. Eurasia Journal of Mathematics Science and Technology Education, 19(10), em2331. https://doi.org/10.29333/ejmste/13540
Chorney, S. (2022). Classroom practice and craft knowledge in teaching mathematics using desmos: Challenges and strategies. International Journal of Mathematical Education in Science and Technology, 53(12), 3203–3227. https://doi.org/10.1080/0020739X.2021.1931974
Clark-Wilson, A., Robutti, O., & Sinclair, N. (Eds.). (2014). The mathematics teacher in the digital era: An ınternational perspective on technology focused professional development. Springer. https://doi.org/10.1007/978-94-007-4638-1
Clark-Wilson, A., Robutti, O., & Sinclair, N. (Eds.). (2023). The mathematics teacher in the digital era: International research on professional learning and practice (2nd edn). Springer. https://doi.org/10.1007/978-3-031-05254-5
Confrey, J., & Maloney, A. (2007). A theory of mathematical modelling in technological settings. In W. Blum, P. L. Galbraith, H. W. Henn & M. Niss (Eds.), Modelling and applications in mathematics education. The 14th ICMI study (pp. 57–68). Springer. https://doi.org/10.1007/978-0-387-29822-1_4
Daher, W., & Shahbari, A. (2015). Pre-service teachers’ modelling processes through engagement with model eliciting activities with a technological tool. International Journal of Science and Mathematics Education, 13, 25–46. https://doi.org/10.1007/s10763-013-9464-2
de Villiers, M. (1998). An alternative approach to proof in dynamic geometry. In R. Lehrer & D. Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 369–393). Lawrence Erlbaum. https://doi.org/10.4324/9780203053461
DeGilio, M. (2022). Creating custom desmos activities using desmos activity builder to create effective lessons for online learning during Covid-19. Master's thesis, SUNY Brockport.
English, L. D. (2016). STEM education K-12: Perspectives on integration. International Journal of STEM Education, 3(1), 1–8. https://doi.org/10.1186/s40594-016-0036-1
Frassia, M. G., & Serpe, A. (2017). Learning geometry through mathematical modelling: An example with GeoGebra. TOJET: The Turkish Online Journal of Educational Technology, Special Issue for INTE 2017 (pp. 411–418)
Fuchs, K. J., & Blum, W. (2008). Selbständiges Lernen Im mathematikunterricht mit, beziehungsreichen‘ aufgaben. In J. Thonhauser (Ed.), Aufgaben als Katalysa- Toren Von Lernprozessen (pp. 135–147). Waxmann.
Galbraith, P., & Stillman, G. (2006). A framework for identifying student blockages during transitions in the modelling process. Zentralblatt für Didaktik Der Mathematik, 38, 143–162. https://doi.org/10.1007/BF02655886
Geiger, V. (2011). Factors affecting teachers’ adoption of innovative practices with technology and mathematical modelling. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in Teaching and Learning of Mathematical Modelling: ICTMA14 (pp. 305–314). Springer. https://doi.org/10.1007/978-94-007-0910-2_31
Greefrath, G. (2011). Using technologies: New possibilities of teaching and learning modelling-Overview. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in teaching and learning of mathematical modelling, ICTMA 14 (pp. 301–304). Springer. https://doi.org/10.1007/978-94-007-0910-2_30
Greefrath, G., & Siller, H. S. (2017). Modelling and simulation with the help of digital tools. In G. A. Stillman, W. Blum, & G. Kaiser (Eds.), Mathematical modelling and applications, ICTMA 17 (pp. 529–539). Springer. https://doi.org/10.1007/978-3-319-62968-1_44
Greefrath, G., & Siller, H. S. (2018). GeoGebra as a tool in modelling processes. In L. Ball, P. Drijvers, S. Ladel, H. Siller, & M. Tabach (Eds.), Uses of technology in primary and secondary mathematics education (pp. 363–374). Springer. https://doi.org/10.1007/978-3-319-76575-4_21
Greefrath, G., & Vorhölter, K. (2016). Teaching and learning mathematical modelling: Approaches and developments from German speaking countries. Springer. https://doi.org/10.1007/978-3-319-45004-9
Greefrath, G. (2020). Mathematical modelling competence: Selected current research developments. Avances De Investigación en Educación Matemática, 17, 38–51.
Greefrath, G., Hertleif, C., & Siller, H. S. (2018). Mathematical modelling with digital tools - a quantitative study on mathematising with dynamic geometry software. Zentralblatt für Didaktik Der Mathematik, 50, 233–244. https://doi.org/10.1007/s11858-018-0924-6
Greefrath, G., Siller, H. S., & Weitendorf, J. (2011). Modelling considering the influence of technology. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillmann (Eds.), Trends in teaching and learning of mathematical modelling (pp. 315–329). Springer. https://doi.org/10.1007/978-94-007-0910-2_32
Greefrath, G., & Vos, P. (2021). Video-based word problems or modelling projects—Classifying ICT-based modelling tasks. In F. K. S. Leung, G. A. Stillman, G. Kaiser, & K. L. Wong (Eds.), Mathematical modelling education in east and west (pp. 489–499). Springer.
Gulati, S. (2017). Create your own interactive activity. At Right Angles, 6(3), 81–88.
Kaiser, G., Blomhøj, M., & Sriraman, B. (2006). Towards a didactical theory for mathematical modelling. Zentralblatt für Didaktik Der Mathematik, 38(2), 82–85. https://doi.org/10.1007/BF02655882
Krippendorff, K. (1980). Validity in content analysis. In E. Mochmann (Ed.), Computerstrategien für die kommunikationsanalyse (pp. 69–112). Campus.
Laborde, C. (2001). Integration of technology in the design of geometry tasks with Cabri geometry. International Journal of Computers for Mathematical Learning, 6, 283–317.
Lingefjaerd, T., et al. (2007). Modelling in teacher education. In W. Blum (Ed.), Modelling and applications in mathematics education (pp. 475–482). Springer.
Lingefjärd, T. (2000). Mathematical Modelling by Prospective Teachers using Technology. Doctoral dissertation. University of Georgia.
Lingefjärd, T. (2013). Teaching mathematical modelling in teacher education: Efforts and results. In X. S. Yang (Ed.), Mathematical modelling with multidisciplinary applications (pp. 57–80). John Wiley and Sons Inc.
Ludwig, M., & Jablonski, S. (2021). Step by step: Simplifying and mathematizing the real world with MathCityMap. Quadrante: Revista De Investigação em Educação Matemática, 30(2), 242–268. https://doi.org/10.48489/quadrante.23604
McCulloch, A. W., Hollebrands, K., Lee, H., Harrison, T., & Mutlu, A. (2018). Factors that influence secondary mathematics teachers’ integration of technology in mathematics lessons. Computers & Education, 123, 26–40. https://doi.org/10.1016/j.compedu.2018.04.008
Merriam, S. B. (1998). Qualitative research and case study applications in education (2nd ed.). Jossey-Bass.
Miles, M. B., & Huberman, A. M. (1994). Qualitative data analysis (2nd ed.). Sage.
Molina-Toro, J. F., Rendón-Mesa, P. A., & Villa-Ochoa, J. A. (2019). Research trends in digital technologies and modelling in mathematics education. Eurasia Journal of Mathematics Science and Technology Education, 15(8), 1–13. https://doi.org/10.29333/ejmste/108438
Molina-Toro, J. F., Rendón-Mesa, P. A., & Villa-Ochoa, J. A. (2022). Contradictions in mathematical modelling with digital technologies. Education and Information Technologies, 27, 1655–1673. https://doi.org/10.1007/s10639-021-10676-z
Patton, M. Q. (2014). Qualitative research and evaluation methods: Integrating theory and practice. Sage.
Ramírez-Montes, G., Carreira, S., & Henriques, A. (2021). Mathematical modelling routes supported by technology in the learning of linear algebra: A study with Costa Rican undergraduate students. Quadrante, 30(1), 219–241.
Schaap, S., Vos, P., & Goedhart, M. (2011). Students overcoming blockages while building a mathematical model: Exploring a framework. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in teaching and learning of mathematical modeling (pp. 137–146). Springer.
Schukajlow, S., Kaiser, G., & Stillman, G. (2018). Empirical research on teaching and learning of mathematical modelling: A survey on the current state-of-the-art. Zentralblatt für Didaktik Der Mathematik, 50, 5–18. https://doi.org/10.1007/s11858-018-0933-5
Siller, H. S., & Greefrath, G. (2010). Mathematical modelling in class regarding to technology. In V. Durand-Guerrier, S. Soury-Lavergne, & F. Arzarello (Eds.), Proceedings of the sixth congress of the European society for research in mathematics education(CERME6) (pp. 2136–2145). Institut National de Recherche Pédagogique.
Siller, H. S., Cevikbas, M., Geiger, V., & Greefrath, G. (2022). The role of digital resources in mathematical modelling research. In C. Fernández, S. Llinares, Á. Gutiérrez & N. Planas (Eds.), The Proceedings of 45th Conference of the International Group for the Psychology of Mathematics Education-PME, vol. 1 (pp. 152–155).
Sinclair, M. (2003). Some implications of the results of a case study for the design of pre constructed, dynamic geometry sketches and accompanying materials. Educational Studies in Mathematics, 52(3), 289–317. https://doi.org/10.1023/A:1024305603330
Sinclair, M. (2004). Working with accurate representations: The case of pre-constructed dynamic geometry sketches. The Journal of Computers in Mathematics and Science Teaching, 23(2), 191–208.
Stake, P. (2005). Qualitative case study. In N. K. Denzin & Y. S. Lincoln (Eds.), The sage handbook of qualitative research (pp. 433–466). Sage.
Tekin-Dede, A., & Bukova-Güzel, E. (2018). A rubric development study for the assessment of modeling skills. The Mathematics Educator, 27(2), 33–72.
Villarreal, M. E., Esteley, C. B., & Smith, S. (2018). Pre-service teachers’ experiences within modelling scenarios enriched by digital technologies. Zentralblatt für Didaktik Der Mathematik, 50, 327–341. https://doi.org/10.1007/s11858-018-0925-5
Viseu, F., & Leite, L. (2019). Developing technologically enhanced mathematics pedagogical content knowledge in initial teacher education. In L. Daniela (Ed.), Didactics of smart pedagogy (pp. 331–351). Springer. https://doi.org/10.1007/978-3-030-01551-0_17
Yiğit Koyunkaya, M., & Tekin Dede, A. (2021). Matematiksel modelleme problemlerinde teknoloji kullanımının rolü. In E. Bukova Güzel, M. F. Doğan, & A. Özaltun Çelik (Eds.), Matematiksel modelleme: Teoriden uygulamaya bütünsel bakış (pp. 295–320). Pegem Akademi.
Yin, R. K. (2018). Case study research: Design and methods (6th ed.). Sage.
Zawojewski, J. (2010). Problem solving versus modelling. In Lesh, R., Galbraith, P., Haines, C., Hurford, A. (Eds.), Modelling Students’ Mathematical Modelling Competencies (pp. 237–243). Springer. https://doi.org/10.1007/978-1-4419-0561-1_20
Funding
Open access funding provided by the Scientific and Technological Research Council of Türkiye (TÜBİTAK). No funding was received for conducting this study.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that there are no conflicts of interest or competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Koyunkaya, M.Y., Dede, A.T. Using different digital tools in designing and solving mathematical modelling problems. Educ Inf Technol (2024). https://doi.org/10.1007/s10639-024-12577-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10639-024-12577-3