Abstract
In this paper we discuss scheduling of semi-cyclic discrete-event systems, for which the set of operations may vary over a limited set of possible sequences of operations. We introduce a unified modeling framework in which different types of semi-cyclic discrete-event systems can be described by switching max-plus linear (SMPL) models. We use a dynamic graph to visualize the evolution of an SMPL system over a certain period in a graphical way and to describe the order relations of the system events. We show that the dynamic graph can be used to analyse the structural properties of the system. In general the model predictive scheduling design problem for SMPL systems can be recast as a mixed integer linear programming (MILP) problem. In order to reduce the number of optimization parameters we introduce a novel reparametrization of the MILP problem. This may lead to a decrease in computational complexity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Scheduling is the process of deciding how to allocate a set of jobs to limited resources over time in such a way that one or more objectives are optimized (Leung 2004; Pinedo 2001). Here, a job is a sequence of operations according to a recipe that specifies a partial ordering among these operations, and resources are the equipment units where operations can take place. In a typical scheduling problem, resources are scarce and constrained in various ways (e.g., in the capacity of resources or the order of activities that can be performed on them), and one is looking for a schedule of the activities that both satisfies the constraints and is optimal according to some criterion (e.g., the length of the schedule) (Fromherz 2001). A lot of research on scheduling has been done since the original work of Johnson (1954). Several books already presented general surveys for these problems such as Blazewicz et al. (2001), Brucker (2001), and Pinedo (2001) for some recent ones.
In scheduling three basic types of control decisions play a major role, namely routing, ordering, and synchronization. Routing decides how a job follows a sequence of resources. Usually a job follows a predetermined route through the system (Johnson 1954). Sometimes there are alternative routes and the routing for each job has to be determined. Once the routes of the jobs have been fixed, conflicts may occur when multiple jobs need to be operated at the same resource. This means we have determine the ordering of concurring jobs in resources. Often job synchronization takes place, i.e. an operation of a job can only start when a specific operation of another job on another resource has finished.
A special type of scheduling problem is the flow shop scheduling problem, in which the routes of the jobs and the order of operations are fixed. All of the resources and jobs contribute to the achievement of some common goal, such as a minimal idle time and a minimal total waiting time. After all jobs in a system have been completed, the cycle is complete and a new cycle begins. An overview of the cyclic scheduling problem is available in Brucker and Kampmeyer (2008) and Hanen and Munier (1995). Many flow shop scheduling problems can be solved very well by considering a class of cyclic discrete event systems (DES), namely the class of max-plus linear systems (Baccelli et al. 1992; Heidergott et al. 2006), which is capable of representing job and resource unavailability. The main reason to use these models is that the max-plus algebra is better adapted for solving sequencing problems than the classical algebra. Flow-shop scheduling problems using max-plus linear models have already been studied in Bouquard et al. (2006), Doustmohammadi and Kamen (1995), Indriyani (2016), Nambiar and Judd (2011), and Yurdakul and Odrey (2004). Model predictive control of a flow shop scheduling problem with a just-in-time cost function and no constraint next to the non-decreasing input constraint can be solved using a semimodule approach (with a lower computational cost) (G~omes da Silva and Maia 2016). More publications on control of max-plus linear system can be found in Boimond and Ferrier (1996), Hardouin et al. (2009), Houssin et al. (2013), Lahaye et al. (2008), Libeaut and Loiseau (1995), Maia et al. (2003), and Menguy et al. (2000).
An example of scheduling a cyclic DES is the synchronization of the legs in a six-legged mobile robot (Lopes et al. 2014). The legs will move in a coordinated pattern, called a gait. For a fixed gait the system will show a cyclic behavior, which can be described by a max-plus linear model. Alirezaei et al. (2012) design an optimal schedule of multiple sheets in a printer using a max-plus framework. The design variables are the feeding time and the handling time of the sheet in the duplex loop. It is shown that the resulting optimization problem can be solved using linear programming optimization methods. The scheduling of energy flows between the parallel processes in the production of calcium silicate stones is discussed in Mutsaers et al. (2012), where the authors use a max-plus linear model in the formulation of the scheduling problem. A railway traffic system with a cyclic timetable can described by a max-plus-linear model (Braker 1993; Heidergott et al. 2006). The use of max-plus algebra allows fast computation of performance indicators and delay propagation in short time even on large networks. Modeling a cyclic DES using max-plus algebra has as advantage that the resulting max-plus-linear (MPL) system can be considered as a linear system that has a strong analogy to conventional linear system theory.
A disadvantage of MPL systems is that the model structure is fixed, whereby changes in the structure of the system (change of route, different order of operations) cannot be modeled.
In the case of semi-cyclic processes the set of operations may vary over a limited set of possible sequences of operations. Every possible set of operations defines a mode of operation. By switching between different modes of operation (in each mode the system is described by an MPL model), we obtain a switching max-plus linear (SMPL) system (van den Boom and De Schutter 2006).
An example of scheduling a semi-cyclic DES is the synchronization of the legs in a six-legged mobile robot with gait changes. The legs can change gait, which means that the legs will move in different coordinated patterns. If gait switching is possible, the system’s behavior is semi-cyclic and can be described by an SMPL model (Kersbergen et al. 2011). Also paper handling in printers with different paper sizes and/or both simplex and duplex printing, can be modeled as an SMPL system (see Section 3). Other examples of scheduling semi-cyclic DESs are operational traffic management of railway systems with changing train orders in case of disturbances (Kersbergen et al. 2016), and the scheduling of automated guided vehicles for unloading ships in seaport container terminals, in which the vehicles transport the containers from the quay cranes to the stack cranes (van Boetzelaer et al. 2014).
Graph-based methods can be used in the scheduling procedure (see Mascis and Pacciarelli 2002). There is a close relation between max-plus linear models and the graph representation of the system (Baccelli et al. 1992). From the precedence graph of the system we can compute the eigenvalue and eigenvector of the system matrix, which play a crucial role in the analysis of the system. For SMPL systems we cannot use the precedence graph because the system matrix may change every event step. In this paper we therefore use the dynamic graph (Murota 2009, 2012). From the dynamic graph we can compute the spectral radius of the system (equivalent to the max-plus eigenvalue for max-plus linear systems). Also controllability of the SMPL system can be studied using the dynamic graph (See Section 6).
Many scheduling problems lead to integer optimization problems, or in many cases, to mixed integer linear programming (MILP) problems (Floudas and Lin 2005; Ku and Karimi 1988; Leung 2004; Pinedo 2001). Also in this paper the final optimization problem will be an MILP problem. This final optimization problem will often be identical to the one we obtain using the MILP optimization problem that arises in conventional scheduling techniques. The contribution this paper is that by considering SMPL systems the performance of the scheduling procedure can be improved by using the properties of SMPL models and dynamic graphs, such as detecting bottlenecks and using reparametrization of the MILP problem based on max-plus expressions to reduce the number of optimization parameters.
Motivation and contribution
There are advantages in using SMPL systems as a basic model for scheduling. First of all there are many system-theoretical results for (S)MPL systems in literature (Baccelli et al. 1992; van den Boom et al. 2013). We can use them for finding bottlenecks in the scheduling process as well as good initial scheduling values by using system properties, based on the max-plus eigenvalue and eigenvectors (Kersbergen et al. 2011). In this paper we discuss model predictive scheduling of semi-cyclic DESs. By using an SMPL model of the system we can make a prediction of its future behavior while searching for an optimal schedule for the future. If the model is perfect, the optimal schedule can be executed without feedback and the system will behave as predicted. However, in general the system is affected by disturbances and/or the model is not perfect, so we deal with model uncertainty. Therefore, the schedule has to be adapted on-line in response to the unexpected events. This is called operational scheduling or rescheduling.
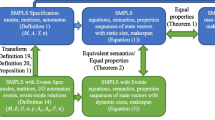
The goal of this paper is to show how SMPL systems and their corresponding dynamic graphs can be used for the scheduling of semi-cyclic systems. We will introduce a unifying modeling approach and use it to analyze the properties of the SMPL systems. The use of a dynamic graphs eases the modeling and gives insight in the routing and order relations of the system events.
This paper extends the results of van den Boom et al. (2013): We introduce the dynamic graph for representing the switching behavior of an SMPL system. We highlight the importance of the dynamic graph concept by discussing controllability and maximum average path weight in terms of dynamic graphs and elaborate on the relation between the makespan of a schedule and the maximum average path weight of the SMPL system. Furthermore, we have added a section on classification of SMPL scheduling problems and a section with two illustrative examples of SMPL systems (with their corresponding dynamic graphs). We prove that under mild conditions the relaxed model predictive scheduling problem will give the same result as the original model predictive scheduling problem. Finally we give a generalized framework for reparametrization of the mixed integer linear programming problem and apply this to reparametrization of the ordering and routing variables.
The paper is organized as follows: In Section 2 we review SMPL systems and introduce the concept of dynamic graphs. Section 3 gives some illustrative examples of semi-cyclic systems that can be modeled as SMPL systems with their corresponding dynamics graphs. Section 4 discusses the classification of SMPL models. Section 5 analyzes the relation between the routing, ordering, and job synchronization of the scheduling operations in the context of SMPL systems. Section 6 presents some tools for the analysis of SMPL systems using dynamic graphs. Section 7 formulates the model predictive scheduling problem and shows how the related optimization problem can be solved. Section 8 concentrates on the case where the problem can be written as a mixed integer optimization problem and shows that by reparametrization the number of optimization variables can be reduced. Finally, in Section 9 some conclusions are drawn.
2 Max-plus linear systems
2.1 Max-plus algebra
Define \(\varepsilon = - \infty \) and \(\mathbb {R}_{\varepsilon } = \mathbb {R} \cup \left \{ \varepsilon \right \}\). The max-plus-algebraic addition \(\left (\oplus \right )\) and multiplication \(\left (\otimes \right )\) are defined as follows Baccelli et al. (1992) and Cuninghame-Green (1979):
for any \(x, y \in \mathbb {R}_{\varepsilon }\), and
for matrices \(A, B \in \mathbb {R}_{\varepsilon }^{m \times n}\) and \(C \in \mathbb {R}_{\varepsilon }^{n \times p}\). The last operation (⊙) is the max-plus Schur product. The matrix ε is the max-plus-algebraic zero matrix: [ε]i,j = ε for all i,j. Define for \(n\in \mathbb {Z}^{+}\) the set \(\underline {n} = \{1,2,\ldots ,n\}\). The matrix \(E_{n} \in \mathbb {R}_{\varepsilon }^{n \times n}\) is the max-plus identity matrix with \([E_{n}]_{i,i}=0\), \(i\in \underline {n}\) and \([E_{n}]_{i,j}=\varepsilon \), \(i\in \underline {n}\), \(j\in \underline {n}\), i≠j. The max-plus-algebraic matrix power of \(A \in \mathbb {R}_{\varepsilon }^{n \times n}\) is defined as follows: \({A}^{{\scriptscriptstyle \otimes }^{\scriptstyle {0}}} = E_{n}\) and \({A}^{{\scriptscriptstyle \otimes }^{\scriptstyle {k}}} = A \otimes {A}^{{\scriptscriptstyle \otimes }^{\scriptstyle {(k-1)}}}\) for \(k=1,2,\dots \).
The max-plus Kleene-star of a matrix \(A \in \mathbb {R}_{\varepsilon }^{n \times n}\) is defined as
Note that A∗ exists for any square matrix A with a precedence graph G(A) having only nonpositive circuit weights (Baccelli et al. 1992).
Let \(u \in {\mathbb {B}_{\varepsilon }} = \{0,\varepsilon \}\) be a max-plus binary variable; then the adjoint variable \(\bar {u}\in {\mathbb {B}_{\varepsilon }}\) is defined as follows:
2.2 Max-plus linear systems
A max-plus linear system is defined as follows Baccelli et al. (1992):
where \(A\in \mathbb {R}_{\varepsilon }^{n \times n}\) and \(B\in \mathbb {R}_{\varepsilon }^{n \times n_{u}}\) are the system matrices, \(x(k)\in \mathbb {R}_{\varepsilon }^{n}\) is the state, \(u(k)\in \mathbb {R}_{\varepsilon }^{n_{u}}\) is the input of the system, and k is the event counter of the system. In this paper k will also be called cycle counter, because in every cycle k a number of jobs are completed using a fixed route and in a specific order.
Remark 1
Note that in this paper we use the dater description of the max-plus linear system, which means that the matrices A and B are constant matrices in \(\mathbb {R}_{\varepsilon }^{n \times n}\) and \(\mathbb {R}_{\varepsilon }^{n \times n_{u}}\), respectively.
2.3 Switching max-plus linear systems
In van den Boom and De Schutter (2006) the class of switching max-plus linear (SMPL) systems was introduced, described by
in which the matrices \(A(\ell (k))\in \mathbb {R}_{\varepsilon }^{n \times n}\), \(B^{\prime }(\ell (k))\in \mathbb {R}_{\varepsilon }^{n \times n_{u}}\) are the system matrices for mode \(\ell (k) \in {\underline {n_{\small \ell }}}\) for cycle k. The moments of switching between modes are determined by a switching mechanism. In general, the mode ℓ(k) will depend on the previous state x(k − 1), the previous mode ℓ(k − 1), the input variable u(k), and an additional control variable v(k). For this purpose we define the switching function ϕs as:
Model (2) is often referred to as an explicit SMPL model. In this paper, we will also consider the implicit SMPL model, given by:
The max-plus Kleene star of A0(ℓ(k)) for mode ℓ(k) at cycle k is given by
Note that for a fixed ℓ(k) the matrix A0(ℓ(k)) is a constant matrix and so [A0(ℓ(k))]∗ can easily be computed. We can use the max-plus Kleene star of A0(ℓ(k)) to rewrite the implicit SMPL model into an explicit one. Consider an implicit SMPL system (3) for which a finite solution of [A0(ℓ(k))]∗ exists. Using Theorem 2.66 of Baccelli et al. (1992) the implicit SMPL system can be written in the explicit form of Eq. 2, where A(ℓ(k)) = [A0(ℓ(k))]∗⊗ A1(ℓ(k)) and \(B^{\prime }(\ell (k)) = [A_{0}(\ell (k))]^{*} \otimes B(\ell (k))\). In the current paper we consider the scheduling of semi-cyclic DES. We study different types of semi-cyclic DES and model them with an SMPL model. In some applications the mode ℓ(k) only depends on the additional integer-valued control vector v(k), so ℓ(k) = ϕs(v(k)). Therefore, we will also use the notation A0(v(k)), A1(v(k)), and B(v(k)).
If we rewrite the implicit SMPL model into an explicit SMPL model the system matrices of the explicit model become A(v(k)) and \(B^{\prime }(v(k))\). These matrices A(v(k)) and \(B^{\prime }(v(k))\) may become very complex functions of v(k). For example, in Kersbergen et al. (2016) a railway traffic management problem was considered with the optimization of the scheduling parameters. A comparison was done using an explicit SMPL model and an implicit SMPL model. The explicit model became very complex and introduced many additional constraints in the final MILP problem. This made the optimization with the explicit model much slower than the optimization with the implicit model. This motivates the use of implicit models in model predictive scheduling.
2.4 Dynamic graphs
There exists a close relation between max-plus algebra and graphs (Baccelli et al. 1992; Gondran and Minoux 1976, 1984). Important properties such as irreducibility, eigenvalues, and structural controllability can be determined from the precedence graph of a max-plus system. If we want to study the switching behavior in the system the precedence graph cannot be used any more because the mode ℓ(k) and thus also the A-matrix of the system may change for every cycle k. Only if the system remains a longer time in one mode (so if ℓ(k) is constant in some event interval {kstart,kstart + 1,…,kend}), we can study the behavior of the system in that specific mode by considering the precedence graph. Examples of systems that often remain a longer time in one mode for some event interval are printers, where the paper type may be constant for some time (Alirezaei et al. 2012), and legged robots that move in a specific gait for some time (Lopes et al. 2014). For a better understanding of the switching behavior we consider the dynamic graph concept, introduced by Murota (2009, 2012). For the analysis of the dynamic graphs we can compute the maximum average path weight, related to the maximum growth rate of the system (van den Boom and De Schutter 2012), and we can check the controllability of the system. This will be discussed in Section 6.
Consider an SMPL system of the form (3) where nℓ is the number of modes. For a given positive integer N, let the set \({\mathscr{L}}_{N}=\{ \>[\>\ell (1)\cdots \ell (N)\>]^{T}\>|\>\ell (m) \in {\underline {n_{\small \ell }}},\> m\in \underline {N}\}\) denote the set of all possible consecutive mode switching vectors within N cycles.
The main advantage of the dynamic graph is that it can handle the switching nature of SMPL systems. In the context of implicit SMPL systems the dynamic graph for a given mode sequence \(\tilde {\ell } =[\>\ell (1)\cdots \ell (N)\>]^{T} \in {\mathscr{L}}_{N}\), is defined as follows:
Definition 1
Consider an implicit SMPL system for a given mode sequence \(\tilde {\ell }\in {\mathscr{L}}_{N}\). The dynamic graph \(G=({G^{1}_{0}},{G^{1}_{1}},{G^{2}_{0}},{G^{2}_{1}},\ldots ,{G^{m}_{0}},\)\({G^{m}_{1}},H^{1},\ldots ,\) Hm) is a sequence of graphs, where \({G^{k}_{0}}= (X^{k},{E^{k}_{0}})\) is a directed graph with only nonpositive circuit weights, \({G^{k}_{1}}= (X^{k},X^{k-1},{E^{k}_{1}})\), is a directed bipartite graph with \({E^{k}_{1}}\) being the set of edges from Xk− 1 to Xk, and \(H^{k}(X^{k},U^{k},E^{k}_{(u)})\) is a directed bipartite graph with \(E^{k}_{(u)}\) being the set of edges from Uk to Xk. The nodes Xk represent the state of a system at cycle k and the nodes Uk correspond to the input of the system at cycle k. The weight of the edge of \({G^{k}_{0}}\) from node [Xk]j to [Xk]i is equal to [A0(ℓ(k))]i,j, the weight of the edge of \({G^{k}_{1}}\) from node [Xk− 1]j to [Xk]i is equal to [A1(ℓ(k))]i,j, and the weight of the edge of Hk from node [Uk]j to [Xk]i is equal to [B(ℓ(k))]i,j.
In the following section we will show that SMPL models and the corresponding dynamic graphs will help in the modeling of semi-cyclic DESs. System analysis with the dynamic graph will be discussed in Section 6.
Example 1
For the implicit SMPL system
with two modes
the dynamic graph for mode-sequence {1,2,1} is given in Fig. 1.
For a periodic mode sequence with ℓ(k + c) = ℓ(k) the dynamic graphs can be obtained from traditional precedence graphs by using a classical state-space expanding technique.
3 Examples of switching max-plus-linear systems
In this section we discuss two applications in which the DES can be modeled as an SMPL system, namely a pro duction system and the paper flow in a simplex/duplex printer. More examples can be found in literature (e.g. a railway network (Kersbergen et al. 2016), a legged robot (Lopes et al. 2014), and a container terminal (van Boetzelaer et al. 2014)). For the mathematical modeling it is convenient if there is a general modeling methodology that one can follow. Moreover, when an adjustment must be made in the obtained model, such as adding a resource, it is desirable that not the whole system needs to be remodeled. It would be time saving if then only that specific part can be added whereby automatically a new model is obtained. Finally, a systematic way of modeling will result in a structured control problem to obtain the optimal schedule.
Due to the switching nature of SMPL systems, the Petri net representation is not useful for SMPL systems because of the changing structure. To study the mode changes in SMPL systems we consider the dynamic graph, which can represent the switching behavior of SMPL systems. In addition the dynamic graph can be used to derive the SMPL model of the system.
3.1 Production system
Consider the production system of Fig. 2. This system consists of five machines M1,…,M5 and operates in batches. The raw material is fed to machines M1 and M2 where preprocessing is done. Afterwards the intermediate product is fed to machine M3 or machine M4 for further processing. Finally, the two parts are assembled in machine M5 and the end product leaves the system. We assume that each machine starts working as soon as possible on each batch, i.e., as soon as the raw material or the required intermediate product is available, and as soon as the machine is idle (i.e., the previous batch of products has been processed and has left the machine). Define ui(k), i = 1,2 as the time instant at which machine Mi is fed for the k th time, y(k) as the time instant at which the k th end product leaves the system, and xi, i = 1,…,5 as the time instant at which machine i starts for the k th time. We define di, i = 1,…5 as the processing time on machine i for the k th batch, and we assume the transportation times between the machines can be neglected.
Assume that the system can run in two modes. In the first mode the product from machine M1 will proceed to machine M3, and the product from machine M2 will proceed to machine M4, while in the second mode the product from machine M1 will proceed to machine M4, and the product from machine M2 will proceed to machine M3. In the first mode the system equations are given by
leading to the following matrices for the first mode:
In the second mode the system equations are given by
leading to the following matrices for the second mode:
In Fig. 3 the dynamic graph of the production system is given for the case where we have mode 1 in cycle k and mode 2 in cycle k + 1.
Dynamic graph of the production system of Section 3.1
3.2 Paper flow in a simplex/duplex printer
In Fig. 4 a schematic representation is given of the paper path in a simplex/duplex printer (see Alirezaei et al. 2012). In mode 1 (duplex mode) the paper runs from the paper input module via the image transfer station, where the image is printed onto the sheet, via the invert module and the re-entry module again to the image transfer station for back side printing. Finally, the sheet leaves the system via the paper output module. If the printer runs in mode 2 (simplex mode), the paper runs via the paper input module and image transfer station directly to the paper output module.
The collision avoidance of the sheets in the printer is the main constraint in the paper path. We will first derive the model and then give the dynamic graph.
Let u(k) be the time instant that the k th sheet enters the PIM, y1(k) the time instant that the k th sheet enters the ITS, y2(k) the time instant that the k th sheet enters the RM, y3(k) the time instant that the k th sheet enters the ITS for the second time, y4(k) the time instant that the k th sheet leaves the printer.
The evolution of the paper path are defined as follows for the duplex mode:
where τ1, τ2, τ3, τ4, and τ5 are the process time for feeding, printing, handling in the first part of the loop, inverting, handling in the second part of the loop and stacking, respectively. Note that when paper sheet k is in the IM/RM, sheet k + 1 also enters the IM/RM. This means that the second time that paper k enters the ITS (x3(k)) is scheduled after the first time that paper k + 1 leaves the ITS (x1(k + 1) + τ2). Therefore, the state x3(k) depends on the future event x1(k + 1). In the same way, the first time paper k enters the ITS (x1(k)) will be scheduled after the second time paper k − 2 leaves the ITS (x3(k − 2) + τ2).
To rewrite the model in the form of Eq. 3 we introduce the state x and a new input \(\bar {u}\) as follows:
The new set of state equations become
For the model description given in Eq. 3 we obtain the system matrices for the first mode:
Now let us consider the case of mode 2 (simplex mode), where paper sheet k only needs to be printed on one side. In that case we skip the states x1(k) and x2(k) in the paper path and immediately go from the input to state x3(k). The evolution of the paper path are defined as follows for the simplex mode:
With the new set x(k) the state equations become
The dynamic graph in Fig. 5 shows the paper flow for the case were sheets k − 2, k − 1, k + 1, and k + 2 are printed in duplex mode (mode 1) and sheet k is printed in simplex mode (mode 2). Note that paper sheet k will enter the system after paper sheet k + 1. Furthermore the states x1(k) and x2(k) are actully redundant but remain in the dynamic graph to facilitate the representation of the synchronization.
Dynamic graph of the printer paper flow system of Section 3.2 in duplex mode in the cycles k − 2, k − 1, k + 1, and k + 2, but in simplex mode in cycle k
4 Classification of switching max-plus-linear systems
In the previous section we have derived SMPL models for various applications. In this section look at six features that classify the SMPL system:
-
1.
Natural cycle.
-
2.
Simultaneous or sequential processing.
-
3.
Fixed or variable route.
-
4.
Input type.
-
5.
Due date or time table.
-
6.
Re-entry.
These features give us information about the types of synchronization that appear in the SMPL model. We will refer to the two applications of Section 3 (production system, printer) and some SMPL systems discussed in the literature (a railway network (Kersbergen et al. 2016), a legged robot (Lopes et al. 2014), and a container terminal (van Boetzelaer et al. 2014)) to illustrate these concepts.
-
1.
Natural cycle
A natural cycle can be seen as a sequence of events whereafter the behavior of the system repeats itself. This means that after one natural cycle, all jobs enter the system again. In a railway network with a cyclic timetable, the cycle period of the timetable can be regarded as a natural cycle. For a printer the processing of one sheet of paper from the input module to the output module can be seen as a natural cycle. Similarly in a container terminal the processing of one container from quay crane to stack crane is a natural cycle. For a legged robot the natural cycle is defined as the timespan between the moment when all legs have lifted off and the moment they have all touched down again.
It is important to notice that if we choose a natural cycle it is not said that all events in a new cycle appear in the same order or appear at all: some jobs may follow another route, or the order of processing operations at the resources may be different, but the (semi-)cyclic behavior is still recognizable.
We can distinguish two cycle types for an SMPL model:
-
Batch cycle or multi-job cycle: Every cycle consists of a batch of jobs. Sometimes the system works according to a specific periodic timetable with a fixed cycle period (railway network); sometimes multiple jobs are clearly linked by synchronization (legged robot).
-
Product cycle or single-job cycle: The system is based on handling products in a (semi-)cyclic way (paper flow in printer, container terminal, production system). The cycle time may be different for each product. The cycle counter can be regarded as a ’product’-counter.
-
-
2.
Simultaneous or sequential processing
The processing on the resources can take place in two different ways: sequentially or simultaneously. In the sequential case there is only one operation possible on a resource at the same time. The next operation on the resource has to wait until the present operation has completely finished (e.g. the printing of paper in the image transfer station has to be done sheet by sheet). In the simultaneous case, multiple operations can take place at the same resource simultaneously (e.g. multiple trains may run on the same track between stations, given a separation by the headway time). Simultaneous processing is usually due to an aggregation of smaller segments. For example most railway systems have block sections with signals to separate the trains. To analyze and control a railway network the overall model will then become too complex. In that case we aggregate a number of blocks to one block and separate trains by headway constraints.
-
3.
Fixed or variable route
In some applications there are multiple possible routes for the jobs. However there are also applications where the routes of the jobs are fixed and only the order of the events may change (this happens in railway systems (Kersbergen et al. 2016)). If both the routes and the order of the jobs are fixed, e.g. because operations from future cycles always come after operations from the current cycle, the SMPL system will only have one mode and we obtain an MPL system.
-
4.
Input type
As mentioned before, u(k) can take different forms. It can represent a reference under which the system needs to be operated: this is the case in a railway network where trains can never leave earlier than indicated by the reference (time table). In a printer the time instant at which paper is fed to the system can be chosen by the user and also in the case of a production system the input can be controlled. Later on in Section 7 we use the input to control the SMPL system.
-
5.
Due date or time table
The due date is defined as the time instant at which a job should be finished. A time table gives the desired time instant at which a job should start. Due dates and time tables are both a kind of reference signal, but they act in a different way on the SMPL system.
The entries of a time table can be seen as a lower bound on the states (e.g. in a railway system). If we consider the time table as a fixed input, the time table constraint becomes a max-plus equation on the state and this fixed input.
For some systems (e.g. the production system) there may be due dates that define when a job should be finished. The due date is a desired upper bound on the state and may be so strict that it cannot be satisfied. The violation of the due date can then be minimized using model predictive scheduling. This will be discussed in Section 7.
-
6.
Re-entry
A job consists of a number of operations on a sequence of resources. Usually each resource in this sequence is only visited once during the job. However, for some applications the job visits the same resource twice or more. We then talk about re-entry. In the printer example we already saw that in the duplex case the paper runs through the image transfer station twice. In the re-entry case we will then assign two states for this operation, to distinguish between the time that the first operation on that particular resource and the second operation.
Overview
In Table 1 the classification of the five examples of SMPL systems (of Section 3 and literature) is given. The six discussed features characterize the types of synchronization and as such the properties of the model. Of course for other applications different combinations of the features are possible.
5 Scheduling and SMPL models
In Section 3 we have reviewed some examples of applications from scheduling in which the system was described by SMPL models. In this section we will discuss how to derive an SMPL model description for scheduling in a structured and generic way.
In the previous sections we have seen that an SMPL model can switch between different modes. In some applications the number of possible mode can be very large. In that case it is often better to parameterize the modes. There are three ways to do this parametrization:
- Mode parametrization::
-
We consider the set of all possible modes and enumerate the set so that the specific mode number is the parameter.
- Integer parametrization::
-
If the set of all possible modes is large it is sometimes easier to describe the mode by a tuple of integers. The integers may describe features like the ordering of the operations for a specific resource, or determine the route for a specific job. For example in the container terminal case the mode is described by which combination quay crane, automated guided vehicle, and stack crane is used for unloading a specific container.
- Binary parametrization::
-
Binary variables can describe which of two operations go first for a resource, or can decide whether a synchronization is made or not.
Each parametrization has it advantages and disadvantages. Mode parametrization can be used if we have a small scheduling problem with a limited number of modes. For medium-size problems integer or binary parametrization will be better. If the number of possible modes is small, we can precompute the system matrices for all modes and scheduling can be done by evaluating all possible modes. When the number of modes gets large integer or binary parametrization will lead to more tractable problems. In this section we will consider binary parametrization and study the three basic types of control decisions, namely routing, synchronization, and ordering.
5.1 Routing in MPL systems
Consider a system that has to operate M jobs. For each job a specific route through the system has to be scheduled and resources have to be ordered accordingly. Let job \(j \in \underline {M}\) consist of pj operations on the resources \(\mathcal {R}_{j}=(r_{j,1},\ldots ,r_{j,p_{j}})\) in processing order, and let \(\mathcal {T}_{j}(k)=(\tau _{j,1}(k),\ldots ,\tau _{j,p_{j}}(k))\) be the corresponding processing times in cycle k with τj,i(k) ≥ 0 for all i,j. Each operation is assigned to a unique machine and is not interruptible.
Finally, let \(\hat {x}_{j}(k)=\left [ \begin {array}{ccc} x_{j,1}(k) & {\ldots } & x_{j,p_{j}}(k) \end {array} \right ]^{T}\) be the vector with all starting times of the operations of job j. This will give us the following inequalities for all \(j\in \underline {M}\):
In max-plus matrix notation this can be written as
or in short notation
If we have M jobs, we can collect all starting times in one state vector x(k) and we obtain:

In many applications jobs are not finished within one cycle, but need another cycle to complete. This can happen for example in a railway network with a cyclic timetable, in which a train that leaves a station in cycle k − 1 will arrive at the next station in cycle k. The state equation is then given by
Note that in (9) we use an inequality sign instead of an equality sign. This is because the starting times may also depend on ordering and synchronization, which can delay the starting times.
Often there are alternative routes available for the jobs. Alternative routes may result in the same ‘product’ (e.g. various machines in production line may execute the same operation) and sometimes the route may be changed to make another ‘product’.
Let there be L alternative sets of routes for this system; then for each set of routes we can define the matrices \(A_{\mu ,\ell }^{\text {job}}(k)\) for μ = 0,1, ℓ = 1,…,nℓ. Let us now define a set of max-plus binary variables \((w_{1}(k),\ldots ,w_{{n_{\small \ell }}}(k))\) such that if we have the ℓ th set of alternative routes for the system in cycle k, we find wℓ(k) = 0 and wj(k) = ε for all j≠ℓ. Now the job system matrices can be written for μ = 0,1 as
5.2 Ordering operations on resources in MPL systems
Consider a system with n operations, divided over N resources. Following the results of the previous paragraph, let the system allow L sets of alternative routes, parameterized by the max-plus binary variables w(k). Furthermore, let \(P_{\ell } \in {\mathbb {B}_{\varepsilon }}^{n \times n},\ell \in \{1,\ldots ,L\}\), be a matrix with max-plus binary entries, where [Pℓ]i,j = 0 if operation i and operation j are executed on the same resource, and [Pℓ]i,j = ε if operation i and operation j are executed on different resources. The matrix P(w(k)) for assignment of the resources can now be expressed as follows:
Let H(k) be a separation time matrix, where Hi,j(k)≠ε is the separation time between operations i and j if they may be scheduled on the same resource and Hi,j(k) = ε if operations i and j can never be scheduled on the same resource. Finally, let Zμ(k), μ = 0,1 be order decision matrices with max-plus binary entries, where [Zμ(k)]i,j = 0 if operation i in cycle k is scheduled after operation j in cycle k + μ, and [Zμ(k)]i,j = ε if operation i in cycle k is scheduled before operation j in cycle k + μ. Define zμ(k) as the vector with the stacked column vectors of matrix Zμ(k), so zμ(k) = vec(Zμ(k)). Then we can use the notation Zμ(k) = Z(zμ(k)).
Finally define the ordering matrices
Now the operation ordering constraints in the system can be formulated as follows:
Note that certain values of zμ(k) may lead to an infeasible schedule because of cycles in the ordering. An infeasible ordering occurs e.g. when in the case of three starting times of operations x1, x2, x3, we choose an ordering x1 > x2, x2 > x3, and x3 > x1.
5.3 Synchronization of operations in MPL systems
Synchronization occurs when a specific operation can only start when a specific operation of another job has finished. In general we can define a number of synchronization modes ℓ = 1,…,Lsyn, where for every mode we obtain a system matrix for μ = 0,1:
Now the operation synchronization constraints in the system can be formulated as follows:
where for μ = 0,1:
where \(s_{\mu }(k) \in {\mathbb {B}^{L_{\text {syn}}}_{\varepsilon }}\) are max-plus binary variables for scheduling the synchronizations, where [sμ(k)]ℓ = 0 means that synchronization ℓ is made and [sμ(k)]ℓ = 0 means that synchronization ℓ is cancelled. Synchronizations may be coupled and appear in groups (e.g. the synchronization of legs in a legged robot (Kersbergen et al. 2011)), but can also be an isolated phenomenon (e.g. the synchronization of two trains on a platform to give passengers the chance to change trains (Braker 1991)).
5.4 Combined A matrix
We have derived four conditions (9), (12), (13), and (16) for x(k). We also have a set of scheduling decision variables from
-
Routing: w(k).
-
Ordering: zμ(k), μ = 0,1.
-
Synchronization: sμ(k), μ = 0,1.
If we now stack all decision variables into one vector
where Ltot is the total number of scheduling variables, then we can write our scheduling model as follows
where for μ = 0,1:
Note that by choosing a specific control vector v(k) the system switches between different modes of operation (van den Boom and De Schutter 2006).
5.5 Reference and input signal
Some DESs work with a predefined schedule that gives a lower bound for the starting time of the operations in the system (e.g. in a railway system we have a timetable with the departure times of the trains). Let ri(k) be the starting time for operation i according to the given time schedule. To guarantees a lower bound ri(k) on operation i we introduce the constraint
For operations without a lower bound on the starting time we choose ri(k) = ε. Some DESs have a input signal that gives the starting time of ta job (e.g. in a production system the input is the time instant at which the raw material is fed into the system). To guarantees a lower bound we introduce the constraint
with
where [Bℓ]ij is the minimum time between the input event uj(k) and state event xi(k) if max-plus binary decision variable vℓ equals 0.
Now Eq. 15 can be replaced by
For systems without an input signal we can discard the second term.
5.6 Final SMPL model
We now have taken into account all the constraints (9), (12), (13), (16), and (17) that determine the starting times x(k). We assume that an event will take place as soon as all constraints are satisfied, which means that we now have an equality in Eq. 18 instead of an inequality:
Example 2
Consider the production system from Section 3. In this system there are two routes, so we introduce the max-plus variables w1(k) and w2(k). Note that because of the fact that the system can only be in one mode at the time, we have \(w_{2}(k) = \bar {w}_{1}(k)\). Now by choosing the scheduling variable v(k) = w1(k) we obtain the system matrices:
6 Analysis of SMPL systems using dynamic graphs
For max-plus linear system (1) we can determine the precedence graph G(A). The maximum average circuit weight in the precedence graph G(A) is then equal to the largest max-plus eigenvalue λ of the system matrix A (Heidergott et al. 2006).
For SMPL systems we use neither the concept of eigenvalue nor the precedence graph because the system matrix A(ℓ(k)) may change in every cycle k. We therefore use the concept of maximum growth rate or spectral radius. This section we start with the relation of the maximum average path weight in the dynamic graph and the maximum autonomous growth rate of the SMPL system (van den Boom and De Schutter 2012). Subsequently, we will discuss the controllability of an SMPL system in terms of the dynamic graph. This controllability is of importance when we want to perform scheduling and control of an SMPL system.
In van den Boom and De Schutter (2012) we introduced the maximum autonomous growth rate σmagr:
Definition 2
van den Boom and De Schutter (2012) Consider an SMPL system of the form (2) with system matrices A(ℓ), \(\ell \in {\underline {n_{\small \ell }}}\). For a given \(\alpha \in \mathbb {R}\), define the matrices Aα(ℓ) with [Aα(ℓ)]i,j = [A(ℓ)]i,j − α. Define the set \(\mathcal {S}_{\text {fin},n}\) of all n × n max-plus diagonal matrices with finite diagonal entries, so \(\mathcal {S}_{\text {fin},n}= \{ \>S\>|\>S=\text {diag}_{\oplus }(s_{1},\ldots ,s_{n}), \>s_{i}\text {is finite}\>\}\). The maximum autonomous growth rate λ of the SMPL system is defined by
Now consider the dynamic graph G of an SMPL system with mode switching vector \(\tilde {\ell }=[\>\ell (1)\cdots \ell (N)\>]^{T} \in {\mathscr{L}}_{N}\).
If the number of cycles N runs to infinity we obtain the maximum average path weight. The maximum average path weight σmapw can be computed as follows:
Let Sσ be such that \([\>S_{\sigma } \otimes A_{\alpha }(\ell ) \otimes {S_{\sigma }}^{{\scriptscriptstyle \otimes }^{\scriptstyle {-1}}} \>]_{i,j} \leq 0\) and define \(S_{\sigma }^{-} = {S_{\sigma }}^{{\scriptscriptstyle \otimes }^{\scriptstyle {-1}}}\). Now we can write
We find the bound
We can now summarize this in the following corollary:
Corollary 1
Consider an SMPL system of the form (2) with system matrices A(ℓ), \(\ell \in {\underline {n_{\small \ell }}} \), and let λℓ, \(\ell \in {\underline {n_{\small \ell }}}\) be the maximum eigenvalue for matrix A(ℓ). Then
Note the maximum average path weight is the worst case average cycle duration over the set of all possible consecutive mode switching vectors for \(N \rightarrow \infty \). In optimal scheduling we optimize over all possible consecutive mode switching vectors. This means that in scheduling the maximum average path weight is an upper bound for the makespan divided by the length of the schedule.
Remark 2
The asymptotic growth rate and maximum average path weight is related to the spectral radius (Peperko 2011) and the Lyapunov exponent. For a max-plus-linear system (so nℓ = 1), the maximum autonomous growth rate λ is equivalent to the largest max-plus-algebraic eigenvalue of the matrix A(1).
The next system property we discuss is structural controllability
Definition 3
Baccelli et al. (1992) and van den Boom and De Schutter (2012) Consider an SMPL system of the form (2) with system matrices A(ℓ), B(ℓ), \(\ell \in {\underline {n_{\small \ell }}} \). The SMPL system is structurally controllable if there exists a finite positive integer N such that for all mode sequences \(\tilde {\ell } = \left [ \begin {array}{ccc} \ell _{1} & {\ldots } & \ell _{N} \end {array} \right ]^{T} \in {\mathscr{L}}_{N}\) the matrices
are row-finite, i.e. in each row there is at least one entry different from ε.
Strong structural controllability means that all system states can be reached from the inputs for all possible mode sequences. If it is possible to choose the mode (like in case of scheduling) this concept of strong structural controllability is not always useful. We therefore also introduce the concept of weak structural controllability.
Weak structural controllability in the context of dynamic graphs is defined as follows:
Definition 4
Kalamboukis (2018) An SMPL system of the form (2) is said to be weakly structurally controllable if there exist a finite positive integer N and a mode sequence \(\tilde {\ell } = \left [ \begin {array}{ccc} \ell _{1} & {\ldots } & \ell _{N} \end {array} \right ]^{T} \in {\mathscr{L}}_{N}\) such that for any initial state x(k), all state vertices at t = k + N in the dynamic graph can be reached by a path originating at an input node.
Strong structural controllability (or just structural controllability) in the context of dynamic graphs is defined as follows:
Definition 5
Kalamboukis (2018) An SMPL system of the form (2) is said to be strongly structurally controllable if if there exists a finite positive integer N such that the system is weakly structurally controllable for all feasible mode sequences.
This last definition corresponds to the definition of structural controllability in van den Boom and De Schutter (2012).
7 Model predictive scheduling
Model predictive control (De Schutter and van den Boom 2001; Maciejowski 2002) is a one of the most popular advanced control strategies in industry. In this paper we will extend this methodology to scheduling and will therefore refer to it as model predictive scheduling (MPS). One of the main advantages of MPS is that we use the receding horizon principle, which means that we do not optimize the whole schedule at once, but we do this at regular time instants, where in each iteration we optimize only the jobs in the nearest future (over a certain horizon), taking into account the available information of past jobs. By using the receding horizon principle we use this available information past and only consider a limited number of future tasks. This reduces the number of scheduling variables to be optimized, which implies a lower computational burden. A too long computation time can cancel out the time gained by optimizing the schedule, or even deteriorate the total solution.
Apart from the MPC methodology to control SMPL system (van den Boom and De Schutter 2006, 2012) one can also using residuation to obtain an appropriate schedule (Alsaba et al. 2006).
In this paper we aim for predictive operational scheduling, which means that based on observations of the system events we can reschedule (reroute, resynchronize, and reorder) the jobs of the system to optimize the performance. This means that in every iteration the optimization has to be done in real time using the available information of the past jobs (accumulated in the state of the SMPL system).
Consider the SMPL system of Eq. 19 and let t be the present time instant. Now we like to compute the optimal future control actions. Define the actual current cycle k as follows:
This means that x(κ) ≤ t for κ ≤ k − 1, so these states are all known at time t. Note that parts of the states x(κ) ≤ t for κ ≥ k may also be known. Define the set \(\mathcal {X}_{t}\) such that for all pairs \((i,j) \in \mathcal {X}_{t}\) we have \(x_{i}(k+j) = x_{i}^{\text {past}}(k+j) \leq t\). Apart from the known states also specific scheduling variables and input variables are fixed at time t. Therefore, define the set \(\mathcal {V}_{t}\) such that for all pairs \((i,j) \in \mathcal {V}_{t}\), \(v_{i}(k+j) = v_{i}^{\text {past}}(k+j)\) is fixed at time t, and likewise define the set \(\mathcal {U}_{t}\) such that for all pairs \((i,j) \in \mathcal {U}_{t}\), \(u_{i}(k+j) = u_{i}^{\text {past}}(k+j) \leq t\) is fixed at time t.
7.1 The optimization problem
The MPS problem can now be formulated as finding the optimal future signal (v(k;t),u(k;t)), j = 0,…,Np − 1 that solves the following optimization problem for cycle k and time instant t:
subject to
where Np is the prediction horizon, and J(k;t) is the performance index for cycle k at time t.
Remark 3
Note that we write x(k;t) rather than x(k), and A(v(k);t) rather than A(v(k)). This is due to the fact that the available information depends on time instant t, leading to a new estimate of the parameters in the system matrices, and therefore a new optimal input sequence (u,v).
The prediction horizon Np determines how far (i.e. how many cycles) we look into the future to optimize the schedule. The choice of Np can be seen as a compromise between global optimality and computation time. Decreasing (increasing) the prediction horizon will result in a shorter (longer) computation time and a worse (better) closed-loop performance.
The performance index J(k;t) expresses a measurement of the efficiency of the chosen control vectors v(k + j;t), j = 0,…,Np − 1. In some problems the makespan (i.e. the time difference between the beginning and the end of a sequence of jobs or tasks) will be the most important measure of performance (i.e. for a printer or a container terminal). The smaller the makespan, the higher the performance. For other applications (e.g. for a production system) there is a (known) due date for the finished products and the performance index will be equal to the penalty we have to pay for all delays. Also for a railway system the performance index will be equal to the penalty we have to pay for all delays with respect to a given time table (note that early departures of trains are usually not allowed). Finally, the performance index for a legged robot may vary from following a reference trajectory (with discrete targets at specific time instants) to reaching a final goal as soon as possible.
The performance index J(k;t) can usually be written as
where
is a conventional binary variable. Further δ, κj,i, λi, ρj,m, and σj,l are weighting scalars, and nu is the number of inputs of the system. The first term of Eq. 27 is related to the makespan over the prediction horizon (i.e. the total production length over the next Np jobs), the second term is related to the weighted sum of all predicted starting times, the third term is related to the delay of the state events with respect to a specific due date signal xd(k), the fourth term maximizes the inputs um(k + j;t) (in manufacturing systems this corresponds to minimizing the number of parts in the input buffers), and the final term denotes the penalty for all changes in routing, ordering, or synchronization during cycle k + j.
Often we like to minimize the global makespan, i.e. the total length of the schedule. Let Ntot be the number of job cycles to be scheduled. Then the aim will be to minimize \(\max \limits _{i} x_{i}(k+N_{\text {tot}};t)\). If Ntot is very big, it is usually better to choose a prediction horizon Np ≪ Ntot, and the criterion will be to minimize (27) where δ = 1, 0 ≤ κj,i ≪ 1, λi = 0 and 0 ≤ ρj,m ≪ 1, and 0 ≤ σj,l ≪ 1. A major advantage of a small prediction horizon Np is that the computational complexity of the optimization problem is drastically reduced.
In other cases we like to minimize the sum of delays with respect to a due date signal xd,i(k) i.e. \(\max \limits \Big (\>x_{i}(k + j;t)-x_{\mathrm {d},i}(k + j)\>,\>0\>\Big )\). We then have δ = 0, 0 ≤ κj,i ≪ 1, 0 ≤ λi ≤ 1 and 0 ≤ ρj,m ≪ 1, and 0 ≤ σj,l ≪ 1.
The relaxed MPS problem is defined as solving (21) subject to Eqs. 23–26, and the inequality constraints
Theorem 1
Let (x#,v#,u#) be an optimal solution of the relaxed model predictive scheduling problem with J# as the optimum. If we define x+(k + j;t) as follows:
and x+(k − 1;t) = x(k − 1;t), then (x+,v#,u#) is a solution of the original model predictive scheduling problem.
Proof
Recal from Eq. 20 that x(k − 1;t) < t is completely known at time instant t.
From (30) we can derive for optimal solution (x#,v#,u#):
Now assume x+(k + j − 1;t) ≤ x#(k + j − 1;t). Then we compute
The term on the right-hand side of the last inequality is equal to x+(k + j;t), and so we find that if x+(k + j − 1;t) ≤ x#(k + j − 1;t) then x+(k + j;t) ≤ x#(k + j;t). For j = 0 we compute
and so x+(k;t) ≤ x#(k;t). This means that x+(k + j;t) ≤ x#(k + j;t) for all j = 0,…,Np − 1.
Associate J# with the value of the cost function for the optimal solution (x#,v#,u#) and J+ with the value of the cost function for the solution (x+,v#,u#). Note that J is a non-decreasing function in the state x. With x+(k + j;t) ≤ x#(k + j;t) we find J+ ≤ J#. On the other hand, note that x+ is a feasible solution for the relaxed model predictive scheduling problem while x∗ is an optimal solution. This means that J+ ≥ J#. Therefore, J+ = J# and (x+,v#,u#) is a solution of the original model predictive scheduling problem. □
Example 3
Consider the production system from Section 3 and Example 2, and let us introduce a signal yd(k) which is a due date for the time instant at which output event y(k) takes place. The cost criterion measures the tracking error or tardiness of the system, which is equal to the delay between the output y(k) and due date yd(k) if y(k) − yd(k) > 0, and zero otherwise. Now define xd(k + j) = yd(k + j) − d5; then y(k + j;t) − yd(k + j) = x5(k + j;t) − xd,5(k + j). Cost criterion (27) with δ = 0, κi = 0, λp = 0, p = 1,…,4, λ5 = 1, 0 ≤ ρj,l ≪ 1, and σj,m = 0, results in
Note that in this example we do not have a reference signal (i.e. r(k) = ε), so constraints (22)–(23) boil down to the set of constraints
for j = 1,…Np − 1. Together with constraints (23)–(26) this gives us the MPS problem for the production system.
7.2 The mixed-integer programming problem
The MPS problem (21), (23)–(30) can be recast into a mixed-integer linear programming (MILP) problem as follows. The scheduling parameters in the MPS problem are either zero or minus infinity. For the actual numerical implementation the infinite value ε cannot be used. The first step will therefore be to replace the max-plus binary variables by conventional binary variables. We use the following approximation
where β ≪ 0 is a very large (in absolute value) negative number and \(v^{\flat }(k;t) \in \{0,1\}^{L_{\text {tot}}}\) is a conventional binary vector. The adjoint of vi(k;t) can be approximated by
Let \(x^{\max \limits } \geq \max \limits _{i,j} x_{i}(k+j) \), then for \(\upbeta \leq -x^{\max \limits }\) the solution using the approximation and the original optimization variables will lead to the same optimal solution.
Now consider constraint (30). This can be written as a set of constraints:
for \(i\in \underline {n}\), \(l\in \underline {n}\), j = 0,…,Np − 1. In the absence of a reference signal, we can drop constraint (34).
Consider cost criterion (27). Note that the first term and the second term are linear in \(\tilde {x}(k;t)\), the fourth term is linear in \(\tilde {u}(k;t)\), and the fifth term is linear in \(\tilde {v}^{\flat }(k;t)\). For the third term we introduce an auxiliary variable \(e(k;t)=\max \limits (x(k;t)-x_{\mathrm {d}}(k),0)\); then minimizing the third term is equal to minimizing \({\sum }_{j} {\sum }_{i} e_{i}(k+j;t)\), subject to
for \(i\in \underline {n}\), j = 0,…,Np − 1.
Define the vectors
Now cost criterion (21) can be rewritten as a linear cost criterion
and the MPS problem can be recast as the following MILP problem:
subject to
where
In general, MILP problems are NP-hard (Schrijver 1986). In practice, this means that the worst case computational complexity of a mixed integer linear programming problem grows exponentially with the number of integer values in the problem. Nevertheless, there exist fast and reliable solvers (e.g. CPLEX, Gurobi, XPRESS (Atamtürk and Savelsbergh 2005)) for these problems. Furthermore, the underlying scheduling problem may be not be NP-hard, and may be polynomially solvable (See also Section 9).
Example 4
Consider the production system from Section 3 and Examples 2 and 3.
The cost criterion measures the tracking error or tardiness of the system, which is equal to the delay between the output y(k) and due date yd(k) if y(k) − yd(k) > 0, and zero otherwise. Define e(k + j;t) = y(k + j;t) − yd(k + j) = x5(k + j;t) + d5 − yd(k + j). Now define xd(k + j) = yd(k + j) − d5; then using cost criterion (27) with δ = 0, κi = 0, λp = 0, p = 1,…,4, λ5 = 1, 0 ≤ ρj,l ≪ 1, and σj,m = 0, results in
with constraints
for j = 1,…Np − 1. Note that cost criterion (40) is of the linear form Eq. 36. The constraints can be rewritten in the linear form Eqs. 38–39. This means that the MPS problem for the production system can be recast as an MILP problem.
8 Reparameterizing the MILP
In this section we will discuss the reparametrization of the binary optimization variables of the MILP. The goal is to reduce the number of binary variables in the MILP. The complexity in MILP depends on, among other things, the number of binary variables and the number of constraints. Based on this exponential behavior, the number of binary variables in a MILP is often used as an indicator of the computational difficulty. If we can reduce the number of binary parameters without adding too many constraints, the computation of the MILP may well be reduced. However, the final computational benefits depends on how the MILP optimization problem (21)–(21) is solved, and may depend on the choice of branch and bound algorithm (Bemporad and Morari 1999; Williams 1993). We start with the general idea of reparametrization and then look at two specific cases, namely routing and ordering.
8.1 Reparametrization with max-plus functions
We start with the definition of a max-plus function:
Definition 6
A scalar max-plus function \(f: \mathbb {R}_{\varepsilon }^{n} \rightarrow \mathbb {R}_{\varepsilon }\) is defined by the recursive grammar
with \(i \in \{{1},\dots ,{n}\}\), \(\alpha \in \mathbb {R}_{\varepsilon }\), and where \(f_{k}: \mathbb {R}_{\varepsilon }^{n} \rightarrow \mathbb {R}_{\varepsilon }\), \(f_{l}: \mathbb {R}_{\varepsilon }^{n} \rightarrow \mathbb {R}_{\varepsilon }\) are again scalar max-plus functions; the symbol | stands for “or”, and \(\max \limits \) is performed entrywise.
A vector function \(f: \mathbb {R}_{\varepsilon }^{n} \rightarrow \mathbb {R}_{\varepsilon }^{m}\) is an max-plus function if all entries are scalar max-plus functions. A max-plus linear function is an max-plus function. Furthermore from the above definition it is immediately clear that the max-plus product of two max-plus functions is again an max-plus function.
Theorem 2
A scalar max-plus function \(f: \mathbb {R}_{\varepsilon }^{n} \rightarrow \mathbb {R}_{\varepsilon }\) can be rewritten in a canonical form
for some integer L, matrix Γ and vector δ, and where Γi stand for the i th row of Γ.
Proof
This theorem is a special case of Theorem 3.1 in De Schutter and van den Boom (2004). □
Introduce a max-plus function \(f: \mathbb {B}^{L_{\text {red}}}_{\varepsilon } \rightarrow \mathbb {B}^{L_{\text {tot}}}_{\varepsilon }\) with Lred < Ltot and let
Now we substitute (42) in constraint (30). We obtain:
with
Note that every entry of Aμ(f(𝜃(k + j;t));t), μ = 0,1, and B(f(𝜃(k + j;t));t) is a max-plus function in the variable 𝜃 and so the right-hand side of Eq. 43 is a max-plus function in 𝜃, x, u, and r.
Next we introduce conventional binary variables 𝜃♭(k + j;t) similar to the previous section, so
We can now find matrices \(\bar {A}(k + j;t)\) such (43) can be rewritten as
and so in the implementation constraint (43) results in a set of linear constraints.
To give an idea how to find an appropriate mapping v(k + j;t) = f(𝜃(k + j;t)) we will discuss reparametrization of the route scheduling variables and the order scheduling variables.
8.2 Reparametrization of the routing variables
We start by looking at the routing of the jobs. From Eqs. 9 and 10 we know the routing constraints can be written as
Now let \(2^{m_{0}-1} < L \leq 2^{m_{o}}\). Then we can parameterize the variables \((w_{1},\ldots ,w_{L})\) by m max-plus binary variables \((\eta _{1},\ldots ,\eta _{m_{0}})\) and their adjoint values \((\bar {\eta }_{1},\ldots ,\bar {\eta }_{m_{0}})\). For example if L = 8 we can parameterize \(w_{1},\ldots ,w_{8}\) as follows:
In general we can define a max-plus function f such that wi(k) = fi(η(k)). By substitution of w(k) = f(η(k)) in Eq. 10 the number of variables can be reduced. Instead of \(A^{\text {job}}_{\mu }(w(k))\) we will use the notation \(A^{\text {job}}_{\mu }(\eta (k))\).
Note that by the reparametrization the number of scheduling variables is reduced from L to \(m_{0}=\lceil \log _{2}{L}\rceil \). The difference between L and m0 will grow rapidly with increasing L, as can be seen in Table 2.
Remark 4
If L is not an exact power of 2, there will be more permutations of ηi(k) and \(\bar {\eta }_{i}(k)\) than necessary. In that case we can introduce a constraint on ηi(k) and \(\bar {\eta }_{i}(k)\) to describe the allowed set. Let \(\eta ^{\flat }_{i}(k)\) be the conventional binary variable associated with the max-plus binary variable ηi(k). Then this constraint can be defined as
For example, for L = 10, and so m0 = 4, we add the constraint:
8.3 Reparametrization of the ordering variables
Next we consider the operation ordering of the p jobs on a resource. From Eq. 12 we know that the ordering constraints can be written as
The vector zμ(k), μ = 0,1 consists of the entries of matrix Zμ(k). Note that if operation i in cycle k is scheduled after operation j, so [Zμ(k)]i,j = 0, then automatically operation j in cycle k is scheduled before operation i, so [Zμ(k)]i,j = ε. In general we will find that \([Z_{\mu }(k)]_{i,j} = \overline {[Z_{\mu }(k)]}_{i,j} \) for i≠j and [Zμ(k)]i,i = ε. This means that for scheduling p operations the vector zμ(k) will have dimension m1 = p(p − 1)/2. Note that certain values of zμ(k) will lead to an infeasible schedule because of cycles in the ordering. To avoid these infeasible schedules we can define the set \(\mathcal {Z}\) with all feasible values zμ(k). For scheduling p operations on one resource we have p! possible permutations. This is also the maximum number of elements in the set \(\mathcal {Z}\). Let \(m_{2}=\lceil \log _{2}{p\text {!}}\rceil \); then we need m binary parameters \(\gamma _{\mu }(k) = \left [ \begin {array}{ccc} [\gamma _{\mu }]_{1}(k) & \ldots &[\gamma _{\mu }]_{m}(k) \end {array} \right ]^{T}\) to model all possible allowed values zμ(k). We can define max-plus function \(f:{(\mathbb {B}_{\varepsilon })}^{m_{1}} \rightarrow {(\mathbb {B}_{\varepsilon }})^{m_{2}}\) such that [zμ]i(k) = [fμ]i((γμ(k)). A way to derive a concise description of the function f can be found in Akers (1978), where a binary decision tree is used to reduce the number of decision parameters.
Example 5
Consider an example for p = 3, where we have a matrix
with p(p − 1)/2 = 3 variables. We have p! = 6 feasible combinations of ([z0]1,[z0]2,[z0]3) and so \(m=\lceil \log _{2}{3\text {!}}\rceil =3\).
Table 3 shows the permutations (last column) with the corresponding values of the entries z0 of the matrix Z0 for the ordering P(1) − P(2) − P(3). From the table we can see that
Subsequently, we can substitute zμ(k) = fμ((γμ(k))) into (11) and we obtain
Using the variables 𝜃(k + j;t) (e.g. η2(k) or γμ(k)) has two important advantages: we need less parameters and there are less infeasible choices for v(k).
Remark 5
Note that for the case in Example 5 there is no reduction because for p = 3 we find m1 = 3 and m2 = 3. For higher values of p however the difference between m1 and m2 grows very rapidly, as can be seen in Table 4
8.4 Parameter reduction
We may conclude that for every job the reduction of the number of routing variables is \(\lceil \log _{2}{L}\rceil \) where L is the number of routes for that particular job and that for every resource the reduction of routing variables is \((\lceil \log _{2}{p\text {!}}\rceil )/p(p-1)\) where p is the number of jobs for that particular resource. Note that in both cases the number of binary variables decreases in a logarithmic way. This is often beneficial for the optimization.
9 Conclusions
In this paper we have shown that various semi-cyclic discrete-event systems can be modeled as switching max-plus linear (SMPL) systems and that dynamic graphs are a useful tool in the modeling and analysis process. The SMPL model can be applied in the context of scheduling. This can be done by formulating the model predictive scheduling problem, which can be recast as a mixed-integer linear program. We have shown how the number of optimization parameters can be reduced in a logarithmic way, which is often beneficial for the optimization.
As was already stated in Section 7, MILP problems are NP-hard (Schrijver 1986). However the underlying scheduling problem is not always NP-hard, and may be polynomially solvable. In future research we will continue our study on the computational complexity of the scheduling problem defined in this paper. Further we will do an in-depth investigation on how to accurately charaterize the effect of the reparametrization of Section 8 on the computation time.
References
Akers SB (1978) Binary decision diagrams. IEEE Trans Comput C–27(6):509–516
Alirezaei M, van den Boom TJJ, Babuška R (2012) Max-plus algebra for optimal scheduling of multiple sheets in a printer. In: Proceedings of the American control conference 2012, Montreal, Canada, pp 1973–1978
Alsaba M, Lahaye S, Boimond J-L (2006) On just in time control of switching max-plus linear systems. In: Proceedings of ICINCO 06, Setubal, Portugal, pp 79–84
Atamtürk A, Savelsbergh MWP (2005) Integer-programming software systems. Ann Oper Res 140(1):67–124
Baccelli F, Cohen G, Olsder GJ, Quadrat JP (1992) Synchronization and linearity. Wiley, New York
Bemporad A, Morari M (1999) Control of systems integrating logic, dynamics, and constraints. Automatica 35:407–427
Blazewicz J, Ecker KH, Pesch E, Schmidt G, Weglarz J (2001) Scheduling computer and manufacturing processes, 2nd edn. Springer, Berlin
Boimond JL, Ferrier JL (1996) Internal model control and max-algebra: Controller design. IEEE Trans Autom Control 41(3):457–461
Bouquard JL, Lenté C, Billaut JC (2006) Application of an optimization problem in max-plus algebra to scheduling problems. Discret Appl Math 154(15):2064–2079
Braker JG (1991) Max-algebra modelling and analysis of time-table dependent transportation networks. In: Proceedings of the 1st European Control Conference, pp 1831–1836
Braker JG (1993) Algorithms and applications in timed discrete event systems. PhD thesis, Delft University of Technology, Delft
Brucker P (2001) Scheduling algorithms, 3rd edn. Springer, Berlin
Brucker P, Kampmeyer T (2008) A general model for cyclic machine scheduling problems. Discret Appl Math 156(13):2561–2572
Cuninghame-Green RA (1979) Minimax algebra, volume 166 Lecture Notes in Economics and Mathematical Systems. Springer, Berlin
G~omes da Silva G., Maia CA (2016) On just-in-time control of timed event graphs with input constraints: a semimodule approach. Discrete Event Dynamic Systems 26(2):351–366
De Schutter B, van den Boom T (2001) Model predictive control for max-plus-linear discrete event systems. Automatica 37(7):1049–1056
De Schutter B, van den Boom TJJ (2004) MPC for continuous piecewise-affine systems. Syst Contr Lett 52(3/4):179–192
Doustmohammadi A, Kamen EW (1995) Direct generation of event-timing equations for generalized flow shop systems. In: Proceedings of the Photonics East’95: International Society for Optics and Photonics, pp 50–62
Floudas CA, Lin X (2005) Mixed integer linear programming in process scheduling Modeling, algorithms, and applications. Ann Oper Res 139:131–162
Fromherz MPJ (2001) Constraint-based scheduling. In: Proceedings of the American Control Conference (ACC’01), Invited tutorial paper, pp 3231–3244
Gondran M, Minoux M (1976) Eigenvalues and eigenvectors in semimodules and their interpretation in graph theory. In: Proceedings of the 9th International Mathematical Programming Symposium, pp 333–348
Gondran M, Minoux M (1984) Graphs and algorithms. Wiley, Chichester
Hanen C, Munier A (1995) Cyclic scheduling on parallel processors: An overview. In: Chretienne P, Coffman EG, Lenstra JK, Liu Z (eds) Scheduling Theory and Its Applications, chapter 9. Wiley, New York
Hardouin L, Cottenceau B, Lhommeau M, Le Corronc E (2009) Interval systems over idempotent semiring. Linear Algebra Appl 431(5-7):855–862
Heidergott B, Olsder GJ, van der Woude J (2006) Max Plus at Work: Modeling and Analysis of Synchronized Systems. Princeton University Press, Princeton
Houssin L, Lahaye S, Boimond J-L (2013) Control of (max,+)-linear systems minimizing delays. Discrete Event Dynamic Systems 23(3):261–276
Indriyani D (2016) Subiono Scheduling of the crystal sugar production system in sugar factory using max-plus algebra. Int J Comput Sci Appl Math 2(3):33–37
Johnson SM (1954) Optimal two- and three-stage production schedule with setup times included. Naval Research Logistics Quarterly 1(1):61–68
Kalamboukis VP (2018) Matrix spans in max-plus algebra and a graph-theoretic approach to switching max-plus linear systems. MSc thesis Delft, University of Technology
Kersbergen B, Lopes GAD, van den Boom T, De Schutter B, Babuška R. (2011) Optimal gait switching for legged locomotion. In: Proceedings of the International Conference on Intelligent Robots and Systems (IROS-2011), San Francisco, USA, pp 2729–2734
Kersbergen B, Rudan J, van den Boom T, De Schutter B (2016) Towards railway traffic management using switching max-plus-linear systems - structure analysis and rescheduling. Discrete Event Dynamic Systems: Theory and Applications 26(2):183–223
Ku H, Karimi IA (1988) Scheduling in serial multiproduct batch processes with finite interstage storage A mixed integer linear programming formulation. Ind Eng Chem Res 27:1840–1848
Lahaye S, Boimond J-L, Ferrier J-L (2008) Just-in-time control of time-varying discrete event dynamic systems in (max,+) algebra. Int J Prod Res 46(19):5337–5348
Leung JY-T (ed) (2004) Handbook of Scheduling: algorithms, Models, and Performance Analysis. CRC Press, Inc, Boca Raton
Libeaut L, Loiseau JJ (1995) Admissible initial conditions and control of timed event graphs. In: Proceedings of the 34th IEEE Conference on Decision and Control, New Orleans, Louisiana, pp 2011–2016
Lopes G, Kersbergen B, van den Boom TJJ, Schutter B. D~. e., Babuška R. (2014) Modeling and control of legged locomotion via switching max-plus models. IEEE Trans Robot 30(3):652–665
Maciejowski JM (2002) Predictive control with constraints. Prentice Hall, Pearson education limited, Harlow
Maia CA, Hardouin L, Santos-Mendes R, Cottenceau B (2003) Optimal closed-loop control of timed event graphs in dioids. IEEE Trans Autom Control 48 (12):2284–2287
Mascis A, Pacciarelli D (2002) Job shop scheduling with blocking and no-wait constraints. European J Oper Res 143(3):498–517
Menguy E, Boimond J, Hardouin L, Ferrier J (2000) Just-in-time control of timed event graphs Update of reference input, presence of uncontrollable input. IEEE Trans Autom Control 45(11):2155– 2158
Murota K (2009) Matrices and Matroids for Systems Analysis. vol 20, Springer Science & Business Media
Murota K (2012) Systems Analysis by Graphs and Matroids: Structural Solvability and Controllability, vol 3, Springer Science & Business Media
Mutsaers M, Özkan L, Backx T (2012) Scheduling of energy flows for parallel batch processes using max-plus systems. In: Proceedings of the 8th IFAC International Symposium on Advanced Control of Chemical Processes 2012, pp 176–181
Nambiar A, Judd R (2011) Max-plus-based mathematical formulation for cyclic permutation flow-shops. International Journal of Mathematical Modelling and Numerical Optimisation 2:85–97
Peperko A (2011) On the continuity of the generalized spectral radius in max-algebra. Linear Algebra Appl 435:902–907
Pinedo M (2001) Scheduling: Theory, Algorithms and Systems, 2nd edn. Prentice-Hall, Englewood Cliffs
Schrijver A (1986) Theory of Linear and Integer Programming. Wiley, Chichester
van Boetzelaer FB, van den Boom TJJ, Negenborn RR (2014) Model predictive scheduling for container terminals. In: Proceedings of the 19th IFAC World Congress (IFAC WC’14), Cape Town, South Africa, pp 5091–5096
van den Boom TJJ, De Schutter B (2006) Modelling and control of discrete event systems using switching max-plus-linear systems. Control Eng Pract 14(10):1199–1211
van den Boom TJJ, De Schutter B (2012) Modeling and control of switching max-plus-linear systems with random and deterministic switching. Discrete Event Dyn Syst 12(3):293–332
van den Boom TJJ, Lopes GAD, De Schutter B (2013) A modeling framework for model predictive scheduling using switching max-plus linear models. In: Proceedings of the 52st IEEE conference on decision and control (CDC 2013), Florence, Italy, December 10-13
Yurdakul M, Odrey NG (2004) Development of a new dioid algebraic model for manufacturing with the scheduling decision making capability. Robot Auton Syst 49:207–218
Williams HP (1993) Model building in mathematical programming, 3rd edn. Wiley, New York
Acknowledgments
The authors would like to thank Vangelis Kalamboukis and Jacob van der Woude of Delft University of Technology for the inspiring discussions on dynamic graphs, and also the anonymous referees for their helpful comments on an earlier draft of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
van den Boom, T.J.J., Muijsenberg, M.v.d. & De Schutter, B. Model predictive scheduling of semi-cyclic discrete-event systems using switching max-plus linear models and dynamic graphs. Discrete Event Dyn Syst 30, 635–669 (2020). https://doi.org/10.1007/s10626-020-00318-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10626-020-00318-w