Modeling and control of switching max-plus-linear systems with random and deterministic switching

Abstract

Switching max-plus-linear (SMPL) systems are discrete-event systems that can switch between different modes of operation. In each mode the system is described by a max-plus-linear state equation and a max-plus-linear output equation, with different system matrices for each mode. The switching may depend on the inputs and the states, or it may be a stochastic process. In this paper two equivalent descriptions for switching max-plus-linear systems will be discussed. We will also show that a switching max-plus-linear system can be written as a piecewise affine system or as a constrained max-min-plus-scaling system. The last translation can be established under (rather mild) additional assumptions on the boundedness of the states and the inputs. We also develop a stabilizing model predictive controller for SMPL systems with deterministic and/or stochastic switching. In general, the optimization in the model predictive control approach then boils down to a nonlinear nonconvex optimization problem, where the cost criterion is piecewise polynomial on polyhedral sets and the inequality constraints are linear. However, in the case of stochastic switching that depends on the previous mode only, the resulting optimization problem can be solved using linear programming algorithms.

1 Introduction

There exist many modeling frameworks for discrete-event systems such as queueing theory, (extended) state machines, formal languages, automata, temporal logic models, generalized semi-Markov processes, Petri nets, and computer simulation models (see Cassandras and Lafortune 1999; Ho 1992; Peterson 1981 and the references therein). In general, models that describe the behavior of a discrete-event system are nonlinear in conventional algebra. However, there is a class of discrete-event systems that can be described by a model that is “linear” in the max-plus algebra (Baccelli et al. 1992; Cuninghame-Green 1979; Heidergott et al. 2006). Such discrete-event systems are called max-plus-linear systems. Essentially, they can be characterized as discrete-event systems in which only synchronization and no choice occurs. So typical examples are serial production lines, production systems with a fixed routing schedule, railway networks, legged robots, transmission lines, and urban traffic systems.

The basic control problem for MPL systems consists in determining the optimal input times (e.g., feeding times of raw material or starting times of processes or activities) for a given reference signal (e.g., due dates for the finished products or completion dates for processes or activities). In the literature many different approaches are described to solve this problem. Among these the most common ones are based on residuation and on model predictive control (MPC). Residuation essentially consists in finding the largest solution to a system of max-plus inequalities with the input times as variables and the due dates as upper bounds. Residuation-based approaches for computing optimal input times are presented or used in Boimond and Ferrier (1996), Cottenceau et al. (2001), Goto (2008), Lahaye et al. (2008), Libeaut and Loiseau (1995), Maia et al. (2003) and Menguy et al. (1997, 2000a, b). The MPC approach is essentially based on the minimization of the error between the actual output times and the due dates, possibly subject to additional constraints on the inputs and the outputs. The MPC approach for MPL systems has been developed in De Schutter and van den Boom (2001), Masuda (2006), Masuda and Goto (2007), Necoara et al. (2009) and van den Boom and De Schutter (2002). Another approach, based on invariant subspaces, is proposed in Katz (2007) and Maia et al. (2011).

In van den Boom and De Schutter (2006) we have introduced the class of switching max-plus-linear (SMPL) systems. This class consists of discrete-event systems that can switch between different modes of operation. In each mode the system is described by a max-plus-linear state equation and a max-plus-linear output equation, with different system matrices for each mode. In van den Boom and De Schutter (2006) the mode switching was a function of the input signals and the previous state; in the current paper the switching can also depend on a stochastic sequence. The class of SMPL systems with deterministic and stochastic switching contains discrete-event systems with synchronization but no choice, in which the order of events may vary randomly and often cannot be determined a priori. This randomness may be due to e.g. (randomly) changing production recipes, varying customer demands or traffic demands, failures in production units, or faults in transmission links.

In this paper we discuss two types of SMPL system descriptions and we show that the two descriptions are equivalent. Furthermore, we show that an SMPL system can be rewritten as a piecewise affine system or as a max-min-plus-scaling system. Using the results of Heemels et al. (2001) we also implicitly prove that an SMPL system can be rewritten as an (extended) linear complementarity (ELC/LC) system or as a mixed logic dynamical (MLD) system, which are system descriptions that are often used in the field of hybrid systems. Using these results we can transfer properties of piecewise affine systems and max-min-plus-scaling systems to SMPL systems. Finally, we will present a design procedure for stabilizing model predictive controllers for SMPL systems with both types of switching procedures.

This paper will review and extend the results of van den Boom and De Schutter (2006, 2007, 2008a, b). The most important changes with respect to van den Boom and De Schutter (2008b) are the revision of the proofs and the improvement of the presentation of the material. The main change with respect to van den Boom and De Schutter (2007, 2008a) is the correction in Theorem 1. We also relaxed the condition of a row-finite matrix C by the condition that the system is structurally observable in Theorem 1. We improved the definitions for the maximum growth rate and we explicitly provide an algorithm to compute this value. Further we have extended the paragraph on the optimization in the MPC algorithm and added some lines to Section 5 to indicate how MPC techniques using PWA and MMPS systems can be used to compute a predictive controller for SMPL systems. Finally we added a paragraph to Section 5 on MPC for SMPL systems with deterministic switching. The paper is organized as follows. In Section 2 we introduce the max-plus algebra and the concept of SMPL systems. In Section 3 we define a second class of SMPL systems and discuss the equivalences between the two classes of SMPL systems. Furthermore we will show that SMPL systems can be rewritten as piecewise affine systems or max-min-plus-scaling systems. Section 4 presents conditions for a stabilizing controller, and in Section 5 we derive a stabilizing model predictive controller for SMPL systems.

2 Max-plus algebra and SMPL systems

2.1 Max-plus algebra

In this section we give the basic definition of the max-plus algebra (Baccelli et al. 1992; Cuninghame-Green 1979).

Define ε = − ∞ and ℝ _ε  = ℝ ∪ {ε}. The max-plus-algebraic addition (⊕) and multiplication (⊗) are defined as follows:

$$ x \oplus y = \max(x,y) , \quad x \otimes y = x + y $$

for any x, y ∈ ℝ _ε , and

$$ \begin{aligned} {[} A \oplus B {]}_{i,j} &= a_{i,j} \oplus b_{i,j} = \max ( a_{i,j}, b_{i,j} ) \\ [ A \otimes C ]_{i,j} &= \mathop\bigoplus\limits_{k=1}^{n} a_{i,k} \otimes c_{k,j} =\max\limits_{k=1,\ldots,n} ( a_{i,k} + c_{k,j} ) \end{aligned} $$

for matrices A, B ∈ ℝ _ε ^m×n and C ∈ ℝ _ε ^n×p. The matrix ε is the max-plus-algebraic zero matrix: [ε] _i,j  = ε for all i, j. A max-plus diagonal matrix S = diag_⊕(s ₁, ..., s _n ) has elements [S] _i,j  = ε for i ≠ j and diagonal elements [S] _i,i  = s _i for i = 1, ..., n. The matrix E = diag_⊕(0, ..., 0) is the max-plus identity matrix. The max-plus-algebraic matrix power of A ∈ ℝ _ε ^n×n is defined as follows: $A^{\otimes^{0}} = E$ and $A^{\otimes^{k}} = A {\otimes} A^{\otimes^{k-1}}$ for k = 1, 2, .... Let $S^{\otimes^{-1}}$ denote the inverse of S in max-plus algebra, so $S \otimes S^{\otimes^{-1}} = S^{\otimes^{-1}} \otimes S = E$. diagonal up to a permutation of rows. S is invertible if it has one and only one entry in each row and column which is different from ϵ. If all s _i are finite, the max-plus inverse of a max-plus diagonal matrix S = diag_⊕(s ₁, ..., s _n ) is equal to $S^{\otimes^{-1}}={\mathrm{diag}}_\oplus(-s_1,\ldots,-s_n)$.

2.2 SMPL systems

Switching Max-Plus-Linear (SMPL) systems are discrete-event systems that can switch between different modes of operation (van den Boom and De Schutter 2006). In each mode $\ell\in\{1,\ldots,{n_{L}} \}$, the system is described by a max-plus-linear state equation and a max-plus-linear output equation:

$$ x(k) = A^{(\ell(k))} \otimes x(k-1) \oplus B^{(\ell(k))} \otimes u(k) $$

(1)

$$ y(k) = C^{(\ell(k))} \otimes x(k)$$

(2)

in which the matrices $A^{(\ell)} \in {{\mathbb{R}}_\varepsilon}^{n_x\times n_x}$, $B^{(\ell)} \in {{\mathbb{R}}_\varepsilon}^{n_x\times n_u}$, $C^{(\ell)} \in {{\mathbb{R}}_\varepsilon}^{n_y\times n_x}$ are the system matrices for the ℓ-th mode.¹ We assume that there are n _L possible modes.

The index k is called the event counter. For SMPL systems the state x(k) typically contains the time instants at which the internal events occur for the kth time, the input u(k) contains the time instants at which the input events occur for the kth time, the output y(k) contains the time instants at which the output events occur for the kth time, and the mode ℓ(k) determines which max-plus linear model is valid during the kth event.

In van den Boom and De Schutter (2006) we have considered SMPL systems with deterministic switching depending on the previous state or on an input signal. In van den Boom and De Schutter (2007) we have introduced SMPL systems with random switching, in which the mode switching depended on a stochastic sequence. In this paper we consider the combination of both switching types (van den Boom and De Schutter 2008a). For the SMPL system (1) and (2), the mode switching variable ℓ(k) then in general depends on both stochastic variables as well as deterministic variables (state and inputs). The switching actions are determined by a switching mechanism. For the SMPL system (1) and (2), the mode switching variable ℓ(k) is a stochastic process that depends on the previous mode ℓ(k − 1), the previous state x(k − 1), the input variable u(k), and an (additional) control variable v(k). We denote the probability of switching to mode ℓ(k) given ℓ(k − 1), x(k − 1), u(k), and v(k) by P[L(k) = ℓ(k)|ℓ(k − 1), x(k − 1), u(k), v(k)], where L(k) is a stochastic variable and ℓ(k) is its value. We assume that for all $\ell(k),\ell(k-1)\in \{1,\ldots,{n_{L}} \}$, the probability P is piecewise affine on polyhedral sets in the variables x(k − 1), u(k), and v(k). Since P is a probability, we have

$$ 0 \leq P[L(k)=\ell(k)|\ell(k-1),x(k-1),u(k),v(k)] \leq 1 $$

and

$$ \sum\limits_{\ell(k)=1}^{n_{\small L}} P[L(k)=\ell(k)|\ell(k-1),x(k-1),u(k),v(k)] = 1 $$

To illustrate the different types of mode switching, we will now present three simple examples. In the first example we discuss deterministic switching, in which the mode switching only depends on the previous state or an input signal. In a second example we discuss random switching, in which the mode switching entirely depends on a stochastic sequence. In a third example we discuss stochastic switching with a probability depending on the state.

Example 1

(Deterministic switching) Consider the system in Fig. 1 with three modes, starting in mode 1 at event step k. Let v(k) be a control variable that determines the system to stay in mode 1 (for v(k) < 0.3), to switch from mode 1 to mode 2 (for 0.3 ≤ v(k) < 0.7), or to switch to mode 3 (for v(k) ≥ 0.7).

Fig. 1

Deterministic switching

We achieve this by defining the probability functions

$$ \begin{aligned} P[L(k)=1|1,x(k-1),u(k),v(k)] & = \left\{ \begin{array}{ll} 1 & \mathrm{for}\;v<0.3\;\;,\; \forall x,u \\ 0 & \mathrm{for}\;v\geq 0.3\;\;,\; \forall x,u \end{array} \right. \\ P[L(k)=2|1,x(k-1),u(k),v(k)] & = \left\{ \begin{array}{ll} 0 & \mathrm{for}\;v < 0.3\;\;,\; \forall x,u \\1 & \mathrm{for}\;0.3 \leq v <0.7\;\;,\; \forall x,u \\ 0 & \mathrm{for}\;v\geq 0.7\;\;,\; \forall x,u \end{array} \right. \\ P[L(k)=3|1,x(k-1),u(k),v(k)] & = \left\{ \begin{array}{ll} 0 & \mathrm{for}\;v<0.7\;\;,\; \forall x,u \\ 1 & \mathrm{for}\;v\geq 0.7\;\;,\; \forall x,u \end{array} \right. \end{aligned} $$

In general for deterministic switching, the probability functions are piecewise constant with values either 0 or 1.

Example 2

(Stochastic switching with fixed probability) Consider the system in Fig. 2 with three modes, starting in mode 1 at event step k. In this case of stochastic switching we assume that the probability to stay in mode 1 is equal to γ, that the probability to switch from mode 1 to mode 2 is equal to β, and that the probability to switch from mode 1 to mode 3 is equal to 1 − β − γ, where β, γ ∈ [0, 1] are constants and γ + β ≤ 1.

Fig. 2

Stochastic switching

We can achieve this by defining the probability functions

$$ \begin{aligned} P[L(k)=1|1,x(k-1),u(k),v(k)] & = \gamma\;\;,\; \forall x,u \\ P[L(k)=2|1,x(k-1),u(k),v(k)] & = \beta\;\;,\; \forall x,u \\ P[L(k)=3|1,x(k-1),u(k),v(k)] & = 1-\beta-\gamma\;\;,\; \forall x,u \end{aligned} $$

In general for stochastic switching with fixed probability, the probability functions are piecewise constant with values between 0 and 1.

Example 3

(Stochastic switching with a probability depending on the state) Consider the system in Fig. 3 with two modes, starting in mode 1 at event step k. In this example, the switching probability depends on the state of the system. Consider a system with state x(k). Let x ₁(k) be the first entry of the state. We assume the system always stays in mode 1 for x ₁(k) < 0, and always switches from mode 1 to a mode 2 for x ₁(k) > 1; for x ₁(k) ∈ [0, 1] we have a probability equal to x ₁(k) to stay in mode 1, and a probability equal to 1 − x ₁(k) to switch from mode 1 to mode 2.

Fig. 3

State-dependent stochastic switching

We can achieve this by defining the probability functions

$$ \begin{aligned} P[L(k)1|1,x(k-1),u(k),v(k)] & = \begin{cases} 1 & \mathrm{for} \;x_1(k) < 0\;\;,\; \forall x,u \\[-1mm] x_1(k) & \mathrm{for} \;0 \leq x_1(k) \leq 1\;\;,\; \forall x,u \\[-1mm] 0 & \mathrm{for} \;x_1(k) > 1\;\;,\; \forall x,u \end{cases}\\ P[L(k)=2|1,x(k-1),u(k),v(k)] & = \begin{cases} 0 & \mathrm{for} \;x_1(k) < 0\;\;,\; \forall x,u \\[-2mm] 1-x_1(k) & \mathrm{for} \;0 \leq x_1(k) \leq 1\;\;,\; \forall x,u \\[-1mm] 1 & \mathrm{for} \;x_1(k) > 1\;\;,\; \forall x,u. \end{cases} \end{aligned} $$

In general for stochastic switching with a probability depending on the state or the input the probability functions are piecewise affine in the state or the input.

Definition 1

A polyhedral partition $\{\Gamma_i\}_{i=1,\ldots,n_{s}}$ of the space ${\mathbb{R}}^{n_w}$ is defined as the partitioning of the space ${\mathbb{R}}^{n_w}$ into non-overlapping polyhedra Γ _i , i = 1, ..., n _s of the form

$$ \Gamma_{i} = \{\; w(k)\; |\; S_{i}\,w(k) {\preceq}_i\, s_{i}\;\}\;,\;\;\mathrm{for}\;\; i = 1,\ldots,n_{s}, $$

for some matrices $S_i \in {\mathbb{R}}^{q \times n_w}$ and vectors $s_i \in {\mathbb{R}}^{q}$, and with ${\preceq}_i$ a vector operator² where the entries stand for either ≤ or < and there holds

$$ \bigcup\limits_{i=1}^{n_s} \Gamma_{i} = {\mathbb{R}}^{n_w} \;\;\;\text{and}\;\;\; \Gamma_{i} \cap \Gamma_{j} = \emptyset \;\;\; \mathrm{for}\;\; i \ne j $$

Definition 2

(van den Boom and De Schutter 2007, 2008a, b) Consider the system (1) and (2) with n _L possible modes and let the probability of switching to mode ℓ(k) given ℓ(k − 1), x(k − 1), u(k), v(k) be denoted by P[L(k) = ℓ(k)|ℓ(k − 1), x(k − 1), u(k), v(k)]. Then the system (1) and (2) is a type-1 Switching Max-Plus-Linear (SMPL) system if for any given ℓ(k) ∈ {1, ..., n _L }, $\>P[L(k)=\ell(k)|\cdot,\cdot,\cdot,\cdot]$ is a probability function that is piecewise affine on polyhedral partition of the space of the variables ℓ(k − 1), x(k − 1), u(k), v(k).

Remark 1

Consider a type-1 SMPL system with switching probability P. If we define the vector $w(k)= \left[{\ell(k-1) \;x^T(k-1) u^T(k) \;v^T(k)}\right]^T \in {\mathbb{R}}^{n_w}$, then there exist a polyhedral partition $\{\Gamma_i\}_{i=1,\ldots,n_{s}}$ of ${\mathbb{R}}^{n_w}$ and vectors α _m,i , and scalars β _m,i for i = 1, ..., n _s , m ∈ {1, ..., n _L } such that the probability P can be written as

$$ P[L(k)=\ell(k)|w(k)] = \alpha^T_{\ell(k),i}\,w(k) + \beta_{\ell(k),i}\;,\;\;\text{if}\;\;w(k) \in \Gamma_{i} $$

(3)

Remark 2

Since P is a probability, for any w(k) we have

$$ 0 \leq P[L(k)=\ell(k)|w(k)] \leq 1\;\;,\;\;\mathrm{for}\;\;\ell(k)=1,\ldots,{n_{L}} $$

and

$$ \sum\limits_{\ell(k)=1}^{n_{L}} P[L(k)=\ell(k)|w(k)] = 1 $$

Remark 3

As was mentioned in Section 1, the switching of the mode cannot always be determined a priori, but may have a stochastic behavior. For example, in the case of a production system we can use the probability P to describe the changing production recipes or varying customer demands; or in transmission links each mode may represent a network with a specific set of faults, and the probability P may describe the chance of this set of faults to occur.

Example 4

(Production system I) Consider the production system of Fig. 4. This system consists of three machines M ₁, M ₂, and M ₃. Three products (A, B, C) can be made with this system, each with its own recipe, meaning that the order in the production sequence is different for every product.

Fig. 4

A production system

For product A (using recipe ℓ(k) = 1) the production order is M ₁-M ₂-M ₃, which means that the raw material is fed to machine M ₁ where it is processed. Next, the intermediate product is sent to machine M ₂ for further processing, and finally the product A is finished in machine M ₃. Similarly, for product B (using recipe ℓ(k) = 2) the processing order is M ₂-M ₁-M ₃, and for product C (using recipe ℓ(k) = 3) the processing order is M ₁-M ₃-M ₂. We assume that the type of the kth product (A, B or C) is available at the start of the production, so that we do know ℓ(k) when computing u(k).

Each machine starts working as soon as possible on each batch, i.e., as soon as the raw material or the required intermediate products are available, and as soon as the machine is idle (i.e., the previous batch has been finished and has left the machine). We define u(k) as the time instant at which the system is fed with the raw material for the kth product, x _i (k) as the time instant at which machine i starts processing the kth product, and y(k) as time instant at which the kth product leaves the system. We assume that all the internal buffers are large enough, and no overflow will occur.

We assume the transportation times between the machines to be negligible, and the processing times of the machines M ₁, M ₂ and M ₃ to be given by d ₁ = 1, d ₂ = 2 and d ₃ = 3, respectively. The system equations for recipe A are given by

$$ \begin{aligned} x_1(k) & = \max(x_1(k-1)+d_1,u(k))\;, \\ x_2(k) & = \max(x_1(k)+d_1, x_2(k-1)+d_2) \\ & = \max(x_1(k-1)+2d_1, x_2(k-1)+d_2,u(k)+d_1)\;, \\ x_3(k) & = \max(x_2(k)+d_2, x_3(k-1)+d_3) \\ & = \max(x_1(k-1)+2d_1+d_2, x_2(k-1)+2d_2, x_3(k-1)+d_3,u(k)+d_1+d_2)\;, \\ y(k) & = x_3(k)+d_3\;, \end{aligned} $$

leading to the system matrices for recipe A:

$$ A^{(1)} = \left[\begin{array}{ccc} d_1 & \varepsilon & \varepsilon \\ 2d_1 & d_2 & \varepsilon \\ 2d_1 + d_2 & 2d_2 & d_3 \end{array}\right]\;\;,\;\;\; B^{(1)} = \left[\begin{array}{c} 0 \\ d_1 \\ d_1 + d_2 \end{array}\right]\;\;,\;\;\; C^{(1)} = \left[\begin{array}{ccc} {\varepsilon} & {\varepsilon} & d_3 \end{array}\right]. $$

Similarly we derive for recipe B:

$$ A^{(2)} = \left[\begin{array}{ccc} d_1 & 2d_2 & {\varepsilon} \\ {\varepsilon} & d_2 & {\varepsilon} \\ 2d_1 & d_1 + 2d_2 & d_3 \end{array}\right]\;\;,\;\;\; B^{(2)} = \left[\begin{array}{c} d_2 \\ 0 \\ d_1 + d_2 \end{array}\right]\;\;,\;\;\; C^{(2)} = \left[\begin{array}{ccc} {\varepsilon} & {\varepsilon} & d_3 \end{array}\right] \;, $$

and for recipe C:

$$ A^{(3)} = \left[\begin{array}{ccc} d_1 & {\varepsilon} & {\varepsilon} \\ 2d_1 + d_3 & d_2 & 2d_3 \\ 2d_1 & {\varepsilon} & d_3 \end{array}\right]\;\;,\;\;\; B^{(3)} = \left[\begin{array}{c} 0 \\ d_1 + d_3 \\ d_1 \end{array}\right]\;\;,\;\;\; C^{(3)} = \left[\begin{array}{ccc} {\varepsilon} & d_2 & {\varepsilon} \end{array}\right]. $$

The switching probability from one recipe to the next one is assumed to be given by:

$$ \begin{array}{l} P[L(k)=1|1,x(k-1),u(k),v(k)] = 0.64 , \\ P[L(k)=2|1,x(k-1),u(k),v(k)] = 0.18 , \\ P[L(k)=1|2,x(k-1),u(k),v(k)] = 0.18 , \\ P[L(k)=2|2,x(k-1),u(k),v(k)] = 0.64 , \\ P[L(k)=1|3,x(k-1),u(k),v(k)] = 0.18 , \\ P[L(k)=2|3,x(k-1),u(k),v(k)] = 0.18 , \\ P[L(k)=3|1,x(k-1),u(k),v(k)] = 0.18 , \\ P[L(k)=3|2,x(k-1),u(k),v(k)] = 0.18 , \\ P[L(k)=3|3,x(k-1),u(k),v(k)] = 0.64 , \end{array} $$

(4)

which means that if we have a specific recipe for product k, then the probability of having the same recipe for product k + 1 is 64%, and the probability of a switching to each other recipe is 18%.

Now define

$$ \begin{aligned} S_1 &= \left[ 1 \; 0 \; \ldots \;0 \right]^T & s_1 &= 2 & {\preceq}_1 \equiv \leq \\ S_2 &= \left[-1 \;0 \; \ldots \; 0 \right]^T & s_2 &= -2 & {\preceq}_2 \equiv < \\[2mm] \alpha_{1,1} &= \left[-0.46 \; 0 \; \ldots \; 0 \right]^T & \beta_{1,1} &= 1.10 \\ \alpha_{1,2} &= \left[ 0 \; 0 \; \ldots \; 0 \right]^T & \beta_{1,2} &= 0.18 \\ \alpha_{2,1} &= \left[ 0.46 \; 0 \; \ldots \; 0 \right]^T & \beta_{2,1} &= -0.28 \\ \alpha_{2,2} &= \left[ 0 \; 0 \; \ldots \; 0 \right]^T & \beta_{2,2} &= 0.18 \\ \alpha_{3,1} &= \left[ 0 \; 0 \; \ldots \; 0 \right]^T & \beta_{3,1} &= 0.18 \\ \alpha_{3,2} &= \left[ 0 \; 0 \; \ldots \; 0 \right]^T & \beta_{3,2} &= 0.64 \end{aligned} $$

then the SMPL system can be written in the form of Definitions 1, 2 and Remark 1.

Example 5

(Production system II) Now consider the production system of Example 4, but assume that the products B and C are equivalent, but are produced using different recipes (so M ₂-M ₁-M ₃ for B and M ₁-M ₃-M ₂ for C). This means that if we need to produce a product B/C we can choose the recipe (so either B or C. We therefore introduce an auxiliary binary control variable v(k) ∈ {0, 1} that can be used to choose between processing recipe B and C. The switching probability from one recipe to the next one is now given by:

$$ \begin{array}{l} P[L(k)=1|1,x(k-1),u(k),v(k)] = 0.64 , \\ P[L(k)=2|1,x(k-1),u(k),v(k)] = 0.36\,v(k) \\ P[L(k)=1|2,x(k-1),u(k),v(k)] = 0.18 , \\ P[L(k)=2|2,x(k-1),u(k),v(k)] = 0.64\,v(k) \\ P[L(k)=1|3,x(k-1),u(k),v(k)] = 0.18 , \\ P[L(k)=2|3,x(k-1),u(k),v(k)] = 0.64\,v(k) \\ P[L(k)=3|1,x(k-1),u(k),v(k)] = 0.36\,(1\!-\!v(k)) , \\ P[L(k)=3|2,x(k-1),u(k),v(k)] = 0.64\,(1\!-\!v(k)) , \\ P[L(k)=3|3,x(k-1),u(k),v(k)] = 0.64\,(1\!-\!v(k)) . \\ \end{array}$$

(5)

Note that for any v(k) ∈ {0, 1} there holds P[L(k) = 1|i, x(k − 1), u(k), v(k)] + P[L(k) = 2|i, x(k − 1), u(k), v(k)] + P[L(k) = 3|i, x(k − 1), u(k), v(k)] = 1 for i = 1, 2, 3.

Now define

$$\begin{aligned} S_1 &= \left[ 1 \; 0 \; \ldots \; 0 \right]^T & s_1 &= 1 & {\preceq}_1 \equiv \leq \\ S_2 &= \left[-1 \; 0 \; \ldots \; 0 \right]^T & s_2 &= -1 & {\preceq}_2 \equiv < \\[2mm] \alpha_{1,1} &= \left[0 \; 0 \; \ldots \; 0 \right]^T & \beta_{1,1} &= 0.64 \\ \alpha_{1,2} &= \left[0 \; 0 \; \ldots \; 0 \right]^T & \beta_{1,2} &= 0.18 \\ \alpha_{2,1} &= \left[0 \; 0 \; \ldots \; 0.36 \right]^T & \beta_{2,1} &= 0 \\ \alpha_{2,2} &= \left[0 \; 0 \; \ldots \; 0.64 \right]^T & \beta_{2,2} &= 0 \\ \alpha_{3,1} &= \left[0 \; 0 \; \ldots \; -0.36 \right]^T & \beta_{3,1} &= 0.36 \\ \alpha_{3,2} &= \left[0 \; 0 \; \ldots \; -0.64 \right]^T & \beta_{3,2} &= 0.64 \end{aligned}$$

then the SMPL system can be written in the form of Definition 1, Definition 2 and Remark 1.

Remark 4

In the Examples 4 and 5 we have assumed sufficiently large internal buffers and negligible transportation times between the machines. Note however that we have done so to simplify the example; it is not a limitation in the theory.

3 Equivalence in classes of SMPL systems

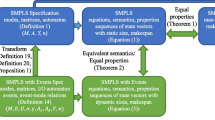
In this section we introduce an alternative class of SMPL systems, called type-2 SMPL systems, and we show that type-1 and type-2 SMPL systems are equivalent. Furthermore we will show that SMPL systems can be rewritten as piecewise affine systems or max-min-plus-scaling systems, two well-known classes of hybrid systems. The relations between the models are depicted in Fig. 5. In Example 6 all equivalent system descriptions will be computed for a type-1 SMPL model.

Fig. 5

Transformations and model classes with the proposition that states the relation

Definition 3

(van den Boom and De Schutter 2008b) A type-2 SMPL system is defined as follows: Consider the system (1) and (2) with n _L possible modes. The mode ℓ(k) = m if

$$ z(k) = \left[\ell(k-1) \; x^T(k-1) \; u^T(k) \; v^T(k) \; d(k)\right]^T \in \Omega_{m} \subset {\mathbb{R}}^{n_z} $$

for $m=1,\ldots,{n_{L}}$, where d(k) ∈ [0, 1] is a uniformly distributed stochastic scalar signal, and where Ω _m is a union of polyhedra, so $\Omega_m={\cup}_{j=1}^{n_m} \Omega_{m,j}$ in which $\{\Omega_{m,j}\}_{\begin{array}{c} m=1,\ldots,{n_{L}} \\ j=1,\ldots,n_m \end{array}}$ is a polyhedral partition.

Remark 5

The polyhedral partion $\{\Omega_{m,j}\}_{\begin{array}{c} m=1,\ldots,{n_{L}} \\ j=1,\ldots,n_m \end{array}}$ can be parameterized by

$$ \Omega_{m,j} = \{\; z(k) \;|\; R_{m,j} \,z(k)\, {\preceq}_{m,j}\, r_{m,j}\;\} \;\;,\;\;\mathrm{for}\;\;j=1,\ldots,n_m $$

where ${\preceq}_i$ is a vector where the entries stand for either ≤ or <.

A type-1 SMPL model is easy for modeling where we consider the probabilities of switching from one mode to another. The model gives a lot of physical insight into the system and is usually more intuitive for the user. A type-2 SMPL model is signal-based and the properties of probabilities of switching are translated into the properties of a stochastic signal. The fact that type-2 SMPL models are signal-based makes that this type of SMPL system can easily be translated into another model in one of the other classes of hybrid systems (see Propositions 3 and 4).

Proposition 1

The class of type-1 SMPL systems and the class of type-2 SMPL systems are equivalent in the sense of input-state-output-mode behavior.

Proof

Type-1 SMPL → type-2 SMPL   Consider a type-1 SMPL system of the form (1) and (2) as given in Definition 2. The probability P is given by

$$ P[L(k)=\ell(k)|w(k)] = \alpha^T_{\ell(k),i}\,w(k) + \beta_{\ell(k),i}\;,\;\;\text{if}\;\;w(k) \in \Gamma_{i} $$

(6)

Now define the function η such that

$$ \begin{aligned} \eta(m,w(k)) = \begin{cases} {\displaystyle}\mathop\sum\limits_{\ell(k)=1}^{m} P[L(k)=\ell(k)|w(k)] & \mathrm{for} \;m=1,\ldots,{n_{\small L}} \\ 0 & \mathrm{for} \;m=0 \end{cases} \end{aligned} $$

Furthermore we observe that $\eta({n_{\small L}} ,w(k)) = \sum_{j=\ell(k)}^{{n_{\small L}} } P[L(k)=\ell(k)|w(k)] = 1$.

For w(k) ∈ Γ _i we find

$$ \eta(m,w(k)) = {\displaystyle}\bar{\alpha}^T_{m,i}\,w(k) + \bar{\beta}_{m,i} $$

(7)

where $\bar{\alpha}_{0,i} = 0$ and $\bar{\beta}_{0,i} = 0$ and $\bar{\alpha}_{m,i} = \sum_{j=1}^{m} \alpha_{j,i}$ and $\bar{\beta}_{m,i} = \sum_{j=1}^{m} \beta_{j,i}$ for $m=1,\ldots,{n_{L}}$.

Now introduce a uniformly distributed stochastic scalar signal d(k) ∈ [0, 1]. Let

$$ L(k) = m \;\;\;\;\;\text{if}\;\;\;\;\;\eta(m-1,w(k)) < d(k) \leq \eta(m,w(k)) $$

(8)

Denote P _d [L(k) = m|w(k)] as the probability that L(k) = m according to Eq. 8. For a uniformly distributed d(k) and scalars a, b with 0 ≤ a ≤ b ≤ 1 there holds P[a < d(k) < b] = b − a . Using this we find that

$$ \begin{aligned} P_d[L(k)=m|w(k)] &= P\Big[\eta(m-1,w(k)) < d(k) \leq \eta(m,w(k)]\Big) \\ &= \eta(m,w(k)) - \eta(m-1,w(k))\\ &= P[L(k)=m|w(k)) \end{aligned} $$

which is equal to the probability (6) in the type-1 SMPL system. If we combine this result with Eq. 8 we obtain

$$ \ell(k) = m \;\;\;\;\;\text{if} \;\;\;\;\; \left[\begin{array}{c} \eta(m-1,w(k))-d(k) < 0\\ -\eta(m,w(k)) +d(k) \leq 0 \end{array}\right] $$

(9)

Note that η : (m, w(k)) → η(m, w(k)) is an affine function if w(k) ∈ Γ _i (or equivalently $S_i\,w(k) - s_i\, {\preceq}^s_i\, 0$), and so we can rewrite Eq. 9 as

$$ \ell(k) = m \;\;\;\;\;\text{if }\; \exists i \;\;\text{such that}\;\;\;\; \left[\begin{array}{c} \bar{\alpha}^T_{m-1,i}\,w(k) + \bar{\beta}_{m-1,i}-d(k)\\[3pt] -\bar{\alpha}^T_{m ,i}\,w(k) - \bar{\beta}_{m ,i} +d(k) \\ S_i\,w(k) - s_i \end{array}\right]{\preceq}\, 0 $$

Define

$$ R_{m,i} = \left[\begin{array}{rr} \bar{\alpha}^T_{m-1,i} & -1 \\[1mm] -\bar{\alpha}^T_{m ,i} & 1 \\ S_{i} & 0 \end{array}\right]\>, r_{m,i} = \left[\begin{array}{r} \bar{\beta}_{m-1,i} \\[1mm] -\bar{\beta}_{m ,i} \\ -s_{i} \end{array}\right]\>, {\preceq}^r_{m,i} = \left[\begin{array}{c} < \\ \leq \\ {\preceq}^s_i \end{array}\right] $$

then with $z^T(k) = \left[w^T(k) \; d^T(k)\right]$ we find that

$$ \ell(k) = m \;\;\; \text{if}\;\;R_{m,i}\, z(k)\, {\preceq}_{m,i}^r\, r_{m,i} \;,\;i=1,\ldots,n_s, $$

which is equal to the switching mechanism of a type-2 SMPL system.

Type-2 SMPL → type-1 SMPL   Consider a type-2 SMPL system, so

$$ L(k) = m \;\;\;\text{if}\;\;\; R_{m,t}\,z(k)\, {\preceq}^r_{m,t}\, r_{m,t} $$

for some index t. Define R _m,t,1 and R _m,t,2 such that

$$ R_{m,t}\,z(k) = R_{m,t}\,\left[\begin{array}{c}w(k) \\ d(k)\end{array}\right] = R_{m,t,1}\,w(k) + R_{m,t,2}\,d(k)\, {\preceq}^r_{m,t}\, r_{m,t} $$

(10)

Note that d(k) ∈ [0, 1] is a scalar. Let d _m,t,max(w(k)) be the maximum value of d such that Eq. 10 is satisfied, and let d _m,t,min(w(k)) be the minimum value of d such that Eq. 10 is satisfied. If for some w(k) there exists no d(k) ∈ [0, 1] such that Eq. 10 is satisfied, we define d _m,t,max(w(k)) = d _m,t,min(w(k)) = 0. Finding d _m,t,max(w(k)) and d _m,t,min(w(k)) can be done using a linear programming algorithm, which means that d _m,t,max(w(k)) and d _m,t,min(w(k)) are piecewise affine in w(k) (Borelli 2003). So there exist matrices S _i,m,t , vectors s _i,m,t , p _m,t,i,max, p _m,t,i,min and scalars q _m,t,i,max and q _m,t,i,min, such that

$$ \begin{aligned} d_{m,t,\max}(w(k)) & = p^T_{m,t,i,\max}\,w(k) + q_{m,t,i,\max} \\ d_{m,t,\min}(w(k)) & = p^T_{m,t,i,\min}\,w(k) + q_{m,t,i,\min} \end{aligned} $$

if $S_{i,m,t}\,w(k){\preceq}^s_{i,m,t}\, s_{i,m,t}$ for i = 1, ..., M _m,t , t = 1, ..., n _m and $m=1,\ldots,{n_{L}}$.

The probability that ℓ(k) = m, given w(k) can be written as

$$ \begin{aligned} P[L(k)=m|w(k)] & = P[d_{m,t,\min}(w(k)) \leq d(k) \leq d_{m,t,\max}(w(k))] \\ & = d_{m,t,\max}(w(k)) - d_{m,t,\min}(w(k)) \\ & = \left(p^T_{m,t,i,\max}-p^T_{m,t,i,\min}\right)\,w(k) + (q_{m,t,i,\max}-q_{m,t,i,\min}) \end{aligned} $$

for $S_{i,m,t}\,w(k){\preceq}^s_{i,m,t}\, s_{i,m,t}$ for i = 1, ..., M _m,t , t = 1, ..., n _m and m = 1, ..., n _L . This is equal to the switching mechanism of a type-1 SMPL system.□

Proposition 2

A type-2 SMPL system can always be rewritten in the form:

$$x(k) = \bar{A}^{(\kappa(k))} \otimes x(k-1) \oplus \bar{B}^{(\kappa(k))} \otimes u(k) $$

(11)

$$y(k) = \bar{C}^{(\kappa(k))} \otimes x(k) $$

(12)

such that the mode κ(k) = m if

$$ z(k) = \left[\kappa(k-1) \; x^T(k-1) \; u^T(k) \; v^T(k) \; d(k)\right]^T \in \bar{\Omega}_{m} $$

(13)

where d(k) ∈ [0, 1] is a uniformly distributed stochastic scalar signal, and where $\{\bar{\Omega}_m\}_{m=1,\ldots,{n_\kappa}}$ is a polyhedral partition and $\bar{\Omega}_{m}$ can be written as

$$ \bar{\Omega}_{m} = \{\; z(k) \;|\; R_{m} \,z(k)\, {\preceq}^r_m\, r_{m}\;\} $$

Proof

Consider the type-2 SMPL system of Definition 3, and introduce a new numbering

$$ \kappa(\ell,j)= j + \sum\limits_{i=1}^{\ell-1} n_{i},\;\;\mathrm{for}\;\; \ell=1,\ldots,{n_{\small L}} \;\; \text{and}\;\; j=1,\ldots,n_\ell $$

If we define

$$ \bar{\Omega}_{\kappa(\ell,j)} = \Omega_{\ell,j} $$

and

$$ \begin{aligned} \bar{A}^{(\kappa(\ell,j))} &= A^{(\ell)} \\ \bar{B}^{(\kappa(\ell,j))} &= B^{(\ell)} \\ \bar{C}^{(\kappa(\ell,j))} &= C^{(\ell)} \end{aligned} $$

for $\ell=1,\ldots,{n_{L}}$, j = 1, ..., n _ℓ, then we obtain a system of the form (11)–(13).□

Remark 6

For the form of Definition 3 every region Ω_ℓ(k) for mode ℓ(k) is a union of polyhedra. For the form of Proposition 2 every region $\bar{\Omega}_{\kappa(k)}$ for mode κ(k) is a polyhedron. The consequence is that we usually need more modes for the latter form than for the original form.

Definition 4

An SMPL system is structurally finite if for any finite (x(k − 1), u(k)) we have that x(k) and y(k) are finite for all $\ell(k-1)\in \{1,\ldots,{n_{ L}} \}$ and any d(k) ∈ [0, 1].

Lemma 1

A SMPL system is structurally finite if and only if the matrix

$$ H^{(\ell)} = \left[\begin{array}{ccc} A^{(\ell)} & B^{(\ell)} & \varepsilon \\ \varepsilon & \varepsilon & C^{(\ell)} \end{array}\right] $$

(14)

is row-finite for all $\ell=1,\ldots,{n_{L}}$ (i.e. for each ℓ every row of the matrix H ^(ℓ) has at least one finite entry).

Proof

Part 1: (if) :

Let x(k − 1) and u(k) be finite. Now

$$ \begin{aligned} x_i(k) & = \max\limits_{j} \left( \left[A^{(\ell)} \; B^{(\ell)}\right]_{i,j}+\left[\begin{array}{c}x(k-1)\\u(k)\end{array}\right]_j\right) \\ y_s(k) & = \max\limits_t \left( [C^{(\ell)}]_{s,t} + x_t(k) \right) \end{aligned} $$

If all elements of x(k − 1) and u(k) are finite and every row of H ^(ℓ) has at least one finite elements, we will find that the elements x _i (k), i = 1, ..., n _x are finite as well. Similarly for finite x(k) we find finite elements y _s (k), s = 1, ..., n _y .

Part 2: (only if) :

We will prove the second part of lemma by contradiction. First, define

$$\begin{array}{rll} \omega(k) &=& \left[\begin{array}{c}x(k) \\ y(k) \end{array}\right] \in {\mathbb{R}}^{n_\omega}={\mathbb{R}}^{n_x+n_y},\\ \theta(k)&=& \left[\begin{array}{c} x(k-1) \\ u(k) \\ x(k) \end{array}\right]\in {\mathbb{R}}^{n_\theta}={\mathbb{R}}^{2n_x+n_y}\end{array}$$

(15)

then system equations (1) and (2) can be written as

$$ \omega(k) = H^{(\ell)} (k) {\otimes}\theta(k) \;\;\;\mathrm{for}\;\; R_\ell\,z(k)\, {\preceq}^r_\ell\, r_\ell $$

and finiteness of x(k) and u(k) implies finiteness of θ(k).

Now suppose that for a given ℓ the i-th row of H ^(ℓ) has no finite entries, so $[H^{(\ell)}]_{i,j}=\varepsilon$, ∀ j. Then $\omega_i(k) = \max\Big( [H^{(\ell)}]_{i,j} (k) + \theta_j(k) \Big) = \varepsilon$, which means that the system is not structurally finite. We may conclude that the system is structurally finite if and only if H ^(ℓ) is row-finite for all ℓ = 1, ..., n _L .□

Remark 7

(van den Boom and De Schutter 2008a) Note that physical systems are typically structurally finite.

Next we will show that SMPL systems can be rewritten as piecewise affine systems or max-min-plus-scaling systems. The following definition is an extension of Sontag (1981):

Definition 5

Type-d piecewise affine systems are described by

$$ \begin{array}{r@{\,}c@{\,}ll} x(k) & = & A_i x(k-1) + B_i u(k) + f_i \\ y(k) & = & C_i x(k) + D_i u(k) + g_i \end{array} \ \ \mathrm{for} \begin{bmatrix} x(k-1) \\ u(k) \\ d(k) \end{bmatrix} \in \Omega_i, $$

(16)

where $f_i \in {\mathbb{R}}^{n_x \times 1}$, $g_i \in {\mathbb{R}}^{n_y \times 1}$, $A_i \in {\mathbb{R}}^{n_x \times n_x}$, $B_i \in {\mathbb{R}}^{n_x \times n_u}$, $C_i \in {\mathbb{R}}^{n_y \times n_x}$, $D_i \in {\mathbb{R}}^{n_y \times n_u}$, for i = 1, ..., N where the signal d(k) ∈ [0, 1] is a uniformly distributed stochastic scalar signal and {Ω _i } _{i = 1,...,N} is a polyhedral partition of ${\mathbb{R}}^{n_x+n_u+1}$.

Proposition 3

Every structurally finite SMPL system of type-2 can be written as type-d piecewise affine system.

Proof

Consider a structurally finite SMPL system of type-2 with state and output equations (1) and (2) where ℓ(k) = m if z(k) satisfies $R_m \,z(k)\, {\preceq}^r_m\, r_m$. Let ω(k) and θ(k) be given by Eq. 15. The SMPL system is structurally finite, which means that if θ is finite, then ω(k) will be finite. Let $h^{(\ell)}_{i,p} = [H^{(\ell)}]_{i,p}$ and define the set

$$ \begin{aligned} \Phi = \Big\{&(\ell_t,p_{1,t},p_{2,t},\ldots,p_{n_\omega,t})\Big|\; \ell_t \in\{0,\ldots,{n_{\small L}} \},\; p_{i,t} \in\{1,\ldots,n_\theta\}, \\ & i=1,\ldots,n_\omega,\;\exists \omega(k), \;\;\text{such that}\;\omega_{i}(k) = \max_p \left( h^{(\ell_t)}_{i,p} + \theta_p(k)\right) = h^{(\ell_t)}_{i,p_{i,t}} + \theta_{p_{i,t}}(k) \Big\} \end{aligned} $$

Define³ n _tot = #Φ, then $n_{\mathrm{tot}} \leq {n_{\small L}} \,n_{\omega}^{n_{\theta}}$. Note that $\omega_{i}(k) = \max_p ( h^{(\ell_t)}_{i,p} + \theta_p(k)) = h^{(\ell_t)}_{i,p_{i,t}} + \theta_{p_{i,t}}(k)$ is equivalent to

$$ h^{(\ell_t)}_{i,p_{i,t}} + \theta_{p_{i,t}}(k) \geq h^{(\ell_t)}_{i,p} + \theta_{p}(k) \;\;\;\mathrm{for}\;\; p = 1,\ldots,n_\omega,\; p = 1,\ldots,n_\theta $$

By collecting all entries for p = 1, ..., n _ω , j = 1, ..., n _θ we obtain that

$$ \omega(k) = H^{(t)}\,\theta(k) + h^{(t)} \;\;\;\; \;\;\text{if} \;\;\; E^{(t)}\,\theta(k) \leq e^{(t)} \;\;\;\; \text{and} \;\;\; R_{\ell_t} \,z(k)\, {\preceq}_{\ell_t}\, r_{\ell_t} $$

(17)

where, for i = 1, ..., n _ω , j = 1, ..., n _θ , and t = 1, ..., n _tot, we have:

$$ \begin{aligned} {[}H^{(t)}]_{i,j} &= \begin{cases} 1 & \mathrm{for}\;\; j=p_{i,t} \\ 0 & \text{otherwise} \end{cases} \\[2mm] [h^{(t)}]_i &= h^{(\ell_t)}_{i,p_{i,t}} \\[2mm] [E^{(t)}]_{(i-1)n_\theta+j,l} &= \begin{cases} 1 & \mathrm{for}\;\; l=j \;\; \text{and} \;\; j \ne p_{i,t} \\ -1 & \mathrm{for}\;\; l=p_{i,t}\;\; \text{and} \;\; j \ne p_{i,t} \\ 0 & \text{otherwise} \end{cases} \\[2mm] [e^{(t)}]_{(i-1)n_\theta+j} &= h^{(\ell_t)}_{i,p_{i,t}}-h^{(\ell_t)}_{i,j} \end{aligned} $$

(Note that in fact the zero rows of [E ^(t) e ^(t)] can be removed.) It is clear that from Eq. 17 we can derive the matrices A _i , B _i , C _i , D _i and vectors f _i and g _i such that we obtain a description of the form Eq. 16. The polyhedra are described by the inequalities E ^(t) θ(k) ≤ e ^(t) and $R_{\ell_t} \,z(k)\, {\preceq}^r_{\ell_t}\, r_{\ell_t}$. The total number of different polyhedra is less than or equal to $N={n_{\small L}} \,n_\omega^{n_\theta}$.□

Definition 6

A max-min-plus-scaling (MMPS) expression f of the variables x ₁, ..., x _n is defined by the syntax⁴

$$ f := x_i | \alpha | \max(f_k,f_l) | \min(f_k,f_l) | f_k + f_l | \beta f_k \enspace $$

(18)

with i ∈ {1, 2, ..., n}, α, β ∈ ℝ, and where f _k , f _l are again MMPS expressions.

Definition 7

Consider systems that can be described by

$$ x(k) = {f_x}(x(k-1),u(k),d(k)) $$

(19)

$$ y(k) = {f_y}(x(k-1),u(k),d(k)), $$

(20)

where the components of f _x , f _y are MMPS expressions in terms of the components of x(k), u(k), and the auxiliary variables d(k), which are all real-valued. Such systems will be called max-min-plus-scaling (MMPS) systems. If in addition, we have a condition of the form

$$ {f_\mathrm{c}}(x(k-1),u(k),d(k))\, {\preceq}\, c(k) , $$

where the components of f _c are MMPS expressions and ${\preceq}_i$ is a vector where the entries stand for either ≤ or <, we speak about constrained MMPS systems.

Proposition 4

Every structurally finite SMPL system of type-2 can be written as a constrained MMPS system provided that the variables x(k − 1) and u(k) are bounded.

Note that this proposition is a direct consequence of the equivalence between the class of type-d piecewise affine systems and MMPS systems (see Heemels et al. 2001). However we will provide a direct proof here that transfers SMPL systems directly into MMPS systems.

Proof

Consider a structurally finite SMPL system of type-2 with state and output equations (1) and (2) where ℓ(k) = m if z(k) satisfies $R_m \,z(k)\, {\preceq}^r_m\, r_m$. Define ω(k), θ(k) and H ^(ℓ(k)) as in Eqs. 15 and 14. Then

$$ \omega(k) = H^{(\ell(k))} {\otimes}\theta(k) \;\;\;\mathrm{for}\;\; R_{\ell(k)}\,z(k)\, {\preceq}^r_\ell\, r_{\ell(k)} $$

so

$$ \omega_i(k) = \max\limits_j \Big(m_{i,j}^{(\ell(k))} + \theta_j(k)\Big) \;\;\;\mathrm{for}\;\; R_{\ell(k)}\,z(k)\, {\preceq}^r_\ell\, r_{\ell(k)}. $$

Now define the (binary) variables δ _m (k) ∈ {0, 1}, for m = 1, ..., n _L such that

$$ \left[\delta_m(k)=1\right] \Leftrightarrow \left[\>R_m\,z(k) {\preceq}^r_m r_m\right] \Leftrightarrow [\ell(k)=m] $$

(21)

Since x(k) and u(k) are bounded, and d ∈ [0, 1] we find that there exist bounded sets ${\mathcal{E}}$ and ${\mathcal{Z}}$ such that $\theta(k) \in {\mathcal{E}}$ and $z(k) \in {\mathcal{Z}}$. Let

$$ \rho^*_m = \max\limits_{z(k) \in {\mathcal{Z}}} \,R_m\,z(k) - r_m $$

then following Bemporad and Morari (1999, p. 5) and using the fact that the sets $\{z(k)|R_m\,z(k)\, {\preceq}^r_m\, r_m\}$ are non-overlapping, we can rewrite Eq. 21 as

$$ R_m\,z(k) - r_m \preceq ^r_m \rho^*_m\Big(1-\delta_m(k)\Big) $$

(22)

$$ \sum\limits_{m=1}^{n_{L}} \delta_m(k) = 1 $$

(23)

Note that constraints (22) and (23) are linear (and thus also MMPS) constraints. Define

$$ \sigma^* =\Big[\max\limits_m \> \max\limits_i \> \max\limits_{ \scriptsize \theta(k) \in {\mathcal{E}}} \> \max\limits_j \, \left( h^{(m)}_{i,j} + \theta_j(k) \right)\Big] - \Big[\min\limits_m \> \min\limits_i \> \min\limits_{ \scriptsize \theta(k) \in {\mathcal{E}}} \> \max\limits_j \, \left( h^{(m)}_{i,j} + \theta_j(k) \right)\Big] $$

(note that σ ^* is finite because the system is structurally finite and x(k − 1) and u(k) are bounded), then the system is described by the following equation

$$\omega_i(k) = \max_{m,j} \Big( h^{(m)}_{i,j} +\theta_j(k) - (1-\delta_m(k))\sigma^* \Big) $$

(24)

subject to Eqs. 22 and 23.

Indeed, if the SMPL system is in mode ℓ(k) = m, then δ _m (k) = 1 and δ _q (k) = 0 for all q ≠ m, and so Eq. 24 reduces to

$$ \omega_i(k) = \max\limits_{j} \Big( h^{(m)}_{i,j} +\theta_j(k)\Big) $$

Note that Eq. 24 is an MMPS function in the variables θ and δ. Hence, we have proven that a type-2 SMPL system, with bounded states and inputs, can be rewritten as a constrained MMPS system.□

Remark 8

Recall that the state x(k) and input u(k) denote the time instant at which a state event or an input event occurs for the kth time, respectively. This means that both state and input are non-decreasing and grow unboundedly. In Section 4 we will introduce a shifted system, in which we consider the deviations of the state and input signals with respect to a reference signal. Therefore in a shifted system the shifted state and shifted input u(k) can be bounded and can thus easily be transformed into a type-d MMPS system.

In the following example we will illustrate some of the equivalences.

Example 6

(Equivalent system descriptions) Consider a type-1 SMPL system

$$ \begin{aligned}[b] x(k) &= \Big(A^{(\ell(k))} {\otimes}x(k-1)\Big) {\oplus}\Big(B^{(\ell(k))} {\otimes}u(k)\Big) ~~ \mathrm{for} ~~\ell(k)=1,2 \\ y(k) &= x(k) \end{aligned} $$

(25)

with x(k), u(k), y(k) ∈ ℝ _ε and⁵

$$ \begin{aligned} A^{(1)} & = 1 & B^{(1)} &= 0.2 & C^{(1)} &= 0\\ A^{(2)} & = -0.1 & B^{(2)} &= 0.1 & C^{(2)} &= 0 \end{aligned} $$

and

$$ \begin{aligned} P[L(k)=1|1,x(k-1),u(k)] & = 0 \\ P[L(k)=2|1,x(k-1),u(k)] & = 1 \\ P[L(k)=1|2,x(k-1),u(k)] & = \begin{cases} 1 & \mathrm{for} \;\;\;x(k-1) < -1 \\[-1mm] -x(k-1) & \mathrm{for} \;\;\;-1 \leq x(k-1) \leq 0 \\[-1mm] 0 & \mathrm{for} \;\;\;x(k-1) > 0 \end{cases} \\ P[L(k)=2|2,x(k-1),u(k),v(k)] & = \begin{cases} 0 & \mathrm{for} \;\;\;x(k-1) <-1 \\[-1mm] 1+x(k-1) & \mathrm{for} \;\;\;-1 \leq x(k-1) \leq 0 \\[-1mm] 1 & \mathrm{for} \;\;\;x(k-1) >0\;. \end{cases} \end{aligned} $$

Note that 0 ≤ P[L(k) = i|j, x(k − 1), u(k)] ≤ 1, for i, j = 1, 2, and

$$\begin{aligned} P[L(k)=1|1,x(k-1),u(k)] + P[L(k)=2|1,x(k-1),u(k)]= 1\;, \\ P[L(k)=1|2,x(k-1),u(k)] + P[L(k)=2|2,x(k-1),u(k)]= 1\;. \end{aligned}$$

Define the vector $w(k) = \left[\ell(k-1) \; x(k-1) \; u(k)\right]^T$. The probability P[L(k) = ℓ(k)|w(k)] can be written as a piecewise function:

$$ P[L(k)=\ell(k)|w(k)] = \alpha^T_{\ell(k),i}\,w(k) + \beta_{\ell(k),i}\;, \;\;\;\;\text{if}\;\;S_{i}\,w(k)\, {\preceq}^s_i\, s_{i}\;,\;\;\mathrm{for} \;i=1,\ldots,4 $$

where

$$ \begin{array}{lrlrlrl} i=1 & S_{1} &= \left[ 1 \; 0 \; 0 \right] & s_{1} &= [1.5] & {\preceq}^s_1 &= [\leq]\\[1mm] & \alpha^T_{1,1} &= \left[ 0 \; 0 \; 0 \right] & \beta_{1,1} &= 0 \\[1mm] & \alpha^T_{2,1} &= \left[ 0 \; 0 \; 0 \right] & \beta_{2,1} &= 1 \\[1mm] i=2 & S_{2} &= \left[\begin{array}{rrr}-1 & 0 & 0 \\ 0 & -1 & 0 \end{array}\right] & s_{2} &= \left[\begin{array}{c}-1.5 \\ 0 \end{array}\right] & {\preceq}^s_2 &= \left[\begin{array}{c} < \\ < \end{array}\right]\\[1mm] & \alpha^T_{1,2} &= \left[ 0 \; 0 \; 0 \right] & \beta_{1,2} &= 0 \\[1mm] & \alpha^T_{2,2} &= \left[ 0 \; 0 \; 0 \right] & \beta_{2,2} &= 1 \\[1mm] i=3 & S_{3} &= \left[\begin{array}{rrr}-1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -1 & 0 \end{array}\right] & s_{3} &= \left[\begin{array}{c}-1.5 \\ 0 \\ 1 \end{array}\right] & {\preceq}^s_3 &= \left[\begin{array}{c} < \\ \leq \\ \leq \end{array}\right]\\[1mm] & \alpha^T_{1,3} &= \left[ 0 \; -1 \; 0 \right] & \beta_{1,3} &= 0 \\[1mm] & \alpha^T_{2,3} &= \left[ 0 \; 1 \; 0 \right] & \beta_{2,3} &= 1 \\[1mm] i=4 & S_{4} &= \left[\begin{array}{rrr}-1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right] & s_{4} &= \left[\begin{array}{c}-1.5 \\ -1 \end{array}\right] & {\preceq}^s_4 &= \left[\begin{array}{c} < \\ < \end{array}\right]\\[1mm] & \alpha^T_{1,4} &= \left[ 0 \; 0 \; 0 \right] & \beta_{1,4} &= 1 \\[1mm] & \alpha^T_{2,4} &= \left[ 0 \; 0 \; 0 \right] & \beta_{2,4} &= 0 \\[1mm] \end{array} $$

Note that the inequality ℓ(k − 1) ≤ 1.5 represents the case ℓ(k − 1) = 1, and the inequality − ℓ(k − 1) < − 1.5 represents the case ℓ(k − 1) = 2.

The presented system is a type-1 SMPL system. We will now rewrite this system as a type-2 SMPL system. Consider a uniformly distributed stochastic scalar signal d(k) ∈ [0, 1], and define $z(k) = \left[w^T(k) \; d(k) \right]^T$.

First we discuss the case ℓ(k − 1) = 2. Let ℓ(k) = 1 if x(k − 1) + d(k) < 0 and let ℓ(k) = 2 if x(k − 1) + d(k) ≥ 0. This defines the regions

$$ \begin{aligned} \Omega_{1,1} &= \{ z(k)\>|\>\ell(k-1) > 1.5, x(k-1)+d(k) < 0\}, \\ \Omega_{2,1} &= \{ z(k)\>|\>\ell(k-1) > 1.5, x(k-1)+d(k) \geq 0\} \end{aligned} $$

For the case ℓ(k − 1) = 1, we always have ℓ(k) = 2, and so

$$ \Omega_{2,2} = \{ z(k)\>|\>\ell(k-1)\leq 1.5 \}$$

Now we can compute the matrices for i = 1, 2:

$$ \begin{aligned} R_{1,1} = \left[\begin{array}{rrrr}\; -1& 0& 0& \;0\\ 0& 1& \;0& 1 \end{array}\right] & r_{1,1}= \left[\begin{array}{ccc}-1.5 \\ 0 \end{array}\right] & {\preceq}^r_{1,1} &= \left[\begin{array}{c} \leq \\ < \end{array}\right]\\[1mm] \\ & \\[-3mm] R_{2,1} = \left[\begin{array}{rrrr}\; -1& 0& 0& \;0\\ 0&-1& \;0&-1 \end{array}\right] & r_{2,1}= \left[\begin{array}{ccc}-1.5 \\ 0 \end{array}\right] & {\preceq}^r_{2,1} &= \left[\begin{array}{c} \leq \\ \leq \end{array}\right]\\[1mm] \\ & \\[-3mm] R_{2,2} = \left[\begin{array}{rrrr}\;\;1& 0& 0& 0 \end{array}\right] & r_{2,2}= \left[ 1.5 \right] & {\preceq}^r_{2,2} &= \left[ < \right]\\[1mm] \end{aligned} $$

To be able to recast the SMPL system as a type-d piecewise affine system using Proposition 3, we will rewrite this type-2 SMPL system as follows. We introduce 3 modes κ = 1, 2, 3, with

$$ \begin{aligned}[b] x(k) &= \max\Big(x(k-1)+1,u(k)+0.2\Big) \mathrm{~for~} \kappa(k)=1 \\ x(k) &= \max\Big(x(k-1)-0.1,u(k)+0.1\Big) \mathrm{~for~} \kappa(k)=2,3 \\ y(k) &= x(k) \end{aligned} $$

(26)

We define

$$\begin{aligned} \bar{R}_1 &= \bar{R}_{1,1} & \bar{r}_1 &= \bar{r}_{1,1} & {\preceq}^{-}_1 &= {\preceq}_{1,1} \\ \bar{R}_2 &= \bar{R}_{2,1} & \bar{r}_2 &= \bar{r}_{2,1} & {\preceq}^{-}_2 &= {\preceq}_{2,1} \\ \bar{R}_3 &= \bar{R}_{2,2} & \bar{r}_3 &= \bar{r}_{2,2} & {\preceq}^{-}_3 &= {\preceq}_{2,2} \end{aligned}$$

and we obtain that the now mode κ(k) = m if

$$ \bar{z}(k) = \left[\kappa(k-1) \; x^T(k-1) \; u^T(k) \; d(k) \right]^T \in \bar{\Omega}_{m}$$

where

$$ \bar{\Omega}_{m} = \{\; \bar{z}(k) \;|\; \bar{R}_{m} \,\bar{z}(k) {\preceq}^{-}_m \bar{r}_{m}\;\} $$

Now it is straightforward to derive the type-d piecewise affine system: Note that

$$\begin{aligned} x(k) &= x(k\!-\!1)+1 & \!\!\!\!\text{if }& \kappa(k) \leq 1.5 ,\; x(k\!-\!1)+1 \geq u(k)+0.2 \\ x(k) &= u(k)+0.2 & \!\!\!\!\text{if }& \kappa(k) \leq 1.5 ,\; x(k\!-\!1)+1 < u(k)+0.2 \\ x(k) &= x(k\!-\!1)-0.1\!\! & \!\!\!\!\text{if }& \kappa(k) > 1.5 ,\; x(k\!-\!1)-0.1 \geq u(k)+0.1 \\ x(k) &= u(k)+0.1 & \!\!\!\!\text{if }& \kappa(k) > 1.5 ,\; x(k\!-\!1)-0.1 < u(k)+0.1 \end{aligned}$$

This translates into the following type-d piecewise affine system:

$$\begin{array}{llll} i=1: & x(k)= x(k-1)+1 & \textrm{if}\;\; & \bar{R}_{1}\,\bar{z}(k) \leq \bar{r}_{1} ,\; x(k\!-\!1)+0.8 \geq u(k) \\ i=2: & x(k)= u(k)+0.2 & \textrm{if}\;\; & \bar{R}_{1}\,\bar{z}(k) \leq \bar{r}_{1} ,\; x(k\!-\!1)+0.8 < u(k) \\ i=3: & x(k)= x(k-1)+1 & \textrm{if}\;\; & \bar{R}_{2}\,\bar{z}(k) \leq \bar{r}_{2} ,\; x(k\!-\!1)-0.2 \geq u(k) \\ i=4: & x(k)= x(k-1)+1 & \textrm{if}\;\; & \bar{R}_{3}\,\bar{z}(k) \leq \bar{r}_{3} ,\; x(k\!-\!1)-0.2 \geq u(k) \\ i=5: & x(k)= u(k)+0.1 & \textrm{if}\;\; & \bar{R}_{2}\,\bar{z}(k) \leq \bar{r}_{2} ,\; x(k\!-\!1)-0.2 < u(k) \\ i=6: & x(k)= u(k)+0.1 & \textrm{if}\;\; & \bar{R}_{3}\,\bar{z}(k) \leq \bar{r}_{3} ,\; x(k\!-\!1)-0.2 < u(k) \end{array}$$

We conclude that this system is a type-d piecewise affine system with 6 polyhedral regions.

Finally we rewrite the system as a constrained MMPS system. Assume the input is in the bounded set − 1 ≤ u(k) ≤ 2 and that the initial state is in the bounded set − 1 ≤ x(0) ≤ 1. Introduce the binary variables δ _m (k) ∈ {0, 1}, for m = 1, 2, 3 such that $\delta_m(k)=1 \;\;\Leftrightarrow \;\;\bar{R}_{m} \,\bar{z}(k)\, {\preceq}^{-}_m\, \bar{r}_{m}$. It is easy to derive that in that case x(k) for k ≥ 0 will be bounded:

$$ -1.1\!\leq\! x(k) \!\leq\! 2.2 \;.$$

We compute

$$ \rho^*_m = \max\limits_{\bar{z(k)} \in {\mathcal{Z}}} \,\bar{R}_m\,\bar{z}(k) - \bar{r}_m = -3.5$$

and

$$\begin{aligned} \sigma^* & = \left[\max\limits_m \> \max\limits_i \> \max\limits_{\theta(k) \in {\mathcal{E}}} \> \max\limits_j \, \left( h^{(m)}_{i,j} + \theta_j(k) \right)\right] - \left[\min\limits_m \> \min\limits_i \> \min\limits_{\theta(k) \in {\mathcal{E}}} \> \max\limits_j \, \left( h^{(m)}_{i,j} + \theta_j(k) \right)\right] \\ & = 3.2- (-1.2) \\ & = 4.4 \end{aligned}$$

Now we obtain the following model:

$$\begin{aligned} x(k) =\max&\left[\Big(\max(x(k\!-\!1)+1,u(k)+0.2) + (1\!-\!\delta_1(k))\sigma^*\Big), \right. \\ & \,\,\,\,\Big(\max(x(k\!-\!1)-0.1,u(k)+0.1) + (1\!-\!\delta_2(k))\sigma^*\Big), \\ &\,\,\,\left.\Big(\max(x(k\!-\!1)-0.1,u(k)+0.1) + (1\!-\!\delta_3(k))\sigma^*\Big)\right] \\ x(k) =\max&\left[\Big(\max(x(k\!-\!1)+1,u(k)+0.2) + (1\!-\!\delta_1(k))\sigma^*\Big), \right. \\ &\,\,\left.\Big(\max(x(k\!-\!1)-0.1,u(k)+0.1) + (1\!-\!\delta_2(k)\!-\!\delta_3(k))\sigma^*\Big)\right] \end{aligned}$$

for δ _m (k) ∈ [0, 1] and subject to

$$ \begin{aligned} \bar{R}_{m} \,\bar{z}(k) &\leq \bar{r}_{m} + \rho^*_m(1-\delta_m(k)) \;\;\mathrm{for}\;\; m=1,2,3 \\ \sum\limits_{m=1}^3 \delta_m(k) &= 1 \end{aligned} $$

This is a constrained MMPS system.

4 Conditions for stability

In this section we will derive conditions for stability in Theorem 1. These conditions will be used in Section 5 to derive a stabilizing model predictive controller for SMPL systems.

Just like in van den Boom and De Schutter (2002), we adopt the notion of stability for discrete-event systems from Passino and Burgess (1998), in which a discrete-event system is called stable if all its buffer levels remain bounded. In this paper we consider discrete-event systems with a due-date signal. This due date signal is a reference for the time that the output event should occur (e.g. in production systems the finished part has to be removed from the output buffer before the due-dates). This means that if the output event occurs after the given due-date there is a delay in the system. For a proper operation of the system, the delays have to remain bounded. In the remainder of the paper the due-date signal will be called “reference signal”, as is usual in MPC literature.

All the buffer levels in a discrete-event system are bounded if the dwelling times of the parts or batches in the system remain bounded. This implies for an MPL system with an asymptotically increasing reference signal r(k) that stability is achieved if and only if there exist finite constants k ₀, M _yr , M _yx and M _xu such that

$$ |\,y_i(k) - r_i(k)\,| \leq M_{yr}, \;\; \forall i $$

(27)

$$ |\,y_i(k) - x_j(k)\,| \leq M_{yx}, \;\; \forall i,j $$

(28)

$$ |\,x_j(k) - u_m(k)\,| \leq M_{xu}, \;\; \forall j,m $$

(29)

for all k > k ₀. Condition (27) means that the delay between the actual output date y(k) and the reference r(k) has to remain bounded, and on the other hand, that the stock time has to remain bounded. Conditions (28) and (29) mean that the throughput time (i.e. the time between the starting date, u(k) and the output date, y(k)) is bounded. Consider a reference signal vector defined as

$$ r(k) = \rho\,k + \xi(k),\;\;\textrm{where} \;|\xi_i(k)|\leq \xi_{\mathrm{max}},\forall i $$

(30)

where ξ is a vector describing the bounded variation of the reference around an average slope k ρ with ρ a positive scalar. (If r(k) is strictly increasing we need the additional constraint ξ _i (k) > ξ _i (k − 1) − ρ.) For the asymptotically increasing reference signal (30), the conditions (27)–(29) imply finite buffer levels.

Similar to max-plus-linear systems, stability is not an intrinsic feature of the SMPL system, but it also depends on the reference signal. In van den Boom and De Schutter (2002) we already observed that for max-plus-linear systems, the max-plus-algebraic eigenvalue of the system matrix A gives an upper bound on the asymptotic slope of the reference sequence. For a max-plus-linear system with a strongly connected A-matrix⁶, this A-matrix only has one max-plus-algebraic eigenvalue λ and a corresponding max-plus-algebraic eigenvector v ≠ ε, such that A ⊗ v = v ⊗ λ (Baccelli et al. 1992). For SMPL systems we cannot use the max-plus-algebraic eigenvalue, but we use the concept of maximum autonomous growth rate:

Definition 8

Consider an SMPL system of the form (1) and (2) with system matrices A ^(ℓ), $\ell=1,\ldots,{n_{L}}$. Define the matrices $A^{(\ell)}_\alpha$ with $[A^{(\ell)}_\alpha]_{i,j} = [A^{(\ell)}]_{i,j} - \alpha$. Define the set ${\mathcal{S}}_{\mathrm{fin},n}$ of all n × n max-plus diagonal matrices with finite diagonal entries, so ${\mathcal{S}}_{\mathrm{fin},n}= \{ \>S\>|\>S={\mathrm{diag}}_\oplus(s_1,\ldots,s_n), \>s_i\;\text{is f\/inite}\>\}$. The maximum autonomous growth rate λ of the SMPL system is defined by

$$ \lambda = \min \left\{ \alpha \>\left|\> \exists S\in {\mathcal{S}}_{\mathrm{fin},n}\;\text{such that}\; [\>S {\otimes}A^{(\ell)}_\alpha {\otimes}S^{\otimes^{-1}} \>]_{i,j} \leq 0 ,\;\;\forall\> i,j,\ell \right.\right\} $$

Remark 9

Note that for any SMPL system the maximum autonomous growth rate λ is finite, or more precisely:

$$ \lambda \leq \max\limits_{i,j,\ell} \left[A^{(\ell)}\right]_{i,j}. $$

This fact is easily verified by noting that if we define $\lambda'=\max_{i,j,\ell} [A^{(\ell)}]_{i,j}$ and use the max-plus identity matrix S = diag_⊕(0, ..., 0) we obtain

$$ \left[\>S {\otimes}A^{(\ell)}_{\lambda'} {\otimes}S^{\otimes^{-1}} \>\right]_{i,j} = \left[A^{(\ell)}_{\lambda'}\right]_{i,j} = \left[A^{(\ell)}\right]_{i,j}-{\lambda'} \leq 0 ,\;\;\forall\> i,j,\ell, $$

and so λ ≤ λ′. The maximum autonomous growth rate λ can be easily computed by solving a linear programming problem:

$$ \min\limits_{\alpha,s_1,\ldots,s_n} \alpha $$

subject to

$$ \left[A^{(\ell)}\right]_{i,j} + s_i - s_j - \alpha \leq 0 ,\;\;\forall\> i,j,\ell $$

The optimizer now gives the maximum autonomous growth rate λ = α ^*.

Remark 10

For a max-plus-linear system (so n _L = 1), the maximum autonomous growth rate λ is equivalent to the largest max-plus-algebraic eigenvalue of the matrix A ⁽¹⁾.

For a given integer N, let the set ${\mathcal{L}}_N=\{ \>[\>\ell_1\;\cdots\;\ell_N\>]^T\>|\>\ell_m \in \{1,\ldots,{n_{\small L}} \},\> m=1,\ldots,N\}$ denote the set of all possible consecutive mode switchings vectors.

Definition 9

(Baccelli et al. 1992) Let α ∈ ℝ be given. Define the matrices $A^{(\ell)}_\alpha$ with $[A^{(\ell)}_\alpha]_{i,j} = [A^{(\ell)}]_{i,j} - \alpha$. An SMPL system is structurally controllable if there exists a finite positive integer N such that for all ${\tilde{\ell}} = \left[ \ell_1 \; \ldots \; \ell_N \right] ^T \in {\mathcal{L}}_N$ the matrices

$$ \Gamma^N_\alpha({\tilde{\ell}}) \!=\! \left[\begin{array}{cccccccc} \! A^{(\ell_N)}_\alpha \!{\otimes}\! \cdots \!{\otimes}A^{(\ell_{2})}_\alpha {\otimes}B^{(\ell_{1})} \;\;\;\; & \ldots \;\;\;\; & \! A^{(\ell_N)}_\alpha\! {\otimes}\! A^{(\ell_{N\!-\!1})}_\alpha \!{\otimes}\! B^{(\ell_{N\!-\!2})}\;\;\;\; & \! A^{(\ell_{N})}_\alpha \!{\otimes}\! B^{(\ell_{N\!-\!1})} \;\;\;\; & \! B^{(\ell_N)}\! \end{array}\right] $$

are row-finite, i.e. in each row there is at least one entry different from ε.

Definition 10

(Baccelli et al. 1992) Let α ∈ ℝ be given. Define the matrices $A^{(\ell)}_\alpha$ with $[A^{(\ell)}_\alpha]_{i,j} = [A^{(\ell)}]_{i,j} - \alpha$. An SMPL system is structurally observable if there exists a finite positive integer M such that for all ${\tilde{\ell}} = \left[ \ell_1 \; \ldots \; \ell_M \right]^T \in {\mathcal{L}}_M$ the matrices

$$ O^M_\alpha({\tilde{\ell}}) = \left[\begin{array}{l} C^{(\ell_N)}_\alpha \!{\otimes}\! A^{(\ell_N)}_\alpha \!{\otimes}\! \cdots \!{\otimes}A^{(\ell_{2})}_\alpha\\ \qquad\qquad\qquad\qquad\vdots \\ C^{(\ell_N)}_\alpha \!{\otimes}\! A^{(\ell_N)}_\alpha\! {\otimes}\! A^{(\ell_{N\!-\!1})}_\alpha \\ C^{(\ell_N)}_\alpha \!{\otimes}\! A^{(\ell_{N})}_\alpha \\ C^{(\ell_N)}_\alpha \end{array}\right] $$

are column-finite, i.e. in each column there is at least one entry different from ε.

Remark 11

Note that the structural controllability and structural observability are structural properties and do not depend on the actual value of α. If a SMPL system is structurally controllable (observable) for one finite value of α it is structurally controllable (observable) for any finite value of α.

Theorem 1

Consider an SMPL system with maximum autonomous growth rate λ and consider a reference signal (30) with growth rate ρ . Define the matrices $A^{(\ell)}_\rho$ with $[A^{(\ell)}_\rho]_{i,j} = [A^{(\ell)}]_{i,j} - \rho$ . Now if

$$ \textrm{$1$.} \;\;\; \rho > \lambda, $$

(31)

$$ \textrm{$2$.} \;\;\; \text{the system is structurally controllable, and } $$

(32)

$$ \textrm{$3$.} \;\;\; \text{the system is structurally observable,} $$

(33)

then any input signal

$$ u(k) = \rho\,k + \mu(k),\;\;\textrm{where}\;\; |\> \mu_i(k)\>| \leq \mu_{\mathrm{max}},\;\forall i,\;\forall k $$

(34)

for a finite value μ _max , will stabilize the SMPL system.

Proof

First note that the condition ρ > λ holds if and only if there exists a max-plus diagonal matrix S such that

$$ \left[ S {\otimes}A^{(\ell)}_\rho {\otimes}S^{\otimes^{-1}} \>\right]_{i,j} < 0 ,\;\;\forall\> i,j,\ell. $$

(35)

Let S be the max-plus diagonal matrix with finite diagonal elements such that (35) is satisfied, and define the signals

$$\begin{aligned} z(k) &= S {\otimes}(x(k) - \rho\,k)\\ w(k) &= y(k) - \rho\,k\\ \mu(k) &= u(k) - \rho\,k \end{aligned}$$

and the matrices ${\bar{A}}^{(\ell)}_\rho$, ${\bar{B}}^{(\ell)}$, and ${\bar{C}}^{(\ell)}$ with

$$ {\bar{A}}^{(\ell)}_\rho = S {\otimes}A^{(\ell)}_\rho {\otimes}S^{\otimes^{-1}} $$

(36)

$$ {\bar{B}}^{(\ell)} = S {\otimes}B^{(\ell)} $$

(37)

$${\bar{C}}^{(\ell)} = C^{(\ell)} {\otimes}S^{\otimes^{-1}}. $$

(38)

Just like we did in Necoara et al. (2007) for max-plus-linear systems we can associate to every ρ a shifted system

$$ z(k) = {\bar{A}}^{(\ell)}_\rho {\otimes}z(k-1) {\oplus}{\bar{B}}^{(\ell)} {\otimes}\mu(k) $$

(39)

$$ w(k) = {\bar{C}}^{(\ell)} {\otimes}z(k). $$

(40)

Stability means that all signals in this system should remain bounded. In other words, we are looking for finite values z _max, w _max, such that

$$ \;|z(k)|\leq z_{\mathrm{max}}\;\;\;, \;\;\;|w(k)|\leq w_{\mathrm{max}}. $$

Now consider the SMPL system (39) and (40) for the input signal $|\>\mu_i(k)\>|\leq \mu_{\max}$, ∀ i,k for a given finite value μ _max. Let $\bar{z}(k) = \max_i z_i(k)$ and $\bar{b}_{\max}=\max_{\ell,i,j}([{\bar{B}}^{(\ell)}]_{i,j})$, then

$$ \begin{aligned} z_i(k) & = \max\left( \max_{j} \left( \left[{\bar{A}}^{(\ell)}_\rho\right]_{i,j} + z_j(k-1)\right), \max_{m} \left(\left[{\bar{B}}^{(\ell)}\right]_{i,m} + \mu_m(k)\right) \right) \\[6pt] & \leq \max\left( \max_{j} \left( \left[{\bar{A}}^{(\ell)}_\rho\right]_{i,j}\right) + \bar{z}(k-1), \max_{\ell,i,m}\left(\left[{\bar{B}}^{(\ell)}\right]_{i,m}\right) + \mu_{\max}\right) \\[6pt] & \leq \max\left(\bar{z}(k-1) , \bar{b}_{\max} + \mu_{\max}\right) \end{aligned}$$

where we use the fact that $[{\bar{A}}^{(\ell)}_\rho]_{i,j} < 0$ because Eqs. 35 and 36. We find

$$\begin{aligned} z_i(k) & \leq \bar{z}(k) \\[6pt] & \leq \max\Big(\bar{z}(k-1) , \bar{b}_{\max} + \mu_{\max}\Big) \\[6pt] & \leq \max\Big(\bar{z}(0) , \bar{b}_{\max} + \mu_{\max}\Big)\\[6pt] & = z_{\max} \end{aligned} $$

where we defined $z_{\max} = \max\Big(\bar{z}(0),\bar{b}_{\max} + \mu_{\max}\Big)$. This means that all entries of the shifted state z(k) have a finite upper bound z _max.

Now again consider the SMPL system (39) and (40) for the input signal μ _i (k) ≥ − μ _max, ∀ i,k, and let N and M be such that $\gamma_{i,\max}({\tilde{\ell}})=\max_{j}([\Gamma^N_\rho({\tilde{\ell}})]_{i,j})$ are finite for all $i,{\tilde{\ell}}$, and $\omega_{i,\max}({\tilde{\ell}})=\max_{j}([{\mathcal{O}}^M_\rho({\tilde{\ell}})]_{i,j})$ are finite for all $i,{\tilde{\ell}}$. Note that a finite N and a finite M exist due to condition 2 and 3 of the theorem (see also Definitions 9 and 10). Now define

$$ \begin{aligned} {\tilde{\ell}}(k) &= \left[\begin{array}{c}\ell(k) \\ \vdots \\ \!\ell(k\!+\!N\!-\!2)\! \\ \!\ell(k\!+\!N\!-\!1)\! \end{array}\right], {\tilde{\mu}_{\tiny N}}(k) = \left[\begin{array}{c}\mu(k) \\ \vdots \\ \!\mu(k\!+\!N\!-\!2)\! \\ \!\mu(k\!+\!N\!-\!1)\! \end{array}\right],\\ {\tilde{z}_{\tiny M}}(k) &= \left[\begin{array}{c}z(k) \\ \vdots \\ \!z(k\!+\!M\!-\!2)\! \\ \!z(k\!+\!M\!-\!1)\! \end{array}\right], \end{aligned} $$

then by successive substitution we find that for any m ≥ N there holds

$$\begin{aligned} z(k+m) =\;& {\bar{A}}^{(\ell(k+m))}_\rho \otimes {\bar{A}}^{(\ell(k+m-1))}_\rho \otimes \ldots \otimes {\bar{A}}^{(\ell(k+m-N\!+\!1))}_\rho \otimes z(k\!+\!m\!-N) \\* & \oplus {\bar{A}}^{(\ell(k+m))}_\rho \otimes {\bar{A}}^{(\ell(k+m-1))}_\rho \otimes \ldots \otimes {\bar{B}}^{(\ell(k+m-N\!+\!1))} \otimes \mu(k\!+\!m\!-N+1) \\* & \oplus {\bar{A}}^{(\ell(k+m))}_\rho \otimes {\bar{B}}^{(\ell(k+m-1))} \otimes \mu(k\!+\!m\!-1) \oplus\ldots\oplus {\bar{B}}^{(\ell(k+m))} \otimes \mu(k\!+\!m) \\ =\;& S{\otimes}A^{(\ell(k+m))}_\rho \otimes A^{(\ell(k+m-1))}_\rho \otimes \ldots \otimes A^{(\ell(k+m-N\!+\!1))}_\rho {\otimes}S^{\otimes^{-1}} \otimes z(k\!+\!m\!-N) \\* & \oplus S{\otimes}A^{(\ell(k+m))}_\rho \otimes A^{(\ell(k+m-1))}_\rho \otimes \ldots \otimes B^{(\ell(k+m-N\!+\!1))}_\rho \otimes \mu(k\!+\!m\!-N+1) \\* & \oplus S{\otimes}A^{(\ell(k+m))}_\rho \otimes B^{(\ell(k+m-1))}_\rho \otimes \mu(k\!+\!m\!-1) \oplus\ldots\oplus S{\otimes}B^{(\ell(k+m))}_\rho \\ & \otimes \mu(k\!+\!m) \\ =\;& S{\otimes}A^{(\ell(k+m))}_\rho \otimes A^{(\ell(k+m-1))}_\rho \otimes \ldots \otimes A^{(\ell(k+m-N\!+\!1))}_\rho {\otimes}S^{\otimes^{-1}} \otimes z(k\!+\!m\!-N) \\* & \oplus S{\otimes}\Gamma^N_\rho({\tilde{\ell}}(k+m-N\!+\!1)) {\otimes}{\tilde{\mu}_{\tiny N}}(k\!+\!m\!-N+1)\;\;. \end{aligned} $$

For every element of z(k + m), m ≥ N we derive:

$$ \begin{aligned} {[}z(k+m)]_i \geq\;& \left[S{\otimes}\Gamma^N_\rho\left({\tilde{\ell}}\left(k+m-N\!+\!1\right)\right) {\otimes}{\tilde{\mu}_{\tiny N}}\left(k\!+\!m\!-N+1\right)\right]_i \\* =\; & \max\limits_j \left(\left[S {\otimes}\Gamma^N_\rho\left({\tilde{\ell}}\left(k+m-N\!+\!1\right)\right) \right]_{i,j} + \left[{\tilde{\mu}_{\tiny N}}\left(k\!+\!m\!-N+1\right)\right]_i\right) \\* \geq\;& \min\limits_p([S]_{p,p}) + \max\limits_j \left(\left[\Gamma ^N_\rho\left({\tilde{\ell}}\left(k+m-N\!+\!1\right)\right) \right]_{i,j}\right)- \mu_{\max} \\* \geq\;& \min\limits_p(s_p) + \gamma_{i,\max}\left({\tilde{\ell}}\left(k+m-N\!+\!1\right)\right) - \mu_{\max}\\* \geq\;& s_{\min} + \gamma_{\min} - \mu_{\max} \end{aligned}$$

where s _min =  min _p (s _p ) and $\gamma_{\min}=\min_{{\tilde{\ell}},i} \gamma_{i,\max}({\tilde{\ell}})$. We conclude that after N event steps we have a lower bound for the shifted state z(k).

By successive substitution we find that for any m ≥ N + M there holds

$$\begin{aligned} w(k+m) =\;& {\bar{C}}^{(\ell(k+m))}_\rho \otimes {\bar{A}}^{(\ell(k+m))}_\rho \otimes {\bar{A}}^{(\ell(k+m-1))}_\rho \otimes \cdots \otimes {\bar{A}}^{(\ell(k+m-N+2))}_\rho\\ &\otimes z(k\!+\!m\!-N+1) \oplus \ldots \oplus {\bar{C}}^{(\ell(k+m))}_\rho \otimes {\bar{A}}^{(\ell(k+m))}_\rho \otimes z(k\!+\!m\!-1) \\ &\oplus {\bar{C}}^{(\ell(k+m))}_\rho \otimes z(k\!+\!m) \\ =\;& C^{(\ell(k+m))}_\rho {\otimes}A^{(\ell(k+m))}_\rho \otimes A^{(\ell(k+m-1))}_\rho \otimes \cdots \otimes A^{(\ell(k+m-N+2))}_\rho \otimes S^{\otimes^{-1}} \\ &{\otimes}z(k\!+\!m\!-M+1) \oplus C^{(\ell(k+m))}_\rho {\otimes}A^{(\ell(k+m))}_\rho \otimes A^{(\ell(k+m-1))}_\rho \otimes S^{\otimes^{-1}} \\ &{\otimes}z(k\!+\!m\!-1) \oplus\ldots\oplus C^{(\ell(k+m))}_\rho \otimes S^{\otimes^{-1}} {\otimes}z(k\!+\!m) \\ =\;& {\mathcal{O}}^M_\rho\left({\tilde{\ell}}\left(k+m-M\!+\!1\right)\right) {\otimes}S^{\otimes^{-1}} {\otimes} {\tilde{z}_{\tiny M}}(k\!+\!m\!-N+1)\;\;. \end{aligned}$$

For every element of w(k + m), m ≥ N + M we derive:

$$\begin{aligned} {[}w(k+m)]_i \geq\;& \left[{\mathcal{O}}^M_\rho\left({\tilde{\ell}}(k+m-M\!+\!1)\right) {\otimes}S^{\otimes^{-1}} {\otimes}{\tilde{z}_{\tiny M}}(k\!+\!m\!-M+1)\right]_i \\*[5pt] =\; & \max\limits_j \left(\left[{\mathcal{O}}^M_\rho\left({\tilde{\ell}}(k+m-M\!+\!1)\right) {\otimes}S^{\otimes^{-1}}\right]_{i,j} + \left[{\tilde{z}_{\tiny M}}(k\!+\!m\!-M+1)\right]_i\right) \\*[5pt] \geq\;& \max\limits_j \left(\left[{\mathcal{O}}^M_\rho\left({\tilde{\ell}}(k+m-M\!+\!1)\right) \right]_{i,j}\right) - \max\limits_p([S]_{p,p}) - \mu_{\max} \\*[5pt] \geq\;& \omega_{i,\max}\left({\tilde{\ell}}(k+m-M\!+\!1)\right) - \max\limits_p(s_p) + s_{\min} + \gamma_{\min} - \mu_{\max}\\*[5pt] \geq\;& \omega_{\min} - s_{\max} + s_{\min} + \gamma_{\min} - \mu_{\max} \end{aligned}$$

where s _max =  max _p (s _p ) and $\omega_{\min}=\min_{{\tilde{\ell}},i} \omega_{i,\max}({\tilde{\ell}})$. Now from (40) it follows that

$$\begin{aligned} {[}w(k+m)]_i & = \left[{\mathcal{O}}^M_\rho\left({\tilde{\ell}}(k+m-M\!+\!1)\right) {\otimes}S^{\otimes^{-1}} {\otimes}{\tilde{z}_{\tiny M}}(k\!+\!m\!-M+1)\right]_i \\*[5pt] & \leq \max\limits_{i,j,{\tilde{\ell}}} \Big({\mathcal{O}}^M_\rho\left({\tilde{\ell}}(k+m-M\!+\!1)\right)\Big) - \min\limits_p([S]_{p,p}) + z_{\max} \\*[5pt] & \leq \omega_{\max} - s_{\min} + z_{\max} \end{aligned}$$

where $\omega_{\max}=\max_{i,j,{\tilde{\ell}}} \Big({\mathcal{O}}^M_\rho({\tilde{\ell}}(k+m-M\!+\!1))\Big)$, and so after N + M event steps w _i (k) will be bounded by

$$ \omega_{\min} - s_{\max} + s_{\min} + \gamma_{\min} - \mu_{\max} \leq w_i(k) \leq \omega_{\max} - s_{\min} + z_{\max} $$

Now for any k > N + M, there holds

$$ \begin{array}{rll} y_i(k) - r_i(k) & =& [w(k) + \rho\,k]_i - [ \zeta(k) + \rho\,k]_i \\ & =& w_i(k) - \xi_i(k) \\ &\leq& \omega_{\max} - s_{\min} + z_{\max} +\xi_{\max} \\ & =& M_{yr1} \;\;\text{(is f\/inite)},\\ r_i(k) - y_i(k) &=& \xi_i(k) - w_i(k) \\ &\leq& \xi_{\max} - \omega_{\min} + s_{\max} - s_{\min} - \gamma_{\min} + \mu_{\max}\\ &=& M_{yr2} \;\;\text{(is f\/inite)}, \end{array} $$

$$ \begin{array}{rll} |y_i(k) - r_i(k)| &=& | w_i(k)-\zeta_i(k) | \\ & \leq& \max(M_{yr1},M_{yr2})\\ & =& M_{yr} \;\;\text{(is f\/inite)} ,\\ y_i(k) - x_j(k) & =& [(S^{\otimes^{-1}} {\otimes}w(k) ) + \rho\,k]_i - [(S^{\otimes^{-1}} {\otimes}z(k) ) + \rho\,k]_j \\ & =& (-s_i + w_i(k) +\rho\,k ) - (-s_j + z_j(k) +\rho\,k) \\ & =& w_i(k) + s_j - z_j(k) \\ &\leq& \omega_{\max} - s_{\min} + z_{\max} + s_{\max} - s_{\min} - \gamma_{\min} + \mu_{\max} \\ &=& M_{yx} \;\;\text{(is f\/inite)}, \\ x_j(k) - u_m(k) & =& [(S^{\otimes^{-1}} {\otimes}z(k) ) + \rho\,k]_j - [\mu(k) + \rho\,k]_m \\ & =& (-s_j + z_j(k) +\rho\,k ) - ( \mu_m(k) +\rho\,k) \\ & =& z_j(k) - \mu_m(k) - s_j \\ &\leq& z_{\max} + \mu_{\max} - s_{\min}\\ &=& M_{xu} \;\;\text{(is f\/inite)} \;, \end{array} $$

In a similar way as y _i (k) − x _j (k) and x _j (k) − u _m (k) we can prove that x _j (k) − y _i (k) and u _m (k) − x _j (k) are bounded. This proves stability for the SMPL system (1) and (2).

Remark 12

For a max-plus-linear system (so ${n_{L}} =1$), condition (31) is equivalent to the condition that the growth rate ρ of the reference signal should be larger than the largest max-plus-linear eigenvalue λ of the matrix A ⁽¹⁾ (cf. van den Boom and De Schutter 2002).

Remark 13

Note that the conditions of structural controllability and structural observability for stability have already been mentioned in Baccelli et al. (1992) and Commault (1998) for the case with one mode.

5 A stabilizing model predictive controller

In this section we develop a stabilizing model predictive controller for SMPL systems with both deterministic and stochastic switching. Model predictive control (MPC) (Maciejowski 2002) is a model-based control approach that has its origins in the process industry and that has mainly been developed for linear or nonlinear time-driven systems. Its main ingredients are: a prediction model, a performance criterion to be optimized over a given horizon, constraints on inputs and outputs, and a receding horizon approach. Just as for time-driven systems (where more than 80% of the advanced controllers are model predictive controllers), we like to use the advantages of the model predictive control strategy for SMPL discrete-event systems. The main advantage of using MPC is that it is the only closed-loop control method that can handle constraints in an adequate way. Feedback is incorporated into MPC by repeating the state measurement and control input calculation at regular time instants. Furthermore, MPC features an simple tuning process and can easily adapt to model changes. The algorithms to compute the optimal input signal are mostly linear programming algorithms, with means that the computational effort is usually very low. In more complicated situations where we deal with different modes and the switching mechanism has stochastic properties, MPC gives a framework to deal with these issues and the controller computes an optimal control input.

A Model Predictive Control (MPC) approach for MPL systems has been introduced in De Schutter and van den Boom (2001). In De Schutter and van den Boom (2001) and van den Boom and De Schutter (2002) it has been shown that for a broad range of performance criteria and constraints, max-plus linear MPC results in a linear programming problem, which can be solved very efficiently. In van den Boom and De Schutter (2006, 2007, 2008a) we have extended this approach to SMPL systems with both stochastic and deterministic switching. In this paper we review these results and discuss the algorithms to solve the MPC problem for different types of switching (stochastic and/or deterministic).

Consider a type-1 SMPL system. In MPC we use predictions of future signals based on this model. Define the prediction vectors

$$ {\tilde{y}}(k) \!= \!\!\left[\begin{array}{c}{\hat{y}}(k|k) \\ \vdots \\ \!{\hat{y}}(k\!+\!{N_{\mathrm{p}}}\!-\!2|k)\! \\ \!{\hat{y}}(k\!+\!{N_{\mathrm{p}}}\!-\!1|k)\! \end{array}\right], {\tilde{u}}(k) \!= \!\!\left[\begin{array}{c}u(k) \\ \vdots \\ \!u(k\!+\!{N_{\mathrm{p}}}\!-\!2)\! \\ \!u(k\!+\!{N_{\mathrm{p}}}\!-\!1)\! \end{array}\right],$$

$$ {\tilde{\ell}}(k) \!= \!\!\left[\begin{array}{c}\ell(k|k) \\ \vdots \\ \!\ell(k\!+\!{N_{\mathrm{p}}}\!-\!2|k)\! \\ \!\ell(k\!+\!{N_{\mathrm{p}}}\!-\!1|k)\! \end{array}\right], {\tilde{r}}(k) \!= \!\!\left[\begin{array}{c}r(k) \\ \vdots \\ \!r(k\!+\!{N_{\mathrm{p}}}\!-\!2)\! \\ \!r(k\!+\!{N_{\mathrm{p}}}\!-\!1)\! \end{array}\right], $$

where $\hat{y}(k\!+\!j|k)$ denotes the prediction of y(k + j) based on knowledge at event step k, u(k + j) denotes the (future) input at event step k + j, ℓ(k + j) denotes the (future) mode at event step k + j, r(k + j) denote the (future) reference at event step k + j, and N _p is the prediction horizon (so it determines how many event steps we look ahead in our control law design).

Define

$$\begin{aligned} {\tilde{A}}_{m}({\tilde{\ell}}(k)) &= A^{(\ell(k+m-1|k))} \otimes \ldots \otimes A^{(\ell(k|k))}, \\ {\tilde{B}}_{m,n}({\tilde{\ell}}(k)) &= \left\{ \begin{array}{ll} A^{(\ell(k\!+\!m\!-\!1|k))} \otimes \ldots \otimes A^{(\ell(k\!+\!n|k))} \otimes B^{(\ell(k\!+\!n\!-\!1|k))} & \!\mbox{if } m\!>\!n \\[3mm] B^{(\ell(k\!+\!m\!-\!1|k))} & \!\mbox{if } m\!=\!n \\[3mm] \!\varepsilon & \!\mbox{if } m\!<\!n \end{array} \right. ,\\ \end{aligned}$$

and

$$\begin{aligned} {\tilde{C}}_{m}({\tilde{\ell}}(k)) &= C^{(\ell(k+m-1|k))} \otimes {\tilde{A}}_{m}({\tilde{\ell}}(k)), \\ {\tilde{D}}_{m,n}({\tilde{\ell}}(k)) &= C^{(\ell(k+m-1|k))} \otimes {\tilde{B}}_{m,n}({\tilde{\ell}}(k)). \end{aligned}$$

For any mode sequence ${\tilde{\ell}}(k)$ the prediction model for Eqs. 1 and 2 is now given by:

$$ {\tilde{y}}(k) = {\tilde{C}}({\tilde{\ell}}(k)) \otimes x(k-1) \oplus {\tilde{D}}({\tilde{\ell}}(k)) \otimes {\tilde{u}}(k) $$

(41)

in which ${\tilde{C}}({\tilde{\ell}}(k))$ and ${\tilde{D}}({\tilde{\ell}}(k))$ are given by

$${\tilde{C}}({\tilde{\ell}}(k)) = \left[\begin{array}{c} {\tilde{C}}_1({\tilde{\ell}}(k)) \\ \vdots \\ {\tilde{C}}_{{N_{\mathrm{p}}}}({\tilde{\ell}}(k)) \end{array}\right], \qquad\qquad{\tilde{D}}({\tilde{\ell}}(k)) = \left[\begin{array}{cccc} \!{\tilde{D}}_{1,1}({\tilde{\ell}}(k)) \!\! & \cdots\!\! & {\tilde{D}}_{1,{N_{\mathrm{p}}}}({\tilde{\ell}}(k)) \!\\ \!\vdots \!\! & \ddots\!\! & \vdots \! \\ \!{\tilde{D}}_{{N_{\mathrm{p}}},1}({\tilde{\ell}}(k)) \!\! & \cdots\!\! & {\tilde{D}}_{{N_{\mathrm{p}}},{N_{\mathrm{p}}}}({\tilde{\ell}}(k)) \!\end{array}\right] $$

Furthermore we can write

$$ x(k\!+\!j) = {\tilde{A}}_j({\tilde{\ell}}(k)) \otimes x(k\!-\!1) \oplus {\bar{B}}_j({\tilde{\ell}}(k)) \otimes {\tilde{u}}(k), $$

(42)

where

$$ {\bar{B}}_j({\tilde{\ell}}(k)) = \left[\begin{array}{cccc}\!{\tilde{B}}_{j,1}({\tilde{\ell}}(k)) & \cdots & {\tilde{B}}_{j,{N_{\mathrm{p}}}}({\tilde{\ell}}(k)) \!\end{array}\right]. $$

With Eq. 42 the probability of switching to mode L(k + j) = ℓ(k + j) given ℓ(k + j − 1), x(k + j − 1), u(k + j), v(k + j)) can be written as

$$ \begin{aligned} & P\big[L(k+j)=\ell(k\!+\!j|k)|\ell(k\!+\!j\!-\!1|k),x(k\!+\!j\!-\!1),u(k\!+\!j),v(k\!+\!j)\big] \\ & = P\big[L(k+j)=\ell(k\!+\!j|k)|\ell(k\!+\!j\!-\!1|k),{\tilde{A}}_j({\tilde{\ell}}(k)) \otimes x(k\!-\!1) \oplus {\bar{B}}_j({\tilde{\ell}}(k)) \\ &\qquad \otimes {\tilde{u}}(k), u(k\!+\!j),v(k\!+\!j)\big] \end{aligned} $$

where P denotes the switching probability (see Section 2.2). Note that from (42) we find that for a fixed ${\tilde{\ell}}(k)$ the state x(k + j) is piecewise affine on polyhedral sets in the variables x(k − 1) and ${\tilde{u}}(k)$. From that we can conclude that for a fixed ${\tilde{\ell}}(k)$, x(k − 1) and ℓ(k − 1) the probability P is piecewise affine on polyhedral sets in the variables ${\tilde{u}}(k)$ and ${\tilde{v}}(k)$. The probability for the switching sequence ${\tilde{\ell}}(k)\in {\mathcal{L}}_{{N_{\mathrm{p}}}}$, given ℓ(k − 1), x(k − 1), ${\tilde{u}}(k)$, ${\tilde{v}}(k)$ is computed as

$$ \begin{aligned} &{\tilde{P}}\big[{\tilde{L}}(k)={\tilde{\ell}}(k)|\ell(k\!-\!1),x(k\!-\!1),{\tilde{u}}(k),{\tilde{v}}(k)\big] \\ &= P\left[L(k)=\ell(k)|\ell(k\!-\!1),x(k\!-\!1),u(k),v(k)\right] \\ &\quad\cdot P\left[L(k\!+\!1)=\ell(k\!+\!1)|\ell(k),x(k),u(k\!+\!1),v(k\!+\!1)\right]\cdot \ldots \cdot \\ &\quad \cdot \ldots \cdot P\big[L(k\!+\!{N_{\mathrm{p}}}\!-\!1)=\ell(k\!+\!{N_{\mathrm{p}}}\!-\!1)|\ell(k\!+\!{N_{\mathrm{p}}}\!-\!2),x(k\!+\!{N_{\mathrm{p}}}\!-\!2),\\ &\,\,\,\qquad\qquad u(k\!+\!{N_{\mathrm{p}}}\!-\!1),v(k\!+\!{N_{\mathrm{p}}}\!-\!1)\big] \end{aligned} $$

The probability function ${\tilde{P}}$ is a product of piecewise affine functions P, and will therefore be a piecewise polynomial function on polyhedral sets in the variables ${\tilde{u}}(k)$, ${\tilde{v}}(k))$ (for a given ${\tilde{\ell}}(k)$, x(k − 1), and ℓ(k − 1)).

In MPC we aim at computing the optimal ${\tilde{u}}(k),{\tilde{v}}(k)$ that minimize the expectation of a cost criterion J(k), subject to linear constraints on the inputs. The cost criterion reflects the input and output cost functions (J _in and J _out, respectively) in the event period k, ..., k + N _p − 1:

$$ J(k) = {J_\mathrm{out}}(k) + \beta {J_\mathrm{in}}(k) \;\;\;, $$

(43)

where β ≥ 0 is a tuning parameter, chosen by the user. The output cost function is defined by

$$ \begin{array}{rll} {J_\mathrm{out}}(k) &=& I\!\!E \left \{\sum\limits_{j=0}^{{N_{\mathrm{p}}}-1} \sum\limits_{i=1}^{n_y} \max(y_i(k+j)-r_i(k+j),0)\right\} \\ &=& I\!\!E \left \{ \sum\limits_{i=1}^{n_y{N_{\mathrm{p}}}} \max({\tilde{y}}_i(k)-{\tilde{r}}_i(k),0)\right\} \\ &=& I\!\!E \left \{ \sum\limits_{i=1}^{n_y{N_{\mathrm{p}}}} [ ({\tilde{y}}(k)-{\tilde{r}}(k)) {\oplus}\bar{0} ]_i \right\} \\ &=&I\!\!E \left \{ \sum\limits_{i=1}^{n_y{N_{\mathrm{p}}}} \Big[ \Big(({\tilde{C}}({\tilde{\ell}}(k)) \otimes x(k-1) \oplus {\tilde{D}}({\tilde{\ell}}(k)) \otimes {\tilde{u}}(k)) -{\tilde{r}}(k)\Big) \oplus \bar{0} \;\Big]_i \right\} \\ &=& \sum\limits_{{\tilde{\ell}}\in {\mathcal{L}}_N} \left\{ \sum\limits_{i=1}^{n_y {N_{\mathrm{p}}}} \left[ \left({\tilde{C}}({\tilde{\ell}}) \otimes x(k\!-\!1) \oplus {\tilde{D}}({\tilde{\ell}}) \otimes {\tilde{u}}(k))\!-\!{\tilde{r}}(k)\right)\!\oplus \!\bar{0} \right]_i \right. \\ && \left. \phantom{ \sum_{i=1}^{n_y{N_{\mathrm{p}}}}} \cdot {\tilde{P}}\left[{\tilde{L}}(k)={\tilde{\ell}}|\ell(k\!-\!1),x(k\!-\!1),{\tilde{u}}(k),{\tilde{v}}(k)\right]\!\right\} \end{array} $$

(44)

where IE stands for the expectation over all possible switching sequences, and $\bar{0}$ is a column vector consisting of zeros. The output cost function J _out measures the tardiness of the system, which is equal to the delay between the output dates ${\tilde{y}}_i(k)$ and reference dates ${\tilde{r}}_i(k)$ if ${\tilde{y}}_i(k)-{\tilde{r}}_i(k)>0$, and zero otherwise.

The input cost function is chosen as

$$ \begin{array}{rll} {J_{\mathrm{in},u}}(k) & =& - \sum\limits_{j=0}^{{N_{\mathrm{p}}}-1} \sum\limits_{i=1}^{n_u} u_i(k+j) + \sum\limits_{j=0}^{{N_{\mathrm{p}}}-1} \sum\limits_{i=1}^{n_v} \alpha_{i,j} v_i(k+j) \\ & =& - \sum\limits_{i=1}^{n_u{N_{\mathrm{p}}}} [{\tilde{u}}(k)]_i + \sum\limits_{i=1}^{n_v{N_{\mathrm{p}}}} {\tilde{\alpha}}_i [{\tilde{v}}(k)]_i \;. \end{array} $$

(45)

where ${\tilde{\alpha}} = \left[\alpha_{1,1} \; \alpha_{2,1} \; \ldots \; \alpha_{n_v, ({N_{\mathrm{p}}}-1)}\right]^T \geq 0$ is a weighting vector. The first term in the input cost function J _in maximizes the input dates ${\tilde{u}}_i(k)$ for just-in-time production, the second term can be used to (possibly) penalize specific actions of the variable ${\tilde{v}}_i(k)$.

Note that the input cost function is linear in ${\tilde{u}}(k)$ and ${\tilde{v}}(k)$.

The MPC problem for structurally controllable and structurally observable SMPL systems with reference signal (30), satisfying Eq. 31 can be defined at event step k as

$$ \min\limits_{{\tilde{u}}(k),{\tilde{v}}(k)} J(k) $$

(46)

subject to

$$ {\tilde{y}}(k) = {\tilde{C}}({\tilde{\ell}}(k)) \otimes x(k-1) \oplus {\tilde{D}}({\tilde{\ell}}(k)) \otimes {\tilde{u}}(k) $$

(47)

$$ u(k+j) - u(k+j-1) \geq 0 ,\;\; j\!=\!0,\ldots,{N_{\mathrm{p}}}\!-\!1 $$

(48)

$$ |\>u_i(k+j) - \rho\cdot(k+j) \>| \leq \mu_{\mathrm{max}},\;\text{for}\;\; i=1,\ldots,n_u,\;\; j\!=\!0,\ldots,{N_{\mathrm{p}}}\!-\!1 $$

(49)

$$ Q{\tilde{v}}(k) \leq q $$

(50)

$$ R\,{\tilde{u}}(k) \leq s ,\;\; $$

(51)

where Eq. 47 describes the system dynamics, Eq. 48 guarantees a non-decreasing input sequence, Eq. 49 guarantees stability (cf. Theorem 1), and Eq. 50 defines the admissible set for the auxiliary input variables ${\tilde{v}}(k)$. Finally Eq. 51 gives the possibility to include linear constraints on ${\tilde{u}}$.

So the optimization in the MPC algorithm boils down to a nonlinear optimization problem, where the cost criterion is piecewise polynomial and the inequality constraints are linear. This problem can be solved in several ways. Let $\mathcal{P}=\{\mathcal{P}_1,\ldots,\mathcal{P}_K\}$ be the set of polyhedral regions formed by the intersection of linear constraints (47)–(51) and the regions on which the piecewise polynomial functions expressing J are defined. If the number K of polyhedral regions in $\mathcal{P}$ is small, one could apply for each region $\mathcal{P}_i$ a multi-start optimization method for smooth, linearly constrained functions such as steepest descent with gradient projection or sequential quadratic programming (Pardalos and Resende 2002), and afterwards take the minimum over all regions $\mathcal{P}_i$. If K is larger, global optimization methods like tabu search (Glover and Laguna 1997), genetic algorithms (Davis 1991), simulated annealing (Eglese 1990), or (multi-start) pattern search (Audet and Dennis 2007) could be applied.⁷

Note that in the special case where each probability P is a piecewise constant function, J will be a piecewise affine function, and then it can be shown (using an approach similar to the one used in Bemporad and Morari 1999) that the optimization problem reduces to a mixed-integer linear programming problem, for which reliable and efficient algorithms are available (Atamtürk and Savelsbergh 2005; Fletcher and Leyffer 1998). If some of the control variables are integer-valued, we get a mixed-integer nonlinear programming problem, which could be solved using branch-and-bound methods (Leyffer 2001).

We can rewrite the SMPL system with both deterministic and stochastic switching as a stochastic MMPS system or as a stochastic PWA system using the algorithms given in Section 3. Necoara et al. (2004) solves the model predictive control problem using a stochastic MMPS system description. In Kerrigan and Mayne (2002), Lazar et al. (2007) and Rakovic et al. (2004) the model predictive control problem using a stochastic PWA system description is solved.

MPC for SMPL systems with deterministic switching   In some applications the mode switching is deterministic, which means that the switching probability is either zero or one (so P[L(k) = ℓ(k)|ℓ(k − 1), x(k − 1), u(k), v(k)] ∈ {0, 1}). If we rewrite such an SMPL system into the type-2 form, the stochastic signal d(k) will not be needed. We can then use the transformation formulas of Section 3 to rewrite the system as a deterministic PWA system or a deterministic MMPS system. For PWA systems there are many MPC algorithms available (see e.g. Alessio and Bemporad 2009; Johansson 2003) and for MMPS systems we can use the MPC algorithm of De Schutter and van den Boom (2004).

Sometimes the mode switching only depends on the auxiliary variable v(k). In that case the MPC problem can be directly recast into a Mixed Integer Linear Program (MILP).

MPC for SMPL systems with mode-dependent stochastic switching   We will now study the MPC algorithm in the special case of a mode-dependent stochastic switching. We will show that for this subclass of SMPL systems the optimization that arises from the MPC problem boils down to a linear programming problem. For SMPL systems with mode-dependent stochastic switching the probability of switching to mode ℓ(k) depends entirely on the previous mode ℓ(k − 1) (and not on the previous state or input signals), so we now define a new probability function P _s such that

$$ P[L(k) = \ell(k)|\ell(k-1),x(k-1),u(k),v(k)] = P_{\mathrm{s}}[L(k)=\ell(k)|\ell(k-1)] $$

(52)

$$ {\tilde{P}}[{\tilde{L}}(k) = {\tilde{\ell}}(k)|\ell(k-1),x(k-1),{\tilde{u}}(k),{\tilde{v}}(k)] = {\tilde{P}}_{\mathrm{s}}[{\tilde{L}}(k)={\tilde{\ell}}(k)|\ell(k-1)] $$

(53)

The performance index (44) then becomes:

$$ \begin{array}{rll} {J_\mathrm{out}}(k) & =& \sum\limits_{{\tilde{\ell}}\in {\mathcal{L}}_N} \left \{\sum\limits_{i=1}^{n_y {N_{\mathrm{p}}}} \Big[ \Big({\tilde{C}}({\tilde{\ell}}) \otimes x(k-1) \oplus {\tilde{D}}({\tilde{\ell}}) \otimes {\tilde{u}}(k))-{\tilde{r}}(k)\Big) \oplus \bar{0} \;\Big]_i \right\} \\ && \times\,{\tilde{P}}_{\mathrm{s}}[{\tilde{L}}(k)={\tilde{\ell}}|\ell(k-1)] \end{array} $$

(54)

Theorem 2

Consider a type-1 SMPL systems with mode-dependent stochastic switching, so the switching probability is given by Eq.  52 and 53 . Assume that ${\mathcal{L}}_{{N_{\mathrm{p}}}}$ can be rewritten as ${\mathcal{L}}_{{N_{\mathrm{p}}}}= \{ {\tilde{\ell}}^1 , {\tilde{\ell}}^2, \ldots, {\tilde{\ell}}^M \}$ for $M = {n_{\small L}} ^{{N_{\mathrm{p}}}}$ . The MPC problem (46)–(49) can be recast as a linear programming problem:

$$ \min\limits_{{\tilde{u}}(k),t_{i,m}} \sum\limits_{i=1}^{n_y{N_{\mathrm{p}}}} \sum\limits_{m=1}^{M} t_{i,m}{\tilde{P}}_{\mathrm{s}}\left[{\tilde{L}}(k)={\tilde{\ell}}^m\big|\ell(k-1)\right] - \beta \sum\limits_{i=1}^{n_u{N_{\mathrm{p}}}} {\tilde{u}}_i(k) $$

(55)

subject to

$$ t_{i,m} \geq \left[{\tilde{C}}\left({\tilde{\ell}}^m\right)\right]_{i,l} + x_l(k-1)-{\tilde{r}}_i(k) \;,\;\;\forall i,m,l $$

(56)

$$t_{i,m} \geq \left[{\tilde{D}}\left({\tilde{\ell}}^m\right)\right]_{i,l} + {\tilde{u}}_l(k)-{\tilde{r}}_i(k) \;,\;\;\forall i,m,l $$

(57)

$$t_{i,m} \geq 0 \;,\;\;\forall i,m $$

(58)

$$ u_i(k+j\,) - u_i(k+j-1) \geq 0 ,\;\; \forall i,j $$

(59)

$$ |\> u_i(k+j\,) - \rho\cdot(k+j\,) \>| \leq \mu_{\mathrm{max}} ,\;\; \forall i,j $$

(60)

$$ R\,{\tilde{u}}(k) \leq s ,$$

(61)

Proof

From Eq. 44 we obtain:

$$\begin{aligned} {J_\mathrm{out}}(k) & = \sum\limits_{i=1}^{n_y{N_{\mathrm{p}}}} \sum\limits_{m=1}^{M} \max \left\{ \left[ {\tilde{C}}\left({\tilde{\ell}}^m(k)\right) \otimes x(k-1) \oplus {\tilde{D}}\left({\tilde{\ell}}^m(k)\right) \otimes {\tilde{u}}(k) \right] _i -{\tilde{r}}_i(k) , 0 \right\} \\[-2pt] &\quad\times {\tilde{P}}_{\mathrm{s}}\left[{\tilde{L}}(k)={\tilde{\ell}}^m|\ell(k-1)\right] \\ & = \sum\limits_{i=1}^{n_y{N_{\mathrm{p}}}} \sum\limits_{m=1}^{M} \max \Big\{ \max\limits_l \Big( \left[{\tilde{C}}\left({\tilde{\ell}}^m(k)\right)\right]_{i,l} + x_l(k-1)- {\tilde{r}}_i(k) \Big), \\ & \qquad\qquad\qquad\max\limits_j \Big( \left[{\tilde{D}}\left({\tilde{\ell}}^m(k)\right)\right]_{i,j} \!+\! {\tilde{u}}_j(k) \!-\!{\tilde{r}}_i(k)\Big), 0 \Big\} {\tilde{P}}_{\mathrm{s}}\left[{\tilde{L}}(k)\!=\!{\tilde{\ell}}^m|\ell(k\!-\!1)\right] \\ & = \sum\limits_{i=1}^{n_y{N_{\mathrm{p}}}} \sum\limits_{m=1}^{M} t_{i,m} {\tilde{P}}_{\mathrm{s}}\left[{\tilde{L}}(k)={\tilde{\ell}}^m|\ell(k-1)\right] \end{aligned}$$

where

$$ \begin{array}{rll} t_{i,m} &=& \max \Big( \max\limits_l \left( \left[{\tilde{C}}\left({\tilde{\ell}}^m(k)\right)\right]_{i,l} + x_l(k-1)-{\tilde{r}}_i(k) \right), \\ &&\qquad \qquad\max\limits_j \left( \left[{\tilde{D}}\left({\tilde{\ell}}^m(k)\right)\right]_{i,j} + {\tilde{u}}_j(k)\right)-{\tilde{r}}_i(k) , 0 \Big) \end{array} $$

(62)

If we would minimize J _out(k) + βJ _in(k) subject to Eqs. 56–61 then, given the fact that the values of ${\tilde{P}}_{\mathrm{s}}[{\tilde{L}}(k)={\tilde{\ell}}^m|\ell(k-1)]$ are nonnegative, and that the variables t _i,m only appear on the left-hand side of the inequalities (56)–(58), one of the inequalities indeed becomes an equality for at least one of the indices and so t _i,m will be equal to the maximum (62).

This implies that the MPC problem (46)–(49) can indeed be written as the linear programming problem (55)–(61).□

So the optimization in the MPC algorithm boils down to a linear programming problem, which is polynomially solvable (Khachiyan 1979). Usually we will find that $M \ll {n_{\small L}} ^{{N_{\mathrm{p}}}}$ (as not all mode transitions are possible and so the corresponding probabilities will be zero) and we can efficiently solve the optimization.

Timing issues   Switching max-plus-linear systems are different from conventional time-driven systems in the sense that the event counter k is not directly related to a specific time. So far we have assumed that at event step k the state x(k) is available (recall that x(k) contains the time instants at which the internal activities or processes of the system start for the kth cycle). Therefore, we will present a method to address the availability issue of the state at a certain time instant t. Since the components of x(k) correspond to event times, they are in general easy to measure. So we consider the case of full state information. Also note that measurements of occurrence times of events are in general not as susceptible to noise and measurement errors as measurements of continuous-time signals involving variables such as temperature, speed, pressure, etc. Let t be the time instant when an MPC problem has to be solved. We can define the initial cycle k as follows:

$$ k = \arg \max \Big \{ l | x_i(l) \leq t \;,\>\>\forall i \in \{1,2,\ldots,n_x\} \Big\} $$

Hence, the state x(k) is completely known at time t and thus u(k − 1) is also available (due to the fact that in practical applications the entries of the system matrices are nonnegative or take the value ε). Note that at time t some components of the future⁸ states and of the forthcoming inputs might be known (so x _i (k + l) ≤ t and u _j (k + l − 1) ≤ t for some i,j and some l > 0). Due to causality, these states are completely determined by the known forthcoming inputs. During the optimization at time instant t the known values of the input have to be fixed by equality constraints, which fits perfectly in the framework of a (mixed-integer) linear programming problem. Due to the information at time t it might be possible to conclude that certain future modes (ℓ(k + l) for l > 0) are not feasible any more. In that case we can set the switching probabilities for this mode at zero, and normalize the switching probabilities of the other modes. With these new probabilities we can perform the MPC optimization at time t.

Examples   The production systems of Examples 4 and 5 are used to demonstrate the design procedure for stabilizing model predictive controllers for SMPL systems with both types of switching procedures. In the first example the switching is purely stochastic, while in the second example the switching is both deterministic and stochastic.

Example: Production system I

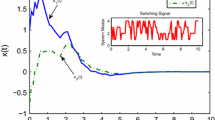
Consider the production system of Example 4. Note that the matrices $\Gamma^1_\rho({\tilde{\ell}}) = B^{(\ell)}$, ℓ ∈ {1, 2, 3} are all row-finite, and the matrices ${\mathcal{O}}^1_\rho({\tilde{\ell}}) = C^{(\ell)}$, ℓ ∈ {1, 2, 3} are all column-finite. This means that the SMPL system is structurally controllable and structurally observable. The maximum growth rate of the system is equal to λ = 6.5. We choose a reference signal given by r(k) = ρ · k , where ρ = 7.15 > λ. The initial state is taken equal to $x(0)= \left[5\;5\;5\right]^T$, and J is given by Eq. 43 for N _p = 4, and β = 10^− 4. In the experiment, the true switching sequence is simulated for a random sequence with the switching probability (4). We apply the presented MPC algorithm to this system. The optimization is done using a linear programming algorithm. Figure 6a gives the tracking error between the reference signal and the output signal y(k), for the switching sequence given in Fig. 6c, when the system is in closed loop with the receding horizon model predictive controller. It can be observed that y(k)  −  r(k) is initially larger than zero, which is due to the initial state. The error decreases rapidly and for k ≥ 13 the error is always equal to zero, which means that the product is delivered in time for all k ≥ 13. Figure 7b gives the difference between the input signal u(k) and the reference signal r(k).

Fig. 6

a Tracking error y(k)  −  r(k) , b control variable wrt. reference u(k)  −  r(k) , and c switching sequence ℓ(k)

Fig. 7

a Reference error y(k)  −  r(k) , b control variable wrt. reference u(k)  −  r(k) , and c switching sequence ℓ(k)

Example: Production system II

Consider the production system of Example 5. Note that also this SMPL system is structurally controllable and structurally observable. The maximum growth rate of the system is equal to λ = 6.5. We choose a reference signal given by r(k) = ρ · k, where ρ = 7.15 > λ. The initial state is equal to $x(0)= \left[5\;5\;5\right]^T$, and J is given by Eq. 43 for N _p = 4, and β = 10^− 4. In the experiment, the true switching sequence is simulated for a random sequence with the switching probability (5). We apply the MPC algorithm as presented in Section 5 to this system. The optimization turns out to be a mixed-integer linear programming problem. Figure 7a gives the reference error between the reference signal r(k) and the output signal y(k), for a switching sequence given in Fig. 7c, when the system is in closed loop with the receding horizon model predictive controller. It can be observed that y(k)  −  r(k) is initially larger than zero, which is due to the initial state. The error decreases rapidly and for k ≥ 9 the error is always equal to zero, which means that the the product is delivered in time for all k ≥ 9. Note that for v(k) = 0 we choose recipe B₁ (so ℓ(k) = 2) and for v(k) = 1 we choose recipe B₂ (so ℓ(k) = 3). For ℓ(k) = 1, the value v(k) is indefinite (which means that for mode 1 the value of signal v(k) has no influence). Figure 7b gives the difference between the input signal u(k) and the reference signal r(k).

6 Discussion

We have considered the control of switching max-plus-linear (SMPL) systems, a subclass of the discrete-event systems, in which the system can switch between different modes of operation. The switching between the modes can be deterministic or stochastic, and in each mode the discrete-event system is described by a max-plus-linear state space model with different system matrices for each mode.

In this paper we have revisited type-1 SMPL and type-2 SMPL systems, and we have shown that these two classes of SMPL systems are equivalent. Furthermore we have proven that every structurally finite SMPL system of these two types can be written as a type-d piecewise affine system or as a constrained max-min-plus-scaling system (provided that the output and state variables are bounded). An advantage of the equivalency is that we can use many tools, derived for piecewise affine system and max-min-plus-scaling systems, to analyze our SMPL systems.

We have also derived a stabilizing model predictive controller for SMPL systems. The resulting optimization problem is nonlinear with a piecewise polynomial cost criterion and linear inequality constraints. In the case of stochastic switching depending only on the previous mode, the resulting optimization problem can be solved using linear programming.

In future research we will continue our study on the relation between the various classes of SMPL systems. Further we will extend the SMPL system by the introduction of stochasticity in the system parameters, as was done in van den Boom and De Schutter (2004) for MPL systems. In this way we will be able to capture more stochastic issues in SMPL systems.