Sok: vector OLE-based zero-knowledge protocols

Abstract

A zero-knowledge proof is a cryptographic protocol where a prover can convince a verifier that a statement is true, without revealing any further information except for the truth of the statement. This article is a survey of recent developments in building practical zero-knowledge proof systems using vector oblivious linear evaluation (VOLE), a tool from secure two-party computation. In this work, we attempt to systematize the recent works on VOLE-based Zero-Knowledge proofs and make the state of the art accessible in one document.

1 Introduction

A zero-knowledge proof is a cryptographic protocol where a prover can convince a verifier that a statement is true, without revealing any further information except for the truth of the statement. More precisely, if x is a statement from an NP language verified by an efficient machine M, then a zero-knowledge proof aims to prove to the verifier that there exists a witness w such that $M(x,w)=1$, without revealing any further information about w. We say that the proof is a proof of knowledge, if the prover additionally convinces the verifier that it knows the witness w, rather than just of its existence. For example, a prover can use a ZK protocol to convince others that it knows an input that can cause stack overflow for some public program (e.g., when submitting a bug report to the Common Vulnerabilities and Exposures system) without revealing the input.

This article is a survey of recent developments in building practical zero-knowledge proof systems using vector oblivious linear evaluation (VOLE), a tool from secure two-party computation. This approach offers several advantages:

Fast prover. VOLE-based proof systems are scalable, meaning that the computational resources required by the prover and verifier are not much larger than what’s needed to verify the statement when given the witness in the clear.¹ Concretely, for statements given in a boolean circuit C, a multi-threaded prover incurs essentially no overhead in wall-clock evaluation time over a single-threaded evaluation of C in the clear. As a more concrete example, the authors of [2] recently demonstrated that evaluating AES as an optimized C-program (without using AES-specific CPU instructions) is 50x faster than evaluating AES in the ZK-proof system of [2].

Small memory. An attractive feature of many VOLE-based protocols is their low memory overhead: just as with plain computation, memory requirements are often only proportional to the cost of verifying the statement (given the witness). This is especially useful for complex statements, where for instance, the witness may be so large that it does not fit into memory, even though the proof can be verified efficiently in a streaming manner.

Post-quantum. With the possibility of large-scale quantum computing on the horizon, protocols based on traditional factoring or discrete log assumptions could become insecure to a quantum attacker. VOLE-based protocols, however, are instead based on variants of the learning parity with noise (LPN) assumption, which is related to the hardness of decoding random linear codes and currently believed to be resistant to quantum attacks.

Conceptual simplicity. VOLE-based protocols can be divided into two phases: a preprocessing phase, which usually consists of running the VOLE protocol on random inputs and which is essentially independent of the statement, and an online phase, where the proof takes place. By abstracting away the properties of the preprocessing, the online phase is very simple to describe, and can even be information-theoretically secure. As one of the simplest, practical ways of constructing zero-knowledge proofs for general statements, it may also be a valuable pedagogical resource.

These benefits also come with a few drawbacks, that can be seen as tradeoffs. Firstly, most VOLE-based ZK proofs have a large communication cost, that is, the amount of data sent between the prover and verifier often scales linearly with the size of the circuit that verifies the statement being proven. This inherently means that the runtime of the verifier must also scale linearly. Another possible drawback is that current constructions of VOLE-based ZK require a designated verifier. That is, the verifier must store a private state needed to verify a proof, which cannot be made public. It’s therefore more difficult to prove the same statement to many different verifiers, or in public, with these techniques.

1.1 Overview of this survey

In this work, we attempt to systematize the recent works on VOLE-based Zero-Knowledge proofs and make the state of the art accessible in one document.

In Sect. 2 we will outline the notation and tools that are the foundation for all VOLE-based ZK. This includes how proven statements can be formalized, the definition of Zero-Knowledge that we achieve as well as an overview of VOLE.

We will then, in Sect. 3, introduce a general abstraction that unifies the ideas behind the main VOLE-based ZK proofs into an Arithmetic Black Box, and how most of the ZK constructions follow given access to VOLE.

Section 4 is devoted to the main differences in which existing works implement the Multiplication in the Arithmetic Black Box, which is one of the main sources of interaction in the proof. Here, we give an introduction into how the Wolverine, Mac’n’Cheese, Line-Point ZK and QuickSilver protocols work.

Section 5 will discuss how follow-up works have added different operations to the Arithmetic Black Box, thus allowing the prove certain statements more efficiently. This includes ideas such as more efficient proofs of polynomial evaluation, SIMD circuits, disjunctions, conversions or proofs over rings instead of fields. We will moreover consider proofs of RAM programs based on VOLE protocols.

Finally, we will mention some interesting open questions in Sect. 6.

1.2 Related techniques in ZK

Zero-knowledge proofs were first introduced by Goldwasser, Micali and Rackoff in 1985 [30]. Since then, there has been a vast body of research in both theoretical and applied settings. Below, we mention a few of the techniques that are most relevant for those in this survey. For a more in-depth coverage, the ZKProof Community Reference² aims to give a comprehensive overview of the state-of-the-art.

1.2.1 Garbled circuits

Zero-knowledge proofs based on garbled circuits were first proposed by Jawurek et al. [35], with the key insight that garbled circuits already provide one-sided malicious security and ZK only needs one-sided privacy. It has many advantages of VOLE-based ZK but requires $\kappa$ bits of communication per AND gate even after optimizations [27, 53]. More recent works have also expanded this approach to support more efficient disjunctive proofs [33].

1.2.2 MPC-in-the-head

MPC-in-the-head by Ishai et al. [34] is an elegant way of constructing ZK proofs based on secure multi-party computation. Its concrete efficiency was first studied by Giacomelli et al. [29], which has led to a long line of practical ZK proofs in recent years, particularly for designing digital signatures. It could be made non-interactive but often needs communication linear in the circuit size.

1.2.3 SNARKs

In recent years, there has been a large focus on Succint non-interactive arguments of knowledge (SNARKS) [28], which are protocols where the communication complexity, that is, the size of the proof, is very small, potentially even constant size or logarithmic in the witness length. A drawback of most SNARKs is that succinctness comes at the cost of a more expensive prover, which often has super-linear computational complexity (with a few exceptions [31, 54]) and large memory requirements (linear to the statement size).

1.3 Applications

VOLE-based ZK proofs enjoy high efficiency and scalability: they could prove tens of millions of gates even under a small bandwidth connection and low-configured hardware. As a result, it has the potential to enable many exciting applications.

• 1. Proofs of program properties. When expressing properties about a program $\Pi$ formally, automated theorem provers can allow formally attesting the presence of certain properties using a proof $\pi$. By encoding the verification of a given proof for a public $\Pi$ as the input to a ZK proof system, a prover can e.g. show that a program shows certain information leakage, without revealing the proof $\pi$ that explains this behavior [43].

• 2. Proofs of machine-learning tasks. Machine-learning tasks often involve sensitive data (e.g. biometric information) or valuable data (e.g., large models) where ZK proofs could help to enhance privacy. Until recent, ZK for ML is limited because statements on ML are usually large. Recent works have shown the feasibility of proving inference of deep neural networks in ZK [37, 49].

• 3. Proofs of signature validity on private messages. [45] considers a case where applicants would like to prove their medical qualification without revealing how they qualify and which healthcare provider signed the evidence. This requires proving that a private digital document is signed by someone from an public authorized list and that the same document implies medical validity.

• 4. Proofs of unsatisfiability. The correctness verification of computer programs is commonly done by showing the unsatisfiability of a certain SAT formula, which is decided by the program and the property to be proven. Proving formula unsatisfiability in ZK [38] could enable applications like 1) showing the correctness of a public program without revealing why; and 2) showing the correctness of a private program.

2 Preliminaries

We use lower case, bold symbols for vectors $\textbf{x}$ and upper case, bold symbols for matrices $\textbf{A}$. We use $\kappa$ as the computational and $\sigma$ as the statistical security parameter. Generally, the prover is denoted as $\mathcal {P}$ while the verifier is $\mathcal {V}$. In our UC functionalities and proofs, $\mathcal {Z}$ denotes the environment, and $\mathcal {S}$ is the simulator, while $\mathcal {A}$ will refer to the adversary. When we say that an algorithm is Probabilistic Polynomial Time (PPT), then we mean that it can be expressed as a probabilistic interactive turing machine whose worst-case runtime can be expressed as a polynomial in $\kappa$. For any finite set S, we denote by |S| the cardinality of S. If instead s is a string, then |s| denotes its length. If $s_1,s_2$ are strings then denotes the concatenation of strings.

2.1 The computational model: arithmetic circuits

The zero-knowledge proofs in this survey are used by a PPT prover $\mathcal {P}$ to convince a PPT verifier $\mathcal {V}$ that a certain statement is true, and furthermore, that $\mathcal {P}$ knows a witness for the statement. This means they are proofs of knowledge. Abstractly, both $\mathcal {P}$ and $\mathcal {V}$ consider a language $\mathcal {L}$ together with a relation $\mathcal {R}_{\mathcal {L}}$. For a string x input to both $\mathcal {P}$ and $\mathcal {V}$, $\mathcal {P}$ will convince $\mathcal {V}$ that it knows a w such that $(x,w)\in \mathcal {R}_{\mathcal {L}}$, i.e. $x\in \mathcal {L}$. Here, $\mathcal {R}_{\mathcal {L}}$ is an NP relation, which means that there exists a Turing Machine (TM) M which, on input x, w, accepts in time poly(|x|) iff $x\in \mathcal {L}$. Instead of expressing computation as happening on a Turing machine M, we will require that each x can, in time poly(|x|), be converted into a circuit C over a ring $(R,+,\times )$ whose gates correspond to efficiently computable³ functions defined over R. We require that $C(w)=0$ iff $(x,w)\in \mathcal {R}_{\mathcal {L}}$, except with negligible probability in $\kappa$. This requirement is without loss of generality, as such a circuit can always be constructed using the Cook-Levin Theorem.

More concretely, our statements are circuits C over a ring R. We define their semantics as follows: Consider the tuple $C=(n_{in},n_{out},n_{g},\texttt{I},\texttt{G})$ where

• $n_{in}\ge 2$ is the number of input wires, $n_{out}\ge 1$ the number of output wires and $n_{g}\ge 1$ the number of gates in the circuit. We let $n_w = n_{in}+n_{g}$ be the number of wires.

• We define the sets $Inputs\leftarrow \{1,\dots ,n_{in}\}$, $Wires\leftarrow \{1,\dots ,n_w\}$ as well as $Outputs\leftarrow \{n_w-n_{out}+1,\dots ,n_w\}$ and $Gates\leftarrow \{n_{in}+1,...,n_w \}$ to identify the respective elements in the circuit.

• The poly-time computable function $\texttt{I}: Gates \mapsto 2^{Wires\setminus Outputs}$ identifies the incoming wires for each gate, with the restrictions that:

  • $\forall g \in Gates: \texttt{I}(g) \ne \emptyset$.

  • $\forall g \in Gates:\text {max}_{s\in \texttt{I}(g)}\{s \}<g$.

• The poly-time computable mapping $\texttt{G}: Gates \mapsto \left( R^+ \mapsto R \right)$ determines the function that is computed by a gate. We require that

  • 1. $\forall g\in Gates:$ The input length of $\texttt{G}(g)$ is identical to $|\texttt{I}(g)|$.

  • 2. $\forall g\in Gates:$ The function $\texttt{G}(g)$ can be computed in time $poly(|\texttt{I}(g)|,\log (|R|))$.

To obtain the outputs of the above circuit when evaluating it on an input

one evaluates C as follows:

eval(C, w):

• 1. For $i\in \{1,\dots , n_{in}\}$ set $x_i=w_i$.

• 2. For $g\in \{n_{in}+1,\dots ,n_w\}$:

  • (a) $(s_1,\dots ,s_{|\texttt{I}(g)|})\leftarrow \texttt{I}(g)$ where $s_i<s_{i+1}$

  • (b) $f \leftarrow \texttt{G}(g)$

  • (c) $x_g\leftarrow f(x_{s_1},\dots ,x_{s_{|\texttt{I}(g)|}})$

• 3. Output

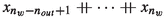
We denote by C(w) the aforementioned evaluation of C on input w.

2.2 Zero knowledge proofs for circuits

We define Zero-Knowledge Proofs (of Knowledge) in the Ideal-Real paradigm. Let $\Pi$ be an interactive protocol between two PPT interactive Turing Machines (iTMs) $\mathcal {P},\mathcal {V}$. This means that parties might send messages to each other, as well as to idealized functionalities. Define the functionality $\mathcal {F}_\textsf{ZK}$ as in Fig. 1.

Fig. 1

Functionality for ZK proofs over the ring R

Let $\mathcal {A}$ be a PPT iTM algorithm, called the adversary. $\mathcal {A}$ is allowed to corrupt either of the parties, or none at all. If a party is corrupted, then $\mathcal {A}$ will have full control over that party and be allowed to read all its secrets and send any messages on its behalf. It has to specify in the beginning which party, if at all, $\mathcal {A}$ will corrupt.

We define security with respect to a PPT iTM $\mathcal {Z}$ called environment. The environment provides inputs to and receives outputs from the parties. Furthermore, the adversary $\mathcal {A}$ will corrupt a party in the name of $\mathcal {Z}$. To define security, let $\Pi \circ \mathcal {A}$ be the distribution of the output of an arbitrary $\mathcal {Z}$ when interacting with $\mathcal {A}$ in a real protocol instance $\Pi$. Furthermore, let $\mathcal {S}$ denote an ideal world adversary and $\mathcal {F}_\textsf{ZK} \circ \mathcal {S}$ be the distribution of the output of $\mathcal {Z}$ when interacting with parties which run with $\mathcal {F}_\textsf{ZK}$ instead of $\Pi$ and where $\mathcal {S}$ takes care of adversarial behavior.

Definition 2.1

(Zero-Knowledge Proof of Knowledge) We say that $\Pi$ is a Zero-Knowledge Proof of Knowledge if for every PPT iTM $\mathcal {A}$ that maliciously corrupts at most 1 party there exists a PPT iTM $\mathcal {S}$ (with black-box access to $\mathcal {A}$) such that no PPT environment $\mathcal {Z}$ can distinguish $\Pi \circ \mathcal {A}$ from $\mathcal {F}_\textsf{ZK} \circ \mathcal {S}$ with non-negligible probability in $\kappa$.

2.3 Vector oblivious linear evaluation (VOLE)

A VOLE correlation is a pair of random variables $(\textbf{u}, \textbf{x})$ and $(\textbf{v}, \Delta )$, where $\textbf{x}, \textbf{u}, \textbf{v}$ are vectors and $\Delta$ is a scalar, which are all random subject to the constraint that

$$\begin{aligned} u_i = v_i + x_i \cdot \Delta \end{aligned}$$

One party, in our case the prover $\mathcal {P}$, is given $\textbf{u}, \textbf{x}$, while the verifier $\mathcal {V}$ learns $(\textbf{v}, \Delta )$.

We model the generation of VOLE correlations as an ideal functionality $\mathcal {F}_{\textsf{VOLE}}^{d}$, given in Fig. 2. Here d is the length of the vectors $\textbf{u}$, $\textbf{x}$, and $\textbf{v}$. The functionality works over a ring R; in most cases, we require that R is a finite field, but in Sect. 5.5 we also discuss how to support non-field rings such as $R=\mathbb {Z}_{2^k}$, the integers modulo $2^k$. On initialization, the functionality samples a MAC key $\Delta \in R_{\textsf{key}}^t$, where $R_{\textsf{key}}\subset R$ for some parameter $t \ge 1$ such that $|R_{\textsf{key}}^t |$ is exponentially large in the security parameter. When R is a field, we typically choose $R_{\textsf{key}}^{}=R$. After initialization, the $\textsf{Extend}$ command may be called repeatedly. On each call, it samples one more “element” of the VOLE correlation, which we view as a MAC M[x] on a random element x given to the prover, where the verifier learns only the corresponding key K[x] (as well as the global key $\Delta$).

In the rest of this paper, we assume that such a functionality can be efficiently realized using a secure VOLE protocol. To justify this, we outline which approaches currently exist to implement $\mathcal {F}_{\textsf{VOLE}}^{d}$ efficiently with active security.

Fig. 2

Functionality for VOLE over $R^t$ with a message from the ring R, and scalar $\Delta$ from $R_{\textsf{key}}^t$, where $R_{\textsf{key}}\subset R$

2.3.1 Instantiate $\mathcal {F}_{\textsf{VOLE}}^{d}$ directly

The two most popular approaches use linearly homomorphic encryption or OT extension protocols. For homomorphic encryption, the approach is usually that $\mathcal {V}$ samples a public key/private key pair, then sends an encryption of $\Delta$ to $\mathcal {P}$. $\mathcal {P}$ picks $x,M[x]$ and, using the homomorphism, computes an encryption of $K[x]$ that it sends to $\mathcal {V}$. Finally, $\mathcal {V}$ can decrypt this result. While it is easy to achieve passive security by rerandomizing the ciphertext containing $K[x]$ appropriately, achieving active security usually requires additional consistency checks such as specialized zero-knowledge proofs. See e.g. [3, 20, 21] for variants on this approach. An alternative solution is to use Oblivious Transfers to perform the multiplications, leading to highly efficient protocols such as [36, 46], or [47] when R is a ring such as $\mathbb {Z}_{2^k}$. The disadvantage of all these protocols is that the communication between $\mathcal {P}$ and $\mathcal {V}$ scales at least linearly in the number of VOLE correlations n, which can easily become a bottleneck when a large number of correlations are needed.

2.3.2 Extend VOLEs efficiently

Current state-of-the-art VOLE extension protocols all stem from the approach of Boyle et al. [10], which builds a pseudorandom correlation generator based on (variants of) the learning parity with noise (LPN) assumption. This approach exploits the fact that sparse LPN errors can be used to compress secret-sharings of pseudorandom vectors, allowing the two parties to generate a long, pseudorandom instance of a VOLE correlation in a succinct manner from a short vector of VOLE correlations.

These protocols usually proceed along the following lines:

• 1. Construct a protocol for single-point VOLE, where the sender’s input vector has only a single non-zero entry.

• 2. The single-point VOLE protocol is repeated t times, to obtain a t-point VOLE where the sender’s input is viewed as a long, sparse, LPN error vector.

• 3. Combine t-point VOLE and the LPN assumption, allowing the parties to locally obtain pseudorandom VOLE by applying a linear mapping.

Using this blueprint leads to (random) VOLE protocols with communication much smaller than the output length, which is sufficient to build Zero-Knowledge protocols as we shall see. It can be seen as a form of VOLE extension, where in the first step, a small “seed” VOLE of length $m \ll n$ is used to create the single-point VOLEs, and then extended into a longer VOLE of length n. In the Ferret protocol [51], it was additionally observed that when repeating this process, it can greatly help communication if m of the n extended outputs are reserved and used to bootstrap the next iteration of the protocol, saving generation of fresh seed VOLEs whose computation is usually more involved as outlined above.

To use VOLE as part of a ZK protocol, we will need that it is actively secure. If R is a field, then VOLE extension can efficiently be done by picking a protocol such as [11, 48]. These also allow the secret x to be from a subfield of R, which yields more efficient constructions when the proof circuit is defined over a small field such as $\mathbb {F}_2$. For $R=\mathbb {Z}_{2^k}$, the recent work of [1] described how to adapt [10, 48] with a consistency check that is secure if the underlying LPN instance tolerates a small amount of leakage on the noise vector.

2.4 Schwartz–Zippel Lemma

A crucial building block in all presented protocols is the Schwartz-Zippel Lemma over finite fields, which allows for efficient polynomial identity tests. The version which we use, proven by Ore [42], works as follows:

Lemma 2.1

(Schwartz-Zippel Lemma) Let $\mathbb {F}$ be a finite field, $S\subseteq \mathbb {F}$ and $P\in \mathbb {F}[X]$ be a non-zero polynomial of degree $d\ge 0$. Then

$$\begin{aligned} \Pr _{s\xleftarrow {\$} S}[P(s)=0]\le \frac{d}{|S|}\text {.} \end{aligned}$$

3 A general framework for VOLE-based ZK

3.1 Homomorphic MACs from VOLE

VOLE can be used to build a simple, information-theoretic MAC scheme with useful homomorphic properties. Prior works have shown numerous MAC schemes with different properties that follow a similar paradigm [6, 14, 18, 19]. The MAC scheme is oblivious, in the sense that the prover will hold MACs on certain values, while only the verifier knows the corresponding MAC key. For example, consider running VOLE over a finite field $\mathbb {F}$, i.e. $\mathcal {F}_{\textsf{VOLE}}^{d}$ with $R=\mathbb {F}$, $R_{\textsf{key}}= R$ and $t=1$. A single output from a random VOLE can be seen as a MAC on the value $x \in \mathbb {F}$ obtained by the prover. The prover also learns the MAC M[x], while the verifier holds the MAC key, which consists of a random $K[x] \in \mathbb {F}$ and the fixed key $\Delta \in \mathbb {F}$, satisfying

$$\begin{aligned} K[x] = M[x] - \Delta \cdot x \end{aligned}$$

If the prover wants to send x to the verifier, this can be authenticated by additionally sending M[x]: the verifier simply checks the above equation holds.

The MAC cannot be forged with probability larger than $1/|\mathbb {F} |$. To see this, consider a cheating prover who sends $x' \ne x$ together with a MAC $M[x']$. If verification succeeds, we have $M[x] - \Delta \cdot x = M[x'] - \Delta \cdot x'$, and so $(M[x] - M[x'])\cdot (x - x')^{-1} = \Delta$. This implies that the prover must have guessed $\Delta$, by coming up with $x',M[x']$ that pass the check. Crucially, this check relies on $x-x'$ being invertible, which in the given case⁴ is of course always true.

3.1.1 Linear homomorphism

Since the MAC equation is linear, and $\Delta$ is fixed for every VOLE output, it’s easy to see that any public, linear function can be applied to MACs. The parties can also create a MAC on a public constant $c \in \mathbb {F}$, by defining $M[c] = 0$ and $K[c] = -c\cdot \Delta$; this allows homomorphically computing affine functions.

3.1.2 Multiplicative homomorphism

The MACs are also multiplicatively homomorphic, with the caveat that the storage complexity increases. To see this, let (x, M[x]) held by the prover define a linear polynomial $p(s) = M[x] + x \cdot s$ in s. The verifier then holds the random key $\Delta$, and the evaluation $p(\Delta )$. Now consider a second such MAC on y, and polynomial $q(s) = M[y] + y \cdot s$. The product p(s)q(s) is now a degree-two polynomial, whose coefficients are held by the prover.

The drawback of homomorphically multiplying MACs is that the size of the resulting MAC scales with the number of multiplications (i.e. the degree of the function). However, this can still be exploited, as we see in Sects. 4.3 and 4.3.3.

3.1.3 MACs over small fields

The approach outlined above does not achieve sufficient security if $|\mathbb {F} |$ is small. For example, when $\mathbb {F} =\mathbb {F} _2$, the MAC only delivers 1 bit of security! Luckily, the approach generalizes to arbitrary $t>1$. Namely, let $R_{\textsf{key}}=R^t$ where $R=\mathbb {F}$ for an arbitrary finite field. The same security argument as before does apply: if a cheating prover who sends $x' \ne x$ together with a MAC $M[x']$ succeeds in verification, then we have $M[x] - \Delta \cdot x = M[x'] - \Delta \cdot x'$, and therefore $(M[x] - M[x'])\cdot (x - x')^{-1} = \Delta$ which can be computed over $R^t$ by coordinate-wise division by $x-x'$. Therefore, a forgery can now only happen with probability $1/|\mathbb {F} |^t$.

$\mathcal {F}_{\textsf{VOLE}}^{d}$ for this setting can efficiently be instantiated by considering R as a subfield of $R^t$ using the machinery from [12]. It also lends itself to updates on the MACed value x with low communication, since only a value over R but not $R^t$ must be communicated to do so. The linear homomorphism of the MAC scheme again follows directly from its setup. By considering $R^t$ as the degree-t extension field of R instead of just a vector space, the multiplicative homomorphism (and how it is exploited in this work) can also be recovered.

In Sect. 5.5, we show how this type of homomorphic MAC can also be made to work over rings, with some differences to the soundness guarantees and repercussions on ring size.

3.2 Arithmetic black box for ZK

The functionality $\mathcal {F}_\textsf{ZK}$ introduced in Fig. 1 is only able to process a circuit C over a ring in a block. However, VOLE-based ZK can often provide a more flexible functionality where parties can prove the circuit progressively in a gate-by-gate manner. This is crucial e.g. for memory-friendliness, since wires which are no longer needed can be dropped from memory. To abstract this capability in VOLE-based ZK, we now refine $\mathcal {F}_\textsf{ZK}$ into $\mathcal {F}_\textsf{ABB}$ in Fig. 3 which performs exactly this job. To use $\mathcal {F}_\textsf{ABB}$ to realize $\mathcal {F}_\textsf{ZK}$, two parties can use the $\textsf{Input}$ to obtain handles to the committed witness; then they can traverse the circuit following topological order: each linear gate can be computed using Affine combination and each non-linear gate can be computed using multiplication check. In the end, two parties hold a handle for the output wire which can be asserted using $\textsf{CheckZero}$.

Fig. 3

Functionality modeling an arithmetic black box over the ring $R$

This functionality $\mathcal {F}_\textsf{ABB}$ is what protocols such as [2, 48] and follow-ups actually implement. Their observation is that Vector-OLEs output by $\mathcal {F}_{\textsf{VOLE}}^{d}$ can be used to securely store inputs by $\mathcal {P}$ such that linear functions of secrets can be computed without interaction. In the following, whenever a value x is stored inside $\mathcal {F}_\textsf{ABB}$, then we denote it as [x]. This is equivalent to the value x being MACed (as outlined in Sect. 3.1), which is why the same notation is used. If $R=\mathbb {Z}_s$ for some $s\in \mathbb {N}$, then we write $[x]_s$ to clarify the modulus used in $\mathcal {F}_\textsf{ABB}$. We leave out the subscript if the ring is clear from the context.

To realize $\mathcal {F}_\textsf{ABB}$ for the case where $R=\mathbb {F}$, both parties initially call Init of $\mathcal {F}_{\textsf{VOLE}}^{d}$ to make commitments available. Then they proceed as follows.

Random

• 1. The parties call Extend on $\mathcal {F}_{\textsf{VOLE}}^{d}$ and assign the returned $(r,M[r],K[r])$ the id $\textsf{id}$.

Input

• 1. The parties call Extend on $\mathcal {F}_{\textsf{VOLE}}^{d}$, which returns $(r,M[r])$ to $\mathcal {P}$ and $K[r]$ to $\mathcal {V}$.

• 2. $\mathcal {P}$ computes $\delta =x-r$ over R and sends $\delta$ to $\mathcal {V}$.

• 3. $\mathcal {P}$ sets $M[x]\leftarrow M[r]$ while $\mathcal {V}$ sets $K[x]\leftarrow K[r]-\Delta \delta$ and both parties assign $(x,M[x],K[x])$ the id $\textsf{id}$.

Check Zero If only one $\textsf{id}$ needs to be checked, then this can be done as follows:

• 1. $\mathcal {P}$ looks up $M[0]$ for the id $\textsf{id}$, while $\mathcal {V}$ looks up $K[0]$. If it is undefined, then abort.

• 2. $\mathcal {P}$ sends $M[0]$ to $\mathcal {V}$, who checks that $K[0]=M[0]$.

If more than one $\textsf{id}$ needs to be checked, then $\mathcal {P},\mathcal {V}$ can also apply a Collision-Resistant Hash Function to compress their values and save communication bandwidth.

Affine Combination

• 1. $\mathcal {P}$ looks up $x_1,\dots ,x_n,M[x_1],\dots ,M[x_n]$ for the ids $\textsf{id}_1,\dots ,\textsf{id}_n$, while $\mathcal {V}$ looks up $K[x_1],\dots ,K[x_n]$. If either of these is undefined, or $\textsf{id}_0$ is already defined, then abort.

• 2. $\mathcal {P}$ locally sets $x_0\leftarrow \alpha _0+\sum _i \alpha _i x_i$ and $M[x_0]\leftarrow \sum _i \alpha _i M[x_i]$, while $\mathcal {V}$ locally sets $K[x_0]=\sum _i \alpha _i K[x_i] - \alpha _0\Delta$.

In the case where $R=\mathbb {F}$ then one can easily write a simulator, following Definition 2.1, to show that the aforementioned subprotocols implement the desired parts of the functionality $\mathcal {F}_\textsf{ABB}$ securely. The main idea is that $\mathcal {V}$ does not learn any information, since the outputs of $\mathcal {F}_{\textsf{VOLE}}^{d}$ leak no information about the outputs given to $\mathcal {P}$, while every input during Input is blinded using a uniformly-random value from $\mathcal {F}_{\textsf{VOLE}}^{d}$. Affine Combination is entirely non-interactive, while the value that $\mathcal {V}$ obtains during Check Zero is predetermined. A cheating $\mathcal {P}$ can only change the outputs during Check Zero such that $\mathcal {V}$ accepts a non-zero value, but as shown in Sect. 3.1, this reduces to $\mathcal {P}$ being able to guess $\Delta$. This value is never revealed to $\mathcal {P}$ by $\mathcal {F}_{\textsf{VOLE}}^{d}$, which finishes the claim. The exact details are shown in the referenced works⁵.

What is left to implement is the Multiplication Check of $\mathcal {F}_\textsf{ABB}$. This is actually the core of much of the early work on VOLE-based Zero Knowledge. We will summarize the state-of-the-art in the following section.

Fig. 4

The Wolverine multiplication check protocol

4 Multiplication checks

4.1 Wolverine multiplication check

The Wolverine multiplication check protocol [48] can be viewed as a direct application of the bucketing technique introduced in the context of malicious secure computation [19, 40, 41]. The only difference is that only the prover has a privacy requirement (i.e. zero-knowledge) and thus the bucketing only needs to be done for one layer. In more detail, the protocol proceeds in the following steps:

• 1. Given a list of authenticated tuples to be checked, two parties generate $nB+c$ number of extra random authenticated multiplication tuples that are correct if the prover is honest.

• 2. The verifier randomly picks c tuples out of the $nB+c$ newly generated ones and checks if they have the correct relationship. If so, the remaining nB random authenticated multiplication triples must have a high proportion of good triples. Since all tuples are committed, the check can be done at the end of the protocol as well.

• 3. For the remaining nB triples, the verifier specifies a random permutation to group them randomly into n buckets each with B triples per bucket.

• 4. For the i-th input triple, all triples in the i-th bucket are “sacrificed” to check the correctness one at a time. The sacrifice procedure does detect cheating unless both the “input” triple and the “sacrificed” triple are incorrect simultaneously.

Details of the protocol can be found in Fig. 4. A careful analysis shows that by setting c, B appropriately, we can ensure that the proportion of incorrect triples that survive after step 2 of the outlined protocol is low. Then, with overwhelming probability during Step 4 not all B “sacrificing” tuples in a bucket can be faulty, as the permutation is chosen at random. Therefore, if any “input” multiplication tuple was faulty, it would be detected during Step 4 and the check would fail. In summary:

Theorem 4.1

For any field $R=\mathbb {F}$ and integer t and if $c\ge B$, the protocol in Fig. 4 securely instantiates CheckMult in Fig. 3 with statistical error of $1/\left( {\begin{array}{c}\ell \\ B\end{array}}\right) +O(\ell /|\mathbb {F}|^t)$.

4.2 Mac’n’Cheese multiplication check

The protocol from Sect. 4.1 requires 3B sent ring elements per verified multiplication. We now discuss two different approaches. The first only sends 2 ring elements per multiplication check for large fields and builds on Beaver’s circuit randomization technique [5]. The second builds on a protocol from Boneh et al. [9], where the idea is to reduce proving n multiplicative relations to checking a dot product of length n. This comes at the cost of communicating $n+O(\log (n))$ R-elements. In particular, for $R=\mathbb {F}_p$ for $p = 2^{61} - 1$ their protocol requires around 64.3 bits of communication per multiplication.

4.2.1 Warm-up: multiplication checks using circuit randomization

Consider $\mathcal {P}$ has created [x], [y], [z] and wants to show that $z=x\cdot y$. To do so, first both $\mathcal {P},\mathcal {V}$ use $\mathcal {F}_{\textsf{VOLE}}^{d}$ to create a random [a]. Additionally, $\mathcal {P}$ creates [c] where $c=a\cdot y$.

Upon obtaining a challenge e from $\mathcal {V}$, both parties now compute $[\varepsilon ]=e\cdot [x]-[a]$ and $\mathcal {P}$ sends $\varepsilon$ to $\mathcal {V}$. Then, $\mathcal {P}$ shows that both $[\varepsilon ]-\varepsilon$ and $e\cdot [z]-[c]-\varepsilon [y]$ are commitments to 0.

Assuming that $[\varepsilon ]$ was indeed opened correctly, consider the case where $[z]=[x\cdot y + \delta ]$ for a non-zero $\delta$, while $[c]=[ay+\gamma ]$ for a possibly non-zero $\gamma$. Assume that $e\cdot [z]-[c]-\varepsilon [y]$ is indeed a commitment to 0. Then once can easily show that this implies that $e\delta =\gamma$, implying that $e=\gamma /\delta$ for $\gamma ,\delta$ that $\mathcal {P}$ has to choose before it knows e. This in turn only succeeds with probability $1/p^k$, as e is chosen uniformly at random. Therefore, for small fields this test has to be repeated multiple times to achieve low enough soundness error.

4.2.2 Multiplication checks via inner product checks

Boneh et al. [9] introduce a logarithmic-sized proof for “parallel-sum” circuits. In a “parallel-sum” circuit, identical subcircuits $C'$ are evaluated in parallel on possibly different inputs, with the sum of the outputs of each $C'$ being the output of the overall circuit. The high-level idea of the proof protocol is to embed checks for different instances of $C'$ within a single polynomial, allowing $\mathcal {V}$ to verify n instances of $C'$ in parallel. When letting $C'$ be a single multiplication of its two inputs, can then be used to simultaneously verify the sum of n multiplications, which is equivalent to a dot product. Denote the protocol that checks the dot product $\textsf{AssertDotProduct}$.

The $\textsf{AssertDotProduct}$ protocol works as follows. Suppose $\mathcal {P}$ wants to prove that $[z] = \sum _{i\in [n]} [x_i] [y_i]$. $\mathcal {P}$ begins by defining n polynomials $f_1, \dots , f_{n/2}, g_1, \dots , g_{n/2}$ such that $f_i(j)^{} = x_{(j-1)n/2 + i}$ and $g_i(j) = y_{(j-1)n/2 + i}$ for $j\in \{1,2\}$, and then computing $h = \sum _{i\in [n/2]} f_i g_i$. $\mathcal {P}$ then commits to h by committing to its coefficients (denoted as [h]). $\mathcal {V}$ defines its own polynomials $f'_i, g'_i$ over the values $[x_{(j-1)n/2 + i}]$ and $[y_{(j-1)n/2 + i}]$ that are stored in $\mathcal {F}_\textsf{ABB}$ to check that $\sum _{i\in [n/2]} f'_i g'_i = h$. By Schwartz-Zippel, this can be done by checking that

$$\begin{aligned} \sum \nolimits _{i\in [n/2]} f'_i(r) g'_i(r) = h(r) \end{aligned}$$

for a random r chosen by $\mathcal {V}$. Here, observe that the evaluation of $f_i',g_i',h$ in a public constant r boils down to multiplying the committed coefficients of each polynomial with appropriate powers of r and summing up the result, both of which are linear operations in $\mathcal {F}_\textsf{ABB}$ that do not require any interaction. Then, verifying the above equation after fixing r is again a dot product check, although over vectors of length n/2, and we can recursively apply $\textsf{AssertDotProduct}$ until n is of constant size. Note that only 4 R-elements are communicated during one iteration of $\textsf{AssertDotProduct}$: 3 when committing to h and one when sending r. See Fig. 5 for a formal presentation of the protocol. There, for the base-case of $\textsf{AssertDotProduct}$, one can e.g. use the multiplication checking procedure from Sect. 4.2.1.

Given $\textsf{AssertDotProduct}$, we can batch-verify n multiplications as follows:

• 1. Assume that n tuples $[x_i],[y_i],[z_i]$ have been committed by $\mathcal {P}$.

• 2. $\mathcal {V}$ chooses a randomization factor r that it sends to $\mathcal {P}$.

• 3. $\mathcal {P}$ shows that $\langle r^i [x_i], [y_i] \rangle = \sum _{i\in [n]} r^i [z_i]$. Since r is public, computing $r^i [x_i]$ and $\sum _{i\in [n]} r^i [z_i]$ is local.

This protocol, called $\textsf{AssertMultVec}$, is presented in Fig. 5.

Fig. 5

Protocols for efficient multiplications. See text for necessary notation

It is clear that both $\textsf{AssertDotProduct}$ and $\textsf{AssertMultVec}$ are complete and zero-knowledge. The following theorem, proven in [2], shows they are also sound.

Theorem 4.2

If $R=\mathbb {F}_{p^k}$ and the protocol $\textsf{AssertMultVec}$ passes, then the input commitments have the required relation except with probability $\frac{n+4\log {n} + 1}{p^k-2}$

The number of rounds of interaction in $\textsf{AssertDotProduct}$ is logarithmic in the number of multiplications n. [2] also show that, using the Fiat-Shamir transform [25], the number of rounds can be made constant by assuming a random oracle.

An alternative version of $\textsf{AssertMultVec}$ with a soundness error that is only logarithmic in n can be achieved as follows:

$\textsf{AssertMultVec} '(\{([x_i], [y_i], [z_i])\}_{i\in [n]})$:

• 1. $\mathcal {V}$ samples $r_1,\dots ,r_n \in _R R$ and sends them to $\mathcal {P}$.

• 2. $\textsf{AssertDotProduct} (r_1[x_1], \dots , r_n [x_n], [y_1], \dots , [y_n], \sum _{i\in [n]} r_i [z_i])$.

One can easily show that $\textsf{AssertMultVec} '$ has the desired soundness, although at the expense of communicating more random elements from $\mathcal {V}$ to $\mathcal {P}$. In practice, one can optimize this by having $\mathcal {V}$ choose a random PRG seed that it sends to $\mathcal {P}$, with $r_1,\dots ,r_n$ derived deterministically from the seed.

4.3 LPZK multiplication check

The Line Point Zero Knowledge (LPZK) work of [23] introduces the concept of an LPZK proof system, where the prover constructs a line and the verifier queries a single point on that line, and determines from this point whether to accept or reject the proof (see Fig. 6). This geometric presentation emphasizes the simplicity and algebraic character of the VOLE commitment scheme, which will be used in a non-black box construction.

In the LPZK multiplication check, the witness and all intermediate wire values are stored in the vector $\textbf{a}$ (see Fig. 6). The underlying intuition is that the verifier will perform a series of calculations on the vector $\textbf{v}:= \textbf{a} \alpha + \textbf{b}$ and the prover will mirror the verifier by performing the same calculations on the vector of formal polynomial expressions given by $\textbf{a} t + \textbf{b}$, treating t as an indeterminate.

The results of these calculations are a collection of values held by the verifier that are the evaluations at $\alpha$ of corresponding polynomials held by the prover. Conditions on the coefficients of these polynomials correspond to conditions on the vectors $\textbf{a},\textbf{b}$, and so can be used to prove that the extended witness satisfies the desired relation. Concretely, the LPZK multiplication check builds a series of quadratic polynomials (one per multiplication gate) whose leading coefficients are zero if and only if the corresponding gates are evaluated correctly. The resulting “polynomial checks” we need to verify these coefficients are zero can be efficiently batched together, saving on communication.

Fig. 6

Geometry of line point zero knowledge

4.3.1 Single gate example

To demonstrate how the above language of LPZK translates into proving multiplication relations, we give a commit-and-prove protocol for the relation $R(x,y,z):= xy-z$ as an LPZK over $\mathbb {F}$ with binding and soundness error $\le 2/|\mathbb {F}|$.

The (honest) prover chooses some triple (x, y, z) and constructs a line $\textbf{a} t + \textbf{b}$ by setting

$$\begin{aligned} \textbf{a} = (a_1,a_2,a_3,a_4):= (x,y,z,xb_2 + yb_1 - b_3) \end{aligned}$$

with $b_1,b_2,b_3$ chosen uniformly at random and $b_4:= b_1 b_2$. We write

$$\begin{aligned} \textbf{v}(t):= \textbf{a} t + \textbf{b}, \end{aligned}$$

for the line held by the prover, and $\textbf{v} = \textbf{a}\alpha + \textbf{b}$ for the point received by the verifier, for a random $\alpha \in \mathbb {F}$. We likewise write the prover’s view of the entries as

$$\begin{aligned} \textbf{v}(t) = (v_1(t),v_2(t),v_3(t),v_4(t)), \end{aligned}$$

and write $v_i$ for $v_i(\alpha )$. The verifier now checks whether

$$\begin{aligned} v_1 v_2 - \alpha v_3 - v_4 = 0. \end{aligned}$$

If the prover is honest, we have

$$\begin{aligned} v_1v_2 - \alpha v_3 - v_4 =&(xy-z)\alpha ^2 + (x b_2 + y b_1 - b_3 - (xb_2+yb_1-b_3)) \alpha \\&+ b_1 b_2 - b_4 \\ =&0 \end{aligned}$$

identically, as long as $xy-z=0$. In other words, $v_1 v_2 - \alpha v_3 - v_4$ is a quadratic in $\alpha$ that is identically zero if and only if the prover is honest. For a cheating prover, $v_1 v_2 - \alpha v_3 - v_4$ will be equal to some nonzero polynomial in $\alpha$, and so breaking the binding property would be equivalent to $\mathcal {P}$ guessing $\alpha$, while breaking soundness would be equivalent to $\mathcal {P}$ constructing a polynomial of degree 2 which has $\alpha$ as a root, which gives binding and soundness error $\le 2/|\mathbb {F}|$, by the Schwartz-Zippel Lemma, as desired. Note that this is a special case of the LPZK construction sketched above, since being identically zero is a stronger condition than having a zero leading coefficient.

When constructing LPZK from a random VOLE, this protocol requires communication for each entry of $\textbf{a}$ and $\textbf{b}$ which cannot be set randomly by the prover. Here, we require communication of five field elements: four elements for the values $a_1,\dots ,a_4$ and an additional element of communication for the value $b_4$.

4.3.2 Polynomial checks

To emphasize the similarity of the one gate example to the IT-MAC that we defined in Sect. 3.1, we can instead write the triple $(\textbf{a}, \textbf{b}, \textbf{v})$ as $(\textbf{x}, M[\textbf{x}], K[\textbf{x}])$. Then setting values of $\textbf{a}$ or $\textbf{x}$ is accomplished by the $\textbf{Input}$ step of $\mathcal {F}_\textsf{ABB}$, and setting values of $\textbf{b}$ or $M[\textbf{x}]$ is accomplished similarly by sending the difference between a random value M[r] and the desired value $M[x_i]$.

When extending this construction to a larger circuit, we generate an authenticated wire [w] for each input wire and each output wire of a multiplication gate, and get authentications of the remaining wires from affine transformations. There are then two variant LPZK protocols, one with information theoretic security without a random oracle, and one in the random oracle model, which we call IT-LPZK and ROM-LPZK.

In both protocols, the prover constructs some quadratic polynomial in $\Delta$ for each multiplication gate, and the verifier learns the evaluation of those polynomials. The $\Delta ^2$ coefficient of the polynomial is the value $xy - z$, so if the prover is honest, the polynomial will be degenerate. For IT-LPZK, the polynomial will also have zero $\Delta$ coefficient, that is, the polynomial constructed by an honest prover is equal to a constant. For ROM-LPZK, the polynomial is linear.

For the ROM-protocol, the degenerate polynomial held by the prover is

$$\begin{aligned} K[x] K[y] - K[z] \Delta = (xy - z)\Delta ^2 + (y \cdot M[x] + x \cdot M[y] - M[z]) \Delta + M[x] \cdot M[y], \end{aligned}$$

which will be linear if $xy = z$, with the prover holding the coefficients of the linear polynomial and the verifier holding the evaluation at $\Delta$. For the IT-LPZK protocol, we set $u:= xM[y] +y M[x] - M[z]$ and subtract $M[u]:= u \Delta + K[u]$ from this polynomial, so that the prover and verifier hold the putative constant

$$\begin{aligned} K[x] K[y] - K[z] \Delta - K[u] = M[x] M[y] - M[u]. \end{aligned}$$

We therefore need two gadgets for ROM-LPZK and IT-LPZK that certify that a batch of quadratic polynomials are degenerate and actually of degree 1 or degree 0, respectively.

In the IT-LPZK protocol, we treat multiplication gates in batches of size n, (not necessarily equal to the total number of multiplication gates in the circuit) resulting in a soundness error of $2n/|\mathbb {F}|$. For each batch of n gates $x_i y_i = z_i$, the prover authenticates an additional $u_i:= x_i M[y_i] + y_i M[x_i] - M[z_i]$, so that the prover holds $(u_i, M[u_i])$ and the verifier holds $K[u_i] = u_i\Delta + M[u_i]$. The verifier then computes the product of n successive instances of the polynomial above

$$\begin{aligned} m:= \prod _{i=1}^{n} \iota (K[x_i] K[y_i] - K[z_i] \Delta - K[u_i]), \end{aligned}$$

where $\iota$ is the identity function on nonzero values, with $\iota (0)=1$ to ensure the product is nonzero. The prover sends the term $\hat{m}:= \prod _{i=1}^n \iota (M[x_i] M[y_i] - M[u_i])$, and the verifier aborts if $m \ne \hat{m}$.

The value the verifier has computed is now the evaluation of a polynomial of degree 2n, which is a constant polynomial if and only if the prover acted honestly on each of the n gates in the batch. Otherwise, a cheating prover must construct a non-constant polynomial that has $\Delta$ as a root, and we can apply the Schwartz-Zippel lemma as above to bound the binding and soundness error. The correctness and security are proven in [23].

Theorem 4.3

The protocol in Fig. 7, using Step 3 securely instantiates CheckMult in Fig. 3 with soundness error $2n/|\mathbb {F}|$.

Fig. 7

The LPZK and QuickSilver multiplication check protocols

4.3.3 QuickSilver extension

The circuit-based QuickSilver [52] multiplication check can be viewed as an extension of the ROM version of the Line-Point ZK protocol [23] to support any field. We provide an overview of the protocol. The key idea to support any field size is by extending the checking on an extension field of the original field. We will abuse the notation and use $\mathbb {F}^t$ to also refer to the extension field; this means that multiplications between two $\mathbb {F}^t$ elements are performed according to field-extension multiplication. For each multiplication gate, the prover ${\mathcal {P}}$ has $(x, M[x])$, $(y, M[y]),$ $(z, M[z])\in \mathbb {F} \times \mathbb {F} ^t$; the verifier ${\mathcal {V}}$ holds $K[x], K[y], K[z], \Delta \in \mathbb {F} ^t$ such that the following four equations hold:

$$\begin{aligned} z = x \cdot y \quad \text { and } \quad M[i] = K[i] - i \cdot \Delta \ \text { for } i \in \{x, y, z\}. \end{aligned}$$

If $\mathcal {P}$ is malicious, the first equation could potentially be incorrect and the main task is to check that this relationship holds for all multiplication gates. Although the last three equations are linear equations from the perspective of the verifier, the first equation is not linear. The crucial observation from line-point ZK is that it is possible to convert the non-linear checking to a linear checking. Specifically, for the i-th multiplication gate with wire values (x, y, z), if it is computed correctly (i.e., $z = x\cdot y$), then we have:

We can see that the above relationship is now linear and very similar to the IT-MAC relationship. What’s more, if the underlying wire values (i.e., x, y, z) are not computed correctly, then the above relationship can hold only with probability $2/|\mathbb {F}|^t$ due to Schwartz-Zippel lemma: now it becomes a quadratic equation of $\Delta$, where there are at most two values of $\Delta$ that satisfy the equation.

Now when we look at a circuit with t multiplication gates, we can obtain one such relationship for each multiplication gate. Namely, for each $i\in [n]$, $\mathcal {P}$ has $A_{0,i},A_{1,i}\in \mathbb {F} ^t$ and $\mathcal {V}$ has $B_i\in \mathbb {F} ^t$ such that $B_i = A_{0,i} + A_{1,i}\cdot \Delta .$ We can check all t linear relations in a batch using a random linear combination. In particular, the verifier samples a uniform element $\chi \in \mathbb {F} ^t$ after the above values have been defined, and then checks that the following relationship holds:

By the verifier sending just one field element (i.e., $\chi$), we are able to reduce checking t equations in the circuit to checking the above single equation, that is $B=A_0+A_1\cdot \Delta$, where $\mathcal {V}$ has B and $\Delta$, while $\mathcal {P}$ has $A_0$ and $A_1$. This could be easily checked by using a random linear relationship $B^*=A_0^*+A_1^* \cdot \Delta$ with $B^*, A_0^*, A_1^* \in \mathbb {F}^t$ to mask field elements $A_0$ and $A_1$, and then opening the masked elements. In particular, $\mathcal {P}$ sends $U = A_0+A_0^*$ and $V=A_1+A_1^*$ to $\mathcal {V}$, who checks that $B+B^* = U+V \cdot \Delta$. Finally, this random linear relationship over $\mathbb {F}^t$ can be easily obtained by generating subfield VOLE correlations on $\mathbb {F} _p$ and packing them to $\mathbb {F}^t$.

The details of the protocol can be found in Fig. 7 and we have the following theorem.

Theorem 4.4

For any field $\mathbb {F}$ and integer t, the protocol in Fig. 7 using Step 2 securely instantiates CheckMult in Fig. 3 with statistical error of $(n+3)/|\mathbb {F}|^t$.

Note that the online phase of the ZK protocol where the circuit and witness are known, can be made non-interactive by computing $\chi$ using a random oracle to hash the transcript up to that point when $|\mathbb {F}|^t\ge 2^{\kappa }$.

4.4 Comparing the multiplication check protocols

To compare the different Multiplication check protocols presented in this section, we focus on the number of communication rounds as well as elements in R that have to be sent per verified multiplication. Moreover, since Wolverine and Mac’n’Cheese become more efficient as n increases, we assume $n=1,000,000$.

In the arithmetic case, i.e. when $R=\mathbb {Z}_p$ for a large p, Wolverine has to send 4 R-elements per multiplication, to achieve statistical security $2^{-40}$ with $B=3$. The warm-up version of Mac’n’Cheese (Sect. 4.2) reduces this to 3 elements. The interactive versions of LPZK & QuickSilver only need to communicate 1 R-element per multiplication in 3 rounds of interaction, while the non-interactive and information-theoretic version of LPZK communicates 2 R-elements. In comparison, using the batch multiplication check in Mac’n’Cheese gives an amortized communication cost of 1 R-element per multiplication and requires 17 rounds with $n=1\,000\,000$. Note that all of these protocols can be collapsed to be non-interactive (excluding the VOLE preprocessing) in the random oracle model using the Fiat-Shamir transform. The main advantage of Mac’n’Cheese over QuickSilver (which has better concrete and asymptotic performance) is that it supports so-called stacking proofs (see Sect. 5.3) which are not known to carry over to QuickSilver as easily. If $R=\mathbb {Z}_2$, i.e. for binary circuits, then Wolverine for $n=1,000,000$ has to communicate 7 bits per proven multiplicative relation. In comparison, QuickSilver and Mac’n’Cheese both take approximately 1 bit. LPZK, on the other hand, only supports computations over large fields.

In terms of practical performance, [2] argue that QuickSilver shows approximately twice the throughput in proven multiplicative relations per time unit in comparison to Mac’n’Cheese. They caution, though, that the systems have not been compared on identical hardware. The benchmarking of [22] shows that the information-theoretic version of LPZK is twice as fast as the interactive version of LPZK in terms of online computational costs, perhaps due to eliminating the cost of invoking a hash function, and only around $2.5\times$ slower than evaluating the circuit in the clear.

5 Extensions

In Sects. 3 and 4, we provided an overview how to efficiently prove any computation provided that it can be written as a circuit over a field with linear and degree-2 multiplication gates only. However, in many settings, representing the statement as a such a circuit may not be ideal: 1) this specific circuit representation may be huge and thus lead to high overhead in the proof as it has to fit into this specific representation; 2) it prevents us from designing customized gadgets and gates that exploit the semantics of the problem and could be potentially more efficient than degree-2 circuit-based protocols.

In this section, we discuss efficient gadgets that are out of the regular degree-2 circuit-modal computation. The modular design of our approach means that these gadgets can be integrated with the main protocol easily, and can e.g. be expressed as higher-degree gates which the model from Sect. 2.1 permits.

5.1 Low-degree polynomials proofs

We introduce proofs for low-degree polynomials from [52]. As a starter, let us first generalize the multiplication check in Sect. 4.3.3 to prove an inner product between two vectors with communication of 1 field element.

5.1.1 Proving degree-2 polynomials

Let f be a degree-2 polynomial such that $f(x_1,\ldots , x_n) = c_0 + \sum _{i\in [n/2]} c_i\cdot x_{i}\cdot x_{n/2+i}$. Both parties hold authenticated values $[w_1],\ldots ,[w_n]$, and the prover wants to prove $f(w_1,\ldots ,w_n)=0$. Using a circuit-based approach, this would need n/2 multiplication gates and thus at least n/2 communication. Here, we show a protocol that can use less communication: Observe that

$$\begin{aligned}&f(K[w_1],\ldots ,K[w_n])= c_0 + \sum _{i\in [n/2]} c_i\cdot K[w_i]\cdot K[w_{n/2+i}]\\&\quad = c_0 + \sum _{i\in [n/2]} c_i\cdot (M[w_i] + w_{i}\cdot \Delta )\cdot (M[w_{n/2+i}] + w_{n/2+i}\cdot \Delta )\\&\quad = c_0 + \sum _{i\in [n/2]} \left( c_i\cdot M[w_i]\cdot M[w_{n/2+i}] \right. \\&\qquad \left. + c_i\cdot (M[w_i]\cdot w_{n/2+i} + M[w_{n/2+i}]\cdot w_{i})\cdot \Delta +c_i\cdot w_{i}\cdot w_{n/2+i}\cdot \Delta ^2\right) \\&\quad = \Big (c_0 + \sum _{i\in [n/2]} c_i\cdot M[w_i]\cdot M[w_{n/2+i}]\Big ) \\&\qquad + \Big (\sum _{i\in [n/2]} c_i\cdot M[w_{i}]\cdot w_{n/2+i} + c_i\cdot M[w_{n/2+i}]\cdot w_{i} \Big )\cdot \Delta +\\&\qquad \Big (\sum _{i\in [n/2]} c_i\cdot w_{i}\cdot w_{n/2+i}\Big )\cdot \Delta ^2\\&\quad = \Big (c_0 + \sum _{i\in [n/2]} c_i\cdot M[w_i]\cdot M[w_{n/2+i}]\Big )\\&\qquad +\Big (\sum _{i\in [n/2]} c_i\cdot M[w_i]\cdot w_{n/2+i} + c_i\cdot M[w_{n/2+i}]\cdot w_{i} \Big )\cdot \Delta - c_0\cdot \Delta ^2. \end{aligned}$$

The last equation is due to the fact that $f(w_1,\ldots ,w_n) = c_0 + \sum _{i\in [n/2]} c_i\cdot w_{i}\cdot w_{n/2+i} = 0$. Reorganizing the above equation a bit, we can obtain the following:

$$\begin{aligned}&\underbrace{f(K[w_1],\ldots ,K[w_n]) + c_0\cdot \Delta ^2}_{\text {known to}~{\mathcal {V}},~\text {denoted as }B} \\&\quad = \underbrace{\Big (c_0 + \sum _{i\in [n/2]} c_i\cdot M[w_i]\cdot M[w_{n/2+i}]\Big )}_{\text {known to}~{\mathcal {P}},~\text {denoted as }A_{0}}\\&\quad + \underbrace{\Big (\sum _{i\in [n/2]} c_i\cdot M[w_i]\cdot w_{n/2+i} + c_i\cdot M[w_{n/2+i}]\cdot w_{i}\Big )}_{\text {known to}~{\mathcal {P}},~\text {denoted as }A_{1}}\cdot \Delta . \end{aligned}$$

This is still a linear relationship $B = A_0 + A_1\cdot \Delta$, which could be proven just as in the Quicksilver protocol. Essentially, we can prove a degree-2 polynomial with n/2 multiplications with a communication cost of just O(1), in addition to the cost of committing the witness. This is independent of the number of multiplications in the polynomial, which could be as many as $n/2=O(n)$. One immediate observation is that if we have t such polynomials to be proven, the total communication cost is still O(1) rather than O(t), by using the same random-linear-combination idea to reduce all linear checks to a single check.

5.1.2 Generalizing to any low-degree polynomial

Now we generalize the above to support checking of low-degree polynomials. We assume that the witness is $(w_1,\ldots ,w_n) \in \mathbb {F}^n$; there are t polynomials to be proven and each multivariate polynomial $f_i(X_1,\ldots , X_n)$ over $\mathbb {F}$ has a degree at most d. The prover wants to prove that $f_i(w_1,\ldots ,w_n)=0$ for all $i \in [t]$. Below, we show how to prove such polynomial set in communication of d field elements over $\mathbb {F}^t$, in addition to the n field elements over $\mathbb {F}$ to commit the witness. For every n-variable d-degree polynomial $f \in \{f_1, \dots , f_t\}$, we will represent it as $f(X_1, \ldots , X_n) = \sum _{h\in [0,d]} g_{h}(X_1,\ldots , X_n)$, where $g_{h}$ is a degree-h polynomial such that all terms in $g_{h}$ have exactly degree h. Here we assume that each polynomial f has been written in a “degree-separated” format, and thus do consider the computation of this decomposition to be beyond scope.

We write each polynomial in a “degree-separated” format and shift each sub-polynomial. The verifier now computes

$$\begin{aligned}&\sum _{h\in [0,d]} g_h(K[w_1],\ldots ,K[w_n])\cdot \Delta ^{d-h}\\&\quad =\sum _{h\in [0,d]} g_h(M[w_1]+w_1\cdot \Delta ,\ldots ,M[w_n]+w_n\cdot \Delta )\cdot \Delta ^{d-h}\\&\quad =\sum _{h\in [0,d]} \Big (g_h(w_1,\ldots ,w_n)\cdot \Delta ^d + \sum _{j\in [0, h-1]} A^j_{h} \cdot \Delta ^{j+d-h} \Big )\\&\quad =\sum _{h\in [0,d]} g_h(w_1,\ldots ,w_n)\cdot \Delta ^d + \sum _{h\in [0,d-1]} A_{h} \cdot \Delta ^h \\&\quad =f(w_1, \dots , w_n)\cdot \Delta ^d+\sum _{h\in [0,d-1]} A_{h} \cdot \Delta ^h \\&\quad =\sum _{h\in [0,d-1]} A_{h} \cdot \Delta ^h. \end{aligned}$$

Here $A_h^j$ is defined as above, and $A_h$ is the aggregated coefficient for all terms with $\Delta ^h$. Note that the prover with witnesses $w_i$ and MACs $M[w_i]$ can compute all the coefficients locally. The coefficients $A_h$ are polynomial coefficients when we treat it as a single-variable polynomial on $\Delta$. Therefore, the prover can compute all $A_h$ efficiently by evaluating the polynomial on $d+1$ points and then computing the polynomial coefficients using Lagrange interpolation. In many practical applications, the polynomial is usually simple and thus the coefficients can be derived without using the above generic approach. This relationship can be viewed as an oblivious polynomial evaluation (OPE), where the verifier has $\Delta$ and the prover has a polynomial $P(x) = \sum _{h\in [0,d-1]} A_{h}\cdot x^h$ over $\mathbb {F}^t$. The verifier wants to check that the resulting evaluation in the above equation is the same as $P(\Delta )$. It is not hard to check the above polynomial relation, as sVOLE can be used to generate (V)OPE in an efficient way. Similarly, we can perform the checks for all t polynomials in a batch using a random linear combination. This results in a total communication of $(n+d r) \log |\mathbb {F}|$ bits in the $\mathcal {F}_{\textsf{VOLE}}^{d}$-hybrid model. When using the interpolation approach to compute the coefficients $A_h$, we have that the computational cost of the prover and verifier is $O(td^2z+dn)$ and O(tdz) respectively, where z is the maximum number of terms in all t polynomials.

5.2 LPZKv2

The follow-up work to LPZK, [22], presents another extension of of VOLE-based ZK that uses an extension of the VOLE correlation and is specialized for particular circuit formats. LPZKv2 improves the online communication cost of LPZKv1 by a factor of roughly two for both the information-theoretic and random oracle variants (IT-LPZKv2 and ROM-LPZKv2, respectively).

There are two technical ideas that enable the improvements of LPZKv2 over LPZKv1. The first technical idea is to store the message in the constant term of the VOLE, instead of the linear term, i.e. to write $K^*[x]:= \Delta M^*[x] + x$ instead of $K[x]:= \Delta x + M[x]$. Storing the value in the constant term instead of the linear term reduces the verifier’s computation, since on the step $\textbf{Input}$ of $\mathcal {F}_\textsf{ABB}$ described in 3.2, when the $\mathcal {P}$ sends $\delta = x - r$ to $\mathcal {V}$, $\mathcal {V}$ now computes $K^*[x] \leftarrow K^*[r] - \delta$ instead of $K[x] \leftarrow K[r] - \Delta \delta$. Because each multiplication gate requires an additional call to $\textbf{Input}$, this change reduces the verifier’s computation by one multiplication per gate in both the information theoretic and random oracle variants.

The second technical idea is the use of an extension of VOLE, quadratically certified VOLE, or qVOLE, which allows for the imposition of additional quadratic relations on the entries of an instance of random VOLE. These quadratic relations essentially allow certain terms needed in LPZK to be precomputed, reducing the communication and computation required in the online step. For example, using qVOLE, we could generate three authenticated random values ([p], [q], [r]) with the guarantee that the quadratic relation $M^*[p] \cdot M^*[q] - M^*[r] = 0$ is satisfied, which in turn would imply that $K^*[p] \cdot K^*[q] - K^*[r]$ is a polynomial with zero $\Delta ^2$ coefficient. This property still holds after calling the modified $\textbf{Input}$ protocol described above to shift $(p,q,r) \rightarrow (x,y,r)$, a fact which we use extensively in the construction below.

The qVOLE functionality can be realized either by bootstrapping off of an existing instance of VOLE, which requires a linear amount of communication in the preprocessing phase (effectively pushing 50% of the communication of LPZKv1 to an offline phase). Alternatively, we can use ring-LPN to give a sublinear-communication qVOLE generation protocol that is concretely efficient in the SIMD setting or for circuits with repeated subcircuits (such as hash trees).

5.2.1 General circuits

The information-theoretic protocol IT-LPZKv2 can be used efficiently with general circuits by realizing the qVOLE functionality by bootstrapping off of an existing instance of VOLE. Then IT-LPZKv2 requires $1+\tfrac{1}{n}$ elements of communication in the online phase, nearly matching the communication cost of ROM-LPZKv1, Quicksilver or Mac’n’Cheese over large fields. Here n is a constant representing batch size, as in IT-LPZKv1. For a multiplication gate $xy = z$, we have

$$\begin{aligned} K^*[x] \cdot K^*[y] = M^*[x] M^*[y] \Delta ^2 + (x M^*[y] + y M^*[x]) \Delta + xy\text {,} \end{aligned}$$

where the leading coefficient can be pre-computed from the qVOLE functionality, and the constant coefficient $xy = z$ is the constant coefficient of the authenticated output value $K^*[z]$. If $K^*[r] = M^*[x] M^*[y] \Delta + M^*[r]$ is the precomputed qVOLE entry, then $K^*[x] K^*[y] - K^*[r] \Delta - K^*[z]$ will be a linear polynomial in $\Delta$ with zero constant term, which can be checked using the same batched proof given in Step 3 of Fig. 7. Therefore the total online communication cost is 1 element for $K^*[z]$ and an amortized cost of 1/n per gate for the batched proofs. Additionally, 1 element of communication per gate is required in a preprocessing step for the generation of the values $K^*[r]$.

5.2.2 Layered circuits and other specialized circuits

As mentioned above, both IT-LPZKv2 and ROM-LPZKv2 give efficiency gains in the SIMD setting or for circuits with repeated subcircuits, since then qVOLE functionality can be efficiently realized using Ring-LPN. Additionally, the polynomial techniques described above allow us to extend the LPZKv2 constructions from arithmetic circuits containing only fan-in 2 addition and multiplication gates to circuits with arbitrary degree 2 polynomial gates.

The ROM-LPZKv2 protocol offers some additional speed-up in online communication time for a broad class of circuits with a certain colorability property described below. The key observation behind the ROM-LPZKv2 protocol change is that the expression $K^*[x] K^*[y] - K^*[p] \Delta$ is a linear polynomial with constant term xy, and so already represents an authentication of xy without any communication required at all. However, for the authenticated value $K^*[z]:= K^*[x] K^*[y] - K^*[p] \Delta$, the linear term is equal to $M^*[z]:= x M^*[y]+ yM^*[x] - M^*[p]$, which depends on the prover’s input. Therefore if we wish to use z as the input wire to another multiplication gate with inputs z, t the prover can no longer compute the quadratic coefficient $M^*[z] M^*[t]$ using only precomputed randomness. This is the motivation behind the colorability property.

For the coloring, we use the color red to denote wires for which the value $M^*[t]$ is determined purely by the correlated randomness, and use blue to denote wires for which the value $M^*[t]$ depends on the prover’s input. Color the input wires red, then color the remaining wires of the circuit such that, for any degree 2 polynomial gate with all blue inputs, or a mix of blue and red inputs, the output wire is red, while for a gate with all red inputs, the output wire may be red or blue. Then the communication cost of ROM-LPZKv2 under this coloring is equal to the number of red wires.

For layered circuits, where each gate is assigned to some layer k, and all the inputs to gates at layer k are outputs to gates at layer $k-1$, either all odd layers or all even layers can be colored red, so the amortized communication per degree 2 polynomial gate is at most $\tfrac{1}{2}$ elements of communication per gate in a layered circuit. For a broad class of non-layered circuits, substantial savings are also possible. For example, as described in [22], for a random circuit made up entirely of multiplication gates and colored with a greedy algorithm, approximately $38 \%$ of the wires will be blue, so that one can achieve an approximately $38 \%$ reduction in communication.

5.3 Disjunctions and r-out-of-n proofs

[2] consider the setting where both $\mathcal {P}$ and $\mathcal {V}$ agree on m circuits $C_1,\dots ,C_m$ that define protocols based on a committed vector $[{\varvec{w}}]$. Let these protocols each be public coin HVZK proofs over the same field $\mathbb {F}_{p^k}$. For this, they construct a communication-efficient protocol showing that from $[{\varvec{w}}]$ one can extract a satisfying input ${\varvec{w}}_{i*}$ to at least one of the circuits.

The classic OR-proof technique by Cramer et al. [16] can be used to construct such a proof with message complexity $\approx \sum _{i\in [m]} \alpha _i$ where $\alpha _i$ is the communication necessary for the proof $\Pi _i$ of $C_i$. This would be done by running all m proofs for all circuits in parallel (which means sending messages for evaluating all of them) and having their outputs being committed as $[y_1],\dots ,[y_m]$. The prover would then show that at least one finished successfully with the expected output using the OR-proof of [16] on $[y_1],\dots ,[y_m]$. [2] show how to reduce the message complexity of such a proof to $2mk + \max \{ \alpha _i \}$, where the soundness error grows by an additional additive $\approx p^{-k}$. What is required for the technique of [2] to work is that all messages from the prover in each protocol $\Pi _i$ appear uniformly random. Moreover, they require that protocol messages in each round are of identical length, for any $\Pi _i,\Pi _j$. Towards this, observe that it is always possible to defer zero-tests in a protocol $\Pi _i$ that relies on $\mathcal {F}_\textsf{ABB}$ to the end, as a verifier doesn’t have a secret that could be leaked through late application of the zero check. Achieving messages of identical length (and same number of rounds in each $\Pi _i$) can be achieved using padding.

At the same time, not all implementations of $\mathcal {F}_\textsf{ABB}$ are compatible with the requirement that messages from the prover are uniform, even with padding: The multiplication checks from Sects. 4.1 and 4.2 reduce to the prover making auxiliary commitments, the verifier sending random challenges and the prover then doing a zero-test. This can be made compatible with the desired protocol structure. Unfortunately, this is not true for the approach from Sect. 4.3.3 as it works directly on a MAC level.

Assume that we start m proofs $\Pi _i$, over $\mathbb {F}_{p^k}$, proving the individual circuits $C_i$. Note that p can be any prime power, with no restrictions on size. We make the simplifying assumption that each $C_i$ has the same number of linear gates and that each $\Pi _i$ has the same number of rounds of interaction and that prover messages in each round are of the same length. [2] show the more general case where these restrictions are not necessary.

5.3.1 Constructing the protocol

We construct a protocol $\Pi _{\texttt{OR}}$, defined over $\mathbb {F}_{p^k}$, for the aforementioned task as follows:

• 1. $\mathcal {P}$, having only $w_{i^*}$ for one of the circuits $C_{i^*}$, will commit to $[{\varvec{w}}]$ such that $\Pi _{i^*}$ can access $w_{i^*}$. It then in its head runs each of the $\Pi _i$ on inputs derived from $[{\varvec{w}}]$. For this, it extends $w_{i^*}$ with a random padding if necessary.

• 2. $\mathcal {P}$ and $\mathcal {V}$ will simultaneously run all $\Pi _1,\dots ,\Pi _m$, with the following modification: $\mathcal {P}$’s message $c_h$ to $\mathcal {V}$ in round h will be chosen as the message created from running $\Pi _{i^*}$, while $\mathcal {V}$ uses the same message from the prover in all instances. Since the messages of all protocols by assumption appear uniformly random and are therefore indistinguishable, $\mathcal {V}$ can now execute all instances in parallel but cannot tell which of these is the true one.

• 3. Conversely, since all $\Pi _i$ are public coin, $\mathcal {V}$ sends a randomness string that is long enough for any of the m instances in round h. $\mathcal {P}$ uses this identical randomness string in all simulated proofs $\Pi _1,\dots ,\Pi _m$.

The challenge now, is that $\mathcal {V}$ cannot simply perform the verification for all $\Pi _i$ using the $\textsf{CheckZero}$ queries for each instance, since this would reveal the index ${i^*}$ of the true statement. Towards resolving this, we first observe that any “pure” zero-test can be turned into a $\Sigma$-protocol-like argument as follows:

• 1. For each $i\in \{1,\dots ,m\}$, let $[\mu _i]$ be the output of the circuit $C_i$ run on $[{\varvec{w}}]$. Assume that there exists a uniformly random commitment $[r_i]$, which can be generated without additional interaction from $\mathcal {F}_{\textsf{VOLE}}^{d}$.

• 2. $\mathcal {P}$ sends $r_i$ to $\mathcal {V}$, but crucially does not open the commitment $[r_i]$ yet.

• 3. $\mathcal {V}$ sends a challenge $f_i$ to $\mathcal {P}$.

• 4. $\mathcal {P}$ uses $\textsf{CheckZero}$ to show that $[r_i]+f_i[\mu _i]-r_i$ opens to 0.

This check, crucially, has a soundness error of $1/p^k$, as any prover knowing $f_i$ in advance can generate $r_i$ appropriately in order to cheat during the sigma-protocol.

[2] now perform a [16]-style OR-proof to show that at least one of the outputs $[\mu _i]$ is zero, using the $\Sigma$-protocol version of $\textsf{CheckZero}$. The basic idea behind [16] is that given m $\Sigma$-protocols for proving relations, an OR proof can be done by having the prover choose the random challenge $f_i$ for $m-1$ of the instances, so it can simulate the correct messages $r_i$ to be sent in every false instance using the simulator for the sigma protocol. This makes the verifier accept for the “false” instances automatically. For the correct instance $i^*$, $\mathcal {P}$ will choose $r_i$ as in the correct $\Sigma$-protocol, which it can complete because the statement is actually true for one instance. Hence, after receiving the m initial messages of each $\Sigma$-protocol (honest in one case, simulated in all others), the verifier picks a challenge f, which defines the challenge $f_{i^*} = f - \sum _{i\ne i^*} f_i$ corresponding to the true instance $i^*$. The prover sends all these $f_i$ to the verifier.

Finally, $\mathcal {V}$ checks that the $f_i$ add up to f and that each $\textsf{CheckZero}$ test for each $C_i$ is indeed valid.

5.3.2 Threshold proofs

In [16] the authors describe how to additionally construct proofs of partial knowledge for any threshold, i.e., how to show that r out of the m statements are true. Their technique, together with a modification of $\Pi _{\texttt{OR}}$, can be used to construct a proof in the VOLE setting where we implicitly only communicate the transcript of r statements, and not all m of them.

Towards this, $\Pi _{\texttt{OR}}$ can then be seen as a special case where $r=1$. To generalize to arbitrary r one now simulates the $m-r$ possibly false proofs using false challenges. The prover then, based on the challenge f, computes the unique degree-$m-t$ polynomial s that evaluates to f at point 0 and to the simulated challenge $f_i$ for each i where the sigma-protocol was simulated. It then derives the honest challenges by evaluating this polynomial at their indices, and sends s to the verifier. Towards compressing the messages, [2] then consider the r messages for the true branches as evaluations of a polynomial t of degree $r-1$. Namely, for each true evaluated branch i, they let t(i) be the message sent by $\Pi _i$. The prover then computes this unique polynomial in canonical coefficient form and sends it to $\mathcal {V}$, who derives the inputs to each simulated $\Pi _i$ from t. Since both s, t are of canonical form, they do not leak which of the branches are actually true.

5.3.3 $\log$-overhead disjunctions

The drafted protocol $\Pi _{\texttt{OR}}$ has the drawback that to verify one out of m statements, we still need O(m) communication complexity in the OR-proof. One can construct an alternative protocol that obtains an overhead only logarithmic in m, as follows:

• 1. Any $\Pi _i$ accepts iff $\textsf{CheckZero}$ is true, i.e. the output commitment $[\mu _i]$ is 0.

• 2. If the prover can then compute the product $\mu _1\cdots \mu _m$, and prove that this is 0, then at least one $\mu _j$ was 0 to begin with, i.e. one output was true.

A naive instantiation of the above approach is to perform $m-1$ multiplications between the m implicit variables $\mu _i$, and open the result. However, this would still give O(m) overhead. Instead, one can carefully apply recursion to make this overhead logarithmic, using the fact that after augmenting the parallel evaluation of two protocols $\Pi _1, \Pi _2$ with a multiplication, we obtain a protocol which can recursively be fed into the same process.

5.4 Conversions between $\mathbb {F}_2$ and $\mathbb {F}_p$

In [4] the authors show how, given two simultaneously running instances of $\mathcal {F}_\textsf{ABB}$ for moduli 2, p, one can efficiently prove that $[c_0]_2,\dots ,[c_m]_2$ is the correct binary decomposition of $[c]_p$. These correct decompositions, called Edabits, were introduced to secure computation protocols in [24] and are useful for computing/proving truncations and comparisons.

On a high level, in [24] first a set of random Edabits is created during a preprocessing phase. Later, one of these Edabits is used to perform the actual conversion in the online phase. [4] adapt and optimize the approach of [24] in multiple ways, mainly by observing that, since the prover already knows the conversions ahead of time, these can directly be checked using the preprocessing protocol and there is no need for the intermediary random Edabits. We want to stress that, concurrently to [4], Weng et al. [49] also introduced an adaptation of Edabits to the ZK setting with a similar construction. In the following, we use the notation of [4].

5.4.1 The protocol

To define the check let us first, in addition to Edabits, define Dabits as pairs of commitments $[x]_2,[x]_p$ that are consistent. On a high level, the Edabits checking protocol of [4] consists of four phases, using a bucketing approach similar to the one already introduced in Sect. 4.1:

• 1. Initially, $\mathcal {P}$ commits to auxiliary random Edabits and Dabits necessary for the check. The Dabits are verified separately for consistency, and then $\mathcal {V}$ chooses a random permutation.

• 2. After permuting the auxiliary Edabits, both parties run an implicit cut-and-choose phase. Here, $\mathcal {P}$ opens C of the auxiliary Edabits, which are checked by $\mathcal {V}$  for consistency.

• 3. Place each input Edabit (that we want to test for correctness) into one of N buckets, each of which also contains a set of B auxiliary Edabits $\{([r_0]_2,\dots ,[r_{m-1}]_2,[r]_p)\}_{i=0}^{B-1}$ that we use to perform verification. None of these auxiliary Edabits have been proven consistent, but C Edabits coming from the same pool have been opened in the previous step.

• 4. Now, over B iterations the prover and verifier for each $j\in [B]$ compute $[c+r_j]_p = [c]_p + [r_j]_p$ and use an addition circuit to check that $([e_0]_2, \dots , [e_{m}]_2) = ([c_0]_2, \dots , [c_{m-1}]_2) + ([r_0]_2, \dots , [r_{m-1}]_2)$. The addition circuit is evaluated using the $\mathcal {F}_\textsf{ABB}$ operations.

For the checks within each bucket, [4] use an additional protocol which converts an authentication of a bit $[b]_2$ into an arithmetic authentication $[b]_p$ which is necessary to do so $[c+r_j]_p$ does not reveal any information. Additionally, the authors also observe that their protocol is still secure if the Dabits are “approximately correct”, meaning that each pair $[x]_2,[x]_p$ has the same parity and x is bounded but $[x]_p$ necessarily commits to a bit. For this, they present a cheaper protocol to check this property.

5.4.2 Truncation and Comparison

[4] provide protocols for verifying integer truncation and comparison. Here, truncation means that given integers l, m and two authenticated values $x,x'$ of l and $l-m$ bits, verify that $x'$ corresponds to the upper $l-m$ bits of $x$, i.e. $x' = \lfloor \frac{x}{2^m} \rfloor$ over the integers. Integer comparison is then the problem of taking two authenticated integers and outputting 0 or 1 (authenticated) depending on which input is the largest. Integers are considered as signed in the interval $[-2^{l-1}, 2^{l-1})$.

5.4.3 Truncation

To perform a truncation check with one call to the conversion check introduced above, the prover in addition to each input $[a]_p$ also provides:

• the truncated value $[a_{tr}]_p$ of $[a]_p$ and its bit decomposition $([a^0_{tr}]_2, \dots , [a^{l-m-1}_{tr}]_2)$

• the lower m bits of $[a]_p$; $[a']_p = [a \mod 2^m]_p$ as well as its bit decomposition $([a'_0]_2, \dots , [a'_{m-1}]_2)$.

Having access to $[a_{tr}]_p$ and $[a']_p$ which are shown to have consistend decompositions then allows the verifier then to check that $a = 2^m \cdot a_{tr} + a'$, which proves the claim.

5.4.4 Comparison

The authors also present a protocol to compare two signed, l-bit integers $\alpha$ and $\beta$. The way their protocol works is by having the prover (and verifier) compute $[\alpha ]_p - [\beta ]_p$ and have the prover compute the truncation of this which is only the most significant bit. Now one can run the aforementioned truncation verification protocol and use the truncation as the output of the comparison. Similarly to previous works in the MPC setting [15, 24], this gives the correct result as long as $\alpha , \beta \in [-2^{l-2},2^{l-2})$, so that $\alpha - \beta \in [-2^{l-1},2^{l-1})$, so this introduces a mild restriction on the range of values that can be supported

5.5 Zero-Knowledge modulo $2^k$

Assume that $\mathcal {P}$ wants to commit to secrets $x\in \mathbb {Z}_{2^k}$ using $\mathcal {F}_{\textsf{VOLE}}^{d}$, such that also $\Delta ,K[x],M[x]$ come from $\mathbb {Z}_{2^k}$. Assuming one would follow the approach from Sect. 3, then $\mathcal {P}$ sends $x,M[x]$ to open [x], such that $\mathcal {V}$ checks that $K[x]+\Delta x=M[x] \bmod 2^k$.

Unfortunately, since $\mathbb {Z}_{2^k}$ is not a ring, such a check is not constraining $\mathcal {P}$ to only one valid opening $x,M[x]$. For example, if $\Delta =2\Delta '$ which happens with probability 1/2, then by setting $x'=x+2^{k-1}$ we have that

$$\begin{aligned} x'\cdot \Delta = (x+2^{k-1})(2\Delta ')= x\Delta +2^k=x\Delta \bmod 2^k\text {,} \end{aligned}$$

meaning that $x',M[x]$ is also a valid opening.

Instead, [1, 4] choose the information-theoretic MAC scheme from [17] as their starting point. For this, let $s$ be an additional parameter, and $\ell =k+s$. To authenticate a value $x \in \mathbb {Z}_{2^k}$ known to $\mathcal {P}$ towards $\mathcal {V}$ (denoted as $[x]$), we choose the MAC keys $\Delta \in \mathbb {Z}_{2^s}$ and $K[x] \in \mathbb {Z}_{2^{\ell }}$, and compute the MAC tag as

$$\begin{aligned} M[x]:= \Delta \cdot \tilde{x} + K[x] \in \mathbb {Z}_{2^{\ell }} \end{aligned}$$

(1)

where $x = \tilde{x} \bmod 2^k$, i.e. $\tilde{x}$ is a representative of the corresponding congruence class of integers modulo $2^k$. Then $\mathcal {P}$ gets $\tilde{x}$ and $M[x]$, whereas $\mathcal {V}$ receives $\Delta$ and $K[x]$. As before, linear operations can be applied in the same way. One can show that this again leads to $\mathcal {P}$ not being able to cheat, unless it can guess $\Delta$ which only succeeds with probability $2^{-s}$. Setting $s=\sigma$ then achieves the required statistical security.

Observe that initially $\tilde{x}$ may be chosen as $\tilde{x} = x \in \{0, \dotsc , 2^k - 1\}$. Applying arithmetic operations can result in larger values though, which do not get reduced modulo $2^k$ because all computation happens modulo $2^{\ell }$. Therefore, to safely open $[x]$ or show that $x=0$, first the upper $s$ bits of $\tilde{x}$ need to be randomized, by computing $[z] \leftarrow [x] + 2^k \cdot [r]$ with random $\tilde{r} \in _R \mathbb {Z}_{2^{\ell }}$ and then opening [z].

5.5.1 Extending Line-Point Multiplication checks to $\mathbb {Z}_{2^k}$

It is clear that Equation 4.3.3 from the efficient multiplication check from Sect. 4.3.3 still holds. Therefore, one might hope that the same security argument still applies. Unfortunately, when just considering general quadratic equations

$$\begin{aligned} f(x) = ax^2 + bx + c \end{aligned}$$

modulo $2^\ell$, then these may have many more than just 2 solutions.

It is clear that Equation 4.3.3 from the efficient multiplication check from Sect. 4.3.3 still holds. Therefore, one might hope that the same security argument still applies. Unfortunately, when just considering general quadratic equations

$$\begin{aligned} f(x) = ax^2 + bx + c \end{aligned}$$

modulo $2^\ell$, then these may have many more than just 2 solutions.

In [1] the authors observe that f(x) actually is constrained in the given setting, since a cannot be chosen from the entire ring by $\mathcal {P}$, as $a\ne 0 \bmod 2^k$ for $\mathcal {P}$ to successfully cheat. Moreover, $\mathcal {P}$ may have to guess a root $\Delta$ of f(x) that comes from $\{ 0,\dots ,2^{s}-1 \}$. They therefore show the following:

Lemma 5.1

Let $f(x)\in \mathbb {Z}[x]$ be a quadratic equation such that $2^r$ is the largest power of 2 dividing all coefficients. Then for any $\ell , s, s' \in \mathbb {N}$ such that $\ell -r>s'$ there are at most $2^{\max \{(2s-s')/2,1\}}$ solutions to $f(x) = 0 \mod 2^{\ell }$ in $\{0,\dots ,2^{s}-1\}$.

This implies that by choosing $\ell =k+2s$, one can achieve the required bound on the number of solutions.

5.5.2 Amortizing multiplication checks in $\mathbb {Z}_{2^k}$

Also with respect to checking many multiplications simultaneously, the solution of QuickSilver from Equation 4.3.3 does not directly carry over. [1] solve this by generalizing the techniques from [17] to their MAC scheme.

Here, [1] show that by letting $\mathcal {V}$ choose the $\chi _i$ independently from the set $\{0,\dots ,2^{s}-1\}$ and requiring $s=\sigma +\log (\sigma )+3$ and $\sigma \ge 7$, then this modified check from Equation 4.3.3 when done modulo $2^\ell$ is sound except with probability $2^{-\sigma }$.

5.6 RAM-based Zero-knowledge Proofs

RAM-based zero-knowledge proofs have been studied in the context of zkSNARKs (starting from [7]). As we show below, the main components needed are zero-knowledge proofs of permutation, packing, and integer comparison. When representing the integers as a list of authenticated values in $\mathbb {F}_2$, proving integer comparison is a fair easy task since comparison becomes a straightforward circuit. For efficient permutation and packing, the problems are somewhat related. The folklore method to prove a permutation is by letting the prover commit to the permuted values and prove equality of the sets, which in turn can be converted to a polynomial identity check [39]. When the field is large, it can be checked in linear time by checking the evaluation on a random point, where the soundness if ensured by the Schwartz-Zippel Lemma. However, converting between $\mathbb {F}_2$ and a large field can be costly even after optimizations such as in Sect. 5.4.

The key observation in [26] is that the Schwartz-Zippel Lemma works for any field as long as it is sufficiently large and thus one can choose a field that is friendly to conversions. In particular, we can embed a bit string either as $\mathbb {F}_2^{\kappa }$ or as $\mathbb {F}_{2^{\kappa }}$. Their authentications are different: authenticating elements in $\mathbb {F}_2^{\kappa }$ requires IT-MACs on each $\mathbb {F}_2$ value; authenticating $\mathbb {F}_{2^{\kappa }}$ only requires one IT-MAC for the whole element. Just like cleartext operation, conversions between authenticated elements in $\mathbb {F}_2^{\kappa }$ and $\mathbb {F}_{2^{\kappa }}$ can also be done efficiently with no communication: if we fix a degree-$\kappa$ irreducible polynomial f(X) and identify $\mathbb {F} _{2^\kappa }$ with $\mathbb {F} _2[X]/(f(X))$, then it can be derived that $x = \sum _{i\in [\kappa ]} x_i\cdot \textsf{X}^i$, where $\textsf{X} \in \mathbb {F} _{2^\kappa }$ denotes the element corresponding to $X \in \mathbb {F} _2[X]/(f(X))$. The parties can compute [x] by having the prover compute $M[x] = \sum _{i\in [\kappa ]} M[x_i]\cdot \textsf{X}^i$ and the verifier compute $K[x] = \sum _{i\in [\kappa ]} K[x_i]\cdot \textsf{X}^i$; we then have

$$\begin{aligned} M[x]&= \sum _{i\in [\kappa ]} M[x_i]\cdot \textsf{X}^i\\&= \sum _{i\in [\kappa ]} (K[x_i]\oplus x_i\Delta ) \cdot \textsf{X}^i\\&= \sum _{i\in [\kappa ]} K[x_i]\cdot \textsf{X}^i \;\oplus \; \Big (\sum _{i\in [\kappa ]} x_i\cdot \textsf{X}^i\Big )\cdot \Delta \\&= K[x] \oplus x\cdot \Delta . \end{aligned}$$

This means that given a vector of bits, we can prove a Boolean predicate by treating them as authenticated bits and, without communication, we can prove arithmetic predicates on vectors of bits by treating vectors as extension field elements. Below we use ZK proof of read-only RAM as an example.

5.6.1 Read-only ZKRAM

Consider the case where the prover wants to prove in zero knowledge to the verifier that there exists an index i for which $\textsf{Mem}_i = t$ (where t is a public value). The protocol in this case roughly proceeds as follows:

• 1. The prover commits to the list of values $\mathcal {L}=\big ((0, \textsf{Mem}_0), (1, \textsf{Mem}_1), \ldots ,$ $(N-1, \textsf{Mem}_{N-1}) \big )$. (This can be done once-and-for-all, and before t is known.)

• 2. The prover commits to (i, t), where t is known to the verifier but i is not, and appends (i, t) to $\mathcal {L}$.

• 3. The prover then sorts the tuples in $\mathcal {L}$ by their first entry, giving an updated list $\mathcal {L}'$, and commits to the tuples in that list.

• 4. The prover proves that $\mathcal {L}'$ is consistent, namely, that if two tuples in $\mathcal {L}'$ agree in their first entry, then they also agree in their second entry. This can be done in a natural way by comparing all adjacent entries in $\mathcal {L}'$. All operations should be proven as a Boolean circuit over $\mathbb {F}_2$.

• 5. The prover proves that $\mathcal {L}'$ is a permuted version of $\mathcal {L}$ using the polynomial equality check ensured by Schwartz-Zippel. Specifically, let $\mathcal {L}=\big (x_0, \ldots \big )$ denote the tuples in $\mathcal {L}$ (where now we represent each tuple as elements in $\mathbb {F}_{2^\kappa }$), and let $\mathcal {L}'=\big (x'_0, \ldots \big )$ denote the tuples in $\mathcal {L}'$. If one defines the polynomials $L(R) = \prod _i (x_i - R)$ and $L'(R) = \prod _i(x'_i - R)$, then note that $\mathcal {L}$ and $\mathcal {L}'$ are permutations of each other iff $L(R)=L'(R)$. The verifier can efficiently test the equality of these polynomials by choosing a uniform field element r and verifying that $L(r) = L(r')$.

To extend the above idea to support write, one just needs to take the timestamp into consideration since a value can be updated in the middle of the execution. The sorting needs to respect both index and time stamp, and the consistency checks need to incorporate the update after the initialization.

6 Open questions

We will now mention some research directions which we believe are interesting to develop VOLE-based ZK protocols further.

6.1 Theoretical questions

There are many intriguing theoretical aspects of VOLE-based Zero Knowledge protocols that are yet unexplored. In the following, we provide a list of interesting theoretical research directions.

• 1. Using other correlations. The efficiency of VOLE-based Zero Knowledge protocols relies on the recent breakthroughs in efficient VOLE extension. But also other pseudorandom correlations (see e.g. [13]) can be efficiently generated. The question is if these, or other, correlations can benefit ZK proofs in a similar way. One step into this direction was already done in [22] (see Sect. 5.2) by using qVOLE.

• 2. Sublinear communication and verification. The idea of ZK proofs with sublinear communication and verification has flourished in the past 10 years, starting from [8, 28, 44] and leading to recent Blockchain-optimized proof systems. In VOLE-based ZK, similar properties may be interesting although non-interactivity is less important. Having a verifier with sublinear (in |C|) computation while keeping a concretely efficient, linear prover has to the best of our knowledge not yet been achieved. For the special case of disjunctions one could achieve an asymptotic solution by extending the techniques of [32], but concrete efficiency is unclear.

• 3. Sublinear communication, also in the input length.A recent work [50], which extends VOLE-based ZK, enables communication sublinear to |C|. Their protocol relies on vector oblivious polynomial evaluation (VOPE), an extension of VOLE. At the same time, it requires the proof to be of size at least |w| (i.e. the circuit input) for knowledge extraction. It would be interesting to explore if VOLE-based protocols can be both sublinear in |C| and |w| by introducing a knowledge assumption or using a random oracle, while keeping the concrete efficiency of [50].

6.2 Practical questions

VOLE-based ZK enjoys many advantages that are intriguing to practical deployment. Here we summarize a list of interesting practical future directions.

• 1. More efficient VOLE. The concrete efficiency of the whole proof system relies on efficient VOLE protocols. Thus it is crucial to design more efficient VOLE protocols with improved computation and communication overhead.

• 2. More applications. State-of-the-art VOLE-based ZK can prove tens of millions of gates with ease. This opens the possibility of proving very large statements, something not feasible before this line of work. It would be interesting to explore the space of applications that need ZK but were limited so far by the scalability problems of existing schemes. The fact that this type of proof is designated-verifier could affect the design and thus poses new questions in designing ZK-based applications.

• 3. Lowering the gap between $\mathbb {Z}_{2^k}$ and $\mathbb {F}_p$. In their work, [1] provide a software implementation of their instantiation of $\mathcal {F}_\textsf{ABB}$ that operates over $\mathbb {Z}_{2^k}$. Their implementation achieves $> rapprox 1$mio multiplications over $\mathbb {Z}_{2^{64}}$, which is up to an order of magnitude slower than what the implementations of the protocols from Sect. 4 can perform in similar settings over fields of similar size. Lowering this gap may be helpful if $\mathbb {Z}_{2^k}$ proof systems should be used for proofs of programs on current hardware architectures.