Abstract
We construct an efficient dynamic group signature (or more generally an accountable ring signature) from isogeny and lattice assumptions. Our group signature is based on a simple generic construction that can be instantiated by cryptographically hard group actions such as the CSIDH group action or an MLWE-based group action. The signature is of size \(O(\log N)\), where N is the number of users in the group. Our idea builds on the recent efficient OR-proof by Beullens, Katsumata, and Pintore (Asiacrypt’20), where we efficiently add a proof of valid ciphertext to their OR-proof and further show that the resulting non-interactive zero-knowledge proof system is online extractable. Our group signatures satisfy more ideal security properties compared to previously known constructions, while simultaneously having an attractive signature size. The signature size of our isogeny-based construction is an order of magnitude smaller than all previously known post-quantum group signatures (e.g., 6.6 KB for 64 members). In comparison, our lattice-based construction has a larger signature size (e.g., either 126 KB or 89 KB for 64 members depending on the satisfied security property). However, since the \(O(\cdot )\)-notation hides a very small constant factor, it remains small even for very large group sizes, say \(2^{20}\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 About
An extended abstract of this work was published in EUROCRYPT 2022 [13]. This is a full version of the paper. In more details, we provide a comparison of this work with two recent concurrent and independent papers which propose isogeny-based group signatures; we prove correctness and security of the proposed generic accountable ring signature \(\Pi _{\textsf{ARS}}\) in Fig. 1; we describe in details the tight variant \(\Pi _{\textsf{ARS}}^\textsf{Tight}\) in Fig. 2 and we prove its security; we prove correctness and security of the traceable OR sigma protocol \(\Pi _{\Sigma }^\textsf{base}\) in Fig. 3; we detail how we incorporate three optimisations to the modification of \(\Pi _{\Sigma }^\textsf{base}\) which enjoys a negligibly-small soundness error, and we prove its security; we give a full description of the base traceable OR sigma protocol \(\Pi _{\Sigma }^{\textsf{base}{{\textsf{T}}}{{\textsf{i}}}}\) for the “tight” relation \(R_{\textsf{sig}}^\textsf{Tight}\) in Fig. 6; we formally show that the \(\textsf{NIZK}\) with labels \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) in Fig. 7 is zero-knowledge. In Sect. 8, the building blocks required for our generic construction are instantiated via isogenies-by using the CSIDH group action—and lattices. Finally, we recall how accountable ring signatures can be naturally viewed as group signatures in the Appendix.
2 Introduction
Group signature schemes, introduced by Chaum and van Heyst [31], allow authorized members of a group to individually sign on behalf of the group while the specific identity of the signer remains anonymous. However, should the need arise, a special entity called the group manager (or sometimes the tracing authority) can trace the signature to the signer, thus holding the group members accountable for their signatures. Group signatures have been an active area of academic research for the past three decades, and have also been gathering practical attention due to the recent real-world deployment of variants of group signatures such as directed anonymous attestation (DAA) [23] and enhanced privacy ID (EPID) [24].
Currently, there are versatile constructions of efficient group signatures from classical assumptions, e.g., [6, 16, 17, 34, 39, 40, 55, 58, 71, 72]. In this work, when we argue the efficiency of a group signature, we focus on one of the quintessential metrics: the signature size. We require it to be smaller than \(c \cdot \log N\) bits, where N is the group size and c is some explicit small polynomial in the security parameter. In their seminal work, Bellare, Micciancio, and Warinschi [8] provided a generic construction of a group signature with signature size O(1) from any signature scheme, public-key encryption scheme, and general non-interactive zero-knowledge (\(\textsf{NIZK}\)) proof system. Unfortunately, this only provides an asymptotic feasibility result, and thus one of the main focuses of subsequent works, including ours, has been to construct a concretely efficient group signature.
In contrast to the classical setting, constructing efficient group signatures from any post-quantum assumptions has been elusive. Since the first lattice-based construction by Gordon, Katz, and Vaikuntanathan [57], there has been a rich line of subsequent works on lattice-based (and one code-based) group signatures, including but not limited to [49, 59, 65, 70, 74]. However, these results remained purely asymptotic. It was not until recently that efficient lattice-based group signatures appeared [22, 38, 47, 48]. In [47], Esgin et al. report a signature size of 12KB and 19KB for a group size of \(N = 2^{6}\) and \(2^{10}\), respectively—several orders of magnitude better than prior constructions.Footnote 1 These rapid improvements in efficiency for lattices originate in the recent progress of lattice-based NIZK proof systems for useful languages [5, 21, 45, 46, 75, 76, 85], most of which rely heavily on the properties of special structured lattices. Thus, it seems impossible to import similar techniques to other post-quantum assumptions or to standard non-structured lattices. For instance, constructing efficient group signatures from isogenies—one of the promising alternative post-quantum tools to lattices—still seems out of reach using current techniques. This brings us to the main question of this work:
Can we construct an efficient group signature secure from isogenies? Moreover, can we have a generic construction that can be instantiated from versatile assumptions, including those based on less structured lattices?
In addition, as we discuss in more detail later, we notice that all works regarding efficient post-quantum group signatures [22, 38, 47, 48, 60] do not satisfy the ideal security properties (which are by now considered standard) formalized by Bootle et al. [20]. Thus, we are also interested in the following question:
Can we construct efficient post-quantum group signatures satisfying the ideal security properties formalized by Bootle et al. [20]?
To address these questions, in this work we focus on accountable ring signatures [84]. An accountable ring signature offers the flexibility of choosing the group of users when creating a signature (like a ring signature [82]), while also enforcing accountability by including one of the openers in the group (like a group signature). Although research on accountable ring signatures is still limited [19, 48, 62, 68, 84], we advocate that they are as relevant and interesting as group and ring signatures. As shown by Bootle et al. [19], accountable ring signatures imply group and ring signatures by naturally limiting or downgrading their functionality. Thus, an efficient post-quantum solution to an accountable ring signature implies solutions for both secure (dynamic) group signatures [9] and ring signatures, making it an attractive target to focus on.
Finally, as an independent interest, we are also concerned with tightly-secure constructions. To the best of our knowledge, all prior efficient post-quantum secure group and ring signatures are in the random oracle model and have a very loose reduction loss. In typical security proofs, given an adversary with advantage \(\epsilon \) that breaks some security property of the group signature, we can only construct an adversary with advantage at most \((N^2 Q)^{-1} \cdot \epsilon ^2\) against the underlying hard problem, where Q is the number of random oracle queries and N is the number of users in the system. If we aim for 128-bit security (i.e., \(\epsilon = 2^{-128}\)), and set for example \((N, Q) = (2^{10}, 2^{50})\), then we need at least 326-bits of security for the hard problem. When aiming for a provably-secure construction, the parameters must be set much larger to compensate for this significant reduction loss, which then leads to a less efficient scheme. This is especially unattractive in the isogeny setting since only the smallest among the CSIDH parameters [28] enjoys properties suitable to achieve concrete efficiency [15].
2.1 Our contribution
In this work, we construct an efficient accountable ring signature based on isogenies and lattices. This in particular implies the first efficient isogeny-based group signature. Our generic construction departs from known general feasibility results such as [8] and builds on primitives that can be efficiently instantiated. Unlike previous efficient post-quantum group signatures, our scheme satisfies all the desired properties provided by Bootle et al. [20] including dynamicity and fully (CCA) anonymity: the former states that the group members can be added and revoked dynamically and are not fixed on setup; the later states that anonymity holds even in the presence of an adversary that sees the signing keys of all honest users, who is additionally granted access to an opening oracle. We also satisfy the ideal variant of non-frameability and traceability [20], where the former is captured by unforgeability in the context of accountable ring signature. Roughly, this ensures that arbitrary collusion among members, even with the help of a corrupted group manager, cannot falsely open a signature to an honest user.
Our accountable ring signature schemes are realized in three steps. We first provide a generic construction of an accountable ring signature from simple cryptographic primitives such as a public-key encryption (\(\textsf{PKE}\)) scheme and an accompanying \(\textsf{NIZK}\) for a specific language. We then show an efficient instantiation of these primitives based on a group action that satisfies certain cryptographic properties. Finally, we instantiate the group action by either the CSIDH group action or the MLWE-based group action. Our generic construction builds on the recent efficient OR-proofs for isogeny and lattice-based hard languages by Beullens, Katsumata, and Pintore [14], which were used to construct ring signatures. The most technical part of this work is to efficiently add a proof of valid ciphertext to their OR-proof and proving full anonymity, which done naively would incur an exponential security loss. At the core of our construction is an efficient online-extractable OR-proof that allows to also prove validity of a ciphertext.
Moreover, thanks to the online extractability, our construction achieves a much tighter reduction loss compared to prior accountable ring signatures (and also group and ring signatures). It suffices to assume that the underlying post-quantum hard problem cannot be solved with advantage more than \(N^{-1} \cdot \epsilon \) rather than \((N^2 Q)^{-1} \cdot \epsilon ^2\) as in prior works whose proofs rely on the forking lemma [50, 81]. Working with the above example, we only lose 10-bits rather than 198-bits of security. We further show how to remove \(N^{-1}\) using the Katz-Wang technique [61] along with some techniques unique to our \(\textsf{NIZK}\). As a side product, we obtain a tightly-secure and efficient isogeny and lattice-based ring signatures, improving upon those by Beullens et al. [14] which have a loose security reduction.
Comparison to prior work. To the best of our knowledge, Esgin et al. [47, 48] are the only other work that (implicitly) provide an efficient post-quantum accountable ring signature.Footnote 2 Since the efficiency of an accountable ring signature is equivalent to those of the group signature obtained through limiting the functionality of the accountable ring signature, we chose to compare the efficiency of our scheme with other state-of-the-art post-quantum group signatures. Table 1 includes a comparison of the signature size and the different notions of security it satisfies. The first two schemes satisfy all the desired security properties of a dynamic group signature formalized by Bootle et al. [20]. Our scheme is the only one to achieve full \(\textsf{CCA}\) anonymity. Esgin et al. [47] achieves full \(\textsf{CPA}\) anonymity, where anonymity is broken once an adversary is given access to an opening oracle; in practice, this means that if a specific signature is once opened to some user, then any signature ever signed by that particular user will lose anonymity. Here, “full” means that the signing key of all the users may be exposed to the adversary. In contrast, Katz, Kolesnikov, and Wang [60] satisfies selfless \(\textsf{CCA}\) anonymity. While their scheme supports opening oracles, anonymity no longer holds if the signing key used to sign the signature is exposed to the adversary. Moreover, our scheme is the only one that also achieves the ideal variant of non-frameability and traceability [9, 20] (illustrated in the “Manager Accountability” column). The two schemes [47, 60] assume the group manager honestly executes the opening algorithm and that everyone trusts the output. Put differently, a malicious group manager can frame any honest members in the group by simply replacing the output of the opening algorithm. In contrast, our scheme remains secure even against malicious group managers since the validity of the output of the opening algorithm is verifiable. That is, even the group manager is held accountable in our group signature.
Not only our group signatures satisfy more ideal security properties compared to previous constructions, Table 1 shows that our signature size remains competitive. Our isogeny-based group signature based on CSIDH provides the smallest signature size among all post-quantum group signatures, which is \(0.6 \log _2(N) + 3\) KB. In contrast, our lattice signature is larger; the scheme in the second (resp. third) row has signature size \(0.5 \log _2(N) + 123.5\) KB (resp. \(0.5 \log _2(N) + 85.9\) KB). It is smaller compared to [60], while larger compared to [47]. Compared to the two constructions, our signature size grows much slower with the group size N (see also Footnote 1) and also satisfies stronger security. We thus leave it as an interesting open problem to lower the constants in our construction.
2.2 Technical overview
An accountable ring signature is like a standard ring signature where the ring \({\textsf{R}}\) also includes an arbitrary opener public key \(\textsf{opk}\) of the signer’s choice when creating a signature \(\sigma \). The signature \(\sigma \) remains anonymous for anybody who does not know the corresponding opener secret key \(\textsf{osk}\), while the designated opener can use \(\textsf{osk}\) to trace the user who created \(\sigma \). A ring signature can be thought of as an accountable ring signature where \(\textsf{opk}= \bot \), while a group signature can be thought as an accountable ring signature where there is only a single opener.
General approach. Our generic construction of an accountable ring signature follows the well-known template of the encrypt-then-prove approach to construct a group signature [27]. The high-level idea is simple. The signer encrypts its verification key \({{\textsf{v}}}{{\textsf{k}}}\) (or another unique identifier) using the opener’s public key \(\textsf{opk}\) for a \(\textsf{PKE}\) scheme and provides a \(\textsf{NIZK}\) proof for the following three facts: the ciphertext \({{\textsf{c}}}{{\textsf{t}}}\) encrypts \({{\textsf{v}}}{{\textsf{k}}}\) via \(\textsf{opk}\); \({{\textsf{v}}}{{\textsf{k}}}\) is included in the ring \({\textsf{R}}\); and that it knows a secret key \({{\textsf{s}}}{{\textsf{k}}}\) corresponding to \({{\textsf{v}}}{{\textsf{k}}}\). To trace the signer, the opener simply decrypts \({{\textsf{c}}}{{\textsf{t}}}\) to recover \({{\textsf{v}}}{{\textsf{k}}}\). Notice that the \(\textsf{NIZK}\) proof implicitly defines a verifiable encryption scheme [25, 26] since it is proving that \({{\textsf{c}}}{{\textsf{t}}}\) is a valid encryption for some message \({{\textsf{v}}}{{\textsf{k}}}\) in \({\textsf{R}}\). Below, although our construction can be based on any cryptographically-hard group action, we mainly focus on isogenies for simplicity.
One of the difficulties in instantiating this template using isogeny-based cryptography is that we do not have an efficient verifiable encryption scheme for an appropriate \(\textsf{PKE}\) scheme. To achieve full anonymity, most of the efficient group signatures, e.g., [38, 39, 55, 58, 71, 72], use an \(\textsf{IND}\text {-}\textsf{CCA}\) secure \(\textsf{PKE}\) as a building block and construct an efficient \(\textsf{NIZK}\) that proves validity of the ciphertext. Full anonymity stipulates that an adversary cannot de-anonymize a signature even if it is provided with an opening oracle, which traces the signatures submitted by the adversary. Roughly, by using an \(\textsf{IND}\text {-}\textsf{CCA} \) secure \(\textsf{PKE}\) as a building block, the reduction can simulate the opening oracle by using the decapsulation oracle provided by the \(\textsf{IND}\text {-}\textsf{CCA} \) game, rather than the opener’s secret key. In the classical setting, constructing such an efficient \(\textsf{IND}\text {-}\textsf{CCA} \) secure verifiable encryption scheme is possible using the Cramer-Shoup \(\textsf{PKE}\) [35] that offers a rich algebraic structure. Unfortunately, in the isogeny setting, although we know how to construct an \(\textsf{IND}\text {-}\textsf{CCA}\) secure \(\textsf{PKE}\) based on the Fujisaki-Okamoto transform [53], it seems quite difficult to provide an accompanying verifiable encryption scheme as the construction internally uses a hash function modeled as a random oracle. Another approach is to rely on the weaker \(\textsf{IND}\text {-}\textsf{CPA}\) secure \(\textsf{PKE}\) but to use a stronger \(\textsf{NIZK}\) satisfying online-extractability [52]. At a high level, the reduction can use the online-extractor to extract the witness in the ciphertext \({{\textsf{c}}}{{\textsf{t}}}\) instead of relying on the decapsulation oracle.Footnote 3 However, it turns out that even this approach is still non-trivial since we do not have any efficient verifiable encryption scheme for existing isogeny-based \(\textsf{PKE}\) s, let alone an accompanying online-extractable \(\textsf{NIZK}\). For instance, most isogeny-based \(\textsf{IND}\text {-}\textsf{CPA}\) secure \(\textsf{PKE}\) s are based on the hashed version of ElGamal, and to the best of our knowledge, there are no efficient verifiable encryption schemes for hashed ElGamal.
Verifiable encryption scheme for a limited class of PKE. In this work, we observe that in the context of accountable ring signatures and group signatures, we do not require the full decryption capability of a standard \(\textsf{PKE}\). Observe that decryption is only used by the opener and that it knows the ciphertext \({{\textsf{c}}}{{\textsf{t}}}\) must be an encryption of one of the verification keys included in the ring (or group) \({\textsf{R}}\). Therefore, given a ciphertext \({{\textsf{c}}}{{\textsf{t}}}\), we only require a mechanism to check if \({{\textsf{c}}}{{\textsf{t}}}\) encrypts a particular message \({\textsf{M}}\), rather than being able to decrypt an arbitrary unknown message. Specifically, the opener can simply run through all the verification keys \({{\textsf{v}}}{{\textsf{k}}}\in {\textsf{R}}\) to figure out which \({{\textsf{v}}}{{\textsf{k}}}\) was encrypted in \({{\textsf{c}}}{{\textsf{t}}}\). This allows us to use a simple \(\textsf{IND}\text {-}\textsf{CPA}\) secure \(\textsf{PKE}\) with limited decryption capability based on the CSIDH group action: Let \(E_0 \in \mathcal {E}\ell \ell _{p}({\mathcal {O}},\pi )\) be a fixed and public elliptic curve. The public key is \({{\textsf{p}}}{{\textsf{k}}}= (E_0, E:= s \star E_0)\), where \({{\textsf{s}}}{{\textsf{k}}}= s\) is sampled uniformly at random from the class group \(\mathcal {C}\ell (\mathcal {O})\). To encrypt a message \({\textsf{M}}\in \mathcal {C}\ell (\mathcal {O})\), we sample \(r \leftarrow \mathcal {C}\ell (\mathcal {O})\) and set \({{\textsf{c}}}{{\textsf{t}}}=({{\textsf{c}}}{{\textsf{t}}}_0:= r \star E_0, {{\textsf{c}}}{{\textsf{t}}}_1:= {\textsf{M}}\star (r \star E))\). To check if \({{\textsf{c}}}{{\textsf{t}}}\) decrypts to \({\textsf{M}}'\), we check whether \({{\textsf{c}}}{{\textsf{t}}}_1\) is equal to \({\textsf{M}}' \star ({{\textsf{s}}}{{\textsf{k}}}\star {{\textsf{c}}}{{\textsf{t}}}_0)\). Note that in general we cannot decrypt when \({\textsf{M}}\) is unknown since we cannot cancel out \({{\textsf{s}}}{{\textsf{k}}}\star {{\textsf{c}}}{{\textsf{t}}}_0\) from \({{\textsf{c}}}{{\textsf{t}}}_1\). Now, observe that proving \({{\textsf{c}}}{{\textsf{t}}}\) encrypts \({\textsf{M}}\in \mathcal {C}\ell (\mathcal {O})\) is easy since there is a simple sigma protocol for the Diffie-Hellman-like statement \(({{\textsf{c}}}{{\textsf{t}}}_0, (-{\textsf{M}}) \star {{\textsf{c}}}{{\textsf{t}}}_1) = (r\star E_0, r\star E)\), where r is the witness, e.g., [43]. Although this comes closer to what we want, this simple sigma protocol is not yet sufficient since the prover must reveal the message \({\textsf{M}}\) to run it. Specifically, it proves that \({{\textsf{c}}}{{\textsf{t}}}\) is an encryption of \({\textsf{M}}\), while what we want to prove is that \({{\textsf{c}}}{{\textsf{t}}}\) is an encryption of some \({\textsf{M}}\in {\textsf{R}}\). In the context of accountable ring signature and group signature, this amounts to the signer being able to hide its verification key \({{\textsf{v}}}{{\textsf{k}}}\in {\textsf{R}}\).
\({{\textit{Constructing }\textsf{NIZK} \textit{ for accountable ring signature}}}\) Let us move forward to the intermediate goal of constructing a (non-online-extractable) \(\textsf{NIZK}\) proof system for the following three facts: the ciphertext \({{\textsf{c}}}{{\textsf{t}}}\) encrypts \({{\textsf{v}}}{{\textsf{k}}}\) via \({{\textsf{p}}}{{\textsf{k}}}\); \({{\textsf{v}}}{{\textsf{k}}}\) is included in the ring \({\textsf{R}}\); and that the prover knows a secret key \({{\textsf{s}}}{{\textsf{k}}}\) corresponding to \({{\textsf{v}}}{{\textsf{k}}}\). Recently, Beullens, Katsumata, and Pintore [14] proposed an efficient sigma protocol (and a non-online-extractable \(\textsf{NIZK}\) via the Fiat-Shamir transform) for proving the last two facts, which in particular constitutes an efficient OR-proof. We show how to glue the above “weak” verifiable encryption scheme with their OR-proof.
We first review a variant of the OR-sigma protocol in [14] with proof size O(N), where N is the size of the ring. Assume each user \(i \in [N]\) in the ring holds \({{\textsf{v}}}{{\textsf{k}}}_i = (E_0, E_i:= s_i \star E_0) \in \mathcal {E}\ell \ell {p}({\mathcal {O}},\pi )^2\) and \({{\textsf{s}}}{{\textsf{k}}}_i = s_i \in \mathcal {C}\ell (\mathcal {O})\). To prove \({{\textsf{v}}}{{\textsf{k}}}_I \in {\textsf{R}}\) and that it knows \({{\textsf{s}}}{{\textsf{k}}}_I\), the prover first sample \(s' \leftarrow \mathcal {C}\ell (\mathcal {O})\) and sets \(R_i = s' \star E_i\) for \(i \in [N]\). It also samples randomness \(\textsf{rand}_i\) and creates commitments \(( {\textsf{C}}_i = \textsf{Com}(R_i, \textsf{rand}_i) )_{i \in [N]}\), where this commitment is simply instantiated by a random oracle. It finally samples a random permutation \(\phi \) over [N] and sends a permuted tuple \(( {\textsf{C}}_{\phi (i)} = \textsf{Com}(R_{i}, \textsf{rand}_{i}) )_{i \in [N]}\). The verifier samples a random bit \(b \in \{ 0,1 \} \). If \(b = 0\), the prover returns all the randomness \(( s', ( \textsf{rand}_i )_{i \in [N]}, \phi )\) used to create the first message. The verifier then checks if the first message sent by the prover is consistent with this randomness. Otherwise, if \(b = 1\), the prover returns \((I'', \textsf{rand}'', s''):= ( \phi (I), \textsf{rand}_{I}, s' + s_I )\). The verifier then checks if \({\textsf{C}}_{I''} = \textsf{Com}(s'' \star E_0, \textsf{rand}'')\) holds. Notice that if the prover is honest, then \(s'' \star E_0 = s' \star E_I\) as desired. It is easy to check it is honest-verifier zero-knowledge. The transcript when \(b = 0\) is independent of the witness, while the transcript when \(b = 1\) can be simulated if the commitment scheme is hiding. Moreover, special soundness can be checked by noticing that given \(s''\) and \(s'\), we can extract some \((i^*, s^*)\) such that \((E_0, E_{i^*} = s^* \star E_0) \in {\textsf{R}}\). A full-fledged OR-sigma protocol with proof size O(N) is then obtained by running this protocol \(\uplambda \)-times in parallel, where \(\uplambda \) denotes the security parameter. [14] showed several simple optimization techniques to compress the proof size from O(N) to \(O(\log N)\), but we first explain our main idea below.
We add our “weakly decryptable” \(\textsf{PKE}\) to this OR-sigma protocol. Since our \(\textsf{PKE}\) only handles messages in \(\mathcal {C}\ell (\mathcal {O})\), the prover with \({{\textsf{v}}}{{\textsf{k}}}_I \in {\textsf{R}}\) encrypts the index \(I \in [N]\) rather than \({{\textsf{v}}}{{\textsf{k}}}_I\), where we assume the verification keys in the ring \({\textsf{R}}\) are ordered lexicographically.Footnote 4 The statement now consists of the ring \({\textsf{R}}\) and the ciphertext \({{\textsf{c}}}{{\textsf{t}}}= ({{\textsf{c}}}{{\textsf{t}}}_0:= r\star E_0, {{\textsf{c}}}{{\textsf{t}}}_1 = I \star (r \star E))\), where \((E_0, E)\) is the opener’s public key \(\textsf{opk}\). Recall the opener can decrypt \({{\textsf{c}}}{{\textsf{t}}}\) with knowledge of the ring \({\textsf{R}}\) by brute-force searching for an \(i \in [N]\) such that \({{\textsf{c}}}{{\textsf{t}}}_1 = i \star (\textsf{osk}\star {{\textsf{c}}}{{\textsf{t}}}_0)\). Now, to prove \({{\textsf{v}}}{{\textsf{k}}}_I\) is an entry in \({\textsf{R}}\) and that it knows \({{\textsf{s}}}{{\textsf{k}}}_I\), the prover samples \(s' \leftarrow \mathcal {C}\ell (\mathcal {O})\) and sets \(R_i = s' \star E_i\) for \(i \in [N]\) as before. It then further samples \(r' \leftarrow \mathcal {C}\ell (\mathcal {O})\) and prepares \({{\textsf{c}}}{{\textsf{t}}}'_i = ( r' \star {{\textsf{c}}}{{\textsf{t}}}_0, (-i) \star (r' \star {{\textsf{c}}}{{\textsf{t}}}_1))\) for all \(i \in [N]\). Observe that \({{\textsf{c}}}{{\textsf{t}}}'_i\) is an encryption of the message \((I - i)\) using randomness \((r' + r)\). Specifically, \({{\textsf{c}}}{{\textsf{t}}}'_I\) is of the form \(((r' + r)\star E_0, (r' + r) \star E)\), which admits a natural sigma protocol as explained above. Finally, the prover samples randomness \(\textsf{rand}_i\) and a random permutation \(\phi \) over [N], and sends the randomly permuted commitments \(( {\textsf{C}}_{\phi (i)} = \textsf{Com}(R_{i} \Vert {{\textsf{c}}}{{\textsf{t}}}'_{i}, \textsf{rand}_{i}) )_{i \in [N]}\). The verifier samples a random bit \(b \in \{ 0,1 \} \). If \(b = 0\), then similarly to the above OR-sigma protocol, the prover simply returns all the randomness and the verifier checks the consistency of the first message. Otherwise, if \(b = 1\), the prover returns \((I'', \textsf{rand}'', s'', r''):= ( \phi (I), \textsf{rand}_{I}, s' + s_I, r' + r )\). The verifier checks if \({\textsf{C}}_{I''} = \textsf{Com}(s'' \star E_0 \Vert (r'' \star E_0, r'' \star E), \textsf{rand}'')\) holds. Correctness and honest-verifier zero-knowledge holds essentially for the same reason as the above OR-sigma protocol. More importantly, special soundness holds as well. Intuitively, since the opening to \(b = 0\) forces the cheating prover to commit to the proper \(({{\textsf{v}}}{{\textsf{k}}}_i, i)\)-pair, a cheating prover cannot encrypt an index \(I'\) and prove that it has \({{\textsf{s}}}{{\textsf{k}}}_I\) corresponding to \({{\textsf{v}}}{{\textsf{k}}}_I\) for a different \(I \ne I'\).
To compile our sigma protocol into an \(\textsf{NIZK}\), we apply the Fiat-Shamir transform. Moreover, we apply similar optimization techniques used in [14] to compress the proof size from O(N) to \(O(\log N)\). Roughly, the prover additionally uses a pseudorandom generator to generate the randomness (i.e., \(s', r', \phi , ( \textsf{rand}_i )_{i \in [N]}\)). Then, in case \(b = 0\), the prover needs to reply only with the seed of size O(1). The prover also uses a Merkle tree to accumulate \(( {\textsf{C}}_{\phi (i)} )_{i \in [N]}\) and sends the root value in the first message. It then only opens to the path necessary for verification when \(b = 1\). This has a positive side-effect that we no longer require a permutation \(\phi \) since the path hides the index if we use a slightly tweaked variant of the standard Merkle tree. Finally, we take advantage of the asymmetry in the prover’s response size for \(b = 0\) and \(b = 1\), which are O(1) and \(O(\log N)\), respectively. Namely, we imbalance the challenge space so that the prover opens to more 0 than 1, while still maintaining negligible soundness error.
Adding online-extractability. To build an accountable ring signature or group signature, we require the above \(\textsf{NIZK}\) to be (multi-proof) online-extractable. This is a strengthening of standard proof of knowledge (PoK) that roughly states that the knowledge extractor, who can see what the adversary queries to the random oracle, is able to directly extract witnesses from the proofs output by the adversary. The OR-proof by [14], which our \(\textsf{NIZK}\) builds on, was only shown to satisfy the standard PoK, which bases on a rewinding extractor.
One simple way to add online-extractability to our \(\textsf{NIZK}\) is to apply the Unruh transform [83]. Namely, we can modify the prover to add two more commitments \(h_0 = \textsf{Com}(s' \Vert r', \textsf{rand}_0)\) and \(h_1 = \textsf{Com}(s'' \Vert r'', \textsf{rand}_1)\) in the first message, where \(\textsf{Com}\) is instantiated by the random oracle. Then, if \(b = 0\) (resp. \(b = 1\)), the prover further opens to \(h_0\) (resp. \(h_1\)). Recall that if the reduction obtains both \((s', r')\) and \((s'', r'')\), then it can invoke the extractor provided by the underlying sigma protocol to extract some \((i^*, s^*)\) such that \((E_0, E_{i^*} = s^* \star E_0) \in {\textsf{R}}\). Therefore, for the cheating adversary to fool the reduction, it must guess the bit b and create \(h_b\) correctly while creating \(h_{1-b}\) arbitrary. Intuitively, if we have \(\uplambda \)-repetition of the sigma protocol, then the cheating prover cannot possibly guess all the challenge bits correctly. Therefore, there must be some challenge where it created \(h_0\) and \(h_1\) honestly. For that challenge bit, the reduction algorithm can then retrieve the corresponding inputs \((s' \Vert r', \textsf{rand}_0)\) and \((s'' \Vert r'', \textsf{rand}_1)\) from simply observing the random oracle, and then, run the extractor to obtain the witness.
This idea works but it comes with an extra two hashes per one execution of the binary-challenge sigma protocol. Although it may sound insignificant in an asymptotic sense, these hashes add up when we execute the sigma protocol many times, and it makes it difficult to apply some of the optimization tricks. Concretely, when we apply this change to the isogeny-based ring signature by Beullen et al. [14], the signature grows by roughly a factor of 2 to 3.
In this work, we show that we can in fact prove online-extractability without making any modification to the aforementioned \(\textsf{NIZK}\). Our main observations are the following: if the prover uses a seed to generate the randomness used in the first message via a random oracle, then the online extractor can observe \((s', r', \phi , ( \textsf{rand}_i )_{i \in [N]})\); and the prover must respond to some execution of the binary-challenge sigma protocol where the challenge bit is 1. The first implies that the seed implicitly acts as a type of commitment to \((s', r')\). The second implies the prover returns a response that includes \((s'', r'')\). Specifically, our online extractor only looks at all the responses for the rounds where the challenge bit was 1, and checks the random oracle for any seed that leads to the commitment provided in the first message of the sigma protocol. If such seed is found, then it succeeds in extracting a witness. The intuition is simple but it turns out that the formal proof is technically more complicated due to the several optimizations performed on the basic sigma protocol to achieve proof size \(O(\log N)\).
Generalizing with group actions. Although we have been explaining our generic construction using the CSIDH group action, it is not unique to them. It works equally well for any group action that naturally induces a \(\textsf{PKE}\). Specifically, we instantiate the above idea also by the MLWE group action defined roughly as \(\star : R^{n + m}_q \times R^m_q: ({{\textbf {s}}}, {{\textbf {e}}}) \star {{\textbf {t}}}\rightarrow {{\textbf {A}}}\star {{\textbf {s}}}+ {{\textbf {e}}}+ {{\textbf {t}}}\), where \(R_q = {\mathbb {Z}}_q[X]/(X^d + 1)\). Since CSIDH and MLWE induce a \(\textsf{PKE}\) with slightly different algebraic structures, we introduce a group-action-based \(\textsf{PKE}\) defined by two group actions to formally capture both instances. This abstraction may be of an independent interest since at first glance, isogeny-based and lattice-based \(\textsf{PKE}\) s seem to rely on different algebraic structures. Finally, one interesting feature unique to our generic construction is that since our sigma protocol is rather combinatorial in nature, we can for instance use CSIDH for the user’s public key \({{\textsf{v}}}{{\textsf{k}}}\) and mix it with an \(\textsf{MLWE}\)-based \(\textsf{PKE}\) for the opener’ public key \(\textsf{opk}\). The practical impact of such mixture is that we can achieve stronger bit-security for anonymity (due to \(\textsf{MLWE}\)) while keeping the user’s public key and signature small (due to CSIDH).
Achieving tight reduction. Since the proofs do not rely on the forking lemma [50, 81] to extract witnesses from the forged proofs, our construction achieves a tighter reduction compared to prior works on efficient group signatures. However, we still lose a factor 1/N in the proof of unforgeability, which may vary from 1/2 to \(1/2^{20}\).Footnote 5 Recall N is the size of the group in group signatures but it is the size of all the users enrolled in the system for accountable ring signatures, which may be far larger than the size of the ring. The main reason for this loss was because the reduction needs to guess one user’s verification key used by the adversary to create its forgery and to embed the hard problem into it.
A well known technique to obtain a tight proof is to rely on the Katz-Wang technique [61] along with the generic OR-composition of sigma protocols, and rely on a multi-instance version of the hard problem (which are believed to be as difficult as the single-instance version for specific hard problems). Namely, we modify the scheme to assign two verification keys \(({{\textsf{v}}}{{\textsf{k}}}^{(1)}, {{\textsf{v}}}{{\textsf{k}}}^{(2)})\) to each user. The users will only hold one signing key \({{\textsf{s}}}{{\textsf{k}}}^{(b)}\) for \(b \in \{ 1,2 \}\) corresponding to the verification key \({{\textsf{v}}}{{\textsf{k}}}^{(b)}\). The user can honestly run the aforementioned sigma protocol where the statement includes \({{\textsf{v}}}{{\textsf{k}}}^{(b)}\), and a simulated sigma protocol using the ZK-simulator where the statement includes \({{\textsf{v}}}{{\textsf{k}}}^{(3-b)}\). We can then use the sequential OR-proof technique as presented in [1, 51] to bridge these two sigma protocols so that it hides the b.Footnote 6
While this generic transform works, it unfortunately doubles the signature size, which may outweigh the motivation for having a tight reduction. In this work, we present a novel and far cheaper technique tailored to our sigma protocol. The signature size overhead is a mere 512B for our concrete lattice-based instantiation. The key observation is that we can view the set of all users’ verification key \(({{\textsf{v}}}{{\textsf{k}}}^{(1)}, {{\textsf{v}}}{{\textsf{k}}}^{(2)})\) as a ring of size 2N, rather than a ring of size N where each ring element consists of two verification keys. This observation itself is not yet sufficient since recall that we typically must encrypt some information bound to the signer for traceability, e.g., encrypt the position/index of \({{\textsf{v}}}{{\textsf{k}}}\) in \({\textsf{R}}\), and it is no longer clear what to encrypt when we have two verification keys in the ring. Luckily, it turns out that our sigma protocol can be easily modified with no loss in efficiency to overcome this apparent issue. Details are provided in Sect. 6.3.
Concurrent works. There are two concurrent and independent works published on the Cryptology ePrint Archive [33, 66]. Both of these works obtain isogeny-based group signatures from variants of ring signatures. Lai et al. [66] base their group signature on revocable ring signatures, while Chung et al. [33] base theirs on accountable ring signatures. Chug et al. follow the security properties formalized in [84], in contrast with our accountable ring signature which follows those formalized in [20]. Since the security properties defined in [20] are stronger, our group signature satisfies more desirable security properties. Concretely, even though the opening algorithm of Chung et al. can output an opening proof, it does not enjoy the security guarantees defined in [20]. In fact, their construction does not have tracing soundness. In other words, their signature can be opened to two distinct parties with distinct valid opening proofs.
Table 2 compares this work with [33, 66] in terms of signature size, anonymity and manager accountability, where the integer N represents the size of the group. The construction in [33] is marked with partial manager accountability for the aforementioned reason. Ours is the only scheme that achieves an \(O(\log N)\) signature size and \(\textsf{CCA}\) anonymity. Additionally, our schem provides a much tighter security since both [33, 66] rely on the forking lemma in their security proofs.
Structure of this paper. We begin in Sect. 3 with some preliminary background on sigma protocols, accountable ring signatures, and other mathematical content which this paper relies on. We then introduce our new, generic constructions of accountable ring signature and dynamic group signature schemes in Sect. 4. These generic constructions are built from various components put forward in the proceeding sections: Sect. 5 defines group-action-based hard instance generators and public-key encryption schemes; Sect. 6 introduces our new “traceable” sigma protocol and proves its security; and Sect. 7 then constructs a NIZK proof system from said sigma protocol through the Fiat-Shamir transform. Finally, Sect. 8 details the instantiation of our schemes from isogenies and lattices.
3 Preliminaries
Notation. We begin by introducing some notation that will be used throughout the paper. For \(N \in {\mathbb {N}}\), we denote by [N] the set \(\{ 1, \dots , N \}\). We use \(\parallel \) to represent concatenation of two strings. We also use \(\{ X_i \}_{i \in S}\) to denote the set of elements \(X_i\) iterating over all values \(i \in S\). For any randomized algorithm A taking as input x, we will write A(x; r) to denote the execution of A on x using the randomness r. With an overload in notation, we write A(x) to denote the set of all possible outputs of A on input x, and \(y \in A(x)\) to indicate that there exists a randomness r such that \(y = A(x; r)\). Finally, we let \(\textsf{negl}(\uplambda )\) be a negligible function, i.e. one dominated by \(O(\uplambda ^{-n})\) for all \(n > 0\).
A note on random oracles. Throughout the paper, we instantiate several standard cryptographic primitives, such as pseudorandom number generators (i.e., \(\textsf{Expand}\)) and commitment schemes, by hash functions modeled as a random oracle \({\mathcal {O}}\). We always assume the input domain of the random oracle is appropriately separated when instantiating several cryptographic primitives by one random oracle. With abuse of notation, we may occasionally write for example \({\mathcal {O}}(\textsf{Expand}\parallel \cdot )\) instead of \(\textsf{Expand}(\cdot )\) to make the usage of the random oracle explicit. Here, we identify \(\textsf{Expand}\) with a unique string when inputting it to \({\mathcal {O}}\). Finally, we denote by \({\mathcal {A}}^{\mathcal {O}}\) an algorithm \({\mathcal {A}}\) that has black-box access to \({\mathcal {O}}\), and we may occasionally omit the superscript \({\mathcal {O}}\) for simplicity when the meaning is clear from context.
3.1 Sigma protocols
A sigma protocol \(\Pi _{\Sigma }\) for a NP relation \(R\subseteq \{ 0,1 \} ^* \times \{ 0,1 \} ^*\) is a public-coin three-move interactive protocol between a prover and a verifier that satisfies a specific flavor of soundness and zero-knowledge. The language \({\mathcal {L}}_R\) is defined as \(\{ {\textsf{X}}\mid ({\textsf{X}}, {\textsf{W}}) \in R \}\). As standard with many sigma protocols for a language defined over post-quantum algebraic structures, we relax the soundness notion to only hold for a slightly wider relation \({\tilde{R}}\) (i.e., \(R\subseteq {\tilde{R}}\)), e.g., [4, 10, 14, 36, 44, 54]. That is, a cheating prover may not be using a witness in \(R\) but is guaranteed to be using some witness in the wider relation \({\tilde{R}}\). Below, we consider a sigma protocol in the random oracle model, where the prover and verifier have access to a random oracle similarly to [14].Footnote 7
Definition 3.1
(Sigma Protocol) A sigma protocol \(\Pi _{\Sigma }\) for the relations \(R\) and \({\tilde{R}}\) such that \(R\subseteq {\tilde{R}}\) (which are implicitly parameterized by the security parameter \(\uplambda \)) consists of oracle-calling PPT algorithms \(({P}= ({P}_1, {P}_2), {V}=({V}_1,{V}_2))\), where \({V}_2\) is deterministic and we assume \({P}_1\) and \({P}_2\) share states. Let \({\textsf{ChSet}}\) denote the challenge space. Then, \(\Pi _{\Sigma }\) has the following three-move flow:
-
The prover, on input \(({\textsf{X}}, {\textsf{W}}) \in R\), runs \(\textsf{com}\leftarrow {P}^{\mathcal {O}}_1({\textsf{X}}, {\textsf{W}})\) and sends a commitment \(\textsf{com}\) to the verifier.
-
The verifier runs \(\textsf{chall}\leftarrow {V}^{\mathcal {O}}_1(1^\uplambda )\) to obtain a random challenge \(\textsf{chall}\) from \({\textsf{ChSet}}\), and sends it to the prover.
-
The prover, given \(\textsf{chall}\), runs \(\textsf{resp}\leftarrow {P}^{\mathcal {O}}_2( {\textsf{X}}, {\textsf{W}}, \textsf{chall})\) and returns a response \(\textsf{resp}\) to the verifier. Here, we allow \({P}_2\) to abort with some probability. In such cases we assign \(\textsf{resp}\) with a special symbol \(\bot \) denoting abort.
-
The verifier runs \({V}^{\mathcal {O}}_2({\textsf{X}}, \textsf{com}, \textsf{chall}, \textsf{resp})\) and outputs \(\top \) (accept) or \(\bot \) (reject).
Here, \({\mathcal {O}}\) is modeled as a random oracle and we often drop \({\mathcal {O}}\) from the superscript for simplicity when the meaning is clear from context. We assume \({\textsf{X}}\) is always given as input to \({P}_2\) and \({V}_2\), and omit it in the following. The protocol transcript \((\textsf{com}, \textsf{chall}, \textsf{resp})\) is said to be valid in case \({V}_2(\textsf{com}, \textsf{chall}, \textsf{resp})\) outputs \(\top \).
We require a sigma protocol \(\Pi _{\Sigma }\) in the random oracle model to satisfy the following standard properties: correctness, high min-entropy, special zero-knowledge and (relaxed) special soundness.
We require the sigma protocol to be correct conditioned on the prover not aborting the protocol. Below, if \(\delta = 0\), then it corresponds to the case when the prover never aborts.
Definition 3.2
(\((1 - \delta )\)-Correctness) A sigma protocol \(\Pi _{\Sigma }\) is \((1 - \delta )\)-correct for \(\delta \in [0, 1]\) if for all \(\uplambda \in {\mathbb {N}}\) and \(({\textsf{X}}, {\textsf{W}}) \in R\), the probability of the prover outputting \(\bot \) is at most \(\delta \), and we have

where the probability is taken over the randomness used by (P, V) and by the random oracle.
Definition 3.3
(High Min-Entropy) We say a sigma protocol \(\Pi _{\Sigma }\) has \(\alpha (\uplambda )\) min-entropy if for any \(\uplambda \in {\mathbb {N}}\), \(({\textsf{X}}, {\textsf{W}}) \in R\), and a possibly computationally-unbounded adversary \({\mathcal {A}}\), we have

where the probability is taken over the randomness used by \(P_1\) and by the random oracle. We say \(\Pi _{\Sigma }\) has high min-entropy if \(2^{-\alpha }\) is negligible in \(\uplambda \).
Definition 3.4
(Non-Abort Special Zero-Knowledge) We say \(\Pi _{\Sigma }\) is (non-abort) special zero-knowledge if there exists a PPT simulator \(\textsf{Sim}^{\mathcal {O}}\) with access to a random oracle \({\mathcal {O}}\) such that for any \(\uplambda \in {\mathbb {N}}\), statement-witness pair \(({\textsf{X}}, {\textsf{W}}) \in R\), \(\textsf{chall}\in {\textsf{ChSet}}\) and any computationally-unbounded adversary \({\mathcal {A}}\) that makes at most a polynomial number of queries to \({\mathcal {O}}\), we have
where \({\widetilde{P}}\) is a non-aborting prover \(P = (P_1, P_2)\) run on \(({\textsf{X}}, {\textsf{W}})\) with a challenge fixed to \(\textsf{chall}\) and the probability is taken over the randomness used by (P, V) and by the random oracle.
Below, for the special soundness property, the extraction algorithm is only required to recover a “weaker” witness in \({\tilde{R}}\) rather than in \(R\) used in the real protocol. In many applications, the capability of extracting from this wider relation suffices.
Definition 3.5
(Special Soundness) We say a sigma protocol \(\Pi _{\Sigma }\) has (relaxed) special soundness if there exists a PT extraction algorithm \({\textsf{Extract}}\) such that, given a statement \({\textsf{X}}\) and any two valid transcripts \((\textsf{com}, \textsf{chall}, \textsf{resp})\) and \((\textsf{com}, \textsf{chall}', \textsf{resp}')\) relative to \({\textsf{X}}\) and such that \(\textsf{chall}\ne \textsf{chall}'\), outputs a witness \({\textsf{W}}\) satisfying \(({\textsf{X}}, {\textsf{W}}) \in {\tilde{R}}\).
3.2 Non-interactive Zero-knowledge proofs of knowledge in the ROM
We consider non-interactive zero-knowledge proof of knowledge protocols (or simply \(\textsf{NIZK}\) (proof system)) in the ROM. Below, we define a variant where the proof is generated with respect to a label. Although syntactically different, such \(\textsf{NIZK}\) is analogous to the notion of signature of knowledge [30]
Definition 3.6
(\(\textsf{NIZK}\) Proof System) Let \({\textsf{L}} \) denote a label space, where checking membership can be done efficiently. A non-interactive zero-knowledge (\(\textsf{NIZK}\)) proof system \(\Pi _\textsf{NIZK} \) for the relations \(R\) and \({\tilde{R}}\) such that \(R\subseteq {\tilde{R}}\) (which are implicitly parameterized by \(\uplambda \)) consists of oracle-calling PPT algorithms \((\textsf{Prove}, \textsf{Verify})\) defined as follows:
- \(\textsf{Prove}^{\mathcal {O}}(\textsf{lbl}, {\textsf{X}}, {\textsf{W}}) \rightarrow \pi /\bot :\):
-
On input a label \(\textsf{lbl} \in {\textsf{L}} \), a statement and witness pair \(({\textsf{X}}, {\textsf{W}}) \in R\), it outputs a proof \(\pi \) or a special symbol \(\bot \) denoting abort.
- \(\textsf{Verify}^{\mathcal {O}}(\textsf{lbl}, {\textsf{X}}, \pi ) \rightarrow \top / \bot :\):
-
On input a label \(\textsf{lbl} \in {\textsf{L}} \), a statement \({\textsf{X}}\), and a proof \(\pi \), it outputs either \(\top \) (accept) or \(\bot \) (reject).
We require a \(\textsf{NIZK}\) proof system in the random oracle model to satisfy the following standard properties: correctness, zero-knowledge, (relaxed) statistical soundness, and online extractability. We assume for simplicity that \(\textsf{Verify}\) always outputs \(\bot \) in case \(\textsf{lbl} \notin {\textsf{L}} \).
Definition 3.7
(\((1-\delta )\)-Correctness) A \(\textsf{NIZK}\) proof system \(\Pi _\textsf{NIZK} \) is \((1-\delta )\)-correct for \(\delta \in [0, 1]\) if for all \(\uplambda \in {\mathbb {N}}\), \(\textsf{lbl} \in {\textsf{L}} \), \(({\textsf{X}}, {\textsf{W}}) \in R\), the probability of \(\textsf{Prove}^{\mathcal {O}}(\textsf{lbl}, {\textsf{X}}, {\textsf{W}})\) outputting \(\bot \) is at most \(\delta \), and we have

where the probability is taken over the randomness used by \((\textsf{Prove}, \textsf{Verify})\) and by the random oracle.
Definition 3.8
(Zero-Knowledge) Let \({\mathcal {O}}\) be a random oracle, \(\Pi _\textsf{NIZK} \) a \(\textsf{NIZK} \) proof system, and \(\textsf{Sim}= (\textsf{Sim}_0,\textsf{Sim}_1)\) a zero-knowledge simulator for \(\Pi _\textsf{NIZK} \), consisting of two algorithms \(\textsf{Sim}_0\) and \(\textsf{Sim}_1\) with a shared state. We say the advantage of an adversary \({\mathcal {A}}\) against \(\textsf{Sim}\) is
where \(\textsf{Prove}\) and \({\mathcal {S}}\) are prover oracles that on input \((\textsf{lbl}, {\textsf{X}},{\textsf{W}})\) return \(\bot \) if \(\textsf{lbl} \not \in {\textsf{L}} \vee ({\textsf{X}},{\textsf{W}}) \not \in R\) and otherwise return \(\textsf{Prove}^{\mathcal {O}}(\textsf{lbl}, {\textsf{X}},{\textsf{W}})\) or \(\textsf{Sim}_1(\textsf{lbl}, {\textsf{X}})\), respectively. Moreover, the probability is taken also over the randomness of sampling \({\mathcal {O}}\).
We say \(\Pi _\textsf{NIZK} \) for \(R\) and \({\tilde{R}}\) is zero-knowledge if there exists a PPT simulator \(\textsf{Sim}\) such that for all (possibly computationally-unbounded) adversary \({\mathcal {A}}\) making at most polynomially many queries to the random oracle and the prover oracle, we have \(\textsf{Adv}_{\Pi _\textsf{NIZK}}^{\textsf{ZK}}({\mathcal {A}}) \le \textsf{negl}(\uplambda )\).
Statistical soundness guarantees that any adversary cannot generate a proof for an invalid statement except with a negligible probability.
Definition 3.9
(Statistical Soundness) Let \({\mathcal {O}}\) be a random oracle and \(\Pi _\textsf{NIZK} \) a \(\textsf{NIZK} \) proof system. We say the advantage of an adversary \({\mathcal {A}}\) against soundness is

where the probability is taken also over the randomness of sampling \({\mathcal {O}}\).
We say the \(\textsf{NIZK} \) proof system \(\Pi _\textsf{NIZK} \) for \(R\) and \({\tilde{R}}\) has (relaxed) statistical soundness if for all (possibly computationally-unbounded) adversary \({\mathcal {A}}\) making at most polynomially many queries to the random oracle, we have \(\textsf{Adv}_{\Pi _\textsf{NIZK}}^{\textsf{soundness}}({\mathcal {A}}) \le \textsf{negl}(\uplambda )\).
Online extractability requires the existence of an extraction algorithm which, on input a valid proof \(\pi \) and the list or random-oracle queries made by an adversary, always extract a (relaxed) witness except with a negligible probability.
Definition 3.10
(Multi-Proof Online Extractability) A \(\textsf{NIZK} \) proof system \(\Pi _\textsf{NIZK} \) is (multi-proof) online extractable if there exists a PPT extractor \(\textsf{OnlineExtract} \) such that for any (possibly computationally-unbounded) adversary \({\mathcal {A}}\) making at most polynomially-many queries has at most a negligible advantage in the following game played against a challenger (with access to a random oracle \({\mathcal {O}}\)).
-
(i)
The challenger prepares empty lists \(L_{\mathcal {O}}\) and \(L_{P}\), and sets \(\textsf{flag}\) to 0.
-
(ii)
\({\mathcal {A}}\) can make random-oracle, prove, and extract queries an arbitrary polynomial number of times:
-
\((\texttt{hash}, x)\): The challenger updates \(L_{\mathcal {O}}\leftarrow L_{\mathcal {O}}\cup \{ x, {\mathcal {O}}(x) \}\) and returns \({\mathcal {O}}(x)\). We assume below that \({\mathcal {A}}\) runs the verification algorithm after receiving a proof from the prover oracle and before submitting a proof to the extract oracle.Footnote 8
-
\((\texttt{prove},\textsf{lbl}, {\textsf{X}},{\textsf{W}})\): The challenger returns \(\bot \) if \(\textsf{lbl} \not \in {\textsf{L}} \) or \(({\textsf{X}},{\textsf{W}}) \not \in R\). Otherwise, it returns \(\pi \leftarrow \textsf{Prove}^{\mathcal {O}}(\textsf{lbl}, {\textsf{X}},{\textsf{W}})\) and updates \(L_{P}\leftarrow L_{P}\cup \{ \textsf{lbl}, {\textsf{X}}, \pi \}\).
-
\((\texttt{extract}, \textsf{lbl}, {\textsf{X}}, \pi )\): The challenger checks if \(\textsf{Verify}^{\mathcal {O}}(\textsf{lbl}, {\textsf{X}}, \pi ) = \top \) and \((\textsf{lbl}, {\textsf{X}}, \pi ) \not \in L_{P}\), and returns \(\bot \) if not. Otherwise, it runs \({\textsf{W}}\leftarrow \textsf{OnlineExtract} ^{\mathcal {O}}(\textsf{lbl}, {\textsf{X}}, \pi , L_{\mathcal {O}})\) and checks if \(({\textsf{X}},{\textsf{W}}) \not \in {\tilde{R}}\), and returns \(\bot \) if yes and sets \(\textsf{flag} = 1\). Otherwise, if all checks pass, it returns \({\textsf{W}}\).
-
-
(iii)
At some point \({\mathcal {A}}\) outputs 1 to indicate that it is finished with the game. We say \({\mathcal {A}}\) wins if \(\textsf{flag} = 1\). The advantage of \({\mathcal {A}}\) is defined as \(\textsf{Adv}_{\Pi _\textsf{NIZK}}^{\textsf{OE}}({\mathcal {A}}) = \Pr [{\mathcal {A}}\text { wins}]\) where the probability is also taken over the randomness used by the random oracle.
Note, importantly, that \(\textsf{OnlineExtract} \) is not given access to the queries \(\textsf{Prove}^{\mathcal {O}}\) makes directly to \({\mathcal {O}}\). Thus, \(\textsf{OnlineExtract} \) is not guaranteed to return a valid witness \({\textsf{W}}\) when called with any output of the \(\textsf{Prove}\) oracle. The requirement that \((\textsf{lbl}, {\textsf{X}}, \pi ) \notin L_{P}\) ensures that this does not allow the adversary to trivially win the game, and in particular by extension ensures that modifying the label \(\textsf{lbl} \) should invalidate any proof obtained from the \(\textsf{Prove}\) oracle.
Remark 3.11
If a \(\textsf{NIZK} \) proof system \(\Pi _\textsf{NIZK} \) is (multi-proof) online extractable, it is statistically sound—that is, online extractability implies statistical soundness. This is clear, because if an adversary is able to generate an accepting tuple \((\textsf{lbl}, {\textsf{X}}, \pi )\) for which \(\not \exists {\textsf{W}}: ({\textsf{X}},{\textsf{W}}) \in {\tilde{R}}\) in the soundness game, then clearly \((\texttt{extract}, \textsf{lbl}, {\textsf{X}}, \pi )\) will allow the adversary to win the online extractability game.
Remark 3.12
(\(\textsf{NIZK}\) s with Labels) If the label space of the \(\textsf{NIZK}\) is \({\textsf{L}} = \{\bot \}\), we say the \(\textsf{NIZK}\) is without labels (or a plain/unlabelled \(\textsf{NIZK}\)). In this case, we omit the \(\textsf{lbl} \) argument from the \(\textsf{Prove}\) and \(\textsf{Verify}\) functions for clarity.
3.3 Public-key encryption
We recall the standard multi-challenge IND-CPA security of a public-key encryption (\(\textsf{PKE}\)) scheme.
Definition 3.13
(Public-Key Encryption) A public-key encryption \(\Pi _{\textsf{PKE}}\) over a message space \({\mathcal {M}}\) consists of four algorithms \(\Pi _{\textsf{PKE}}= ( \textsf{Setup}, \textsf{KeyGen}, \textsf{Enc}, \textsf{Dec})\):
-
\(\textsf{Setup}(1^\uplambda ) \rightarrow {{\textsf{p}}}{{\textsf{p}}}:\) On input the security parameter \(1^\uplambda \), it outputs a public parameter \({{\textsf{p}}}{{\textsf{p}}}\).
-
\(\textsf{KeyGen}({{\textsf{p}}}{{\textsf{p}}}) \rightarrow ({{\textsf{p}}}{{\textsf{k}}}, {{\textsf{s}}}{{\textsf{k}}}):\) On input a public parameter \({{\textsf{p}}}{{\textsf{p}}}\), it outputs a pair of public key and secret key \(({{\textsf{p}}}{{\textsf{k}}}, {{\textsf{s}}}{{\textsf{k}}})\).
-
\(\textsf{Enc}( {{\textsf{p}}}{{\textsf{k}}}, {\textsf{M}}) \rightarrow {{\textsf{c}}}{{\textsf{t}}}\): On input a public key \({{\textsf{p}}}{{\textsf{k}}}_i\) and a message \({\textsf{M}}\in {\mathcal {M}}\), it outputs a ciphertext \({{\textsf{c}}}{{\textsf{t}}}\).
-
\(\textsf{Dec}( {{\textsf{s}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}) \rightarrow {\textsf{M}}\text { or } \bot :\) On input a secret key \({{\textsf{s}}}{{\textsf{k}}}\) and a ciphertext \({{\textsf{c}}}{{\textsf{t}}}\), it outputs either \({\textsf{M}}\in {\mathcal {M}}\) or a special symbol \(\bot \not \in {\mathcal {M}}\).
We will denote by \({\mathcal {R}}\) the set containing the randomness used by the encryption algorithm \(\textsf{Enc}\).
We omit the standard definition of correctness as we provide a more generalized version in Sect. 4.1,Def. 4.1. Below, we define the standard \(\textsf{IND}\text {-}\textsf{CPA} \) security extended to the multi-challenge setting. Using a textbook hybrid argument, it is clear that the multi-challenge definition is polynomially related to the standard single-challenge definition. The motivation for introducing the multi-challenge variant is because in some cases, we can show that the two definitions are equally difficult without incurring any reduction loss.
Definition 3.14
(Multi-Challenge IND-CPA Security) A \(\textsf{PKE}\) scheme \(\Pi _{\textsf{PKE}}=(\textsf{Setup}, \textsf{KeyGen}, \textsf{Enc}, \textsf{Dec})\) is multi-challenge IND-CPA secure against Q challenges if, for any \(\uplambda \in {\mathbb {N}}\), any PPT adversary \({\mathcal {A}}\) has at most a negligible advantage in the following game played against a challenger.
-
(i)
The challenger runs \({{\textsf{p}}}{{\textsf{p}}}\leftarrow \textsf{Setup}(1^\uplambda )\), \(({{\textsf{p}}}{{\textsf{k}}}, {{\textsf{s}}}{{\textsf{k}}}) \leftarrow \textsf{KeyGen}({{\textsf{p}}}{{\textsf{p}}})\) and samples a bit \(b \in \{ 0,1 \} \). The challenger provides \(({{\textsf{p}}}{{\textsf{p}}}, {{\textsf{p}}}{{\textsf{k}}})\) to \({\mathcal {A}}\).
-
(ii)
\({\mathcal {A}}\) can adaptively query the challenge oracle at most Q times. In each query, \({\mathcal {A}}\) sends a pair of messages \(({\textsf{M}}_0, {\textsf{M}}_1) \in {\mathcal {M}}^2\), and the challenger returns \({{\textsf{c}}}{{\textsf{t}}}_b \leftarrow \textsf{Enc}( {{\textsf{p}}}{{\textsf{k}}}, {\textsf{M}}_b )\) to \({\mathcal {A}}\).
-
(iv)
\({\mathcal {A}}\) outputs a bit \(b^* \in \{0,1\}\). We say \({\mathcal {A}}\) wins if \(b^* = b\).
The advantage of \({\mathcal {A}}\) is defined as \(\textsf{Adv}^{\mathsf {Multi \text {-} CPA}}_{\Pi _{\textsf{PKE}},Q}({\mathcal {A}}) = \left|\Pr [{\mathcal {A}}\text { wins}] - 1/2 \right|\).
3.4 Accountable ring signatures
We provide the definition of accountable ring signatures (\(\textsf{ARS}\) s), following the formalization introduced by Bootle et al. [19].
Definition 3.15
(Accountable Ring Signature) An accountable ring signature \(\Pi _{\textsf{ARS}}\) consists of PPT algorithms \((\textsf{Setup}, \textsf{OKGen}, \textsf{UKGen}, \textsf{Sign}, \textsf{Verify}, \textsf{Open}, \textsf{Judge})\) defined as follows:
- \(\textsf{Setup}(1^\uplambda ) \rightarrow {{\textsf{p}}}{{\textsf{p}}}:\):
-
On input a security parameter \(1^\uplambda \), it returns a public parameter \({{\textsf{p}}}{{\textsf{p}}}\) (sometimes implicitly) used by the scheme. We assume \({{\textsf{p}}}{{\textsf{p}}}\) defines openers’ public-key space \({\mathcal {K}}_{\textsf{opk}}\) and users’ verification-key space \({\mathcal {K}}_{{{\textsf{v}}}{{\textsf{k}}}}\), with efficient algorithms to decide membership.
- \(\textsf{OKGen}({{\textsf{p}}}{{\textsf{p}}}) \rightarrow (\textsf{opk}, \textsf{osk}):\):
-
On input a public parameter \({{\textsf{p}}}{{\textsf{p}}}\), it outputs a pair of public and secret keys \((\textsf{opk}, \textsf{osk})\) for an opener.
- \(\textsf{UKGen}({{\textsf{p}}}{{\textsf{p}}}) \rightarrow ({{\textsf{v}}}{{\textsf{k}}}, {{\textsf{s}}}{{\textsf{k}}}):\):
-
On input a public parameter \({{\textsf{p}}}{{\textsf{p}}}\), it outputs a pair of verification and signing keys \(({{\textsf{v}}}{{\textsf{k}}}, {{\textsf{s}}}{{\textsf{k}}})\) for a user.
- \(\textsf{Sign}(\textsf{opk}, {{\textsf{s}}}{{\textsf{k}}}, {\textsf{R}}, {\textsf{M}}) \rightarrow \sigma :\):
-
On input an opener’s public key \(\textsf{opk}\), a signing key \({{\textsf{s}}}{{\textsf{k}}}\), a list of verification keys, i.e., a ring, \({\textsf{R}}=\{{{\textsf{v}}}{{\textsf{k}}}_1,\dots ,{{\textsf{v}}}{{\textsf{k}}}_N\}\), and a message \({\textsf{M}}\), it outputs a signature \(\sigma \).
- \(\textsf{Verify}( \textsf{opk}, {\textsf{R}}, {\textsf{M}}, \sigma ) \rightarrow \top /\bot :\):
-
On input an opener’s public key \(\textsf{opk}\), a ring \({\textsf{R}}=\{{{\textsf{v}}}{{\textsf{k}}}_1,\dots ,{{\textsf{v}}}{{\textsf{k}}}_N\}\), a message \({\textsf{M}}\), and a signature \(\sigma \), it (deterministically) outputs either \(\top \) (accept) or \(\bot \) (reject).
- \(\textsf{Open}(\textsf{osk}, {\textsf{R}}, {\textsf{M}}, \sigma ) \rightarrow ({{\textsf{v}}}{{\textsf{k}}}, \pi )/\bot :\):
-
On input an opener’s secret key \(\textsf{osk}\), a ring \({\textbf {R}}=\{{{\textsf{v}}}{{\textsf{k}}}_1,\dots ,{{\textsf{v}}}{{\textsf{k}}}_N\}\), a message \({\textsf{M}}\), a signature \(\sigma \), it (deterministically) outputs either a pair of verification key \({{\textsf{v}}}{{\textsf{k}}}\) and a proof \(\pi \) that the owner of \({{\textsf{v}}}{{\textsf{k}}}\) produced the signature, or \(\bot \).
- \(\textsf{Judge}(\textsf{opk}, {\textsf{R}}, {{\textsf{v}}}{{\textsf{k}}}, {\textsf{M}}, \sigma , \pi ) \rightarrow \top /\bot :\):
-
On input an opener’s public key \(\textsf{opk}\), a ring \({\textsf{R}}=\{{{\textsf{v}}}{{\textsf{k}}}_1,\dots ,{{\textsf{v}}}{{\textsf{k}}}_N\}\), a verification key \({{\textsf{v}}}{{\textsf{k}}}\), a message \({\textsf{M}}\), a signature \(\sigma \), and a proof \(\pi \), it (deterministically) outputs either \(\top \) (accept) or \(\bot \) (reject). We assume without loss of generality that \(\textsf{Judge}(\textsf{opk}, {\textsf{R}}, {{\textsf{v}}}{{\textsf{k}}}, {\textsf{M}}, \sigma , \pi )\) outputs \(\bot \) if \(\textsf{Verify}( \textsf{opk}, {\textsf{R}}, {\textsf{M}}, \sigma )\) outputs \(\bot \).
An accountable ring signature is required to satisfy the following properties: correctness, anonymity, traceability, unforgeability, and tracing soundness.
First, we require correctness to hold even if the ring contains maliciously-generated user keys or the signature has been produced for a maliciously-generated opener key. Note that the correctness guarantee for the open and judge algorithms are defined implicitly in the subsequent security definitions.
Definition 3.16
(Correctness) An accountable ring signature \(\Pi _{\textsf{ARS}}\) is correct if, for all \(\uplambda \in {\mathbb {N}}\), any PPT adversary \({\mathcal {A}}\) has at most a negligible advantage in \(\uplambda \) in the following game played against a challenger.
-
(i)
The challenger runs \({{\textsf{p}}}{{\textsf{p}}}\leftarrow \textsf{Setup}(1^\uplambda )\) and generates a user key \(({{\textsf{v}}}{{\textsf{k}}}, {{\textsf{s}}}{{\textsf{k}}}) \leftarrow \textsf{UKGen}({{\textsf{p}}}{{\textsf{p}}})\). It then provides \(({{\textsf{p}}}{{\textsf{p}}}, {{\textsf{v}}}{{\textsf{k}}}, {{\textsf{s}}}{{\textsf{k}}})\) to \({\mathcal {A}}\).
-
(ii)
\({\mathcal {A}}\) outputs an opener’s public key, a ring, and a message tuple \((\textsf{opk}, {\textsf{R}}, {\textsf{M}})\) to the challenger.
-
(iii)
The challenger runs \(\sigma \leftarrow \textsf{Sign}(\textsf{opk}, {{\textsf{s}}}{{\textsf{k}}}, {\textsf{R}}, {\textsf{M}})\). We say \({\mathcal {A}}\) wins if
-
\(\textsf{opk}\in {\mathcal {K}}_{\textsf{opk}}\), \({\textsf{R}}\subseteq {\mathcal {K}}_{{{\textsf{v}}}{{\textsf{k}}}}\), and \({{\textsf{v}}}{{\textsf{k}}}\in {\textsf{R}}\),
-
\(\textsf{Verify}(\textsf{opk}, {\textsf{R}}, {\textsf{M}}, \sigma ) = \bot \).
-
The advantage of \({\mathcal {A}}\) is defined as \(\textsf{Adv}^{\textsf{Correct}}_{\Pi _{\textsf{ARS}}}({\mathcal {A}}) = \Pr [ {\mathcal {A}}\text { wins} ]\).
Anonymity requires that a signature does not leak any information on who signed it. We consider the standard type of anonymity notion where the adversary gets to choose the signing key used to generate the signature. Moreover, we allow the adversary to make (non-trivial) opening queries that reveal who signed the messages. This notion is often called full (CCA) anonymity [8, 20] to differentiate between weaker notions of anonymity such as selfless anonymity that restricts the adversary from exposing the signing key used to sign the signature or CPA anonymity where the adversary is restricted from querying the open oracle.
Definition 3.17
(Anonymity) An accountable ring signature \(\Pi _{\textsf{ARS}}\) is (CCA) anonymous (against full key exposure) if, for all \(\uplambda \in {\mathbb {N}}\), any PPT adversary \({\mathcal {A}}\) has at most a negligible advantage in the following game played against a challenger.
-
(i)
The challenger runs \({{\textsf{p}}}{{\textsf{p}}}\leftarrow \textsf{Setup}(1^\uplambda )\) and generates an opener key \((\textsf{opk}, \textsf{osk}) \leftarrow \textsf{OKGen}({{\textsf{p}}}{{\textsf{p}}})\). It also prepares an empty list \({\textsf{Q}}_{\texttt{sign}}\) and samples a random bit \(b \leftarrow \{ 0,1 \} \).
-
(ii)
The challenger provides \(({{\textsf{p}}}{{\textsf{p}}}, \textsf{opk})\) to \({\mathcal {A}}\).
-
(iii)
\({\mathcal {A}}\) can make signing and opening queries an arbitrary polynomial number of times:
-
\((\texttt{sign}, {\textsf{R}}, {\textsf{M}}, {{\textsf{s}}}{{\textsf{k}}}_0, {{\textsf{s}}}{{\textsf{k}}}_1)\): The challenger runs \(\sigma _i \leftarrow \textsf{Sign}(\textsf{opk}, {{\textsf{s}}}{{\textsf{k}}}_i, {\textsf{R}}, {\textsf{M}})\) for \(i \in \{ 0,1 \} \) and returns \(\bot \) if \(\textsf{Verify}(\textsf{opk}, {\textbf {R}}, {\textsf{M}}, \sigma _i)= \bot \) for either of \(i \in \{ 0,1 \} \). Otherwise, it updates \({\textsf{Q}}_{\texttt{sign}}\leftarrow {\textsf{Q}}_{\texttt{sign}}\cup \{ ( {\textsf{R}}, {\textsf{M}}, \sigma _b) \}\) and returns \(\sigma _b\).
-
\((\texttt{open}, {\textsf{R}}, {\textsf{M}}, \sigma )\): The challenger returns \(\bot \) if \(({\textsf{R}}, {\textsf{M}},\sigma ) \in {\textsf{Q}}_{\texttt{sign}}\). Otherwise, it returns \(\textsf{Open}(\textsf{osk}, {\textsf{R}}, {\textsf{M}}, \sigma )\).
-
-
(iv)
\({\mathcal {A}}\) outputs a guess \(b^*\). We say \({\mathcal {A}}\) wins if \(b^*=b\).
The advantage of \({\mathcal {A}}\) is defined as \(\textsf{Adv}^{\textsf{Anon}}_{\Pi _{\textsf{ARS}}}({\mathcal {A}}) = \left|\Pr [ {\mathcal {A}}\text { wins} ] - 1/2 \right|\).
Unforgeability considers two types of forgeries. The first captures the natural notion of unforgeability where an adversary cannot forge a signature for a ring of honest users, i.e., a ring of users for which it does not know any of the corresponding secret keys. The second captures the fact that an adversary cannot accuse an honest user of producing a signature even if the ring contains malicious users and the opener is malicious.
Definition 3.18
(Unforgeability) An accountable ring signature scheme \(\Pi _{\textsf{ARS}}\) is unforgeable (with respect to insider corruption) if, for all \(\uplambda \in {\mathbb {N}}\), any PPT adversary \({\mathcal {A}}\) has at most negligible advantage in the following game played against a challenger.
-
(i)
The challenger runs \({{\textsf{p}}}{{\textsf{p}}}\leftarrow \textsf{Setup}(1^\uplambda )\) and initializes an empty keyed dictionary \({\textsf{D}}_{\texttt{UKey}}[\cdot ]\) and three empty sets \({\textsf{Q}}_{\texttt{UKey}}\), \({\textsf{Q}}_{\texttt{sign}}\) and \({\textsf{Q}}_{\texttt{cor}}\). It provides \({{\textsf{p}}}{{\textsf{p}}}\) to \({\mathcal {A}}\).
-
(ii)
\({\mathcal {A}}\) can make user key generation, signing, and corruption queries an arbitrary polynomial number of times:
-
\((\texttt{ukeygen})\): The challenger runs \(({{\textsf{v}}}{{\textsf{k}}}, {{\textsf{s}}}{{\textsf{k}}}) \leftarrow \textsf{UKGen}({{\textsf{p}}}{{\textsf{p}}})\). If \({\textsf{D}}_{\texttt{UKey}}[{{\textsf{v}}}{{\textsf{k}}}] \ne \bot \), then it returns \(\bot \). Otherwise, it updates \({\textsf{D}}_{\texttt{UKey}}[{{\textsf{v}}}{{\textsf{k}}}] = {{\textsf{s}}}{{\textsf{k}}}\) and \({\textsf{Q}}_{\texttt{UKey}}\leftarrow {\textsf{Q}}_{\texttt{UKey}}\cup \{ {{\textsf{v}}}{{\textsf{k}}} \}\), and returns \({{\textsf{v}}}{{\textsf{k}}}\).
-
\((\texttt{sign}, \textsf{opk},{{\textsf{v}}}{{\textsf{k}}},{\textsf{R}}, {\textsf{M}})\): The challenger returns \(\bot \) if \({{\textsf{v}}}{{\textsf{k}}}\not \in {\textsf{Q}}_{\texttt{UKey}}\cap {\textsf{R}}\). Otherwise, it runs \(\sigma \leftarrow \textsf{Sign}(\textsf{opk}, {\textsf{D}}_{\texttt{UKey}}[{{\textsf{v}}}{{\textsf{k}}}],{\textsf{R}}, {\textsf{M}})\). The challenger updates \({\textsf{Q}}_{\texttt{sign}}\leftarrow {\textsf{Q}}_{\texttt{sign}}\cup \{ (\textsf{opk}, {{\textsf{v}}}{{\textsf{k}}}, {\textsf{R}}, {\textsf{M}}, \sigma ) \}\) and returns \(\sigma \).
-
\((\texttt{corrupt}, {{\textsf{v}}}{{\textsf{k}}})\): The challenger returns \(\bot \) if \({{\textsf{v}}}{{\textsf{k}}}\not \in {\textsf{Q}}_{\texttt{UKey}}\). Otherwise, it updates \({\textsf{Q}}_{\texttt{cor}}\leftarrow {\textsf{Q}}_{\texttt{cor}}\cup \{ {{\textsf{v}}}{{\textsf{k}}} \}\) and returns \({\textsf{D}}_{\texttt{UKey}}[{{\textsf{v}}}{{\textsf{k}}}]\).
-
-
(iv)
\({\mathcal {A}}\) outputs \((\textsf{opk}, {{\textsf{v}}}{{\textsf{k}}}, {\textsf{R}}, {\textsf{M}}, \sigma , \pi )\). We say \({\mathcal {A}}\) wins if
-
\((\textsf{opk}, *, {\textsf{R}}, {\textsf{M}}, \sigma ) \not \in {\textsf{Q}}_{\texttt{sign}}\), \({\textsf{R}}\subseteq {\textsf{Q}}_{\texttt{UKey}}\backslash {\textsf{Q}}_{\texttt{cor}}\),
-
\(\textsf{Verify}(\textsf{opk}, {\textsf{R}}, {\textsf{M}}, \sigma ) = \top \),
or
-
\((\textsf{opk}, {{\textsf{v}}}{{\textsf{k}}}, {\textsf{R}}, {\textsf{M}}, \sigma ) \not \in {\textsf{Q}}_{\texttt{sign}}\), \({{\textsf{v}}}{{\textsf{k}}}\in {\textsf{Q}}_{\texttt{UKey}}\backslash {\textsf{Q}}_{\texttt{cor}}\),
-
\(\textsf{Judge}(\textsf{opk}, {\textsf{R}}, {{\textsf{v}}}{{\textsf{k}}}, {\textsf{M}}, \sigma , \pi ) = \top \).
-
The advantage of \({\mathcal {A}}\) is defined as \(\textsf{Adv}_{\Pi _{\textsf{ARS}}}^{\textsf{Unf}}({\mathcal {A}}) =\Pr [ {\mathcal {A}}\text { wins}]\).
Traceability requires that any opener key pair \((\textsf{opk}, \textsf{osk})\) in the range of the opener key-generation algorithm can open a valid signature \(\sigma \) to some user \({{\textsf{v}}}{{\textsf{k}}}\) along with a proof valid \(\pi \). This ensures that any opener can trace the user and produce a proof for its decision. Below, rather than assuming an efficient algorithm that checks set membership \((\textsf{opk}, \textsf{osk}) \in \textsf{OKGen}({{\textsf{p}}}{{\textsf{p}}})\), we simply ask the adversary to output the randomness used to generate \((\textsf{opk}, \textsf{osk})\). Note that this definition contains the prior definitions where \(\textsf{opk}\) was assumed to be uniquely defined and efficiently computable from \(\textsf{osk}\) [19].
Definition 3.19
(Traceability) An accountable ring signature scheme \(\Pi _{\textsf{ARS}}\) is traceable if, for all \(\uplambda \in {\mathbb {N}}\), any PPT adversary \({\mathcal {A}}\) has at most negligible advantage in the following game played against a challenger.
-
(i)
The challenger runs \({{\textsf{p}}}{{\textsf{p}}}\leftarrow \textsf{Setup}(1^\uplambda )\) and provides \({{\textsf{p}}}{{\textsf{p}}}\) to \({\mathcal {A}}\).
-
(ii)
\({\mathcal {A}}\) returns a randomness, a ring, a message, and a signature tuple \(({{\textsf{r}}}{{\textsf{r}}}, {\textsf{R}}, {\textsf{M}}, \sigma )\). We say \({\mathcal {A}}\) wins if
-
\(\textsf{Verify}(\textsf{opk}, {\textsf{R}}, {\textsf{M}}, \sigma ) = \top \), where \((\textsf{opk}, \textsf{osk})\leftarrow \textsf{OKGen}({{\textsf{p}}}{{\textsf{p}}}; {{\textsf{r}}}{{\textsf{r}}})\), and
-
\(\textsf{Judge}(\textsf{opk}, {\textsf{R}}, {{\textsf{v}}}{{\textsf{k}}}, {\textsf{M}}, \sigma , \pi ) = \bot \), where \(({{\textsf{v}}}{{\textsf{k}}}, \pi ) \leftarrow \textsf{Open}(\textsf{osk}, {\textsf{R}}, {\textsf{M}}, \sigma )\).
-
The advantage of \({\mathcal {A}}\) is defined as \(\textsf{Adv}_{\Pi _{\textsf{ARS}}}^{\textsf{Tra}}({\mathcal {A}}) =\Pr [ {\mathcal {A}}\text { wins}]\).
Finally, tracing soundness requires that a signature cannot trace to two different users in the ring. This must hold even if all the users in the ring and the opener are corrupt.
Definition 3.20
(Tracing Soundness) An accountable ring signature scheme \(\Pi _{\textsf{ARS}}\) is traceable sound if, for all \(\uplambda \in {\mathbb {N}}\), any PPT adversary \({\mathcal {A}}\) has at most negligible advantage in the following game played against a challenger.
-
(i)
The challenger runs \({{\textsf{p}}}{{\textsf{p}}}\leftarrow \textsf{Setup}(1^\uplambda )\) and provides \({{\textsf{p}}}{{\textsf{p}}}\) to \({\mathcal {A}}\).
-
(ii)
\({\mathcal {A}}\) returns an opener’s public key, a ring, a message, a signature, and two verification keys and proofs \((\textsf{opk}, {\textsf{R}}, {\textsf{M}}, \sigma , \{ ({{\textsf{v}}}{{\textsf{k}}}_b, \pi _b) \}_{b \in \{ 0,1 \} })\). We say \({\mathcal {A}}\) wins if
-
\({{\textsf{v}}}{{\textsf{k}}}_0 \ne {{\textsf{v}}}{{\textsf{k}}}_1\),
-
\(\textsf{Judge}(\textsf{opk}, {\textsf{R}}, {{\textsf{v}}}{{\textsf{k}}}_0, {\textsf{M}}, \sigma , \pi _0) = \top \),
-
\(\textsf{Judge}(\textsf{opk}, {\textsf{R}}, {{\textsf{v}}}{{\textsf{k}}}_1, {\textsf{M}}, \sigma , \pi _1) = \top \).
-
The advantage of \({\mathcal {A}}\) is defined as \(\textsf{Adv}_{\Pi _{\textsf{ARS}}}^{\textsf{TraS}}({\mathcal {A}}) =\Pr [ {\mathcal {A}}\text { wins}]\).
3.5 Isogenies and ideal class group actions
Let \({\mathbb {F}}_p\) be a prime field, with \(p \ge 5\). In the following E and \(E'\) denote elliptic curves defined over \({\mathbb {F}}_p\). An isogeny \(\varphi : E \rightarrow E'\) is a non-constant morphism mapping \(0_E\) to \(0_{E'}\). Each coordinate of \(\varphi (x,y)\) is then the fraction of two polynomials in \(\overline{{\mathbb {F}}}_p[x,y]\), where \(\overline{{\mathbb {F}}}_p\) denotes the algebraic closure of \({\mathbb {F}}_p\). If the coefficients of the polynomials lie in \({\mathbb {F}}_p\), then \(\varphi \) is said to be defined over \({\mathbb {F}}_{p}\). We restrict our attention to separable isogenies (which induce separable extensions of function fields) between supersingular elliptic curves defined over \({\mathbb {F}}_p\), i.e., curves whose set of rational points \(E({\mathbb {F}}_p)\) has cardinality \(p+1\).
An isogeny \(\varphi :E \rightarrow E'\) is an isomorphism if its kernel is equal to \(\{0_E\}\), and an endomorphism of E if \(E=E'\). The set \(\text {End}_p(E)\) of all endomorphisms of E that are defined over \({\mathbb {F}}_p\), together with the zero map, form a commutative ring under pointwise addition and composition. \(\text {End}_p(E)\) is isomorphic to an order \({\mathcal {O}}\) of the quadratic field \({\mathbb {K}}={\mathbb {Q}}(\sqrt{-p})\) [28]. We recall that an order is a subring of \({\mathbb {K}}\), which is also a finitely-generated \({\mathbb {Z}}\)-module containing a basis of \({\mathbb {K}}\) as a \({\mathbb {Q}}\)-vector space. A fractional ideal \({\mathfrak {a}}\) of \({\mathcal {O}}\) is a finitely generated \({\mathcal {O}}\)-submodule of \({\mathbb {K}}\). We say that \({\mathfrak {a}}\) is invertible if there exists another fractional ideal \({\mathfrak {b}}\) of \({\mathcal {O}}\) such that \({\mathfrak {a}}{\mathfrak {b}}={\mathcal {O}}\), and that it is principal if \({\mathfrak {a}}=\alpha {\mathcal {O}}\) for some \(\alpha \in {\mathbb {K}}\). The invertible fractional ideals of \({\mathcal {O}}\) form an Abelian group whose quotient by the subgroup of principal fractional ideals is finite. This quotient group is called the ideal class group of \({\mathcal {O}}\), and denoted by \(\mathcal {C}\ell (\mathcal {O})\).
The ideal class group \(\mathcal {C}\ell (\mathcal {O})\) acts freely and transitively on the set \(\mathcal {E}\ell \ell {p}({\mathcal {O}},\pi )\), which contains all supersingular elliptic curves E over \({\mathbb {F}}_p\) - modulo isomorphisms defined over \({\mathbb {F}}_p\) - such that there exists an isomorphism between \({\mathcal {O}}\) and \(\text {End}_p(E)\) mapping \(\sqrt{-p} \in {\mathcal {O}}\) into the Frobenius endomorphism \((x,y) \mapsto (x^p,y^p)\). We denote this action by \(*\). Recently, it has been used to design several cryptographic primitives [15, 28, 37, 67], whose security proofs rely on (variations of) the Group Action Inverse Problem (\(\textsf{GAIP}\)), defined as follows.
Definition 3.21
(Group Action Inverse Problem (\(\textsf{GAIP}\))) Let \([E_0]\) be an element in \(\mathcal {E}\ell \ell {p}({\mathcal {O}},\pi )\), where p is an odd prime and \({\mathcal {O}}\) an order in \({\mathbb {Q}}(\sqrt{-p})\). Given [E] sampled from the uniform distribution over \(\mathcal {E}\ell \ell {p}({\mathcal {O}},\pi )\), the \(\textsf{GAIP}_p\) problem consists in finding an element \([{\mathfrak {a}}] \in \mathcal {C}\ell (\mathcal {O})\) such that \([{\mathfrak {a}}] *[E_0]=[E]\).
The best known classical algorithm to solve the \(\textsf{GAIP}\) problem has time complexity \(O(\sqrt{N})\), where \(N=|\mathcal {C}\ell (\mathcal {O})|\). The best known quantum algorithm, on the other hand, is Kuperberg’s algorithm for the hidden shift problem [63, 64]. It has a subexponential complexity, for which the concrete security estimates are still an active area of research [12, 18, 32, 80].
For the security of the isogeny-based instantiations, we will also rely on a multi-instance variant the GAIP problem which is trivially equivalent to the GAIP problem.
Definition 3.22
(Multi-Instance GAIP (\({{\textsf{M}}}{{\textsf{I}}}\text {-}\textsf{GAIP}\)) Problem) Let \([E_0]\) be an element in \(\mathcal {E}\ell \ell {p}({\mathcal {O}},\pi )\), where p is an odd prime and \({\mathcal {O}}\) an order in \({\mathbb {Q}}(\sqrt{-p})\). Given \([E_1],\cdots ,[E_N] \) sampled uniformly at random from \(\mathcal {E}\ell \ell {p}({\mathcal {O}},\pi )\), where \(N \in {\mathbb {N}}\), the \({{\textsf{M}}}{{\textsf{I}}}\text {-}\textsf{GAIP}_{p,N}\) problem consists in finding an element \([{\mathfrak {a}}] \in \mathcal {C}\ell (\mathcal {O})\) such that \([{\mathfrak {a}}] *[E_0]=[E_i]\) for some \(i \in [N]\).
To see the equivalence (informally), given an instance of the GAIP problem \(([E_0], [E])\), sample \([{\mathfrak {r}}_1], \ldots , [{\mathfrak {r}}_N] \in \mathcal {C}\ell (\mathcal {O})\), and compute \([E_i] = [{\mathfrak {r}}_i] *[E]\) for each i. Then a solution for the MT-GAIP on \(([E_0], [E_1], \ldots , [E_N])\), say \([{\mathfrak {a}}] *[E_0]=[E_j]\), results in a solution to the GAIP by computing \([{\mathfrak {a}}][{\mathfrak {r}}_j]^{-1}\).
We also need the following assumption, the decisional CSIDH Problem. Looking ahead, the distinguishing problems will ensure (multi-instance) IND-CPA for our PKE in Sect. 8.1 and therefore anonymity for our ring/group signature schemes. Note that we will require the class group to be of odd order to avoid the attack presented in [29]. Equivalently, we require \(p=3 \mod 4\).
Definition 3.23
(Decisional CSIDH (\(\textsf{dCSIDH}\)) Problem) Let \([E_0]\) be an element in \(\mathcal {E}\ell \ell {p}({\mathcal {O}},\pi )\), where p is an odd prime. The decisional CSIDH problem is that given a tuple \(([{\mathfrak {a}}_1] *[E_0],[{\mathfrak {a}}_2] *[E_0], E)\) where \([{\mathfrak {a}}_1],[{\mathfrak {a}}_2]\) are sampled uniformly from \(\mathcal {C}\ell (\mathcal {O})\) and [E] is either sampled uniformly from \(\mathcal {E}\ell \ell {p}({\mathcal {O}},\pi )\) or \([E]=[{\mathfrak {a}}_1 {\mathfrak {a}}_2]*[E_0]\), and decide which distribution [E] is drawn from.
3.6 Lattices
Let R and \(R_q\) denote the rings \({\mathbb {Z}}[X]/(X^n + 1)\) and \({\mathbb {Z}}[X]/ (q, X^n + 1)\) for integers n and q, respectively. Norms over R are defined through the coefficient vectors of the polynomials, which lie over \({\mathbb {Z}}^n\). Norms over \(R_q\) are defined in the conventional way by uniquely representing coefficients of elements over \(R_q\) by elements in the range \((-q/2, q/2] \) when q is even and \([ -(q-1)/2, (q-1)/2 ]\) when q is odd (see for example [42] for more details).
The hard problems we will rely on are the module short integer solution (\(\textsf{MSIS} \)) problem and module learning with errors (\(\textsf{MLWE} \)) problem, first introduced in [69].
Definition 3.24
(Module Short Integer Solution) Let \(n, q, k, \ell , \gamma \) be integers. The advantage for the (Hermite normal form) module short integer solution problem \(\textsf{MSIS} _{n, q, k, \ell , \gamma }\) for an algorithm \({\mathcal {A}}\) is defined as

Definition 3.25
(Module Learning with Errors) Let \(n, q, k, \ell \) be integers and D a probability distribution over \(R_q\). For any \({{\textbf {A}}}\in R^{k \times \ell }_q\), define two oracles as follows:
-
\({\mathcal {O}}_{{{\textbf {A}}}}\): Sample \(({{\textbf {s}}}, {{\textbf {e}}}) \leftarrow D^k \times D^\ell \) and output \({{\textbf {A}}}{{\textbf {s}}}+ {{\textbf {e}}}\in R_q^k\),
-
\({\mathcal {O}}_{\$}\): Output a random \({{\textbf {b}}}\leftarrow R_q^k\).
The advantage for the decision module learning with errors problem \(\textsf{sMLWE} _{n, q, k, \ell , D}\) for an algorithm \({\mathcal {A}}\) is defined as
where the probability is taken also over the random choice of \({{\textbf {A}}}\leftarrow R_q^{k \times \ell }\).
The advantage for the search learning with errors problem \(\textsf{sMLWE} _{n, q, k, \ell , D}\) is defined as

where \({{\textbf {v}}}\) is one of the vectors returned by \({\mathcal {O}}_{{{\textbf {A}}}}\).
In this work, we consider the \(\textsf{MLWE}\) problem where an adversary is given oracle access to a \(\textsf{MLWE}\) sample generator. For any PPT adversary \({\mathcal {A}}\), this is polynomially related to the conventional single-instance \(\textsf{MLWE}\) problem via a standard hybrid argument. There is also a simple tight reduction from the single-instance to the multi-instance \(\textsf{MLWE}\) problem à la “noise-flooding,” where (roughly) the support of the distribution D considered by the multi-instance problem is required to be super-polynomially larger than those considered by the single-instance problem. However, practically speaking, to the best of our knowledge, we are not aware of any attacks that exploit the multiplicity of the \(\textsf{MLWE}\) sample. Therefore, throughout this work, we assume the multi-instance \(\textsf{MLWE}\) problem to be as difficult as the single-instance \(\textsf{MLWE}\) problem.
The assumption on the hardness of (multi-instance) \(\textsf{MLWE} \) is believed to hold even when D is the uniform distribution over ring elements with infinity norm at most a fixed value B, say \(B \approx 5\), for appropriate choices of \(n, q, k, \ell \) [2]. We write \(\textsf{MLWE} _{n, q, k, \ell , B}\) when we consider such distribution D. For example, the round-2 NIST candidate signature scheme Dilithium [42] uses such parameters for the (single-instance) \(\textsf{MLWE}\) problem, and in particular, our scheme borrows the same parameter sets.
4 Generic construction of accountable ring signature and dynamic group signature
In this section, we present novel generic frameworks for accountable ring signature, dynamic group signature, and their tightly secure variants. Firstly, we introduce a generic construction of an accountable ring signature in Sect. 4.1. Constructing a dynamic group signature immediately follows by limiting the functionality of accountable ring signature. Our construction achieves a tighter reduction compared to prior works on efficient group signatures as it does not rely on the forking lemma [50, 81]. However, since we still lose a factor of 1/N in the reduction, we finally show how to modify our construction to be truly tight using the Katz-Wang technique [61] in Sect. 4.3.
4.1 Generic construction of accountable ring signature
In this subsection, we present our generic construction of an accountable ring signature scheme. Before diving in the details we give a brief overview of our generic construction. The setup is as follows. The opening authorities generate a \(\textsf{PKE}\) key-pair, denoted as \((\textsf{opk},\textsf{osk})\) to indicate that they are the opener’s keys, and publish the opening public key \(\textsf{opk}\). The users generate an element \(({\textsf{x}},{\textsf{w}})\) in a hard relation \(R\), and publish the statement \({\textsf{x}} \) as verification key, and keep the witness \({\textsf{w}} \) as secret signing key. A signature for our \(\textsf{ARS}\) scheme for a ring \(R = \{{\textsf{x}} _1,\dots , {\textsf{x}} _N\}\) consists of a ciphertext \({{\textsf{c}}}{{\textsf{t}}}\), and a \(\textsf{NIZK}\) proof that: 1) The ciphertext is an encryption of an index \(I \in [N]\) under an opener public key \(\textsf{opk}\), and 2) that the signer knows a witness \({\textsf{w}} \) corresponding to the I-th statement \({\textsf{x}} _I\) in the ring R. The second property ensures that the signature is unforgeable, and the first property ensures that the opener (who has the secret key \(\textsf{opk}\)) can decrypt the ciphertext to find out who the real signer is. To convince others that a signature was produced by the I-th member of the ring, the opener uses a second \(\textsf{NIZK}\) proof to prove that he knows an opener secret key \(\textsf{osk}\) that is consistent with \(\textsf{opk}\), and such that \(\textsf{Dec}(\textsf{osk},{{\textsf{c}}}{{\textsf{t}}}) = I\). If the opener could find a second secret key \(\textsf{osk}'\), consistent with \(\textsf{opk}\) and such that \({{\textsf{c}}}{{\textsf{t}}}\) decrypts to \(I' \ne I\) under \(\textsf{osk}'\), then the opener could frame \(I'\) for signing a signature, which breaks the tracing soundness of the signature scheme. To prevent this we require the \(\textsf{PKE}\) to satisfy a strong correctness property, which says that an encryption of I will always decrypt to I, even if the encryption randomness and decryption key are invalid (in some specific, controlled way). More formally we define the following special correctness notion for a \(\textsf{PKE}\) scheme.
Definition 4.1
(\(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness) Consider a public-key encryption scheme \(\Pi _{\textsf{PKE}}=(\textsf{Setup}, \textsf{KeyGen}, \textsf{Enc}, \textsf{Dec})\), with \({\mathcal {R}}\) the set containing all possible randomness used by \(\textsf{Enc}\) and \({{\mathcal {K}}}{{\mathcal {R}}}\) the binary relation that contains all the key pairs \(({{\textsf{p}}}{{\textsf{k}}},{{\textsf{s}}}{{\textsf{k}}})\) that can be generated by running \(\textsf{KeyGen}\). Let \({\mathcal {R}}'\) be a set containing \({\mathcal {R}}\), and \({{\mathcal {K}}}{{\mathcal {R}}}'\) a relation containing \({{\mathcal {K}}}{{\mathcal {R}}}\). Then we say that \(\Pi _{\textsf{PKE}}\) is \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correct if, for all \(\uplambda \in {\mathbb {N}}\), and for all but a negligible fraction of \({{\textsf{p}}}{{\textsf{p}}}\in \textsf{Setup}(1^\uplambda )\), we have for all \(({{\textsf{p}}}{{\textsf{k}}},{{\textsf{s}}}{{\textsf{k}}}) \in {{\mathcal {K}}}{{\mathcal {R}}}'\), for all messages m in the plaintext space \({\mathcal {M}}\), and all \(r \in {\mathcal {R}}'\) that
Remark 4.2
Note that \({{\textsf{p}}}{{\textsf{p}}}\) is also implicitly used in the relations \({{\mathcal {K}}}{{\mathcal {R}}},{{\mathcal {K}}}{{\mathcal {R}}}'\). If \({\mathcal {R}}' = {\mathcal {R}}\) and \({{\mathcal {K}}}{{\mathcal {R}}}' = {{\mathcal {K}}}{{\mathcal {R}}}\), then the \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness is exactly the standard correctness property for \(\textsf{PKE} \)s. If \({\mathcal {R}}'\) or \({{\mathcal {K}}}{{\mathcal {R}}}'\) is larger than \({\mathcal {R}}\) or \({{\mathcal {K}}}{{\mathcal {R}}}\), respectively, then the definition becomes a stronger property, because the decryption algorithm is required to decrypt correctly even when the encryption algorithm used some invalid randomness, and/or when the keypair is invalid. (\({\mathcal {R}}'\) and \({{\mathcal {K}}}{{\mathcal {R}}}'\) control how “invalid” randomness and secret key are allowed to be.)
Generic construction of an accountable ring signature \(\Pi _{\textsf{ARS}}\) obtained from a hard instance generator \((\textsf{RelSetup},\textsf{IGen})\), a public-key encryption algorithm \((\mathsf {PKE.Setup},\textsf{KeyGen},\textsf{Enc},\textsf{Dec})\) satisfying some suitable security and correctness properties, a \(\textsf{NIZK}\) with labels \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) for \(R_{\textsf{sig}}\), and a \(\textsf{NIZK} \) without labels \(\Pi _\textsf{NIZK} \) for \(R_{\textsf{open}}\). The public parameter \({{\textsf{p}}}{{\textsf{p}}}\) is provided to all algorithms where we may omit them for readability
Our generic construction of an accountable ring signature scheme \(\Pi _{\textsf{ARS}}=(\textsf{ARS}.\textsf{Setup}, \textsf{ARS}.\textsf{OKGen}, \textsf{ARS}.\textsf{UKGen}, \textsf{ARS}.\textsf{Sign}, \textsf{ARS}.\textsf{Verify},\textsf{ARS}.\textsf{Open}, \textsf{ARS}.\textsf{Judge})\), provide in Fig. 1, is based on the following building blocks:
-
A hard-instance generator contains a setup algorithm \(\textsf{RelSetup}\) that, on input a security parameter \(\uplambda \), outputs a description \({{\textsf{p}}}{{\textsf{p}}}\) of a pair of binary relations \(R_{{\textsf{p}}}{{\textsf{p}}}\subseteq {\tilde{R}}_{{\textsf{p}}}{{\textsf{p}}}\), and an instance generator \(\textsf{IGen}\) for those pairs of relations. That is, \(\textsf{RelSetup}\) and \(\textsf{IGen}\) are PPT algorithms such that \( \Pr [ ({\textsf{x}},{\textsf{w}}) \in R_{{\textsf{p}}}{{\textsf{p}}}~ \mid ~ {{\textsf{p}}}{{\textsf{p}}}\leftarrow \textsf{RelSetup}(1^\uplambda ); ({\textsf{x}},{\textsf{w}}) \leftarrow \textsf{IGen}({{\textsf{p}}}{{\textsf{p}}})] = 1\), and such that if we define the advantage of an adversary \({\mathcal {A}}\) against \((\textsf{RelSetup},\textsf{IGen})\) as

then \(\textsf{Adv}^{\textsf{Hard}}_{\textsf{RelSetup},\textsf{IGen}}({\mathcal {A}})\) is a negligible function of \(\uplambda \) for every PPT adversary \({\mathcal {A}}\).
-
A public-key encryption scheme \(\Pi _\textsf{PKE} = (\mathsf {PKE.Setup}, \textsf{KeyGen}, \textsf{Enc}, \textsf{Dec})\) with multi-challenge IND-CPA security, and with \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness for some relaxed randomness set \({\mathcal {R}}'\) and some relaxed key relation \({{\mathcal {K}}}{{\mathcal {R}}}'\). The message space of the encryption scheme contains a set of indices [N] for any polynomially large \(N \in {\mathbb {N}}\).
-
A multi-proof online extractable \(\textsf{NIZK}\) proof system with labels \(\Pi _{\textsf{NIZK},\textsf{lbl}} = (\textsf{NIZK}.\textsf{Setup}_\textsf{lbl},\textsf{NIZK}.\textsf{Prove}_\textsf{lbl}, \textsf{NIZK}.\textsf{Verify}_\textsf{lbl})\) for the relations
$$\begin{aligned} R_{\textsf{sig}}&= \left\{ \left( (\{{\textsf{x}} _i\}_{i\in [N]}, {{\textsf{p}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}), (I,{\textsf{w}},r) \right) \begin{array}{c} ({\textsf{x}} _I,{\textsf{w}}) \in R_{{\textsf{p}}}{{\textsf{p}}}\wedge {{\textsf{c}}}{{\textsf{t}}}=\textsf{Enc}({{\textsf{p}}}{{\textsf{k}}},I;r) \end{array} \right\} \,\\ {\tilde{R}}_{\textsf{sig}}&= \left\{ \left( (\{{\textsf{x}} _i\}_{i\in [N]}, {{\textsf{p}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}), (I,{\textsf{w}},r) \right) \begin{array}{c} ({\textsf{x}} _I, {\textsf{w}}) \in {\tilde{R}}_{{\textsf{p}}}{{\textsf{p}}}\wedge {{\textsf{c}}}{{\textsf{t}}}=\textsf{Enc}({{\textsf{p}}}{{\textsf{k}}},I;r) \end{array} \right\} \, . \end{aligned}$$To be precise, we need to also include the public parameters output by \(\textsf{RelSetup}\) and \(\mathsf {PKE.Setup}\) in the statement. We omit them for better readability.
-
A statistically sound \(\textsf{NIZK}\) proof system (without labels) \(\Pi _\textsf{NIZK} = (\textsf{NIZK}.\textsf{Setup}, \textsf{NIZK}.\textsf{Prove}, \textsf{NIZK}.\textsf{Verify})\) for the relations
$$\begin{aligned} R_{\textsf{open}}&= \left\{ (({{\textsf{p}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}, I),{{\textsf{s}}}{{\textsf{k}}}) ({{\textsf{p}}}{{\textsf{k}}},{{\textsf{s}}}{{\textsf{k}}}) \in {{\mathcal {K}}}{{\mathcal {R}}}\wedge \textsf{Dec}({{\textsf{s}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}) = I \right\} \\ {\tilde{R}}_{\textsf{open}}&= \left\{ (({{\textsf{p}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}, I),{{\textsf{s}}}{{\textsf{k}}}) ({{\textsf{p}}}{{\textsf{k}}},{{\textsf{s}}}{{\textsf{k}}}) \in {{\mathcal {K}}}{{\mathcal {R}}}' \wedge \textsf{Dec}({{\textsf{s}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}) = I \right\} . \, \end{aligned}$$Similarly to above, we omit the public parameter output by \(\mathsf {PKE.Setup}\) in the statement. We emphasize that \(\Pi _\textsf{NIZK} \) does not need to be online extractable.
Correctness and security of the proposed accountable ring signature scheme \(\Pi _{\textsf{ARS}}\) are shown in the following theorems.
Theorem 4.3
The accountable ring signature scheme \(\Pi _{\textsf{ARS}}\) in Fig. 1 is correct.
Proof
Due to the correctness of the underlying \(\textsf{NIZK}\) proof system, \(\Pi _{\textsf{NIZK},\textsf{lbl}} \), any signature output by \(\textsf{ARS}.\textsf{Sign}\) will be accepted by \(\textsf{ARS}.\textsf{Verify}\) with probability 1. \(\square \)
Theorem 4.4
The accountable ring signature scheme \(\Pi _{\textsf{ARS}}\) in Fig. 1 is (CCA) anonymous (against full key exposure) in the random oracle model, assuming \(\Pi _\textsf{PKE} \) is multi-challenge \(\textsf{IND}\text {-}\textsf{CPA}\) secure and \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correct, \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) is zero-knowledge, multi-challenge online-extractable, and \(\Pi _\textsf{NIZK}\) is zero-knowledge. Precisely, for an adversary \({\mathcal {A}}\), running in time T, there exist PPT adversaries \({\mathcal {B}}_1,{\mathcal {B}}_2,{\mathcal {B}}_3,{\mathcal {B}}_4\), with running times O(T) such that
Proof
We prove anonymity using a hybrid argument with the following series of games. Let the advantage of the adversary \({\mathcal {A}}\) in \(\textsf{Game}_i\) be denoted by \(\textsf{Adv}_i({\mathcal {A}})\).
- \(\textsf{Game}_1:\):
-
This is the original anonymity game defined in Def. 3.17. The adversary’s advantage in this game is \(\textsf{Adv}_1({\mathcal {A}})= \textsf{Adv}^{\textsf{Anon}}_{\Pi _{\textsf{ARS}}}({\mathcal {A}})\) by definition.
- \(\textsf{Game}_2:\):
-
This is the same as \(\textsf{Game}_1\), except that it uses the simulator \(\textsf{NIZK}.\textsf{Sim}= (\textsf{NIZK}.\textsf{Sim}_0,\textsf{NIZK}.\textsf{Sim}_1)\) for \(\Pi _\textsf{NIZK} \) to answer random-oracle and opening queries from the adversary. When \({\mathcal {A}}\) makes a random oracle query, the challenger forwards the query to \(\textsf{NIZK}.\textsf{Sim}_0\), records the query and answers, and forwards the answer to \({\mathcal {A}}\). When \({\mathcal {A}}\) makes an opening query, rather than computing \(\pi _\texttt{open}\) using \(\textsf{NIZK}.\textsf{Prove}\) and \(\textsf{osk}\), the challenger instead uses the output of \(\textsf{NIZK}.\textsf{Sim}_1\). We consider an adversary \({\mathcal {B}}_1\) against the zero-knowledge property of \(\Pi _\textsf{NIZK} \) which simulates \(\textsf{Game}_2\) for \({\mathcal {A}}\). Let \(\textsf{Prove}\) and \({\mathcal {S}}\) be as in the definition of zero-knowledge for the \(\textsf{NIZK}\) proof system. Then, if \({\mathcal {B}}_1's\) oracle queries are answered by \(({\mathcal {O}},\textsf{Prove})\) the game is identical to \(\textsf{Game}_1\), and if queries are answered by \((\textsf{NIZK}.\textsf{Sim}_0,{\mathcal {S}})\), then the game is identical to \(\textsf{Game}_2\). Therefore, assuming \({\mathcal {B}}_1\) outputs 1 when \({\mathcal {A}}\) wins, we have \(\textsf{Adv}_1({\mathcal {A}}) \le \textsf{Adv}_2({\mathcal {A}}) + \textsf{Adv}_{\Pi _\textsf{NIZK}}^{\textsf{ZK}}({\mathcal {B}}_1)\).
- \(\textsf{Game}_3:\):
-
This is the same as \(\textsf{Game}_2\), except that the way the challenger answers opening queries is further modified. Rather than using the secret key \(\textsf{osk}\) to decrypt the ciphertext \({{\textsf{c}}}{{\textsf{t}}}\) and identify the index I of the real signing key (as \(\textsf{ARS}.\textsf{Open}\) does in the honest protocol), the challenger instead runs the online extractor \(\textsf{OnlineExtract} \) for \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) to extract the witness \((I, {{\textsf{s}}}{{\textsf{k}}}, r)\) from \(({{\textsf{c}}}{{\textsf{t}}}, \pi _\texttt{sign})\), and then returns the user \(R_I\). We consider an adversary \({\mathcal {B}}_2\) against the online extractability of \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) that simulates \(\textsf{Game}_3\) for \({\mathcal {A}}\) such that
- \(\bullet \):
-
random-oracle queries from \({\mathcal {A}}\) are replied by querying \((\texttt{hash},\cdot )\) (see Def. 3.10);
- \(\bullet \):
-
instead of computing \(\pi _\texttt{sign}\) when answering a signing query, \({\mathcal {B}}_2\) makes a query \((\texttt{prove}, {\textsf{M}}, {\textsf{x}}, {\textsf{w}})\), where \(({\textsf{x}}, {\textsf{w}}) = (({\textsf{R}}, \textsf{opk}, {{\textsf{c}}}{{\textsf{t}}}), (I,{{\textsf{s}}}{{\textsf{k}}},r))\), and
- \(\bullet \):
-
instead of running \(\textsf{OnlineExtract} \), \({\mathcal {B}}_2\) makes a query \((\texttt{extract}, {\textsf{M}}, {\textsf{x}}, \pi _\texttt{sign})\).
Note that \(\texttt{extract}\) for proofs originating from \(\texttt{prove}\) queries are answered with \(\bot \), which is compatible with the fact that the challenger outputs \(\bot \) for opening queries that correspond to signatures originating from the signing oracle in \(\textsf{Game}_3\). If \({\mathcal {B}}_2\) loses the multi-proof online extractability game (i.e., \({\mathcal {B}}_2\) did not cause the extractor to fail), then it follows from the \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness of \(\Pi _{\textsf{PKE}}\) that for each extraction \({\textsf{W}}= (I,{{\textsf{s}}}{{\textsf{k}}},r)\) we have \(\textsf{Dec}(\textsf{osk}, {{\textsf{c}}}{{\textsf{t}}}) = \textsf{Dec}(\textsf{osk}, \textsf{Enc}(\textsf{opk},I;r)) = I\), so the view of \({\mathcal {A}}\) is not affected by whether I was obtained from \(\textsf{OnlineExtract} \) or by decrypting \({{\textsf{c}}}{{\textsf{t}}}\) with \(\textsf{osk}\). Therefore, we have \(\textsf{Adv}_2({\mathcal {A}}) \le \textsf{Adv}_3({\mathcal {A}}) + \textsf{Adv}_{\Pi _{\textsf{NIZK},\textsf{lbl}}}^{\textsf{OE}}({\mathcal {B}}_2)\).
- \(\textsf{Game}_4:\):
-
This is the same as \(\textsf{Game}_3\), except that we change how the challenger answers signing queries from the adversary: The challenger generates \({{\textsf{c}}}{{\textsf{t}}}\) as in \(\textsf{Game}_3\), but uses the zero-knowledge simulator \(\textsf{Sim}\) for \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) to create the proof \(\pi _\texttt{sign}\) rather than using \(\textsf{NIZK}.\textsf{Prove}_\textsf{lbl} \). It then outputs \(({{\textsf{c}}}{{\textsf{t}}}, \pi _\texttt{sign})\) as the signature. Similarly to the transition from \(\textsf{Game}_1\) to \(\textsf{Game}_2\), we can define an adversary \({\mathcal {B}}_3\) against the zero-knowledge property of \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) such that \(\textsf{Adv}_3({\mathcal {A}}) \le \textsf{Adv}_4({\mathcal {A}}) + \textsf{Adv}_{\Pi _{\textsf{NIZK},\textsf{lbl}}}^{\textsf{ZK}}({\mathcal {B}}_3)\).
- \(\textsf{Game}_5:\):
-
This is the same as \(\textsf{Game}_4\), except we further change how the challenger answers signing queries: Instead of encrypting the correct index I to obtain \({{\textsf{c}}}{{\textsf{t}}}\), the challenger encrypts a random index \(I'\). We define a multi-challenge \(\textsf{IND}\text {-}\textsf{CPA}\) adversary \({\mathcal {B}}_4\) for \(\Pi _{\textsf{PKE}}\) that simulates \(\textsf{Game}_5\) for \({\mathcal {A}}\), but instead of generating \((\textsf{opk},\textsf{osk})\), the adversary \({\mathcal {B}}_4\) receives \(\textsf{opk}\) from the multi-challenge \(\textsf{IND}\text {-}\textsf{CPA}\) challenger, and instead of producing the ciphertexts \({{\textsf{c}}}{{\textsf{t}}}\) the adversary \({\mathcal {B}}_4\) makes encryption queries \((I,I')\), where I is the correct index, and \(I'\) is a random index. Note that, say on input \((\texttt{sign},{\textbf {R}},{\textsf{M}},{{\textsf{s}}}{{\textsf{k}}}_0,{{\textsf{s}}}{{\textsf{k}}}_1)\), the I-th key in \({\textsf{R}}\) is the verification key corresponding to \({{\textsf{s}}}{{\textsf{k}}}_0\). We can make this replacement because in \(\textsf{Game}_5\), the challenger does not use \(\textsf{osk}\). (The purpose of \(\textsf{Game}_2\) and \(\textsf{Game}_3\) were to remove the use of \(\textsf{osk}\) for this reason.) If the hidden bit b in the \(\textsf{IND}\text {-}\textsf{CPA} \) game is 0, then the \(\textsf{IND}\text {-}\textsf{CPA} \) experiment is identical to \(\textsf{Game}_4\), and if the bit is 1, then the experiment is equal to \(\textsf{Game}_5\). Therefore, we have that \(\textsf{Adv}_4({\mathcal {A}}) \le \textsf{Adv}_5({\mathcal {A}}) + \textsf{Adv}^{\mathsf {Multi \text {-} CPA}}_{\Pi _{\textsf{PKE}}}({\mathcal {B}}_4)\).
Finally, observe that in \(\textsf{Game}_5\) the challenger leaks no information about the secret bit b because b is not used. Hence, \(\textsf{Adv}_5({\mathcal {A}}) = 0\). \(\square \)
Remark 4.5
In the previous proof we really relied on the online extractability property (without rewinding). This is because, even if we allow for a non-tight reduction, we cannot resort to rewinding (i.e., the forking lemma) since there can be polynomially many open queries and the reduction loss will be exponential if we try to extract from all of them. Here, keep in mind that the online extractor must succeed with (roughly) \(1-\textsf{negl}(\uplambda )\) rather than any non-negligible function \(1/\textsf{poly}(\uplambda )\) since there can be polynomially many open queries. Namely, even a success probability of 1/2 will not be good enough. Most, if not all, prior works circumvent this issue by using an IND-CCA \(\textsf{PKE}\) as building block rather than a (possibly inefficient) online extractable \(\textsf{NIZK}\) to simulate the decryption of \({{\textsf{c}}}{{\textsf{t}}}\).
Theorem 4.6
The accountable ring signature scheme \(\Pi _{\textsf{ARS}}\) in Fig. 1 is unforgeable in the random oracle model. More precisely, for any adversary \({\mathcal {A}}\) that runs in time T and makes \({\mathcal {Q}}_{u}\) queries to the \(\texttt{ukeygen}\) oracle, there exist adversaries \({\mathcal {B}}_1,{\mathcal {B}}_2,{\mathcal {B}}_3\), running in time O(T), such that
Proof
We prove unforgeability using a hybrid argument with the following series of games. Let the advantage of the adversary \({\mathcal {A}}\) in \(\textsf{Game}_i\) be denoted by \(\textsf{Adv}_i({\mathcal {A}})\).
- \(\textsf{Game}_1:\):
-
This is the original unforgeability game defined in Def. 3.18. The adversary’s advantage in this game is \(\textsf{Adv}_1({\mathcal {A}}) = \textsf{Adv}^{\textsf{Unf}}_{\Pi _{\textsf{ARS}}}({\mathcal {A}})\) by definition.
- \(\textsf{Game}_2:\):
-
This is the same as \(\textsf{Game}_1\), but the winning condition is changed. We let the challenger maintain a list \(L_{\mathcal {O}}\) of all the random oracle queries that \({\mathcal {A}}\) makes. When \({\mathcal {A}}\) finishes the game by outputting \((\textsf{opk}, {{\textsf{v}}}{{\textsf{k}}}, {\textsf{R}}, {\textsf{M}}, \sigma = ({{\textsf{c}}}{{\textsf{t}}}, \pi _\texttt{sign}), \pi )\), the challenger runs \((I, {{\textsf{s}}}{{\textsf{k}}}, r) \leftarrow \textsf{OnlineExtract} ({\textsf{M}}, ({\textsf{R}}, \textsf{opk}, {{\textsf{c}}}{{\textsf{t}}}), \pi _\texttt{sign},\) \(L_{\mathcal {O}})\). The game results in a loss if \((({\textsf{R}}, \textsf{opk}, {{\textsf{c}}}{{\textsf{t}}}), (I,{{\textsf{s}}}{{\textsf{k}}}, r)) \not \in {\tilde{R}}_{\textsf{sig}}\), otherwise, the winning condition is not changed. We construct an online-extractability adversary \({\mathcal {B}}_1\) for \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) that simulates \(\textsf{Game}_2\) for \({\mathcal {A}}\). He replies random-oracle queries from \({\mathcal {A}}\) by querying \((\texttt{hash}, \cdot )\) (see Def. 3.10), signing queries by making an oracle call \((\texttt{prove}, {\textsf{M}}, ({\textsf{R}}, \textsf{opk}, {{\textsf{c}}}{{\textsf{t}}}), (I,{{\textsf{s}}}{{\textsf{k}}},r))\) instead of computing \(\pi _\texttt{sign}\) himself, and makes the oracle call \((\texttt{extract}, {\textsf{M}}, ({\textsf{R}}, \textsf{opk}, {{\textsf{c}}}{{\textsf{t}}}),\pi _\texttt{sign})\) instead of running \(\textsf{OnlineExtract} \). The view of \({\mathcal {A}}\) during the game simulated by \({\mathcal {B}}_1\) is identical to its view during \(\textsf{Game}_1\) and \(\textsf{Game}_2\). Suppose that the output received by \({\mathcal {A}}\) is a win for the winning condition of \(\textsf{Game}_1\), but a loss for the winning condition of \(\textsf{Game}_2\). This means that \(\textsf{NIZK}.\textsf{Verify}_\textsf{lbl} ^{\mathcal {O}}({\textsf{M}}, ({\textsf{R}}, \textsf{opk}, {{\textsf{c}}}{{\textsf{t}}}), \pi _\texttt{sign}) = \top \) and \(({{\textsf{c}}}{{\textsf{t}}},\pi _\texttt{sign})\) was not the output of a query \((\texttt{sign}, \textsf{opk}, {{\textsf{v}}}{{\textsf{k}}}', {\textsf{R}}, {\textsf{M}})\) for any \({{\textsf{v}}}{{\textsf{k}}}'\), otherwise the winning condition of \(\textsf{Game}_1\) would not be met. Moreover, we would have \((({\textsf{R}}, \textsf{opk}, {{\textsf{c}}}{{\textsf{t}}}), (I,{{\textsf{s}}}{{\textsf{k}}}, r)) \not \in {\tilde{R}}_{\textsf{sig}}\), otherwise the winning condition of \(\textsf{Game}_2\) would be met. This is precisely the situation \({\mathcal {B}}_1\) needs in order to win the online extractability game. Therefore, we have \(\textsf{Adv}_1({\mathcal {A}}) \le \textsf{Adv}_2({\mathcal {A}}) + \textsf{Adv}_{\Pi _{\textsf{NIZK},\textsf{lbl}}}^{\textsf{OE}}({\mathcal {B}}_1)\)
- \(\textsf{Game}_3:\):
-
This is the same as \(\textsf{Game}_2\) except that we change the way the challenger answers signing queries from \({\mathcal {A}}\). Specifically, the challenger generates \({{\textsf{c}}}{{\textsf{t}}}\) as in \(\textsf{Game}_2\) but uses the zero-knowledge simulator \(\textsf{Sim}=(\textsf{Sim}_0,\textsf{Sim}_1)\) for \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) to create the proof \(\pi _\texttt{sign}\). That is, it forwards the random-oracle queries to \(\textsf{Sim}_0\), and runs \(\textsf{Sim}_1\) to get \(\pi _\texttt{sign}\). It then outputs \(({{\textsf{c}}}{{\textsf{t}}}, \pi _\texttt{sign})\) as the signature. Let \({\mathcal {B}}_2\) be an adversary against the zero-knowledge property of \(\Pi _{\textsf{NIZK},\textsf{lbl}} \), which simulates \(\textsf{Game}_3\) for \({\mathcal {A}}\) by forwarding random-oracle queries and proving queries to the oracles \(\textsf{Sim}_0\) and \(\textsf{Sim}_1\), respectively. If \({\mathcal {B}}_2\) is given access to oracles \({\mathcal {O}}\) and \(\textsf{Prove}\) (see Def. 3.8), then \({\mathcal {A}}\)’s view is identical to \(\textsf{Game}_2\), and if \({\mathcal {B}}_2\) is run with access to \(\textsf{Sim}_0, \textsf{Sim}_1\), then \({\mathcal {A}}\)’s view is identical to \(\textsf{Game}_3\). Therefore, we have \(\textsf{Adv}_2({\mathcal {A}}) \le \textsf{Adv}_3({\mathcal {A}}) + \textsf{Adv}_{\Pi _{\textsf{NIZK},\textsf{lbl}}}^{\textsf{ZK}}({\mathcal {B}}_2)\).
- \(\textsf{Game}_4:\):
-
This is the same as \(\textsf{Game}_3\) except that we change the winning condition again: the challenger guesses a random index \({\widetilde{I}}\in \{1,\dots ,{\mathcal {Q}}_{u}\}\) at the outset of the game. If \({\mathcal {A}}\) makes a corruption query to corrupt the verification key returned in the \({\widetilde{I}}\)-th user key generation query, then \(\textsf{Game}_4\) aborts. The game results in a win if the winning condition of \(\textsf{Game}_3\) is met and if \({\widetilde{I}}= I\). Since \({\widetilde{I}}\) is information-theoretically hidden during the execution of the game, we have \({\widetilde{I}}= I\) with probability \(1/{\mathcal {Q}}_{u}\). Therefore, we have \(\textsf{Adv}_3({\mathcal {A}}) = {\mathcal {Q}}_{u}\textsf{Adv}_4({\mathcal {A}})\).
Finally, let \({\mathcal {B}}_3\) be an adversary against \((\textsf{RelSetup},\textsf{IGen})\) which simulates \(\textsf{Game}_4\) for \({\mathcal {A}}\). At the beginning of the game, \({\mathcal {B}}_3\) is given an instance \(({{\textsf{p}}}{{\textsf{p}}}_1,{\textsf{x}})\). The adversary \({\mathcal {B}}_3\) simulates an execution of \(\textsf{Game}_4\) by using the public parameter \({{\textsf{p}}}{{\textsf{p}}}_1\) that is given to him, rather than generating a new \({{\textsf{p}}}{{\textsf{p}}}_1\) himself using \(\textsf{RelSetup}\), and by answering the \({\widetilde{I}}\)-th \(\texttt{ukeygen}\) query assigning \({{\textsf{v}}}{{\textsf{k}}}_{{\widetilde{I}}} = {\textsf{x}} \) instead of running \(({\textsf{x}}, {\textsf{w}}) \leftarrow \textsf{IGen}({{\textsf{p}}}{{\textsf{p}}}_1)\). Note that \({\mathcal {B}}_3\) does not need \({\textsf{w}} \) because if \({\mathcal {A}}\) makes a query to corrupt \({{\textsf{v}}}{{\textsf{k}}}_{{\widetilde{I}}}\) then the game aborts. The view of \({\mathcal {A}}\) during \({\mathcal {B}}_3\)’s simulation is the same as its view during a real execution of \(\textsf{Game}_4\), so \(\textsf{OnlineExtract} \) outputs a valid witness \(({\widetilde{I}},{{\textsf{s}}}{{\textsf{k}}},r)\) with probability at least \(\textsf{Adv}_4({\mathcal {A}})\). If this is the case, then \({\mathcal {B}}_3\) wins his game against the hardness of \((\textsf{RelSetup}, \textsf{IGen})\) by outputting \({{\textsf{s}}}{{\textsf{k}}}\). Therefore, we have \(\textsf{Adv}_4({\mathcal {A}}) \le \textsf{Adv}^{\textsf{Hard}}_{\textsf{RelSetup},\textsf{IGen}}({\mathcal {B}}_3)\). \(\square \)
Theorem 4.7
The accountable ring signature scheme \(\Pi _{\textsf{ARS}}\) in Fig. 1 is traceable and tracing sound in the random oracle model. More precisely, for any adversary \({\mathcal {A}}\) that runs in time T, we have adversaries \({\mathcal {B}}_1,{\mathcal {B}}_2,{\mathcal {B}}_3\) that run in time O(T), such that
and
Proof
We prove the two properties separately as follows:
Traceability Traceability follows from the statistical soundness of \(\Pi _{\textsf{NIZK},\textsf{lbl}} \), the \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness of \(\Pi _{\textsf{PKE}}\), and the correctness of \(\Pi _\textsf{NIZK} \). Observe that if \({\mathcal {A}}\) wins an execution of the traceability game, then \(\textsf{NIZK}.\textsf{Verify}_\textsf{lbl} ({\textsf{M}},\) \({\textsf{X}}= ({\textsf{R}}, \textsf{opk}, {{\textsf{c}}}{{\textsf{t}}}), \pi _\texttt{sign}) = \top \), but still there cannot be a witness \({\textsf{W}}= (I,{{\textsf{s}}}{{\textsf{k}}},r)\) such that \(({\textsf{X}},{\textsf{W}}) \in {\tilde{R}}_{\textsf{sig}}\). Towards a contradiction, suppose that such a witness does exist, then the \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness of the \(\textsf{PKE} \) implies that \(\textsf{Dec}(\textsf{osk},{{\textsf{c}}}{{\textsf{t}}}= \textsf{Enc}(\textsf{opk}, I; r)) = I\), which implies that \(((\textsf{opk},{{\textsf{c}}}{{\textsf{t}}},I), \textsf{osk}) \in R_{\textsf{open}}\), so the correctness of \(\Pi _\textsf{NIZK} \) implies that \(\textsf{NIZK}.\textsf{Verify}((\textsf{opk}, {{\textsf{c}}}{{\textsf{t}}}, I), \pi _\texttt{open}) = \top \). This means that \({\mathcal {A}}\) did not win the traceability game. Therefore, \({\mathcal {A}}\) produces valid proofs for statements not in \({\tilde{R}}_{\textsf{sig}}\) with probability at least \(\textsf{Adv}_{\Pi _{\textsf{ARS}}}^{\textsf{Tra}}({\mathcal {A}})\). We can use this to construct an adversary \({\mathcal {B}}_1\) against the statistical soundness of \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) that generates \({{\textsf{p}}}{{\textsf{p}}}\leftarrow \textsf{ARS}.\textsf{Setup}(1^\uplambda )\) for a security parameter \(\uplambda \), runs \(({{\textsf{r}}}{{\textsf{r}}}, {\textsf{R}}, {\textsf{M}}, \sigma ) \leftarrow {\mathcal {A}}({{\textsf{p}}}{{\textsf{p}}})\) where \(\sigma =({{\textsf{c}}}{{\textsf{t}}},\pi _\texttt{sign})\), and \((\textsf{osk},\textsf{opk}) \leftarrow \textsf{ARS}.\textsf{OKGen}({{\textsf{p}}}{{\textsf{p}}};{{\textsf{r}}}{{\textsf{r}}})\), and outputs \(({\textsf{M}}, {\textsf{x}}:= (R,\textsf{opk}, {{\textsf{c}}}{{\textsf{t}}}), \pi _{\texttt{sign}})\), which makes \({\mathcal {B}}_1\) win. \({\mathcal {B}}_1\)’s advantage is therefore \(\textsf{Adv}_{\Pi _{\textsf{ARS}}}^{\textsf{Tra}}({\mathcal {A}}) \le \textsf{Adv}_{\Pi _{\textsf{NIZK},\textsf{lbl}}}^{\textsf{soundness}}({\mathcal {B}}_1)\).
Tracing soundness Similarly, tracing soundness follows from the statistical soundness of \(\Pi _\textsf{NIZK}\) and \(\Pi _{\textsf{NIZK},\textsf{lbl}}\), and the \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness of the \(\Pi _{\textsf{PKE}}\). In order for \({\mathcal {A}}\) to win the tracing soundness game, it needs to output valid proofs \(\pi _\texttt{sign}\), \(\pi _0\), \(\pi _1\) (the former is part of the produced signature \(\sigma =({{\textsf{c}}}{{\textsf{t}}},\pi _\texttt{sign})\)) such that there exist witnesses \((I,{{\textsf{s}}}{{\textsf{k}}},r)\), \(\textsf{osk}_0\) and \(\textsf{osk}_1\) where
with \(I_0 \not = I_1\). However, it follows from the \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness of \(\Pi _{\textsf{PKE}}\) that no three such witnesses can exist. Suppose, towards a contradiction, that those witnesses exist. Then we have \(I_0 = \textsf{Dec}(\textsf{osk}_0,{{\textsf{c}}}{{\textsf{t}}}= \textsf{Enc}(\textsf{opk},I;r))\), so the \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness implies that \(I_0 = I\), and similarly it follows from \(I_1 = \textsf{Dec}(\textsf{osk}_1,\) \({{\textsf{c}}}{{\textsf{t}}}= \textsf{Enc}(\textsf{opk},I;r))\) that \(I_1 = I\), which contradicts \(I_0 \ne I_1\). Therefore, at least one of \(\pi _\texttt{sign}, \pi _0, \pi _1\) is a valid proof of an invalid statement, i.e. a \({\textsf{X}}\) for which does not exist \({\textsf{W}}\) such that \(({\textsf{X}}, {\textsf{W}}) \in {\tilde{R}}_{\textsf{sig}}\) (or \((v) \in {\tilde{R}}_{\textsf{open}}\)), with probability at least \(\textsf{Adv}_{\Pi _{\textsf{ARS}}}^{\textsf{TraS}}({\mathcal {A}})\). Let \({\mathcal {B}}_2\) and \({\mathcal {B}}_3\) be statistical-soundness adversaries for \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) and \(\Pi _\textsf{NIZK} \), respectively, that simulate the tracing soundness game and output \(\pi _\texttt{sign}\) or \(\pi _b\), respectively, where b is a random bit. Then we have \(\textsf{Adv}_{\Pi _{\textsf{ARS}}}^{\textsf{TraS}}({\mathcal {A}}) \le \textsf{Adv}_{\Pi _{\textsf{NIZK},\textsf{lbl}}}^{\textsf{soundness}}({\mathcal {B}}_2) + 2 \textsf{Adv}_{\Pi _\textsf{NIZK}}^{\textsf{soundness}}({\mathcal {B}}_3)\). \(\square \)
4.2 Accountable ring signature to dynamic group signature
Accountable ring signatures are known to trivially imply dynamic group signatures [19, 20]. A formal treatment is provided by Bootle et al. [20]. We remark that the transformation provided in [20] retains the same level of security provided by the underlying accountable ring signature. That is, all reductions between unforgeability, full-anonymity and traceability are tight. For completeness, we provide more details on group signatures and the transformation in App. B.
4.3 Tightly secure variant
Observe the only source of loose reduction in the previous section was in the unforgeability proof (see Theorem 4.6), where we assume each building blocks, i.e., \(\textsf{NIZK}\) and \(\textsf{PKE}\), are tightly reduced to concrete hardness assumptions. In this subsection, we apply the Katz-Wang technique [61] to modify our construction in Fig. 1 to obtain a tight reduction.
We firstly give an intuition of the method. Recall that in the proof of Theorem 4.6, the reduction is given a challenge instance \({\textsf{x}} \), guesses which user’s signature the adversary will forge, and assigns \({\textsf{x}} \) to the verification key \({{\textsf{v}}}{{\textsf{k}}}\) of the selected user. If the adversary queries the corruption oracle on the key \({{\textsf{v}}}{{\textsf{k}}}\), the reduction fails and aborts since it will not be able to produce the corresponding secret key for \({{\textsf{v}}}{{\textsf{k}}}\). If the guess is correct and the adversary successfully forges the signature, then the reduction can recover a witness \({\textsf{w}} '\) such that \(({\textsf{x}},{\textsf{w}} ')\) is in the relation \({\widetilde{R}}_{{{\textsf{p}}}{{\textsf{p}}}_1}\). Therefore, if the adversary makes \({\mathcal {Q}}_{u}\) user key generation queries and its advantage is \(\epsilon \), then the reduction can extract a witness with probability roughly \(\epsilon /{\mathcal {Q}}_{u}\).
A high-level viewpoint of the Katz-Wang method is that each user is given a pair of statements \(({\textsf{x}} ^{(1)},{\textsf{x}} ^{(2)})\) as the verification key \({{\textsf{v}}}{{\textsf{k}}}\), with only one witness \({\textsf{w}} \) as the secret signing key, such that either \(({\textsf{x}} ^{(1)},{\textsf{w}})\) or \(({\textsf{x}} ^{(2)},{\textsf{w}})\) is in the relation \({\widetilde{R}}_{{{\textsf{p}}}{{\textsf{p}}}_1}\). Also, we assume that now the reduction is given \({\mathcal {Q}}_{u}\) challenge instances \(\{ {\textsf{x}} _i \}_{i\in [{\mathcal {Q}}_{u}]}\) and it is required to solve any one of them. The reduction in this case needs no guessing steps as above. Specifically, the reduction can use \(\textsf{IGen}\) to generate pairs \(({\widetilde{{\textsf{x}}}}_i,{\widetilde{{\textsf{w}}}}_i)\) for \(i \in [{\mathcal {Q}}_{u}]\), randomly permutes \({\textsf{x}} _i,{\widetilde{{\textsf{x}}}}_i\) and assigns the obtained ordered pair to \({{\textsf{v}}}{{\textsf{k}}}_i\). Therefore, the reduction can always answer any corruption query with \({\widetilde{{\textsf{w}}}}_i\). As long as the adversary wins the unforgeability game by forging a signature, the reduction can return a witness for one of the \(\{ {\textsf{x}} _i \}_{i\in [{\mathcal {Q}}_{u}]}\) with probability 1/2. Roughly speaking, if the success rate of the adversary is \(\epsilon \), then the reduction can extract the answer for the challenge \((\star ,X_0,\{ {\textsf{x}} _i \}_{i\in [{\mathcal {Q}}_{u}]})\) with probability around \(\epsilon /2\). Here, it is important that the information on which verification key the user knows the corresponding signing key remains hidden from the adversary. Otherwise, the adversary may always create a forgery with respect to the signing key the reduction already knows.
To turn the above idea into a formal proof, we require two new ingredients: an instance generator that outputs multiple challenges and a \(\textsf{NIZK}\) that additionally hides the information on which signing key is used. More formally, we build a tightly secure accountable ring signature scheme \(\Pi _{\textsf{ARS}}^\textsf{Tight}=(\textsf{ARS}.\textsf{Setup}, \textsf{ARS}.\textsf{OKGen}, \textsf{ARS}.\textsf{UKGen}, \textsf{ARS}.\textsf{Sign}, \textsf{ARS}.\textsf{Verify}, \textsf{ARS}.\textsf{Open}, \textsf{ARS}.\textsf{Judge})\) based on the following tools. The only difference between the tools used in Sect. 4.1 are the hard multi-instance generator and the \(\textsf{NIZK}\) for the relation \(R_{\textsf{sig}}^\textsf{Tight}\).
-
A hard multi-instance generator \((\textsf{RelSetup},\textsf{IGen})\) contains a setup algorithm \(\textsf{RelSetup}\) that outputs a description \({{\textsf{p}}}{{\textsf{p}}}\) of a pair of relations \(R_{{\textsf{p}}}{{\textsf{p}}}\subseteq {\tilde{R}}_{{\textsf{p}}}{{\textsf{p}}}\), and an instance generator \(\textsf{IGen}\) for these pairs of relations. That is, \(\textsf{RelSetup}\) and \(\textsf{IGen}\) are PPT algorithms such that \(\Pr [ ({\textsf{x}} _i,{\textsf{w}} _i) \in R_{{\textsf{p}}}{{\textsf{p}}}~ \mid ~ {{\textsf{p}}}{{\textsf{p}}}\leftarrow \textsf{RelSetup}(1^\uplambda ); \{({\textsf{x}} _i, {\textsf{w}} _i)\}_{i \in [N]} \leftarrow \textsf{IGen}({{\textsf{p}}}{{\textsf{p}}}, N)] = 1\). Moreover, if we define the advantage of an adversary \({\mathcal {A}}\) against \((\textsf{RelSetup},\textsf{IGen})\) as
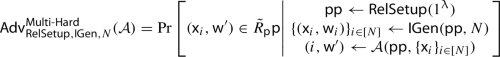
then \(\textsf{Adv}^{\mathsf {Multi{\text{- }}Hard}}_{\textsf{RelSetup},\textsf{IGen},N}({\mathcal {A}})\) is a negligible function in \(\uplambda \) for every PPT adversary \({\mathcal {A}}\).
-
A public-key encryption scheme \(\Pi _\textsf{PKE} = (\mathsf {PKE.Setup}, \textsf{KeyGen}, \textsf{Enc}, \textsf{Dec})\) with multi-challenge IND-CPA security, and with \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness for some relaxed randomness set \({\mathcal {R}}'\) and some relaxed key relation \({{\mathcal {K}}}{{\mathcal {R}}}'\). The message space of the encryption scheme contains a set of indices [N] for any polynomially large \(N \in {\mathbb {N}}\).
-
A multi-proof online extractable NIZK proof system with labels \(\Pi _{\textsf{NIZK},\textsf{lbl}} = (\textsf{NIZK}.\textsf{Setup}_\textsf{lbl},\) \(\textsf{NIZK}.\textsf{Prove}_\textsf{lbl},\) \(\textsf{NIZK}.\textsf{Verify}_\textsf{lbl})\) for the family of relations

-
A second \(\textsf{NIZK}\) proof system (without labels) \(\Pi _\textsf{NIZK} = (\textsf{NIZK}.\textsf{Setup}, \textsf{NIZK}.\textsf{Prove}, \textsf{NIZK}.\textsf{Verify})\) for the family of relations
$$\begin{aligned} R_{\textsf{open}}&= \left\{ (({{\textsf{p}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}, I),{{\textsf{s}}}{{\textsf{k}}}) ({{\textsf{p}}}{{\textsf{k}}},{{\textsf{s}}}{{\textsf{k}}}) \in {{\mathcal {K}}}{{\mathcal {R}}}\wedge \textsf{Dec}({{\textsf{s}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}) = I \right\} \\ {\tilde{R}}_{\textsf{open}}&= \left\{ (({{\textsf{p}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}, I),{{\textsf{s}}}{{\textsf{k}}}) ({{\textsf{p}}}{{\textsf{k}}},{{\textsf{s}}}{{\textsf{k}}}) \in {{\mathcal {K}}}{{\mathcal {R}}}' \wedge \textsf{Dec}({{\textsf{s}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}) = I \right\} \, , \end{aligned}$$with statistical soundness (Def. 3.9).
The building blocks listed above are combined similarly to Fig. 1. For the sake of completeness, we detail the resulting protocol in Fig. 2. For the security properties, we only focus on unforgeability. The others are a direct consequence of the proofs given for the non-tight construction in Fig. 1.
Modified tightly-secure construction of an accountable ring signature \(\Pi _{\textsf{ARS}}^{\textsf{Tight}}\) obtained from a hard multi-instance generator \((\textsf{RelSetup},\textsf{IGen})\), a public-key encryption algorithm \((\mathsf {PKE.Setup},\textsf{KeyGen},\textsf{Enc},\textsf{Dec})\) satisfying some suitable correctness and security properties, a \(\textsf{NIZK}\) proof system with labels \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) for \(R_{\textsf{sig}}^\textsf{Tight}\), and a \(\textsf{NIZK} \) proof system without labels \(\Pi _\textsf{NIZK} \) for \(R_{\textsf{open}}\)
Theorem 4.8
The accountable ring signature scheme \(\Pi _{\textsf{ARS}}^\textsf{Tight}\) in Fig. 2 is unforgeable in the random oracle model. More precisely, for any adversary \({\mathcal {A}}\) that runs in time T and makes \({\mathcal {Q}}_{u}\) queries to the \(\texttt{ukeygen}\) oracle, there exist adversaries \({\mathcal {B}}_1,{\mathcal {B}}_2,{\mathcal {B}}_3\), running in time O(T), such that
Proof
We prove unforgeability using a hybrid argument with the following series of games. Let the advantage of an adversary \({\mathcal {A}}\) in \(\textsf{Game}_i\) be denoted by \(\textsf{Adv}_i({\mathcal {A}})\).
-
The first game, \(\textsf{Game}_1\), is the original unforgeability game defined in Def. 3.18. The adversary’s advantage in this game is \(\textsf{Adv}_1({\mathcal {A}}) = \textsf{Adv}^{\textsf{Unf}}_{\textsf{ARS}}({\mathcal {A}})\) by definition.
-
\(\textsf{Game}_2\) is the same as \(\textsf{Game}_1\), but with a modified winning condition. We let the challenger maintain a list \(L_{\mathcal {O}}\) of all the random-oracle queries that \({\mathcal {A}}\) makes. When \({\mathcal {A}}\) finishes the game by outputting \((\textsf{opk}, {{\textsf{v}}}{{\textsf{k}}}, {\textsf{R}}, {\textsf{M}}, \sigma = ({{\textsf{c}}}{{\textsf{t}}}, \pi _\texttt{sign}), \pi )\), the challenger runs \((I, b, {{\textsf{s}}}{{\textsf{k}}}, r) \leftarrow \textsf{OnlineExtract} ({\textsf{M}}, ({{\textsf{p}}}{{\textsf{p}}}_1, {\textsf{R}}, \textsf{opk}, {{\textsf{c}}}{{\textsf{t}}}),\) \(\pi _\texttt{sign}, L_{\mathcal {O}})\). The game results in a loss if \((({{\textsf{p}}}{{\textsf{p}}}_1, {\textsf{R}}, \textsf{opk}, {{\textsf{c}}}{{\textsf{t}}}), (I,,b,{{\textsf{s}}}{{\textsf{k}}}, r)) \not \in {\tilde{R}}_{\textsf{sig}}^\textsf{Tight}\), otherwise, the winning condition is not changed. As we have shown in the proof of Theorem 4.6, there exists an online-extractability adversary \({\mathcal {B}}_1\) for \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) running in time O(T) such that \(\textsf{Adv}_1({\mathcal {A}}) \le \textsf{Adv}_2({\mathcal {A}}) + \textsf{Adv}_{\Pi _{\textsf{NIZK},\textsf{lbl}}}^{\textsf{OE}}({\mathcal {B}}_1)\).
-
The third game, \(\textsf{Game}_3\), is the same as \(\textsf{Game}_2\) except that we change the way the challenger answers signing queries from \({\mathcal {A}}\). Specifically, the challenger generates \({{\textsf{c}}}{{\textsf{t}}}\) as in \(\textsf{Game}_2\) but uses the \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) zero-knowledge simulator \(\textsf{Sim}=(\textsf{Sim}_0,\textsf{Sim}_1)\) to create the proof \(\pi _\texttt{sign}\). As we have shown in the proof of Theorem 4.6, there exists a zero-knowledge adversary \({\mathcal {B}}_2\) for \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) running in time O(T) and such that \(\textsf{Adv}_2({\mathcal {A}}) \le \textsf{Adv}_3({\mathcal {A}}) + \textsf{Adv}_{\Pi _{\textsf{NIZK},\textsf{lbl}}}^{\textsf{ZK}}({\mathcal {B}}_2)\).
-
Finally, we consider an adversary \({\mathcal {B}}_3\) against the hardness of \((\textsf{RelSetup},\textsf{IGen})\) which simulates \(\textsf{Game}_3\) for \({\mathcal {A}}\). At the beginning of the game, the adversary \({\mathcal {B}}_3\) is given the instances \(({{\textsf{p}}}{{\textsf{p}}}_1,\{ {\textsf{x}} \}_{i \in [{\mathcal {Q}}_{u}]})\). \({\mathcal {B}}_3\) uses the public parameter \({{\textsf{p}}}{{\textsf{p}}}_1\) that is given to him, rather than generating new \({{\textsf{p}}}{{\textsf{p}}}_1\) himself using \(\textsf{RelSetup}\). Moreover, when answering the i-th \(\texttt{ukeygen}\) query, \({\mathcal {B}}_3\) uniformly draws \(b_i\) from \(\{ 1,2 \}\), generates \(({\widetilde{{\textsf{x}}}}_i,{\widetilde{{\textsf{w}}}}_i) \leftarrow \textsf{IGen}({{\textsf{p}}}{{\textsf{p}}}_1)\), and assigns \({{\textsf{v}}}{{\textsf{k}}}_{i} = ({\textsf{x}} _i^{(1)},{\textsf{x}} _i^{(2)})\) where \(({\textsf{x}} _i^{(b_i)},{\textsf{x}} _i^{(3-b_i)})=({\widetilde{{\textsf{x}}}}_i,{\textsf{x}} _i)\). Note that now \({\mathcal {B}}_3\) is able to respond to any valid corruption query \(\texttt{corrupt}\). In fact, for any \(i\in [{\mathcal {Q}}_{u}]\), if \({\mathcal {A}}\) makes a corruption query to corrupt \({{\textsf{v}}}{{\textsf{k}}}_{i}\), then \({\mathcal {B}}_3\) responds by \({{\textsf{s}}}{{\textsf{k}}}=(b_i,{\widetilde{{\textsf{w}}}}_i)\). The view of \({\mathcal {A}}\) during \({\mathcal {B}}_3\)’s simulation is the same as its view during a real execution of \(\textsf{Game}_3\), so \(\textsf{OnlineExtract} \) outputs a valid witness \(({\widetilde{I}},{{\textsf{s}}}{{\textsf{k}}}=(b',{\textsf{w}} '),r)\) with probability at least \(\textsf{Adv}_3({\mathcal {A}})\). Since the sampling of the statements and witnesses follows the same distribution determined by \(\textsf{IGen}({{\textsf{p}}}{{\textsf{p}}}_1)\) in the real execution, there is an 1/2 chance that \(b'=(3-b_{{\widetilde{I}}})\). That is, \(({\textsf{x}} _{{\widetilde{I}}},{\textsf{w}} ') \in {\widetilde{R}}_{{{\textsf{p}}}{{\textsf{p}}}_1}\). Therefore, we have \(\textsf{Adv}_3({\mathcal {A}})/2 \le \textsf{Adv}^{\mathsf {Multi{\text{- }}Hard}}_{\textsf{RelSetup},\textsf{IGen},{\mathcal {Q}}_{u}}({\mathcal {B}}_3)\).
\(\square \)
5 Group-action-based hard instance generators and PKEs
In this section, we introduce group-action-based hard instance generators (\(\textsf{HIG}\) s) and group-action-based \(\textsf{PKE}\) s. These are classes of \(\textsf{HIG}\) s and \(\textsf{PKE}\) s, that derive their security from cryptographic group actions, and which have some specific internal structure. We define these concepts because, as we will see in Sects. 6 and 7, if we instantiate our generic accountable ring signature construction with a group-action-based \(\textsf{HIG}\) and a group-action-based \(\textsf{PKE}\), then we can construct a very efficient multi-proof online extractable \(\textsf{NIZK}\) for the \(R_{\textsf{sig}}\) relation. We provide concrete instantiations of group-action-based \(\textsf{HIG}\) s and \(\textsf{PKE}\) s from lattices and isogenies in Sect. 8.
5.1 Group-action-based hard instance generator
We consider a special class of hard instance generators naturally induced by cryptographic hard actions.
Definition 5.1
(Group-Action-based Hard Instance Generator) A group-action-based hard instance generator, \(\textsf{GA}\text {-}\textsf{HIG} \) in short, is a pair of efficient algorithms \((\textsf{RelSetup}, \textsf{IGen})\) with the following properties:
-
On input a security parameter \(\uplambda \), \(\textsf{RelSetup}\) outputs \({{\textsf{p}}}{{\textsf{p}}}= (G,S_1,S_2,\delta ,X_0,{\mathcal {X}},\star )\) such that: G is an additive group whose elements can be represented uniquely, \(S_1 \subseteq S_2\) are symmetric subsets of G, such that membership in \(S_1\) and \(S_2\) can be decided efficiently, and such that the group law can be computed efficiently for elements in \(S_1 \cup S_2\). Moreover, the intersection \(S_3 = \cap _{g \in S_1} g + S_2\) has cardinality \(\delta |S_2 |\) and membership of \(S_3\) can be decided efficiently. \(\star \) is an action \(\star : G \times {\mathcal {X}}\rightarrow {\mathcal {X}}\) of G on a set \({\mathcal {X}}\) that contains the element \(X_0\). \(\star \) can be evaluated efficiently on elements of \(S_1 \cup S_2\). These parameters describe an NP-relation
$$\begin{aligned} R_{{\textsf{p}}}{{\textsf{p}}}= \left\{ (X,s) \, \, s \in S_1: s \star X_0 = X \right\} , \end{aligned}$$and a relaxed NP-relation
$$\begin{aligned} {\tilde{R}}_{{\textsf{p}}}{{\textsf{p}}}= \left\{ (X,s) \, \, s \in S_2 + S_3: s \star X_0 = X \right\} . \end{aligned}$$ -
On input \({{\textsf{p}}}{{\textsf{p}}}\), \(\textsf{IGen}\) samples an element s from \(S_1\) and outputs \((s~\star ~X_0,s) \in ~R_{{\textsf{p}}}{{\textsf{p}}}\).
-
\((\textsf{RelSetup}, \textsf{IGen})\) is a hard instance generator as defined in Sect. 4.
5.2 Group-action-based PKE
We also consider group actions provided with a corresponding public-key encryption scheme, as specified in the following definition.
Definition 5.2
(Group-action-based \(\textsf{PKE}\)) A group-action-based public-key encryption scheme, \(\textsf{GA}\text {-}\textsf{PKE}\) in short, is a public-key encryption scheme \(\Pi _\textsf{GA}\text {-}\textsf{PKE}=(\textsf{Setup}, \textsf{KeyGen}, \textsf{Enc}, \textsf{Dec})\) with the following properties:
-
\(\textsf{Setup}(1^\uplambda ) \rightarrow {{\textsf{p}}}{{\textsf{p}}}:\) On input a security parameter \(1^\uplambda \), it returns the public parameter \({{\textsf{p}}}{{\textsf{p}}}= (G, G_{\textsf{M}}, {\mathcal {X}}, S_1, S_2, \delta , D_{{\mathcal {X}}}, \star _{\textsf{M}}, {\mathcal {M}})\) (sometimes implicitly) used by the scheme. Here, \(G, G_{\textsf{M}}\) are additive groups, \(S_1,S_2\) two symmetric subsets of G, \({\mathcal {X}}\) a finite set, \(\delta \) a real number in [0, 1], \(D_{{\mathcal {X}}}\) a distribution over a set of group actions \(\star _{{\textsf{p}}}{{\textsf{k}}}: G \times {\mathcal {X}}\rightarrow {\mathcal {X}}\) and elements in \({\mathcal {X}}\), \(\star _{\textsf{M}}: G_{\textsf{M}}\times {\mathcal {X}}\rightarrow {\mathcal {X}}\) a group action, \({\mathcal {M}}\subseteq G_{\textsf{M}}\) a message space. For any polynomially large \(N \in {\mathbb {N}}\), we assume that there exists a feasible and invertible embedding \(\tau \) from the set of index [N] into the message space \({\mathcal {M}}\). For simplicity, we will write \(\tau (i) \star _{\mathcal {M}}X\), \(\textsf{Enc}({{\textsf{p}}}{{\textsf{k}}},\tau (i))\) as \(i \star _{\textsf{M}}X\), \(\textsf{Enc}({{\textsf{p}}}{{\textsf{k}}},i)\) respectively without causing confusion.
-
\(\textsf{KeyGen}({{\textsf{p}}}{{\textsf{p}}}) \rightarrow ({{\textsf{p}}}{{\textsf{k}}}, {{\textsf{s}}}{{\textsf{k}}}):\) On input a public parameter \({{\textsf{p}}}{{\textsf{p}}}\), it returns a public key \({{\textsf{p}}}{{\textsf{k}}}\) and a secret key \({{\textsf{s}}}{{\textsf{k}}}\). We assume \({{\textsf{p}}}{{\textsf{k}}}= (\star _{{\textsf{p}}}{{\textsf{k}}}, X_{{\textsf{p}}}{{\textsf{k}}})\) to be drawn from \(D_{{\mathcal {X}}}\), where \(\star _{{\textsf{p}}}{{\textsf{k}}}: G \times {\mathcal {X}}\rightarrow {\mathcal {X}}\) is a group action and \(X_{{\textsf{p}}}{{\textsf{k}}}\in {\mathcal {X}}\), and \({{\textsf{s}}}{{\textsf{k}}}\in G\). We also assume \({{\textsf{p}}}{{\textsf{k}}}\) includes \({{\textsf{p}}}{{\textsf{p}}}\) w.l.o.g.
-
\(\textsf{Enc}({{\textsf{p}}}{{\textsf{k}}}, {\textsf{M}}; r) \rightarrow {{\textsf{c}}}{{\textsf{t}}}:\) On input a public key \({{\textsf{p}}}{{\textsf{k}}}= (\star _{{\textsf{p}}}{{\textsf{k}}}, X_{{\textsf{p}}}{{\textsf{k}}})\) and a message \({\textsf{M}}\in {\mathcal {M}}\), it returns a ciphertext \({{\textsf{c}}}{{\textsf{t}}}\). We assume \({{\textsf{c}}}{{\textsf{t}}}\) is generated as \({\textsf{M}}\star _{\textsf{M}}(r \star _{{\textsf{p}}}{{\textsf{k}}}X_{{\textsf{p}}}{{\textsf{k}}}) \in {\mathcal {X}}\), where the encryption randomness is sampled as \(r \overset{_{\tiny \$}}{\leftarrow } S_1\).
-
\(\textsf{Dec}({{\textsf{s}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}) \rightarrow {\textsf{M}}:\) On input a secret key \({{\textsf{s}}}{{\textsf{k}}}\) and a ciphertext \({{\textsf{c}}}{{\textsf{t}}}\), it (deterministically) returns a message \({\textsf{M}}\in {\mathcal {M}}\).
In addition, we assume the following properties hold for the group actions defined by \({{\textsf{p}}}{{\textsf{p}}}\).
-
1.
There exists a positive-valued polynomial T such that for all \(\uplambda \in {\mathbb {N}}\), \({{\textsf{p}}}{{\textsf{p}}}\in \textsf{Setup}(1^\uplambda )\), and \(({{\textsf{p}}}{{\textsf{k}}}, {{\textsf{s}}}{{\textsf{k}}}) \in \textsf{KeyGen}({{\textsf{p}}}{{\textsf{p}}})\), one can efficiently compute \(g \star _{{\textsf{p}}}{{\textsf{k}}}X\) for all \(g \in S_1 \cup S_2\) and all \(X \in {\mathcal {X}}\) in time at most \(T(\uplambda )\), sample uniformly from \(S_1\) and \(S_2\), and represent elements of G and \({\mathcal {X}}\) uniquely. It is also efficient to compute the action \(\star _{\textsf{M}}\) for every possible input.
-
2.
The intersection \(S_3\) of the sets \(S_2 + g\), with g varying in \(S_1\), is such that its cardinality is equal to \(\delta |S_2 |\). Furthermore, it is efficient to check whether an element \(g \in G\) belongs to \(S_3\).
We further require a group-action-based \(\textsf{PKE} \) to satisfy standard correctness and decryption efficiency.
Definition 5.3
(Correctness and Decryption Efficiency) We say a group-action-based \(\textsf{PKE}\) \(\Pi _\textsf{GA}\text {-}\textsf{PKE}\) is correct if for all \(\uplambda \in {\mathbb {N}}\), and for all but a negligible fraction of \({{\textsf{p}}}{{\textsf{p}}}\in \textsf{Setup}(1^\uplambda )\), we have \(\textsf{Dec}({{\textsf{s}}}{{\textsf{k}}}, \textsf{Enc}({{\textsf{p}}}{{\textsf{k}}}, {\textsf{M}})) = {\textsf{M}}\) for all \(({{\textsf{p}}}{{\textsf{k}}}, {{\textsf{s}}}{{\textsf{k}}}) \in \textsf{KeyGen}({{\textsf{p}}}{{\textsf{p}}})\) and \({\textsf{M}}\in {\mathcal {M}}\).
Moreover, we require \(\textsf{Dec}\) to run in \(\textsf{poly}(\uplambda )\) for a fixed polynomial function \(\textsf{poly}\) and for all possible inputs.
As we show in Sect. 4.1, in order to construct an accountable ring signature, a group-action-based \(\textsf{PKE}\) is also required to be (multi-challenge) \(\textsf{IND}\text {-}\textsf{CPA} \) secure and \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correct for some relaxed randomness set \({\mathcal {R}}'\) and some relaxed key relation \({{\mathcal {K}}}{{\mathcal {R}}}'\) (Def. 4.1).
The concrete choice of \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\) may depend on the instantiation. For instance, while we define \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}') = ({\mathcal {R}},{{\mathcal {K}}}{{\mathcal {R}}})\) for our isogeny-based instantiation in Sect. 8.1, we must rely on a strictly wider relation for our lattice-based instantiation to compensate for the relaxed soundness. In slightly more detail, in our lattice-based \(\textsf{NIZK}\), we are only able to argue that an adversary created a ciphertext \({{\textsf{c}}}{{\textsf{t}}}\) using message \({\textsf{M}}\) and randomness \(r \in {\mathcal {R}}'\), and/or that a \({{\textsf{c}}}{{\textsf{t}}}\) can be decrypted to \({\textsf{M}}\) using secret key \({{\textsf{s}}}{{\textsf{k}}}\) such that \(({{\textsf{p}}}{{\textsf{k}}}, {{\textsf{s}}}{{\textsf{k}}}) \in {{\mathcal {K}}}{{\mathcal {R}}}'\). Roughly, \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness guarantees that such an argument suffices to prove that \({{\textsf{c}}}{{\textsf{t}}}\) can only be decrypted to a unique \({\textsf{M}}\).
6 Sigma protocol for a “Traceable” OR relation
In this section, we present an efficient sigma protocol for the relation \(R_{\textsf{sig}}\) introduced in Sect. 4.1, using group-action-based \(\textsf{HIG}\) and a group-action-based \(\textsf{PKE}\) from the previous section. Recall this relation was used to define the multi-proof online extractable \(\textsf{NIZK}\) with labels \(\Pi _\textsf{NIZK} \), which allowed an OR proof along with a proof of opening to a ciphertext. Looking ahead, in Sect. 7, we show that our sigma protocol can be turned into a multi-proof online extractable \(\textsf{NIZK}\) using the Fiat-Shamir transform. This is in contrast to the common application of the Fiat-Shamir transform that only provides a proof of knowledge via the rewinding argument [50, 81]. We note that we do not focus on the other \(\textsf{NIZK}\) for the relation \(R_{\textsf{open}}\) in Sect. 4.1 since they can be obtained easily from prior works.
We call the sigma protocol we present in this section as a traceable OR sigma protocol since it allows to trace the prover. This section is structured as follows. Firstly, we introduce a base traceable OR sigma protocol \(\Pi _{\Sigma }^\textsf{base}\) for the relation \(R_{\textsf{sig}}\) with proof size \(O(\log N)\) but with a binary challenge space. Secondly, we amplify the soundness of the sigma protocol by performing parallel repetitions. Here, instead of applying \(\uplambda \)-parallel repetitions naively, we optimize it using three approaches developed in [14] to obtain our main traceable OR sigma protocol \(\Pi _{\Sigma }^\textsf{tOR}\). Finally, we show a sigma protocol for the “tight” relation \(R_{\textsf{sig}}^\textsf{Tight}\) introduced in Sect. 4.3.
6.1 From a group-action-based HIG and PKE to base traceable OR sigma protocol
In this section, we present a base OR sigma protocol for the relation \(R_{\textsf{sig}}\) with a binary challenge space from which the main OR sigma protocol will be deduced.
Parameters and Binary Relation The sigma protocol is based on a group-action-based \(\textsf{HIG}\) and \(\textsf{PKE}\). Let \({{\textsf{p}}}{{\textsf{p}}}_1 = (G, {\mathcal {X}}, S_1, S_2, \delta _x, \star , X_0)\) and \({{\textsf{p}}}{{\textsf{p}}}_2 = ({\overline{G}}, {\overline{G}}_{\textsf{T}}, {\mathcal {Y}}, {\overline{S}}_1, {\overline{S}}_2, \delta _y, D_{\mathcal {Y}}, \star _{\textsf{M}}, {\mathcal {M}})\) be public parameters in the image of \(\textsf{RelSetup}\) and \(\mathsf {PKE.Setup}\), respectively. Moreover, let \(({{\textsf{p}}}{{\textsf{k}}}, {{\textsf{s}}}{{\textsf{k}}}) \in \textsf{KeyGen}({{\textsf{p}}}{{\textsf{p}}}_2)\). The relation \(R_{\textsf{sig}}\) in Sect. 4.1 can be equivalently rewritten as follows:

Recall that by definition of \(\textsf{GA}\text {-}\textsf{PKE}\) (Def. 5.2), the ciphertext \({{\textsf{c}}}{{\textsf{t}}}\) is restricted to the simple form \( I \star _{\textsf{M}}(r \star _{{\textsf{p}}}{{\textsf{k}}}Y_{{\textsf{p}}}{{\textsf{k}}}) \in {\mathcal {Y}}\), where \(r \in {\overline{S}}_1\subseteq {\overline{G}}\).
Sigma Protocol for \(R_{\textsf{sig}}\). We now sketch the base traceable OR sigma protocol \(\Pi _{\Sigma }^\textsf{base}\). A prover with witness \((I, s, r) \in [N] \times S_1 \times {\overline{S}}_1\) first samples  . Then, it computes commitments
. Then, it computes commitments
and builds a Merkle tree with \(({\textsf{C}}_1, \dots , {\textsf{C}}_N)\) as its leaves, obtaining \(\textsf{root}\). Here, notice \(r' \star _{{{\textsf{p}}}{{\textsf{k}}}} (-i \star _{\textsf{M}}{{\textsf{c}}}{{\textsf{t}}}) = r' \star _{{{\textsf{p}}}{{\textsf{k}}}} (-i+I) \star _{\textsf{M}}(r \star _{{{\textsf{p}}}{{\textsf{k}}}} Y_{{{\textsf{p}}}{{\textsf{k}}}})\) is simply \( (r' + r) \star _{{\textsf{p}}}{{\textsf{k}}}Y_{{\textsf{p}}}{{\textsf{k}}}\) when \(i= I\). Then, the prover sends \(\textsf{com}=\textsf{root}\) to the verifier as the commitment of the sigma protocol. The verifier, in turn, responds with a uniform challenge \(\textsf{chall}\in \{ 0,1 \} \).
If the challenge bit \(\textsf{chall}\) is 0, then the prover sends \((s',r')\) and the commitment randomness \(\{\textsf{bits}_i\}_{i\in [N]}\). That is, all the randomness it generated in the first round. The verifier then can reconstruct the Merkle tree and verify that the root of the obtained tree is equal to \(\textsf{root}\).
If the challenge bit \(\textsf{chall}\) is equal to 1, then the prover computes \(s'' = s'+s\), \(r'' = r'+r\). The prover aborts the protocol if \(s'' \not \in S_3\) or \(r'' \not \in {\overline{S}}_3\). The first event will occur with probability \((1-\delta _x)\) and, similarly, the second event will occur with probability \((1-\delta _y)\). Otherwise, the prover sends \((r'',s'')\) together with the path connecting \({\textsf{C}}_I\) to \(\textsf{root}\) in the Merkle tree, and the corresponding commitment randomness \(\textsf{bits}_I\) to the verifier. The verifier computes \({\widetilde{{\textsf{C}}}}_I={\mathcal {O}}(\textsf{Com}\parallel s'' \star X_0 \parallel r'' \star _{{\textsf{p}}}{{\textsf{k}}}Y_{{\textsf{p}}}{{\textsf{k}}}\parallel \textsf{bits}_I)\) and uses the received path to reconstruct \({\widetilde{\textsf{root}}}\) of the Merkle tree. The verifier checks whether \({\widetilde{\textsf{root}}}=\textsf{root}\).
To reduce the communication cost, a pseudorandom number generator (PRG) \(\textsf{Expand}\) can be run over a uniform seed \(\textsf{seed}\in \{0,1\}^{\uplambda }\) to produce the group elements \(s',r'\) and all commitment randomness values \(\textsf{bits}_1,\dots ,\textsf{bits}_N\) (part of the response for \(\textsf{chall}=0)\). As a consequence, if the challenge bit is 0, the prover responds with \(\textsf{seed}\) so that the verifier can generate \((s',r',\textsf{bits}_1,\cdots , \textsf{bits}_N )\) with the PRG \(\textsf{Expand}\). The response corresponding to the challenge bit \(\textsf{chall}=1\) remains unchanged. We instantiate the PRG by a random oracle \({\mathcal {O}}(\textsf{Expand}\parallel \cdot )\). Looking ahead, using a PRG not only provides efficiency, but it proves to be essential when proving multi-proof online extractability when compiled into a \(\textsf{NIZK}\). Roughly, the seed binds the cheating prover from using arbitrary \((s',r',\textsf{bits}_1,\cdots , \textsf{bits}_N )\) and the random oracle allows for efficient extraction. Finally, we instantiate the collision-resistant hash function \({\mathcal {H}}_{\textsf{Coll}}(\cdot )\) used in our Merkle tree by a random oracle \({\mathcal {O}}(\textsf{Coll}\parallel \cdot )\).
A formal description of \(\Pi _{\Sigma }^\textsf{base}\) is provided in Fig. 3
Construction of the base traceable OR sigma protocol \(\Pi _{\Sigma }^{\textsf{base}} = (P'=(P'_1,P'_2),V'=(V_1',V'_2))\) for the relation \(R_{\textsf{sig}}\). Informally, \(O(\textsf{Expand}\Vert \cdot )\) and \(O(\textsf{Com}\Vert \cdot )\) are a PRG and a commitment scheme instantiated by the random oracle, respectively
Security of Sigma Protocol \(\Pi _{\Sigma }^{\textsf{base}}\). The following Theorems 6.1 and 6.2 summarize the security of our sigma protocol. We point out that in Theorem 6.1, we show our sigma protocol satisfies special soundness for the relations \(R_{\textsf{sig}}\) and \({\tilde{R}}_{\textsf{sig}}'\) such that \(R_{\textsf{sig}}\subset {\tilde{R}}_{\textsf{sig}}'\), rather than for the relations \(R_{\textsf{sig}}\) and \({\tilde{R}}_{\textsf{sig}}\) such that \(R_{\textsf{sig}}\subseteq {\tilde{R}}_{\textsf{sig}}\), where \({\tilde{R}}_{\textsf{sig}}\) is the relaxed relation introduced in Sect. 4.1. The subtle difference is that \({\tilde{R}}_{\textsf{sig}}'\) captures the scenario where the extractor may extract a witness that forms a collision in the random oracle. This has no concrete impact as we are able to turn such a sigma protocol into a multi-proof online extractable \(\textsf{NIZK}\) for the relations \(R_{\textsf{sig}}\) and \({\tilde{R}}_{\textsf{sig}}\).
Theorem 6.1
The sigma protocol \(\Pi _{\Sigma }^{\textsf{base}}\) has correctness with abort rate \((1-\delta _x \delta _y)/2\) and relaxed special soundness for the relations \(R_{\textsf{sig}}\) and \({\tilde{R}}_{\textsf{sig}}'\), where

Here, \({\tilde{R}}_{\textsf{sig}}'\) is identical to the one defined in Sect. 4.1 if we ignore the hash collision \({\textsf{W}}=(x_1,x_2)\) and set \({\mathcal {R}}' = {\overline{S}}_2 + {\overline{S}}_3\) in the \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness of \(\textsf{GA}\text {-}\textsf{PKE}\).
Proof
Correctness. Say the prover honestly runs \(\Pi _{\Sigma }^{\textsf{base}}\) on an input (I, s, r) satisfying \(X_I =s \star X_0\) and \({{\textsf{c}}}{{\textsf{t}}}=\textsf{Enc}({{\textsf{p}}}{{\textsf{k}}},I;r) \), and does not abort. If \(\textsf{chall}=0\), then the verifier repeats the computation in the commitment phase (see Round 1 in Fig. 3) and therefore obtains the same output. If \(\textsf{chall}=1\), then the verifier computes \({\widetilde{T}}=s'' \star X_0\) and \({\widetilde{{{\textsf{c}}}{{\textsf{t}}}}}=r''\star _{{\textsf{p}}}{{\textsf{k}}}Y_{{\textsf{p}}}{{\textsf{k}}}\) where \(s''=s'+s\) and \(r''=r'+r\). Besides, since \({\widetilde{T}}\) is equal to \(T_I = s' \star X_I\), \({\widetilde{{{\textsf{c}}}{{\textsf{t}}}}}\) is equal to \({{\textsf{c}}}{{\textsf{t}}}_I = r' \star _{{\textsf{p}}}{{\textsf{k}}}(-I \star _{\textsf{M}}{{\textsf{c}}}{{\textsf{t}}})\) and \({\widetilde{{\textsf{C}}}}= {\mathcal {O}}(\textsf{Com}\parallel {\widetilde{T}}\parallel {\widetilde{{{\textsf{c}}}{{\textsf{t}}}}}\parallel \textsf{bits})\) is equal to the leaf \({\widetilde{{\textsf{C}}}}={\textsf{C}}_I \in \{{\textsf{C}}_1,\cdots ,{\textsf{C}}_N\}\), the verifier reconstructs the root \({\widetilde{\textsf{root}}}\) which is equal to \(\textsf{root}\). Hence, the protocol has (non-abort) correctness.
Abort rate. The prover will not abort in the case \(\textsf{chall}=0\). When \(\textsf{chall}=1\) (which occurs with probability 1/2) the prover aborts if \(s''=s'+s \notin S_3\) or \(r''=r'+r \notin {\overline{S}}_3\). We note that s is in \(S_1\) and \(s'\) is drawn uniformly at random from \(S_2\) (in the random oracle model). We can therefore say \(s''\) is drawn uniformly at random from \(S_2+s\), which contains \(S_3\) as a subset. So the probability that \(s''=s'+s \in S_3\) is \(|S_3 |/ |S_2 |=\delta _x\). The same reasoning applies to \(r''\), so the probability of both \(s'', r''\) lying in \(S_3,{\overline{S}}_3\) respectively is \(\delta _x \delta _y\) and the total abort rate is \((1-\delta _x \delta _y)/2\)
Relaxed special soundness. Given two valid transcripts for the same statement and on the same commitment, \((\textsf{com},0,\textsf{seed})\) and \((\textsf{com},1,(s'',r'',\textsf{path},\textsf{bits}))\) where \(\textsf{com}=\textsf{root}\), an extraction algorithm \({\textsf{Extract}}\) for a witness for the relation \({\widetilde{R}}'_{{\textsf{p}}}{{\textsf{k}}}\) proceeds as follows. \({\textsf{Extract}}\) firstly generates \((s',r',\textsf{bits}_1,\cdots ,\textsf{bits}_N) \leftarrow {\mathcal {O}}(\textsf{Expand}\parallel \textsf{seed})\) and constructs \({\textsf{C}}_1,\cdots ,{\textsf{C}}_N\) such that the Merkle Tree with leaves \(({\textsf{C}}_1,\cdots ,{\textsf{C}}_N)\) has root equal to \(\textsf{root}\). \({\textsf{Extract}}\) outputs \({\textsf{W}}= (\textsf{Coll}\parallel x_1, \textsf{Coll}\parallel x_2)\) as the witness if it there exists \(x_1 \ne x_2\) such that \({\mathcal {O}}(\textsf{Coll}\parallel x_1)= {\mathcal {O}}(\textsf{Coll}\parallel x_2)\). Otherwise, by Lem. A.1, we can assume \({\widetilde{{\textsf{C}}}}={\mathcal {O}}(\textsf{Com}\parallel s'' \star X_0 \parallel r'' \star _{{\textsf{p}}}{{\textsf{k}}}Y_{{\textsf{p}}}{{\textsf{k}}}\parallel \textsf{bits})\) is equal to \({\textsf{C}}_{{\widetilde{I}}} \in \{{\textsf{C}}_1,\cdots ,{\textsf{C}}_N\}\) for some \({\widetilde{I}}\in [N]\). Then, \({\textsf{Extract}}\) outputs \({\textsf{W}}= (\textsf{Com}\parallel x_1, \textsf{Com}\parallel x_2)\) as the witness if it there exists \(x_1 \ne x_2\) such that \({\mathcal {O}}(\textsf{Com}\parallel x_1)= {\mathcal {O}}(\textsf{Com}\parallel x_2)\). Otherwise, from \({\widetilde{{\textsf{C}}}}={\textsf{C}}_{{\widetilde{I}}}\), we can assume \(s' \star X_{{\widetilde{I}}}=s'' \star X_0\), \(r' \star _{{\textsf{p}}}{{\textsf{k}}}({\widetilde{I}}\star _{\textsf{M}}{{\textsf{c}}}{{\textsf{t}}})=r'' \star _{{\textsf{p}}}{{\textsf{k}}}Y_{{\textsf{p}}}{{\textsf{k}}}\), and \(\textsf{bits}=\textsf{bits}_{{\widetilde{I}}}\). Let \({\widetilde{s}}=-s'+s'' \in S_2 + S_3\) and \({\widetilde{r}}=-r'+r'' \in {\overline{S}}_2 + {\overline{S}}_3\). Finally, \({\textsf{Extract}}\) outputs \({\textsf{W}}=({\widetilde{I}}, {\widetilde{s}}, {\widetilde{r}})\). Here, the equalities \({\widetilde{s}}\star X_0=X_{{\widetilde{I}}}\) and \({\widetilde{I}}\star _{\textsf{M}}({\widetilde{r}}\star _{{\textsf{p}}}{{\textsf{k}}}Y_{{\textsf{p}}}{{\textsf{k}}})={{\textsf{c}}}{{\textsf{t}}}\) follow directly from the relations \(s' \star X_{{\widetilde{I}}}=s'' \star X_0\) and \(r' \star _{{\textsf{p}}}{{\textsf{k}}}({\widetilde{I}}\star _{\textsf{M}}{{\textsf{c}}}{{\textsf{t}}})=r'' \star _{{\textsf{p}}}{{\textsf{k}}}Y_{{\textsf{p}}}{{\textsf{k}}}\), respectively. Therefore, \({\textsf{W}}=({\widetilde{I}}, {\widetilde{s}}, {\widetilde{r}})\) is a witness for the “relaxed” relation \({\widetilde{R}}'_{{{\textsf{p}}}{{\textsf{k}}}}\). Hence, the protocol \(\Pi _{\Sigma }^{\textsf{base}}\) has relaxed special soundness. \(\square \)
Theorem 6.2
The sigma protocol \(\Pi _{\Sigma }^{\textsf{base}}\) has non-abort special zero-knowledge. Precisely, there exists a PPT simulator \(\textsf{Sim}^{\mathcal {O}}\) with access to a random oracle \({\mathcal {O}}\) such that, for any statement-witness pair \(({\textsf{X}}, {\textsf{W}}) \in R_{\textsf{sig}}\), \(\textsf{chall}\in \{ 0,1 \}\), and any computationally-unbounded adversary \({\mathcal {A}}\) that makes at most Q queries to the random oracle \({\mathcal {O}}\), we have
where \({\widetilde{P}}\) is a non-aborting prover \(P' = (P'_1, P'_2)\) run on \(({\textsf{X}}, {\textsf{W}})\) with a challenge fixed to \(\textsf{chall}\).
Proof
Assume the adversary makes \(Q_\textsf{Expand}\) and \(Q_{\textsf{Com}}\) queries to the random oracles of the form \({\mathcal {O}}(\textsf{Expand}\parallel \cdot )\) and \({\mathcal {O}}(\textsf{Com}\parallel \cdot )\), respectively. We have \(Q_\textsf{Expand}+Q_{\textsf{Com}} \le Q\). The PPT simulator \(\textsf{Sim}^{\mathcal {O}}\), on input \(({\textsf{X}}, \textsf{chall})\), proceeds as follows.
-
If \(\textsf{chall}= 0\), the simulator executes as \(P^{' {\mathcal {O}}}({\textsf{X}}, \bot ,\textsf{chall})\), where notice \(P'\) does not require the witness when \(\textsf{chall}= 0\). Concretely, the simulator outputs \((\textsf{com}=\textsf{root},\textsf{chall}=0,\textsf{resp}=\textsf{seed})\) where \(\textsf{root},\textsf{seed}\) are honestly generated as in the execution of \(P_1^{' {\mathcal {O}}}\).
-
If \(\textsf{chall}= 1\), the simulator uniformly samples \((s'',r'')\) from \(S_3 \times {\overline{S}}_3\), and \(\textsf{bits}\) from \(\{ 0,1 \}^{\uplambda }\). It computes \({\textsf{C}}_1 = {\mathcal {O}}(\textsf{Com}\parallel s'' \star X_0 \parallel r'' \star _{{\textsf{p}}}{{\textsf{k}}}Y_{{\textsf{p}}}{{\textsf{k}}}\parallel \textsf{bits})\). It then uniformly samples dummy commitments \({\textsf{C}}_i\) for \(i \in \{ 2, \ldots , N \}\) from \(\{ 0,1 \}^{2\uplambda }\), and computes the (index-hiding) Merkle tree \((\textsf{root}, \textsf{tree}) \leftarrow \textsf{MerkleTree}({\textsf{C}}_1, \ldots , {\textsf{C}}_N)\). After that, it extracts the path \(\textsf{path}\leftarrow \textsf{getMerklePath}(\textsf{tree}, 1)\) in the tree and sets \(\textsf{com}= \textsf{root}\), and \(\textsf{resp}= (s'',r'', \textsf{path}, \textsf{bits})\). Finally, the simulator returns \((\textsf{com}, \textsf{chall}=1, \textsf{resp})\).
In the first case, the whole transcript is generated exactly as in the protocol. Hence transcripts generated by \({\widetilde{P}}^{\mathcal {O}}\) and \(\textsf{Sim}^{\mathcal {O}}\) are indistinguishable to the adversary \({\mathcal {A}}\). Therefore, we have
To conclude the proof, it suffices to show that the difference between the probabilities that the adversary \({\mathcal {A}}\) outputs 1 for the other case, \(\textsf{chall}=1\), is also bounded by \(\frac{Q}{2^\uplambda }\).
We use a hybrid argument by introducing a series of simulators \(\textsf{Sim}_{0}={\widetilde{P}}, \ldots , \textsf{Sim}_{4}=\textsf{Sim}\), gradually changing from the honest prover \({\widetilde{P}}\) to \(\textsf{Sim}\), to show that they are indistinguishable with overwhelming probability. We fix an adversary \({\mathcal {A}}\), \(({\textsf{X}},{\textsf{W}}) \in R_{\textsf{sig}}\), and for each \(i \in \{0,1,\dots ,4\}\), we denote by \({\textsf{E}}_i\) the event that \({\mathcal {A}}^{\mathcal {O}}(1^\uplambda , \textsf{Sim}^{{\mathcal {O}}}_i({\textsf{X}}, \textsf{chall}=1)) = 1\).
-
\(\textsf{Sim}_{1}\) is identical to \(\textsf{Sim}_{0}\) except that instead of using \(\textsf{Expand}\) to generate \(s', r', \{\textsf{bits}_{i}\}_{i \in [N]}\), the simulator generates these by sampling uniformly at random from the corresponding domains. This does not change the view of \({\mathcal {A}}\), unless the adversary queries \({\mathcal {O}}\) on input \((\textsf{Expand}\parallel \textsf{seed})\). Since \(\textsf{seed}\) has \(\uplambda \) bits of min-entropy and because it is information-theoretically hidden from \({\mathcal {A}}\), the probability that \({\mathcal {A}}\) queries \({\mathcal {O}}\) on this input is bounded by \(Q_\textsf{Expand}/2^\uplambda \). That is, \(\left|\Pr [{\textsf{E}}_1] - \Pr [{\textsf{E}}_0] \right|\le \frac{Q_\textsf{Expand}}{2^\uplambda }\).
-
\(\textsf{Sim}_{2}\) is identical to \(\textsf{Sim}_{2}\) except that all the commitments \({\textsf{C}}_i\) for \(i \in [N] \setminus \{I\}\) are generated uniformly at random. This does not change the view of \({\mathcal {A}}\), unless the adversary queries \({\mathcal {O}}\) on input \((\textsf{Com}\parallel T_i \parallel {{\textsf{c}}}{{\textsf{t}}}_i \parallel \textsf{bits}_i)\) for any \(i\in [N] {\setminus } \{ I \}\), where \(T_i= s' \star X_i \) and \({{\textsf{c}}}{{\textsf{t}}}_i=r' \star _{{\textsf{p}}}{{\textsf{k}}}(-i \star _{\textsf{M}}{{\textsf{c}}}{{\textsf{t}}})\). Since for any \(i\in [N] \setminus \{ I \}\) the string \(\textsf{bits}_i\) has \(\uplambda \) bits of min-entropy and because it is information-theoretically hidden from \({\mathcal {A}}\), the probability that \({\mathcal {A}}\) queries \({\mathcal {O}}\) on input \((\textsf{Com}\parallel T_i \parallel {{\textsf{c}}}{{\textsf{t}}}_i \parallel \textsf{bits}_i)\) is bounded by \(Q_{\textsf{Com}}/2^\uplambda \). That is, \(|\Pr [{\textsf{E}}_2] - \Pr [{\textsf{E}}_1] |\le \frac{Q_{\textsf{Com}}}{2^\uplambda }\).
-
\(\textsf{Sim}_{3}\) is identical to \(\textsf{Sim}_{3}\) except that instead of computing \(s'',r''\) as \(s'+s,r'+r\) (conditioned on them respectively lying in \(S_3,{\overline{S}}_3\), due to non-aborting transcripts), the simulator generates these two values by sampling uniformly at random from \(S_3,{\overline{S}}_3\), respectively. Both the distributions are uniform over \(S_3\) and \({\overline{S}}_3\). Therefore, we have \(|\Pr [{\textsf{E}}_3] - \Pr [{\textsf{E}}_2] |= 0\).
-
\(\textsf{Sim}_{4} = \textsf{Sim}\) is identical to \(\textsf{Sim}_{4}\) except that the simulator uses \(I=1\) instead of the value I in the witness \({\textsf{W}}\). These two simulators are indistinguishable because the Merkle tree is index-hiding (by Lemma A.2). Precisely, we have \(|\Pr [{\textsf{E}}_4] - \Pr [{\textsf{E}}_3] |= 0\).
Collecting the bounds, we obtain the bound in the statement. \(\square \)
6.2 From base to main traceable OR sigma protocol
In this section, compile \(\Pi _{\Sigma }^\textsf{base}\) to make the soundness error negligibly small. This is straightforward if we run the OR sigma protocol in parallel \(\uplambda \)-times. However, we show how to do much better by incorporating the three optimizations developed in [14] explained in the technical overview. Our main traceable OR sigma protocol, denote by \(\Pi _{\Sigma }^\textsf{tOR}\), is detailed in Fig. 4.
Main traceable OR sigma protocol \(\Pi _{\Sigma }^{\textsf{tOR}} = (P=(P_1,P_2),V=(V_1,V_2))\) for the relation \(R_{\textsf{sig}}\) built on the the base traceable OR sigma protocol \(\Pi _{\Sigma }^{\textsf{base}} = (P'=(P'_1,P'_2),V'=(V'_1,V'_2))\) in Fig. 3. The challenge space is defined as \(C_{M, K}:= \{ {{\textbf {c}}}\in \{ 0,1 \} ^M \mid \Vert {{\textbf {c}}} \Vert _1 = K \}\). Both the seed tree and \(\Pi _{\Sigma }^{\textsf{base}}\) have access to salted random oracles derived from \({\mathcal {O}}\)
Unbalanced Challenge Space Given the construction \(\Pi _{\Sigma }^\textsf{base}\), one can observe that the response produced by the prover by running \(P'_2\) when the challenge is 1 is larger than the response produced when the challenge is 0, which is a single seed of \(\uplambda \) bits. Concretely, the response for the challenge \(\textsf{chall}=1\) consists of a Merkle tree path, two elements in \(S_3, {\overline{S}}_3\) respectively, and a \(\uplambda \) bit string. We leverage this fact by preparing an unbalanced challenge space \(C_{M,K}\), where each element in \(C_{M, K}\) is a string containing K 1’s and \(M-K\) 0’s. We chose \(K \ll M\) to chose more 0’s, while satisfying \(\left( {\begin{array}{c}M\\ K\end{array}}\right) \ge 2^{\uplambda }\) for negligible soundness error.
Seed Trees The seed tree described in Sect. A.2 allows the prover to generate all seeds \(\textsf{seed}\) by using a single seed \(\textsf{seed}_\textsf{root}\), and reveal parts of the tree according to the challenge. A smaller signature size follows directly from this approach.
Adding Salt We prefix a salt and the session identifier, i.e. \((\textsf{salt}\parallel i)\), to the random oracle when used within the i-th parallel execution of \(\Pi _{\Sigma }^\textsf{base}\). In particular, throughout such execution, \({\mathcal {O}}_i( \cdot )= {\mathcal {O}}(\textsf{salt}\parallel i \parallel \cdot )\) is used. The salt is used as a prefix also within the construction of Merkle trees and seed trees. Adding salt benefits the protocol in having a tighter reduction and resisting multi-target attacks, such as those in [41]. The approach appears to make no difference in a sigma protocol but it is quite beneficial for a group (ring) signature scheme after we apply the Fiat-Shamir transform. Roughly, in the anonymity game (Def. 3.17) each oracle \({\mathcal {O}}\) query made by the adversary will only give useful information to at most one challenge signature due to distinct prefix salts. In contrast, without salts an oracle query of \({\mathcal {O}}\) can give useful information to each challenge signature.
Theorem 6.3
The sigma protocol \(\Pi _{\Sigma }^{\textsf{tOR}}\) has correctness with abort rate \((1-\delta _x^K \delta _y^K)\), high min-entropy, and relaxed special soundness for the relations \(R_{\textsf{sig}}\) and \({\tilde{R}}_{\textsf{sig}}'\), where the relations are identical to those used in Theorem 6.1.
Proof
As a starting remark, we note that in the following lines we will use the notation of Fig. 4.
Correctness and abort rate. If the execution of \(\Pi _{\Sigma }^{\textsf{tOR}}\) does not abort, then the verifier will accept with probability 1 due to the correctness of \(\Pi _{\Sigma }^{\textsf{base}}\) and \(\textsf{SeedTree}\). We recall that in the case of challenge equal to 1 the execution of \(\Pi _{\Sigma }^{\textsf{base}}\) will abort with probability \((1-\delta _x \delta _y)\). Since the challenge \({{\textbf {c}}}\), sampled from \(C_{M,K}\), is of Hamming weight K, the abort rate of \(\Pi _{\Sigma }^{\textsf{tOR}}\) is \((1-\delta _x^K \delta _y^K)\).
High min-entropy. Since a random salt of length \(2\uplambda \) is included in the commitment \(\textsf{com}\), it has at least \(2\uplambda \) bits of min-entropy.
Relaxed special Soundness. The proof is similar to the one for the relaxed special soundness of \(\Pi _{\Sigma }^{\textsf{base}}\). Let \((\textsf{com}, \textsf{chall}={{\textbf {c}}}, \textsf{resp})\) \((\textsf{com}, \textsf{chall}'={{\textbf {c}}}', \textsf{resp}')\) be two accepting transcripts for the same statement. Without loss of generality, say \(c_j=0,c'_j=1\), i.e. the \(j^{th}\) components of \({{\textbf {c}}}\) and \({{\textbf {c}}}'\) are different. By computing \(\{ \textsf{resp}_i \}_{i \text { s.t. } c_i = 0} \leftarrow \textsf{RecoverLeaves}^{{\mathcal {O}}'}( {\textsf{seeds}_\textsf{internal}}, 1^{M} \oplus {{\textbf {c}}})\), the extraction algorithm gets \(\textsf{resp}_j\). In this way, two valid transcripts \((\textsf{com}_j,0,\textsf{resp}_j)\) and \((\textsf{com}_j,1,\textsf{resp}'_j)\) for \(\Pi _{\Sigma }^{\textsf{base}}\) have been obtained, and the extractor of \(\Pi _{\Sigma }^{\textsf{base}}\) in Theorem 6.1 can be invoked to extract the witness for the relation \({\tilde{R}}_{\textsf{sig}}\). To be concrete, in case a witness \({\textsf{W}}=(x_1,x_2)\) is extracted by the extractor of Theorem 6.1 such that it forms a collision in the random oracle \({\mathcal {O}}_j={\mathcal {O}}(\textsf{salt}\parallel j \parallel \cdot )\), then the extractor appends \(x_1\) and \(x_2\) by either \(\textsf{salt}\parallel j \parallel \textsf{Coll}\) or \(\textsf{salt}\parallel j \parallel \textsf{Com}\) to produce a collision in \({\mathcal {O}}\). \(\square \)
Theorem 6.4
The sigma protocol \(\Pi _{\Sigma }^{\textsf{tOR}}\) has non-abort special zero-knowledge. Precisely, there exists a PPT simulator \(\textsf{Sim}^{\mathcal {O}}\) with access to a random oracle \({\mathcal {O}}\) such that, for any statement-witness pair \(({\textsf{X}}, {\textsf{W}}) \in R_{\textsf{sig}}\), \(\textsf{chall}\in C_{M,K}\) and any computationally-unbounded adversary \({\mathcal {A}}\) that makes at most Q queries of the form \((\textsf{salt}\parallel \cdot )\) to the random oracle \({\mathcal {O}}\), where \(\textsf{salt}\) is the salt value included in the transcript returned by \({\widetilde{P}}\) or \(\textsf{Sim}\), we have
where \({\widetilde{P}}\) is a non-aborting prover \(P = (P_1, P_2)\) run on \(({\textsf{X}}, {\textsf{W}})\) with a challenge fixed to \(\textsf{chall}\).
Proof
The PPT simulator \(\textsf{Sim}^{\mathcal {O}}({\textsf{X}},\textsf{chall})\) for the main sigma protocol \(\Pi _{\Sigma }^{\textsf{tOR}}\) proceeds as in Fig. 5, where the simulator used for the base sigma protocol \(\Pi _{\Sigma }^{\textsf{base}}\) in Theorem 6.2, denoted by \(\textsf{Sim}'\) is a subroutine. Say the adversary makes \(Q_i\) queries to the random oracle of the form \({\mathcal {O}}( \textsf{salt}\parallel i \parallel \cdot )\) for \(i \in \{ 0 \}\cup [M]\). We have \(\Sigma ^M_0 Q_i \le Q\).
We use a hybrid argument by introducing a sequence of simulators \(\textsf{Sim}_0,\cdots ,\textsf{Sim}_2\) that gradually change from \(\textsf{Sim}_0={\widetilde{P}}\) to \(\textsf{Sim}_2=\textsf{Sim}\). We fix an adversary \({\mathcal {A}}\), \(({\textsf{X}},{\textsf{W}}) \in R_{\textsf{sig}}\), and for each \(i \in \{0,1,2\}\), we denote by \({\textsf{E}}_i\) the event \({\mathcal {A}}^{\mathcal {O}}(1^\uplambda , \textsf{Sim}_i^{{\mathcal {O}}}({\textsf{X}}, \textsf{chall})) = 1\).
-
\(\textsf{Sim}_{1}\) is identical to \(\textsf{Sim}_{0}\), except that, rather than using a \(\textsf{SeedTree}\) with root \(\textsf{seed}_\textsf{root}\) to generate \({\textsf{seeds}_\textsf{internal}}\) and \(\{ \textsf{seed}_i \}_{i \text { s.t. } c_i = 0}\), the simulator instead runs \(\textsf{SimulateSeeds}(1^M \oplus {{\textbf {c}}})\) to obtain \({\textsf{seeds}_\textsf{internal}}\), and then \(\{ \textsf{seed}_i \}_{i \text { s.t. } c_i = 0}\) via \(\textsf{RecoverLeaves}({\textsf{seeds}_\textsf{internal}},1^M \oplus {{\textbf {c}}})\). The simulator picks the remaining seeds (for the challenge components \(c_i\) equal to 1) \(\{ \textsf{seed}_i \}_{i \text { s.t. } c_i = 1}\) uniformly at random from \(\{ 0,1 \}^\uplambda \). Lemma A.3 for the bit string \(1^M \oplus {{\textbf {c}}}\) implies that the distributions of \({\textsf{seeds}_\textsf{internal}}\) and \(\{ \textsf{seed}_i \}_{i \text { s.t. } c_i = 1}\) generated in this way rather than as in the honest protocol can be distinguished with an advantage not greater than \(\frac{Q_0}{2^\uplambda }\). That is, \(|\Pr [{\textsf{E}}_1] - \Pr [{\textsf{E}}_0] |\le \frac{Q_0}{2^\uplambda }\).
-
\(\textsf{Sim}_{2}\) is identical to \(\textsf{Sim}_{1}\) except that the simulator uses the base simulator subroutine \(\textsf{Sim}'\) to compute, for each \(i \in [M]\) such that \(c_i=1\), \(\textsf{com}_i\) and \(\textsf{resp}_i\) on randomness \(\textsf{bits}_i\) by \(\textsf{seed}_i \overset{_{\tiny \$}}{\leftarrow } \{0,1\}^\uplambda \). By Theorem 6.2, the distinguishing advantage of the adversary is bounded by \(\frac{Q_i}{2^\uplambda }\) for each \(i \in [M]\) such that \(c_i=1\). That is, \(|\Pr [{\textsf{E}}_3] - \Pr [{\textsf{E}}_2] |\le \frac{\Sigma ^M_1 Q_i}{2^\uplambda }\).
Collecting the bounds, we obtain the bound in the statement. \(\square \)
6.3 Base sigma protocol for the “Tight” relation \(R_{\textsf{sig}}^\textsf{Tight}\)
In this section, we show how to slightly tweak our base sigma protocol for the relation \(R_{\textsf{sig}}\) to obtain a sigma protocol for the “tight” relation \(R_{\textsf{sig}}^\textsf{Tight}\) (see Sect. 4.3). This can then be used to construct the desired \(\textsf{NIZK}\) for \(R_{\textsf{sig}}^\textsf{Tight}\) required for our tightly secure accountable ring signature construction (see the full version of this paper).
As explained in the technical overview, we can use the sigma protocol for \(R_{\textsf{sig}}\) along with the sequential OR-proof [51] to construct a sigma protocol for the “tight” relation \(R_{\textsf{sig}}^\textsf{Tight}\). Unfortunately, this approach requires to double the proof size. Instead, we present a small tweak to our sigma protocol for \(R_{\textsf{sig}}\) to directly support statements in \(R_{\textsf{sig}}^\textsf{Tight}\). Concretely, we use the same Merkle tree to commit to the 2N instances \(\{X^{(j)}_i\}_{(i,j)\in [N]\times [2]}\) and for each \(X^{(1)}_i\) and \(X^{(2)}_i\), we encrypt the same index i. The main observation is that when the prover opens to the challenge bit 1 (which is the only case that depends on the witness), the path does no leak which \(X^{(1)}_i\) and \(X^{(2)}_i\) it opened to, and hence hides \(b \in [2]\).
Notice the only increase in the size of the response is due to the path. Since the accumulated commitment only grows from N to 2N, the overhead in the size of the path is merely \(2\uplambda \) bits. By using the unbalanced challenge space \(C_{M,K}\) for the optimized parallel repetition, which consists of M-bit strings of Hamming weight K, the additional cost is only \(2 K \uplambda \) where we typically set K to be a small constant (e.g., \(K \le 20\) for our concrete instantiation). This is much more efficient than the generic approach that doubles the proof size.
Formally, the sigma protocol for the “tight” relation \(R_{\textsf{sig}}^\textsf{Tight}\), denoted as \(\Pi _{\Sigma }^{\textsf{base}\textsf{Ti}}\), is provided in Fig. 6. We can turn it into a full-fledged sigma protocol with negligible soundness error by applying exactly the same argument in Sect. 6.1. We omit the proof of correctness and security for \(\Pi _{\Sigma }^{\textsf{base}\textsf{Ti}}\) as they are almost identical to those of our sigma protocol \(\Pi _{\Sigma }^\textsf{base}\) for \(R_{\textsf{sig}}\).
Construction of the base traceable OR sigma protocol \(\Pi _{\Sigma }^{\textsf{base}\textsf{Ti}} = (P'=(P'_1,P'_2),V'=(V_1',V'_2))\) for the “tight” relation \(R_{\textsf{sig}}^\textsf{Tight}\). The box indicates the difference between the “non-tight” relation \(R_{\textsf{sig}}\). Informally, \(O(\textsf{Expand}\parallel \cdot )\) and \(O(\textsf{Com}\parallel \cdot )\) are a PRG and a commitment scheme instantiated by the random oracle, respectively
7 Multi-proof online extractable NIZK from sigma protocol \(\Pi _{\Sigma }^\textsf{tOR}\)
In this section, we show that applying the Fiat-Shamir transform to our traceable OR sigma protocol \(\Pi _{\Sigma }^\textsf{tOR}\) from the previous section results in a multi-proof online extractable \(\textsf{NIZK}\) with labels \(\Pi _{\textsf{NIZK},\textsf{lbl}} \). The construction of our \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) for the relation \(R_{\textsf{sig}}\) is provide in Fig. 7.Footnote 9 We assume the output of \({\mathcal {O}}({{\textsf{F}}}{{\textsf{S}}}\parallel \cdot )\) is an M-bit string of Hamming weight K, i.e., the image is the challenge set \(C_{M,K}\).
A multi-proof online extractable \(\textsf{NIZK}\) with labels \(\Pi _{\textsf{NIZK},\textsf{lbl}}\) for the relation \(R_{\textsf{sig}}\) obtained by applying the Fiat-Shamir transform to the traceable OR sigma protocol \(\Pi _{\Sigma }^{\textsf{tOR}} = (P=(P_1,P_2),V=(V_1,V_2))\) in Fig. 4
Correctness of \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) for the relation \(R_{\textsf{sig}}\) follows directly from the correctness of the underlying traceable OR sigma protocol \(\Pi _{\Sigma }^\textsf{tOR}\). We show in Theorems. 7.1 and 7.4 that \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) is multi-proof online extractable and zero-knowledge. We highlight that while we show special soundness for \(\Pi _{\Sigma }^\textsf{tOR}\) with respect to the relaxed relation \({\tilde{R}}_{\textsf{sig}}'\) (see Theorem 6.1), \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) is multi-proof online extractable with respect to the relaxed relation \({\tilde{R}}_{\textsf{sig}}\) originally considered in Sect. 4.1 for the generic construction of accountable ring signature. At a high level, we upper bound the probability that a cheating prover finds a collision in the random oracle, which was the only difference between \({\tilde{R}}_{\textsf{sig}}\) and \({\tilde{R}}_{\textsf{sig}}'\). This subtle difference makes the resulting \(\textsf{NIZK}\) more handy to use as a building block, since we can ignore the edge case where the extractor accidentally extracts a collision in the random oracle. Below, we provide the proof of the multi-proof online extractability.
Theorem 7.1
The \(\textsf{NIZK}\) with labels \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) in Fig. 7 is multi-proof online extractable for the family of relations \(R_{\textsf{sig}}\) and \({\tilde{R}}_{\textsf{sig}}\) considered in Sect. 4.1, where \(R_{\textsf{sig}}\) was formally redefined using notations related to group actions in Sect. 6.1 and \({\tilde{R}}_{\textsf{sig}}\) is formally redefined as follows:

More precisely, for any (possibly computationally-unbounded) adversary \({\mathcal {A}}\) making at most Q queries to the random oracle and T queries to the extract oracle, we have
where \(C_{M, K}\) is the challenge space (or equivalently the output space of \({\mathcal {O}}({{\textsf{F}}}{{\textsf{S}}}\parallel ~cdot)\)).
Proof
We begin the proof by providing the description of the online extractor \(\textsf{OnlineExtract} \). Below, it is given as input \((\textsf{lbl}, {\textsf{X}}, \pi , L_{\mathcal {O}})\), where \(\pi \) is guaranteed to be valid by definition.
-
1.
It parses \((\{ X_i \}_{i \in [N]}, {{\textsf{p}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}) \leftarrow {\textsf{X}}\), \((\overline{\textsf{com}}, \overline{\textsf{chall}}, \overline{\textsf{resp}}) \leftarrow \pi \), \(((\textsf{salt}, \textsf{com}_1, \cdots , \textsf{com}_M), {{\textbf {c}}}= (c_1, \cdots , c_M)) \leftarrow (\overline{\textsf{com}}, \overline{\textsf{chall}})\), \( ({\textsf{seeds}_\textsf{internal}}, \{ \textsf{resp}_j \}_{j \text { s.t. } c_j = 1}) \leftarrow \overline{\textsf{resp}}\), and \(\textsf{root}_j \leftarrow \textsf{com}_j\) for \(j \in [M]\).Footnote 10
-
2.
For \(j \in [M]\) such that \(c_j = 1\), it proceeds as follows:
-
(a)
It parses \((s''_j, r''_j, \textsf{path}_j) \leftarrow \textsf{resp}_j\).
-
(b)
For every \(\big ( (\textsf{salt}\parallel j \parallel \textsf{Expand}\parallel \textsf{seed}), (s', r', \textsf{bits}_1, \cdots , \textsf{bits}_N) \big ) \in L_{\mathcal {O}}\), where \(\textsf{salt}\parallel j \parallel \textsf{Expand}\) is fixed, it proceeds as follows:
-
(i)
It sets \((s, r) = (s''_j - s', r''_j - r')\) and checks if \((s, r) \in (S_2 + S_3) \times ({\overline{S}}_2 + {\overline{S}}_3)\).
-
(ii)
It then checks if there exists \(I \in [N]\) such that \(X_I = s \star X_0\) and \({{\textsf{c}}}{{\textsf{t}}}= \textsf{Enc}({{\textsf{p}}}{{\textsf{k}}}, I; r)\).
-
(iii)
If all the check above passes, it returns \({\textsf{W}}= (I, s, r)\).
-
(i)
-
(a)
-
3.
If it finds no witness \({\textsf{W}}\) of the above form, then it returns \({\textsf{W}}= \bot \).
We analyze the probability of \({\mathcal {A}}\) winning the multi-proof online extractability game with the above online extractor \(\textsf{OnlineExtract}\). Below, \(P'\) and \(V'\) are the prover and verifier of the base traceable OR sigma protocol \(\Pi _{\Sigma }^{\textsf{base}}\) in Fig. 3.
-
We say a tuple \(\textsf{input}_\textsf{base} = ({\textsf{X}}, \textsf{salt}, j, \textsf{com}, \textsf{chall}, \textsf{resp})\) is \(\textsf{valid}\) if the following properties hold:
-
\(\textsf{chall}= 1\);
-
\(V'^{{\mathcal {O}}(\textsf{salt}\parallel j \parallel \cdot )}_2(\textsf{com}, \textsf{chall}, \textsf{resp})\) outputs \(\textsf{accept}\) (i.e., it is a valid transcript for \(\Pi _{\Sigma }^{\textsf{base}}\) with challenge 1);
-
there exists \((\textsf{seed}, s', r', \textsf{bits}_1, \cdots , \textsf{bits}_N)\) such that \(\big ( (\textsf{salt}\parallel j \parallel \textsf{Expand}\parallel \textsf{seed}), (s', r', \textsf{bits}_1, \cdots , \textsf{bits}_N) \big ) \in L_{\mathcal {O}}\), and if we execute \({P}'^{{\mathcal {O}}(\textsf{salt}\parallel j \parallel \cdot )}_1\) with randomness \(\textsf{seed}\), it produces \(\textsf{com}\). Here, we use the fact that \({P}'^{{\mathcal {O}}(\textsf{salt}\parallel j \parallel \cdot )}_1\) can be executed without the witness. By correctness of \(\Pi _{\Sigma }^{\textsf{base}}\), this implies that \((\textsf{com}, 0, \textsf{seed})\) is a valid transcript.
-
-
We say a tuple \(\textsf{input}_\textsf{base} = ({\textsf{X}}, \textsf{salt}, j, \textsf{com}, \textsf{chall}, \textsf{resp})\) is \(\textsf{invalid}\) if \(\textsf{chall}= 1\), \(V'^{{\mathcal {O}}(\textsf{salt}\parallel j \parallel \cdot )}_2(\textsf{com}, \textsf{chall}, \textsf{resp})\) outputs \(\textsf{accept}\), but it is not \(\textsf{valid}\).
Observe that if \(\textsf{input}_\textsf{base}\) is \(\textsf{valid}\), then the online extractor can recover a valid transcript \((\textsf{com}, 0, \textsf{seed})\) from \(\textsf{input}_\textsf{base} \). Then, it can (informally) extract a witness by combining it with \((\textsf{com}, 1, \textsf{resp})\) and using the extractor from \(\Pi _{\Sigma }^{\textsf{base}}\) constructed in Theorem 6.1. In contrast, if \(\textsf{input}_\textsf{base}\) is \(\textsf{invalid}\), then intuitively, no adversary would be able to prepare a valid response \(\textsf{resp}= \textsf{seed}\) for the challenge \(\textsf{chall}= 0\) since \(L_{\mathcal {O}}\) (i.e., the random oracle query the adversary makes) does not contain a valid response. However, to make this claim formal, we need to also take into account the fact that the adversary may learn non-trivial information about \(\textsf{resp}= \textsf{seed}\) via the proof output by the prove query. That is, when the challenger runs \({P}^{\mathcal {O}}\), the adversary may learn non-trivial input/output pairs without directly querying the random oracle itself. In this case, even though no useful information is stored in \(L_{\mathcal {O}}\), the adversary may still be able to forge a proof.
We formally show in Lem. 7.2 below that if an adversary \({\mathcal {A}}\) submits an extract query on a valid input \((\textsf{lbl}, {\textsf{X}}, \pi )\), then a \(\textsf{valid}\) \(\textsf{input}_\textsf{base}\) must be included in \(\pi \) (i.e., it cannot consist of \(\textsf{input}_\textsf{base}\) that are all \(\textsf{invalid}\)). This allows us to argue that the online extractor will be able to recover two valid transcripts with overwhelming probability, which then further allows the online extractor to extract the witness by running the extractor for the special soundness of the base traceable OR sigma protocol \(\Pi _{\Sigma }^{\textsf{base}}\).
Lemma 7.2
Assume an adversary \({\mathcal {A}}\) submits a total of T extract queries of the form \(\{(\textsf{lbl} _k, {\textsf{X}}_k, \pi _k)\}_{k \in [T]}\), where every \(\pi _k\) is a valid proof including the same \(\textsf{salt}\) and satisfies \((\textsf{lbl} _k, {\textsf{X}}_k, \pi _k) \not \in L_{P}\). Let \(\{ (\textsf{com}_{k, j}, \textsf{chall}_{k, j}, \textsf{resp}_{k, j}) \}_{j \in [M]}\) be the transcript of the base traceable OR sigma protocol \(\Pi _{\Sigma }^{\textsf{base}}\) that the verification algorithm reconstructs when verifying \(\pi _k\) (see Line 7 of Verification \(V^{\mathcal {O}}_2\) in Fig. 4). Then, with probability at least \(1 - T \cdot \big ( Q_{\textsf{salt}}/2^{2\uplambda -1} + (M \cdot Q_{\textsf{salt}}) / 2^\uplambda + 1/|C_{M, K} | \big )\), for all \(k \in T\) there exists at least one \(j \in [M]\) such that \(\textsf{input}_\textsf{base} = ({\textsf{X}}_k, \textsf{salt}, j, \textsf{com}_{k, j}, \textsf{chall}_{k, j} = 1, \textsf{resp}_{k, j})\) is \(\textsf{valid}\).
Proof
For any \(k \in [T]\), let us redefine \(\pi _k = (\overline{\textsf{com}}, \overline{\textsf{chall}}, \overline{\textsf{resp}})\), \( (\overline{\textsf{com}}, \overline{\textsf{chall}}) = ((\textsf{salt}, \textsf{com}_1, \cdots , \textsf{com}_M), {{\textbf {c}}}= (c_1, \cdots , c_M))\) where \({{\textbf {c}}}= {\mathcal {O}}({{\textsf{F}}}{{\textsf{S}}}\parallel \textsf{lbl} \parallel {\textsf{X}}\parallel \overline{\textsf{com}})\), \(\overline{\textsf{resp}}= ({\textsf{seeds}_\textsf{internal}}, \{ \textsf{resp}_j \}_{j \text { s.t. } c_j = 1})\). Namely, we omit the subscript k for better readability. We consider two cases: (1) there exists \((\textsf{lbl}, {\textsf{X}}, \pi ') \in L_{P}\) such that \(\pi ' = (\overline{\textsf{com}}, \overline{\textsf{chall}}, \overline{\textsf{resp}}')\) and \(\overline{\textsf{resp}}' \ne \overline{\textsf{resp}}\) and (2) no such entry in \(L_{P}\) exists.
We consider the first case (1). This corresponds to the case where \({\mathcal {A}}\) reuses the proof \(\pi '\) obtained through the prove query by simply modifying the response. We claim that this cannot happen with overwhelming probability. Let \(\overline{\textsf{resp}}' = (\textsf{seed}'_{\textsf{internal}}, \{ \textsf{resp}'_j \}_{j \text { s.t. } c_j = 1})\). It is clear if \(\textsf{seed}'_{\textsf{internal}}\) is different from \({\textsf{seeds}_\textsf{internal}}\), then \({\mathcal {A}}\) finds a collision in the random oracle. Since we use a seed tree to generate the randomness used in each base sigma protocol, we can very loosely upper bound the probability of \({\mathcal {A}}\) outputting such transcript for any \(k \in [T]\) by \( Q_{\textsf{salt}}/2^{2\uplambda }\). Similarly, consider \(\textsf{resp}'_j \ne \textsf{resp}_j\) for some j such that \(c_j = 1\). Then, it either finds a collision in \({\mathcal {O}}(\textsf{Coll}\parallel \cdot )\) (used by the Merkle tree) or \({\mathcal {O}}(\textsf{Com}\parallel \cdot )\). We can again very loosely upper bound the probability of \({\mathcal {A}}\) outputting such transcript for any \(k \in [T]\) by \( Q_{\textsf{salt}}/2^{2\uplambda }\). Thus, case (1) occurs with probability at most \( Q_{\textsf{salt}}/2^{2\uplambda -1}\).
We next consider the second case (2). If \(\overline{\textsf{com}}\) included in \(\pi \) is the same as \(\pi '\), then \(\overline{\textsf{chall}}\) is the same challenge included in \(\pi \) since the challenge is generated as \({\mathcal {O}}({{\textsf{F}}}{{\textsf{S}}}\parallel \textsf{lbl} \parallel {\textsf{X}}\parallel \overline{\textsf{com}})\). However, this results in a tuple that falls in the first case (1). Therefore, there exists no \(\pi '\) in \(L_{P}\) that contains the same \(\overline{\textsf{com}}\) as \(\pi \). This, in particular, implies that the output \(\overline{\textsf{chall}}\leftarrow {\mathcal {O}}({{\textsf{F}}}{{\textsf{S}}}\parallel \textsf{lbl} \parallel {\textsf{X}}\parallel \overline{\textsf{com}})\) is distributed uniform random from the view of \({\mathcal {A}}\) before it makes the hash query.
Now, for the sake of contradiction, we assume \(\textsf{input}_{\textsf{base}, {j}} = ( {\textsf{X}}, \textsf{salt}, j, \textsf{com}_j, c_j, \textsf{resp}_j)\) is \(\textsf{invalid}\) for all \(j \in [M]\) such that \(c_j = 1\). Let \(L_{{\mathcal {O}}_{P}}\) be a list that contains all the inputs/outputs of the random oracle queries \(\textsf{Prove}^{\mathcal {O}}\) makes when the challenger answers the prove query made by \({\mathcal {A}}\). We prove the following corollary.
Corollary 7.3
For any \(j^* \in [M]\), if \(\textsf{input}_{\textsf{base}, {j^*}} \) is \(\textsf{invalid}\), then either of the following holds:
-
there exists no tuple \((s', r', \textsf{bits}_1, \cdots , \textsf{bits}_N, \textsf{seed})\) and \(j' \in [M]\) such that \(\big ( (\textsf{salt}\parallel j' \parallel \textsf{Expand}\parallel \textsf{seed}), (s', r',\textsf{bits}_1, \cdots , \textsf{bits}_N) \big ) \in L_{{\mathcal {O}}_{P}}\), but if we execute \({P}'^{{\mathcal {O}}(\textsf{salt}\parallel j' \parallel \cdot )}_1\) with randomness \(\textsf{seed}\), it produces \(\textsf{com}_{j^*}\);
-
there exists such a tuple but \(\textsf{seed}\) retains \(\uplambda \)-bits of min-entropy from the view of \({\mathcal {A}}\) except with probability at most \((MQ_{\textsf{salt}})/ 2^\uplambda \).
Proof
Assume such an entry is found in \(L_{{\mathcal {O}}_{P}}\). This corresponds to the case \({\mathcal {A}}\) is reusing \(\textsf{com}_{j^*}\) that was included in a proof \(\pi \) obtained through the prove query. Let \(\{ (\textsf{com}'_j, c'_j, \textsf{resp}'_j) \}_{j \in [M]}\) be the transcript of the base traceable OR sigma protocol \(\Pi _{\Sigma }^{\textsf{base}}\) that the verification algorithm reconstructs from such \(\pi \) (see Line 7 of Verification \(V^{\mathcal {O}}_2\) in Fig. 4), where \(\textsf{com}'_{j'} = \textsf{com}_{j^*}\). Our current goal is to prove that \(c'_{j'} = 1\) (i.e., \(\textsf{seed}\) was not used as a response). Since \(\textsf{com}'_{j'}\) and \(\textsf{com}_{j^*}\) are roots of a Merkle tree and the indices \(j'\) and \(j^*\) are used as prefix to the hash when constructing the roots, respectively, the probability of \({\mathcal {A}}\) outputting \(\textsf{com}_{j^*}\) such that \(j' \ne j^*\) is upper bounded by \(((M-1)Q_{\textsf{salt}})/2^\uplambda \). Below, we assume \(j' = j^*\). Recall by definition of the online extractability game (see Def. 3.10), \({\mathcal {A}}\) runs the verification algorithm to check if \(\pi \) is valid. Therefore, if \(\textsf{input}_{\textsf{base}, {j^*}} \) is \(\textsf{invalid}\), then we have \(c'_{j'} = 1\). Otherwise, there must exist an entry \(\big ( (\textsf{salt}\parallel j^* \parallel \textsf{Expand}\parallel \textsf{seed}), (s', r', \textsf{bits}_1, \cdots , \textsf{bits}_N) \big ) \in L_{{\mathcal {O}}}\), which contradicts that \(\textsf{input}_{\textsf{base}, {j^*}} \) is \(\textsf{invalid}\). This further implies that \(\textsf{resp}'_{j'}\) does not include \(\textsf{seed}\). Then, by Lem. A.3 regarding the seed tree, \(\textsf{seed}\) that was used to construct \(\textsf{com}_{j'} = \textsf{com}_{j^*}\) is statistically hidden to the adversary with all but probability \(Q_{\textsf{salt}}/ 2^\uplambda \). The proof is completed by collecting all the bounds. \(\square \)
By Lem. 7.3, if \(\textsf{input}_{\textsf{base}, {j}} \) is \(\textsf{invalid}\), then \({\mathcal {A}}\) cannot prepare a valid response for the challenge \(c_j = 0\) with all but probability at most \((MQ_{\textsf{salt}})/2^{\uplambda }\). This is because such response is either not recorded in both \(L_{{\mathcal {O}}}\) and \(L_{{\mathcal {O}}_{P}}\), or it is recorded in \(L_{{\mathcal {O}}_{P}}\) but the \(\textsf{seed}\) retains \(\uplambda \)-bits of min-entropy from the view of \({\mathcal {A}}\) except with probability \((MQ_{\textsf{salt}})/2^\uplambda \). Moreover, since \(\overline{\textsf{chall}}\) is statistically hidden to \({\mathcal {A}}\) before it queries the random oracle, the probability that \(\overline{\textsf{chall}}\) coincides with challenges for which \({\mathcal {A}}\) can open to is at most \(1 - 1/|C_{M, K}|\), where recall \(C_{M, K}\) is the challenge space (or equivalently the output space of \({\mathcal {O}}({{\textsf{F}}}{{\textsf{S}}}\parallel \cdot )\)).
Taking the union bound and collecting all the bounds together, at least one of the \(\textsf{input}_\textsf{base} \) must be \(\textsf{valid} \) with the probability stated in the statement. This completes the proof of the lemma. \(\square \)
We are now prepared to analyze the probability that \({\mathcal {A}}\) wins the multi-proof online extractability game with the aforementioned online extractor \(\textsf{OnlineExtract}\). By Lem. 7.2, if \({\mathcal {A}}\) makes at most T extract queries, then by a simple union bound and using the inequality \(\sum _{i}Q_{\textsf{salt}_i} \le Q\), with probability at least \(1 - T \cdot \big ( (2 Q)/2^{2\uplambda } + (M \cdot Q) / 2^\uplambda + 1/|C_{M, K} | \big )\), all the \(\textsf{input}_\textsf{base} \) included in the queried proof are \(\textsf{valid}\). Then, by the definition of \(\textsf{valid} \) and the description of \(\textsf{OnlineExtract}\), \(\textsf{OnlineExtract}\) is able to extract two valid transcripts for all T proofs queried by \({\mathcal {A}}\). Recalling Thms. 6.1 and 6.3, \(\textsf{OnlineExtract}\) either succeeds in extracting a witness \({\textsf{W}}= (I, s, r) \in [N] \times (S_2 + S_3) \times ({\overline{S}}_2 + {\overline{S}}_3)\) or a witness that consists of a collision in \({\mathcal {O}}(\textsf{salt}\parallel j \parallel \textsf{Coll}\parallel \cdot )\) or \({\mathcal {O}}(\textsf{salt}\parallel j \parallel \textsf{Com}\parallel \cdot )\) for some \(j \in [M]\). Hence, with all but probability \(Q^2/2^{2\uplambda }\), \(\textsf{OnlineExtract}\) succeeds in extracting a witness \({\textsf{W}}= (I, s, r)\) as desired, conditioned on all the \(\textsf{input}_\textsf{base} \) included in the queried proof are \(\textsf{valid}\). Collecting the bounds, we arrive at our statement. \(\square \)
Theorem 7.4
The \(\textsf{NIZK}\) with labels \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) in Fig. 7 is zero-knowledge. Precisely, there exists a PPT simulator \(\textsf{Sim}= (\textsf{Sim}_0, \textsf{Sim}_1)\) such that, for any statement-witness pair \(({\textsf{X}}, {\textsf{W}}) \in R_{\textsf{sig}}\) and any computationally-unbounded adversary \({\mathcal {A}}\) that makes at most \(Q_1\) queries to \({\mathcal {O}}\) or \(\textsf{Sim}_0\), and \(Q_2\) queries to \(\textsf{Prove}\) or \({\mathcal {S}}\), we have
Proof
To prove the zero-knowledge property of \(\Pi _{\textsf{NIZK},\textsf{lbl}} = (\textsf{Prove}^{\mathcal {O}},\textsf{Verify}^{\mathcal {O}})\), we define a zero-knowledge simulator \(\textsf{Sim}= (\textsf{Sim}_0,\textsf{Sim}_1)\) in Fig. 8, where \(\textsf{Sim}_0\) and \(\textsf{Sim}_1\) share states, including a list L which is initially empty. At a high level, \(\textsf{Sim}_0\) simulates the random oracle \({\mathcal {O}}\) in an on-the-fly manner but replaces certain queries for consistency with \(\textsf{Sim}_1\). On the other hand, \(\textsf{Sim}_1\) simulates the prover oracle using the simulator from the underlying sigma protocol, which we denote here by \(\textsf{Sim}_\Sigma \) (see Theorem 6.4), as a subroutine. Specifically, \(\textsf{Sim}_1\) is given a valid statement \({\textsf{X}}= (\{X_i \}_{i\in [N]}, {{\textsf{p}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}})\), and samples a random challenge \(\textsf{chall}\) from the challenge space \(C_{M,K}\), which is also the output space of \({\mathcal {O}}({{\textsf{F}}}{{\textsf{S}}}\parallel \cdot )\). It then runs \(\textsf{Sim}_\Sigma \) on challenge \(\textsf{chall}\) by providing it oracle access to \(\textsf{Sim}_0\), and updates the list L accordingly. In Fig. 8, we denote by \(D_x\) the distribution of \({\mathcal {O}}(x)\), where the probability is taken over the random choice of the random oracle \({\mathcal {O}}\). Without loss of generality, we assume \(D_x\) to be efficiently sampleable.
To show the indistinguishability of \(({\mathcal {O}},\textsf{Prove})\) and \((\textsf{Sim}_0,{\mathcal {S}})\), we use a hybrid argument by introducing an intermediate pair of simulators \((\textsf{Sim}_0,\textsf{Sim}_\textsf{int})\), where \(\textsf{Sim}_\textsf{int}\) is defined in Fig. 9. Let \({\mathcal {S}}_\textsf{int}\), analog to \(\textsf{Prove}\) and \({\mathcal {S}}\), be an oracle that on input \((\textsf{lbl}, {\textsf{X}},{\textsf{W}})\) returns \(\bot \) if \(\textsf{lbl} \not \in {\textsf{L}} \vee ({\textsf{X}},{\textsf{W}}) \not \in R_{\textsf{sig}}\) and otherwise returns \(\textsf{Sim}_\textsf{int}(\textsf{lbl}, {\textsf{X}},{\textsf{W}})\).
Intermediate simulator \(\textsf{Sim}_\textsf{int}\), where \(P=(P_1,P_2)\) is the prover of the traceable OR sigma protocol \(\Pi _{\Sigma }^{\textsf{tOR}}\) in Fig. 4
Suppose \({\mathcal {A}}\) makes \(Q_1\) queries to the oracles \({\mathcal {O}}\) or \(\textsf{Sim}_0\), and \(Q_2\) queries to the oracles \(\textsf{Prove}, {\mathcal {S}}_\textsf{int}\), or \({\mathcal {S}}\). For each \(i\in \{ 1,2,3 \}\), we denote by \({\textsf{E}}_i\) the event that \({\mathcal {A}}\) returns 1 respectively. We analyze the differences by defining three games as follows:
- \(\textsf{Game}_1:\):
-
This is the real zero-knowledge game where \({\mathcal {A}}\) is given access to \({\mathcal {O}}\) and \(\textsf{Prove}\).
- \(\textsf{Game}_2:\):
-
The game is modified to provide \({\mathcal {A}}\) access to \(\textsf{Sim}_0\) and \({\mathcal {S}}_\textsf{int}\) instead. The view of \({\mathcal {A}}\) is identical to the previous game unless \(\textsf{Sim}_\textsf{int}\) outputs \(\bot \) in Line 4. Roughly, this occurs when the reprogramming of the random oracle fails due to the input being already defined. By Theorem 6.3, \(\textsf{com}\) has \(2\uplambda \) bits of min-entropy. Since at most \(Q_1 + Q_2\) queries of the form \(({{\textsf{F}}}{{\textsf{S}}}\parallel \textsf{lbl} \parallel {\textsf{X}}\parallel \textsf{com})\) are made in this game, we have \(|\Pr [E_1] - \Pr [E_2] |\le \frac{Q_2\cdot (Q_1+Q_2)}{2^{2\uplambda }}\).
- \(\textsf{Game}_3:\):
-
The game is modified to provide \({\mathcal {A}}\) access to \(\textsf{Sim}_0\) and \({\mathcal {S}}\) instead. The only difference is that rather than computing honestly via \((P_1, P_2)\) from the traceable OR sigma protocol \(\Pi _{\Sigma }^{\textsf{tOR}}\), the simulator \(\textsf{Sim}_1\) simulates these using the simulator \(\textsf{Sim}_\Sigma \) provided by \(\Pi _{\Sigma }^{\textsf{tOR}}\). Let \(\textsf{salt}_i\) represent the salt that \(\textsf{Sim}_\textsf{int}\) or \(\textsf{Sim}_1\) samples on its i-th invocation. For \(i \in [Q_2]\), let \(Q'_i\) be the number of queries the adversary makes to oracle \(\textsf{Sim}_0\) of the form \((\textsf{salt}_i \parallel \cdot )\). By Theorem 6.4, the advantage of the adversary in distinguishing \(\textsf{Sim}_\textsf{int}\) or \(\textsf{Sim}_1\) is bounded by \(\frac{Q'_i}{2^\uplambda }\) for each \(i\in [Q_2]\). Therefore, \(|\Pr [E_2] - \Pr [E_3] |\le \frac{\sum ^{Q_2}_1 Q'_i }{2^\uplambda } \le \frac{Q_1}{2^{\uplambda }}\)
Collecting the bounds, we obtain the bound in the statement. \(\square \)
8 Instantiations
We instantiate the building blocks required for our generic construction of an accountable ring signature scheme presented in Sect. 4 via isogenies based on CSIDH group action and lattices.
8.1 Instantiation from isogenies
We instantiate a group-action-based \(\textsf{HIG}\) and \(\textsf{PKE}\), and the corresponding \(\textsf{NIZK}\) s for the relations \(R_{\textsf{sig}}\) and \(R_{\textsf{open}}\) based on the CSIDH paradigm. In particular we assume that the structure of the ideal class group \(\mathcal {C}\ell (\mathcal {O})\) is known, and cyclic of odd order n, so that it is isomorphic to \({\mathbb {Z}}_n\). Given a generator \({\mathfrak {g}}\) of \(\mathcal {C}\ell (\mathcal {O})\), \({\mathbb {Z}}_n\) acts freely and transitively on \(\mathcal {E}\ell \ell {p}({\mathcal {O}},\pi )\) via the group action \(\star : (a,E) \mapsto {\mathfrak {g}}^a *E\), which we can compute efficiently. Note that in case the class group structure is not known (e.g., at higher security levels where computing the class group is currently not feasible.) we can still instantiate all the building blocks using rejection sampling à la SeaSign.
Group-Action-Based \(\textsf{HIG}\). We instantiate the group-action-based \(\textsf{HIG}\) defined by the algorithms \((\textsf{RelSetup},\textsf{IGen})\) as follows. The output of \(\textsf{RelSetup}\) describes a setup for a CSIDH group action \(\star : \mathcal {C}\ell (\mathcal {O})\times \mathcal {E}\ell \ell {p}({\mathcal {O}},\pi )\rightarrow \mathcal {E}\ell \ell {p}({\mathcal {O}},\pi )\), sets \(G = S_1 = S_2 = \mathcal {C}\ell (\mathcal {O})\), \(\delta = 1\), \({\mathcal {X}}= \mathcal {E}\ell \ell {p}({\mathcal {O}},\pi )\), and \(X_0 = E_0\), where \(E_0\) is the elliptic curve \(E_0:y^2=x^3+x\) over \({\mathbb {F}}_{p}\). The output of \(\textsf{IGen}\) is then \((E_0, {\mathfrak {a}} \star E_0)\), where \({\mathfrak {a}}\) is uniformly sampled from \(\mathcal {C}\ell (\mathcal {O})\). Then the properties of Def. 5.1 are easily verified. In particular, the security of the hard instance generator is equivalent to the hardness of \(\textsf{GAIP}\) for CSIDH. Moreover, it is not difficult to see that the group-action-based \(\textsf{HIG}\) is also a hard multi-instance generator based on the same assumption. Concretely, given one instance \((E_0, E)\), the reduction can rerandomize this arbitrarily many times to obtain fresh statements \((E_0, {\mathfrak {b}} \star E)\), where \({\mathfrak {b}}\) is uniformly sampled from \(\mathcal {C}\ell (\mathcal {O})\). If an adversary succeeds in breaking any of these instances, then the reduction can subtract \({\mathfrak {b}}\) from it to solve its original instance.
Group-Action-Based \(\textsf{PKE}\). We can define an ElGamal-like public-key encryption scheme \(\Pi _\textsf{GA}\text {-}\textsf{PKE}= (\textsf{Setup}, \textsf{KeyGen}, \textsf{Enc}, \textsf{Dec})\) based on the CSIDH group action, as follows. Note that the decryption algorithm works by enumerating the message space, so the \(\textsf{PKE}\) is only efficient when the message space \({\mathcal {M}}\) (which is a subset of \(\mathcal {C}\ell (\mathcal {O})\)) is polynomially large. This relaxed notion of decryption suffices for our \(\textsf{ARS}\) generic construction.
- \(\textsf{Setup}(1^\uplambda ) \rightarrow {{\textsf{p}}}{{\textsf{p}}}\)::
-
On input a security parameter \(1^\uplambda \), it returns the setup for a CSIDH group action \(\star : \mathcal {C}\ell (\mathcal {O})\times \mathcal {E}\ell \ell {p}({\mathcal {O}},\pi )\rightarrow \mathcal {E}\ell \ell {p}({\mathcal {O}},\pi )\), and sets \(G = G_M = S_1 = S_2 =\mathcal {C}\ell (\mathcal {O}), {\mathcal {Y}}=\mathcal {E}\ell \ell {p}({\mathcal {O}},\pi )\times \mathcal {E}\ell \ell {p}({\mathcal {O}},\pi ), \delta _y=1\). The “message” group action \(\star _{\textsf{M}}: G \times {\mathcal {Y}}\rightarrow {\mathcal {Y}}\) is defined as \((a,(E_1,E_2)) \mapsto (E_1, a \star E_2)\) (i.e., \(\star _{\textsf{M}}\) acts on the second component only).
- \(\textsf{KeyGen}({{\textsf{p}}}{{\textsf{p}}}) \rightarrow ({{\textsf{p}}}{{\textsf{k}}}, {{\textsf{s}}}{{\textsf{k}}})\)::
-
On input a public parameter \({{\textsf{p}}}{{\textsf{p}}}\), it returns a secret key \({{\textsf{s}}}{{\textsf{k}}}\) sampled uniformly from \(\mathcal {C}\ell (\mathcal {O})\), and a public key \({{\textsf{p}}}{{\textsf{k}}}=(\star _{{\textsf{p}}}{{\textsf{k}}}, Y_{{\textsf{p}}}{{\textsf{k}}})\), where \(\star _{{\textsf{p}}}{{\textsf{k}}}: G \times {\mathcal {Y}}\rightarrow {\mathcal {Y}}\) is defined as \((a,(E_1,E_2)) \mapsto (a \star E_1, a \star E_2)\) (i.e., \(\star _{{\textsf{p}}}{{\textsf{k}}}\) acts on both components), and \(Y_{{\textsf{p}}}{{\textsf{k}}}=(E_0, {{\textsf{s}}}{{\textsf{k}}}\star E_0)\).
- \(\textsf{Enc}({{\textsf{p}}}{{\textsf{k}}}, {\textsf{M}}; r) \rightarrow {{\textsf{c}}}{{\textsf{t}}}\)::
-
On input a public key \({{\textsf{p}}}{{\textsf{k}}}= (\star _{{\textsf{p}}}{{\textsf{k}}}, Y_{{\textsf{p}}}{{\textsf{k}}})\) and a message \({\textsf{M}}\in {\mathcal {M}}\), it returns the ciphertext \({{\textsf{c}}}{{\textsf{t}}}= ({\textsf{M}}\star _{\textsf{M}}(r \star _{{\textsf{p}}}{{\textsf{k}}}Y_{{\textsf{p}}}{{\textsf{k}}})) \in {\mathcal {Y}}\), where \(r \leftarrow G\).
- \(\textsf{Dec}({{\textsf{s}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}) \rightarrow {\textsf{M}}\)::
-
On input a secret key \({{\textsf{s}}}{{\textsf{k}}}\) and a ciphertext \({{\textsf{c}}}{{\textsf{t}}}=({{\textsf{c}}}{{\textsf{t}}}_1,{{\textsf{c}}}{{\textsf{t}}}_2)\), the decryption algorithm tries all messages \({\textsf{M}}\in {\mathcal {M}}\) until it finds a message \({\textsf{M}}\) such that \({\textsf{M}}\star {{\textsf{c}}}{{\textsf{t}}}_1=-{{\textsf{s}}}{{\textsf{k}}}\star {{\textsf{c}}}{{\textsf{t}}}_2\). If such a message exists, it is unique, and the algorithm outputs it; otherwise, \(\bot \) is output.
It is not difficult to verify that the above-defined \(\Pi _\textsf{GA}\text {-}\textsf{PKE}\) is correct (with probability 1). The decryption scheme of \(\Pi _\textsf{GA}\text {-}\textsf{PKE}\) differs from that of ElGamal since it is not possible to divide out \(sk \star {{\textsf{c}}}{{\textsf{t}}}_1\) from \({{\textsf{c}}}{{\textsf{t}}}_2\). Therefore, retrieving \({\textsf{M}}\) from \({{\textsf{c}}}{{\textsf{t}}}_1,{{\textsf{c}}}{{\textsf{t}}}_2,{{\textsf{s}}}{{\textsf{k}}}\) requires the resolution of an instance of \(\textsf{GAIP}\) with input \(({{\textsf{s}}}{{\textsf{k}}}\star {{\textsf{c}}}{{\textsf{t}}}_1,{{\textsf{c}}}{{\textsf{t}}}_2)\). \(\textsf{Dec}\) solves this problem by a brute force over the message space \({\mathcal {M}}\). In case \({\mathcal {M}}\) is polynomially large, then we have efficient decryption as desired.
\({\textit{Multi-challenge} \textsf{IND}\text {-}\textsf{CPA} \textit{ Security.}}\) The scheme is multi-challenge \(\textsf{IND}\text {-}\textsf{CPA}\) secure based on the \(\textsf{dCSIDH}\) assumption. Since \(\Pi _\textsf{GA}\text {-}\textsf{PKE}\) is an ElGamal-like encryption scheme in the CSIDH setting — where each exponentiation is replaced by a group action — for the security proof it is sufficient to adapt the usual proof for the group-based ElGamal encryption scheme. Note that the the reduction loses a factor \(1/Q_{{\textsf{c}}}{{\textsf{t}}}\), where \(Q_{{\textsf{c}}}{{\textsf{t}}}\) is the number of challenge ciphertext the adversary observes. This is the only reason why we do not achieve tight security for our accountable ring signature and group signature.
We point out that by ignoring the \(\textsf{PKE}\), we obtain a ring signature identical to Beullens et al. [14]. Thus we obtain the first tightly secure and efficient isogeny-based ring signature in this work.
\(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness. In the isogeny setting, it is not needed to relax the key relation (contrary to our lattice instantiation where some relaxation is necessary in order to get an efficient opening proof). We can simply set  . Similarly, since \(S_2 = S_1\), there is no relaxation in the encryption randomness. Therefore \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness is equivalent to the standard correctness property (with probability 1), which is satisfied by our \(\textsf{PKE}\).
. Similarly, since \(S_2 = S_1\), there is no relaxation in the encryption randomness. Therefore \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness is equivalent to the standard correctness property (with probability 1), which is satisfied by our \(\textsf{PKE}\).
Multi-Proof Online Extractable \(\textsf{NIZK}\) with Labels \(\Pi _{\textsf{NIZK},\textsf{lbl}} \). Using the group-action-based \(\textsf{HIG} \) and \(\textsf{PKE} \), we can instantiate \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) for the signing relation \(R_{\textsf{sig}}\) (see Sect. 4.1) as explained in Sects. 6 and 7.
Statistically Sound \(\textsf{NIZK}\) without Labels \(\Pi _\textsf{NIZK} \). The last ingredient for our \(\textsf{ARS}\) is a \(\textsf{NIZK}\) for the opening relation \(R_{\textsf{open}}\), which in our instantiation is

A sigma protocol for this relation was introduced in [43, Sect. 3.2]. We can then turn this sigma protocol into an \(\textsf{NIZK}\) by applying the Fiat-Shamir transform. (Note that we do not need this \(\textsf{NIZK}\) to be online-extractable.)
Concrete Instantiation for Tab. 1. For our isogeny-based instantiation, we chose an \(\textsf{HIG}\) and a \(\textsf{PKE}\) based on the CSIDH-512 group action. The structure of this class group has been computed [15], which allows for more efficient proofs. We chose the challenge space as string of length \(M = 855\) with Hamming weight \(K=19\). Most of the signature is independent of N, and contains a fixed number of curves and class group elements as well as some overhead from the generic construction such as a hash value, the internal nodes in the seed tree, and commitment randomness to open the commitments. The only reason the signature size increases with N is that the signature contains a fixed amount of paths in a Merkle tree of depth \(\log _2 N\). This makes for a very mild dependence on N.
8.2 Instantiation from lattices
We instantiate a group-action-based \(\textsf{HIG}\) and \(\textsf{PKE}\), and the corresponding \(\textsf{NIZK}\) s for the relations \(R_{\textsf{sig}}\) and \(R_{\textsf{open}}\) based on lattices under the \(\textsf{MSIS}\) and \(\textsf{MLWE}\) assumptions. The choices for the integer n, modulus q, and ring \(R_q\) are provided in Sect. 3.6.
Group-Action-Based \(\textsf{HIG}\). By Def. 5.1, it suffices to define the public parameter \({{\textsf{p}}}{{\textsf{p}}}_1 = (G,S_1,S_2,\delta _x,X_0,{\mathcal {X}},\star )\) generated by \(\textsf{RelSetup}\) and to check that the output of \(\textsf{IGen}\) defines a hard relation. The public parameters \({{\textsf{p}}}{{\textsf{p}}}\) are defined as follows:
-
\((G, {\mathcal {X}}) = (R^\ell _q \times R^k_q, R^k_q)\), where \(X_0\) is an arbitrary element in \({\mathcal {X}}\),
-
For \(b \in \{ 0,1 \} \), \(S_b = \{ ({{\textbf {s}}}, {{\textbf {z}}}) \in G \vert \Vert {{\textbf {s}}}\Vert _{\infty }, \Vert {{\textbf {e}}}\Vert _{\infty } \le B_b \}\), where \(B_1, B_2\) are positive integers such that \(B_1< B_2 < q\),
-
\(\delta _x = \big ( \frac{2(B_2 - B_1) +1}{2 B_2 + 1} \big )^{n (k + \ell )}\),
-
The group action \(\star : G \times {\mathcal {X}}\rightarrow {\mathcal {X}}\) is defined as \(({{\textbf {s}}}, {{\textbf {e}}}) \star {{\textbf {w}}}= ({{\textbf {A}}}{{\textbf {s}}}+ {{\textbf {z}}}) + {{\textbf {w}}}\), where \({{\textbf {A}}}\in R^{k \times \ell }_q\) is a fixed matrix sampled uniformly by \(\textsf{RelSetup}\).
We define \(S_3\) to be a subset of G with coefficients all bounded by \(B_2 - B_1\). It can be checked that \({{\textsf{p}}}{{\textsf{p}}}\) satisfies all the conditions in Def. 5.1, where \(\delta _x\) follows by simply counting the points included in \(S_2\) and \(S_3\). It remains to check that the relation \({\widetilde{R}}_{{\textsf{p}}}{{\textsf{p}}}= \{ ({{\textbf {b}}}, ({{\textbf {s}}}, {{\textbf {z}}})) \vert {{\textbf {b}}}= {{\textbf {A}}}{{\textbf {s}}}+ {{\textbf {e}}}\wedge ({{\textbf {s}}}, {{\textbf {e}}}) \in S_2 + S_3 \}\) defines a hard relation as defined in Sect. 4.1, where \(S_2 + S_3\). Note that if the adversary \({\mathcal {A}}\) is restricted to output a witness \(({{\textbf {s}}}, {{\textbf {e}}}) \in S_1\), then this follows directly from the \(\textsf{MLWE} _{n, q, B_1}\) assumption. For our application, we have to further consider the scenario where \({\mathcal {A}}\) may output a witness \(({{\textbf {s}}}, {{\textbf {e}}})\) outside of \(S_1\). We need to consider this case since our online extractor for the \(\textsf{NIZK}\) can only extract a witness in the relaxed relation \({\widetilde{R}}_{{\textsf{p}}}{{\textsf{p}}}\) rather than \(R_{{\textsf{p}}}{{\textsf{p}}}\).
The hardness of our group-action-based \(\textsf{HIG}\) follows naturally from the \(\textsf{MSIS} _{n, q, k, \ell , 2B_2}\) and \(\textsf{sMLWE} _{n, q, k, \ell , B_1}\) assumptions. We only focus on an adversary \({\mathcal {A}}\) that outputs a witness \(({{\textbf {s}}}, {{\textbf {e}}})\) outside of \(S_1\), since the other case simply follows from \(\textsf{MLWE} \) as we seen above. Let us construct an adversary \({\mathcal {B}}\) against the \(\textsf{MSIS} _{n, q, k, \ell , 2B_2}\) problem by using \({\mathcal {A}}\) as a subroutine. \({\mathcal {B}}\), given \({{\textbf {A}}}\) as input, samples a random \(({{\textbf {s}}}, {{\textbf {e}}}) \leftarrow S_1\), sets \({{\textbf {b}}}= {{\textbf {A}}}{{\textbf {s}}}+ {{\textbf {e}}}\) and invokes \({\mathcal {A}}\) on input \({{\textsf{p}}}{{\textsf{p}}}, {{\textbf {b}}}\), where \({{\textsf{p}}}{{\textsf{p}}}\) includes \({{\textbf {A}}}\). When \({\mathcal {A}}\) outputs \(({{\textbf {s}}}', {{\textbf {e}}}')\), \({\mathcal {B}}\) submits \(({{\textbf {s}}}+ {{\textbf {s}}}', {{\textbf {e}}}+ {{\textbf {e}}}')\) as its solution. By assumption, \(\Vert {{\textbf {s}}}+ {{\textbf {s}}}'\Vert _{\infty }, \Vert {{\textbf {e}}}+ {{\textbf {e}}}'\Vert _{\infty } \le B_1 + B_2 + B_3 = 2 B_2\) and they are non-zero. Therefore, \({\mathcal {B}}\) breaks the \(\textsf{MSIS} _{n, q, k, \ell , 2B_2}\) problem as desired.
Finally, the same proof shows that our group-action-based \(\textsf{HIG}\) is a hard multi-instance generator based on the same assumptions.
Group-Action-Based \(\textsf{PKE}\). We use a \(\textsf{PKE}\) scheme based on the Lindner-Peikert framework [73]. We first explain the public parameters \({{\textsf{p}}}{{\textsf{p}}}_2 = ({\overline{G}}, {\overline{G}}_{\textsf{T}}, {\mathcal {Y}}, {\overline{S}}_1, {\overline{S}}_2, \delta _y, D_{\mathcal {Y}}, \star _{\textsf{M}}, {\mathcal {M}})\) generated by \(\mathsf {PKE.Setup}\).Footnote 11
-
\(({\overline{G}}, {\overline{G}}_{\textsf{T}}, {\mathcal {Y}}) = (R^k_q \times R^\ell _q \times R_q, R_q, R^k_q \times R_q)\),
-
For \(b \in \{ 0,1 \} \), \({\overline{S}}_b = \{ ({{\textbf {r}}}, {{\textbf {e}}}, e) \in {\overline{G}}\vert \Vert {{\textbf {r}}}\Vert _{\infty }, \Vert {{\textbf {e}}}\Vert _{\infty }, \Vert e\Vert _{\infty } \le B_b \}\), where \(B_1, B_2\) are positive integers such that \(B_1< B_2 < q\) and \(4(nk + 1) (2B_2 - B_1) \le q\),
-
\(\delta _y = \big ( \frac{2(B_2 - B_1) +1}{2 B_2 + 1} \big )^{n (k + \ell + 1)}\),
-
\(D_{\mathcal {Y}}\) is a distribution that samples a uniform random \(({{\textbf {A}}}, {{\textbf {s}}}, {{\textbf {z}}}) \in R^{k \times \ell } \times R^\ell _q \times R^k_q\) and outputs a group action \(\star : {\overline{G}}\times {\mathcal {Y}}\rightarrow {\mathcal {Y}}\) defined as \(({{\textbf {r}}}, {{\textbf {e}}}, e) \star ({{\textbf {w}}}, w) = (( {{\textbf {A}}}^\top {{\textbf {r}}}+ {{\textbf {e}}}+ {{\textbf {w}}}, {{\textbf {b}}}^\top {{\textbf {r}}}+ e + w)\) and an element \(Y = ({{\textbf {w}}}, w) \in {\mathcal {Y}}\), where \({{\textbf {b}}}= {{\textbf {A}}}{{\textbf {s}}}+ {{\textbf {z}}}\),
-
\(\star _{\textsf{M}}: {\overline{G}}_{\textsf{T}}\times {\mathcal {Y}}\rightarrow {\mathcal {Y}}\) is a group action defined as \({\textsf{M}}\star _{\textsf{M}}({{\textbf {c}}}, c) = ( {{\textbf {c}}}, c + {\textsf{M}}\cdot \lfloor q/2 \rceil )\),
-
The message space \({\mathcal {M}}\) is a subset of \({\overline{G}}_{\textsf{T}}= R_q\) with coefficients in \( \{ 0,1 \} \).
We define \(S_3\) to be a subset of G with coefficients all bounded by \(B_2 - B_1\). It can be checked that \({{\textsf{p}}}{{\textsf{p}}}\) satisfies the conditions in Def. 5.2, where \(\delta _y\) follows by simply counting the points included in \(S_2\) and \(S_3\). The remaining algorithms \((\textsf{KeyGen}, \textsf{Enc}, \textsf{Dec})\) are defined as follows, where U(B) denotes elements in \(R_q\) with infinity norm at most \(B \in {\mathbb {N}}\):
- \(\textsf{KeyGen}({{\textsf{p}}}{{\textsf{p}}})\)::
-
It samples a uniform random \(({{\textbf {A}}}, {{\textbf {s}}}, {{\textbf {z}}}) \in R^{k \times \ell } \times U(B_1)^\ell \times U(B_1)^k\) and outputs \(({{\textsf{p}}}{{\textsf{k}}}, {{\textsf{s}}}{{\textsf{k}}}) = ((\star _{{\textsf{p}}}{{\textsf{k}}}, {{\textbf {0}}}), {{\textbf {s}}})\), where \({{\textbf {0}}}\) is the zero polynomial in \({\mathcal {Y}}\) and \(\star _{{\textsf{p}}}{{\textsf{k}}}\) is a group action defined as \(({{\textbf {r}}}, {{\textbf {e}}}, e) \star _{{\textsf{p}}}{{\textsf{k}}}({{\textbf {w}}}, w) = ( {{\textbf {A}}}^\top {{\textbf {r}}}+ {{\textbf {e}}}+ {{\textbf {w}}}, {{\textbf {b}}}^\top {{\textbf {r}}}+ e + w)\), where \({{\textbf {b}}}= {{\textbf {A}}}{{\textbf {s}}}+ {{\textbf {z}}}\). Note that \({{\textsf{p}}}{{\textsf{k}}}\) is distributed as a sample from \(D_{\mathcal {Y}}\).
- \(\textsf{Enc}({{\textsf{p}}}{{\textsf{k}}}, {\textsf{M}})\)::
-
On input a public key \({{\textsf{p}}}{{\textsf{k}}}= (\star _{{\textsf{p}}}{{\textsf{k}}}, Y_{{\textsf{p}}}{{\textsf{k}}}= {{\textbf {0}}})\) and a message \({\textsf{M}}\in {\mathcal {M}}\), it samples \(({{\textbf {r}}}, {{\textbf {e}}}, e) \leftarrow {\overline{S}}_1\) and returns \({{\textsf{c}}}{{\textsf{t}}}= {\textsf{M}}\star _{\textsf{M}}(({{\textbf {r}}}, {{\textbf {e}}}, e) \star _{{\textsf{p}}}{{\textsf{k}}}{{\textbf {0}}}) = ({{\textbf {A}}}^\top {{\textbf {r}}}+ {{\textbf {e}}}, {{\textbf {b}}}^\top {{\textbf {r}}}+ e + {\textsf{M}}\cdot \lfloor q/2 \rceil ) \in {\mathcal {Y}}\).
- \(\textsf{Dec}({{\textsf{s}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}) \rightarrow {\textsf{M}}\)::
-
It parses \(({{\textbf {c}}}, c) \leftarrow {{\textsf{c}}}{{\textsf{t}}}\) and computes \(w = c - {{\textbf {c}}}^\top {{\textbf {s}}}\) over \(R_q\). It rounds each coefficient back to either 0 or \(\lfloor q/2 \rceil \) whichever is closest modulo q and outputs the polynomial.
Correctness is a consequence of \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness, which we show below, and decryption efficiency clearly holds as well. We discuss the remaining properties.
\({\textit{Multi-challenge} \textsf{IND}\text {-}\textsf{CPA} \textit{ Security.}}\) The security follows by a standard proof using \(\textsf{dMLWE} \). For completeness, we provide the proof: We consider a sequence of games and prove that the adversary’s advantage only changes negligibly in each adjacent games. The first game is the original security game. In the second game, we modify the group action \(\star _{{\textsf{p}}}{{\textsf{k}}}\) included in the public key to be defined by a random \(({{\textbf {A}}}, {{\textbf {b}}}) \leftarrow R^{k \times \ell } \times R^k_q\). By the \(\textsf{dMLWE} _{n, q, k, \ell , B_1}\) assumption, this game is indistinguishable from the previous game. In the final game, we sample each ciphertext as \({{\textsf{c}}}{{\textsf{t}}}\leftarrow R^{k} \times R_q\). By the \(\textsf{dMLWE} _{n, q, \ell + 1, k, B_1}\) assumption, this game is indistinguishable from the previous game. Note that we appropriately parse the matrix \({{\textbf {A}}}' \in R_q^{(\ell + 1) \times k}\) provided by the challenge as \({{\textbf {A}}}\) and \({{\textbf {b}}}\), and query the oracle once for each ciphertext. Since the challenge bit b is statistically hidden from the adversary, no adversary has advantage in winning this game. This concludes the proof.
We note that we can prove multi-challenge \(\textsf{IND}\text {-}\textsf{CPA}\) security while only relying on the \(\textsf{dMLWE}\) assumption with a fixed number of instances (i.e., those that do not rely on the number of challenge ciphertexts), if we can tolerate choosing slightly less efficient parameters. Specifically, we can use the dual-Regev encryption [56], where \({{\textbf {A}}}\) is a tall matrix. When \({{\textbf {A}}}\) is tall enough, \({{\textbf {A}}}^\top {{\textbf {r}}}\) and \({{\textbf {b}}}^\top {{\textbf {r}}}\) is distributed statistically close to random under appropriate choices of parameters owing to the regularity lemma [77]. Hence, we only need the \(\textsf{dMLWE} \) assumption to jump from the first to second game above.
\({{({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')-\textit{ correctness}}}\) We define \({\mathcal {R}}'\) and \({{\mathcal {K}}}{{\mathcal {R}}}'\) as follows, where the choice of \({\mathcal {R}}'\) coincides with those considered in Theorem 6.1:
-
\(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}') = ({\overline{S}}_2 + {\overline{S}}_3, U(2B_2 - B_1)^\ell \times U(2B_2 - B_1)^k)\), where recall \(S_3\) is a subset of G with ring elements whose coefficients are all bounded by \(B_2 - B_1\). Specifically, \({\overline{S}}_2 + {\overline{S}}_3 = \{ ({{\textbf {r}}}, {{\textbf {e}}}, e) \in {\overline{G}}\vert \Vert {{\textbf {r}}}\Vert _{\infty }, \Vert {{\textbf {e}}}\Vert _{\infty }, \Vert e\Vert _{\infty } \le 2B_2 - B_1 \}\).
We check that correctness holds even if the ciphertext is encrypted using randomness \(({{\textbf {r}}}, {{\textbf {e}}}, e) \in {\mathcal {R}}'\) and a secret key \({{\textsf{s}}}{{\textsf{k}}}= ({{\textbf {s}}}, {{\textbf {e}}}) \in {{\mathcal {K}}}{{\mathcal {R}}}'\). Let \({{\textsf{c}}}{{\textsf{t}}}= ({{\textbf {A}}}^\top {{\textbf {r}}}+ {{\textbf {e}}}, {{\textbf {b}}}^\top {{\textbf {r}}}+ e + {\textsf{M}}\cdot \lfloor q/2 \rceil )\), then \(c- {{\textbf {c}}}^\top {{\textbf {s}}}= {\textsf{M}}\cdot \lfloor q/2 \rceil + e + {{\textbf {e}}}^\top {{\textbf {s}}}- {{\textbf {z}}}^\top {{\textbf {r}}}\). Then, \(\Vert e + {{\textbf {e}}}^\top {{\textbf {s}}}- {{\textbf {z}}}^\top {{\textbf {r}}}\Vert _{\infty } \le \Vert e\Vert _{\infty } + \Vert {{\textbf {e}}}^\top {{\textbf {s}}}\Vert _{\infty } + \Vert {{\textbf {z}}}^\top {{\textbf {r}}}\Vert _{\infty } \le (2B_2 - B_1) + 2 n k (2B_2 - B_1)^2 \le q/4\), where the last inequality follows from our parameter choice. Thus, \({\textsf{M}}\) can be correctly decrypted with probability 1.
Multi-Proof Online Extractable \(\textsf{NIZK}\) with Labels \(\Pi _{\textsf{NIZK},\textsf{lbl}} \). Using the group-action-based \(\textsf{HIG} \) and \(\textsf{PKE} \), we can instantiate \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) for the signing relations \(R_{\textsf{sig}}\) and \(R_{\textsf{sig}}'\) (see Sect. 4.1) as explained in Sects. 6 and 7.
Statistically Sound \(\textsf{NIZK}\) without Labels \(\Pi _\textsf{NIZK} \). It remains to show how to construct \(\Pi _\textsf{NIZK} \) for the opening relations \(R_{\textsf{open}}\) and \(R_{\textsf{open}}'\). We can rewrite the relation \(R_{\textsf{open}}\) (see Sect. 4.1) as follows:

Notice we can rewrite the righthand side as
where d is some element in \(R_q\) such that \(\Vert d\Vert _{\infty } \le q/4\). Since d is not secret, we can think d is included in the statement \(({{\textsf{p}}}{{\textsf{k}}}, {{\textsf{c}}}{{\textsf{t}}}, {\textsf{M}})\). Then, \(\Pi _\textsf{NIZK} \) can simply viewed as an \(\textsf{NIZK} \) for the standard \(\textsf{MLWE}\)-based statement \({\tilde{{{\textbf {A}}}}} {{\textbf {s}}}+ {\tilde{{{\textbf {z}}}}} = {\tilde{{{\textbf {b}}}}}\), where \(\Vert {{\textbf {s}}}\Vert _{\infty }, \Vert {\tilde{{{\textbf {z}}}}}\Vert _{\infty } \le B_1\). Notice that such a statement is implicitly used in \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) for the relation \(R_{\textsf{sig}}\) since this statement is essentially the group-action-based \(\textsf{HIG}\). Specifically, if we remove all the components regarding the OR proof and leave the proof regarding the group-action-based \(\textsf{HIG}\) from Figs. 3,4 and 7, we arrive at our desired \(\textsf{NIZK}\). Similarly to \(\Pi _{\textsf{NIZK},\textsf{lbl}} \) for the relation \(R_{\textsf{sig}}\), we can only prove that a cheating prover was using a witness (i.e., secret key) satisfying \(\Vert {{\textbf {s}}}\Vert _{\infty }, \Vert {\tilde{{{\textbf {z}}}}}\Vert _{\infty } \le B_2 + B_3\). This is exactly the \({{\mathcal {K}}}{{\mathcal {R}}}'\) defined above and coincides with the relaxed relation \({\tilde{R}}_{\textsf{open}}\).
One may wonder if we can construct an \(\textsf{NIZK} \) for this standard \(\textsf{MLWE}\) relation based on a sigma protocol with a non-binary challenge set. Although the proof size of \(\Pi _\textsf{NIZK}\) is already constant, this may further minimize the proof size of the opening proof. We claim that this may be difficult. The main reason is that when we use a non-binary challenge space, the extracted witness \(({{\textbf {s}}}, {\tilde{{{\textbf {z}}}}})\) typically comes from a furthered relaxed relation such that not only they have a larger norm, they are guaranteed to only satisfy \({\tilde{{{\textbf {A}}}}} {{\textbf {s}}}+ {\tilde{{{\textbf {z}}}}} = t \cdot {\tilde{{{\textbf {b}}}}}\) for some short \(t \in R_q\). This relaxation may suffice in some settings but it turns out that it won’t for ours as we can no longer prove \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness. When restricted to binary challenges, we can control t to be \(1 \in R_q\).
Remark 8.1
(Bai-Galbraith Optimization [7]) We can apply the Bai-Galbraith optimization [7] by exploiting the lattice structure. This is a common and simple optimization used in various lattice-based interactive protocols based on the Fiat-Shamir with aborts paradigm [78] that allows to roughly halve the proof size, or signature size when viewing the proof as a signature, with no additional cost. Intuitively, for \(\textsf{MLWE} \), proving knowledge of a short \({{\textbf {s}}}\) indirectly proves knowledge of a short \({{\textbf {e}}}\) since it is uniquely defined as \({{\textbf {b}}}- {{\textbf {A}}}{{\textbf {s}}}\). Therefore, we can remove the components that are used to explicitly prove that \({{\textbf {e}}}\) is short. Since the size of \({{\textbf {s}}}\) and \({{\textbf {e}}}\) are about the same in our construction, this allows to almost halve the proof size. For further details, see for example [7, 14, 42].
Concrete Instantiation for Tab. 1. For the concrete instantiation in Tab. 1, we use \(M = 1749, K=16\). For the \(\textsf{HIG}\), we chose the parameters according to the parameters used in the Security Level II variant of the (round 3) NIST submission of the Dilithium signature scheme. Concretely, we use the ring \(R_q = {\mathbb {Z}}_q[X]/(X^n+1)\), with \(n = 256\) and \(q = 2^{23} - 2^{13} + 1\), and we put \(l=k=4\), \(B_1 = 2, B_2 = 2^{17}\). These parameters are chosen by the Dilithium team such that the relevant \(\textsf{MLWE}\) and \(\textsf{MSIS}\) problems are hard enough to reach NIST SL II.
For the \(\textsf{PKE}\), we use the ring \(R_q'\) with \(n = 256\) and \(q' \approx 2^{49}\), and we put \(k=l=8, B_1 = 1, B_2 \approx 2^{16.3}\). The LWE estimator of Albrecht et al. estimates that this \(\textsf{MLWE}\) instance has 141 bits of security [3]. Moreover, the \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}}')\)-correctness holds, because we have \((2B_2 - B_1) + 2 n k (2B_2 - B_1)^2 \le q/4\). For the parameter set without manager accountability, we only require \(({\mathcal {R}}',{{\mathcal {K}}}{{\mathcal {R}}})\)-correctness, so we only need \((2B_2 - B_1) + 2 n k (2B_2 - B_1)B_1 \le q/4\). Therefore, we can choose our parameters as \(q' \approx 2^{30}, l=k=5, B_1 = 1\), and \(B_2 = 2^{15.9}\) for better signature sizes. The LWE estimator of Albrecht et al. estimates that this \(\textsf{MLWE}\) instance has also 141 bits of security. In either cases, we use an optimization due to Bai and Galbraith to reduce the size of the proofs (and therefore the size of the signature).
Similar to the isogeny instantiation, the signature size depends very mildly on N because N only affects the length of some paths in the signature. Finally, we can use Sect. 6.3 to obtain a tightly secure scheme. Since \(K=16\), the overhead compared to the non-tight scheme is a mere 512B.
Notes
We note that their signature size grows by \(\log ^t N\) for a small constant \(t > 1\) rather than simply by \(\log N\).
To be precise, they consider a weaker variant of standard accountable ring signature where no \(\textsf{Judge}\) algorithm is considered.
Note that extractability via rewinding is insufficient for full anonymity as it will cause an exponential reduction loss when trying to extract the witness from adaptively chosen signatures [11].
The choice of what to encrypt is rather arbitrary. The same idea works if for instance we hash \({{\textsf{v}}}{{\textsf{k}}}\) into \(\mathcal {C}\ell (\mathcal {O})\) and view the digest as the message.
We note that we also have some independent looseness in the anonymity proof since we rely on the “multi-challenge” \(\textsf{IND}\text {-}\textsf{CPA}\) security from our \(\textsf{PKE}\). This is handled in a standard way, and this is also why we only achieve a truly tight group signature from lattices and not from isogenies.
We note that it seems difficult to use the parallel OR-proof for our sigma protocol since the challenge space is structured.
This should not be confused with the random oracle used to compile a sigma protocol into an \(\textsf{NIZK}\) proof system.
This is w.l.o.g., and guarantees that the list \(L_{\mathcal {O}}\) is updated with the input/output required to verify the proof \({\mathcal {A}}\) receives or sends.
An astute reader may notice that the prover is only expected polynomial time. We can always assign an upper bound on the runtime of the prover, but did not do so for better readability. In practice, for concrete choices of the parameter, the number of repetition never exceeds, say 10.
Throughout the proof, we use overlines for \((\overline{\textsf{com}}, \overline{\textsf{chall}}, \overline{\textsf{resp}})\) to indicate that it is a transcript of of \(\Pi _{\Sigma }^\textsf{tOR}\). We use \(\textsf{resp}_i\) without overlines to indicate elements of \(\overline{\textsf{resp}}\).
Note that although we use the same \((q, B_1, B_2)\) as those used by the group-action-based \(\textsf{HIG} \), they can be set differently. We only use the same notations for better readability.
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.
References
Abe M., Ohkubo M., Suzuki K.: 1-out-of-n signatures from a variety of keys. In: Zheng, Y. (ed.) ASIACRYPT 2002. LNCS, vol. 2501, pp. 415–432. Springer (2002). https://doi.org/10.1007/3-540-36178-2_26
Albrecht M.R., Curtis B.R., Deo A., Davidson A., Player, R., Postlethwaite E.W., Virdia F., Wunderer T.: Estimate all the LWE, NTRU schemes! In: Catalano D., De Prisco R. (eds.) SCN 18. LNCS, vol. 11035, pp. 351–367. Springer (2018). https://doi.org/10.1007/978-3-319-98113-0_19
Albrecht M.R., Player R., Scott S.: On The Concrete Hardness Of Learning With Errors. Cryptology ePrint Archive, Report 2015/046. https://eprint.iacr.org/2015/046 (2015)
Asharov G., Jain A., López-Alt A., Tromer E., Vaikuntanathan V., Wichs D.: Multiparty computation with low communication, computation and interaction via threshold FHE. In: Pointcheval D., Johansson T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 483–501. Springer (2012). https://doi.org/10.1007/978-3-642-29011-4_29
Attema T., Lyubashevsky V., Seiler G.: Practical product proofs for lattice commitments. In: Micciancio D., Ristenpart T. (eds.) CRYPTO 2020, Part II. LNCS, vol. 12171, pp. 470–499. Springer (2020). https://doi.org/10.1007/978-3-030-56880-1_17
Backes M., Hanzlik L., Schneider-Bensch J.: Membership privacy for fully dynamic group signatures. In: Cavallaro L., Kinder J., Wang X., Katz, J. (eds.) ACM CCS 2019, pp. 2181–2198. ACM Press (2019). https://doi.org/10.1145/3319535.3354257
Bai S., Galbraith S.D.: An improved compression technique for signatures based on learning with errors. In: Benaloh J. (ed.) CT-RSA 2014. LNCS, vol. 8366, pp. 28–47. Springer (2014). https://doi.org/10.1007/978-3-319-04852-9_2
Bellare M., Micciancio D., Warinschi, B.: Foundations of group signatures: Formal definitions, simplified requirements, and a construction based on general assumptions. In: Biham E. (ed.) EUROCRYPT 2003. LNCS, vol. 2656, pp. 614–629. Springer (2003). https://doi.org/10.1007/3-540-39200-9_38
Bellare M., Shi H., Zhang C.: Foundations of group signatures: The case of dynamic groups. In: Menezes A. (ed.) CT-RSA 2005. LNCS, vol. 3376, pp. 136–153. Springer (2005). https://doi.org/10.1007/978-3-540-30574-3_11
Benhamouda F., Camenisch J., Krenn S., Lyubashevsky V., NevenG.: Better zero-knowledge proofs for lattice encryption and their application to group signatures. In: Sarkar P., Iwata T. (eds.) ASIACRYPT 2014, Part I. LNCS, vol. 8873, pp. 551–572. Springer (2014). https://doi.org/10.1007/978-3-662-45611-8_29
Bernhard D., Fischlin M., WarinschiB.: Adaptive proofs of knowledge in the random oracle model. In: Katz J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 629–649. Springer (2015). https://doi.org/10.1007/978-3-662-46447-2_28
Bernstein D.J., Lange T., Martindale C., Panny L.: Quantum circuits for the CSIDH: Optimizing quantum evaluation of isogenies. In: Ishai Y., Rijmen V. (eds.) EUROCRYPT 2019, Part II. LNCS, vol. 11477, pp. 409–441. Springer (2019). https://doi.org/10.1007/978-3-030-17656-3_15
Beullens W., Dobson S., Katsumata S., Lai Y.-F., Pintore F.: Group signatures and more from isogenies and lattices: Generic, simple, and efficient. In: EUROCRYPT 2022, Part II. LNCS, pp. 95–126. Springer, (2022). https://doi.org/10.1007/978-3-031-07085-3_4
Beullens W., Katsumata S., Pintore F.: Calamari and Falafl: Logarithmic (linkable) ring signatures from isogenies and lattices. In: Moriai S., Wang H. (eds.) ASIACRYPT 2020, Part II. LNCS, vol. 12492, pp. 464–492. Springer (2020). https://doi.org/10.1007/978-3-030-64834-3_16
Beullens W., Kleinjung T., Vercauteren F.: CSI-FiSh: Efficient isogeny based signatures through class group computations. In: Galbraith S.D., Moriai S. (eds.) ASIACRYPT 2019, Part I. LNCS, vol. 11921, pp. 227–247. Springer (2019). https://doi.org/10.1007/978-3-030-34578-5_9
Bichsel P., Camenisch J., Neven G., Smart, N.P., Warinschi, B.: Get shorty via group signatures without encryption. In: Garay J.A., Prisco R.D. (eds.) SCN 10. LNCS, vol. 6280, pp. 381–398. Springer (2010). https://doi.org/10.1007/978-3-642-15317-4_24
Boneh D., Boyen X., Shacham H.: Short group signatures. In: Franklin M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer (2004). https://doi.org/10.1007/978-3-540-28628-8_3
Bonnetain X., Schrottenloher A.: Quantum security analysis of CSIDH. In: Canteaut A., Ishai Y. (eds.) EUROCRYPT 2020, Part II. LNCS, vol. 12106, pp. 493–522. Springer (2020). https://doi.org/10.1007/978-3-030-45724-2_17
Bootle J., Cerulli A., Chaidos P., Ghadafi E., Groth J., Petit C.: Short accountable ring signatures based on DDH. In: Pernul G., Ryan P.Y.A., Weippl E.R. (eds.) ESORICS 2015, Part I. LNCS, vol. 9326, pp. 243–265. Springer (2015). https://doi.org/10.1007/978-3-319-24174-6_13
Bootle J., Cerulli A., Chaidos P., Ghadafi E., Groth J.: Foundations of fully dynamic group signatures. In: Manulis M., Sadeghi A.-R., Schneider S. (eds.) ACNS 16. LNCS, vol. 9696, pp. 117–136. Springer (2016). https://doi.org/10.1007/978-3-319-39555-5_7
Bootle J., Lyubashevsky V., Seiler G.: Algebraic techniques for short(er) exact lattice-based zero-knowledge proofs. In: Boldyreva A., Micciancio D. (eds.) CRYPTO 2019, Part I. LNCS, vol. 11692, pp. 176–202. Springer (2019). https://doi.org/10.1007/978-3-030-26948-7_7
Boschini C., Camenisch J., Neven G.: Floppy-sized group signatures from lattices. In: Preneel B., Vercauteren F. (eds.) ACNS 18. LNCS, vol. 10892, pp. 163–182. Springer (2018). https://doi.org/10.1007/978-3-319-93387-0_9
Brickell E.F., Camenisch J., Chen L.: Direct anonymous attestation. In: Atluri V., Pfitzmann B., McDaniel P. (eds.) ACM CCS 2004, pp. 132–145. ACM Press, (2004). https://doi.org/10.1145/1030083.1030103
Brickell E., Li J.: Enhanced privacy id: A direct anonymous attestation scheme with enhanced revocation capabilities. In: Proceedings of the 2007 ACM Workshop on Privacy in Electronic Society, pp. 21–30 (2007)
Camenisch J., Damgård I.: Verifiable encryption, group encryption, and their applications to separable group signatures and signature sharing schemes. In: Okamoto T. (ed.) ASIACRYPT 2000. LNCS, vol. 1976, pp. 331–345. Springer (2000). https://doi.org/10.1007/3-540-44448-3_25
Camenisch J., Shoup, V.: Practical verifiable encryption and decryption of discrete logarithms. In: Boneh D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 126–144. Springer (2003). https://doi.org/10.1007/978-3-540-45146-4_8
Camenisch J.: Efficient and generalized group signatures. In: Fumy W. (ed.) EUROCRYPT’97. LNCS, vol. 1233, pp. 465–479. Springer (1997). https://doi.org/10.1007/3-540-69053-0_32
Castryck W., Lange T., Martindale C., Panny L., Renes J.: CSIDH: An efficient post-quantum commutative group action. In: Peyrin T., Galbraith S. (eds.) ASIACRYPT 2018, Part III. LNCS, vol. 11274, pp. 395–427. Springer (2018). https://doi.org/10.1007/978-3-030-03332-3_15
Castryck W., Sotáková J., Vercauteren, F.: Breaking the decisional Diffie-Hellman problem for class group actions using genus theory. In: Micciancio D., Ristenpart T. (eds.) CRYPTO 2020, Part II. LNCS, vol. 12171, pp. 92–120. Springer (2020). https://doi.org/10.1007/978-3-030-56880-1_4
Chase M., Lysyanskaya A.: On signatures of knowledge. In: Dwork C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 78–96. Springer (2006). https://doi.org/10.1007/11818175_5
Chaum D., van Heyst E.: Group signatures. In: Davies D.W. (ed.) EUROCRYPT’91. LNCS, vol. 547, pp. 257–265. Springer, (1991). https://doi.org/10.1007/3-540-46416-6_22
Chávez-Saab J., Chi-Domínguez J.-J., Jaques S., Rodríguez-Henríquez F.: The SQALE of CSIDH: square-root vélu quantum-resistant isogeny action with low exponents. IACR Cryptol. ePrint Arch. 2020, 1520 (2020).
Chung K.-M., Hsieh Y.-C., Huang M.-Y., Huang Y.-H., Lange T., Yang B.-Y.: Group signatures and accountable ring signatures from isogeny-based assumptions. Cryptology ePrint Archive, Report 2021/1368. https://ia.cr/2021/1368 (2021)
Clarisse R., Sanders O.: Group signature without random oracles from randomizable signatures. In: Nguyen K., Wu W., Lam K.-Y., Wang H. (eds.) ProvSec 2020. LNCS, vol. 12505, pp. 3–23. Springer, (2020). https://doi.org/10.1007/978-3-030-62576-4_1
Cramer R., Shoup V.: A practical public key cryptosystem provably secure against adaptive chosen ciphertext attack. In: Krawczyk H. (ed.) CRYPTO’98. LNCS, vol. 1462, pp. 13–25. Springer (1998). https://doi.org/10.1007/BFb0055717
Damgård I., Fujisaki E.: A statistically-hiding integer commitment scheme based on groups with hidden order. In: Zheng Y. (ed.) ASIACRYPT 2002. LNCS, vol. 2501, pp. 125–142. Springer (2002). https://doi.org/10.1007/3-540-36178-2_8
De Feo L., Galbraith S.D.: SeaSign: Compact isogeny signatures from class group actions. In: Ishai Y., Rijmen V. (eds.) EUROCRYPT 2019, Part III. LNCS, vol. 11478, pp. 759–789. Springer (2019). https://doi.org/10.1007/978-3-030-17659-4_26
del Pino R., Lyubashevsky V., Seiler G.: Lattice-based group signatures and zero-knowledge proofs of automorphism stability. In: Lie D., Mannan M., Backes M., Wang X. (eds.) ACM CCS 2018, pp. 574–591. ACM Press (2018). https://doi.org/10.1145/3243734.3243852
Delerablée C., Pointcheval,D.: Dynamic fully anonymous short group signatures. In: Nguyen P.Q. (ed.) Progress in Cryptology - VIETCRYPT 06. LNCS, vol. 4341, pp. 193–210. Springer (2006)
Derler D., Slamanig D.: Highly-efficient fully-anonymous dynamic group signatures. In: Kim J., Ahn G.-J., Kim S., Kim Y., López J., Kim T. (eds.) ASIACCS 18, pp. 551–565. ACM Press, (2018)
Dinur I., Nadler N.: Multi-target attacks on the Picnic signature scheme and related protocols. In: Ishai Y., Rijmen V. (eds.) EUROCRYPT 2019, Part III. LNCS, vol. 11478, pp. 699–727. Springer (2019). https://doi.org/10.1007/978-3-030-17659-4_24
Ducas L., Kiltz E., Lepoint T., Lyubashevsky V., Schwabe P., Seiler G., Stehlé D.: CRYSTALS-Dilithium: a lattice-based digital signature scheme. IACR TCHES 1, 238–268 (2018). https://doi.org/10.13154/tches.v2018.i1.238-268.
El Kaafarani A., Katsumata S., Pintore F.: Lossy CSI-FiSh: Efficient signature scheme with tight reduction to decisional CSIDH-512. In: Kiayias A., Kohlweiss M., Wallden P., Zikas V. (eds.) PKC 2020, Part II. LNCS, vol. 12111, pp. 157–186. Springer (2020). https://doi.org/10.1007/978-3-030-45388-6_6
El Kaafarani A., Katsumata S.: Attribute-based signatures for unbounded circuits in the ROM and efficient instantiations from lattices. In: Abdalla M., Dahab R. (eds.) PKC 2018, Part II. LNCS, vol. 10770, pp. 89–119. Springer (2018). https://doi.org/10.1007/978-3-319-76581-5_4
Esgin M.F., Nguyen N.K., Seiler G.: Practical exact proofs from lattices: New techniques to exploit fully-splitting rings. In: Moriai S., Wang H. (eds.) ASIACRYPT 2020, Part II. LNCS, vol. 12492, pp. 259–288. Springer (2020). https://doi.org/10.1007/978-3-030-64834-3_9
Esgin M.F., Steinfeld R., Liu J.K., Liu D.: Lattice-based zero-knowledge proofs: New techniques for shorter and faster constructions and applications. In: Boldyreva A., Micciancio D. (eds.) CRYPTO 2019, Part I. LNCS, vol. 11692, pp. 115–146. Springer (2019). https://doi.org/10.1007/978-3-030-26948-7_5
Esgin M.F., Steinfeld R., Zhao R.K.: MatRiCT+: More Efficient Post-Quantum Private Blockchain Payments. Cryptology ePrint Archive, Report 2021/545 (To appear in IEEE S &P 2022)
Esgin M.F., Zhao R.K., Steinfeld R., Liu J.K., Liu D.: MatRiCT: Efficient, scalable and post-quantum blockchain confidential transactions protocol. In: Cavallaro L., Kinder J., Wang X., Katz J. (eds.) ACM CCS 2019, pp. 567–584. ACM Press (2019). https://doi.org/10.1145/3319535.3354200
Ezerman M.F., Lee H.T., Ling S., Nguyen K., Wang,H.: A provably secure group signature scheme from code-based assumptions. In: Iwata T., Cheon J.H. (eds.) ASIACRYPT 2015, Part I. LNCS, vol. 9452, pp. 260–285. Springer (2015). https://doi.org/10.1007/978-3-662-48797-6_12
Fiat A., Shamir A.: How to prove yourself: Practical solutions to identification and signature problems. In: Odlyzko A.M. (ed.) CRYPTO’86. LNCS, vol. 263, pp. 186–194. Springer (1987). https://doi.org/10.1007/3-540-47721-7_12
Fischlin M., Harasser P., Janson C.: Signatures from sequential-OR proofs. In: Canteaut A., Ishai Y. (eds.) EUROCRYPT 2020, Part III. LNCS, vol. 12107, pp. 212–244. Springer (2020). https://doi.org/10.1007/978-3-030-45727-3_8
Fischlin M.: Communication-efficient non-interactive proofs of knowledge with online extractors. In: Shoup V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 152–168. Springer (2005). https://doi.org/10.1007/11535218_10
Fujisaki E., Okamoto T.: Secure integration of asymmetric and symmetric encryption schemes. In: Wiener M.J. (ed.) CRYPTO’99. LNCS, vol. 1666, pp. 537–554. Springer (1999). https://doi.org/10.1007/3-540-48405-1_34
Fujisaki E., Okamoto T.: Statistical zero knowledge protocols to prove modular polynomial relations. In: Kaliski Jr., B.S. (ed.) CRYPTO’97. LNCS, vol. 1294, pp. 16–30. Springer (1997). https://doi.org/10.1007/BFb0052225
Furukawa J., Imai H.: An efficient group signature scheme from bilinear maps. IEICE Trans. Fund. Electron. Commun. Comput. Sci. 89(5), 1328–1338 (2006).
Gentry C., Peikert C., Vaikuntanathan V.: Trapdoors for hard lattices and new cryptographic constructions. In: Ladner R.E., Dwork C. (eds.) 40th ACM STOC, pp. 197–206. ACM Press (2008). https://doi.org/10.1145/1374376.1374407
Gordon S.D., Katz J., Vaikuntanathan V.: A group signature scheme from lattice assumptions. In: Abe M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 395–412. Springer (2010). https://doi.org/10.1007/978-3-642-17373-8_23
Groth J.: Fully anonymous group signatures without random oracles. In: Kurosawa K. (ed.) ASIACRYPT 2007. LNCS, vol. 4833, pp. 164–180. Springer (2007). https://doi.org/10.1007/978-3-540-76900-2_10
Katsumata S., Yamada S.: Group signatures without NIZK: From lattices in the standard model. In: Ishai Y., Rijmen V. (eds.) EUROCRYPT 2019, Part III. LNCS, vol. 11478, pp. 312–344. Springer (2019). https://doi.org/10.1007/978-3-030-17659-4_11
Katz J., Kolesnikov V., Wang X.: Improved non-interactive zero knowledge with applications to post-quantum signatures. In: Lie, D., Mannan M., Backes M., Wang X. (eds.) ACM CCS 2018, pp. 525–537. ACM Press (2018). https://doi.org/10.1145/3243734.3243805
Katz J., Wang N.: Efficiency improvements for signature schemes with tight security reductions. In: Jajodia S., Atluri V., Jaeger T. (eds.) ACM CCS 2003, pp. 155–164. ACM Press (2003). https://doi.org/10.1145/948109.948132
Kumawat S., Paul S.: A new constant-size accountable ring signature scheme without random oracles. In: International Conference on Information Security and Cryptology, pp. 157–179 (2017). Springer
Kuperberg G.: Another subexponential-time quantum algorithm for the dihedral hidden subgroup problem. In: 8th Conference on the Theory of Quantum Computation, vol. 22, pp. 20–34. Communication and Cryptography (TQC 2013). Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, Dagstuhl (2013).
Kuperberg G.: A subexponential-time quantum algorithm for the dihedral hidden subgroup problem. SIAM J. Comput. 35(1), 170–188 (2005).
Laguillaumie F., Langlois A., Libert B., Stehlé D.: Lattice-based group signatures with logarithmic signature size. In: Sako K., Sarkar P. (eds.) ASIACRYPT 2013, Part II. LNCS, vol. 8270, pp. 41–61. Springer (2013). https://doi.org/10.1007/978-3-642-42045-0_3
Lai Y.-F., Dobson S.: Collusion Resistant Revocable Ring Signatures and Group Signatures from Hard Homogeneous Spaces. Cryptology ePrint Archive, Report 2021/1365. https://ia.cr/2021/1365 (2021)
Lai Y.-F., Galbraith S.D., de Saint Guilhem C.: Compact, efficient and UC-secure isogeny-based oblivious transfer. In: Canteaut A., Standaert F.-X. (eds.) EUROCRYPT 2021, Part I. LNCS, vol. 12696, pp. 213–241. Springer (2021). https://doi.org/10.1007/978-3-030-77870-5_8
Lai R.W.F., Zhang T., Chow S.S.M., Schröder D.: Efficient sanitizable signatures without random oracles. In: Askoxylakis I.G., Ioannidis S., Katsikas S.K., Meadows C.A. (eds.) ESORICS 2016, Part I. LNCS, vol. 9878, pp. 363–380. Springer (2016). https://doi.org/10.1007/978-3-319-45744-4_18
Langlois A., Stehlé D.: Worst-case to average-case reductions for module lattices. Des. Codes Cryptogr. 75(3), 565–599 (2015). https://doi.org/10.1007/s10623-014-9938-4.
Libert B., Ling S., Nguyen K., Wang H.: Zero-knowledge arguments for lattice-based accumulators: Logarithmic-size ring signatures and group signatures without trapdoors. In: Fischlin M., Coron J.-S. (eds.) EUROCRYPT 2016, Part II. LNCS, vol. 9666, pp. 1–31. Springer (2016). https://doi.org/10.1007/978-3-662-49896-5_1
Libert B., Mouhartem F., Peters T., Yung M.: Practical “signatures with efficient protocols” from simple assumptions. In: Chen X., Wang X., Huang X. (eds.) ASIACCS 16, pp. 511–522. ACM Press (2016)
Libert B., Peters T., Yung M.: Short group signatures via structure-preserving signatures: Standard model security from simple assumptions. In: Gennaro R., Robshaw M.J.B. (eds.) CRYPTO 2015, Part II. LNCS, vol. 9216, pp. 296–316. Springer (2015). https://doi.org/10.1007/978-3-662-48000-7_15
Lindner R., Peikert C.: Better key sizes (and attacks) for LWE-based encryption. In: Kiayias A. (ed.) CT-RSA 2011. LNCS, vol. 6558, pp. 319–339. Springer (2011). https://doi.org/10.1007/978-3-642-19074-2_21
Ling S., Nguyen K., Wang H., Xu Y.: Constant-size group signatures from lattices. In: Abdalla M., Dahab R. (eds.) PKC 2018, Part II. LNCS, vol. 10770, pp. 58–88. Springer (2018). https://doi.org/10.1007/978-3-319-76581-5_3
Lyubashevsky V., Nguyen N.K., Seiler G.: Practical lattice-based zero-knowledge proofs for integer relations. In: Ligatti J., Ou X., Katz J., Vigna G. (eds.) ACM CCS 2020, pp. 1051–1070. ACM Press (2020). https://doi.org/10.1145/3372297.3417894
Lyubashevsky V., Nguyen N.K., Seiler G.: SMILE: Set membership from ideal lattices with applications to ring signatures and confidential transactions. In: Malkin T., Peikert C. (eds.) CRYPTO 2021, Part II. LNCS, vol. 12826, pp. 611–640. Springer, Virtual Event (2021). https://doi.org/10.1007/978-3-030-84245-1_21
Lyubashevsky V., Peikert C., Regev O.: A toolkit for ring-LWE cryptography. In: Johansson T., Nguyen P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 35–54. Springer (2013). https://doi.org/10.1007/978-3-642-38348-9_3
Lyubashevsky V.: Lattice signatures without trapdoors. In: Pointcheval D., Johansson T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 738–755. Springer (2012). https://doi.org/10.1007/978-3-642-29011-4_43
Merkle R.C.: A digital signature based on a conventional encryption function. In: Pomerance C. (ed.) CRYPTO’87. LNCS, vol. 293, pp. 369–378. Springer (1988). https://doi.org/10.1007/3-540-48184-2_32
Peikert C.: He gives C-sieves on the CSIDH. In: Canteaut A., Ishai Y. (eds.) EUROCRYPT 2020, Part II. LNCS, vol. 12106, pp. 463–492. Springer (2020). https://doi.org/10.1007/978-3-030-45724-2_16
Pointcheval D., Stern J.: Security arguments for digital signatures and blind signatures. J. Cryptol. 13(3), 361–396 (2000). https://doi.org/10.1007/s001450010003.
Rivest R.L., Shamir A., Tauman Y.: How to leak a secret. In: Boyd C. (ed.) ASIACRYPT 2001. LNCS, vol. 2248, pp. 552–565. Springer (2001). https://doi.org/10.1007/3-540-45682-1_32
Unruh D.: Non-interactive zero-knowledge proofs in the quantum random oracle model. In: Oswald E., Fischlin M. (eds.) EUROCRYPT 2015, Part II. LNCS, vol. 9057, pp. 755–784. Springer (2015). https://doi.org/10.1007/978-3-662-46803-6_25
Xu S., Yung M.: Accountable ring signatures: A smart card approach. In: Smart Card Research and Advanced Applications VI, pp. 271–286. Springer (2004)
Yang R., Au M.H., Zhang Z., Xu Q., Yu Z., Whyte W.: Efficient lattice-based zero-knowledge arguments with standard soundness: Construction and applications. In: Boldyreva A., Micciancio D. (eds.) CRYPTO 2019, Part I. LNCS, vol. 11692, pp. 147–175. Springer (2019). https://doi.org/10.1007/978-3-030-26948-7_6
Acknowledgements
Yi-Fu Lai was supported by the Ministry for Business, Innovation and Employment in New Zealand. Shuichi Katsumata was supported by JST CREST Grant Number JPMJCR19F6, Japan. This work was supported by CyberSecurity Research Flanders with reference number VR20192203, and in part by the Research Council KU Leuven grant C14/18/067 on Cryptanalysis of post-quantum cryptography. Ward Beullens is funded by FWO Junior Postdoc- toral Fellowship 1S95620N.
Funding
Open access funding provided by Universitá degli Studi di Bari Aldo Moro within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Data sharing
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Conflict of interest
The authors declare they have no financial and non-financial interests.
Additional information
Communicated by A. Enge.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
Omitted primitives
1.1 Index-hiding Merkle trees
The definition an index-hiding Merkle tree is taken almost verbatim from [14]. Merkle trees [79] allow one to hash a list of elements \(A = ( a_0, \cdots , a_N )\) into one hash value (often called the \(\textsf{root}\)). At a later point, one can efficiently prove to a third party that an element \(a_i\) was included at a certain position in the list A. In the following, we consider a slight modification of the standard Merkle tree construction, such that one can prove that a single element \(a_i\) was included in the tree without revealing its position in the list.
Formally, the Merkle tree technique consists of three algorithms (\(\textsf{MerkleTree}\), \(\textsf{getMerklePath}\), \(\textsf{ReconstructRoot}\)) with access to a common hash function \({\mathcal {H}}_{\textsf{Coll}}:\{0,1\}^{\star } \rightarrow \{0,1\}^{2\uplambda }\).
-
\(\textsf{MerkleTree}(A) \rightarrow (\textsf{root}, \textsf{tree})\): On input a list of \(2^k\) elements \(A = (a_1, \cdots , a_{2^k})\), with \(k \in {\mathbb {N}}\), it constructs a binary tree of height k with \(\{ l_i = {\mathcal {H}}_{\textsf{Coll}}(a_i) \}_{i\in [2^k]}\) as its leaf nodes, and where every internal node h with children \(h_{\textsf{left}}\) and \(h_{\textsf{right}}\) equals the hash digest of a concatenation of its two children. While it is standard to consider the concatenation \(h_{\textsf{left}} \parallel h_{\textsf{right}}\), we consider a variation which consists in ordering the two children according to the lexicographical order (or any other total order on binary strings). We denote by (\(h_{\textsf{left}},h_{\textsf{right}})_{\textsf{lex}}\) this modified concatenation. The algorithm then outputs the root \(\textsf{root}\) of the Merkle tree, as well as a description of the entire tree \(\textsf{tree}\).
-
\(\textsf{getMerklePath}(\textsf{tree}, I) \rightarrow \textsf{path}\): On input the description of a Merkle tree \(\textsf{tree}\) and an index \(i \in [2^k]\), it outputs the list \(\textsf{path}\), which contains the sibling of \(l_i\) (i.e. a node, different from \(l_i\), that has the same parent as \(l_i\)), as well as the sibling of any ancestor of \(l_i\), ordered by decreasing height.
-
\(\textsf{ReconstructRoot}( a, \textsf{path})\rightarrow \textsf{root}\): On input an element a in the list of elements \(A = ( a_1, \cdots , a_{2^k} )\) and \(\textsf{path}= (n_1,\cdots ,n_k)\), it outputs a reconstructed root \(\textsf{root}' = h_k\), which is calculated by putting \(h_0 = {\mathcal {H}}_{\textsf{Coll}}(a)\) and defining \(h_i\) for \(i \in [k]\) recursively as \(h_i = {\mathcal {H}}_{\textsf{Coll}}((h_{i-1},n_i)_{\textsf{lex}})\).
If the hash function \({\mathcal {H}}_{\textsf{Coll}}\) that is used in the Merkle tree is collision-resistant, then the following easy lemma implies that the Merkle tree construction is binding, i.e. that one cannot construct a path that “proves" that a value \(b \notin A=(a_1,\dots ,a_N)\) is part of the list A that was used to construct the Merkle tree without breaking the collision-resistance of the underlying hash function \({\mathcal {H}}_{\textsf{Coll}}\).
Lemma A.1
(Binding for merkle tree) There is an efficient extractor algorithm that, given the description \(\textsf{tree}\) of a Merkle tree (having root \(\textsf{root}\) and constructed using the list of elements A) and \((b,\textsf{path})\) such that \(b \notin A\) and \(\textsf{ReconstructRoot}(b,\textsf{path})=\textsf{root}\), outputs a collision for the hash function \({\mathcal {H}}_{\textsf{Coll}}\).
The use of the lexicographical order to concatenate two children nodes in the Merkle tree construction implies that the output \(\textsf{path}\) of the \(\textsf{getMerklePath}\) algorithm information-theoretically hides the index \(i \in [N]\) given as input. Formally, we have the following.
Lemma A.2
(Index Hiding for Merkle Tree) Let \(N \in {\mathbb {N}}\) be a power of 2, \(D,D'\) be two arbitrary distributions over \(\{0,1\}^{*}\) and \( D_{I} \), with \(I \in [N]\), be the distribution defined as

where \(A = (a_1,\dots ,a_{N})\). Then we have \(D_{I} = D_{J} \) for all \( I,J \in [N]\).
1.2 Seed tree
The definition seed tree is taken almost verbatim from [14]. The purpose of a seed tree is to first generate a number of pseudorandom values and later disclose an arbitrary subset of them, without revealing information on the remaining values. The seed tree is a complete binary treeFootnote 12 of \(\uplambda \)-bit seed values such that the left (resp. right) child of a seed \(\textsf{seed}_h\) is the left (resp. right) half of \(\textsf{Expand}(\textsf{seed}\parallel h)\), where \(\textsf{Expand}\) is a pseudorandom generator (PRG). The unique identifier h of the parent seed is appended to separate the input domains of the different calls to the PRG. A sender can efficiently reveal the seed values associated with a subset of the set of leaves by revealing the appropriate set of internal seeds in the tree. We provide the full detail of the seed tree below. Let \(\textsf{Expand}: \{ 0,1 \} ^{\uplambda + \lceil \log _2 (M-1) \rceil } \rightarrow \{ 0,1 \} ^{2\uplambda }\) be a PRG for any \(\uplambda , M \in {\mathbb {N}}\), instantiated by a random oracle \({\mathcal {O}}\). Then, a seed tree consists of the following four oracle-calling algorithms.
-
\(\textsf{SeedTree}^{\mathcal {O}}(\textsf{seed}_\textsf{root}, M) \rightarrow \{ \textsf{leaf}_i \}_{i \in [M]}:\) On input a root seed \(\textsf{seed}_\textsf{root}\in \{ 0,1 \} ^{\uplambda }\) and an integer \(M \in {\mathbb {N}}\), it constructs a complete binary tree with M leaves by recursively expanding each seed to obtain its children seeds. Calls are of the form \({\mathcal {O}}(\textsf{Expand}\parallel \textsf{seed}_h \parallel h )\), where \(h \in [M-1]\) is a unique identifier for the position of \(\textsf{seed}\) in the binary tree.
-
\(\textsf{ReleaseSeeds}^{\mathcal {O}}( \textsf{seed}_\textsf{root}, {{\textbf {c}}}) \rightarrow {\textsf{seeds}_\textsf{internal}}:\) On input a root seed \(\textsf{seed}_\textsf{root}\in \{ 0,1 \} ^\uplambda \), and a challenge \({{\textbf {c}}}\in \{ 0,1 \} ^M\), it outputs the list of seeds \({\textsf{seeds}_\textsf{internal}}\) that covers all the leaves with index i such that \(c_i = 1\). Here, we say that a set of nodes D covers a set of leaves S if the union of the leaves of the subtrees rooted at each node \(v \in D\) is exactly the set S.
-
\(\textsf{RecoverLeaves}^{\mathcal {O}}({\textsf{seeds}_\textsf{internal}}, {{\textbf {c}}}) \rightarrow \{ \textsf{leaf}_i \}_{i \text { s.t. } c_i = 1}:\) On input a set \({\textsf{seeds}_\textsf{internal}}\) and a challenge \({{\textbf {c}}}\in \{ 0,1 \} ^M\), it computes and outputs all the leaves of subtrees rooted at seeds in \({\textsf{seeds}_\textsf{internal}}\). By construction, this is exactly the set \(\{ \textsf{leaf}_i \}_{i \text { s.t. } c_i = 1}\).
-
\(\textsf{SimulateSeeds}^{\mathcal {O}}( {{\textbf {c}}}) \rightarrow {\textsf{seeds}_\textsf{internal}}:\) On input a challenge \({{\textbf {c}}}\in \{ 0,1 \} ^{M}\), it computes the set of nodes covering the leaves with index i such that \(c_i = 1\). It then randomly samples a seed from \( \{ 0,1 \} ^\uplambda \) for each of these nodes, and finally outputs the set of these seeds as \({\textsf{seeds}_\textsf{internal}}\).
By construction, the leaves \(\{ \textsf{leaf}_i \}_{i \text { s.t. } c_i = 1}\) output by \(\textsf{SeedTree}(\textsf{seed}_\textsf{root}, M)\) are the same as those output by \(\textsf{RecoverLeaves}( \textsf{ReleaseSeeds}(\textsf{seed}_\textsf{root}, {{\textbf {c}}}), {{\textbf {c}}})\) for any \({{\textbf {c}}}\in \{ 0,1 \} ^M\). The last algorithm \(\textsf{SimulateSeeds}\) can be used to argue that the seeds associated with all the leaves with index i such that \(c_i = 0\) are indistinguishable from uniformly random values for a recipient that is only given \({\textsf{seeds}_\textsf{internal}}\) and \({{\textbf {c}}}\). More formally, we have the following.
Lemma A.3
Fix any \(M \in {\mathbb {N}}\) and any \({{\textbf {c}}}\in \{ 0,1 \} ^M\). If we model \(\textsf{Expand}\) as a random oracle \({\mathcal {O}}\), then any (computationally unbounded) adversary \(A^{\mathcal {O}}\) that makes Q queries to the random oracle \({\mathcal {O}}\) can distinguish the following two distributions \(D_1\) and \(D_2\) with distinguishing advantage bounded by \(\frac{Q}{2^\uplambda }\):

Here, the distributions take into account the randomness used by the random oracle as well.
Dynamic group signatures from accountable ring signatures
In this section, we review briefly the definition of group signatures and explain how accountable ring signatures can be naturally viewed as group signatures. A formal treatment can be found in Bootle et al. [20]
1.1 Preliminaries on group signatures
Group signatures can be divided into two primary types: static schemes [8] and dynamic schemes [9]. Roughly, while static group signature require the group to be fixed at setup, dynamic group signatures allow members to join and leave the group at any time. This joining and leaving is administered by the group manager, who has the power to add and revoke membership — as well as the ability to revoke anonymity and reveal the specific signer of a certain signature. For a dynamic group signature scheme, the revocation mechanism can be handled by a separate entity called opening or tracing authority to offer better flexibility in the scheme and this makes only little difference regarding the security notions.
Informally, a dynamic group signature scheme consists of a setup algorithm \(\textsf{Setup}\), key generation algorithms \(\textsf{MKGen}\) and \(\textsf{UKGen}\) for the group manager and group members (or users) respectively, and \(\textsf{Sign}\), \(\textsf{Verify}\), \(\textsf{Open}\), and \(\textsf{Judge}\) algorithms which are counterparts of the ARS scheme functions of the same names. Additionally, an interactive \(\textsf{Join}\) protocol run between the group manager and a user allows users to be added to the group, while an \(\textsf{UpdateGroup}\) function allows the group manager to revoke a user’s membership in the group dynamically (this is done via some publicly-published group info \(\textsf{info}\)).
Dynamic group signature schemes should satisfy standard security properties of correctness, anonymity, traceability and non-frameability [9, 20]. Correctness ensures that a signature produced by a user running \(\textsf{Sign}\) after joining the group via \(\textsf{Join}\) is accepted by \(\textsf{Verify}\). The inclusion of the \(\textsf{Join}\) function in this definition ensures joining works as intended, beyond just guaranteeing the signing algorithms’s correctness. Full \(\textsf{CCA}\)-anonymity (often refereed simply as full anonymity) states that even under full key exposure of all group members (other than the group manager, who can trivially revoke anonymity via \(\textsf{Open}\)), and with access to an opening oracle, the user who generated a certain signature cannot be identified. More specifically, an adversary should be unable to distinguish between signatures generated by any two members of the adversary’s choice— even if the adversary knows all secret keys involved. This notion is almost identical to its namesake in the ARS setting (Sect. 3.4). In contrast, \(\textsf{CPA}\)-anonymity is a weaker notion which still allows the adversary to learn all group members’ keys, but removes access to the opening oracle. Weaker variants of these two are selfless \(\textsf{CCA}\)-anonymity and selfless \(\textsf{CPA}\)-anonymity where the adversary cannot obtain any secret keys of targeted members in the anonymity game. Traceability states that an adversary who is able to corrupt any members is not able to produce a signature for which \(\textsf{Open}\) fails to return an active member of the group even if the group manager’s secret key is leaked. Finally, non-frameability states that even if the group manager and all but one of the group members are corrupted, they cannot forge or falsely attribute a signature to an honest member who did not produce it. These properties also imply what is usually called unforgeability, because if an adversary could produce a signature for a group they knew no secret keys for, the signature must either fail to \(\textsf{Open}\) to an active user, or would frame an honest member of the group—violating either traceability or non-frameability. We also remark a difference, usually being neglected, that the group manager can be corrupted in the security model of a dynamic group while a static variant only takes into account the exposure of the opening secret key [8]. We refer the reader to [20] for more thorough definitions.
1.2 Constructing group signatures from ARS
For completeness, we now review the generic construction of a dynamic group signature scheme from an accountable ring signature scheme, by Bootle et al. [19, 20]. Let \(\Pi _{\textsf{ARS}}\) be a secure ARS scheme, then we define a group signature scheme \(\Pi _{\textsf{GS}}\) as follows:
Let the group manager be the opening authority of \(\Pi _{\textsf{ARS}}\), and let the group manager’s keypair be \((\textsf{gmpk}= \textsf{opk}, \textsf{gmsk}= \textsf{osk})\). The group public key \(\textsf{gpk}\) is then set to \((\textsf{gmpk}, {{\textsf{p}}}{{\textsf{p}}})\), where \({{\textsf{p}}}{{\textsf{p}}}\) is the output of \({{\textsf{G}}}{{\textsf{S}}}.\textsf{Setup}:= \textsf{ARS}.\textsf{Setup}\). Define \({{\textsf{G}}}{{\textsf{S}}}.\textsf{UKGen}:= \textsf{ARS}.\textsf{UKGen}\), so that users generate their own keypairs directly. The \(\textsf{Join}\) protocol proceeds by a user submitting their public key \({{\textsf{p}}}{{\textsf{k}}}\) to the group manager, who appends it to the list of keys in \(\textsf{info}_{\tau }:= [{{\textsf{v}}}{{\textsf{k}}}_0, \ldots , {{\textsf{v}}}{{\textsf{k}}}_i]\) (the group \(\textsf{info}\) at epoch \(\tau \)) and publishes \(\textsf{info}_{\tau +1}\). Membership is similarly revoked by the group manager via \(\textsf{UpdateGroup}\) by removing the user’s public key from \(\textsf{info}_\tau \) and publishing the updated \(\textsf{info}\). Finally, define:
-
\({{\textsf{G}}}{{\textsf{S}}}.\textsf{Sign}(\textsf{gpk}, \textsf{info}_\tau , {{\textsf{s}}}{{\textsf{k}}}_i, {\textsf{M}}):= \textsf{ARS}.\textsf{Sign}(\textsf{gmpk}, {{\textsf{s}}}{{\textsf{k}}}_i, \textsf{info}_\tau , {\textsf{M}})\).
-
\({{\textsf{G}}}{{\textsf{S}}}.\textsf{Verify}(\textsf{gpk}, \textsf{info}_\tau , {\textsf{M}}, \sigma ):= \textsf{ARS}.\textsf{Verify}(\textsf{gmpk}, \textsf{info}_\tau , {\textsf{M}}, \sigma )\).
-
\({{\textsf{G}}}{{\textsf{S}}}.\textsf{Open}(\textsf{gpk}, \textsf{info}_tau, \textsf{gmsk}, {\textsf{M}}, \sigma )\) calls \(({{\textsf{v}}}{{\textsf{k}}}_j, \pi ) \leftarrow \textsf{ARS}.\textsf{Open}(\textsf{gmsk}, \textsf{info}_\tau , {\textsf{M}}, \sigma )\) and returns \((j, \pi )\).
-
\({{\textsf{G}}}{{\textsf{S}}}.\textsf{Judge}(\textsf{gpk}, \textsf{info}_\tau , {\textsf{M}}, \sigma , (j,\pi )):= \textsf{ARS}.\textsf{Judge}(\textsf{gmpk}, \textsf{info}_\tau , {{\textsf{v}}}{{\textsf{k}}}_j, {\textsf{M}}, \sigma , \pi )\).
Note that \(\textsf{info}_\tau \) defines the ring of signers at epoch \(\tau \) and should be publicly accessible, as too should be the index-to-public-key (\(j \leftrightarrow {{\textsf{v}}}{{\textsf{k}}}_j\)) correspondence table, maintained by the group manager. As shown in [20], this generic construction of a group signature from an ARS is tightly secure assuming the ARS is secure. Hence, our ARS construction in Sect. 4.1 implies a secure dynamic group signature scheme. The type of security notions satisfied by the resulting group signature, e.g., full or selfless, \(\textsf{CCA}\) or \(\textsf{CPA}\) anonymity, is directly inherited from the ARS.
We note that this scheme’s group \(\textsf{info}\) grows linearly in the number of group members. This is the same as all other proposed efficient post-quantum group signature constructions such as [48]. It remains an interesting open problem to construct a efficient group signature where the group \(\textsf{info}\) grows at most logarithmically in the number of group members.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Beullens, W., Dobson, S., Katsumata, S. et al. Group signatures and more from isogenies and lattices: generic, simple, and efficient. Des. Codes Cryptogr. 91, 2141–2200 (2023). https://doi.org/10.1007/s10623-023-01192-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10623-023-01192-x
Keywords
- Isogeny-based cryptography
- Lattice-based cryptography
- Linkable ring signature
- Post-quantum cryptography