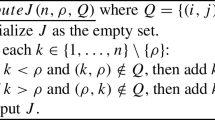Decentralized multi-client functional encryption for set intersection with improved efficiency

Abstract

Functional encryption (FE) is a new paradigm of public key encryption that can control the exposed information of plaintexts by supporting computation on encrypted data. In this paper, we propose efficient multi-client FE (MCFE) schemes that compute the set intersection of ciphertexts generated by two clients. First, we propose an MCFE scheme that calculates the set intersection cardinality (MCFE-SIC) and prove its static security under dynamic assumptions. Next, we extend our MCFE-SIC scheme to an MCFE scheme for set intersection (MCFE-SI) and prove its static security under dynamic assumptions. The decryption algorithm of our MCFE-SI scheme is more efficient than the existing MCFE-SI scheme because it requires fewer pairing operations to calculate the intersection of two clients. Finally, we propose a decentralized MCFE scheme for set intersection (DMCFE-SI) that decentralizes the generation of function keys. Our MCFE schemes can be effectively applied to a privacy-preserving contact tracing system to prevent the spread of recent infectious diseases.

1 Introduction

Functional encryption (FE) is a cryptographic technique that supports a controlled functional evaluation on encrypted data and has an interesting feature that the result of the function evaluation is directly revealed in the decryption [14]. In FE, a user creates a ciphertext CT for a plaintext x using a public key, and an entity who possesses a function key $DK_f$ for a function f issued by a trusted center can obtain f(x) by decrypting the ciphertext. As interesting extensions of FE, multi-input FE (MIFE) that handles multiple ciphertexts during decryption and multi-client FE (MCFE) that provides independent encryption keys for each client were proposed [21]. FE schemes that support arbitrary functions can be constructed by using indistinguishability obfuscation, but indistinguishability obfuscation is still inefficient to implement. In order to construct efficient FE schemes, research on FE that supports only special functions instead of general functions has been actively conducted [2, 3, 6].

Recently, FE schemes that support the set intersection operation were proposed [32, 37]. An interesting application of the FE schemes for set intersection is privacy-preserving contact tracing [1], which allows a user to check the possibility of contact with a confirmed patient while preserving the location privacy of the user. A specific example is as follows. First, a hospital cloud server encrypts and stores the visited places of a confirmed patient by associating with time periods. If a user wants to know whether he or she has been in contact with the confirmed patient, the user encrypts visited places associated with time periods and uploads them to the cloud server. Then, the cloud server receives a function key that computes the set intersection cardinality between the confirmed patient and the user, and calculates the cardinality of an intersection set between them. If the cardinality has a positive value, then the cloud server notifies the user that the probability of contact is high. In the later, if the user wants to determine the exact intersection place, the user can calculate the intersection by requesting a function key for set intersection.

The first FE schemes for set intersection were proposed by Kamp et al. [37], but their schemes have some problems such that the result of set intersection is publicly revealed to anybody since there is no function key and the setup algorithm should be independently performed among all pairs of clients. To solve these problems, Lee and Seo proposed MCFE for set intersection (MCFE-SI) schemes that support the generation of function keys between multiple clients after running the setup algorithm just once initially [32]. They designed their MCFE-SI schemes in bilinear groups by inventing the equal-then-derive technique. That is, a client with an index i who has a set $X = \{ x_k \}$ of items creates a ciphertext element $H(x_k)^{\alpha _i}$ for each item, and it additionally sets a temporal key $K = e(H(x_k), {\hat{g}})^{\beta _i}$ as a symmetric key to encrypt an item $x_k$. If both i and j clients encrypt the equal item x, then the temporal key $K = e(H(x)^{\alpha _i} H(x)^{\alpha _j}, {\hat{g}}^{\beta _i / (\alpha _i + \alpha _j)})$ can be derived if a function key ${\hat{g}}^{\beta _i / (\alpha _i + \alpha _j)}$ is provided.

In this paper, we intend to improve the performance and functionality of the MCFE-SI schemes of Lee and Seo [32]. The first problem with the MCFE-SI schemes of Lee and Seo is that their decryption algorithm is inefficient. In other words, the decryption algorithm of their MCFE-SI schemes require the process of decrypting all combinations of ciphertext elements of two clients i and j and checking that a correct value is derived. Thus, this decryption algorithm requires approximately $\ell ^2$ pairing operations where $\ell$ is the number of items in a set, and it causes a serious problem in performance when the number of items increases. The second problem is that their MCFE-SI schemes require a trusted center to generate function keys. The existence of a trusted center can hinder the deployment of this system to the real environment since there are issues such that a central authority can monitor the activities of users. Therefore, in this paper, we ask whether it is possible to design an MCFE-SI scheme that supports efficient decryption and decentralized function key generation.

1.1 Our contributions

Table 1 Comparison of functional encryption schemes for set intersection

In this paper, we devise efficient MCFE-SI schemes and give positive answers to the preceding questions. The detailed results of our contributions are summarized as follows.

MCFE for set intersection cardinality We first propose an MCFE for set intersection cardinality scheme (MCFE-SIC) that calculates the cardinality of the intersection of two client’s sets. To support the set intersection cardinality, we use the ciphertext structure of the MCFE-SI scheme proposed by Lee and Seo [32] and modify their scheme to provide a new function key to check whether the ciphertext elements generated by different clients contain equal items. At this time, in order to test the equality of the ciphertext elements generated by different clients, we notice that the ciphertext structure of Lee and Seo uses an algebraic pseudo-random function (PRF) which is defined as $H(x)^{\alpha _i}$ where x is an item and $\alpha _i$ is the secret key of an i-index client and H is a hash function. If a function key is provided as $({\hat{g}}^{\alpha _i r}, {\hat{g}}^{\alpha _j r})$ where r is a random exponent, it is possible to check whether the ciphertext elements of two clients i and j are encryption of the same item through the equation $e(H(x)^{\alpha _i}, {\hat{g}}^{\alpha _j r}) = e(H(x)^{\alpha _j}, {\hat{g}}^{\alpha _j r})$ by using a pairing operation. The decryption algorithm of this scheme additionally exposes the equality pattern between ciphertext elements in addition to the set intersection cardinality. The ciphertext of our MCFE-SIC scheme consists of $\ell$ ciphertext elements, the function key consists of two group elements, and the decryption algorithm requires $2\ell$ pairing operations and $O(\ell \log \ell )$ comparison operations for sorting where $\ell$ is the number of items in a set.

MCFE for set intersection Next, we propose an MCFE for Set Intersection (MCFE-SI) scheme with improved decryption performance compared to the previous MCFE-SI scheme. The idea of improving the decryption performance is to efficiently find a matching pair of ciphertext elements that contain the same item from two client ciphertexts by using the function key of our MCFE-SIC scheme. To decrypt the ciphertext elements of the actual set item in the ciphertext, we use the same equal-then-derive method proposed by Lee and Seo [32]. That is, when two matching ciphertext elements of two clients are $H(x)^{\alpha _i}$ and $H(x)^{\alpha _j}$, we can derive a temporal key $K = e(H(x)^{\alpha _i} H(x)^{\alpha _j}, {\hat{g}}^{\beta _i / (\alpha _i + \alpha _j)}) = e(H(x), {\hat{g}})^{\beta _i}$ for symmetric-key decryption if a function key ${\hat{g}}^{\beta _i / (\alpha _i + \alpha _j)}$ is provided. To analyze the security of our MCFE-SI scheme, we prove the security of our scheme by using newly introduced complexity assumptions in the static-IND security model in which function key queries, corrupted clients, and challenge messages are initially submitted by an attacker. Compared to the MCFE-SI scheme of Lee and Seo that requires $\ell ^2$ pairing operations in decryption, Our MCFE-SI scheme is more efficient since the decryption algorithm requires only $2\ell$ pairing operations and $O(\ell \log \ell )$ comparison operations where $\ell$ is the number of items in a set. The comparison of our MCFE schemes with other similar schemes is given in Table 1.

Decentralized MCFE for set intersection Finally, we propose a decentralized MCFE scheme for set intersection (DMCFE-SI) that removes the trusted center that generates function keys in our MCFE-SI scheme. The function key of our MCFE-SI scheme is composed of two key elements ${\hat{g}}^{\alpha _i r}$ and ${\hat{g}}^{\alpha _j r}$ for calculating the set intersection cardinality and one key element ${\hat{g}}^{\beta _i / (\alpha _i + \alpha _j)}$ for deriving a temporal key. The difficulty of decentralizing the generation of function keys is that two clients i and j should select the same random exponent r and the exponent inverse operation $(\alpha _i + \alpha _j)^{-1}$ which includes client secret keys should be decentralized. To select the same random exponent, each client exposes a public key and runs the Diffie–Hellman non-interactive key exchange scheme between two clients. Decentralizing the exponent inverse operation cannot be solved in a simple way. To solve this problem, each client creates an encoded secret key by encrypting a secret key with one-time pad, and an entity that combines the partial function keys to perform the exponent inversion operation by itself after combining the encoded secret keys of two clients. We can prove the security of our DMCFE-SI scheme because the additionally exposed encoded secret keys are information theoretically secure.

1.2 Related work

Functional encryption Boneh et al. [14] introduced the concept of functional encryption (FE) as a new paradigm for public key encryption. They showed that identity-based encryption [11], attribute-based encryption [23, 34], and predicate encryption [12, 28] are all special forms of FE. The first FE scheme that supports arbitrary functions was designed by Garg et al. [19] by using indistinguishability obfuscation, public-key encryption, and non-interactive zero-knowledge proof. In addition, there have been various attempts to design FE schemes that support arbitrary functions with bounded collusion by using weaker cryptographic primitives instead of using indistinguishability obfuscation [20, 22]. In order to improve the practicality of FE schemes, an FE scheme for inner-products (FE-IP) that support the inner product operation between attributes in a ciphertext and a function key was proposed by Abdalla et al. [2]. Since then, the research on FE-IP has been expanded to support function hiding, full security, and quadratic functions [6, 9, 10].

Multi-input and multi-client functional encryption Goldwasser et al. [21] extended the concept of FE that handles only one ciphertext in decryption to the concept of multi-input functional encryption (MIFE) and multi-client functional encryption (MCFE) that support the evaluation of a function on multiple ciphertexts. They also showed that these MIFE and MCFE schemes can be constructed by using indistinguishability obfuscation. MIFE and MCFE are the same in terms of processing multiple ciphertexts, but MCFE has an important difference in that ciphertexts are additionally associated time periods and only ciphertexts associated with the same time period are processed during decryption. The research on FE-IP has been expanded to support multiple inputs, multiple clients, and decentralized key generation [3,4,5, 15, 31]. In addition, FE for quadratic function also can be extended to support multiple inputs [7]. As another efficient MCFE schemes, MCFE schemes that support the set intersection operation and MCFE scheme that support conjunctive equality and range query operations between multiple clients have been proposed [30, 32, 37].

Private set intersection Private set intersection (PSI) is a cryptographic technique that allows two parties compute the intersection of their private sets without revealing any other information of the sets. Compared to an FE scheme that supports the set intersection operation, a PSI protocol requires additional interactions between two parties when calculating the set intersection. A simple way to implement a PSI protocol is to use the Diffie–Hellman key exchange protocol, which is efficient in the terms of communication, but it requires public key operations [26]. A PSI protocol by using oblivious polynomial evaluation that expresses sets as polynomials was proposed by Freedman et al. [17]. After that, oblivious PRF based PSI protocols, garbled circuit based PSI protocols, and oblivious transfer based PSI protocols have been proposed [24, 25, 29, 33]. In order to reduce the communication overhead of PSI protocols, delegated PSI protocols in which a cloud server performs most of the computation of clients were proposed [27]. Recently, private set intersection cardinality (PSI-CA) protocols for contact tracing have been proposed [16, 36].

2 Preliminaries

In this section, we define functional encryption, symmetric-key encryption, and pseudo-random function. We also introduce complexity assumptions to prove the security of our functional encryption schemes.

2.1 Multi-client functional encryption

Multi-client functional encryption (MCFE) is an extension of functional encryption (FE) that supports computation on encrypted data, and it requires a client secret key for encryption and handles multiple ciphertexts during decryption [21]. In MCFE, the client of an index i encrypts a plaintext $x_i$ with a time label T using the client secret key $SK_i$ to generate a ciphertext $CT_{i,T}$. Subsequently, an entity who has a function key $DK_f$ for a function f decrypts ciphertexts $CT_{1,T}, \ldots , CT_{n,T}$ with the same time label T and obtains a decrypted result $f(x_1, \ldots , x_n)$. The IND security model of MCFE is defined by Goldwasser et al. [21]. A more detailed syntax of MCFE is given as follows.

Definition 1

(Multi-Client Functional Encryption) A multi-client functional encryption (MCFE) scheme consists of four algorithms Setup, GenKey, Encrypt, and Decrypt, which are defined as follows:

• Setup($1^{\lambda }, n$) The setup algorithm takes as input the security parameter $\lambda$ in unary and the number of clients n. It outputs a master key MK, client secret keys $(SK_1, \ldots , SK_n)$, and public parameters PP.

• GenKey(f, MK, PP) The key generation algorithm takes as input a function f, the master key MK, and public parameters PP. It outputs a function key $DK_f$.

• Encrypt($x, T, SK_i, PP$) The encryption algorithm takes as input a message x, a time period T, a client secret key $SK_i$, and public parameters PP. It outputs a ciphertext $CT_{i,T}$.

• Decrypt($(CT_{1,T}, \ldots , CT_{n,T}), DK_f, PP$) The decryption algorithm takes as input ciphertexts $(CT_{1,T}, \ldots , CT_{n,T})$ in which each $CT_{i,T}$ is an encryption of a message $x_i$ on the same time period T, a function key $DK_f$ corresponding to a function f, and public parameters PP. It outputs a value $f(x_1, \ldots , x_n)$.

The correctness of the MCFE scheme is defined as follows: For all $(MK, (SK_1, \ldots , SK_n), PP) [0]\leftarrow {\textbf {Setup}}(1^{\lambda }, n)$, $DK_f \leftarrow {\textbf {GenKey}}(f, MK, PP)$ for any function $f \in \mathcal {F}$, and $CT_{i,T} \leftarrow {\textbf {Encrypt}}[0](x_i, T, SK_i, PP)$ for $i \in [n]$ and any $x_i \in \mathcal {X}$, it is required that Decrypt$((CT_{1,T}, \ldots , CT_{n,T}), DK_f, [0]PP) = f(x_1, \ldots , x_n)$.

2.2 Symmetric key encryption

Symmetric key encryption (SKE) is an encryption method that uses the same key for encryption and decryption. The general security model of SKE is the IND security model that allows multiple challenge ciphertext queries. For this paper, we use a one-message IND security model that only allows only one challenge ciphertext query. The detailed syntax of SKE is given as follows.

Definition 2

(Symmetric Key Encryption) A symmetric key encryption (SKE) scheme consists of three algorithms GenKey, Encrypt, and Decrypt, which are defined as follows:

• GenKey($1^{\lambda }$) The key generation algorithm takes as input the security parameter $\lambda$. It outputs a symmetric key K.

• Encrypt(M, K) The encryption algorithm takes as input a message $M \in \mathcal {M}$ and the symmetric key K. It outputs a ciphertext C.

• Decrypt(C, K) The decryption algorithm takes as input a ciphertext CT and the symmetric key K. It outputs a message M or a symbol $\perp$.

The correctness of the SKE scheme is defined as follows: For all K generated by ${\textbf {GenKey}}$ and any message $M \in \mathcal {M}$, it is required that ${\textbf {Decrypt}} ({\textbf {Encrypt}}(M, K), K) = M$.

2.3 Pseudo-random function

A pseudo-random function (PRF) is a function $F:\mathcal {K}\times \mathcal {X} \rightarrow \mathcal {Y}$ where $\mathcal {K}$ is a key space, $\mathcal {X}$ is a domain, and $\mathcal {Y}$ is a codomain. Let $F(k, \cdot )$ be an oracle for a uniformly chosen $k \in \mathcal {K}$ and $f(\cdot )$ be an oracle for a uniformly chosen function $f : \mathcal {X} \rightarrow \mathcal {Y}$. We say that a PRF F is secure if for all efficient adversaries $\mathcal {A}$, the advantage of $\mathcal {A}$ defined as ${\textbf {Adv}}_{\mathcal {A}}^{PRF}(\lambda ) = \big | \Pr [\mathcal {A}^{F(k,\cdot )} = 1] - \Pr [\mathcal {A}^{f(\cdot )} = 1] \big |$ is negligible in the security parameter $\lambda$.

2.4 Bilinear groups

A bilinear group generator $\mathcal {G}$ takes as input a security parameter $\lambda$ and outputs a tuple $(p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e)$ where p is a random prime and ${\mathbb {G}}, {\hat{{\mathbb {G}}}}$, and ${\mathbb {G}}_T$ are three cyclic groups of prime order p. Let g and ${\hat{g}}$ be generators of ${\mathbb {G}}$ and ${\hat{{\mathbb {G}}}}$, respectively. The bilinear map $e : {\mathbb {G}}\times {\hat{{\mathbb {G}}}} \rightarrow {\mathbb {G}}_{T}$ has the following properties:

• 1. Bilinearity: $\forall u \in {\mathbb {G}}, \forall {\hat{v}} \in {\hat{{\mathbb {G}}}}$ and $\forall a,b \in {\mathbb {Z}}_p$, $e(u^a,{\hat{v}}^b) = e(u,{\hat{v}})^{ab}$.

• 2. Non-degeneracy: $\exists g \in {\mathbb {G}}, {\hat{g}} \in {\hat{{\mathbb {G}}}}$ such that $e(g,{\hat{g}})$ has order p in ${\mathbb {G}}_T$.

We say that ${\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T$ are asymmetric bilinear groups with no efficiently computable isomorphisms if the group operations in ${\mathbb {G}}, {\hat{{\mathbb {G}}}}$, and ${\mathbb {G}}_T$ as well as the bilinear map e are all efficiently computable, but there are no efficiently computable isomorphisms between ${\mathbb {G}}$ and ${\hat{{\mathbb {G}}}}$.

2.5 Complexity assumptions

We introduce complexity assumptions necessary to prove the security of our MCFE schemes. These complexity assumptions are dynamic assumptions that are defined depending on the key queries of an attacker. Note that these assumptions are slight modifications of the assumptions introduced by Lee and Seo [32]. We analyze that these complexity assumptions hold in the generic group model in Sect. 7.

Let n be a positive integer, $\rho$ be a target index such that $\rho \in [n]$, and $Q = \{ (i,j) \}$ be a set of index pairs that $i, j \in [n]$ and $i < j$. From $n, \rho$, and Q, we define an index set $J = \{ k : 1 \le k \ne \rho \le n \text { such that } (k,\rho ) \notin Q \text { if } k < \rho \text { and } (\rho ,k) \notin Q \text { if } k > \rho \}$. This set can be computed by using the function ComputeJ which is described as follows:

$\underline{{ComputeJ}(n, \rho , Q)}$ where $Q = \{ (i,j) \}$

1. Initialize a set $J = \emptyset$.

2. For each $k \in \{ 1, \ldots , n \} \setminus \{ \rho \}$:

If $k < \rho$ and $(k,\rho ) \notin Q$, then add k to J.

If $k > \rho$ and $(\rho ,k) \notin Q$, then add k to J.

3. Output the set J.

For example, if we let $n = 4$, $\rho = 2$, and $Q = \{ (1,4), (2,3), (2,4) \}$, then we obtain $J = \{ 1 \}$ since $(1,2) \notin Q$, $(2,3) \in Q$, and $(2,4) \in Q$.

Assumption 1

Let $(p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e)$ be a bilinear group randomly generated by $\mathcal {G}(1^\lambda )$. Let $g, {\hat{g}}$ be random generators of ${\mathbb {G}}, {\hat{{\mathbb {G}}}}$ respectively. Let $n, \rho , Q, J$ be defined above. The Assumption 1 for $(n, \rho , Q, J)$ is that if the challenge tuple

$$\begin{aligned} D = \big (&(p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e),~ g,~ g^a,~ \{ g^{b_i} \}_{i=1}^n,~ \{ g^{a b_k} \}_{k \in J},~ {\hat{g}},~ \{ ( {\hat{g}}^{b_i c_{i,j}},~ {\hat{g}}^{b_j c_{i,j}} ) \}_{(i,j) \in Q} \big ) \text{ and } Z \end{aligned}$$

are given, no probabilistic polynomial-time (PPT) algorithm $\mathcal {A}$ can distinguish $Z = Z_0 = g^{a b_{\rho }}$ from $Z = Z_1 = g^d$ with more than a negligible advantage. The advantage of $\mathcal {A}$ is defined as ${\textbf {Adv}}_{\mathcal {A}}^{A1\text {-}(n,\rho ,Q,J)} (\lambda ) = \big | \Pr [\mathcal {A}(D,Z_0) = 0] - \Pr [\mathcal {A}(D,Z_1) = 0] \big |$ where the probability is taken over random choices of parameters to $\mathcal {A}$ and over the coin tosses of $\mathcal {A}$.

Assumption 2

Let $(p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e)$ be a bilinear group randomly generated by $\mathcal {G}(1^\lambda )$. Let $g, {\hat{g}}$ be random generators of ${\mathbb {G}}, {\hat{{\mathbb {G}}}}$ respectively. Let $n, \rho , Q, J$ be defined above. The Assumption 2 for $(n, \rho , Q, J)$ is that if the challenge tuple

$$\begin{aligned} D = \big (&(p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e),~ g,~ g^a,~ \{ g^{b_i} \}_{i=1}^n,~ \{ g^{a b_k} \}_{k \in J},~ \\&{\hat{g}},~ \{ ( {\hat{g}}^{b_i c_{i,j}},~ {\hat{g}}^{b_j c_{i,j}},~ {\hat{g}}^{1 / (b_i + b_j)} ) \}_{(i,j) \in Q} \big ) \text{ and } Z \end{aligned}$$

are given, no probabilistic polynomial-time (PPT) algorithm $\mathcal {A}$ can distinguish $Z = Z_0 = g^{a b_{\rho }}$ from $Z = Z_1 = g^d$ with more than a negligible advantage. The advantage of $\mathcal {A}$ is defined as ${\textbf {Adv}}_{\mathcal {A}}^{A2\text {-}(n,\rho ,Q,J)} (\lambda ) = \big | \Pr [\mathcal {A}(D,Z_0) = 0] - \Pr [\mathcal {A}(D,Z_1) = 0] \big |$ where the probability is taken over random choices of parameters to $\mathcal {A}$ and over the coin tosses of $\mathcal {A}$.

Assumption 3

Let $(p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e)$ be a bilinear group randomly generated by $\mathcal {G}(1^\lambda )$. Let $g, {\hat{g}}$ be random generators of ${\mathbb {G}}, {\hat{{\mathbb {G}}}}$ respectively. Let $n, \rho , Q$ be defined above. The Assumption 3 for $(n, \rho , Q)$ is that if the challenge tuple

$$\begin{aligned} D = \big (&(p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e),~ g,~ g^a,~ \{ g^{b_i} \}_{i=1}^n,~ \{ g^{a b_k} \}_{1 \le k \ne \rho \le n},~ \\&{\hat{g}},~ \{ ( {\hat{g}}^{b_i c_{i,j}},~ {\hat{g}}^{b_j c_{i,j}},~ {\hat{g}}^{d_i / (b_i + b_j)} ) \}_{(i,j) \in Q},~ \{ {\hat{g}}^{d_i} \}_{1 \le i \ne \rho \le n},~ e(g, {\hat{g}})^{d_\rho } \big ) \text{ and } Z \end{aligned}$$

are given, no probabilistic polynomial-time (PPT) algorithm $\mathcal {A}$ can distinguish $Z = Z_0 = e(g, {\hat{g}})^{a d_\rho }$ from $Z = Z_1 = e(g, {\hat{g}})^f$ with more than a negligible advantage. The advantage of $\mathcal {A}$ is defined as ${\textbf {Adv}}_{\mathcal {A}}^{A3\text {-}(n,\rho ,Q)} (\lambda ) = \big | \Pr [\mathcal {A}(D,Z_0) = 0] - \Pr [\mathcal {A}(D,Z_1) = 0] \big |$ where the probability is taken over random choices of parameters to $\mathcal {A}$ and over the coin tosses of $\mathcal {A}$.

3 MCFE for set intersection cardinality

In this section, we define the syntax and security model of MCFE that calculates the set intersection cardinality. And then we propose an efficient MCFE-SIC scheme by using a bilinear map and analyze the security of our scheme.

3.1 Definition

We define the syntax of MCFE for set intersection cardinality (MCFE-SIC). MCFE-SIC is a special form of FE and supports a function key for calculating the set intersection cardinality in which a ciphertext is associated with a time label T and each client has its own secret key $SK_i$ for encryption. In MCFE-SIC, a trusted center creates client secret keys and public parameters. After that, an individual client associates an item set $X_i$ with a time label T and generate a ciphertext $CT_{i,T}$ by using its secret key $SK_i$. A third entity who wants to calculate the set intersection cardinality receives a function key DK for client indexes (i, j) from the trusted center. After that, the third entity decrypts the ciphertexts of the i-index client and the j-index client by using the function key, and obtains the value $| X_i \cap X_j |$. The detailed syntax of MCFE-SIC is described as follows.

Definition 3

(MCFE for Set Intersection Cardinality) A multi-client functional encryption for set intersection cardinality (MCFE-SIC) scheme for an item space $\mathcal {D}$ and a time space $\mathcal {T}$ consists of four algorithms Setup, GenKey, Encrypt, and Decrypt, which are defined as follows:

• Setup($1^{\lambda }, n$) The setup algorithm takes as input the security parameter $\lambda$ and the number of clients n. It outputs a master key MK, client secret keys $(SK_1, \ldots , SK_n)$, and public parameters PP.

• GenKey(f, MK, PP) The function key generation algorithm takes as input a function $f = (i,j)$, the master key MK, and public parameters PP. It outputs a function key $DK_{f}$.

• Encrypt($X_i, T, SK_i, PP$) The encryption algorithm takes as input a set $X_i = \{ x_{i,1}, \ldots , x_{i,\ell _i} \}$ of items where $x_{i,k} \in \mathcal {D}$, a time period $T \in \mathcal {T}$, a client secret key $SK_i$, and public parameters PP. It outputs a ciphertext $CT_{i,T}$.

• Decrypt($CT_{i,T}, CT_{j,T}, DK_{f}, PP$) The decryption algorithm takes as input two ciphertexts $CT_{i,T}$ and $CT_{j,T}$ for the same time T, a function key $DK_{f}$ for a function $f = (i,j)$, and public parameters PP. It outputs $|X_i \cap X_j|$ where $X_i$ and $X_j$ are associated with $CT_{i,T}$ and $CT_{j,T}$ respectively.

The correctness of the MCFE-SIC scheme is defined as follows: For all $MK, (SK_i)_{i=1}^n, PP \leftarrow {\textbf {Setup}}(1^{\lambda }, n)$, any $DK_{f} \leftarrow {\textbf {GenKey}}(f, MK, PP)$ of a function $f = (i,j)$, and all $CT_{i,T} \leftarrow {\textbf {Encrypt}}(X_i, T, SK_i, PP)$ and $CT_{j,T} \leftarrow {\textbf {Encrypt}}[0](X_j, T, SK_j, PP)$ for any $X_i, X_j$ and the same time period T, it is required that

• Decrypt$(CT_{i,T}, CT_{j,T}, DK_{f}, PP) = |X_i \cap X_j|$ except with negligible probability.

We define the IND security model of MCFE-SIC. The security model of MCFE was first defined by Goldwasser et al. [21]. For the security model of MCFE-SIC, we use the static IND security model of MCFE-SI defined by Lee and Seo with slight modification [32]. The static IND security model defined by Lee and Seo is a security model in which an attacker fixes function key queries and a list of corrupted clients in advance and submits the target challenge sets $X_0^*$ and $X_1^*$ in advance. At this time, we set a constraint that the cardinality of set intersection exposed in the challenge sets is the same even if many function keys are provided to an attacker. We consider a limited security model in which the cardinality of set intersections and the equality patterns of the challenge ciphertexts are exposed when an attacker decrypts the challenge ciphertexts using function keys.

We first define a function $CSIC( (X_k)_{k \in I}, Q)$ for a tuple $( X_k )_{k \in I}$ of item sets $X_k$ and a set $Q = \{ (i,j) \}$ that computes the set intersection cardinality of $X_i$ and $X_j$ for each $(i,j) \in Q$ as follows:

$\underline{{CSIC}((X_k)_{k \in I}, Q)}$ where $Q = \{ (i,j) \}$

1. Initialize a set $C = \emptyset$.

2. For each $(i,j) \in Q$:

Calculate $c = |X_i \cap X_j|$ and add ((i, j), c) to C.

3. Output the set C.

Additionally, we define a function $CSIP( (X_k)_{k \in I}, Q)$ for a tuple $( X_k )_{k \in I}$ of item sets $X_k$ and a set $Q = \{ (i,j) \}$ that computes the set intersection pattern of $X_i$ and $X_j$ for each $(i,j) \in Q$ as follows:

$\underline{{CSIPA}(i^*, (X_k)_{k \in I}, Q)}$

1. For each $x \in X_{i^*}$, initialize a set $S_x = \emptyset$.

2. For each $(i,j) \in Q$ such that $i = i^*$ or $j = i^*$:

Calculate $Y = X_i \cap X_j$.

For each $x \in Y$:

If $i=i^*$, add j to $S_x$.

If $j=i^*$, add i to $S_x$.

3. Output a pattern multiset $P_{i^*} = \{ S_x \}_{x \in X_{i^*}}$.

$\underline{{CSIP}((X_k)_{k \in I}, Q)}$ where $Q = \{ (i,j) \}$

1. For each $i \in I$:

Calculate $P_i$ by calling $CSIPA(i, (X_k)_{k \in I}, Q)$.

2. Output a tuple $(P_i)_{i \in I}$ of pattern multisets.

For example, if we let $n = 3, (X_1 = \{ a, b, c \}, X_2 = \{ b, c \}, X_3 = \{ c, a \})$, and $Q = \{ (1,2), (2,3) \}$, then we have $CSIC((X_k), Q) = \{ ((1,2),2), ((2,3),1) \}$ and $CSIP((X_k), Q) = ( P_1 = \{ \emptyset , \{ 2 \}, \{ 2 \} \}, [0]P_2 = \{ \{ 1 \}, \{ 1, 3 \} \}, P_3 = \{ \{ 2 \}, \emptyset \} )$.

Definition 4

(Static-IND Security) The static-IND security of MCFE-SIC with corruptions is defined in the following experiment ${\textbf {EXP}}_{MCFE\text {-}SIC,\mathcal {A}}^{ST\text {-}IND} (1^\lambda )$ between a challenger $\mathcal {C}$ and a PPT adversary $\mathcal {A}$:

• 1. Init: $\mathcal {A}$ initially submits an index set ${\overline{I}} \subset [n]$ of corrupted clients. Let $I = \{ 1, \ldots , n \} \setminus {\overline{I}}$ be an index set of uncorrupted clients. $\mathcal {A}$ also submits two challenge tuples $( X_{0,k}^* )_{k \in I}$ and $( X_{1,k}^* )_{k \in I}$ of item sets $X_{b,k}^* = \{ x_{b,k,j} \}$, a challenge time period $T^*$, and a set $Q = \{ (i,j) \}$ of function key queries with the three restrictions such that (a) $i,j \in I$ for each $(i,j) \in Q$, (b) $CSIC(( X_{0,k}^* )_{k \in I}, Q) = CSIC(( X_{1,k}^* )_{k \in I}, Q)$, and (c) $CSIP(( X_{0,k}^* )_{k \in I}, Q) = CSIP(( X_{1,k}^* )_{k \in I}, Q)$.

• 2. Setup: $\mathcal {C}$ generates a master key MK, client secret keys $( SK_i )_{i=1}^n$, and public parameters PP by running Setup$(1^{\lambda }, n)$. It keeps MK and $( SK_i )_{i \in I}$ to itself and gives $( SK_i )_{i \in {\overline{I}}}$ and PP to $\mathcal {A}$.

• 3. Challenge: $\mathcal {C}$ flips a random bit $\mu \in \{0,1\}$ and obtains a ciphertext $CT_{i,T^*}$ by running Encrypt$(X_{\mu ,i}^*, [0]T^*, SK_i, PP)$ for each $i \in I$. $\mathcal {C}$ gives the challenge ciphertexts $( CT_{i,T^*} )_{i \in I}$ to $\mathcal {A}$

• 4. Query: $\mathcal {A}$ requests function keys and ciphertexts. $\mathcal {C}$ handles these queries as follows:

  • If this is a function key query for a function $f = (i,j) \in Q$, then $\mathcal {C}$ gives a function key $DK_{f}$ to $\mathcal {A}$ by running GenKey(f, MK, PP).

  • If this is a ciphertext query for a client index $k \in I$, an item set $X_k$, and a time period $T \ne T^*$, then $\mathcal {C}$ gives a ciphertext $CT_{k,T}$ to $\mathcal {A}$ by running Encrypt$(X_k, T, SK_k, PP)$.

• 5. Guess: $\mathcal {A}$ outputs a guess $\mu ' \in \{0,1\}$ of $\mu$. $\mathcal {C}$ outputs 1 if $\mu = \mu '$ or 0 otherwise.

An MCFE-SIC scheme is static-IND secure with corruptions if for all PPT adversary $\mathcal {A}$, the advantage of $\mathcal {A}$ defined as ${\textbf {Adv}}_{MCFE\text {-}SIC,\mathcal {A}}^{ST\text {-}IND} (\lambda ) [0]= \big | \Pr [ {\textbf {EXP}}_{MCFE\text {-}SIC,\mathcal {A}}^{ST\text {-}IND} (1^\lambda ) = 1 ] - \frac{1}{2} \big |$ is negligible in the security parameter $\lambda$.

3.2 Construction

The basic idea of designing an MCFE scheme that computes the set intersection cardinality of two clients is to provide a function key that can check whether ciphertext elements generated by two clients are related to the same item. For this, we can consider to provide a function key $({\hat{g}}^{\alpha _i}, {\hat{g}}^{\alpha _j})$ because ciphertext elements are in the form of $H(T \Vert x)^{\alpha _i}$ and $H(T \Vert x)^{\alpha _j}$. In this case, by deriving the same $e(H(T \Vert x), {\hat{g}})^{\alpha _i, \alpha _j}$ through the pairing operation, it is possible to compare whether the ciphertext elements are associated to the same item x. However, providing a function key in this simple form has the risk of a collusion attack, so we provide a function key $({\hat{g}}^{\alpha _i r}, {\hat{g}}^{\alpha _j r})$ with additional randomization to prevent the collusion attack. In this case, only the set intersection of two clients i and j can be compared due to the additionally included random exponent, and comparison with the ciphertexts of other clients is impossible. An MCFE-SIC scheme is described as follows:

• Setup($1^{\lambda }, n$) Let n be the maximum number of clients. It first generates a bilinear group $(p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e)$ of prime order p with random generators $g \in {\mathbb {G}}$ and ${\hat{g}} \in {\hat{{\mathbb {G}}}}$. It chooses a hash function $H: \{0,1\}^* \rightarrow {\mathbb {G}}$. Next, it selects random exponents $\alpha _1, \ldots , \alpha _n \in {\mathbb {Z}}_p$. It outputs a master key $MK = (\alpha _1, \ldots , \alpha _n)$, client secret keys $( SK_i = \alpha _i )_{i=1}^n$, and public parameters $PP = \big ( (p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e), g, {\hat{g}}, H, n \big )$.

• GenKey(f, MK, PP) Let $f = (i,j)$ such that $i < j$ and $MK = (\alpha _1, \ldots , \alpha _n)$. It selects a random exponent $r \in {\mathbb {Z}}_p$ and outputs a function key $DK_{f} = \big ( K_1 = {\hat{g}}^{\alpha _i r}, K_2 = {\hat{g}}^{\alpha _j r} \big )$.

• Encrypt($X_i, T, SK_i, PP$) Let $X_i = \{ x_{i,1}, \ldots , x_{i,\ell _i} \}$ be a set of items where $|X_i| = \ell _i$ and $SK_i = \alpha _i$. For each $k \in [\ell _i]$, it computes $C_{i,k} = H(T \Vert x_{i,k})^{\alpha _i}$. It chooses a random permutation $\pi$ and outputs a ciphertext $CT_{i,T} = \big ( C_{i,\pi (k)} \big )_{k=1}^{\ell _i}$ by implicitly including i, T.

• Decrypt($CT_{i,T}, CT_{j,T}, DK_{f}, PP$) Let $CT_{i,T} = ( C_{i,k} )_{k=1}^{\ell _i}$ and $CT_{j,T} = ( C_{j,k} )_{k=1}^{\ell _j}$ be ciphertexts such that $i < j$. Let $DK_{f} = (K_1, K_2)$ for a function $f = (i,j)$.

  • 1. For each $k \in [\ell _i]$, it computes $E_{i,k} = e(C_{i,k}, K_2)$. For each $k \in [\ell _j]$, it computes $E_{j,k} = e(C_{j,k}, K_1)$.

  • 2. It prepares two sets $E_i = \{ E_{i,k} \}_{k=1}^{\ell _i}$ and $E_j = \{ E_{j,k} \}_{k=1}^{\ell _j}$ and computes the intersection $S = E_i \cap E_j$ by comparing group elements.

  • 3. It outputs the cardinality of S by counting the number of elements.

3.3 Correctness

We show the correctness of the MCFE-SIC scheme. For this, it is sufficient to show that the same group element is derived by combining a ciphertext element and a function key when the items of two clients are the same. We can derive the following equation when the item x of the client i and the item $x'$ of the client j are the same.

$$\begin{aligned} e(C_{i,k}, K_2) = e(H(T \Vert x)^{\alpha _i}, {\hat{g}}^{\alpha _j r}) = e(H(T \Vert x), {\hat{g}})^{\alpha _i \alpha _j r} = e(H(T \Vert x')^{\alpha _j}, {\hat{g}}^{\alpha _i r}) = e(C_{j,k'}, K_1). \end{aligned}$$

3.4 Security analysis

We define a function $CIQ( ( X_k ), Q)$ for a tuple $( X_k )$ of item sets and a set $Q = \{ (i,j) \}$ of index pairs that computes the collected intersection of $X_i$ and $X_j$ for each $(i,j) \in Q$ as follows:

$\underline{{CIQ}(( X_k )_{k \in I}, Q)}$ where $Q = \{ (i,j) \}$

1. For each $i \in I$, initialize a set $E_i = \emptyset$.

2. For each $(i,j) \in Q$:

Calculate $Y = X_i \cap X_j$.

For each $x \in Y$: Add x to $E_i$ and $E_j$ respectively.

3. Output a tuple $( E_i )_{i \in I}$ of common sets.

Theorem 4

The above MCFE-SIC scheme is static-IND secure with no corruptions in the random oracle model if the Assumption 1 holds.

Proof

Suppose there exists an adversary that breaks the static-IND security of the MCFE-SIC scheme with no corruptions. We can assume that $I = \{ 1, \ldots , n \}$ and ${\overline{I}} = \emptyset$. Let $( X_{0,1}^*, \ldots , [0]X_{0,n}^* )$ and $( X_{1,1}^*, \ldots , X_{1,n}^* )$ be the challenge tuples of item sets where $X_{b,i}^* = \{ x_{b,i,1}^*, \ldots , x_{b,i,\ell _i}^* \}$ and $| X_{b,i}^* | = \ell _i$. Let $Q = \{ (i,j) \}$ be the set of function key queries. We derive a tuple $( E_1^*, \ldots , E_n^* )$ by calling $CIQ(( X_{\mu ,k}^* )_{k \in [n]}, Q)$ where $\mu$ is the challenge random bit of the security game. To argue that the adversary cannot win this game, we define a sequence of hybrid games ${\textbf {G}}_0$, and ${\textbf {G}}_1$. The game ${\textbf {G}}_i$ is defined as follows:

• Game ${\textbf {G}}_0$. The first game ${\textbf {G}}_0$ is the original security game defined in Definition 4.

• Game ${\textbf {G}}_1$. This game ${\textbf {G}}_1$ is similar to the game ${\textbf {G}}_0$ except that the challenge ciphertext components $\{ C_{i,k} \}$ are generated as random for all $x_{\mu ,i,k}^* \notin E_i^*$.

Let $S_{\mathcal {A}}^{{\textbf {G}}_i}$ be the event that an adversary wins in a game ${\textbf {G}}_i$. From the following Lemmas 1 and 2, we obtain the following result

$$\begin{aligned} {\textbf {Adv}}_{MCFE\text {-}SIC,\mathcal {A}}^{ST\text {-}IND}(\lambda ) \le&| \Pr [S_{\mathcal {A}}^{{\textbf {G}}_0}] - \Pr [S_{\mathcal {A}}^{{\textbf {G}}_1}] | + \Pr [S_{\mathcal {A}}^{{\textbf {G}}_1}] \le n\ell {\textbf {Adv}}_{\mathcal {B}}^{A1\text {-}(n,\rho ,Q,J)}(\lambda ) \end{aligned}$$

where n is the number of clients, $\ell$ is the maximum size of the challenge item set. This completes our proof. $\square$

Lemma 1

If the Assumption 1 for $(n, \rho , Q, J)$ holds, then no polynomial-time adversary can distinguish between ${\textbf {G}}_0$ and ${\textbf {G}}_1$ with a non-negligible advantage.

Proof

To prove this lemma, we additionally define hybrid games ${\textbf {H}}_{1,0}, {\textbf {H}}_{1,1}, \ldots , {\textbf {H}}_{1,\ell _1}, {\textbf {H}}_{2,1}, [0]\ldots , {\textbf {H}}_{i,k}, [0]\ldots , {\textbf {H}}_{n,\ell _n}$ where ${\textbf {H}}_{1,0} = {\textbf {G}}_0$ and ${\textbf {H}}_{n,\ell _n} = {\textbf {G}}_1$. The game ${\textbf {H}}_{\rho ,\delta }$ is defined as follows:

• Game ${\textbf {H}}_{\rho ,\delta }$. This game ${\textbf {H}}_{\rho ,\delta }$ is almost identical to the game ${\textbf {G}}_1$ except the generation of the components $\{ C_{i,k} \}$ in the challenge ciphertexts.

  • Case $(i < \rho )$ or $(i = \rho \wedge k \le \delta )$: If $x_{\mu ,i,k}^* \in E_i^*$, then the component $C_{i,k}$ is generated as normal. Otherwise ($x_{\mu ,i,k}^* \notin E_i^*$), the component $C_{i,k}$ is generated as random.

  • Case $(i = \rho \wedge k > \delta )$ or $(i > \rho )$: The component $C_{i,k}$ is generated as normal.

Suppose there exists an adversary $\mathcal {A}$ that distinguishes between ${\textbf {H}}_{\rho ,\delta -1}$ and ${\textbf {H}}_{\rho ,\delta }$ with a non-negligible advantage. Without loss of generality, we assume that $x_{\mu ,\rho ,\delta }^* \notin E_{\rho }^*$ since ${\textbf {H}}_{\rho ,\delta -1}$ and ${\textbf {H}}_{\rho ,\delta }$ are equal if $x_{\mu ,\rho ,\delta }^* \in E_{\rho }^*$. A simulator $\mathcal {B}$ that solves the Assumption 1 for $(n, \rho , Q, J)$ is described as follows:

Init: $\mathcal {A}$ submits challenge tuples $( X_{0,1}^*, \ldots , X_{0,n}^* )$ and $( X_{1,1}^*, \ldots , X_{1,n}^* )$, a challenge time period $T^*$, and a set $Q = \{ (i,j) \}$ of function key queries. $\mathcal {B}$ proceeds as follows:

• 1. From $n, \rho , Q$, it derives an index set J by calling $ComputeJ(n, \rho , Q)$.

• 2. It receives a challenge tuple $D = ( g, g^a, \{ g^{b_i} \}_{i=1}^n, \{ g^{a b_k} \}_{k \in J}, {\hat{g}}, \{ ( {\hat{g}}^{b_i c_{i,j}}, {\hat{g}}^{b_j c_{i,j}} ) \}_{(i,j) \in Q} )$ and Z of the Assumption 1 for $(n, \rho , Q, J)$ where $Z = g^{a b_\rho }$ or $Z = R \in {\mathbb {G}}$.

• 3. It flips a random bit $\mu \in \{0,1\}$ internally and derives a tuple $( E_1^*, \ldots , E_n^* )$ by calling $CIQ(( X_{\mu ,k}^* ), Q)$.

Setup: $\mathcal {B}$ sets $PP = ((p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e), g, {\hat{g}}, H, n)$. It prepares a hash table H-list for the H hash function as the empty set. For each $i \in [n]$ and $k \in [\ell _i]$, it updates the H-list as follows:

• Case $i \ne \rho$ or $k \ne \delta$: If $T^* \Vert x_{\mu ,i,k}^*$ does not exist in the H-list, then it adds $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ to the H-list by selecting a random exponent $u'_{i,k} \in {\mathbb {Z}}_p$.

• Case $i = \rho$ and $k = \delta$: It adds $(T^* \Vert x_{\mu ,\rho ,\delta }^*, -, g^a)$ to the H-list.

Challenge: $\mathcal {B}$ creates challenge ciphertexts $CT_{1,T^*}, \ldots , CT_{n,T^*}$ as follows:

• 1. For each $i \in [n]$ and $k \in [\ell _i]$, it generates ciphertext elements $C_{i,k}$ depending on the following cases:

  • Case $i < \rho$:

    • If $(x_{\mu ,i,k}^* \in E_i^*) \wedge (x_{\mu ,i,k}^* = x_{\mu ,\rho ,\delta }^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, -, g^a)$ from the H-list and sets $C_{i,k} = g^{a b_i}$. For this case, we show that $g^{a b_i}$ is given in the assumption. If a function key for $(i,\rho )$ was queried, we have $x_{\mu ,\rho ,\delta }^* \in E_\rho ^*$ by the definition of CIQ. However, we assumed that $x_{\mu ,\rho ,\delta }^* \notin E_\rho ^*$ for this game. Thus a function key for $(i,\rho )$ was not queried and it means that $i \in J$ by the definition of J.

    • If $(x_{\mu ,i,k}^* \in E_i^*) \wedge (x_{\mu ,i,k}^* \ne x_{\mu ,\rho ,\delta }^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ from the H-list and creates $C_{i,k} = (g^{b_i})^{u'_{i,k}}$.

    • If $(x_{\mu ,i,k}^* \notin E_i^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ from the H-list and chooses a random $C_{i,k} \in {\mathbb {G}}$.

  • Case $i = \rho$:

    • If $(k < \delta ) \wedge (x_{\mu ,\rho ,k}^* \in E_\rho ^*)$, it retrieves $(T^* \Vert x_{\mu ,\rho ,k}^*, u'_{\rho ,k}, g^{u'_{\rho ,k}})$ from the H-list and creates $C_{\rho ,k} = (g^{b_\rho })^{u'_{\rho ,k}}$ since $x_{\mu ,\rho ,k}^* \ne x_{\mu ,\rho ,\delta }^*$.

    • If $(k < \delta ) \wedge (x_{\mu ,\rho ,k}^* \notin E_\rho ^*)$, it retrieves $(T^* \Vert x_{\mu ,\rho ,k}^*, u'_{\rho ,k}, g^{u'_{\rho ,k}})$ from the H-list and chooses a random $C_{\rho ,k} \in {\mathbb {G}}$.

    • If $(k = \delta )$, it sets $C_{\rho ,\delta } = Z$ since we assumed that $x_{\mu ,\rho ,\delta }^* \notin E_\rho ^*$.

    • If $(k > \delta )$, it retrieves $(T^* \Vert x_{\mu ,\rho ,k}^*, u'_{\rho ,k}, g^{u'_{\rho ,k}})$ from the H-list and creates $C_{\rho ,k} = (g^{b_\rho })^{u'_{\rho ,k}}$ since $x_{\mu ,\rho ,k}^* \ne x_{\mu ,\rho ,\delta }^*$.

  • Case $i > \rho$:

    • If $(x_{\mu ,i,k}^* = x_{\mu ,\rho ,\delta }^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, -, g^a)$ from the H-list and sets $C_{i,k} = g^{a b_i}$. For this case, we show that $g^{a b_i}$ is given in the assumption. If a function key for $f = (\rho ,i)$ was queried, we have $x_{\mu ,\rho ,\delta }^* \in E_\rho ^*$ by the definition of CIQ. However, we assumed that $x_{\mu ,\rho ,\delta }^* \notin E_\rho ^*$ for this game. Thus a function key for $f = (\rho ,i)$ was not queried and it means that $i \in J$ by the definition of J.

    • If $(x_{\mu ,i,k}^* \ne x_{\mu ,\rho ,\delta }^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ from the H-list and creates $C_{i,k} = (g^{b_i})^{u'_{i,k}}$.

• 2. For each client $i \in [n]$, it chooses a random permutation $\pi _i$ and sets $CT_{i,T^*} = ( C_{i,\pi _i(k)} )_{k=1}^{\ell _i}$.

Query: $\mathcal {B}$ handles hash, function key, and ciphertext queries of $\mathcal {A}$ as follows:

• If this is a hash query for a time period T and an item x, then it proceeds as follows: If $T \Vert x$ exists in the H-list, then it retrieves $(T \Vert x, -, h)$ from the H-list and gives h to $\mathcal {A}$. Otherwise, it adds $(T \Vert x, u', g^{u'})$ to the H-list by selecting a random exponent $u' \in {\mathbb {Z}}_p$ and gives $g^{u'}$ to $\mathcal {A}$.

• If this is a function key query for a function $f = (i,j) \in Q$, then it generates a function key $DK_{f} = ( {\hat{g}}^{b_i c_{i,j}}, {\hat{g}}^{b_j c_{i,j}} )$ since these elements are given in the assumption.

• If this is a ciphertext query for a client index i, a set $X_i = \{ x_{i,1}, \ldots , x_{i,\ell } \}$, and a time period $T \ne T^*$, then it generates a ciphertext as follows: For each $k \in [\ell _i]$, it retrieves $(T \Vert x_{i,k}, u'_k, g^{u'_k})$ from the H-list and sets $C_{i,k} = (g^{b_i})^{u'_k}$. It chooses a random permutation $\pi$ and sets $CT_{i,T} = ( C_{i,\pi (k)} )_{k=1}^{\ell _i}$.

Guess: $\mathcal {A}$ outputs a guess $\mu '$. If $\mu = \mu '$, it outputs 1. Otherwise, it outputs 0. $\square$

Lemma 2

No adversary can win the game ${\textbf {G}}_1$ with a non-negligible advantage in the random oracle model.

Proof

Let $\mathcal {A}$ be a statistical adversary. A simulator $\mathcal {B}$ is described as follows:

Init: $\mathcal {A}$ submits challenge tuples $( X_{0,1}^*, \ldots , X_{0,n}^* )$ and $( X_{1,1}^*, \ldots , X_{1,n}^* )$, a challenge time period $T^*$, and a set $Q = \{ (i,j) \}$ of function key queries. $\mathcal {B}$ proceeds as follows:

• 1. It flips a random bit $\mu \in \{0,1\}$ internally and derives a tuple $( E_1^*, \ldots , E_n^* )$ by calling $CIQ(( X_{\mu ,k}^* )_{k \in [n]}, Q)$.

Setup: $\mathcal {B}$ first chooses random exponents $\alpha _1, \ldots , \alpha _n \in {\mathbb {Z}}_p$. Next, it sets $( SK_i = \alpha _i )_{i=1}^n$ and $PP = ((p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e), [0]g, {\hat{g}}, H, n)$. It prepares a hash table H-list for the H hash function as the empty set.

• 1. For each $i \in [n]$ and $k \in [\ell _i]$, it updates the H-list as follows: If $T^* \Vert x_{\mu ,i,k}^*$ does not exist in the H-list, then it adds $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ to the H-list by selecting a random exponent $u'_{i,k} \in {\mathbb {Z}}_p$.

• 2. It sets ${\overline{\mu }} = 1 - \mu$. For each $i \in [n]$ and $k \in [\ell _i]$, it also updates the H-list as follows: If $T^* \Vert x_{{\overline{\mu }},i,k}^*$ does not exist in the H-list, then it adds $(T^* \Vert x_{{\overline{\mu }},i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ to the H-list by selecting a random exponent $u'_{i,k} \in {\mathbb {Z}}_p$.

Challenge: $\mathcal {B}$ creates challenge ciphertexts $CT_{1,T^*}, \ldots , CT_{n,T^*}$ as follows:

• 1. For each $i \in [n]$ and $k \in [\ell _i]$, it proceeds as follows: If $x_{\mu ,i,k}^* \in E_i^*$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, [0]u'_{i,k}, g^{u'_{i,k}})$ from the H-list and sets $C_{i,k} = g^{u'_{i,k} \alpha _i}$. If $x_{\mu ,i,k}^* \notin E_i^*$, it chooses a random element $C_{i,k} \in {\mathbb {G}}$.

• 2. For each $i \in [n]$, it chooses a random permutation $\pi _i$ and sets $CT_{i,T^*} = ( C_{i,\pi _i(k)} )_{k=1}^{\ell _i}$.

Query: $\mathcal {B}$ handles hash, function key, and ciphertext queries of $\mathcal {A}$ as follows:

• If this is a hash query for a time period T and an item x, then it proceeds as follows: If $T \Vert x$ exists in the H-list, then it retrieves $(T \Vert x, u', g^{u'})$ from the H-list. Otherwise, it selects a random exponent $u' \in {\mathbb {Z}}_p$ and adds $(T \Vert x, u', g^{u'})$ to the H-list. It gives $g^{u'}$ to $\mathcal {A}$.

• If this is a function key query for $f = (i, j) \in Q$, then $\mathcal {B}$ generates $DK_{f}$ by running GenKey since it knows $SK_i$ and $SK_j$.

• If this is a ciphertext query for a client index i, a set $X_i = \{ x_{i,1}, \ldots , x_{i,\ell } \}$, and a time period $T \ne T^*$, then $\mathcal {B}$ generates a ciphertext $CT_{i,T}$ by running Encrypt algorithm since it knows $SK_i$.

Guess: $\mathcal {A}$ outputs a guess $\mu '$. If $\mu = \mu '$, it outputs 1. Otherwise, it outputs 0.

We first show that the simulation described above is correct. Since the simulator knows all the secret key $SK_i$ of individual clients, it is possible to correctly generate function keys and all ciphertexts. When the simulator creates the challenge ciphertext, it creates the correct ciphertext element if $x_{\mu ,i,k}^* \in E_i^*$ is established as in the definition of the game ${\textbf {G}}_1$, and generates a random element if $x_{\mu ,i,k}^* \notin E_i^*$ is established.

Now we show that the advantage of the statistical adversary is zero in the game ${\textbf {G}}_1$. To do this, we show that it is possible to change the challenge ciphertext for the challenge bit $\mu$ to the challenge ciphertext for the complement bit $1-\mu$ by modifying the mapping of the random oracle table. Such a change only modifies the mapping of the simulator’s random oracle table without modifying the challenge ciphertexts. A detailed description of how to change the random oracle table is given as follows.

• 1. For each $i \in [n]$, it proceeds as follows:

  • (a) It obtains $P_{\mu ,i} = \{ S_{x} \}$ by running $CSIPA(i, (X_{\mu ,k}^*), Q)$. It also obtains $P_{{\overline{\mu }},i} = \{ S_{x} \}$ by running $CSIPA(i, (X_{{\overline{\mu }},k}^*), Q)$.

  • (b) It derives a list $XL_{\mu ,i}^* = (x_{\mu ,i,1}^*, \ldots , x_{\mu ,i,\ell _i}^*)$ from the challenge item set $X_{\mu ,i}^* = \{ x_{\mu ,i,k}^* \}$ in which each challenge ciphertext element $C_{i,k}^*$ is associated with the item $x_{\mu ,i,k}^*$.

  • (c) It builds $XL_{{\overline{\mu }},i}^* = (x_{{\overline{\mu }},i,1}, \ldots , x_{{\overline{\mu }},i,\ell _i}^*)$ from the challenge item set $X_{{\overline{\mu }},i}^* = \{ x_{{\overline{\mu }},i,k}^* \}$ by changing the order of items with the condition that the pattern set $S_{x_{\mu ,i,k}^*}$ of $x_{\mu ,i,k}^*$ is equal to the pattern set $S_{x_{{\overline{\mu }},i,k}^*}$ of $x_{{\overline{\mu }},i,k}^*$.

• 2. It initializes a set $R = \emptyset$. For each $i \in [n]$ and $k \in [\ell _i]$, it takes $x_{\mu ,i,k}^*$ and $x_{{\overline{\mu }},i,k}^*$ from $XL_{\mu ,i}^*$ and $XL_{{\overline{\mu }},i}^*$ respectively, and modifies the H-list as follows:

  • (a) If $(x_{\mu ,i,k}^* \notin E_i^*) \vee (x_{\mu ,i,k}^* = x_{{\overline{\mu }},i,k}^*) \vee (x_{\mu ,i,k}^* \in R) \vee (x_{{\overline{\mu }},i,k}^* \in R)$, then it skips to the next iteration.

  • (b) It deletes $(T^* \Vert x_{\mu ,i,k}^*, u'_1, g^{u'_1})$ and $(T^* \Vert x_{{\overline{\mu }},i,k}^*, u'_2, g^{u'_2})$ from the H-list, and then adds $(T^* \Vert x_{{\overline{\mu }},i,k}^*, u'_1, g^{u'_1})$ and $(T^* \Vert x_{\mu ,i,k}^*, u'_2, g^{u'_2})$ to the H-list.

  • (c) It adds $x_{\mu ,i,k}^*$ and $x_{{\overline{\mu }},i,k}^*$ to R.

If the random oracle table is changed in the same way as above, the actual elements of the challenge ciphertext is maintained as it is, so the equality pattern of the challenge ciphertext is not changed. Thus, if the challenge tuples of item sets with the same equality pattern are given, it is possible to change the challenge bit without changing the ciphertext through the above process. Therefore, the statistical adversary cannot distinguish the challenge ciphertext. $\square$

Theorem 5

The above MCFE-SIC scheme is static-IND secure with corruptions in the random oracle model if the MCFE-SIC scheme is static-IND secure with no corruptions.

Proof

To prove this theorem, we use the fact that in the static-IND security model, the two indexes i and j of a function $f=(i,j)$ in a function key query requested by an attacker must be uncorrupted clients. In other words, the simulator of this proof generates the secret keys of corrupted clients ${\overline{I}}$, and it can handle all other challenge ciphertext, ciphertext, and function key queries requested by the attacker by using the queries of the MCFE-SIC scheme with no corruptions. We omit the detailed description of this simulator. $\square$

3.5 Discussions

Efficiency analysis We analyze the efficiency of our MCFE-SIC scheme described above. First, the function key generation algorithm requires two exponentiation operations, and a function key consists of two group elements. The encryption algorithm requires $\ell$ map-to-point hash operations and $\ell$ exponentiation operations, and a ciphertext consists of $\ell$ group elements where $\ell$ is the number of items in a set. Finally, the decryption algorithm requires $2\ell$ pairing operations and $2\ell \log \ell$ comparison operations for sorting to perform the intersection of pairing elements since it requires a pairing operation for each individual ciphertext element. The detailed comparison of MCFE schemes is given in Table 1.

Decentralized function key generation The function key generation algorithm of our MCFE-SIC scheme should be performed by a trusted center that knows the secret keys of all clients. To reduce trust in the trusted center, it is necessary to decentralize the function key generation so that individual clients are involved to generate function keys without the trusted center. One method is that when creating a function key for a function $f = (i,j)$, two clients with indexes i, j generate partial function keys independently of each other, and the requestor of the function key later combines these partial function keys to derive a complete function key. At this time, in order for the two clients to generate the same random exponent r, a non-interactive key exchange (NIKE) scheme can be used. For more detailed description of this method, refer to the DMCFE-SI scheme in Sect. 5.

Multi-party set intersection cardinality The MCFE-SIC scheme can only process the set intersection cardinality between two clients. To process the set intersection cardinality between three clients, we may consider to provide a function key $({\hat{g}}^{\alpha _j \alpha _k r}, {\hat{g}}^{\alpha _i \alpha _k r}, {\hat{g}}^{\alpha _i \alpha _j r})$ for the client indexes (i, j, k). However, this method has a problem of exposing information on the set intersection cardinality of clients (i, j), (j, k), and (i, k) as well as the set intersection cardinality of clients (i, j, k). Another way is to select random exponents $r_i, r_j, r_k$ to satisfy $r_i + r_j + r_k = 0$ and provide a function key $({\hat{g}}^{r_i / \alpha _i}, {\hat{g}}^{r_j / \alpha _j}, {\hat{g}}^{r_k / \alpha _k})$. At this time, the decryption algorithm calculates $e(H(T \Vert x)^{\alpha _i}, {\hat{g}}^{r_i / \alpha _i}) = e(H(T \Vert x), {\hat{g}})^{r_i}$ for each ciphertext elements of each client. And then it multiplies all combinations to check that $e(H(T \Vert x), {\hat{g}})^{r_i + r_j + r_k} = 1$ holds. This method can prevent the leakage of additional information, but it requires $3\ell$ pairing operations and $O(\ell ^3)$ multiplication operations since all combinations must be considered to calculate the set intersection cardinality.

4 MCFE for set intersection

In this section, we define the syntax and security model of MCFE for set intersection. Then, we propose an MCFE-SI scheme with efficient decryption using a bilinear map and analyze the security of our scheme.

4.1 Definition

We define the syntax of MCFE for set intersection (MCFE-SI). The definition of MCFE-SI was introduced by Lee and Seo [32], and it was modified to issue a function key for the set intersection instead of the function key for the set intersection cardinality in MCFE-SIC we introduced in the previous section. Thus, the decryption algorithm of MCFE-SI outputs the set intersection $X_i \cap X_j$ of two item sets $X_i$ and $X_j$ associated with two client ciphertexts $CT_{i,T}$ and $CT_{j,T}$. The detailed syntax of MCFE-SI is described as follows.

Definition 5

(MCFE for set intersection) A multi-client functional encryption for set intersection (MCFE-SI) scheme for an item space $\mathcal {D}$ and a time space $\mathcal {T}$ consists of four algorithms Setup, GenKey, Encrypt, and Decrypt, which are defined as follows:

• Setup($1^{\lambda }, n$) The setup algorithm takes as input the security parameter $\lambda$ and the number of clients n. It outputs a master key MK, client secret keys $( SK_i )_{i=1}^n$, and public parameters PP.

• GenKey(f, MK, PP) The key generation algorithm takes as input a function $f = (i,j)$, the master key MK, and public parameters PP. It outputs a function key $DK_{f}$.

• Encrypt($X_i, T, SK_i, PP$) The encryption algorithm takes as input a set $X_i = \{ x_{i,1}, \ldots , x_{i,\ell _i} \}$ of items where $x_{i,k} \in \mathcal {D}$, a time period $T \in \mathcal {T}$, the client secret key $SK_i$, and public parameters PP. It outputs a ciphertext $CT_{i,T}$.

• Decrypt($CT_{i,T}, CT_{j,T}, DK_{f}, PP$) The decryption algorithm takes as input two ciphertexts $CT_{i,T}$ and $CT_{j,T}$ for the same time T, a function key $DK_{f}$ for a function $f = (i,j)$, and public parameters PP. It outputs a set $X_i \cap X_j$ where $X_i$ and $X_j$ are associated with $CT_{i,T}$ and $CT_{j,T}$ respectively.

The correctness of the MCFE-SI scheme is defined as follows: For all $MK, ( SK_i )_{i=1}^n, PP \leftarrow {\textbf {Setup}}(1^{\lambda }, n)$, any $DK_{f} \leftarrow {\textbf {GenKey}}(f, MK, PP)$ for a function $f = (i,j)$, and all $CT_{i,T} \leftarrow {\textbf {Encrypt}}(X_i, T, SK_i, PP)$ and $CT_{j,T} \leftarrow {\textbf {Encrypt}}[0](X_j, T, SK_j, PP)$ for any $X_i, X_j$ and the same time T, it is required that

• Decrypt$(CT_{i,T}, CT_{j,T}, DK_{f}, PP) = X_i \cap X_j$ except with negligible probability.

We define the IND security model of MCFE-SI. The IND security model of MCFE was defined by Goldwasser et al. [21], and Lee and Seo modified this model to define a static IND security model of MCFE-SI [32]. We adopt the same static IND security model defined by Lee and Seo. In the static IND security model, an attacker first submits challenge sets $X_0^*, X_1^*$, a challenge time period $T^*$, and all function key queries, and corrupted client indexes with additional constraints. After that, the attacker receives the challenge ciphertext, and can request additional function key and ciphertext queries. Finally, if the attacker correctly guesses the challenge set of the challenge ciphertext, it wins the security game. A more detailed definition of the static IND security model is given as follows.

We first define a function $CSI( ( X_k )_{k \in I}, Q)$ for a tuple $( X_k )_{k \in I}$ of item sets $X_k$ and a set $Q = \{ (i,j) \}$ that computes the set intersection of $X_i$ and $X_j$ for each $(i,j) \in Q$ as follows:

$\underline{{CSI}(( X_k )_{k \in I}, Q)}$ where $Q = \{ (i,j) \}$

1. Initialize a set $S = \emptyset$.

2. For each $(i,j) \in Q$:

Calculate $A = X_i \cap X_j$ and add ((i, j), A) to S.

3. Output the set S.

For example, if we let $n = 3, (X_1 = \{ a, b, c \}, X_2 = \{ b, c \}, X_3 = \{ c, a \})$, and $Q = \{ (1,2), (2,3) \}$, then we have $CSI((X_k), Q) = \{ ((1,2), \{ b, c \}), ((2,3), \{ c \}) \}$.

Definition 6

(Static-IND Security) The static-IND security of MCFE-SI with corruptions is defined in the following experiment ${\textbf {EXP}}_{MCFE\text {-}SI,\mathcal {A}}^{ST\text {-}IND} (1^\lambda )$ between a challenger $\mathcal {C}$ and a PPT adversary $\mathcal {A}$:

• 1. Init: $\mathcal {A}$ initially submits an index set ${\overline{I}} \subset [n]$ of corrupted clients. Let $I = \{ 1, \ldots , n \} \setminus {\overline{I}}$ be the index set of uncorrupted clients. $\mathcal {A}$ also submits two challenge tuples $( X_{0,k}^* )_{k \in I}$ and $( X_{1,k}^* )_{k \in I}$ of item sets, a challenge time period $T^*$, and a set $Q = \{ (i,j) \}$ of function key queries with the two restrictions that (1) $i,j \in I$ for each $(i,j) \in Q$ and (2) $CSI(( X_{0,k}^* )_{k \in I}, Q) = CSI(( X_{1,k}^* )_{k \in I}, Q)$.

• 2. Setup: $\mathcal {C}$ generates a master key MK, secret keys $( SK_i )_{i=1}^n$, and public parameters PP by running Setup$(1^{\lambda }, n)$. It keeps MK and $( SK_i )_{i \in I}$ to itself and gives $( SK_i )_{i \in {\overline{I}}}$ and PP to $\mathcal {A}$.

• 3. Challenge: $\mathcal {C}$ flips a random bit $\mu \in \{0,1\}$ and obtains a ciphertext $CT_{i,T^*}$ by running Encrypt$(X_{\mu ,i}^*, [0]T^*, SK_i, PP)$ for each $i \in I$. $\mathcal {C}$ gives the challenge ciphertexts $( CT_{i,T^*} )_{i \in I}$ to $\mathcal {A}$

• 4. Query: $\mathcal {A}$ requests function keys and ciphertexts. $\mathcal {C}$ handles these queries as follows:

  • If this is a function key query for a function $f = (i,j) \in Q$, then $\mathcal {C}$ gives a function key $DK_{f}$ to $\mathcal {A}$ by running GenKey(f, MK, PP).

  • If this is a ciphertext query for a client index $k \in I$, an item set $X_k$, and a time period $T \ne T^*$, then $\mathcal {C}$ gives a ciphertext $CT_{k,T}$ to $\mathcal {A}$ by running Encrypt$(X_k, T, SK_k, PP)$.

• 5. Guess: $\mathcal {A}$ outputs a guess $\mu ' \in \{0,1\}$ of $\mu$. $\mathcal {C}$ outputs 1 if $\mu = \mu '$ or 0 otherwise.

An MCFE-SI scheme is static-IND secure with corruptions if for all PPT adversary $\mathcal {A}$, the advantage of $\mathcal {A}$ defined as ${\textbf {Adv}}_{MCFE\text {-}SI,\mathcal {A}}^{ST\text {-}IND} (\lambda ) [0]= \big | \Pr [ {\textbf {EXP}}_{MCFE\text {-}SI,\mathcal {A}}^{ST\text {-}IND} (1^\lambda ) = 1 ] - \frac{1}{2} \big |$ is negligible in the security parameter $\lambda$.

4.2 Construction

We combine our MCFE-SIC scheme of the previous section and the MCFE-SI scheme of Lee and Seo [32] in order to design an efficient MCFE-SI scheme with improved decryption. The MCFE-SI scheme of Lee and Seo uses an equal-then-derive technique in which if the items of two client ciphertext elements are equal, then a temporal key is derived by combining these ciphertexts and a function key. However, their MCFE-SI scheme has a disadvantage that the decryption algorithm requires approximately $\ell ^2$ pairing operations because the pairing operation must be performed for all possible combinations of two client ciphertext elements to calculate the set intersection. To improve the decryption performance, we first use our MCFE-SIC scheme to find matching pairs of ciphertext elements corresponding to the set intersection. And then we apply the equal-then-derive method to derive a temporal key to obtain an encrypted item. In this case, the total number of pairing operations can be reduced to $3\ell$.

Let SKE = (GenKey, Encrypt, Decrypt) be an SKE scheme. An MCFE-SI scheme is described as follows.

• Setup($1^{\lambda }, n$) Let n be the maximum number of clients. It first generates a bilinear group $(p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e)$ of prime order p with random generators $g \in {\mathbb {G}}$ and ${\hat{g}} \in {\hat{{\mathbb {G}}}}$. It chooses two hash functions $H: \{0,1\}^* \rightarrow {\mathbb {G}}$ and $F: {\mathbb {G}}_T \rightarrow \{0,1\}^{\lambda }$. Next, it selects random exponents $\alpha _1, \ldots , \alpha _n, \beta _1, \ldots , \beta _n \in {\mathbb {Z}}_p$. It outputs a master key $MK = ((\alpha _i, \beta _i))_{i=1}^n$, secret keys $( SK_i = (\alpha _i, \beta _i) )_{i=1}^n$ for clients, and public parameters $PP = \big ( (p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e), g, {\hat{g}}, H, F, n \big )$.

• GenKey(f, MK, PP) Let $f = (i,j)$ such that $i < j$ and $MK = ((\alpha _i, \beta _i))_{i=1}^n$. It selects a random exponent $r \in {\mathbb {Z}}_p$ and outputs a function key $DK_{f} = \big ( K_1 = {\hat{g}}^{\alpha _i r}, K_2 = {\hat{g}}^{\alpha _j r}, K_3 = {\hat{g}}^{\beta _i / (\alpha _i + \alpha _j)} \big )$.

• Encrypt($X_i, T, SK_i, PP$) Let $X_i = \{ x_{i,1}, \ldots , x_{i,\ell _i} \}$ be a set of items where $|X_i| = \ell _i$ and $SK_i = (\alpha _i, \beta _i)$.

  • 1. For each $k \in [\ell _i]$, it proceed as follows: It computes $C_{i,k} = H(T \Vert x_{i,k})^{\alpha _i}$ and derives a temporal key $TK_{i,k} = e( H(T \Vert x_{i,k}), {\hat{g}} )^{\beta _i}$. It obtains $D_{i,k}$ by running SKE.Encrypt$(T \Vert x_{i,k}, [0]F(TK_{i,k}))$.

  • 2. It chooses a random permutation $\pi$ and outputs a ciphertext $CT_{i,T} = \big ( ( C_{i,\pi (k)}, D_{i,\pi (k)} ) \big )_{k=1}^{\ell _i}$ by implicitly including i, T.

• Decrypt($CT_{i,T}, CT_{j,T}, DK_{f}, PP$) Let $CT_{i,T} = ( ( C_{i,k}, D_{i,k} ) )_{k=1}^{\ell _i}$ and $CT_{j,T}$ $= ( ( C_{j,k}, D_{j,k} ) )_{k=1}^{\ell _j}$ be ciphertexts such that $i < j$ for the same T. Let $DK_{f} = (K_1, K_2, K_3)$ for a function $f = (i,j)$. It first initializes a set $Y = \emptyset$.

  • 1. For each $k \in [\ell _i]$, it computes $E_{i,k} = e(C_{i,k}, K_2)$. For each $k \in [\ell _j]$, it computes $E_{j,k} = e(C_{j,k}, K_1)$.

  • 2. It prepares two sets $E_i = \{ E_{i,k} \}_{k=1}^{\ell _i}$ and $E_j = \{ E_{j,k} \}_{k=1}^{\ell _j}$ and computes the intersection $S = E_i \cap E_j$ by comparing the group elements.

  • 3. For each $E_k \in S$, it proceeds as follows:

    • 1. It finds $(C_{i,k_i}, D_{i,k_i})$ from $CT_{i,T}$ and $(C_{j,k_j}, D_{j,k_j})$ from $CT_{j,T}$ such that $C_{i,k_i}$ and $C_{j,k_j}$ are used to derive $E_k$.

    • 2. It computes $TK_k = e(C_{i,k_i} \cdot C_{j,k_j}, K_3)$ and obtains $T \Vert x$ by running SKE.Decrypt$[0](D_{i,k_i}, F(TK_k))$.

    • 3. It adds an item x into Y.

  • 4. It outputs the set Y.

4.3 Correctness

We show the correctness of the above MCFE-SI scheme. To this end, we need to show that when the ciphertext elements of two clients are the encryption of the same item, the matching ciphertext elements of the set intersection can be found, and when these matching ciphertext elements are decrypted with a function key, the set intersection item can be obtained. First, we already showed that if client ciphertext elements are the encryption of the same item, then matching ciphertext elements can be found by using a function key through the correctness of the MCFE-SIC scheme. Now, we can confirm that the correct item is decrypted from the matching ciphertext elements since a correct temporal key is derived by the following equation

$$\begin{aligned} e(C_{i,k} C_{j,k'}, K_3) = e(H(T \Vert x)^{\alpha _i} H(T \Vert x)^{\alpha _j}, {\hat{g}}^{\beta _i / (\alpha _i + \alpha _j)}) = e(H(T \Vert x), {\hat{g}})^{\beta _i}. \end{aligned}$$

4.4 Security analysis

Theorem 6

The above MCFE-SI scheme is static-IND secure with no corruptions in the random oracle model if the Assumptions 2 and 3 hold.

Proof

Suppose there exists an adversary that breaks the static-IND security of the MCFE-SI scheme with no corruptions. We can assume that $I = \{ 1, \ldots , n \}$ and ${\overline{I}} = \emptyset$. Let $( X_{0,1}^*, \ldots , X_{0,n}^* )$ and $( X_{1,1}^*, \ldots , X_{1,n}^* )$ be the challenge tuples where $X_{b,i}^* = \{ x_{b,i,1}^*, \ldots , x_{b,i,\ell _i}^* \}$ and $| X_{b,i}^* | = \ell _i$. Let $Q = \{ (i,j) \}$ be the set of index pairs related to function key queries. We can derive a tuple $( E_1^*, \ldots , E_n^* )$ by calling $CIQ(( X_{\mu ,k}^* ), Q)$ where $\mu$ is the challenge random bit of the security game. To argue that the adversary cannot win this game, we define a sequence of hybrid games ${\textbf {G}}_0, {\textbf {G}}_1, {\textbf {G}}_2$, and ${\textbf {G}}_3$. The game ${\textbf {G}}_i$ is defined as follows:

• Game ${\textbf {G}}_0$. The first game ${\textbf {G}}_0$ is the original security game defined in Definition 6.

• Game ${\textbf {G}}_1$. This game ${\textbf {G}}_1$ is similar to the game ${\textbf {G}}_0$ except that the challenge ciphertext components $\{ C_{i,k} \}$ are generated as random for all $x_{\mu ,i,k}^* \notin E_i^*$.

• Game ${\textbf {G}}_2$. This game ${\textbf {G}}_2$ is slightly changed from the game ${\textbf {G}}_1$. That is, the challenge temporal keys $\{ TK_{i,k} \}$ are generated as random for all $x_{\mu ,i,k}^* \notin E_i^*$.

• Game ${\textbf {G}}_3$. In the final game ${\textbf {G}}_3$, we change the generation of challenge ciphertext components $\{ D_{i,k} \}$. That is, the challenge ciphertext components $\{ D_{i,k} \}$ are the encryption of random values for all $x_{\mu ,i,k}^* \notin E_i^*$. Note that the advantage of the adversary in this game is zero since challenge ciphertext components $\{ C_{i,k} \}$ are random and $\{ D_{i,k} \}$ are the encryption of random values for all $x_{\mu ,i,k}^* \notin E_i^*$.

Let $S_{\mathcal {A}}^{{\textbf {G}}_i}$ be the event that an adversary wins in a game ${\textbf {G}}_i$. From the following lemmas 3, 4, and 5, we obtain the following result

$$\begin{aligned} {\textbf {Adv}}_{MCFE\text {-}SI,\mathcal {A}}^{ST\text {-}IND}(\lambda ) \le&\left| \Pr [S_{\mathcal {A}}^{{\textbf {G}}_0}] - \Pr [S_{\mathcal {A}}^{{\textbf {G}}_3}] \right| + \Pr [S_{\mathcal {A}}^{{\textbf {G}}_3}] \le \sum _{i=1}^3 \left| \Pr [S_{\mathcal {A}}^{{\textbf {G}}_{i-1}}] - \Pr [S_{\mathcal {A}}^{{\textbf {G}}_i}] \right| + \Pr [S_{\mathcal {A}}^{{\textbf {G}}_3}] \\ \le&n\ell {\textbf {Adv}}_{\mathcal {B}}^{A2\text {-}(n,\rho ,Q,J)}(\lambda ) + n\ell {\textbf {Adv}}_{\mathcal {B}}^{A3\text {-}(n,\rho ,Q)}(\lambda ) + n\ell {\textbf {Adv}}_{\mathcal {B}}^{SKE}(\lambda ) \end{aligned}$$

where n is the number of clients, $\ell$ is the maximum size of the challenge item set. This completes our proof. $\square$

Lemma 3

If the Assumption 2 for $(n, \rho , Q, J)$ holds, then no polynomial-time adversary can distinguish between ${\textbf {G}}_0$ and ${\textbf {G}}_1$ with a non-negligible advantage.

Proof

To prove this lemma, we additionally define hybrid games ${\textbf {H}}_{1,0}, {\textbf {H}}_{1,1}, \ldots , {\textbf {H}}_{1,\ell _1}, {\textbf {H}}_{2,1}, [0]\ldots , {\textbf {H}}_{i,k}, [0]\ldots , {\textbf {H}}_{n,\ell _n}$ where ${\textbf {H}}_{1,0} = {\textbf {G}}_0$ and ${\textbf {H}}_{n,\ell _n} = {\textbf {G}}_1$. The game ${\textbf {H}}_{\rho ,\delta }$ is defined as follows:

• Game ${\textbf {H}}_{\rho ,\delta }$. This game ${\textbf {H}}_{\rho ,\delta }$ is almost identical to the game ${\textbf {G}}_0$ except the generation of the components $\{ C_{i,k} \}$ in the challenge ciphertexts.

  • Case $(i < \rho )$ or $(i = \rho \wedge k \le \delta )$: If $x_{\mu ,i,k}^* \in E_i^*$, then the component $C_{i,k}$ is generated as normal. Otherwise ($x_{\mu ,i,k}^* \notin E_i^*$), the component $C_{i,k}$ is generated as random.

  • Case $(i = \rho \wedge k > \delta )$ or $(i > \rho )$: The component $C_{i,k}$ is generated as normal.

Suppose there exists an adversary $\mathcal {A}$ that distinguishes between ${\textbf {H}}_{\rho ,\delta -1}$ and ${\textbf {H}}_{\rho ,\delta }$ with a non-negligible advantage. Without loss of generality, we assume that $x_{\mu ,\rho ,\delta }^* \notin E_{\rho }^*$ since ${\textbf {H}}_{\rho ,\delta -1}$ and ${\textbf {H}}_{\rho ,\delta }$ are equal if $x_{\mu ,\rho ,\delta }^* \in E_{\rho }^*$. A simulator $\mathcal {B}$ that solves the Assumption 2 for $(n, \rho , Q, J)$ which will be defined later is described as follows:

Init: $\mathcal {A}$ submits challenge tuples $( X_{0,1}^*, \ldots , X_{0,n}^* )$ and $( X_{1,1}^*, \ldots , X_{1,n}^* )$, a challenge time period $T^*$, and a set $Q = \{ (i,j) \}$ of function key queries. $\mathcal {B}$ proceeds as follows:

• 1. From $n, \rho , Q$, it derives an index set J by calling $ComputeJ(n, \rho , Q)$.

• 2. It receives a challenge tuple $D = ( g, g^a, \{ g^{b_i} \}_{i=1}^n, \{ g^{a b_k} \}_{k \in J}, {\hat{g}}, \{({\hat{g}}^{b_i c_{i,j}}, {\hat{g}}^{b_j c_{i,j}}, {\hat{g}}^{1/(b_i + b_j)}) [0]\}_{(i,j)\in Q})$ and Z of the Assumption 2 for $(n, \rho , Q, J)$ where $Z = g^{a b_\rho }$ or $Z = R \in {\mathbb {G}}$.

• 3. It flips a random bit $\mu \in \{0,1\}$ internally and derives a tuple $( E_1^*, \ldots , E_n^* )$ by calling $CIQ(( X_{\mu ,k}^* ), Q)$.

Setup: $\mathcal {B}$ first chooses random exponents $\beta _1, \ldots , \beta _n \in {\mathbb {Z}}_p$. Next, it sets $PP = ((p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e), [0]g, {\hat{g}}, H, F, n)$. It prepares a hash table H-list for the H hash function as follows:

• 1. For each $i \in [n]$ and $k \in [\ell _i]$, it proceeds as follows: If $i \ne \rho$ or $k \ne \delta$, then it selects a random exponent $u'_{i,k} \in {\mathbb {Z}}_p$ and adds $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ to the H-list. Otherwise ($i = \rho \wedge k = \delta$), it adds $(T^* \Vert x_{\mu ,\rho ,\delta }^*, -, g^a)$ to the H-list.

Challenge: $\mathcal {B}$ creates challenge ciphertexts $CT_{1,T^*}, \ldots , CT_{n,T^*}$ as follows:

• 1. For each $i \in [n]$ and $k \in [\ell _i]$, it generates ciphertext elements $C_{i,k}$ and $TK_{i,k}$ depending on the following cases:

  • Case $i < \rho$:

    • If $(x_{\mu ,i,k}^* \in E_i^*) \wedge (x_{\mu ,i,k}^* = x_{\mu ,\rho ,\delta }^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, -, g^a)$ from the H-list, and sets $C_{i,k} = g^{a b_i}$ and creates $TK_{i,k} = e(g^a, {\hat{g}})^{\beta _i}$. For this case, we show that $g^{a b_i}$ is given in the assumption. If a function key for $f = (i,\rho )$ was queried, we have $x_{\mu ,\rho ,\delta }^* \in E_\rho ^*$ by the definition of CIQ. However, we assumed that $x_{\mu ,\rho ,\delta }^* \notin E_\rho ^*$ for this game. Thus a function key for $f = (i,\rho )$ was not queried and it means that $i \in J$ by the definition of J.

    • If $(x_{\mu ,i,k}^* \in E_i^*) \wedge (x_{\mu ,i,k}^* \ne x_{\mu ,\rho ,\delta }^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ from the H-list, and creates $C_{i,k} = (g^{b_i})^{u'_{i,k}}$ and $TK_{i,k} = e(g^{u'_{i,k}}, {\hat{g}})^{\beta _i}$.

    • If $(x_{\mu ,i,k}^* \notin E_i^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ from the H-list, and chooses a random $C_{i,k} \in {\mathbb {G}}$ and creates $TK_{i,k} = e(g^{u'_{i,k}}, {\hat{g}})^{\beta _i}$.

  • Case $i = \rho$:

    • If $(k < \delta ) \wedge (x_{\mu ,\rho ,k}^* \in E_\rho ^*)$, it retrieves $(T^* \Vert x_{\mu ,\rho ,k}^*, u'_{\rho ,k}, g^{u'_{\rho ,k}})$ from the H-list, and creates $C_{\rho ,k} = (g^{b_\rho })^{u'_{\rho ,k}}$ and $TK_{\rho ,k} = e(g^{u'_{\rho ,k}}, {\hat{g}})^{\beta _\rho }$ since $x_{\mu ,\rho ,k}^* \ne x_{\mu ,\rho ,\delta }^*$.

    • If $(k < \delta ) \wedge (x_{\mu ,\rho ,k}^* \notin E_\rho ^*)$, it retrieves $(T^* \Vert x_{\mu ,\rho ,k}^*, u'_{\rho ,k}, g^{u'_{\rho ,k}})$ from the H-list, and chooses a random $C_{\rho ,k} \in {\mathbb {G}}$ and creates $TK_{\rho ,k} = e(g^{u'_{\rho ,k}}, {\hat{g}})^{\beta _\rho }$.

    • If $(k = \delta )$, it sets $C_{\rho ,\delta } = Z$ and creates $TK_{\rho ,\delta } = e(g^a, {\hat{g}})^{\beta _\rho }$ since we assumed that $x_{\mu ,\rho ,\delta }^* \notin E_\rho ^*$.

    • If $(k > \delta )$, it retrieves $(T^* \Vert x_{\mu ,\rho ,k}^*, u'_{\rho ,k}, g^{u'_{\rho ,k}})$ from the H-list, and creates $C_{\rho ,k} = (g^{b_\rho })^{u'_{\rho ,k}}$ and $TK_{\rho ,k} = e(g^{u'_{\rho ,k}}, {\hat{g}})^{\beta _\rho }$ since $x_{\mu ,\rho ,k}^* \ne x_{\mu ,\rho ,\delta }^*$.

  • Case $i > \rho$:

    • If $(x_{\mu ,i,k}^* = x_{\mu ,\rho ,\delta }^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, -, g^a)$ from the H-list, and sets $C_{i,k} = g^{a b_i}$ and creates $TK_{i,k} = e(g^a, {\hat{g}})^{\beta _i}$. For this case, we show that $g^{a b_i}$ is given in the assumption. If a function key for $f = (\rho ,i)$ was queried, we have $x_{\mu ,\rho ,\delta }^* \in E_\rho ^*$ by the definition of CIQ. However, we assumed that $x_{\mu ,\rho ,\delta }^* \notin E_\rho ^*$ for this game. Thus a function key for $f = (\rho ,i)$ was not queried and it means that $i \in J$ by the definition of J.

    • If $(x_{\mu ,i,k}^* \ne x_{\mu ,\rho ,\delta }^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ from the H-list, and creates $C_{i,k} = (g^{b_i})^{u'_{i,k}}$ and $TK_{i,k} = e(g^{u'_{i,k}}, {\hat{g}})^{\beta _i}$.

  Next, it generates a ciphertext element $D_{i,k}$ by running SKE.Encrypt$(T^* \Vert x_{\mu ,i,k}^*, TK_{i,k})$

• 2. For each $i \in [n]$, it chooses a random permutation $\pi _i$ and sets $CT_{i,T^*} = ( (C_{i,\pi _i(k)}, D_{i,\pi _i(k)}) )_{k=1}^{\ell _i}$.

Query: $\mathcal {B}$ handles hash, function key, and ciphertext queries of $\mathcal {A}$ as follows:

• If this is a hash query for a time period T and an item x, then $\mathcal {B}$ proceeds as follows: If $T \Vert x$ exists in the H-list, then it retrieves $(T \Vert x, -, u)$ from H-list and gives u to $\mathcal {A}$. Otherwise, it selects a random exponent $u' \in {\mathbb {Z}}_p$ and adds $(T \Vert x, u', g^{u'})$ to the H-list, and then it gives the hash value $g^{u'}$ to $\mathcal {A}$.

• If this is a function key query for a function $f = (i,j) \in Q$, then $\mathcal {B}$ generates $DK_{f} = \big ( {\hat{g}}^{b_i c_{i,j}}, {\hat{g}}^{b_j c_{i,j}}, [0]({\hat{g}}^{1/(b_i + b_j)})^{\beta _i} \big )$ since these elements are given in the assumption.

• If this is a ciphertext query for a client index i, a set $X_i = \{ x_{i,1}, \ldots , x_{i,\ell } \}$, and a time period $T \ne T^*$, then $\mathcal {B}$ generates a ciphertext as follows:

  • 1. For each $k \in [\ell _i]$, it proceeds as follows: It retrieves $(T \Vert x_{i,k}, u'_k, g^{u'_k})$ from the H-list, and sets $C_{i,k} = (g^{b_i})^{u'_k}$ and $TK_{i,k} = e(g^{u'_k}, {\hat{g}})^{\beta _i}$. Next, it obtains $D_{i,k}$ by running SKE.Encrypt$(T \Vert x_{i,k}, TK_{i,k})$.

  • 2. It chooses a random permutation $\pi$ and sets $CT_{i,T} = ( (C_{i,\pi (k)}, D_{i,\pi (k)}) )_{k=1}^{\ell _i}$.

Guess: $\mathcal {A}$ outputs a guess $\mu '$. If $\mu = \mu '$, it outputs 1. Otherwise, it outputs 0. $\square$

Lemma 4

If the Assumption 3 for $(n, \rho , Q)$ holds, then no polynomial-time adversary can distinguish between ${\textbf {G}}_1$ and ${\textbf {G}}_2$ with a non-negligible advantage.

Proof

To prove this lemma, we additionally define hybrid games ${\textbf {H}}'_{1,0}, {\textbf {H}}'_{1,1}, \ldots , {\textbf {H}}'_{1,\ell _1}, \ldots , {\textbf {H}}'_{i,k}, [0]\ldots , {\textbf {H}}'_{n,\ell _n}$ where ${\textbf {H}}'_{1,0} = {\textbf {G}}_1$ and ${\textbf {H}}'_{n,\ell _n} = {\textbf {G}}_2$. The game ${\textbf {H}}'_{\rho ,\delta }$ is defined as follows:

• Game ${\textbf {H}}'_{\rho ,\delta }$. This game ${\textbf {H}}'_{\rho ,\delta }$ is almost identical to the game ${\textbf {G}}_1$ except the generation of temporal keys $\{ TK_{i,k} \}$ in the challenge ciphertexts.

  • Case $(i < \rho )$ or $(i = \rho \wedge k \le \delta )$: If $x_{\mu ,i,k}^* \in E_i^*$, then the temporal key $TK_{i,k}$ is generated as normal. Otherwise ($x_{\mu ,i,k}^* \notin E_i^*$), the temporal key $TK_{i,k}$ is generated as random.

  • Case $(i = \rho \wedge k > \delta )$ or $(i > \rho )$: The temporal key $TK_{i,k}$ is generated as normal.

Suppose there exists an adversary $\mathcal {A}$ that distinguishes between ${\textbf {H}}'_{\rho ,\delta -1}$ and ${\textbf {H}}'_{\rho ,\delta }$ with a non-negligible advantage. Without loss of generality, we assume that $x_{\mu ,\rho ,\delta }^* \notin E_{\rho }^*$ since ${\textbf {H}}'_{\rho ,\delta -1}$ and ${\textbf {H}}'_{\rho ,\delta }$ are equal if $x_{\mu ,\rho ,\delta }^* \in E_{\rho }^*$. A simulator $\mathcal {B}$ that solves the Assumption 3 for $(n, \rho , Q)$ which will be defined later is described as follows:

Init: $\mathcal {A}$ submits challenge tuples $( X_{0,1}^*, \ldots , X_{0,n}^* )$ and $( X_{1,1}^*, \ldots , X_{1,n}^* )$, a challenge time period $T^*$, and a set $Q = \{ (i,j) \}$ of function key queries. $\mathcal {B}$ proceeds as follows:

• 1. It receives a challenge tuple $D = ( g, g^a, \{ g^{b_i} \}_{i=1}^n, \{ g^{a b_k} \}_{1 \le k \ne \rho \le n}, {\hat{g}}, \{ ( {\hat{g}}^{b_i c_{i,j}}, {\hat{g}}^{b_j c_{i,j}}, {\hat{g}}^{d_i / (b_i + b_j)} ) [0]\}_{(i,j) \in Q}, [0]\{ {\hat{g}}^{d_i} \}_{1 \le i \ne \rho \le n}, e(g,{\hat{g}})^{d_\rho } )$ and Z of the Assumption 3 for $(n, \rho , Q)$ where $Z = e(g, {\hat{g}})^{a d_\rho }$ or $Z = R \in {\mathbb {G}}_T$.

• 2. It flips a random bit $\mu \in \{0,1\}$ internally and derives a tuple $( E_1^*, \ldots , E_n^* )$ by calling $CIQ(( X_{\mu ,k}^* ), Q)$.

Setup: $\mathcal {B}$ sets $PP = ((p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e), g, {\hat{g}}, H, F, n)$. It prepares a hash table H-list for the H hash function as follows:

• 1. For each $i \in [n]$ and $k \in [\ell _i]$, it proceeds as follows: If $i \ne \rho$ or $k \ne \delta$, then it selects a random exponent $u'_{i,k} \in {\mathbb {Z}}_p$ and adds $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ to the H-list. Otherwise ($i = \rho \wedge k = \delta$), it adds $(T^* \Vert x_{\mu ,\rho ,\delta }^*, -, g^a)$ to the H-list.

Challenge: $\mathcal {B}$ creates challenge ciphertexts $CT_{1,T^*}, \ldots , CT_{n,T^*}$ as follows:

• 1. For each $i \in [n]$ and $k \in [\ell _i]$, it generates ciphertext elements $C_{i,k}$ and $TK_{i,k}$ depending on the following cases:

  • Case $i < \rho$:

    • If $(x_{\mu ,i,k}^* \in E_i^*) \wedge (x_{\mu ,i,k}^* = x_{\mu ,\rho ,\delta }^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, -, g^a)$ from the H-list, and sets $C_{i,k} = g^{a b_i}$ and $TK_{i,k} = e(g^a, {\hat{g}}^{d_i})$. In this case, $g^{ab_i}$ is given in the assumption since $i \ne \rho$.

    • If $(x_{\mu ,i,k}^* \in E_i^*) \wedge (x_{\mu ,i,k}^* \ne x_{\mu ,\rho ,\delta }^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ from the H-list, and sets $C_{i,k} = (g^{b_i})^{u'_{i,k}}$ and $TK_{i,k} = e(g^{u'_{i,k}}, {\hat{g}}^{d_i})$.

    • If $(x_{\mu ,i,k}^* \notin E_i^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ from the H-list, and selects random $C_{i,k} \in {\mathbb {G}}$ and $TK_{i,k} \in {\mathbb {G}}_T$.

  • Case $i = \rho$:

    • If $(k < \delta ) \wedge (x_{\mu ,\rho ,k}^* \in E_\rho ^*)$, it retrieves $(T^* \Vert x_{\mu ,\rho ,k}^*, u'_{\rho ,k}, g^{u'_{\rho ,k}})$ from the H-list, and sets $C_{\rho ,k} = (g^{b_\rho })^{u'_{\rho ,k}}$ and $TK_{\rho ,k} = (e(g, {\hat{g}})^{d_\rho })^{u'_{\rho ,k}}$ since $x_{\mu ,\rho ,k}^* \ne x_{\mu ,\rho ,\delta }^*$.

    • If $(k < \delta ) \wedge (x_{\mu ,\rho ,k}^* \notin E_\rho ^*)$, it retrieves $(T^* \Vert x_{\mu ,\rho ,k}^*, u'_{\rho ,k}, g^{u'_{\rho ,k}})$ from the H-list, and selects random $C_{\rho ,k} \in {\mathbb {G}}$ and random $TK_{\rho ,k} \in {\mathbb {G}}_T$.

    • If $(k = \delta )$, it chooses a random $C_{\rho ,\delta } \in {\mathbb {G}}$ and sets $TK_{\rho ,\delta } = Z$ since we assumed that $x_{\mu ,\rho ,\delta }^* \notin E_\rho ^*$.

    • If $(k > \delta ) \wedge (x_{\mu ,\rho ,k}^* \in E_\rho ^*)$, it retrieves $(T^* \Vert x_{\mu ,\rho ,k}^*, u'_{\rho ,k}, g^{u'_{\rho ,k}})$ from the H-list, and sets $C_{\rho ,k} = (g^{b_\rho })^{u'_{\rho ,k}}$ and $TK_{\rho ,k} = (e(g, {\hat{g}})^{d_\rho })^{u'_{\rho ,k}}$ since $x_{\mu ,\rho ,k}^* \ne x_{\mu ,\rho ,\delta }^*$.

    • If $(k > \delta ) \wedge (x_{\mu ,\rho ,k}^* \notin E_\rho ^*)$, it retrieves $(T^* \Vert x_{\mu ,\rho ,k}^*, u'_{\rho ,k}, g^{u'_{\rho ,k}})$ from the H-list, and selects a random $C_{\rho ,k} \in {\mathbb {G}}$ and creates $TK_{\rho ,k} = ( e(g,{\hat{g}})^{d_\rho } )^{u'_{\rho ,k}}$.

  • Case $i > \rho$:

    • If $(x_{\mu ,i,k}^* \in E_i^*) \wedge (x_{\mu ,i,k}^* = x_{\mu ,\rho ,\delta }^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, -, g^a)$ from the H-list, and sets $C_{i,k} = g^{a b_i}$ and $TK_{i,k} = e(g^a, {\hat{g}}^{d_i})$. In this case, $g^{ab_i}$ is given in the assumption since $i \ne \rho$.

    • If $(x_{\mu ,i,k}^* \in E_i^*) \wedge (x_{\mu ,i,k}^* \ne x_{\mu ,\rho ,\delta }^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ from the H-list, and sets $C_{i,k} = (g^{b_i})^{u'_{i,k}}$ and $TK_{i,k} = e(g^{u'_{i,k}}, {\hat{g}}^{d_i})$.

    • If $(x_{\mu ,i,k}^* \notin E_i^*)$, it retrieves $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ from the H-list, and selects a random $C_{i,k} \in {\mathbb {G}}$ and creates $TK_{i,k} = e(g^{u'_{i,k}}, {\hat{g}}^{d_i})$.

  Next, it generates a ciphertext element $D_{i,k}$ by running SKE.Encrypt$(T^* \Vert x_{\mu ,i,k}^*, TK_{i,k})$

• 2. For each $i \in [n]$, it chooses a random permutation $\pi _i$ and sets $CT_{i,T^*} = ( (C_{i,\pi _i(k)}, D_{i,\pi _i(k)}) )_{k=1}^{\ell _i}$.

Query: $\mathcal {B}$ handles hash, function key, and ciphertext queries of $\mathcal {A}$ as follows:

• If this is a hash query for a time period T and an item x, then $\mathcal {B}$ proceeds as follows: If $T \Vert x$ exists in the H-list, then it retrieves $(T \Vert x, -, u)$ from H-list and gives u to $\mathcal {A}$. Otherwise, it selects a random exponent $u' \in {\mathbb {Z}}_p$ and adds $(T \Vert x, u', g^{u'})$ to the H-list, and then it gives the hash value $g^{u'}$ to $\mathcal {A}$.

• If this is a function key query for a function $f = (i,j) \in Q$, then $\mathcal {B}$ generates $DK_{f} = \big ( {\hat{g}}^{b_i c_{i,j}}, {\hat{g}}^{b_j c_{i,j}}, {\hat{g}}^{d_i / (b_i + b_j)} \big )$ since these elements are given in the assumption.

• If this is a ciphertext query for a client index i, a set $X_i = \{ x_{i,1}, \ldots , x_{i,\ell } \}$, and a time period $T \ne T^*$, then $\mathcal {B}$ generates a ciphertext as follows:

  • 1. For each $k \in [\ell _i]$, it proceeds as follows: It retrieves $(T \Vert x_{i,k}, u'_{k}, g^{u'_{k}})$ from the H-list and sets $C_{i,k} = (g^{b_i})^{u'_{k}}$. Next, it sets $TK_{i,k} = (e(g, {\hat{g}})^{d_\rho })^{u'_{k}}$ if $i = \rho$, and it sets $TK_{i,k} = e(g^{u'_{k}}, {\hat{g}}^{d_i})$ if $i \ne \rho$. It obtains $D_{i,k}$ by running SKE.Encrypt$(T \Vert x_{i,k}, TK_{i,k})$.

  • 2. It chooses a random permutation $\pi$ and creates $CT_{i,T} = ( (C_{i,\pi (k)}, D_{i,\pi (k)}) )_{k=1}^{\ell _i}$.

Guess: $\mathcal {A}$ outputs a guess $\mu '$. If $\mu = \mu '$, it outputs 1. Otherwise, it outputs 0. $\square$

Lemma 5

If the SKE scheme is one-message secure, then no polynomial-time adversary can distinguish between ${\textbf {G}}_2$ and ${\textbf {G}}_3$ with a non-negligible advantage.

Proof

To prove this lemma, we additionally define hybrid games ${\textbf {H}}''_{1,0}, {\textbf {H}}''_{1,1}, \ldots , {\textbf {H}}''_{1,\ell _1}, {\textbf {H}}''_{2,1}, [0]\ldots , {\textbf {H}}''_{i,k}, [0]\ldots , {\textbf {H}}''_{n,\ell _n}$ where ${\textbf {H}}''_{1,0} = {\textbf {G}}_2$ and ${\textbf {H}}''_{n,\ell _n} = {\textbf {G}}_3$. The game ${\textbf {H}}''_{\rho ,\delta }$ is defined as follows:

• Game ${\textbf {H}}''_{\rho ,\delta }$. This game ${\textbf {H}}''_{\rho , \delta }$ is almost identical to the game ${\textbf {G}}_2$ except the generation of components $\{ D_{i,k} \}$ in the challenge ciphertexts.

  • Case $(i < \rho )$ or $(i = \rho \wedge k \le \delta )$: If $x_{\mu ,i,k}^* \in E_i^*$, then the component $D_{i,k}$ is generated as normal. Otherwise ($x_{\mu ,i,k}^* \notin E_i^*$), the component $D_{i,k}$ is generated as the encryption of a random value.

  • Case $(i = \rho \wedge k > \delta )$ or $(i > \rho )$: The component $D_{i,k}$ is generated as normal.

Suppose there exists an adversary $\mathcal {A}$ that distinguishes between ${\textbf {H}}''_{\rho ,\delta -1}$ and ${\textbf {H}}''_{\rho ,\delta }$ with a non-negligible advantage. Without loss of generality, we assume that $x_{\mu ,\rho ,\delta }^* \notin E_{\rho }^*$ since ${\textbf {H}}''_{\rho ,\delta -1}$ and ${\textbf {H}}''_{\rho ,\delta }$ are equal if $x_{\mu ,\rho ,\delta }^* \in E_{\rho }^*$. Then $\mathcal {B}$ that interacts with $\mathcal {A}$ is described as follows:

Init: $\mathcal {A}$ submits challenge tuples $( X_{0,1}^*, \ldots , X_{0,n}^* )$ and $( X_{1,1}^*, \ldots , X_{1,n}^* )$ of item sets, a challenge time period $T^*$, and a set $Q = \{ (i,j) \}$ of function key queries. $\mathcal {B}$ then flips a random bit $\mu \in \{0,1\}$ internally and derives a tuple $( E_1^*, \ldots , E_n^* )$ by calling $CIQ(( X_{\mu ,k}^* ), Q)$.

Setup: $\mathcal {B}$ first chooses random exponents $\alpha _1, \ldots , \alpha _n$, $\beta _1, \ldots , \beta _n \in {\mathbb {Z}}_p$. Next, it sets $PP = ((p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e), g, {\hat{g}}, [0]H, F, n)$. It prepares a hash table H-list for the H hash function as follows:

• 1. For each $i \in [n]$ and $k \in [\ell _i]$, it selects a random exponent $u'_{i,k} \in {\mathbb {Z}}_p$ and adds $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, [0]g^{u'_{i,k}})$ to the H-list.

Challenge: $\mathcal {B}$ creates challenge ciphertexts $CT_{1,T^*}, \ldots , CT_{n,T^*}$ as follows:

• 1. For each $i \in [n]$ and $k \in [\ell _i]$, it generates ciphertext elements $C_{i,k}$ and $TK_{i,k}$ depending on the following cases:

  • Case $x_{\mu ,i,k}^* \in E_i$: It retrieves $(T^* \Vert x_{\mu ,i,k}^*, u'_{i,k}, g^{u'_{i,k}})$ from the H-list, and creates $C_{i,k} = g^{u'_{i,k} \alpha _i}$ and $TK_{i,k} = e(g^{u'_{i,k}}, {\hat{g}})^{\beta _i}$.

  • Case $x_{\mu ,i,k}^* \notin E_i$: It selects random $C_{i,k} \in {\mathbb {G}}$ and random $TK_{i,k} \in {\mathbb {G}}_T$.

  Next, it also generates a ciphertext element $D_{i,k}$ depending on the following cases:

  • Case $(i < \rho )$ or $(i = \rho \wedge k < \delta )$: If $x_{\mu ,i,k}^* \in E_i^*$, it creates $D_{i,k}$ by running SKE.Encrypt$[0](T^* \Vert x_{\mu ,i,k}^*, [0]TK_{i,k})$. Otherwise ($x_{\mu ,i,k}^* \notin E_i^*$), it selects a random $y \in \mathcal {D}$ and creates $D_{i,k}$ by running SKE.Encrypt$[0](T^* \Vert y, TK_{i,k})$.

  • Case $(i = \rho \wedge k = \delta )$: It selects a random $y \in \mathcal {D}$ and submits challenge message $x_{\mu ,\rho ,\delta }^*$ and y to the encryption oracle of SKE. Next, it receives a challenge ciphertext $CT_{SKE}^*$ from SKE and sets $D_{\rho ,\delta } = CT_{SKE}^*$. Recall that we assumed $x_{\mu ,\rho ,\delta }^* \notin E_\rho ^*$.

  • Case $(i = \rho \wedge k > \delta )$ or $(i > \rho )$: It creates $D_{i,k}$ by running SKE.Encrypt$(T^* \Vert x_{\mu ,i,k}^*, [0]TK_{i,k})$.

• 2. For each $i \in [n]$, it chooses a random permutation $\pi _i$ and sets $CT_{i,T^*} = ( (C_{i,\pi _i(k)}, D_{i,\pi _i(k)}) )_{k=1}^{\ell _i}$.

Query: $\mathcal {B}$ handles hash, function key, and ciphertext queries of $\mathcal {A}$ as follows:

• If this is a hash query for a time period T and an item x, then $\mathcal {B}$ proceeds as follows: If $T \Vert x$ exists in the H-list, then it retrieves $(T \Vert x, -, u)$ from H-list and gives u to $\mathcal {A}$. Otherwise, it selects a random exponent $u' \in {\mathbb {Z}}_p$ and adds $(T \Vert x, u', g^{u'})$ to the H-list, and then it gives the hash value $g^{u'}$ to $\mathcal {A}$.

• If this is a function key query for a function $f = (i,j)$, then $\mathcal {B}$ simply generates $DK_{f}$ by using $\alpha _i, \alpha _j, \beta _i$.

• If this is a ciphertext query for a client index i, a set $X_i$, and a time period $T \ne T^*$, then $\mathcal {B}$ simply generates a ciphertext $CT_{i,T}$ by using $\alpha _i, \beta _i$.

Guess: $\mathcal {A}$ outputs a guess $\mu '$. If $\mu = \mu '$, it outputs 1. Otherwise, it outputs 0. $\square$

Theorem 7

The above MCFE-SI scheme is static-IND secure with corruptions in the random oracle model if the MCFE-SI scheme is static-IND secure with no corruptions.

Proof

The proof of this theorem is similar to that of Theorem 5. In other words, the simulator of this proof generates the secret keys of corrupted clients by itself, and processes all other queries of an attacker using the queries of the MCFE-SI scheme with no corruptions. We omit the description of more detailed proofs. $\square$

4.5 Discussions

Efficiency analysis We analyze the efficiency of the proposed MCFE-SI scheme. First, the function key is composed of two group elements for the set intersection cardinality and one group element for deriving a temporal key. The encryption algorithm requires $\ell$ map-to-point hash operations, $\ell$ exponentiation operations, and $\ell$ pairing operations since it requires operations in proportion to the size of a set. The decryption algorithm requires $2\ell$ pairing operations, $\ell \log \ell$ comparison operations for sorting of group elements, and $\ell$ pairing operations for deriving temporal keys to decrypt intersection items. The detailed comparison of MCFE schemes is given in Table 1. Compared to the decryption algorithm of the MCFE-SI scheme of Lee and Seo [32] that requires approximately $\ell ^2$ pairing operations, the decryption algorithm of our scheme is more efficient since it only requires $2\ell$ pairing operations.

Outsourcing the decryption of MCFE If the ciphertexts generated by clients are stored on a cloud server, we can consider outsourcing part of the decryption operation to the cloud server. At this time, since the cloud server is not a trusted entity, we must be careful not to expose the set intersection information of the ciphertext to the cloud server. To this end, a client owning a function key $DK = (K_1, K_2, K_3)$ for indexes (i, j) selects a random exponent z and provides an outsourcing function key $oDK = (K_1, K_2, K_3^{z})$ to the cloud server. Then, the cloud server finds ciphertext elements that satisfy the set intersection by using $K_1$ and $K_2$, derives outsourced temporal keys $oTK = e(C_{i,k} C_{j,k'}, K_3^z) = e(H(T \Vert x), {\hat{g}}^{\beta _i})^{z}$, and then it passes these keys back to the client. Then, the client raises all outsourced temporal keys to $z^{-1}$ and decrypts corresponding ciphertexts with the temporal keys. At this time, the cloud server obtains information on the set intersection cardinality and information on the equality patterns but does not obtain the set intersection items.

Multi-party set intersection In the previous section, we presented a method of extending the MCFE-SIC scheme to support the set intersection cardinality for multiple parties. Using this method, our MCFE-SI scheme can also be extended to support multi-party set intersection. That is, for calculating the set intersection cardinality, random exponents $r_i, r_j$, and $r_k$ that satisfy $r_i + r_j + r_k = 0$ are selected and key elements ${\hat{g}}^{r_i / \alpha _i}, {\hat{g}}^{r_j / \alpha _j}, {\hat{g}}^{r_k / \alpha _k}$ are created. After that, an additional key element ${\hat{g}}^{\beta _i / (\alpha _i + \alpha _j + \alpha _k)}$ is provided to derive temporal keys. This method has the disadvantage that it requires $O(\ell ^3)$ multiplication operations to find matching ciphertext elements, but it only requires $O(\ell )$ pairing operations.

5 Decentralized MCFE for set intersection

In this section, we define the syntax and security model of DMCFE-SI that generates function keys in a distributed way. And we propose an efficient DMCFE-SI scheme and analyze the security of the proposed scheme.

5.1 Definition

We define the syntax of decentralized MCFE-SI (DMCFE-SI). DMCFE-SI is a decentralized version of MCFE-SI in the previous section so that individual clients generate partial function keys instead of a trusted center generating a function key. In DMCFE-SI, individual clients set their own private key $SK_i$ and public key $PK_i$ using the ClientSetup algorithm. And then individual clients generate partial function keys using the GenPartKey algorithm, and a third entity combines the partial function keys using the CombPartKey algorithm to derive a correct function key. That is, if the third entity wants to obtain a function key for client indexes (i, j), it receives a partial function key $pDK_i$ from the i-index client and a partial function key $pDK_j$ from the j-index client. And then, it combines the two partial function keys to derive the correct function key DK to decrypt a ciphertext. At this point, the encryption and decryption algorithms of DMCFE-SI are the same as those of MCFE-SI. The detailed syntax of DMCFE-SI is described as follows.

Definition 7

(Decentralized MCFE for Set Intersection) A decentralized multi-client functional encryption for set intersection (DMCFE-SI) scheme for an item space $\mathcal {D}$ and a time space $\mathcal {T}$ consists of six algorithms Setup, ClientSetup, GenPartKey, CombPartKey, Encrypt, and Decrypt, which are defined as follows:

• Setup($1^{\lambda }, n$) The global setup algorithm takes as input the security parameter $\lambda$ and the number of clients n. It outputs public parameters PP.

• ClientSetup(i, PP) The client setup algorithm takes as input an index i of a client and public parameters PP. It outputs a secret key $SK_i$ and a public key $PK_i$.

• GenPartKey($f, SK_i, PK, PP$) The partial key generation algorithm takes as input a function f, a secret key $SK_i$, and a tuple PK of public keys, and public parameters PP. It outputs a partial function key $pDK_{i,f}$.

• CombPartKey($pDK_{i,f}, pDK_{j,f}, PP$) The partial key combining algorithm takes as input two partial decryption keys $pDK_{i,f}$ and $pDK_{j,f}$ for a function $f = (i,j)$ and public parameters PP. It outputs a function key $DK_{f}$.

• Encrypt($X_i, T, SK_i, PP$) The encryption algorithm takes as input a set $X_i = \{ x_{i,1}, \ldots , x_{i,\ell _i} \}$ of items where $x_{i,j} \in \mathcal {D}$, a time period $T \in \mathcal {T}$, a secret key $SK_i$, and public parameters PP. It outputs a ciphertext $CT_{i,T}$.

• Decrypt($CT_{i,T}, CT_{j,T}, DK_{f}, PP$) The decryption algorithm takes as input two ciphertexts $CT_{i,T}$ and $CT_{j,T}$ for the same time T, a function key $DK_{f}$, and public parameters PP. It outputs a set $X_i \cap X_j$ where $X_i$ and $X_j$ are associated with $CT_{i,T}$ and $CT_{j,T}$ respectively.

The correctness of the DMCFE-SI scheme is defined as follows: For any $PP \leftarrow {\textbf {Setup}}(1^{\lambda }, n)$, all $SK_i, PK_i \leftarrow {\textbf {ClientSetup}}[0](i, PP)$, and all $CT_{i,T} \leftarrow {\textbf {Encrypt}}(X_i, T, SK_i, PP)$ and $CT_{j,T} \leftarrow {\textbf {Encrypt}}(X_j, T, SK_j, PP)$ for any $X_i, X_j$ and the same time T, it is required that

• CombPartKey$({\textbf {GenPartKey}}(f, SK_i, PK, PP), {\textbf {GenPartKey}}(f, SK_j, PK, PP), PP) = DK_f$.

• Decrypt$(CT_{i,T}, CT_{j,T}, DK_{f}, PP) = X_i \cap X_j$ except with negligible probability.

We define the security model of DMCFE-SI. We define the static IND security model of DMCFE-SI by modifying the static IND security model of MCFE-SI defined in the previous section. This security model of DMCFE-SI is the same as that of MCFE-SI in Sect. 4.1, except that it allows partial function key queries instead of function key queries. In this security model of DMCFE-SI, partial function key queries requested by an attacker have two limitations. If a partial function key for a function $f = (i,j)$ requested by the attacker belongs to the predefined function key query set, then the attacker can request both a partial function key for a client i and a partial function key for a client j. However, if a partial function key for $f = (i,j)$ does not belong to the predefined function key query set, then the attacker can request only one partial function key for a client i or j. Thus, the attacker of DMCFE-SI allows not only predefined function key queries, but also additional partial function key queries. The more detailed security model of DMCFE-SI is defined as follows.

Definition 8

(Static-IND Security) The static-IND security of DMCFE-SI with corruptions is defined in the following experiment ${\textbf {EXP}}_{DMCFE\text {-}SI,\mathcal {A}}^{ST\text {-}IND} (1^\lambda )$ between a challenger $\mathcal {C}$ and a PPT adversary $\mathcal {A}$:

• 1. Init: $\mathcal {A}$ initially submits an index set ${\overline{I}} \subset [n]$ of corrupted clients. Let $I = \{ 1, \ldots , n \} \setminus {\overline{I}}$ be the index set of uncorrupted clients. $\mathcal {A}$ also submits two challenge tuples $( X_{0,k}^* )_{k \in I}$ and $( X_{1,k}^* )_{k \in I}$ of item sets, a challenge time period $T^*$, and a set $Q = \{ (i,j) \}$ of function key queries with the two restrictions that (1) $i,j \in I$ for each $(i,j) \in Q$ and (2) $CSI(( X_{0,k}^* )_{k \in I}, Q) = CSI(( X_{1,k}^* )_{k \in I}, Q)$.

• 2. Setup: $\mathcal {C}$ generates public parameters PP by running Setup$(1^\lambda , n)$. It also generates secret keys and public keys $(SK_i, PK_i)$ of clients by running ClientSetup(i, PP) for each $i \in [n]$. It keeps $( SK_i )_{i \in I}$ to itself and gives $( SK_i )_{i \in {\overline{I}}}$, $PK = (PK_i)_{i=1}^n$, and PP to $\mathcal {A}$.

• 3. Challenge: $\mathcal {C}$ flips a random bit $\mu \in \{0,1\}$ and obtains a ciphertext $CT_{i,T^*}$ by running Encrypt$(X_{\mu ,i}^*, [0]T^*, SK_i, PP)$ for each $i \in I$. $\mathcal {C}$ gives the challenge ciphertexts $( CT_{i,T^*} )_{i \in I}$ to $\mathcal {A}$

• 4. Query: $\mathcal {A}$ requests function keys and ciphertexts. $\mathcal {C}$ handles these queries as follows:

  • If this is a partial function key query for a tuple $f = (i,j)$ and a client index k such that $k = i$ or $k = j$, then $\mathcal {C}$ gives a partial function key $pDK_{k,f}$ to $\mathcal {A}$ by running GenPartKey$(f, SK_k, PK, PP)$ with the restrictions that (1) if $f \in Q$, then two partial function keys of i and j can be queried and (2) if $f \notin Q$, then only one partial function key of i or j can be queried.

  • If this is a ciphertext query for a client index $k \in I$, an item set $X_k$, and a time period $T \ne T^*$, then $\mathcal {C}$ gives a ciphertext $CT_{k,T}$ to $\mathcal {A}$ by running Encrypt$(X_k, T, SK_k, PP)$.

• 5. Guess: $\mathcal {A}$ outputs a guess $\mu ' \in \{0,1\}$ of $\mu$. $\mathcal {C}$ outputs 1 if $\mu = \mu '$ or 0 otherwise.

A DMCFE-SI scheme is static-IND secure with corruptions if for all PPT adversary $\mathcal {A}$, the advantage of $\mathcal {A}$ defined as ${\textbf {Adv}}_{DMCFE\text {-}SI,\mathcal {A}}^{ST\text {-}IND} (\lambda ) [0]= \big | \Pr [ {\textbf {EXP}}_{DMCFE\text {-}SI,\mathcal {A}}^{ST\text {-}IND} (1^\lambda ) = 1 ] - \frac{1}{2} \big |$ is negligible in the security parameter $\lambda$.

5.2 Construction

The function key of the MCFE-SI scheme proposed in the previous section consist of $K_1$ and $K_2$ for set intersection cardinality and $K_3$ for deriving a temporal key for set intersection. We first devise a method to decentralize the generation of $K_1$ and $K_2$. In order for individual clients to generate these two group elements in an independent way, it is necessary to generate a common random exponent r. To this end, we derive the same shared key K by using a non-interactive key exchange NIKE scheme and we use PRF to derive the exponent r from the shared key K. That is, if an individual client additionally selects a private key $\gamma _i$ and exposes a public key $h_i = g^{\gamma _i}$, then it can derive a shared key $K = g^{\gamma _i \gamma _j}$ by using a NIKE scheme. Thus, individual clients can generate partial function keys of ${\hat{g}}^{\alpha _i r}$ and ${\hat{g}}^{\alpha _j r}$ where $r = PRF(K,1)$.

Now we devise a method to decentralize the generation of $K_3$ for derivation of a temporal key. However, it cannot be decentralized by a simple method since it requires the inverse operation of an exponent. In order to decentralize the calculation of the inverse operation while hiding the secret keys of two clients, we introduce a method in which the secret key is encrypted with a one-time pad scheme and a client requesting the partial function key combines the encrypted keys to calculate the inverse operation. That is, individual clients first derive the same shared key $K_{i,j}$ using the NIKE scheme, and derives the same random exponents s and t. Then, each client encrypts its secret key as $E_i = s \alpha _i + t$ and $E_j = s \alpha _j - t$, respectively. At this time, if the i index client additionally provides ${\hat{g}}^{\beta _i s}$, the client that received $E_i$ and $E_j$ can compute a key $({\hat{g}}^{\beta _i s})^{1/(E_i + E_j)}$. Note that, since $E_i$ and $E_j$ have a one-to-one correspondence with random exponents s and t, the information of the secret keys is not exposed.

Let SKE = (GenKey, Encrypt, Decrypt) be an SKE scheme. A DMCFE-SI scheme is described as follows.

• Setup($1^{\lambda }, n$) Let n be the maximum number of clients. It first generates a bilinear group $(p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e)$ of prime order p with random generators $g \in {\mathbb {G}}$ and ${\hat{g}} \in {\hat{{\mathbb {G}}}}$. It chooses two hash functions $H: \{0,1\}^* \rightarrow {\mathbb {G}}$ and $F: {\mathbb {G}}_T \rightarrow \{0,1\}^{\lambda }$. It outputs public parameters $PP = \big ( (p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e), g, {\hat{g}}, H, F, n \big )$.

• ClientSetup(i, PP) Let i be the index of a client. It selects random exponents $\alpha _i, \beta _i, \gamma _i \in {\mathbb {Z}}_p$, and then it outputs a secret key $SK_i = (\alpha _i, \beta _i, \gamma _i)$ and a public key $PK_i = \big ( h_i = g^{\gamma _i} \big )$.

• GenPartKey($f, SK_k, PK, PP$) Let $f = (i,j)$ such that $i < j$. Let $SK_k = (\alpha _k, \beta _k, \gamma _k)$ such that $k = i$ or $k = j$ and $PK = (PK_1, \ldots , PK_n)$.

  • 1. If $k = i$, it retrieves $PK_j = h_j$ from PK and computes a shared key $K_{i,j} = h_j^{\gamma _i}$. Otherwise ($k = j$), it retrieves $PK_i = h_i$ from PK and computes a shared key $K_{i,j} = h_i^{\gamma _j}$. Next, it derives random exponents $r, s, t \in {\mathbb {Z}}_p$ by running $PRF(K_{i,j},1)$, $PRF(K_{i,j},2)$, $PRF(K_{i,j},3)$ respectively.

  • 2. If $k = i$, it sets $A_2 = {\hat{g}}^{\beta _i \cdot s}$ and $E = s \cdot \alpha _i + t \mod p$. Otherwise, it sets $A_2 = 1_{{\hat{{\mathbb {G}}}}}$ and $E = s \cdot \alpha _j - t \mod p$. It outputs a partial function key $pDK_{k,f} = \big ( A_1 = {\hat{g}}^{\alpha _k \cdot r}, A_2, E \big )$.

• CombPartKey($pDK_{i,f}, pDK_{j,f}, PP$) Let $f = (i,j)$ such that $i < j$. Let $pDK_{i,f} = (A_1, A_2, E)$ and $pDK_{j,f} = (A'_1, A'_2, E')$. It selects a random exponent $r \in {\mathbb {Z}}_p$ and outputs a function key $DK_{f} = \big ( K_1 = (A_1)^{r}, K_2 = (A'_1)^{r}, K_3 = A_2^{1/(E + E')} \big )$.

• Encrypt($X_i, T, SK_i, PP$) Let $X_i = \{ x_{i,1}, \ldots , x_{i,\ell _i} \}$ be a set of items where $|X_i| = \ell _i$ and $SK_i = (\alpha _i, \beta _i, \gamma _i)$.

  • 1. For each $k \in [\ell _i]$, it proceed as follows: It computes $C_{i,k} = H(T \Vert x_{i,k})^{\alpha _i}$ and derives a temporal key $TK_{i,k} = e( H(T \Vert x_{i,k}), {\hat{g}} )^{\beta _i}$. It obtains $D_{i,k}$ by running SKE.Encrypt$[0](T \Vert x_{i,k}, F(TK_{i,k}))$.

  • 2. It chooses a random permutation $\pi$ and outputs a ciphertext $CT_{i,T} = \big ( ( C_{i,\pi (k)}, D_{i,\pi (k)} ) \big )_{k=1}^{\ell _i}$ by implicitly including i, T.

• Decrypt($CT_{i,T}, CT_{j,T}, DK_{f}, PP$) Let $CT_{i,T} = ( ( C_{i,k}, D_{i,k} ) )_{k=1}^{\ell _i}$ and $CT_{j,T} = ( ( C_{j,k}, D_{j,k} ) )_{k=1}^{\ell _j}$ be ciphertexts such that $i < j$ for the same T. Let $DK_{f} = (K_1, K_2, K_3)$ where $f = (i,j)$. It first initializes a set $Y = \emptyset$.

  • 1. For each $k \in [\ell _i]$, it computes $E_{i,k} = e(C_{i,k}, K_2)$. For each $k \in [\ell _j]$, it computes $E_{j,k} = e(C_{j,k}, K_1)$.

  • 2. It prepares two sets $E_i = \{ E_{i,k} \}_{k=1}^{\ell _i}$ and $E_j = \{ E_{j,k} \}_{k=1}^{\ell _j}$ and computes the intersection $S = E_i \cap E_j$ by comparing the group elements.

  • 3. For each $E_k \in S$, it proceeds as follows:

    • 1. It finds $(C_{i,k_i}, D_{i,k_i})$ from $CT_{i,T}$ and $(C_{j,k_j}, D_{j,k_j})$ from $CT_{j,T}$ such that $C_{i,k_i}$ and $C_{j,k_j}$ are used to derive $E_k$.

    • 2. It computes $TK_k = e(C_{i,k_i} \cdot C_{j,k_j}, K_3)$ and obtains $T \Vert x$ by running SKE.Decrypt$[0](D_{i,k_i}, F(TK_k))$.

    • 3. It adds an item x into Y.

  • 4. It outputs the set Y.

5.3 Correctness

We show the correctness of the DMCFE-SI scheme. First, two clients i and j can obtain the same shared key $K_{i,j}$ from the correctness of the Diffie–Hellman non-interactive key exchange scheme. And two clients i and j can derive the same random exponents r, s, and t since PRF is a deterministic function. Now, when a combing client combines the partial function key elements generated by using the same random exponents r, s, and t, it can derive a function key by the following equation

$$\begin{aligned} A_1 = {\hat{g}}^{\alpha _i r},~ A'_1 = {\hat{g}}^{\alpha _j r},~ A_2^{1/(E + E')} = \big ( {\hat{g}}^{\beta _i \cdot s} \big )^{1/(s \alpha _i + t + s \alpha _j - t)}&= \big ( {\hat{g}}^{\beta _i \cdot s} \big )^{1/(s \alpha _i + s \alpha _j)}\\ {}&= {\hat{g}}^{\beta _i / (\alpha _i + \alpha _j)}. \end{aligned}$$

Since the correct function key is derived from the partial function key, it is guaranteed that the set intersection is correctly calculated from the ciphertexts of two clients from the correctness of the MCFE-SI scheme.

5.4 Security analysis

Theorem 8

The above DMCFE-SI scheme is static-IND secure with no corruptions in the random oracle model if the PRF scheme is secure and the Assumptions 2 and 3 hold.

Proof

Suppose there exists an adversary that breaks the static-IND security of the DMCFE-SI scheme with no corruptions. We can assume that $I = \{ 1, \ldots , n \}$ and ${\overline{I}} = \emptyset$. Let $( X_{0,1}^*, \ldots , X_{0,n}^* )$ and $( X_{1,1}^*, \ldots , X_{1,n}^* )$ be the challenge tuples where $X_{b,i}^* = \{ x_{b,i,1}^*, \ldots , x_{b,i,\ell _i}^* \}$ and $| X_{b,i}^* | = \ell _i$. Let $Q = \{ (i,j) \}$ be the set of index pairs related to function key queries. We can derive a tuple $( E_1^*, \ldots , E_n^* )$ by calling $CIQ(( X_{\mu ,k}^* ), Q)$ where $\mu$ is the challenge random bit of the security game. To argue that the adversary cannot win this game, we define a sequence of hybrid games ${\textbf {G}}_0, {\textbf {G}}_1, {\textbf {G}}_2$, and ${\textbf {G}}_3$. The game ${\textbf {G}}_i$ is defined as follows:

• Game ${\textbf {G}}_0$. The first game ${\textbf {G}}_0$ is the original security game defined in Definition 8.

• Game ${\textbf {G}}_1$. In this game ${\textbf {G}}_1$, when processing partial function key queries, we change all shared keys $\{ K_{i,j} \}$ derived by non-interactive key agreement to random elements.

• Game ${\textbf {G}}_2$. In this game, we modify the previous game ${\textbf {G}}_1$ to generate random exponents r, s, t by using the a truly random function instead of using a pseudo-random function when processing partial function key queries.

• Game ${\textbf {G}}_3$. This game ${\textbf {G}}_3$ is similar to the game ${\textbf {G}}_2$ except that the challenge ciphertext components $\{ C_{i,k} \}$ are generated as random for all $x_{\mu ,i,k}^* \notin E_i^*$.

• Game ${\textbf {G}}_4$. This game ${\textbf {G}}_4$ is slightly changed from the game ${\textbf {G}}_3$. That is, the challenge temporal keys $\{ TK_{i,k} \}$ are generated as random for all $x_{\mu ,i,k}^* \notin E_i^*$.

• Game ${\textbf {G}}_5$. In the final game ${\textbf {G}}_5$, we change the generation of challenge ciphertext components $\{ D_{i,k} \}$. That is, the challenge ciphertext components $\{ D_{i,k} \}$ are the encryption of random values for all $x_{\mu ,i,k}^* \notin E_i^*$. Recall that the advantage of the adversary in this game is zero since challenge ciphertext components $\{ C_{i,k} \}$ are random and $\{ D_{i,k} \}$ are the encryption of random values for all $x_{\mu ,i,k}^* \notin E_i^*$.

Let $S_{\mathcal {A}}^{{\textbf {G}}_i}$ be the event that an adversary wins in a game ${\textbf {G}}_i$. From the following Lemmas 6, 7, 8, 9, and 10, we obtain the following result

$$\begin{aligned}&{{\textbf {Adv}}_{DMCFE\text {-}SI,\mathcal {A}}^{ST\text {-}IND}(\lambda )} \\ {}&\le \left| \Pr [S_{\mathcal {A}}^{{\textbf {G}}_0}] - \Pr [S_{\mathcal {A}}^{{\textbf {G}}_5}] \right| + \Pr [S_{\mathcal {A}}^{{\textbf {G}}_5}] \le \sum _{i=1}^5 | \Pr [S_{\mathcal {A}}^{{\textbf {G}}_{i-1}}] - \Pr [S_{\mathcal {A}}^{{\textbf {G}}_i}] | + \Pr [S_{\mathcal {A}}^{{\textbf {G}}_5}] \\&\le {\textbf {Adv}}_{\mathcal {B}}^{XDH}(\lambda ) + n^2 {\textbf {Adv}}_{\mathcal {B}}^{PRF}(\lambda ) + n\ell {\textbf {Adv}}_{\mathcal {B}}^{A2\text {-}(n,\rho ,Q,J)}(\lambda ) + n\ell {\textbf {Adv}}_{\mathcal {B}}^{A3\text {-}(n,\rho ,Q)}(\lambda ) \\&\quad + n\ell {\textbf {Adv}}_{\mathcal {B}}^{SKE}(\lambda ) \end{aligned}$$

where n is the number of clients, $\ell$ is the maximum size of the challenge item set. This completes our proof. $\square$

Lemma 6

If the XDH assumption holds, then no polynomial-time adversary can distinguish between ${\textbf {G}}_0$ and ${\textbf {G}}_1$ with a non-negligible advantage.

Proof

To prove this lemma, we introduce a multi-XDH assumption that is modified from the XDH assumption. Let $(p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e)$ be a bilinear group and $g, {\hat{g}}$ be random generators of ${\mathbb {G}}, {\hat{{\mathbb {G}}}}$ respectively. The multi-XDH assumption is that if the challenge tuple $D = \big ( (p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e),~ g,~ g^{a_1}, \ldots , g^{a_n},~ {\hat{g}} \big )$ and Z are given, no PPT algorithm $\mathcal {A}$ can distinguish $Z = Z_0 = ( g^{a_1 a_2}, \ldots , g^{a_1 a_n}, \ldots , g^{a_i a_j}, \ldots , g^{a_{n-1} a_n} )_{1 \le i < j \le n}$ from $Z = Z_1 = ( g^{c_{1,2}}, \ldots , g^{c_{i,j}} \ldots , [0]g^{c_{n-1,n}} )_{1 \le i < j \le n}$ with more than a negligible advantage where the probability is taken over random choices of $a_1, \ldots , a_n, \{ c_{i,j} \} \in {\mathbb {Z}}_p$.

The multi-XDH assumption is actually the same as the XDH assumption by using the random self-reducibility of the XDH assumption. We omit the detailed proof of this lemma since the proof of randomly changing all shared keys is simply processed by using the multi-XDH assumption. $\square$

Lemma 7

If the PRF is secure, then no polynomial-time adversary can distinguish between ${\textbf {G}}_1$ and ${\textbf {G}}_2$ with a non-negligible advantage.

Proof

To prove this lemma, we play additional hybrid games that convert pseudo-random functions into truly random functions one by one. When the number of clients is n, the maximum number of shared keys is $n(n-1)/2$, so the hybrid games consist of a maximum of $n^2/2$. Note that the exponents r, s, and t derived by a truly random function are distributed as random values. We omit the detailed proof of this lemma. $\square$

Lemma 8

If the Assumption 2 for $(n, \rho , Q, J)$ holds, then no polynomial-time adversary can distinguish between ${\textbf {G}}_2$ and ${\textbf {G}}_3$ with a non-negligible advantage.

Proof

The proof of this lemma is almost the same as Lemma 3 except for client public key generation and partial function key query processing. To perform the proof, we define a number of additional hybrid games as in Lemma 3 and show the indistinguishability of individual hybrid games. The simulator of this lemma generates public parameters, challenge ciphertexts, and challenge ciphertexts in the same manner as in Lemma 3. Note that function key query processing in Lemma 3 is unnecessary for this lemma. In the proof of individual hybrid games, the simulator handles additional client public key generation and partial function key queries.

In the setup phase, the simulator selects a random exponent $\gamma _i \in {\mathbb {Z}}_p$ for each client and sets $h_i = g^{\gamma _i}$ as the corresponding client public key. The public key generated in this way has the same distribution as that of the original game.

In the query phase, the simulator handles a partial function key query for a function $f = (i,j)$ and a client index k as follows:

• Case $f = (i,j) \in Q$: It first sets a function key $DK_{f} = \big ( K_1 = {\hat{g}}^{b_i c_{i,j}}, K_2 = {\hat{g}}^{b_j c_{i,j}}, K_3 = ({\hat{g}}^{1/(b_i + b_j)})^{\beta _i} \big )$ since these elements are given in the assumption. Next, it selects random exponents $r', s', t' \in {\mathbb {Z}}_p$. If $k = i$, then it creates $pDK_{i,f} = \big ( A_1 = K_1^{r'}, A_2 = K_3^{s'}, E = s' + t' \mod p \big )$. Otherwise ($k = j$), it creates $pDK_{j,f} = \big ( A'_1 = K_2^{r'}, A'_2 = 1_{{\hat{{\mathbb {G}}}}}, E' = -t' \mod p \big )$. Now we show that the distribution of the generated partial function keys has the same distribution as that of the original game. We implicitly define the random exponents of the partial function key as follows:

  $$\begin{aligned} r = c_{i,j} r',~ s = \frac{1}{(b_i + b_j)} s',~ t = \frac{b_j}{(b_i + b_j)} s' + t'. \end{aligned}$$

  Then, we can show that the elements of the partial function key are correctly distributed by the following equations:

  $$\begin{aligned}&A_1 = {\hat{g}}^{b_i r} = {\hat{g}}^{b_i c_{i,j} r'} = K_1^{r'},~A'_1 = {\hat{g}}^{b_j r} = {\hat{g}}^{b_j c_{i,j} r'} = K_2^{r'},~\\ {}&A_2 = {\hat{g}}^{\beta _i s} = {\hat{g}}^{\beta _i \cdot s' / (b_i + b_j)} = K_3^{s'},~ \\&E = s b_i + t = \frac{s'}{(b_i + b_j)} b_i + \frac{b_j}{(b_i + b_j)} s' + t' = s' + t',~ \\&E' = s b_j - t = \frac{s'}{(b_i + b_j)} b_j - \frac{b_j}{(b_i + b_j)} s' - t' = - t'. \end{aligned}$$

• Case $f = (i,j) \notin Q$: It first selects random exponents $r', s', t' \in {\mathbb {Z}}_p$. If $k = i$, then it creates $pDK_{i,f} = \big ( A_1 = {\hat{g}}^{r'}, A_2 = {\hat{g}}^{s'}, E = t' \mod p \big )$. Otherwise ($k = j$), it creates $pDK_{j,f} = \big ( A'_1 = {\hat{g}}^{r'}, A'_2 = 1_{{\hat{{\mathbb {G}}}}}, E' = t' \mod p \big )$. Now we should show that the distribution of the partial function keys generated in this way has the same distribution as that of the original game. Note that in the case of $f \notin Q$, an attacker can obtain only one of $pDK_{i,f}$ or $pDK_{j,f}$ due to the constraints of the security model. First, in the case of $k=i$, if we define the random exponents as follows, then we can see that the elements of the partial function key are correctly distributed by the following equations:

  $$\begin{aligned}&r = \frac{1}{b_i} r',~ s = \frac{1}{\beta _i} s',~ t = -\frac{b_i}{\beta _i} s' + t',\\&A_1 = {\hat{g}}^{b_i r} = {\hat{g}}^{b_i \cdot r'/b_i} = {\hat{g}}^{r'},~ A_2 = {\hat{g}}^{\beta _i s} = {\hat{g}}^{\beta _i \cdot s'/\beta _i} = {\hat{g}}^{s'},~ \\&E = s b_i + t = \frac{1}{\beta _i} s' b_i - \frac{b_i}{\beta _i} s' + t' = t'. \end{aligned}$$

  Next, in the case of $k=j$, if we define the random exponents as follows, then we can see that the elements of the partial function key are correctly distributed by the following equations:

  $$\begin{aligned} r = \frac{1}{b_j} r',~ s = \frac{1}{\beta _i} s',~ t = \frac{b_j}{\beta _i} s' - t', \end{aligned}$$
  $$\begin{aligned}&A'_1 = {\hat{g}}^{b_j r} = {\hat{g}}^{b_j \cdot r'/b_j} = {\hat{g}}^{r'},~ E' = s b_j - t = \frac{s'}{\beta _i} b_j - \frac{b_j}{\beta _i} s' + t' = t'. \end{aligned}$$

This completes our proof. $\square$

Lemma 9

If the Assumption 3 for $(n, \rho , Q, J)$ holds, then no polynomial-time adversary can distinguish between ${\textbf {G}}_3$ and ${\textbf {G}}_4$ with a non-negligible advantage.

Proof

The proof of this lemma is the same as that of Lemma 4 by removing the function key query and adding additional client public key generation and partial function key query. In order to perform the proof, we define additional hybrid games, identical to Lemma 4, and perform indistinguishability proof of individual hybrid games. In the proof of individual hybrid games, a simulator proceeds client public key generation and partial function key query processing as the similar manner as in Lemma 8. We omit the detailed proof. $\square$

Lemma 10

If the SKE scheme is one-message secure, then no polynomial-time adversary can distinguish between ${\textbf {G}}_4$ and ${\textbf {G}}_5$ with a non-negligible advantage.

Proof

The proof of this lemma is almost the same by removing the function key generation from the proof of Lemma 5, and adding client public key generation and partial function key query processing. A simulator can easily handle client public key generation and partial function key query by using $\alpha _i, \beta _i$, and $\gamma _i$ selected by the simulator. We omit the detailed description of this proof. $\square$

Theorem 9

The above DMCFE-SIC scheme is static-IND secure with corruptions in the random oracle model if the DMCFE-SIC scheme is static-IND secure with no corruptions.

Proof

The proof of this theorem is almost the same as Theorem 7 by replacing the function key query with a partial function key query. In other words, the simulator of this theorem generates the secret keys of corrupted clients by itself, and partial function key queries requested by an attacker are also processed by using the queries of the DMCFE-SI scheme with no corruption. Since all other parts of this proof are the same as Theorem 7, we will omit the detailed proof. $\square$

5.5 Discussions

Efficiency analysis The encryption and decryption algorithms of our DMCFE-SI scheme has the same performance as those of our MCFE-SI scheme in the previous section. The partial function key generation algorithm requires three exponentiations and three PRF operations to generate random exponents. And the partial function key combining algorithm requires one inverse and one exponentiation operations. Thus, the partial function key generation and partial function key combining algorithms are very efficient. The detailed comparison of MCFE schemes is given in Table 1.

Public verification of function keys A client that performs the partial function key combination algorithm needs to check whether the derived function key is correct or not. In order to publicly verify the function key, it is necessary to additionally expose public keys for private keys of individual clients. In other words, individual clients publish a public key $(g^{\alpha _i}, e(g, {\hat{g}})^{\beta _i}, g^{\gamma _i})$ for their private key $(\alpha _i, \beta _i, \gamma _i)$. Since the function key is composed of $({\hat{g}}^{\alpha _i r}, {\hat{g}}^{\alpha _j r}, {\hat{g}}^{\beta _i / (\alpha _i + \alpha _j)})$, it is possible to verify the function key by checking the following equations. $e(g^{\alpha _j}, {\hat{g}}^{\alpha _i r}) = e(g^{\alpha _i}, {\hat{g}}^{\alpha _j r}) \wedge e(g^{\alpha _i} g^{\alpha _j}, {\hat{g}}^{\beta _i / (\alpha _i + \alpha _j)}) = e(g, {\hat{g}})^{\beta _i}$. Note that it is secure for a client to expose $g^{\alpha _i}, e(g, {\hat{g}})^{\beta _i}$ in the public key since these elements are already included in the two assumptions used to prove the security of the DMCFE-SI scheme.

Decentralized three-party set intersection Previously, we could extend the MCFE-SIC and MCFE-SI schemes to support the set intersection between multiple parties. Here, we extend our DMCFE-SI scheme to support multi-party set intersection. In the case of the DMCFE-SI scheme, the function key generation is divided into partial function key generation and partial function key combination algorithms. Thus, it is necessary to modify the partial function key generation algorithm to support the multi-party set intersection. The partial function key generation algorithm needs to derive a shared key through non-interactive key exchange between entities involved in the set intersection. Fortunately, three-party non-interactive key exchange is possible by using the pairing operation. In other words, we first derive a shared key $K_{i,j,k} = e(g^{\gamma _i}, {\hat{g}}^{\gamma _j})^{\gamma _k}$ for three clients (i, j, k). We then select random exponents $r_1, r_2, s, t_1, t_2$ and set $r_3 = - r_1 - r_2, t_3 = - t_1 - t_2$. Then the partial key of the client i is $(g^{\alpha _i r_1}, g^{\beta _i s}, E_i = s \alpha _i + t_1)$, and the partial key of the client j is $(g^{\alpha _j r_2}, 1, E_j = s \alpha _j + t_2)$, and the partial key of the client k is $(g^{\alpha _k r_3}, 1, E_k = s \alpha _k + t_3)$. In this case, the correct function key $({\hat{g}}^{\beta _i s})^{1/(E_i + E_j + E_k)} = {\hat{g}}^{\beta _i / (\alpha _i + \alpha _j + \alpha _k)}$ is derived from the partial function keys.

6 Efficiency comparison

In this section, we estimate the performance of our MCFE schemes for set intersection when our schemes are instantiated in asymmetric bilinear groups. To do this, we first measure the speed of basic group operations in asymmetric pairing groups by using the Charm library [8], which is a framework for quickly implementing public-key cryptographic schemes in the Python language. To measure the performance of these basic operations, we used a desktop computer with Intel Core i9-11900 2.5GHz CPU and 16GB RAM. The Charm library supports the MNT159, MNT201, and MNT224 pairing curves as asymmetric bilinear groups that provide 80-bit, 100-bit, and 112-bit security, respectively. The performance of basic operators in these curves is given in Table 2.

We compare the performance of our MCFE schemes with the MCFE scheme of Lee and Seo [32]. For this comparison, we estimate the performance of these MCFE schemes by using the number of basic operations in Table 1 and the speed of basic operations in Table 2 instead of actually implementing these MCFE schemes. We select the MNT224 curve that provides 112-bit security as an asymmetric bilinear group, and analyze the performance of individual algorithms while changing the number of items in a set differently. The performance comparison between MCFE schemes is given in Table 3. In this table, we did not describe the performance of our DMCFE-SI scheme because the encryption and decryption algorithms of our DMCFE-SI scheme are the same as those of our MCFE-SI scheme. The estimated performance is based on a single-threaded environment, and this performance can be improved as much as the number of physical cores if multiple-threads are used.

First, the function key generation algorithms of three schemes are very efficient regardless of the size of a set because all of them only require constant number of exponentiations. Next, the encryption algorithms of three schemes require basic group operations in proportion to the size of a set. The encryption algorithm of our MCFE-SIC scheme is the most efficient because there is no pairing operation, and the encryption algorithms of the MCFE scheme of Lee and Seo and our MCFE-SI scheme have the same performance. Lastly, the decryption algorithms have the biggest difference in three schemes. The decryption algorithm of the MCFE scheme of Lee and Seo is efficient only for small-sized sets because it requires $\ell ^2$ pairing operations. In contrast, the decryption algorithm of our MCFE-SI scheme takes about 38 seconds for the $\ell = 2048$ size set because it only requires $3\ell$ pairing operations. Thus, our decryption algorithm is about 700 times faster than that of the MCFE scheme of Lee and Seo when $\ell = 2048$.

7 Generic group model

In this section, we describe the master theorem of Freeman [18] and analyze our three complexity assumptions in the generic group model of Shoup [35].

7.1 Master theorem

We use the master theorem of Freeman [18] to analyze the complexity assumptions introduced in the previous section. This master theorem is the generalization of the master theorem of Boneh et al. [13] so that the target challenge element is either ${\mathbb {G}}$ or ${\mathbb {G}}_T$ in asymmetric bilinear groups of prime order.

Table 2 Comparison of basic group operations in asymmetric bilinear groups

Table 3 Efficiency comparison of MCFE schemes for set intersection in MNT224

Let ${\mathbb {G}}, {\hat{{\mathbb {G}}}}$, and ${\mathbb {G}}_T$ be asymmetric bilinear groups of prime order p equipped with the bilinear map $e:{\mathbb {G}}\times {\hat{{\mathbb {G}}}} \rightarrow {\mathbb {G}}_T$. A group element $u \in {\mathbb {G}}$ can be represented as a multi-variate polynomial, which indicates the exponent of u relative to some fixed generator g. We can also represent group elements in ${\hat{{\mathbb {G}}}}$ and ${\mathbb {G}}_T$ as similar way. For instance, the general Diffie–Hellman tuple is represented as the expression (1, X, Y, XY) where X and Y are random variables.

The generalized dependence and independence of variables is defined by Freeman [18] as follows:

Definition 9

[18, Definition D.1] Let $P = (p_1, \ldots , p_u)$, $R = (r_1, \ldots , r_w)$, $T = (t_1, \ldots , t_v)$, $S = (s_1, \ldots , s_t)$ be tuples of multi-variate polynomials in ${\mathbb {F}}_p[X_1, \ldots , X_n]$. Let f be a multi-variate polynomial in ${\mathbb {F}}_p[X_1, \ldots , X_n]$. We say that $f \cdot S$ is dependent on (P, R, T) if there exist integers $\{ \alpha _{i,j} \}, \{ \beta _k \}, \{ \gamma _\ell \}$ such that

$$\begin{aligned} \sum _{i=1}^u \sum _{j=1}^w \alpha _{i,j} \cdot p_i r_j + \sum _{k=1}^v \beta _k \cdot t_k + \sum _{\ell =1}^t \gamma _\ell \cdot s_\ell Y \end{aligned}$$

is nonzero in ${\mathbb {F}}_p[X_1, \ldots , X_n, Y]$ but becomes zero when we set $Y = f$. We say that $f \cdot S$ is independent of (P, R, T) if $f \cdot S$ is not dependent on (P, R, T). We say that f is independent of (P, R, T) if $f \cdot \{ 1 \}$ is not dependent on (P, R, T).

In this definition, the multi-variate polynomials $p_i, r_j, t_k$ represent the exponents of group elements in ${\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T$ respectively, and the polynomial f represents the exponent of the challenge element in complexity assumptions. Additionally, the polynomials $s_\ell$ represent the exponents of group elements in which the challenge element can be paired.

Freeman defined the (P, R, T, f)-DDH problem in ${\mathbb {G}}$ and ${\mathbb {G}}_T$ by extending the (P, R, T, f)-DDH problem of Boneh et al. [13] as follows:

Definition 10

[18, Definition D.2] Let $(p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e)$ be a bilinear group randomly generated by $\mathcal {G}(1^\lambda )$. Let $g, {\hat{g}}$ be random generators of ${\mathbb {G}}, {\hat{{\mathbb {G}}}}$ respectively. Let P, R, T, f be as in Definition 9. We select $\textbf{x} {\mathop {\leftarrow }\limits ^{R}} {\mathbb {F}}_p^n$ and define the following distribution:

$$\begin{aligned} D = \big (&(p, {\mathbb {G}}, {\hat{{\mathbb {G}}}}, {\mathbb {G}}_T, e),~ g^{p_1(\textbf{x})}, \ldots , g^{p_u(\textbf{x})},~ {\hat{g}}^{r_1(\textbf{x})}, \ldots , {\hat{g}}^{r_w(\textbf{x})},~ \\&e(g, {\hat{g}})^{t_1(\textbf{x})}, \ldots , e(g, {\hat{g}})^{t_v(\textbf{x})} \big ),~ Z_0 \leftarrow g^{f(\textbf{x})},~ Z_1 {\mathop {\leftarrow }\limits ^{R}} {\mathbb {G}}\end{aligned}$$

We define the advantage of an algorithm $\mathcal {A}$ that outputs $b \in \{0,1\}$ in solving the (P, R, T, f)-decision Diffie–Hellman problem in ${\mathbb {G}}$ to be

$$\begin{aligned} {\textbf {Adv}}_{\mathcal {A}}^{(P,R,T,f)\text {-}DDH}(\lambda ) = \left| \Pr [\mathcal {A}(D, Z_0) = 1] - \Pr [\mathcal {A}(D, Z_1) = 1] \right| \end{aligned}$$

We define the analogous problem in ${\mathbb {G}}_T$ by taking $Z_0 \leftarrow e(g, {\hat{g}})^{f(\textbf{x})}, Z_1 {\mathop {\leftarrow }\limits ^{R}} {\mathbb {G}}_T$.

The master theorem of Boneh et al. [13] gives the complexity lower bound of the (P, R, T, f)-DDH problem in ${\mathbb {G}}_T$, but the same argument also works for the (P, R, T, f)-DDH problem in ${\mathbb {G}}$ as indicated by Freeman [18] using the generalized definition of independence in Definition 9.

Theorem 10

[13, 18] Let $P = (p_1, \ldots , p_u)$, $R = (r_1, \ldots , r_w)$, $T = (t_1, \ldots , t_v)$ be tuples of polynomials in ${\mathbb {F}}_p[X_1, \ldots , X_n]$. Let f be a polynomial in ${\mathbb {F}}_p[X_1, \ldots , X_n]$. Let $d = 2 \cdot max(d_P, d_R, [0]d_T, d_f)$ where $d_f$ is the total degree of f and $d_X = max\{ d_f | f \in X \}$ for a set X. If f is independent of (P, R, T), then any algorithm $\mathcal {A}$ that solves the (P, R, T, f)-DDH problem in ${\mathbb {G}}_T$ with advantage 1/2 must take at least $\Omega (\sqrt{p/d} - n)$. If $f \cdot R$ is independent of (P, R, T), then the same statement holds for the (P, R, T, f)-DDH problem in ${\mathbb {G}}$.

7.2 Analysis of Assumption 1 for $(n, \rho , Q, J)$

We analyze the Assumption 1 for $(n, \rho , Q, J)$ in the generic group model by using Theorem 10. The Assumption 1 is described as follows:

$$\begin{aligned}&D = \big ( g, g^a, \{ g^{b_k} \}_{k=1}^n, \{ g^{a b_k} \}_{k \in J}, {\hat{g}}, \{ ( {\hat{g}}^{b_i c_{i,j}}, {\hat{g}}^{b_j c_{i,j}} ) \}_{(i,j) \in Q} \big ),~ Z_0 = g^{ab_\rho },~ Z_1 = g^d. \end{aligned}$$

The Assumption 1 is described again as the following set of multi-variate polynomials:

$$\begin{aligned}&P = \{ 1, A \} \cup \{ B_k \}_{k=1}^n \cup \{ A B_k \}_{k \in J},~ R = \{ 1 \} \cup \{ B_i C_{i,j}, B_j C_{i,j} \}_{(i,j) \in Q},~ T = \{ \},~ \\&f_0 = A B_\rho ,~ f_1 = D. \end{aligned}$$

To apply the master theorem, we must show that $f_0$ and $f_1$ are independent of (P, R, T) by following Definition 9. We can easily show that $f_1 \cdot R$ is independent of (P, R, T) by using the fact that the random variable D in $f_1$ does not exist in P, R, T. To show that $f_0 \cdot R$ is independent of (P, R, T), we derive two sets $f_0 \cdot R$ and $P \cdot R$ as follows:

$$\begin{aligned} f_0 \cdot R =&\{ A B_\rho \} \cup \{ A B_\rho B_i C_{i,j}, A B_\rho B_j C_{i,j} \}_{(i,j) \in Q}, \\ P \cdot R =&\{ 1, A \} \cup \{ B_k \}_{1 \le k \le n} \cup \{ A B_k \}_{k \in J} \cup \\&\{ B_i C_{i,j}, B_j C_{i,j} \}_{(i,j) \in Q} \cup \{ A B_i C_{i,j}, A B_j C_{i,j} \}_{(i,j) \in Q} \cup \\&\{ B_k B_i C_{i,j}, B_k B_j C_{i,j} \}_{(i,j) \in Q, 1 \le k \le n} \cup \{ A B_k B_i C_{i,j}, A B_k B_j C_{i,j} \}_{(i,j) \in Q, k \in J}. \end{aligned}$$

The set $f_0 \cdot R$ consists of three component types: $A B_\rho$, $A B_\rho B_i C_{i,j}$, and $A B_\rho B_j C_{i,j}$. Since these component types are independent of each other, we can analyze these types separately.

• First, we show that $A B_\rho$ is independent of $P \cdot R$. At this time, since $A B_\rho$ includes random variables A and $B_\rho$, only $\{ A B_k \}$ can have a dependency. However, $A B_\rho$ is independent because of $\rho \notin J$.

• Next, we show that $A B_\rho B_i C_{i,j}$ is independent of $P \cdot R$. The subsets of $P \cdot R$ that contain the random variables $A, B_\rho , B_i, C_{i,j}$ are $\{ A B_k B_i C_{i,j} \}$. However, the index k cannot be the index $\rho$ because of $\rho \notin J$. Thus $A B_\rho B_i C_{i,j}$ is independent.

• We can also show that $A B_\rho B_j C_{i,j}$ is independent similarly.

Therefore, we have that $f_0 \cdot R$ is independent of (P, R, T).

7.3 Analysis of Assumption 2 for $(n, \rho , Q, J)$

We analyze the Assumption 2 for $(n, \rho , Q, J)$ in the generic group model by using Theorem 10. However, we cannot directly apply the theorem to the assumption because the assumption contains negative exponents. To solve this negative exponent problem, we set ${\hat{h}} = {\hat{g}}^{\prod _{(i,j) \in Q} (b_i + b_j)}$ and use ${\hat{h}}$ instead of ${\hat{g}}$. In this case, the Assumption 2 is described again as follows:

$$\begin{aligned}&D = \big ( g, g^a, \{ g^{b_k} \}_{k=1}^n, \{ g^{a b_k} \}_{k \in J}, {\hat{h}}, \{ {\hat{h}}^{b_i c_{i,j}}, {\hat{h}}^{b_j c_{i,j}}, {\hat{h}}^{1 / (b_i + b_j)} \}_{(i,j) \in Q} \big ),~ Z_0 = g^{ab_\rho },~ Z_1 = g^d. \end{aligned}$$

Let $\eta = \prod _{(i,j) \in Q} (B_i + B_j)$ be a random variable where the maximum degree of $\eta$ is $n(n-1)/2$. The Assumption 2 is described again as the following set of multi-variate polynomials:

$$\begin{aligned}&P = \{ 1, A \} \cup \{ B_k \}_{k=1}^n \cup \{ AB_k \}_{k \in J},~ \\&R = \{ \eta \} \cup \{ \eta B_i C_{i,j}, \eta B_j C_{i,j}, \eta / (B_i + B_j) \}_{(i,j) \in Q},~ T = \{ \},~ \\&f_0 = A B_\rho ,~ f_1 = D. \end{aligned}$$

To apply the master theorem, we must show that $f_0$ and $f_1$ are independent of (P, R, T) by following Definition 9. We can easily show that $f_1 \cdot R$ is also independent of (P, R, T) by using the fact that the random variable D in $f_1$ does not exist in P, R, T. To show that $f_0 \cdot R$ is independent of (P, R, T), we derive two sets $f_0 \cdot R$ and $P \cdot R$ as follows:

$$\begin{aligned} f_0 \cdot R =&\{ \eta A B_\rho \} \cup \{ \eta A B_\rho B_i C_{i,j}, \eta A B_\rho B_j C_{i,j}, \eta A B_\rho / (B_i + B_j) \}_{(i,j) \in Q}, \\ P \cdot R =&\{ \eta , \eta A \} \cup \{ \eta B_k \}_{1 \le k \le n} \cup \{ \eta A B_k \}_{k \in J} \cup \\&\{ \eta B_i C_{i,j}, \eta B_j C_{i,j} \}_{(i,j) \in Q} \cup \{ \eta A B_i C_{i,j}, \eta A B_j C_{i,j} \}_{(i,j) \in Q} \cup \\&\{ \eta B_k B_i C_{i,j}, \eta B_k B_j C_{i,j} \}_{(i,j) \in Q, 1 \le k \le n} \cup \{ \eta A B_k B_i C_{i,j}, \eta A B_k B_j C_{i,j} \}_{(i,j) \in Q, k \in J} \cup \\&\{ \eta / (B_i + B_j) \}_{(i,j) \in Q} \cup \{ \eta A / (B_i + B_j) \}_{(i,j) \in Q} \cup \\&\{ \eta B_k / (B_i + B_j) \}_{(i,j) \in Q, 1 \le k \le n} \cup \{ \eta A B_k / (B_i + B_j) \}_{(i,j) \in Q, k \in J}. \end{aligned}$$

The set $f_0 \cdot R$ consists of four component types: $\eta A B_\rho$, $\eta A B_\rho B_i C_{i,j}$, $\eta A B_\rho B_j C_{i,j}$, and $\eta A B_\rho / (B_i + B_j)$. Since these component types are independent of each other, we can analyze these types separately.

• First, we show that $\eta A B_\rho$ is independent of $P \cdot R$. At this time, since $\eta AB_\rho$ includes random variables $\eta , A$, and $B_\rho$, only $\{ \eta A B_k \}$ can have a dependency. However, $\eta AB_\rho$ is independent because of $\rho \notin J$.

• We show that $\eta A B_\rho B_i C_{i,j}$ is independent of $P \cdot R$. The subsets of $P \cdot R$ that contain the random variables $A, B_\rho , B_i, C_{i,j}$ are $\{ \eta A B_k B_i C_{i,j} \}$. However, $\eta A B_\rho B_i C_{i,j}$ is independent because of $\rho \notin J = \{ k \}$.

• We can also show that $\eta A B_\rho B_j C_{i,j}$ is independent similarly.

• Next, we show that $\eta A B_\rho / (B_i + B_j)$ is independent of $P \cdot R$. The subsets of $P \cdot R$ that contain the random variables $\eta , A$ are $\{ \eta A \}, \{ \eta A B_k \}, \{ \eta A / (B_i + B_j) \}$, and $\{ \eta AB_k / (B_i + B_j) \}$. Here, the subset $\{ \eta AB_k \}$ need not be considered because of $\rho \notin J$. The subset $\{ \eta A / (B_i + B_j) \}$ does not need to be considered because it does not contain $B_\rho$. Now using the remaining subsets $\{ \eta A = \eta A (B_i + B_j)/(B_i + B_j) \}$ and $\{ \eta AB_k / (B_i + B_j) \}$, we may try to compose a linear equation with $\eta AB_\rho / (B_i +B_j)$. Here, the index k cannot be the index $\rho$ because of $\rho \notin J$. Thus the only way to create a linear equation is to derive

  $$\begin{aligned} \frac{\eta AB_\rho }{(B_\rho + B_k)} = \frac{\eta A (B_\rho + B_k)}{(B_\rho + B_k)} - \frac{\eta A B_k}{(B_\rho + B_k)} \end{aligned}$$

  when $(\rho , k) \in Q$. To satisfy the above equation, it is required that $k \in J$ when $(\rho , k) \in Q$. However, if $(\rho , k) \in Q$, we have $k \notin J$ according to the definition of J. Thus $\eta AB_\rho / (B_i + B_j)$ is independent because $AB_k \notin P$ when $(\rho , k) \in Q$.

Therefore, we have that $f_0 \cdot R$ is independent of (P, R, T).

7.4 Analysis of Assumption 3 for $(n, \rho , Q)$

We analyze the Assumption 3 for $(n, \rho , Q)$ in the generic group model by using Theorem 10. However, we cannot directly apply the theorem to the assumption because the assumption contains negative exponents. To solve this negative exponent problem, we set ${\hat{h}} = {\hat{g}}^{\prod _{(i,j) \in Q} (b_i + b_j)}$ and use ${\hat{h}}$ instead of ${\hat{g}}$. In this case, the Assumption 3 is described as follows:

$$\begin{aligned}&D = \big ( g, g^a, \{ g^{b_i} \}_{i=1}^n, \{ g^{a b_k} \}_{1 \le k \ne \rho \le n}, {\hat{h}}, \{ {\hat{h}}^{b_i c_{i,j}}, {\hat{h}}^{b_j c_{i,j}}, {\hat{h}}^{d_i / (b_i + b_j)} \}_{(i,j) \in Q},\\ {}&\qquad \qquad \{ {\hat{h}}^{d_i} \}_{1 \le i \ne \rho \le n}, e(g, {\hat{h}})^{d_\rho } \big ), \\&Z_0 = e(g, {\hat{h}})^{ad_\rho },~ Z_1 = e(g, {\hat{h}})^f. \end{aligned}$$

Let $\eta = \prod _{(i,j) \in Q} (B_i + B_j)$ be a random variable where the maximum degree of $\eta$ is $n(n-1)/2$. The Assumption 3 is described again as the following set of multi-variate polynomials:

$$\begin{aligned}&P = \{ 1, A \} \cup \{ B_k \}_{k=1}^n \cup \{ A B_k \}_{1 \le k \ne \rho \le n},~ \\&R = \{ \eta \} \cup \{ \eta B_i C_{i,j}, \eta B_j C_{i,j}, \eta D_i / (B_i + B_j) \}_{(i,j) \in Q} \cup \{ \eta D_i \}_{1 \le i \ne \rho \le n},~ T = \{ \eta D_{\rho } \},~ \\&f_0 = \eta A D_\rho ,~ f_1 = \eta F. \end{aligned}$$

To apply the master theorem, we must show that $f_0$ and $f_1$ are independent of (P, R, T) by following Definition 9. We can easily show that $f_1$ is independent of (P, R, T) by using the fact that the random variable F in $f_1$ does not exist in P, R, T. To show that $f_0$ is independent of (P, R, T), we derive the set $P \cdot R$ as follows:

$$\begin{aligned} P \cdot R =&\{ \eta , \eta A \} \cup \{ \eta B_k \}_{i=k}^n \cup \{ \eta A B_k \}_{1 \le k \ne \rho \le n} \cup \{ \eta D_i, \eta A D_i \}_{1 \le i \ne \rho \le n} \cup \\&\{ \eta B_k D_i \}_{1 \le i \ne \rho \le n, 1 \le k \le n} \cup \{ \eta A B_k D_i \}_{1 \le i \ne \rho \le n, 1 \le k \le n} \cup \\&\{ \eta B_i C_{i,j}, \eta B_j C_{i,j} \}_{(i,j) \in Q} \cup \{ \eta A B_i C_{i,j}, \eta A B_j C_{i,j} \}_{(i,j) \in Q} \cup \\&\{ \eta B_k B_i C_{i,j}, \eta B_j B_k C_{i,j} \}_{(i,j) \in Q, 1 \le k \ne \rho \le n} \cup \{ \eta A B_k B_i C_{i,j}, \eta A B_k B_j C_{i,j} \}_{(i,j) \in Q, 1 \le k \ne \rho \le n} \cup \\&\{ \eta D_i / (B_i + B_j) \}_{(i,j) \in Q} \cup \{ \eta A D_i / (B_i + B_j) \}_{(i,j) \in Q} \cup \\&\{ \eta B_k D_i / (B_i + B_j) \}_{(i,j) \in Q, 1 \le k \ne \rho \le n} \cup \{ \eta A B_k D_i / (B_i + B_j) \}_{(i,j) \in Q, 1 \le k \ne \rho \le n}. \end{aligned}$$

We show that $f_0 = \eta A D_\rho$ is independent of $P \cdot R$ and T. The subsets of $P \cdot R$ that contain the random variables $A, D_\rho$ are $\{ \eta A D_i / (B_i + B_j) \}$ and $\{ \eta A B_k D_i / (B_i + B_j) \}$. Here, the subset $\{ \eta A D_i / (B_i + B_j) \}$ does not need to be considered because it lacks $(B_i + B_j)$. By using the remaining subset $\{ \eta A B_k D_i / (B_i + B_j) \}$, we may try to compose a linear equation with $\eta A D_\rho$. The only way to create a linear equation is to derive

$$\begin{aligned} \eta A D_\rho = \frac{\eta A B_{k_1} D_\rho }{(B_\rho + B_j)} + \frac{\eta A B_{k_2} D_\rho }{(B_\rho + B_j)} \end{aligned}$$

when $(\rho , j) \in Q$, $k_1 = \rho$, and $k_2 = j$. To satisfy the above equation, it is required that $k_1 = \rho$ where $k_1$ is an index for $\{ A B_k \}$. However, we have $k_1 \ne \rho$ from the restriction of the Assumption 3. Therefore, $f_0$ is independent of (P, R, T).

8 Conclusion

In this paper, we proposed various MCFE schemes that support set intersection operations and proved the security of our schemes by using the newly introduced complexity assumptions. Our first MCFE-SIC scheme supports the computation of set intersection cardinality and can efficiently find matching ciphertext elements by using a pairing operation. Our second MCFE-SI scheme supports the set intersection operation, and it requires $2\ell$ pairing operations in the decryption. Our third DMCFE-SI scheme decentralizes the generation of function keys by removing a trusted center. Using our MCFE-SI schemes, it is possible to construct an effective contact tracing system that preserves privacy of people.

We leave two interesting problems related to this study. The first problem is to devise an MCFE-SI scheme that is secure under standard assumptions. Since all our MCFE-SI schemes have disadvantages that they are secure under complex and dynamic assumptions, it is an important problem to prove the security under weaker assumptions. The second problem is to devise an MCFE-SI scheme that can efficiently compute the set intersection between n patients and m users. If our MCFE-SI scheme is directly used, the computation requires $2 nm \ell$ pairing operations with additional comparison operations. Thus, if we can improve the performance, it can be used for more efficient contact tracing.