On sets of subspaces with two intersection dimensions and a geometrical junta bound

Abstract

In this article, constant dimension subspace codes whose codewords have subspace distance in a prescribed set of integers, are considered. The easiest example of such an object is a junta (Combin Probab Comput 18(1–2):107–122, 2009); i.e. a subspace code in which all codewords go through a common subspace. We focus on the case when only two intersection values for the codewords, are assigned. In such a case we determine an upper bound for the dimension of the vector space spanned by the elements of a non-junta code. In addition, if the two intersection values are consecutive, we prove that such a bound is tight, and classify the examples attaining the largest possible dimension as one of four infinite families.

1 Introduction and preliminaries

Let $\mathbb {V}=V(\mathbb {F})$ be a finite dimensional vector space over a (possibly finite) field $\mathbb {F}$, and let $k \in \mathbb {Z}^+$ be a positive integer and $\ell \in \mathbb {N}$, such that $\ell < k$. A $(k;\ell )$-SCID (Subspaces with Constant Intersection Dimension) in $\mathbb {V}$, is a set of k-dimensional subspaces of $\mathbb {V}$ (k-spaces in the following) pairwise intersecting in an $\ell$-dimensional space [1]. The easiest way of constructing such an object is by considering a so-called $\ell$-sunflower. Precisely, by taking a family $\mathcal {S}$ of k-spaces of $\mathbb {V}$ containing an $\ell$-space $V'$ and having no points in common outside of $\mathbb {V}'$. In the following, we will refer to $V'$ as the center of the sunflower, and will call the elements of $\mathcal {S}$, the petals of $\mathcal {S}$.

Of course, not all $\ell$-sunflowers with the same number of petals span a subspace of the same dimension in $\mathbb {V}$. A sunflower $\mathcal {S}$ is said to be of maximal dimension if among all sunflowers with the same number of petals, it spans a subspace of $\mathbb {V}$ of largest dimension.

In this article we focus on a natural generalization of the concept of $(k;\ell )$-SCID. More precisely, let $\ell _1,\ell _2,...,\ell _v \in \mathbb {N}$ be non-negative integers such that $\ell _1,\ell _2, ..., \ell _v < k$. We give the following definition.

Definition 1.1

A set $\mathcal {S}$ of k-spaces of $\mathbb {V}$ is a $(k;\ell _1,\ell _2,...,\ell _v)$-SPID (Subspaces with Pre-assigned Intersection Dimensions) if for each pair of distinct subspaces $\pi _i,\pi _j\in \mathcal {S}$, we have $\dim (\pi _i \cap \pi _j) \in \{\ell _1,\ell _2,...,\ell _v\}$, and for each integer $\ell _m \in \{\ell _1,\ell _2,...,\ell _v\},$ there exist at least two k-spaces in $\mathcal {S}$ such that $\dim (\pi _i \cap \pi _j)=\ell _m$.

For our purposes, we always suppose that the dimension of $\mathbb {V}$ to be large enough in order to assure the existence of such an object. Clearly, in the case when $v=1$, we get back the definition of a $(k;\ell )$-SCID in $\mathbb {V}$.

The notion of $\ell$-sunflower in $\mathbb {V}$ can also be naturally generalized. We say that a $(k;\ell _1,\ell _2,...,\ell _v)$-SPID $\mathcal {S}$ is an $\ell$-junta in $\mathbb {V}$, if all elements of $\mathcal {S}$ pass through a common $\ell$-space of $\mathbb {V}$.

These geometric objects arise from a more general problem stated in [2, 4, 6], and recently gained a particular interest due to the fact that they provide constant subspace codes, which are a main tool in random network coding [7,8,9].

In this paper, we elaborate on finite $(k;\ell _1,\ell _2,...,\ell _v)$-SPIDs, mainly focusing on the case when only two intersection values are assigned. Moreover, if $\tilde{\ell } = \min \{\ell _1,\ell _2,...,\ell _v\}$, we will assume that $\dim (\mathbb {V}) \ge |\mathcal {S}|(k-\tilde{\ell })+\tilde{\ell }$. Under this hypothesis, it is easy to see that $\mathcal {S}$ is an $\tilde{\ell }$-sunflower of $\mathbb {V}$ of maximal dimension if any element $\pi \in \mathcal {S}$ meets the subspace generated by all others precisely in the center. In this case, we determine an upper bound for the dimension of the vector space spanned by the elements of a non-junta code, providing the smallest intersection value is strictly larger than zero. In addition, if these two possible intersection values are consecutive integers, we prove that this bound is tight and classify the examples attaining the largest dimension as one of four infinite families.

Let $\mathcal {S}=\{\pi _{1},\pi _{2},\ldots ,\pi _{n}\}$ be a $(k;\ell _1,\ell _2,\ldots ,\ell _v)$-SPID. As in [1], for each $j \in \{1,...,n\}$, the differences

$$\begin{aligned} \delta _{j}(\mathcal {S})=\dim \langle \pi _{1},\ldots ,\pi _{j} \rangle -\dim \langle \pi _{1},\ldots ,\pi _{j-1} \rangle \end{aligned}$$

will be an important arithmetic tool in order to prove our results. We underline here that we consider the span of the empty set as the null subspace; accordingly we put $\delta _1=k$. Clearly, the values $\delta _j(\mathcal {S})$ depend on the labeling of the subspaces in $\mathcal {S}$. In the following, we will enclose these integers in an array, say $\delta (\mathcal {S})=(\delta _1(\mathcal {S}),\ldots ,\delta _n(\mathcal {S}))$. Regarding this array, we show the following fact which also will play a crucial role.

Proposition 1.2

Let $k,t_1,t_2,\ldots ,t_v \in \mathbb {Z}^+$ be integers such that $k\ge t_1> t_2> \cdots >t_v \ge 1$. Let $\mathcal {S}=\{\pi _1,\ldots ,\pi _n\}$ be a $(k;k-t_1,k-t_2,\ldots ,k-t_v)$-SPID in a vector space $\mathbb {V}$, with $n \ge 3$. Then there exists a permutation $\sigma$ of the indices in the set $I_n=\{1,2,\dots ,n\}$ such that

$$\begin{aligned} t _1= \delta _2(\mathcal {S}_\sigma )\ge \delta _3(\mathcal {S}_\sigma ) \ge \ldots \ge \delta _n(\mathcal {S}_\sigma ), \end{aligned}$$

where $\mathcal {S}_{\sigma }=\{\pi _{\sigma (1)},\ldots ,\pi _{\sigma (n)}\}$, and

$$\begin{aligned} \delta _j(\mathcal {S}_\sigma )=\dim \langle \pi _{\sigma (1)},\ldots ,\pi _{\sigma (j)} \rangle -\dim \langle \pi _{\sigma (1)},\ldots ,\pi _{\sigma (j-1)} \rangle . \end{aligned}$$

Proof

Let $m \in \mathbb {Z}^+$ be the maximum integer for which there exist m k-spaces, $\pi _{i_1},\pi _{i_2},\ldots ,\pi _{i_m}$, of $\mathcal {S}$, forming a $(k-t_1)$-sunflower of maximal dimension; obviously $m \ge 2$.

Consider

$$\begin{aligned} \underset{i \not = i_1,\ldots ,i_m}{\max _{1\le i \le n }} \dim (\pi _i \cap \langle \pi _h \,|\,h\not =i \rangle ), \end{aligned}$$

and denote by $i_n$ an integer in $\{1,\ldots ,n\}\setminus \{i_1,\ldots ,i_m\}$ such that

$$\begin{aligned} \dim (\pi _{i_n} \cap \langle \pi _h \,|\,h\not =i_n \rangle )= \underset{i \not = i_1,\ldots ,i_m}{\max _{1\le i \le n }} \dim (\pi _i \cap \langle \pi _h \,|\,h\not =i \rangle ). \end{aligned}$$

Similarly, consider

$$\begin{aligned} \underset{i \not = i_1,\ldots ,i_m,i_n}{\max _{1\le i \le n }} \dim (\pi _i \cap \langle \pi _h \,|\,h\not =i,i_n \rangle ), \end{aligned}$$

then there exists an integer, say $i_{n-1} \in \{1,\ldots ,n\}\setminus \{i_1,\ldots ,i_m,i_n\}$, such that

$$\begin{aligned} \dim (\pi _{i_{n-1}} \cap \langle \pi _h \,|\,h\not =i_{n-1}, i_n \rangle )= \underset{i \not = i_1,\ldots ,i_m,i_n}{\max _{1\le i \le n }} \dim (\pi _i \cap \langle \pi _h \,|\,h\not =i,i_n \rangle ). \end{aligned}$$

After $n-m$ steps, we obtain a sequence of indices $(i_{m+1},\ldots ,i_n)$.

Let $\sigma$ be a permutation of the indices $\{1,\ldots ,n\}$, fixing the set $\{i_1,i_2,\ldots ,i_m\}$ and such that $\sigma (j)=i_j$, for every $j=m+1,\ldots ,n$. Consider $\mathcal {S}_\sigma = \{ \pi _{\sigma (1)},\ldots ,\pi _{\sigma (n)}\}$, we will show that

$$\begin{aligned} \delta _{j+1}(\mathcal {S}_\sigma ) \le \delta _j(\mathcal {S}_\sigma ) \,\,\,\, \text {for all }\,\, j=2,\ldots ,n-1.\end{aligned}$$

First of all, $\delta _j(\mathcal {S}_\sigma )\le t_1$, for each $j=2,\ldots ,n$; indeed

$$\begin{aligned} \delta _j(\mathcal {S}_\sigma )=k-\dim (\pi _{\sigma (j)} \cap \langle \pi _{\sigma (1)},\ldots ,\pi _{\sigma (j-1)} \rangle ) \le k - \dim (\pi _{\sigma (j)} \cap \pi _{\sigma (1)}) \le t_1. \end{aligned}$$

Also, since $\pi _{\sigma (1)},\ldots ,\pi _{\sigma (m)}$ form a $(k-t_1)$-sunflower of maximal dimension, then we have $\delta _j(\mathcal {S}_\sigma )=t_1$, with $2\le j \le m$. Note that

$$\begin{aligned} \dim (\pi _{i_{j+1}} \cap \langle \pi _h \,|\,h\not = i_{j+1},\ldots ,i_n \rangle ) \ge \dim (\pi _{i_{j}} \cap \langle \pi _h \,|\,h\not = i_{j},\ldots ,i_n \rangle ) \end{aligned}$$

for all $m+1 \le j \le n-1$, because otherwise we would have

$$\begin{aligned} \begin{aligned} \dim (\pi _{i_{j+1}} \cap \langle \pi _h \,|\,h\not = i_{j+1},\ldots ,i_n \rangle )&< \dim (\pi _{i_{j}} \cap \langle \pi _h \,|\,h\not = i_{j},\ldots ,i_n \rangle ) \\&\le \dim (\pi _{i_j} \cap \langle \pi _h \,|\, h \not =i_j,i_{j+2},\ldots ,i_n \rangle ), \end{aligned} \end{aligned}$$

which is a contradiction by the definition of $i_{j+1}$. Then

$$\begin{aligned} \delta _{j+1}(\mathcal {S}_\sigma )= & {} k-\dim (\pi _{i_{j+1}} \cap \langle \pi _h \,|\,h\not = i_{j+1},\ldots ,i_n \rangle ) \\\le & {} k- \dim (\pi _{i_{j}} \cap \langle \pi _h \,|\,h\not = i_{j},\ldots ,i_n \rangle )=\delta _j(\mathcal {S}_\sigma ). \end{aligned}$$

This concludes the proof. $\square$

In other terms, it is always possible to sort k-spaces in $\mathcal {S}$ in such a way that the associated array $\delta (\mathcal {S})$, is non-increasing (see also [1, Theorem 2]).

Remark 1.3

We note explicitly that for a $(k;k-t)$-SCID $\mathcal {S}=\{\pi _1,\ldots ,\pi _n\} \subset \mathbb {V},$ we have

$$\begin{aligned} \delta (\mathcal {S}):= (\delta _1,\delta _2,\ldots ,\delta _n)=(k,t,\ldots ,t) \end{aligned}$$

(1)

if and only if $\mathcal {S}$ is a $(k-t)$-sunflower of maximal dimension. The necessary condition is in fact trivial. While, regarding the sufficiency we may observe that since $\delta _n(\mathcal {S})=t$ and

$$\begin{aligned}\pi _n \cap \langle \pi _1,\ldots ,\pi _{n-1} \rangle \supseteq \pi _n \cap \pi _i,\end{aligned}$$

we get for each $i \in \{1,...,n-1\},$ $\pi _n \cap \pi _i= V'$, where $V'=\pi _n \cap \langle \pi _1,\ldots ,\pi _{n-1} \rangle$. This implies that $\mathcal {S}$ is a $(k-t)$-sunflower. Finally, by using Grassmann’s formula, it is easy to show that $\mathcal {S}$ is of maximal dimension.

2 A junta-property bound for $(k;k-t_1,k-t_2)$-SPIDs

In this section, we restrict our discussion to the case where only two values for the intersection dimensions are possible.

We start by showing a result which appears as a quite natural generalization of [1, Theorem 2] to $(k;k-t_1,k-t_2)$-SPID, with $k-t_1 \ne 0$.

Theorem 2.1

Let $k,t_1,t_2 \in \mathbb {Z}^+$ such that $k> t_1 > t_2 \ge 2$. Let $\mathcal {S}$ be a $(k;k-t_1,k-t_2)$-SPID in $\mathbb {V}$, with $n=| \mathcal {S}| \ge 3$. If $\dim \langle \mathcal {S} \rangle \ge k+(t_1-1)(n-1)+2$, then $\mathcal {S}$ is a $(k-t_1)$-junta.

Proof

Let $\delta (\mathcal {S})$ be any non-increasing array associated with $\mathcal {S}$. In particular, arguing as in the proof of Proposition 1.2, we can choose as first m spaces, $m \ge 2$, those forming a $(k-t_1)$-sunflower of maximal dimension. By Remark 1.3, the integer m is the largest index for which $\delta _m=t_1$. Let $V'$ be the center of the sunflower formed by $\pi _1,\ldots ,\pi _m$. Hence, we get $\dim V'=k-t_1$. Assume that $\mathcal {S}$ is not a $(k-t_1)$-junta, so we can find a subspace $\pi _r \in \mathcal {S}\setminus \{\pi _1,\ldots ,\pi _m\}$ not containing $V'$. We denote $k-t_1-\dim (\pi _r \cap V')$ by $\varepsilon$; hence, $\varepsilon \ge 1$. Also, in the quotient vector space $\Pi =\langle \mathcal {S} \rangle /(V'\cap \pi _r)$, we have that $\dim _{\Pi }\pi _r=t_1+\varepsilon$, and that $\dim _{\Pi }(\pi _r \cap \pi _i) \in \{\varepsilon ,\varepsilon +t_1-t_2\}$, for each $1 \le i \le m$. Also, the subspaces $(\pi _r \cap \pi _i)/(V' \cap \pi _r)$ of $\Pi$, with $1 \le i \le m$, are linearly independent. Hence,

$$\begin{aligned} \begin{aligned} \delta _{r}&= \dim \pi _r -\dim (\langle \pi _1, \pi _2, \ldots ,\pi _{r-1} \rangle \cap \pi _r)\le \dim _\Pi \pi _r - \dim _\Pi \langle \pi _1 \cap \pi _r, \ldots , \pi _m \cap \pi _r \rangle \\&= t_1+\varepsilon - \sum ^m_{i=1} \dim _{\Pi }(\pi _r \cap \pi _i) \le t_1+\varepsilon - m \cdot \varepsilon \le t_1-m+1.\end{aligned} \end{aligned}$$

Since $\delta (\mathcal {S})=(\delta _1,\ldots , \delta _n)$ is non-increasing, it is easy to see that

$$\begin{aligned} \begin{aligned} \dim \langle {\mathcal {S}} \rangle&= \sum ^n_{i=1} \delta _i= k + \sum ^m_{i=2} \delta _i +\sum ^{r-1}_{i=m+1}\delta _i+\sum ^n_{i=r} \delta _i \\&\le k + (m-1)t_1+(r-m-1)(t_1-1)+(n-r+1)(t_1-m+1) \\&=k+(n-1)(t_1-1)-(n-r)(m-2)+1 \\&\le k+(n-1)(t_1-1)+1, \end{aligned} \end{aligned}$$

(2)

which proves the theorem. $\square$

Remark 2.2

We point out here that unlike what happens for SCIDs, in general the bound stated above is not tight. For instance, with the same notation as used in Theorem 2.1; if $t_1 > t_2 \ge 2$ and there exists an integer s such that $r>s>m$ with $\delta _s \le t_2$, we can slightly improve on the upper bound stated in Theorem 2.1. In fact, if this is the case we can repeat the proof of Theorem 2.1, and by re-writing Inequality (2), we get

$$\begin{aligned} \begin{aligned} \dim \langle {\mathcal {S}} \rangle&= \sum ^n_{i=1}\delta _i= k + \sum ^m_{i=2}\delta _i +\sum ^{s-1}_{i=m+1}\delta _i+\sum ^{r-1}_{i=s}\delta _i+\sum ^n_{i=r}\delta _i \\&\le k + (m-1)t_1+(s-m-1)(t_1-1)+(r-s)t_2+(n-r+1)(t_1-m+1) \\&=k+(n-1)(t_1-1)-(n-r)(m-2)-(r-s)(t_1-t_2-1)+1 \\&\le k+(n-1)(t_1-1)-(t_1-t_2)+2. \end{aligned} \end{aligned}$$

(3)

This possibility can be realised if the first $r-1$ spaces form a $(k-t_1)$-junta with $\dim (\pi _s \cap \pi _j)=k-t_2$ for some $j\in \{1,\ldots ,s-1\}$. In what follows, we exhibit a concrete example.

Let $k,t_1,t_2 \in \mathbb {Z}^+$ such that $k> t_1> t_2+1 > 2$ and consider $t_1-t_2+1 \le m \le \min \{t_1+1,n-1\}$. Let $V',X,N_1,\ldots ,N_m$, $M_{m+1},\ldots ,M_{s-1}$ and $P_s, \ldots ,P_{n-1}$ be linearly independent subspaces of $\mathbb {V}$ such that

(a):

$\dim V'=k-t_1$,

(b):

$\dim X=t_1-m+1$,

(c):

$\dim N_i=t_1$,   for $i=1,\ldots ,m$,

(d):

$\dim M_j = t_1-1$,   for $j=m+1,\ldots ,s-1$,

(e):

$\dim P_\ell =t_2$,   for $\ell =s,\ldots ,n-1$.

Let $A_i=\{a_{i1},\ldots ,a_{i,t_1-t_2}\}$ be a set of linearly independent 1-spaces in $N_i$, for $i=1,\ldots ,m$, $|A_i|=t_1-t_2$, and we choose in $A_i$ a 1-space, for example $a_{i1}$. Now, let $b_{m+1},\ldots , b_{s-1}$ be distinct 1-spaces in $\langle a_{11},\ldots ,a_{m1} \rangle \setminus \{a_{11},\ldots ,a_{m1}\}$ (where $\frac{q^m-1}{q-1}\ge s-m-1$ when $\mathbb {V}$ is a vector space over the Galois field of order q, $\mathbb {F}_q$) and let W be a $(k-t_1-1)$-space in $V'$. Then we define the k-spaces $\pi _1,\ldots ,\pi _n$ as follows.

$\circ$:

$\pi _1=\langle V',N_1 \rangle$, $\pi _2=\langle V',N_2 \rangle$, $\ldots$, $\pi _m=\langle V',N_m \rangle$,

$\circ$:

$\pi _{m+1}=\langle V',b_{m+1}, M_{m+1} \rangle$, $\ldots$, $\pi _{s-1}=\langle V',b_{s-1},M_{s-1} \rangle$,

$\circ$:

$\pi _s=\langle V',Q_s,P_s \rangle$,$\ldots$,$\pi _{n-1}=\langle V',Q_{n-1},P_{n-1} \rangle$,

$\circ$:

$\pi _{n}=\langle W,a_{11},\ldots ,a_{m1},X \rangle$,

where $Q_s,\ldots ,Q_{n-1}$ are $(t_1-t_2)$-spaces equal to $\langle A_i \rangle$, for some $i \in \{1,\ldots ,m\}$. It is easy to verify that

(i):

$\pi _i \cap \pi _j =V'$, with $i,j=1,\ldots ,s-1,$

(ii):

$\pi _i \cap \pi _j=V'$, with $i=m+1,\ldots ,s-1$ and $j=s,\ldots ,n-1,$

(iii):

$\dim (\pi _i \cap \pi _j) \in \{k-t_1,k-t_2\}$, for $i=1,\ldots ,m$ and $j=s,\ldots ,n$.

Fig. 1

The $(k;k-t_1,k-t_2)$-SPID described in Remark 2.2

Hence, $\mathcal {S}=\{\pi _1,\ldots ,\pi _n\}$ is a set of n distinct k-spaces pairwise meeting either in a space of dimension $k-t_1$ or of dimension $k-t_2$, i.e. a $(k; k-t_1,k-t_2)$-SPID. Also, it is clear that $\mathcal {S}$ is not a $(k-t_1)$-junta. Now, we have that

$$\begin{aligned} \langle \mathcal {S} \rangle =\langle \pi _1,\ldots ,\pi _n \rangle =\langle V',N_1,\ldots ,N_m,M_{m+1},\ldots ,M_{s-1},P_s,\ldots ,P_{n-1},X \rangle . \end{aligned}$$

So, by hypothesis,

$$\begin{aligned} \begin{aligned} \dim \langle \mathcal {S} \rangle&= k + (m-1)t_1+(s-m-1)(t_1-1)+(n-s)t_2+(t_1-m+1) \\&=k+(n-1)(t_1-1)-(n-s)(t_1-t_2-1)+1 \\&\le k+(n-1)(t_1-1)-(t_1-t_2)+2. \end{aligned} \end{aligned}$$

We find that the array $\delta (\mathcal {S})$ corresponding to such a SPID is as follows:

$$\begin{aligned} \delta (\mathcal {S})=(k,\underbrace{t_1,\ldots , t_1}_{m-1 \,\,\text {times}}, \underbrace{t_1-1, \ldots , t_1-1}_{s-m-1\,\, \text {times}}, \underbrace{t_2, \ldots , t_2}_{n-s\,\, \text {times}}, t_1-m+1). \end{aligned}$$

In the following, we will show that if in addition we ask that the two possible values for the dimensions of the intersection between elements of the SPID are consecutive integers, then the bound in Theorem 2.1 is sharp. Towards this aim, we put beforehand the following result.

Proposition 2.3

Let $t_1,t_2 \in \mathbb {Z}^+$ with $k> t_1 > t_2 \ge 2$. Let $\mathcal {S}$ be a $(k;k-t_1,k-t_2)$-SPID in a vector space $\mathbb {V}$, with $n=|\mathcal {S}| \ge 3$, such that $\dim \langle \mathcal {S} \rangle =k+(n-1)(t_1-1)+1$. Also let $\delta (\mathcal {S})$ be any non-increasing array associated with $\mathcal {S}$.

Then, there is no $(k-t_1)$-sunflower of maximal dimension with at least three petals in $\mathcal {S}$, if and only if

$$\begin{aligned} \delta (\mathcal {S})=(k,t_1,t_1-1,\ldots ,t_1-1). \end{aligned}$$

(4)

Moreover, if $\mathcal {S}=\{\pi _1,\pi _2,\ldots ,\pi _n\}$ has associated non-increasing array $\delta (\mathcal {S})$ like in (4), then any permutation $\sigma$, fixing $\pi _1$ and $\pi _2$, does not change $\delta (\mathcal {S})$.

Proof

The necessity is obvious because if any such a $\delta (\mathcal {S})$ is like in (4), then, by Proposition 1.2 and by Remark 1.3, $\mathcal {S}$ can not contain a $(k-t_1)$-sunflower of maximal dimension with at least three petals.

Regarding sufficiency, clearly we have $\dim (\pi _1 \cap \pi _2)=k-t_1$ and by hypothesis in any non-increasing array the largest index m for which $\delta _m=t_1$, is 2. Now, if $\delta _n \le t_1-2$, then

$$\begin{aligned} \dim \langle \mathcal {S} \rangle= & {} \sum ^n_{i=1}\delta _i=k+t_1+\sum ^{n-1}_{i=3} \delta _i+\delta _n \le k+ t_1 +(n-3)(t_1-1)+t_1-2 \\= & {} k+(n-1)(t_1-1), \end{aligned}$$

a contradiction. Hence, $(\delta _1,\delta _2,\ldots ,\delta _n)=(k,t_1,t_1-1,\ldots ,t_1-1)$.

Now, we show that any permutation of the k-spaces in $\mathcal {S}$, fixing $\pi _1$ and $\pi _2$, does not change the array (4). First of all, we notice that

$$\begin{aligned} \dim ( \pi _j \cap \langle \pi _1,\pi _2 \rangle ) = k-t_1+1, \quad \text {for all} \,\,j=3,\ldots ,n. \end{aligned}$$

Indeed, for $3 \le j \le n$,

$$\begin{aligned}&k-t_1 \le \dim (\pi _j \cap \pi _1) \le \dim ( \pi _j \cap \langle \pi _1, \pi _2 \rangle )\\&\le \dim ( \pi _j \cap \langle \pi _1,\pi _2,\ldots ,\pi _{j-1} \rangle )=k-t_1+1. \end{aligned}$$

If $\dim (\pi _j \cap \langle \pi _1,\pi _2 \rangle )=k-t_1$, then

$$\begin{aligned} \pi _j \cap \pi _1=\pi _j \cap \langle \pi _1 ,\pi _2 \rangle =\pi _j \cap \pi _2. \end{aligned}$$

Consequently, we also have $\pi _j \cap \langle \pi _1 ,\pi _2 \rangle =\pi _1 \cap \pi _2$. This implies that $\pi _1,\pi _2,\pi _j$ form a $(k-t_1)$-sunflower of maximal dimension; in fact, $\dim \langle \pi _1,\pi _2,\pi _j \rangle =k+2t_1$ and, eventually applying the same procedure as in the proof of Proposition 1.2, we would get a non-increasing array $\delta (\mathcal {S})$ with $\delta _2=\delta _3=t_1$; a contradiction. Hence, $\dim ( \pi _j \cap \langle \pi _1,\pi _2 \rangle ) = k-t_1+1$.

Nevertheless, since any non-increasing array $\delta (\mathcal {S})$ is as in (4), we have

$$\begin{aligned} k-t_1+1= & {} \max _{3 \le i \le n} \dim (\pi _i \cap \langle \pi _h \,|\, h \not = i \rangle ) \ge \dim (\pi _j \cap \langle \pi _h \,| \,h \not = j \rangle ) \\\ge & {} \dim (\pi _j \cap \langle \pi _1,\pi _2 \rangle )=k-t_1+1. \end{aligned}$$

Hence, for any $I \subset I_n=\{1,\ldots ,n\}$, with $1,2\in I$ and $j \not \in I$,

$$\begin{aligned} \dim (\pi _j \cap \langle \pi _h \,| \,h \in I \rangle )=k-t_1+1. \end{aligned}$$

Now, let $\sigma$ be any permutation of $I_n$ such that $\sigma (1)=1$ and $\sigma (2)=2$, then

$$\begin{aligned} \begin{aligned} \delta _j(\mathcal {S}_\sigma )&= k-\dim (\pi _{\sigma (j)} \cap \langle \pi _{\sigma (1)},\pi _{\sigma (2)}, \ldots ,\pi _{\sigma (j-1)} \rangle )\\&= k-\dim (\pi _{\sigma (j)} \cap \langle \pi _{1},\pi _{2},\pi _{\sigma (3)}, \ldots ,\pi _{\sigma (j-1)} \rangle )=t_1-1, \end{aligned} \end{aligned}$$

for all $j=3,\ldots ,n$. $\square$

Next, we exhibit four families of $(k;k-t,k-t+1)$-SPIDs which are not ($k-t$)-juntas, and such that $\dim \langle \mathcal {S} \rangle = k+ (n-1)(t-1)+1$.

In the following, we will denote by $\delta '(\mathcal {S})$ any non-increasing array obtained as described in Proposition 1.2.

2.1 SPIDs with $\delta '=(k,t,\dots ,t,t-1,\dots ,t-1,t+1-m)$

Let $t \in \mathbb {Z}^+$ such that $2 \le t \le k-1$. Let $m \in \mathbb {Z}^+$ be a positive integer such that $m>2$. We provide a class of $(k;k-t,k-t+1)$-SPIDs with non-increasing array

$$\begin{aligned} \delta '(\mathcal {S}) = (k,\underbrace{t, \ldots , t}_{m-1 \,\,\text {times}}, \underbrace{t-1, \ldots , t-1}_{n-m-1\,\, \text {times}}, t+1-m). \end{aligned}$$

Fig. 2

The ($k;k-t,k-t+1$)-SPID described in Class I

$\bullet$  Class I

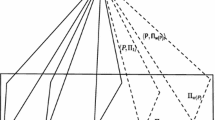
Let $2<m \le \min \{t+1,n-1\}$. Let $V',X,N_1,\ldots ,N_m$ and $M_{m+1},\ldots ,M_{n-1}$ be linearly independent subspaces of $\mathbb {V}$ such that $\dim V'=k-t$, $\dim X=t-m+1$, $\dim N_i=t$ for $i=1,\ldots ,m,$ and $\dim M_j = t-1$ for $j=m+1,\ldots ,n-1$ (Fig. 2). Let $a_1,\ldots ,a_m$ be 1-spaces in $N_1,\ldots ,N_m$, respectively. Also, let $b_{m+1},\ldots , b_{n-1}$ be 1-spaces in $\langle a_1,\ldots ,a_m \rangle$ such that either

(i):

at least two of them are the same 1-space, or

(ii):

at least one of them is equal to $a_i$, with $i \in \{1,\ldots ,m\}$.

Let W be a $(k-t-1)$-space in $V'$. Then we define the k-spaces $\pi _1,\ldots ,\pi _n$ as follows.

$\circ$:

$\pi _1=\langle V',N_1 \rangle$, $\pi _2=\langle V',N_2 \rangle$, $\ldots$, $\pi _m=\langle V',N_m \rangle$,

$\circ$:

$\pi _{m+1}=\langle V',M_{m+1},b_{m+1} \rangle$, $\ldots$, $\pi _{n-1}=\langle V',M_{n-1},b_{n-1} \rangle$,

$\circ$:

$\pi _{n}=\langle W,a_1,\ldots ,a_m,X \rangle$.

By Requests (i) and (ii), it is clear that the pairwise intersection of distinct spaces $\pi _i$ and $\pi _j$, $i,j=1, \ldots , n-1$, either is the $(k-t)$-space $V'$ or it is a $(k-t+1)$-space containing $V'$. Moreover, since each of the spaces $\pi _1,\ldots ,\pi _{n-1}$ contains a unique 1-space from the set $\{a_1,\ldots ,a_m,b_{m+1},\ldots ,b_{n-1}\}$ (note that by Properties (i) and (ii), some of the 1-spaces could be equal), we have $\dim (\pi _n \cap \pi _i)=k-t$, for all $i=1,\ldots ,n-1$. Hence, the set $\mathcal {S}=\{\pi _1,\ldots ,\pi _n\}$ is a set of n distinct k-spaces pairwise meeting in a space of dimension $k-t$ or $k-t+1$. Also, since not all pairwise intersections equal the same $(k-t)$-space, $\mathcal {S}$ is not a $(k-t)$-junta. The set $\{a_1,\ldots ,a_m,b_{m+1},\ldots ,b_{n-1}\}$ is contained in $\langle N_1,\ldots ,N_m \rangle$ and $W \subset V'$. Then

$$\begin{aligned} \langle \mathcal {S} \rangle =\langle \pi _1,\ldots ,\pi _n \rangle =\langle V',N_1,\ldots ,N_m,M_{m+1},\ldots ,M_{n-1},X \rangle . \end{aligned}$$

Clearly, since $V',X,N_1,\ldots ,N_m$ and $M_{m+1},\ldots ,M_{n-1}$ are linearly independent spaces of $\mathbb {V}$, we have that

$$\begin{aligned} \dim \langle \mathcal {S} \rangle&= k-t+m \cdot t+ (n-1-m) \cdot (t-1) + t-m+1 \\&= k+ (n-1)(t-1)+1. \end{aligned}$$

Arguing as in Proposition 1.2, we find

$$\begin{aligned} \delta '(\mathcal {S})=(k,\underbrace{t, \ldots , t}_{m-1 \,\,\text {times}}, \underbrace{t-1, \ldots , t-1}_{n-m-1\,\, \text {times}}, t+1-m). \end{aligned}$$

Lemma 2.4

Let $\mathcal {S}$ be a $(k;k-t, k-t+1)$-SPID of $\mathbb {V}$, where $2 \le t \le k-1$, such that $\mathcal {S}$ is not a $(k-t)$-junta, with $| \mathcal {S}|= n \ge 3$. If $\dim \langle \mathcal {S} \rangle =k+(n-1)(t-1)+1$ and there exists a $(k-t)$-sunflower of maximal dimension with at least three petals in $\mathcal {S}$, then $\mathcal {S}$ belongs to Class I.

Proof

Since $\dim \langle \mathcal {S} \rangle =k+(n-1)(t-1)+1$, from the proof of Theorem 2.1 we get

$$\begin{aligned} \sum ^n_{i=1} \delta _i=k+(n-1)(t_1-1)-(n-r)(m-2)+1.\end{aligned}$$

Moreover, since this implies that $(n-r)(m-2)=0$ and $m \ge 3$, necessarily $r=n$. Then,

$$\begin{aligned} \delta '(\mathcal {S})=(k,\underbrace{t, \ldots , t}_{m-1 \,\,\text {times}}, \underbrace{t-1, \ldots , t-1}_{n-m-1\,\, \text {times}}, t+1-m). \end{aligned}$$

(5)

Consider $\mathcal {S}'=\{\pi _1,\ldots ,\pi _{n-1}\}$. Since $\dim \langle \mathcal {S}' \rangle =k+(n-2)(t-1)+m-1 \ge k+(n-2)(t-1)+2$, then, by Theorem 2.1, we have that $\mathcal {S}'$ is a $(k-t)$-junta. Let $V'$ be the common $(k-t)$-space through which the k-spaces $\pi _1, \ldots , \pi _{n-1}$ pass, and denote $k-t-\dim (\pi _n \cap V')$ by $\varepsilon$. Since $\mathcal {S}$ is not a junta, $\varepsilon \ge 1$; indeed, by the proof of Theorem 2.1, necessarily $\varepsilon =1$. Let W denote the $(k-t-1)$-subspace $\pi _n \cap V'$. Furthermore, we note the first k-spaces form a sunflower of maximal dimension since $\delta _2=\cdots =\delta _m=t$. Hence, there exist t-spaces $N_1, \ldots ,N_m$, with $i=1,\ldots ,m$, such that $N_1,\ldots ,N_m,V'$ are linearly independent, and $\pi _i=\langle V', N_i \rangle$. Also, by hypothesis, there exist at least two k-spaces in $\mathcal {S}$ such that they meet in a $(k-t+1)$-space. We first show that

$$\begin{aligned} \dim (\pi _n \cap \pi _j)=k-t, \text {for all} \,\, j \in \{1,\ldots ,n-1\}. \end{aligned}$$

For this purpose, suppose by way of contradiction that there exists a $j \in \{1,\ldots ,n-1\}$ such that $\dim (\pi _n \cap \pi _j)=k-t+1$; we may distinguish between two cases:

(a):

$j \in \{1, \ldots , m\}$. Then there are two 1-spaces $a_{j_1}$ and $a_{j_2}$ in $\pi _n \cap \pi _j$ not in $V'$, and there is at least another 1-space $a_i \in \pi _n \cap \pi _i$, for all $i \in \{1,\ldots ,m\} \setminus \{j\}$ not in $V'$. Without loosing any generality, we may choose the $N_i$’s in such a way that $a_1 \in N_1, \ldots , a_m \in N_m$ and $\langle a_{j_1}, a_{j_2} \rangle \subseteq N_j$. Hence,

$$\begin{aligned} \pi _n \cap \langle \pi _1, \ldots , \pi _{n-1} \rangle \supseteq \langle W, a_1,\ldots ,a_{j-1},a_{j_1},a_{j_2},a_{j+1},\ldots ,a_{m} \rangle , \end{aligned}$$

obtaining that

$$\begin{aligned} t-m+1=\delta _n \le k- \dim \langle W, a_1,\ldots ,a_{j-1},a_{j_1},a_{j_2},a_{j+1},\ldots ,a_{m} \rangle =t-m, \end{aligned}$$

a contradiction.

(b):

$j \in \{m+1, \ldots , n-1\}$. Since, by Point (a), $\dim (\pi _n \cap \pi _i)=k-t$ for every $i=1,\ldots ,m$, $\pi _n$ contains the 1-spaces $a_1 \in \pi _1,\ldots , a_m \in \pi _m$, meeting $V'$ trivially. Furthermore, since $\dim (\pi _n \cap \pi _j)=k-t+1$, there must be two 1-spaces $a',a'' \in \pi _n \cap \pi _j$ not in $V'$ and such that $\langle a', a'' \rangle \cap W$ is trivial. Also, the subspace $\langle a',a'' \rangle$ can not be contained in $\langle V',a_1,\ldots ,a_m \rangle$, otherwise we would have

$$\begin{aligned} \pi _{j} \cap \langle V', a_1,\ldots , a_m \rangle \supseteq \langle V',a',a'' \rangle , \end{aligned}$$

and, consequently,

$$\begin{aligned} t-1=\delta _{j}\le k- \dim \langle V',a',a'' \rangle =t-2. \end{aligned}$$

Moreover, $\langle a',a'' \rangle$ meets $\langle V',a_1,\ldots ,a_m \rangle$ in a 1-space, otherwise

$$\begin{aligned} \pi _n \cap \langle \pi _1,\ldots ,\pi _{n-1} \rangle \supseteq \langle W,a_1,\ldots ,a_m,a',a'' \rangle \end{aligned}$$

obtaining again $t-m+1=\delta _n \le t-m-1$. However, if $b \in \langle a',a'' \rangle \setminus \langle V',a_1,\ldots ,a_m \rangle$, then

$$\begin{aligned} t-m+1=\delta _n \le k- \dim \langle W,a_1\ldots ,a_m,b \rangle =t-m; \end{aligned}$$

which is again a contradiction.

Hence, definitely $\dim (\pi _n \cap \pi _j)=k-t$, for each $j \in \{1,\ldots ,n-1\}$.

Now, since $\delta _n=t-m+1$ and $\pi _n$ intersects $V'$ in the $(k-t-1)$-dimensional subspace W, we get that the k-space $\pi _n$ may be realised as follows

$$\begin{aligned} \pi _n=\langle W,a_1,\ldots ,a_m,X \rangle , \end{aligned}$$

for suitable points $a_1 \in N_1,\ldots , a_m\in N_m$ and X a $(t-m+1)$-dimensional subspace such that $V',N_1,\ldots ,N_m,X$ are linearly independent.

Fig. 3

The $(k;k-t,k-t+1)$-SPIDs described in Class II

Since $\pi _n \cap \pi _j$, $j=m+1,\ldots ,n-1$, is a $(k-t)$-space contained in $\langle W,a_1,\ldots ,a_m \rangle ,$ there must exist a 1-space $b_j$ in $\langle a_1,\ldots ,a_m \rangle \setminus W$ such that $\pi _n \cap \pi _j=\langle W,b_j \rangle$ otherwise

$$\begin{aligned} t-m+1=\delta _n=k-\dim (\pi _n \cap \langle \pi _1,\ldots ,\pi _{n-1} \rangle )\le k-\dim \langle W,a_1,\ldots ,a_m,b_j \rangle =t-m, \end{aligned}$$

a contradiction. Moreover, since $\delta _j=t-1$, it is immediate that for any $j=m+1,\ldots ,n-1$, we have $\pi _{j}= \langle V',b_j,M_j\rangle$, with $M_j$ a $(t-1)$-space and such that $V',N_1,\ldots , N_m, M_{m+1},\ldots ,$ $M_{n-1}$ and X are linearly independent. Note explicitly that if $\dim (\pi _i \cap \pi _j)=k-t+1$, with $i,j \in \{m+1,\ldots ,n-1\}$, then $b_i=b_j$. Indeed, let $\pi _i \cap \pi _j=\langle V',a' \rangle$. This space is contained in $\langle \pi _1,\pi _2,\ldots ,\pi _m \rangle$, since if $a' \not \in \langle \pi _1, \pi _2,\ldots ,\pi _m \rangle$, assuming $j >i$, we have

$$\begin{aligned} \pi _j \cap \langle \pi _1,\ldots ,\pi _i \rangle \supseteq \langle V',b_j,a' \rangle , \end{aligned}$$

obtaining $\delta _j \le t-2$. So, $\langle V',a' \rangle \subseteq \langle \pi _1,\ldots ,\pi _m \rangle$. Now, since $\pi _i \cap \langle \pi _1,\pi _2,\ldots , \pi _m \rangle =\langle V',b_i \rangle$ and $\pi _j \cap \langle \pi _1,\pi _2,\ldots ,\pi _m \rangle =\langle V',b_j \rangle$ have dimension $k-t+1$ and

$$\begin{aligned} \pi _i \cap \pi _j= \pi _i \cap \pi _j \cap \langle \pi _1, \pi _2, \ldots , \pi _m \rangle , \end{aligned}$$

we get that both $\langle V',b_i \rangle$ and $\langle V',b_j \rangle$ are equal to $\pi _i \cap \pi _j$. Now, since we assumed $j > i$, if $b_i \not = b_j$ then again we would have $t-1=\delta _j \le t-2$, which is not the case. Suppose that there exist $i \in \{1,\ldots ,m\}$ and $j \in \{m+1, \ldots ,n-1\}$ such that $\dim (\pi _i \cap \pi _j)=k-t+1$, then there exists a 1-space $a' \in N_i$ such that

$$\begin{aligned} \langle V',a' \rangle =\pi _i \cap \pi _j \subseteq \pi _j \cap \langle \pi _1,\ldots ,\pi _m \rangle =\langle V',b_j \rangle . \end{aligned}$$

Hence, $b_j \in \langle V',a' \rangle$ and, since $\delta _j=t-1$, $b_j \in \langle a_1,\ldots ,a_m \rangle \cap N_i$ otherwise

$$\begin{aligned} t-1=\delta _j=k-\dim (\pi _j \cap \langle \pi _1,\ldots ,\pi _{j-1} \rangle ) \le k -\dim \langle V',a',b_j \rangle =t-2; \end{aligned}$$

this implies that $b_j=a_i$. Note explicitly that a k-space $\pi _j$ in $\mathcal {S}$, with $j \in \{m+1,\ldots ,n-1\}$, can meet at most one $\pi _i$, with $i \in \{1,\ldots ,m\}$, in a $(k-t+1)$-space. Finally, it is possible that in $\mathcal {S}$ there exists a k-space $\pi _j$, with $j \in \{m+1,\ldots ,n-1\}$, that intersects $\pi _i$, with $i \in \{1,\ldots ,m\}$, and $\pi _h$, with $h\in \{m+1,\ldots ,n-1\}$, in two $(k-t+1)$-spaces. From previous results, $b_h=b_j=a_i$. So, $\mathcal {S}$ belongs to Class I. $\square$

2.2 SPIDs with $\delta '=(k,t,t-1,t-1,\ldots ,t-1)$

$\bullet$  Class II

Choose integers $n \ge 3$ and k, t such that $2 \le t \le k-1$. Let W be a $(k-t+1)$-subspace of $\mathbb {V}$, and $X_1,X_2$ t-spaces such that $\dim \langle X_1,X_2 \rangle =2t-1$. Moreover, consider $M_3,\ldots , M_n$ $(t-1)$-subspaces of $\mathbb {V}$ such that W, $\langle X_1,X_2 \rangle$, $M_3,\ldots ,M_n$ are linearly independent. Let $W_1$ and $W_2$ be two $(k-t)$-spaces in W (Fig. 3). Then we define the sets $\pi _1,\ldots ,\pi _n$ as follows:

$\circ$:

$\pi _1=\langle W_1,X_1 \rangle$, $\pi _2=\langle W_2,X_2 \rangle$,

$\circ$:

$\pi _{3}=\langle W,M_{3} \rangle$, ...$,\pi _{n}=\langle W,M_n \rangle$.

Now, since $\dim (X_1 \cap X_2)=1$, $\pi _1 \cap \pi _2$ is a $(k-t)$-space. Moreover, these two spaces meet other ones either in $W_1$ or in $W_2$, and $\{\pi _3,\ldots ,\pi _n\}$ is a $(k-t+1)$-sunflower with center W. Clearly,

$$\begin{aligned} \langle \mathcal {S} \rangle =\langle \pi _1,\ldots ,\pi _n \rangle =\langle W,X_1,X_2,M_3,\ldots ,M_{n} \rangle . \end{aligned}$$

Since W, $\langle X_1,X_2 \rangle$, $M_3,\ldots ,M_n$ are linearly independent, we find that

$$\begin{aligned} \dim \langle \mathcal {S} \rangle&= k-t+1 +2t-1+(n-2)\cdot (t-1) \\&= k+ (n-1)(t-1)+1. \end{aligned}$$

Again arguing as in Proposition 1.2, we get

$$\begin{aligned} \delta '(\mathcal {S})=(k,t,t-1, \ldots , t-1). \end{aligned}$$

Fig. 4

The $(k;k-t,k-t+1)$-SPIDs described in Class III

We observe that particular examples in this class contain $(k-t+1)$-sunflowers of maximal dimension, but do not contain $(k-t)$-sunflowers of maximal dimension. Nonetheless, they are $(k-t-1)$-juntas.

$\bullet$  Class III

Choose integers $n\ge 3$, $2\le s<n$ and k, t such that $2 \le t \le k-1$. Let $\mathbb {V}$ be a vector space over a field $\mathbb {F}$ which is either infinite or else a finite field $\mathbb {F}$ of order q with q a prime power such that $q+1 \ge s$. Let $V'$, $\langle X_1,X_2 \rangle ,M_3,\ldots ,M_n$ be linearly independent subspaces of $\mathbb {V}$ such that $\dim V'=k-t+2$, and $\dim X_1=t$, $\dim X_2=t-1$ with $\dim (X_1 \cap X_2)=1$ and $\dim M_i=t-1$, for $i=3,\ldots ,n$. Let $W_0,W_1,\ldots ,W_s$ be distinct $(k-t+1)$-spaces in $V'$ such that $W_1,\ldots ,W_s$ go through a $(k-t)$-space W (Fig. 4), and $W_0$ does not pass through W. We define the sets

$$\begin{aligned} \pi _1= & {} \langle W,X_1 \rangle , \, \pi _2=\langle W_0,X_2 \rangle , \\ \pi _{3}= & {} \langle W_1,M_{3} \rangle , \ldots ,\, \pi _{m_1}=\langle W_1,M_{m_1} \rangle , \\ \pi _{m_1+1}= & {} \langle W_2,M_{m_1+1} \rangle , \ldots ,\, \pi _{m_2}=\langle W_2,M_{m_2} \rangle , \\&\qquad \quad \qquad \quad \ldots \\ \pi _{m_{s-1}+1}= & {} \langle W_s,M_{m_{s-1}+1} \rangle ,\ldots ,\, \pi _{n}=\langle W_s,M_n \rangle . \end{aligned}$$

Clearly, $\mathcal {S}=\{\pi _1,\ldots ,\pi _n\}$ is a $(k;k-t,k-t+1)$-SPID which is not a $(k-t)$-junta and

$$\begin{aligned} \langle \mathcal {S} \rangle =\langle \pi _1,\ldots ,\pi _n \rangle =\langle V',X_1,X_2,M_3,\ldots ,M_{n} \rangle . \end{aligned}$$

Since $V'$, $\langle X_1,X_2 \rangle ,M_3,\ldots ,M_n$ are linearly independent, we find that

$$\begin{aligned} \dim \langle \mathcal {S} \rangle&= k-t+2+ 2t-2 +(n-2)(t-1) \\&= k+ (n-1)(t-1)+1. \end{aligned}$$

Also in this case we have $\delta '(\mathcal {S})=(k,t,t-1, \ldots , t-1)$.

Fig. 5

The $(k;k-t,k-t+1)$-SPIDs described in Class IV

Examples in this class may contain $(k-t)$-sunflowers not of maximal dimension and $(k-t+1)$-sunflowers of maximal dimension.

$\bullet$  Class IV

Choose integers $n\ge 3$, $2\le s<n$ and k, t such that $2 \le t \le k-1$. Let $\mathbb {V}$ be a vector space over a field $\mathbb {F}$ which is either infinite or else a finite field $\mathbb {F}$ of order q with q a prime power such that $\frac{q^{k-t+2}-1}{q-1} \ge s+2$. Let $V'$, $M_1,\ldots ,M_n$ be linearly independent subspaces of $\mathbb {V}$ such that $\dim V'=k-t+2$, and $\dim M_i=t-1$, for $i=1,\ldots ,n$. Let $V_0,W_0,W_1,\ldots ,W_s$ be $s+2$ $(k-t+1)$-spaces in $V'$ such that they do not go through the same $(k-t)$-space, with $W_1,\ldots ,W_s$ distinct (Fig. 5) (which in the case $\mathbb {V}$ is a vector space over a finite field of order q, exist for the above assumption on q). We define the sets

$$\begin{aligned} \pi _1= & {} \langle V_0,M_1 \rangle , \, \pi _2=\langle W_0,M_2 \rangle , \\ \pi _{3}= & {} \langle W_1,M_{3} \rangle , \ldots ,\, \pi _{m_1}=\langle W_1,M_{m_1} \rangle , \\ \pi _{m_1+1}= & {} \langle W_2,M_{m_1+1} \rangle , \ldots ,\, \pi _{m_2}=\langle W_2,M_{m_2} \rangle , \\&\qquad \quad \qquad \quad \ldots \\ \pi _{m_{s-1}+1}= & {} \langle W_s,M_{m_{s-1}+1} \rangle ,\ldots ,\, \pi _{n}=\langle W_s,M_n \rangle . \end{aligned}$$

Clearly, the set $\mathcal {S}$ is a $\{k;k-t,k-t+1\}$-SPID such that it is not a $(k-t)$-junta and

$$\begin{aligned} \langle \mathcal {S} \rangle =\langle \pi _1,\ldots ,\pi _n \rangle =\langle V',M_1,M_2,M_3,\ldots ,M_{n} \rangle . \end{aligned}$$

Since $V'$, $M_1,M_2,M_3,\ldots ,M_n$ are linearly independent, we find that

$$\begin{aligned} \dim \langle \mathcal {S} \rangle&= k-t+2 +n\cdot (t-1) = k+ (n-1)(t-1)+1, \end{aligned}$$

and $\delta '(\mathcal {S})=(k,t,t-1, \ldots , t-1).$

Examples in this last class may contain $(k-t+1)$-sunflowers of maximal dimension and $(k-t)$-sunflowers not of maximal dimension.

3 Tightness of the junta-property bound for $(k;k-t,k-t+1)$-SPIDs

We will prove the following classification result.

Theorem 3.1

Let $\mathcal {S}$ be a $(k;k-t,k-t+1)$-SPID in a vector space $\mathbb {V}$, with $| \mathcal {S}|= n \ge 3$ and $2 \le t \le k-1$. If the dimension of $\langle \mathcal {S} \rangle$ is $k+(n-1)(t-1)+1$, then $\mathcal {S}$ is either a $(k-t)$-junta or $\mathcal {S}$ is one of the examples described in Classes I, II, III or IV.

First, we state the following lemma.

Lemma 3.2

Let $\mathcal {S}$ be a $(k;k-t,k-t+1)$-SPID ($2 \le t \le k-1$) in a vector space $\mathbb {V}$ such that $n=| \mathcal {S}| \ge 3$ and $\mathcal {S}$ is not a $(k-t)$-junta.

If $\dim \langle \mathcal {S} \rangle =k+(n-1)(t-1)+1$ and there is not a $(k-t)$-sunflower of maximal dimension with at least three petals in $\mathcal {S}$, then $\mathcal {S}$ is equivalent to one of the examples described in Classes II, III, or IV.

Proof

By Propositions 1.2 and 2.3, we may sort k-subspaces in $\mathcal {S}$ in such a way that

$$\begin{aligned} (\delta _1,\delta _2, \ldots ,\delta _n)=(k,t,t-1,\ldots ,t-1). \end{aligned}$$

(6)

Also, arguing as in the proof of Proposition 2.3, we get that $\dim (\pi _4 \cap \langle \pi _1,\pi _2,\pi _3 \rangle )=\dim (\pi _4 \cap \langle \pi _1,\pi _2 \rangle )=k-t+1$, and hence

$$\begin{aligned} \pi _4 \cap \pi _3 \subseteq \pi _4 \cap \langle \pi _1,\pi _2,\pi _3 \rangle =\pi _4 \cap \langle \pi _1,\pi _2 \rangle \subseteq \langle \pi _1,\pi _2 \rangle . \end{aligned}$$

Eventually rearranging the spaces $\pi _3,\ldots ,\pi _n$ in $\mathcal {S}$, we can repeat the previous argument, getting

$$\begin{aligned} \pi _i \cap \pi _j \subseteq \langle \pi _1,\pi _2 \rangle , \end{aligned}$$

for all distinct $\pi _i$ and $\pi _j$, with $i,j \in \{3,\ldots ,n\}$. Moreover, $\dim (\pi _i \cap \langle \pi _1,\pi _2 \rangle )=\dim (\pi _j \cap \langle \pi _1, \pi _2 \rangle )=k-t+1$.

Now, define in $\mathcal {S}'=\{\pi _3,\ldots ,\pi _n\}$, the following binary relation

$$\begin{aligned} \pi _i \sim \pi _j \Longleftrightarrow \pi _i \cap \langle \pi _1,\pi _2 \rangle = \pi _j \cap \langle \pi _1,\pi _2 \rangle , \end{aligned}$$

for $i,j=3,\ldots ,n$.

Clearly, $\sim$ is an equivalence relation on $\mathcal {S}'$. The k-spaces of an equivalence class meet $\langle \pi _1,\pi _2 \rangle$ in the same $(k-t+1)$-space. In this way, we get s distinct $(k-t+1)$-dimensional spaces in $\langle \pi _1,\pi _2 \rangle$, say $W_1,\ldots ,W_s$, where s is a given integer, $1 \le s \le n-2$, pairwise intersecting in a $(k-t)$-space. Indeed, let $\pi _i$ and $\pi _j$ be k-spaces of $\mathcal {S}'$ in different equivalence classes. Then, by the proof of Proposition 2.3, $\dim (\pi _i \cap \langle \pi _1,\pi _2 \rangle )=\dim (\pi _j \cap \langle \pi _1, \pi _2 \rangle )=k-t+1$,

$$\begin{aligned} \pi _i \cap \langle \pi _1,\pi _2 \rangle =W_\ell \,\,\text {and}\,\, \pi _j \cap \langle \pi _1,\pi _2 \rangle =W_m, \end{aligned}$$

for some distinct $\ell ,m \in \{1, \ldots ,s\}$. Hence,

$$\begin{aligned} \pi _i \cap \pi _j= \pi _i \cap \pi _j \cap \langle \pi _1,\pi _2 \rangle =W_\ell \cap W_m. \end{aligned}$$

Since $k-t \le \dim (\pi _i \cap \pi _j)=\dim (W_\ell \cap W_m)$ and $W_\ell ,W_m$ are distinct $(k-t+1)$-subspaces,

$$\begin{aligned} \dim (W_\ell \cap W_m)=k-t. \end{aligned}$$

Now, since the relation $\sim$ induces a partition $J_1,J_2,\ldots ,J_s$ on the elements of the index set $\{3,4,\ldots ,n\}$, by Proposition 2.3, we can label appropriately the elements of $\mathcal {S}$, obtaining

$$\begin{aligned} \begin{aligned} \pi _{j_1}&=\langle W_1,M_{j_1} \rangle \quad \text {with} \,\, j_1 \in J_1, \\& \pi _{j_2}=\langle W_2,M_{j_2} \rangle \quad \text {with} \,\, j_2 \in J_2, \\&\quad \quad \quad \quad \ldots \\& \pi _{j_s}=\langle W_s,M_{j_s} \rangle \quad \text {with} \,\, j_s \in J_s, \end{aligned} \end{aligned}$$

where the elements in the set $\{M_{j_{h}} : j_{h}\in J_h,\,\,h\in \{1,2,\ldots ,s\}\}$, are certain linearly independent $(t-1)$-spaces in $\mathbb {V}$.

We divide the remainder of the proof in two steps:

• (1) First, we look at the case where all elements in $\mathcal {S}'$ meet $\langle \pi _1,\pi _2 \rangle$ in the same $(k-t+1)$-space, say W. It is clear that for $3 \le j \le n$ and $i=1,2$, $\pi _i \cap \pi _j=\pi _i \cap W$. Indeed, since $W = \pi _j \cap \langle \pi _1, \pi _2 \rangle$; we have

  $$\begin{aligned} \pi _i \cap \pi _j \subseteq W. \end{aligned}$$

  Hence, $\pi _i \cap \pi _j \subseteq W \cap \pi _i$. On the other hand, since

  $$\begin{aligned} W = \pi _j \cap \langle \pi _i ,\pi _2 \rangle \subseteq \pi _j, \end{aligned}$$

  then we also have $W \cap \pi _i \subseteq \pi _j \cap \pi _i$. Next we show that

  $$\begin{aligned} \dim (\pi _i \cap \pi _j)=k-t, \end{aligned}$$

  for $3 \le j \le n$ and $i=1,2$. To this aim, suppose that either the space $\pi _1$ or $\pi _2$ contains W ($W \not \subseteq \pi _1 \cap \pi _2$, since $\dim (\pi _1 \cap \pi _2)=k-t$). For instance, let $\pi _1$ contain W. Then, $\pi _2 \cap W=\pi _1 \cap \pi _2$; in fact, we have that $\pi _1 \cap \pi _2 \supseteq \pi _2 \cap W = \pi _2 \cap \pi _j$ with $j \in \{3,...,n\}$. But then $\mathcal {S}$ is a $(k-t)$-junta; a contradiction. Hence, $\pi _1 \cap W=W_1$ and $\pi _2 \cap W=W_2$ are $(k-t)$-spaces, and they are distinct otherwise $\mathcal {S}$ is again a $(k-t)$-junta. Precisely, they are two hyperplanes of W. We denote by $W'$ the $(k-t-1)$-space of W in which they meet, and choose a basis of $\mathbb {V}$ in such a way that the following happens

  $$\begin{aligned} \pi _1 \cap W=\langle W',a_1 \rangle \quad \text {and} \quad \pi _2 \cap W=\langle W',a_2 \rangle , \end{aligned}$$

  with $a_1,a_2$ distinct 1-spaces in $W_1 \setminus W'$ and $W_2 \setminus W'$, with $W', a_1,a_2$ linearly independent. Then, there also exist two t-spaces $X_1$ and $X_2$, having a 1-space in common and such that

  $$\begin{aligned} \pi _1=\langle W',a_1,X_1 \rangle , \quad \pi _2=\langle W',a_2,X_2 \rangle . \end{aligned}$$

  This finally means that $\mathcal {S}$ is one of the examples in Class II.

• (2) Now, we suppose that $s \ge 2$. In this case, $W_1, \ldots , W_s$ are $(k-t+1)$-spaces pairwise intersecting in a $(k-t)$-space. Hence, by [3, Sect. 9.3], either

  (a):

  they have a $(k-t)$-space in common, or

  (b):

  they lie in a $(k-t+2)$-space $V'$.

  Note explicitly that for $s=2$, (a) and (b) are equivalent. If $s \ge 3$, we will show that

  $$\begin{aligned} \dim \langle W_1,W_2,\ldots ,W_s \rangle =k-t+2, \end{aligned}$$

  (7)

  which is equivalent to prove that, for all $1\le h \le s,$

  $$\begin{aligned} W_h \subseteq \langle W_1,W_2 \rangle . \end{aligned}$$

  (8)

  Suppose that $W_1,W_2,\ldots ,W_s$ go through a $(k-t)$-space in $\langle \pi _1,\pi _2 \rangle$ and let $\pi _{j_1}$, $\pi _{j_2},\pi _{j_h}$ be k-spaces belonging to different equivalence classes with respect to $\sim$, such that

  $$\begin{aligned} \pi _{j_1} =\langle W_1,M_{j_1} \rangle \pi _{j_2}=\langle W_2,M_{j_2} \rangle \pi _{j_h}=\langle W_h,M_{j_h} \rangle . \end{aligned}$$

  Since there is not a sunflower of maximal dimension with at least three petals contained in $\mathcal {S}$, we have

  $$\begin{aligned} \dim (\pi _{j_h} \cap \langle \pi _{j_1},\pi _{j_2} \rangle )\ge k-t+1. \end{aligned}$$

  Then, by applying Grassmann’s Formula, we obtain

  $$\begin{aligned} \begin{aligned} k-t+1&\le \dim (\pi _{j_h} \cap \langle \pi _{j_1},\pi _{j_2} \rangle )=2k+t -\dim \langle W_1,W_2,W_h,M_{j_1},M_{j_2},M_{j_h} \rangle \\&= 2k+t- 3(t-1)- (\dim W_h + \dim \langle W_1,W_2 \rangle - \dim (W_h \cap \langle W_1,W_2 \rangle ). \end{aligned} \end{aligned}$$

  This implies $\dim (W_h \cap \langle W_1,W_2 \rangle ) \ge k-t+1$ and hence we get property (8). So, all $(k-t+1)$-spaces $W_1,\ldots ,W_s$ lie in a $(k-t+2)$-space, say $V'$. Obviously, $V'$ is contained in $\langle \pi _1,\pi _2 \rangle$ and

  $$\begin{aligned} k-t \le \dim (\pi _i \cap V') \le k-t+1, \text {for}\,\,\, i=1,2. \end{aligned}$$

  (9)

  Indeed, since for $i \in \{1,2\}$ and for any $j \in \{3,\ldots ,n\}$,

  $$\begin{aligned} \pi _i \cap \pi _j= \pi _i \cap \pi _j \cap \langle \pi _1,\pi _2 \rangle =\pi _i \cap W_h \subseteq \pi _i \cap V', \end{aligned}$$

  for some $h\in \{1,\ldots ,s\}$, then the first inequality in (9) follows. On the other hand, if $\dim (\pi _i \cap V') \ge k-t+2$, for $i=1$ or 2, then $V'$ is contained either in $\pi _1$ or in $\pi _2$ (not in both since $\dim (\pi _1 \cap \pi _2)=k-t$). Without loss of generality, we can suppose that $V'$ is contained in $\pi _1$. Then

  $$\begin{aligned} \pi _2 \cap \pi _{j_h}=\pi _2 \cap W_h \subseteq \pi _2 \cap V' \subseteq \pi _1 \cap \pi _2, \end{aligned}$$

  for $h \in \{1,\ldots ,s\}.$ This implies that $\pi _1 \cap \pi _2$ is contained in all elements of $\mathcal {S}$ and hence it is a $(k-t)$-junta. Furthermore, $\pi _1 \cap V'$ and $\pi _2 \cap V'$ are distinct subspaces. Indeed,

  $(\diamond )$:

  if $\pi _1 \cap V'=\pi _2 \cap V'$ and it is a $(k-t+1)$-space, then $\pi _1 \cap \pi _2$ is a $(k-t+1)$-space, a contradiction;

  $(\diamond \diamond )$:

  if $\pi _1 \cap V'=\pi _2 \cap V'$ is a $(k-t)$-space, since for $i=1,2$ and $h=1,\ldots ,s$, $\pi _i \cap W_h$ has dimension at least $k-t$ and $W_h \subseteq V'$, we have that

  $$\begin{aligned} \pi _1 \cap W_h= \pi _1 \cap V'=\pi _2 \cap V' =\pi _2 \cap W_h. \end{aligned}$$

  This implies that $\pi _1 \cap \pi _2$ is contained in all elements of $\mathcal {S}$; again this is not the case.

  Now, let $W_h$ be a $(k-t+1)$-space with $1 \le h \le s$, then

  $$\begin{aligned} \begin{aligned} k-t&= \dim (\pi _1 \cap \pi _2) \ge \dim (\pi _1 \cap \pi _2 \cap W_h) \\&\ge \dim (\pi _1 \cap W_h)+ \dim (\pi _2 \cap W_h)-\dim W_h \ge 2(k-t)-k+t-1=k-t-1. \end{aligned} \end{aligned}$$

  (10)

  By taking into account Inequalities (9) and (10), the discussion may be reduced to one of the following three cases:

  (i):

  $\dim (\pi _1 \cap V')=\dim (\pi _2 \cap V')=k-t$   (and   $\dim (\pi _1 \cap \pi _2 \cap V')=k-t-1$).

  (ii):

  $\pi _1$ and $\pi _2$ meet $V'$ in subspaces with different dimensions.

  (iii):

  $\pi _1 \cap V'$ and $\pi _2 \cap V'$ are two hyperplanes of $V'$.

  Case (i): We shall show that for all $3 \le j \le n$,

  $$\begin{aligned} \pi _j \cap \langle \pi _1,\pi _2 \rangle = \langle \pi _1 \cap V', \pi _2 \cap V' \rangle . \end{aligned}$$

  (11)

  Since $\pi _j \cap \langle \pi _1,\pi _2 \rangle \subseteq V'$, and $\pi _1$ and $\pi _2$ meet $V'$ in a $(k-t)$-space, $\pi _j \cap \pi _1=\pi _1 \cap V'$ and $\pi _j \cap \pi _2=\pi _2 \cap V'$ , obtaining that

  $$\begin{aligned} \pi _j \cap \langle \pi _1,\pi _2 \rangle \supseteq \langle \pi _j \cap \pi _1, \pi _j \cap \pi _2 \rangle =\langle \pi _1 \cap V', \pi _2 \cap V' \rangle . \end{aligned}$$

  However, since they both are $(k-t)$-spaces in $V'$, we obtain equality stated in (11). Hence, every $\pi _j$, $j=3,\ldots ,n$, meets $\langle \pi _{1},\pi _2 \rangle$ in the same $(k-t+1)$-subspace. But this contradicts $s \ge 2$. Case (ii): We can suppose, without loss of generality, that $\dim (\pi _1 \cap V')=k-t$     and     $\dim (\pi _2 \cap V')=k-t+1$. Clearly, $\pi _1 \cap V' \not \subseteq \pi _2 \cap V'$, otherwise

  $$\begin{aligned} \pi _1 \cap W_h =\pi _1 \cap V' \subseteq \pi _2 \cap V'. \end{aligned}$$

  This implies that $\pi _1 \cap \pi _2 \subseteq W_h$, for $h=1,\ldots ,s$, and then $\mathcal {S}$ is a $(k-t)$-junta with center $\pi _1 \cap \pi _2$. Since $W=\pi _1 \cap \pi _2 \cap V'$ is a $(k-t-1)$-space, there exists a t-space $X_1$ contained in $\pi _1$ and a $(t-1)$-space $X_2$ contained in $\pi _2$ both disjoint from $V'$, for $i=1,2$, and such that $\langle X_1,X_2 \rangle =2t-2$. Then

  $$\begin{aligned} \pi _1=\langle \pi _1 \cap V',X_1 \rangle \,\,\,\text {and}\,\,\,\pi _2=\langle \pi _2\cap V',X_2 \rangle . \end{aligned}$$

  We note explicitly that

  $$\begin{aligned} \pi _1 \cap V' = \pi _1 \cap W_h \subseteq W_h, \end{aligned}$$

  (12)

  for $h\in \{1,\ldots ,s\}$, since $\dim (\pi _1 \cap V')=k-t$. Case (iii): Now, we suppose that $\pi _1 \cap V'$ and $\pi _2 \cap V'$ are hyperplanes of $V'$, say $V_0$ and $W_0$, respectively. Then, there exists $X_i$, $i=1,2$, a $(t-1)$-space in $\pi _i$ disjoint from $V'$, such that

  $$\begin{aligned} \pi _1=\langle V_0,X_1 \rangle \,\,\,\text {and}\,\,\,\pi _2=\langle W_0,X_2 \rangle . \end{aligned}$$

  Again, by Grassmann’s Formula, we obtain that $X_1,X_2,V'$ are linearly independent and $\dim \langle X_1,X_2 \rangle =2t-2$.

So, the discussion in Case (ii) provides us with an example described in Class III, while Case (iii) gives an example in Class IV. $\square$

Remark 3.3

Let $\mathcal {W}= \{W_1,\ldots ,W_s,\pi _2 \cap V' \}$ be the set of $(k-t+1)$-spaces in $V'$ with $2 \le s \le n-3$.

In Case (ii), if $s \ge 3$ by Formula (12), the first s subspaces in $\mathcal {W}$ form a sunflower with center $\pi _1 \cap V'$, and $\pi _2 \cap V'$ not through $\pi _1 \cap V'$.

In Case (iii), considering $\pi _1 \cap V'$ and $\pi _2\cap V'$, one of them or both could be in $\{W_1,\ldots ,W_s\}$.

If $s=2$, at most one of $\pi _1 \cap V'$ and $\pi _2\cap V'$ can coincide with $W_1$ or $W_2$. Otherwise, $W_1 \cap W_2=\pi _1 \cap \pi _2$ and it is contained in all elements of $\mathcal {S}$.

In particular, if $s=2$ and $n=4$, it is straightforward to see that exactly one of $\pi _1 \cap V'$ and $\pi _2 \cap V'$ must necessarily be equal to $W_1$ or $W_2$.

We are now in the position to prove the main result of this section.

Proof of Theorem 3.1

We assume that $\mathcal {S}$ is not a $(k-t)$-junta and denote the elements of $\mathcal {S}$ by $\pi _1,\pi _2, \ldots , \pi _n$. We will consider all possible orderings of the spaces in $\mathcal {S}$ such that the parameters $(\delta _2,\ldots ,\delta _n)$ are non-increasing. Since $\dim \langle \mathcal {S} \rangle =k+(n-1)(t-1)+1$, we have the equality in (2) of Theorem 2.1. Hence, if $m \ge 3$, we have

$$\begin{aligned} (\delta _2, \ldots , \delta _n)=(\underbrace{t, \ldots , t}_{m-1 \,\,\text {times}}, \underbrace{t-1, \ldots , t-1}_{n-m-1\,\, \text {times}}, t+1-m), \end{aligned}$$

(13)

otherwise $m=2$ and we have

$$\begin{aligned} (\delta _2, \ldots , \delta _n)=(t, t-1, \ldots ,t-1). \end{aligned}$$

(14)

$\circ$:

Suppose that we can find a permutation of the elements in $\mathcal {S}$ such that $\delta (\mathcal {S})$ is as in (13), for $m \ge 3$. Then, by Lemma 2.4, it follows that $\mathcal {S}$ belongs to Class I.

$\circ$:

If otherwise $(\delta _2, \ldots , \delta _n)$ is as in (14), by Proposition 2.3, there is no $(k-t)$-sunflower of maximal dimension with at least three petals. The result then follows by Lemma 3.2.

$\square$

The authors thank the referees for careful reading of the paper and for their valuable suggestions which improved the article.