Abstract
We propose a generic construction for fully secure decentralized multiauthority predicate encryption. In such multiauthority predicate encryption scheme, ciphertexts are associated with one or more predicates from various authorities and only if a user has a set of decryption keys that evaluates all predicates to true, the user is able to recover the message. In our decentralized system, anyone can create a new authority and issue decryption keys for their own predicates. We introduce the concept of a multi-authority admissible pair encoding scheme and, based on these encodings, we give a generic conversion algorithm that allows us to easily combine various predicate encryption schemes into a multi-authority predicate encryption variant. The resulting encryption schemes are proven fully secure under standard subgroup decision assumptions in the random oracle model. Finally, by instantiating several concrete multi-authority admissible pair encoding schemes and applying our conversion algorithm, we are able to create a variety of novel multi-authority predicate encryption schemes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Predicate encryption (PE) is a type of public-key encryption, where the outcome of decryption is controlled by a relation R. A user possessing a decryption key associated with value y, is only able to recover the plaintext of a ciphertext associated with value x, if the relation R(x, y) holds. Many different types of PE have been proposed, each characterizable by the family of relations they support. Examples of PE types include identity-based encryption (IBE) [10] (where the relation is equality testing), attributebased encryption (ABE) [28] (equality testing joined with logical and and or gates), hidden vector encryption [11] (vector equality testing with wildcard support), and innerproduct predicate encryption (IPPE) [18] (testing whether two vectors are orthogonal). Even more advanced schemes, such as schemes capable of evaluating relations based on regular languages, exist as well [30].
A drawback of standard PE is that a single party, the authority, is responsible for creating the decryption keys for all users in the system. As a direct consequence, this authority can decrypt all messages since the authority has to be able to create every possible decryption key. Thus, relying on a single authority has not only consequences for the scalability of the system, but also for the trust relations. In natural situations, we would rather appoint multiple authorities, where each authority is responsible for issuing keys in their own realm. For example, when handling data from a clinical trial, we demand that only medical doctors affiliated to a research institute have access to the data. A hospital could then be responsible for issuing a decryption key for “medical doctor,” while a university would be responsible for issuing the decryption key for “researcher.”
The question whether it is possible to construct such a multi-authority scheme was first raised by Sahai and Waters [28]. In a multi-authority predicate encryption (MA-PE) scheme, ciphertexts are associated with one or more predicates from various authorities. Users are then only able to decrypt the ciphertext if their keys make all predicates associated with the ciphertext evaluate to true. The first proposed MA-PE constructions [12, 13, 25] either require interaction between all authorities, or solely address the scalability problem and still require a master secret which can be used to decrypt all messages. To address both problems at the same time, Lewko and Waters [21] proposed a decentralized scheme. However, a limitation of all previous proposed MA-PE constructions, is that they only address the special case of multiauthority attribute-based encryption (MA-ABE), rather than the more general MA-PE.
We propose a generic framework for creating decentralized multi-authority predicate encryption. Our framework supports several predicate types, such as multi-authority IBE, multi-authority ABE, and multi-authority IPPE. We also provide an instantiation for each of these predicate families. Since our solution is decentralized, we address both the trust and scalability issues: no party is required to hold a master secret and new authorities can be created without requiring any form of interaction. Lastly, we prove that the encryption schemes resulting from our framework are fully secure.
Our construction for an MA-PE scheme can be seen as the combination of multiple parallel instantiations of a (modified) single authority PE scheme with a “multi-authority layer” on top. Basically, the MA-PE scheme first fixes the group parameters and then instantiates a new PE scheme in this group for every new authority. To encrypt a message, a user blinds the message with a random number and split this random number using additive secret sharing into various shares. Next, each of the shares are encrypted using the PE scheme’s public key. Decryption works by first decrypting all shares to recover the random number and then unblinding the blinded message. However, described as such, the scheme would be vulnerable to a collusion attack, i.e., users combining knowledge to gain access to messages they should not have access to. To see this, assume we have a ciphertext that may only be decrypted by students older than 21. Now, two colluding users, one with the “student” attribute and another one with the “over-21” attribute, can each obtain part of the shares. If they combine their shares they are able to unblind the blinded message, while neither of them should have been able to. To prevent this attack, we make sure that during the decryption of a share, randomness specific to the user is added. Only if the shares of the same user are combined, this user specific randomness cancels out.
To support a variety of PE schemes for the use in a decentralized MA-PE scheme, we introduce the concept of multi-authority admissible pair encoding schemes (MA-PESs). An MA-PES can be “compiled” into PE scheme compatible with MA-PE scheme using our conversion algorithm. The definition of an MA-PES is an extended variant of the recently introduced concept of pair encoding schemes (PESs) [2, 3, 5]. Such a (multi-authority admissible) pair encoding scheme describes how a predicate can be encoded in an encryption scheme, without having to consider the group structure the scheme is instantiated in. This separation of encoding and group structure greatly simplifies the construction of new (multi-authority) PE schemes since it is relatively easy to prove an MA-PES secure compared to proving the entire encryption scheme secure. After proving the MA-PES secure, we can simply apply our conversion algorithm to turn the secure MA-PES into a secure MA-PE scheme.
Using the proposed conversion algorithm, we are able to combine various PE schemes for different predicates (e.g., IBE, ABE, or IPPE) into an MA-PE scheme using and gates between the predicates. While the need for or gates can be circumvented by writing the global policy in disjunctive normal form (DNF) and encrypting the plaintext for each of the conjunctive clauses, we could also directly support or gates by slightly chaning the algorithm: By using Shamir secret sharing (SSS) instead of additive secret sharing, policies can also contain or gates [21].
We prove that applying our conversion algorithm on a secure MA-PES results in a fully secure MA-PE scheme in the random oracle model. In our full security game for multiple authorities, several authorities may be corrupted while the adversary may query the challenger for both the creation of new authorities and for decryption keys of its choice. We use a variant of the dual system encryption technique to prove our construction secure. The dual system proof technique, first introduced in the seminal work by Waters [29] and later refined by a series of subsequent work [14, 20, 22, 23], uses semi-functional ciphertexts and keys in the proofs. A semi-functional ciphertext can be decrypted using a normal key, and a normal ciphertext can be decrypted by a semi-functional key (of course, in both cases we still require that the relation R holds). However, a semi-functional ciphertext can never be decrypted by a semi-functional key, not even if the relation R holds. To prove a scheme secure, we use a series of hybrid games. In the final game, the adversary receives a semi-functional challenge ciphertext and only semi-functional keys, meaning that the adversary has no chance in correctly decrypting the challenge ciphertext, and thus making it impossible for the adversary to gain a non-negligible advantage in winning the game.
1.1 Our contributions
We summarize our contributions as follows. Firstly, we introduce new multi-authority encryption schemes with novel functionality. This newly introduced functionality has two distinct advantages; it allows for
the creation of ciphertexts with predicates spanning multiple authoritative domains. Our construction allows for different predicate types per authority. For example, it allows for policies over two authorities where one authority uses ABE, while the other uses IPPE.
the combination of various PE types to obtain more efficient or more expressive predicates. For example, combining a large-universe PE scheme with PE scheme supporting non-monotonic access structures to allow for revocation.
Secondly, we introduce MA-PESs and their security requirement, give a conversion algorithm from MA-PES to MA-PE, and prove that the resulting MA-PE scheme is fully secure. We do so by unifying and extending several works. This leads to new insights, such as the symmetry in the definition of EncCt and EncKey in MA-PESs. These insights help in constructing more efficient MA-PE schemes and conversions among MA-PESs (e.g., dual predicate).
Finally, we give examples of various MA-PESs and also prove them secure. By applying our construction to these examples we achieve novel types of MA-PE for IBE, ABE, and IPPE.
1.2 Organization of the work
After the related work in Sect. 2, we continue with the preliminaries in Sect. 3, containing the definition of an MA-PE scheme and its security. In Sect. 4, we detail the definition of our MA-PES, and in Sect. 5, we explain how to convert an MA-PES into MA-PE scheme. The security proof of our conversion algorithm is in Sect. 6. Finally, in Sect. 7, we give several examples of MA-PESs for predicates of the type IBE, ABE, and IPPE.
2 Related work
Up until now, the vast majority of multi-authority predicate encryption (MA-PE) schemes proposed in literature are MA-ABE schemes. The first MA-ABE schemes either require the introduction of a central party that is even able to decrypt all ciphertexts [12, 25] or do not allow for the addition of new authorities once the system is set up [13]. The first practical MA-ABE scheme came with the introduction of decentralized MA-ABE [21]. A decentralized MA-PE scheme does not require any central party and anyone can start a new authority completely independent of all other parties. However, the current decentralized MA-ABE schemes [21, 26, 27] only support a single fixed construction and lack the ability to be used with any predicate family other than ABE. Moreover, in our construction, each authority can choose its own predicate family, which allows for the combination of several predicate systems, e.g., we can combine ABE and IPPE in a single MA-PE scheme.
In 2014, both Wee [31] and Attrapadung [5] observed that many of the schemes proven secure under the dual system encryption technique could be split into an encoding of the predicate and the group structure this encoding is instantiated in. Three variants of these encodings exist: predicate encoding [31], pair encoding [5], and the later introduced tag-based encoding [19]. Several newer works build on various improvements of the concepts of predicate encodings [4, 16] and pair encodings [2,3,4]. Because pair encodings are the most general of the three, we base our work on pair encodings. For the instantiation of the group structure, composite order and prime order groups can be used [2, 14, 15]. In this work, we instantiate our decentralized MA-PE scheme in a composite order group setting, resulting in the first generic MA-PE scheme. The previously proposed prime order group structure cannot be directly used, since our construction uses a system based on three subgroups, instead of the more common two subgroups.
The MA-PE schemes resulting from our conversion algorithm are fully secure, similar to notions used before [21, 26]. Our notion is slightly more permissive in the sense that not all authorities need to be announced at the start of the game, but the adversary can query for new authorities throughout the game. Weaker security notions, e.g., selective or static security games [27], or the use of the generic group model often allow for simpler and more efficient constructions at the costs of security.
A special use of our MA-PE construction is the combination of various predicate families into a single authority PE scheme, i.e., the (single) authority creates multiple key pairs, each for a distinct predicate family. Constructions of these combined PE schemes was first studied for the combination of ciphertext-policy attribute-based encryption (CP-ABE) with key-policy attribute-based encryption (KP-ABE) [6, 7]. Recently, Ambrona, Barthe, and Schmidt [4] give generic transformations to combine arbitrary predicate encodings into a new (single authority) predicate encoding scheme. Their approach differs from ours, since we do not transform encodings into an encoding for a combined predicate, but convert special encodings into an encryption scheme for combined predicates.
Our achieved functionality of decentralized multi-authority inner-product predicate encryption (MA-IPPE) is different from the works on multi-input inner product encryption (MI-IPE) [1, 17]. In inner product encryption,, the decryption algorithm outputs the inner product of two encrypted vectors, while in IPPE, the orthogonality of two vectors determines whether an encrypted message can be decrypted. The work by Michalevsky and Joye [24] achieves a specific form of MA-IPPE under a notion of decentralization that requires a semi-honest authority and coordination among the authorities during key generation. Their paper brings up the challenge to realize what the authors call “full decentralization” which we tackle in this paper. Moreover, our construction achieves this type of “full” decentralization for various MA-PE types, including MA-IPPE.
3 Preliminaries
In this work, we use lower case variables for vectors, denoted as \({\mathbf {\varvec{v}}}\). For matrices we use upper case variables such as \(\mathbf {\varvec{\mathrm {M}}}\). We often work with vectors of group elements \((g^{v_1}, \dotsc , g^{v_n})\), written as \(g^{{\mathbf {\varvec{v}}}}\). To denote that we draw an element uniformly at random from a finite set S, we use \(x {\mathop {\leftarrow }\limits ^{R}}S\). If an element \(x \in S\) is a uniformly random element from the finite set S, we write \(x \in _RS\). The ordered set of number \(\{ 1, \dotsc , n \}\) is denoted by [n], while we denote the set \(\{ 0, \dotsc , n \}\) by \([n]^+\). Computational indistinguishability is denoted by the binary relation \(\approx _c\).
We use the notation for a predicate family by Attrapadung [5]. Let \(P = \{ P_\kappa \}_{\kappa \in {\mathbb {N}}^c}\), for some constant \(c \in {\mathbb {N}}\), denote the predicate family for relations \(P_\kappa :{\mathcal {X}}_\kappa \times {\mathcal {Y}}_\kappa \rightarrow \{ \textsc {true}, \textsc {false}\}\). Here, a relation is equivalent to a predicate function where \({\mathcal {X}}_\kappa \), the ciphertext attribute space, and \({\mathcal {Y}}_\kappa \), the key attribute space, are mapped to a true/false output. A predicate \(P_\kappa \) can be described by its family index \(\kappa \). We often use  to denote that the index is specific to an authority
to denote that the index is specific to an authority
 .
.
3.1 Composite order bilinear map
Our construction uses a composite order bilinear map.
Definition 1
(Composite order bilinear map of three primes [21]) Let \({\mathbb {G}}\), \({\mathbb {G}}_T\) be cyclic multiplicative groups of composite order \(N = p_1p_2p_3\), where \(p_1\), \(p_2\), and \(p_3\) are distinct large primes of bit length \(\Theta ({ \lambda })\) for some security parameter \({ \lambda }\). The map \(e:{\mathbb {G}} \times {\mathbb {G}} \rightarrow {\mathbb {G}}_T\) is a composite order bilinear map if the following two conditions hold.
The map is bilinear; \(\forall g, h \in {\mathbb {G}}\; a, b \in {\mathbb {Z}}_N:e(g^a, h^b) = e(g, h)^{ab}\).
The map is non-degenerate; generator g of the group \({\mathbb {G}}\) is chosen such that the order of the element \(e(g, g) \in {\mathbb {G}}_T\) equals N, the order of group \({\mathbb {G}}_T\).
We use the function \({\mathcal {G}}(1^{ \lambda })\) to generate the parameters for a composite order bilinear map for security parameter \({ \lambda }\). We refer to the subgroups of \({\mathbb {G}}\) of prime order \(p_1\), \(p_2\), and \(p_3\), as \({\mathbb {G}}_1\), \({\mathbb {G}}_2\), and \({\mathbb {G}}_3\), respectively. Similarly, we write \(g_1\), \(g_2\), and \(g_3\) for the generators of the respective subgroups. The orthogonality property of composite order bilinear groups, i.e., \(e(g_i, g_j) = 1\) for \(i \ne j\), is a crucial property used in the security proofs.
3.2 Multi-authority predicate encryption
A decentralized multi-authority predicate encryption (MA-PE) scheme differs from a single authority PE scheme in several key aspects. Most importantly, any party can use the global public parameters to create a new authority
 . Using these global parameters, it creates its own public/private key pair for a predicate indexed by
. Using these global parameters, it creates its own public/private key pair for a predicate indexed by  .
.
Furthermore, since every authority has its own public key, the encryption algorithm requires one or more public keys as input. Naturally, only the public keys of the authorities
 involved in the access policy are required to encrypt a message. Besides the public keys, the algorithm also requires the ciphertext values
involved in the access policy are required to encrypt a message. Besides the public keys, the algorithm also requires the ciphertext values  for each of the authorities
for each of the authorities  . Note that these values may come from distinct domains, as this value space
. Note that these values may come from distinct domains, as this value space  depends on the predicate index
depends on the predicate index  .
.
Finally, to prevent user collusion, every user in the system get its own globally unique identity gid from an identity space \({\mathcal {I}}\). Decryption keys are issued to a specific user and are bound to their personal gid. This prevents collusion attacks in which distinct users try to combine their key to decrypt a ciphertext that may only be decrypted by users that possess all required keys themselves.
A decentralized multi-authority predicate encryption (MA-PE) scheme is a collection of the following five probabilistic polynomial time algorithms.
\({\mathbf {\mathsf{{GlobalSetup}}}}{\mathbf {\mathsf{{(}}}}1^{ \lambda }{\mathbf {\mathsf{{)}}}}\rightarrow { \textsf {pp}}\). On input of the security parameter \({ \lambda }\), the algorithm outputs the global public parameters pp of the scheme. The output of GlobalSetup additionally defines the message space \({\mathcal {M}}\), the identity space \({\mathcal {I}}\), and a number \(N \in {\mathbb {N}}\) (these may be implicitly defined by pp).
 . On input of the public parameters pp and some additional parameters
. On input of the public parameters pp and some additional parameters  , the algorithm outputs a public key
, the algorithm outputs a public key  and an authority secret key
and an authority secret key  for authority
for authority  . The algorithm AuthoritySetup (implicitly) sets
. The algorithm AuthoritySetup (implicitly) sets  to
to  .
.
 . The algorithm Encrypt takes a set of public keys
. The algorithm Encrypt takes a set of public keys  from authorities
from authorities  , values
, values  , and a message \(m \in {\mathcal {M}}\) as input and outputs a ciphertext ct.
, and a message \(m \in {\mathcal {M}}\) as input and outputs a ciphertext ct.
 . The algorithm KeyGen takes an authority secret key
. The algorithm KeyGen takes an authority secret key  of authority
of authority
 , a value
, a value  , and an identity \({ \textsf {gid}}\in {\mathcal {I}}\) as input and outputs a user secret key \({ \textsf {usk}}_{y,{ \textsf {gid}}}\).
, and an identity \({ \textsf {gid}}\in {\mathcal {I}}\) as input and outputs a user secret key \({ \textsf {usk}}_{y,{ \textsf {gid}}}\).
\({\mathbf {\mathsf{{Decrypt}}}}{\mathbf {\mathsf{{(}}}}{ \textsf {pp}}, \{ { \textsf {usk}}_{y,{ \textsf {gid}}} \}_{y}, { \textsf {ct}}{\mathbf {\mathsf{{)}}}} \rightarrow \{ m, \bot \}\). On input of a set of user secret keys \(\{ { \textsf {usk}}_{y,{ \textsf {gid}}} \}\), all issued to the same identity gid, and a ciphertext ct, the algorithm outputs either a message m or the distinctive symbol \(\bot \).
Correctness is defined such that if all predicates  can be evaluated to true, the ciphertext can be decrypted with an overwhelming probability.
can be evaluated to true, the ciphertext can be decrypted with an overwhelming probability.
Definition 2
(Correctness) A multi-authority predicate encryption (MA-PE) scheme is correct if for any combination of ciphertext ct, created using Encrypt with any message \(m \in {\mathcal {M}}\) and values  , together with keys for the authorities
, together with keys for the authorities
 specified in the ciphertext ct,
specified in the ciphertext ct,  for any identity \({ \textsf {gid}}\in {\mathcal {I}}\),
for any identity \({ \textsf {gid}}\in {\mathcal {I}}\),  , then
, then

where the probability is taken over the coins of GlobalSetup, AuthoritySetup, Encrypt, and KeyGen.
3.3 Multi-authority predicate encryption security
We define security in terms of an indistinguishability game where the adversary may query for several decryption keys and has to decide on the message encrypted in the challenge ciphertext. The adversary may also query for the creation of new authorities and also statically corrupt new authorities. The static corruption of an authority is modeled by letting the adversary create a public/private key pair for a new authority. The adversary may then request the challenger to encrypt the challenge message using the public keys of uncorrupted and corrupted authorities. Note that this implies a static corruption model similar to [21], as none of the authorities associated with the challenge ciphertext may be corrupted after the challenge phase. The difference is that we do not require all authorities to be specified during Setup, but allow for “Authority Setup” queries.
Definition 3
(Full security) A multi-authority predicate encryption scheme is fully secure if any p.p.t. adversary \({\mathcal {A}}\) has at most a negligible advantage in winning the following game.
Setup The GlobalSetup algorithm is run and the challenger creates an empty set \(I\) to hold the uncorrupted authorities in the system.
Query 1 The adversary may query the challenger for two types of queries. Additionally, it can also create new authorities using the global parameters, i.e., without needing to query the challenger.
Authority setup The adversary queries for a new authority by sending the parameters
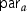 (describing a predicate) to the challenger. The challenger runs AuthoritySetup using
(describing a predicate) to the challenger. The challenger runs AuthoritySetup using 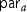 and gives the resulting public key
and gives the resulting public key 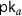 to the adversary. Additionally, it adds
to the adversary. Additionally, it adds
 to the set of uncorrupted authorities \(I\).
to the set of uncorrupted authorities \(I\).User secret key By sending a tuple
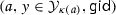 , where
, where 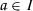 , to the challenger, the adversary requests the user secret key
, to the challenger, the adversary requests the user secret key 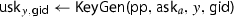 from the challenger. If the challenger has received a key request for the combination
from the challenger. If the challenger has received a key request for the combination 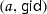 before, it aborts the game.Footnote 1 Otherwise, it returns the user secret key \({ \textsf {usk}}_{y,{ \textsf {gid}}}\).
before, it aborts the game.Footnote 1 Otherwise, it returns the user secret key \({ \textsf {usk}}_{y,{ \textsf {gid}}}\).
Challenge The adversary sends a tuple  to the challenger, where
to the challenger, where
 is a set of authorities chosen by the adversary. For each authority
is a set of authorities chosen by the adversary. For each authority  the adversary created itself, it also sends the public key
the adversary created itself, it also sends the public key  to the challenger. We denote these authorities created by the adversary by the set
to the challenger. We denote these authorities created by the adversary by the set  .
.
For each gid that was used in a key query, the challenger checks if there exists an uncorrupted authority  , such that either no query
, such that either no query  has been made, or
has been made, or  for the queried
for the queried  . If so, it chooses a bit \(b {\mathop {\leftarrow }\limits ^{R}}\{0, 1\}\) and returns the challenge
. If so, it chooses a bit \(b {\mathop {\leftarrow }\limits ^{R}}\{0, 1\}\) and returns the challenge  . Otherwise, the challenger aborts the game.
. Otherwise, the challenger aborts the game.
Query 2 Same as Query 1, with the additional restriction that new key queries must not violate the constraint described in Challenge.
Guess The adversary makes a guess \(b'\) for bit b. We define the advantage of the adversary in winning the game as
3.4 Complexity assumptions
The security of our construction relies on several instances of the family of the General Subgroup Decision Assumption [8]. These assumptions are identical to the assumptions used by the MA-ABE scheme of Lewko and Waters [21].
Assumption 1
Let the bilinear map parameters \({ \textsc {gp}}= (N = p_1p_2p_3, {\mathbb {G}}, {\mathbb {G}}_T, e, g)\) be generated by \({\mathcal {G}}(1^{ \lambda })\) and \(g_1 {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\). Given \(g_1\), it is hard to distinguish \({\hat{h}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}\) from \({\hat{h}}_1 {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\). That is, the advantage of any p.p.t. adversary \({\mathcal {A}}\) in distinguishing,
is negligible in the security parameter \({ \lambda }\).
Assumption 2
Let the bilinear map parameters \({ \textsc {gp}}= (N = p_1p_2p_3, {\mathbb {G}}, {\mathbb {G}}_T, e, g)\) be generated by \({\mathcal {G}}(1^{ \lambda })\), and \(g_1, h_1, {\hat{h}}_1 {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\), \(h_2, {\hat{h}}_2 {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_2\), and \(g_3 {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_3\). Given \(g_1\), \(h_1h_2\), and \(g_3\), it is hard to distinguish \({\hat{h}}_1\) from \({\hat{h}}_1{\hat{h}}_2\). That is, the advantage of any p.p.t. adversary \({\mathcal {A}}\) in distinguishing,
is negligible in the security parameter \({ \lambda }\).
Assumption 3
Let the bilinear map parameters \({ \textsc {gp}}= (N = p_1p_2p_3, {\mathbb {G}}, {\mathbb {G}}_T, e, g)\) be generated by \({\mathcal {G}}(1^{ \lambda })\), and \(g_1, h_1, {\hat{h}}_1 {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\), \(h'_2, {\hat{h}}_2 {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_2\), and \(h_3, h'_3, {\hat{h}}_3 {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_3\). Given \(g_1\), \(h_1h_3\), and \(h'_2h'_3\), it is hard to distinguish \({\hat{h}}_1{\hat{h}}_2\) from \({\hat{h}}_1{\hat{h}}_3\). That is, the advantage of any p.p.t. adversary \({\mathcal {A}}\) in distinguishing,
is negligible in the security parameter \({ \lambda }\).
Assumption 4
Let the bilinear map parameters \({ \textsc {gp}}= (N = p_1p_2p_3, {\mathbb {G}}, {\mathbb {G}}_T, e, g)\) be generated by \({\mathcal {G}}(1^{ \lambda })\), and \(g_1 {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\), \(g_2 {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_2\), \(g_3 {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_3\), and \(a, b, c, d, \xi {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N\). Given \(g_1\), \(g_2\), \(g_3\), \(g_1^{\,a}\), \((g_1g_3)^b\), \(g_1^{\,c}\), and \(g_1^{\,ac}g_3^{\,d}\), it is hard to distinguish \(e(g_1, g_1)^{abc}\) from \(e(g, g)^{\xi }\). That is, the advantage of any p.p.t. adversary \({\mathcal {A}}\) in distinguishing,
is negligible in the security parameter \({ \lambda }\).
4 Multi-authority admissible pair encoding
We extend the definition of a pair encoding [3, 5] to a multi-authority setting. A multiauthority admissible pair encoding scheme (MA-PES) is defined for a single authority
 . We will later show how we can convert several MA-PESs into a single MA-PE scheme.
. We will later show how we can convert several MA-PESs into a single MA-PE scheme.
We choose to extend the definition of PES as defined by Agrawal and Chase [3] since it is well-structured— although it may be a bit difficult to grasp at first. To get a better understanding of the scheme, it is convenient to think of the encodings as the variables in the exponents in the encryption scheme. The values \({\mathbf {\varvec{b}}}\) correspond to an authority’s public key, while \({\mathbf {\varvec{s}}}, {\mathbf {\varvec{{\hat{s}}}}}\) and \({\mathbf {\varvec{r}}}, {\mathbf {\varvec{{\hat{r}}}}}\) correspond to the randomness used in the encryption and key generation algorithms, respectively. The algorithms EncCt and EncKey encode the ciphertext value x and key value y, respectively, by returning one or more multivariate polynomials of a restricted form. The variables \(b_1, \dotsc , b_n\) can occur in both the ciphertext and the key encoding, so they are termed common. These common variables may be multiplied with non-lone a variable \(s_i\) (in a ciphertext encoding) or \(r_i\) (in a key encoding). A lone variable, indicated by a hat, e.g., \({\hat{r}}_i\), is never multiplied with a common variable, but may be added as an independent term to the polynomial. Two special variables, \(\alpha \) in the key encodings—corresponding to the authority’s secret key—and \(\omega \) in the ciphertext encodings, are always present in at least one of the polynomials. Basically, the encodings of a ciphertext contain linear combinations of monomials \(\omega \), \({\hat{s}}_i\), and \(s_ib_j\), while key encodings contain linear combinations of \(\alpha \), \({\hat{r}}_i\), and \(r_ib_j\).
Recall that our construction can be understood as a combination of several multi-authority admissible PE schemes using a “multi-authority layer” that withstands collusion attacks. During the decryption of such a multi-authority admissible PE scheme, randomness specific to the user is added to prevent collusion attacks. In our MA-PES, this randomness is represented in the correctness requirement by the newly added term \(\omega r_0\), where \(r_0\) corresponds to the user’s gid.
Our changes with respect to the PES definition by Agrawal and Chase [3] are highlighted in
 .
.
Definition 4
(Multi-authority admissible pair encoding scheme) A multiauthority admissible pair encoding scheme (MA-PES) for a predicate function \(P_\kappa :{\mathcal {X}}_\kappa \times {\mathcal {Y}}_\kappa \rightarrow \{ \textsc {false}, \textsc {true}\}\) indexed by \(\kappa = (N, { \textsf {par}})\), where par specifies some parameters, is given by the following four deterministic polynomial-time algorithms.
\({\mathbf {\mathsf{{AuthorityParam(par)}}}} \rightarrow n\) When given par as input, AuthorityParam outputs \(n \in {\mathbb {N}}\) that specifies the number of common variables, which we denote by \({\mathbf {\varvec{b}}} = (b_1, \dotsc , b_{n})\).
 On input \(N \in {\mathbb {N}}\) and \(x \in {\mathcal {X}}_{(N, { \textsf {par}})}\), EncCt outputs a vector of polynomials \({\mathbf {\varvec{c}}} = (c_1, \dotsc , c_{w_3})\) in non-lone variables \({\mathbf {\varvec{s}}} = (s_0, s_1, \dotsc , s_{w_1})\) and lone variables
On input \(N \in {\mathbb {N}}\) and \(x \in {\mathcal {X}}_{(N, { \textsf {par}})}\), EncCt outputs a vector of polynomials \({\mathbf {\varvec{c}}} = (c_1, \dotsc , c_{w_3})\) in non-lone variables \({\mathbf {\varvec{s}}} = (s_0, s_1, \dotsc , s_{w_1})\) and lone variables  and \({\mathbf {\varvec{{\hat{s}}}}} = ({\hat{s}}_1, \dotsc , {\hat{s}}_{w_2})\). For \(\ell \in [w_3]\), where
and \({\mathbf {\varvec{{\hat{s}}}}} = ({\hat{s}}_1, \dotsc , {\hat{s}}_{w_2})\). For \(\ell \in [w_3]\), where  , the \(\ell \hbox {th}\) polynomial is given by
, the \(\ell \hbox {th}\) polynomial is given by

\({\mathbf {\mathsf{{EncKey}}}}{\mathbf {\mathsf{{(}}}}N, y{\mathbf {\mathsf{{)}}}} \rightarrow (m_1, m_2, {\mathbf {\varvec{k}}}(\alpha , {\mathbf {\varvec{r}}}, {\mathbf {\varvec{{\hat{r}}}}}, {\mathbf {\varvec{b}}}))\) On input \(N \in {\mathbb {N}}\) and \(y \in {\mathcal {Y}}_{(N, { \textsf {par}})}\), EncKey outputs a vector of polynomials \({\mathbf {\varvec{k}}} = (k_1, \dotsc , k_{m_3})\) in non-lone variables and  and lone variables \(\alpha \) and \({\mathbf {\varvec{{\hat{r}}}}} = ({\hat{r}}_1, \dotsc , {\hat{r}}_{m_2})\). For \(\ell \in [m_3]\), where \(\phi _\ell , \phi _{\ell ,z}, \phi _{\ell ,i,j} \in {\mathbb {Z}}_N\), the \(\ell \hbox {th}\) polynomial is given by
and lone variables \(\alpha \) and \({\mathbf {\varvec{{\hat{r}}}}} = ({\hat{r}}_1, \dotsc , {\hat{r}}_{m_2})\). For \(\ell \in [m_3]\), where \(\phi _\ell , \phi _{\ell ,z}, \phi _{\ell ,i,j} \in {\mathbb {Z}}_N\), the \(\ell \hbox {th}\) polynomial is given by

\({\mathbf {\mathsf{{Pair}}}}(N,x,y) \rightarrow (\mathbf {\varvec{\mathrm {E}}}, {\hat{\mathbf {\varvec{\mathrm {E}}}}})\) On input N and both x and y, Pair outputs two matrices \(\mathbf {\varvec{\mathrm {E}}}\) and \({\hat{\mathbf {\varvec{\mathrm {E}}}}}\) of size \((w_1 + 1) \times m_3\) and  , respectively.
, respectively.
For clarity, in cases where the specific MA-PES that is being used is relevant, we index the algorithms by the authority that chooses to use the scheme, e.g.,
 or
or
 .
.
Definition 5
(Correctness) An MA-PES is correct if for every \(\kappa = (N, { \textsf {par}})\), \(x \in {\mathcal {X}}_\kappa \), \(y \in {\mathcal {Y}}_\kappa \) such that \(P_\kappa (x, y) = \textsc {true}\), the following holds symbolically,

Note that in this extended definition EncCt and EncKey are up to the variable names identically defined. Furthermore, if we set \(\omega = 0\), then we have the definition of pair encodings back as defined by [3] (except for the extra term \(r_0\), however, we can see this as an alternative numbering of the components in \({\mathbf {\varvec{r}}}\)).
4.1 Security
For a multi-authority pair encoding scheme to be secure, we require statistical security, similar to the perfect security notion by Attrapadung [5]. For the security of the encoding, it is helpful to realize that we will apply the dual system encryption technique by (partially) replicating the scheme in the various subgroups. The security properties of the encoding will be used in the semi-functional subgroups, allowing us to prove indistinguishability among several variants of semi-functional ciphertexts and keys.
Instead of requiring that the value \(\alpha \) is hidden in the adversary’s view, as required in a PES, we require, as a security property for our MA-PES, that the value \(\omega \) is hidden in the adversary’s view. This property allows us to prove that an adversary cannot distinguish a correctly distributed challenge ciphertext from a challenge ciphertext taken from a more restricted distribution. The property should hold even if user secret keys are given, but only as long as the values y associated to these keys do not let the predicate evaluate to true.
Definition 6
(Statistical security) A multi-authority admissible pair encoding scheme (MA-PES) is statistically secure for \(\kappa = (N, { \textsf {par}}) \in {\mathbb {N}}^c\), if for all \(x \in {\mathcal {X}}_\kappa \) and \(y \in {\mathcal {Y}}_\kappa \), the values \((w_1, w_2, {\mathbf {\varvec{c}}}(\omega , {\mathbf {\varvec{s}}}, {\mathbf {\varvec{{\hat{s}}}}}, {\mathbf {\varvec{b}}})) \leftarrow \textsf {EncCt}\textsf {(}{ N, x}\textsf {)}\) and \((m_1, m_2, {\mathbf {\varvec{k}}}(\alpha , {\mathbf {\varvec{r}}}, {\mathbf {\varvec{{\hat{r}}}}}, {\mathbf {\varvec{b}}})) \leftarrow \textsf {EncKey}\textsf {(}{ N, y}\textsf {)}\), if \(P_\kappa (x, y) = \textsc {false}\), the distributions
are statistically indistinguishable, where the probability is taken over \({\mathbf {\varvec{b}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_p^n\), \(\omega {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_p\), \({\mathbf {\varvec{s}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_p^{(w_1+1)}\), \({\mathbf {\varvec{{\hat{s}}}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_p^{w_2}\), \({\mathbf {\varvec{r}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_p^{(m_1+1)}\), and \({\mathbf {\varvec{{\hat{r}}}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_p^{m_2}\) (i.e., the distributions need to be statistically close in the size of p), for every prime \(p |N\).
In our security proof for the conversion algorithm (see Sect. 6), we additionally need to restrict the output of EncKey(\(N, y\)) of an MA-PES. We require that if, for some \(\ell \in [m_3]\), the polynomial \(k_\ell \) contains \(\alpha \), also \(r_0b_1\) needs to be present in the polynomial. More specifically, we require that \(\phi _\ell = \phi _{\ell ,0,1}\). Note that combining this constraint with the correctness property, we also have that \(\eta _\ell = \eta _{\ell ,0,1}\).
We give several examples of an MA-PES in Sect. 7.
5 Conversion from encoding to encryption
A collection of statistically secure MA-PESs can be converted to a fully secure MA-PE scheme using a generic algorithm.
The encryption algorithm can be seen as a combination of the encryption algorithms of several (modified) PE schemes. First, we encrypt a message \(m \in {\mathbb {G}}_T\) by blinding the message with a random element \(e(g_1, g_1)^\Delta \). Next, we (additively) secret share \(\Delta \) into shares  for each of the involved authorities
for each of the involved authorities  . For each authority, we encrypt the value
. For each authority, we encrypt the value  using the randomness
using the randomness  . From the correctness of the MA-PES, we know that a user having the appropriate keys can combine the ciphertext and keys in such a way that it obtains the value
. From the correctness of the MA-PES, we know that a user having the appropriate keys can combine the ciphertext and keys in such a way that it obtains the value  . Hence, the user can recover the value
. Hence, the user can recover the value  up to a newly introduced random element that has
up to a newly introduced random element that has  in the exponent. We use this randomness
in the exponent. We use this randomness  to prevent user collusion. Recall that EncCt determines the value
to prevent user collusion. Recall that EncCt determines the value  , while EncKey determines the value \(r_0\). So, if we additively secret share 0 into the values
, while EncKey determines the value \(r_0\). So, if we additively secret share 0 into the values  and choose a fixed value \(r_0\) for each gid, we have that, only if a user is able to obtain
and choose a fixed value \(r_0\) for each gid, we have that, only if a user is able to obtain  for all all authorities
for all all authorities
 , the user can combine these values to obtain the randomness used in the encryption of the message m,
, the user can combine these values to obtain the randomness used in the encryption of the message m,  .
.
Although our employed technique is similar to conversion algorithms used in single authority predicate encryption (SA-PE) [2, 3, 15], we use the fact that the symbol \(\omega \), an element part of the ciphertext, is statistically hidden. In contrast, SA-PE requires \(\alpha \), an element part of a key, to be statistically hidden. Therefore, in our employed proof technique, we can only randomize \(\omega \) as part of the ciphertext and not \(\alpha \) as part of the keys. As an consequence, we require a composite order pairing group with three subgroups, instead of the common two subgroups. This also implies that we cannot use the existing constructions for dual system groups [2, 15].
We require that identities are random elements from the identity space \({\mathcal {I}} = {\mathbb {G}}\). We achieve this by choosing a cryptographic hash function \(H:\{ 0, 1 \}^* \rightarrow {\mathbb {G}}\) and hash the gid to obtain a random element in \({\mathbb {G}}\). In our security proof, we require that the challenger can decide on the image of \(H({ \textsf {gid}})\), \({{\,\mathrm{Im}\,}}(H) = {\mathbb {G}}' \subseteq {\mathbb {G}}\). This requirement is fulfilled by proving the construction secure in the programmable random oracle model.
\({\mathbf {\mathsf{{GlobalSetup}}}}{\mathbf {\mathsf{{(}}}}1^{ \lambda }{\mathbf {\mathsf{{)}}}}\) The GlobalSetup algorithm first runs \({\mathcal {G}}(1^{ \lambda })\) to obtain \({ \textsc {gp}}= (N = p_1p_2p_3, {\mathbb {G}}, {\mathbb {G}}_T, e, g)\) and \(g_1 {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\). It sets the message space \({\mathcal {M}} = {\mathbb {G}}_T\) and the identity space \({\mathcal {I}} = {\mathbb {G}}\). It defines a hash function \(H:\{0, 1\}^* \rightarrow {\mathbb {G}}\) and outputs \(({ \textsc {gp}}, g_1, H)\) as the global public parameters pp.
 Given an MA-PES for
Given an MA-PES for  , the algorithm runs
, the algorithm runs
 to obtain n. It picks \({\mathbf {\varvec{v}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N^{\,n}\) and \(\alpha {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\), and sets
to obtain n. It picks \({\mathbf {\varvec{v}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N^{\,n}\) and \(\alpha {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\), and sets  . The authority’s
. The authority’s  is
is  . The authority’s
. The authority’s  is
is  .
.
 Choose an
Choose an  , pick
, pick  for each authority
for each authority  , and set
, and set  . Additionally, pick
. Additionally, pick  for all
for all  and define
and define  . Blind the message \(m \in {\mathbb {G}}_T\) using \(e(g_1, g_1)^\Delta \) to obtain \({ \textsf {ct}}_0 = m \cdot e(g_1, g_1)^\Delta \).
. Blind the message \(m \in {\mathbb {G}}_T\) using \(e(g_1, g_1)^\Delta \) to obtain \({ \textsf {ct}}_0 = m \cdot e(g_1, g_1)^\Delta \).
Now, for each authority  continue as follows (we frequently drop the index
continue as follows (we frequently drop the index  —when there is no ambiguity—to simplify notation). Run
—when there is no ambiguity—to simplify notation). Run
 to obtain \(w_1\), \(w_2\), and polynomials \((c_1, \dotsc , c_{w_3})\). For \(k \in [w_1 + w_2]^+\), pick
to obtain \(w_1\), \(w_2\), and polynomials \((c_1, \dotsc , c_{w_3})\). For \(k \in [w_1 + w_2]^+\), pick  , and set
, and set  for \(i \in [w_1]^+\) and
for \(i \in [w_1]^+\) and

for \(\ell \in [w_3]\). Blind the value  by setting
by setting  .
.
The complete ciphertext is

 The algorithm
The algorithm
 is run to obtain \(m_1\), \(m_2\), and polynomials \((k_1, \dotsc , k_{m_3})\). Set
is run to obtain \(m_1\), \(m_2\), and polynomials \((k_1, \dotsc , k_{m_3})\). Set  and pick \(r_i {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N\) to set
and pick \(r_i {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N\) to set  for \(i \in [m_1 + m_2]\). Set
for \(i \in [m_1 + m_2]\). Set

for \(\ell \in [m_3]\). The complete user secret key for  is
is

Note that  for \(z \in [m_2]\) are not included in the complete usk.
for \(z \in [m_2]\) are not included in the complete usk.
\({\mathbf {\mathsf{{Decrypt}}}}{\mathbf {\mathsf{{(}}}}{ \textsf {pp}}, \{ { \textsf {usk}}_{y,{ \textsf {gid}}} \}_{y}, { \textsf {ct}}{\mathbf {\mathsf{{)}}}}\). To decrypt the ciphertext ct, we first decrypt  for each authority
for each authority  . Run
. Run
 to obtain
to obtain  and
and  . Now compute
. Now compute

for some value \(r_0\) independent of
 . We can now combine these results to obtain
. We can now combine these results to obtain

and recover the plaintext \(m = { \textsf {ct}}_0 \cdot e(g_1, g_1)^{-\Delta }\).
Remark 1
(One-use requirement) If the values \({\mathbf {\varvec{b}}}\) of an MA-PES are used multiple times in the same ciphertext, they might not be statistically hidden anymore and information on \(\omega \) might be leaked. Therefore, if we want to make sure to avoid using (part) of the same \({\mathbf {\varvec{b}}}\) multiple times, we may require that an authority may occur only once in a ciphertext of a corresponding MA-PE scheme. Such a requirement is similar to the one-use requirement as found in several ABE schemes [5, 21, 23] where the attributes may only occur once.
Remark 2
(Type of secret sharing) Instead of using additive secret sharing as described above, we could have also decided to use SSS. By using SSS, we allow for combining the predicates from different authorities in the ciphertext using both and and or gates—like in the MA-ABE scheme by Lewko and Waters [21]— while additive secret sharing only allows for combining them using and gates. However, we can easily emulate or gates by writing the desired combination of predicates for different authorities in DNF and creating a new ciphertext for each of the conjunctive clauses. The main advantage of choosing to use additive secret sharing, is that it simplifies the construction and the corresponding security proofs.
6 Security of the conversion algorithm
We prove security similarly to the dual system encryption technique [29] variant that was used to prove MA-ABE secure before [21]. As such, we first introduce semi-functional ciphertext and semi-functional keys. These semi-functional ciphertexts and keys are solely used in the security proofs and not in the actual scheme.
6.1 Semi-functional ciphertext
A semi-functional ciphertext can be created by slightly modifying the encryption algorithm for normal ciphertexts as given before. We define the various types of semi-functional ciphertext through the algorithm
 .
.
 . This algorithm is similar to Encrypt, but also takes a set \({\mathcal {C}} \subseteq \{1, 2, 3\}\) and the authorities’
. This algorithm is similar to Encrypt, but also takes a set \({\mathcal {C}} \subseteq \{1, 2, 3\}\) and the authorities’  as input.
as input.
While in normal ciphertext, we use  , where
, where  , in semi-functional ciphertext, we use
, in semi-functional ciphertext, we use  and require
and require  only for \(i \in {\mathcal {C}}\). For the values \(i \in \{1,2,3\} \setminus {\mathcal {C}}\), we pick
only for \(i \in {\mathcal {C}}\). For the values \(i \in \{1,2,3\} \setminus {\mathcal {C}}\), we pick  without any constraint on the sum of these values.
without any constraint on the sum of these values.
Additionally, the construction of the values  and
and  is dependent on whether the authority
is dependent on whether the authority
 was created by the challenger (i.e.,
was created by the challenger (i.e.,  ) or by the adversary (i.e.,
) or by the adversary (i.e.,  ). If
). If  , all of the encoding variables
, all of the encoding variables  are mapped to elements in \({\mathbb {G}}\). However, if
are mapped to elements in \({\mathbb {G}}\). However, if  , only \(\omega \) is mapped to an element in \({\mathbb {G}}\) (i.e.,
, only \(\omega \) is mapped to an element in \({\mathbb {G}}\) (i.e.,  ), while all other encoding variables are mapped to elements in \({\mathbb {G}}_1 \subset {\mathbb {G}}\) just like in normal ciphertext.
), while all other encoding variables are mapped to elements in \({\mathbb {G}}_1 \subset {\mathbb {G}}\) just like in normal ciphertext.
In the proofs, we will use several types of semi-functional ciphertext. We use
 for \({\mathcal {C}} = \{ 1, 2, 3 \}\), \({\mathcal {C}} = \{ 1, 2 \}\), and \({\mathcal {C}} = \{ 1 \}\).
for \({\mathcal {C}} = \{ 1, 2, 3 \}\), \({\mathcal {C}} = \{ 1, 2 \}\), and \({\mathcal {C}} = \{ 1 \}\).
Pseudo normal ciphertext In case we use \({\mathcal {C}} = \{ 1, 2, 3 \}\), we say that the ciphertext is pseudo normal.
Nominally semi-function ciphertext In case we use \({\mathcal {C}} = \{ 1, 2 \}\), we say that the ciphertext is nominally semi-functional.
6.2 Semi-functional keys
Besides normal keys, we define pseudo normal keys and two types of semi-functional keys. We conveniently define these non-normal keys through the algorithm
 .
.
 . The algorithm is similarly defined as
. The algorithm is similarly defined as
 , however, instead of using the generator \(g_1\) and the hash function \(H:\{0, 1\}^* \rightarrow {\mathbb {G}}\), the generator \(g'\) and the function \(H:{ \textsf {gid}}\mapsto (g')^{r_0}\) are used. As a consequence, all elements of
, however, instead of using the generator \(g_1\) and the hash function \(H:\{0, 1\}^* \rightarrow {\mathbb {G}}\), the generator \(g'\) and the function \(H:{ \textsf {gid}}\mapsto (g')^{r_0}\) are used. As a consequence, all elements of
 are elements of the group \(\langle g'\rangle \).
are elements of the group \(\langle g'\rangle \).
Normal key Note that a normal key cannot be described using
 : While we can set \(g' \in {\mathbb {G}}_1\), the hash function H is defined as \(H:\{0, 1\}^* \rightarrow {\mathbb {G}}\) and not as \(H:\{0, 1\}^* \rightarrow {\mathbb {G}}_1\).
: While we can set \(g' \in {\mathbb {G}}_1\), the hash function H is defined as \(H:\{0, 1\}^* \rightarrow {\mathbb {G}}\) and not as \(H:\{0, 1\}^* \rightarrow {\mathbb {G}}_1\).
Pseudo normal key A pseudo normal key is created using
 with \(g' \in {\mathbb {G}}_1\). It differs from a normal key in that H maps to an element in \({\mathbb {G}}_1\), \(H:\{ 0, 1 \} \rightarrow {\mathbb {G}}_1\), instead of mapping to an element in \({\mathbb {G}}\).
with \(g' \in {\mathbb {G}}_1\). It differs from a normal key in that H maps to an element in \({\mathbb {G}}_1\), \(H:\{ 0, 1 \} \rightarrow {\mathbb {G}}_1\), instead of mapping to an element in \({\mathbb {G}}\).
Semi-functional key of type I A semi-functional key of type I is created using
 with \(g' = g_1g_2\), where \(g_1 \in {\mathbb {G}}_1\) and \(g_2 \in {\mathbb {G}}_2\).
with \(g' = g_1g_2\), where \(g_1 \in {\mathbb {G}}_1\) and \(g_2 \in {\mathbb {G}}_2\).
Semi-functional key of type II A semi-functional key of type II is created using
 with \(g' = g_1g_3\), where \(g_1 \in {\mathbb {G}}_1\) and \(g_3 \in {\mathbb {G}}_3\).
with \(g' = g_1g_3\), where \(g_1 \in {\mathbb {G}}_1\) and \(g_3 \in {\mathbb {G}}_3\).
6.3 Hybrids and proof outline
We will prove security through a series of hybrid games. Let Gameoriginal be the original full security game as defined in Definition 3. Game0 is defined similarly, except that in this game only pseudo normal keys are used, by both the challenger and the adversary, instead of normal keys. In Game1 the challenger answers the challenge query with a semi-functional ciphertext instead of a normal ciphertext as used in Game0. Let q denote the number of distinct gids for which the adversary queries keys for. We define two types of games for each j from 1 to q. In Game2,j,1, the queries for the first \(j-1\) identities are answered with semi-functional keys of type II, while key queries for the \(j\hbox {th}\) identity are answered with a semi-functional key of type I. In Game2,j,2, the challenger answers key queries for the first j identities with a semi-functional key of type II. We define Game3 as the game where all key queries are answered by semi-functional keys of type II and where the challenge ciphertext is replaced by an encryption of a random message.
A summary of the sequence of games can be found in Fig. 1. In this figure, we also indicate the exact type of semi-functional challenge ciphertext the adversary receives by specifying the input \({\mathcal {C}}\) to
 . In the cases where the values
. In the cases where the values  or
or  sum to a random value (i.e., \({\mathcal {C}} = \{1, 2\}\) and \({\mathcal {C}} = \{1\}\)), we have to show that the adversary cannot distinguish this from the case where the values
sum to a random value (i.e., \({\mathcal {C}} = \{1, 2\}\) and \({\mathcal {C}} = \{1\}\)), we have to show that the adversary cannot distinguish this from the case where the values  and
and  are guaranteed to sum to zero (i.e., \({\mathcal {C}} = \{1, 2, 3\}\)).
are guaranteed to sum to zero (i.e., \({\mathcal {C}} = \{1, 2, 3\}\)).
Summary of the sequence of games used in the proof. An explanation of the difference between the games is given in Sect. 6.3
For example, in the hybrid from Game2,j,1 to Game2,j,2, we have to show that the adversary \({\mathcal {A}}\) cannot distinguish a ciphertext created with  from a ciphertext created with
from a ciphertext created with  . In this case, we know that
. In this case, we know that  , i.e., there exists at least one
, i.e., there exists at least one  such that
such that  or no query for
or no query for  has been made. Furthermore, observe that the value
has been made. Furthermore, observe that the value  only occurs in the ciphertext part
only occurs in the ciphertext part  of authority
of authority  , corresponding to the values
, corresponding to the values  of
of
 . By the statistical security requirement (see Definition 6), we know that this
. By the statistical security requirement (see Definition 6), we know that this  is statistically hidden in the adversary’s view. From this fact, it clearly follows that the sum of all
is statistically hidden in the adversary’s view. From this fact, it clearly follows that the sum of all  (i.e.,
(i.e.,  ) includes
) includes  and thus the value of the sum is statistically hidden in the adversary’s view as well. Hence, the adversary cannot distinguishing whether it received a ciphertext where the
and thus the value of the sum is statistically hidden in the adversary’s view as well. Hence, the adversary cannot distinguishing whether it received a ciphertext where the  are shares of zero, or independently random shares.
are shares of zero, or independently random shares.
In Game2,q,2, all key queries are answered with a type II key, and we know that the values  do not need to sum to 0. Since there are no further constraints on
do not need to sum to 0. Since there are no further constraints on  , we can set all
, we can set all  . Thus, we essentially have that an adversary cannot distinguish whether the ciphertext components for any authority have been randomized or not. We use this fact to show that the sum of the values \(\delta _i\), as appearing in the semi-functional ciphertext, is computationally indistinguishable from random as well.
. Thus, we essentially have that an adversary cannot distinguish whether the ciphertext components for any authority have been randomized or not. We use this fact to show that the sum of the values \(\delta _i\), as appearing in the semi-functional ciphertext, is computationally indistinguishable from random as well.
We prove indistinguishability of the hybrids using several lemmas. Combining Lemmata 1, 2, 3, 4, and 5 proves the following theorem.
Theorem 1
For any collection of predicate families for authorities  ,
,  , if each MA-PES for
, if each MA-PES for  satisfies \(\phi _\ell = \phi _{\ell ,0,1}\) for all \(\ell \in [m_3]\) and is statistically secure (see Definition 6), then the MA-PE scheme converted from these MA-PESs (see Sect. 5) is fully secure (see Definition 3) in the random oracle model under Assumptions 1, 2, 3, and 4.
satisfies \(\phi _\ell = \phi _{\ell ,0,1}\) for all \(\ell \in [m_3]\) and is statistically secure (see Definition 6), then the MA-PE scheme converted from these MA-PESs (see Sect. 5) is fully secure (see Definition 3) in the random oracle model under Assumptions 1, 2, 3, and 4.
Lemma 1
(Gameoriginal\(\approx _c\)Game0) Any adversary \({\mathcal {A}}\) having at most a negligible advantage in breaking Assumption 1, has at most a negligible advantage in distinguishing Gameoriginal from Game0.
Proof
The challenger \({\mathcal {B}}\) receives \(\{ ({ \textsc {gp}}, g_1), T \}\) as input, where either \(T \in _R{\mathbb {G}}\) or \(T \in _R{\mathbb {G}}_1\). Now, \({\mathcal {B}}\) plays the following game with \({\mathcal {A}}\).
Hash oracle Upon receiving oracle query gid for the hash function H, the challenger \({\mathcal {B}}\) checks if it received the query before, and if so, answers with the same reply as before. If \({\mathcal {A}}\) has not queried for the hash value of gid before, \({\mathcal {B}}\) picks a value \(u_{ \textsf {gid}}{\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N\) and replies with \(T^{u_{ \textsf {gid}}}\).
Setup The challenger \({\mathcal {B}}\) sets \({ \textsf {pp}}= ({ \textsc {gp}}, g_1)\) and sends pp to the adversary \({\mathcal {A}}\).
Authority queries Request for a new authority
 using
using  are answered by the challenger by running
are answered by the challenger by running
 . The challenger first uses
. The challenger first uses
 to obtain n, picks \({\mathbf {\varvec{v}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N^{\,n}\) and \(\alpha {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\), and sets
to obtain n, picks \({\mathbf {\varvec{v}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N^{\,n}\) and \(\alpha {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\), and sets  . It sets the public key
. It sets the public key  as
as  and the authority secret key
and the authority secret key  as \()\). It sends
as \()\). It sends  to the adversary and adds
to the adversary and adds
 to the set \(I\).
to the set \(I\).
Key queries Upon receiving a key query  for an uncorrupted authority
for an uncorrupted authority  , \({\mathcal {B}}\) answers the query by first running
, \({\mathcal {B}}\) answers the query by first running
 to obtain \(m_1\), \(m_2\), and polynomials \((k_1, \dotsc , k_{m_3})\). Next, it sets
to obtain \(m_1\), \(m_2\), and polynomials \((k_1, \dotsc , k_{m_3})\). Next, it sets  and picks \(r_i {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N\) for \(i \in [m_1 + m_2]\) to set
and picks \(r_i {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N\) for \(i \in [m_1 + m_2]\) to set  for \(i \in [m_1]\). Additionally, it sets
for \(i \in [m_1]\). Additionally, it sets

for \(\ell \in [m_3]\). Finally, it returns the secret key for  as
as

Challenge ciphertext Whenever \({\mathcal {A}}\) requests the ciphertext challenge by sending  along with the public keys
along with the public keys  , the challenger \({\mathcal {B}}\) picks \(b {\mathop {\leftarrow }\limits ^{R}}\{0, 1\}\) and encrypts message \(m_b\) as a normal challenge ciphertext using
, the challenger \({\mathcal {B}}\) picks \(b {\mathop {\leftarrow }\limits ^{R}}\{0, 1\}\) and encrypts message \(m_b\) as a normal challenge ciphertext using

Now, observe that \({\mathcal {A}}\) is playing Gameoriginal if \(T \in _R{\mathbb {G}}\), while it is playing Game0 if \(T \in _R{\mathbb {G}}_1\). Therefore, if \({\mathcal {A}}\) has a non-negligible advantage in deciding which game it is playing, \({\mathcal {B}}\) has a non-negligible advantage in breaking Assumption 1. \(\square \)
Lemma 2
(Game0\(\approx _c\)Game1) Any adversary \({\mathcal {A}}\) having at most a negligible advantage in breaking Assumption 1, has at most a negligible advantage in distinguishing Game0 from Game1.
Proof
The challenger \({\mathcal {B}}\) receives \(\{ ({ \textsc {gp}}, g_1), T \}\) as input, where either \(T \in _R{\mathbb {G}}\) or \(T \in _R{\mathbb {G}}_1\). Now, \({\mathcal {B}}\) plays the game with \({\mathcal {A}}\) as follows.
Hash oracle Upon receiving oracle query gid for the hash function H, the challenger \({\mathcal {B}}\) checks if it received the query before, and if so, answers with the same reply as before. If \({\mathcal {A}}\) has not queried for the hash value of gid before, \({\mathcal {B}}\) picks a value \(u_{ \textsf {gid}}{\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N\) and replies with \(g_1^{\,u_{ \textsf {gid}}}\).
Setup The challenger \({\mathcal {B}}\) sets \({ \textsf {pp}}= ({ \textsc {gp}}, g_1)\) and sends pp to the adversary \({\mathcal {A}}\).
Authority queries Request for a new authority
 using
using  are answered by the challenger by running
are answered by the challenger by running
 . The challenger first uses
. The challenger first uses
 to obtain n, picks \({\mathbf {\varvec{v}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N^{\,n}\) and \(\alpha {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\), and sets
to obtain n, picks \({\mathbf {\varvec{v}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N^{\,n}\) and \(\alpha {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\), and sets  . It sets the public key
. It sets the public key  as
as  and the authority secret key
and the authority secret key  as
as  . It sends
. It sends  to the adversary and adds
to the adversary and adds
 to the set \(I\).
to the set \(I\).
Key queries Upon receiving a key query  for an uncorrupted authority
for an uncorrupted authority  , \({\mathcal {B}}\) answers the query using a pseudo normal key using \(u_{ \textsf {gid}}\) as \(r_0\),
, \({\mathcal {B}}\) answers the query using a pseudo normal key using \(u_{ \textsf {gid}}\) as \(r_0\),
 .
.
Challenge ciphertext Whenever \({\mathcal {A}}\) requests the ciphertext challenge by sending  , the challenger \({\mathcal {B}}\) picks \(b {\mathop {\leftarrow }\limits ^{R}}\{0, 1\}\) and encrypts message \(m_b\) as a challenge ciphertext using T.
, the challenger \({\mathcal {B}}\) picks \(b {\mathop {\leftarrow }\limits ^{R}}\{0, 1\}\) and encrypts message \(m_b\) as a challenge ciphertext using T.
Choose an  , pick
, pick  for each authority
for each authority  , and set
, and set  . Additionally, pick
. Additionally, pick  , set
, set  for all
for all  , and define
, and define  . Blind the message \(m_b \in {\mathbb {G}}_T\) using \(e(g_1, g_1)^\Delta \) to obtain \({ \textsf {ct}}_0 = m_b \cdot e(g_1, g_1)^\Delta \).
. Blind the message \(m_b \in {\mathbb {G}}_T\) using \(e(g_1, g_1)^\Delta \) to obtain \({ \textsf {ct}}_0 = m_b \cdot e(g_1, g_1)^\Delta \).
Now, for each authority  continue as follows (we frequently drop the index
continue as follows (we frequently drop the index
 —when there is no ambiguity—to simplify notation). Run
—when there is no ambiguity—to simplify notation). Run
 to obtain \(w_1\), \(w_2\), and polynomials \((c_1, \dotsc , c_{w_3})\).
to obtain \(w_1\), \(w_2\), and polynomials \((c_1, \dotsc , c_{w_3})\).
If  , pick
, pick  , and set
, and set  for \(i \in [w_1]^+\) and, for \(\ell \in [w_3]\), set
for \(i \in [w_1]^+\) and, for \(\ell \in [w_3]\), set

Blind the value  by setting
by setting  .
.
If  , pick
, pick  for \(k \in [w_1 + w_2]^+\), and set
for \(k \in [w_1 + w_2]^+\), and set  for \(i \in [w_1]^+\) and, for \(\ell \in [w_3]\), set
for \(i \in [w_1]^+\) and, for \(\ell \in [w_3]\), set

Blind the value  by setting
by setting  .
.
The complete challenge ciphertext is

Note that \(T = g_1^{\,t \pmod {p_1}}g_2^{\,t \pmod {p_2}}g_3^{\,t \pmod {p_3}}\) for unknown t, and so we have implicitly used  in
in  , making the ciphertext identically distributed to a normal ciphertext if \(T \in {\mathbb {G}}_1\). Moreover, we have
, making the ciphertext identically distributed to a normal ciphertext if \(T \in {\mathbb {G}}_1\). Moreover, we have  ,
,  , and
, and  . Thus, if \(T \in _R{\mathbb {G}}_1\) the resulting ciphertext is normal, while if \(T \in _R{\mathbb {G}}\), the resulting ciphertext is pseudo normal, with
. Thus, if \(T \in _R{\mathbb {G}}_1\) the resulting ciphertext is normal, while if \(T \in _R{\mathbb {G}}\), the resulting ciphertext is pseudo normal, with  . Moreover, depending on the value of T, \({\mathcal {B}}\) either plays Game0 or Game1. \(\square \)
. Moreover, depending on the value of T, \({\mathcal {B}}\) either plays Game0 or Game1. \(\square \)
Observe that, by definition, Game1\(\equiv \)Game2,0,2.
Lemma 3
(Game2,j-1,2\(\approx _c\)Game2,j,1) Any adversary \({\mathcal {A}}\) having at most a negligible advantage in breaking Assumption 2, has at most a negligible advantage in distinguishing Game2,j-1,2 from Game2,j,1.
Proof
The challenger \({\mathcal {B}}\) receives \(\{ ({ \textsc {gp}}, g_1, h_1h_2, g_3), T \}\) as input, where either \(T \in _R{\mathbb {G}}_1\) or \(T \in _R{\mathbb {G}}_{12}\). Now, \({\mathcal {B}}\) plays the game with \({\mathcal {A}}\) as follows.
Hash oracle Upon receiving oracle query gid for the hash function H, the challenger \({\mathcal {B}}\) checks if it received the query before, and if so, answers with the same reply as before. If \({\mathcal {A}}\) has not queried for the hash value of gid before, \({\mathcal {B}}\) picks a value \(u_{ \textsf {gid}}{\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N\). Then, the first \(j-1\) queries for some gid are answered with \((g_1g_3)^{u_{ \textsf {gid}}}\), the \(j\hbox {th}\) query is answered with \(T^{u_{ \textsf {gid}}}\), while other queries are answered with \(g_1^{\,u_{ \textsf {gid}}}\).
Setup The challenger \({\mathcal {B}}\) sets \({ \textsf {pp}}= ({ \textsc {gp}}, g_1)\) and sends pp to the adversary \({\mathcal {A}}\).
Authority queries Request for a new authority
 using
using  are answered by the challenger by running
are answered by the challenger by running
 . The challenger first uses
. The challenger first uses
 to obtain n, picks \({\mathbf {\varvec{v}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N^{\,n}\) and \(\alpha {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\), and sets
to obtain n, picks \({\mathbf {\varvec{v}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N^{\,n}\) and \(\alpha {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\), and sets  . It sets the public key
. It sets the public key  as
as  and the authority secret key
and the authority secret key  as
as  . It sends
. It sends  to the adversary and adds
to the adversary and adds
 to the set \(I\).
to the set \(I\).
Key queries Upon receiving a key query  for an uncorrupted authority
for an uncorrupted authority  , \({\mathcal {B}}\) answers the query depending on the number distinct gid that have been queried before. If gid is one of the \((j-1)\hbox {th}\) first gids being queried, \({\mathcal {B}}\) answers with a semi-functional key of type II by sending
, \({\mathcal {B}}\) answers the query depending on the number distinct gid that have been queried before. If gid is one of the \((j-1)\hbox {th}\) first gids being queried, \({\mathcal {B}}\) answers with a semi-functional key of type II by sending
 . If the query is for the \(j\hbox {th}\) gid, \({\mathcal {B}}\) answers by sending
. If the query is for the \(j\hbox {th}\) gid, \({\mathcal {B}}\) answers by sending
 . Otherwise, \({\mathcal {B}}\) answers with a pseudo normal key by sending
. Otherwise, \({\mathcal {B}}\) answers with a pseudo normal key by sending
 .
.
Note that all in cases the key queries are answered with elements from the hash oracle’s range, creating properly distributed (semi-functional) keys. Also, observe that if \(T \in _R{\mathbb {G}}_1\), a query for the \(j\hbox {th}\) gid is answered with a pseudo normal key. Otherwise, if \(T \in _R{\mathbb {G}}_{12}\), the query is answered with a semi-functional key of type I.
Challenge ciphertext Whenever \({\mathcal {A}}\) requests the ciphertext challenge by sending  , the challenger \({\mathcal {B}}\) picks \(b {\mathop {\leftarrow }\limits ^{R}}\{0, 1\}\) and encrypts message \(m_b\) as a challenge ciphertext using \(h_1h_2\) and \(g_3\).
, the challenger \({\mathcal {B}}\) picks \(b {\mathop {\leftarrow }\limits ^{R}}\{0, 1\}\) and encrypts message \(m_b\) as a challenge ciphertext using \(h_1h_2\) and \(g_3\).
Choose an  , pick
, pick  for each authority
for each authority  , and set
, and set  . Additionally, pick
. Additionally, pick  , and set
, and set  for all
for all  , and define
, and define  . Blind the message \(m_b \in {\mathbb {G}}_T\) using \(e(g_1, g_1)^\Delta \) to obtain \({ \textsf {ct}}_0 = m_b \cdot e(g_1, g_1)^\Delta \).
. Blind the message \(m_b \in {\mathbb {G}}_T\) using \(e(g_1, g_1)^\Delta \) to obtain \({ \textsf {ct}}_0 = m_b \cdot e(g_1, g_1)^\Delta \).
Now, for each authority  continue as follows (we frequently drop the index
continue as follows (we frequently drop the index
 —when there is no ambiguity—to simplify notation). Run
—when there is no ambiguity—to simplify notation). Run
 to obtain \(w_1\), \(w_2\), and polynomials \((c_1, \dotsc , c_{w_3})\).
to obtain \(w_1\), \(w_2\), and polynomials \((c_1, \dotsc , c_{w_3})\).
If  , pick
, pick  for \(k \in [w_1 + w_2]^+\), and set
for \(k \in [w_1 + w_2]^+\), and set  for \(i \in [w_1]^+\) and, for \(\ell \in [w_3]\), set
for \(i \in [w_1]^+\) and, for \(\ell \in [w_3]\), set

Blind the value  by setting
by setting  .
.
If  , pick
, pick  for \(k \in [w_1 + w_2]^+\), and set
for \(k \in [w_1 + w_2]^+\), and set  for \(i \in [w_1]^+\) and, for \(\ell \in [w_3]\), set
for \(i \in [w_1]^+\) and, for \(\ell \in [w_3]\), set

Blind the value  by setting
by setting  .
.
The complete challenge ciphertext is

To see that this is properly distributed as a nominally semi-functional ciphertext, observe that  is independent of
is independent of  . Moreover, note that (for all i) the values
. Moreover, note that (for all i) the values  ,
,  , and
, and  are mutually independent. So, the given ciphertext is distributed as a nominally semi-functional one, and thus, we are left to prove that adversary \({\mathcal {A}}\) cannot distinguish a pseudo normal ciphertext (with \({\mathcal {C}} = \{1, 2, 3\}\)) from a nominally semi-functional ciphertext (with \({\mathcal {C}} = \{1, 2\}\)).
are mutually independent. So, the given ciphertext is distributed as a nominally semi-functional one, and thus, we are left to prove that adversary \({\mathcal {A}}\) cannot distinguish a pseudo normal ciphertext (with \({\mathcal {C}} = \{1, 2, 3\}\)) from a nominally semi-functional ciphertext (with \({\mathcal {C}} = \{1, 2\}\)).
Let  be an authority for which \({\mathcal {A}}\) cannot decrypt the ciphertext component
be an authority for which \({\mathcal {A}}\) cannot decrypt the ciphertext component  because
because  . Such an authority exists as otherwise \({\mathcal {A}}\) would be able to trivially decrypt the challenge ciphertext. Now, observe that all values
. Such an authority exists as otherwise \({\mathcal {A}}\) would be able to trivially decrypt the challenge ciphertext. Now, observe that all values  look random for
look random for  , while
, while  for nominally semi-functional ciphertext and
for nominally semi-functional ciphertext and  for pseudo normal ciphertext. Hence, \({\mathcal {A}}\)’s view can at most contain information about
for pseudo normal ciphertext. Hence, \({\mathcal {A}}\)’s view can at most contain information about  on the values
on the values  in the subgroup \({\mathbb {G}}_3\) (remember,
in the subgroup \({\mathbb {G}}_3\) (remember,  for the
for the  of the \(j\hbox {th}\) gid). No other information about the values in these subgroups is given by any of the key query responses (note
of the \(j\hbox {th}\) gid). No other information about the values in these subgroups is given by any of the key query responses (note  is independent of
is independent of  ). By the statistical security property (see Definition 6), we know that this view is now indistinguishable from
). By the statistical security property (see Definition 6), we know that this view is now indistinguishable from  , the view of a nominally semi-functional ciphertext. Hence, the ciphertext is distributed correctly according to the adversary’s view. Moreover, depending on the value of T, \({\mathcal {B}}\) either plays Game2,j-1,2 or Game2,j,1. \(\square \)
, the view of a nominally semi-functional ciphertext. Hence, the ciphertext is distributed correctly according to the adversary’s view. Moreover, depending on the value of T, \({\mathcal {B}}\) either plays Game2,j-1,2 or Game2,j,1. \(\square \)
Lemma 4
(Game2,j,1\(\approx _c\)Game2,j,2) Any adversary \({\mathcal {A}}\) having at most a negligible advantage in breaking Assumption 3, has at most a negligible advantage in distinguishing Game2,j,1 from Game2,j,2.
Proof
The challenger \({\mathcal {B}}\) receives \(\{ ({ \textsc {gp}}, g_1, h_1h_3, h'_2h'_3), T \}\) as input, where either \(T \in _R{\mathbb {G}}_{12}\) or \(T \in _R{\mathbb {G}}_{13}\). Now, \({\mathcal {B}}\) plays the game with \({\mathcal {A}}\) as follows.
Hash oracle Upon receiving oracle query gid for the hash function H, the challenger \({\mathcal {B}}\) checks if it received the query before, and if so, answers with the same reply as before. If \({\mathcal {A}}\) has not queried for the hash value of gid before, \({\mathcal {B}}\) picks a value \(u_{ \textsf {gid}}{\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N\). Then, the first \(j-1\) queries for some gid are answered with \((h_1h_3)^{u_{ \textsf {gid}}}\), the \(j\hbox {th}\) query is answered with \(T^{u_{ \textsf {gid}}}\), while other queries are answered with \(g_1^{\,u_{ \textsf {gid}}}\).
Setup The challenger \({\mathcal {B}}\) sets \({ \textsf {pp}}= ({ \textsc {gp}}, g_1)\) and sends pp to the adversary \({\mathcal {A}}\).
Authority queries Request for a new authority
 using
using  are answered by the challenger by running
are answered by the challenger by running
 . The challenger first uses
. The challenger first uses
 to obtain n, picks \({\mathbf {\varvec{v}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N^{\,n}\) and \(\alpha {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\), and sets
to obtain n, picks \({\mathbf {\varvec{v}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N^{\,n}\) and \(\alpha {\mathop {\leftarrow }\limits ^{R}}{\mathbb {G}}_1\), and sets  . It sets the public key
. It sets the public key  as
as  and the authority secret key
and the authority secret key  as
as  . It sends
. It sends  to the adversary and adds
to the adversary and adds
 to the set \(I\).
to the set \(I\).
Key queries Upon receiving a key query  for an uncorrupted authority
for an uncorrupted authority  , \({\mathcal {B}}\) answers the query depending on the number distinct gid that have been queried before. If gid is one of the \((j-1)\hbox {th}\) first gids being queried, \({\mathcal {B}}\) answers with a semi-functional key of type II by sending
, \({\mathcal {B}}\) answers the query depending on the number distinct gid that have been queried before. If gid is one of the \((j-1)\hbox {th}\) first gids being queried, \({\mathcal {B}}\) answers with a semi-functional key of type II by sending
 . If the query is for the \(j\hbox {th}\) gid, \({\mathcal {B}}\) answers by sending
. If the query is for the \(j\hbox {th}\) gid, \({\mathcal {B}}\) answers by sending
 . Otherwise, \({\mathcal {B}}\) answers with a pseudo normal key by sending
. Otherwise, \({\mathcal {B}}\) answers with a pseudo normal key by sending
 .
.
Note that all cases the key queries are answered with elements from the hash oracle’s range, creating properly distributed semi-functional keys. Also, observe that if \(T \in _R{\mathbb {G}}_{12}\), a query for the \(j\hbox {th}\) gid is answered with a semi-functional key of type I, and otherwise, if \(T \in _R{\mathbb {G}}_{13}\), the query is answered with a semi-functional key of type II.
Challenge ciphertext Whenever \({\mathcal {A}}\) requests the ciphertext challenge by sending  , the challenger \({\mathcal {B}}\) picks \(b {\mathop {\leftarrow }\limits ^{R}}\{0, 1\}\) and encrypts message \(m_b\) as a challenge ciphertext using \(g_1\) and \(h'_2h'_3\).
, the challenger \({\mathcal {B}}\) picks \(b {\mathop {\leftarrow }\limits ^{R}}\{0, 1\}\) and encrypts message \(m_b\) as a challenge ciphertext using \(g_1\) and \(h'_2h'_3\).
Choose an  , pick
, pick  for each authority
for each authority  , and set
, and set  . Additionally, pick
. Additionally, pick  , and set
, and set  for all
for all  , and define
, and define  . Blind the message \(m_b \in {\mathbb {G}}_T\) using \(e(g_1, g_1)^\Delta \) to obtain \({ \textsf {ct}}_0 = m_b \cdot e(g_1, g_1)^\Delta \).
. Blind the message \(m_b \in {\mathbb {G}}_T\) using \(e(g_1, g_1)^\Delta \) to obtain \({ \textsf {ct}}_0 = m_b \cdot e(g_1, g_1)^\Delta \).
Now, for each authority  continue as follows (we frequently drop the index
continue as follows (we frequently drop the index
 —when there is no ambiguity—to simplify notation). Run
—when there is no ambiguity—to simplify notation). Run
 to obtain \(w_1\), \(w_2\), and polynomials \((c_1, \dotsc , c_{w_3})\).
to obtain \(w_1\), \(w_2\), and polynomials \((c_1, \dotsc , c_{w_3})\).
If  , pick
, pick  for \(k \in [w_1 + w_2]^+\), and set
for \(k \in [w_1 + w_2]^+\), and set  for \(i \in [w_1]^+\) and, for \(\ell \in [w_3]\), set
for \(i \in [w_1]^+\) and, for \(\ell \in [w_3]\), set

Blind the value  by setting
by setting  .
.
If  , pick
, pick  for \(k \in [w_1 + w_2]^+\), and set
for \(k \in [w_1 + w_2]^+\), and set  and, for \(\ell \in [w_3]\), set
and, for \(\ell \in [w_3]\), set

Blind the value  by setting
by setting  .
.
The complete challenge ciphertext is

To see that this is properly distributed as a semi-functional ciphertext, first observe that  is independent of
is independent of  . Moreover, note that (for all i) the values
. Moreover, note that (for all i) the values  ,
,  , and
, and  are mutually independent. So, the given ciphertext is distributed as a semi-functional one, and thus, we are left to prove that adversary \({\mathcal {A}}\) cannot distinguish a nominally semi-functional ciphertext (with \({\mathcal {C}} = \{1, 2\}\)) from a semi-functional ciphertext (with \({\mathcal {C}} = \{1\}\)).
are mutually independent. So, the given ciphertext is distributed as a semi-functional one, and thus, we are left to prove that adversary \({\mathcal {A}}\) cannot distinguish a nominally semi-functional ciphertext (with \({\mathcal {C}} = \{1, 2\}\)) from a semi-functional ciphertext (with \({\mathcal {C}} = \{1\}\)).
Let  be an authority for which \({\mathcal {A}}\) cannot decrypt the ciphertext component
be an authority for which \({\mathcal {A}}\) cannot decrypt the ciphertext component  because
because  . Such an authority exists, as otherwise \({\mathcal {B}}\) would have aborted the game or \({\mathcal {A}}\) would have been able to trivially decrypt the challenge ciphertext. Now, observe that all values
. Such an authority exists, as otherwise \({\mathcal {B}}\) would have aborted the game or \({\mathcal {A}}\) would have been able to trivially decrypt the challenge ciphertext. Now, observe that all values  look random for
look random for  , while
, while  for semi-functional ciphertext and
for semi-functional ciphertext and  for nominally semi-functional ciphertext. (In both nominally semi-functional and semi-functional ciphertext, all values
for nominally semi-functional ciphertext. (In both nominally semi-functional and semi-functional ciphertext, all values  for
for  , are already random.) Hence, \({\mathcal {A}}\)’s view can at most contain information about
, are already random.) Hence, \({\mathcal {A}}\)’s view can at most contain information about  on the values
on the values  in the subgroup \({\mathbb {G}}_2\) (remember,
in the subgroup \({\mathbb {G}}_2\) (remember,  for the
for the  of the \(j\hbox {th}\) gid). No other information about the values in these subgroups is given by any of the key query responses (note
of the \(j\hbox {th}\) gid). No other information about the values in these subgroups is given by any of the key query responses (note  is independent of
is independent of  ). By the statistical security property (see Definition 6), we know that this view is now indistinguishable from
). By the statistical security property (see Definition 6), we know that this view is now indistinguishable from  , the view corresponding to a semi-functional ciphertext. Hence, the ciphertext is distributed correctly according to the adversary’s view. Moreover, depending on the value of T, \({\mathcal {B}}\) either plays Game2,j,1 or Game2,j,2. \(\square \)
, the view corresponding to a semi-functional ciphertext. Hence, the ciphertext is distributed correctly according to the adversary’s view. Moreover, depending on the value of T, \({\mathcal {B}}\) either plays Game2,j,1 or Game2,j,2. \(\square \)
Lemma 5
(Game2,q,2\(\approx _c\)Game3) Any p.p.t. adversary \({\mathcal {A}}\), making at most q key queries for distinct gids and having at most a negligible advantage in breaking Assumption 4, has at most a negligible advantage in distinguishing Game2,q,2 from Game3.
Proof
Note that in Game2,q,2, the challenge ciphertext is semi-functional and all key queries are answered with a semi-functional key of type II. We have to prove that the adversary \({\mathcal {A}}\) cannot distinguish whether, for some  ,
,  is replaced by a random element in \({\mathbb {Z}}_N\) or not.
is replaced by a random element in \({\mathbb {Z}}_N\) or not.
The challenger \({\mathcal {B}}\) receives \(\{ ({ \textsc {gp}}, g_1, g_2, g_3, g_1^{\,a}, (g_1g_3)^b, g_1^{\,c}, g_1^{\,ac}g_3^{\,d}), T \}\), where either \(T = e(g_1, g_1)^{abc}\) or \(T \in _R{\mathbb {G}}_T\). Now, \({\mathcal {B}}\) plays the game with \({\mathcal {A}}\) as follows.
Hash oracle Upon receiving oracle query gid for the hash function H, the challenger \({\mathcal {B}}\) checks if it received the query before, and if so, answers with the same reply as before. If \({\mathcal {A}}\) has not queried for the hash value of gid before, \({\mathcal {B}}\) picks a value \(u_{ \textsf {gid}}{\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N\). It answers the query with \(B^{-1} (g_1g_3)^{u_{ \textsf {gid}}} = (g_1g_3)^{-b + u_{ \textsf {gid}}}\).
Setup The challenger \({\mathcal {B}}\) sets \({ \textsf {pp}}= ({ \textsc {gp}}, g_1)\) and sends pp to the adversary \({\mathcal {A}}\).
Authority queries Request for a new authority
 using
using  are answered by the challenger by running
are answered by the challenger by running
 . The challenger first uses
. The challenger first uses
 to obtain n, picks \({\mathbf {\varvec{v}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N^n\) and \({\tilde{\alpha }} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N\), and sets the public key
to obtain n, picks \({\mathbf {\varvec{v}}} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N^n\) and \({\tilde{\alpha }} {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_N\), and sets the public key  as \((g_1^{\,a+{\tilde{v}}_1}, g_1^{\,v_2}, \dotsc , g_1^{\,v_n}, e(g_1^{\,a}, (g_1g_3)^b)e(g_1, g_1)^{{\tilde{\alpha }}})\) and (thereby indirectly) setting the authority secret key
as \((g_1^{\,a+{\tilde{v}}_1}, g_1^{\,v_2}, \dotsc , g_1^{\,v_n}, e(g_1^{\,a}, (g_1g_3)^b)e(g_1, g_1)^{{\tilde{\alpha }}})\) and (thereby indirectly) setting the authority secret key  . It sends
. It sends  to the adversary and adds
to the adversary and adds
 to the set \(I\).
to the set \(I\).
Key queries Upon receiving a key query  for an uncorrupted authority
for an uncorrupted authority  , \({\mathcal {B}}\) answers the query with a semi-functional key of type II. The challenger \({\mathcal {B}}\) computes
, \({\mathcal {B}}\) answers the query with a semi-functional key of type II. The challenger \({\mathcal {B}}\) computes
 as follows. First, it sets
as follows. First, it sets  and
and  . Next, to construct the values
. Next, to construct the values  , consider two cases. Either \(k_\ell \) contains both the symbol \(\alpha \) and \(b_1r_0\), or it does not contain this combination (i.e., \(\phi _\ell = \phi _{\ell ,0,1}\), see Sect. 4.1; symbols \(b_1\) and \(r_0\) may occur separately, but not in the combination \(b_1r_0\)). In the case that \(\alpha \) and \(b_1r_0\) do not occur in \(k_\ell \), \({\mathcal {B}}\) can create
, consider two cases. Either \(k_\ell \) contains both the symbol \(\alpha \) and \(b_1r_0\), or it does not contain this combination (i.e., \(\phi _\ell = \phi _{\ell ,0,1}\), see Sect. 4.1; symbols \(b_1\) and \(r_0\) may occur separately, but not in the combination \(b_1r_0\)). In the case that \(\alpha \) and \(b_1r_0\) do not occur in \(k_\ell \), \({\mathcal {B}}\) can create  using the values
using the values  and \(r_1, \dotsc , r_{m_2}\); and \(g_1^{\,a + {\tilde{v}}_1}g_3^{\,{\tilde{v}}_1}\) and \(v_2, \dotsc , v_n\) (and, of course, the values \(\phi _\ell \), \(\phi _{\ell ,z}\), and \(\phi _{\ell ,i,j}\)). In the case that both \(\alpha \) and \(b_1r_0\) occur in \(k_\ell \), observe that \({\mathcal {B}}\) needs to compute \((g_1g_3)^{\phi _\ell \alpha + \sum _{z \in [m_2]}\phi _{\ell ,z} {\hat{r}}_z + \sum _{i \in [m_1]^+, j \in [n]}\phi _{\ell ,i,j} r_i b_j}\), where we have that
and \(r_1, \dotsc , r_{m_2}\); and \(g_1^{\,a + {\tilde{v}}_1}g_3^{\,{\tilde{v}}_1}\) and \(v_2, \dotsc , v_n\) (and, of course, the values \(\phi _\ell \), \(\phi _{\ell ,z}\), and \(\phi _{\ell ,i,j}\)). In the case that both \(\alpha \) and \(b_1r_0\) occur in \(k_\ell \), observe that \({\mathcal {B}}\) needs to compute \((g_1g_3)^{\phi _\ell \alpha + \sum _{z \in [m_2]}\phi _{\ell ,z} {\hat{r}}_z + \sum _{i \in [m_1]^+, j \in [n]}\phi _{\ell ,i,j} r_i b_j}\), where we have that
And so it sets (we slightly abuse notation and write \((g_1g_3)^{v_1}\) for \((g_1^{\,a})^{{\tilde{v}}_1}(g_3)^{{\tilde{v}}_1}\))

Note that the key queries are answered with elements from the hash oracle’s range and create properly distributed semi-functional keys of type II.
Challenge ciphertext Whenever \({\mathcal {A}}\) requests the ciphertext challenge by sending  , the challenger \({\mathcal {B}}\) picks \(b {\mathop {\leftarrow }\limits ^{R}}\{0, 1\}\) and encrypts message \(m_b\) as a semi-functional challenge ciphertext.
, the challenger \({\mathcal {B}}\) picks \(b {\mathop {\leftarrow }\limits ^{R}}\{0, 1\}\) and encrypts message \(m_b\) as a semi-functional challenge ciphertext.
Choose an uncorrupted authority  . For each authority
. For each authority  , pick
, pick  , and set
, and set  and indirectly set
and indirectly set  . Additionally, pick
. Additionally, pick  for all
for all  . Blind the message \(m_b \in {\mathbb {G}}_T\) using T to obtain \({ \textsf {ct}}_0 = m_b \cdot T\). Note that if \(T = e(g_1, g_1)^{abc}\), the challenger simulates Game2,q,2 using \(\Delta = abc\) and otherwise, if \(T \in _R{\mathbb {G}}_T\), the challenger simulates Game3.
. Blind the message \(m_b \in {\mathbb {G}}_T\) using T to obtain \({ \textsf {ct}}_0 = m_b \cdot T\). Note that if \(T = e(g_1, g_1)^{abc}\), the challenger simulates Game2,q,2 using \(\Delta = abc\) and otherwise, if \(T \in _R{\mathbb {G}}_T\), the challenger simulates Game3.
Now, for each authority  continue as follows (we frequently drop the index
continue as follows (we frequently drop the index
 —when there is no ambiguity—to simplify notation). Run
—when there is no ambiguity—to simplify notation). Run
 to obtain \(w_1\), \(w_2\), and polynomials \((c_1, \dotsc , c_{w_3})\).
to obtain \(w_1\), \(w_2\), and polynomials \((c_1, \dotsc , c_{w_3})\).
If  , pick
, pick  and
and  for \(k \in [w_1 + w_2]\). Set
for \(k \in [w_1 + w_2]\). Set  and
and  for \(i \in [w_1]\). Next, \({\mathcal {B}}\) constructs the values
for \(i \in [w_1]\). Next, \({\mathcal {B}}\) constructs the values  . The challenger \({\mathcal {B}}\) needs to compute (among others)
. The challenger \({\mathcal {B}}\) needs to compute (among others)

where the occurance of \(s_0b_1\) in \(c_\ell \) can be computed by

So, \({\mathcal {B}}\) sets (we slightly abuse notation and write \((g_1g_2g_3)^{v_1}\) for \((g_1^{\,a})^{{\tilde{v}}_1}(g_2g_3)^{{\tilde{v}}_1}\) and  for
for  )
)

Note that by using this, \({\mathcal {B}}\) indirectly uses  in subgroup \({\mathbb {G}}_3\) instead of
in subgroup \({\mathbb {G}}_3\) instead of  . However, since
. However, since  and no constraint is imposed on the sum
and no constraint is imposed on the sum  , the distribution of the ciphertext component is identical to a semi-functional ciphertext.
, the distribution of the ciphertext component is identical to a semi-functional ciphertext.
Blind the value  by setting
by setting

If  , but
, but  , pick
, pick  for \(k \in [w_1 + w_2]^+\), and set
for \(k \in [w_1 + w_2]^+\), and set  for \(i \in [w_1]^+\) and, for \(\ell \in [w_3]\), set (we slightly abuse notation and write \((g_1g_2g_3)^{v_1}\) for \((g_1^{\,a})^{{\tilde{v}}_1}(g_2g_3)^{{\tilde{v}}_1}\))
for \(i \in [w_1]^+\) and, for \(\ell \in [w_3]\), set (we slightly abuse notation and write \((g_1g_2g_3)^{v_1}\) for \((g_1^{\,a})^{{\tilde{v}}_1}(g_2g_3)^{{\tilde{v}}_1}\))

Blind the value  by setting
by setting

If  , pick
, pick  for \(k \in [w_1 + w_2]^+\), and set
for \(k \in [w_1 + w_2]^+\), and set  for \(i \in [w_1]^+\) and, for \(\ell \in [w_3]\), set
for \(i \in [w_1]^+\) and, for \(\ell \in [w_3]\), set

Blind the value  by setting
by setting  .
.
The complete challenge ciphertext is
This semi-functional ciphertext is properly distributed, with  . So, if \(T = e(g_1, g_1)^{abc}\), the adversary \({\mathcal {A}}\) is playing Game2,q,2 and otherwise, if \(T \in _R{\mathbb {G}}_T\), \({\mathcal {A}}\) is playing Game3. \(\square \)
. So, if \(T = e(g_1, g_1)^{abc}\), the adversary \({\mathcal {A}}\) is playing Game2,q,2 and otherwise, if \(T \in _R{\mathbb {G}}_T\), \({\mathcal {A}}\) is playing Game3. \(\square \)
Finally, note that in Game3, the challenger gives the adversary an encryption of a random message. Hence, \({\mathcal {A}}\) has no advantage in winning the game.
7 Multi-authority pair encoding examples
We give several examples of multi-authority admissible pair encoding schemes (MAPESs) for various predicate families.
7.1 Multi-authority identity-based encoding
We can see the MA-ABE construction by Lewko and Waters [21] as a special case of our general MA-PE scheme. Their construction combines the same IBE scheme multiple times with a “multi-authority layer” on top. Based on their scheme, we extract the underlying MA-PES for an identity-based predicate. However, note that if we apply our conversion algorithm on the resulting encoding, we obtain a multi-authority IBE scheme, not an MA-ABE scheme, since our conversion uses additive secret sharing instead of Shamir secret sharing. Furthermore, the resulting MA-PES can be seen as an encoding for an IBE scheme which only allows for a single identity.
Example 1
(MA-PES based on [21]) We derive an MA-PES for multi-authority identity-based encryption from the MA-ABE scheme by Lewko and Waters [21]. The pair encoding for an authority
 is the following:
is the following:
For Pair we have
Correctness follows by simple substitutions,
We can extend the construction to obtain a small universe construction for t identities, by setting
where \(\rho \) is an injective function that maps an identity to an identity index in [t].
Remark 3
(One-use requirement) Similar to the one-use requirement for attributes, as found in several ABE schemes [5, 21, 23], the MA-PES of Example 1 has this one-use requirement as well, i.e., a ciphertext ct from a corresponding MA-PE scheme may only contain the identity x, encoded by \(b_{\rho (x)}\), once.
Theorem 2
(MA-PES based on [21]) The (extended) MA-PES described in Example 1 is statistically secure (see Definition 6).
Proof
If \(P_\kappa (x, y) = \textsc {false}\), we have to show that the distributions
are statically indistinguishable, where \(b_{\rho (x)}, b_{\rho (y)}, \omega , s_0, r_0 {\mathop {\leftarrow }\limits ^{R}}{\mathbb {Z}}_p\) for any prime p, \(\log _2 p = \Theta ({ \lambda })\). Since \(P_\kappa (x, y) = \textsc {false}\), we know that \(x \ne y\) and thus \(\rho (x) \ne \rho (y)\).
We distinguish two cases:
\(s_0 \in {\mathbb {Z}}_{p}^*\), i.e., \(s_0\) is a generator of the multiplicative group \({\mathbb {Z}}_{p}^*\).
Then, \(b_{\rho (x)}s_0\) is uniformly distributed in \({\mathbb {Z}}_p\). On the other hand, \(\omega + b_{\rho (x)}s_0\) is also uniformly distributed in \({\mathbb {Z}}_p\). Hence, the distributions are identical.
\(s_0 = 0\), i.e., \(s_0\) is not a generator for the multiplicative group \({\mathbb {Z}}_{p}^*\).
Then, \(b_{\rho (x)}s_0 = 0\), while \(\omega + b_{\rho (x)}s_0 \in _R{\mathbb {Z}}_p\). However, this case only occurs with a probability negligible in \({ \lambda }\).
Combining the two cases, we have proven that the two distributions are statistically indistinguishable. \(\square \)
7.2 Multi-authority attribute-based encoding
We adapt the PES for CP-ABE from the full version of Attrapadung [5, Scheme 11] to MA-PES. The PES is, in its turn, based on a small universe CP-ABE scheme by Lewko et al. [23].
Example 2
(MA-PES based on [5, 23]) The PES by Attrapadung [5] can be turned into an MA-PES. Let t denote the number of attributes in the universe. For a linear secret sharing scheme (LSSS) using \((\mathbf {\varvec{\mathrm {A}}}^{w_3 \times w_2}, \pi )\), where we denote the \(i\hbox {th}\) row of \(\mathbf {\varvec{\mathrm {A}}}\) by \({\mathbf {\varvec{a}}}_i\) and \(\pi \) is an injective function that maps a row in \(\mathbf {\varvec{\mathrm {A}}}\) to an attribute index in [t], the pair encoding for an authority
 is the following:
is the following:
The matrices returned by the Pair algorithm are indirectly defined by the combination of keys required to satisfy the access policy as described in the ciphertext.
Correctness follows by first computing
for the attributes \(\pi (i)\) the user has the key components \(y = \pi (i)\) for. Then, if the user obtained enough shares \({\mathbf {\varvec{a}}}_i(\omega + s_0b', {\hat{s}}_2, \dotsc , {\hat{s}}_{w_2})^{{\mathsf {T}}}\cdot r_0\), he can combine the shares to recover the secret \([\omega + s_0b'] \cdot r_0\) and then use this to symbolically obtain
Theorem 3
(MA-PES based on [5]) The MA-PES described in Example 2 is statistically secure (see Definition 6).
Proof
The proof is very similar to the proof presented in the full version of [5].
When \(P(x, y) = \textsc {false}\), we have that \((\mathbf {\varvec{\mathrm {A}}}, \pi )\) does not accept y. We need to prove that \(\omega \) is hidden. We may assume \(s_1 \ne 0\) since the probability of \(s_1 = 0\) is negligible in \({ \lambda }\). For \(j = 1, \dotsc , w_3\), we consider two cases. If \(\pi (j) \not \in y\), then \(b_{\pi (j)}\) does not appear anywhere except for in \(c_i\) and hence the information on \(\omega + s_0b'\) will not be leaked from \(c_i\). Now consider \(\pi (j) \in y\). In this case, both \(s_1\) and \(b_{\pi (j)}\) are available (since \(r_0\) and \(r_0b_{\pi (j)}\) are), hence \({\mathbf {\varvec{a}}}_i(\omega + s_0b', {\hat{s}}_2, \dotsc , {\hat{s}}_{w_2})^{{\mathsf {T}}}\) is known. Now from the lemma of LSSS (similar to [5, Proposition 40]), there exists a vector \({\mathbf {\varvec{u}}} \in {\mathbb {Z}}_N^{w_3}\) with \(u_1 \ne 0\), such that \({\mathbf {\varvec{u}}}\) is orthogonal to all \({\mathbf {\varvec{a}}}_j\), where \(\pi (j) \in y\). Hence, \({\mathbf {\varvec{a}}}_j(\omega + s_0b', {\hat{s}}_2, \dotsc , {\hat{s}}_{w_2})^{{\mathsf {T}}}= {\mathbf {\varvec{a}}}_j\big ((\omega + s_0b', {\hat{s}}_2, \dotsc , {\hat{s}}_{w_2})^{{\mathsf {T}}}+ z{\mathbf {\varvec{u}}}^{{\mathsf {T}}}\big )\) for any unknown random \(z \in {\mathbb {Z}}_N\). Therefore, \({\mathbf {\varvec{a}}}_j(\omega + s_0b', {\hat{s}}_2, \dotsc , {\hat{s}}_{w_2})^{{\mathsf {T}}}\) does not leak information on \(\omega + s_0b'\) as \(u_1 \ne 0\). In either case \(\omega + s_0b'\) is hidden in the encoding. Since \(\omega \) only occurs in this expression \(\omega + s_0b'\), no information on \(\omega \) is revealed. \(\square \)
7.3 Multi-authority inner-product encoding
To create a multi-authority admissible pair encoding scheme (MA-PES) for an inner-product predicate, we extend the “short secret key encoding” presented by Wee [31, Section 5.1]
Example 3
(MA-PES based on [9, 31]) Based on the predicate encoding of Wee [31] for an IPPE scheme, which, in its turn, is based on the scheme of Boneh and Boyen [9], we create an MA-PES for the inner-product predicate. Such a predicate evaluates to true if and only if the inner product of the, with the ciphertext associated, vector \({\mathbf {\varvec{x}}}\) and the, with the key associated, vector \({\mathbf {\varvec{y}}}\) equals 0, i.e., if \(\langle {\mathbf {\varvec{x}}}, {\mathbf {\varvec{y}}}\rangle = 0\). Let t be the length of the vectors \({\mathbf {\varvec{x}}}\) and \({\mathbf {\varvec{y}}}\). The pair encoding for an authority
 is the following:
is the following:
Similar to Example 2, Pair(\(N, x, y\)) relies on the value y, which is in this case is the vector \({\mathbf {\varvec{y}}}\). Algorithm Pair outputs matrices to compute \(s_0 \cdot k_1 + \langle {\mathbf {\varvec{c}}}, (1, {\mathbf {\varvec{y}}})\rangle \cdot r_0\).
Correctness follows by simple substitutions and simplifying the expression,
Theorem 4
(MA-PES based on [9, 31]) The MA-PES described in Example 3 is statistically secure (see Definition 6).
Proof
When \(P(x, y) = \textsc {false}\), we have that \(\langle {\mathbf {\varvec{x}}}, {\mathbf {\varvec{y}}}\rangle \ne 0\). We need to prove that \(\omega \) is hidden. We may assume \(s_0 \ne 0\) since the probability of \(s_0 = 0\) is negligible in \({ \lambda }\). Since \(\omega \) only appears in \(c_0\), we need to show that \(b's_0\) is uniformly distributed in \({\mathbb {Z}}_p\) and therefore no information on \(\omega \) is revealed. The value \(b'\) only appears in the adversary’s view elsewhere as \(r_0(b' + \langle {\mathbf {\varvec{b}}}^+, {\mathbf {\varvec{y}}}\rangle )\) in \(k_1\). Thus, we now need to show that \(r_0\langle {\mathbf {\varvec{b}}}^+, {\mathbf {\varvec{y}}}\rangle \) is statistically hidden. The value \({\mathbf {\varvec{b}}}^+\) only appears as \(s_0(b''{\mathbf {\varvec{x}}} + {\mathbf {\varvec{b}}}^+)\) in the adversary’s view. However, no information on the value of \(b''\) is revealed and so, if \(\langle {\mathbf {\varvec{x}}}, {\mathbf {\varvec{y}}}\rangle \ne 0\), the value \(\langle {\mathbf {\varvec{b}}}^+, {\mathbf {\varvec{y}}}\rangle \) is hidden. We may conclude that \(b'\) is hidden and so is \(\omega \). \(\square \)
8 Conclusion
We show that the concept of a multi-authority attribute-based encryption scheme can be generalized to a multi-authority predicate encryption (MA-PE) scheme for a variety of predicate families. Our generic approach allows us to combine the best features of several predicates into a single MA-PE scheme specific to an application’s needs. We achieve our result by defining a multi-authority admissible pair encoding scheme (MA-PES) and proposing a conversion technique from such an encoding to an MA-PE scheme. The obtained MA-PE schemes are decentralized, meaning that new authorities can be created without requiring any form of interaction, while no party needs to have access to a master secret. If started from statistically secure MA-PESs, the resulting MA-PE schemes are proven to be fully secure—allowing for the static corruption of authorities—in the random oracle model.
Notes
The construction of Lewko and Waters [21] also requires that no authority may issue a key to the same user twice, although they do not make this requirement explicit.
References
Abdalla M., Gay R., Raykova M., Wee H.: Multi-input inner-product functional encryption from pairings. In: Coron J.S., Nielsen J.B. (eds.) Advances in Cryptology—EUROCRYPT 2017. LNCS, vol. 10210, pp. 601–626. Springer, New York (2017).
Agrawal S., Chase M.: A study of pair encodings: predicate encryption in prime order groups. In: Kushilevitz E., Malkin T. (eds.) Theory of Cryptography (TCC). LNCS, vol. 9563, pp. 259–288. Springer, New York (2016).
Agrawal S., Chase M.: Simplifying design and analysis of complex predicate encryption schemes. In: Coron J.S., Nielsen J.B. (eds.) Advances in Cryptology—EUROCRYPT 2017. LNCS, vol. 10210, pp. 627–656. Springer, New York (2017).
Ambrona M., Barthe G., Schmidt B.: Generic transformations of predicate encodings: constructions and applications. In: Katz J., Shacham H. (eds.) Advances in Cryptology—CRYPTO 2017. LNCS, vol. 10401, pp. 36–66. Springer, New York (2017).
Attrapadung N.: Dual system encryption via doubly selective security: framework, fully secure functional encryption for regular languages, and more. In: Nguyen P.Q., Oswald E. (eds.) Advances in Cryptology—EUROCRYPT 2014. LNCS, vol. 8441, pp. 557–577. Springer, New York (2014).
Attrapadung N., Imai H.: Dual-policy attribute based encryption. In: Abdalla M., Pointcheval D., Fouque P.A., Vergnaud D. (eds.) Applied Cryptography and Network Security. LNCS, vol. 5536, pp. 168–185. Springer, New York (2009).
Attrapadung N., Yamada S.: Duality in ABE: converting attribute based encryption for dual predicate and dual policy via computational encodings. In: Nyberg K. (ed.) Topics in Cryptology—CT-RSA 2015. LNCS, vol. 9048, pp. 87–105. Springer, New York (2015).
Bellare M., Waters B., Yilek S.: Identity-based encryption secure against selective opening attack. In: Ishai Y. (ed.) Theory of Cryptography (TCC). LNCS, vol. 6597, pp. 235–252. Springer, New York (2011).
Boneh D., Boyen X.: Efficient selective-ID secure identity-based encryption without random oracles. In: Cachin C., Camenisch J.L. (eds.) Advances in Cryptology—EUROCRYPT 2004. LNCS, vol. 3027, pp. 223–238. Springer, New York (2004).
Boneh D., Franklin M.: Identity-based encryption from the Weil pairing. In: Kilian J. (ed.) Advances in Cryptology—CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, New York (2001).
Boneh D., Waters B.: Conjunctive, subset, and range queries on encrypted data. In: Vadhan S.P. (ed.) Theory of Cryptography (TCC). LNCS, vol. 4392, pp. 535–554. Springer, New York (2007).
Chase M.: Multi-authority attribute based encryption. In: Vadhan S.P. (ed.) Theory of Cryptography (TCC). LNCS, vol. 4392, pp. 515–534. Springer, New York (2007).
Chase M., Chow S.S.M.: Improving privacy and security in multi-authority attribute-based encryption. In: Proceedings of the 16th ACM Conference on Computer and Communications Security. ACM, pp. 121–130 (2009)
Chen J., Wee H.: Fully, (almost) tightly secure IBE and dual system groups. In: Canetti R., Garay J.A. (eds.) Advances in Cryptology—CRYPTO. LNCS, vol. 8043, pp. 435–460. Springer, New York (2013).
Chen J., Wee H.: Dual system groups and its applications—compact HIBE and more. Cryptology ePrint Archive, Report 2014/265 (2014)
Chen J., Gay R., Wee H.: Improved dual system ABE in prime-order groups via predicate encodings. In: Oswald E., Fischlin M. (eds.) Advances in Cryptology—EUROCRYPT 2015. LNCS, vol. 9057, pp. 595–624. Springer, New York (2015).
Datta P., Okamoto T., Tomida J.: Full-hiding (unbounded) multi-input inner product functional encryption from the $k$-linear assumption. In: Abdalla M., Dahab R. (eds.) Public Key Cryptography—PKC. LNCS, vol. 10770, pp. 245–277. Springer, New York (2018).
Katz J., Sahai A., Waters B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart N. (ed.) Advances in Cryptology—EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, New York (2008).
Kim J., Susilo W., Guo F., Au M.H.: A tag based encoding: an efficient encoding for predicate encryption in prime order groups. In: Zikas V., De Prisco R. (eds.) Security and Cryptography for Networks. LNCS, vol. 9841, pp. 3–22. Springer, New York (2016).
Lewko A., Waters B.: New techniques for dual system encryption and fully secure HIBE with short ciphertexts. In: Micciancio D. (ed.) Theory of Cryptography (TCC). LNCS, vol. 5978, pp. 455–479. Springer, New York (2010).
Lewko A., Waters B.: Decentralizing attribute-based encryption. In: Paterson K.G. (ed.) Advances in Cryptology—EUROCRYPT 2011. LNCS, vol. 6632, pp. 568–588. Springer, New York (2011).
Lewko A., Waters B.: New proof methods for attribute-based encryption: achieving full security through selective techniques. In: Safavi-Naini R., Canetti R. (eds.) Advances in Cryptology—CRYPTO. LNCS, vol. 7417, pp. 180–198. Springer, New York (2012).
Lewko A., Okamoto T., Sahai A., Takashima K., Waters B.: Fully secure functional encryption: attribute-based encryption and (hierarchical) inner product encryption. In: Gilbert H. (ed.) Advances in Cryptology—EUROCRYPT 2010. LNCS, vol. 6110, pp. 62–91. Springer, New York (2010).
Michalevsky Y., Joye M.: Decentralized policy-hiding ABE with receiver privacy. In: Lopez J., Zhou J., Soriano M. (eds.) Computer Security. LNCS, vol. 11099, pp. 548–567. Springer, New York (2018).
Müller S., Katzenbeisser S., Eckert C.: Distributed attribute-based encryption. In: Lee P.J., Cheon J.H. (eds.) Information Security and Cryptology (ICISC). LNCS, vol. 5461, pp. 20–36. Springer, New York (2009).
Okamoto T., Takashima K.: Decentralized attribute-based signatures. In: Kurosawa K., Hanaoka G. (eds.) Public-Key Cryptography—PKC. LNCS, vol. 7778, pp. 125–142. Springer, New York (2013).
Rouselakis Y., Waters B.: Efficient statically-secure large-universe multi-authority attribute-based encryption. In: Böhme R., Okamoto T. (eds.) Financial Cryptography and Data Security, pp. 315–332. Springer, New York (2015).
Sahai A., Waters B.: Fuzzy identity-based encryption. In: Cramer R. (ed.) Advances in Cryptology—EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, New York (2005).
Waters B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi S. (ed.) Advances in Cryptology—CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, New York (2009).
Waters B.: Functional encryption for regular languages. In: Safavi-Naini R., Canetti R. (eds.) Advances in Cryptology—CRYPTO. LNCS, vol. 7417, pp. 218–235. Springer, New York (2012).
Wee H.: Dual system encryption via predicate encodings. In: Lindell Y. (ed.) Theory of Cryptography (TCC). LNCS, vol. 8349, pp. 616–637. Springer, New York (2014).
Acknowledgements
This work was supported by the Netherlands Organisation for Scientific Research (Nederlandse Organisatie voor Wetenschappelijk Onderzoek, NWO) in the context of the CRIPTIM project. The authors additionally thank Bence Bakondi for his help in checking part of the MA-PES proofs and proofreading part of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by K. Matsuura.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
van de Kamp, T., Peter, A. & Jonker, W. A multi-authority approach to various predicate encryption types. Des. Codes Cryptogr. 88, 363–390 (2020). https://doi.org/10.1007/s10623-019-00686-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10623-019-00686-x





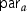 (describing a predicate) to the challenger. The challenger runs
(describing a predicate) to the challenger. The challenger runs 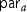 and gives the resulting public key
and gives the resulting public key 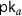 to the adversary. Additionally, it adds
to the adversary. Additionally, it adds
 to the set of uncorrupted authorities
to the set of uncorrupted authorities 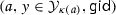 , where
, where 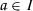 , to the challenger, the adversary requests the user secret key
, to the challenger, the adversary requests the user secret key 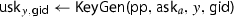 from the challenger. If the challenger has received a key request for the combination
from the challenger. If the challenger has received a key request for the combination 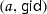 before, it aborts the game.
before, it aborts the game.