1 Introduction

Graphs are a powerful mechanism to represent data. Applications range from social networks, over gene analysis, to smart sensor systems. Due to the ubiquitous nature of graphs, analyzing them is a highly active research field with clustering/community detection being one of the most important and frequently applied tasks. While classical graph clustering approaches have considered merely structural information, in recent years attributed graph clustering has gained strong attention: it integrates additional attribute data about individual instances into the clustering task, to enhance its result. In a social network, e.g., the attributes describing each user’s characteristics might be combined with the underlying friendship network to form an attributed graph.Footnote 1

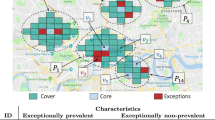
Figure 1 shows an example, in which each vertex is, for the sake of presentation, labeled with a set of items.

In the last few years, a number of clustering approaches for attributed graphs have been introduced. The discussion in the related work sections of publications on the topic tends to focus on whether different methods allow finding overlapping communities or not, or considers the technical methodology of the approaches (e.g., distance-based, model-based, random walk-based, etc.). In this survey, we choose a different way of looking at this issue based on the following observation: There are essentially two ways of exploiting attribute values. 1) to improve community detection by leveraging attribute value similarities, and 2) to derive a concrete description of discovered communities. The latter one enables us to better understand the structure of the detected communities, i.e.  in order to answer the question why this set of vertices is a reasonable community. This is particularly relevant not only relating to interpretability but also given the recently renewed focus on explainable results of data analysis processes.

To return to the example shown in Fig. 1, the rectangular boxes show two communities—two groups of vertices that are strongly connected to each other but that have few connections among each other. It can also be seen, however, that neither of those communities can be described by only one single set of items. The communities marked within grey rectangles, on the other hand, are still strongly connected within, weakly connected to each other, and describable with the items “A” (top-left community) and “B” (bottom-right community), respectively. Clearly, those are not the only two describable communities. It is easy to see that we can further find subcommunities which are described by more complex descriptions, e.g., considering the set of items “A, B” focussing on the four central vertices of the top-left community. Notably, the set of items “B, C” describes two communities, one on the left of the upper rectangle, and one in the center of the lower one, showing that descriptions are not necessarily unique to communities. Another example, referring to two communities described “C, D” is given in Fig. 2.

The approaches we discuss in this work do this at different levels of explicitness. There are approaches that identify for each community the attribute-value combinations that describe the community, returning ready-made descriptions. Additionally, there are approaches that explicitly identify attributes for which all vertices in a community have the same or similar values, without, however, also explicitly returning those values themselves. Finally, there are methods that derive indicators for the importance that attributes have for different communities but that would require post-processing of those indicators to enumerate the attributes. We discuss all three of those approaches. In summary, the main focus of this survey are methods that explicitly treat attributes and therefore (can) derive descriptive communities.

Indeed, this is in marked contrast to the survey by Bothorel et al. (2015), which discusses works that exploit the attribute information in graphs for improving clustering results, i.e.  improving community detection—by calculating distances or by augmenting density information. That is, the primary goal of these methods is to improve clustering performance by using multiple data sources—not to find descriptive communities. This also means that attributes are not treated explicitly but the information that is contained in them is mixed with the information inherent in the network. This takes the form of, for instance, defining quality measures that also take attribute similarity into account. Because the returned results of those approaches are only the communities, and no information about the contribution of the attributes is included, even post-processing might then not result in community descriptions. Therefore, these are outside the scope of our survey.

We start our discussion by introducing fundamental definitions in Sect. 2, followed by a concrete description of our selection methodology in Sect. 3. We then continue with an in-depth survey and categorization of description-oriented approaches in Sect. 4. Next, we briefly touch the aspect of evaluation and graph generation for attributed graphs in Sect. 5 before Sect. 6 concludes the survey with a summary and an outlook on further promising research directions.

Fig. 1
figure 1

Attributed graph with natural communities (indicated by rectangular box) and describable communities (grey background)

Full size image

2 Definitions

In the following, we outline and summarize fundamental definitions on graphs and communities.

Definition 1

(Graph) A graph is a tuple \(G = \langle V,E\rangle \), where V is a set of vertices and E a set of edges \(E\subseteq V\times V\). We refer to the number of edges a vertex \(v \in V\) is incident to as the vertex’ degree, \(\deg (v) = |\{(u,v) \in E\mid u \in V\}|\).

Definition 2

(Attributed Graph) An attributed graph is a graph G in which each \(v\in V\) is associated to a vector of attribute values \(\mathbf {x} = (x_1,\ldots ,x_d)\), and each edge \(e\in E\) to a vector \(\mathbf {y} = (y_1,\ldots ,y_t)\). We use \(a_i(v)\) to refer to the ith attribute value of a vertex v, and \(a_i(e)\) for the edge e respectively. We denote with \(A_V\) the set of vertex attributes, \(d = |A_V|\), and with \(A_E\) the set of edge attributes, \(t = |A_E|\). If \(|A_V| > 0,|A_E| = 0\), we refer to G as vertex-attributed; similarly if \(|A_V|=0,|A_E|>0\), we call it edge-attributed. If \(|A_V| = 0,|A_E| = 0\), then we refer to a plain graph.

Note, that this definition subsumes the widely used labeled graph definition, in which each vertex has a label, and each edge a label or a weight, as a special case.

Definition 3

(Projected Graph) Given a set of vertex attributes \(A_V\), an attributed graph G, a description \(p = \{A_1 \boxdot val_1, \ldots , A_d\boxdot val_d\}\) with \(A_i \in A_V\), \(val_j \in dom(A_j)\), and \(\boxdot \in \{<,\le ,=,\ge ,>\}\), a projected graph \(G_p\) is defined as follows: the subgraph \(G_p = \langle V_p,E_p\rangle \), \(V_p = \{v_j \in V\mid a_i(v_j) \boxdot val_i\}\), \(E_p =\{(u,v)\in E\mid u\in V_p, v\in V_p\}\), is referred to as the projected graph according to description p.

Fig. 2
figure 2

Projection of vertices of the graph shown in Fig. 1 labeled with “C, D”

Full size image

The graph shown in Fig. 2 depicts the result of projecting the graph shown in Fig. 1 on the description “C,D”. The projection acts as a filter on the vertices, and creates two communities that can both be described by a single set of items, which we also call an itemset.

Definition 4

(Graph partition) A partition of a graph G is a set of sets of vertices \(P_G = \{C_1,\ldots ,C_k\}\), with \(C_i \cap C_j = \emptyset \), and \(\bigcup _i C_i = C\); the individual \(C_i\) are also referred to as clusters or communities. The external (internal) degree of a vertex v refers to the number of edges connecting it to vertices in other (the same) communities:

  • \(deg_{ext}(v) = |\{(u,v)\in E\mid v\in C_i, u\in C_j, i\ne j\}|\,,\)

  • \(deg_{int}(v) = |\{(u,v)\in E\mid v\in C_i, u\in C_i\}|\,.\)

This definition is equivalent to the standard community detection definition, in which it is assumed that vertices can belong to a single community only, and that the graph is partitioned w.r.t. vertices, not w.r.t. edges. A consequence of the latter is that edges can have end points belonging to different communities, a characteristic that is exploited in calculating the quality of communities. When the assumption of strict vertex membership is relaxed, we refer to overlapping communities.

Overall, how to define communities is a rather complex topic, on which no consensus has been reached yet in the literature. We do not discuss all possible aspects but refer the interested reader to Fortunato (2010). An often enforced requirement is connectedness.

Definition 5

(Path) Given a graph G, a path of length \(p \in \mathbb {N}\) between two vertices v, u is a list of edges \(\langle (v_1,v_2),(v_2,v_3),\ldots ,(v_{p},v_{p+1})\rangle \) for distinct vertices \(v_i, v_i \in V\), i.e.  \(v_i \ne v_j, i \ne j,\) with \(v=v_1,u=v_{p+1}\).

Definition 6

(Connectedness/Reachability) A community \(C\subseteq V\) is considered connected if and only if there is a path between any two vertices \(v,u\in C\). The n-reachability of a community derives from the existence of a path of maximally length n between any two vertices in the community.

Yet given that reachability requirements could be satisfied by chains of vertices, stronger connectivity requirements are often imposed, such as that vertices need to form a k-core (Seidman 1983).

Definition 7

(k-Core) A community C is referred to as a k-Core if and only if \(deg_{int}(v) \ge k\) for every \(v \in C\), i.e.  each vertex is adjacent to at least k vertices of the community, and the community is maximal, i.e.  one cannot add additional vertices without violating that property.

A sufficient criterion for communities, finally, is that they are not only connected but have more internal connections than external ones, focusing on the density. This is in general related to the notion of density, e.g., (Charikar 2000; Diestel 2006), where we focus on edge density differentiating between edges internal/external to a given community.

Definition 8

((Edge) Density) Given a community \(V_i\), its intra-community density is the ratio of existing internal edges to the maximum possible number of internal edges:

$$\begin{aligned} \delta _{int}(C_i) = \frac{|\{(u,v)\mid u, v \in C_i\}|}{|C_i|(|C_i|-1)/2} = \frac{\sum _{v\in C_i} deg_{int}(v)}{|C_i|(|C_i|-1)}. \end{aligned}$$

Its inter-community density is the ratio of existing edges external edges to possible external edges:

$$\begin{aligned} \delta _{ext}(C_i) = \frac{|\{(u,v)\mid u\in C_i, v\in C_j, i\ne j\}|}{|C_i||V\setminus C_i|}= \frac{\sum _{v\in C_i} deg_{ext}(v)}{|C_i||V\setminus C_i|}. \end{aligned}$$

Such criteria can be absolute, using the definition above with a threshold, but also relative. There are too many different measures for relative density to list them here, which is why we only mention the widely-known modularity.

Definition 9

(Modularity) The modularity (Newman 2004; Newman and Girvan 2004) of a graph clustering with k communities \(C_1, \ldots , C_k\subseteq V\) focuses on the number of edges within a community and compares that with the expected such number given a null-model (i.e. , a corresponding random graph where the vertex degrees of G are preserved). It is given by

$$\begin{aligned} {Modularity(C_1, \ldots , C_k)} = \frac{1}{2m}\sum _{i=1}^k \sum _{u, v \in C_i}A_{u,v} - \frac{\deg (u)\deg (v)}{2m}\,, \end{aligned}$$

where \(A_{u,v}\) is the entry of the adjacency matrix referring to vertices u and v, and m is the number of edges of the whole graph.

Modularity has been used as optimization criterion driving a number of different classical community detection algorithms, i.e.  ones not taking attribute information into account.

When it comes to communities in attributed graphs, finally, structural density is not enough but vertices should also agree with respect to attributes, which can be assessed using a cohesion function (Moser et al. 2009), for instance.

Definition 10

(Cohesion function) A cohesion function is a function

$$\begin{aligned} f: P(V) \times P(A_V) \times \mathbb {R} \mapsto \{\text {true},\text {false}\} \end{aligned}$$

This function is required to satisfy both a maximality characteristic, i.e. for any set of vertices \(V'\) and set of attributes \(A_V'\), the latter contains all attributes for which \(V'\) is cohesive,

$$\begin{aligned}&(f(V',A'_V,\theta _s) = \mathrm {true} \wedge \not \exists A''_V\supset A'_V: f(V',A''_V,\theta _s) = \mathrm {true}) \Rightarrow \\&(f(V',A^{*}_V,\theta _s) = \mathrm {true} \Rightarrow A^{*}_V \subseteq A'_V), \end{aligned}$$

and an anti-monotonicity characteristic, i.e. given a set of vertices and a set of attributes that are cohesive, any subsets of those attributes/vertices stay cohesive:

$$\begin{aligned} f(V',A'_V,\theta _s) = \mathrm {true} \Rightarrow f(V'',A''_V,\theta _s) = \mathrm {true}, \forall V''\subseteq V', A''_{V} \subseteq A'_V \end{aligned}$$

Moser et al. (2009) also provide a concrete example of such a definition:

$$\begin{aligned} f(V',A'_V,\theta _s) = \forall A_i \in A'_V: |\max _{v\in V'} a_i(v) - \min _{v\in V'} a_i(v)| \le \theta _s \end{aligned}$$

As an illustration, consider Fig. 4: assuming \(\theta _s = 0.2\), \(A'_V\) for the upper shaded community would be \(\{A,B\}\), and for the lower shaded one \(\{A,B,C\}\).

3 Scope and overview: algorithm selection and categorization

The numerous techniques that are capable of putting a concrete description on discovered communities rely on the following mechanisms: (a) descriptions drive community detection—they are explicitly enumerated and restrict the vertices that can be used to form communities, (b) communities drive description formation—only those attribute values appearing for vertices in a community can be used, or (c) vertex and attribute membership probabilities for communities are optimized together. The first two approaches are not necessarily exclusive: as we will see later, some methods iterate between the two.

Hence, there are different options for constructing a description. Following the local pattern mining view (Hand 2002; Morik 2002; Morik et al. 2005), we focus on attributes, and attribute values; and a description combines these in a suitable way, e.g., by a conjunction, disjunction, or combination thereof. Also, please note that such descriptions (patterns) induce local structures that can be regarded as the result themselves, or can be integrated into a global approach that partitions the complete (graph) data space.

In this paper, we intend to explore these issues in detail, drawing explicit connections between the different methods, in the same spirit as has been done in (Novak et al. 2009) for supervised rule induction. A comparison between (Pool et al. 2014) and (Galbrun et al. 2014), for example, has been reported in the latter, showing that the description language and discriminative learning of the former leads to rather different results. However, the remaining techniques that we consider (see below), notwithstanding their similarities, have not been compared against each other before.

3.1 Algorithmic selection criteria

Our selection methodology is based on different aspects of description-oriented approaches, focusing on ideas from community detection and local pattern mining. For the latter, we first need to consider what makes up a local pattern. For that, we take some ideas and definitions from local pattern detection (Hand 2002; Morik 2002; Morik et al. 2005) which we also illustrate with an example below: According to Hand (2002) a local pattern can be regarded as a data vector exhibiting an anomalously high local density of data points compared to a background model. A local pattern has two important characteristics (Hand 2002; Klösgen 2002)—exemplified by the gray boxes in Fig. 3: (1) Local patterns cover small parts of the data space. (2) Local patterns deviate from the distribution of the population of which they are part. This deviation is usually measured by interestingness measures that contrast their behavior with that of the entire data or of other patterns.

As a simple illustration, consider Fig. 3: item “A” occurs in five vertices, item “B” in only four but the set of items “A,B” in four vertices out of 11. The expected frequency of that set of items is \((5 \cdot 4)/11 = 1.81\), so its observed frequency deviates clearly from the background distribution. The expected distribution of “C, D”, on the other hand, is \((9*9)/11 = 7.36\) and its observed distribution 7, it can therefore be regarded as not local.

Fig. 3
figure 3

Attributed graph with a community describable by a local, discriminative description (top), and one describable by a non-local, non-discriminative one (bottom)

Full size image

Therefore, in an unsupervised view on local pattern detection, no information but the data itself is given to find out what patterns may be present in the database. In contrast, a supervised view exploits some information about a concept of interest, or some target distribution in order to identify interesting patterns. Then, a local pattern can be regarded as a subgroup, for example, covering a set of instances that contrasts the global model, cf.  Morik (2002). If we consider the edge distribution to be the target distribution, “A,B” is also a local pattern from a supervised perspective since the described community is denser than expected.

Thus, our main focus in this survey is on techniques that have two important aspects in common: (1) Each algorithm identifies a subset of attribute dimensions, i.e.  attributes or attribute–values, that are relevant for the detected communities. (2) These subsets can be mapped to individual communities and their respective induced subgraphs (according to the idea of a local pattern).

While communities (i.e.  set of vertices) are local structures more or less by definition, different categories how to handle the attributes have been proposed. We are specifically interested in local methods where the focus is on subsets of attribute dimensions that are locally relevant. Also, we focus on methods that create concise attributive descriptions, in contrast to those approaches for which the derived descriptions often only take the form of certain values appearing in the majority of vertices in a community, instead of all of them.

Based on these intuitions we can identify three possible categories of algorithms/methods, allowing different potential for interpretation/description:

Fig. 4
figure 4

Projection of vertices of the graph shown in Fig. 4 labeled with “C, D”

Full size image
  1. 1.

    Description via (explicit) attribute selection: Considering Fig. 4, such a method would select \(\{A, B\}\) for the upper shaded community because their values are rather close for all vertices, as well as \(\{A,B,C\}\) for the lower one.

  2. 2.

    Description via (explicit) attribute-value selection: Considering Fig. 4, such a method could find the description \(A\ge 0.75 \wedge B=0.75\) for the upper shaded community, for instance, and \(B\le 0.3 \wedge C \le 0.65 \wedge C \ge 0.5\) for the lower one.

  3. 3.

    Description via implicit attribute selection/attribute weighting, i.e.  post-processing algorithmic output w.r.t. attributes: For Fig. 4, such a method could for instance derive the following weights:

Attribute

Upper communities

Lower communities

Complete

Shaded

Complete

Shaded

A

1.18

5

\(\infty \)

\(\infty \)

B

2

\(\infty \)

3.33

6.67

C

1.11

1.25

2.5

6.67

D

1.11

1.43

1.11

1.11

E

1.11

1.11

1.11

1.43

F

1.11

1.43

1.43

1.43

If we apply a threshold of 3 to select relevant attributes, the non-shaded upper community cannot be described at all, the shaded one by attributes “A” and “B”, the lower non-shaded one with “A” and “B”, and the shaded one with “A”, “B”, and “C”.

As we will outline in Sect. 4.3, the third option differs from the first two in that attributes are not explicitly selected. Instead, all methods discussed in that section derive some kind of indicator for attributes that could be post-processed to create a description.

Table 1 provides an overview of all considered techniques according to this selection methodology in the order as discussed above, i.e.  (1) attribute selection, (2) attribute-value selection, and (3) postprocessing. Here, the methods in the upper part (and the respective algorithms) will be discussed in detail in Sects. 4.1 and 4.2, and the ones in the lower part in Sect. 4.3, including explicit methods and options for postprocessing, as well as more implicit ones, i.e.  postprocessing left to the user.

Table 1 Categorization of algorithms (references in alphabetical order) based on the presented selection criteria. The top part shows the selected methods based on the inclusion criteria (1 and 2), while the bottom part includes the algorithms based on post-processing; the latter will be discussed in less detail in Sect. 4.3
Full size table

3.2 Algorithmic categorization

Considering the above selection of approaches based on their type of description, we provide in the following sections a more detailed categorization of the first two groups according to different criteria. While this section presents an overview on the given criteria, the next section summarizes and categorizes the techniques in more detail.

The first three subcategories concern the informativeness of the descriptions:

  1. 1.

    Does the technique select explicit attribute values as part of the description? All techniques surveyed in detail select a subset, or subspace, of attributes that are specific to the given communities. Not all of them also select the attribute values that describe the community. While those can usually be extracted in a post-processing step, given the community and the relevant attribute subspace, selecting values allows to present the user with communities and their actual descriptions directly.

  2. 2.

    Can found communities overlap? The ability to mine overlapping communities gives additional flexibility and therefore a higher chance to find high-quality results. On the other hand, this can lead to redundancy among communities and reduce interpretability.

  3. 3.

    Does the technique identify local patterns as descriptions, according to the criteria given in Sect. 3.1?

  • In addition, we assess whether found descriptions are discriminative, i.e.  whether they are found by contrasting different communities, or, in other words, whether knowing any of the descriptions allows one to recover a particular community. Notably, a non-local description will not be discriminative but a local one will not automatically help to discriminate between communities.

To illustrate this sub-characteristic, we can again consider Fig. 3. “A,B”, is discriminative in that this description occurs in all vertices of the upper highlighted community and only there. “C,D”, on the other hand, while correcting describing the lower highlighted community, also occurs in other vertices.

Additional categories concern the applicability of the techniques:

  1. 4.

    In which language are descriptions enumerated? Most commonly, description languages are sets of attributes, or conjunctions of attribute-value pairs, but more expressive languages are also possible.

  2. 5.

    Does the technique work on discrete attribute values, continuous ones, or both?

  3. 6.

    Are attributes considered on vertices, edges, or both?

  4. 7.

    Does the technique consider a single graph, or does it allow for multi-layer graphs/multiplex networks?

Finally, techniques can traverse the search space either heuristically or in an exact manner, trading off execution speed against qualitative guarantees. A summary of the approaches and their corresponding characteristics is presented in Table 2.

Table 2 Detailed algorithmic categorization of the algorithms discussed in Sects. 4.1 and 4.2
Full size table

4 Survey on relevant algorithms

In the following three subsections, we describe the selected techniques in more detail. We focus mainly on the first four characteristics (1.-4.) since the applicability criteria (4.-8.) do not lend themselves to much interpretation, and add some information about the traversal strategy. The order of the discussed techniques will be chronological, allowing the reader to follow the methodological developments.

4.1 Attribute selection

We subdivide techniques according to whether they select attribute values or not, and the first class of techniques identifies attribute subspaces that are relevant for particular communities but not the values of those attributes, which could however be derived in a post-processing step.

CoPaM Moser et al. (2009) propose to mine so-called cohesive patterns. A cohesive pattern is a tuple of a set attributes D and a subgraph \(G=(V,E)\) that fulfills three criteria: (1) D satisfies a cohesion function, (2) G is dense, and (3) G is connected.

To find patterns, the approach first removes all non-cohesive edges, i.e.  edges for which the vertices violate the cohesion function. The resulting connected components are processed independently in an Apriori-like manner, joining edges until they violate the cohesive pattern constraint, i.e.  the approach is community-driven. Attribute subspaces are identified via a maximal attribute subspace for a subgraph that is still cohesive. This implies several characteristics of the found patterns: as mentioned above, while attribute subspaces are explicitly selected, attribute values are not. Since edges are joined, it is possible that communities (vertex-)overlap. Furthermore, because attribute subspaces are chosen without recurrence to the full graph or even communities resulting from the same connected community, it is neither guaranteed that they are local, nor that they are discriminative.

GAMER Günnemann et al. (2010), Günnemann et al. (2013c) enhance the above principle by taking the possible redundancy of subgraphs into account. While CoPaM reports all maximal dense subgraphs—which might overlap to a high extent—the works by Günnemann et al. (2010), Günnemann et al. (2013c) focus on finding a set of non-redundant dense subgraphs with maximal interestingness. Here, interestingness can be any function taking the density, size, or number of attributes of the subgraph into account. Furthermore, the attributes of the community need to satisfy a cohesion function. To find clusters, a set enumeration tree operating on the set of vertices is exploited. The tree is traversed in a best-first approaches leading to an exact, non-heuristic solution.

EDCAR Günnemannet al. (2013a) use the same modeling approach as the work above. In contrast, however, they exploit a heuristic search principle, thus leading to much better scalability. More precisely, the set enumeration tree is explored via the GRASP (Greedy Randomized Adaptive Search) principle.

DB-CSC Deviating from the above scenario that the attribute values of a cluster are bounded by a specific interval, Günnemann et al. (2012), Günnemann et al. (2011) propose a density-based cluster definition. More precisely, in the selected attribute subspace the cluster needs to follow the well-known DBSCAN (Ester et al. 1996) clustering definition; while in the graph space an extension of k-cores has been proposed. Again, a set of non-redundant clusters is generated. Since DBSCAN allows to find arbitarly shaped clusters, no specific attribute values selection is provided per cluster. For finding the clusters, an apriori-like search principle combined with fixed-point iteration is exploited: starting with 1-dimensional clusters, higher dimensional clusters are iteratively constructed. Within each subspace, clusters can be detected via a fixpoint iteration. The subspaces are neither contrasted to the overall distribution, nor to other communities.

SSCG Günnemann et al. (2013b) extend the principle of spectral clustering to find subspace clusters in attributed graphs. Following the idea of subspace clustering, each cluster is associated with an individual set of relevant attributes. The selected attributes subsequently determine the similarity/weight of two adjacent vertices; that is, the affinity matrix used in spectral clustering is no longer static but depends on the selected subspaces. Overall, since neither the subspaces nor the clusters are known, both aspect are learned in a joint fashion by minimizing the so-called normalized subspace cut—an extension of the normalized cut. The approach does not identify local patterns but optimizes a global model. Since solving this optimization problem is NP-hard, the authors propose an approximative alternating optimization scheme.

ConSub Sánchez et al. (2013) use a Monte Carlo process to generate interval constraints on vertex attributes, which are used to create projected subgraphs. If the number of edges in the subgraph is higher than expected, a congruent subspace and corresponding subgraph has been found. To derive larger attribute subspaces, the authors propose a bottom-up, Apriori-like approach, similar to Günnemann et al. (2010). The authors view their approach rather as dimensionality reduction to make community (outlier) detection more effective.

There are two common threads to the techniques described so far: 1) descriptions drive community discovery, and 2) vertex attributes’ values’ similarity are considered, either via explicit thresholding or via clustering.

OSCom Starting from ego-networks, Du et al. (2017), Sun et al. (2018) apply a metric-based greedy strategy for detecting a set of subnetworks based on the respective attributed neighborhood, i.e.  the common attributes. After that, subcommunities are extracted, forming an overall supergraph. Finally, global semantic communities are identified on this supergraph.

MIMAG Orthogonal to the above works that mostly consider vertex-attributed graphs, Boden et al. (2013), Boden et al. (2012) focuse on edge-attributed graphs. Similar to the work of Günnemann et al. (2010) they build on extensions of quasi-cliques (i.e.  \(\delta _{int} \ge 0.5\)), now taking multiple graph layers into account and finding descriptions operating on the edge attributes. They propose a joint set enumeration tree to efficiently generate the communities in an informed best first search.

4.2 Attribute-value selection

The second class of techniques identifies both attributes and their relevant values directly. This obviates the need for a post-processing step of the discovered patterns to discover the appropriate values for the description. These techniques in many cases also use descriptions to drive community detection directly in order to establish a mapping between attribute dimensions and induced subgraph. The presented techniques below are somewhat younger than those proposed in the preceding section, and not surprisingly, there are clear connections to existing (local) pattern mining approaches.

SCPM Silva et al. (2012) binarize attributes, allowing them to treat attribut-value combinations as items, and apply frequent itemset mining to find promising candidates. By projecting the graph on the itemset, certain vertices will be removed, and the remaining connected components can be checked for the satisfaction of a minimum density constraint. By calculating upper bounds on the structural correlation of itemsets, the pruning capabilities of the approach are enhanced. Clearly, overlap is entirely possible for the communities found by this approach. In addition, while frequent patterns have been considered the first instance of local patterns in the literature, there is in fact no locality as such—a frequent pattern can be so frequent that it applies to different sections of the network. The literature on frequent patterns includes quite many examples of interestingness measures that relate the frequency of a pattern to background models (Vreeken and Tatti 2014).

ParaminerLC / MinerLC Soldano and Santini (2014) take this approach towards the logical conclusion in terms of frequent itemset mining, mining closed frequent itemsets as candidate descriptions. As in Silva et al. (2012), the graph is projected and connected components identified. A difference to the older technique is the use of the Galois operator on the candidate community, refining both community and description further. Both enumeration options, descriptions driving community discovery and communities driving description enumeration, are therefore interleaved.

A follow-up work (Soldano et al. 2015) turns the approach into an iterative one, treating found communities as networks in which sub-communities should be found. The similarity to the preceding approach means that Soldano et al. also inherit the limitations, such as the lack of true locality, while they also apply a different definition of local (abstract) patterns; essentially, they add the idea of graph abstractions which lead to further constrained subnetworks where communities are identified, as described above. This is implemented in the MinerLC algorithm (as an adaptation of the ParaminerLC algorithm) for undirected but also regarding directed networks (Soldano et al. 2017) and further graph abstractions. If a (strong) constraining graph abstraction constraint is applied (e.g., a k-core (Seidman 1983) constraint, where \(k > 1\)), then MinerLC basically focuses on those (locally) induced (constrained) subgraphs, thus advancing on purely frequent pattern based approaches for community detection on attributed networks. There are further extensions, e.g., regarding two-mode attributed networks (Soldano et al. 2019) with according constraints as well.

DCM Instead of starting from the description side, as the approaches discussed above, Pool et al. (2014) start with communities (as groups of vertices). The space of possible communities is larger than that of (conjunctive) descriptions, which means that they have to use a heuristic approach to find high-scoring ones, as is usual in community detection. Concretely, the approach starts from basic community candidates and greedily adds/removes vertices to improve a community score. Once those candidates stabilize, a pattern mining approach is used to find discriminative conjunctive patterns that predict vertices’ community membership. For each community, corresponding patterns are combined into a disjunction. This gives DCM a much richer description language than other methods discussed in this section. Vertices matching the description are included in the community (and non-matching ones removed). Since this will result in changes to the communities, the process is iterated until the community structure remains unchanged.

To ensure interpretability and control redundancy, the top-k communities are selected in a post-processing step, scored by a measure trading off community quality and description complexity, and controlled by a redundancy threshold on the Jaccard-similarity between communities vertices. The use of the discriminative pattern miner results in local patterns, and the redundancy threshold can be used to control community overlap—typically some overlap will be accepted.

Spectral, LDense, PivotGalbrun et al. (2014) also consider the problem of finding a set of at most k communities in a labeled graph, the cumulative densities of which are maximal. Vertices are described by labels, i.e.  by words. Since a bag-of-words shows the same characteristics as an itemset, the two problem settings are interchangeable. After translating their problem into the generalized maximum coverage problem and showing guarantees for a greedy algorithm that always adds the community having highest residual density, they propose three different techniques for finding the best community. To control redundancy, edges already included in communities are removed between iterations but can be re-added in later iterations to improve the formed communities.

  • One of the three techniques, Spectral, begins with calculating a similarity matrix between attribute-values, using Jaccard over vertices having the respective attribute values as similarity measure. Using the Laplacian of this matrix, attribute values are ordered according to the fiedler vector, and continuous intervals in this ordering considered to identify candidates for communities. The set of communities found by this approach can be vertex-overlapping but edge-overlap is explicitly excluded. Descriptions are not compared to those of other communities or the background graph.

  • Next, LDense, greedily—i.e.  heuristically—adds labels such that the corresponding vertex set has the highest density, until the description becomes too specific and matches no vertices anymore. Among the vertex sets formed during this search process, the densest (and its description) is included into the solution set.

  • The third approach, Pivot, heuristically forms communities, and after formation greedily constructs the description best matching it. As in Pool et al. (2014), vertices are then added and removed according to whether they match the description or not.

COMODO Atzmueller et al. (2016), propose a technique that explicitly aims at identifying local patterns. Inspired by subgroup discovery methods (Atzmueller 2015), their approach exhaustively enumerates conjunctions of attribute-value tests, and calculates (standard) community quality measures such as the modularity (Newman and Girvan 2004), the segregation index (Freeman 1978), or the inverted average out degree fraction (Yang and Leskovec 2012) on the corresponding communities, using upper bounds/optimistic estimates of these measures to aid in pruning. Comodo returns the top-k community patterns, with an optional redundancy check using a minimal improvement filter, e.g., Bayardo et al. (2000). The use of the community quality measure implies discriminative descriptions, such that a description covering several communities (components) receives a low score.

Atzmueller (2016) applies the algorithm also to more complex community quality functions for anomaly detection on labeled edges. The measures used to score descriptions compare community densities to that of the entire graph, satisfying the locality property. (Atzmueller et al. 2016; Atzmueller 2016) build on Atzmueller and Mitzlaff (2010), Atzmueller and Mitzlaff (2011), which used fewer measures. These papers precede the other works discussed in this section.

MinerLSDAtzmueller et al. (2018), Atzmueller et al. (2019) combine central ideas of the discussed COMODO (Atzmueller et al. 2016) and MinerLC (Soldano et al. 2015, 2017) algorithms for explicitly mining closed local patterns into the MinerLSD algorithm. It focuses both on local pattern mining, applying the standard local modularity metric (Newman 2004; Atzmueller et al. 2016), as possible for COMODO. In addition, MinerLSD can utilize graph abstractions which reduce graphs to k-core subgraphs (Soldano et al. 2015) for enabling further graph (interestingness) constraints. Then, local patterns are identified in a similar way as for MinerLC, while the applied community measure (local modularity) also favors discriminative descriptions as for COMODO. In particular, in order to prevent the typical pattern explosion in pattern mining, MinerLSD employs closed patterns. Then, the top-k patterns or those above a certain local modularity threshold are returned.

RoSi Kalofolias et al. (2019) apply the same approach as Comodo—treat community detection as subgroup discovery, let description enumeration drive discovery, use optimistic estimates—but propose a different, k-core based measure to discover more robust communities.

With the exception of DCM, all techniques in this section have very much in common with each other. SCPM, ParaminerLC, Spectral, LDense, and Pivot all use an itemset representation. While the conjunctions of attribute-value combinations used by Comodo, MinerLSD and RoSi would give them more flexibility in the case of numerical attributes, for discrete attributes these can be translated into items, as SCPM shows.

Most of the methods also let descriptions drive community discovery, although DCM and ParaminerLC interleave the two processes to a certain degree, and Pivot also starts from communities.

Table 3 Algorithmic categorization of the algorithms discussed in Sect. 4.3
Full size table

4.3 Attribute-guided graph mining (post-processing possibilities)

There are a number of techniques that employ option three in Sect. 3.1, i.e.  that utilize descriptive information for mining attributed graphs but do not explicitly select attributes or attribute values directly. The post-processing necessary would therefore be more extensive than in the case of the methods described in Sect. 4.1. Strictly speaking, most of these methods fall into the class of algorithms only exploiting attribute information to improve community detection that are described by Bothorel et al. (2015).

They differ from those methods that integrate attribute information via combined similarity functions or by introducing virtual vertices, however. In the former case, inverting the function to derive attribute importance is far from obvious, and in the latter there may be parts of a community that depend not at all on attribute vertices and others that fall apart if one removed these vertices.

Whereas the methods described in Sect. 4.2 explicitly enumerate both attributes and their values, and those in Sect. 4.1 at least return the attributes that need to be processed, the techniques in this section calculate the relative importance of attributes and this information has to be post-processed to derive descriptions. We therefore discuss most of these techniques in less detail, giving more attention to those that demonstrated this kind of post-processing.

We summarize the different methods in Table 3, indicating whether overlapping communities can be found, the used algorithmic technique, whether the method considers vertex or edge attributes, and whether attributes are discrete or continuous.

4.3.1 Explicit post-processing

We start with methods including explicit post-processing options.

GT model We begin with the work of McCallum et al. (2006), which has several interesting characteristics: (1) this is, to the best of our knowledge, the first such work, (2) they consider attributes on edges, not vertices, and (3) they explicitly post-process their results to retrieve the most relevant attributes. Concretely, they consider edges to be labeled with words, equivalent to items, and employ a topic model taking both labels and group membership into account. They extract the five to eight (depending on experimental setting) most relevant words from the topic model.

Block-LDA Balasubramanyan and Cohen (2011) combine block models with LDA to estimate both community membership and conditional topic distributions. By Gibbs sampling fifteen terms per community, they recover the most relevant terms.

CESNA Yang et al. (2013) use a model in which each vertex has community affiliation probabilities. Those affiliation probabilities predict both edges between vertices and attribute values, and the formation process consists of estimating those affiliations in such a way that they align with the edges and attributes observed in the data. Vertices are annotated with words or phrases, by exploiting the estimated conditional attribute weights, the authors extract the top attributes per community.

SENC Revelle et al. (2015) use a topic model for finding relevant topics for communities, as well as vertex membership probabilities, and employ an EM algorithm to optimize the two. They assume that vertices are described by words but differ from other work in using term weights (TFIDF), i.e.  switching from an itemset-like setting to one of numerical values. In the experimental evaluation, they present the top-40 terms per community according to learned conditional probabilities.

SCI Wang et al. (2016) employ non-negative matrix factorization (NMF). Vertices are described by bags-of-words, or itemsets, and the objective function combines topology and attribute similarity, using a trade-off parameter. As a result of their formulation, one of the derived matrices encodes the relationships between communities and attributes, which they exploit to extract the top-10 words.

ASCD The work of Qin et al. (2018) differs only to a small degree from SCI, mainly due to a focus on the fact that topology and shared attribute values can disagree, requiring the ability to fine-tune the trade-off between the two. They also extract the top-10 words.

4.3.2 Post-processing left to the user

Finally, we focus on approaches which do not include explicit post-processing, but leave that to the user for potentially extracting descriptions from the discovered communities. Steinhaeuser and Chavla (2008) annotate edges with the similarity between vertices’ attribute values, and group them into communities by thresholding those similarity values. By post-processing those communities, one could identify those attributes for which vertices are similar, as well as their values but the descriptions could be rather general. Li et al. (2010) first form communities using the Girvan-Newman method (Girvan and Newman 2002), and then identify relevant topics using Latent Dirichlet Allocation. Community detection is not informed by descriptions, and communities are not adjusted afterwards, however, meaning that descriptions could be unreliable or non-existent. Xu et al. (2012) propose building an MAP model over vertex attribute values to cluster vertices. While one could use model values to identify the most relevant attributes for each cluster, this is not an output of the approach. Smith et al. (2016) use a random-walk based method for identifying communities, and derive weights for attribute values based on their frequency in the network and the visitation frequency of the random walker. Those walks could be used to identify the description corresponding to a community in post-processing. Newman and Clauset (2016) use a Bayesian modeling technique based on stochastic block models for estimating community allocations including structural and attributive information, however no description is targeted. Baldominos et al. (2017) find stereotypes from communities detected using a modularity-optimizing algorithm by weighting labels according to the proportion of vertices in the community that support them. Conversely, Martínez-Seis (2017) use homophilic principles for obtaining a ranking of the attributes and then only apply those for community detection.

5 Evaluation and attributed graph generation

A glaring issue for finding descriptions of communities is evaluation. It is already a difficult challenge in the case of classical community detection because the ground truth is often not known, and evaluating whether the description of a community is appropriate is arguably even harder. There are some benchmark graph generators for creating plain networks, e.g., (Lancichinetti et al. 2008; Baldesi et al. 2018; Bojchevski et al. 2018), however, these do not take attribute information into account when creating the respective graphs.

Attributed graph generators aim to generate graphs following natural properties, e.g., power-law behaviour of the degree distribution. Existing works cover extensions of preferential attachment models (Zheleva et al. 2009; Lee et al. 2015), stochastic block models (Newman and Clauset 2016), or sampling approaches (Robles-Granda et al. 2016). Kaytoue et al. (2017) generate attributed graphs incorporating connected components with attributive structure. Furthermore, Serratosa (2018) presents a methodology for generating pairs of attributed graphs with a bounded graph edit distance, focussing on graph matching problems. Note that all these approaches for generating attributed graphs usually do not explicitely model communities. That is, the ‘true’ community structure will not be known for the generated graphs. In contrast, Largeron et al. (2015), Largeron et al. (2017) introduce a graph generator for attributed graphs that is able to incorporate community structure in the generated attributed graphs. However, the work does not propose how to find these communities.

It is worth noting that all attributed graph clustering models based on probabilistic generative models (e.g. Kim (2011), Yang et al. (2013), Xu et al. (2014)) could in principle also be used for generating data; usually, however, they are used for inference only.

6 Conclusion

Even though community detection in attributed graphs, and more concretely detecting communities and their descriptions together, is still a relatively young research direction, progress has been quick and a variety of mature techniques exist already. Surveying those approaches, we have identified three main families, one which employs subspace clustering ideas, i.e.  identifying those attribute-subspaces for which communities occur in the graph/network, a second one that adapts ideas developed in local pattern mining, and a third one that identifies the conditional importance of attributes in certain communities.

For the first class of methods, this allows exploiting the rich set of clustering techniques developed over several decades of research to address the similarity question in the attribute space, giving those approaches both high flexibility and good running times. Accordingly, multiple established clustering notions such as degree-based clustering, spectral clustering, or density-based clustering have been transfered to the attributed graph domain.

The second class of techniques has undergone the same progression as previous forms of pattern mining: starting from frequent patterns, via condensed representations, to exhaustive techniques employing sophisticated upper bounds to find the best patterns according to established quality criteria. As was to be expected, this progression happened much faster than for the original pattern mining settings, which also means that the field has completely caught up to the state of the art. Any future developments in pattern mining could be ported to the communities-plus-descriptions-setting without problems, giving rise to new powerful methods.

The third class draws liberally from anything that allows to assess attribute importance, whether via clustering, learning, probabilistic modeling etc. This gives that class the highest flexibility when it comes to integrating recent advances, and makes it the largest of the three algorithmic classes we considered. Yet matching attributes or their combinations to communities will in most cases only be approximate, as opposed to the more concrete descriptions of the other two classes.

One of the benefits of surveying the state of the art lies in seeing what potential research directions remain underexplored.

  1. 1.

    Existing approaches have arguably picked the low-hanging fruit in focusing on itemset or attribute-value annotations. Yet vertices could as well be described by sequences, graphs (molecules), or logical formulas. Given that clustering and pattern mining techniques for such complex data representations exist, there is no reason that one could not port existing work to the—admittedly challenging—problem setting of finding communities that have more complex descriptions than attribute-value combinations.

  2. 2.

    The real-life data captured in graphs is often not static but changes over time, whether in collaboration networks or networks modeling human mobility, e.g., Giannotti et al. (2016). Dynamic attributed graphs have been studied (Desmier et al. 2014; Boulicaut et al. 2016), as has community detection in dynamic graphs (Mucha et al. 2010; Nguyen et al. 2011; Xie et al. 2013) but the two have yet to be married.

  3. 3.

    While we pointed out a few approaches that address edge-attributed graphs, i.e.  characterizations of the relationships among entities, the vast majority of existing work focuses on vertex-attributed graphs, i.e.  characterizations of the entities themselves.

  4. 4.

    Richer network representations like multi-layer and multiplex networks (Mucha et al. 2010) provide a rich set of analysis options concerning the network structure which can be exploited in community detection.

  5. 5.

    Finally, while each of the previously mentioned future directions should be expected to be challenging, we fully expect that at some point they will be combined, if only because the problem setting offers a very rich descriptive model of the world. Finding communities in dynamic multiplex networks that can be described (and therefore understood) by complex descriptions on vertices and edges is the foreseeable endpoint of a development of which we have only sketched the beginnings in this work.

It is not entirely clear, however, whether developments in this direction can be expected anytime soon. Research on graph and network analysis has exceedingly focussed on embedding techniques in recent years, even if it is not clear that such techniques represent clear improvements (Mara et al. 2020). It is therefore entirely possible that we will see the same development as in deep learning-based machine learning: opaque models are learned, and symbolic methods added afterwards to make those models interpretable, instead of deriving interpretable results directly.