Keywords

1 Introduction

Identifying community structure in graphs is a challenging task in many applications: computer networks, social networks, etc. Graphs have an expressive power that enables an efficient representation of relations between objects as well as their properties. Attributed graphs where vertices or edges are endowed with a set of attributes are now widely available, many of them being created and curated by the semantic web community. While these so-called knowledge graphsFootnote 1 contain a lot of information, their exploration can be challenging in practice. In particular, common approaches to find communities in such graphs rely on rather complex transformations of the input graph.

In this paper, we propose a decision tree based method that we call GraphTrees (GT) to compute dissimilarities between vertices in a straightforward manner. The paper is organized as follows. In Sect. 2, we briefly survey related work. We present our method in Sect. 3, and we discuss its performance in Sect. 4 through an empirical study on real and synthetic datasets. In the last section of the paper, we present a brief discussion of our results and state some perspectives for future research.

Main Contributions of the Paper:

  1. 1.

    We propose a first step to bridge the gap between random decision trees and graph clustering and extend it to vertex attributed graphs (Subsect. 4.1).

  2. 2.

    We show that the vertex-vertex dissimilarity is meaningful and can be used for clustering in graphs (Subsect. 4.2).

  3. 3.

    Our method GT applies directly on the input graph without any preprocessing, unlike the many community detection in vertex-attributed graphs that rely on the transformation of the input graph.

2 Related Work

Community detection aims to find highly connected groups of vertices in a graph. Numerous methods have been proposed to tackle this problem [1, 8, 24]. In the case of vertex-attributedFootnote 2 graph, clustering aims at finding homogeneous groups of vertices sharing (i) common neighbourhoods and structural properties, and (ii) common attributes. A vertex-attributed graph is thought of as a finite structure \(G=(V, E, A)\), where

  • \(V=\{v_1,v_2,\dots ,v_n\}\) is the set of vertices of G,

  • \(E \subseteq V \times V \) is the set of edges between the vertices of V, and

  • \(A=\{x_1,x_2,\dots ,x_n\}\) is the set of feature tuples, where each \(x_i\) represents the attribute value of the vertex \(v_i\).

In the case of vertex-attributed graphs, the problem of clustering refers to finding communities (i.e., clusters), where vertices in the same cluster are densely connected, whereas vertices that do not belong to the same cluster are sparsely connected. Moreover, as attributes are also taken into account, the vertices in the same cluster should be similar w.r.t. attributes.

In this section, we briefly recall existing approaches to tackle this problem.

Weight-Based Approaches. The weight-based approach consists in transforming the attributed graphs in weighted graphs. Standard clustering algorithms that focus on structural properties can then be applied.

The problem of mapping attribute information into edge weight have been considered by several authors. Neville et al. define a matching coefficient [20] as a similarity measure S between two vertices \(v_i\) and \(v_j\) based on the number of attribute values the two vertices have in common. The value \(S_{v_i, v_j}\) is used as the edges weight between \(v_i\) and \(v_j\). Although this approach leads to good results using Min-Cut [15], MajorClust [26] and spectral clustering [25], only nominal attributes can be handled. An extended matching coefficient was proposed in [27] to overcome this limitation, based on a combination of normalized dissimilarities between continuous attributes and increments of the resulting weight per pair of common categorical attributes.

Optimization of Quality Functions. A second type of methods aim at finding an optimal clustering of the vertices by optimizing a quality function over the partitions (clusters).

A commonly used quality function is modularity [21], that measures the density differences between vertices within the same cluster and vertices in different clusters. However, modularity is only based on the structural properties of the graph. In [6], the authors use entropy as the quality metric to optimize between attributes, combined with a modularity-based optimization. Another method, recently proposed by Combe et al. [5], groups similar vertices by maximizing both modularity and inertia.

However, these methods suffer from the same drawbacks as any other modularity optimization based methods in simple graphs. Indeed, it was shown by [17] that these methods are biased, and do not always lead to the best clustering. For instance, such methods fail to detect small clusters in graphs with clusters of different sizes.

Aggregated Distance Measures. Another type of methods used to find communities in vertex-attributed graphs is to define an aggregated vertex-vertex distance between the topological distance and the symbolic distance. All these methods express a distance \(d_{v_i,v_j}\) between two vertices \(v_i\) and \(v_j\) as \(d_{v_i,v_j} = \alpha d_T(v_i,v_j) + (1-\alpha ) d_S(v_i,v_j)\) where \(d_T\) is a structural distance and \(d_S\) is a distance in the attribute space. These structural and attribute distances represent the two different aspects of the data. These distances can be chosen from the vast number of available ones in the literature. For instance, in [4] a combination of geodesic distance and cosine similarities are used by the authors. The parameter \(\alpha \) is useful to control the importance of each aspect of the overall similarity in each use case. These methods are appealing because once the distances between vertices are obtained, many clustering algorithms that cannot be applied to structures such as graphs can be used to find communities.

Miscellaneous. There is yet another family of methods that enable the use of common clustering methods on attributed graphs. SA-cluster [3, 32] is a method performing the clustering task by adding new vertices. The virtual vertices represent possible values of the attributes. This approach, although appealing by its simplicity, has some drawbacks. First, continuous attributes cannot be taken into account. Second, the complexity can increase rapidly as the number of added vertices depends on the number of attributes and values for each attribute. However, the authors proposed an improvement of their method named Inc-Cluster in [33], where they reduce its complexity.

Some authors have worked on model-based approaches for clustering in vertex-attributed settings. In [29], the authors proposed a method based on a bayesian probabilistic model that is used to perform the clustering of vertex-attributed graphs, by transforming the clustering problem into a probabilistic inference problem. Also, graph embeddings can be used for this task of vertex-attributed graph clustering. Examples of these techniques include node2vec [13] or deepwalk [23], and aim to efficiently learn a low dimensional vector representation of each vertex. Some authors focused on extending vertex embeddings to vertex-attributed networks [11, 14, 30].

In this paper, we take a different approach and present a tree-based method enabling the computation of vertex-vertex dissimilarities. This method is presented in the next section.

3 Method

Previous works [7, 28] have shown that random partitions of data can be used to compute a similarity between the instances. In particular, in Unsupervised Extremely Randomized Trees (UET), the idea is that all instances ending up in the same leaves are more similar to each other than to other instances. The pairwise similarities s(i, j) are obtained by increasing s(i, j) for each leaf where both i and j appear. A normalisation is finally performed when all trees have been constructed, so that values lie in the interval [0, 1]. Leaves, and, more generally, nodes of the trees can be viewed as partitions of the original space. Enumerating the number of co-occurrences in the leaves is then the same as enumerating the number of co-occurrence of instances in the smallest regions of a specific partition.

So far, this type of approach has not been applied to graphs. The intuition behind our proposed method, GT, is to leverage a similar partition in the vertices of a graph. Instead of using the similarity computation that we described previously, we chose to use the mass-based approach introduced by Ting et al. [28] instead. The key property of their measure is that the dissimilarity between two instances in a dense region is higher than the same interpoint dissimilarity between two instances in a sparse region of the same space. One of the interesting aspects of this approach is that a dissimilarity is obtained without any post-processing.

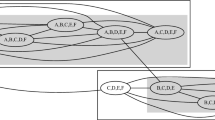
Let \(H \in \mathcal {H}(D)\) be a hierarchical partitioning of the original space of a dataset D into non-overlapping and non-empty regions, and let R(x, y|H) be the smallest local region covering x and y with respect to H. The mass-based dissimilarity \(m_e\) estimated by a finite number t of models – here, random trees – is given by the following equation:

$$\begin{aligned} m_e(x,y|D)=\frac{1}{t}\sum _{i=1}^t \tilde{P}(R(x,y|H_i)) \end{aligned}$$
(1)

where \(\tilde{P}(R)=\frac{1}{|D|} \sum _{z \in D} \mathbbm {1} (z \in R) \). Figure 1 presents an example of a hierarchical partition H of a dataset D containing 8 instances. These instances are vertices in our case. For the sake of the example, let us compute \(m_e(1,4)\) and \(m_e(1,8)\). We have \(m_e(1,4) = \frac{1}{8}(2) = 0.25\), as the smallest region where instances 1 and 4 co-appear contains 2 instances. However, \(m_e(1,8) = \frac{1}{8}(8) = 1\), since instances 1 and 8 only appear in one region of size 8, the original space. The same approach can be applied to graphs.

Fig. 1.
figure 1

Example of partitioning of 8 instances in non-overlapping non-empty regions using a random tree structure. The blue and red circles denote the smallest nodes (i.e., regions) containing vertices 1 and 4 and vertices 1 and 8, respectively. (Color figure online)

Full size image

Our proposed method is based on two steps: (i) obtain several partitions of the vertices using random trees, (ii) use the trees to obtain a relevant dissimilarity measure between the vertices. The Algorithm 1 describes how to build one tree, describing one possible partition of the vertices. Each tree corresponds to a model of (1). Finally, the dissimilarity can be obtained using Eq. 1.

figure a

The computation of pairwise vertex-vertex dissimilarities using Graph Trees and the mass-based dissimilarity we just described has a time complexity of \(O(t\cdot \varPsi log(\varPsi ) + n^2 t log(\varPsi ))\) [28], where t is the number of trees, \(\varPsi \) the maximum height of the trees, and n is the number of vertices. When \(\varPsi<< n\), this time complexity becomes \(O(n^2)\).

To extend this approach to vertex-attributed graphs, we propose to build a forest containing trees obtained by GT over the vertices and trees obtained by UET on the vertex attributes. We can then compute the dissimilarity between vertices by averaging the dissimilarities obtained by both types of trees.

In the next section, we evaluate GT on both real-world and synthetic datasets.

4 Evaluation

This section is divided into 2 subsections. First, we assess GT’s performance on graphs without vertex attributes (Subsect. 4.1). Then we present the performance of our proposed method in the case of vertex-attributed graphs (Subsect. 4.2). An implementation of GT, as well as these benchmarks are available on https://github.com/jdalleau/gt.

4.1 Graph Trees on Simple Graphs

We first evaluate our approach on simple graphs with no attributes, in order to assess if our proposed method is able to discriminate clusters in such graphs. This evaluation is performed on both synthetic and real-world graphs, presented Table 1.

Table 1. Datasets used for the evaluation of clustering on simple graphs using graph-trees
Full size table

The graphs we call SBM are synthetic graphs generated using stochastic block models composed of k blocks of a user-defined size, that are connected by edges depending on a specific probability which is a parameter. The Football graph represents a network of American football games during a given season [12]. The Email-Eu-Core graph [18, 31] represents relations between members of a research institution, where edges represents communication between those members. We also use a random graph in our first experiment. This graph is an Erdos-Renyi graph [10] generated with the parameters \(n=300\) and \(p=0.2\). Finally, the PolBooks data [16] is a graph where nodes represent books about US politics sold by an online merchant and edges books that were frequently purchased by the same buyers.

Our first empirical setting aims to compare the differences between the mean intracluster and the mean intercluster dissimilarities. These metrics enable a comparison that is agnostic to a subsequent clustering method.

The mean difference is computed as follows. First, the arithmetic mean of the pairwise similarities between all vertices with the same label is computed, corresponding to the mean intracluster dissimilarity \(\mu _{intra}\). The same process is performed for vertices with a different label, giving the mean intercluster similarity \(\mu _{inter}\). We finally compute the difference \(\varDelta = |\mu _{intra}-\mu _{inter}|\). In our experiments, this difference \(\varDelta \) is computed 20 times. \(\bar{\varDelta }\) denotes the mean of differences between runs, and \(\sigma \) its standard deviation. The results are presented Table 2. We observe that in the case of the random graph, \(\bar{\varDelta }\) is close to 0, unlike the graphs where a cluster structure exists. A projection of the vertices based on their pairwise dissimilarity obtained using GT is presented Fig. 2.

Table 2. Mean difference between intercluster and intracluster similarities in different settings.
Full size table
Fig. 2.
figure 2

Projection of the vertices obtained using GT on (left) a random graph, (middle) an SBM generated graph (middle) and (right) the football graph. Each cluster membership is denoted by a different color. Note how in the case of the random graph, no clear cluster can be observed. (Color figure online)

Full size image

We then compare the Normalized Mutual Information (NMI) obtained using GT with the NMI obtained using two well-known clustering methods on simple graphs, namely MCL [8] and Louvain [1]. NMI is a clustering quality metric when a ground truth is available. Its values lie in the range [0, 1], with a value of 1 being a perfect matching between the computed clusters and the reference one. The empirical protocol is the following:

  1. 1.

    Compute the dissimilarity matrices using GT, with a total number of trees \(n_{trees}=200\).

  2. 2.

    Obtain a 2D projection of the points using t-SNE [19] (\(k=2\)).

  3. 3.

    Apply k-means on the points of the projection and compute the NMI.

We repeated this procedure 20 times and computed means and standard deviations of the NMI.

The results are presented Table 3. We compared the mean NMI using the t-test, and checked that the differences between the obtained values are statistically significant.

We observe that our approach is competitive with the two well-known methods we chose in the case of non-attributed graphs on the benchmark datasets. In one specific case, we even observe that Graph trees significantly outperforms state of the art results, on the graphs generated by the SBM model. Since the dissimilarity computation is based on the method proposed by [28] to find clusters in regions of varying densities, this may indicate that our approach performs particularly well in the case of clusters of different size.

Table 3. Comparison of NMI on benchmark graph datasets. Best results are in boldface.
Full size table

4.2 Graph Trees on Attributed Graphs

Now that we have tested GT on simple graphs, we can assess its performance on vertex-attributed graphs. The datasets that we used in this subsection are presented Table 4.

WebKB represents relations between web pages of four universities, where each vertex label corresponds to the university and the attributes represent the words that appear in the page. The Parliament dataset is a graph where the vertices represent french parliament members, linked by an edge if they cosigned a bill. The vertex attributes indicate their constituency, and each vertex has a label that corresponds to their political party.

Table 4. Datasets used for the evaluation of clustering on attributed graphs using GT
Full size table

The empirical setup is the following. We first compute the vertex-vertex dissimilarities using GT, and the vertex-vertex dissimilarities using UET. In this first step, a forest of trees on the structures and a forest of trees on the attributes of each vertex are constructed. We then compute the average of the pairwise dissimilarities. Finally, we then apply t-SNE and use the k-means algorithm on the points in the embedded space. We set k to the number of clusters, since we have the ground truths. We repeat these steps 20 times and report the means and standard deviations. During our experiments, we found out that preprocessing the dissimilarities prior to the clustering phase may lead to better results, in particular with Scikit learn’s [22] QuantileTransformer. This transformation tends to spread out the most frequent values and to reduce the impact of outliers. In our evaluations, we performed this quantile transformation prior to every clustering, with \(n_{quantile}=10\).

The NMI obtained after the clustering step are presented in Table 5.

Table 5. NMI using GT on the structure only, UET on the attributes only and GT+UET. Best results are indicated in boldface.
Full size table

We observe that for two datasets, namely WebKB and HVR, considering both structural and attribute information leads to a significant improvement in NMI. For the other dataset considered in this evaluation, while the attribute information does not improve the NMI, we observe that is does not decrease it either. Here, we give the same weight to structural and attribute information.

In Fig. 3 we present the projection of the WebKB dataset, where we observe that the structure and attribute information both bring a different view of the data, each with a strong cluster structure.

Fig. 3.
figure 3

Projection of the WebKB data based on the dissimilarities computed (left) using GT on structural data, (middle) using UET on the attributes data and (right) using the aggregated dissimilarity. Each cluster membership is denoted by a different color. (Color figure online)

Full size image

HVR and Parliament datasets are extracted from [2]. Using their proposed approach, they obtain an NMI of 0.89 and 0.78, respectively. Although the NMI we obtained using our approach are not consistently better in this first assessment, the methods still seems to give similar results without any fine tuning.

5 Discussion and Future Work

In this paper, we presented a method based on the construction of random trees to compute dissimilarities between graph vertices, called GT. For vertex clustering purposes, our proposed approach is plug-and-play, since any clustering algorithm that can work on a dissimilarity matrix can then be used. Moreover, it could find application beyond graphs, for instance in relational structures in general.

Although the goal of our empirical study was not to show a clear superiority in terms of clustering but rather to assess the vertex-vertex dissimilarities obtained by GT, we showed that our proposed approach is competitive with well-known clustering methods, Louvain and MCL. We also showed that by computing forests of graph trees and other trees that specialize in other types of input data, e.g, feature vectors, it is then possible to compute pairwise dissimilarities between vertices in attributed graphs.

Some aspects are still to be considered. First, the importance of the vertex attributes is dataset dependent and, in some cases, considering the attributes can add noise. Moreover, the aggregation method between the graph trees and the attribute trees can play an essential role. Indeed, in all our experiments, we gave the same importance to the attribute and structural dissimilarities. This choice implies that both the graph trees and the attribute trees have the same weight, which may not always be the case. Finally, we chose here a specific algorithm to compute the dissimilarity in the attribute space, namely, UET. The poor results we obtained for some datasets may be caused by some limitations of UET in these cases.

It should be noted that our empirical results depend on the choice of a specific clustering algorithm. Indeed, GT is not a clustering method per se, but a method to compute pairwise dissimilarities between vertices. Like other dissimilarity-based methods, this is a strength of the method we propose in this paper. Indeed, the clustering task can be performed using many algorithms, leveraging their respective strengths and weaknesses.

As a future work, we will explore an approach where the choice of whether to consider the attribute space in the case of vertex-attributed graphs is guided by the distribution of the variables or the visualization of the embedding. We also plan to apply our methods on bigger graphs than the ones we used in this paper.