1 Introduction

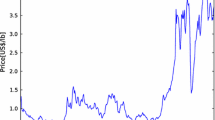
As one of the most widely traded commodities in the world, the coffee industry has around a USD 83 billion market value, with 70 per cent of production exported and a 5.5 per cent CAGR from 2018 to 2023. However, as the retail market booms, the international commodity price for coffee is reaching similar levels to those during the 2000–2004 coffee crisis. In September of 2018, the ICO Composite price for coffee reached a level below USD 1.00/lb for the first time in over 13 years, due to the long lasting effects of the last coffee price crisis. With a mean production cost of USD 0.95/lb, a price shock on coffee bears a dire financial and humanitarian burden on producers that counterparts within the coffee supply chain do not. Hence, there is worldwide concern whether the current price shock on coffee will be permanent, and if not, how long it will take for global prices to revert to a sustainable price level.

Hence, we investigate in this paper persistence within coffee prices by using fractional integration methods, which are appropriate to determine the nature and the duration of shocks. The study will utilize monthly data from the ICO of five coffee price categories (ICO Composite, Brazilian Naturals, Other Milds, Colombian Milds, and Robusta) between the period of 1965 and 2020 so as to encompass different coffee-producing countries more effectively throughout the study. The overall purpose of this paper is to test whether the different coffee prices have long memory, meaning that in the case of a price shock, prices will take a very long time to disappear. To test the level of persistence within the price levels of the different coffee varieties, using fractional integration will allow us to test for an order of integration in the range of values [0, 1] but also above one, rather than the traditional application of ARMA/ARIMA models and others in which only the values zero (for I(0) stationary) and one (for I(1) non-stationary) are available. In fractional integration, a value equal to or higher than one for the order of integration entails a permanent effect on the price level in the case of an exogenous shock. On the other hand, if the order of integration is below one, this would entail transitory effects and the price would settle back towards the mean level. However, the degree to which the price level reverts to the mean depends on how close the order of integration is to zero. The closer the order of integration is to zero, the faster the price will revert to its mean, and vice versa. The results of the fractional integration test could be useful regarding what types of measures should be taken in the case of an exogenous shock in coffee prices. In the case where the order of fractional integration is closer to zero, this would imply that between little and no initiative should be taken since prices are expected to revert to their original level quickly. However, if the prices are above, equal to, or close to one, it would be necessary for action to be taken to prevent a permanent effect from the shock and for prices to revert to their mean level. Thus, this paper is univariate in nature and does not consider relevant factors such as coffee farmers' salaries, climate change, etc. that might influence coffee prices. In that respect, we follow the line of research of “let the data speak by themselves “, investigating if shocks in the series have permanent or transitory effects based on their own history.

There are two main innovations in the present work. Firstly, the use of fractional integration as a methodological tool, that, though not new, has not been very much used in the analysis of persistence in commodity prices. This methodology overcomes the classical ones based on unit roots and that simply use integer degrees of differentiation. Moreover, within the context of fractional integration, we use a testing procedure (Robinson, 1994) that has numerous advantages with respect to other approaches, in particular, the fact that it does not require preliminary differentiation in the case of nonstationary data. Among other things, it is also the most efficient method in the Pitman sense against local departures from the null, which is very relevant in the context of fractional differentiation. The second contribution is the empirical application based on five different groups of coffee prices, and the results reported, which show strong evidence against the hypothesis of trend stationary models and reversion to the mean.

The paper is organized as follows: Sect. 2 presents the relevant literature on coffee price modelling and persistence, as well as presenting applications of fractional integration for other commodities; Sect. 3 displays the methodology with which we gather our results; Sect. 4 describes the data utilized within the study; Sect. 5 presents the empirical results; and finally, Sect. 6 offers some concluding remarks.

2 Literature Review

Over the last two decades, there has been an array of published literature focused on modelling coffee prices. Specifically, there has been a large emphasis on cointegration analysis when it comes to modelling coffee prices. Vogelvang (1992) conducted a study on modelling the spot prices of four different coffee groups using 1960–1982 quarterly data and tested for long-run relationships between those coffee types. The study conducted Johansen (1988) and Johansen and Juselius’ (1989) cointegration tests, in which they determined the number of cointegrating relationships between the coffee types. The study found strong evidence of two cointegrated vectors: (1) a long-run relationship between Colombian Milds (CM) and Other Milds (OM), and (2) one between Robustas (ROB), Other Milds (OM), and Colombian Milds (CM). Otero and Milas (2001) conducted similar tests to that of Vogelvang (1992), however using more recent quarterly data (1962–1998). The authors argue that due to exogenous factors such as adverse weather conditions and then-newly established trade agreements, a new set of cointegrating relationships likely occurred. As expected, the authors found the following new cointegrated vectors: (1) a long-run relationship between three types of Arabica coffees (Unwashed Arabicas UA, Other Milds OM, Colombian Milds COM), and (2) one between Unwashed Arabicas UA and Robustas ROB. Furthermore, Otero and Milas (2001) also tested for the degree of persistence of the two cointegrated vectors by using a persistent profile analysis (Pesaran & Shin, 1996) to determine the speed of convergence towards their long-run equilibrium after a price shock. The results showed full adjustments for both vectors within a year.

The paper by Milas et al. (2004) evaluates the forecast performance of multivariate linear and non-linear error correction models for spot prices of different types of coffee. The study uses multivariate non-linear error correction models, allowing the examination of asymmetric effects (positive and negative deviations from equilibrium) and size effects (small and large discrepancies). The main findings indicate that different coffee type prices are highly integrated, prices tend to adjust back to equilibrium more slowly when too high and faster when too low, and that adjustment is faster when the deviations from the equilibrium get larger. Furthermore, the authors find that multivariate linear and non-linear error correction models performed better for Colombian Milds but not for the other types when compared to the random walk model.

Naveena et al. (2015) also examined cointegration to study price transmission between Indian coffee prices (Arabica and Robusta) on global coffee prices by using Johansen's (1988) cointegration test and Engle and Granger's (1987) cointegration and error-correction model. They found that although a long-run relationship existed between both Indian coffees and their respective world price, the coefficient estimate was insignificant enough to infer a price transmission mechanism. The same authors also tested for the speed of adjustment towards the long-run equilibrium and concluded that the speed of convergence was remarkably slow for both Arabica and Robusta (18% and 12.3% monthly adjustments, respectively).

Yeshiwas and Tesfa (2020) modelled coffee Arabica and Brent Crude Oil price volatility using GARCH models for each commodity. The study did not test for the degree of persistence aside from utilizing the traditional unit root tests for stationarity, for which they found coffee prices to follow GARCH (1,1). However, the study does not test for the degree of persistence aside from utilizing the traditional unit root tests for stationarity or differentiates among the different types of coffee prices.

A more recent paper by Otero et al. (2022) utilizes 1962–2018 coffee data to test how increasing the sample data’s frequency (monthly, quarterly, and yearly) and span affects Johansen’s (1988, 1995) multivariate cointegration Trace test, and the bootstrap and wild bootstrap implementations discussed by Cavaliere et al., (2012, 2014). The authors study these effects by implementing a set of Monte Carlo simulations. The results show that cointegration is not present in the shortest data span, even when extending the frequency. However, as the span is extended, the authors find two cointegration vectors with quarterly and monthly data and one vector with annual data. Although the authors find supporting evidence for the importance of the frequency and span of the data and its effect on the power of Johansen’s (1988, 1995) cointegration test, they do not discuss the cointegrated relationships between the specific coffee price types.

Thus, most of the works that have since been published have focused on the multivariate approach of testing for cointegration and used unit root methods for testing persistence. Hence, few have utilized a univariate approach for testing the degree of stationarity of coffee utilizing fractional integration. However, fractional integration has been used frequently to test for persistency within commodity prices (Crato & Rothman, 1994; Cunado et al., 2012; Gil-Alana & Robinson, 1997; Wang & Tomek, 2007; etc.) as well as in other disciplines like tourism (Gil-Alana & Huijbens, 2018), climatology (Vera-Valdes, 2021), environmental studies (Barassi et al., 2011), etc.

3 Methodology

As earlier mentioned, we use fractional integration or I(d) techniques in the analysis of persistence in the coffee prices. This is a very appropriate technique for analysing shocks if we want to know if they will be permanent or be of a transitory nature.

An I(d) process {x(t), t = 1, 2, …] is defined by using the lag operator L (Lkx(t) = xt(t-k)) as:

$$ (1\,\, - \,\,L)^{d} \,x(t)\,\,\, = \,\,\,u(t),\,\,\,\,\,\,t\,\,\, = \,\,\,1\,,\,\,2\,,\,\,...\,, $$
(1)

where u(t) is integrated of order 0, or an I(0) process, also termed short memory and that is characterized because its spectral density function is positive and bounded at all frequencies in the spectrum. In this context, if u(t) is, for example, an ARMA(p,q) process of the form:

$$ \varphi_{p} (L)\,u(t)\,\,\, = \,\,\,\theta_{q} (L)\,\varepsilon (t),\,\,\,\,\,\,t\,\,\, = \,\,\,1\,,\,\,2\,,\,\,...\,, $$
(2)

with white noise ε(t), then, x(t) is said to be a fractionally integrated ARMA, i.e., ARFIMA(p, d, q) model, where p and q are the orders respectively for the AR and MA parts, and d is the number of differences required in the series to get I(0).

Allowing d to be a real value, we can consider a wide range of alternatives, including.

i. anti-persistence (if d < 0),

ii. short memory (d = 0),

iii. stationary long memory (0 < d < 0.5),

iv. nonstationary with mean reversion (0.5 ≤ d < 1),

v. unit roots (d = 1),

and

vi. explosive patterns (d > 1).

Thus, from a policy perspective, the crucial value is 1, since reversion to the mean occurs as long as d is smaller than and closer to 1 from below, the longer-lasting the effects of the shocks are. Note that the I(d) model specified above is more general and flexible than other approaches that simply consider integer degrees of differentiation. Thus, the unit root methods, widely employed in the literature for testing nonstationary data (e.g., Dickey and Fuller, ADF, 1979; Phillips and Perron, PP, 1988; Elliot et al., ERS, 1996; etc.) can be viewed as particular cases of our model when d = 0 or 1. Moreover, it has been proved that the above-mentioned unit root tests have very low power when the true data generating process is fractionally integrated (see, e.g., Dickey and Rudebusch, 1989; Hassler & Wolters, 1994; Lee & Schmidt, 1996), this being one of the main arguments for the use of fractional integration.

The estimation is carried out based on the Whittle function, which is an approximation to the likelihood function, expressed in the frequency domain as in Dahlhaus (1989) by using a testing approach developed by Robinson (1994). Following this approach, we test the null hypothesis:

$$ {\text{H}}_{{\text{o}}} :{\text{d}} = {\text{d}}_{{\text{o}}} , $$
(3)

in a fractional integration framework as the one reported in Eq. (1) where do can be any real value, including the value 1 for the unit root case but also fractional alternatives. Robinson’s (1994) method is based on the Lagrange Multiplier (LM) principle and thus use the null hypothesis in the estimated model. This is precisely one of the attracting features of this method since do can include values outside the stationary region (do ≥ 0.5). In addition, the limit distribution is standard Normal, which is another distinguishing feature of this approach, and this asymptotic behavior holds independently of the inclusion or not of deterministic terms. Thus, x(t) in (1) can be the errors in a regression model that may include a constant and/or a time trend. Finally, as earlier mentioned, it is supposed to be the most efficient method in the Pitman sense against local departures, which is also of interest based on the fractional nature of the test proposed. The functional form of this version of the tests can be found in Gil-Alana and Robinson (1997), Abbritti et al., (2016, 2023), etc.Footnote 1

4 Data

The data utilized for the analysis comes from the International Coffee Organization (ICO) database, which includes monthly prices in US cents per pound for five coffee groups. The data from 1990 and onwards was publicly available from their website, and the data from 1965 to 1989 was acquired and requested through the ICO's statistics department. The five coffee groups analyzed are Colombian Milds, Other Milds, Brazilian Naturals, Robustas, and the ICO Composite Indicator. The ICO Composite Indicator acts as a benchmark for the price of coffee of all origins and types. The dataset includes monthly prices for all groups between 1965 and 2020. The prices included in the dataset were not adjusted for inflation. The monthly value for all coffee groups was determined by weighing the value from both the New York market and the German market for Colombian Milds, Other Milds, and Brazilian Naturals, and the New York market and the French market for Robustas (for the years where both values were available). A few months of the data for Colombian Milds had missing values for the New York market, hence for those periods, only the German market price value was utilized. Furthermore, Brazilian Naturals had values missing in both markets for two periods, and Colombian Milds had values missing in both markets for three periods. Various arithmetic means (using pre- and post- values along with pre- and post- monthly values) were used to solve this issue, in all cases obtaining almost identical results.

We display in Table 1 some descriptive statistics and we observe that the coffee group with the highest mean is Colombian Milds, followed by Other Milds. Furthermore, Robustas has the lowest mean value across the five groups. This can be explained since Robustas usually produces the lowest quality coffee bean across the five groups. In Fig. 1, we observe that most coffee prices reached their maximum around 1979. All groups reached their maximum value (see Table 1) in April of 1979 due to one of Brazil's most severe frosts, which had damaging effects on the global market for coffee.

Table 1 Descriptive statistics
Full size table
Fig. 1
figure 1

Price series

Full size image

Figure 2 displays the periodograms of the price series, in which we observe that the maximized values within all five groups occur at a zero-level frequency, meaning that differentiation is necessary within the time series. Figure 3 displays the periodograms for the first-degree differenced series of all five groups, in which we observe values close to zero at the zero-frequency. This entails that the series were over-differentiated and that a fractional I(d) process may be better suited. In fact, this was the feature observed by Nobel Prize Clive W. J. Granger in his pioneering works on fractional integration (Granger, 1980; Granger & Joyeux, 1980).

Fig. 2
figure 2

Price series periodogram

Full size image
Fig. 3
figure 3

First-difference price series periodogram

Full size image

5 Empirical Results

First, we consider the following regression model,

$$y\left(t\right) = \alpha + \beta t+ x\left(t\right), {\left(1-B\right)}^{d}x\left(t\right) = u(t), t=1, 2, 3, \dots .,$$
(4)

where y(t) refers to the time series of the coffee group observed, α and β are unknown coefficients determined within the model, and \({(1-L)}^{d}\) being the fractional integration polynomial in L with fractional degree d, which makes the model integrated of order I(0).

Using a version of the Lagrange Multiplier (LM) tests proposed by Robinson (1994), we estimated the value of d in three scenarios: with no deterministic terms (i.e., \(\alpha = \beta = 0)\), including the intercept (i.e.,\(\alpha \ne 0,\) \(\beta = 0)\), and with a linear trend (i.e., \(\alpha \ne \beta \ne 0)\).

In Table 2 we display the estimates of d and their 95% confidence intervals following the previous model (3) across the different coffee groups using first the assumption that the error term u(t) is a white noise process. Thus, all time dependence is modelled throughout the differencing parameter d. We have marked in bold in Table 2 the selected specifications for the deterministic terms, observing that the model with only an intercept is sufficient to describe this deterministic component in all cases. Table 3 displays the respective estimated coefficients. We see that for all groups and their respective scenarios, the d estimate lies above 1, meaning that none of the time series are mean reverting in the case of a price shock.

Table 2 Estimates of d: White Noise Errors
Full size table
Table 3 Estimated coefficients: white noise case
Full size table

The assumption that u(t) in (3) is white noise might be too restrictive. In that respect, in what follows, we suppose u(t) is autocorrelated. However, instead of imposing a standard ARMA approach, we consider a nonparametric method proposed by Bloomfield (1973) based on the frequency domain. This method approximates ARMA structures with a reduced number of parameters and works extremely well in the context of fractional integration (see, e.g. Gil-Alana, 2004). Using this approach based on autocorrelated errors, the results are reported in Tables 4 and 5. We observe that the values are now smaller than in the previous case of white noise errors, and the I(1) null hypothesis cannot be rejected in any of the series examined. Moreover, statistical evidence of mean reversion (d < 1) is not found in any single case, supporting the hypothesis of permanency of shocks in all cases. As a robustness approach, we also employed alternative methods of estimation for the differencing parameter, both parametric (Sowell, 1992) and semiparametric (Abadir et al., 2007; Robinson, 1995; Shimotsu, 2010). In some these cases, we need first to differentiate the data, adding then the value 1 to the estimated orders of integration, and the results, though not reported, were fully consistent with those presented in the paper.

Table 4 Estimates of d: autocorrelated errors
Full size table
Table 5 Estimated coefficients: autocorrelated case
Full size table

6 Conclusions

In this paper we have analyzed the degree of persistence of five coffee group prices by using a long memory approach based on fractional integration. We apply this technique on the monthly ICO Composite, Brazilian Naturals, Other Milds, Colombian Milds, and Robusta price series from the International Coffee Organization (ICO) using data from 1965 to 2020. When assuming that the errors are white noise, our results show that all series are highly persistent with orders of integration greater than 1, meaning that any price shock will result in permanent effects on the long-run price level.

Similarly, when employing the non-parametric method of Bloomfield (1973), based on a factorized spectral density function, our results show that all series are again very persistent, though the values are smaller than in the case of uncorrelated errors. Using logged transformed data, the results were fairly similar. (See the Appendix A).

Our results propose that in the case of a price shock in coffee prices, there will be permanent effects on the long-run price level among all coffee categories, as all of the categories were fractionally integrated with degrees of integration (d) equal to or greater than one. Thus, this would require interventional measures to be taken to allow prices to return to their original long-run price level. This is crucial information for policymakers, coffee industry stakeholders, and investors, as it highlights the need for strategies and interventions to address the long-term impacts of such shocks on the coffee market.

Our results imply that in an industry highly prone to exogenous shocks due to climate, natural disasters, and overproduction, price-stabilizing mechanisms must be established to reduce the risks that come with such exogenous shocks. This is relevant as many developing and emerging economies are dependent on their coffee sector, and a persistent negative shock can have negative implications for economic growth (see Anderson and Bruckner, 2012) in such highly dependent countries. Furthermore, being that exogenous shocks in coffee prices have disproportionate effects on low-income, small-scale coffee farmers, such mechanisms must also ensure their economic welfare.

This poses a question regarding what policies might be effective in mitigating the aforementioned issues. As coffee is a highly fragmented market varying between low-quality and high-quality as well as productive and unproductive coffee bean production, small-scale farmers can benefit from a price premium or increased productivity during the harvesting season. However, this transition from low- to high-quality and/or productivity requires increased levels of investment that might be unattainable by small-holder farmers. A possible policy response that can be implemented is that of input subsidies for productivity-enhancing inputs such as fertilizers, higher premium and/or more resilient coffee varieties, harvesting equipment, etc. Agricultural input subsidy programmes have shown previous success such as that of maize input subsidies in Malawi (see Dorward & Chirwa, 2011). Other policy alternatives are cash transfers or improved access to financial services within the coffee sector (see Gertler et al., 2012; Stoeffler et al., 2016). Lastly, international trade agreements and regulations implemented by the International Coffee Organization have previously shown positive effects in stabilizing coffee prices and reducing risk for producers (see Akiyama & Varangis, 1990). However, these policy suggestions fall outside of the main scope of our paper.

Our paper opens up other lines of future empirical research into fractional integration and I(d) processes within the coffee industry, such as the applications for local economies. In addition, the possibility of GARCH effects is an interesting issue that may deserve further investigation. Appendix B displays the results for each series based on a GARCH (1, 1) specification. The significance of all four coffee type prices in the GARCH(1,1) model reveals the presence of significant explosive volatility clustering \((\alpha +\beta >1)\) and autocorrelations in the coffee market. Due to these results, we apply an integrated GARCH model (IGARCH) introduced by Engle and Bollerslev (1986). The results imply that extreme price movements tend to cluster together over time with high levels of persistence and suggest that alternative richer models like the Fractionally Integrated GARCH (FIGARCH) model of Baillie et al. (1996) and Chen et al. (2022) can be examined on these data to determine the persistence also in the volatility processes. Furthermore, other recent developments in time series econometrics such as the tests for structural breaks (Gil-Alana, 2008), non-linearities (Cuestas & Gil-Alana, 2016; Yaya et al., 2021) and fractional cointegration (Johansen & Nielsen, 2010, 2012) between the different coffee varieties will be examined in future papers.