Bayesian Inference for Mixed Gaussian GARCH-Type Model by Hamiltonian Monte Carlo Algorithm

Abstract

MCMC algorithm is widely used in parameters’ estimation of GARCH-type models. However, the existing algorithms are either not easy to implement or not fast to run. In this paper, Hamiltonian Monte Carlo (HMC) algorithm, which is easy to perform and also efficient to draw samples from posterior distributions, is firstly proposed to estimate for the Gaussian mixed GARCH-type models. And then, based on the estimation of HMC algorithm, the forecasting of volatility prediction is investigated. Through the simulation experiments, the HMC algorithm is more efficient and flexible than the Griddy-Gibbs sampler, and the credibility interval of forecasting for volatility prediction is also more accurate. A real application is given to support the usefulness of the proposed HMC algorithm well.

1 Introduction

Financial time series, such as exchange rates and stock returns, often have exhibited time-varying volatility, excess kurtosis and volatility clustering reported by Mandelbrot (1963) and Fama (1965). The family of autoregressive conditional heteroskedastic (ARCH) model of Engle (1982) and the generalized ARCH (GARCH) model of Bollerslev (1986) provide effective techniques to fit the volatility of the financial time series. Since then, huge research works for the GARCH model and its extensions can be found in the literature for the past three decades, such as the GJR-GARCH model of Glosten et al. (1993), the threshold GARCH (TGARCH) model of Zakoian (1994), the exponential GARCH (EGARCH) model of Nelson (1991), the integrated GARCH (IGARCH) model of Engle and Bollerslev (1986), the power-transformed and threshold GARCH model (PTTGARCH) of Pan et al. (2008). For the GARCH type models, Westerfield (1977) and McFarland et al. (1982) have shown that the assumption of the GARCH model with normal errors can not provide an appropriate framework for some return series with excessive kurtosis and volatility clustering. Bollerslev (1987) suggested that the GARCH models with t-student innovations should be considered to describe the conditional distributions of the stock returns. However, these models can not capture volatility clustering, high kurtosis, heavy-tailed distributions and the phenomenon of extreme events. A mixture normal GARCH-type model with zero mean and different variances is generated by a normal density with a small variance, while a small number of innovations are generated by a normal density with a large variance. Therefore it becomes very popular to model the financial return data, and provide a better fitting and forecasting than the GARCH-type models with normal or t-student innovations. See Bauwens et al. (1999), McLachlan and Peel (2000), Bai et al. (2003), Wong and Li (2001), Haas et al. (2004), Zhang et al. (2006) and Alexander and Lazar (2006) among others.

In the literature, maximum likelihood, quasi-maximum likelihood, the generalized method of moments and the least absolute deviations approach are traditionally carried out to infer the GARCH-type models, see Bollerslev and Wooldridge (1992) and Pan et al. (2008) for details. It is well known that the Bayesian inference offers a natural way to overcome computing problems and to avoid analytical difficulties in the estimation of volatilities. Some authors have applied Markov chain Monte Carlo (MCMC) algorithm to approximate the posterior distributions of the parameters for the GARCH-type models. For example, Geweke (1994) suggested the importance sampling to provide an efficient and generic method for updating posterior distributions. The Griddy-Gibbs sampler suggested by Ritter and Tanner (1992) has been used by Bauwens and Lubrano (1998) and Xia et al. (2017) for a GARCH-type model with normal or t-distributed errors, and Ausín and Galeano (2007) for a GARCH model with Gaussian mixture errors. In fact, finding an appropriate proposal distribution in the Metropolis-Hastings algorithm suggested by Metropolis et al. (1953) and Hastings (1970) or an importance function is not easy. Although the Griddy-Gibbs sampler is easier to implement than other methods, it takes much computation time. Therefore, designing an algorithm that is easier to implement and less heavy to run, is very important for inferring the mixed normal distribution GARCH-type models in practise.

In recent years, attention has been paid for Hamiltonian Monte Carlo (HMC) algorithm proposed by Neal (2011) in the literature, because people realized that it can search the typical set of parameters effectively by using the gradient information of the target distribution. Different from the Metropolis-Hastings algorithm, the HMC sampler may not lead to random walk. Hence, the HMC algorithm has been introduced for inferring the time series models. For instance, Paixão and Ehlers (2017) used the HMC algorithm to estimate the GJR-GARCH model proposed by Glosten et al. (1993) with normal and t-Student errors. Burda and Bélisle (2019) applied HMC algorithm to overcome the difficulty of inferring the Copula-GARCH model, of which the distribution of parameters is skewness, asymmetry and truncation. Kreuzer and Czado (2021) proposed Bayesian inference for a single factor copula stochastic volatility model. Their related results show that the HMC algorithm can be implemented more easily in practice. Stan suggested by Carpenter et al. (2016) can provide HMC and No-U-Turn [NUTS, Hoffman and Gelman (2014)] methods to carry out Bayesian inference, but it aim at the models with continuous-variable. In the GARCH-type models with mixed normal errors, the latent variable is regarded as discrete parameter to define the likelihood function, thus we can not implement HMC procedure directly by Stan. Therefore, the main objective of this article is to propose a procedure for Bayesian inference and prediction of the general GARCH-type models with the Gaussian mixture innovations based on the HMC algorithm.

The arrangements of this paper are as follows. Section 2 presents the general GARCH-type models with mixed normal innovations and describes a Bayesian inference of the model. A Hamiltonian Monte Carlo algorithm for sampling the posterior density of volatilities and VaR forecasts is also addressed. Section 3 provides some simulation experiments and a real data application, which illustrate the accuracy in the estimation of the parameters and the prediction of volatilities and VaR. Section 4 is our conclusions.

2 Gaussian Mixture GARCH-Type Models and Bayesian Inference

2.1 GARCH-type Models with Mixed Gaussian Innovations

A series $\{y_t\}$ is said to follow the normal mixture GARCH-type models given by

$$\begin{aligned} y_t= & {} \sqrt{h_t}\epsilon _t, \nonumber \\ h_t= & {} \text {var}(y_t|F_{t-1}) = f(\Theta , {F}_{t-1}), \end{aligned}$$

(2.1)

where $f(\Theta , F_{t-1})$ is a differentiable function of $\Theta$ and given the previous information ${F}_{t-1}=\{y_{t-1},y_{t-2},\ldots \}$. The error term $\epsilon _t$ is taken from independent mixed normal distributions as follows,

$$\begin{aligned} \varphi (\epsilon _t) = \left\{ \begin{array}{llllllll} \varphi _1(\epsilon _t), \quad {\text with\; probability} \,\rho ,\\ \varphi _2(\epsilon _t), \quad {\text with\; probability} \,1-\rho , \end{array} \right. \end{aligned}$$

(2.2)

where $\varphi _1(\epsilon _t)= \frac{1}{ \sqrt{2\pi \sigma ^2 }} \exp (-\frac{\epsilon _t^2}{2 \sigma ^{2}} )$, $\varphi _2(\epsilon _t) = \frac{\sqrt{\lambda }}{ \sqrt{2\pi \sigma ^2}} \exp (-\frac{\lambda \epsilon _t^2 }{2 \sigma ^{2}} )$ and $\sigma ^2 = \frac{\lambda }{1+ (\lambda -1) \rho }$ with $0<\lambda <1$. Then $E (\epsilon _{t})=0$, $var (\epsilon _{t}) = 1$.

As we can see, model (2.1) includes the following conditional heteroscedasticity models:

• (1) If $f(\Theta , F_{t-1}) = \alpha _0 + \sum _{i=1}^{p}\alpha _i y_{t-i}^2 + \sum _{j=1}^{q}\beta _j h_{t-j}$, then (2.1) becomes the standard GARCH model [Bollerslev (1986)];

• (2) If $f(\Theta , F_{t-1}) = \alpha _0 + \sum _{i=1}^{p}\alpha _i y_{t-i}^2$, then (2.1) is the ARCH model [Engle (1982)], which is a special case of GARCH;

• (3) If $f(\Theta , F_{t-1}) = \alpha _0 + \sum _{i=1}^{p}(\alpha _i + \gamma _i N_{t-i})y_{t-i}^2 + \sum _{j=1}^{q}\beta _j h_{t-j}$, where $\gamma _i > 0,i = 1,..,p$ and $N_{t-i} = 1$ if $y_{t-i} < 0$ or $N_{t-i} = 0$ if $y_{t-i} \geqslant 0$, then (2.1) is the GJR-GARCH model [Glosten et al. (1993)];

• (4) If $f(\Theta , F_{t-1}) = \alpha _0 + \beta _1 h_{t-1} + (1-\beta _1)y_{t-1}^2$, then (2.1) is the IGARCH(1,1) model [Engle and Bollerslev (1986)];

• (5) If $\ln f(\Theta , F_{t-1}) = \alpha _0 + \sum _{i=1}^{p} \alpha _i g(\epsilon _{t-i}) + \sum _{j=1}^{q}\beta _j \ln h_{t-j}$, then (2.1) becomes the EGARCH model [Nelson (1991)], where $\alpha _1 = 1$, $g(\epsilon _{t}) = \theta \epsilon _{t} + \gamma [|\epsilon _{t}| - \text {E}(|\epsilon _{t}|) ]$.

• (6) If $f(\Theta , F_{t-1}) = \left[ \alpha _0 + \sum _{i=1}^{p}\alpha _{1i} (y_{t-i}^{+})^{2\delta }+ \sum _{i=1}^{p}\alpha _{2i} (y_{t-i}^{-})^{2\delta } + \sum _{j=1}^{q}\beta _j h_{t-j}^{\delta } \right] ^{1 /\delta }$, (2.1) represents the PTTGARCH model [Pan et al. (2008)], where $\delta$ is a known positive number.

Remark 2.1

Diebolt and Robert (1994) defined the latent variables ${\textbf {z}} = \{z_t, 1\le t\le n\}$, where $z_t$ is a Bernoulli random variable with probability $\rho$, and $I_{\left\{ \cdot \right\} }$ is the indicator function. Then (2.2) can be interpreted as

$$\begin{aligned}{} & {} \epsilon _t = \epsilon _{t}^{(1)}I_{\{z_t=1\}} + \epsilon _{t}^{(2)}I_{\{z_t=0\}}, \end{aligned}$$

(2.3)

$$\begin{aligned}{} & {} \epsilon _{t}^{(1)} \sim N(0,\sigma ^2), \epsilon _{t}^{(2)}\sim N(0,\sigma ^2/\lambda ). \end{aligned}$$

(2.4)

Thus, if $z_t$ can be identified, then the distribution of $\epsilon _t$ can be determined.

2.2 The Posterior Distribution

Let $\Theta$ denote the parameter vector of the Gaussian mixed GARCH-type models (2.1), and ${\textbf {y}} =\{y_t, t=1,2,\ldots ,n\}$ is observed series with n sample size. Then the posterior density can be written as

$$\begin{aligned} p(\Theta |{\textbf {y}} ) \propto \pi (\Theta ) l(\Theta ; {\textbf {y}}, {\textbf {z}} ), \end{aligned}$$

(2.5)

where $\pi (\Theta )$ is the prior and $l(\Theta ; {\textbf {y}}, {\textbf {z}})$ is the likelihood function, which can be derived in terms of latent variables ${\textbf {z}} = \{z_t, t=1, 2,\ldots , n\}$, i.e.,

$$\begin{aligned} l(\Theta ;{\textbf {y}} , {\textbf {z}} ) \propto \prod _{t:z_t=1}\rho \varphi _1 \left[ \frac{y_t}{f(\Theta , F_{t-1})}\right] \prod _{t:z_t=0}(1-\rho ) \varphi _2\left[ \frac{y_t}{f(\Theta , F_{t-1})}\right] . \end{aligned}$$

(2.6)

The parameter $\rho$ controls the proportion of the two normal distributions. When $\rho$ goes to 1, the innovations $\epsilon _t$ will almost come from the first normal distribution; when $\rho$ tends to 0, $\epsilon _t$ will almost come from the second normal distribution. It would be assumed that $0.5< \rho < 1$, so that most of the innovation $\epsilon _t$ comes from the first part.

To implement the Bayesian inference about the parameters $\Theta$ in model (2.1), we need the joint posterior distribution $P(\Theta | {\textbf {y}})$, which can be obtained by using the conditional posterior distribution in a HMC process. Therefore, we need to choose priors to derive the conditional posterior distribution for the unknown parameters.

For any priors $\pi (\Theta )$, as $h_t$ is a function of $\Theta$ in (2.1), the conditional posterior densities of most parameters in $\Theta$ will contain $h_t$ in (2.5). Consequently, they cannot be a normal or any other well known density, from which random numbers could be easily generated. Also, they are less likely to have the property of conjugacy. Therefore, the uninformative prior distributions will be preferred, and the relevant posterior distribution will be obtained.

If model (2.1) is the standard GARCH model, the uniform prior of $\Theta = (\alpha _0,\alpha _1,\ldots ,\alpha _p,\beta _1, \ldots ,\beta _q,\rho ,\lambda )'$ can be chosen as follows:

$$\begin{aligned}&\alpha _0 \sim U(0,+\infty ); \quad \alpha _i \sim U(0,1), i=1,\ldots , p; \nonumber \\&\beta _j \sim U(0,1), j= 1,\ldots , q; \quad \rho \sim U(0.5,1); \quad \lambda \sim U(0,1). \end{aligned}$$

(2.7)

Therefore, according to the uninformative prior distribution, the joint posterior distribution function of $\Theta$ is,

$$\begin{aligned} p(\Theta |{\textbf {y}},{\textbf {z}}) \propto \prod _{t:z_t=1}\rho \frac{1}{\sqrt{\sigma ^2 h_t}} \exp \left[ \frac{- y^2_t}{2\sigma ^2 h_t} \right] \prod _{t:z_t=0}(1-\rho ) \sqrt{\frac{\lambda }{\sigma ^2 h_t}} \exp \left[ \frac{- \lambda y^2_t}{2\sigma ^2 h_t} \right] . \end{aligned}$$

(2.8)

2.3 Sampling Scheme Using HMC

Since Neal (2011) introduced the HMC algorithm, which originated from the algorithm when Duane et al. (1987) studied molecular dynamics simulation, the statistical inference method based on Hamiltonian dynamics became popular. According to Betancourt (2017), Girolami and Calderhead (2011) and Neal (2011), the HMC algorithm has an excellent performance in solving some difficult high-dimensional inference problems and pathological behaviors of distribution functions.

In Hamiltonian dynamics, there are two parameters with the same dimension, the position vector $\Theta$ and the momentum vector $\Phi$, to describe the motion process. The system is described by a function $H(\Theta , \Phi )$ defined on the phase space $(\Theta , \Phi )$. At the point $(\Theta , \Phi )$, $H(\Theta , \Phi )$ is known as the Hamiltonian, and can be decomposed into two parts, i.e.,

$$\begin{aligned} H(\Theta , \Phi ) = U(\Theta ) + K(\Phi ), \end{aligned}$$

(2.9)

where $U(\Theta )$ and $K(\Phi )$ are called the potential energy and the kinetic energy, respectively. In particular, the canonical distribution of $H(\Theta , \Phi )$ has the form $\pi (\Theta , \Phi ) = \exp (-H(\Theta , \Phi ))$. From Hamilton’s equations (2.10), we can know how $\Theta$ and $\Phi$ change over time t,

$$\begin{aligned} \frac{\textrm{d} \Theta _i }{\textrm{d} t}= & {} +\frac{\partial H}{\partial \Phi _i},\nonumber \\ \frac{\textrm{d} \Phi _i }{\textrm{d} t}= & {} -\frac{\partial H}{\partial \Theta _i}. \end{aligned}$$

(2.10)

In a non-physical context, the position parameter corresponds to the parameter of interest with the density $\pi (\Theta )$, and the parameter momentum is assumed to be a normal distribution random vector with the density $\pi (\Phi )$ independent of the parameter position. The joint probability distribution is written as the product of two densities,

$$\begin{aligned} \pi (\Theta , \Phi ) = \pi (\Theta )\pi (\Phi ). \end{aligned}$$

(2.11)

Since the joint distribution is regarded as a canonical distribution, then the Hamiltonian function can be written as follows,

$$\begin{aligned} H(\Theta , \Phi ) = -\ln \pi (\Theta ) \pi (\Phi ) = -\ln \pi (\Theta ) - \ln \pi (\Phi ) = U(\Theta ) + K(\Phi ). \end{aligned}$$

(2.12)

In the mixed normal GARCH-type models, the parameter $\Theta$ corresponds to the position in Hamiltonian function $H(\Theta ,\Phi )$, and the momentum variable is denoted as $\Phi$ with the same dimension as $\Theta$. In order to calculate the Hamiltonian $H(\Theta ,\Phi )$ of the Gaussian mixed GARCH type models, we adopt $\Phi$ follows a normal distribution with mean zero and covariance $\Sigma$, then the Hamiltonian function can be further written as,

$$\begin{aligned} H(\Theta ,\Phi ) = U(\Theta )+ K(\Phi ) = -\ln p(\Theta |{\textbf {y}},{\textbf {z}}) + \frac{1}{2} \Phi '\Sigma ^{-1}\Phi . \end{aligned}$$

The normalising constant omitted in the HMC iteration will not affect the program. Using the above Hamiltonian function, we perform the HMC algorithm to update the parameter $\Theta$.

Each iteration of the HMC algorithm has two steps. The first changes only the momentum, while the second can change both position and momentum. Both steps leave the canonical joint distribution of $(\Theta , \Phi )$ invariant, and hence their combination also maintains the distribution invariant. In the first step, new value of $\Phi$ is randomly drawn from its Gaussian distribution, independently of the current value of $\Theta$. Because $\Theta$ is not changed, and $\Phi$ is drawn from its correct conditional distribution. Thus, this step obviously keeps the canonical joint distribution invariant. In the second step, a Metropolis update is performed to propose a new state by using Hamiltonian dynamics. Starting with the current state $(\Theta , \Phi )$, Hamiltonian dynamics is simulated for L steps using the leapfrog method with a stepsize of $\Delta s$. Here, L and $\Delta s$ are parameters of the algorithm, which need to be tuned to obtain good performance. The momentum variables at the end of this L-step trajectory are then negated, giving a proposed state $(\Theta _L, \Phi _L)$. It is easy to obtain $P(\Theta ,\Phi )/P(\Theta _L,\Phi _L)= \exp \{-H(\Theta ,\Phi )+H(\Theta _L,\Phi _L)\}$. Then this proposed state is accepted as the next state of the Markov chain with probability

$$\begin{aligned} \min \left[ 1,\pi (\Theta _L, \Phi _L)/\pi (\Theta , \Phi ) \right] = \min \left[ 1,\exp \big (-H(\Theta _L, \Phi _L)+H(\Theta , \Phi )\big )\right] . \end{aligned}$$

(2.13)

If the proposed state is not accepted, the next state is the same as the current state. The negation of the momentum variables at the end of the trajectory makes the Metropolis proposal symmetrical, as needed for the acceptance probability (2.13) to be valid.

For the mixed normal GARCH-type models, the gradient of the kinetic function $\nabla K(\Phi )$ is $\Sigma ^{-1} \Phi$, and the potential function $U(\Theta ) = U(\Theta |{\textbf {y}},{\textbf {z}})$ is first-order differentiable. Then the gradient $\nabla U(\Theta )$ can be calculated. Note that $\rho , \lambda$ is different from the other parameters in $U(\Theta )$. The partial derivatives of U with respect to $\rho$ and $\lambda$ can be calculated directly.

However, the other parameters in $U(\Theta )$ can not be expressed as the explicit formula, and can be calculated according to the chain rule as follows:

$$\begin{aligned} \frac{\partial U}{\partial \Theta _i}= & {} \sum _{t} (U(\Theta |{\textbf {y}},{\textbf {z}}))'_{f(\Theta ,F_{t-1})} (f(\Theta ,F_{t-1}))'_{\Theta _i} \nonumber \\= & {} \sum _{t} (U(\Theta |{\textbf {y}},{\textbf {z}}))'_{h_{t}} (h_{t})'_{\Theta _i}. \end{aligned}$$

(2.14)

Example 2.1

Notice that the partial derivative $(h_t)'_{\Theta _i}$ can be obtained indirectly. For example, for the standard GARCH model, the parameters in $f(\Theta ,F_{t-1})$ are $\alpha _0, \alpha _i, \beta _j, i=1,2, \ldots , p, j=1,2, \ldots , q$. The derivative of $\alpha _0$ can be written as follows,

$$\begin{aligned}{} & {} (h_{t} )_{\alpha _0}' =1 + \beta _1 (h_{t-1} )_{\alpha _0}' + \ldots + \beta _q (h_{t-q} )_{\alpha _0}', \end{aligned}$$

(2.15)

$$\begin{aligned}{} & {} \partial U / \partial \alpha _0 = \sum _{t = l}^{n} (h_{t} )_{\alpha _0}' {u_t}, \end{aligned}$$

(2.16)

where $l = \max (p+1,q+1)$, ${u_t} = \frac{1}{2}(\frac{1}{h_t}-\frac{y_t^2}{\sigma ^2 h_t^2}) I_{\{t:z_t=1 \}}+\frac{1}{2}(\frac{1}{h_t}-\frac{\lambda y_t^2}{\sigma ^2 h_t^2}) I_ {\{ t:z_t=0 \}}$. $(h_{t-k} )_{\alpha _i}'$, $(h_{t-k} )_{\beta _j }'$ and $h_{k}$, for $l-q \le k \le l-1$, $i = 0, 1, 2, \dots , p$, $j = 1, 2, \dots , q$ are assumed to be known. The derivatives of other parameters $\alpha _i, \beta _j$ have similar expressions, for $i = 1,2,\dots ,p, j =1,2,\dots ,q$ . Thus using the above formula, the gradient of $U(\Theta )$ can be calculated.

If $f(\Theta ,F_{t-1})$ is the case 5 in (2.1), one can treat $\ln h_t$ as $h_t$ to calculate the partial derivatives.

In the mixed normal GARCH-type models, generating the latent data ${\textbf {z}}$ is very important for inferring the interested parameter. There are several methods can be found in the literature. For example, Tanner and Wong (1987) led to the posterior of the interested parameter by combining the observed data with latent data. Diebolt and Robert (1994) presented a Bayesian method to evaluate the interested mixture distribution in terms of the missing data scheme. Denote ${\textbf {y}}=(y_1,y_2,\dots ,y_n)'$ to be the observed data. Referring to Tanner and Wong (1987) and Diebolt and Robert (1994), we first generate the missing values ${\textbf {z}} =(z_1,z_2,\dots ,z_n)'$, and then sample the parameters from the posterior function $p(\Theta |{\textbf {y}}, {\textbf {z}})$ based on the complete data $(y_t,z_t), t=1,2,\ldots , n$. The algorithm works at the step m for $m =1, \ldots , N$ as follows:

• (1) Use $\Theta ^{(m)}$ and ${\textbf {y}}$ to generate $z_t^{(m)}$ from posterior $p(z_t|\Theta ^{(m)},y_t)$, where

  $$\begin{aligned} p(z_t|\Theta ^{(m)},y_t)= B\left(1, \frac{pr_1}{pr_1+pr_2}\right), \end{aligned}$$

  (2.17)

  $B(1,\frac{pr_1}{pr_1+pr_2})$ is the Bernoulli distribution with probability $\frac{pr_1}{pr_1+pr_2}$ and $pr_1 = \frac{\rho }{\sqrt{\sigma ^2h_t}}\exp (-\frac{y_t^2}{2\sigma ^2 h_t})$, $pr_2 = \frac{(1-\rho )}{\sqrt{\sigma ^2 h_t/\lambda }}\exp (-\frac{\lambda y_t^2}{2\sigma ^2h_t})$.

• (2) Draw momentum variable $\Phi$ from a zero-mean Gaussian distribution with covariance matrix $\Sigma =diag (1,1,\dots ,1)$, $\Phi \sim N({\textbf {0}},\Sigma )$.

• (3) Use the Algorithm 1 to propose a new state $(\Theta ^*,\Phi ^*)$.

• (4) Accept the proposal $(\Theta ^*,\Phi ^*)$ with probability Pr and reject the proposal with probability $1-Pr$, where

  $$\begin{aligned} Pr = \min \left[ 1, \exp (-H(\Theta ^*,\Phi ^*)+H(\Theta ,\Phi )) \right] . \end{aligned}$$

  (2.18)

Remark 2.2

In fact, Algorithm 1 is the leapfrog method. Here, $UB_i$ and $LB_i$ represent the upper and lower bounds of each parameter respectively.

The simplest method of discretization equations (2.10) is leapfrog method with order $(\Delta s)^3$ local error, while Euler’s method and its modified version have order $(\Delta s)^2$ local error [See Leimkuhler and Reich (2004) for details]. Because a big step size will lead to a poor acceptance rate and a small step size will waste computation time. As Neal’s comments, a relatively suitable step size $\Delta s$ should be considered based on computational efficiency. The adjustment of parameter $\Delta s$ is necessary as well as misleading. Hence, it is essential to run multiple Markov chains with different initial values to ensure that the parameter $\Delta s$ is sufficient to keep the algorithm stable.

According to Beskos et al. Beskos et al. (2013) and Hoffman and Gelman Hoffman and Gelman (2014), tuning of parameters $\Delta s$ and L determines the performance of the HMC algorithm. An inappropriate step size $\Delta s$ will destroy the stability of simulated trajectory, and then affects the acceptance rate. The steps L means the total run in the leapfrog trajectory. Care must be taken when we choose the step size of HMC algorithm, because too small step size can maintain the stability of the trajectory. After a leapfrog iteration we can only get proposal point, which is close to the previous one. Moreover, an overlong step size will destroy the stability. A selected critical step size can keep the algorithm stable and efficient. The initial L is assumed to be 1. Given the initial $\Theta _0, \Phi _0$ and s, then one use the leapfrog method to get $\Theta _L, \Phi _L$. If $\exp \{-H(\Theta _L,\Phi _L) + H(\Theta _0, \Phi _0)\} > 0.5$, then $s = 1/2s$; otherwise, $s=2s$. In simulation experiments and empirical analysis, taking into account the acceptance rate of these two stages, we set a threshold 0.5 and run the Metropolis update multiple times. According to Algorithm 1, repeating this process until the algorithm remains stable. The final acceptance rate for the proposed points is about 0.85. After getting the stable step size, the number of steps L can be increased according to the correlation of the sampling results. One can find an appropriate step size through sufficient preliminary runs of several chains. Furthermore, it’s necessary to choose an appropriate L that avoids producing a dependent point.

In the previous works, the HMC algorithm performs well in sampling unconstrained parameters. As for handling distributions with the constraints on the variables, we can reparameterize the variables. Taking the GARCH model as an example, because the coefficients of autoregressive term $\alpha _i$ is on interval (0,1), we can take logarithm of $\alpha _i$. Under the transformation $\alpha _i^* = \ln (\alpha _i/(1-\alpha _i))$, the HMC algorithm also performs well. However, the reparameterization will take more arithmetic operations. Another way for the posterior with restricted variables can produce similar results. In order to deal with the constraints, once the variable violates any constraints, we set the value of the potential energy and obtain an acceptance rate of almost zero immediately. Thus the parameters will fall in the limited interval, see e.g. Algorithm 1. In each leapfrog iteration, the boundaries of variables can be seen as “walls”. If $\Theta _i$ is beyond the boundaries, the state $(\Theta _i,\Phi _i)$ bounces off the “walls" perpendicularly, see Betancourt (2011) for details.

2.4 Bayesian Forecasting

Volatility and VaR forecasting are important in analyzing derivative pricing, yielding a good portfolio for investments and managing market risks in financial markets. In this section, the estimation of in-sample volatilities and the prediction of future volatilities are also investigated. In order to predict the volatility and VaR, based on the HMC iterations, a simulation-based approach is used to obtain the posterior samples and distributions of volatilities $h_t,t=1,2,\dots ,n$, where $h_t= f(\Theta , F_{t-1})$ is a function of parameter $\Theta$. For each HMC iteration of $\Theta ^{(m)}, m=1,2,\dots ,N$, we estimate the in-sample volatilities $h_t^{(1)},\dots ,h_t^{(N)}$,

$$\begin{aligned} {\hat{h}}_t \simeq E(h_t|{\textbf {y}} _n) \simeq \frac{1}{N}\sum _{m=1}^{N}h_t^{(m)}, ~ t=1,2,\dots ,n, \end{aligned}$$

(2.19)

where ${\textbf {y}}_n = (y_1,y_2,\dots ,y_n)'$.

For one-step ahead prediction of $y_{n+1}$ and $h_{n+1}$, one can obtain samples from the predictive distributions $f(y_{n+1}|{\textbf {y}}_n)$ and $f(h_{n+1}|{\textbf {y}}_n)$, respectively. Note that $h_{n+1}^{(m)}$ is the function of parameter $\Theta ^{(m)}$ and ${\textbf {y}}_n$. Then $h_{n+1}^{(1)},h_{n+1}^{(2)},\dots ,h_{n+1}^{(N)}$ can be obtained and form a sample of the predictive distribution $f(h_{n+1}|{\textbf {y}}_n)$. The posterior distribution $f(y_{n+1}|{\textbf {y}}_n, \Theta ^{(m)})$ has a simple form, so $y_{n+1}^{(m)}$ can be drawn from a zero mean mixed normal distribution with variance $h_{n+1}^{(m)}$. Hence, $y_{n+1}^{(1)},y_{n+1}^{(2)},\dots ,y_{n+1}^{(N)}$ is a sample of the predictive distribution $f(y_{n+1}|{\textbf {y}}_n)$. From this perspective, the distribution of $y_{n+1}$ can be calculated by means of the posterior sample mean, that is

$$\begin{aligned} f(y_{k+1}|{\textbf {y}}_n)\simeq & {} \frac{1}{N}\sum _{m=1}^{N}f(y_{k+1}|{\textbf {y}}_n,\Theta ^{(m)}). \end{aligned}$$

(2.20)

For the prediction of two-step ahead volatility, we can obtain the predictive distribution of $h_{n +2}$ through the calculated $y_{n+1}$ and $h_{n +1}$. According to the $\Theta ^{(m)}$ and $h^{(m)}_{n+1}$, the predictive $y^{(m)}_{n+1}$ and $h^{(m)}_{n+2}$ can be obtained in the same way. Similarly, $y^{(m)}_{n+2}$ also follows the mixed normal distribution given $h^{(m)}_{n+2}$. Then it can be generated from the mixed normal density with known $\Theta ^{(m)}$ and $h^{(m)}_{n+1}$. For $t= n+j, j\ge 2$, the prediction of the volatilities $h_{t}$ and $y_{t}$ can be carried out through the above process. If we need to obtain the predicted distributions $f(h_{t}|{\textbf {y}} _{n+j-1} )$ and $f(y_{t}|{\textbf {y}} _{n+j-1})$, we can repeat the prediction process above. The final prediction distribution can help us compute the prediction interval and the prediction mean at time t.

Due to the common presence of extreme events in financial time series, VaR has become a widely used measure of market risk. It is usually defined as the loss of a financial asset or securities portfolio, which is exceeded with a predetermined probability $\alpha$ over a time horizon of d periods,

$$\begin{aligned} Pr(y[d] \le -VaR) =\alpha , \end{aligned}$$

(2.21)

where $y[d]= y_{n+1}+y_{n+2}+\dots +y_{n+d}$. In fact, VaR is the $\alpha$-quantile of distribution of y[d] at a given confidence level $\alpha$. To forecast VaR, we need to estimate the extreme $\alpha$th percentiles. In this paper, the probability $\alpha$ of interest is 0.01 and 0.05. Given $y^{(m)}_{n+1},y^{(m)}_{n+2},\dots ,y^{(m)}_{n+d}, m=1,2,\dots ,N$, the d-period $\alpha$% VaR can be evaluated from distribution of $f(y[d]|{\textbf {y}} )$, see Jorion (2000) for details.

3 Simulated Example and Real Data Example

In this section, we first use the simulated experiment to illustrate the performance of the HMC method for the standard GARCH model with mixed normal errors, and then apply the proposed method to a real data analysis. The program is written based on R.

3.1 Simulation Experiment

Here, the mixed Gaussian GARCH(1,1) model is adopted as the simulated example, that is

$$\begin{aligned} y_t= & {} \sqrt{h_t}\epsilon _t, \nonumber \\ h_t= & {} \alpha _0 + \alpha _1y_{t-1}^2 + \beta _1h_{t-1}, \end{aligned}$$

(4.1)

where $\epsilon _t$ follows a mixture Gaussian distribution (2.3) and the true values are set as follows,

$$\begin{aligned} \alpha _0 =0.1, \alpha _1= 0.2, \beta _1= 0.5, \rho =0.8, \lambda =0.15. \end{aligned}$$

(4.2)

We first generated three series with sample size 800, 1000, 2000, which are denoted as (s1), (s2) and (s3) respectively. Then 10,000 HMC iterations are carried out for all series with the same initial value $\Theta ^{(0)}=(0.5,0.4,0.4,0.65,0.5)$. The first 5000 iterations considered as burn-in, the trace plots and histograms of all series are shown in Figs 9–14 in Appendix. The trace plots indicate that the HMC algorithm is successful in exploring the posterior density of the parameters. The CUMSUM plots for simulated s2 are displayed in Fig. 1, which shows that the estimates of parameters have good convergence. Meanwhile, convergence diagnosis was investigated by the Geweke test [Geweke (1992)], and the results are more convinced that the chains have converged from Table 8.

Remark 3.1

In Algorithm 1, as Neal (2011) discussed, the stability and periodicity of the trajectory needs to be considered when the HMC algorithm is executed. The leapfrog step $L=59$ and multiple step sizes $\Delta s$ are 0.003, 0.002, 0.002, 0.012 and 0.003 are reasonable. They ensure the stability as well as take into account the excellent performance of the program. The multiple step sizes used here can reduce the correlation of the samples. As discussed above, when discretizing the Hamilton equations, the discretization error can be kept equal to 0 theoretically. However, if the discretization error exists, then the acceptance rate is less than 1, that is round 85%.

Remark 3.2

Here two tests are used to test the convergence of the Markov chain. One is the visual inspection of CUMSUM statistics proposed by Yu and Mykland (1994), and defined by

$$ CS_{t} = {{\left( {\frac{1}{t}\sum\limits_{{i = 1}}^{t} {\theta ^{i} } - \mu _{\theta } } \right)} \mathord{\left/ {\vphantom {{\left( {\frac{1}{t}\sum\limits_{{i = 1}}^{t} {\theta ^{i} } - \mu _{\theta } } \right)} {\sigma _{\theta } }}} \right. \kern-\nulldelimiterspace} {\sigma _{\theta } }}, $$

(4.3)

where $\mu _{\theta }$ and $\sigma _{\theta }$ are the empirical mean and standard deviation of the N draws. Another is the Geweke test, which can be obtained by the R package “coda" [see Plummer et al. (2008) for details].

Fig. 1

The CUMSUM plots of posterior mean estimates for s2 of the model 4.1

Table 1 Comparison results for the mixture normal GARCH(1,1) model using HMC algorithm and GG sampler based on 100 replicates samples

To verify the usefulness of our method a bit further, we conduct an comparison between the HMC algorithm and the Griddy-Gibbs (GG) sampler through 100 simulations. The summary of the results for the two methods is recorded in Table 1, which includes the posterior means, medians and standard deviations (SD) in parentheses.

From Table 1, we can see that the estimated results of two methods are very well. The average of 100 samples of all estimated parameters is very close to the true parameters, excluding a little bias for $\beta _1$. In particular, the posterior estimate of $\rho$ is good and equal to 0.7922, its SD is small. Meanwhile, the median and mean of each parameter are very close, which indicate that the distributions are approximately symmetrical.

Table 2 Comparisons of HMC algorithm and GG sampler in terms of MSE, ESS/min and MAD for each parameter

The posterior estimates of the HMC algorithm are close to the GG sampler. However, the HMC algorithm runs more quickly than the Griddy-Gibbs sampler. As shown in the last column of Table 1, the computation time of the HMC algorithm for the mixed Gaussian GARCH(1,1) model is 12.23 minutes (mins), while the GG sampler is 56.22 mins. In other words, with the same sample size, the time consumption of the GG sampler is almost 5 times that of the HMC algorithm.

In addition, Table 2 shows the detailed comparisons of the two methods, including mean square error (MSE), mean absolute deviation (MAD) for each parameter and effective sample size per minute (ESS/min). We can see that compared with GG sampler, HMC algorithm has a lower MAD and a lower MSE for most parameters. However, ESS/min of HMC algorithm is much higher than GG sampler.

Furthermore, we consider the forecasting by the proposed HMC algorithm. 1005 time series data by model (4.1) is used for predictions, while the first 1000 data are used for the posterior estimation of the model. The HMC algorithm is also performed 10000 iterations with the initial value $\Theta ^{(0)}=(0.5,0.4,0.4,0.65,0.5)'$, and the first 5000 iterations are as burn-in values. We repeat the process to obtain the posterior means, SD’s, 95% credibility intervals and predictive distributions of volatilities and VaR. Moreover, in order to ensure the validity of the prediction, we calculate the results of 100 replicates and obtain the absolute error (AE) of volatilities, which are $|{\hat{h}}_{1000+m}-h_{1000+m}|, m=1,2,\ldots ,5$ plotted in Fig. 2.

Fig. 2

The boxplot of AE of predictive volatilities for future times $T=1001,..,1005$

Fig. 3

The histograms of predictive dsitribution of volatilities for simulated series at times $T=1001,..,1005$ with sample size 1000

Remark 3.3

Ausín and Galeano (2007) and Xia et al. (2017) suggested choosing fixed grids with 40 points to compute the value of GG sampler. For the GG sampler, we choose 40 griddy points and the same initial value $\Theta ^{(0)}$, which can explore the parameter space sufficiently. In addition, linear interpolation is used to implement the approximation of the cumulative distribution function.

Fig. 4

The predicitve distributions of $VaR_{1001}$ $\sim$ $VaR_{1005}$ at 5% (top) and 1% (bottom) level

Table 3 The predictive means, SD’s and 95% credibility intervals for volatilities at times $T=1001,..,1005$ based on 100 replicates

Using the steps described above, one can obtain the estimation of predictive distribution. The histograms of the predictive distributions of volatilities and VaR are shown in Figs. 3 and 4. The estimated means, SD’s and 95% credibility intervals are summarized in Tables 3 and  4. From the histograms of predictive volatilities in Fig. 3, we believe that the distributions of future volatilities are nearly symmetric. For the forecasting of volatility, the predictive mean is very close to the true value, and the SD’s are very small. For the boxplot of predictive volatilities in Fig. 2, we can see that AE plots are pretty small, which indicates that our suggested method provides an accurate estimation. Figure 4 shows that most of the predictive distributions of VaR are symmetric, while a small part of them are skewed.

Table 4 The predictive means, SD’s and 95% credibility intervals of VaR at times $T=1001,..,1005$ with probabilities $\alpha$=0.05 and 0.01 based on 100 replicates

Compared with GG sampler, the simulation results show that HMC algorithm not only provides more accurate estimations and predictions, but also performs higher efficiency for the mixture normal GARCH model.

3.2 Real Data Example

Fig. 5

The the log return plot of SP 500

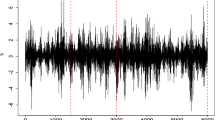
In order to illustrate the good performance of the mixed GARCH type models in practice, we demonstrate the feasibility of the model with the real data analysis. The daily closing prices of SP500 index from Sep./3/2015 to Apr./7/2021 are selected with T = 1407 observed data. The sample mean, variance, skewness and kurtosis of log return series are 0.0525, 1.196, −1.0865 and 24.1190 respectively. The return of the observation series is defined by $y_t = 100(\log P_t-\log P_{t-1})$ shown in Fig. 5, where $P_{t}$ is the closing price at time t. The Dickey-Fuller test is used to verify the stationarity of this time series, and the results show that the log return series is stationary. $P_t$ is used to study the estimation problem of the volatility model. The volatility means the movement of the stock price. For example, the bigger volatility indicates that the stock will increase in price at a future point in time. Then, the prediction of volatilities in the future time can help investors to judge whether to hold the stock or not. Meanwhile, the predicted distribution of VaR is also carried out, which is concerned with a forecast of the possible losses of the investment portfolio over a given time interval. Thus, using the forecast results, financial institutions or individuals can respond in time to reduce losses when dealing with market risks.

The analysis of the real data is based on model (4.1). We use the HMC algorithm to estimate parameters of the model, and GG sampler is also used for the comparison. 10,000 iterations are carried out for the HMC algorithm and the GG sampler with discarding the first 5000 iterations. The posterior means, medians and SD’s in parentheses are shown in Table 5.

Table 5 The posterior estimations for SP500 by using HMC algorithm and GG sampler

Table 5 shows that the estimation for posterior mean of the two methods are very close, indicating that the HMC algorithm is as much reliable as the GG sampler. Although the posterior results of the parameters are generally close, the SD’s of the estimated parameters of the HMC method is smaller, and HMC algorithm consumes less time in terms of running time. Moreover, the posterior mean of parameter $\rho$ equals to 0.8873 and SD is 0.0426. That is to say, about 89% of the data may come from a normal distribution with a small variance 0.64, and the other 11% of the data may come from a normal distribution with a big variance 3.96. In reality, this finding result is very close to the features of the log return series. For example, there were many trade disputes around the world in 2018, which caused the daily closing price of stocks to fall. Another notable example is the global epidemic of COVID-19 in 2020. The epidemic has caused unprecedented trauma to the economies of countries around the world, and the stock market has also experienced severe shocks. Many stock prices, including the SP500 index, have been strongly affected by the epidemic. The observed data in Fig. 5 has a little volatility for most of the period before 2020, and large fluctuations in the short term after 2020. The excess kurtosis of the observed series is 24.12, which implies that capturing the extreme events using t or normal distribution is not a good choice. Under the framework of the mixture normal GARCH model, the heavy-tailed distributions of the returns can be well fitted.

In addition, the diagrams and histograms of the posterior estimation for each parameter are shown in Figs. 15, 16 of Appendix. It can be seen from trace plots of each parameter that the HMC algorithm explores the parameter space well and does not fall into the local region in Fig. 15. According to the histograms in Fig. 16, except that the histogram of $\rho$ is slightly right skew, the marginal posterior distribution of the other parameter is almost symmetrical.

We use the visual inspection of CUMSUM statistics to check convergence of the HMC algorithm, and the plots based on 5000 draws with discarding the first 5000 draws are reported in Fig. 6. In the CUMSUM plots, we can see that the convergence of parameter $\rho$ is slower than other parameters, and the convergence is relatively good for the parameters $\alpha _0$, $\alpha _1$, $\beta _1$ and $\lambda$. The Geweke statistics of $\alpha _0$, $\alpha _1$, $\beta _1$, $\rho$ and $\lambda$ are 0.6575, −0.3713, −0.1276, −0.2118 and 0.1332, respectively, indicating that all estimated results are convergent. For the parameters of the HMC algorithm, we run several Markov chains to find a suitable step size. In fact, we can refer to Beskos et al. (2013), which provided theoretical analysis of optimal step sizes for HMC algorithm. It’s worth noting that the multiple step size $\Delta s$ selected to keep a good performance are $\{0.0025, 0.0017, 0.0025, 0.0067, 0.0042\}$, and the leapfrog step is 55. Considering the discretization error of the leapfrog, the selection of $\Delta s$ and L results in an acceptance rate of 77%.

Fig. 6

The CUMSUM plots of posterior mean estimates for mixed normal GARCH model

Table 6 The predictive means, SD’s and 95% credibility intervals for volatilities $h_{T}$ at times $T=1408,\ldots ,1412$ of SP 500 using HMC method

For the future prediction, we use the same approach described in Sect. 2.4, which is to perform 10000 iterations in each HMC algorithm. We consider 5-step predictions of 1407 observations. Table 6 displays the estimations and confidence intervals of volatilities. As can be seen from Table 6, the length of confidence intervals and the SD’s of volatilities are quite small, although the SD’s of volatilities increases over time. The results of credibility intervals show that HMC algorithm provides an accurate forecasting intervals. The predictive histogram of $y_t$ and forecasts of $h_t$ are shown in Fig. 7, which can be found that the predictive distributions of $y_t$ and $h_t$ are nearly symmetric. The mean of $y_t$ in the next 5 steps is about zero, which indicates that the future log returns are unlikely to occur large volatilities.

The predictive distributions of VaR at 1% and 5% level can be seen from Fig. 8 that they are almost symmetric. The posterior estimations of VaR are shown to be well in Table 7. From the results shown in Table 7 and Fig. 8, the predictive distributions and credibility intervals for VaR are fairly symmetric. From the Table 7, we can see that the estimated values of VaR increase over time, which imply that the maximum possible loss increases as the future period [d] increases. VaR is related to the market risk, investors should choose a reasonable trading time to prevent from loss.

The log return of the SP500 index exhibits heavy-tailed distributions and volatility cluster. The GARCH model with mixed normal distribution can capture the extreme events of market risk as well as the heavy-tailed distribution of the real data well. Meanwhile, the final estimated results illustrate that HMC algorithm performs more accurate and faster than GG sampler. Therefore, we can conclude that the HMC algorithm provides a good estimate and forecast for the log return of the SP500 index using GARCH model with mixed normal errors.

Fig. 7

The histograms of predictive $h_{1408} \sim h_{1412}$ and $y_{1408} \sim y_{1412}$ for SP 500

Fig. 8

The predicitve distributions of $VaR_{1408}$ $\sim$ $VaR_{1412}$ for SP 500 at 5%(top) and 1%(bottom) level

Table 7 The predictive means, SD’s and 95% credibility intervals of VaR at times $T=1408..,1412$ with probabilities $\alpha$=0.05 and 0.01 for SP 500

4 Conclusion

In this article, we carry out Bayesian inference and prediction for the GARCH-type models with mixed normal errors by the HMC algorithm. This new approach can be simply constructed to capture the GARCH effect in the heavy-tailed behavior of the distributions. Comparing with the GG sampler, the HMC algorithm performs higher sampling efficiency and accuracy for the mixture normal GARCH model in the simulation experiments as well as the empirical analysis.

Because the step size and the number of steps will affect the performance of the HMC algorithm, attention should be paid to design the scheme for adjusting the parameters to obtain best performance in the HMC algorithm. Meanwhile, the extension of the multiple mixture distribution is a challenging problem, it is not easy to identify mixture components. These issues are still worthy of further study and explore.

Appendix

See Figures 9, 10, 11, 12, 13, 14, 15 and 16, Tables 8, 9 and 10.

Fig. 9

The trace plots of parameters for s1

Fig. 10

The histograms of parameters for s1

Fig. 11

The trace plots of parameters for s2

Fig. 12

The histograms of parameters for s2

Fig. 13

The trace plots of parameters for s3

Fig. 14

The histograms of parameters for s

Fig. 15

The trace plots of parameters for SP 500

Fig. 16

The histograms of parameters for SP 500

Table 8 Convergence diagnosis by Geweke test for each parameter

Table 9 Statistics summay of three simulation series

Table 10 Posterior means for the simulated s1, s2 and s3 using HMC sampler