Bayesian Estimation of Economic Simulation Models Using Neural Networks

Abstract

Recent advances in computing power and the potential to make more realistic assumptions due to increased flexibility have led to the increased prevalence of simulation models in economics. While models of this class, and particularly agent-based models, are able to replicate a number of empirically-observed stylised facts not easily recovered by more traditional alternatives, such models remain notoriously difficult to estimate due to their lack of tractable likelihood functions. While the estimation literature continues to grow, existing attempts have approached the problem primarily from a frequentist perspective, with the Bayesian estimation literature remaining comparatively less developed. For this reason, we introduce a widely-applicable Bayesian estimation protocol that makes use of deep neural networks to construct an approximation to the likelihood, which we then benchmark against a prominent alternative from the existing literature. Overall, we find that our proposed methodology consistently results in more accurate estimates in a variety of settings, including the estimation of financial heterogeneous agent models and the identification of changes in dynamics occurring in models incorporating structural breaks.

1 Introduction and Literature Review

Recent years have, to some extent, seen the emergence of a paradigm shift in how economic models are constructed. Traditionally, a need to facilitate mathematical tractability and limited computational resources have led to a dependence on strong assumptions,¹ many of which are inconsistent with the heterogeneity and non-linearity that characterise real economic systems (Geanakoplos and Farmer 2008; Farmer and Foley 2009; Fagiolo and Roventini 2017). Ultimately, the Great Recession of the late 2000s and the perceived failings of traditional approaches, particularly those built on general equilibrium theory, would lead to the birth of a growing community arguing that the adoption of new paradigms harnessing contemporary advances in computing power could lead to richer and more robust insights (Farmer and Foley 2009; Fagiolo and Roventini 2017).

Perhaps the most prominent examples of this new wave of computational approaches are agent-based models (ABMs), which attempt to model systems by directly simulating the actions of and interactions between their microconstituents (Macal and North 2010). In theory, the flexibility offered by simulation should allow for more empirically-motivated assumptions and this, in turn, should result in a more principled approach to the modelling of the economy (Chen 2003; LeBaron 2006). The extent to which this has been achieved in practice, however, remains open for debate (Hamill and Gilbert 2016).

While ABMs initially found success by demonstrating an ability to replicate a wide array of stylised facts not recovered by more traditional approaches (LeBaron 2006; Barde 2016), their simulation-based nature makes their estimation nontrivial (Fagiolo et al. 2019). Therefore, while the last decade has seen the emergence of increasingly large and more realistic macroeconomic models, such as the Eurace (Cincotti et al. 2010) and Schumpeter Meeting Keynes (Dosi et al. 2010) models, their acceptance in mainstream policy-making circles remains limited due to these and other challenges.

The aforementioned estimation difficulties largely stem from the simulation-based nature of ABMs, which, in all but a few exceptional cases,² renders it impossible to obtain a tractable expression for the likelihood function. As a result, most existing approaches have attempted to circumvent these difficulties by directly comparing model-simulated and empirically-measured data using measures of dissimilarity (or similarity) and searching the parameter space for appropriate values that minimise (or maximise) these metrics (Grazzini et al. 2017; Lux 2018). The most pervasive of these approaches, which Grazzini and Richiardi (2015) call simulated minimum distance (SMD) methods, is the method of simulated moments (MSM), which constructs an objective function by considering weighted sums of the squared errors between simulated and empirically-measured moments (or summary statistics).

Though MSM has been widely applied in a number of different contexts³ and has desirable mathematical properties,⁴ it suffers from a critical weakness. In more detail, the choice of moments or summary statistics is entirely arbitrary and the quality of the associated parameter estimates depends critically on selecting a sufficiently comprehensive set of moments, which has proven to be nontrivial in practice. In response, recent years have seen the development of a new generation of SMD methods that largely eliminate the need to transform data into a set of summary statistics and instead harness its full informational content (Grazzini et al. 2017).

These new methodologies vary substantially in their sophistication and theoretical underpinnings. Among the simplest of these approaches is attempting to match time series trajectories directly, as suggested by Recchioni et al. (2015). More sophisticated alternatives include information-theoretic approaches (Barde 2017, 2020; Lamperti 2018a), simulation-based approaches to maximum likelihood estimation (Kukacka and Barunik 2017), and comparing the causal mechanisms underlying real and simulated data through the use of SVAR regressions (Guerini and Moneta 2017). In addition to the development of similarity metrics, attempts have also been made to reduce the large computational burden imposed by SMD methods by replacing the costly model simulation process with computationally efficient surrogates (Salle and Yildizoglu 2014; Lamperti et al. 2018).

Many of the above metrics have also been applied in the context of the related problem of model selection, where the output generated by various candidate models⁵ is compared to empirically-observed data and the model associated with the lowest (highest) dissimilarity (similarity) score is predicted to be the most appropriate description of the empirical data-generating process. In particular, Franke and Westerhoff (2012) propose several variants of a novel financial heterogeneous agent model and make use of a moment-based approach to select the best performing candidate. Using more sophisticated information-theoretic techniques, Barde (2016) pits several prominent ABMs against each another and traditional time series models in a comprehensive series of head-to-head tests. Finally, Lamperti (2018b), who employs similar techniques, compares several variants of the Brock and Hommes (1998) model.⁶

Interestingly, the aforementioned approaches are all frequentist in nature, with Bayesian techniques not generating much interest up until very recently.⁷ This is perhaps rather surprising, given the plethora of Bayesian methods available for dynamic stochastic general equilibrium models (Fagiolo and Roventini 2017). The first major Bayesian study was conducted by Grazzini et al. (2017) and makes use of a relatively simple kernel density estimation-based likelihood approximation. This was later followed by the work of Lux (2018), who employs sequential Monte Carlo methods. While this investigation does make some attempts at Bayesian estimation, the vast majority of the experiments conducted still adopt a frequentist paradigm. In what appears to be a modest paradigm shift, the last year has seen a number of interesting new contributions. These include the work of Delli Gatti and Grazzini (2019), which applies similar techniques to those developed by Grazzini et al. (2017) to a medium-scale macroeconomic model,⁸ the work of Lux (2020), which applies the methodology considered by Lux (2018) to additional Bayesian examples involving several small-scale financial models, and finally the probabilistic programming study conducted by Bertschinger and Mozzhorin (2020), which makes use of the Stan language to perform a calibration and model selection exercise on similar models to those considered by Lux (2020).

While the estimation literature has certainly been growing, it still suffers from a number of key weaknesses. Perhaps the most significant of these is a lack of a standard benchmark against which to compare the performance of new methods. As a result, most new approaches have traditionally only been tested in isolation and comparative exercises have been relatively rare. For this reason, we compared a number of prominent estimation techniques in a previous investigation (Platt 2020) and found, rather surprisingly, that the Bayesian estimation procedure proposed by Grazzini et al. (2017) consistently outperformed a number of prominent SMD methods in a series of head-to-head tests, despite its relative simplicity. We therefore argued that more interest in Bayesian methods is warranted and suggested that increased emphasis should be placed on their development.

Additionally, it is also worth noting that while the approaches of Lux (2020) and Bertschinger and Mozzhorin (2020) may achieve a modest degree of success when applied to small-scale models, they cannot be readily applied to models of a larger scale due to issues of computational tractability, a weakness not shared by the approach of Grazzini et al. (2017), which we found was able to achieve some success when confronted by a large-scale model of the UK housing market.

In line with the above findings and recommendations, we now introduce a method for the Bayesian estimation of economic simulation models⁹ that relaxes a number of the assumptions made by the approach of Grazzini et al. (2017) through the use of a neural network-based likelihood approximation. We then benchmark our proposed methodology through a series of computational experiments and finally conclude with discussions related to practical considerations, such as the setting of the method’s hyperparameters and the associated computational costs.

2 Estimation and Experimental Procedures

In this section, we introduce the reader to a number of the essential elements of our investigation, including a brief discussion of the fundamentals of Bayesian estimation, a description of the approach of Grazzini et al. (2017) (our chosen benchmark), and an introduction to our proposed estimation methodology.

2.1 Bayesian Estimation of Simulation Models

For our purposes, we consider a simulation model to be any mathematical or algorithmic representation of a real world system capable of producing time series (panel) data of the form

$$\begin{aligned} \varvec{X} ^{sim} (\varvec{\theta }, T, i) = \left[ \varvec{x} ^{sim} _{1, i}(\varvec{\theta }), \varvec{x} ^{sim} _{2, i}(\varvec{\theta }), \dots , \varvec{x} ^{sim} _{T, i}(\varvec{\theta }) \right] , \end{aligned}$$

(1)

where $\varvec{\theta }$ is a model parameter set in the space of feasible parameter values, T is the length of the simulation, i represents the seed used to initialise the model’s random number generators, and $\varvec{x} ^{sim} _{t, i}(\varvec{\theta }) \in \mathbb {R}^{n}$ for all $t = 1, 2, \dots , T$.

In general, estimation or calibration procedures aim to determine appropriate values for $\varvec{\theta }$ such that $\varvec{X} ^{sim} (\varvec{\theta }, T, i)$ produces dynamics that are as close as possible to those observed in an empirically-measured equivalent,

$$\begin{aligned} \varvec{X} = \left[ \varvec{x}_{1}, \varvec{x}_{2}, \dots , \varvec{x}_{T} \right] , \end{aligned}$$

(2)

where $\varvec{x}_{t} \in \mathbb {R}^{n}$ for all $t = 1, 2, \dots , T$.

Bayesian estimation attempts to achieve the above by first assuming that the parameter values follow a given distribution, $p(\varvec{\theta })$, which is chosen to reflect one’s prior knowledge or beliefs regarding the parameter values. This is then updated in light of empirically-measured data, yielding a modified distribution, $p(\varvec{\theta } | \varvec{X})$, called the posterior. Bayesian estimation can therefore be framed in terms of Bayes’ theorem as follows:

$$\begin{aligned} p(\varvec{\theta } | \varvec{X}) = \frac{p(\varvec{X} | \varvec{\theta })p(\varvec{\theta })}{p(\varvec{X})}. \end{aligned}$$

(3)

Unfortunately, obtaining an analytical expression for the posterior is typically not feasible. Firstly, the normalisation constant, $p(\varvec{X})$, is unknown or determining it is nontrivial. Secondly, the likelihood, $p(\varvec{X} | \varvec{\theta })$, is intractable for most simulation models, particularly large-scale macroeconomic ABMs. Nevertheless, these limitations can be overcome to some extent. Grazzini et al. (2017) provide a method for approximating $p(\varvec{X} | \varvec{\theta })$ for a particular value of $\varvec{\theta }$, which then allows us to evaluate the right-hand side of

$$\begin{aligned} p(\varvec{\theta } | \varvec{X}) \propto p(\varvec{X} | \varvec{\theta })p(\varvec{\theta }). \end{aligned}$$

(4)

The above may then be used along with Markov chain Monte Carlo (MCMC) methods, such as the Metropolis–Hastings algorithm, to sample the posterior. This is possible since most MCMC techniques only require that we are able to determine the value of a function proportional to the density function of interest rather than the density function itself. It should be apparent, however, that the overall estimation error will depend critically on the method used to approximate the likelihood.

2.2 The Approach of Grazzini et al. (2017)

As previously stated, Grazzini et al. (2017) provide a method to approximate the likelihood for simulation models, which we now discuss in more detail.

In essence, the approach is based on the assumption that, for all $t \ge \tilde{T}$, we reach a statistical equilibrium such that $\varvec{x}_{t, i} ^{sim}(\varvec{\theta })$ fluctuates around a stationary level, $\mathbb {E}[\varvec{x}_{t, i} ^{sim}(\varvec{\theta }) | t \ge \tilde{T}]$, which allows us to further assume that $\varvec{x}_{\tilde{T}, i} ^{sim}(\varvec{\theta }), \varvec{x}_{\tilde{T} + 1} ^{sim}(\varvec{\theta }), \dots , \varvec{x}_{T, i} ^{sim}(\varvec{\theta })$ constitutes a random sample from a given distribution.¹⁰ It is then possible to determine a density function that describes this distribution, which we denote by $\tilde{f}(\varvec{x} | \varvec{\theta })$, using kernel density estimation (KDE), finally allowing us to approximate the likelihood of the empirically-sampled data¹¹ for a given value of $\varvec{\theta }$ as follows:

$$\begin{aligned} p(\varvec{X} | \varvec{\theta }) = \prod _{t = 1} ^{T} \tilde{f}(\varvec{x}_t | \varvec{\theta }). \end{aligned}$$

(5)

It should be apparent that the above results in a simple strategy that is easy to apply in most contexts. It must be noted, however, that this is largely made possible through strong assumptions that seldom hold in practice. In more detail, notice that ordered time series (panel) data is essentially being treated as an i.i.d. random sample, implying that $\varvec{x}_{t, i} ^{sim}(\varvec{\theta }) \perp \varvec{x}_{1, i} ^{sim}(\varvec{\theta }), \dots , \varvec{x}_{t - 1, i} ^{sim}(\varvec{\theta })$ for all $t = 2, 3, \dots , T$. Unfortunately, such independence assumptions do not hold for most simulation models, since $\varvec{x}_{t, i} ^{sim}(\varvec{\theta })$ is likely to be dependent on at least some of the previously realised values, whether this dependence is explicit or mediated through latent variables. Additionally, such assumptions result in a likelihood function that makes no distinction between $\varvec{\theta }$ values that result in identical unconditional distributions but differing temporal trends. Since many economic simulation models and particularly large-scale macroeconomic ABMs produce datasets that are characterised by seasonality or structural breaks, there is likely to be some impact on the quality of the resultant parameter estimates.

Nevertheless, Platt (2020) demonstrates that despite the above shortcomings, the method of Grazzini et al. (2017) is able to provide reasonable parameter estimates in many contexts, while also outperforming several more sophisticated SMD methods. This warrants further investigation and naturally leads one to ask whether relaxing the required independence assumptions would allow for the construction of a superior Bayesian estimation method.

2.3 Likelihood Approximation Using Neural Networks

We now begin our discussion of a relatively simple extension to the likelihood approximation procedure proposed by Grazzini et al. (2017) that is capable of capturing some of the dependence of $\varvec{x}_{t, i} ^{sim}(\varvec{\theta })$ on past realised values. As a starting point, we assume that

$$\begin{aligned} p \left( \varvec{x}_{t, i} ^{sim} \big | \varvec{x}_{1, i} ^{sim}, \dots , \varvec{x}_{t - 1, i} ^{sim}: \varvec{\theta }\right) = p \left( \varvec{x}_{t, i} ^{sim} \big | \varvec{x}_{t - L, i} ^{sim}, \dots , \varvec{x}_{t - 1, i} ^{sim}: \varvec{\theta }\right) \end{aligned}$$

(6)

for all $L < t \le T$, implying that $\varvec{x}_{t, i} ^{sim}(\varvec{\theta })$ depends only on the past L realised values. Our task, therefore, is the estimation of the above conditional densities,

$$\begin{aligned} \tilde{f}\left( \varvec{x}_{t - L, i} ^{sim}, \dots , \varvec{x}_{t - 1, i} ^{sim}, \varvec{x}_{t, i} ^{sim}, \varvec{\phi } \right) \simeq p \left( \varvec{x}_{t, i} ^{sim} \big | \varvec{x}_{t - L, i} ^{sim}, \dots , \varvec{x}_{t - 1, i} ^{sim}: \varvec{\theta }\right) , \end{aligned}$$

(7)

for all $L < t \le T$, where $\varvec{\phi } = \varvec{\phi }(\varvec{\theta })$ are parameters associated with the density estimation procedure.

In our context, we make use of a mixture density network (MDN), a neural network-based approach¹² to conditional density estimation introduced by Bishop (1994). The aforementioned scheme consists of two primary components,¹³ a mixture of K Gaussian random variables,

$$\begin{aligned} \tilde{f}\left( \varvec{x}, \varvec{y}, \varvec{\phi } \right) = \sum _{k = 1} ^{K} \alpha _k \left( \varvec{x}\right) \mathcal {N}\left( \varvec{y} \big | \varvec{\mu }_k\left( \varvec{x}\right) , \varvec{\varSigma }_k\left( \varvec{x}\right) \right) , \end{aligned}$$

(8)

where we denote $\varvec{x}_{t, i} ^{sim}$ by $\varvec{y}$ and $\varvec{x}_{t - L, i} ^{sim}, \dots , \varvec{x}_{t - 1, i} ^{sim}$ by $\varvec{x}$, and functions $\alpha _k$, $\varvec{\mu }_k$ and $\varvec{\varSigma }_k$ of $\varvec{x}$ which determine the mixture parameters. Here, $\alpha _k$, $\varvec{\mu }_k$ and $\varvec{\varSigma }_k$ are the outputs of a feedforward neural network taking $\varvec{x}$ as input and having weights and biases $\varvec{\phi }(\varvec{\theta })$, which are determined by training the network on an ensemble of R Monte Carlo replications simulated by the candidate model for parameter set $\varvec{\theta }$. Using the trained MDN, it is then possible to approximate the likelihood of the empirically-sampled data for a given value of $\varvec{\theta }$ as follows:¹⁴

$$\begin{aligned} p(\varvec{X} | \varvec{\theta }) = \prod _{t = 1} ^{T - L} \tilde{f}(\varvec{x}_{t}, \dots , \varvec{x}_{t + L - 1}, \varvec{x}_{t + L}, \varvec{\phi }). \end{aligned}$$

(9)

While alternative density estimation procedures could potentially have been employed, our consideration of MDNs is motivated primarily by their desirable properties. Specifically, MDNs are, in theory, capable of approximating fairly complex conditional distributions. This follows directly from the fact that mixtures of normal random variables are universal density approximators for sufficiently large K (Scott 2015) and the fact that neural networks are universal function approximators (Hornik et al. 1989), provided they are sufficiently expressive. Therefore, provided that K is sufficiently large and the constructed neural network sufficiently deep (and wide), the above methodology should result in accurate conditional density estimates. Additionally, a number of empirical studies, including those of Sugiyama et al. (2012) and Rothfuss et al. (2019), have found MDNs to produce consistently superior performance when compared to a number of prominent alternatives, further motivating their consideration.

2.4 Method Comparison and Benchmarking

Given that we have now described our proposed estimation methodology, we proceed to discuss our strategy for benchmarking it against the approach of Grazzini et al. (2017), where we follow a similar strategy to that employed in Platt (2020).

We begin by letting $\varvec{X}^{sim}(\varvec{\theta }, T, i)$ be the output of a candidate model, M. Since empirically-observed data is nothing more than a single realisation of the true data-generating process, which may itself be viewed as a model with its own set of parameters, it follows that we may consider $\varvec{X} = \varvec{X}^{sim}(\varvec{\theta }^{true}, T_{emp}, i^{*})$ as a proxy for real data to which M may be calibrated.

In this case, we are essentially estimating a perfectly-specified model using data for which the true parameter values, $\varvec{\theta }^{true}$, are known. It can be argued that a good estimation method would, in this idealised setting, be able to recover these true values to some extent and that methods which produce estimates closer to $\varvec{\theta }^{true}$ would be considered superior. This leads us to define the following loss function

$$\begin{aligned} LS(\varvec{\theta }^{true}, \hat{\varvec{\theta }}) = || \varvec{\theta }^{true} - \hat{\varvec{\theta }} ||_{2}, \end{aligned}$$

(10)

where $\hat{\varvec{\theta }}$ is the parameter estimate (posterior mean) produced by a given Bayesian estimation method.

In practice, it is important that both $\hat{\varvec{\theta }}$ and $\varvec{\theta }^{true}$ are normalised to take values in the interval [0, 1] before the loss function value is calculated. This is because even relatively small estimation errors associated with parameters that typically take on larger values will increase the loss function value substantially more than relatively large estimation errors associated with parameters that typically take on smaller values if no normalisation is performed. Therefore, for each free parameter, $\theta _j \in [a, b]$, we set

$$\begin{aligned} \hat{\theta }_{j} ^{[0, 1]} = \frac{\hat{\theta }_{j} - a}{b - a}, \end{aligned}$$

(11)

with an analogous transformation being applied to $\theta ^{true} _{j}$.

The above allows us to develop a series of benchmarking exercises in which we compare the loss function values associated with our proposed method and that of Grazzini et al. (2017) for a number of different models, free parameter sets, and $\varvec{\theta }^{true}$ values.¹⁵ In all of these comparative exercises, we aim to ensure that the overall conditions of the experiments are consistent throughout, regardless of the method used to approximate the likelihood. Therefore, in all cases, we set the length of the proxy for real data to be $T_{emp} = 1000$, the number of Monte Carlo replications in the simulated ensembles to be $R = 100$, the length of each series in the simulated ensembles to be $T_{sim} = 1000$, and the priors for all free parameters to be uniform over the explored parameter ranges, unless stated otherwise. Additionally, we have also used the same lag length, $L = 3$, for all estimation attempts involving our neural network-based method. While seemingly arbitrary, this choice has very clear motivations that are discussed in detail in Sect. 5.1.

Finally, the MCMC algorithm used to sample the posterior and its associated hyperparameters remain unchanged in most experiments. Rather than using a standard random walk Metropolis–Hastings algorithm, we have instead employed the adaptive scheme proposed by Griffin and Walker (2013), which allows for more effective initialisation, faster convergence, and better handling of multimodal posteriors.¹⁶

3 Candidate Models

With our estimation and benchmarking strategies now described, we introduce the candidate models that we attempt to estimate. Their selection is primarily justified by their ubiquity; each has appeared in a number of calibration, estimation, and model selection studies,¹⁷ leading them to become standard test cases in the field. While computationally-inexpensive to simulate, most are capable of producing nuanced dynamics and thus still prove to be a reasonable challenge for most contemporary estimation approaches.

3.1 Brock and Hommes (1998) Model

The first model we introduce, and by far the most popular in the existing literature, is the Brock and Hommes (1998) model, an early example of a class of simulation models that attempt to model the trading of assets on an artificial stock market by simulating the interactions of heterogenous traders that follow various trading strategies.

We focus on a particular version of the model that can be expressed as a system of coupled equations,¹⁸

$$\begin{aligned} y_{t + 1}&= \frac{1}{1 + r} \left[ \sum _{h = 1} ^{H} n_{h, t + 1} (g_h y_t + b_h) + \epsilon _{t + 1}\right] \text {, } \epsilon _t \sim \mathcal {N}(0, \sigma ^2), \end{aligned}$$

(12)

$$\begin{aligned} n_{h, t + 1}&= \frac{\exp (\beta U_{h, t})}{\sum _{h = 1} ^{H}\exp (\beta U_{h, t})}, \end{aligned}$$

(13)

$$\begin{aligned} U_{h, t}&= (y_t - R y_{t - 1})(g_h y_{t - 2} + b_h - R y_{t - 1}), \end{aligned}$$

(14)

where $y_{t}$ is the asset price at time t (in deviations from the fundamental value $p_{t} ^{*}$), $n_{h, t}$ is the fraction of trader agents following strategy $h \in \left\{ 1, 2, \dots , H \right\}$ at time t, and $R = 1 + r$.

Each strategy, h, has an associated trend following component, $g_h$, and bias, $b_h$, both of which are real-valued parameters. The model also includes positive-valued parameters that affect all trader agents, regardless of the strategy they are currently employing, specifically $\beta$, which controls the rate at which agents switch between various strategies, and the prevailing market interest rate, r.

Finally, assuming an i.i.d. dividend process, the fundamental value $p_{t} ^{*} = p^{*}$ is constant, allowing us to obtain the asset price at time t,

$$\begin{aligned} p_t = y_t + p^{*}. \end{aligned}$$

(15)

3.2 Random Walks with Structural Breaks

The second model we consider is a random walk capable of replicating simple structural breaks, defined according to

$$\begin{aligned} x_{t + 1}= x_{t} + d_{t + 1} + \epsilon _{t + 1} \text {, } \epsilon _t \sim \mathcal {N}(0, \sigma _t ^2), \end{aligned}$$

(16)

where

$$\begin{aligned} d_t, \sigma _t = {\left\{ \begin{array}{ll} d_1, \sigma _1 &{} t \le \tau \\ d_2, \sigma _2 &{} t > \tau . \end{array}\right. } \end{aligned}$$

(17)

Unlike the Brock and Hommes (1998) model, the above is not a representation of a real-world system, but rather an artificially-constructed test example designed to challenge estimation and model selection methodologies.¹⁹ Its inclusion is justified on the grounds that, as previously discussed, many large-scale ABMs produce dynamics that are characterised by structural breaks and the fact that it allows us to compare our approach against that of Grazzini et al. (2017) in cases where the considered data demonstrates clear temporal changes in the prevailing dynamics.

3.3 Franke and Westerhoff (2012) Model

The third model we discuss shares a number of conceptual similarities with the previously described Brock and Hommes (1998) model, being a heterogeneous agent model that simulates the interactions of traders following a number of trading strategies. It is, however, different in a number of key areas, particularly in how the probability of an agent switching from one strategy to another is determined and in its incorporation of only two trader types, chartists and fundamentalists.

As in the case of the Brock and Hommes (1998) model, the core elements of the model can be expressed as a system of coupled equations

$$\begin{aligned} p_t&= p_{t - 1} + \mu \left( n_{t - 1} ^{f} d_{t - 1} ^{f} + n_{t - 1} ^{c} d_{t - 1} ^{c} \right) , \end{aligned}$$

(18)

$$\begin{aligned} d_{t} ^{f}&= \phi (p^{*} - p_t) + \epsilon _{t} ^{f} \text {, } \epsilon _{t} ^{f} \sim \mathcal {N}(0, \sigma _{f} ^{2}),\end{aligned}$$

(19)

$$\begin{aligned} d_{t} ^{c}&= \chi (p_{t} - p_{t - 1}) + \epsilon _{t} ^{c} \text {, } \epsilon _{t} ^{c} \sim \mathcal {N}(0, \sigma _{c} ^{2}),\end{aligned}$$

(20)

$$\begin{aligned} n_{t} ^{f}&= \frac{1}{1 + \exp (-\beta a_{t - 1})},\end{aligned}$$

(21)

$$\begin{aligned} n_{t} ^{c}&= 1 - n_{t} ^{f}, \end{aligned}$$

(22)

where $p_t$ is the log asset price at time t, $p^{*}$ is the log of the (constant) fundamental value, $n_{t} ^{f}$ and $n_{t} ^{c}$ are the market fractions of fundamentalists and chartists respectively at time t, $d_{t} ^{f}$ and $d_{t} ^{c}$ are the corresponding average demands, and the remaining symbols all correspond to positive-valued parameters.

At this point, it is worth pointing out that Franke and Westerhoff (2012) do not introduce a single model, but rather a family of related formulations built on the same foundation²⁰ (Eqs. 18–22). These models differ in how they define $a_{t}$, the attractiveness of fundamentalism relative to chartism at the end of period t, and incorporate a number of different mechanisms, including wealth, herding and price misalignment. This makes the consideration of multiple versions of the model worthwhile and we thus consider two of the proposed versions:²¹

$$\begin{aligned} a_t = \alpha _n (n_{t} ^ {f} - n_{t} ^{c}) + \alpha _0 + \alpha _p (p_t - p^{*}) ^{2}, \end{aligned}$$

(23)

referred to as herding, predisposition and misalignment (HPM), and

$$\begin{aligned} g_{t} ^{s}&= \left[ \exp (p_t) - \exp (p_{t - 1})\right] d_{t - 2} ^{s} \text {, } s = \{f, c\}, \end{aligned}$$

(24)

$$\begin{aligned} w_{t} ^{s}&= \eta w_{t - 1} ^{s} + (1 - \eta ) g_{t} ^{s}, \end{aligned}$$

(25)

$$\begin{aligned} a_t&= \alpha _w (w_{t} ^ {f} - w_{t} ^{c}) + \alpha _0, \end{aligned}$$

(26)

referred to as wealth and predisposition (WP).

As a final remark, we consider $r_t = p_t - p_{t - 1}$, the log return process, rather than $p_t$ in our estimation attempts.

3.4 AR(2)-GARCH(1, 1) Model

In addition to the three main models that we consider in our method comparison study, Sect. 4.2 also provides supplementary exercises involving the application of our proposed methodology to a standard ARMA-GARCH variant. In this case, the model functions primarily as a benchmark against which to compare the performance of the Franke and Westerhoff (2012) model and hence forms part of an elementary model selection investigation, the details of which are elaborated upon in subsequent sections.

Variants of the ARMA-GARCH framework remain ubiquitous in econometric and financial literature and are, despite being conceptually simple, capable of replicating a number of important features of financial returns, such as volatility clustering, ultimately motivating their inclusion as a benchmark. For the purposes of this investigation, we make use of an AR(2)-GARCH(1, 1) model, defined by

$$\begin{aligned} x_{t + 1}&= a_1 x_{t} + a_2 x_{t - 1} + \epsilon _{t + 1}, \end{aligned}$$

(27)

$$\begin{aligned} \sigma _{t + 1} ^{2}&= \omega + \alpha _1 \epsilon _{t} ^{2} + \beta _1 \sigma _{t} ^{2}, \end{aligned}$$

(28)

$$\begin{aligned} \epsilon _{t}&= \sigma _{t} z_{t}, \end{aligned}$$

(29)

where $\omega > 0$, $\alpha _1, \beta _1 \ge 0$, and $z_t \sim \mathcal {N}(0, 1)$.

4 Results and Discussion

We now proceed with the presentation of the results of a comprehensive set of estimation experiments designed to assess the estimation performance of our proposed methodology. These include a set of comparative exercises contrasting its performance with that of the approach of Grazzini et al. (2017) and an additional set of exercises applying it to a number of empirical examples.

4.1 Comparative Exercises

In our comparative exercises, we primarily follow the approach laid out in Platt (2020), in which a subset of each model’s parameters is estimated using different methods in order to determine loss function values that facilitate direct comparison, as outlined in Sect. 2.4. All parameters not estimated are simply set to their true values (those used to generate the pseudo-empirical time series to which the models are calibrated) when generating the data required to construct a likelihood approximation.

The consideration of parameter subsets is necessitated on a number of grounds. Firstly, the use of such subsets allows us to consider a wide variety of interesting models, while maintaining a level of computational tractability. Secondly, the consideration of additional parameters can, in some models, introduce parameter identification difficulties that stem from collinear or similar relationships between model parameters that render them unidentifiable regardless of the estimation method employed. As an example, a similar protocol is used by Lux (2018) when estimating the Alfarano et al. (2008) model, for which only a subset of the model parameters can be estimated due to the existence of such relationships.

4.1.1 Brock and Hommes (1998) Model

We now begin our discussion of the obtained results by focusing on the Brock and Hommes (1998) model.²²

In these experiments, we consider a market with $H = 4$ trading strategies and focus on estimating $g_2$, $b_2$, $g_3$, and $b_3$, the trend following and bias components for two of these strategies. For the first free parameter set, we consider $g_2 \in [-2.5, 0]$, $b_2 \in [-1.5, 0]$, $g_3 \in [0, 2.5]$, and $b_3 \in [0, 1.5]$, corresponding to a contrarian strategy with a negative bias and a trend following strategy with a positive bias respectively. For the second free parameter set, we instead consider $g_2, g_3 \in [0, 2.5]$, $b_2 \in [0, 1.5]$, and $b_3 \in [-1.5, 0]$, corresponding to trend following strategies with positive and negatives biases respectively.

At this point, it is imperative that a number of important features of the Brock and Hommes (1998) model are highlighted, particularly as they relate to our chosen parameter ranges. From Eqs. (12)–(14), it should be apparent that the model makes no distinction between individual trend following ($g_1$, $g_2$, $g_3$, and $g_4$) and bias ($b_1$, $b_2$, $b_3$, and $b_4$) parameters; each is subject to identical calculations and plays the same role in each equation. It thus follows that it is the addition of constraints on the values of each of these parameters that defines a given strategy and such constraints are an intrinsic part of the model definition.²³ Therefore, our considered parameter ranges may be seen as defining two distinct variants of the model for which two of the four strategy types differ, as discussed when introducing them above.

Fig. 1

Marginal posterior distributions for free parameter set 1 of the Brock and Hommes (1998) model

The above features also have important consequences for the estimation of the model in general. To illustrate, the model output would be identical if, for example, we considered two different model configurations, $\{g_2 = -0.7, b_2 = -0.4, g_3 = 0.5, b_3 = 0.3\}$ and $\{g_2 = 0.5, b_2 = 0.3, g_3 = -0.7, b_3 = -0.4\}$, with the values of the remaining parameters being identical. This is because the model is generally agnostic to differences in the value of the index h to which a particular strategy is assigned, provided that the overall composition of strategies remains unchanged, as is the case for the two example model configurations given above. This implies that if we were to instead consider symmetric parameter ranges, such as $g_2, g_3 \in [-2.5, 2.5]$, and $b_2, b_3 \in [-1.5, 1.5]$ for the first free parameter set, the considered free parameters would become unidentifiable, regardless of the estimation approach employed. It is therefore vital that we constrain the explored parameter ranges to ensure that the model and corresponding estimation problem are well-specified and that the associated strategies are distinct.²⁴

Table 1 Estimation result summary for the Brock and Hommes (1998) model

Now, referring to Fig. 1, which presents a graphical illustration of the estimation results associated with the first free parameter set, we observe that there are a number of key differences in performance that emerge between our proposed methodology and that of Grazzini et al. (2017). While both approaches seem to perform somewhat comparably when estimating $b_2$, $g_3$, and $b_3$, producing posterior means within reasonably close proximity to the corresponding true parameter values, more significant differences emerge when considering $g_2$. Specifically, we see that while the posterior mean associated with the method of Grazzini et al. (2017) is a relatively poor estimate, our proposed methodology fares far better and maintains a consistent level of performance. Additionally, we also observe that the posteriors associated with our proposed methodology are significantly narrower and more peaked, with their density concentrated in a smaller region of the parameter space. This can be seen as indicative of reduced estimation uncertainty.

Table 1 elaborates on these findings and reveals that similar behaviours also emerge in the case of the second free parameter set. Specifically, we find that differences in estimation performance are generally more pronounced when considering the posterior means for $g_2$ as opposed to those associated with $g_3$, $b_2$, and $b_3$. Since our proposed methodology produces significantly more accurate $g_2$ estimates, we ultimately observe lower loss function values for both free parameter sets. We also observe that our approach results in reduced posterior standard deviations ($\varvec{\sigma }_{posterior}$) consistently for all but one of the free parameters,²⁵ in line with our observation of reduced estimation uncertainty in Fig. 1. It can thus be concluded that our proposed methodology results in meaningful improvements in estimation performance in the context of the Brock and Hommes (1998) model.

Finally, in Appendix 2, where we describe the method used to sample the posteriors, we indicate that we run the procedure multiple times from different starting points in the parameter space and combine the obtained samples into a single, larger sample from which we estimate $\varvec{\mu }_{posterior}$ and $\varvec{\sigma }_{posterior}$. We can, however, estimate the posterior mean for each of these runs individually and determine the standard deviation of $\varvec{\mu }_{posterior}$ across the instantiations of the algorithm, which we call $\varvec{\sigma }_{sampling}$. As shown in Table 1, this standard deviation is generally very small for both methods, suggesting that the posterior mean estimates are robust to changes in the initial conditions of the MCMC algorithm.²⁶

4.1.2 Random Walks with Structural Breaks

Moving on from the Brock and Hommes (1998) model, we now discuss the estimation of a random walk incorporating a structural break. In these experiments, we consider a fixed structural break location,²⁷$\tau = 700$, and determine the extent to which both methods are capable of estimating the pre- and post-break drift, $d_1, d_2 \in [-2, 2]$, and volatility, $\sigma _1, \sigma _2 \in [0, 10]$, for differing underlying changes in the dynamics. While the loss function described in Sect. 2.4 will still be used as our primary metric, we note that since the considered free parameters directly define the dynamics that characterise the different regimes of the data, it would also be worthwhile to assess the extent to which the competing approaches are able to correctly identify the relationships between the parameters and hence the shift in the pre- and post-break dynamics ($\varDelta _d$ and $\varDelta _{\sigma }$).

Table 2 Estimation result summary for the random walk model (increasing volatility)

Before proceeding, however, there are a number of nuances that should be highlighted. Being a random walk, the model clearly produces non-stationary time series and therefore violates a key assumption of the method of Grazzini et al. (2017). For this reason, it is necessary to consider the series of first differences, $x_t - x_{t - 1}$, rather than $x_t$ itself. While our approach does not make stationarity assumptions, we have none the less considered the series of first differences when applying both methods to make the comparison as fair as possible. It should also be noted that we have assumed the location of the structural break to be unknown or difficult to determine a-priori (as is the case in most practical problems), meaning that we apply both estimation approaches to the full time series data to estimate both the pre- and post-break parameters simultaneously. If, however, the location of the structural break was known, it would be possible to estimate the relevant parameters separately using appropriate subsets of the data, a less challenging undertaking that we do not consider here.

Table 3 Estimation result summary for the random walk model (increasing drift)

Now, referring to Table 2, we see that both our proposed estimation methodology and that of Grazzini et al. (2017) perform similarly well when attempting to estimate the pre- and post-break volatility, with both producing reasonable estimates for the free parameters and both being able to identity the correct shift in the dynamics. Referring to Tables 3 and 4, however, we see that more pronounced differences emerge when attempting to estimate the pre- and post-break drift. While this is clearly evident from the fact that the loss function values associated with our proposed methodology are noticeably lower in all cases, a more detailed analysis reveals further distinctions worth mentioning. Table 3, which presents the results for cases involving an increasing drift, reveals that our proposed methodology has correctly identified an increasing trend in both cases and has also more or less correctly identified that the increase in drift for parameter set 4 is three times that of parameter set 3. In contrast to this, the method of Grazzini et al. (2017) incorrectly suggests a decreasing trend in both cases. Table 4, which presents the results for cases involving a decreasing drift, similarly shows that our proposed methodology delivers superior performance when attempting to identify the change in drift.

Table 4 Estimation result summary for the random walk model (decreasing drift)

This change in the relative performances of each method when estimating the drift rather than the volatility is a direct consequence of the relationship between the deterministic and stochastic components of the model. For the selected parameter ranges, the random fluctuations, $\epsilon _t$, dominate the evolution of the model, with the drift producing a more subtle effect, particularly after the structural break occurs. For this reason, correctly estimating the pre- and post-break volatility is a far less challenging task than estimating the pre- and post-break drift. Therefore, while both methods perform well when estimating parameters associated with dominant effects like volatility, our method’s incorporation of dependence on previously observed values seems to be important when estimating parameters related to more nuanced and less dominant aspects of a model.

4.1.3 Franke and Westerhoff (2012) Model

Table 5 Estimation result summary for the Franke and Westerhoff (2012) model

As stated in Sect. 3.3, the final model we consider has a number of alternate configurations differing in how the attractiveness of fundamentalism relative to chartism, $a_t$, is determined during each period. For this reason, we consider two of these configurations, HPM and WP, and focus on estimating the parameters associated with the rules governing $a_t$: $\alpha _n \in [0, 2]$, $\alpha _0 \in [-1, 1]$, $\alpha _p \in [0, 20]$, $\alpha _w \in [0, 15000]$, and $\eta \in [0, 1]$, while also estimating the standard deviation of the noise term appearing in the chartist demand equation, $\sigma _c \in [0, 5]$. Our selected parameter ranges take the intervals presented in Table 1 of Barde (2016) as a basis, with only slight modifications being made for the purposes of our investigation.²⁸

Fig. 2

Marginal posterior distributions for the WP parameter set of the Franke and Westerhoff (2012) model

Referring to Table 5, we see that our proposed estimation methodology appears slightly more effective than that of Grazzini et al. (2017) for the HPM parameter set, producing competitive estimates for all of the considered free parameters and resulting in a lower loss function value. Nevertheless, the estimates do not differ substantially when comparing the methods. Despite this, we see, in what is a seemingly analogous trend to what was observed in the random walk experiments, that the differences in performance are more pronounced for the WP parameter set. In particular, we see a substantial difference in the loss function values associated with each method, brought about by differences in the quality of estimates produced for $\eta$.

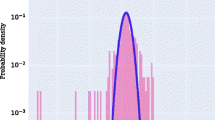
As illustrated in Fig. 2, the method of Grazzini et al. (2017) produces a wide posterior for $\eta$ that is dispersed across the entirety of the explored parameter range, which results in a relatively poor estimate. In contrast to this, we see that the proposed methodology fares better, producing a far narrower posterior and a significantly more accurate estimate. While it is nontrivial to identify any definitive causes for the observed behaviours due to the nonlinear nature of heterogeneous agent models, it is worth pointing out that the inclusion of wealth dynamics in the WP version of the model introduces a dependence of $a_t$ on the previous return via Eqs. (24)–(26), which may in turn increase the strength of the relationship between the current and previously observed values in the log return time series.

As a final remark, notice that for the vast majority of the free parameters considered, the proposed methodology also results in lower posterior standard deviations, as was the case for the previously considered models.

4.1.4 Overall Summary

In the preceding subsections, we have focused primarily on analysing the results on a case-by-case basis. Here, however, we provide a summative comparison across all of the considered models. This is achieved though the consideration of a number of key performance metrics, presented in Table 6, which compare the approaches at both a global and individual parameter level.

The first of the aforementioned metrics, and the most important, $LS_{mdn} < LS_{kde}$, indicates how often the proposed methodology results in lower loss function values, and hence measures its relative ability to recover the true parameter set. We observe that in all cases considered, our methodology results in lower loss function values, which can be seen as indicative of dominance at the global level.

Table 6 Estimation result summary across all models

The second metric, $|\mu _{mdn} ^{i} - \theta _{true} ^{i}| < |\mu _{kde} ^{i} - \theta _{true} ^{i}|$, determines how often our proposed methodology produces superior estimates for individual parameters. In some situations, one might find that the estimates obtained for a subset of the free parameters by the method of Grazzini et al. (2017) are superior, even if the overall estimate for the entire free parameter set is not as good. Nevertheless, we find that in over $70\%$ of cases, our methodology also results in superior estimates at the level of individual parameters, a comfortable majority. It should also be noted that in almost all situations where $|\mu _{mdn} ^{i} - \theta _{true} ^{i}| > |\mu _{kde} ^{i} - \theta _{true} ^{i}|$, such as $\sigma _1$ in the random walk model and $\sigma _c$ in the Franke and Westerhoff (2012) model (HPM parameter set), the differences in the estimates produced by both methods are incredibly small. In contrast to this, a sizeable number of cases where $|\mu _{mdn} ^{i} - \theta _{true} ^{i}| < |\mu _{kde} ^{i} - \theta _{true} ^{i}|$, such as $g_2$ in the first free parameter set of the Brock and Hommes (1998) model and $\eta$ in the second free parameter set of the Franke and Westerhoff (2012) model, are characterised by comparatively large differences in the estimates obtained by the competing approaches. This suggests that our proposed methodology also demonstrates a degree of dominance at the level of individual parameters.

The final metric, $\sigma _{mdn} ^{i} < \sigma _{kde} ^{i}$, indicates how frequently our proposed methodology results in reduced posterior standard deviations for individual parameters, which can be viewed as roughly quantifying estimation uncertainty. We find that our approach again delivers consistently superior performance along these lines, producing a smaller posterior standard deviation in over $81\%$ of the considered cases.

Based on the evidence presented by the above metrics as a whole, it would appear that our proposed methodology does indeed compare favourably to that of Grazzini et al. (2017), which was itself already shown to dominate a number of other contemporary approaches in the literature by Platt (2020). This ultimately validates our method as a worthwhile addition to the growing toolbox of estimation methods for economic simulation models.

4.2 Empirical Examples

In the preceding exercises, we focused primarily on a comparison of the estimation performance of our proposed methodology with that of the approach of Grazzini et al. (2017) in the context of pseudo-empirical data. We now proceed to empirical applications of our approach involving the DCA-HPM variant²⁹ of the Franke and Westerhoff (2012) model, which we benchmark against a standard and widely-used approach for modelling financial returns, an AR(2)-GARCH(1, 1) model, in an attempt to provide a simple example of the competitiveness of the ABM paradigm relative to other approaches.

4.2.1 Full Model Estimation

Unlike in the previously considered cases, we estimate all model parameters simultaneously in each exercise rather than limiting ourselves to parameter subsets. It is therefore imperative that, before attempting to fit both models to empirical data using our proposed methodology, we first demonstrate our approach’s ability to recover reasonable values for each of the considered free parameters. Therefore, as in Sect. 4.1, we begin by calibrating both models to pseudo-empirical time series data as a validation step.

To account for the increased number of free parameters considered in these experiments, we are required to adjust certain aspects of our overall procedure. In particular, we increase the length of the pseudo-empirical data and model Monte Carlo replications, $T_{emp}$ and $T_{sim}$ respectively, to 2000, while reducing the number of model Monte Carlo replications,³⁰R, to 50. Additionally, we also increase the number of sample sets and burning-in period associated with the adaptive Metropolis–Hastings algorithm to 15000 and 10000 respectively.

Table 7 Estimation result summary for the full Franke and Westerhoff (2012) model on several datasets

As before, we employ uniform priors over the considered parameter ranges. For the AR-GARCH model, we assume $a_1, a_2 \in [-1.5, 1.5]$ and $\omega$, $\alpha _1$, $\beta _1 \in [0, 2]$. For the Franke and Westerhoff (2012) model, we again slightly modify the ranges originally considered in the comparative exercise conducted by Barde (2016), leading us to assume $\phi , \chi \in [0, 4]$, $\alpha _0 \in [-1, 1]$, $\alpha _n \in [0, 2]$, $\alpha _p \in [0, 20]$, $\sigma _f \in [0, 1.25]$, and $\sigma _c \in [0, 5]$. It should be noted that, as pointed out by both Franke and Westerhoff (2012) and Bertschinger and Mozzhorin (2020), $\mu$ and $\beta$ are redundant parameters that simply act as multiplicative constants for $\phi , \chi , \sigma _f, \sigma _c$ and $\alpha _0, \alpha _n, \alpha _p$ respectively and should therefore not be estimated, leading us to fix their values to the defaults suggested by Franke and Westerhoff (2012), as indicated in Table 7.

Additionally, particular attention should be paid to $\sigma _f$, where we consider a more constrained range of variation compared to that of $\sigma _c$. This is necessitated primarily due to idiosyncrasies that emerge regardless of the estimation methodology employed. Consistent with the findings of Bertschinger and Mozzhorin (2020), who employ a probabilistic programming approach, we find that the estimation of the DCA-HPM variant of the Franke and Westerhoff (2012) model can, in certain situations, lead to a bimodal posterior that renders certain parameters unidentifiable. When comparing the two obtained modes, it emerges that it is in fact the values of $\sigma _c$ and $\sigma _f$ that drive the observed bimodality, with one mode being associated with $\sigma _f < \sigma _c$ and another with $\sigma _f > \sigma _c$,³¹ despite both modes having very similar log-likelihoods. This necessitates the addition of a constraint that enforces parameter identifiability, leading us to consider a reduced range of variation for $\sigma _f$ as indicated above, ensuring that the mode for which $\sigma _f < \sigma _c$ is always returned in cases where the posterior is bimodal. As stated by Bertschinger and Mozzhorin (2020), the mode in which $\sigma _f > \sigma _c$ leads to model dynamics in which fundamentalist agents are the primary drivers of volatility. This is in contrast to the original intent of the model, where fundamentalists are expected to instead produce a stabilising effect and chartists are intended to drive volatile price movements, motivating our choice.

Table 8 Estimation result summary for the full AR(2)-GARCH(1, 1) model on several datasets

Directly following the preceding validation exercise, we apply an identical protocol³² to the log-return time series associated with the closing prices of two major stock market indices, the FTSE 100 from 03-01-2012 to 30-12-2019, and the Nikkei 225 from 01-03-2011 to 30-12-2019, with the date ranges selected to ensure that the resulting empirical time series are both recent and of a similar length to the pseudo-empirical series used in the validation step.³³ The complete sets of estimation results for both the Franke and Westerhoff (2012) and AR-GARCH models are presented in Tables 7 and 8 respectively, with a number of aspects worth highlighting. To begin, we notice that, for both models, the validation exercises involving simulated data demonstrate that, despite an increase in the considered number of free parameters, the quality of the obtained estimation results remains in line with those associated with the benchmarking exercises presented in Sect. 4.1, with the posterior means of all free parameters being within reasonably close proximity to their true values. This is ultimately very reassuring, and provides some level of confidence in the validity of the results obtained when applying our protocol to empirical data. Proceeding to the empirical results themselves, it should additionally be noted that, unlike the parameters of the AR-GARCH model, the parameters of the Franke and Westerhoff (2012) model are readily interpretable, and may thus provide a number of meaningful insights regarding the considered markets. In particular, we notice that despite very similar estimates for $\sigma _f$, the Nikkei dataset results in a noticeably larger estimate for $\phi$ when compared to that obtained for the FTSE, suggesting that fundamentalist traders in the former market have a greater tendency to buy or sell in response to a given level of perceived mispricing. Additionally, we also observe that despite virtually identical estimates for $\chi$, the Nikkei dataset results in a noticeably larger estimate for $\sigma _c$, suggesting greater heterogeneity in the demands of chartist traders in the Japanese market. As a final remark, it is also worth noting that the Nikkei is associated with a stronger herding tendency and a more significant (though still relatively weak) predisposition to chartist trading.

4.2.2 Model Comparison

With both models now being calibrated to empirical data, it is relatively straightforward to also provide a simple model comparison exercise. Indeed, given that ABMs are often positioned as more interpretable alternatives to traditional time series models, it is worth considering whether the calibrated Franke and Westerhoff (2012) model is competitive when benchmarked against a more traditional AR-GARCH model. Along these lines, we compare the two candidate models according to two distinct criteria.

As a first step, we perform a simple moment-based comparison in the vein of Franke and Westerhoff (2012), where we initialise each model using the final parameter estimates obtained in our previous exercise ($\varvec{\mu }_{posterior}$ in Tables 7 and 8) and proceed to generate 200 Monte Carlo replications of the log return process of length $T_{sim} = 2000$ (one set of replications for each model). For each of these replications, we estimate the values of 6 moments, which may then be used to determine the means and associated standard errors³⁴ for the ensembles and hence facilitate an elementary comparative exercise.³⁵ As with any moment-based investigation, the choice of moments is of critical importance, leading us to select quantities that correspond to well-known return time series stylised facts. In particular, we consider the standard deviation, excess kurtosis, and skewness of the raw return series, and autocorrelation coefficients of the absolute return series at lags 1, 3, and 5. The inclusion of the kurtosis and skewness is motivated chiefly by the fat-tailed and negatively-skewed distributions associated with empirically-observed returns and, along with the standard deviation, is intended to capture key features of the unconditional return distribution. In contrast, the inclusion of the aforementioned autocorrelation coefficients is intended to capture the phenomenon of volatility clustering and thus instead focuses on the conditional distribution and temporal dynamics of the return process.

Referring to Table 9, which presents the results of our moment comparison exercise, we find that the Franke and Westerhoff (2012) model generally delivers the best performance, with the mean values of 5 and 4 of the considered moments being closer to their empirical values than the corresponding AR-GARCH equivalents for the Nikkei and FTSE datasets respectively, providing some evidence of the competitiveness of ABMs relative to more traditional approaches. Of course, moment-based model selection techniques suffer from identical weaknesses to those encountered in the estimation context,³⁶ leading us to keep our discussion of the above results relatively brief and additionally necessitating the consideration of a more principled set of model comparison tools.

Along these lines, we also compare the estimated models to the empirical data using the Markov Information Criterion (MIC), an information-theoretic approach³⁷ developed by Barde (2017) and applied empirically to several ABMs in Barde (2016).³⁸ In essence, the MIC can be viewed as a generalisation of the Akaike Information Criterion (AIC) in the sense that it calculates a bias-corrected estimate of the cross-entropy between the output generated by a candidate model and an empirically-observed equivalent. Such cross-entropy estimates can be calculated for various models and the candidate with the lowest MIC score would then be predicted to be most appropriate given the empirical data.

Table 9 Estimated Model Comparison

When constructing the aforementioned cross-entropy estimates, a number of operations are applied to an ensemble of model-generated Monte Carlo replications, including a binary discretisation step,³⁹ to construct an Nth order Markov process using an algorithm known as context tree weighting (CTW) (Willems et al. 1995). The obtained transition probabilities and the associated sum of the binary log scores along the length of the empirically-observed data are then used to produce the estimate. In our case, we make use of the same ensembles of 200 Monte Carlo replications considered in the moment-based comparative exercise as input to the CTW algorithm to calculate the corresponding MIC scores for both models and both empirical datasets. Since the MIC does not require the selection of an arbitrary set of moments for comparison and makes use of the original time series data, it is preferable to a moment-based approach (Barde 2016; Platt 2020).

Once again referring to Table 9, which also presents the aforementioned MIC scores, we see that the Franke and Westerhoff (2012) model again delivers the best performance, providing further evidence of its competitiveness relative to the more-established AR-GARCH model and reinforcing the findings of Barde (2016) and Bertschinger and Mozzhorin (2020). Ultimately, the provided comparative exercises are primarily illustrative and included to provide a simple demonstration of the ability of our approach to facilitate model comparison and selection. The preceding exercises could, of course, be extended to a larger set of candidate models and incorporate additional Bayesian model selection techniques, such as cross-validation, to further explore these findings and yield a more comprehensive and robust set of model selection experiments. We leave this to future research.

5 Practical Considerations

5.1 Choosing the Lag Length

As previously stated, we set $L = 3$ in all estimation experiments involving our proposed method. Naturally, one may wonder whether this is an arbitrary choice or if there is a systematic way of choosing L. Similarly, one may also wonder if the obtained results are robust to this choice, even if only to some extent. We now address both issues.

When applying the proposed methodology, we observed a phenomenon that appeared to be relatively consistent throughout the experiments. In more detail, we observe that while increasing L initially has a pronounced effect on the estimated conditional densities, there exists some $L^{*} \ge 0$ such that for $L \ge L^{*}$,

$$\begin{aligned} p \left( \varvec{x}_{t, i} ^{sim} \big | \varvec{x}_{t - L, i} ^{sim}, \dots , \varvec{x}_{t - 1, i} ^{sim}: \varvec{\theta }\right) \simeq p \left( \varvec{x}_{t, i} ^{sim} \big | \varvec{x}_{t - L - 1, i} ^{sim}, \dots , \varvec{x}_{t - 1, i} ^{sim}: \varvec{\theta }\right) , \end{aligned}$$

(30)

or, in other words, the MDN essentially ignores the additional lags.

We illustrate this graphically in Fig. 3. Here, we train an MDN using a similar process to that employed in our estimation experiments on an ensemble of 100 realisations of length 1000 generated using the Brock and Hommes (1998) model initialised using the true values associated with the first free parameter set (see Table 1). We then randomly draw an arbitrary sequence of 6 consecutive values, $\{z_1, z_2, z_3, z_4, z_5, z_6\}$, from any time series of length 1000 generated by the Brock and Hommes (1998) model for the above parameter configuration, i.e. any series in the ensemble. This then allows us to use the trained MDN to plot the conditional density functions, $p \left( y \big | z_{6 - L + 1}, \dots , z_6 \right)$, for differing choices of $L \le 6$, and observe the aforementioned trend.

Fig. 3

A demonstration of the sensitivity of the conditional density estimates to the choice of lag length for a typical example of the Brock and Hommes (1998) model

In more detail, the upper left panel of Fig. 3 contrasts the density function obtained when conditioning on none of the previous observations to that obtained when conditioning on a single past realised value. Here we see that, in this case, there is a clear difference in the obtained density functions, with differences in the associated means being apparent and the lag 1 density being significantly more peaked around its mean. A similar trend is also observed in the upper middle panel, which analogously compares the density functions obtained by conditioning on one and two of the previous observations. When examining the additional comparisons represented in subsequent panels, however, we see that the consideration of three as opposed to two previous observations, four as opposed to three previous observations, and so on, results in almost no perceivable difference between the obtained density functions, suggesting that we eventually reach a point, in this case $L^{*} \simeq 2$, at which the consideration of additional lags has a negligible effect on the obtained conditional density estimates.

Repeating this exercise on models for which the true number of lags, $L_{true}$, is known a-priori, we see that $L^{*} = L_{true}$, providing some evidence that the MDN is able to ignore uninformative lags. To elaborate, Fig.4 shows that, when applying the above procedure to i.i.d. log-normal random samples, the obtained density functions are virtually identical, regardless of the considered number of lags. This is exactly as we would expect, as each observation is, by construction, independent ($L_{true}$ = 0), meaning past observations should not have any influence on the resultant density estimates. Analogously, Fig. 5, which considers a standard AR(2) model, illustrates behaviours consistent with those observed in Fig. 3, with marked changes in the obtained density functions initially being observed as the number of lags is increased, until reaching $L^{*} \simeq 2$, at which point the addition of further lags no longer produces a noticeable effect. As in the case of the log-normal samples, this is exactly as we would expect, since the AR(2) model produces, by construction, time series in which observations are dependent only on the last two values ($L_{true} = 2$).

Fig. 4

A demonstration of the sensitivity of the conditional density estimates to the choice of lag length for i.i.d. random samples following a log-normal distribution, LN(0, 0.0625). The upper left panel compares the conditional density estimate for $L = 1$ to the known, true unconditional density function

This has a number of important implications. Firstly, it implies that plots of the type we have constructed here could be used as a means to systematically inform the choice of L for arbitrary models. Secondly, and perhaps more importantly, it implies that if $L \ge L_{true}$, the procedure should demonstrate at least a modest degree of robustness to the choice of lag at the level of individual conditional density estimates, which would, by extension, result in some level of robustness in the likelihood approximation, provided that the MDN is sufficiently expressive and sufficiently well-trained. This may explain why simply setting $L = 3$ resulted in a high level of estimation performance in our experiments, regardless of the considered model, since the models considered are not characterised by long-range dependencies.⁴⁰

Fig. 5

A demonstration of the sensitivity of the conditional density estimates to the choice of lag length for an AR(2) model, $x_{t + 1} = 0.45 x_t + 0.45 x_{t - 1} + \epsilon _t$, where $\epsilon _t \sim \mathcal {N}(0, 1)$

5.2 Computational Costs and Applicability to Large-Scale Models

At this point, one may ask whether the proposed estimation routine compares favourably to other contemporary alternatives in terms of computational costs and, perhaps more importantly, whether it may be applied to more complex models. As stated by Grazzini et al. (2017), the cost of generating simulated data using a candidate model is generally dominant, particularly for large-scale models that may need to be run for several minutes in order to generate a single realisation. It is therefore imperative that any estimation methodology keep the simulated ensemble size, which we call R, to a minimum.

As previously stated, we consider at most $R = 100$ replications, which results in a relatively large training set of $R(T_{sim} - L) = 99700$ training examples. This compares favourably to most alternatives in the literature on a number of grounds. Firstly, most studies which have attempted to estimate models of similar complexity make use of ensembles consisting of a far greater number of realisations, typically between 500 and 2000 (Barde 2017; Lamperti 2018a; Lux 2018). Secondly, the training set associated with $R = 100$ is already large relative to the complexity of the network architecture we employ, which is described in “Neural Network Architecture” in Appendix 1.

To illustrate this point, we repeat the experiment associated with parameter set 1 of the Brock and Hommes (1998) model, changing only the simulated ensemble size, which has been halved to $R = 50$. We find that even with this drastic decrease in the number of Monte Carlo replications, the proposed methodology still performs well and results in a lower loss function value than was obtained using the method of Grazzini et al. (2017) in the original experiments, with a ratio⁴¹ of $LS_{MDN} / LS_{KDE} = 0.2899$. This provides some evidence that even for greatly reduced ensemble sizes, our approach remains viable, and implies that the complexity of the candidate model and hence the employed neural network would likely need to be increased substantially before any increase in R beyond 100 might be required.

Fig. 6

Training time for various MDN configurations on the same ensemble of 100 realisations of length 1000 generated using the Brock and Hommes (1998) model initialised using parameter set 1. The point indicated on both the left and right panels corresponds to the configuration employed in our estimation experiments

In addition to concerns related to the size of the simulated ensemble, it is also worthwhile to consider the actual computational costs of the neural network training procedure relative to those associated with the generation of a single model realisation. For this reason, Fig. 6 demonstrates the total training time required by various neural network configurations, most of which are larger than that of the network employed in this investigation, which typically takes $\sim 5$ s to be completely trained. We find that even for substantially more complex neural networks than those considered in our investigation, the overall training time is still typically less than 40 s, which compares favourably to the simulation time of large-scale models, and we additionally find that the increase in computational time is linear for both increases in the lag length and network width.

Further, it should be noted that GPU parallelisation was not employed when generating the aforementioned computational cost diagrams. Given the significant speedup that could be expected with the use of such hardware, typically in the region of $20\times$ (Oh and Jung 2004), we find there to be at least some evidence that the time taken to train the neural network should be negligible in comparison to the time taken to generate a single model realisation, even for far more sophisticated neural networks and candidate models.

Of course, a natural next step would be a detailed examination of the ability of our methodology, and particularly the neural network configuration introduced in “Neural Network Architecture” in Appendix 1, to estimate large-scale models. Unfortunately, a thorough analysis is significantly beyond the scope of this investigation. We can, however, provide an illustrative example of the applicability of our approach to models significantly larger in scope than those considered in Sect. 4. In particular, Platt (2020) provides an example of the use of the method of Grazzini et al. (2017) to estimate four key parameters of a large-scale model of the UK housing market (Baptista et al. 2016). The model in question involves the simulation of thousands of discrete household agents, is computationally-expensive to simulate, and produces more nuanced dynamics than the other models considered in this investigation. It would thus be worthwhile to determine the extent to which our proposed methodology maintains its previously established level of performance in this more challenging context.

Fig. 7

Marginal posterior distributions for the housing market model. The plotted density functions are obtained by applying KDE to the posterior samples obtained using each method. The results associated with the method of Grazzini et al. (2017) were originally presented by Platt (2020)

We therefore repeat the exercise presented in Section 4.2.1 of Platt (2020), making no changes to the experimental procedure,⁴² with the exception of the approach used to estimate the likelihood, where we now consider our proposed methodology, as it is applied in Sect. 4 of this manuscript. The results of the above exercise, along with those obtained when instead employing the method of Grazzini et al. (2017), are presented in Fig. 7, and demonstrate that the performance of our proposed methodology is comparable to that yielded in the case of the simpler models considered in Sect. 4.1. To be more precise, we see that our approach typically results in marginal posteriors that are more strongly peaked around their respective means, with those means tending to, in most cases, be noticeably closer to the true parameter values when compared to those associated with the method of Grazzini et al. (2017). This is particularly evident in the case of the Sale Epsilon parameter. Further, we also observe that the aforementioned posterior means are all reasonable estimates of the true parameter values.

It thus follows that the above exercise provides promising evidence that our approach may indeed be suitable for the estimation of large-scale models and further provides a concrete demonstration of the computational tractability of such exercises. This is particularly relevant, as approaches similar to the particle filter considered by Lux (2018) would generally not be well-suited to such models due to their incorporation of high-dimensional latent spaces.⁴³ Additionally, the probabilistic programming approach employed by Bertschinger and Mozzhorin (2020) cannot be applied to models with discrete agents due to theoretical restrictions induced by the sampling methodology. It would therefore be worthwhile to consider more ambitious exercises involving larger free parameter sets and similarly complex models in future research.

6 Conclusion

In the preceding sections, we have introduced a neural network-based protocol for the Bayesian estimation of economic simulation models (with a particular focus on ABMs) and demonstrated its estimation capabilities relative to a leading method in the existing literature.

Overall, we find that our method delivers compelling performance in a number of scenarios, including the estimation of heterogeneous agent models typically used to test estimation procedures and simple empirical model selection exercises, as well as less orthodox examples, such as identifying dynamic shifts in data generated by a random walk model. In all of the cases tested, we find that our proposed methodology produces estimates closer to known ground truth values than the approach proposed by Grazzini et al. (2017) and find that it also typically results in narrower and more sharply peaked posteriors.

In addition to our primary findings, we also discuss practical issues related to the applicability of the proposed routine. We demonstrate that the lag length, which can be viewed as our approach’s primary hyperparameter, can be systematically chosen and that the overall estimation performance demonstrates at least some robustness to this choice. Further, we provide a number of arguments as to the protocol’s computational efficiency relative to a number of prominent alternatives in the literature and provide a simple example of how it may be applied to models of a larger scale in future research.

Appendices

Appendix 1: Technical Details of the Proposed Estimation Procedure

While we presented an overview of our estimation procedure in Sect. 2, the associated discussions were primarily illustrative and omitted several key details. We thus provide a more technical, step-by-step discussion of our approach in this section.

1.1 Training Set Construction

The primary aim of our methodology is the construction of an approximation to the likelihood function for a given set of parameter values, $\varvec{\theta }$. In order to facilitate this process, we make the simplifying assumption that $\varvec{x} ^{sim} _{t, i}(\varvec{\theta })$ depends only on $\varvec{x} ^{sim} _{t - L, i}(\varvec{\theta }), \dots , \varvec{x} ^{sim} _{t - 1, i}(\varvec{\theta })$, for all $L < t \le T$. Our problem therefore reduces to the estimation of conditional densities of the form $p \left( \varvec{x}_{t, i} ^{sim} \big | \varvec{x}_{t - L, i} ^{sim}, \dots , \varvec{x}_{t - 1, i} ^{sim}: \varvec{\theta }\right)$.

In order to estimate the above conditional densities, we will require an appropriate dataset, which is constructed in a number of stages. The first of these stages involves the use of the candidate model to generate an ensemble of R Monte Carlo replications,⁴⁴$\varvec{X} ^{sim} (\varvec{\theta }, T _{sim}, i), i = i_0, i_0 + 1, \dots , i_0 + R - 1$, for a given value of $\varvec{\theta }$. This is then followed by the construction of two ordered sets for each Monte Carlo replication i in the ensemble,

$$\begin{aligned} \varvec{X} ^{train}_i(\varvec{\theta }) =&\Big \{\left\{ \varvec{x} ^{sim} _{1, i}(\varvec{\theta }), \dots , \varvec{x} ^{sim} _{L, i}(\varvec{\theta })\right\} , \left\{ \varvec{x} ^{sim} _{2, i}(\varvec{\theta }), \dots , \varvec{x} ^{sim} _{L + 1, i}(\varvec{\theta })\right\} , \dots , \nonumber \\&\left\{ \varvec{x} ^{sim} _{T - L, i}(\varvec{\theta }), \dots , \varvec{x} ^{sim} _{T - 1, i}(\varvec{\theta })\right\} \Big \}, \end{aligned}$$

(31)

and

$$\begin{aligned} \varvec{Y} ^{train}_i(\varvec{\theta }) = \left\{ \varvec{x} ^{sim} _{L + 1, i}(\varvec{\theta }), \varvec{x} ^{sim} _{L + 2, i}(\varvec{\theta }), \dots , \varvec{x} ^{sim} _{T, i}(\varvec{\theta })\right\} . \end{aligned}$$

(32)

Finally, the sets $\varvec{X} ^{train}_i(\varvec{\theta }), i = i_0, i_0 + 1, \dots , i_0 + R - 1$ are concatenated, in order, to produce a single, larger ordered set, $\varvec{X} ^{train}(\varvec{\theta })$, with an analogous procedure being applied to $\varvec{Y} ^{train}_i(\varvec{\theta })$ to yield $\varvec{Y} ^{train}(\varvec{\theta })$.

In essence, $\varvec{X} ^{train}(\varvec{\theta })$ consists of rolling windows of length L drawn from the ensemble of Monte Carlo replications, while $\varvec{Y} ^{train}(\varvec{\theta })$ consists of the $\varvec{x} ^{sim} _{t, i}(\varvec{\theta })$ values that directly follow each window in $\varvec{X} ^{train}(\varvec{\theta })$. Together, they form a training set of size $R(T_{sim} - L)$ that can be used to approximate the required conditional densities.

1.2 Neural Network Specification and Training

With an appropriate dataset now constructed, we proceed with a more detailed discussion of the MDN itself.

As a starting point, let H be a feedforward neural network with input layer $\varvec{h}_0$ (taking in windows of length L), hidden layers $\varvec{h}_1, \varvec{h}_2, \dots , \varvec{h}_{n - 1}$, output layer $\varvec{h}_{n}$, and weights and biases $\varvec{\psi }$. The mixture parameters are then defined as

$$\begin{aligned} \varvec{\alpha }= & {} softmax(\varvec{W}_{\alpha }\varvec{h}_{n} + \varvec{b}_{\alpha }), \end{aligned}$$

(33)

$$\begin{aligned} \varvec{\mu }_{k}= & {} \varvec{W}_{\mu _k}\varvec{h}_{n} + \varvec{b}_{\mu _k}, \end{aligned}$$

(34)

and

$$\begin{aligned} \varvec{\varSigma }_{k} = diag(\varvec{\sigma }_{k} ^2), \end{aligned}$$

(35)

where $diag(\varvec{x})$ is a diagonal matrix with diagonal $\varvec{x}$ and

$$\begin{aligned} \log \varvec{\sigma } ^{2} _{k} = \varvec{W}_{\sigma _k}\varvec{h}_{n} + \varvec{b}_{\sigma _k}. \end{aligned}$$

(36)

This results in an expanded neural network with weights and biases

$$\begin{aligned} \varvec{\phi } = \left\{ \varvec{\psi }, \varvec{W}_{\alpha }, \varvec{b}_{\alpha }, \varvec{W}_{\mu _k}, \varvec{b}_{\mu _k}, \varvec{W}_{\sigma _k}, \varvec{b}_{\sigma _k}\right\} \end{aligned}$$

(37)

that takes windows of length L as input and outputs $\varvec{\alpha }$, $\varvec{\mu }_{k}$, and $\varvec{\varSigma }_{k}$ as defined above.

At this stage, there are a number of nuances worth highlighting. In Eq. (33), notice that we make use of the softmax function.⁴⁵ This ensures that the mixture weights, $\varvec{\alpha }$, are strictly positive and sum to one, as required. Additionally, notice that in Eq. (35) we consider a diagonal rather than a full covariance matrix.⁴⁶ If we had not made such an assumption, we would have to ensure that the covariance matrices returned by our neural network were positive definite. Though possible in principle, this would significantly increase the number of network parameters and have a potentially detrimental effect on computational performance (Rothfuss et al. 2019). Finally, it should be apparent from Eq. (36) that the neural network outputs a vector of log variances rather than the diagonal covariance matrix, allowing us to avoid imposing positivity constraints on the network output.

Now, all that remains is the training of our constructed network, which is achieved through the application of maximum likelihood estimation to our training set. Denoting by $\varvec{X}_m ^{train}$ the mth entry in $\varvec{X} ^{train}(\varvec{\theta })$ (with $\varvec{Y}_m ^{train}$ being similarly defined), maximum likelihood estimation is equivalent to solving

$$\begin{aligned} \arg \min _{\varvec{\phi }} -\sum _{m = 1} ^{R (T - L)} \log \sum _{k = 1} ^{K} \alpha _k \left( \varvec{X}_m ^{train}\right) \mathcal {N}\left( \varvec{Y}_m ^{train} \big | \varvec{\mu }_k\left( \varvec{X}_m ^{train}\right) , \varvec{\varSigma }_k\left( \varvec{X}_m ^{train}\right) \right) \end{aligned}$$

(38)

using stochastic gradient descent methods, where $\alpha _k\left( \varvec{X}_m ^{train}\right)$ is the kth element of $\varvec{\alpha }\left( \varvec{X}_m ^{train}\right)$.

1.3 Data Normalisation and Regularisation

While the scheme we have just described could be applied as is, it is likely to perform suboptimally in its current form. This is because neural networks, like most machine learning techniques with a large number of free parameters, have a tendency to overfit the training data and thus perform poorly out-of-sample, particularly when the training set is small (Murphy 2012). In practice, this is often addressed using early stopping, a technique that requires a percentage of the data to be kept separate from the training set in order to evaluate out-of-sample performance during each epoch (Prechelt 1998). Such a solution is, however, undesirable in our context, since it requires the generation of additional data, an expensive undertaking for large-scale simulation models.

Fortunately, Rothfuss et al. (2019) present a set of best practices for conditional density estimation using neural networks that provides an alternative solution for overfitting. In particular, a technique called noise regularisation is employed, in which small random perturbations are applied to the data during the training process. It can be shown that this ultimately results in a complexity penalty that favours smoother density estimates that are less prone to overfitting (Rothfuss et al. 2019). For this reason, we apply Gaussian perturbations to training examples in $\varvec{X} ^{train}(\varvec{\theta })$ and $\varvec{Y} ^{train}(\varvec{\theta })$, which we denote by

$$\begin{aligned} \varvec{\xi }_{x} \sim \mathcal {N}(0, \eta _x ^{2}\varvec{I}) \text { and } \varvec{\xi }_{y} \sim \mathcal {N}(0, \eta _y ^{2}\varvec{I}), \end{aligned}$$

(39)

respectively.

It should be apparent that the degree of regularisation depends directly on the magnitudes of the standard deviations $\eta _x$ and $\eta _y$ relative to the range of variation in the training data.⁴⁷ This implies that $\eta _x$ and $\eta _y$ would have to be adjusted for each candidate model in order to result in the same degree of regularisation. Rothfuss et al. (2019) therefore propose a data normalisation scheme that ensures the training data exhibits zero mean and unit variance, eliminating the need to retune these hyperparameters for each candidate model. This is achieved through the application of a simple transformation to each training example.

Letting $\hat{\varvec{\mu }}_x$ and $\hat{\varvec{\sigma }}_x$ be vectors that contain estimates of the mean and standard deviation along each dimension for training examples in $\varvec{X} ^{train}(\varvec{\theta })$, this transformation is given by

$$\begin{aligned} \tilde{\varvec{X}}_m ^{train} = diag(\hat{\varvec{\sigma }}_x) ^{-1} (\varvec{X}_m ^{train} - \hat{\varvec{\mu }}_x), \end{aligned}$$

(40)

with $\hat{\varvec{\mu }}_y$, $\hat{\varvec{\sigma }}_y$ and $\tilde{\varvec{Y}}_m ^{train}$ being defined analogously.

Once the network has been trained on the normalised dataset, we are required to evaluate $\tilde{f}(\varvec{x}, \varvec{y}, \varvec{\phi })$, originally defined in Eq. (8). This is achieved through a simple procedure. Firstly, the normalisation transform is applied to $\varvec{x}$ and $\varvec{y}$ using the same $\hat{\varvec{\mu }}_y$, $\hat{\varvec{\sigma }}_y$, $\hat{\varvec{\mu }}_x$ and $\hat{\varvec{\sigma }}_x$ values defined in Eq. (40), yielding $\tilde{\varvec{x}}$ and $\tilde{\varvec{y}}$. $\tilde{\varvec{x}}$ is then fed through the trained neural network to yield corresponding mixture parameters, allowing us to evaluate the density at $\tilde{\varvec{y}}$, which we denote by $\tilde{g}(\tilde{\varvec{x}}, \tilde{\varvec{y}}, \tilde{\varvec{\phi }})$. It should be noted that $\tilde{g}$ does not directly correspond to $\tilde{f}$, since we have made a change of variables and the volume of the probability density is not preserved under the normalisation transform for $\hat{\varvec{\sigma }}_y \ne 1$. Rothfuss et al. (2019) do, however, prove that

$$\begin{aligned} \tilde{f}(\varvec{x}, \varvec{y}, \varvec{\phi }) = \frac{1}{\prod _{j = 1} ^{J} \hat{\sigma }_y ^{(j)}} \tilde{g}(\tilde{\varvec{x}}, \tilde{\varvec{y}}, \tilde{\varvec{\phi }}), \end{aligned}$$

(41)

where $\hat{\sigma }_y ^{(j)}$ is the jth element of $\hat{\varvec{\sigma }}_y$, allowing us to easily calculate the required density.

1.4 Neural Network Architecture

In essence, we have defined a general neural network-based approach to simulation model estimation that is independent of the specific network architecture (number of hidden layers, number of neurons, type of activation functions, and so on) used. Nevertheless, for the sake of completeness, we briefly introduce the (relatively simple) architecture employed in our study, which is used consistently throughout unless stated otherwise.

For the mixture model itself, we set the number of mixture components to be $K = 16$, with the associated mixture parameter network consisting of 3 hidden layers, each with 32 neurons and ReLU activations. This was trained using the well-known Adam optimiser (Kingma and Ba 2015) over 12 epochs,⁴⁸ with a batch size of 512 and noise regularisation parameters $\eta _x = \eta _y = 0.2$.

The above architecture, which performed well for all of the estimation tasks conducted, was, perhaps rather surprisingly, the first architecture we considered and was chosen by hand rather than through an automated optimisation procedure. Attempts to improve performance by increasing the number of hidden layers, neurons, and mixture components seemed to have little effect (see “Neural Network Architecture” in Appendix 4), suggesting that the proposed network is sufficiently expressive to produce high-quality density estimates for our considered set of problems.

Further, it should also be noted that, as shown in Sect. 5.2, there is at least some evidence that the above architecture is also effective when confronted with large-scale, complex economic ABMs. We suspect that this will likely hold for other models of similar complexity and therefore make the recommendation that our proposed architecture be used as a baseline for future investigations employing this estimation methodology. Of course, it may certainly be the case that it becomes necessary to construct more expressive networks for some problems and that some form of hyperparameter optimisation would need be carried out. This is beyond the scope of our investigation, however, and we thus leave it to future research.

Finally, it is worth mentioning that neural networks are, as a result of their weight initialisation process and training via stochastic gradient descent, random in nature, meaning that a different set of weights and biases would be learnt each time the same network architecture is trained on the same dataset. It thus follows that the obtained conditional density estimates would, to some extent, be dependent on the random seed, $j^{*}$, used to initialise the random number generators associated with the neural network weight initialisation and training procedure. As stated in Footnote 44, it is important that any random seeds be kept consistent across evaluations of the posterior for different values of $\varvec{\theta }$, and this is no exception. Therefore, in line with this discussion, we fix $j^{*}$ to an arbitrary and non-optimised value, which is kept identical throughout the entire investigation (across all models, parameter sets, and posterior density evaluations). Further discussions and experiments considering the effects of alternative $j^{*}$ choices are presented in “Neural Network Architecture” in Appendix 4.

Appendix 2: Technical Details of the Employed Sampling Strategy

1.1 Basic Algorithm

In this section, we briefly discuss the adaptive Metropolis–Hastings algorithm that has been employed in all of the conducted estimation experiments, which was also considered by Platt (2020). Our discussion here is mainly illustrative and positioned in the context of our investigation. The interested reader should therefore refer to the original contribution by Griffin and Walker (2013) for theoretical justifications and a more general discussion.

In essence, the approach is centred on the idea of maintaining a set of samples, $\varvec{\theta }_s = \left\{ \varvec{\theta }_{s} ^{(1)}, \varvec{\theta }_{s} ^{(2)}, \dots , \varvec{\theta }_{s} ^{(N)} \right\} , s = 1, 2, \dots , S$, that is updated for a desired number of iterations. Initially, the set consists of samples drawn uniformly from the space of feasible parameter values, $\varvec{\varTheta }$, but eventually converges to be distributed according to $p(\varvec{\theta }|\varvec{X})$. This is achieved through the construction of an adaptive proposal distribution that is dependent on the current samples, $\varvec{\theta }_s$, which can be summarised algorithmically as follows:

• 1. Sample $\varvec{z}$ according to $\tilde{p}\left( \varvec{z} \big | \varvec{\theta }_{s} ^{(1)}, \varvec{\theta }_{s} ^{(2)}, \dots , \varvec{\theta }_{s} ^{(N)} \right)$, which is determined by applying KDE to $\varvec{\theta }_{s} ^{(1)}, \varvec{\theta }_{s} ^{(2)}, \dots , \varvec{\theta }_{s} ^{(N)}$.

• 2. Propose the switch of $\varvec{z}$ with $\varvec{\theta }_{s} ^{(n)}$, where n is chosen uniformly from $\left\{ 1, 2, \dots , N \right\}$.

• 3. Accept the switch with probability

  $$\begin{aligned} \alpha = \min \left\{ 1, \frac{p\left( \varvec{z} \big | \varvec{X}\right) \tilde{p}\left( \varvec{\theta }_{s} ^{(n)} | \varvec{\theta }_{s} ^{(1)}, \varvec{\theta }_{s} ^{(2)}, \dots , \varvec{\theta }_{s} ^{(n - 1)}, \varvec{z}, \varvec{\theta }_{s} ^{(n + 1)}, \dots , \varvec{\theta }_{s} ^{(N)}\right) }{p\left( \varvec{\theta }_{s} ^{(n)} | \varvec{X}\right) \tilde{p}\left( \varvec{z} | \varvec{\theta }_{s} ^{(1)}, \varvec{\theta }_{s} ^{(2)}, \dots , \varvec{\theta }_{s} ^{(N)}\right) } \right\} . \end{aligned}$$

  (42)

• 4. If accepted, set $\varvec{\theta }_{s + 1} = \varvec{\theta }_{s}$ with $\varvec{\theta }_{s} ^{(n)}$ replaced by $\varvec{z}$, otherwise simply set $\varvec{\theta }_{s + 1} = \varvec{\theta }_{s}$.

Repeating the above for S iterations, we obtain a sequence of sample sets that can be used to compute expectations of the form

$$\begin{aligned} \mathbb {E}\left[ g(\varvec{\theta })\right] = \frac{1}{NS} \sum _{s = 1} ^{S} \sum _{n = 1} ^{N} g\left( \varvec{\theta }_{s} ^{(n)}\right) . \end{aligned}$$

(43)

In our investigation, we set $S = 5000$ and $N = 70$ unless stated otherwise, with convergence typically observed at some point before $s = 1500$, leading us to discard the first 1500 sets as part of a burn-in period.⁴⁹ When constructing the posterior samples, we repeat this entire sampling process 5 times and collect the obtained sets to form a larger collection of $5 \times 3500 \times 70 = 1225000$ samples.⁵⁰

Ultimately, this has become our MCMC algorithm of choice for two main reasons:

• 1. The number of iterations required to reach convergence in random walk Metropolis–Hastings algorithms depends significantly on the initialisation of the algorithm. If, for example, the initial candidate parameter set has a particularly low posterior density, it could take a substantial period of time before convergence is observed. Since the algorithm proposed by Griffin and Walker (2013) is initialised using a sample of points from a number of areas of the parameter space, this problem is less pronounced.

• 2. Most random walk Metropolis–Hastings algorithms require careful tuning of the proposal distribution, usually with the aim of obtaining an acceptance rate of roughly $25\%$, in order to ensure a good balance between local exploration of high density areas of the parameter space and global coverage of the parameter space as a whole (Robert and Casella 2010). This can be difficult to achieve in practice, making an adaptive approach that determines the proposal distribution automatically particularly appealing.

1.2 Modifications

It should be noted that while our implementation of the algorithm is almost identical to that introduced by Griffin and Walker (2013) and later considered in Platt (2020), some small, but important modifications have been made.

To elaborate, although the above routine delivers robust convergence to the posterior without careful manual step-size adjustments and is able to handle complex multimodal distributions, the original procedure can introduce a degree of noise into the resultant samples. In more detail, notice from the discussion above that the N points in the initial sample set are drawn uniformly from the space of feasible parameter values and, with each subsequent step of the algorithm, are replaced, one-by-one, to generate subsequent sample sets. After a sufficient number of these iterations, the points in the current sample set should be distributed according to the posterior distribution. In some cases, however, and particularly when the posterior is very narrow relative to the prior, a very small number of low-likelihood points (usually only a single point) at a significant distance from the actual posterior samples may remain in the current sample set, regardless of the number of algorithm iterations considered.

This occurs because a new proposal is learnt using the points in the current sample set during each iteration of the procedure. To illustrate, consider the case where all but one of the points in the current sample set have converged to be distributed according to the posterior distribution and the single remaining point is relatively far away from these posterior samples. Calling this point $\varvec{\theta }_{s} ^{(n)}$, notice that $\tilde{p}\left( \varvec{\theta }_{s} ^{(n)} | \varvec{\theta }_{s} ^{(1)}, \varvec{\theta }_{s} ^{(2)}, \dots , \varvec{\theta }_{s} ^{(n - 1)}, \varvec{z}, \varvec{\theta }_{s} ^{(n + 1)}, \dots , \varvec{\theta }_{s} ^{(N)}\right)$ in the numerator of Eq. (42) would be extremely small, or practically 0 given finite machine precision, as $\varvec{\theta }_{s} ^{(n)}$ could not be reached using a proposal based on the remaining points. Therefore, even if $p\left( \varvec{z} \big | \varvec{X}\right) / p\left( \varvec{\theta }_{s} ^{(n)} | \varvec{X}\right)> > 1$, or, in other words, $\varvec{\theta }_{s} ^{(n)}$ were a low-likelihood point far away from the true posterior, the acceptance probability would always be 0 and $\varvec{\theta }_{s} ^{(n)}$ would not be replaced by any subsequent candidate points, even if $S \rightarrow \infty$.

In practice, such low-likelihood points tend to represent a very small fraction of the final samples (typically significantly less than 1%) and in practically all cases have a very small effect on the accuracy of point estimates, such as the posterior mean, making the original algorithm suitable for the purposes for which it was employed by Platt (2020). Nevertheless, we did find that these points do, in some cases, have a noticeable effect on the accuracy of estimates of the posterior variance, which could be considered problematic given our consideration of the posterior standard deviation as a measure of estimation uncertainty. We therefore introduce a simple, but principled correction to the algorithm to account for the possibility of encountering invalid samples of the type described above.

In brief, we observe that since all points in the current sample set should eventually converge to be distributed according to the posterior, any point $\varvec{\theta }_{s} ^{(n)}$ in the current sample set should have a non-negligible probability of being drawn from the distribution implied by the points in the current sample set, even if $\varvec{\theta }_{s} ^{(n)}$ were to be removed and replaced by another candidate. In other words, $\tilde{p}\left( \varvec{\theta }_{s} ^{(n)} | \varvec{\theta }_{s} ^{(1)}, \varvec{\theta }_{s} ^{(2)}, \dots , \varvec{\theta }_{s} ^{(n - 1)}, \varvec{z}, \varvec{\theta }_{s} ^{(n + 1)}, \dots , \varvec{\theta }_{s} ^{(N)}\right)$ should not be dramatically smaller than $\tilde{p}\left( \varvec{\theta }_{s} ^{(n)} | \varvec{\theta }_{s} ^{(1)}, \varvec{\theta }_{s} ^{(2)}, \dots , \varvec{\theta }_{s} ^{(N)}\right)$. If the opposite were instead true and the former was indeed several orders of magnitude smaller, this would imply that the probability of drawing $\varvec{\theta }_{s} ^{(n)}$ dramatically decreases if it is not contained in the sample set and that it is therefore unlikely to have been sampled from the same distribution as the remaining points.

In line with the above, and before determining the acceptance probability of a candidate point as in Eq. (42), we first determine if

$$\begin{aligned} \frac{\tilde{p}\left( \varvec{\theta }_{s} ^{(n)} | \varvec{\theta }_{s} ^{(1)}, \varvec{\theta }_{s} ^{(2)}, \dots , \varvec{\theta }_{s} ^{(n - 1)}, \varvec{z}, \varvec{\theta }_{s} ^{(n + 1)}, \dots , \varvec{\theta }_{s} ^{(N)}\right) }{\tilde{p}\left( \varvec{\theta }_{s} ^{(n)} | \varvec{\theta }_{s} ^{(1)}, \varvec{\theta }_{s} ^{(2)}, \dots , \varvec{\theta }_{s} ^{(N)}\right) } < \epsilon , \end{aligned}$$

(44)

where $\epsilon > 0$ and $\epsilon<< 1$.

If the above condition holds, this would imply that $\varvec{\theta }_{s} ^{(n)}$ is likely one of the aforementioned problematic points and should thus be replaced, leading us to set $\alpha = 1$. If, however, the above condition does not hold, we simply calculate $\alpha$ as in Eq. (42).

Naturally, the above requires us to choose an appropriate value for $\epsilon$. While any relatively small value could be chosen, we found $10^{-8}$ to be an appropriate choice for all of the considered cases.⁵¹

As a final remark, Fig. 8a and Fig. 8b provides a simple comparison of the unmodified and modified algorithms respectively in the context of a normal distribution, $\mathcal {N}(-2, 4)$. Here, we see that while both sampling algorithms perform well and produce very similar mean estimates, the unmodified algorithm is characterised by the presence of a very small number of the aforementioned low-likelihood points (see $x \simeq 13$ and $x \simeq -23$) and produces a noticeably less accurate standard deviation estimate, justifying the use of the augmented version in this investigation. Additionally, Fig. 8c applies our version of the algorithm to a simple mixture model,

$$\begin{aligned} \sum _{i = 1} ^3 \alpha _i \mathcal {N}(\mu _i, \sigma _i ^2), \end{aligned}$$

(45)

where $\mu _1 = -12$, $\mu _2 = -7$, $\mu _3 = 12$, $\sigma _1, \sigma _2, \sigma _3 = 2$, $\alpha _1 = 0.5$, and $\alpha _2, \alpha _3 = 0.25$, and demonstrates that the introduced modifications do not have any impact on the ability of the algorithm to sample multimodal posteriors.

Fig. 8

Examples of the application of both the modified and unmodified versions of the adaptive Metropolis–Hastings algorithm proposed by Griffin and Walker (2013) to the problem of sampling known distributions. All examples make use of samples drawn from 5 separate chains, each with $S = 5000$ and a burn-in period of 1500 sample sets. $\mu$ is the true mean of the distribution and $\hat{\mu }$ and $\hat{\sigma }$ are the sample mean and standard deviation respectively

Appendix 3: Supplementary Brock and Hommes (1998) Model Exercises

In Sect. 4.1.1, we provided a detailed discussion regarding how restrictions on the ranges of values taken by the trend following and bias parameters associated with each strategy in the Brock and Hommes (1998) model are an intrinsic part of the model definition and further elaborated on how such restrictions are essential for ensuring model identifiability. Along these lines, we assumed $g_2 \in [-2.5, 0]$, $b_2 \in [-1.5, 0]$, $g_3 \in [0, 2.5]$, and $b_3 \in [0, 1.5]$ for the first free parameter set, in line with our definition of a model including a contrarian strategy with a negative bias and a trend following strategy with a positive bias.

We note, however, that the model should, at least in theory, remain identifiable if we were to instead assume $g_2, g_3 \in [-2.5, 2.5]$, since the remaining restrictions on $b_2$ and $b_3$ would ensure that the estimation problem remains well-specified.⁵² It would thus be interesting to observe if such a change induces any meaningful effects on the performance of both our proposed methodology and that of Grazzini et al. (2017), leading us to repeat the exercises associated with the first free parameter set of the Brock and Hommes (1998) model with these new parameter ranges.⁵³

Referring to Fig. 9, which presents a graphical illustration of the results of the above exercise, we observe that the performance of our proposed methodology is unaffected, with it yielding near-identical estimation performance to that observed in the original experiments. The same cannot be said for the method of Grazzini et al. (2017), however, which now produces a rather poorly-behaved bimodal posterior, which can be taken as evidence of the inability of the approach to effectively discriminate between the effects associated with positive and negative values of $g_2$ and $g_3$. Further, it should also be noted that although we do provide the posterior means for reference, Murphy (2012) suggests that point estimates are generally uninformative when derived from multimodal posteriors and should thus be interpreted with caution, further highlighting the shortcomings of the approach of Grazzini et al. (2017) in this more challenging context and reinforcing the findings of the original comparative exercise in Sect. 4.1.1.

Fig. 9

Marginal posterior distributions obtained for free parameter set 1 of the Brock and Hommes (1998) model after relaxing assumptions on the ranges of $g_2$ and $g_3$

Appendix 4: Robustness Tests

1.1 Number of Lags

In Sect. 5.1, we provided evidence that the conditional density estimates produced by the MDN, and by extension our proposed likelihood approximation, demonstrate some robustness relative to the choice of the number of lags, L. Here, we provide a more complete examination by repeating all of the estimation experiments conducted in Sect. 4.1 that are associated with our methodology, changing only the number of lags, which we have increased to $L = 4$. Referring to the summary presented in Table 10, we find that the overall performance of the procedure relative to our chosen benchmark is virtually unchanged.⁵⁴ This indicates that any differences resulting from the consideration of the additional lag are generally smaller than the performance differences between the considered methods in virtually all cases and thus verifies the robustness of our overall conclusions regarding the competitiveness of our proposed methodology.

Table 10 Estimation result summary across all models for $L = 4$

1.2 Neural Network Architecture

In all of the preceding experiments involving the application of our proposed methodology, we have employed the neural network architecture described in “Neural Network Architecture” in Appendix 1 exclusively. Naturally, some readers may wonder if modifying the aforementioned architecture would have a strong effect on the overall estimation performance. For this reason, we aim to provide some insight into the effects of various MDN components on the loss function values through a set of supplementary experiments.

Fig. 10

Loss function values associated with the application of our proposed methodology to the HPM parameter set of the Franke and Westerhoff (2012) model for various neural network architectures. $LS_{kde}$ and $LS_{mdn}$ refer to the loss function values associated with the method of Grazzini et al. (2017) and the default network architecture introduced in “Neural Network Architecture” in Appendix 1 respectively. The point indicated in purple represents our default architecture

In these experiments, we repeat the exercises associated with the HPM parameter set of the Franke and Westerhoff (2012) model,⁵⁵ each time modifying a single feature of the MDN (number of hidden layers, number of nodes per layer, and number of mixture components), while keeping the remainder of the network architecture identical to that described in “Neural Network Architecture” in Appendix 1 and recording the final loss function value.

Our focus on the HPM parameter set of the Franke and Westerhoff (2012) model is justified on a number of grounds. Firstly, in order to obtain a sufficiently large number of data points to deduce loss function trends, we consider 30 different network architectures, each of which is associated with a full Bayesian estimation exercise. This is, of course, a computationally-demanding undertaking that requires us to limit ourselves to a single example case. Additionally, it should also be noted that the performance of the method of Grazzini et al. (2017) is relatively close to that of our proposed methodology in this case, with only a very small difference in the loss function values being observed in the original experiments in Table 5. It therefore follows that the differences between the loss function values obtained in these previously conducted experiments would provide a challenging benchmark against which to compare the differences induced by the consideration of alternative network architectures.

Elaborating on the above point, we would expect to see one of two behaviours as the complexity of the network is increased. These include a decreasing loss function trend, indicating that the increased network complexity facilitates greater accuracy in the obtained conditional density estimates, or oscillatory behaviour, indicating that the MDN is already sufficiently expressive and that increasing network complexity does not improve performance. In the latter case, these fluctuations emerge due to the stochastic nature of neural networks and the resultant changes in the training process induced by altering the network architecture. Here, it is especially important that the loss function differences induced by these fluctuations are insignificant relative to the performance differences between the methodologies if the overall procedure is to be considered robust. This clearly justifies our choice of the HPM parameter set of the Franke and Westerhoff (2012) model, for which the performance difference is extremely small and for which both methods perform relatively well.

Now, referring to Fig. 10a, which illustrates the effect of increasing the number of hidden layers, we observe that the loss function value initially exceeds that yielded by the method of Grazzini et al. (2017) and follows a decreasing trend, before reaching a minimum at 4 hidden layers and settling into a series of small oscillations about the loss function value obtained in the original experiments. This initial decreasing trend is not at all surprising, as the number of hidden layers in a neural network has a strong effect on its overall expressiveness and the consideration of too few hidden layers would have a detrimental effect on its ability to approximate functions. The aforementioned convergent behaviour is also exactly as expected in our discussion above. It therefore follows that although it should be ensured that the neural network is sufficiently deep, the consideration of a network with significantly more than 3 or 4 hidden layers is unlikely to lead to meaningful improvements in performance. Further, it appears that the overall estimation performance is relatively stable for deeper networks, implying that there does not appear to be a significant performance penalty for considering unnecessarily complex networks, other than increased computational time.

Proceeding to Fig. 10b, which illustrates the effect of increasing the number of nodes per hidden layer, we now observe a somewhat different trend. To summarise, we encounter oscillatory behaviour throughout, with the aforementioned loss function value fluctuations being more or less negligible relative to the differences in method performance. To elaborate, all of the considered network configurations result in loss function values noticeably less than the corresponding value obtained when employing the method of Grazzini et al. (2017) and these loss function values are, in $70\%$ of cases, bounded above by $LS_{mdn} + \frac{1}{4}\left( LS_{kde} - LS_{mdn}\right)$. This suggests that, in most cases, changes to the network width do not alter the loss function value by more than $25\%$ of the performance difference between the methods. This is particularly relevant, given that the aforementioned performance difference is, as previously discussed, very small. Further, all loss function values not bounded above by this line do not greatly exceed it.

The above factors suggest that increases in the network width are unlikely to lead to improvements in estimation performance and further imply that the choice of the number of nodes per hidden layer is not critical. Interestingly, this is also not surprising. Recent years have seen the emergence of several studies suggesting that network depth is a more important determinant of expressiveness than width (Eldan and Shamir 2016; Lu et al. 2017; Safran and Shamir 2017) and this ultimately seems to have been reflected in our findings. Further, Lu et al. (2017) demonstrate that for ReLU networks, which we consider in our investigation, universal approximation theorems hold for widths of $n + 4$ or greater, where n is the number of inputs. Since we consider exactly 3 inputs (for $L = 3$), all of the network widths presented in Fig. 10b would meet this criterion and therefore be predicted to be sufficient, likely explaining the lack of improvement in the obtained loss function values for increased widths.

A similar discussion applies to Fig. 10c, which illustrates the effect of increasing the number of mixture components. Again, we observe fluctuations throughout that are negligible relative to the differences in method performance, and, as before, can offer an explanation for the encountered trends. In more detail, Bertschinger and Mozzhorin (2020) demonstrate that the conditional distribution of returns produced by the Franke and Westerhoff (2012) model can be approximated by a normal distribution. Therefore, even a single mixture component would be sufficient, indicating that the choice of the number of mixture components is not critical and, perhaps more importantly, that the consideration of significantly more mixture components than is required, such as the 16 we employ in our investigation, does not result in a significant performance penalty, as in the case of the network depth and width.

Based on the examples given above, it thus follows that there is at least some evidence that our approach may be robust to the choice of neural network architecture and number of mixture components, provided that the number of hidden layers is sufficient, and that increasing the complexity of the considered network, while not detrimental, does not seem to result in much improvement in estimation performance. We therefore suggest that, in future, if the default architecture presented in “Neural Network Architecture” in Appendix 1 does not seem sufficient for more complex problems, that emphasis should be placed on increasing the number of hidden layers, rather than the number of mixture components or nodes per layer.

1.3 Neural Network Random Seed

Recall that in “Neural Network Architecture” in Appendix 1, we indicated that the random seed associated with the neural network weight initialisation and training procedures is fixed to an arbitrary value, $j^{*}$, and kept identical for every posterior density evaluation performed in this investigation, in other words, across all $\varvec{\theta }$ values and models. As previously explained, this is necessary to ensure that it is the effect of changes in the parameter values and not randomness in the initial network weights that underlies differences between subsequent posterior density evaluations.

Since our initial choice of $j^{*}$ is entirely arbitrary, the same value is used throughout this investigation for many different models and parameter sets, and our proposed methodology performs relatively well in all of these cases, it would appear that either initial weight configurations that perform well in one example are likely to perform well in others,⁵⁶ or alternatively, that for many problems, the choice of $j^{*}$ may not be particularly important. Naturally, a definitive answer to the above would be extremely difficult to determine. Nevertheless, it is likely that some readers would, as in the case of the underlying neural network architecture, wish to be given some indication of the sensitivity of some of our results to alternative choices of $j^{*}$.

Table 11 Neural Network Seed Robustness Testing for the Franke and Westerhoff (2012) Model

Therefore, much like in the case of our experiments involving various neural network architectures, we repeat the exercises involving the application of our proposed methodology to the HPM parameter set of the Franke and Westerhoff (2012) model a total of 50 times,⁵⁷ each time considering a different value for $j^{*}$. This ultimately results in a set of 50 estimates for the posterior means of the parameters, posterior standard deviations of the parameters, and the final loss function value that may be used to determine various descriptive statistics.

As in “Neural Network Architecture” in Appendix 4, the use of a single example model is necessitated due to computational limitations.⁵⁸ Further, the consideration of the HPM parameter set of the Franke and Westerhoff (2012) model is again justified due to the relatively small difference in performance between the method of Grazzini et al. (2017) and our proposed methodology in this context.

To elaborate, we would generally expect that, if our results were robust to the choice of $j^{*}$, loss function differences arising from different seed choices would be small relative to the performance difference between the methods, or, in other words, that choosing a different random seed would not lead to our methodology being beaten by the benchmark in most cases. Clearly, in such an exercise, the obtained results would be most informative when the performance difference between the methods is small.

Now, referring to Table 11, which presents the means and standard errors⁵⁹ of various quantities of interest over the 50 considered neural network random seeds, we observe evidence of the robustness of our results in this case. Firstly, notice that the averages of the posterior means, posterior standard deviations, and the final loss function value over the ensemble demonstrate a high degree of similarity when compared to the equivalent values obtained for our single fixed random seed in Table 5. Additionally, notice that, in all cases, the associated standard errors are also relatively small.