Unified Approach for the Affine and Non-affine Models: An Empirical Analysis on the S&P 500 Volatility Dynamics

Abstract

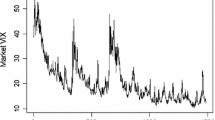
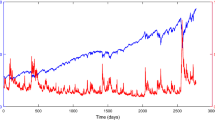
Being able to generate a volatility smile and adequately explain how it moves up and down in response to changes in risk, stochastic volatility models have replaced BS model. A single-factor volatility model can generate steep smiles or flat smiles at a given volatility level, but it cannot generate both for given parameters. In order to match the market implied volatility surface precisely, Grasselli introduced a 4/2 stochastic volatility model that includes the Heston model and the 3/2 model, performing as affine and non-affine model respectively. The present paper is intended to further investigate the 4/2 model, which falls into four parts. First, we apply Lewis’s fundamental transform approach instead of Grasselli’s method to deduce PDEs, which is intuitional and simple; Then, we use a result derived by Craddock and Lennox using Lie Symmetries theory for PDEs, and the results are more objective and reasonable; Finally, through adopting the data on S&P 500, we estimate the parameters of the 4/2 model; Furthermore, we investigate the 4/2 model along with the Heston model and the 3/2 model and compare their different performances. Our results illustrate that the 4/2 model outperforms the Heston and the 3/2 model for the fitting problem.

Appendix

Proposition 2

If$\gamma \ne 2$, the PDE (9) has a nontrivial Lie symmetry group if and only if$h$, which is given by$h = x^{1 - \gamma } f\left( x \right)$, satisfies one of the following families of drift equations

$$ \begin{aligned} & \sigma xh^{\prime} - \sigma h + \frac{1}{2}h^{2} + 2\sigma x^{2 - \gamma } g\left( x \right) = 2\sigma Ax^{2 - \gamma } + B, \\ & \sigma xh^{\prime} - \sigma h + \frac{1}{2}h^{2} + 2\sigma x^{2 - \gamma } g\left( x \right) = \frac{{Ax^{4 - 2\gamma } }}{{2\left( {2 - \gamma } \right)^{2} }} + \frac{{Bx^{2 - \gamma } }}{2 - \gamma } + C, \\ & \sigma xh^{\prime} - \sigma h + \frac{1}{2}h^{2} + 2\sigma x^{2 - \gamma } g\left( x \right) = \frac{{Ax^{4 - 2\gamma } }}{{2\left( {2 - \gamma } \right)^{2} }} + \frac{{Bx^{{3 - \frac{3}{2}\gamma }} }}{{3 - \frac{3}{2}\gamma }} + \frac{{Cx^{2 - \gamma } }}{2 - \gamma } - \frac{\gamma }{8}\left( {\gamma - 4} \right)\sigma^{2} . \\ \end{aligned} $$

(23)

Proof

The proof of this result is Proposition 2.1 in Craddock and Lennox (2009) or Theorem 4.4.1 in Baldeaux and Platen (2013), Craddock and Platen (2004) also proved this theorem.

Readers interested in the technical details of Lie symmetry analysis are referred to Bluman and Kumei (1989), and Olver (1993). For a survey of some recent work on Lie symmetries, see Craddock et al. (2009).

Theorem 1

Suppose $\gamma \ne 2$ and $h = x^{1 - \gamma } f\left( x \right)$ is a solution of the Riccati equation

$$ \sigma xh^{\prime} - \sigma h + \frac{1}{2}h^{2} + 2\sigma x^{2 - \gamma } g\left( x \right) = 2\sigma Ax^{2 - \gamma } + B $$

Then the PDE (9) has a symmetry of the form

$$ \begin{aligned} \bar{U}_{ \in } \left( {x,t} \right) & = \frac{1}{{\left( {1 + 4 \in t} \right)^{{\frac{1 - \gamma }{2 - \gamma }}} }}exp\left\{ {\frac{{ - 4 \in \left( {x^{2 - \gamma } + A\sigma \left( {2 - \gamma } \right)^{2} t^{2} } \right)}}{{\sigma \left( {2 - \gamma } \right)^{2} \left( {1 + 4 \in t} \right)}}} \right\} \\ & \quad \times \exp \left\{ {\frac{1}{2\sigma }\left( {F\left( {\frac{x}{{\left( {1 + 4 \in t} \right)^{{\frac{2}{2 - \gamma }}} }}} \right) - F\left( x \right)} \right)} \right\} \\ & \quad \times u\left( {\frac{x}{{\left( {1 + 4 \in t} \right)^{{\frac{2}{2 - \gamma }}} }},\frac{t}{1 + 4 \in t}} \right). \\ \end{aligned} $$

where$F^{\prime}\left( x \right) = f\left( x \right)/x^{\gamma }$and$u$is a solution of PDE (9). That is, for$\in$sufficiently small,$U_{ \in }$is a solution of PDE (9) whenever$u$is. If$u\left( {x,t} \right) = u_{0} \left( x \right)$with$u_{0}$an analytic, stationary solution, then there is a fundamental solution$p\left( {x,y,t} \right)$of (9) such that

$$ \mathop \smallint \limits_{0}^{\infty } exp\left\{ { - \lambda y^{2 - \gamma } } \right\}u_{0} \left( y \right)p\left( {x,y,t} \right)dy = U_{\lambda } \left( {x,t} \right) $$

(24)

Here$U_{\lambda } \left( {x,t} \right) = \bar{U}_{{\frac{1}{4}\sigma \left( {2 - \gamma } \right)^{2} \lambda }} \left( {x,t} \right).$Further, if$u_{0} = 1$, then$\mathop \smallint \limits_{0}^{\infty } p\left( {x,y,t} \right)dy = 1.$

Proof

The proof follows that of Theorem 3.1 in Craddock and Lennox (2009) or Theorem 4.4.3 in Baldeaux and Platen (2013).

Equation (24) is a generalized Laplace transform. We may recover the fundamental solution $p\left( {x,y,t} \right)$ by inverting the transform and dividing by $u_{0} \left( y \right)$.

Proof of Proposition 1

The drift function $f\left( v \right) = \alpha - \beta v$ in (12) satisfies the first Ricatti Eq. (23), where $x = v, \sigma = \in , \gamma = 1, g\left( v \right) = a_{1} v + \frac{{a_{2} }}{v}$. Using the Proposition 2 and Theorem 1, We obtain a fundamental solution to the PDE (10) of the form

$$ \begin{aligned}& p\left( {v,w,t} \right) = \frac{{\sqrt {\frac{Av}{w}} }}{{2 \in \sinh \left( {\sqrt A t/2} \right)}} \times e^{{ - \left( {Bt + \sqrt A \left( {v + w} \right)coth\left( {\sqrt A t/2} \right) + F\left( v \right) - F\left( w \right)} \right)/\left( {2 \in } \right)}} \\ & \quad \times \left( {C_{1} \left( w \right)I_{{\frac{{\sqrt { \in^{2} + 2C} }}{ \in }}} \left( {\frac{{\sqrt {\frac{Av}{w}} }}{{ \in \sinh \left( {\sqrt A t/2} \right)}}} \right)+ C_{2} \left( w \right)I_{{ - \frac{{\sqrt { \in^{2} + 2C} }}{ \in }}} \left( {\frac{{\sqrt {\frac{Av}{w}} }}{{ \in \sinh \left( {\sqrt A t/2} \right)}}} \right)} \right) \\ \end{aligned} $$

where $F^{\prime}\left( v \right) = f\left( v \right)/v, A = \beta^{2} + 4 \in a_{1} , B = - \alpha \beta , C = \frac{1}{2}\left( {\alpha^{2} - 2 \in \alpha + 4 \in a_{2} } \right)$. $I_{ - x} \left( z \right) = K_{x} \left( z \right)$

If $x$ is an integer, and $I_{x} ,K_{x}$ denote resp. the modified Bessel function of the first kind and second kind. Following the discussion in Craddock and Lennox (2009), we must consider the case $C_{1} = 1, C_{2} = 0.$

Using the fundamental solution $p\left( {v,w,t} \right)$, we can obtain

$$ \begin{aligned} {\mathbb{E}}\left( {e^{{ - \lambda v_{t} - a_{1} \mathop \smallint \limits_{0}^{t} v_{s} ds - a_{2} \mathop \smallint \limits_{0}^{t} \frac{1}{{v_{s} }}ds}} } \right) & = \mathop \smallint \limits_{0}^{\infty } e^{ - \lambda w} p\left( {v,w,t} \right)dw \\ & = \frac{{\sqrt A v^{{\frac{1}{2} - \frac{\alpha }{2 \in }}} }}{{2 \in \sinh \left( {\frac{\sqrt A t}{2}} \right)}}\left( {\frac{B}{2}} \right)^{m} \left( {K + \lambda } \right)^{{ - \left( {\frac{\alpha }{2 \in } + \frac{1}{2} + \frac{m}{2}} \right)}} \\ & \quad \times \exp \left\{ {\frac{{\beta \left( {v + \alpha t} \right) - \sqrt A v\coth \left( {\frac{\sqrt A t}{2}} \right)}}{2 \in }} \right\} \\ & \quad \times \frac{{\varGamma \left( {\frac{\alpha }{2 \in } + \frac{1}{2} + \frac{m}{2}} \right)}}{{\varGamma \left( {1 + m} \right)}} M\left( {\frac{\alpha }{2 \in } + \frac{1}{2} + \frac{m}{2},1 + m,\frac{{B^{2} }}{{4\left( {K + \lambda } \right)}}} \right) \\ \end{aligned} $$

where $A = \beta^{2} + 4a_{1} \in ,\,\,m = \frac{1}{ \in }\sqrt {\left( {\alpha - \in } \right)^{2} + 4 \in a_{2} } ,\quad B = \frac{{\sqrt {Av} }}{{ \in \sinh \left( {\frac{\sqrt A t}{2}} \right)}},\,\,K = \frac{{\sqrt A + \beta \tanh \left( {\frac{\sqrt A t}{2}} \right)}}{{2 \in \tanh \left( {\frac{\sqrt A t}{2}} \right)}}.$

We give a very direct evidence based on Lie symmetries in the spirit of Baldeaux and Platen (2013) (see their Proposition 7.3.9) and Craddock and Lennox (2009) (Example 5.3 for a special case).

Then, setting $\lambda = 0$, which gives Proposition 1.