Human and Machine Learning

Abstract

In this paper, we consider learning by human beings and machines in the light of Herbert Simon’s pioneering contributions to the theory of Human Problem Solving. Using board games of perfect information as a paradigm, we explore differences in human and machine learning in complex strategic environments. In doing so, we contrast theories of learning in classical game theory with computational game theory proposed by Simon. Among theories that invoke computation, we make a further distinction between computable and computational or machine learning theories. We argue that the modern machine learning algorithms, although impressive in terms of their performance, do not necessarily shed enough light on human learning. Instead, they seem to take us further away from Simon’s lifelong quest to understand the mechanics of actual human behaviour.

Introduction

How do human beings make decisions? By his own admission, this question provided Herbert Simon the impetus to shape his unparalleled research pursuits (Feigenbaum 2001). In the search for answers to various aspects of it, Simon transcended and redefined conventional disciplinary boundaries by venturing in to multiple subject areas. To the best of our knowledge, no one scholar in recent times has been as prolific in their contributions across so many areas, a list of which includes economics, political science, cognitive psychology, artificial intelligence, computer science, philosophy of science, management, organizational theory, complex systems, statistics and econometrics. Simon’s contributions were not only original but also almost always challenged the perceived wisdom and orthodoxy that prevailed in each field.

In this paper, we take up a theme that is intimately related to decision making, viz., learning, which was also on the radar of Simon’s explorations. Although he returned to theme now and then, he was relatively more focused on human decision making (especially in Newell and Simon (1972)). This may be explained by the fact that an acceptable model of decision making is a prerequisite for a theory of learning. Once such a model of performance is agreed upon, learning can be seen as an improvement or augmentation in the capabilities of this performing system in the same (or similar) problem domain.

Learning, however, is not unique to human beings alone. Other organisms and even artificial systems are capable of exhibiting learning behaviour. In fact, conceptualizing thinking and learning machines has been of interest from the genesis of research on Artificial Intelligence (AI) since Turing (1950). With the recent advances in machine learning algorithms in a variety of domains, interest in AI has been rekindled. In this backdrop, we revisit some of the questions that occupied the pioneers of AI, who saw machines – digital computers in particular – as a vehicle to gain insights into human cognition, intelligence and learning. More specifically, we ask whether the current advances in machine learning explain the mechanics of human learning. If not, the differences between them are of natural interest.¹

To study this, we choose board games of perfect information (eg. Chess and Go) as a paradigm. The reasons behind this choice are partly historical, given their prominent place in the development of AI over the years because of their amenability to investigation via computational methods. These games are complex and the impressive ability displayed by human beings in playing them was seen as providing an ideal ground for understanding the ingenuity of human intelligence. If one could find satisfactory answers, it was hoped that relevant invariants about behaviour across domains could potentially shed light on how people behaved in complex environments, such as the economy. In addition, modern advances in machine learning algorithms have shown remarkable performance in games previously thought to pose considerable challenges (Silver et al. 2016). Despite their suitability and performance, there are fundamental differences between human and machine learning that exist within this paradigm. Our central argument in this paper is the following: unlike Simon’s approach, the focus and contents of most contemporary machine learning algorithms render them inadequate to explain human learning despite their impressive performance.

Our paper is structured as follows: in Sect. 2, we outline different approaches to learning in classical game theory (another prominent area of research on games) and contrast it with Simon’s approach. Unlike the former approach, the latter focuses on procedural rationality exhibited by boundedly rational agents, for whom optimization in such complex environments is out of reach. Section 3 examines different theories of learning which specifically emphasise procedural and computational aspects. In particular, we focus on deep learning employed in AlphaGo, that defeated top players. In Sect. 4, we outline the essential differences between human and machine learning and argue that the current machine learning approach takes us further away from understanding actual human learning.

Learning in Games

Our interest here is to explore the aims, methods, relative strengths and limitations of human and machine learning in the context of games. To this end, it might be useful to distinguish between learning to play a game and learning to play a game intelligently.² A mere ability to play a game only requires a knowledge of the rules – allowable or legal operations – of the game in question. This in itself may involve specific skills from human beings and require detailed instructions in terms of programs for a machine (digital computer). However, this aspect of learning is relatively straightforward for the present purpose and can be taught. On the other hand, we will be primarily concerned with learning to play in the latter sense, where the play is explicitly goal-oriented and there is an improvement in performance (in terms of some defined criterion) or capability of the decision-making entity.³

Learning: A Game-Theoretic View

Learning has been a well-researched subject in different branches of game theory. We briefly (even if only inadequately) review how learning is conceived within the conventional game-theoretic literature and behavioural game theory (Camerer 2003). Learning in situations that called for strategic interaction can be traced as far back as Cournout’s analysis of duopoly, but research in this area has been revitalized only since the 1950s. To speak about learning in a meaningful manner, the setting must naturally be dynamic (at least in principle), where agents can be seen as learning something over time through experience, trial and error, acquiring new information and so on.⁴ Hence, much of the discussion on learning in the literature on game-theory concerns dynamic, repeated games.

There are broadly two classes of models of learning in conventional non-cooperative game theory. We will call them, for want of better terms, the rational and adaptive class of models. In the former class, agents are rational, but may not necessarily be in equilibrium. The learning activity for these agents involves forecasting the behaviour of their opponents and responding to them optimally. These learning processes can vary greatly in terms of the sophistication that the agents employ while forecasting their opponent’s behaviour. Typically, agents possess a prediction rule that maps the history of the game until a given point to a probability distribution over the future actions of the opponent. This prediction rule can be deterministic or stochastic, with perfect or imperfect information, and agents are assumed to respond optimally with respect to it when choosing their actions at every stage of the game. The broader question of interest is whether and how these rational agents learn to play equilibrium strategies of the game starting from out-of-equilibrium situations. Learning in this context is seen as a dynamic adjustment process of agents groping to equilibrium. A well researched learning model in this class is belief learning in which agents dynamically update their beliefs about what their opponent will do based on actions carried out in previous periods of the game. Models such as best-response dynamics, fictitious play (Brown 1951) fall under this category. In the case of fictitious play, the agent tracks the relative frequency with which different strategies are played by their opponent in the past. This information is then used to form beliefs or expectations about strategic choices of the opponent in the current period.⁵ Agents are typically assumed to choose a strategy which maximizes their expected payoffs in the light of their beliefs about opponent’s behaviour. In contrast, agents in Bayesian learning models choose a strategy that is a best-response to a prior, i.e., a probability distribution over the strategies of the opponent.⁶ Apart from these relatively unsophisticated models of learning which focus only on information about the history of the game, we also have models of sophisticated learning (Kalai and Lehrer 1993) that take in to account the information available to the opponents, their payoffs and degree of rationality.⁷

The second class of learning models, viz., adaptive models, do not assume that the agents optimize and behave rationally as understood in the conventional sense. Instead, they employ heuristic methods or behavioural rules to choose their actions at every stage of the game. A simple example of such a behavioural rule is imitation, which is a basic form of social learning. Another learning rule that has received a lot of attention in the literature is reinforcement learning (or stimulus response learning), which has its origins in behavioural psychology (Bush and Mosteller 1951; Roth and Erev 1995; Erev and Roth 1998). The intuition behind this learning scheme is that better performing choices are reinforced over time (and hence more likely to chosen in the future), while those that lead to unfavourable outcomes are not. Other examples of adaptive learning methods include regret minimization(Hart and Mas-Colell 2000), imitate the best (Axelrod 1984), learning direction theory (Selten and Stoecker 1986).⁸ In addition, there are hybrid learning models, such as experience-weighted attraction (EWA) model (Camerer and Ho 1999), which combine elements from belief-learning and reinforcement learning models. Note that belief learning pays no heed to choices made by agents themselves in the past (the focus is only on the history of the opponent’s strategies and choices). Similarly, in reinforcement learning, agents ignore the structure of the game, information about strategies used by their opponents and foregone payoffs. EWA combines this potentially relevant information taking into account both forces, i.e., attraction and experience weight, in a single learning model.

The extent to which the above game-theoretic models shed light on how players might actually play games in reality and learn is a relevant question. Research on experimental and behavioural game theory (Camerer 2003) explore the empirical relevance of these models. However much of this research is limited to laboratory experiments and fitting learning models to experimental data, which poses a restriction.⁹ In this paper, we are concerned in particular with learning and gaining expertise in perfect information, complex games like chess and Go. These games typically contain very large search spaces and the possibility of a player optimizing over all possible strategies is near impossible. We will analyse this in the next section.

Learning, Chess and Procedural Rationality: A Simonian View

Board games, chess in particular, have always piqued the interest of many scholars interested in the holy grail of human intelligence and AI. Chess has often been viewed as the Drosophila of artificial intelligence (Ensmenger 2012) and cognitive science (Simon and Schaeffer 1992, p. 2)¹⁰. What makes chess (and Go) different from the games considered in traditional non-cooperative game theory and why is it a conducive and fertile ground to study actual human intelligence?

First, the game of chess may be considered as being trivial or uninteresting from the classical game-theoretic standpoint.¹¹ Chess is a finite, alternating, two-person, zero-sum game of perfect information, without any chance moves.¹²$^{,}$¹³ For such games, a classical game theorist might prescribe a potential rational strategy in which one goes through every branch of the game tree to see whether it leads to a win, loss or a draw, assign values to each of those accordingly and employ a minimax strategy backwards. But, lo and behold, the existence of a strategy does not necessarily imply that learning such a strategy or implementing it is a trivial task. Second, classical game theory focuses largely on substantive rationality (the focus is on what), focusing on optimal strategies and consequently, often remains silent on how agents might choose a particular move. The actual decision processes and their plausibility are not of central concern. Third, skills such as pattern recognition, knowledge acquisition, long-term memory and intuition are often vital in the actual game of chess. However, these factors, or cognitive limitations in general, are seldom seriously considered in games investigated by classical game theory.

Apart from these differences, a crucial distinguishing factor is that games like chess have deterministic but very large search spaces. The state-space and size of the game tree associated are too big and agents cannot realistically engage in exhaustive search and calculations as they do in conventional game theoretic models. These considerations qualitatively hold, pari passu, for the game of Go, if anything with increasing severity given the relatively larger and wider search space. Consequently, highly selective search may be the only viable option in the light of computational limitations faced by agents. Yet the skill which human players display in games like chess and Go is truly astounding. Players who are relatively good often employ highly selective search and engage in in-depth reasoning of a select few variations.

Not surprisingly, these factors made games – at least chess – an ideal experimental bed for AI attempting to gain insights into human intelligence. The goal was to unearth how computationally constrained humans coped with complex and rich task environments like chess. Decision processes which transformed insights from the weird and mysterious world of intuition into actual intelligent behaviour were seen to embody the essence of human thought. Thus, chess presented an ideal microcosm within which to develop and test theories concerning intelligence and cognition. The relatively straightforward rules of chess, its discrete nature that was readily amenable to analysis by digital computers together with centuries of accumulated knowledge together cemented the position of chess as a testing bed for AI. Newell and Simon, who were among the participants in the seminal AI conference in Dartmouth in 1956, shortly declared: ‘chess is the intellectual game par excellence....If one could devise a successful chess machine, one would seem to have penetrated to the core of human intellectual endeavor.’ (Newell et al. 1958, p. 320, italics added).

For Simon, human decision makers are constrained by computational limitations while operating in complex environments. In such environments, Simon argued that they are best seen as problem solvers (not maximisers or optimizers), who in turn are characterized as Information Processing Systems (IPS) performing symbolic manipulations (Newell and Simon 1972, pp. 4–13 and ch. 14). They engage in a structured search in the problem space and only the relevant aspects of the task environment are represented while structuring. The possibility of optimization or rational play is out of reach for such players in these complex problems. Unlike those agents in classical game theory who maximize or optimize, these agents can satisfice at best.¹⁴ According to him, ‘The task is not to characterize optimality or substantive rationality, but to define strategies for finding good moves – procedural rationality’ (Simon and Schaeffer 1992). All of these render Simon’s research program a completely different character from that of von Neumann–Morgenstern approach.

In chess,the practical amount of computation feasible for players and the inability to exhaustively search the entire search space creates a wedge between the best moves in the shorter and longer horizons. The task of choosing a‘best move’ to respond to a given problem on the board involving a smaller search space may differ from strategy or choices which might be better when the entire course of the game, i.e., when larger search spaces (or horizons) are considered.¹⁵ This is because the actual search space under consideration by the problem solver varies over different stages of the game. The oft-discussed distinction between well-structured and ill-structured problems can be understood in terms of this wedge. According to this view, the actual problems presented to agents are best seen as ill-structured problems that are continually transformed into well-structured problems. These transformations in structuring the problem representation and using relevant heuristics for a particular representation are at the core of problem solving (Simon 1973, p. 185–187). It is here that the notion of learning in Simon becomes evident:

If the continuing alteration of the problem representation is short-term and reversible, we generally call it “adaptation” or “feedback”, if the alteration is more or less permanent (e.g., revising the “laws of nature”), we refer to it as “learning”. Thus the robot modifies its problem representation temporarily by attending in turn to selected features of the environment; it modifies it more permanently by changing its conceptions of the structure of the external environment or the laws that govern it.

Borrowing from Miller, Simon postulated that learning involves an increasing complexity of informative cognitive representations, or chunks in the long-term memory. Since short-term memory is rather limited, the number of chunks that agents can handle at any given point in time cannot be more than a handful (seven plus or minus two according to Miller). A learned or an expert player is seen as employing processes that recall only a few, but increasingly complex chunks (or groups) from her long term memory. In addition to this, Newell and Simon also distinguish between adaptive changes in heuristics in the short and long-run. For them, learning is a change in the repertoire of heuristics itself and not just a change in specific heuristics that are actively guiding a search. Thus, learning from a Simonian standpoint can be seen as a mixture of (i) increasing nuance in structuring problems, (ii) the ability to group relevant information or knowledge into chunks in the long-term memory and (iii) reshaping the repertoire of heuristics that can be employed to chose a good move for the problem at hand (Simon 1979, p. 167). When Simon speaks about learning, note however that there is no reference to equilibrium of any sort or a presumed movement towards it.

It is quite evident that the approaches of classical game theory and Simon are drastically different. Taking the route of classical game theory, one would consider a simplified approximation of the actual game, and focus on a game-theoretic optimum for that approximation. Simon’s route was to depart more ‘from exhaustive minimax search in the approximation and use a variety of pattern-recognition and selective search strategies to seek satisfactory moves’(Simon and Schaeffer 1992, p.16). The second approach to game theory is inherently computational (procedural) and intimately related to the idea of bounded rationality and satisficing.

What is emerging, therefore, from research on games like chess, is a computational theory of games: a theory of what it is reasonable to do when it is impossible to determine what is best - a theory of bounded rationality. - (Simon and Schaeffer 1992, p.16)

Before we end this section, two remarks are in order: first, as Simon has clarified in various places, he concerned himself with procedures that agents use to solves problems at hand. In this goal-oriented problem-solving set up, agents who are boundedly rational should not be viewed against the benchmark of substantive rationality or utility maximization in economics. Bounded rationality is, in fact, a more general notion and a procedural theory that can sufficiently account for bounded rational behaviour can naturally accommodate substantive rationality, but not vice-versa.¹⁶ They are best viewed as different approaches altogether. Second, considering the computational limitations of the decision maker alone does not make the approach Simonian since it is insufficient to understanding the nature and emergence of procedural rationality. For Simon, the complexity of the task environment and the practical limitations on the computational capabilities of the agent are equally important.¹⁷

Computation and Models of Learning

In the previous section, we noted that Simon’s approach was explicitly computational and his focus was on procedural rationality. What exactly is a procedure or method that agents can use for solving problems or learning? Efforts to characterize the idea of intuitive calculability in terms of a formal notion gave rise to several definitions of an effective method in the early 1930s, which were later proved to be equivalent. Intuitive or effective calculability was seen to be encapsulated by the mathematical notion of computability. Turing’s formulation of this notion, in what came to be known as a Turing machine, presents one of the simplest yet powerful models of computation. The Church-Turing thesis (not a theorem) claims that the class of functions that are intuitively computable is same as the class of functions that are recursive or Turing computable. For a decision maker to be procedural in this framework, one needs characterize an agent with a model of computation (for instance, a Turing machine).¹⁸ The process of decision making is then one of solving problems algorithmically (Velupillai 2012).¹⁹

Before we discuss computable learning in games, brief remarks on computability in games is apposite. The first step in a computable approach to studying games would require that game theoretic models be cast in appropriate recursion-theoretic or constructive formalisms.²⁰ Classical game theory is replete with games whose decision rules and strategies are non-effective and non-constructive. Making these games conducive to analyse procedural and computational aspects would mean effectivising these games: i.e., identifying and replacing the source of non-effectivities and couching them in recursion-theoretic formalisms or endowing them with constructive processes. Only after this is done, we can pose questions such as whether a given game is (effectively) playable; if so, whether a best or an optimal strategy, if it exists, can be actually employed by the player.( Even within classical game theory, there are results concerning the (un)computability and computational complexity of Nash equilibria (Prasad 1997; Daskalakis et al. 2009; Velupillai 2009; Nachbar and Zame 1996). However, discussing complexity considerations concerning the computation of Nash or other types of equilibria make little sense when discussed in the context of models which are themselves uncomputable.²¹

A notable contribution in effective games has been by Rabin (1957). A fertile interpretation of effective games in terms of a more general class of arithmetic games is presented in (Velupillai 2000, ch.7). Rabin’s theorem is particularly relevant to the discussion in the subsequent sections concerning learning. Intuitively, it asserts that there exist finite, determined, perfect information games ‘in which the player who in theory can always win cannot do so in practise because it is impossible to supply him with effective instructions regarding how he should play in order to win’ (Rabin 1957, p. 148).

In this backdrop, we will consider two major approaches to learning that are viewed as being computational and outline the differences between these two.

Computable Learning

First, we consider a class of models related to the learning paradigm proposed by Gold (1967) and further developed in Osherson et al. (1986). This was primarily intended as a model for understanding language acquisition by children. The necessary elements for describing this learning paradigm include a learner, hypotheses, the environment in which learning takes place and finally that which needs to be learned: a language. All of these necessary ingredients are formalized in terms of natural numbers: languages are seen as a set of natural numbers(N), more specifically to recursively enumerable subsets of N. Hypotheses or learner’s conjectures are identified with Turing machines, environments with texts, which are sequence of natural numbers. Learners in this model are viewed as functions which convert the finite evidence available into theories. Both evidences and theories are interpreted in terms of natural numbers, and hence the mapping is from $N\rightarrow N$. In this framework, learning is interpreted as being successful if the learner’s hypotheses stabilize and become accurate. More precisely, successful learning means identification in the limit – conjectures are made and refuted until they converge.

The learning function, in general, can be recursive or non-recursive, thus not merely restricted to a set of partial and total recursive functions. If such a restriction were to be placed in the context of human learning, then it can be related to a (rather strong) position that identifies all human thought and intellectual activities as being simulable by a Turing machine. However, imposing computability constraints in learning functions can help identify boundaries and limits of algorithmic reasoning. In this paradigm, learning can viewed as an act of inductive inference where a learner infers theories from the finite evidence that is available. This can also be interpreted in terms of the modern theory of inductive inference proposed by Ray Solomonoff (Velupillai 2000, ch: 5.2), which is grounded in recursion theoretic ideas. In the context of this paper, this could be viewed as a game played against nature where agents are provided with sequences of information at different stages as the play evolves. Although appealing at a theoretical level, one potential drawback of this paradigm could be that it may only have limited applicability to study empirical data arising from actual games since it lacks explicit efficiency bounds. In principle, this convergence can take an infinite amount of time.²²

Computational (Statistical) Theories of Learning

The second class of learning models that we will discuss are collectively referred to as computational learning theories or statistical learning theories. These are also often referred to as machine learning models. Most of these models focus on learning from actual data and are geared towards making predictions or classifications. Typically, the task is to find the underlying functional relationships that characterize the data. To see this in a bit more detail, let X be the input data set and Y be some output measure. In the case of supervised learning, the task is to infer or approximate the functional relationship between the input-output pairs (X, Y) based on the features in X with an eye on predicting or classifying new data based on this approximation. The learning agent (or a digital computer) is rendered with abilities to learn from data without explicit or detailed programming. The act of learning involves the formulation and alteration of this prediction model, call it f, by minimizing the error. In the case of unsupervised learning, the task is to uncover hidden structures within a given dataset X, without a training sample to rely on.

Examples of supervised learning methods include Gaussian kernels, linear and logistic regression, linear discriminant analysis, separating hyperplanes, Bayesian methods, classification trees and regression trees among others. Examples of unsupervised learning methods include various clustering algorithms such as k-means, hierarchical clustering, to name a few. An important learning model that features in both supervised and unsupervised categories is artificial neural networks.²³ There are also ensemble learning methods which use a collection of learning methods to infer the predictive model in question. Another model of computational learning that is widely employed is reinforcement learning (discussed earlier), which has been found to be extremely useful in devising machines which play games.

Having discussed two major approaches to learning that involve computation, what distinguishes computable and computational models of learning? First, computable learning models resort to the formalisms of computability theory and are endowed with a recursive structure. In contrast, computational or machine learning models are computational in a more narrow, instrumental sense: they rely on algorithmic or computational methods for approximations of their predictive models. Second, one needs to note the assumptions concerning the domains of input and output data. Those in latter models are not natural or rational numbers as in the case of computable learning models, they are almost always real numbers. Thus, computational learning models are closer to statistical learning theory, where statistical issues concerning estimation and prediction dominate.

We now return to the employment of these models to learn and play actual complex games in an intelligent fashion. Computers – especially digital computers – playing games has been viewed as a possible window to understanding intelligence from their invention. Alan Turing, the pioneer of computability theory, was one of the early advocates of this idea. His attempts to understanding machine intelligence utilized the idea of a chess-playing digital computer (Turing 1948, 1953). Turing also went on to construct one of the first ever chess playing programs.²⁴ Other early chess playing programs such as the Los Alamos program, Bernstein’s program and Newell-Shaw-Simon program offered some thrust during the first wave of AI. In particular, Shannon’s typology of solutions to prune large search trees – through either brute force (Type-A) or through intelligent heuristics performing selective search (Type-B) – set out two distinct approaches to constructing chess playing programs.

Simon’s view was that both for humans and machines, reliance on intelligent heuristics for highly selective search was important. Simon and Newell’s approach focused on symbolic representations of the problem and on information and manipulations of these strings of symbols. It is now broadly referred to as Classical AI, symbolic-AI or the Good Old-Fashioned Artificial Intelligence (GOFAI). This ought be distinguished from sub-symbolic AI, which eschews explicit representation. For sub-symbolic AI, performance alone matters and the computational learning algorithms were not expected to reason like humans do.²⁵ Artificial neural nets, reinforcement learning and other statistical learning approaches outlined earlier belong to this category. One of the limitations of Gold’s learning paradigm which has been pointed out is that, despite its elegance, it lacks practical applicability as a theory. On the other hand, computational models of learning are often applied to a variety of tasks and have been shown to be fairly efficient. One such example of the statistical approach to learning in machines is Deep Learning and it has had remarkable success in playing complex games, which is the subject of the following section.

Deep Learning and Go

Until recently, the game of Go was regarded as one of the few unconquered frontiers of AI. The features that made it one of the most challenging games for machine play is its enormous search space – which is much larger than chess – and the notoriously difficult issues concerning positional evaluation on the board. Go is shown to be PSPACE-Hard (Lichtenstein and Sipser 1980) and that no PSPACE algorithm can exist (Robson 1983) for Go.²⁶ Brute-force approaches like those that were relatively successful in chess (in the case of Deep Blue) are believed to be infeasible when it comes to Go. Just like with chess, Go piqued the curiosity of cognitive science and AI researchers with the clear superiority that human beings displayed.²⁷ However, there has been notable progress in computational learning algorithms employing artificial neural networks to play Go in the recent times. AlphaGo, developed by Google DeepMind has recently managed to defeat some of the top Go players in the world. The key idea underlying this success is deep learning, which in turn is a representational learning method. Unlike traditional machine learning, the representations are themselves expressed in a hierarchy of simpler representations (Goodfellow et al. 2016, pp. 5–10) and these different layers of features and mapping from features to output are to be learned from data.

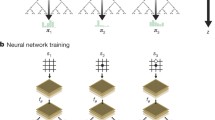
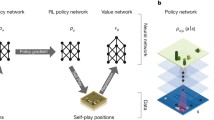
A sketch of the strategy and architecture of AlphaGo in a bit more detail may be useful here. Let us consider a board game like chess and let b and d be the breadth and depth of game. Then there is approximately $b^{d}$ sequence of moves possible. Since this number, i.e., $b^{d}$, for the game of Go is a very large and an exhaustive search is practically impossible even for very powerful machines. Type-B strategies, which were outlined Shannon’s initial proposal (to constructing chess programs) to reduce the effective search space become important and indispensable. The main innovation in AlphaGo is the way in which this depth and breadth reduction is achieved using convolutional neural networks and the use of Monte Carlo Tree Search (Silver et al. 2016). Go, in this setting, is viewed as an alternating Markov game between two players. The probability distribution over possible legal actions at any given state is referred to as policy. Value function of the game refers to the expected outcome, provided that the actions by both are selected in accordance with the policy.²⁸ It employs a value network for evaluating different positions and the moves are then selected using a policy network.

In terms of the process, first, real life expert Go games (160,000 games, consisting of 29.4 million moves) are fed as input to train the policy network, which is a convolutional neural network. The output of this supervised learning process, which is a probability distribution over legal actions, is then fed as initial input into another policy network which employs reinforcement learning for improvement. This reinforcement learning policy network undertakes self-play and generates a new policy, which is an improved probability distribution over legal moves. Using this policy as an input, the value networks predict the expected outcome of the game (a single scalar value) using regression from a given position on the board. The actions then are selected based on a search algorithm (MCTS) that combines both policy and value networks.²⁹ Similar deep learning approaches have also had considerable success in games like chess and Atari (Lai 2015; Mnih et al. 2015).

Even within the computational modes of learning and playing games that we have discussed, two distinct conceptual approaches to learning can be categorized. First, learning as understood in machine learning models, involving an alteration of the internal configurations, prediction models and associated parameters without much interference or explicit instructions. Performance alone matters in this approach. Second, along the lines advocated by Simon, learning involves a permanent alteration in the repertoire of heuristics to guide search and actions of an IPS, involving knowledge acquisition and increasing complexity of perceptual chunks. This involves explicit programming of the rules and pays attention to both performance and the correspondence of processes to those implemented by an actual human player.

Human and Machine Learning: Lessons from Chess and Go

Deep Blue plays very good chess–so what? Does that tell you something about how we play chess? No. Does it tell you about how Kasparov envisions, understands a chessboard? ...I don’t want to be involved in passing off some fancy program’s behavior for intelligence when I know that it has nothing to do with intelligence. And I don’t know why more people aren’t that way. (Somers 2013)

Given the success of various deep learning algorithms, one naturally wonders whether we are finally closer to understanding how human cognition and learning works. However, despite the impressive performance by machine learning methods in games like Go and chess, they do not seem to shed enough light on how human beings decide and learn in real life.

First, note that the features that are well known to characterise humans – limitations on information processing capabilities, attention, short-term memory – and their learning processes are not shared by these programs. This omission of psychological characteristics poses difficulties in inferring corresponding human learning mechanisms based on performance alone.

Second, human-like or even superhuman performance of these machine learning programs should not be confused with them being ‘explanations’ of actual human learning. While their achievement may be impressive, they provide little or no explanation regarding how human beings reason and learn. Kasparov (2017) points precisely to this concern:

We confuse performance – the ability of a machine to replicate or surpass the results of a human – with method, how those results are achieved. This fallacy has proved irresistible in the domain of higher intelligence that is unique to Homo Sapiens.

There are actually two separate but related versions of the fallacy. The first is “the only way a machine will ever be able to do X is if it reaches a level of general intelligence close to a human’s.” The second, “if we can make a machine that can do X as well as a human, we will have figured out something very profound about the nature of intelligence. (Kasparov 2017, p. 26)

One might argue that these programs can be viewed as imitating the ways in which underlying neural architectures in our brains aid learning and recognition of patterns. In other words, they belong to the ‘as if’ category. However, this may not be a compelling argument, at least as yet, since we have not been able to conclusively verify such a claim. Also it is worth noting that the computational power of artificial neural networks – convolutional or not – do not exceed those of Turing machines. Insofar as one accepts the thesis that all intuitively calculable functions (by humans) are Turing computable and that all human decision making and learning are through computational processes (in the sense of digital computation),³⁰ theoretically uncomputable problems concerning learning still remain beyond the reach of human beings.³¹

Third, one of the important characteristics of human learning processes is that it is terribly slow. This may be related to the specific information processing character of the human beings. For modern machine learning programs, efficiency is a key criterion and they do not focus on explaining the causes for these peculiarities in learning and why they are unique to human beings.³² This was to be a priority for machine learning according to Simon. In Simon (1983, p. 26), he makes a useful distinction concerning two goals of AI that may be of worth pointing out here:

Artificial intelligence has two goals. First, AI is directed toward getting computers to be smart and do smart things so that human beings don’t have to do them. And second, AI (sometimes called cognitive simulation, or information processing psychology) is also directed at using computers to simulate human beings, so that we can find out how humans work and perhaps can help them to be a little better in their work - (italics added)

Fourth, a hallmark of human learning is that they rely heavily on the use of analogical reasoning while learning. Human beings routinely employ analogies across different problem domains. This clearly is a sign of intelligent behaviour that is missing in machine learning such as deep learning. They are often designed for a specific problem and focus on associations rather than analogy.

Fifth, the essence of human learning on the other hand can be seen as an accumulation of a set of principles or models that can employed across problem domains. The role of pattern recognition may be an important component of learning in human beings, but it is by no means the only feature involved. Human learning activity seem to involve continuously building causal models of reasoning (however imperfect they may be), deducing patterns and also a component involving finding meta-patterns in inferential procedures underlying pattern deduction across a variety of problems. This meta-level transferability of knowledge is rarely captured in many of the machine learning models that we have discussed above. Learning, seen this way, is about extracting, retaining and transferring knowledge and interesting patterns.³³

Sixth, constructing causal models – or building any model for that matter – necessarily involves excluding a lot of the information in an environment and relying only on a subset that the learner considers relevant. In the case of board games, it involves discriminating attention and focusing only on those structures that are relevant, and exploring various consequences. This is also what seems to underlie the act of structured search and much of human learning. As Simon points out, human decision making involves human beings structuring what may appear to be a complex problem through relevant representations based on selective features. Learning would then involve the process of refining and enriching these (internal) representations and the associated set of actions or heuristics.³⁴ In modern machine learning, the role of internal representation of the problem and the task environment is trivialized.³⁵

Seventh, an aspect that is often ignored in machine learning models is the role of natural language in learning. Human beings do learn from each other and this often involves communication, mainly through natural language. For instance, specific terms associated with various patterns in Go (or chess) that have been developed and communicated to players over the years as they learn. It helps players drastically reduce descriptive complexity of patterns on the board, remember and recall them easily (Kao 2013, pp. 95–98). This important aspect of human learning where players accumulate relevant vocabulary is often absent in machine learning.³⁶ Thus, for humans, learning constitutes more or less a permanent change in their knowledge structure, contents of which can be readily employed in the future, even in entirely different task environments.³⁷

Finally, machine learning algorithms often need a vast amount of data to learn – as in AlphaGo – and in contrast human beings seem to be good at learning from relatively fewer examples. By this, we do not mean human beings necessarily learn faster, but only that they do so with fewer examples. Note that the training sets in the supervised learning in the case of AlphaGo and the knowledge base of Deep Blue are in fact actual games of expert human players. The objective behind research on human learning should therefore be one of unearthing processes that lie behind how human beings gain such expertise overtime and not merely using that expertise to build engines that generate human-like performance. It is reasonable to envisage developments that would enable future programs like AlphaGo gaining impressive expertise purely through self-play. An argument can be made about the crucial role of self-play in machine learning programs, justifying it as a plausible way to account for counter-factual or fictitious mental games. However, this argument is tenuous at best since it does not explain how exactly learning occurs and it is silent on the associated change in knowledge structures. Corresponding aspects of human learning, in our opinion, can be better explained through the lens of chunking: increasing modularity and sophistication of chunks in the memory and a refinement in mapping them to appropriate actions and heuristics.

It may argued that programs such as AlphaGo are at least not brute-force based and are akin to Shannon’s Type-B programs. There may be some merit to this argument and it is a welcome change. Unlike Deep Blue, they consider much fewer moves while making decisions by pruning the search space using smart heuristics. However, despite this attractive feature, we note that the lack of brute force or the presence of pruning alone does not make it human-like. Instead, it is the nature and contents of these heuristics that need to be taken in to account.

There is another issue that is relevant in this context: how are we to discriminate among many potential machine learning programs that exhibit the same level of performance? We argue that the possibility of executing these learning processes by actual human beings should be the criteria to discriminate between different sufficient explanations. It is here that empirical and experimental studies in cognitive and behavioural psychology would play an important role. Among those computational learning theories which meet the criteria of actual human implementability, preference should be given to parsimonious – not merely simple – theories.³⁸

Computational Model Versus Computational Explanation

This is a grail worthy of a holy quest, especially “explain”. Even the strongest chess programs in the world can’t explain any rationales behind their brilliant moves beyond elementary tactical sequences. They play a strong move simply because it was evaluated to be better than anything else, not by using the type of applied reasoning a human would understand.

A distinction between a computational model and a computational explanation in this context may be of use. In a computational model, one strives to describe the behaviour of a system without necessarily implying that the underlying system or its components perform computation. On the other hand, in a computational explanation, one explains the behaviour of a system by specific computational processes that are internal to the system (Piccinini 2015, p. 60). Differences between Simon’s approach to human problem solving and bounded rationality and the contrasting position of modern machine learning programs using deep learning can be seen through this lens. For Simon, the use of computers to learn and play complex games was a ‘deliberate attempt to simulate human thought processes’ (Newell et al. 1958, p. 334, italics added). It was not for the chess programs to achieve human-like performances alone. In this sense, one can argue that computational methods were not just reasonable vehicles or devices for modelling for Simon, but they were intended to explain how computationally constrained human beings operate in complex environments.

A few remarks concerning computability and computational complexity in Simon’s approach may be pertinent. Although Simon’s human problem solving and learning can be legitimately interpreted in terms of computability theory, he himself seems to be uninterested in them. He felt that limits to computability, though relevant as a potential outer boundary for human procedural reasoning, may not be binding or important for actual human decision makers since they are severely constrained in their abilities to compute. He made a distinction between computability in principle and practical computability (Simon 1973, pp. 185–186). Similarly, he expressed scepticism about the relevance of results on computational complexity as it mainly addressed worst-case complexity of algorithms. Instead, for him, it was the average-case complexity that human beings encounter in their day-to-day which merits focus (Simon 2000, p. 247).

Conclusion

In this paper, we considered the problem of learning by humans and machines with a particular focus on complex board games like chess and Go. These games have been viewed as ideal grounds for understanding the ingenuity of human intelligence and they have been amenable to investigation through computational methods. We surveyed the approaches to learning in classical game theory which resorts to substantive rationality and optimization. We contrasted it with Herbert Simon’s approach, which focused on procedural rationality exhibited by boundedly rational agents for whom optimization in such complex environments is out of reach. Given that computational methods play an important role in the procedural theories of Simon, we examined various computational theories of learning.

Although recent achievements of machine learning algorithms in playing against human players have been commendable in complex board games, we argued that these are not particularly illuminating in providing reasonable explanations concerning how humans actually learn. Consequently, we find them departing from Simon’s life long quest to understand the mechanics of human problem solving. We feel that impressive developments in model-free learning and in the areas of pattern recognition algorithms can be imaginatively integrated with the classical approach to AI. Studies such as Lake et al. (2016) point us in this direction.

Simon’s research program on bounded rationality, human problem solving and learning was not merely subversive, intended solely to challenge the established view regarding human decision making in economics. Instead, it was a much broader, ambitious project in which he studied actual human beings and their decision making processes closely. He seems to have never shied away from dirtying his hands with all the messiness and glory associated with human decision making, always seeking explanations and trying to unlock its mysteries. He was more akin to a renaissance man, not lured by highly technical, mathematical models or their performance alone. In his efforts, Simon, much like Turing, was always a firm believer in ‘the inadequacy of reason unsupported by common sense’ (Turing 1954).