Introduction

Informed management decisions require reliable data about the distribution and abundance of an endangered species. When it was listed as endangered in 1967, the San Joaquin kit fox (SJKF; Vulpes macrotis mutica) had been substantially reduced from its historic range, with kit foxes restricted primarily to the western and southern ends of the San Joaquin Valley (U.S. Fish and Wildlife Service 1967, 2010) within the San Joaquin Desert biotic province (Germano et al. 2011). Since then, the status of SJKF throughout much of its current range, particularly in the northern and central portions, has remained poorly known due to a lack of large-scale surveys and many areas where surveys cannot be conducted due to private land ownership (U.S. Fish and Wildlife Service 1998, 2010). In 1998, a recovery plan identified three geographically-distinct core populations whose enhanced protection and management was critical to a sound conservation strategy: the Carrizo Plain, western Kern County (including Elk Hills, Buena Vista Valley, and Lokern Natural Area), and the Ciervo-Panoche Natural Area (CPNA; U.S. Fish and Wildlife Service 1998; Phillips 2013). Both the Carrizo Plain and western Kern County are located in the southwest end of the range and are known to have high SJKF densities. The CPNA is a rural area in the central range of the SJKF that has been used mainly for grazing and contains relatively few man-made structures. Although little is known about SJKF in the CPNA, the area contains large portions of habitat with moderate and high suitability for SJKF and is thought to have a substantial fox population (Cypher et al. 2013).

Non-invasive genetic sampling offers an effective way to survey wildlife species, even when rare or endangered (Taberlet et al. 1999; Waits and Paetkau 2005; Ruell and Crooks 2007; Beja-Pereira et al. 2009). DNA obtained from scat samples can be used to identify individuals and estimate population size, alleviating challenges in gathering population data on low density species (Marucco et al. 2009; Solberg et al. 2006). Moreover, detection dogs trained to locate the scat of a specific species can reliably increase sample size(s) and number of observations of both fresh and aged scats (MacKay et al. 2008; Woollett et al. 2014). Conservation dog-handler teams have proven to be a useful tool for detecting SJKF scats, increasing the number of samples recovered in genetic surveys (Smith et al. 2003, 2006; Wilbert et al. 2015).

We used conservation dog-handler teams to locate SJKF scats in the CPNA, followed by DNA analysis of the collected scats. Using the genetic data, we documented the distribution of SJKF in the area and identified individuals present. We assessed genetic diversity and investigated how individuals in the area are related. We tested for population structure and connectivity within the CPNA. We used our data to estimate contemporary effective population size (Ne) as well as demographic or census population size (N). With this new information about SJKF in the CPNA, we discuss the relevance of our findings to the conservation of this population and of the species rangewide.

Materials and methods

Study area

The CPNA comprises ~ 372 km2 of moderate to highly suitable SJKF habitat (Cypher et al. 2013). This area includes the Panoche Hills, Panoche Valley, Griswold Hills, Vallecitos Valley, Tumey Hills and Ciervo Hills, as well as a narrow stretch of habitat east of these hills and west of Interstate 5. Altogether the CPNA represents a large continuous stretch of relatively undisturbed land from Mercy Hot Springs through the Panoche Valley to Silver Creek Ranch, and Vallecitos (Fig. 1). The Panoche Valley (PV) itself was the basin of a Pleistocene lake (Barrows and Ingersoll 1893), resulting in a fertile valley supplied by the Panoche Creek and consisting mainly of grasslands. Like other areas in the San Joaquin Valley, parts of the PV have been used for grazing and cultivation of crops since the mid-1800s (Frusetta 1991). However, the majority of the PV has not been further developed, with many ranchers and farmers living outside of the valley and using the land for livestock grazing or agriculture over the past centuries (Frusetta 1991). Today the PV is a mosaic of land uses with public and private ownership. Ten percent of the land is federally owned and protected from development. Another 105 km2 (~ 50%) are protected through a conservation easement, while approximately 8 km2 are slated for development as a large-scale solar plant. Thus, most of the PV has very suitable habitat for SJKF and is the largest area of land in the northern and central range of the fox that still shows lower levels of human impact.

Fig. 1
figure 1

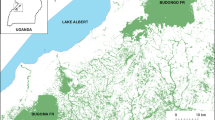
Survey areas and transects (green lines) are demarcated on the topographic map of the Ciervo-Panoche Natural Area (CPNA; purple boundary). Yellow triangles represent all of the scats genetically identified as SJKF and used in the population analyses (n = 330) while red circles represent the central location from all scat samples collected from each individual (n = 91)

Full size image

Surveys

Between 2009 and 2011, professional conservation detection dog-handler teams (Working Dogs for Conservation, Bozeman, MT) were used to locate scats of kit fox in multiple areas of the CPNA. Survey effort and locations varied each year, and consisted of a combination of targeted repeat and opportunistic surveys, driven by the dual aims of surveying new areas each year and increasing the likelihood of detecting more individuals overall. Several transects covering a total distance of approximately 56, 41, and 24 km were searched in suitable kit fox habitat in July of 2009, July of 2010, and May of 2011, respectively (Fig. 1). As determined by a freshness rating method based on their physical characteristics (see Smith et al. 2003), both fresh and aged scats were collected for DNA analysis.

The majority of transects were on public properties and right-of-ways, though private lands were also surveyed when access was permitted. Many transect routes utilized unpaved roads, as kit foxes frequently deposit a high number of scats on these roads (Smith et al. 2005). Additionally, various transects (or legs) were in vegetation or alongside paved roads bordering suitable habitat.

In order to augment the overall sample size for genetic analyses, all scats collected from 2009 to 2011 were combined with scats from a separate SJKF monitoring study that several of the co-authors were involved with in the PV area from July to September of 2010. In that study, surveys of approximately 352 km of transects on two adjacent sites included an initial and a repeat survey session approximately one week apart during which only fresh scats were collected for DNA analysis, since the goal was to obtain current presence and population information. Because that study included different areas, combining data also expanded our understanding of SJKF occupancy across the CPNA.

Locations of all scats were geo-referenced and recorded using Global Positioning System (GPS) units. Scats were stored in plastic bags with silica gel for desiccation (Fisher Scientific, Pittsburgh, PA) and shipped to the Center for Conservation Genomics laboratory at the Smithsonian Institution. All samples were used to map kit fox scat distribution and an individual’s recapture area.

Molecular techniques

DNA was extracted using the QIAamp DNA stool mini kit in a separate room to avoid contamination of PCR products from the main lab. Species identification, molecular sexing, and microsatellite genotyping were conducted following protocols detailed in Wilbert et al. (2015). Although conservation dogs can detect more scats and with greater accuracy in identification of species than humans (Hurt and Smith 2009), a handler may inadvertently collect non-target scat when a dog correctly locates a latrine containing fresh scats from multiple canids (i.e. fox/coyote; Ralls and Smith 2004); when a dog errs in scent discrimination and keys on a similar (yet incorrect) target; or when a dog selects an incorrect target when few target scats are present in order to receive a reward (Schoon 1996; Smith et al. 2003). Therefore, we determined the species of each scat sample by amplifying a fragment of the mitochondrial control region, which is species-specific by size (Bozarth et al. 2010). During this step, we diluted samples with poor amplification (1:15 up to 1:45) to minimize interference from PCR inhibitors from prey items such as insects (Panasci et al. 2011). These dilutions served as an optimization step for the following molecular steps because amplification issues were usually related to the quality of the scat sample. We then used canid-specific primers that use differences in the zinc finger gene to identify sex—two bands for males and one for females (Ortega et al. 2004; Ralls et al. 2010). Only samples that amplified successfully in both species and sex identification were then characterized for six microsatellites (FH2137, FH2140, FH2226, FH2535, FH2561, Pez19) that have been used reliably for individual identification of kit foxes in our lab (Smith et al. 2006). Because DNA samples extracted from scats are prone to genotyping error and contamination, we used a modification of the multi-tube approach (Taberlet et al. 1996). Briefly, each DNA extract was subject to a minimum of five independent PCR amplifications for each homozygous locus and a minimum of three times for each heterozygous locus to verify allele size and detect allelic dropout. Each amplification was conducted with a positive and negative control to detect any contamination and to standardize allele sizes across all data. We used fluorescently labeled forward primers in all PCRs to visualize them on an ABI PRISM* 3130 Genetic Analyzer (Applied Biosystems Inc. Foster City, CA).

We used the Excel Microsatellite Toolkit (Park 2001) to compare genotypes and defined individuals by unique genotypes and samples from the same individual by matching alleles at all loci. We checked all genotypes carefully but paid particular attention to those that differed at only one or two loci for accuracy of genotype and data entry. We also compared genotypes between samples collected in 2009–2011 to determine if any individuals had been recaptured in subsequent years. We checked for evidence of allelic dropout and/or null alleles using the program Micro-Checker (vanOosterhout et al. 2004).

We assessed our ability to differentiate individuals by estimating the probability of identity (PID) (i.e. the probability of different individuals sharing an identical genotype by chance) and the PID between siblings (Mills et al. 2000; Waits et al. 2001). Both PID unbiased and PID sibs values were low enough to suggest that we can differentiate between individuals, including close relatives (PID unbiased = 1.4 × 10− 5, PID sibs = 9.9 × 10− 3). Because we identified many individuals, we genotyped individuals at 5 additional microsatellites previously characterized in canids (AHTh171, FH2054, FH2328, FH2848, and Ren162; Spiering et al. 2009) to increase our statistical power in subsequent analyses. We selected one representative scat sample that amplified most reliably for each individual and genotyped these samples at the additional loci using the same protocols and conditions described above. We then used the final genotype of 11 microsatellites to assess genetic diversity and population structure.

Genetic diversity

We used GenAlEx to calculate expected (HE) and observed (HO) heterozygosity, and SPAGeDi to calculate allelic richness (AR) as defined by Nielsen (2003), effective number of alleles (Ne), and global estimates of FIS. We tested for departure from Hardy–Weinberg equilibrium with a global test of heterozygote deficiency using the Markov chain method in GenePop 3.4 (Raymond and Rousset 1995). We also used GenePop to test for linkage disequilibrium (LD) between pairs of loci. We calculated relatedness using the mean Queller and Goodnight estimator (1989) in GenAlEx.

Genetic patterns of population structure

We investigated genetic differentiation and structure within the CPNA through Bayesian analyses and statistical measures of variance. We used three Bayesian clustering approaches to detect population structure in individuals in the CPNA, one non-spatial (STRUCTURE version 2.3.2; Pritchard et al. 2000) and two spatially sensitive (TESS version 2.3.1, Chen et al. 2007; GENELAND version 2, Guedj and Guillot 2011). STRUCTURE assigns genotypes to genetic clusters that maximize Hardy–Weinberg and linkage equilibrium. We investigated the likelihood of the number of genetic clusters (K) from 1 to 8 with 10 independent replicates, admixture ancestry and correlated allele frequency models, and Markov chain Monte Carlo resampling for 400,000 generations following a burn-in of 100,000. We visualized the STRUCTURE results using STRUCTURE Harvester (Earl and vonHoldt 2012) and determined the number of clusters using the Evanno et al. (2005) method. Results from the ten replicates of the chosen K were averaged using CLUMPP 1.1.2 (Jakobsson and Rosenberg 2007) and the appropriate .ind file created from Harvester. We assigned individuals to a cluster if they had an ancestry assignment of at least 0.70, following Marsden et al. (2012).

The spatially sensitive analyses, TESS and GENELAND, use the same principles as STRUCTURE but also incorporate the geographic coordinates for each individual. Because we found two or more scats for many individuals and there are no programs that can incorporate more than one geographic location per individual for this type of analysis, we chose one GPS point for each individual that was located in the middle of its sample distribution. When an individual had only two scat locations, we chose the point that was closer to other individuals. In TESS, we analyzed our data using the default geospatial weighting of 0.6, and analyzed values of K from 1 to 10, with 10,000 burn-in sampling and 50,000 recorded steps. Each potential population was run 10 times for three models: no admixture (HMRF model), the CAR admixture model, and the BYM admixture model. The most appropriate number of populations was chosen using the highest 30% DIC scores for all runs and looking at two indicators: (1) determining the lowest value, and (2) graphing the average DIC scores for each model as the value of K increased. In GENELAND, we ran the correlated frequency model for 500,000 steps with every 100th step recorded and a burnin of 100,000 steps. This model was run for 10 replicates of 1–10 populations.

We performed a hierarchical analysis of molecular variance (AMOVA) using GenAlEx to test for the proportion of genetic variation between subpopulations previously identified using STRUCTURE. We tested the significance of the percentage of variance between and within populations using an F-test. We calculated the F ratio and probability of variance in Excel using 1 degree of freedom for the numerator (number of groups, K, − 1) and 180 degrees of freedom for the denominator (total sample size equals two alleles per individual − 2). We visualized genetic differentiation with a principal coordinate analysis (PCoA) conducted in GenAlEx. We also calculated the mean eigenvalues for principal coordinates 1 and 2 for both populations and plotted this mean on the PCoA to display the population separation. Using GenAlEx, we also calculated two measures of genetic differentiation: FST as described by Slatkin (1995) and Dest (Jost 2008) as calculated by Meirmans and Hedrick’s equation 2 (2011).

To examine alternative causes for genetic structure, we tested for isolation by distance (IBD) and kin clustering. We generated matrices of genotypic distance (GD) and linearized geographic distance (LnGGD). We executed Mantel tests between GD and LnGGD with 10,000 permutations to test for IBD. We created matrices of pairwise relatedness using the mean Queller and Goodnight estimator (Queller and Goodnight 1989) and tested for correlation with LnGGD using the same Mantel test parameters. We also performed a spatial autocorrelation analysis (SAA) to see if individuals next to each other were more related than average, which would be expected because kit foxes live in family groups (Cypher et al. 2000), and at what spatial scale this kin clustering might occur. SAA is a multivariate analysis that measures the genetic similarity of individuals within a distance class. We chose a distance class of 2 km because we needed the ability to detect fine scale structure resulting from family groups inhabiting typical SJKF home ranges of 4–11 km2 (Cypher et al. 2000; Koopman et al. 2000). The autocorrelation coefficient (r) ranges from − 1 to + 1 and is closely related to Moran’s I, a measure of genetic relatedness. We ran SAA in GenAlEx using 10,000 bootstraps around r and 10,000 permutations to calculate the 95% upper and lower confidence limits of random sampling of the data assuming no spatial structure. Heterogeneity of spatial structure (omega) was used to test significance of the correlogram.

Population estimates

We used two methods to calculate Ne: an Ne estimator based on sibship frequency (SF; Wang and Santure 2009) as implemented in the program COLONY (Jones and Wang 2010), and the commonly used LD method (Hill 1981; Waples and Do 2008) as implemented in NeEstimator v.2.01 (Do et al. 2014) with a correction for bias from low frequency alleles (Waples 2006). These are the most robust methods available to estimate Ne from one sample. We could not use two-sample methods because they require samples collected at least 3–5 generations apart for species with overlapping generations (Waples and Yokota 2007). For both methods, we used the random mating model. We calculated Ne using individuals that were detected during all 3 years since this period represents 1–2 kit fox generations. While combining years, we calculated Ne for each subpopulation separately because combining them would violate population closure, which is assumed by the models in these programs (Ne calculations that combined the subpopulations showed a Wahlund effect as expected; data not shown). For Ne estimates based on SF, we assumed polygamy for males and females and used the population allele frequencies, no sibship prior, two medium length runs with the full-likelihood method, and we report 95% confidence intervals. For the LD estimate, we used a minimum allele frequency cutoff (Pcrit) of 0.02, which is suggested for our sample sizes in order to balance Ne precision and upward bias from rare alleles (Waples and Do 2010). We report 95% confidence intervals from the jackknife approach.

We also explored possible bias in LD-based Ne estimates due to immigration or the presence of highly related individuals (Waples and Anderson 2017). Because scat samples do not allow us to directly determine the age of individuals nor definitive kinship relationships, we performed this analysis using three subsets of data: (1) all individuals from a population, (2) individuals from a population without those identified as migrants or genetically admixed, and (3) individuals from a population without those that were highly related. We removed migrants or genetically admixed individuals that were identified previously with STRUCTURE. We used the Queller and Goodnight estimator to calculate pairwise relatedness between individuals and removed the smallest number of individuals required to reduce pairwise relatedness to < 0.5.

We calculated census population size (N) using two methods: (1) Capwire (Miller et al. 2005) and (2) inference from Ne/N ratios. Capwire uses the number of samples per individual to estimate detection probability and then runs urn simulations to estimate population size using two capture probability models—the equal capture probability (ECM) and the two innate rates model (TIRM). The appropriate model is chosen using a likelihood-ratio test. TIRM is used when capture rate is heterogeneous between individuals. We calculated a population estimate for each subpopulation for all 3 years combined (with and without highly related individuals), as well as for each subpopulation for each year. We did not calculate N for each subpopulation for each year without highly related individuals because our sample sizes were too small.

To estimate N from Ne/N ratios, we used the Ne estimates for the full dataset (individuals over all 3 years for each subpopulation) from the SF method (from COLONY, see above) because it is more robust than the LD estimator to violations of model assumptions such as random sampling and nonrandom mating (Wang 2016). In addition, the Ne values from the SF estimator were slightly lower and therefore would produce a more conservative number of individuals. Previous research showed that the harmonic mean of the Ne/N ratio was 0.55 for kit fox at the Naval Petroleum Reserves in California (Otten and Cypher 1998). However, these authors suggested using an Ne/N ratio of 0.2–0.3 to be conservative. A meta-analysis of life history traits across taxa suggested Ne/N = 0.76 for a similar species, the gray fox (Waples et al. 2013). Therefore, we calculated N using Ne/N = 0.55 and bounded our estimate with a low Ne/N of 0.25 (and thus higher inferred N) and a high Ne/N of 0.76 (and thus lower inferred N).

Results

We collected a total of 597 scat samples (aged and fresh): 159 scats in 2009, 344 in 2010, and 94 in 2011. We were able to isolate mitochondrial DNA from 69% (n = 411) of the total scat samples, of which 398 or 97% were confirmed as SJKF. We assigned 332 samples to unique genotypes, identifying 93 individuals, 56 males and 37 females, giving a 1:0.66 sex ratio. Half of the individuals carried a mtDNA haplotype with the length of 252 bp, which is found in all SJKF in other locations (Wilbert et al. 2015), while the other half possessed a regionally unique haplotype with a 16 bp deletion (236 bp; Table 1). We collected an average of 3.6 scats per individual, although we found 10–20 scat samples for a few individuals. We recaptured four individuals in 2009 and 2010 and four individuals in 2010 and 2011. One female was found every year although we only found six of her scats. SJKF scats were found in the central Panoche Valley, Mercy Hot Springs, Silver Creek Ranch, the eastern foothills of the Tumey and Ciervo Hills, and the Vallecitos area (Fig. 1).

Table 1 Measures of genetic diversity in the Panoche Valley and I-5 populations
Full size table

We only included individuals for the population analysis that we could confidently genotype for at least 8 of the 11 microsatellite loci. We had high-quality data for 91 individuals (n8 = 3, n9 = 5, n10 = 10, n11 = 74; from 330 scat samples) that we used in all subsequent analyses. We found moderate levels of heterozygosity (HO=0.576 ± 0.055, unbiased HE=0.641 ± 0.048; Table 1). Microsatellite loci had 4–13 alleles per locus and we found no evidence of large allelic dropout at any locus. Potential null alleles were indicated by an excess of homozygotes at two microsatellite loci (AHTh171 and FH2848). However, these calculations may have been affected by missing data as these loci could not be genotyped in 10% of the individuals. Allelic richness was 7.79 and the effective number of alleles was 3.18. The global estimate of FIS for the overall population was 0.100. The CPNA was not in Hardy Weinberg (HW) equilibrium due to heterozygote deficit (p = 0.0001).

Bayesian clustering analysis in STRUCTURE indicated strong population subdivision, with the ΔK statistic (Evanno et al. 2005) showing a peak at K = 2 (Supplemental Fig. 1). Cluster 1 was comprised of individuals located in the Panoche Valley (west of the Panoche and Tumey Hills) including individuals at Silver Creek Ranch and along Little Panoche Road through Mercy Hot Springs. Cluster 2 included individuals on the eastern slope of the Tumey Hills and Ciervo Hills, between the foothills and I-5. Using the ancestry assignments of at least 70% with 10 replicates, 56 individuals were assigned to cluster 1 and 22 were assigned to cluster 2. Two of the individuals assigned to cluster 1 were located to the east of the Ciervo Hills and two individuals from cluster 2 were located in the Panoche Valley (asterisks in Fig. 2b). We classified these four individuals as putative migrants. We found 13 individuals with mixed ancestry (between 30 and 70%) that were assigned to the location where they were found, including 12 located in the valley and one to the east of the Ciervo Pass. These migrants and individuals of mixed ancestry are delineated in Fig. 2b by a dashed line separating the individuals with > 70% ancestry. We found the same number of migrants and admixed individuals if we modified the STRUCTURE cutoff values from 70% assignment to the 80% used by Crawford et al. (2009) and Cullingham et al. (2009) or the 60% used by Coulon et al. (2008).

Fig. 2
figure 2

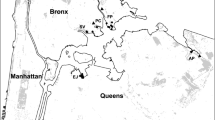
Two defined kit fox subpopulations within the CPNA. a Habitat suitability of the CPNA (figure created by Scott Phillips based on data compiled for Cypher et al. 2013) split into two areas that relate to the two genetically distinct kit fox groups. b Percent ancestry of each individual (n = 91) identified by Structure; Cluster 1 in light grey and Cluster 2 in dark grey, separated by a black solid line. The dotted lines represent a 70% cutoff, where by individuals are either admixed or migrants (asterisks) if they are located between the dotted line and the solid line. c Clustering of individuals (n = 91) from TESS using geospatial weighting and the clear division that corresponds to the ridgeline

Full size image

Population structuring differed slightly between STRUCTURE and the spatially explicit programs, TESS and GENELAND. TESS detected two subpopulations with 71 individuals in cluster 1 and 20 individuals in cluster 2 (Fig. 2c). TESS combined all individuals detected in the Panoche Valley (cluster 1) with the two migrant individuals from cluster 2 into one group. GENELAND supported the same structuring found by TESS, assigning higher posterior probabilities for migrants and mixed ancestry to the location of sampling (results not shown). These differences from STRUCTURE may be expected due to the nature of their algorithms and the biological importance of geographic isolation. When TESS used spatial information to assign individuals to clusters, it tended to assign individuals to the locations where they were sampled and was biased to assign individuals to cluster 1. In subsequent analyses, we compared the two geographically designated subpopulations—the Panoche Valley (PV, n = 68) and the I-5 (n = 23), with mixed ancestry and migrant individuals assigned to the group where the samples were collected. The geographic areas inhabited by these two subpopulations are shown in Fig. 2a with the split between them based on high elevation (Scott Phillips personal communication), which is likely a barrier to kit fox movements.

Separation between individuals in the PV and I-5 was also supported by statistical measures of variance. The hierarchical AMOVA found 10% variance between populations and 90% within populations. The one-tailed F-test of variance of the AMOVA detected significant differentiation between subpopulations (F = 8.892, F1,180<0.003). The first two coordinates of the PCoA represented 47.8% of the total variation (coordinate 1 = 31.0%, coordinate 2 = 16.8%; Supplemental Fig. 2). Measures of genetic differentiation also showed significant separation between the two subpopulations: F’ST = 0.278 and Jost’s D = 0.190 (all p < 0.0001).

Mantel tests showed a weak but significant correlation between genetic diversity and geographic distance, even within subpopulations (CPNA: r = 0.200, p < 0.0001; PV: r = 0.111, p < 0.013; I-5: r = 0.225, p < 0.003). Mantel tests showed a significant negative correlation between relatedness and geographic distance (CPNA: r = − 0.314, p < 0.0001, PV: r = − 0.180, p < 0.0001; I-5: r = − 0.325, p < 0.0001). Spatial autocorrelation analysis of all SJKF in the CPNA area indicated that individuals within 6 km of each other are significantly more related than average (p < 0.0001; Fig. 3). Estimates of relatedness across the CPNA and within each subpopulation were similarly low; for example, the Queller and Goodnight relatedness estimate for the CPNA was − 0.012 (QGM), PV = − 0.017, and I-5 = − 0.043 (Table 1).

Fig. 3
figure 3

Spatial autocorrelation analysis of SJKF in the CPNA shows that individuals within 6 km of each other are significantly more related than average (p < 0.0001). The autocorrelation coefficient (r), shown in solid line, represents the genetic similarity of individuals within a distance class. The dotted lines signify the upper (U) and lower (L) bounds of the 95% confidence interval of a random distribution of the data

Full size image

Genetic diversity was similar between the two subpopulations. The PV subpopulation had 3–11 alleles per locus with AR = 6.72 and 3.12 effective number of alleles. The I-5 subpopulation had 3–9 alleles per locus with AR = 5.50 and 2.87 effective number of alleles. Expected and observed heterozygosities were lower for each subpopulation as compared to the overall CPNA (see Table 1). The FIS value for PV was higher (0.08) than I-5 (0.01), but both were lower than overall CPNA FIS = 0.103. Tests in Genepop showed the I-5 subpopulation is in HW and linkage equilibrium. However, the PV subpopulation had 3/55 pairs of loci showing LD. There was no evidence that any particular locus was more often involved in linkage and three significant tests are expected by chance at the 0.05 level (0.05 × 55 = 3).

We created subsets of our data to look at potential influences on the estimates of Ne. Mean relatedness across each subpopulation did not change appreciably when we removed individuals that had mixed ancestry or were identified as migrants, nor when we removed highly related pairs (see Supplemental Table 1). However, removal of these individuals greatly changed the estimates of Ne (Table 2). When we removed individuals that showed mixed ancestry or identification to the other population, Ne was reduced, which is expected because we removed the genetic diversity of individuals from the other subpopulation. When we removed individuals that were highly related, the estimate of Ne increased, which is also expected because a smaller number of individuals contained a comparable amount of genetic diversity as the full dataset.

Table 2 Estimates of effective population size (Ne) based on linkage disequilibrium (LD) calculated with NeEstimator with Pcrit = 0.02, the random mating model, and confidence intervals from jackknifing, and the Ne based on sibship frequency (SF) calculated in COLONY with random mating, polygamy, the full-likelihood method, and 95% confidence intervals
Full size table

In estimating census size (N), we first used the number of times that an individual was resampled to estimate the subpopulation size of each year with the program Capwire. The TIRM model, which indicates capture heterogeneity, was selected by the program as the most likely model of capture probability for each year and subpopulation. The average number of scat samples per individual per year in both subpopulations was > 1.7, which was the minimum level of resampling to produce accurate Capwire results in grey wolves (Stenglein et al. 2010; Stansbury et al. 2014). As survey effort and locations varied each year, the estimated subpopulation size varied across each year and no year was representative of the total number of individuals in either location (Table 3).

Table 3 Estimates of census population size (N) calculated using Capwire for each year in each population. Capwire estimates are reported with 95% confidence intervals in parentheses
Full size table

We then estimated the number of individuals across all 3 years using Capwire and extrapolated the number of individuals from Ne/N ratios, with and without highly related individuals. The number of individuals estimated in the Panoche Valley ranged from 60 to 90, while the number of individuals in the I-5 ranged from 17 to 27 (Fig. 4). The Capwire estimates have smaller confidence intervals due to less variation in urn model simulations, while the large confidence intervals around estimates from Ne/N method result from the use of Ne/N ratios with and without migrant and admixed individuals and close relatives. Because Capwire uses recapture rates to estimate size, the combination of both subpopulations (overall CPNA) will make variation across recapture rates lower, which in turn will make the population appear to be more thoroughly surveyed than it actually was and the estimates low. Additionally, the yearly subpopulation estimates are low because all areas were not surveyed in any given year. Population estimates extrapolated from Ne for the entire CPNA display a Wahlund effect, as expected from the inclusion of genetically differentiated subpopulations (Fig. 4).

Fig. 4
figure 4

Population estimates (N) from Capwire (95% confidence intervals) and Ne/N ratios (confidence intervals from high and low Ne/N ratios) using data across all 3 years, with and without highly related individuals. For comparison, the number of foxes estimated from a family group size of 3 (confidence intervals ± 1 individual) with all home ranges occupied in moderate and high suitable habitat are shown in grey. *Numbers of individuals in the overall CPNA are underestimates of true values (Wahlund effect)

Full size image

Discussion

Non-invasive sampling can be difficult due to low quality and low quantity DNA that leads to low amplification rates (Taberlet et al. 1999; Waits and Paetkau 2005; Beja-Pereira et al. 2009). Despite a broad range in quality of scat samples used in this study, we successfully obtained species information on 69% of all scats (both aged and fresh). As we expected, and found in other fecal DNA studies (DeMatteo et al. 2014; Panasci et al. 2011; Piggott 2004; Santini et al. 2007), fresh scat had higher success downstream in the genetic analysis (important in studying population dynamics) but aged scat was very useful in identifying kit fox presence. Even when being conservative in classifying scat samples as SJKF and demanding clear and consistent data before assigning a unique genotype, we were able to identify 398 scats to kit fox and ascertain 93 individuals.

Species identification based on mtDNA showed that SJKF in this area had two control region haplotypes of different fragment sizes, with half of the individuals carrying each type. These are the only two haplotypes that have been found in SJKF (Wilbert et al. 2015). The smaller 236 bp haplotype has only been found in one individual outside of the CPNA (Wilbert et al. 2015), suggesting that this haplotype is largely restricted to the CPNA.

We identified two male SJKF individuals in the Vallecitos area, one in 2010 and one in 2011. The presence of these two males is significant because the last official sighting of kit fox in the area occurred in the 1970s. Two other samples from Vallecitos had mixed genetic signatures of SJKF and coyote but we could not determine if this was due to cross-contamination in the field, or evidence of a coyote preying on a kit fox or a kit fox scavenging on a coyote.

Multiple analyses consistently split our individuals into two subpopulations, one in the PV and one in the strip of habitat between I-5 and eastern side of the Tumey and Ciervo Hills. The degree of genetic differentiation is large and unexpected given the small geographic scale of this study, but some degree of differentiation has also been observed within the region in other San Joaquin Desert species (Richmond et al. 2017; Statham et al. 2018). The PV and the I-5 area are partially separated by a geographic barrier to kit fox dispersal because of high elevation and unsuitable habitat, but there is a pass at the base of the Tumey and Panoche Hills that connects the two areas at a low elevation with habitat that appears to be suitable for kit foxes. No SJKF scat samples were found on transects searched in this connecting habitat but handlers visually observed scats of coyotes (Canis latrans) in this zone, and red foxes (Vulpes vulpes), gray foxes (Urocyon cinereoargenteus) and bobcats (Lynx rufus) may be present in the area. Larger carnivores using this area may displace or kill most kit foxes that move into or through it (Cypher et al. 2000; Cypher and Spencer 1998; Nelson et al. 2007; Ralls and White 1995; Spiegel and Tom 1996).

However, our analyses indicate that the two subpopulations are still biologically connected. While a handful of migrants were identified in each subpopulation (PV and I-5), most of the admixed individuals were located in the PV population. This suggests that dispersing individuals may have greater ability to move westward than eastward, or that migrants are more likely to survive if they move into the valley.

The CPNA is one of three core SJKF populations and it is geographically isolated from other relatively larger SJKF populations. Our surveys were designed to detect kit fox in as many locations as possible, not to estimate population size. However, we calculated several estimates from our data for the conservation management of this endangered species. We identified a minimum of 93 individuals in the CPNA over the 3 years of surveys, though all areas were not surveyed in any given year. Population estimates from Capwire and Ne/N ratios suggest there are about 60–90 individuals in the Panoche Valley subpopulation and 17–27 individuals in the I-5 subpopulation, giving an overall estimate of 73–114 individuals across the CPNA (Fig. 4).

For comparison, we also calculated how many foxes could inhabit the CPNA based on the amount and quality of habitat. Nelson et al. (2007) estimated that 6 km2 are required for each kit fox family group in optimal habitat, so the total CPNA could support 225 kit foxes at most. However, Cypher et al. (2013) found only 65% of the CPNA contains habitat with moderate or high suitability for kit foxes, and that family groups require a home range of 16 km2 in moderately suitable habitat, which corresponds well to our finding of highly related individuals—potential family groups—within a 6 km distance. If all home ranges are occupied with a kit fox pair, the area could support a total of 38 kit fox pairs, 23 in the PV and 15 in the I-5 area (Fig. 2a). We multiplied the probable number of pairs in each subpopulation by three as a conservative estimate that represents two adults and one surviving pup, which seems reasonable given the surveys were conducted during the late spring to early fall (May–September), a time of year when many pups were still with their parents (Koopman et al. 2000). This produces an estimate of 69 individuals in PV and 44 in the I-5 area, which corresponds closely to the genetic population estimates (Fig. 4).

Kit foxes are seasonal breeders and are known to have fluctuating population sizes during the year. There are higher numbers of foxes in the spring and early summer due to the presence of adults and their offspring and smaller numbers of foxes in the winter after high juvenile mortality rates during dispersal in late summer and fall (up to 65%, Koopman et al. 2000). This population fluctuation has been documented in long-term spotlighting data (Ralls and Eberhardt 1997). In addition to these within-year differences in population size, there are also between-year variations in population size due to varying precipitation levels that influence kit fox reproduction through a trophic cascade of resource availability (Standley et al. 1992; White and Ralls 1993; Williams and Germano 1992; Cypher et al. 2000). Our Capwire analysis detected heterogeneous capture rates (as indicated by the TIRM model), which may reflect changing numbers of kit foxes at different times of the year and at different locations. Because our surveys were conducted from the late spring to early fall (May–September), our higher estimates of N based on all individuals detected probably better reflect the numbers of foxes present during our surveys while the lower estimates after removing relatives probably better reflect the number of breeding adults (Fig. 4).

Our estimate of roughly 90 kit foxes in the CPNA provides a baseline for future comparisons. In addition, our estimates suggest that most, if not all, of the suitable habitat for kit fox in this area is occupied. This is significant for three reasons. First, small populations are vulnerable to extirpation from ecological events, demographic fluctuations, or human activity. Only a few kit foxes are thought to exist in areas adjacent or near the CPNA so if the current population were lost, reestablishment by natural immigration would not be rapid. Secondly, we found that this population has a unique mtDNA haplotype not found in other locations, and further studies may discover more genetic distinctions. Finally, although we recognize that populations fluctuate in size, we were surprised to find a substantial population that was close to carrying capacity. Other areas in the central portion of SJKF range, such as the San Luis Reservoir in western Merced County, also have medium and high suitable kit fox habitat (Cypher et al. 2013). More extensive surveys in nearby areas with suitable habitat might reveal the presence of SJKF and determine whether or not foxes disperse between the small pockets of suitable habitat adjacent to the CPNA. Our results highlight the importance of continued conservation efforts to preserve SJKF habitat in the CPNA as well as connectivity between the two subpopulations in this area.

Furthermore, habitat connectivity across the entire range of SJKF is important because the majority of SJKF inhabit the southern portion of the range. The other two core areas are very different from the CPNA; they are located in the southern portion of the range, have much more suitable habitat, higher numbers of individuals, and are close to many other areas with SJKF (Cypher et al. 2013). The CPNA is a small population with unique genetic diversity that is largely isolated from other SJKF. When possible, efforts should be made to reduce habitat fragmentation throughout the range of the SJKF, for example by restoring unproductive farmlands to more natural conditions (Cypher et al. 2013; Lortie et al. 2018), thus improving connectivity between the CPNA and other areas to the south with large areas of highly suitable SJKF habitat.